Modified Integral Control Globally Counters Symmetry-Breaking Biases
Abstract
1. Introduction
- The state space and therefore the error space is not a linear vector space, but a nonlinear manifold, more precisely a compact Lie group. This requires to revisit the concept of “integrating the error”, since summing up or integrating variables relies on a vector space structure. The solution in [7,8] proposes to integrate instead the error-proportional feedback action, brought back to the Lie algebra (which is a vector space) thanks to standard Lie group operations. This error-proportional feedback is the main controller in standard studies without bias, like [1,4,5], and we thus only suggest to add a small multiple of its integral. The idea is that, similarly, if an error-proportional feedback action constantly fights against the same bias, then the integral would keep increasing; so if the controlled system stabilizes it must be at a situation with zero error-proportional feedback action, hence in principle (under some conditions, and at least locally) with zero error. By assuming full actuation, Refs. [7,8] prove that any constant bias on a Lie group can be countered in this way.
- A new challenge in the present paper is the nonholonomic actuation typical of such systems, also sometimes called underactuation. This means that, if a bias pushes the system with some vector v, it is not necessarily physically possible with our actuator to push in the direction even if we knew it. Think for instance of a ship subject to lateral drift, or of a steering-controlled vehicle with translation velocity fixed at a wrong value. In standard linear control, this situation can appear as well. Consider with perturbation force that lies outside the range of actuation ; then, there is no way to stabilize exactly, since this simply cannot be made a steady state. In the coordination application, the goal is to stabilize a manifold of relative equilibria corresponding to any configuration compatible with synchronized right-invariant Lie group velocities [9,10]. Configurations where the vehicles can keep moving in a coordinated way appear feasible even for nonholonomic systems with uncountered bias.
- In Section 2, we describe the abstract Lie group model for stabilizing an underactuated rigid body in a fixed relative configuration with respect to a swarm leader, which is thus the geometric invariant related to the symmetry of rigid body motions. While Refs. [4,5,10], among others, have derived corresponding controllers for perfectly modeled vehicles, we insist on achieving the same performance when the controlled vehicle is subject to biases or calibration errors on its translation velocity, both on actuated and on unactuated directions of motion. We progressively explain why coordinated motion/restoring symmetry is a proper objective in the presence of bias. We end this section by proposing a moderating integral controller (MIC) to solve this task.
- In Section 3, we carry out a detailed convergence analysis for stabilizing the steering controlled vehicle into a given circular motion ([4], see [3] for a concrete application), despite the actuation biases. We start the section by a more concrete formulation for the steering controlled vehicle in the plane. The main result proves how our MIC allows for still ensuring global convergence towards exact coordinated motion. The result combines a Lyapunov function adapted from the bias-less case [5,10], with a detailed analysis of averaging theory along the lines of [11], and showing that the averaging approximation becomes exact as we approach the target.
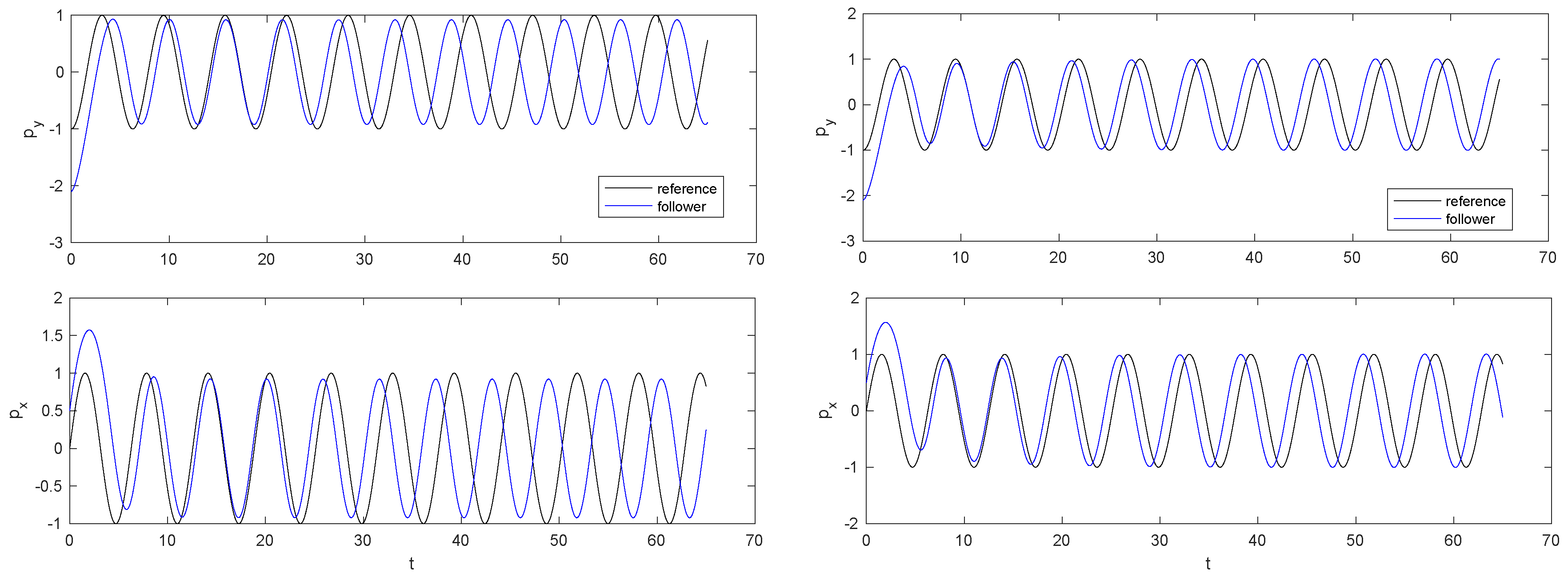
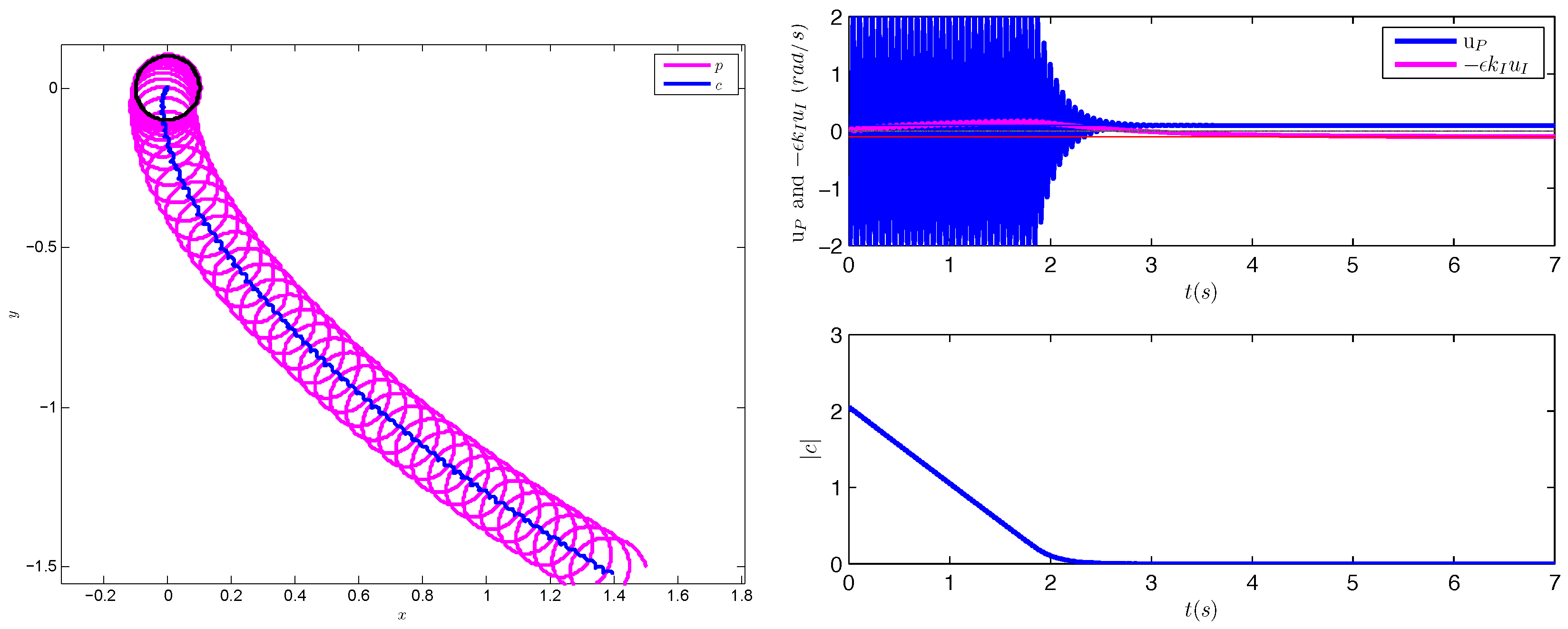
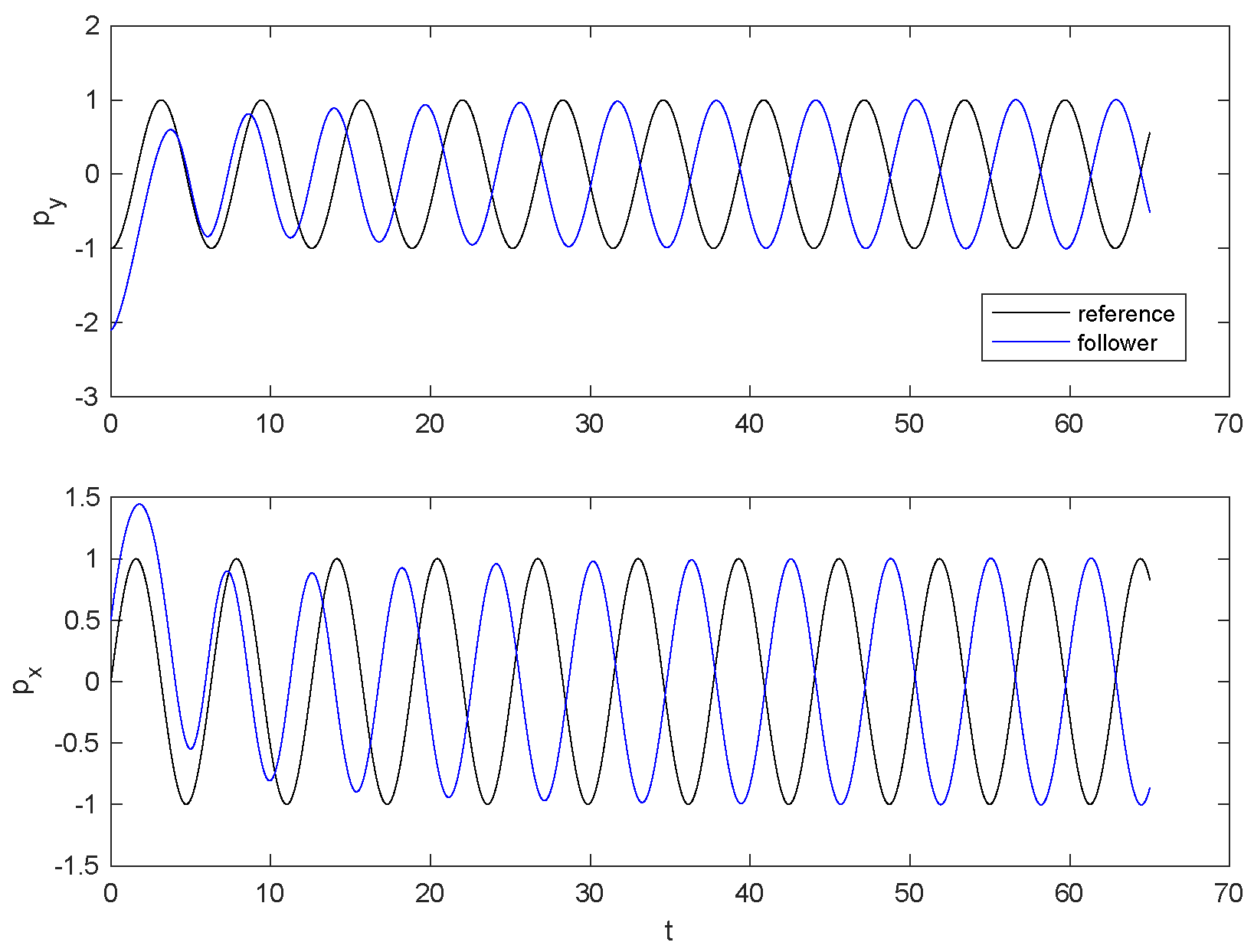
- Section 4 provides simulation results illustrating the working of our controller for the steering controlled vehicle and giving a hint at expected performance.
- In Section 5, we note how the MIC can be reformulated in an abstract context of output biases, to possibly solve problems beyond symmetry-preservation. In particular, we discuss its application to linear systems, where it enables a trade-off between rejecting biases on the input or on the output.
2. General Problem Setting and Controller Definition
2.1. Underactuated Rigid Body Motion
2.2. Coordinated Motion
2.3. A “Moderating” Integral Controller (MIC)
3. Steering Control Application
3.1. Explicit Nominal Dynamics with Coordination Control
- equal rotation rate ;
- equal -conditioned center of rotation .
3.2. Bias-Rejecting Controller and Proof Strategy
- First (Section 3.3), we study more accurately the local stability, specifying a region of exponential attraction , a ball of radius around where saturation is inactive, and we fix a value such that our conclusions are valid for all .
- Then, (Section 3.4) we analyze the system behavior for , with , and we prove that for all the system starting in will end up in .
3.3. Local Exponential Stability
3.4. Global Stability
- By Lemma 1, after an initial transient, the system reaches the subset where the bound (13) holds and stays there for all future times.
- Assume by contradiction that the system would stay in for all times. Then, by Proposition 3, the Lyapunov function would decrease like for some constant for all times, which is not possible since V must stay positive (in fact even larger than if we stayed in ). Thus, the system cannot stay in forever.
- This means that, at some time, the system must enter , and thus it also enters since . Once the system is in , we know by Proposition 2 that it converges to exactly.
4. Simulations
5. Towards Other Applications of the Modified Integral Controller
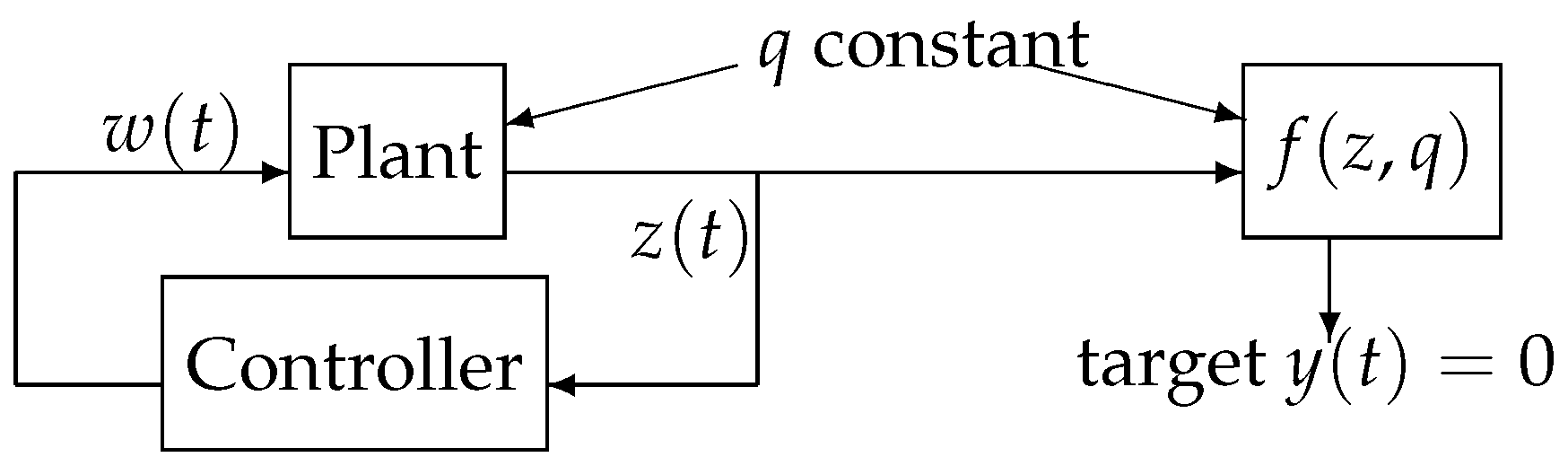
- a system with state , variable of interest , must be stabilized to some target by the control command .
- unlike standard, the value of is not measured, but deduced from actual measurements through the static function where q are some constant parameters.
- the exact value of q is not known; without loss of generality, is nominal and .
- x the rigid body configuration g, for the planar vehicle ;
- w the part of the input that corrects w.r.t. the target steady state motion, thus for the planar vehicle;
- the measured relative configuration between vehicle and reference, corresponding for the planar vehicle to with three scalar components;
- the parameter mismatch, corresponding to ;
- is the target variable to be put to zero, according to (4). For the vehicle, it has three scalar components . The last component is equivalent to . Referring to (11), the others take the formindeed involving known constants, the unknown q, and observed variables z.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bai, H.; Arcak, M.; Wen, J.T. Rigid body attitude coordination without inertial frame information. Automatica 2008, 44, 3170–3175. [Google Scholar] [CrossRef]
- Sarlette, A.; Sepulchre, R.; Leonard, N. Autonomous rigid body attitude synchronization. Automatica 2009, 45, 572–577. [Google Scholar] [CrossRef]
- Leonard, N.; Paley, D.; Lekien, F.; Sepulchre, R.; Frantantoni, D.; Davis, R. Collective motion, sensor networks and ocean sampling. Proc. IEEE 2007, 95, 48–74. [Google Scholar] [CrossRef]
- Justh, E.W.; Krishnaprasad, P. Equilibria and steering laws for planar formations. Syst. Control Lett. 2004, 52, 25–38. [Google Scholar] [CrossRef]
- Sepulchre, R.; Paley, D.A.; Leonard, N.E. Stabilization of planar collective motion: All-to-all communication. Autom. Control IEEE Trans. 2007, 52, 811–824. [Google Scholar] [CrossRef]
- Aström, K.J.; Murray, R.M. Feedback Systems: an Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Zhang, Z.; Alain, S.; Zhihao, L. Integral control on Lie groups. Syst. Control Lett. 2015, 80, 9–15. [Google Scholar] [CrossRef]
- Maithripala, D.; Berg, J.M. An intrinsic PID controller for mechanical systems on Lie groups. Automatica 2015, 54, 189–200. [Google Scholar] [CrossRef]
- Hanssmann, H.; Leonard, N.; Smith, T. Symmetry and Reduction for Coordinated Rigid Bodies. Eur. J. Control 2006, 12, 176–194. [Google Scholar] [CrossRef]
- Sarlette, A.; Bonnabel, S.; Sepulchre, R. Coordinated motion design on Lie groups. IEEE Trans. Autom. Control 2010, 55, 1047–1058. [Google Scholar] [CrossRef]
- Aeyels, D.; Peuteman, J. On exponential stability of nonlinear time-varying differential equations. Automatica 1999, 35, 1091–1100. [Google Scholar] [CrossRef]
- Bonnabel, S.; Martin, P.; Rouchon, P. Symmetry-preserving observers. IEEE Trans. Autom. Control 2008, 53, 2514–2526. [Google Scholar] [CrossRef]
- Lageman, C.; Trumpf, J.; Mahony, R. Gradient-like observers for invariant dynamics on a Lie group. IEEE Trans. Autom. Control 2010, 55, 367–377. [Google Scholar] [CrossRef]
- Khosravian, A.; Trumpf, J.; Mahony, R.; Lageman, C. Observers for invariant systems on Lie groups with biased input measurements and homogeneous outputs. Automatica 2015, 55, 19–26. [Google Scholar] [CrossRef][Green Version]
- Aguiar, P.; Hespanha, J. Trajectory-tracking and path-following of underactuated autonomous vehicles with parametric modeling uncertainty. IEEE Trans. Autom. Control. 2007, 52, 1362–1379. [Google Scholar] [CrossRef]
- Sanders, J.A.; Verhulst, F.; Murdock, J. Averaging Methods in Nonlinear Dynamical Systems; Springer: Berlin, Germany, 1985. [Google Scholar]
- Gorinevsky, D.; Boyd, S.; Stein, G. Design of low-bandwidth spatially distributed feedback. IEEE Trans. Autom. Control. 2008, 53, 257–272. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Ling, Z.; Sarlette, A. Modified Integral Control Globally Counters Symmetry-Breaking Biases. Symmetry 2019, 11, 639. https://doi.org/10.3390/sym11050639
Zhang Z, Ling Z, Sarlette A. Modified Integral Control Globally Counters Symmetry-Breaking Biases. Symmetry. 2019; 11(5):639. https://doi.org/10.3390/sym11050639
Chicago/Turabian StyleZhang, Zhifei, Zhihao Ling, and Alain Sarlette. 2019. "Modified Integral Control Globally Counters Symmetry-Breaking Biases" Symmetry 11, no. 5: 639. https://doi.org/10.3390/sym11050639
APA StyleZhang, Z., Ling, Z., & Sarlette, A. (2019). Modified Integral Control Globally Counters Symmetry-Breaking Biases. Symmetry, 11(5), 639. https://doi.org/10.3390/sym11050639



