Abstract
Characteristically, most fluids are not linear in their natural deeds and therefore fractional order models are very appropriate to handle these kinds of marvels. In this article, we studied the base solvents of water and ethylene glycol for the stable dispersion of graphene oxide to prepare graphene oxide-water (GO-W) and graphene oxide-ethylene glycol (GO-EG) nanofluids. The stable dispersion of the graphene oxide in the water and ethylene glycol was taken from the experimental results. The combined efforts of the classical and fractional order models were imposed and compared under the effect of the Marangoni convection. The numerical method for the non-integer derivative that was used in this research is known as a predictor corrector technique of the Adams–Bashforth–Moulton method (Fractional Differential Equation-12) or shortly (FDE-12). The impact of the modeled parameters were analyzed and compared for both GO-W and GO-EG nanofluids. The diverse effects of the parameters were observed through a fractional model rather than the traditional approach. Furthermore, it was observed that GO-EG nanofluids are more efficient due to their high thermal properties compared with GO-W nanofluids.
1. Introduction
Fractional order models are very useful in the study of nanofluids that contain small nanosized particles at the rate of small intervals rather than the traditional concept of integer order derivatives. A fractional order study has the credibility to explain the actual behavior of the physical parameters and is possible only in the case of the small intervals. The influences of the physical parameters in the classical models are limited and, in some cases, different from the fractional order models near the wall surface. Caputo [1] introduced the idea of fractional derivatives from the modified Darcy’s law using the concept of unsteadiness. This idea was further modified by the researchers El Amin [2], Atangana and Alqahtani [3], and Alkahtani [4] by introducing varieties of new fractional derivatives and their applications. The fractional derivative concept can potentially be applied to the study of complicated control system problems. Yilun Shang [5] studied finite-time state consensus problems in continuous multi-agent systems with non-linear particles. Liu et al. [6] investigated the fixed-time event-triggered consensus control problem for multi-agent systems with non-linear uncertainties.
Advanced energy assets are the hot issue amid engineers and researchers as a response to rising energy demands. The base liquids have no sufficient thermal efficiency to fulfill the required demands of the industry. The small size of metal particles are used in common solvents to improve the thermal efficiency of the liquids. Water-, ethylene glycol-, and mineral oil-like convectional heat transfer fluids play an imperative role in many industrial and technological approaches such as heat generation, air-conditioning, chemical production, microelectronics, and transportation. The rate of change at small intervals has been examined by Atangana and Baleanu [7] to investigate the physical constraints of nanofluids for the heat transfer applications.
The physical aspects of the nanofluids and the role of the small sized nanoparticles in the enhancement of heat transfer applications using the traditional concept were introduced by Choi [8] to enhance the thermal efficiency of the nanofluids through nanoparticles.
The carbon family has the tendency to provide rapid cooling and fast thermal productivities. The experimental results demonstrated for carbon materials include the results of graphite nanoparticles, graphene oxides, and carbon nanotubes. Ellahi et al. [9] comprehensively discussed the effect of Carbon Nanotubes (CNT) nanofluid flow along a vertical cone with variable wall temperature. The results of both types of nanofluid can be obtained. Gul et al. [10] discussed effective Prandtl number model influences on and nanofluids’ spray along a stretching cylinder. Ellahi [11] worked on the effects of Magneto Hydrodynamic (MHD) and temperature-dependent viscosity on the flow of a non-Newtonian nanofluid in a pipe, using the analytical solution. Ellahi et al. [12] studied shiny film coating for multi-fluid flows of a rotating disk suspended with nanosized silver and gold particles. Khan et al. [13] worked on the Optimal Homotopy Analysis Method (OHAM) solution of Multi Walled Carbon Nanotubes and Single Walled Carbon Nanotubes (MWCNT/SWCNT) nanofluid thin film flow over a nonlinear extending disc.
Hummers and Offeman [14] developed a speedy and comparatively safe technique for the production of graphitic oxide from graphite in what is basically a crystalline substance of sulfuric acid H2SO4, potassium permanganate KMnO4, and sodium nitrate NaNO3.
The high thermal conductivity and characteristic lubricity of graphene make it a perfect claimant for the alteration of functional fluids. The solid particles, having an efficient thermal conductivity, are assorted to the base fluid to enhance the overall thermal conductivity of the fluid, as depicted in Maxwell [15]. Balandin et al. [16] examined the efficient thermal conductivity of single layer graphene in different solvents. Wei et al. [17] were pioneers in expressing the use of graphene oxide in ethylene glycol to enhance the thermal conductivity of ethylene glycol (EG). The graphene oxide nanosheets were set and isolated in EG and water at 5% capacity concentrations to enhance the thermal conductivity up to 60% compared with the base liquid EG.
Recently, Gul and Firdous [18] experimentally examined the stable dispersion of the graphene oxide in water and then analyzed the numerical study of the graphene oxide-water (GO-W) nanofluid between two rotating discs for the thermal applications.
Another type of convection which is used for temperature-dependent situations is called Marangoni convection. The existence of a spontaneous interface was first reported in 1855 by Thomson [19] and later represented in detail in 1865 by Marangoni [20] by spreading an oil droplet on a water surface, revealing that lower surface tension will spread on a liquid with higher surface tension.
In light of the previous meaningful discussion, the aim of this study was to examine the GO-W and graphene oxide and ethylene glycol (GO-EG) nanofluid flow under the effect of Marangoni convection using the classical and fractional order models. The comparison of the two types of nanofluids was conducted to investigate the impacts of the physical parameters. The physical and numerical outputs of the classical and fractional models were also compared and discussed. Sheikholeslami and Ganji [21] examined the Cu–H2O nanofluid flow under the impact of Marangoni convection. The numerical approach to find the solution of a different type of problem was previously discussed [22,23,24,25,26,27]. The numerical scheme of Runge Kutta method of order 4 (RK-4) was used in their study to determine the impact of the physical parameters and numerical outputs.
The published work of Gul and Kiran [18] was extended by including the GO-EG nanofluid and a comparison of GO-EG and GO-W was made. Furthermore, integer and non-integer models h were compared under the effect of Marangoni convection. The fractional order differential equations were tackled numerically with the help of the Fractional Differential Equation-12 (FDE-12) technique [28,29,30,31,32]. A variety of numerical techniques are used to find the solutions of the classical models [33] and these techniques are further combined for the solutions of fractional order problems. Agarwal et al. [34] studied the neural network models using the GML synchronization and impulsive Caputo fractional differential equations. Morales-Delgado et al. [35] worked on the analytic solution for oxygen diffusion from capillaries to tissues involving external force effects using a fractional calculus approach. Khan et al. [36] researched the dynamics of the Zika virus with the Caputo fractional derivative. The physical configuration of the problem is shown in Figure 1.
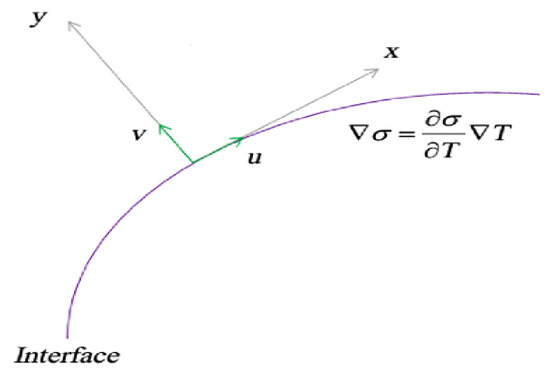
Figure 1.
Geometry of the problem.
2. Problem Formulation
The two-dimensional Marangoni boundary layer flow of GO-W and GO-EG nanofluids is considered. The magnetic field is functional to the flow pattern in the transverse direction. The interface temperature is vigilant as a function of . Assume that both base solvents (water and EG) contain GO nanoplatelets that are present in the thermally stable stage and no slippage. The flow under observation can be put into the following plan for GO nanofluids [14]:
where Equation (1) is the continuity equation, Equation (2) is the momentum equation, and Equation (3) is the energy equation. Exposed boundary conditions are expressed as:
The Marangoni conditions at the interface are revealed in Equation (4), taking the surface tension where stands for the surface tension temperature coefficient and represents the surface tension constant at the origin.
Also, specify velocity components in the x-, y-directions. The interface and external flow of the temperature are represented by respectively.
The effective indicate the density, dynamic viscosity, electrical conductivity, thermal conductivity, and specific heat capacity of nanoplatelets, respectively, and are defined as:
where is the solid volume fraction and , , are the electrical conductivity, density, and specific heat capacity of the base fluids, respectively.
The similarity transformations are considered as [14]:
Using the aforementioned assumption and condition, Equation (1) is verified identically, whereas Equations (2)–(4) are transformed in the following form:
where indicate the transformation of the magnetic parameter and Prandtl number, respectively, and are defined individually as:
The local Nusselt number Nu is:
3. Preliminaries on the Caputo Fractional Derivatives
The basic definition and properties related to non-integer or fractional derivatives derived by Caputo are as follows.
3.1. Definition 1
Let . The Caputo fractional derivative of order of function is given by:
3.2. Property 1
Let be such that and exist almost everywhere and let Then exists almost everywhere and:
3.3. Property 2
The function is constant and therefore the fractional derivative is zero: The general description of the fractional differential equation is assumed, including the Caputo concept:
with the initial conditions
4. Solution Methodology
The variables were selected to alter Equations (7)–(9) into the system of the first order differential equations:
The variables selected in Equation (15) were used for the classical (integer) system and Equations (7)–(9) are settled as:
with initial conditions:
The first order ordinary differential equations system (15) is further transformed into the Caputo fractional order derivatives.
The FDE-12 technique was adopted for the fractional order differential equations. The final system and initial conditions are as follows:
5. Results and Discussions
The GO-W and GO-EG nanofluid flows under the effect of Marangoni convection were analyzed using the classical and fractional models for heat transfer applications. The impact of the physical parameters was obtained through the classical and fractional order models and compared. Moreover, the impact of the embedded parameters, comprising GO-W and GO-EG nanofluids, was compared, and it was observed that due to rich thermophysical properties the GO-EG nanofluid is a comparatively better heat transfer solvent.
In the following figures, an upward arrow shows an increasing effect while a downward arrow shows a decreasing effect.
The effect of the nanofluid volume fraction using the classical model versus the velocity profile for the GO-W and GO-EG nanofluids is depicted in Figure 2. The rising values of lead to enhance the velocity field linearly in the classical model. Physically, the larger amount of nanoparticle volume fraction generates the friction force, and this force is more visible near the wall, reducing the flow motion. However, this impact is unclear in the classical model. The increase in the flow motion due to the rising values of indicates that the thermal efficiency of the nanofluid provides strength to the flow field. Moreover, this impact is comparatively high using the GO-EG nanofluids.

Figure 2.
The impact of versus classical , when .
The effect of the nanofluid volume fraction using the fractional model for the same values of is shown in Figure 3. Near the wall surface the velocity field falls, because near the wall surface friction increases, which retards the velocity and increases after the critical point due to the reduction in friction. Physically, the larger nanoparticle volume fraction generates the friction force and this force is more visible near the wall, reducing the flow motion. This effect is clearer using the fractional model. The impact of the increasing values of versus the radial velocity field using the integer model is shown in Figure 4. The same effect as discussed above was observed. The larger amount of increases the value of in the integer order model. The impact of the increasing values of versus the radial velocity field using the fractional model is shown in Figure 5. The larger amount of reduces in the fractional order model near the wall surface and after the point of inflection the velocity enhances, as shown in Figure 5.
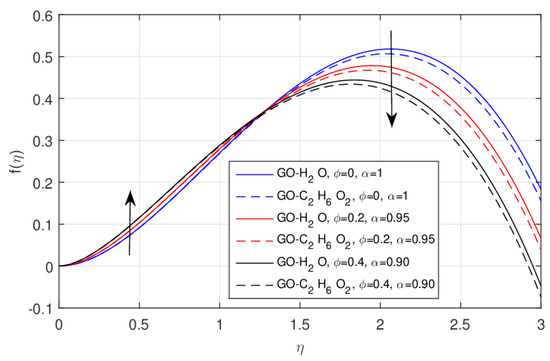
Figure 3.
The impact of versus fractional , when .
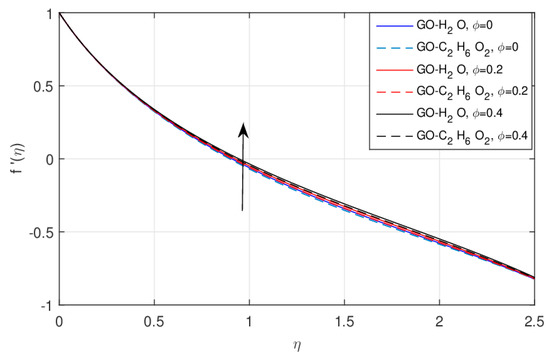
Figure 4.
The impact of versus classical , when .
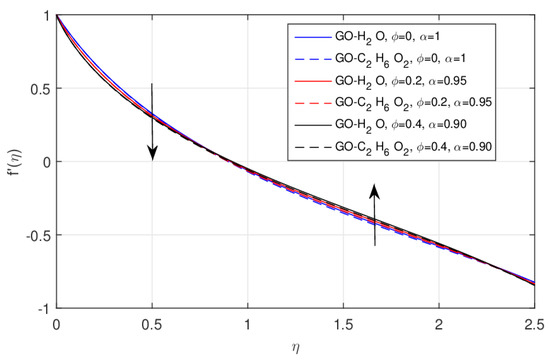
Figure 5.
The impact of versus fractional , when .
The influence of the larger values of the magnetic parameter versus the temperature profile for the integer order and fractional order problems is shown in Figure 6 and Figure 7, respectively. This is due to the Lorentz force, which results in resistance to the transport phenomena. This retarding force controls the GO-W and GO-EG nanofluid velocities, which is useful in numerous industrial and engineering applications such as heat transferring, industrial cooling, and nanofluid coolant. Mathematically, the magnetic parameter represents the ratio of the magnetic induction to the viscous force. Moreover, GO-EG was found to show more dominant results than GO-W.
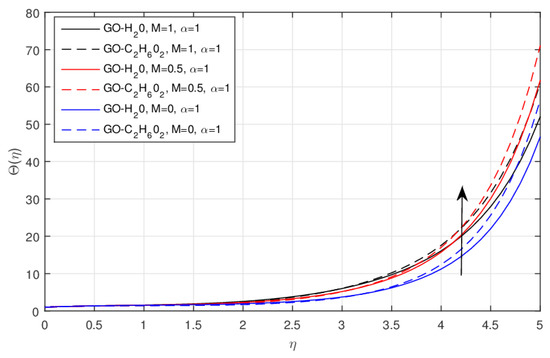
Figure 6.
The impact of versus classical , when .

Figure 7.
The impact of versus fractional , when .
The impact of using the classical model and the fractional order model versus the temperature profile for the GO-W and GO-EG nanofluids is depicted in Figure 8 and Figure 9. The nanoparticle volume fraction is basically used as the heat transport agent parameter and its increase boosts up the temperature profile. In fact, the cohesive forces among the liquid molecules release with the increasing amount of and as a result the thermal boundary layer enhancement. This effect is comparatively efficient in GO-EG nanofluids due to their enriching thermophysical properties.
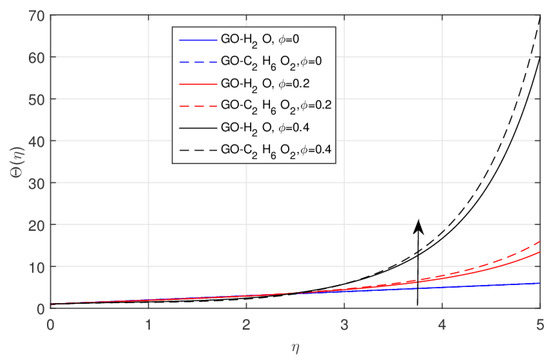
Figure 8.
The impact of versus the integer order of , when .
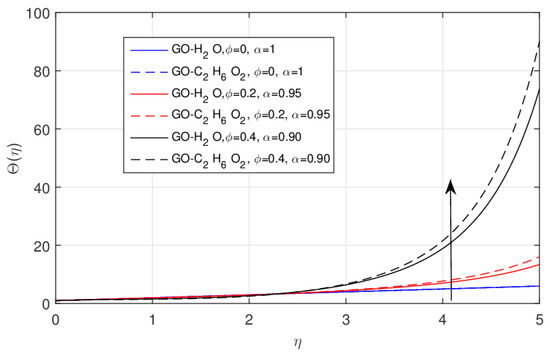
Figure 9.
The impact of versus fractional , when .
The impact of the magnetic parameter versus the Nusselt number of integer and fraction order problems is displayed in Figure 10 and Figure 11, respectively. A higher value of the magnetic parameter enhances the temperature field and reduces the Nusselt number. This effect is slightly clearer using the fractional model for similar values of , as shown in Figure 11. We noticed that in the cases of GO-EG and GO-W the temperature distribution is dominant and almost completely closed.

Figure 10.
The impact of versus classical , when .
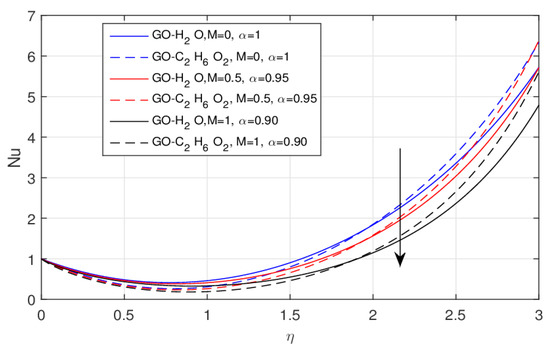
Figure 11.
The impact of versus fractional , when .
The impact of the fractional order versus for both sorts of nanofluids is depicted in Figure 12. It was observed that the heat transfer and cooling efficiency of the GO-EG nanofluid is comparatively higher than the GO-W nanofluid. The Nusselt number increases near the wall surface and declines towards the free surface.

Figure 12.
versus when .
The thermophysical properties of the two sorts of nanofluids (GO-W and GO-EG) were examined from the experimental results and are displayed in Table 1. These properties of the base fluids were initially calculated at 25 °C. The thermophysical properties were examined at a different temperature level from 25 °C to 40 °C.

Table 1.
The experimental values (thermophysical properties) of water, ethylene glycol, and graphene oxide nanoparticles.
The numerical outputs for the heat transfer rate using the fractional order problem are displayed in Table 2. The fractional order enhances the heat transfer rate in increasing intervals and this effect is relatively high in the GO-W nanofluid.

Table 2.
versus , when .
6. Conclusions
The flow of the two types of nanofluids, GO-W and GO-EG, were analyzed for the augmentation of temperature. Numerical and theoretical analyses were carried out under the effect of Marangoni convection. The classical and fractional models were used to investigate the impact of the physical parameters for similar values of the constraint. It was observed that the outputs of the physical parameters over the velocity and temperature profiles in the classical model are limited, but in utilizing the fractional model the effect varies in each interval. The fractional order model specifies the outputs at the small number of intervals, leading to the accurate determination of the physical parameters, which is very necessary for industrial and engineering applications.
The main features of this study are as follows:
- The rising values of lead to the linear enhancement of the velocity field, which was observed more clearly in the non-integer case compared with the classical model.
- The increasing values of the magnetic parameter increase the temperature field and decrease the Nusselt number. This effect is somewhat better in the fractional case compared to the integer model.
- Due to the rising values of , the thermal boundary layer increases and this effect is somewhat better in the GO-EG nanofluid rather than the GO-W nanofluid.
- The cooling efficiency and heat transfer of the GO-EG nanofluid is far better than that of the GO-W nanofluid.
- With the Lorentz force, resistance arises in the transport phenomenon. This particular phenomenon controls the GO-W and GO-EG nanofluid velocities. Also, this effect is more visible in GO-EG than in GO-W.
- Due to the fractional order the heat transfer rate enhances in growing increments and this effect is far better in the GO-W nanofluid compared with the GO-EG nanofluid.
7. Future Work
This mathematical model is extendable for future work considering gold nanoparticles, carbon nanotubes, porous media, variable viscosity, thermal radiation, and hall effects. The fractional ordered derivative scheme is also extendable using the Caputo–Fabrizio and Atangana–Baleanu operators.
Author Contributions
T.G. and H.A.; conceptualization, M.A.K. and T.G.; methodology, I.K.; software, I.K.; and P.K.; validation, T.G., M.A.K. and H.A.; formal analysis, I.K.; P.K.; investigation, T.G.; I.K.; writing—original draft preparation, T.G.; M.A.K. and P.K. I.K.; writing—review and editing.
Funding
This research was funded by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
Acknowledgments
This project was supported by the Theoretical and Computational Science (TaCS) Center under Computational and Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Caputo, M. Models of flux in porous media with memory. Water Resour. Res. 2000, 36, 693–705. [Google Scholar] [CrossRef]
- El Amin, M.F.; Radwan, A.G.; Sun, S. Analytical solution for fractional derivative gas-flow equation in porous media. Results Phys. 2017, 7, 2432–2438. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. Numerical approximation of the space-time Caputo-Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 2016, 156–169. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T.; Koca, I.; Atangan, A. A novel approach of variable order derivative: Theory and Methods. J. Nonlinear Sci. Appl. 2016, 9, 4867–4876. [Google Scholar] [CrossRef]
- Shang, Y. Finite-time consensus for multi-agent systems with fixed topologies. Int. J. Syst. Sci. 2012, 43, 499–506. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Y.; Wang, Q.; Sun, C. Fixed-time event-triggered consensus control for multi-agent systems with nonlinear uncertainties. Neurocomputing 2017, 260, 497–504. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. FED-231lMD 1995, 66, 99–105. [Google Scholar]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of Natural Convection MHD Nanofluid by Means of Single and Multi-Walled Carbon Nanotubes Suspended in a Salt-Water Solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Gul, T.; Nasir, S.; Islam, S.; Shah, Z.; Khan, M.A. Effective prandtl number model influences on the Al2O3-H2O and Al2O3-C2H6O2 nanofluids spray along a stretching cylinder. Arab. J. Sci. Eng. 2019, 2, 1601–1616. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of a non-Newtonian nanofluid in a pipe, Analytical solution. Appl. Math. Model. 2013, 37, 1451–1457. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Study of Shiny Film Coating on Multi-Fluid Flows of a Rotating Disk Suspended with Nano-Sized Silver and Gold Particles: A Comparative Analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Taza, G.; Waris, K.; Muhammad, S.; Muhammad, A.K.; Ebenezer, B. MWCNTs/SWCNTs Nanofluid Thin Film Flow over a Nonlinear Extending Disc: OHAM solution. J. Therm. Sci. 2019, 28, 115–122. [Google Scholar] [CrossRef]
- Hummers, W.S.; Offeman, R.E. Preparation of graphitic oxide. J. Am. Chem. Soc. 1958, 80, 1339. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Maxwell, J.C. Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1873. [Google Scholar]
- Wei, Y.; Huaqing, X.; Dan, B. Enhanced thermal conductivities of nanofluids containing graphene oxide nanosheets. Nanotechnology 2010, 21, 055705. [Google Scholar]
- Gul, T.; Ferdous, K. The experimental study to examine the stable dispersion of the graphene nanoparticles and to look at the GO–H2O nanofluid flow between two rotating disks. Appl. Nanosci. 2018, 8, 1711–1728. [Google Scholar] [CrossRef]
- Thomson, J. On certain curious motions observable at the surface of wine and other alcoholic liquors. Philos. Mag. 1855, 10, 330–333. [Google Scholar] [CrossRef]
- Marangoni, C. Ueber die Ausbreitung der Tropfeneiner Flussigkeit auf der Oberflache einer anderen. Ann. Phys. 1871, 143, 337–354. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Influence of magnetic field on CuOeH2O nanofluid flow considering Marangoni boundary layer. Int. J. Hydrog. Energy 2017, 42, 2748–2755. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Ellahi, R.; Sheikholeslami, T.F.; Behzadmehr, A. Numerical investigation of heat and mass transfer flow under the influence of silicon carbide by means of plasmaenhanced chemical vapor deposition vertical reactor. Neural Comput. Appl. 2018, 30, 3721–3731. [Google Scholar] [CrossRef]
- Barikbin, Z.; Ellahi, R.; Abbasbandy, S. The Ritz-Galerkin method for MHD Couette Fow of non-Newtonian fluid. Int. J. Ind. Math. 2014, 6, 235–243. [Google Scholar]
- Hayat, T.; Saif, R.S.; Ellahi, R.; Muhammad, T.; Ahmad, B. Numerical study of boundary-layer flow due to a nonlinear curved stretching sheet with convective heat and mass conditions. Results Phys. 2017, 7, 2601–2606. [Google Scholar] [CrossRef]
- Hayat, T.; Saif, R.S.; Ellahi, R.; Muhammad, T.; Ahmad, B. Numerical study for Darcy-Forchheimer flow due to a curved stretching surface with Cattaneo-Christov heat flux and homogeneous heterogeneous reactions. Results Phys. 2017, 7, 2886–2892. [Google Scholar] [CrossRef]
- Javeed, S.; Baleanu, D.; Waheed, A.; Khan, M.S.; Affan, H. Analysis of Homotopy Perturbation Method for Solving Fractional Order Differential Equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef]
- Srivastava, H.M.; El-Sayed, A.M.A.; Gaafar, F.M. A Class of Nonlinear Boundary Value Problems for an Arbitrary Fractional-Order Differential Equation with the Riemann-Stieltjes Functional Integral and Infinite-Point Boundary Conditions. Symmetry 2018, 10, 508. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The Frac PECE subroutine for the numerical solution of differential equations of fractional order. In Forschung und Wissenschaftliches Rechnen; Heinzel, S., Plesser, T., Eds.; 1998 Gessellschaft fur Wissenschaftliche Datenverarbeitung: Gottingen, Germany, 1999; pp. 57–71. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Saifullah Khan, M.A.; Farooq, M. A fractional model for the dynamics of TB virus. Chaos Solitons Fractals 2018, 116, 63–71. [Google Scholar]
- Gul, T.; Khan, M.A.; Khan, A.; Shuaib, M. Fractional-order three-dimensional thin-film nanofluid flow on an inclined rotating disk. Eur. Phys. J. Plus 2018, 133, 500–5011. [Google Scholar] [CrossRef]
- Gul, T.; Khan, M.A.; Noman, W.; Khan, I.; Alkanhal, T.A.; Tlili, I. Fractional Order Forced Convection Carbon Nanotubes Nanofluid Flow Passing Over a Thin Needle. Symmetry 2019, 11, 312. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.A.; Farooq, M.; Gul, T.; Hussai, F. A fractional order HBV model with hospitalization. Discret. Contin. Dyn. Syst. 2019, 957–974. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Global Mittag-Leffler Synchronization for Neural Networks Modeled by Impulsive Caputo Fractional Differential Equations with Distributed Delays. Symmetry 2018, 10, 473. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Saad, K.M.; Khan, M.A.; Agarwal, P. Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: A fractional calculus approach. Phys. A Stat. Mech. Its Appl. 2019, 523, 48–65. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, S.; Farhan, M. The dynamics of Zika virus with Caputo fractional derivative. AIMS Math. 2019, 4, 134–146. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).