Effectiveness of Nature-Inspired Algorithms using ANFIS for Blade Design Optimization and Wind Turbine Efficiency
Abstract
1. Introduction
2. Power Coefficient of Horizontal Axis Wind Turbine Blade
3. Nature-Inspired Algorithms
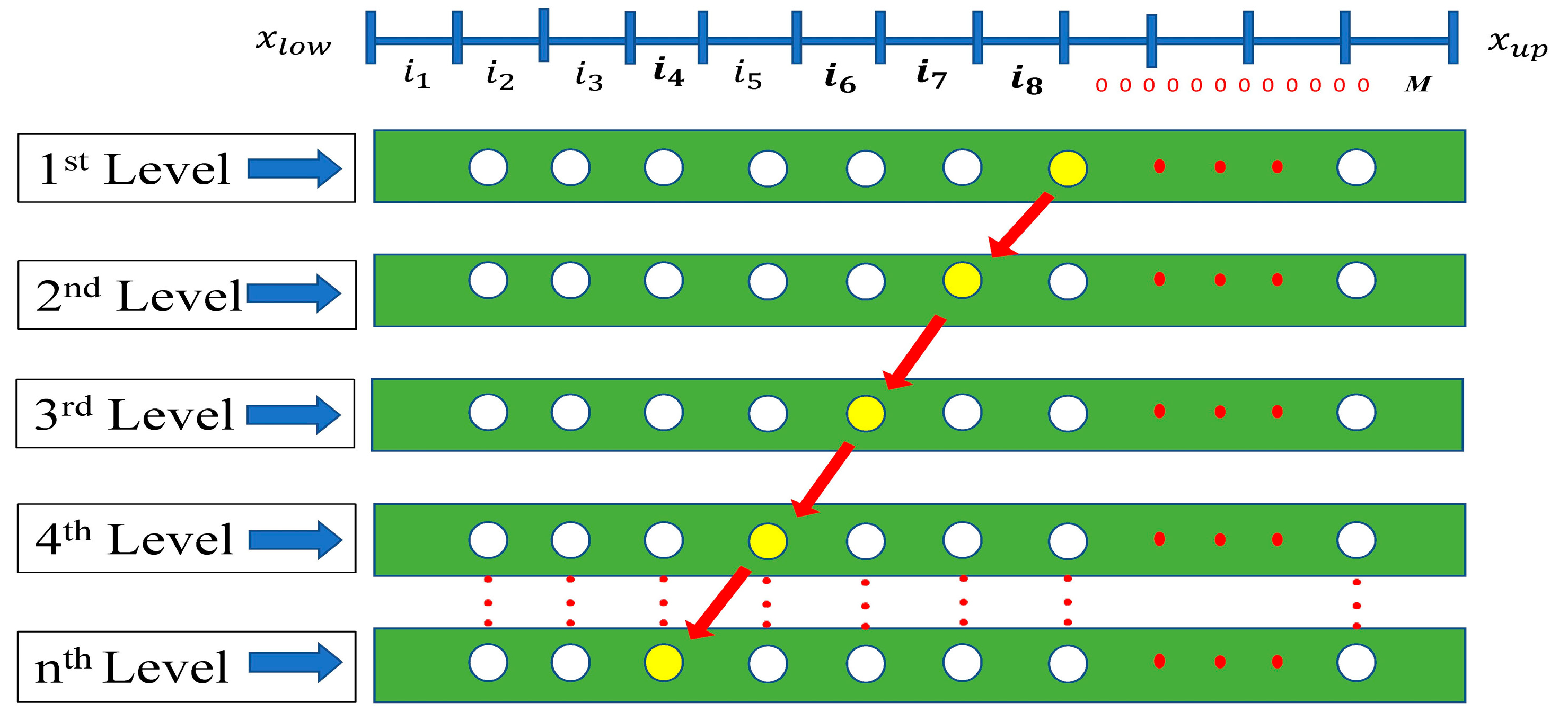
3.1. Ant Colony Algorithm
3.2. Artificial Bee Colony
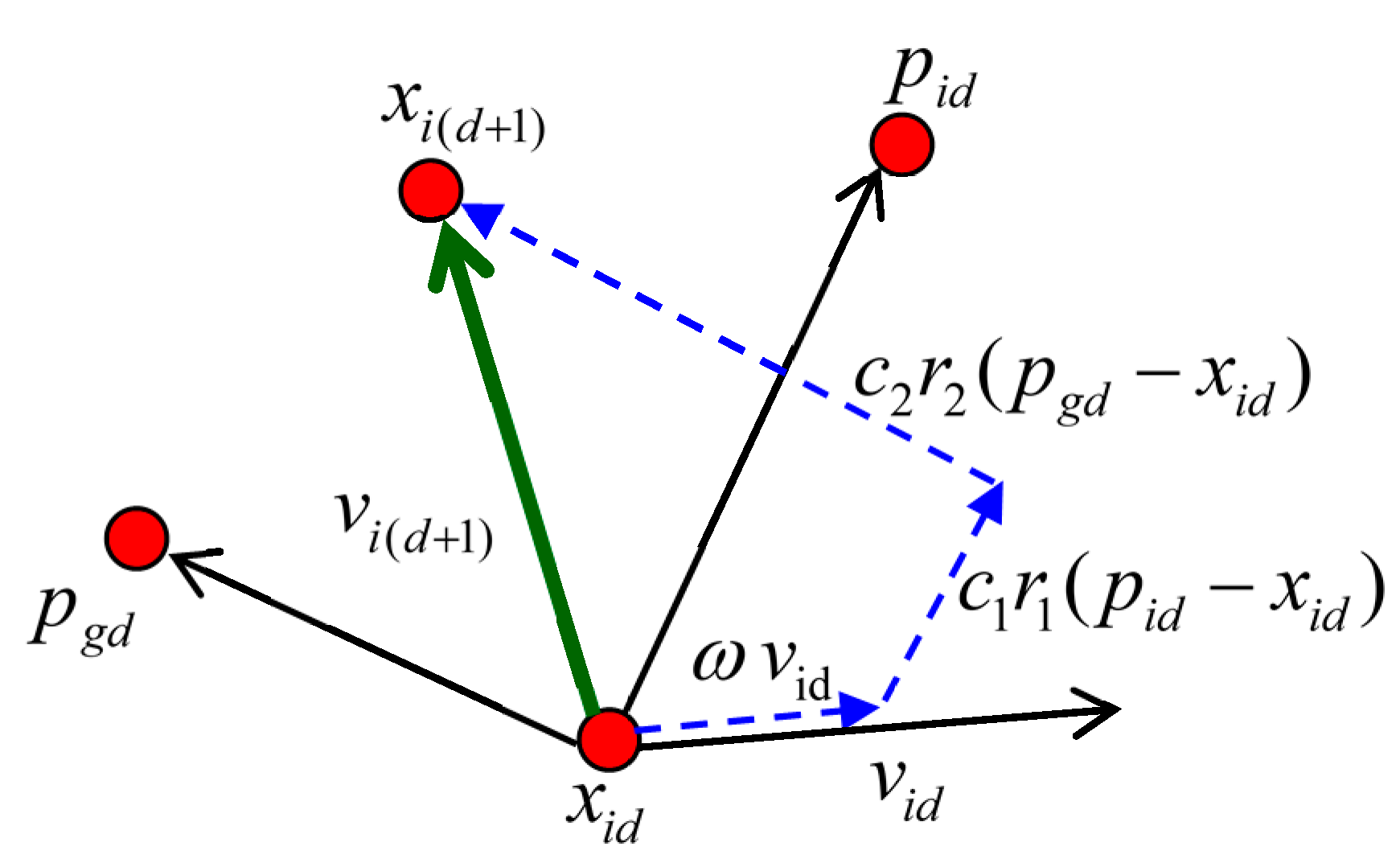
3.3. Particle Swarm Optimization
4. Adaptive Neuro-Fuzzy Interface System
5. Results and Discussion
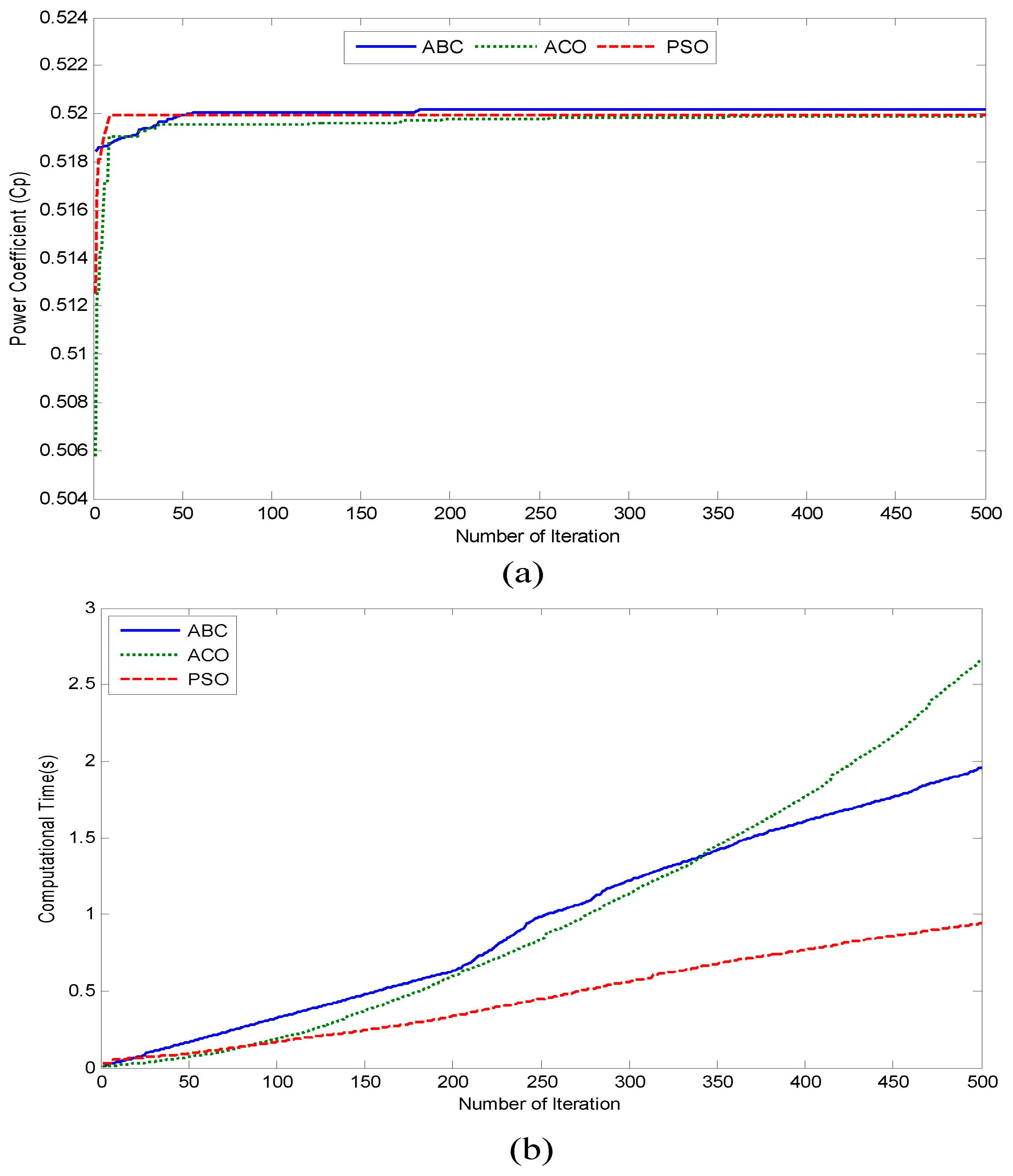
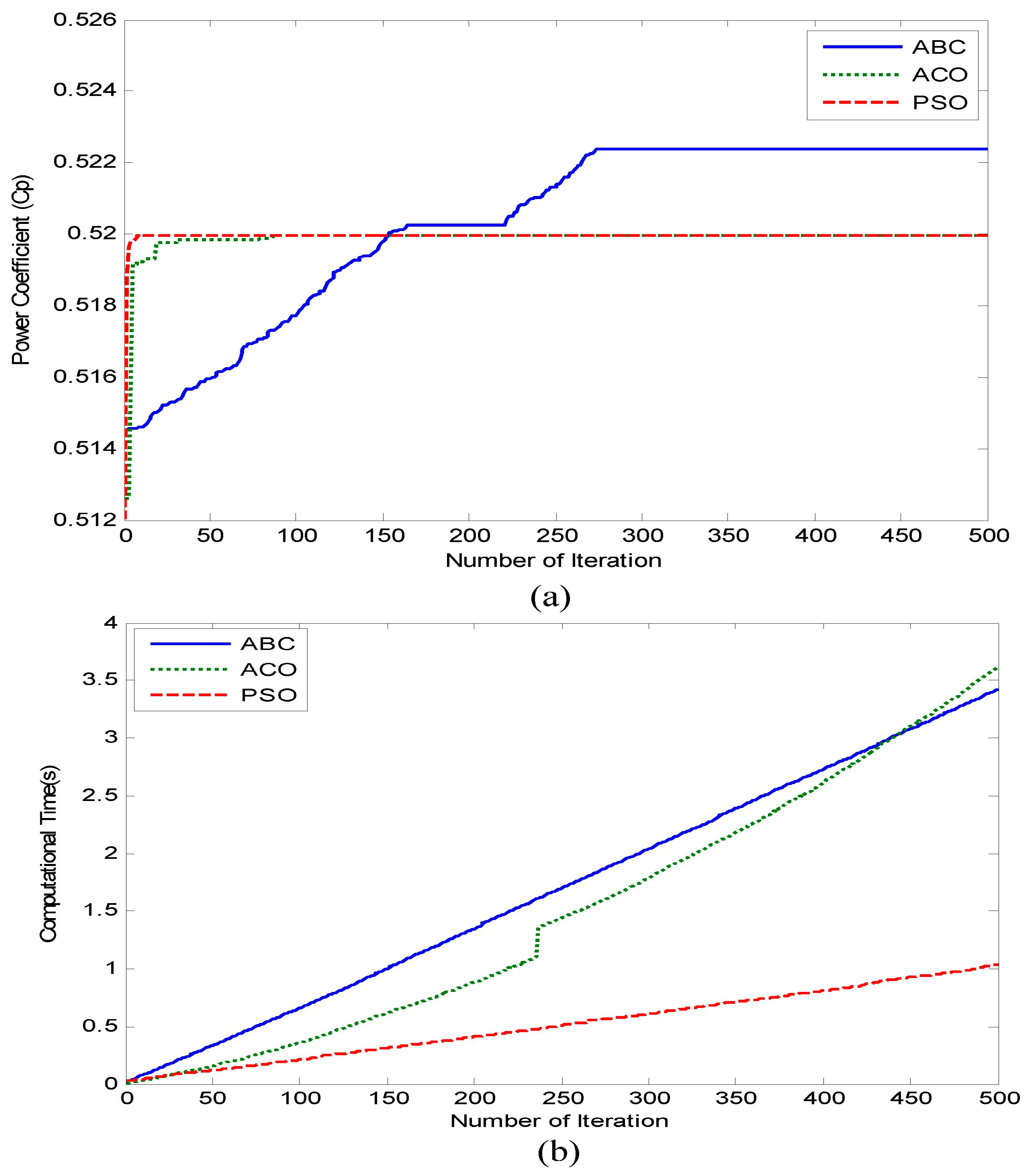
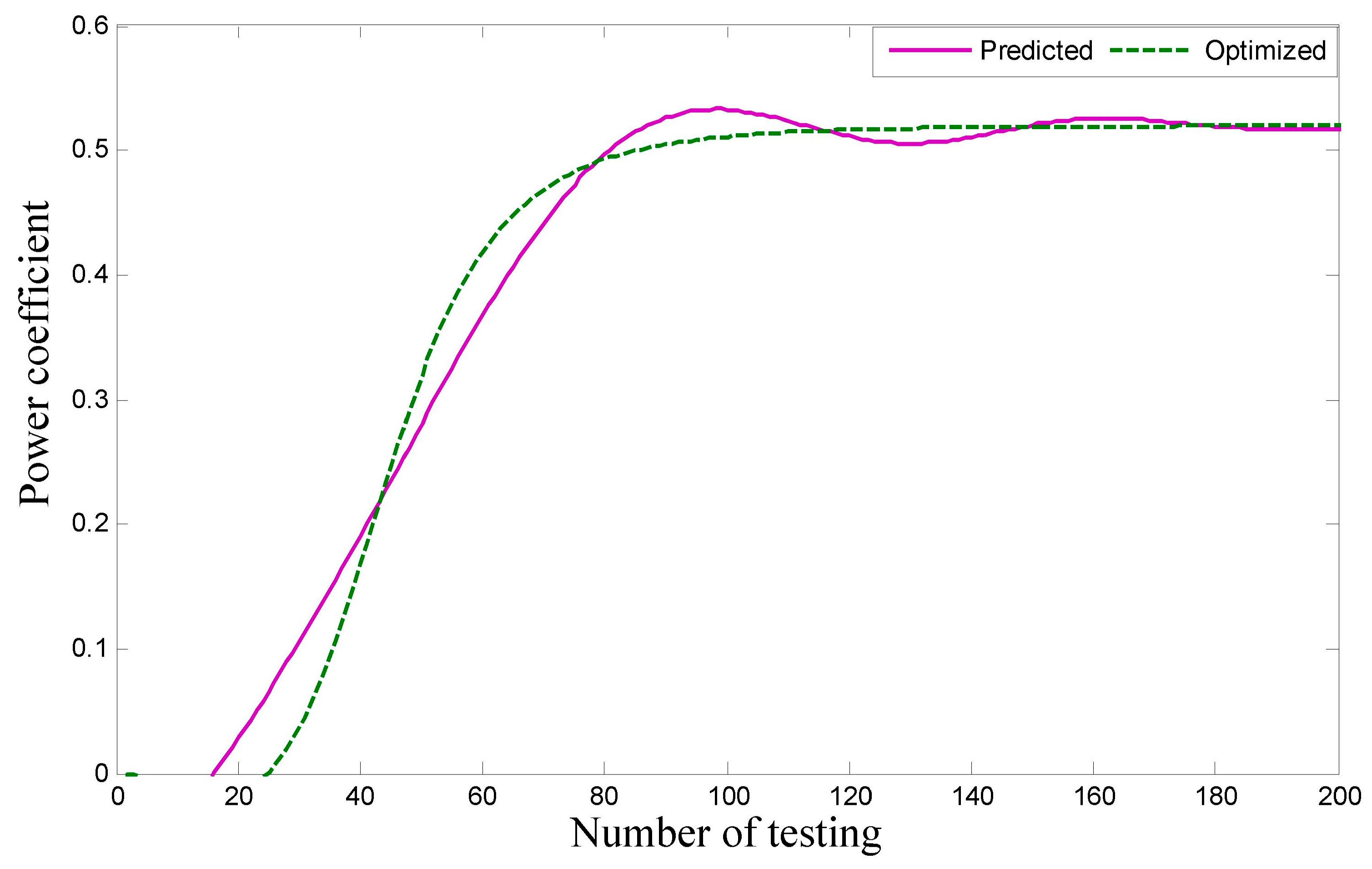
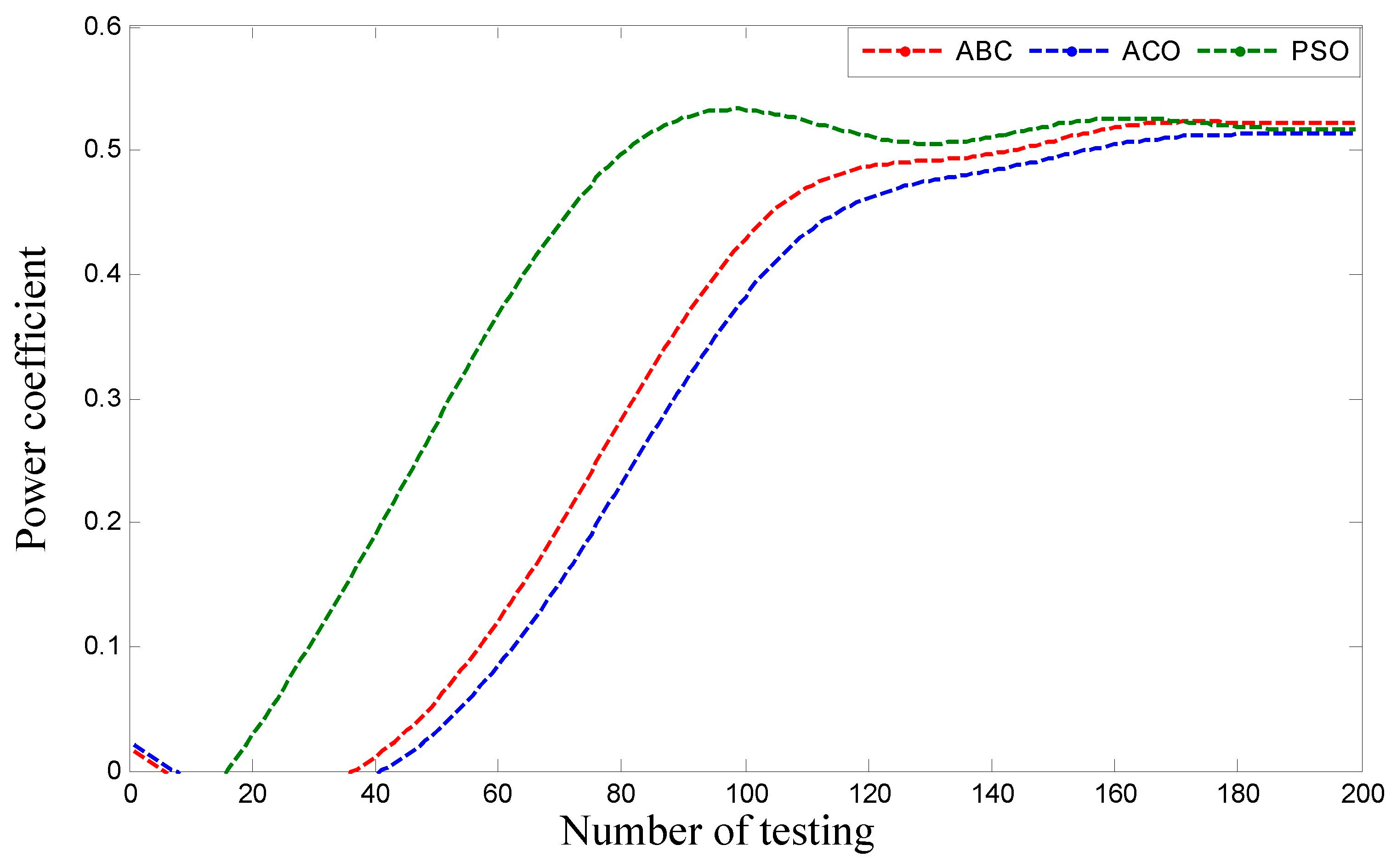
5.1. Convergence Graph Power Coefficient and Computational Time
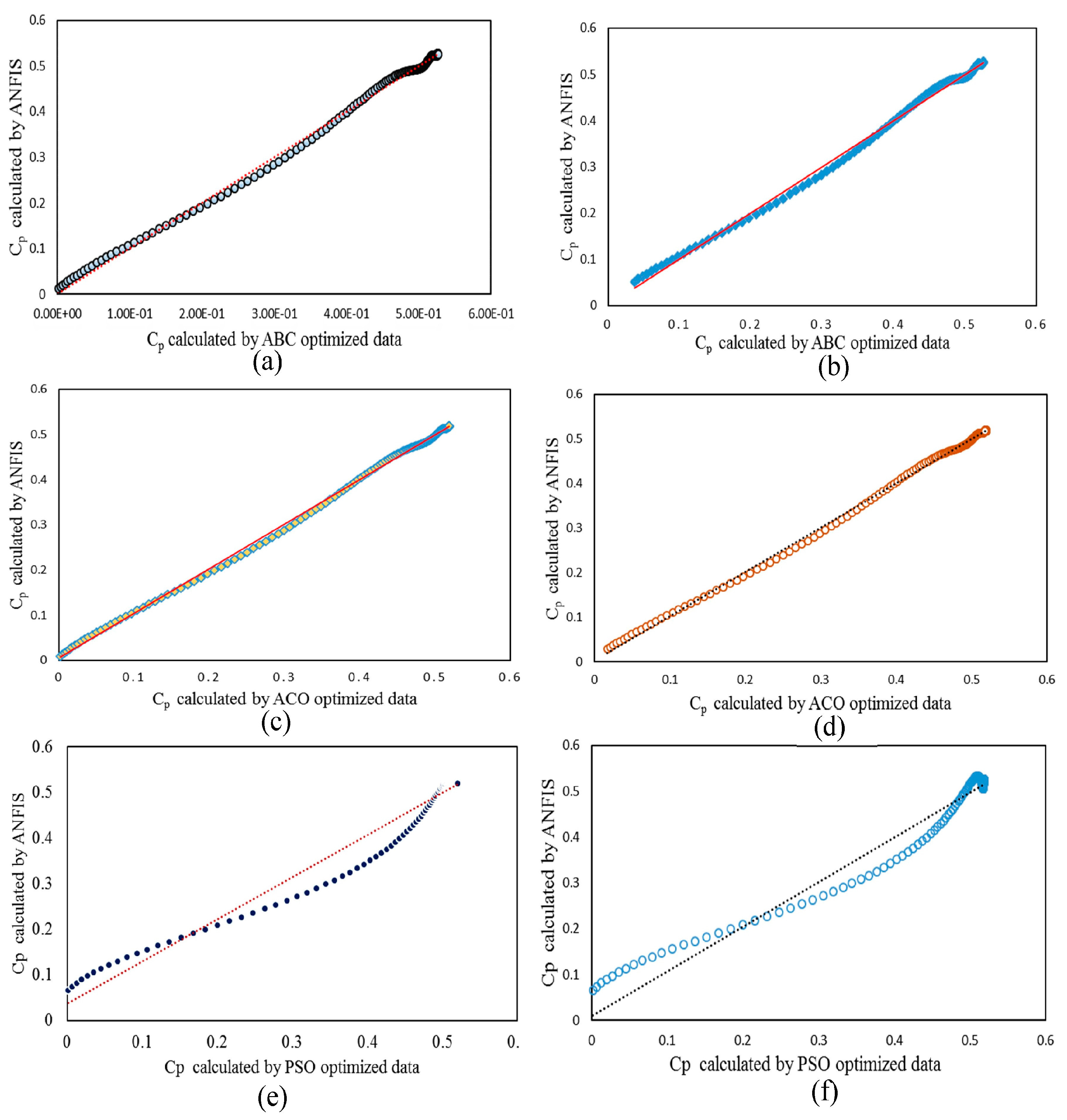
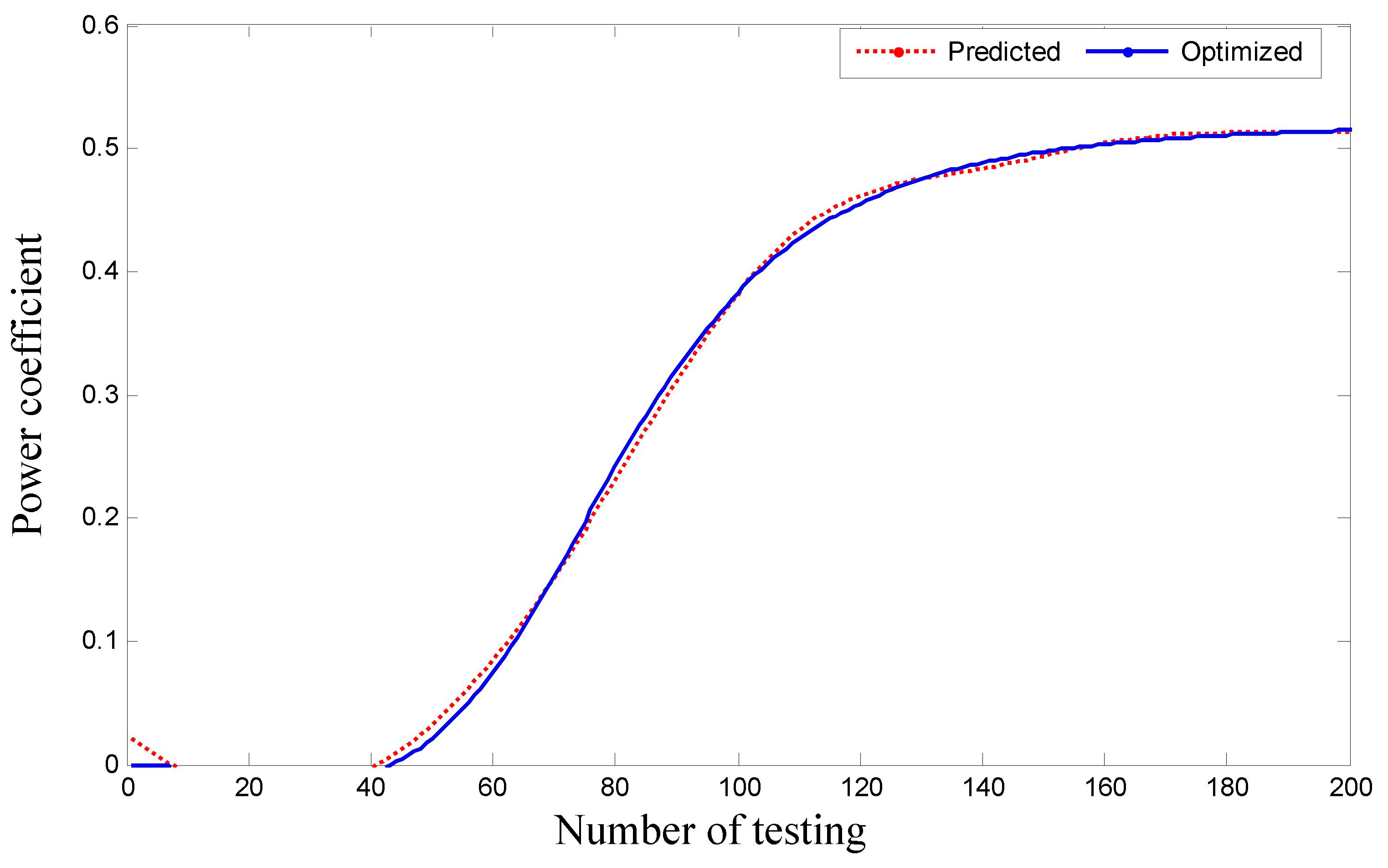
5.2. Prediction of Power Coefficient Using ANFIS
5.3. Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eltamaly, A.M.; Farh, H.M. Maximum power extraction from wind energy system based on fuzzy logic control. Electr. Power Syst. Res. 2013, 97, 144–150. [Google Scholar] [CrossRef]
- Oghafy, V.; Nikkhajoei, H. Maximum power extraction for a wind-turbine generator with no wind speed sensor. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–6. [Google Scholar]
- Marques, J.; Pinheiro, H.; Gründling, H.; Pinheiro, J.; Hey, H. A survey on variable-speed wind turbine system. Network 2003, 24, 26. [Google Scholar]
- Lanzafame, R.; Messina, M. Horizontal axis wind turbine working at maximum power coefficient continuously. Renew. Energy 2010, 35, 301–306. [Google Scholar] [CrossRef]
- Rajakumar, S.; Ravindran, D. Iterative approach for optimising coefficient of power, coefficient of lift and drag of wind turbine rotor. Renew. Energy 2012, 38, 83–93. [Google Scholar] [CrossRef]
- Petković, D.; Ćojbašić, Ž.; Nikolić, V.; Shamshirband, S.; Kiah, M.L.M.; Anuar, N.B.; Wahab, A.W.A. Adaptive neuro-fuzzy maximal power extraction of wind turbine with continuously variable transmission. Energy 2014, 64, 868–874. [Google Scholar] [CrossRef]
- Eroğlu, Y.; Seçkiner, S.U. Design of wind farm layout using ant colony algorithm. Renew. Energy 2012, 44, 53–62. [Google Scholar] [CrossRef]
- Fuchs, I.; Gjengedal, T. Ant colony optimization and analysis of time step resolution in transmission expansion computations for wind power integration. In Proceedings of the 2011 16th International Conference on Intelligent System Application to Power Systems (ISAP2011), Hersonissos, Greece, 25–28 September 2011; pp. 1–6. [Google Scholar]
- Jovanovic, R.; Tuba, M.; Voß, S. An ant colony optimization algorithm for partitioning graphs with supply and demand. Appl. Soft Comput. 2016, 41, 317–330. [Google Scholar] [CrossRef]
- Abd-Allah, M.; Said, A.; Ali, M.N. Mitigation of lightning hazards at the more sensitive points in wind farms using ant-colony optimization technique. Int. Electr. Eng. J. 2015, 6, 1856–1868. [Google Scholar]
- Mustafar, M.F.; Musirin, I.; Kalil, M.R.; Idris, M.K. Ant colony optimization (aco) based technique for voltage control and loss minimization using transformer tap setting. In Proceedings of the 2007 5th Student Conference on Research and Development (SCOReD 2007), Selangor, Malaysia, 11–12 December 2007; pp. 1–6. [Google Scholar]
- Delgarm, N.; Sajadi, B.; Delgarm, S. Multi-objective optimization of building energy performance and indoor thermal comfort: A new method using artificial bee colony (ABC). Energy Build. 2016, 131, 42–53. [Google Scholar] [CrossRef]
- Song, J.; Romero, C.E.; Yao, Z.; He, B. Improved artificial bee colony-based optimization of boiler combustion considering NOX emissions, heat rate and fly ash recycling for on-line applications. Fuel 2016, 172, 20–28. [Google Scholar] [CrossRef]
- Ebrahim, E.A. Artificial Bee Colony-Based Design of Optimal On-Line Self-tuning PIDController Fed AC Drives. Int. J. Eng. Res. 2014, 3, 807–811. [Google Scholar]
- Derakhshan, S.; Tavaziani, A.; Kasaeian, N. Numerical shape optimization of a wind turbine blades using artificial bee colony algorithm. J. Energy Resour. Technol. 2015, 137, 051210. [Google Scholar] [CrossRef]
- Habbi, H.; Boudouaoui, Y.; Karaboga, D.; Ozturk, C. Self-generated fuzzy systems design using artificial bee colony optimization. Inf. Sci. 2015, 295, 145–159. [Google Scholar] [CrossRef]
- Safaei, A.; Vahidi, B.; Askarian-Abyaneh, H.; Azad-Farsani, E.; Ahadi, S. A two step optimization algorithm for wind turbine generator placement considering maximum allowable capacity. Renew. Energy 2016, 92, 75–82. [Google Scholar] [CrossRef]
- Wan, C.; Wang, J.; Yang, G.; Zhang, X. Optimal micro-siting of wind farms by particle swarm optimization. In Proceedings of the International Conference in Swarm Intelligence, Beijing, China, 12–15 June 2010; pp. 198–205. [Google Scholar]
- Pookpunt, S.; Ongsakul, W. Optimal placement of wind turbines within wind farm using binary particle swarm optimization with time-varying acceleration coefficients. Renew. Energy 2013, 55, 266–276. [Google Scholar] [CrossRef]
- Maleki, A.; Ameri, M.; Keynia, F. Scrutiny of multifarious particle swarm optimization for finding the optimal size of a PV/wind/battery hybrid system. Renew. Energy 2015, 80, 552–563. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Petković, D.; Ćojbašič, Ž.; Nikolić, V. Adaptive neuro-fuzzy approach for wind turbine power coefficient estimation. Renew. Sustain. Energy Rev. 2013, 28, 191–195. [Google Scholar] [CrossRef]
- Shamshirband, S.; Petković, D.; Saboohi, H.; Anuar, N.B.; Inayat, I.; Akib, S.; Ćojbašić, Ž.; Nikolić, V.; Kiah, M.L.M.; Gani, A. Wind turbine power coefficient estimation by soft computing methodologies: Comparative study. Energy Convers. Manag. 2014, 81, 520–526. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mirhosseini, M. Aerodynamic design of a 300kW horizontal axis wind turbine for province of Semnan. Energy Convers. Manag. 2012, 63, 87–94. [Google Scholar] [CrossRef]
- Rajakumar, S.; Durairaj, R.; Kumar, M.; Venkatachalam, G.; Muthukumar, S. Optimization of power coefficient of wind turbine using genetic algorithm. J. Inst. Eng. (India) 2017, 98, 111–118. [Google Scholar] [CrossRef]
- Arifujjaman, M. Modeling and optimization of power coefficient using 2K factorial methodology. In Proceedings of the 2010 IEEE Electrical Power & Energy Conference, Halifax, NS, Canada, 25–27 August 2010; pp. 1–6. [Google Scholar]
- Selig, M.S.; Coverstone-Carroll, V.L. Application of a genetic algorithm to wind turbine design. J. Energy Resour. Technol. 1996, 118, 22–28. [Google Scholar] [CrossRef]
- Jureczko, M.; Pawlak, M.; Mężyk, A. Optimisation of wind turbine blades. J. Mater. Process. Technol. 2005, 167, 463–471. [Google Scholar] [CrossRef]
- Khalfallah, M.G.; Koliub, A.M. Suggestions for improving wind turbines power curves. Desalination 2007, 209, 221–229. [Google Scholar] [CrossRef]
- Sayed, M.A.; Kandil, H.A.; Shaltot, A. Aerodynamic analysis of different wind-turbine-blade profiles using finite-volume method. Energy Convers. Manag. 2012, 64, 541–550. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: West Sussex, UK, 2010. [Google Scholar]
- Zhu, J.; Cai, X.; Gu, R. Aerodynamic and Structural Integrated Optimization Design of Horizontal-Axis Wind Turbine Blades. Energies 2016, 9, 66. [Google Scholar] [CrossRef]
- Kim, B.; Kim, W.; Lee, S.; Bae, S.; Lee, Y. Developement and verification of a performance based optimal design software for wind turbine blades. Renew. Energy 2013, 54, 166–172. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Aerodynamics of horizontal axis wind turbines. In Wind Energy Handbook, 2nd ed.; John Wiley & Sons: West Sussex, UK, 2011. [Google Scholar]
- Bai, C.-J.; Chen, P.-W.; Wang, W.-C. Aerodynamic design and analysis of a 10 kW horizontal-axis wind turbine for Tainan, Taiwan. Clean Technol. Environ. Policy 2016, 18, 1151–1166. [Google Scholar] [CrossRef]
- Singh, M.; Chandra, A. Application of adaptive network-based fuzzy inference system for sensorless control of PMSG-based wind turbine with nonlinear-load-compensation capabilities. IEEE Trans. Power Electron. 2011, 26, 165–175. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the travelling salesman problem. BioSystems 1997, 43, 73–81. [Google Scholar] [CrossRef]
- Shen, Q.; Jiang, J.-H.; Tao, J.-C.; Shen, G.-L.; Yu, R.-Q. Modified ant colony optimization algorithm for variable selection in QSAR modeling: QSAR studies of cyclooxygenase inhibitors. J. Chem. Inf. Model. 2005, 45, 1024–1029. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Kıran, M.S.; Özceylan, E.; Gündüz, M.; Paksoy, T. A novel hybrid approach based on particle swarm optimization and ant colony algorithm to forecast energy demand of Turkey. Energy Convers. Manag. 2012, 53, 75–83. [Google Scholar] [CrossRef]
- Galdi, V.; Piccolo, A.; Siano, P. Designing an adaptive fuzzy controller for maximum wind energy extraction. IEEE Trans. Energy Convers. 2008, 23, 559–569. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Singh, S.; Kaushik, S.C. Optimal sizing of grid integrated hybrid PV-biomass energy system using artificial bee colony algorithm. IET Renew. Power Gener. 2016, 10, 642–650. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. A modified artificial bee colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A modified artificial bee colony (ABC) algorithm for constrained optimization problems. Appl. Soft Comput. 2011, 11, 3021–3031. [Google Scholar] [CrossRef]
- Song, X.; Gu, H.; Tang, L.; Zhao, S.; Zhang, X.; Li, L.; Huang, J. Application of artificial bee colony algorithm on surface wave data. Comput. Geosci. 2015, 83, 219–230. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L.; Contreras, J. Optimization of control strategies for stand-alone renewable energy systems with hydrogen storage. Renew. Energy 2007, 32, 1102–1126. [Google Scholar] [CrossRef]
- Bai, Q. Analysis of particle swarm optimization algorithm. Comput. Inf. Sci. 2010, 3, 180. [Google Scholar] [CrossRef]
- Kennedy, J.; Kennedy, J.F.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Morgan Kaufmann: Burlington, MA, USA, 2001. [Google Scholar]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; pp. 84–88. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Parameter selection in particle swarm optimization. In Proceedings of the International Conference on Evolutionary Programming, San Diego, CA, USA, 24–27 March 1998; pp. 591–600. [Google Scholar]
- Eberhart, R.C.; Shi, Y.; Kennedy, J. Swarm Intelligence (Morgan Kaufmann Series in Evolutionary Computation); Morgan Kaufmann: Burlington, MA, USA, 2001. [Google Scholar]
- Dilmac, S.; Nizam, A.; Korurek, M. Evaluation of a new heart beat classification method based on ABC algorithm, comparison with GA, PSO and ACO classifiers. Int. J. Reason.-Based Intell. Syst. 2014, 6, 98–108. [Google Scholar] [CrossRef]
- Petković, D.; Shamshirband, S. Soft methodology selection of wind turbine parameters to large affect wind energy conversion. Int. J. Electr. Power Energy Syst. 2015, 69, 98–103. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Al-Hmouz, A.; Shen, J.; Al-Hmouz, R.; Yan, J. Modeling and simulation of an Adaptive Neuro-Fuzzy Inference System (ANFIS) for mobile learning. IEEE Trans. Learn. Technol. 2012, 5, 226–237. [Google Scholar] [CrossRef]
- Tangler, J.L.; Somers, D.M. NREL Airfoil Families for HAWTs; Citeseer: Golden, CO, USA, 1995. [Google Scholar]
- Giguere, P.; Selig, M.S. Low Reynolds number airfoils for small horizontal axis wind turbines. Wind Eng. 1997, 21, 367–380. [Google Scholar]
- Dai, J.; Liu, D.; Wen, L.; Long, X. Research on power coefficient of wind turbines based on SCADA data. Renew. Energy 2016, 86, 206–215. [Google Scholar] [CrossRef]



| Input/output Parameters | Input Variables | ABC | ACO | PSO |
|---|---|---|---|---|
| Tip Speed Ratio | 3 to 10 [24] | 6.4479 | 6.0032 | 6.00 |
| Blade Radius | 1 to 5 [61] | 4.016 | 4.3089 | 4.50 |
| Lift to drag ratio | 1 to 110 [61] | 109.4848 | 109.9935 | 110.00 |
| Solidity ratio | 0.01 to 0.45 [35] | 0.3885 | 0.35 | 0.45 |
| Chord length | 0.01 to 0.45 [62] | 0.193 | 0.232 | 0.40 |
| Power coefficient | 0.529 | 0.52 | 0.52 |
| Model | Training | Testing | ||
|---|---|---|---|---|
| ABC-ANFIS | 0.00654 | 0.999 | 0.363 | 0.9985 |
| ACO-ANFIS | 0.00544 | 0.9989 | 0.814 | 0.997 |
| PSO-ANFIS | 0.235 | 0.9711 | 1.911 | 0.9777 |
| Subject | Theory | Blade Model | Maximum CP |
|---|---|---|---|
| Present Investigation | ABC algorithms | Airfoil S822 | 0.529 |
| ACO algorithms | 0.52 | ||
| PSO algorithms | 0.52 | ||
| ABC-ANFIS | 0.5215 | ||
| ACO-ANFIS | 0.5175 | ||
| PSO0-ANFIS | 0.5135 | ||
| Validation | Blade element momentum theory (BEM) [24] | Airfoil is RISØ-A1-18 | 0.51 |
| CFD analysis [5] | NACA 4410 | 0.48 | |
| NACA 2415 | 0.45 | ||
| Supervisory control and data acquisition (SCADA) system [63] | ---------- | 0.508 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarkar, M.R.; Julai, S.; Wen Tong, C.; Toha, S.F. Effectiveness of Nature-Inspired Algorithms using ANFIS for Blade Design Optimization and Wind Turbine Efficiency. Symmetry 2019, 11, 456. https://doi.org/10.3390/sym11040456
Sarkar MR, Julai S, Wen Tong C, Toha SF. Effectiveness of Nature-Inspired Algorithms using ANFIS for Blade Design Optimization and Wind Turbine Efficiency. Symmetry. 2019; 11(4):456. https://doi.org/10.3390/sym11040456
Chicago/Turabian StyleSarkar, Md. Rasel, Sabariah Julai, Chong Wen Tong, and Siti Fauziah Toha. 2019. "Effectiveness of Nature-Inspired Algorithms using ANFIS for Blade Design Optimization and Wind Turbine Efficiency" Symmetry 11, no. 4: 456. https://doi.org/10.3390/sym11040456
APA StyleSarkar, M. R., Julai, S., Wen Tong, C., & Toha, S. F. (2019). Effectiveness of Nature-Inspired Algorithms using ANFIS for Blade Design Optimization and Wind Turbine Efficiency. Symmetry, 11(4), 456. https://doi.org/10.3390/sym11040456







