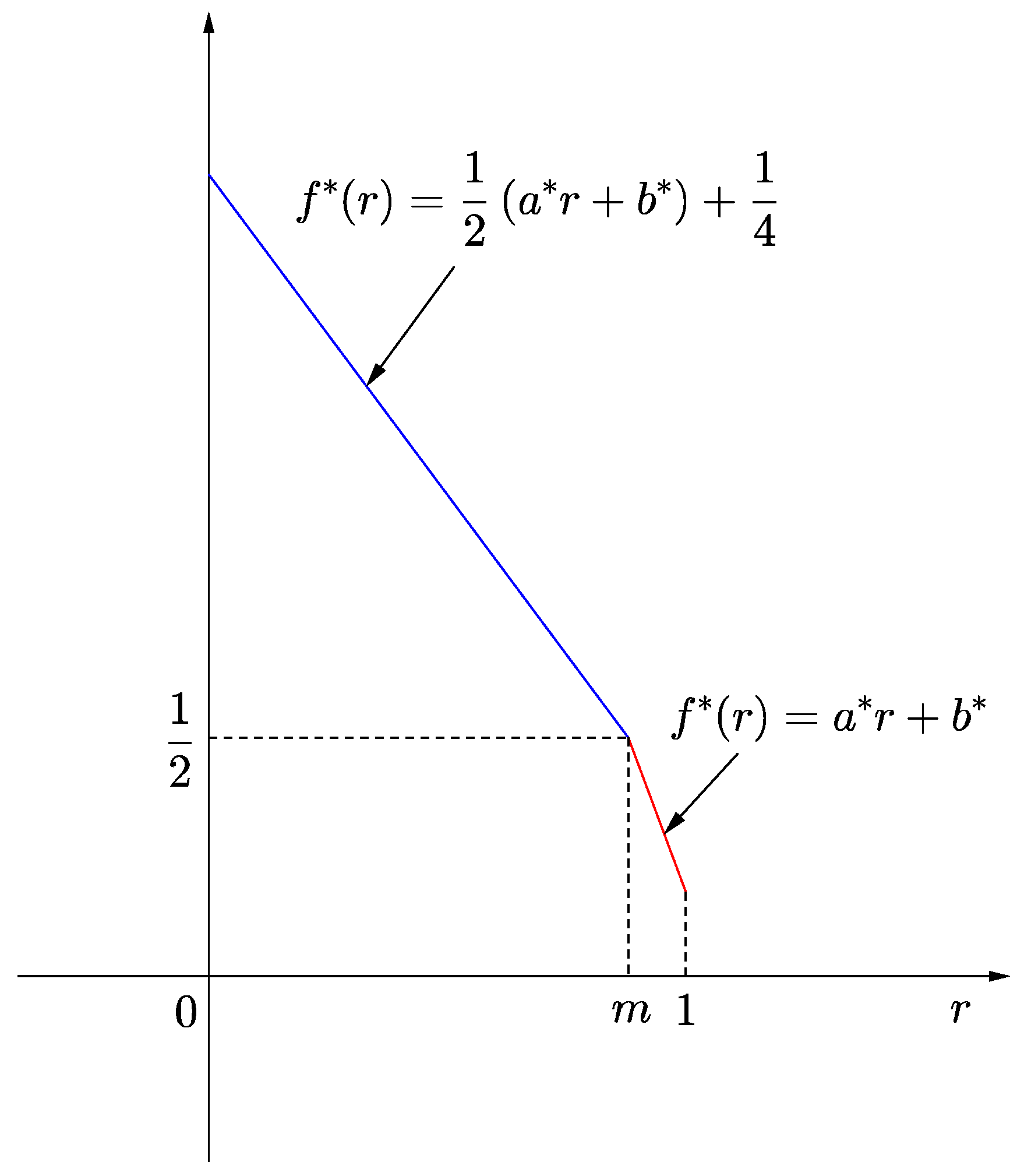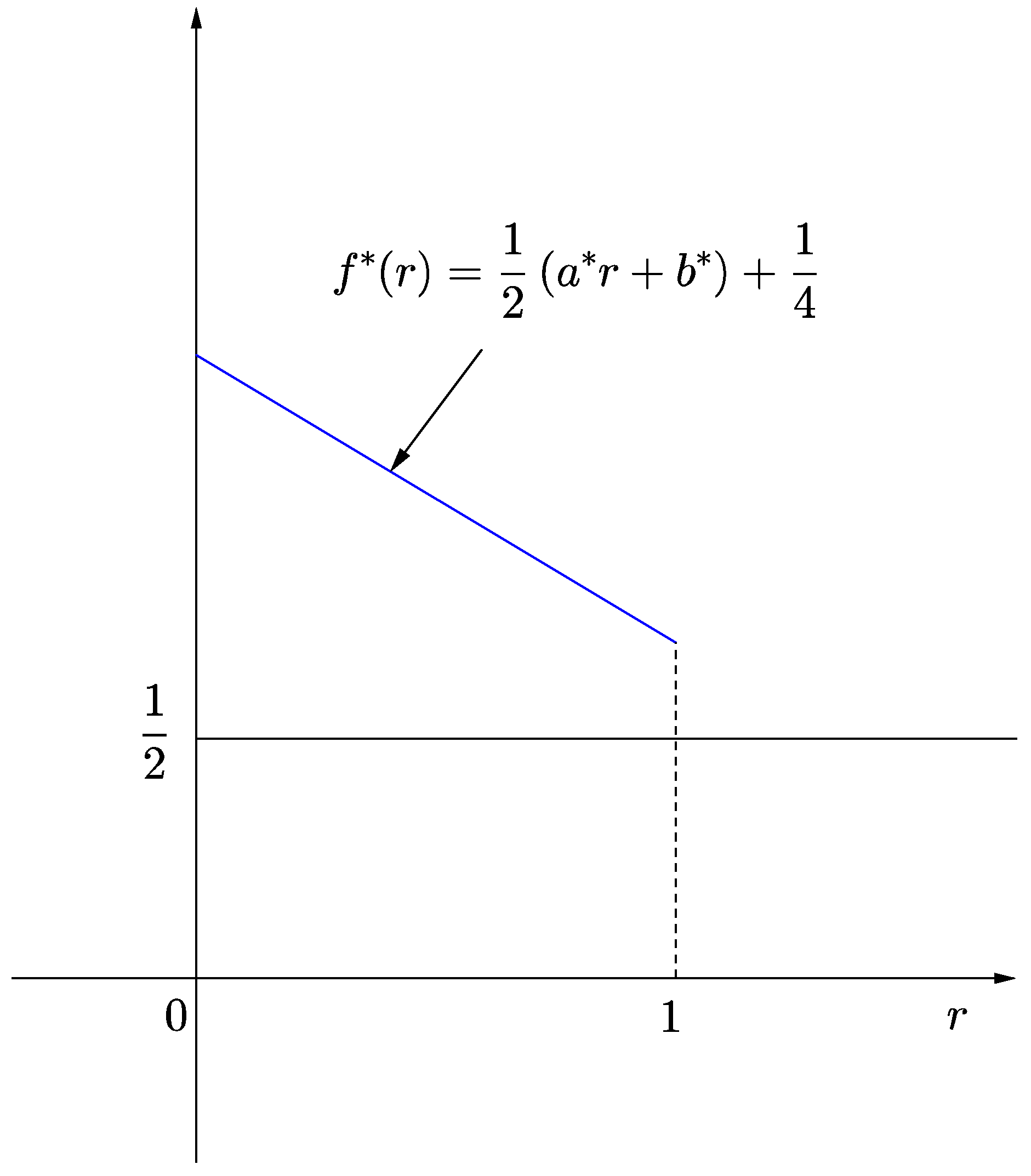The Solution Equivalence to General Models for the RIM Quantifier Problem

Abstract

Hong investigated the relationship between the minimax disparity minimum variance regular increasing monotone (RIM) quantifier problems. He also proved the equivalence of their solutions to minimum variance and minimax disparity RIM quantifier problems. Hong investigated the relationship between the minimax ratio and maximum entropy RIM quantifier problems and proved the equivalence of their solutions to the maximum entropy and minimax ratio RIM quantifier problems. Liu proposed a general RIM quantifier determination model and proved it analytically by using the optimal control technique. He also gave the equivalence of solutions to the minimax problem for the RIM quantifier. Recently, Hong proposed a modified model for the general minimax RIM quantifier problem and provided correct formulation of the result of Liu. Thus, we examine the general minimum model for the RIM quantifier problem when the generating functions are Lebesgue integrable under the more general assumption of the RIM quantifier operator. We also provide a solution equivalent relationship between the general maximum model and the general minimax model for RIM quantifier problems, which is the corrected and generalized version of the equivalence of solutions to the general maximum model and the general minimax model for RIM quantifier problems of Liu’s result.

1. Introduction

One of the important topics in the theory of ordered weighted averaging (OWA) operators is the determination of the associated weights. Several authors have suggested a number of methods for obtaining associated weights in various areas such as decision-making, approximate reasoning, expert systems, data mining, fuzzy systems and control [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Yager [12] proposed RIM quantifiers as a method for finding OWA weight vectors through fuzzy linguistic quantifiers. Liu [15] and Liu and Da [16] gave solutions to the maximum-entropy RIM quantifier model when the generating functions are differentiable. Liu and Lou [9] studied the equivalence of solutions to the minimax ratio and maximum-entropy RIM quantifier models, and the equivalence of solutions to the minimax disparity and minimum-variance RIM quantifier problems. Hong [17,18] gave the proof of the minimax ratio RIM quantifier problem and the minimax disparity RIM quantifier model when the generating functions are absolutely continuous. He also gave solutions to the maximum-entropy RIM quantifier model and the minimum-variance RIM quantifier model when the generating functions are Lebesgue integrable.

Based on these results, Hong [17,18] provided a relationship between the minimax disparity and minimum-variance RIM quantifier problems. He also provided a correct relationship between the minimax ratio and maximum-entropy RIM quantifier models. Liu [19] suggested a general RIM quantifier determination model and proved it analytically using the optimal control methods. He also studied the solution equivalence to the minimax problem for the RIM quantifier.

This paper investigates the general minimax model for the RIM quantifier problem for the case in which the generating functions are absolutely continuous and a generalized solution to the general minimum model for the RIM quantifier problem for the case in which the generating functions are Lebesgue integrable. Moreover, this paper provides a solution equivalent relationship between the general maximum model and the general minimax model for RIM quantifier problems and generalizes the results of Hong [17,18]. In this paper, we improve and extend Liu’s theorems to be suitable for absolutely continuous generating functions. We have corrected and improved Theorem 13 [19] by using the absolutely continuous condition of generating functions and the absolute continuity condition of $F^{\prime }$ for the general minimax model for the RIM quantifier problem. Theorem 9 [19] has been improved using the Lebesgue integrability condition of generating functions and the continuity condition of $F^{\prime }$ for the general maximum model for the RIM quantifier problem.

Based on these results, we give a correct relationship between the general minimum model and the general minimax model for RIM quantifier problems.

2. Preliminaries

Yager [11] proposed a new aggregation technique based on OWA operators. An OWA operator of dimension n is a mapping $F:R^n\to R$ that has an associated weight vector $W={(w_1,\cdots ,w_n)}^T$ with the properties $w_1+\cdots +w_n=1,0\le w_i\le 1,i=1,\cdots ,n$, such that

$$F(a_1,\cdots ,a_n)=\sum _{i=1}^n{w}_i{b}_i,$$

where $b_j$ is the jth largest element of the collection of the aggregated objects $\{a_1,\cdots ,a_n\}.$ In [11], Yager introduced a measure of “orness” associated with the weight vector W of an OWA operator:

$$orness\left(W\right)=\sum _{i=1}^n\frac{n-i}{n-1}{w}_i.$$

This measure characterizes the degree to which the aggregation is like an $OR$ operation.

Here, $min,max,$ and $average$ correspond to $W^{*},W_{*}$ and $W_A$ respectively, where $W^{*}=(1,0,\cdots ,0),W_{*}=(0,0,\cdots ,1)$ and $W_A=(1/n,1/n,\cdots ,1/n).$ Clearly, $orness\left(W^{*}\right)=1,orness\left(W_{*}\right)=0$ and $orness\left(W_A\right)=1/2.$

Yager [12] introduced RIM quantifiers as a method for obtaining OWA weight vectors through fuzzy linguistic quantifiers.

Definition 1 

([12]). A fuzzy subset Q on the real line is called a RIM quantifier if $Q\left(0\right)=0,Q\left(1\right)=1$ and $Q\left(x\right)\ge Q\left(y\right)$ for $x>y$.

The quantifier $forall$ is represented by the fuzzy set

$$\begin{array}{c}{Q}_{*}\left(r\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}x=1,\hfill \\ 0,\hfill & \mathrm{if}x\ne 1.\hfill \end{array}\right.\hfill \end{array}$$

The quantifier $thereexists$ is defined as

$$\begin{array}{c}{Q}^{*}\left(r\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}x=0,\hfill \\ 1,\hfill & \mathrm{if}x\ne 0.\hfill \end{array}\right.\hfill \end{array}$$

Both of these are examples of the RIM quantifier. A generating function representation of RIM quantifiers has been proposed for analyzing the relationship between OWA operators and RIM quantifiers.

Definition 2.

For $f\left(t\right)$ on [0, 1] and the RIM quantifier $Q\left(x\right),$$f\left(t\right)$ is called the generating function of $Q\left(x\right),$ if it satisfies

$$Q\left(x\right)={\int }_0^{x}f\left(t\right)dt,$$

where $f\left(t\right)\ge 0$ and ${\int }_0^{1}f\left(t\right)dt=1.$

If the RIM quantifier $Q\left(x\right)$ is smooth, then $f\left(x\right)$ should be continuous; if $Q\left(x\right)$ is a piecewise linear function, then $f\left(x\right)$ is a jump piecewise function of some constants; and if $Q\left(x\right)$ is an absolutely continuous function, then $f\left(x\right)$ is a Lesbegue integrable function and unique in the sense of being “almost everywhere” [23].

Yager extended the $orness$ measure of OWA operators, and defined the $orness$ of RIM quantifiers [10] as:

$$orness\left(Q\right)={\int }_0^{1}Q\left(x\right)dx={\int }_0^1(1-t)f\left(t\right)dt.$$

We see that $Q_{*}$ leads to the weight vector $W_{*}$, $Q^{*}$ leads to the weight vector $W^{*}$, and the ordinary $average$ RIM quantifier $Q_A\left(x\right)=x$ leads to the weight vector $W_A.$ We also have $orness\left(Q^{*}\right)=1,rness\left(Q_{*}\right)=0,$ and $orness\left(Q_A\right)=1/2.$

As the RIM quantifier can be seen as a continuous form of OWA, an operator with a generating function, the OWA optimization problem can be extended to the case of the RIM quantifier.

3. The General Model for the Minimax RIM Quantifier Problem

In this section, we consider the general model for the minimax RIM quantifier problem and generalize some results of Hong [17,18]. Hong [7] provided a modified model for the minimax RIM quantifier problem and the correct formulation of a result of Liu [19]. We summarize briefly.

∗ The minimax disparity RIM quantifier problem [15,17].

The minimax disparity RIM quantifier problem with a given orness level $0<\alpha <1$ consists of finding a solution $f:[0,1]\to [0,1]$ to the following optimization problem:

$$\begin{array}{cc}\mathrm{Minimize}\hfill & \underset{t\in (0,1)}{\max }\mid f^{\prime }\left(t\right)\mid ,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\int }_0^1(1-r)f\left(r\right)dr=\alpha ,0<\alpha <1,\hfill \\ & {\int }_0^{1}f\left(r\right)dr=1,\hfill \\ & f\left(r\right)\ge 0.\hfill \end{array}$$

∗ The minimax ratio RIM quantifier problem [9,18].

The minimax ratio RIM quantifier problem with a given orness level $0<\alpha <1$ consists of finding a solution $f:[0,1]\to [0,1]$ to the following optimization problem:

$$\begin{array}{cc}\mathrm{Minimize}\hfill & \underset{t\in (0,1)}{\max }\left|\frac{f^{\prime }\left(t\right)}{f\left(t\right)}\right|,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\int }_0^1(1-r)f\left(r\right)dr=\alpha ,0<\alpha <1,\hfill \\ & {\int }_0^{1}f\left(r\right)dr=1,\hfill \\ & f\left(r\right)>0.\hfill \end{array}$$

In regard to the above optimization problem, Liu [19] considered a general model for the minimax RIM quantifier problem:

$$\begin{array}{cc}\mathrm{Minimize}& M_f=\underset{r\in (0,1)}{\max }\left|F^{″}\left(f\left(r\right)\right)f^{\prime }\left(r\right)\right|,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\int }_0^{1}rf\left(r\right)dr=\alpha ,0<\alpha <1,\hfill \\ & {\int }_0^{1}f\left(r\right)dr=1,\hfill \\ & f\left(r\right)>0,\hfill \end{array}$$

(1)

where the generating functions are continuous and F is a strictly convex function on $[0,\infty ),$ which is differentiable to at least the 2nd order.

The above two cases are special cases of this model with $F\left(x\right)=x^2$ and $F\left(x\right)=x\ln x.$ Hong [7] gave a corrected and modified general model for the minimax RIM quantifier problem as follows:

∗ The general model for the minimax RIM quantifier problem.

$$\begin{array}{cc}\mathrm{Minimize}& M_f=esssu{p}_{r\in (0,1)}\left|F^{″}\left(f\left(x\right)\right)f^{\prime }\left(x\right)\right|,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\int }_0^{1}rf\left(r\right)dr=\alpha ,0<\alpha <1,\hfill \\ & {\int }_0^{1}f\left(r\right)dr=1,\hfill \\ & f\left(r\right)>0.\hfill \end{array}$$

(2)

Theorem 1.

Supposing that the generating functions are absolutely continuous, F is a strictly convex function on $[0,\infty ),$ and $F^{\prime }$ is absolutely continuous, then there is a unique optimal solution for problem (2), and that the optimal solution has the form

$$\begin{array}{c}{f}^{*}\left(r\right)=\max \left\{{\left(F^{\prime }\right)}^{-1}\left(a^{*}r+b^{*}\right),0\right\},\hfill \end{array}$$

where $a^{*}$ and $b^{*}$ are determined by the constraints:

$$\begin{array}{c}\left\{\begin{array}{c}{\int }_0^{1}r{f}^{*}\left(r\right)dr=\alpha ,\hfill \\ {\int }_0^1{f}^{*}\left(r\right)dr=1,\hfill \\ f^{*}\left(r\right)\ge 0.\hfill \end{array}\right.\hfill \end{array}$$

The next example shows that the condition of $F^{\prime }$ being absolutely continuous on $[0,\infty )$ in Theorem 1 is essential.

Example 1.

Letting $F_1\left(x\right)={\int }_0^x(C\left(r\right)+r)dr$ where $C\left(x\right)$ is a Cantor function, then $F^{\prime }\left(x\right)=C\left(x\right)+x$ and $F_1^{″}\left(x\right)=1a.e.$ but $F_1^{\prime }\left(x\right)\ne {\int }_0^x{F}_1^{″}\left(r\right)dr,$ that is, $F_1^{\prime }$ is not absolutely continuous on $[0,\infty ).$ Let $F_2\left(x\right)=(1/2)x^2,$ then $F_2^{″}\left(x\right)=1$. Since

$$esssu{p}_{r\in (0,1)}\left|F_1^{″}\left(f\left(x\right)\right)f^{\prime }\left(x\right)\right|=esssu{p}_{r\in (0,1)}\left|f^{\prime }\left(x\right)\right|=esssu{p}_{r\in (0,1)}\left|F_2^{″}\left(f\left(x\right)\right)f^{\prime }\left(x\right)\right|,$$

the optimal solution of problem (2) with respect to $F_1$ and $F_1$ are the same. However, since $F_1^{\prime }\left(x\right)\ne F_2^{\prime }\left(x\right),$ the optimal solution of problem (2) with respect to $F_1$ and $F_1$ cannot be the same by Theorem 2, which is a contradiction. This example shows the Theorem 2 is incorrect if $F^{\prime }$ is not absolutely continuous on $[0,\infty ).$

4. The General Model for the Minimum RIM Quantifier Problem

In this section, we consider the general model for the minimum RIM quantifier problem. We improve the results of Liu [19] and generalize Theorem 4 of Hong [17] and Theorem 5 of Hong [18]. Liu [19] obtained solutions to the general minimum RIM quantifier problem for the case in which the generating functions are continuous and F is differentiable to at least the 2nd order by considering a variational optimization problem using the Lagrangian multiplier method ([24], Chapter 2). In this section, we consider a generalized result for this problem.

∗ The minimum variance RIM quantifier problem [17,18].

The minimum variance RIM quantifier problem under a given orness level is

$$\begin{array}{cc}\mathrm{Minimize}\hfill & D_f={\int }_0^1{f}^2\left(r\right)dr,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\int }_0^{1}rf\left(r\right)dr=\alpha ,0<\alpha <1,\hfill \\ & {\int }_0^{1}f\left(r\right)dr=1,\hfill \\ & f\left(r\right)>0.\hfill \end{array}$$

∗ The maximum entropy RIM quantifier problem [9,18].

The maximum entropy RIM quantifier problem with a given orness level $0<\alpha <1$ consists of finding a solution $f:[0,1]\to [0,1]$ to the following optimization problem:

$$\begin{array}{ll}\mathrm{Maximize}& -{\int }_0^{1}f\left(r\right)\ln f\left(r\right)dr,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\int }_0^{1}rf\left(r\right)dr=\alpha ,0<\alpha <1,\hfill \\ & {\int }_0^{1}f\left(r\right)dr=1,\hfill \\ & f\left(r\right)>0.\hfill \end{array}$$

Recently, Liu [19] considered the general model for the minimum variance and maximum entropy RIM quantifier problems, under a given orness level formulated as follows:

∗ The general model for the minimum RIM quantifier problem.

$$\begin{array}{cc}\mathrm{Minimize}\hfill & V_f={\int }_0^{1}F\left(f\left(r\right)\right)dr,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & {\int }_0^{1}rf\left(r\right)dr=\alpha ,0<\alpha <1,\hfill \\ & {\int }_0^{1}f\left(r\right)dr=1,\hfill \\ & f\left(r\right)>0,\hfill \end{array}$$

(3)

where F is a strictly convex function on $[0,\infty ),$ and differentiable to at least the 2nd order.

The above two cases are special cases of the model where $F\left(x\right)=x^2$ and $F\left(x\right)=xlnx.$

Liu (Theorem 9, [19]) proved the following problem for the case in which generating functions are continuous and F is differentiable to at least the 2nd order:

Theorem 2 

(Theorem 9, [19]). There is a unique optimal solution for (3), and the optimal solution has the form

$$\begin{array}{c}{f}^{*}\left(r\right)=\left\{\begin{array}{cc}{\left(F^{\prime }\right)}^{-1}(a^{*}r+b^{*}),\hfill & if{\left(F^{\prime }\right)}^{-1}(a^{*}r+b^{*})\ge 0,\hfill \\ 0,\hfill & elsewhere,\hfill \end{array}\right.\hfill \end{array}$$

where $a^{*},b^{*}$ are determined by the constraints:

$$\begin{array}{c}\left\{\begin{array}{c}{\int }_0^{1}r{f}^{*}\left(r\right)dr=\alpha ,\hfill \\ {\int }_0^1{f}^{*}\left(r\right)dr=1,\hfill \\ f^{*}\left(r\right)\ge 0.\hfill \end{array}\right.\hfill \end{array}$$

Here, we consider a generalized result for Theorem 3 when $f\left(x\right)$ is Lebesgue integrable and $F^{\prime }$ is continuous.

Theorem 3.

Suppose that the generating functions are Lebesgue integrable, F is a strictly convex function on $[0,\infty )$, and $F^{\prime }$ is continuous. Then, there is a unique optimal solution for problem (3), and that optimal solution has the form

$$\begin{array}{c}{f}^{*}\left(r\right)=\left\{\begin{array}{cc}{\left(F^{\prime }\right)}^{-1}(a^{*}r+b^{*})a.e.,\hfill & if{\left(F^{\prime }\right)}^{-1}(a^{*}r+b^{*})>0,\hfill \\ 0a.e.,\hfill & elsewhere,\hfill \end{array}\right.\hfill \end{array}$$

where $a^{*}$ and $b^{*}$ are determined by the constraints:

$$\begin{array}{c}\left\{\begin{array}{c}{\int }_0^{1}r{f}^{*}\left(r\right)dr=\alpha ,\hfill \\ {\int }_0^1{f}^{*}\left(r\right)dr=1,\hfill \\ f^{*}\left(r\right)\ge 0.\hfill \end{array}\right.\hfill \end{array}$$

Proof. 

As shown in Theorem 2, we consider the case where $\alpha \in (0,1/2]$ and assume that $\{r<1:f^{*}\left(r\right)>0\}=[0,t)$ for some $t\in (0,1)$ and $\{r<1:f^{*}\left(r\right)=0\}=[t,1).$ We also note that for $r\in [0,t]$,

$$F^{\prime }\left(f^{*}\left(r\right)\right)=a^{*}r+b^{*}$$

and for $r\in (t,1)$,

$$a^{*}r+b^{*}<F^{\prime }\left(0\right)$$

if $F^{\prime }\left(0\right)$ exists. Let the nonnegative function f satisfy $1={\int }_0^{1}f\left(r\right)dr$ and ${\int }_0^{1}rf\left(r\right)dr=\alpha$. We set $f\left(r\right)=f^{*}\left(r\right)+g\left(r\right),r\in [0,1].$ Then, noting that $f\left(r\right)=g\left(r\right),r\in [t,1],$ we have

$$\begin{array}{c}{\int }_0^{t}g\left(r\right)dr+{\int }_t^{1}f\left(r\right)dr={\int }_0^{1}g\left(r\right)dr=0,\hfill \end{array}$$

(4)

since $1={\int }_0^{1}f\left(r\right)dr={\int }_0^1{f}^{*}\left(r\right)dr+{\int }_0^{1}g\left(r\right)dr=1+{\int }_0^{1}g\left(r\right)dr$. We also have

$$\begin{array}{c}{\int }_0^{t}rg\left(r\right)dr+{\int }_t^{1}rf\left(r\right)dr={\int }_0^{1}rg\left(r\right)dr=0,\hfill \end{array}$$

(5)

since $\alpha ={\int }_0^{1}rf\left(r\right)dr={\int }_0^{1}r{f}^{*}\left(r\right)dr+{\int }_0^{1}rg\left(r\right)dr=\alpha +{\int }_0^{1}rg\left(r\right)dr$. We now show that

$$\begin{array}{c}{\int }_0^{1}F\left(f\left(r\right)\right)dr\ge {\int }_0^{1}F\left(f^{*}\left(r\right)\right)dr.\hfill \end{array}$$

Since $F\left(x\right)-F\left(x_0\right)\ge F^{\prime }\left(x_0\right)(x-x_0)$ (the equality holds if and only if $x=x_0$), we have that

$$\begin{array}{cc}& {\int }_0^{1}F\left(f\left(r\right)\right)dr-{\int }_0^{1}F\left(f^{*}\left(r\right)\right)dr\hfill \\ =\hfill & {\int }_0^{1}F\left((f^{*}\left(r\right)+g\left(r\right))\right)dr-{\int }_0^{1}F\left(f^{*}\left(r\right)\right)dr\hfill \\ \ge & {\int }_0^1{F}^{\prime }\left(f^{*}\left(r\right)\right)g\left(r\right)dr\hfill \\ =& {\int }_0^t(a^{*}r+b^{*})g\left(r\right)dr+{\int }_t^1{F}^{\prime }\left(0\right)g\left(r\right)dr\hfill \\ =& a^{*}{\int }_0^{t}rg\left(r\right)dr+b^{*}{\int }_0^{t}g\left(r\right)dr+{\int }_t^1{F}^{\prime }\left(0\right)g\left(r\right)dr\hfill \\ =& a^{*}(-{\int }_t^{1}rf\left(r\right)dr)+b^{*}(-{\int }_t^{1}f\left(r\right)dr)+{\int }_t^1{F}^{\prime }\left(0\right)g\left(r\right)dr\hfill \\ =& {\int }_t^1(F^{\prime }\left(0\right)-a^{*}r-b^{*})f\left(r\right)dr\hfill \\ \ge & 0,\hfill \end{array}$$

where the fourth equality comes from (4) and (5) and the second inequality comes from the fact that $a^{*}r+b^{*}\le F^{\prime }\left(0\right)a.e.$ for $r\in [t,1]$. The equalities hold if and only if $f^{*}=fa.e.$ This completes the proof. □

Combining Theorems 2 and 4, we now have a solution equivalent relationship between the general minimum RIM quantifier problem and the general minimax RIM quantifier problem. This result generalizes Theorem 6 of Hong [17] and Theorem 5 of Hong [18] and provides a corrected version of Theorem 13 [19].

Theorem 4.

Suppose that the generating functions are absolutely continuous and $F^{\prime }$ is increasing and absolutely continuous. Then, the general minimum RIM quantifier problem has the same solution as the general minimax RIM quantifier problem.

5. Numerical Example

We consider a RIM quantifier operator F which is not differentiable to at least the second order, but $F^{\prime }$ is absolutely continuous, and find an optimal solution of two RIM quantifier problems.

Let a RIM quantifier operator F be

$$F\left(x\right)=\left\{\begin{array}{cc}\frac{x^2}{2,}\hfill & \mathrm{if}0\le x<\frac{1}{2},\hfill \\ x^2-\frac{1}{2}x+\frac{1}{8},\hfill & \mathrm{if}\frac{1}{2}\le x\le 1.\hfill \end{array}\right.$$

Then,

$$F^{\prime }\left(x\right)=\left\{\begin{array}{cc}x,\hfill & \mathrm{if}0\le x<\frac{1}{2},\hfill \\ 2x-\frac{1}{2},\hfill & \mathrm{if}\frac{1}{2}\le x\le 1.\hfill \end{array}\right.$$

Hence, $F\left(x\right)$ is strictly convex and $F^{\prime }\left(x\right)$ is absolutely continuous, but $F\left(x\right)$ is not the second order differentiable. Let

$$\begin{array}{c}{f}^{*}\left(r\right)=\left\{\begin{array}{cc}{\left(F^{\prime }\right)}^{-1}(a^{*}r+b^{*}),\hfill & \mathrm{if}{\left(F^{\prime }\right)}^{-1}\left(a^{*}r+b^{*}\right)>0,\hfill \\ 0,\hfill & \mathrm{elsewhere},\hfill \end{array}\right.\hfill \end{array}$$

where $a^{*}$ and $b^{*}$ are determined by the constraints:

$$\begin{array}{c}\left\{\begin{array}{c}{\int }_0^{1}r{f}^{*}\left(r\right)dr=\alpha ,\hfill \\ {\int }_0^1{f}^{*}\left(r\right)dr=1,\hfill \\ f^{*}\left(r\right)\ge 0.\hfill \end{array}\right.\hfill \end{array}$$

(6)

We consider the case for $0<\alpha \le 1/2$. Then, $a^{*}\le 0$ and $b^{*}>0$.

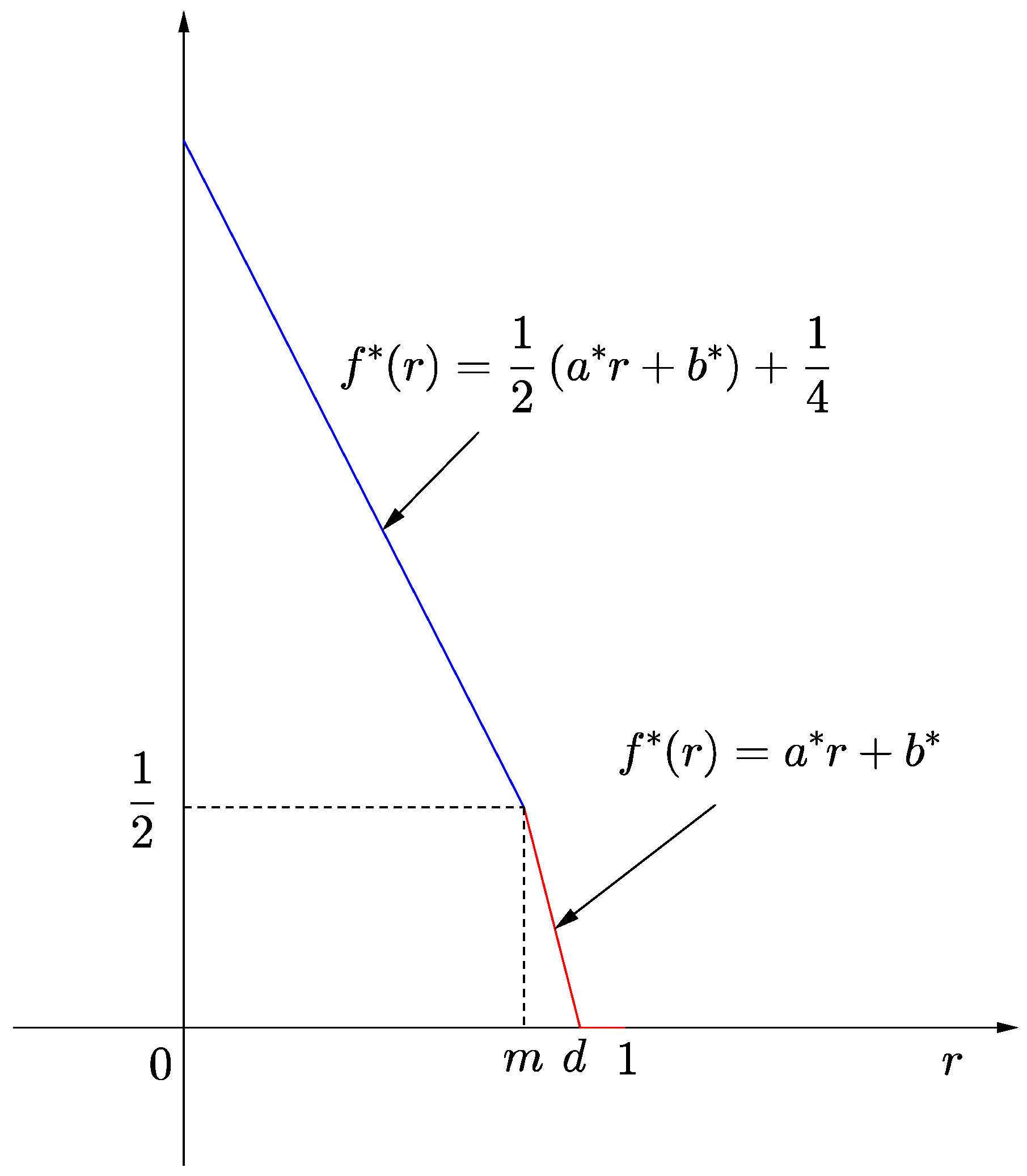
Case (1) (See Figure 1) There exists $m,d\in [0,1]$ such that $m<d$ and

$$\begin{array}{c}{f}^{*}\left(r\right)=\left\{\begin{array}{cc}\frac{1}{2}(a^{*}r+b^{*})+\frac{1}{4},\hfill & \mathrm{if}0\le r\le m,\hfill \\ a^{*}r+b^{*},\hfill & m<r\le d,\hfill \\ 0,\hfill & d<r\le 1.\hfill \end{array}\right.\hfill \end{array}$$

Figure 1. The graph of $f^{*}$ ($0<\alpha <\frac{17-4\sqrt{10}}{12}$).

Since $a^{*}m+b^{*}=\frac{1}{2}$ and $a^{*}d+b^{*}=0$, $b^{*}=-a^{*}m+\frac{1}{2}$ and $d=m-\frac{1}{2a^{*}}$. Hence,

$$\begin{array}{c}{f}^{*}\left(r\right)=\left\{\begin{array}{cc}\frac{1}{2}{a}^{*}(r-m)+\frac{1}{2},\hfill & \mathrm{if}0\le r\le m,\hfill \\ a^{*}(r-m)+\frac{1}{2},\hfill & m<r\le m-\frac{1}{2a^{*}},\hfill \\ 0,\hfill & m-\frac{1}{2a^{*}}<r\le 1.\hfill \end{array}\right.\hfill \end{array}$$

From (6),

$$\begin{array}{ccc}{a}^{*}\hfill & =& \frac{2m-4-\sqrt{2m^2-16m+16}}{2m^2},\hfill \\ \alpha \hfill & =& -\frac{4m^3{a^{*}}^3-12m^2{a^{*}}^2+6m{a}^{*}-1}{48{a^{*}}^2}\hfill \end{array}$$

hold. In addition, since $a^{*}<0$ and $f^{*}\left(1\right)<0$,

$$0<m<4-\sqrt{10},0<\alpha <\frac{17-4\sqrt{10}}{12}.$$

Case (2) (See Figure 2) There exists $m\in [0,1]$ such that

$$\begin{array}{c}{f}^{*}\left(r\right)=\left\{\begin{array}{cc}\frac{1}{2}(a^{*}r+b^{*})+\frac{1}{4},\hfill & \mathrm{if}0\le r\le m,\hfill \\ a^{*}r+b^{*},\hfill & m<r\le 1.\hfill \end{array}\right.\hfill \end{array}$$

Figure 2. The graph $f^{*}$ ($\frac{17-4\sqrt{10}}{12}\le \alpha \le \frac{5}{12}$).

Since $a^{*}m+b^{*}=\frac{1}{2}$,

$$\begin{array}{c}{f}^{*}\left(r\right)=\left\{\begin{array}{cc}\frac{1}{2}{a}^{*}(r-m)+\frac{1}{2},\hfill & \mathrm{if}0\le r\le m,\hfill \\ a^{*}(r-m)+\frac{1}{2},\hfill & m<r\le 1.\hfill \end{array}\right.\hfill \end{array}$$

From (6),

$$\begin{array}{ccc}{a}^{*}\hfill & =& \frac{2}{m^2-4m+2},\hfill \\ \alpha \hfill & =& \frac{2m^3+3m^2-24m+14}{12(m^2-4m+2)}\hfill \end{array}$$

hold. In addition, since $a^{*}<0$ and $f^{*}\left(1\right)\ge 0$,

$$4-\sqrt{10}\le m\le 1,\frac{17-4\sqrt{10}}{12}\le \alpha \le \frac{5}{12}.$$

Case (3) (See Figure 3) For all $0\le r\le 1$,

$$\begin{array}{c}{f}^{*}\left(r\right)=\frac{1}{2}(a^{*}r+b^{*})+\frac{1}{4}.\hfill \end{array}$$

Figure 3. The graph $f^{*}$ ($\frac{5}{12}<\alpha \le \frac{1}{2}$).

From (6),

$$\begin{array}{ccc}{a}^{*}\hfill & =& -12+24\alpha ,\hfill \\ b^{*}\hfill & =& \frac{15}{2}-12\alpha \hfill \end{array}$$

hold. In addition, since $a^{*}\le 0$ and $f^{*}\left(1\right)>\frac{1}{2}$, $\frac{5}{12}<\alpha \le \frac{1}{2}$.

6. Conclusions

In this paper, we examined the general minimax model for the RIM quantifier problem for the case in which the generating functions are absolutely continuous and a generalized solution to the general minimum model for the RIM quantifier problem for the case in which the generating functions are Lebesgue integrable. In addition, we provided a solution equivalent relationship between the general maximum model and the general minimax model for RIM quantifier problems and generalizes results of Hong based on these results. We also corrected Liu’s theorems from a mathematical perspective as their theorems are not suitable for absolutely continuous generating functions.