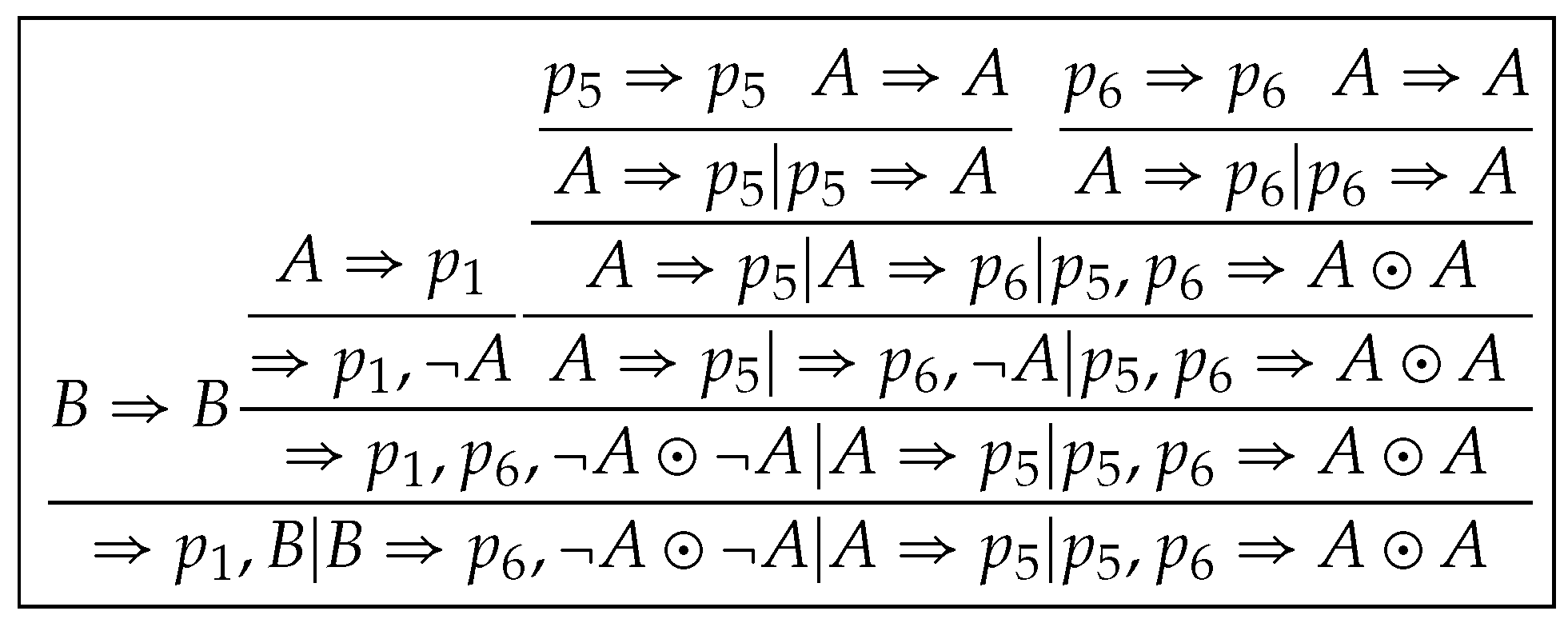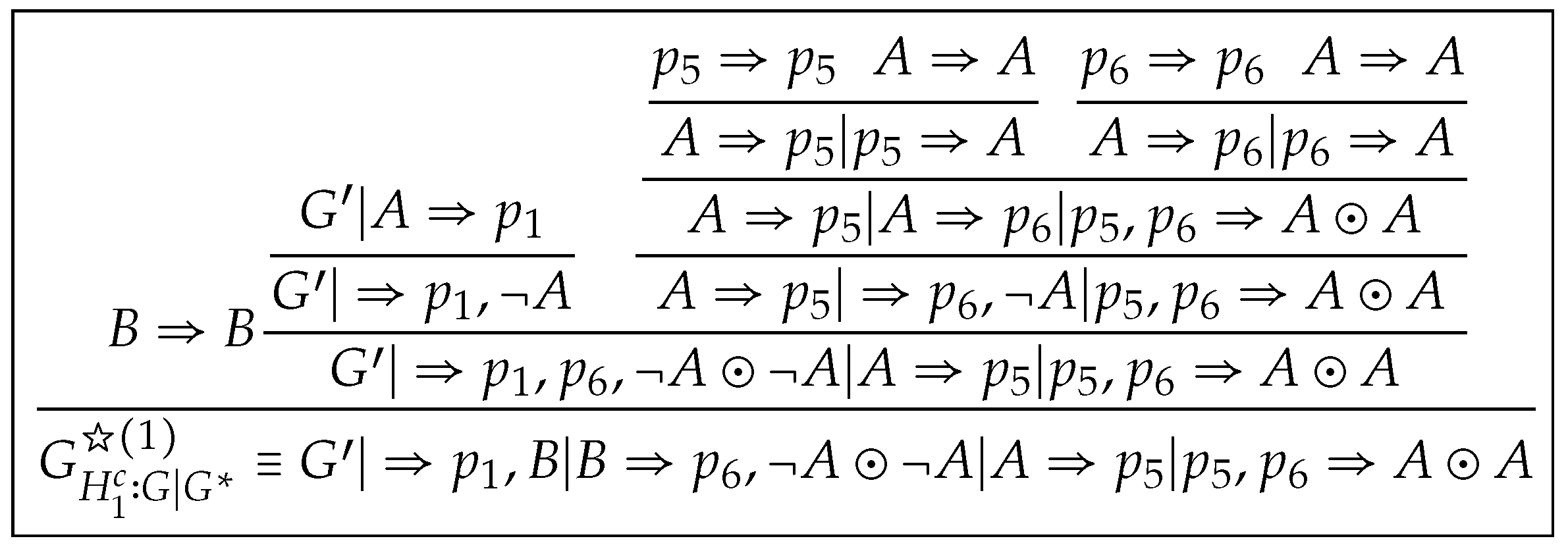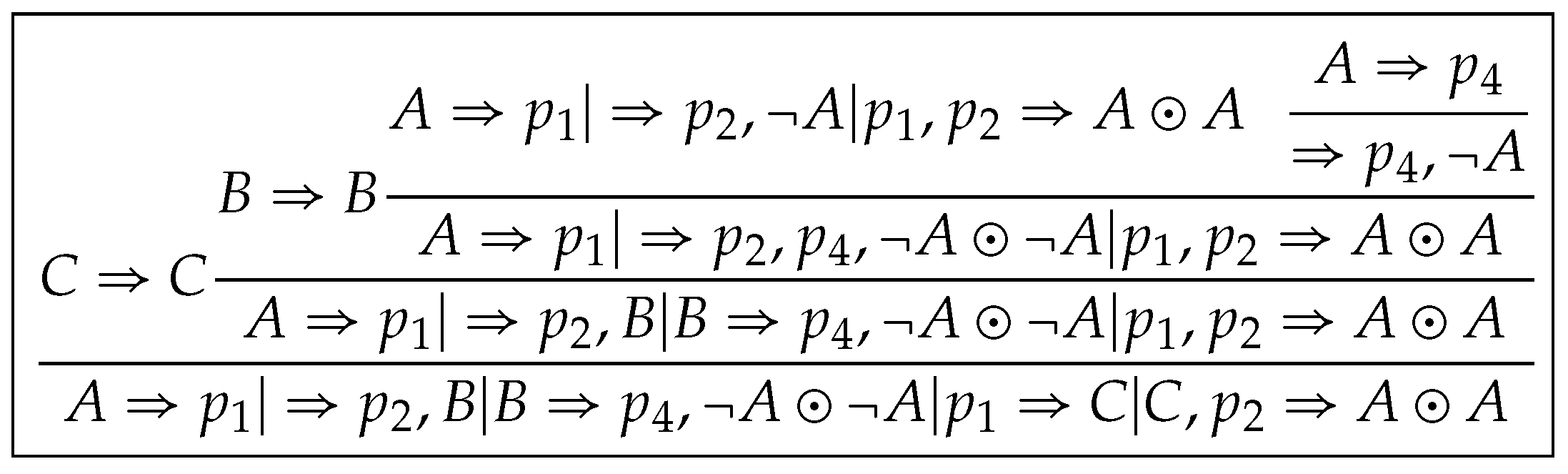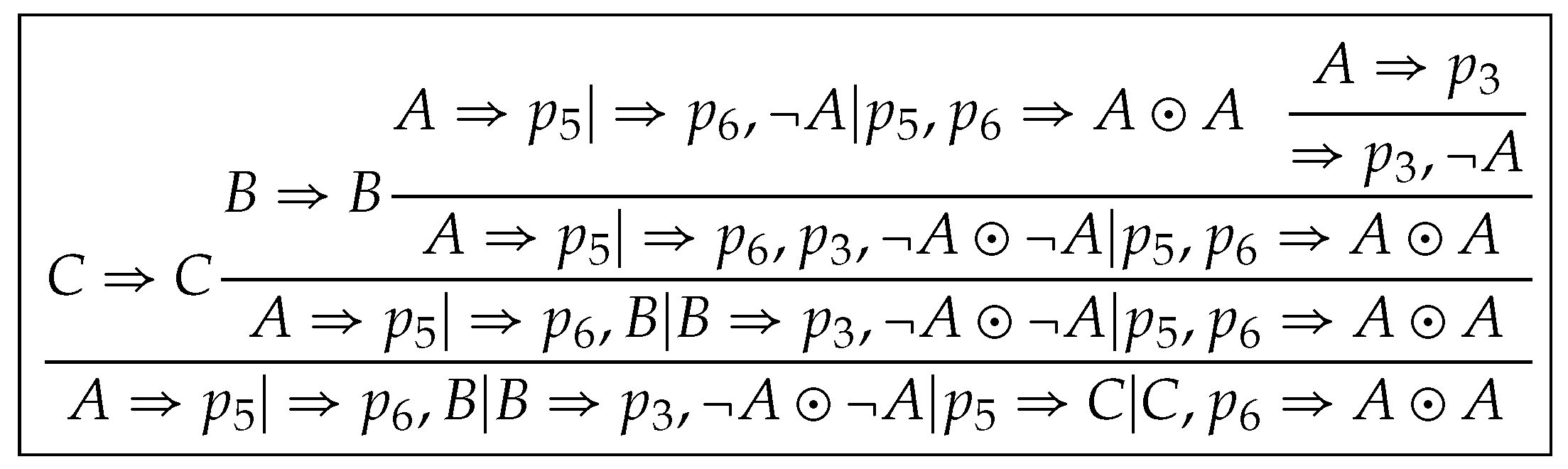A Proof of the Standard Completeness for the Involutive Uninorm Logic

Abstract

In this paper, we solve a long-standing open problem in the field of fuzzy logics, that is, the standard completeness for the involutive uninorm logic IUL. In fact, we present a uniform method of density elimination for several semilinear substructural logics. Especially, the density elimination for IUL is proved. Then the standard completeness for IUL follows as a lemma by virtue of previous work by Metcalfe and Montagna.

1. Introduction

The problem of the completeness of Łukasiewicz infinite-valued logic (Ł, for short) was posed by Łukasiewicz and Tarski in the 1930s. It was twenty-eight years later that it was syntactically solved by Rose and Rosser [1]. Chang [2] developed at almost the same time a theory of algebraic systems for Ł, which are called MV-algebras, with an attempt to make MV-algebras correspond to Ł as Boolean algebras to the classical two-valued logic. Chang [3] subsequently finished another proof for the completeness of Ł by virtue of his MV-algebras.

It was Chang who observed that the key role in the structure theory of MV-algebras is not locally finite MV-algebras but linearly ordered ones. The observation was formalized by Hájek [4] who showed the completeness for his basic fuzzy logic (BL for short) with respect to linearly ordered BL-algebras. Starting with the structure of BL-algebras, Hájek [5] reduced the problem of the standard completeness of BL to two formulas to be provable in BL. Here and thereafter, by the standard completeness we mean that logics are complete with respect to algebras with lattice reduct [0, 1]. Cignoli et al. [6] subsequently proved the standard completeness of BL, i.e., BL is the logic of continuous t-norms and their residua.

Hajek’s approach toward fuzzy logic has been extended by Esteva and Godo in [7], where the authors introduced the logic MTL which aims at capturing the tautologies of left-continuous t-norms and their residua. The standard completeness of MTL was proved by Jenei and Montagna in [8], where the major step is to embed linearly ordered MTL-algebras into the dense ones under the situation that the structure of MTL-algebras have been unknown as of yet.

Esteva and Godo’s work was further promoted by Metcalfe and Montagna [9] who introduced the uninorm logic UL and involutive uninorm logic (IUL) which aims at capturing tautologies of left-continuous uninorms and their residua and those of involutive left-continuous ones, respectively. Recently, Cintula and Noguera [10] introduced semilinear substructural logics which are substructural logics complete with respect to linearly ordered models. Almost all well-known families of fuzzy logics such as Ł, BL, MTL, UL and IUL belong to the class of semilinear substructural logics.

Metcalfe and Montagna’s method to prove standard completeness for UL and its extensions is of proof theory in nature and consists of two key steps. Firstly, they extended UL with the density rule of Takeuti and Titani [11]:

$$\frac{\mathsf{\Gamma }⊢(A\to p)\vee (p\to B)\vee C}{\mathsf{\Gamma }⊢(A\to B)\vee C}(D),$$

where p does not occur in $\mathsf{\Gamma },A,B$ or C, and then prove the logics with $(D)$ are complete with respect to algebras with lattice reduct [0, 1]. Secondly, they give a syntactic elimination of $(D)$ that was formulated as a rule of the corresponding hypersequent calculus.

Hypersequents are a natural generalization of sequents which were introduced independently by Avron [12] and Pottinger [13] and have proved to be particularly suitable for logics with prelinearity [9,14]. Following the spirit of Gentzen’s cut elimination, Metcalfe and Montagna succeeded to eliminate the density rule for GUL and several extensions of GUL by induction on the height of a derivation of the premise and shifting applications of the rule upwards, but failed for GIUL and therefore left it as an open problem.

There are several relevant works about the standard completeness of IUL as follows. With an attempt to prove the standard completeness of IUL, we generalized Jenei and Montagna’s method [15] for IMTL in [16], but our effort was only partially successful. It seems that the subtle reason why it does not work for UL and IUL is the failure of the finite model property of these systems [17]. Jenei [18] constructed several classes of involutive FL${}_e$-algebras, as he said, in order to gain a better insight into the algebraic semantic of the substructural logic IUL, and also to the long-standing open problem about its standard completeness. Ciabattoni and Metcalfe [19] introduced the method of density elimination by substitutions which is applicable to a general class of (first-order) hypersequent calculi but fails in the case of GIUL.

We reconsidered Metcalfe and Montagna’s proof-theoretic method to investigate the standard completeness of IUL, because they have proved the standard completeness of UL by their method and we cannot prove such a result by the Jenei and Montagna’s model-theoretic method. In order to prove the density elimination for GUL, they prove that the following generalized density rule $({\mathcal{D}}_1)$:

$$\frac{G_0\equiv {\{{\mathsf{\Gamma }}_i,{\lambda }_{i}p\Rightarrow {\mathsf{\Delta }}_i\}}_{i=1\cdots n}|{\{{\mathsf{\Sigma }}_k,({\mu }_k+1)p\Rightarrow p\}}_{k=1\cdots o}|{\{{\mathsf{\Pi }}_j\Rightarrow p\}}_{j=1\cdots m}}{{\mathcal{D}}_1(G_0)\equiv {\{{\mathsf{\Gamma }}_i,{\lambda }_i{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_i\}}_{i=1\cdots n}^{j=1\cdots m}|{\{{\mathsf{\Sigma }}_k,{\mu }_k{\mathsf{\Pi }}_j\Rightarrow t\}}_{k=1\cdots o}^{j=1\cdots m}}({\mathcal{D}}_1)$$

is admissible for GUL, where they set two constraints to the form of $G_0$: (i) $n,m⩾1$ and ${\lambda }_i⩾1$ for some $1⩽i⩽n$; (ii) p does not occur in ${\mathsf{\Gamma }}_i$, ${\mathsf{\Delta }}_i$, ${\mathsf{\Pi }}_j$, ${\mathsf{\Sigma }}_k$ for $i=1\cdots n$, $j=1\cdots m$, $k=1\cdots o$.

We may regard $({\mathcal{D}}_1)$ as a procedure whose input and output are the premise and conclusion of $({\mathcal{D}}_1)$, respectively. We denote the conclusion of $({\mathcal{D}}_1)$ by ${\mathcal{D}}_1(G_0)$ when its premise is $G_0$. Observe that Metcalfe and Montagna had succeeded in defining the suitable conclusion for an almost arbitrary premise in $({\mathcal{D}}_1)$, but it seems impossible for GIUL (see Section 3 for an example). We then define the following generalized density rule $({\mathcal{D}}_0)$ for

$$\mathbf{GL}\in \{\mathbf{GUL},\mathbf{GIUL},\mathbf{GMTL},\mathbf{GIMTL}\}$$

and prove its admissibility in Section 9.

Theorem 1 (Main theorem).

Let $n,m⩾1$, p does not occur in $G^{\prime },{\mathsf{\Gamma }}_i,{\mathsf{\Delta }}_i,{\mathsf{\Pi }}_j$ or ${\mathsf{\Sigma }}_j$ for all $1⩽i⩽n$,$1⩽j⩽m$. Then the strong density rule

$$\frac{G_0\equiv G^{\prime }|{\left\{{\mathsf{\Gamma }}_i,p\Rightarrow {\mathsf{\Delta }}_i\right\}}_{i=1\cdots n}|{\left\{{\mathsf{\Pi }}_j\Rightarrow p,{\mathsf{\Sigma }}_j\right\}}_{j=1\cdots m}}{{\mathcal{D}}_0\left(G_0\right)\equiv G^{\prime }|\{{\mathsf{\Gamma }}_i,{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_i,{\mathsf{\Sigma }}_j\}{}_{i=1\cdots n;j=1\cdots m}}({\mathcal{D}}_0)$$

is admissible in $\mathbf{GL}$.

In proving the admissibility of $({\mathcal{D}}_1)$, Metcalfe and Montagna made some restriction on the proof $\tau$ of $G_0$, i.e., converted $\tau$ into an r-proof. The reason why they need an r-proof is that they set the constraint (i) to $G_0$. We may imagine the restriction on $\tau$ and the constraints to $G_0$ as two pallets of a balance, i.e., one is strong if another is weak and vice versa. Observe that we select the weakest form of $G_0$ in $({\mathcal{D}}_0)$ that guarantees the validity of $(D)$. Then it is natural that we need make the strongest restriction on the proof $\tau$ of $G_0$. But it seems extremely difficult to follow such a way to prove the admissibility of $({\mathcal{D}}_0)$.

In order to overcome such a difficulty, we first of all choose Avron-style hypersequent calculi as the underlying systems (see Appendix A.1). Let $\tau$ be a cut-free proof of $G_0$ in $\mathbf{GL}$. Starting with $\tau$, we construct a proof ${\tau }^{*}$ of $G|G^{*}$ in a restricted subsystem ${\mathbf{GL}}_{\mathsf{\Omega }}$ of $\mathbf{GL}$ by a systematic novel manipulations in Section 4. Roughly speaking, each sequent of G is a copy of some sequent of $G_0$, and each sequent of $G^{*}$ is a copy of some contraction sequent in $\tau$. In Section 5, we define the generalized density rule $(\mathcal{D})$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$ and prove that it is admissible.

Now, starting with $G|G^{*}$ and its proof ${\tau }^{*}$, we construct a proof ${\tau }^{☆}$ of $G^{☆}$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$ such that each sequent of $G^{☆}$ is a copy of some sequent of G. Then ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}\mathcal{D}(G^{☆})$ by the admissibility of $(\mathcal{D})$. Then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$ by Lemma 29. Hence the density elimination theorem holds in $\mathbf{GL}$. Especially, the standard completeness of IUL follows from Theorem 62 of [9].

$G^{☆}$ is constructed by eliminating $(pEC)$-sequents in $G|G^{*}$ one by one. In order to control the process, we introduce the set $I=\{H_{i_1}^c,\cdots ,H_{i_m}^c\}$ of $(pEC)$-nodes of ${\tau }^{*}$ and the set $\mathbf{I}$ of the branches relative to I and construct $G_{\mathbf{I}}^{☆}$ such that $G_{\mathbf{I}}^{☆}$ does not contain $(pEC)$-sequents lower than any node in I, i.e., $S_j^c\in G_{\mathbf{I}}^{☆}$ implies $H_j^c||H_i^c$ for all $H_i^c\in I$. The procedure is called the separation algorithm of branches in which we introduce another novel manipulation and call it derivation-grafting operation in Section 7 and Section 8.

2. Preliminaries

In this section, we recall the basic definitions and results involved, which are mainly from [9]. Substructural fuzzy logics are based on a countable propositional language with formulas built inductively as usual from a set of propositional variables VAR, binary connectives $\odot ,\to ,\wedge ,\vee ,$ and constants $\perp ,\top ,t,f$ with definable connective $\neg A:=A\to f.$

Definition 1.

([9,12]) A sequent is an ordered pair $(\mathsf{\Gamma },\mathsf{\Delta })$ of finite multisets (possibly empty) of formulas, which we denote by $\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }$. Γ and Δ are called the antecedent and succedents, respectively, of the sequent and each formula in Γ and Δ is called a sequent-formula. A hypersequent G is a finite multiset of the form ${\mathsf{\Gamma }}_1\Rightarrow {\mathsf{\Delta }}_1|\cdots |{\mathsf{\Gamma }}_n\Rightarrow {\mathsf{\Delta }}_n$, where each ${\mathsf{\Gamma }}_i\Rightarrow {\mathsf{\Delta }}_i$ is a sequent and is called a component of G for each $1⩽i⩽n$. If ${\mathsf{\Delta }}_i$ contains at most one formula for $i=1\cdots n$, then the hypersequent is single-conclusion, otherwise it is a multiple-conclusion.

Definition 2.

Let S be a sequent and $G=S_1|\cdots |S_m$ a hypersequent. We say that $S\in G$ if S is one of $S_1,\cdots ,S_m$.

Notation 1.

Let $G_1$ and $G_2$ be two hypersequents. We will assume from now on that all set terminology refers to multisets, adopting the conventions of writing $\mathsf{\Gamma },\mathsf{\Delta }$ for the multiset union of Γ and Δ, A for the singleton multiset $\{A\}$, and $\lambda \mathsf{\Gamma }$ for the multiset union of λ copies of Γ for $\lambda \in \mathbf{N}$. By $G_1\subseteq G_2$ we mean that $S\in G_2$ for all $S\in G_1$ and the multiplicity of S in $G_1$ is not more than that of S in $G_2$. We will use $G_1=G_2$, $G_1\bigcap G_2$, $G_1\bigcup G_2$, $G_1\backslash G_2$ by their standard meaning for multisets by default and we will declare when we use them for sets. We sometimes write $S_1|\cdots |S_m$ and $G|\stackrel{\stackrel{ncopies}{︷}}{S|\cdots |S}$ as $\{S_1,\cdots ,S_m\}$, $G|S^n$ (or ${G|\{S\}}^n$), respectively.

Definition 3.

([12]) A hypersequent rule is an ordered pair consisting of a sequence of hypersequents $G_1,\cdots ,G_n$ called the premises (upper hypersequents) of the rule, and a hypersequent G called the conclusion (lower hypersequent), written by $\frac{G_1\cdots G_n}{G}.$ If $n=0$, then the rule has no premise and is called an initial sequent. The single-conclusion version of a rule adds the restriction that both the premises and conclusion must be single-conclusion; otherwise the rule is multiple-conclusion.

Definition 4.

([9])GULandGIULconsist of the single-conclusion and multiple-conclusion versions of the following initial sequents and rules, respectively:

Initial sequents

$$\frac{}{A\Rightarrow A}(ID)\frac{}{\mathsf{\Gamma }\Rightarrow \top ,\mathsf{\Delta }}({\top }_r)\frac{}{\mathsf{\Gamma },\perp \Rightarrow \mathsf{\Delta }}({\perp }_l)\frac{}{\Rightarrow t}(t_r)\frac{}{f\Rightarrow }(f_l)$$

Structural rules

$$\frac{G|\mathsf{\Gamma }\Rightarrow A|\mathsf{\Gamma }\Rightarrow A}{G|\mathsf{\Gamma }\Rightarrow A}(EC)\frac{G}{G|\mathsf{\Gamma }\Rightarrow A}(EW)$$

$$\frac{G_1|{\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1\Rightarrow {\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1{G}_2|{\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2\Rightarrow {\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2}{G_1|G_2|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2\Rightarrow {\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2|{\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2\Rightarrow {\mathsf{\Sigma }}_1,{\mathsf{\Sigma }}_2}(COM)$$

Logical rules

$$\begin{array}{cc}\begin{array}{c}\hfill \frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma },t,\Rightarrow \mathsf{\Delta }}(t_l)\\ \hfill \frac{G_1|{\mathsf{\Gamma }}_1\Rightarrow A,{\mathsf{\Delta }}_1{G}_2|{\mathsf{\Gamma }}_2,B\Rightarrow {\mathsf{\Delta }}_2}{G_1|G_2|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,A\to B\Rightarrow {\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2}({\to }_l)\\ \hfill \frac{G|\mathsf{\Gamma },A,B\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma },A\odot B\Rightarrow \mathsf{\Delta }}({\odot }_l)\\ \hfill \frac{G|\mathsf{\Gamma },A\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma },A\wedge B\Rightarrow \mathsf{\Delta }}({\wedge }_{lr})\\ \hfill \frac{G_1|\mathsf{\Gamma }\Rightarrow A,\mathsf{\Delta }{G}_2|\mathsf{\Gamma }\Rightarrow B,\mathsf{\Delta }}{G_1|G_2|\mathsf{\Gamma }\Rightarrow A\wedge B,\mathsf{\Delta }}({\wedge }_r)\\ \hfill \frac{G|\mathsf{\Gamma }\Rightarrow B,\mathsf{\Delta }}{G|\mathsf{\Gamma }\Rightarrow A\vee B,\mathsf{\Delta }}({\vee }_{rl})\end{array}& \begin{array}{c}\hfill \frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma }\Rightarrow f,\mathsf{\Delta }}(f_r)\\ \hfill \frac{G|\mathsf{\Gamma },A\Rightarrow B,\mathsf{\Delta }}{G|\mathsf{\Gamma }\Rightarrow A\to B,\mathsf{\Delta }}({\to }_r)\\ \hfill \frac{G_1|{\mathsf{\Gamma }}_1\Rightarrow A,{\mathsf{\Delta }}_1{G}_2|{\mathsf{\Gamma }}_2\Rightarrow B,{\mathsf{\Delta }}_2}{G_1|G_2|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2\Rightarrow A\odot B,{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2}({\odot }_r)\\ \hfill \frac{G|\mathsf{\Gamma },B\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma },A\wedge B\Rightarrow \mathsf{\Delta }}({\wedge }_{ll})\\ \hfill \frac{G|\mathsf{\Gamma }\Rightarrow A,\mathsf{\Delta }}{G|\mathsf{\Gamma }\Rightarrow A\vee B,\mathsf{\Delta }}({\vee }_{rr})\\ \hfill \frac{G_1|\mathsf{\Gamma },A\Rightarrow \mathsf{\Delta }{G}_2|\mathsf{\Gamma },B\Rightarrow \mathsf{\Delta }}{G_1|G_2|\mathsf{\Gamma },A\vee B\Rightarrow \mathsf{\Delta }}({\vee }_l)\end{array}\end{array}$$

Cut rule

$$\frac{G_1|{\mathsf{\Gamma }}_1,A\Rightarrow {\mathsf{\Delta }}_1{G}_2|{\mathsf{\Gamma }}_2\Rightarrow A,{\mathsf{\Delta }}_2}{G_1|G_2|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2\Rightarrow {\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2}(CUT)$$

Definition 5.

([9])GMTLandGIMTLareGULandGIULplus the single conclusion and multiple-conclusion versions, respectively, of:

$$\frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma },A\Rightarrow \mathsf{\Delta }}(WL),\frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma }\Rightarrow A,\mathsf{\Delta }}(WR).$$

Definition 6.

(i) $(I)\in \{(t_l),(f_r),({\to }_r),({\odot }_l),({\wedge }_{lr}),({\wedge }_{ll}),({\vee }_{rr}),({\vee }_{rl}),(WL),(WR)\}$ and

$(II)\in \{({\to }_l),({\odot }_r),({\wedge }_r),({\vee }_l),(COM)\}$;

(ii) By $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{G^{\prime }|G^{″}|H^{\prime }}(II)$ (or $\frac{G^{\prime }|S^{\prime }}{G^{\prime }|H^{\prime }}(I))$ we denote an instance of a two-premise rule $(II)$ (or one-premise rule $(I)$) of $\mathbf{GL}$, where $S^{\prime }$ and $S^{″}$ are its focus sequents and $H^{\prime }$ is its principle sequent (for $({\to }_l)$, $({\odot }_r)$, $({\wedge }_r)$ and $({\vee }_l))$ or hypersequent (for $(COM)$, $({\wedge }_{rw})$ and $({\vee }_{lw})$, see Definition 12).

Definition 7.

([9]) ${\mathbf{GL}}^{\mathrm{D}}$ is $\mathbf{GL}$ extended with the following density rule:

$$\frac{G|{\mathsf{\Gamma }}_1,p\Rightarrow {\mathsf{\Delta }}_1|{\mathsf{\Gamma }}_2\Rightarrow p,{\mathsf{\Delta }}_2}{G|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2\Rightarrow {\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2}(D)$$

where p does not occur in $G,{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,{\mathsf{\Delta }}_1$ or ${\mathsf{\Delta }}_2$.

Definition 8.

([12]) A derivation τ of a hypersequent G from hypersequents $G_1,\cdots ,G_n$ in a hypersequent calculus $\mathbf{GL}$ is a labeled tree with the root labeled by G, leaves labeled initial sequents or some $G_1,\cdots ,G_n$, and for each node labeled $G_0^{\prime }$ with parent nodes labeled $G_1^{\prime },\cdots ,G_m^{\prime }$ (where possibly $m=0)$, $\frac{G_1^{\prime }\cdots G_m^{\prime }}{G_0^{\prime }}$ is an instance of a rule of $\mathbf{GL}$.

Notation 2.

(i) $\frac{\underline{G_1\cdots G_n}}{G_0}⟨\tau ⟩$ denotes that τ is a derivation of $G_0$ from $G_1,\cdots ,G_n$;

(ii) Let H be a hypersequent. $H\in \tau$ denotes that H is a node of τ. We call H a leaf hypersequent if H is a leaf of τ, the root hypersequent if it is the root of τ. $\frac{G_1^{\prime }\cdots G_m^{\prime }}{G_0^{\prime }}\in \tau$ denotes that $G_0^{\prime }\in \tau$ and its parent nodes are $G_1^{\prime },\cdots ,G_m^{\prime }$;

(iii) Let $H\in \tau$ then $\tau (H)$ denotes the subtree of τ rooted at H;

(iv) τ determines a partial order ${⩽}_{\tau }$ with the root as the least element. $H_1\parallel H_2$ denotes $H_1{\nleqq }_{\tau }{H}_2$ and $H_2{\nleqq }_{\tau }{H}_1$ for any $H_1,H_2\in \tau$. By $H_1{=}_{\tau }{H}_2$ we mean that $H_1$ is the same node as $H_2$ in τ. We sometimes write ${⩽}_{\tau }$ as ⩽;

(v) An inference of the form $\frac{G^{\prime }|S^n}{G^{\prime }|S}\in \tau$ is called the full external contraction and denoted by $(E{C}^{*})$, if $n⩾2$, $G^{\prime }|S^n$ is not a lower hypersequent of an application of $(EC)$ whose contraction sequent is S, and $G^{\prime }|S$ not an upper one in τ.

Definition 9.

Let τ be a derivation of G and $H\in \tau$. The thread $T{h}_{\tau }(H)$ of τ at H is a sequence $H_0,\cdots ,H_n$ of node hypersequents of τ such that $H_0{=}_{\tau }H$, $H_n{=}_{\tau }G$, $\frac{H_k}{H_{k+1}}\in \tau$ or there exists $G^{\prime }\in \tau$ such that $\frac{H_k{G}^{\prime }}{H_{k+1}}$ or $\frac{G^{\prime }{H}_k}{H_{k+1}}$ in τ for all $0⩽k⩽n-1$.

Proposition 1.

Let $H_1,H_2\in \tau$. Then

(i) $H_1⩽H_2$ if and only if $H_1\in T{h}_{\tau }(H_2)$;

(ii) $H_1\parallel H_2$ and $H_1⩽H_3$ imply $H_2\parallel H_3$;

(iii) $H_1⩽H_3$ and $H_2⩽H_3$ imply $H_1\nparallel H_2$.

We need the following definition to give each node of $\tau$ an identification number, which is used in Construction 3 to differentiate sequents in a hypersequent in a proof.

Definition 10.

(Appendix A.5.2) Let $H\in \tau$ and $Th(H)=(H_0,\cdots ,H_n)$. Let $b_n:=1$,

$$b_k:=\left\{\begin{array}{c}1\mathrm{if}\frac{G^{\prime }{H}_k}{H_{k+1}}\in \tau ,\hfill \\ 0\mathrm{if}\frac{H_k}{H_{k+1}}\in \tau \mathrm{or}\frac{H_k{G}^{\prime }}{H_{k+1}}\in \tau \hfill \end{array}\right.$$

for all $0⩽k⩽n-1$. Then $\mathcal{P}(H):={\sum }_{k=0}^{k=n}{2}^k{b}_k$ and call it the position of H in τ.

Definition 11.

A rule is admissible for a calculusGLif whenever its premises are derivable inGL, then so is its conclusion.

Lemma 1.

([9]) Cut-elimination holds for $\mathbf{GL}$, i.e., proofs using $(CUT)$ can be transformed syntactically into proofs not using $(CUT)$.

3. Proof of the Main Theorem: A Computational Example

In this section, we present an example to illustrate the proof of the main theorem.

Let $G_0\equiv \Rightarrow p,B|B\Rightarrow p,\neg A\odot \neg A|p\Rightarrow C|C,p\Rightarrow A\odot A$. $G_0$ is a theorem of $\mathbf{IUL}$ and a cut-free proof $\tau$ of $G_0$ is shown in Figure 1, where we use an additional rule $\frac{\mathsf{\Gamma },A\Rightarrow \mathsf{\Delta }}{\mathsf{\Gamma }\Rightarrow \neg A,\mathsf{\Delta }}({\neg }_r)$ for simplicity. Note that we denote three applications of $(EC)$ in $\tau$ respectively by ${(EC)}_1,{(EC)}_2,{(EC)}_3$ and three $({\odot }_r)$ by ${({\odot }_r)}_1,{({\odot }_r)}_2$ and ${({\odot }_r)}_3$.

Figure 1. A proof $\tau$ of $G_0$.

By applying (D) to free combinations of all sequents in $\Rightarrow p,B|B\Rightarrow p,\neg A\odot \neg A$ and in $p\Rightarrow C|C,p\Rightarrow A\odot A$, we get that $H_0\equiv \Rightarrow B,C|C\Rightarrow A\odot A,B|B\Rightarrow C,\neg A\odot \neg A|C,B\Rightarrow A\odot A,\neg A\odot \neg A$. $H_0$ is a theorem of $\mathbf{IUL}$ and a cut-free proof $\rho$ of $H_0$ is shown in Figure 2. It supports the validity of the generalized density rule $({\mathcal{D}}_0)$ in Section 1, as an instance of $({\mathcal{D}}_0)$.

Figure 2. A proof $\rho$ of $H_0$.

Our task is to construct $\rho$, starting from $\tau$. The tree structure of $\rho$ is more complicated than that of $\tau$. Compared with UL, MTL and IMTL, there is no one-to-one correspondence between nodes in $\tau$ and $\rho$.

Following the method given by G. Metcalfe and F. Montagna, we need to define a generalized density rule for IUL. We denote such an expected unknown rule by $({\mathcal{D}}_x)$ for convenience. Then ${\mathcal{D}}_x(H)$ must be definable for all $H\in \tau$. Naturally,

$${\mathcal{D}}_x(p\Rightarrow p)=\Rightarrow t;$$

$${\mathcal{D}}_x(A\Rightarrow p|p\Rightarrow A)=A\Rightarrow A;$$

$${\mathcal{D}}_x(\Rightarrow p,\neg A|p,p\Rightarrow A\odot A)=\Rightarrow \neg A,\neg A,A\odot A;$$

$${\mathcal{D}}_x(\Rightarrow p,B|B\Rightarrow p,\neg A\odot \neg A|p,p\Rightarrow A\odot A)=$$

$$\Rightarrow B,B,A\odot A|B,B\Rightarrow A\odot A,\neg A\odot \neg A,\neg A\odot \neg A|B\Rightarrow A\odot A,B,\neg A\odot \neg A;$$

$${\mathcal{D}}_x(G_0)={\mathcal{D}}_0(G_0)=H_0.$$

However, we could not find a suitable way to define ${\mathcal{D}}_x(H_{\times \times })$ and ${\mathcal{D}}_x(H_{\times })$ for $H_{\times \times }$ and $H_{\times }$ in $\tau$, see Figure 1. This is the biggest difficulty we encounter in the case of $\mathbf{IUL}$ such that it is hard to prove density elimination for IUL. A possible way is to define ${\mathcal{D}}_x(\Rightarrow p,p,\neg A\odot \neg A|p,p\Rightarrow A\odot A)$ as $\Rightarrow t,A\odot A,\neg A\odot \neg A$. Unfortunately, it is not a theorem of $\mathbf{IUL}$.

Notice that two upper hypersequents $\Rightarrow p,\neg A|p,p\Rightarrow A\odot A$ of ${({\odot }_r)}_3$ are permissible inputs of $({\mathcal{D}}_x)$. Why is $H_{\times \times }$ an invalid input? One reason is that, two applications ${(EC)}_1$ and ${(EC)}_2$ cut off two sequents $A\Rightarrow p$ such that two $p^{\prime }s$ disappear in all nodes lower than upper hypersequent of ${(EC)}_1$ or ${(EC)}_2$, including $H_{\times \times }$. These make occurrences of $p^{\prime }s$ to be incomplete in $H_{\times \times }$. We then perform the following operation in order to get complete occurrences of $p^{\prime }s$ in $H_{\times \times }$.

Step 1 (preprocessing of $\tau$). Firstly, we replace H with $H|S^{\prime }$ for all $\frac{G^{\prime }|S^{\prime }|S^{\prime }}{G^{\prime }|S^{\prime }}{(EC)}_k\in \tau$, $H⩽G^{\prime }|S^{\prime }$ then replace $\frac{G^{\prime }|S^{\prime }|S^{\prime }}{G^{\prime }|S^{\prime }|S^{\prime }}{(EC)}_k$ with $G^{\prime }|S^{\prime }|S^{\prime }$ for all $k=1,2,3$. Then we construct a proof without $(EC)$, which we denote by ${\tau }_1$, as shown in Figure 3. We call such manipulations sequent-inserting operations, which eliminate applications of $(EC)$ in $\tau$.

Figure 3. A proof ${\tau }_1$.

However, we also cannot define ${\mathcal{D}}_x(H_{\times \times }^{\prime })$ for $H_{\times \times }^{\prime }\in {\tau }_1$ in that $\Rightarrow p,p,\neg A\odot \neg A|p,p\Rightarrow A\odot A\subseteq H_{\times \times }^{\prime }$. The reason is that the origins of $p^{\prime }s$ in $H_{\times \times }^{\prime }$ are indistinguishable if we regard all leaves in the form $p\Rightarrow p$ as the origins of $p^{\prime }s$ which occur in the inner node. For example, we do not know which p comes from the left subtree of ${\tau }_1(H_{\times \times }^{\prime })$ and which from the right subtree in two occurrences of $p^{\prime }s$ in $\Rightarrow p,p,\neg A\odot \neg A\in H_{\times \times }^{\prime }$. We then perform the following operation in order to make all occurrences of $p^{\prime }s$ in $H_{\times \times }^{\prime }$ distinguishable.

We assign the unique identification number to each leaf in the form $p\Rightarrow p\in {\tau }_1$ and transfer these identification numbers from leaves to the root, as shown in Figure 4. We denote the proof of $G|G^{*}$ resulting from this step by ${\tau }^{*}$, where $G\equiv \Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A$ in which each sequent is a copy of some sequent in $G_0$ and $G^{*}\equiv A\Rightarrow p_1|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A$ in which each sequent is a copy of some external contraction sequent in $(EC)$-node of $\tau$. We call such manipulations eigenvariable-labeling operations, which make us to trace eigenvariables in $\tau$.

Figure 4. A proof ${\tau }^{*}$ of $G|G^{*}$.

Then all occurrences of p in ${\tau }^{*}$ are distinguishable and we regard them as distinct eigenvariables (See Definition 18 (i)). Firstly, by selecting $p_1$ as the eigenvariable and applying $(D)$ to $G|G^{*}$, we get

$$G^{\prime }\equiv A\Rightarrow C|\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|C,p_2\Rightarrow A\odot A|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A.$$

Secondly, by selecting $p_2$ and applying $(D)$ to $G^{\prime }$, we get

$$G^{″}\equiv A\Rightarrow C|B\Rightarrow p_4,\neg A\odot \neg A|C\Rightarrow B,A\odot A|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A.$$

Repeatedly, we get

$$G^{″″}\equiv A\Rightarrow C|A,B\Rightarrow A\odot A,\neg A\odot \neg A|C\Rightarrow A\odot A,B.$$

We define such iterative applications of $(D)$ as $\mathcal{D}$-rule (See Definition 20). Lemma 10 shows that ${⊢}_{\mathbf{GIUL}}\mathcal{D}(G|G^{*})$ if ${⊢}_{\mathbf{GIUL}}G|G^{*}$. Then we obtain ${⊢}_{\mathbf{GIUL}}\mathcal{D}(G|G^{*})$, i.e., ${⊢}_{\mathbf{GIUL}}{G}^{″″}$.

A miracle happens here! The difficulty that we encountered in GIUL is overcome by converting $H_{\times \times }^{\prime }=A\Rightarrow p|\Rightarrow p,p,\neg A\odot \neg A|p,p\Rightarrow A\odot A|A\Rightarrow p|p,p\Rightarrow A\odot A$ into $A\Rightarrow p_1|\Rightarrow p_2,p_4,\neg A\odot \neg A|p_1,p_2\Rightarrow A\odot A|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A$ and using $(\mathcal{D})$ to replace $({\mathcal{D}}_x)$.

Why do we assign the unique identification number to each $p\Rightarrow p\in {\tau }_1$? We would return back to the same situation as that of ${\tau }_1$ if we assign the same indices to all $p\Rightarrow p\in {\tau }_1$ or, replace $p_3\Rightarrow p_3$ and $p_4\Rightarrow p_4$ by $p_2\Rightarrow p_2$ in ${\tau }^{*}$.

Note that $\mathcal{D}(G|G^{*})=H_1$. So we have built up a one-one correspondence between the proof ${\tau }^{*}$ of $G|G^{*}$ and that of $H_1$. Observe that each sequent in $G^{*}$ is not a copy of any sequent in $G_0$. In the following steps, we work on eliminating these sequents in $G^{*}$.

Step 2 (extraction of elimination rules). We select $A\Rightarrow p_2$ as the focus sequent in $H_1^c$ in ${\tau }^{*}$ and keep $A\Rightarrow p_1$ unchanged from $H_1^c$ downward to $G|G^{*}$ (See Figure 4). So we extract a derivation from $A\Rightarrow p_2$ by pruning some sequents (or hypersequents) in ${\tau }^{*}$, which we denote by ${\tau }_{H_1^c:A\Rightarrow p_2}^{*}$, as shown in Figure 5.

Figure 5. A derivation ${\tau }_{H_1^c:A\Rightarrow p_2}^{*}$ from $A\Rightarrow p_2$.

A derivation ${\tau }_{H_1^c:A\Rightarrow p_1}^{*}$ from $A\Rightarrow p_1$ is constructed by replacing $p_2$ with $p_1$, $p_3$ with $p_5$ and $p_4$ with $p_6$ in ${\tau }_{H_1^c:A\Rightarrow p_2}^{*}$, as shown in Figure 6. Notice that we assign new identification numbers to new occurrences of p in ${\tau }_{H_1^c:A\Rightarrow p_1}^{*}$.

Figure 6. A derivation ${\tau }_{H_1^c:A\Rightarrow p_1}^{*}$ from $A\Rightarrow p_1$.

Next, we apply ${\tau }_{H_1^c:A\Rightarrow p_1}^{*}$ to $A\Rightarrow p_1$ in $G|G^{*}$. Then we construct a proof ${\tau }_{H_1^c:G|G^{*}}^{☆(1)}$, as shown in Figure 7, where $G^{\prime }\equiv G|G^{*}\backslash \{A\Rightarrow p_1\}$.

Figure 7. A proof ${\tau }_{H_1^c:G|G^{*}}^{☆(1)}$ of $G_{H_1^c:G|G^{*}}^{☆(1)}$.

However, $G_{H_1^c:G|G^{*}}^{☆(1)}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A|\Rightarrow p_1,B|B\Rightarrow p_6,\neg A\odot \neg A|A\Rightarrow p_5|p_5,p_6\Rightarrow A\odot A$ contains more copies of sequents from $G^{*}$ and seems more complex than $G|G^{*}$. We will present a unified method to tackle with it in the following steps. Other derivations are shown in Figure 8, Figure 9, Figure 10 and Figure 11.

Figure 8. A derivation ${\tau }_{H_2^c:A\Rightarrow p_4}^{*}$ from $A\Rightarrow p_4$.

Figure 9. A derivation ${\tau }_{H_2^c:A\Rightarrow p_3}^{*}$ from $A\Rightarrow p_3$.

Figure 10. ${\tau }_{\{H_1^c:A\Rightarrow p_2,H_2^c:A\Rightarrow p_4\}}^{*}$ and ${\tau }_{\{H_1^c:A\Rightarrow p_5,H_2^c:A\Rightarrow p_3\}}^{*}$

Figure 11. ${\tau }_{H_3^c:p_1,p_2\Rightarrow A\odot A}^{*}$, ${\tau }_{H_3^c:p_3,p_4\Rightarrow A\odot A}^{*}$ and ${\tau }_{H_3^c:p_5,p_6\Rightarrow A\odot A}^{*}$.

Step 3 (separation of one branch). A proof ${\tau }_{H_1^c:G|G^{*}}^{☆(2)}$ is constructed by applying sequentially

$${\tau }_{H_3^c:p_3,p_4\Rightarrow A\odot A}^{*},{\tau }_{H_3^c:p_5,p_6\Rightarrow A\odot A}^{*}$$

to $p_3,p_4\Rightarrow A\odot A$ and $p_5,p_6\Rightarrow A\odot A$ in $G_{H_1^c:G|G^{*}}^{☆(1)}$, as shown in Figure 12, where $G^{″}\equiv G_{H_1^c:G|G^{*}}^{☆(1)}\backslash \{p_3,p_4\Rightarrow A\odot A,p_5,p_6\Rightarrow A\odot A\}$

$$G_{H_1^c:G|G^{*}}^{☆(2)}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|A\Rightarrow p_3|\Rightarrow p_1,B|$$

$$B\Rightarrow p_6,\neg A\odot \neg A|A\Rightarrow p_5|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A|p_5\Rightarrow C|C,p_6\Rightarrow A\odot A.$$

Figure 12. A proof ${\tau }_{H_1^c:G|G^{*}}^{☆(2)}$ of $G_{H_1^c:G|G^{*}}^{☆(2)}$.

Notice that

$$\begin{array}{l}\mathcal{D}(B\Rightarrow p_4,\neg A\odot \neg A|A\Rightarrow p_3|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A)\\ =\mathcal{D}(B\Rightarrow p_6,\neg A\odot \neg A|A\Rightarrow p_5|p_5\Rightarrow C|C,p_6\Rightarrow A\odot A)\hfill \\ =A\Rightarrow C|C,B\Rightarrow A\odot A,\neg A\odot \neg A.\hfill \end{array}$$

Then it is permissible to cut off the part

$$B\Rightarrow p_6,\neg A\odot \neg A|A\Rightarrow p_5|p_5\Rightarrow C|C,p_6\Rightarrow A\odot A$$

of $G_{H_1^c:G|G^{*}}^{☆(2)}$, which corresponds to applying $(EC)$ to $\mathcal{D}(G_{H_1^c:G|G^{*}}^{☆(2)})$. We regard such a manipulation as a constrained contraction rule applied to $G_{H_1^c:G|G^{*}}^{☆(2)}$ and denote it by $(E{C}_{\mathsf{\Omega }})$. Define $G_{H_1^c:G|G^{*}}^{☆}$ to be

$$\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|$$

$$A\Rightarrow p_3|\Rightarrow p_1,B|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A.$$

Then we construct a proof of $G_{H_1^c:G|G^{*}}^{☆}$ by $\frac{G_{H_1^c:G|G^{*}}^{☆(2)}}{G_{H_1^c:G|G^{*}}^{☆}}(E{C}_{\mathsf{\Omega }})$, which guarantees the validity of

$${⊢}_{\mathbf{GIUL}}\mathcal{D}(G_{H_1^c:G|G^{*}}^{☆})$$

under the condition

$${⊢}_{\mathbf{GIUL}}\mathcal{D}(G_{H_1^c:G|G^{*}}^{☆(2)}).$$

A change happens here! There is only one sequent which is a copy of a sequent in $G^{*}$ in $G_{H_1^c:G|G^{*}}^{☆}$. It is simpler than $G|G^{*}$. So we are moving forward. The above procedure is called the separation of $G|G^{*}$ as a branch of $H_1^c$ and reformulated as follows (See Section 7 for details).

$$\begin{array}{|c|}\hline \frac{\underline{\frac{\underline{\frac{\underline{G|G^{*}}}{G_{H_1^c:G|G^{*}}^{☆(1)}}⟨{\tau }_{H_1^c:A\Rightarrow p_1}^{*}⟩}}{G_{H_1^c:G|G^{*}}^{☆(2)}}⟨{\tau }_{H_3^c:p_3,p_4\Rightarrow A\odot A}^{*},{\tau }_{H_3^c:p_5,p_6\Rightarrow A\odot A}^{*}⟩}}{G_{H_1^c:G|G^{*}}^{☆}}⟨E{C}_{\mathsf{\Omega }}⟩\\ \hline\end{array}$$

The separation of $G|G^{*}$ as a branch of $H_2^c$ is constructed by a similar procedure as follows.

$$\begin{array}{|c|}\hline \frac{\underline{\frac{\underline{\frac{\underline{G|G^{*}}}{G_{H_2^c:G|G^{*}}^{☆(1)}}⟨{\tau }_{H_2^c:A\Rightarrow p_3}^{*}⟩}}{G_{H_2^c:G|G^{*}}^{☆(2)}}⟨{\tau }_{H_3^c:p_3,p_4\Rightarrow A\odot A}^{*}⟩}}{G_{H_2^c:G|G^{*}}^{☆}}⟨E{C}_{\mathsf{\Omega }}⟩\\ \hline\end{array}$$

Note that $\mathcal{D}(G_{H_1^c:G|G^{*}}^{☆})=H_2$ and $\mathcal{D}(G_{H_2^c:G|G^{*}}^{☆})=H_3$. So we have built up one-one correspondences between proofs of $G_{H_1^c:G|G^{*}}^{☆},G_{H_1^c:G|G^{*}}^{☆}$ and those of $H_2,H_3$.

Step 3 (separation algorithm of multiple branches). We will prove ${⊢}_{\mathbf{GIUL}}{\mathcal{D}}_0(G_0)$ in a direct way, i.e., only the major step of Theorem 2 is presented in the following. (See Appendix A.5.4 for a complete illustration.) Recall that

$$G_{H_1^c:G|G^{*}}^{☆}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|$$

$$A\Rightarrow p_3|\Rightarrow p_1,B|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A,$$

$$G_{H_2^c:G|G^{*}}^{☆}=A\Rightarrow p_1|\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|$$

$$B\Rightarrow p_3,\neg A\odot \neg A|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A.$$

By reassigning identification numbers to occurrences of $p^{\prime }s$ in $G_{H_2^c:G|G^{*}}^{☆}$,

$$G_{H_2^c:G|G^{*}}^{☆}=A\Rightarrow p_5|\Rightarrow p_6,B|B\Rightarrow p_8,\neg A\odot \neg A|p_5\Rightarrow C|C,p_6\Rightarrow A\odot A|$$

$$B\Rightarrow p_7,\neg A\odot \neg A|p_7\Rightarrow C|C,p_8\Rightarrow A\odot A.$$

By applying ${\tau }_{\{H_1^c:A\Rightarrow p_5,H_2^c:A\Rightarrow p_3\}}^{*}$ to $A\Rightarrow p_3$ in $G_{H_1^c:G|G^{*}}^{☆}$ and $A\Rightarrow p_5$ in $G_{H_2^c:G|G^{*}}^{☆}$, we get ${⊢}_{\mathbf{GIUL}}{G}^{\prime }$, where

$$G^{\prime }\equiv \Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|\Rightarrow p_1,B|$$

$$p_3\Rightarrow C|C,p_4\Rightarrow A\odot A|\Rightarrow p_6,B|B\Rightarrow p_8,\neg A\odot \neg A|p_5\Rightarrow C|C,p_6\Rightarrow A\odot A|$$

$$B\Rightarrow p_7,\neg A\odot \neg A|p_7\Rightarrow C|C,p_8\Rightarrow A\odot A|\Rightarrow p_5,B|B\Rightarrow p_3,\neg A\odot \neg A.$$

Why reassign identification numbers to occurrences of $p^{\prime }s$ in $G_{H_2^c:G|G^{*}}^{☆}$? It makes different occurrences of $p^{\prime }s$ to be assigned different identification numbers in two nodes $G_{H_1^c:G|G^{*}}^{☆}$ and $G_{H_2^c:G|G^{*}}^{☆}$ of the proof of $G^{\prime }$.

By applying $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$ to $G^{\prime }$, we get ${⊢}_{{\mathbf{GIUL}}_{\mathsf{\Omega }}}{G}_{\mathbf{I}}^{☆}$, where

$$G_{\mathbf{I}}^{☆}\equiv \Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|\Rightarrow p_1,B|$$

$$p_3\Rightarrow C|C,p_4\Rightarrow A\odot A|B\Rightarrow p_3,\neg A\odot \neg A.$$

A great change happens here! We have eliminated all sequents which are copies of some sequents in $G^{*}$ and converted $G|G^{*}$ into $G_{\mathbf{I}}^{☆}$ in which each sequent is some copy of a sequent in $G_0$.

Then ${⊢}_{\mathbf{GIUL}}\mathcal{D}(G_{\mathbf{I}}^{☆})$ by Lemma 8, where $\mathcal{D}(G_{\mathbf{I}}^{☆})=H_0$ =

$$\Rightarrow C,B|C\Rightarrow B,A\odot A|B\Rightarrow C,\neg A\odot \neg A|C,B\Rightarrow A\odot A,\neg A\odot \neg A.$$

So we have built up one-one correspondences between the proof of $G_{\mathbf{I}}^{☆}$ and that of $H_0$, i.e., the proof of $H_0$ can be constructed by applying $(\mathcal{D})$ to the proof of $G_{\mathbf{I}}^{☆}$. The major steps of constructing $G_{\mathbf{I}}^{☆}$ are shown in the following figure, where $\mathcal{D}(G|G^{*})=H_1$, $\mathcal{D}(G_{H_1^c:G|G^{*}}^{☆})=H_2$, $\mathcal{D}(G_{H_2^c:G|G^{*}}^{☆})=H_3$ and $\mathcal{D}(G_{\mathbf{I}}^{☆})=H_0$.

In the above example, $\mathcal{D}(G_{\mathbf{I}}^{☆})={\mathcal{D}}_0(G_0)$. But that is not always the case. In general, we can prove that ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$ if ${⊢}_{\mathbf{GL}}\mathcal{D}(G_{\mathbf{I}}^{☆})$, which is shown in the proof of the main theorem in Page 42. This example shows that the proof of the main theorem essentially presents an algorithm to construct a proof of ${\mathcal{D}}_0(G_0)$ from $\tau$.

4. Preprocessing of Proof Tree

Let $\tau$ be a cut-free proof of $G_0$ in the main theorem in $\mathbf{GL}$ by Lemma 1. Starting with $\tau$, we will construct a proof ${\tau }^{*}$ which contains no application of $(EC)$ and has some other properties in this section.

Lemma 2.

(i) If ${⊢}_{\mathbf{GL}}{\mathsf{\Gamma }}_1\Rightarrow A,{\mathsf{\Delta }}_1$ and ${⊢}_{\mathbf{GL}}{\mathsf{\Gamma }}_2\Rightarrow B,{\mathsf{\Delta }}_2$

$$then{⊢}_{\mathbf{GL}}{\mathsf{\Gamma }}_1\Rightarrow A\wedge B,{\mathsf{\Delta }}_1|{\mathsf{\Gamma }}_2\Rightarrow A\wedge B,{\mathsf{\Delta }}_2;$$

(ii) If ${⊢}_{\mathbf{GL}}{\mathsf{\Gamma }}_1,A\Rightarrow {\mathsf{\Delta }}_1$ and ${⊢}_{\mathbf{GL}}{\mathsf{\Gamma }}_2,B\Rightarrow {\mathsf{\Delta }}_2$

$$then{⊢}_{\mathbf{GL}}{\mathsf{\Gamma }}_1,A\vee B\Rightarrow {\mathsf{\Delta }}_1|{\mathsf{\Gamma }}_2,A\vee B\Rightarrow {\mathsf{\Delta }}_2.$$

Proof. 

(i)

$$\frac{{\mathsf{\Gamma }}_2\Rightarrow B,{\mathsf{\Delta }}_2\frac{{\mathsf{\Gamma }}_1\Rightarrow A,{\mathsf{\Delta }}_1\frac{B\Rightarrow B\frac{A\Rightarrow A\frac{A\Rightarrow AB\Rightarrow B}{A\Rightarrow B|B\Rightarrow A}(COM)}{A\Rightarrow A\wedge B|B\Rightarrow A}({\wedge }_r)}{A\Rightarrow A\wedge B|B\Rightarrow A\wedge B}({\wedge }_r)}{{\mathsf{\Gamma }}_1\Rightarrow A\wedge B,{\mathsf{\Delta }}_1|B\Rightarrow A\wedge B}(CUT)}{{\mathsf{\Gamma }}_1\Rightarrow A\wedge B,{\mathsf{\Delta }}_1|{\mathsf{\Gamma }}_2\Rightarrow A\wedge B,{\mathsf{\Delta }}_2}(CUT)$$

(ii) is proved by a procedure similar to that of (i) and omitted.  □

We introduce two new rules by Lemma 2.

Definition 12.

$\frac{G_1|{\mathsf{\Gamma }}_1\Rightarrow A,{\mathsf{\Delta }}_1{G}_2|{\mathsf{\Gamma }}_2\Rightarrow B,{\mathsf{\Delta }}_2}{G_1|G_2|{\mathsf{\Gamma }}_1\Rightarrow A\wedge B,{\mathsf{\Delta }}_1|{\mathsf{\Gamma }}_2\Rightarrow A\wedge B,{\mathsf{\Delta }}_2}({\wedge }_{rw})$and $\frac{G_1|{\mathsf{\Gamma }}_1,A\Rightarrow {\mathsf{\Delta }}_1{G}_2|{\mathsf{\Gamma }}_2,B\Rightarrow {\mathsf{\Delta }}_2}{G_1|G_2|{\mathsf{\Gamma }}_1,A\vee B\Rightarrow {\mathsf{\Delta }}_1|{\mathsf{\Gamma }}_2,A\vee B\Rightarrow {\mathsf{\Delta }}_2}({\vee }_{lw})$ are called the generalized $({\wedge }_r)$ and $({\vee }_l)$ rules, respectively.

Now, we begin to process $\tau$ as follows.

Step 1. A proof ${\tau }^1$ is constructed by replacing inductively all applications of

$$\frac{G_1|\mathsf{\Gamma }\Rightarrow A,\mathsf{\Delta }{G}_2|\mathsf{\Gamma }\Rightarrow B,\mathsf{\Delta }}{G_1|G_2|\mathsf{\Gamma }\Rightarrow A\wedge B,\mathsf{\Delta }}({\wedge }_r)(\mathrm{or}\frac{G_1|\mathsf{\Gamma },A\Rightarrow \mathsf{\Delta }{G}_2|\mathsf{\Gamma },B\Rightarrow \mathsf{\Delta }}{G_1|G_2|\mathsf{\Gamma },A\vee B\Rightarrow \mathsf{\Delta }}({\vee }_l))$$

in $\tau$ with

$$\frac{\frac{G_1|\mathsf{\Gamma }\Rightarrow A,\mathsf{\Delta }{G}_2|\mathsf{\Gamma }\Rightarrow B,\mathsf{\Delta }}{G_1|G_2|\mathsf{\Gamma }\Rightarrow A\wedge B,\mathsf{\Delta }|\mathsf{\Gamma }\Rightarrow A\wedge B,\mathsf{\Delta }}({\wedge }_{rw})}{G_1|G_2|\mathsf{\Gamma }\Rightarrow A\wedge B,\mathsf{\Delta }}(EC)$$

$$(\mathrm{accordingly}\frac{\frac{G_1|\mathsf{\Gamma },A\Rightarrow \mathsf{\Delta }{G}_2|\mathsf{\Gamma },B\Rightarrow \mathsf{\Delta }}{G_1|G_2|\mathsf{\Gamma },A\vee B\Rightarrow \mathsf{\Delta }|\mathsf{\Gamma },A\vee B\Rightarrow \mathsf{\Delta }}({\vee }_{lw})}{G_1|G_2|\mathsf{\Gamma },A\vee B\Rightarrow \mathsf{\Delta }}(EC)\mathrm{for}({\vee }_l)).$$

The replacements in Step 1 are local and the root of ${\tau }^1$ is also labeled by $G_0$.

Definition 13.

We sometimes may regard $\frac{G^{\prime }}{G^{\prime }}$ as a structural rule of $\mathbf{GL}$ and denote it by $(I{D}_{\mathsf{\Omega }})$ for convenience. The focus sequent for $(I{D}_{\mathsf{\Omega }})$ is undefined.

Lemma 3.

Let $\frac{G^{\prime }|S^m}{G^{\prime }|S}(E{C}^{*})\in {\tau }^1$, $T{h}_{{\tau }^1}(G^{\prime }|S)=(H_0,H_1,\cdots ,H_n)$, where $H_0=G^{\prime }|S$ and $H_n=G_0$. A tree ${\tau }^{\prime }$ is constructed by replacing each $H_k$ in ${\tau }^1$ with $H_k|S^{m-1}$ for all $0⩽k⩽n$. Then ${\tau }^{\prime }$ is a proof of $G_0|S^{m-1}$.

Proof. 

The proof is by induction on n. Since ${\tau }^1(G^{\prime }|S^m)$ is a proof and $\frac{G^{\prime }|S^m}{H_0|S^{m-1}}(I{D}_{\mathsf{\Omega }})$ is valid in $\mathbf{GL}$, then ${\tau }^{\prime }(H_0|S^{m-1})$ is a proof. Suppose that ${\tau }^{\prime }(H_{n-1}|S^{m-1})$ is a proof. Since $\frac{H_{n-1}{G}^{″}}{H_n}(II)$ (or $\frac{H_{n-1}}{H_n}(I))$ in ${\tau }^1$, then $\frac{H_{n-1}|S^{m-1}{G}^{″}}{H_n|S^{m-1}}$ (or $\frac{H_{n-1}|S^{m-1}}{H_n|S^{m-1}})$ is an application of the same rule $(II)$ (or $(I)$). Thus ${\tau }^{\prime }(H_n|S^{m-1})$ is a proof.  □

Definition 14.

The manipulation described in Lemma 3 is called a sequent-inserting operation.

Clearly, the number of $(E{C}^{*})$-applications in ${\tau }^{\prime }$ is less than ${\tau }^1$. Next, we continue to process $\tau$.

Step 2. Let $\frac{G_1^{‴}|{\{S_1^c\}}^{m_1^{\prime }}}{G_1^{\prime }|S_1^c}(E{C}^{*}),\cdots ,\frac{G_N^{‴}|{\{S_N^c\}}^{m_N^{\prime }}}{G_N^{\prime }|S_N^c}(E{C}^{*})$ be all applications of $(E{C}^{*})$ in ${\tau }^1$ and $G_0^{*}:={\{S_1^c\}}^{m_1^{\prime }-1}|\cdots |{\{S_N^c\}}^{m_N^{\prime }-1}$. By repeatedly applying sequent-inserting operations, we construct a proof of $G_0|G_0^{*}$ in $\mathbf{GL}$ without applications of $(E{C}^{*})$ and denote it by ${\tau }^2$.

Remark 1.

(i) ${\tau }^2$ is constructed by converting $(EC)$ into $(I{D}_{\mathsf{\Omega }})$; (ii) Each node of ${\tau }^2$ has the form $H_0|H_0^{*}$, where $H_0\in {\tau }^1$ and $H_0^{*}$ is a (possibly empty) subset of $G_0^{*}$.

We need the following construction to eliminate applications of $(EW)$ in ${\tau }^2$.

Construction 1.

Let $H\in {\tau }^2$, $H^{\prime }\subseteq H$ and $T{h}_{{\tau }^2}(H)=(H_0,\cdots ,H_n)$, where $H_0=H$, $H_n=G_0|G_0^{*}$. Hypersequents ${⟨H_k⟩}_{H:H^{\prime }}$ and trees ${\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }})$ for all $0⩽k⩽n$ are constructed inductively as follows.

(i) ${⟨H_0⟩}_{H:H^{\prime }}:=H^{\prime }$ and ${\tau }_{H:H^{\prime }}^2({⟨H_0⟩}_{H:H^{\prime }})$ consists of a single node $H^{\prime }$;

(ii) Let $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{G^{\prime }|G^{″}|H^{″}}(II)$ (or $\frac{G^{\prime }|S^{\prime }}{G^{\prime }|S^{″}}(I))$ be in ${\tau }^2$, $H_k=G^{\prime }|S^{\prime }$ and $H_{k+1}=G^{\prime }|G^{″}|H^{″}$ (accordingly $H_{k+1}=G^{\prime }|S^{″}$ for $(I)$) for some $0⩽k⩽n-1$.

If $S^{\prime }\in {⟨H_k⟩}_{H:H^{\prime }}$

$${⟨H_{k+1}⟩}_{H:H^{\prime }}:={⟨H_k⟩}_{H:H^{\prime }}\backslash \{S^{\prime }\}|G^{″}|H^{″}$$

$$(\mathrm{accordingly}{⟨H_{k+1}⟩}_{H:H^{\prime }}:={⟨H_k⟩}_{H:H^{\prime }}\backslash \{S^{\prime }\}|S^{″}\mathrm{for}(I))$$

and ${\tau }_{H:H^{\prime }}^2({⟨H_{k+1}⟩}_{H:H^{\prime }})$ is constructed by combining trees

$${\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }}),{\tau }^2(G^{″}|S^{″})\mathrm{with}\frac{{⟨H_k⟩}_{H:H^{\prime }}{G}^{″}|S^{″}}{{⟨H_{k+1}⟩}_{H:H^{\prime }}}(II)$$

$$(\mathrm{accordingly}{\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }})\mathrm{with}\frac{{⟨H_k⟩}_{H:H^{\prime }}}{{⟨H_{k+1}⟩}_{H:H^{\prime }}}(I)\mathrm{for}(I))$$

otherwise ${⟨H_{k+1}⟩}_{H:H^{\prime }}:={⟨H_k⟩}_{H:H^{\prime }}$ and ${\tau }_{H:H^{\prime }}^2({⟨H_{k+1}⟩}_{H:H^{\prime }})$ is constructed by combining

$${\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }})\mathrm{with}\frac{{⟨H_k⟩}_{H:H^{\prime }}}{{⟨H_{k+1}⟩}_{H:H^{\prime }}}(I{D}_{\mathsf{\Omega }}).$$

(iii) Let $\frac{G^{\prime }}{G^{\prime }|S^{\prime }}(EW)\in {\tau }^2$, $H_k=G^{\prime }$ and $H_{k+1}=G^{\prime }|S^{\prime }$ then ${⟨H_{k+1}⟩}_{H:H^{\prime }}:={⟨H_k⟩}_{H:H^{\prime }}$ and ${\tau }_{H:H^{\prime }}^2({⟨H_{k+1}⟩}_{H:H^{\prime }})$ is constructed by combining ${\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }})\mathrm{with}\frac{{⟨H_k⟩}_{H:H^{\prime }}}{{⟨H_{k+1}⟩}_{H:H^{\prime }}}(I{D}_{\mathsf{\Omega }}).$

Lemma 4.

(i) ${⟨H_k⟩}_{H:H^{\prime }}\subseteq H_k$ for all $0⩽k⩽n$;

(ii) ${\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }})$ is a derivation of ${⟨H_k⟩}_{H:H^{\prime }}$ from $H^{\prime }$ without $(EC)$.

Proof. 

The proof is by induction on k. For the base step, ${⟨H_0⟩}_{H:H^{\prime }}=H^{\prime }$ and ${\tau }_{H:H^{\prime }}^2({⟨H_0⟩}_{H:H^{\prime }})$ consists of a single node $H^{\prime }$. Then ${⟨H_0⟩}_{H:H^{\prime }}\subseteq H_0=H$, ${\tau }_{H:H^{\prime }}^2({⟨H_0⟩}_{H:H^{\prime }})$ is a derivation of ${⟨H_0⟩}_{H:H^{\prime }}$ from $H^{\prime }$ without $(EC)$.

For the induction step, suppose that ${⟨H_k⟩}_{H:H^{\prime }}$ and ${\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }})$ be constructed such that (i) and (ii) hold for some $0⩽k⩽n-1$. There are two cases to be considered.

Case 1. Let $\frac{G^{\prime }|S^{\prime }}{G^{\prime }|S^{″}}(I)\in {\tau }^2$, $H_k=G^{\prime }|S^{\prime }$ and $H_{k+1}=G^{\prime }|S^{″}$. If $S^{\prime }\in {⟨H_k⟩}_{H:H^{\prime }}$ then ${⟨H_k⟩}_{H:H^{\prime }}\backslash \{S^{\prime }\}\subseteq G^{\prime }$ by ${⟨H_k⟩}_{H:H^{\prime }}\subseteq H_k=G^{\prime }|S^{\prime }$. Thus ${⟨H_{k+1}⟩}_{H:H^{\prime }}=({⟨H_k⟩}_{H:H^{\prime }}\backslash \{S^{\prime }\})|S^{″}\subseteq G^{\prime }|S^{″}=H_{k+1}.$ Otherwise $S^{\prime }\notin {⟨H_k⟩}_{H:H^{\prime }}$ then ${⟨H_k⟩}_{H:H^{\prime }}\subseteq G^{\prime }$ by ${⟨H_k⟩}_{H:H^{\prime }}\subseteq H_k=G^{\prime }|S^{\prime }$. Thus ${⟨H_{k+1}⟩}_{H:H^{\prime }}\subseteq H_{k+1}$ by ${⟨H_{k+1}⟩}_{H:H^{\prime }}={⟨H_k⟩}_{H:H^{\prime }}\subseteq G^{\prime }\subseteq H_{k+1}$. ${\tau }_{H:H^{\prime }}^2({⟨H_{k+1}⟩}_{H:H^{\prime }})$ is a derivation of ${⟨H_{k+1}⟩}_{H:H^{\prime }}$ from $H^{\prime }$ without $(EC)$ since ${\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }})$ is such one and $\frac{{⟨H_k⟩}_{H:H^{\prime }}}{{⟨H_{k+1}⟩}_{H:H^{\prime }}}(I)$ is a valid instance of a rule $(I)$ of $\mathbf{GL}$. The case of applications of the two-premise rule is proved by a similar procedure and omitted.

Case 2. Let $\frac{G^{\prime }}{G^{\prime }|S^{\prime }}(EW)\in {\tau }^2$, $H_k=G^{\prime }$ and $H_{k+1}=G^{\prime }|S^{\prime }$. Then ${⟨H_{k+1}⟩}_{H:H^{\prime }}\subseteq H_{k+1}$ by ${⟨H_{k+1}⟩}_{H:H^{\prime }}={⟨H_k⟩}_{H:H^{\prime }}\subseteq H_k\subseteq H_{k+1}$. ${\tau }_{H:H^{\prime }}^2({⟨H_{k+1}⟩}_{H:H^{\prime }})$ is a derivation of ${⟨H_{k+1}⟩}_{H:H^{\prime }}$ from $H^{\prime }$ without $(EC)$ since ${\tau }_{H:H^{\prime }}^2({⟨H_k⟩}_{H:H^{\prime }})$ is such one and $\frac{{⟨H_k⟩}_{H:H^{\prime }}}{{⟨H_{k+1}⟩}_{H:H^{\prime }}}(I{D}_{\mathsf{\Omega }})$ is valid by Definition 13.   □

Definition 15.

The manipulation described in Construction 1 is called a derivation-pruning operation.

Notation 3.

We denote ${⟨H_n⟩}_{H:H^{\prime }}$ by $G_{H:H^{\prime }}^2$, ${\tau }_{H:H^{\prime }}^2({⟨H_n⟩}_{H:H^{\prime }})$ by ${\tau }_{H:H^{\prime }}^2$ and say that $H^{\prime }$ is transformed into $G_{H:H^{\prime }}^2$ in ${\tau }^2$.

Then Lemma 4 shows that $\frac{\underline{H^{\prime }}}{G_{H:H^{\prime }}^2}⟨{\tau }_{H:H^{\prime }}^2⟩$, $G_{H:H^{\prime }}^2\subseteq G_0|G_0^{*}$. Now, we continue to process $\tau$ as follows.

Step 3. Let $\frac{G^{\prime }}{G^{\prime }|S^{\prime }}(EW)\in {\tau }^2$ then ${\tau }_{G^{\prime }|S^{\prime }:G^{\prime }}^2({⟨H_n⟩}_{G^{\prime }|S^{\prime }:G^{\prime }})$ is a derivation of ${⟨H_n⟩}_{G^{\prime }|S^{\prime }:G^{\prime }}$ from $G^{\prime }$ thus a proof of ${⟨H_n⟩}_{G^{\prime }|S^{\prime }:G^{\prime }}$ is constructed by combining ${\tau }^2(G^{\prime })$ and ${\tau }_{G^{\prime }|S^{\prime }:G^{\prime }}^2({⟨H_n⟩}_{G^{\prime }|S^{\prime }:G^{\prime }})$ with $\frac{G^{\prime }}{G^{\prime }}(I{D}_{\mathsf{\Omega }})$. By repeatedly applying the procedure above, we construct a proof ${\tau }^3$ of $G_1|G_1^{*}$ without $(EW)$ in $\mathbf{GL}$, where $G_1\subseteq G_0,G_1^{*}\subseteq G_0^{*}$ by Lemma 4(i).

Step 4. Let $\mathsf{\Gamma },p,\perp \Rightarrow \mathsf{\Delta }\in {\tau }^3$ (or $\mathsf{\Gamma },p\Rightarrow \top ,\mathsf{\Delta }$, $\frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma },p\Rightarrow \mathsf{\Delta }}(WL))$ then there exists ${\mathsf{\Gamma }}^{\prime }\Rightarrow {\mathsf{\Delta }}^{\prime }\in H$ such that $p\in {\mathsf{\Gamma }}^{\prime }$ for all $H\in T{h}_{{\tau }^3}(\mathsf{\Gamma },p,\perp \Rightarrow \mathsf{\Delta })$ (accordingly $H\in T{h}_{{\tau }^3}(\mathsf{\Gamma },p\Rightarrow \top ,\mathsf{\Delta })$, $H\in T{h}_{{\tau }^3}(\mathsf{\Gamma },p\Rightarrow \mathsf{\Delta }))$ thus a proof is constructed by replacing top-down p in each ${\mathsf{\Gamma }}^{\prime }$ with ⊤.

Let $\mathsf{\Gamma },\perp \Rightarrow p,\mathsf{\Delta }$ (or $\mathsf{\Gamma }\Rightarrow \top ,p,\mathsf{\Delta }$, $\frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma }\Rightarrow p,\mathsf{\Delta }}(WR))$ is a leaf of ${\tau }^3$ then there exists ${\mathsf{\Gamma }}^{\prime }\Rightarrow {\mathsf{\Delta }}^{\prime }\in H$ such that $p\in {\mathsf{\Delta }}^{\prime }$ for all $H\in T{h}_{{\tau }^3}(\mathsf{\Gamma },\perp \Rightarrow p,\mathsf{\Delta })$ (accordingly $H\in T{h}_{{\tau }^3}(\mathsf{\Gamma }\Rightarrow \top ,p,\mathsf{\Delta })$ or $H\in T{h}_{{\tau }^3}(\mathsf{\Gamma }\Rightarrow p,\mathsf{\Delta }))$ thus a proof is constructed by replacing top-down p in each ${\mathsf{\Gamma }}^{\prime }$ with ⊥.

Repeatedly applying the procedure above, we construct a proof ${\tau }^4$ of $G_2|G_2^{*}$ in $\mathbf{GL}$ such that there does not exist occurrence of p in $\mathsf{\Gamma }$ or $\mathsf{\Delta }$ at each leaf labeled by $\mathsf{\Gamma },\perp \Rightarrow \mathsf{\Delta }$ or $\mathsf{\Gamma }\Rightarrow \top ,\mathsf{\Delta }$, or p is not the weakening formula A in $\frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma }\Rightarrow A,\mathsf{\Delta }}(WR)$ or $\frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma },A\Rightarrow \mathsf{\Delta }}(WL)$ when $(WR)$ or $(WL)$ is available. Define two operations ${\sigma }_l$ and ${\sigma }_r$ on sequents by ${\sigma }_l(\mathsf{\Gamma },p\Rightarrow \mathsf{\Delta }):=\mathsf{\Gamma },\top \Rightarrow \mathsf{\Delta }$ and ${\sigma }_r(\mathsf{\Gamma }\Rightarrow p,\mathsf{\Delta }):=\mathsf{\Gamma }\Rightarrow \perp ,\mathsf{\Delta }$. Then $G_2|G_2^{*}$ is obtained by applying ${\sigma }_l$ and ${\sigma }_r$ to some designated sequents in $G_1|G_1^{*}$.

Definition 16.

The manipulation described in Step 4 is called eigenvariable-replacing operation.

Step 5. A proof ${\tau }^{*}$ is constructed from ${\tau }^4$ by assigning inductively one unique identification number to each occurrence of p in ${\tau }^4$ as follows.

One unique identification number, which is a positive integer, is assigned to each leaf of the form $p\Rightarrow p$ in ${\tau }^4$ which corresponds to $p_k\Rightarrow p_k$ in ${\tau }^{*}$. Other nodes of ${\tau }^4$ are processed as follows.

• Let $\frac{G_1|\mathsf{\Gamma },\lambda p\Rightarrow \mu p,\mathsf{\Delta }}{G_1|{\mathsf{\Gamma }}^{\prime },\lambda p\Rightarrow \mu p,{\mathsf{\Delta }}^{\prime }}(I)\in {\tau }^4$. Suppose that all occurrences of p in $G_1|\mathsf{\Gamma },\lambda p\Rightarrow \mu p,\mathsf{\Delta }$ are assigned identification numbers and have the form $G_1^{\prime }|\mathsf{\Gamma },p_{i_1},\cdots ,p_{i_{\lambda }}\Rightarrow p_{j_1},\cdots ,p_{j_{\mu }},\mathsf{\Delta }$ in ${\tau }^{*}$, which we often write as $G_1^{\prime }|\mathsf{\Gamma },{\{p_{i_k}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_k}\}}_{k=1}^{\mu },\mathsf{\Delta }.$ Then $G_1|{\mathsf{\Gamma }}^{\prime },\lambda p\Rightarrow \mu p,{\mathsf{\Delta }}^{\prime }$ has the form $G_1^{\prime }|{\mathsf{\Gamma }}^{\prime },{\{p_{i_k}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_k}\}}_{k=1}^{\mu },{\mathsf{\Delta }}^{\prime }.$
• Let $\frac{G^{\prime }{G}^{″}}{G^{‴}}({\wedge }_{rw})\in {\tau }^4$, where $G^{\prime }\equiv G_1|\mathsf{\Gamma },\lambda p\Rightarrow \mu p,A,\mathsf{\Delta },$ $G^{″}\equiv G_2|\mathsf{\Gamma },\lambda p\Rightarrow \mu p,B,\mathsf{\Delta },$ $G^{‴}\equiv G_1|G_2|\mathsf{\Gamma },\lambda p\Rightarrow \mu p,A\wedge B,\mathsf{\Delta }|\mathsf{\Gamma },\lambda p\Rightarrow \mu p,A\wedge B,\mathsf{\Delta }.$ Suppose that $G^{\prime }$ and $G^{″}$ have the forms $G_1^{\prime }|\mathsf{\Gamma },{\{p_{i_{1k}}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_{1k}}\}}_{k=1}^{\mu },A,\mathsf{\Delta }$ and $G_2^{\prime }|\mathsf{\Gamma },{\{p_{i_{2k}}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_{2k}}\}}_{k=1}^{\mu },B,\mathsf{\Delta }$ in ${\tau }^{*}$, respectively. Then $G^{‴}$ has the form $G_1^{\prime }|G_2^{\prime }|\mathsf{\Gamma },{\{p_{i_{1k}}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_{1k}}\}}_{k=1}^{\mu },A\wedge B,\mathsf{\Delta }|\mathsf{\Gamma },{\{p_{i_{2k}}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_{2k}}\}}_{k=1}^{\mu },A\wedge B,\mathsf{\Delta }.$ All applications of $({\vee }_{lw})$ are processed by the procedure similar to that of $({\wedge }_{rw})$.
• Let $\frac{G^{\prime }{G}^{″}}{G^{‴}}({\odot }_r)\in {\tau }^4$, where $G^{\prime }\equiv G_1|{\mathsf{\Gamma }}_1,{\lambda }_{1}p\Rightarrow {\mu }_{1}p,A,{\mathsf{\Delta }}_1,$
  $G^{″}\equiv G_2|{\mathsf{\Gamma }}_2,{\lambda }_{2}p\Rightarrow {\mu }_{2}p,B,{\mathsf{\Delta }}_2,$$G^{‴}\equiv G_1|G_2|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,({\lambda }_1+{\lambda }_2)p\Rightarrow ({\mu }_1+{\mu }_2)p,A\odot B,{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2.$ Suppose that $G^{\prime }$ and $G^{″}$ have the forms $G_1^{\prime }|{\mathsf{\Gamma }}_1,{\{p_{i_{1k}}\}}_{k=1}^{{\lambda }_1}\Rightarrow {\{p_{j_{1k}}\}}_{k=1}^{{\mu }_1},A,{\mathsf{\Delta }}_1$ and $G_2^{\prime }|{\mathsf{\Gamma }}_2,{\{p_{i_{2k}}\}}_{k=1}^{{\lambda }_2}\Rightarrow {\{p_{j_{2k}}\}}_{k=1}^{{\mu }_2},B,{\mathsf{\Delta }}_2$ in ${\tau }^{*}$, respectively. Then $G^{‴}$ has the form $G_1^{\prime }|G_2^{\prime }|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,{\{p_{i_{1k}}\}}_{k=1}^{{\lambda }_1},{\{p_{i_{2k}}\}}_{k=1}^{{\lambda }_2}\Rightarrow {\{p_{j_{1k}}\}}_{k=1}^{{\mu }_1},{\{p_{j_{2k}}\}}_{k=1}^{{\mu }_2},A\odot B,{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2.$ All applications of $({\to }_l)$ are processed by the procedure similar to that of $({\odot }_r)$.
• Let $\frac{G^{\prime }{G}^{″}}{G^{‴}}(COM)\in {\tau }^4$, where $G^{\prime }\equiv G_1|{\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1,{\lambda }_{1}p\Rightarrow {\mu }_{1}p,{\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1,$
  $G^{″}\equiv G_2|{\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\lambda }_{2}p\Rightarrow {\mu }_{2}p,{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2,$$G^{‴}\equiv G_1|G_2|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,({\lambda }_{11}+{\lambda }_{21})p\Rightarrow ({\mu }_{11}+{\mu }_{21})p,{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2|$
  ${\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2,({\lambda }_{12}+{\lambda }_{22})p\Rightarrow ({\mu }_{12}+{\mu }_{22})p,{\mathsf{\Sigma }}_1,{\mathsf{\Sigma }}_2,$ where ${\lambda }_{11}+{\lambda }_{12}={\lambda }_1,{\lambda }_{21}+{\lambda }_{22}={\lambda }_2$, ${\mu }_{11}+{\mu }_{12}={\mu }_1,{\mu }_{21}+{\mu }_{22}={\mu }_2$.

Suppose that $G^{\prime }$ and $G^{″}$ have the forms $G_1^{\prime }|{\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1,{\{p_{i_k^1}\}}_{k=1}^{{\lambda }_1}\Rightarrow {\{p_{j_k^1}\}}_{k=1}^{{\mu }_1},{\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1$ and $G_2^{\prime }|{\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\{p_{i_k^2}\}}_{k=1}^{{\lambda }_2}\Rightarrow {\{p_{j_k^2}\}}_{k=1}^{{\mu }_2},{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2$ in ${\tau }^{*}$, respectively. Then $G^{‴}$ has the form

$$G_1^{\prime }|G_2^{\prime }|{\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,{\{p_{i_{1k}^1}\}}_{k=1}^{{\lambda }_{11}},{\{p_{i_{1k}^2}\}}_{k=1}^{{\lambda }_{21}}\Rightarrow {\{p_{j_{1k}^1}\}}_{k=1}^{{\mu }_{11}},{\{p_{j_{1k}^2}\}}_{k=1}^{{\mu }_{21}},{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2|$$

$${\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2,{\{p_{i_{2k}^1}\}}_{k=1}^{{\lambda }_{12}},{\{p_{i_{2k}^2}\}}_{k=1}^{{\lambda }_{22}}\Rightarrow {\{p_{j_{2k}^1}\}}_{k=1}^{{\mu }_{12}},{\{p_{j_{2k}^2}\}}_{k=1}^{{\mu }_{22}},{\mathsf{\Sigma }}_1,{\mathsf{\Sigma }}_2,$$

where

$${\{p_{i_k^w}\}}_{k=1}^{{\lambda }_w}={\{p_{i_{1k}^w}\}}_{k=1}^{{\lambda }_{w1}}\bigcup {\{p_{i_{2k}^w}\}}_{k=1}^{{\lambda }_{w2}},{\{p_{j_k^w}\}}_{k=1}^{{\mu }_w}={\{p_{j_{1k}^w}\}}_{k=1}^{{\mu }_{w1}}\bigcup {\{p_{j_{2k}^w}\}}_{k=1}^{{\mu }_{w2}}$$

for $w=1,2$.

Definition 17.

The manipulation described in Step 5 is called eigenvariable-labeling operation.

Notation 4.

Let $G_2$ and $G_2^{*}$ be converted to G and $G^{*}$ in ${\tau }^{*}$, respectively. Then ${\tau }^{*}$ is a proof of $G|G^{*}$.

In the preprocessing of $\tau$, each $\frac{G_i^{‴}|{\{S_i^c\}}^{m_i^{\prime }}}{G_i^{‴}|S_i^c}{(E{C}^{*})}_i$ is converted into $\frac{G_i^{″}|{\{S_i^c\}}^{m_i^{\prime }}}{G_i^{″}|{\{S_i^c\}}^{m_i^{\prime }}}{(I{D}_{\mathsf{\Omega }})}_i$ in Step 2, where $G_i^{‴}\subseteq G_i^{″}$ by Lemma 3. $\frac{G^{\prime }}{G^{\prime }|S^{\prime }}(EW)\in {\tau }^2$ is converted into $\frac{G^{″}}{G^{″}}(I{D}_{\mathsf{\Omega }})$ in Step 3, where $G^{″}\subseteq G^{\prime }$ by Lemma 4(i). Some $G^{\prime }|{\mathsf{\Gamma }}^{\prime },p\Rightarrow {\mathsf{\Delta }}^{\prime }\in {\tau }^3$ (or $G^{\prime }|{\mathsf{\Gamma }}^{\prime }\Rightarrow p,{\mathsf{\Delta }}^{\prime }$) is revised as $G^{\prime }|{\mathsf{\Gamma }}^{\prime },\top \Rightarrow {\mathsf{\Delta }}^{\prime }$ (or $G^{\prime }|{\mathsf{\Gamma }}^{\prime }\Rightarrow \perp ,{\mathsf{\Delta }}^{\prime }$) in Step 4. Each occurrence of p in ${\tau }^4$ is assigned the unique identification number in Step 5. The whole preprocessing above is depicted by Figure 13.

Figure 13. Preprocessing of $\tau$.

Notation 5.

Let $\frac{G_i^{‴}|{\{S_i^c\}}^{m_i^{\prime }}}{G_i^{‴}|S_i^c}{(E{C}^{*})}_i,1⩽i⩽N$ be all $(E{C}^{*})$-nodes of ${\tau }^1$ and $G_i^{‴}|{\{S_i^c\}}^{m_i^{\prime }}$ be converted to $G_i^{″}|{\{S_i^c\}}^{m_i}$ in ${\tau }^{*}$. Note that there are no identification numbers for occurrences of variable p in $S_i^c\in G_i^{‴}|{\{S_i^c\}}^{m_i^{\prime }}$ meanwhile they are assigned to p in $S_i^c\in G_i^{″}|{\{S_i^c\}}^{m_i}$. But we use the same notations for $S_i^c\in G_i^{‴}|{\{S_i^c\}}^{m_i^{\prime }}$ and $S_i^c\in G_i^{″}|{\{S_i^c\}}^{m_i}$ for simplicity.

In the whole paper, let $H_i^c=G_i^{\prime }|{\{S_i^c\}}^{m_i}$ denote the unique node of ${\tau }^{*}$ such that $H_i^c⩽G_i^{″}|{\{S_i^c\}}^{m_i}$ and $S_i^c$ is the focus sequent of $H_i^c$ in ${\tau }^{*}$, in which case we denote the focus one $S_{i1}^c$ and others $S_{i2}^c|\cdots |S_{i{m}_i}^c$ among ${\{S_i^c\}}^{m_i}$. We sometimes denote $H_i^c$ also by $G_i^{\prime }|{\{S_{iv}^c\}}_{v=1}^{m_i}$ or $G_i^{\prime }|S_{i1}^c|{\{S_{iv}^c\}}_{v=2}^{m_i}$. We then write $G^{*}$ as ${\{S_{iv}^c\}}_{i=1\cdots N}^{v=2\cdots m_i}$.

We call $H_i^c$, $S_{iu}^c$ the i-th pseudo-$(EC)$ node of ${\tau }^{*}$ and pseudo-$(EC)$ sequent, respectively. We abbreviate pseudo-$EC$ as $pEC.$ Let $H\in {\tau }^{*}$, by $S_i^c\in H$ we mean that $S_{iu}^c\in H$ for some $1⩽u⩽m_i$.

It is possible that there does not exist $H_i^c⩽G_i^{″}|{\{S_i^c\}}^{m_i}$ such that $S_i^c$ is the focus sequent of $H_i^c$ in ${\tau }^{*}$, in which case ${\{S_i^c\}}^{m_i}\subseteq G|G^{*}$, then it has not any effect on our argument to treat all such $S_i^c$ as members of G. So we assume that all $H_i^c$ are always defined for all $G_i^{″}|{\{S_i^c\}}^{m_i}$ in ${\tau }^{*}$, i.e., $H_i^c>G|G^{*}$.

Proposition 2.

(i) ${\{S_{iv}^c\}}_{v=2\cdots m_i}\subseteq H$ for all $H⩽H_i^c$; (ii) $G^{*}={\{S_{iv}^c\}}_{i=1\cdots N}^{v=2\cdots m_i}$.

Now, we replace locally each $\frac{G^{\prime }}{G^{\prime }}(I{D}_{\mathsf{\Omega }})$ in ${\tau }^{*}$ with $G^{\prime }$ and denote the resulting proof also by ${\tau }^{*}$, which has no essential difference with the original one, but could simplify subsequent arguments. We introduce the system ${\mathbf{GL}}_{\mathsf{\Omega }}$ as follows.

Definition 18.

${\mathbf{GL}}_{\mathsf{\Omega }}$ is a restricted subsystem of $\mathbf{GL}$ such that

(i) p is designated as the unique eigenvariable by which we mean that it is not used to built up any formula containing logical connectives and only used as a sequent-formula.

(ii) Each occurrence of p on each side of every component of a hypersequent in $\mathbf{GL}$ is assigned one unique identification number i and written as $p_i$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$. Initial sequent $p\Rightarrow p$ of $\mathbf{GL}$ has the form $p_i\Rightarrow p_i$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$.

(iii) Each sequent S of $\mathbf{GL}$ in the form $\mathsf{\Gamma },\lambda p\Rightarrow \mu p,\mathsf{\Delta }$ has the form

$$\mathsf{\Gamma },{\{p_{i_k}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_k}\}}_{k=1}^{\mu },\mathsf{\Delta }$$

in ${\mathbf{GL}}_{\mathsf{\Omega }}$, where p does not occur in Γ or Δ, $i_k\ne i_l$ for all $1⩽k<l⩽\lambda$, $j_k\ne j_l$ for all $1⩽k<l⩽\mu$. Define $v_l(S)=\{i_1,\cdots ,i_{\lambda }\}$ and $v_r(S)=\{j_1,\cdots ,j_{\mu }\}$. Let G be a hypersequent of ${\mathbf{GL}}_{\mathsf{\Omega }}$ in the form $S_1|\cdots |S_n$ then $v_l(S_k)\bigcap v_l(S_l)=\varnothing$ and $v_r(S_k)\bigcap v_r(S_l)=\varnothing$ for all $1⩽k<l⩽n$. Define $v_l(G)={\bigcup }_{k=1}^n{v}_l(S_k)$, $v_r(G)={\bigcup }_{k=1}^n{v}_r(S_k)$. Here, l and r in $v_l$ and $v_r$ indicate the left side and right side of a sequent, respectively.

(iv) A hypersequent G of ${\mathbf{GL}}_{\mathsf{\Omega }}$ is called closed if $v_l(G)=v_r(G)$. Two hypersequents $G^{\prime }$ and $G^{″}$ of ${\mathbf{GL}}_{\mathsf{\Omega }}$ are called disjoint if $v_l(G^{\prime })\bigcap v_l(G^{″})=\varnothing$, $v_l(G^{\prime })\bigcap v_r(G^{″})=\varnothing$, $v_r(G^{\prime })\bigcap v_l(G^{″})=\varnothing$ and $v_r(G^{\prime })\bigcap v_r(G^{″})=\varnothing$. $G^{″}$ is a copy of $G^{\prime }$ if they are disjoint and there exist two bijections ${\sigma }_l:v_l(G^{\prime })\to v_l(G^{″})$ and ${\sigma }_r:v_r(G^{\prime })\to v_r(G^{″})$ such that $G^{″}$ can be obtained by applying ${\sigma }_l$ to antecedents of sequents in $G^{\prime }$ and ${\sigma }_r$ to succedents of sequents in $G^{\prime }$, i.e., $G^{″}={\sigma }_r\circ {\sigma }_l(G^{\prime })$.

(v) A closed hypersequent $G^{\prime }|G^{″}|G^{‴}$ can be contracted as $G^{\prime }|G^{″}$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$ under the condition that $G^{″}$ and $G^{‴}$ are closed and $G^{‴}$ is a copy of $G^{″}$. We call it the constraint external contraction rule and denote it by

$$\frac{G^{\prime }|G^{″}|G^{‴}}{G^{\prime }|G^{″}}(E{C}_{\mathsf{\Omega }}).$$

Furthermore, if there do not exist two closed hypersequents $H^{\prime },H^{″}\subseteq G^{\prime }|G^{″}$ such that $H^{″}$ is a copy of $H^{\prime }$ then we call it the fully constraint contraction rule and denote by $\frac{\underline{G^{\prime }|G^{″}|G^{‴}}}{G^{\prime }|G^{″}}⟨E{C}_{\mathsf{\Omega }}^{*}⟩$.

(vi) $(EW)$ and $(CUT)$ of $\mathbf{GL}$ are forbidden. $(EC)$, $({\wedge }_r)$ and $({\vee }_l)$ of $\mathbf{GL}$ are replaced with $(E{C}_{\mathsf{\Omega }})$, $({\wedge }_{rw})$ and $({\vee }_{lw})$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$, respectively.

(vii) $G_1|S_1$ and $G_2|S_2$ are closed and disjoint for each two-premise rule

$\frac{G_1|S_1{G}_2|S_2}{G_1|G_2|H^{\prime }}(II)$ of ${\mathbf{GL}}_{\mathsf{\Omega }}$ and, $G^{\prime }|S^{\prime }$ is closed for each one-premise rule $\frac{G^{\prime }|S^{\prime }}{G^{\prime }|S^{″}}(I)$.

(viii) p does not occur in Γ or Δ for each initial sequent $\mathsf{\Gamma },\perp \Rightarrow \mathsf{\Delta }$ or $\mathsf{\Gamma }\Rightarrow \top ,\mathsf{\Delta }$ and, p does not act as the weakening formula A in $\frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma }\Rightarrow A,\mathsf{\Delta }}(WR)$ or $\frac{G|\mathsf{\Gamma }\Rightarrow \mathsf{\Delta }}{G|\mathsf{\Gamma },A\Rightarrow \mathsf{\Delta }}(WL)$ when $(WR)$ or $(WL)$ is available.

Lemma 5.

Let τ be a cut-free proof of $G_0$ in $\mathbf{L}$ and ${\tau }^{*}$ be the tree resulting from preprocessing of τ.

(i) If $\frac{G^{\prime }|S^{\prime }}{G^{\prime }|S^{″}}(I)\in {\tau }^{*}$ then $v_l(G^{\prime }|S^{″})=v_r(G^{\prime }|S^{″})=v_r(G^{\prime }|S^{\prime })=v_l(G^{\prime }|S^{\prime })$;

(ii) If $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{G^{\prime }|G^{″}|H^{\prime }}(II)\in {\tau }^{*}$ then $v_l(G^{\prime }|G^{″}|H^{\prime })=$ $v_l(G^{\prime }|S^{\prime })\bigcup v_l(G^{″}|S^{″})=v_r(G^{\prime }|G^{″}|H^{\prime })=v_r(G^{\prime }|S^{\prime })\bigcup v_r(G^{″}|S^{″})$;

(iii) If $H\in {\tau }^{*}$ and $k\in v_l(H)$ then $k\in v_r(H)$;

(iv) If $H\in {\tau }^{*}$ and $k\in v_l(H)$ (or $k\in v_r(H)$) then $H⩽p_k\Rightarrow p_k$;

(v) ${\tau }^{*}$ is a proof of $G|G^{*}$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$ without $(E{C}_{\mathsf{\Omega }})$;

(vi) If $H^{\prime },H^{″}\in {\tau }^{*}$ and $H^{\prime }\parallel H^{″}$ then $v_l(H^{\prime })\bigcap v_l(H^{″})=\varnothing$, $v_r(H^{\prime })\bigcap v_r(H^{″})=\varnothing$.

Proof. 

Claims from (i) to (iv) follow immediately from Step 5 in preprocessing of $\tau$ and Definition 18. Claim (v) is from Notation 4 and Definition 18. Only (vi) is proved as follows.

Suppose that $k\in v_l(H^{\prime })\bigcap v_l(H^{″})$. Then $H^{\prime }⩽p_k\Rightarrow p_k$, $H^{″}⩽p_k\Rightarrow p_k$ by Claim (iv). Thus $H^{\prime }⩽H^{″}$ or $H^{″}⩽H^{\prime }$, a contradiction with $H^{\prime }\parallel H^{″}$ hence $v_l(H^{\prime })\bigcap v_l(H^{″})=\varnothing$.

$v_r(H^{\prime })\bigcap v_r(H^{″})=\varnothing$ is proved by a similar procedure and omitted.  □

5. The Generalized Density Rule $(\mathcal{D})$ for ${\mathbf{GL}}_{\mathsf{\Omega }}$

In this section, we define the generalized density rule $(\mathcal{D})$ for ${\mathbf{GL}}_{\mathsf{\Omega }}$ and prove that it is admissible in ${\mathbf{GL}}_{\mathsf{\Omega }}$.

Definition 19.

Let G be a closed hypersequent of ${\mathbf{GL}}_{\mathsf{\Omega }}$ and $S\in G$. Define ${\left[S\right]}_G=\bigcap \{H:S\in H\subseteq G,v_l(H)=v_r(H)\}$, i.e., ${\left[S\right]}_G$ is the minimal closed unit of G containing $S.$ In general, for $G^{\prime }\subseteq G$, define ${\left[G^{\prime }\right]}_G=\bigcap \{H:G^{\prime }\subseteq H\subseteq G,v_l(H)=v_r(H)\}$.

Clearly, ${\left[S\right]}_G=S$ if $v_l(S)=v_r(S)$ or p does not occur in S. The following construction gives a procedure to construct ${\left[S\right]}_G$ for any given $S\in G$.

Construction 2.

Let G and S be as above. A sequence $G_1,G_2,\cdots ,G_n$ of hypersequents is constructed recursively as follows. (i) $G_1=\{S\}$; (ii) Suppose that $G_k$ is constructed for $k⩾1$. If $v_l(G_k)\ne v_r(G_k)$ then there exists $i_{k+1}\in v_l(G_k)\backslash v_r(G_k)$ (or $i_{k+1}\in v_r(G_k)\backslash v_l(G_k))$ thus there exists the unique $S_{k+1}\in G\backslash G_k$ such that $i_{k+1}\in v_r(S_{k+1})\backslash v_l(S_{k+1})$ (or $i_{k+1}\in v_l(S_{k+1})\backslash v_r(S_{k+1}))$ by $v_l(G)=v_r(G)$ and Definition 18 then let $G_{k+1}=G_k|S_{k+1}$ otherwise the procedure terminates and $n:=k$.

Lemma 6.

(i) $G_n={\left[S\right]}_G$;

(ii)Let $S^{\prime }\in {\left[S\right]}_G$ then ${\left[S^{\prime }\right]}_G={\left[S\right]}_G$;

(iii)Let $G^{\prime }\equiv G|H^{\prime }$, $G^{″}\equiv G|H^{″}$,$v_l(G^{\prime })=v_r(G^{\prime })$, $v_l(G^{″})=v_r(G^{″})$, $v_l(H^{\prime })\ominus v_r(H^{\prime })=v_l(H^{″})\ominus v_r(H^{″})$ then ${\left[H^{\prime }\right]}_{G^{\prime }}\backslash H^{\prime }={\left[H^{″}\right]}_{G^{″}}\backslash H^{″}$, where $A\ominus B$ is the symmetric difference of two multisets $A,B$;

(iv)Let $v_{lr}(G_k)=v_l(G_k)\bigcap v_r(G_k)$ then $\left|v_{lr}(G_k)\right|+1⩾\left|G_k\right|$ for all $1⩽k⩽n$;

(v) $\left|v_l({\left[S\right]}_G)\right|+1⩾\left|{\left[S\right]}_G\right|.$

Proof. 

(i) Since $G_k\subseteq G_{k+1}$ for $1⩽k⩽n-1$ and $S\in G_1$ then $S\in G_n\subseteq G$ thus ${\left[S\right]}_G\subseteq G_n$ by $v_l(G_n)=v_r(G_n)$. We prove $G_k\subseteq {\left[S\right]}_G$ for $1⩽k⩽n$ by induction on k in the following. Clearly, $G_1\subseteq {\left[S\right]}_G$. Suppose that $G_k\subseteq {\left[S\right]}_G$ for some $1⩽k⩽n-1$. Since $i_{k+1}\in v_l(G_k)\backslash v_r(G_k)$ (or $i_{k+1}\in v_r(G_k)\backslash v_l(G_k))$ and $i_{k+1}\in v_r(S_{k+1})$ (or $i_{k+1}\in v_l(S_{k+1}))$ then $S_{k+1}\in {\left[S\right]}_G$ by $G_k\subseteq {\left[S\right]}_G$ and $v_l({\left[S\right]}_G)=v_r({\left[S\right]}_G)$ thus $G_{k+1}\subseteq {\left[S\right]}_G$. Then $G_n\subseteq {\left[S\right]}_G$ thus $G_n={\left[S\right]}_G$.

(ii) By (i), ${\left[S\right]}_G=S_1|S_2|\cdots |S_n$, where $S_1=S$. Then $S^{\prime }=S_k$ for some $1⩽k⩽n$ thus $i_k\in v_r(S_k)\backslash v_l(S_k)$ (or $i_k\in v_l(S_k)\backslash v_r(S_k))$ hence there exists the unique $k^{\prime }<k$ such that $i_k\in v_l(S_{k^{\prime }})\backslash v_r(S_{k^{\prime }})$ (or $i_k\in v_r(S_{k^{\prime }})\backslash v_l(S_{k^{\prime }}))$ if $k\ge 2$ hence $S_{k^{\prime }}\in {\left[S_k\right]}_G$. Repeatedly, $S_1\in {\left[S_k\right]}_G$, i.e., $S\in {\left[S^{\prime }\right]}_G$ then ${\left[S\right]}_G\subseteq {\left[S^{\prime }\right]}_G$. ${\left[S^{\prime }\right]}_G\subseteq {\left[S\right]}_G$ by $S^{\prime }\in {\left[S\right]}_G$ then ${\left[S^{\prime }\right]}_G={\left[S\right]}_G$.

(iii) It holds immediately from Construction 2 and (i).

(iv) The proof is by induction on k. For the base step, let $k=1$ then $\left|G_k\right|=1$ thus $\left|v_{lr}(G_k)\right|+1⩾\left|G_k\right|$ by $\left|v_{lr}(G_k)\right|⩾0$. For the induction step, suppose that $\left|v_{lr}(G_k)\right|+1⩾\left|G_k\right|$ for some $1⩽k<n$. Then $\left|v_{lr}(G_{k+1})\right|⩾\left|v_{lr}(G_k)\right|+1$ by $i_{k+1}\in v_{lr}(G_{k+1})\backslash v_{lr}(G_k)$ and $v_{lr}(G_k)\subseteq v_{lr}(G_{k+1})$. Then $\left|v_{lr}(G_{k+1})\right|+1⩾\left|G_{k+1}\right|$ by $\left|G_{k+1}\right|=\left|G_k\right|+1=k+1$.

(v) It holds by (iv) and $v_{lr}({\left[S\right]}_G)=v_l({\left[S\right]}_G)$.  □

Definition 20.

Let $G=S_1|\cdots |S_r$ and $S_l$ be in the form ${\mathsf{\Gamma }}_l,{\{p_{i_k^l}\}}_{k=1}^{{\lambda }_l}\Rightarrow {\{p_{j_k^l}\}}_{k=1}^{{\mu }_l},{\mathsf{\Delta }}_l$ for $1⩽l⩽r$.

(i) If $S\in G$ and ${\left[S\right]}_G$ be $S_{k_1}|\cdots |S_{k_u}$ then ${\mathcal{D}}_G(S)$ is defined as

${\mathsf{\Gamma }}_{k_1},\cdots ,{\mathsf{\Gamma }}_{k_u}\Rightarrow (\left|v_l({\left[S\right]}_G)\right|-\left|{\left[S\right]}_G\right|+1)t,{\mathsf{\Delta }}_{k_1},\cdots ,{\mathsf{\Delta }}_{k_u};$

(ii) Let ${\bigcup }_{k=1}^v{\left[S_{q_k}\right]}_G=G$ and ${\left[S_{q_k}\right]}_G\bigcap {\left[S_{q_l}\right]}_G=\varnothing$ for all $1⩽k<l⩽v$ then $\mathcal{D}(G)$ is defined as ${\mathcal{D}}_G(S_{q_1})|\cdots |{\mathcal{D}}_G(S_{q_v})$.

(iii) We call $(\mathcal{D})$ the generalized density rule of ${\mathbf{GL}}_{\mathsf{\Omega }}$, whose conclusion $\mathcal{D}(G)$ is defined by (ii) if its premise is G.

Clearly, $\mathcal{D}(p_k\Rightarrow p_k)$ is $\Rightarrow t$ and $\mathcal{D}(S)=S$ if p does not occur in S.

Lemma 7.

Let $G^{\prime }\equiv G|S$ and $G^{″}\equiv G|S_1|S_2$ be closed and ${\left[S_1\right]}_{G^{″}}\bigcap {\left[S_2\right]}_{G^{″}}=\varnothing$, where $S_1={\mathsf{\Gamma }}_1,{\{p_{i_k^1}\}}_{k=1}^{{\lambda }_1}\Rightarrow {\{p_{j_k^1}\}}_{k=1}^{{\mu }_1},{\mathsf{\Delta }}_1;$ $S_2={\mathsf{\Gamma }}_2,{\{p_{i_k^2}\}}_{k=1}^{{\lambda }_2}\Rightarrow {\{p_{j_k^2}\}}_{k=1}^{{\mu }_2},{\mathsf{\Delta }}_2;$$S={\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,{\{p_{i_k^1}\}}_{k=1}^{{\lambda }_1},{\{p_{i_k^2}\}}_{k=1}^{{\lambda }_2}\Rightarrow {\{p_{j_k^1}\}}_{k=1}^{{\mu }_1},{\{p_{j_k^2}\}}_{k=1}^{{\mu }_2},{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2;$ ${\mathcal{D}}_{G^{″}}(S_1)={\mathsf{\Gamma }}_1,{\mathsf{\Sigma }}_1\Rightarrow {\mathsf{\Pi }}_1,{\mathsf{\Delta }}_1$ and ${\mathcal{D}}_{G^{″}}(S_2)={\mathsf{\Gamma }}_2,{\mathsf{\Sigma }}_2\Rightarrow {\mathsf{\Pi }}_2,{\mathsf{\Delta }}_2.$ Then ${\mathcal{D}}_{G^{\prime }}(S)={\mathsf{\Gamma }}_1,{\mathsf{\Sigma }}_1,{\mathsf{\Gamma }}_2,{\mathsf{\Sigma }}_2\Rightarrow {\mathsf{\Pi }}_1,{\mathsf{\Delta }}_1,{\mathsf{\Pi }}_2,{\mathsf{\Delta }}_2.$

Proof. 

Since ${\left[S_1\right]}_{G^{″}}\bigcap {\left[S_2\right]}_{G^{″}}=\varnothing$ then ${\left[S\right]}_{G^{\prime }}={\left[S_1\right]}_{G^{″}}\backslash \{S_1\}\bigcup {\left[S_2\right]}_{G^{″}}\backslash \{S_2\}\bigcup \{S\}$ by $v_l(S)=v_l(S_1|S_2)$, $v_r(S)=v_r(S_1|S_2)$ and Lemma 6 (iii). Thus $\left|v_l({\left[S\right]}_{G^{\prime }})\right|=\left|v_l({\left[S_1\right]}_{G^{″}})\right|+\left|v_l({\left[S_2\right]}_{G^{″}})\right|$, $\left|{\left[S\right]}_{G^{\prime }}\right|=\left|{\left[S_1\right]}_{G^{″}}\right|+\left|{\left[S_2\right]}_{G^{″}}\right|-1.$ Hence

$$\left|v_l({\left[S\right]}_{G^{\prime }})\right|-\left|{\left[S\right]}_{G^{\prime }}\right|+1=\left|v_l({\left[S_1\right]}_{G^{″}})\right|-\left|{\left[S_1\right]}_{G^{″}}\right|+1+\left|v_l({\left[S_2\right]}_{G^{″}})\right|-\left|{\left[S_2\right]}_{G^{″}}\right|+1.$$

Therefore ${\mathcal{D}}_{G^{\prime }}(S)={\mathsf{\Gamma }}_1,{\mathsf{\Sigma }}_1,{\mathsf{\Gamma }}_2,{\mathsf{\Sigma }}_2\Rightarrow {\mathsf{\Pi }}_1,{\mathsf{\Delta }}_1,{\mathsf{\Pi }}_2,{\mathsf{\Delta }}_2$ by

$${\mathsf{\Pi }}_1=(\left|v_l({\left[S_1\right]}_{G^{″}})\right|-\left|{\left[S_1\right]}_{G^{″}}\right|+1)t,{\mathsf{\Pi }}_1\backslash (\left|v_l({\left[S_1\right]}_{G^{″}})\right|-\left|{\left[S_1\right]}_{G^{″}}\right|+1)t$$

$${\mathsf{\Pi }}_2=(\left|v_l({\left[S_2\right]}_{G^{″}})\right|-\left|{\left[S_2\right]}_{G^{″}}\right|+1)t,{\mathsf{\Pi }}_2\backslash (\left|v_l({\left[S_2\right]}_{G^{″}})\right|-\left|{\left[S_2\right]}_{G^{″}}\right|+1)t$$

$${\mathcal{D}}_{G^{\prime }}(S)={\mathsf{\Gamma }}_1,{\mathsf{\Sigma }}_1,{\mathsf{\Gamma }}_2,{\mathsf{\Sigma }}_2\Rightarrow (\left|v_l({\left[S\right]}_{G^{\prime }})\right|-\left|{\left[S\right]}_{G^{\prime }}\right|+1)t,$$

$${\mathsf{\Pi }}_1\backslash (\left|v_l({\left[S_1\right]}_{G^{″}})\right|-\left|{\left[S_1\right]}_{G^{″}}\right|+1)t,{\mathsf{\Delta }}_1,{\mathsf{\Pi }}_2\backslash (\left|v_l({\left[S_2\right]}_{G^{″}})\right|-\left|{\left[S_2\right]}_{G^{″}}\right|+1)t,{\mathsf{\Delta }}_2$$

where $\lambda t=\underset{\lambda }{\underbrace{\{t,\cdots ,t\}}}$.  □

Lemma 8.

(Appendix A.5.1) If there exists a proof τ of G in ${\mathbf{GL}}_{\mathsf{\Omega }}$ then there exists a proof of $\mathcal{D}(G)$ in $\mathbf{GL}$, i.e., $(\mathcal{D})$ is admissible in ${\mathbf{GL}}_{\mathsf{\Omega }}$.

Proof. 

We proceed by induction on the height of $\tau$. For the base step, if G is $p_k\Rightarrow p_k$ then $\mathcal{D}(G)$ is $\Rightarrow t$ otherwise $\mathcal{D}(G)$ is G then ${⊢}_{\mathbf{GL}}\mathcal{D}(G)$ holds. For the induction step, the following cases are considered.

Case 1 Let

$$\frac{G^{\prime }|S^{\prime }}{G^{\prime }|S^{″}}({\to }_r)\in \tau$$

where

$$S^{\prime }\equiv A,\mathsf{\Gamma },{\{p_{i_k}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_k}\}}_{k=1}^{\mu },\mathsf{\Delta },B,$$

$$S^{″}\equiv \mathsf{\Gamma },{\{p_{i_k}\}}_{k=1}^{\lambda }\Rightarrow {\{p_{j_k}\}}_{k=1}^{\mu },\mathsf{\Delta },A\to B.$$

Then ${\left[S^{″}\right]}_{G^{\prime }|S^{″}}={\left[S^{\prime }\right]}_{G^{\prime }|S^{\prime }}\backslash \{S^{\prime }\}|S^{″}$ by $v_l(S^{\prime })=v_l(S^{″})$, $v_r(S^{\prime })=v_r(S^{″})$ and Lemma 6(iii). Let ${\mathcal{D}}_{G^{\prime }|S^{\prime }}(S^{\prime })=A,\mathsf{\Gamma },{\mathsf{\Gamma }}^{″}\Rightarrow {\mathsf{\Delta }}^{″},\mathsf{\Delta },B$ then ${\mathcal{D}}_{G^{\prime }|S^{″}}(S^{″})=\mathsf{\Gamma },{\mathsf{\Gamma }}^{″}\Rightarrow {\mathsf{\Delta }}^{″},\mathsf{\Delta },A\to B$ thus a proof of $\mathcal{D}(G^{\prime }|S^{″})$ is constructed by combining the proof of $\mathcal{D}(G^{\prime }|S^{\prime })$ and $\frac{{\mathcal{D}}_{G^{\prime }|S^{\prime }}(S^{\prime })}{{\mathcal{D}}_{G^{\prime }|S^{″}}(S^{″})}({\to }_r)$. Other rules of type $(I)$ are processed by a procedure similar to above.

Case 2 Let

$$\frac{G_1|S_1{G}_2|S_2}{G_1|G_2|S_3}({\odot }_r)\in \tau$$

where

$$S_1\equiv {\mathsf{\Gamma }}_1,{\{p_{i_k^1}\}}_{k=1}^{{\lambda }_1}\Rightarrow {\{p_{j_k^1}\}}_{k=1}^{{\mu }_1},A,{\mathsf{\Delta }}_1$$

$$S_2\equiv {\mathsf{\Gamma }}_2,{\{p_{i_k^2}\}}_{k=1}^{{\lambda }_2}\Rightarrow {\{p_{j_k^2}\}}_{k=1}^{{\mu }_2},B,{\mathsf{\Delta }}_2$$

$$S_3\equiv {\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,{\{p_{i_k^1}\}}_{k=1}^{{\lambda }_1},{\{p_{i_k^2}\}}_{k=1}^{{\lambda }_2}\Rightarrow {\{p_{j_k^2}\}}_{k=1}^{{\mu }_2},{\{p_{j_k^1}\}}_{k=1}^{{\mu }_1},A\odot B,{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2.$$

Let

$${\mathcal{D}}_{G_1|S_1}(S_1)={\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_{11}\Rightarrow {\mathsf{\Delta }}_{11},(\left|v_l({\left[S_1\right]}_{G_1|S_1})\right|-\left|{\left[S_1\right]}_{G_1|S_1}\right|+1)t,A,{\mathsf{\Delta }}_1,$$

$${\mathcal{D}}_{G_2|S_2}(S_2)={\mathsf{\Gamma }}_2,{\mathsf{\Gamma }}_{21}\Rightarrow {\mathsf{\Delta }}_{21},(\left|v_l({\left[S_2\right]}_{G_2|S_2})\right|-\left|{\left[S_2\right]}_{G_2|S_2}\right|+1)t,B,{\mathsf{\Delta }}_2.$$

Then ${\mathcal{D}}_{G_1|G_2|S_3}(S_3)$ is

$${\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,{\mathsf{\Gamma }}_{11},{\mathsf{\Gamma }}_{21}\Rightarrow {\mathsf{\Delta }}_{11},{\mathsf{\Delta }}_{21},A\odot B,{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2,$$

$$(\left|v_l({\left[S_1\right]}_{G_1|S_1})\right|+\left|v_l({\left[S_2\right]}_{G_2|S_2})\right|-\left|{\left[S_1\right]}_{G_1|S_1}\right|-\left|{\left[S_2\right]}_{G_2|S_2}\right|+2)t$$

by ${\left[S_3\right]}_{G_1|G_2|S_3}=({\left[S_1\right]}_{G_1|S_1}\backslash \{S_1\})\bigcup ({\left[S_2\right]}_{G_2|S_2}\backslash \{S_2\})\bigcup \{S_3\}$. Then the proof of $\mathcal{D}(G_1|G_2|S_3)$ is constructed by combining ${⊢}_{\mathbf{GL}}\mathcal{D}(G_1|S_1)$ and

${⊢}_{\mathbf{GL}}\mathcal{D}(G_2|S_2)$ with $\frac{{\mathcal{D}}_{G_1|S_1}(S_1){\mathcal{D}}_{G_2|S_2}(S_2)}{{\mathcal{D}}_{G_1|G_2|S_3}(S_3)}({\odot }_r)$. All applications of $({\to }_l)$ are processed by a procedure similar to that of ${\odot }_r$ and omitted.

Case 3 Let

$$\frac{G^{\prime }{G}^{″}}{G^{‴}}({\wedge }_{rw})\in \tau$$

where

$$G^{\prime }\equiv G_1|S_1,G^{″}\equiv G_2|S_2,G^{‴}\equiv G_1|G_2|S_1^{\prime }|S_2^{\prime },$$

$$S_w\equiv {\mathsf{\Gamma }}_w,{\{p_{i_k^w}\}}_{k=1}^{{\lambda }_w}\Rightarrow {\{p_{j_k^w}\}}_{k=1}^{{\mu }_w},A_w,{\mathsf{\Delta }}_w,$$

$$S_w^{\prime }\equiv {\mathsf{\Gamma }}_w,{\{p_{i_k^w}\}}_{k=1}^{{\lambda }_w}\Rightarrow {\{p_{j_k^w}\}}_{k=1}^{{\mu }_w},A_1\wedge A_2,{\mathsf{\Delta }}_w$$

for $w=1,2.$ Then ${\left[S_1^{\prime }\right]}_{G^{‴}}={\left[S_1\right]}_{G^{\prime }}\backslash \{S_1\}|S_1^{\prime }$, ${\left[S_2^{\prime }\right]}_{G^{‴}}={\left[S_2\right]}_{G^{″}}\backslash \{S_2\}|S_2^{\prime }$ by Lemma 6 (iii). Let

$${\mathcal{D}}_{G_w|S_w}(S_w)={\mathsf{\Gamma }}_w,{\mathsf{\Gamma }}_{w1}\Rightarrow {\mathsf{\Delta }}_{w1},(\left|v_l({\left[S_w\right]}_{G_w|S_w})\right|-\left|{\left[S_w\right]}_{G_w|S_w}\right|+1)t,A_w,{\mathsf{\Delta }}_1$$

for $w=1,2.$ Then

$${\mathcal{D}}_{G^{‴}}(S_w^{\prime })={\mathsf{\Gamma }}_w,{\mathsf{\Gamma }}_{w1}\Rightarrow {\mathsf{\Delta }}_{w1},(\left|v_l({\left[S_w\right]}_{G_w|S_w})\right|-\left|{\left[S_w\right]}_{G_w|S_w}\right|+1)t,A_1\wedge A_2,{\mathsf{\Delta }}_w$$

for $w=1,2.$ Then the proof of $\mathcal{D}(G^{‴})$ is constructed by combining ${⊢}_{\mathbf{GL}}\mathcal{D}(G^{\prime })$ and ${⊢}_{\mathbf{GL}}\mathcal{D}(G^{″})$ with $\frac{{\mathcal{D}}_{G^{\prime }}(S_1){\mathcal{D}}_{G^{″}}(S_2)}{{\mathcal{D}}_{G^{‴}}(S_1^{\prime }|S_2^{\prime })}({\wedge }_{rw})$. All applications of $({\vee }_{lw})$ are processed by a procedure similar to that of $({\wedge }_{rw})$ and omitted.

Case 4 Let

$$\frac{G^{\prime }{G}^{″}}{G^{‴}}(COM)\in \tau$$

where

$$G^{\prime }\equiv G_1|S_1,G^{″}\equiv G_2|S_2,G^{‴}\equiv G_1|G_2|S_3|S_4$$

$$S_1\equiv {\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1,{\{p_{i_k^1}\}}_{k=1}^{{\lambda }_1}\Rightarrow {\{p_{j_k^1}\}}_{k=1}^{{\mu }_1},{\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1,$$

$$S_2\equiv {\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\{p_{i_k^2}\}}_{k=1}^{{\lambda }_2}\Rightarrow {\{p_{j_k^2}\}}_{k=1}^{{\mu }_2},{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2,$$

$$S_3\equiv {\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,{\{p_{i_{1k}^1}\}}_{k=1}^{{\lambda }_{11}},{\{p_{i_{1k}^2}\}}_{k=1}^{{\lambda }_{21}}\Rightarrow {\{p_{j_{1k}^1}\}}_{k=1}^{{\mu }_{11}},{\{p_{j_{1k}^2}\}}_{k=1}^{{\mu }_{21}},{\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2,$$

$$S_4\equiv {\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2,{\{p_{i_{2k}^1}\}}_{k=1}^{{\lambda }_{12}},{\{p_{i_{2k}^2}\}}_{k=1}^{{\lambda }_{22}}\Rightarrow {\{p_{j_{2k}^1}\}}_{k=1}^{{\mu }_{12}},{\{p_{j_{2k}^2}\}}_{k=1}^{{\mu }_{22}},{\mathsf{\Sigma }}_1,{\mathsf{\Sigma }}_2$$

where ${\{p_{i_k^w}\}}_{k=1}^{{\lambda }_w}={\{p_{i_{1k}^w}\}}_{k=1}^{{\lambda }_{w1}}\bigcup {\{p_{i_{2k}^w}\}}_{k=1}^{{\lambda }_{w2}},{\{p_{j_k^w}\}}_{k=1}^{{\mu }_w}={\{p_{j_{1k}^w}\}}_{k=1}^{{\mu }_{w1}}\bigcup {\{p_{j_{2k}^w}\}}_{k=1}^{{\mu }_{w2}}$ for $w=1,2.$

Case 4.1.$S_3\in {\left[S_4\right]}_{G^{‴}}$. Then ${\left[S_3\right]}_{G^{‴}}={\left[S_4\right]}_{G^{‴}}$ by Lemma 6(ii) and

${\left[S_3\right]}_{G^{‴}}={\left[S_1\right]}_{G^{\prime }}|{\left[S_2\right]}_{G^{″}}|S_3|S_4\backslash \{S_1,S_2\}$ by Lemma 6(iii). Then

$$\left|v_l({\left[S_3\right]}_{G^{‴}})\right|-\left|{\left[S_3\right]}_{G^{‴}}\right|+1=\left|v_l({\left[S_1\right]}_{G^{\prime }})\right|+\left|v_l({\left[S_2\right]}_{G^{″}})\right|-\left|{\left[S_1\right]}_{G^{\prime }}\right|-\left|{\left[S_2\right]}_{G^{″}}\right|+1⩾0.$$

Thus $\left|v_l({\left[S_1\right]}_{G^{\prime }})\right|-\left|{\left[S_1\right]}_{G^{\prime }}\right|+1⩾1$ or $\left|v_l({\left[S_2\right]}_{G^{″}})\right|-\left|{\left[S_2\right]}_{G^{″}}\right|+1⩾1$. Hence we assume that, without loss of generality,

$${\mathcal{D}}_{G^{\prime }}(S_1)={\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1,{\mathsf{\Gamma }}^{\prime }\Rightarrow {\mathsf{\Delta }}^{\prime },t,{\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1,$$

$${\mathcal{D}}_{G^{″}}(S_2)={\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\mathsf{\Gamma }}^{″}\Rightarrow {\mathsf{\Delta }}^{″},{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2.$$

Then

$${\mathcal{D}}_{G^{‴}}(S_3|S_4)={\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1,{\mathsf{\Gamma }}^{\prime },{\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\mathsf{\Gamma }}^{″}\Rightarrow {\mathsf{\Delta }}^{\prime },{\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1,{\mathsf{\Delta }}^{″},{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2.$$

Thus the proof of $\frac{\underline{{\mathcal{D}}_{G^{\prime }}(S_1){\mathcal{D}}_{G^{″}}(S_2)}}{{\mathcal{D}}_{G^{‴}}(S_3|S_4)}$ is constructed by

$$\frac{{\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1,{\mathsf{\Gamma }}^{\prime }\Rightarrow {\mathsf{\Delta }}^{\prime },t,{\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1\frac{{\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\mathsf{\Gamma }}^{″}\Rightarrow {\mathsf{\Delta }}^{″},{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2}{{\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\mathsf{\Gamma }}^{″},t\Rightarrow {\mathsf{\Delta }}^{″},{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2}(t_l)}{{\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1,{\mathsf{\Gamma }}^{\prime },{\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\mathsf{\Gamma }}^{″}\Rightarrow {\mathsf{\Delta }}^{\prime },{\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1,{\mathsf{\Delta }}^{″},{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2}(CUT).$$

Case 4.2.$S_3\notin {\left[S_4\right]}_{G^{‴}}$. Then ${\left[S_3\right]}_{G^{‴}}\bigcap {\left[S_4\right]}_{G^{‴}}=\varnothing$ by Lemma 6(ii). Let

$$S_{3w}\equiv {\mathsf{\Gamma }}_w,{\{p_{i_{1k}^w}\}}_{k=1}^{{\lambda }_{w1}}\Rightarrow {\{p_{j_{1k}^w}\}}_{k=1}^{{\mu }_{w1}},{\mathsf{\Delta }}_w,$$

$$S_{4w}\equiv {\mathsf{\Pi }}_w,{\{p_{i_{2k}^w}\}}_{k=1}^{{\lambda }_{w2}}\Rightarrow {\{p_{j_{2k}^w}\}}_{k=1}^{{\mu }_{w2}},{\mathsf{\Sigma }}_w,$$

for $w=1,2.$ Then

$${\left[S_3\right]}_{G^{‴}}={\left[S_{31}\right]}_{G_1|S_{31}|S_{41}}\backslash \{S_{31}\}\bigcup {\left[S_{32}\right]}_{G_2|S_{32}|S_{42}}\backslash \{S_{32}\}\bigcup \{S_3\},$$

$${\left[S_4\right]}_{G^{‴}}={\left[S_{41}\right]}_{G_1|S_{31}|S_{41}}\backslash \{S_{41}\}\bigcup {\left[S_{42}\right]}_{G_2|S_{32}|S_{42}}\backslash \{S_{42}\}\bigcup \{S_4\}$$

by $v_l(S_3)=v_l(S_{31}|S_{32})$, $v_l(S_1)=v_l(S_{31}|S_{41})$, $v_l(S_2)=v_l(S_{32}|S_{42})$ and $v_l(S_4)=v_l(S_{41}|S_{42})$. Let

$${\mathcal{D}}_{G_w|S_{3w}|S_{4w}}(S_{3w})={\mathsf{\Gamma }}_w,{\mathrm{X}}_{3w}\Rightarrow {\mathsf{\Psi }}_{3w},{\mathsf{\Delta }}_w,$$

$${\mathcal{D}}_{G_w|S_{3w}|S_{4w}}(S_{4w})={\mathsf{\Pi }}_w,{\mathrm{X}}_{4w}\Rightarrow {\mathsf{\Psi }}_{4w},{\mathsf{\Sigma }}_w$$

for $w=1,2.$ Then

$${\mathcal{D}}_{G^{\prime }}(S_1)={\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1,{\mathrm{X}}_{31},{\mathrm{X}}_{41}\Rightarrow {\mathsf{\Psi }}_{31},{\mathsf{\Psi }}_{41},{\mathsf{\Sigma }}_1,{\mathsf{\Delta }}_1,$$

$${\mathcal{D}}_{G^{″}}(S_2)={\mathsf{\Gamma }}_2,{\mathsf{\Pi }}_2,{\mathrm{X}}_{32},{\mathrm{X}}_{42}\Rightarrow {\mathsf{\Psi }}_{32},{\mathsf{\Psi }}_{42},{\mathsf{\Sigma }}_2,{\mathsf{\Delta }}_2,$$

$${\mathcal{D}}_{G^{‴}}(S_3)={\mathsf{\Gamma }}_1,{\mathrm{X}}_{31},{\mathsf{\Gamma }}_2,{\mathrm{X}}_{32}\Rightarrow {\mathsf{\Psi }}_{31},{\mathsf{\Delta }}_1,{\mathsf{\Psi }}_{32},{\mathsf{\Delta }}_2,$$

$${\mathcal{D}}_{G^{‴}}(S_4)={\mathsf{\Pi }}_1,{\mathrm{X}}_{41},{\mathsf{\Pi }}_2,{\mathrm{X}}_{42}\Rightarrow {\mathsf{\Psi }}_{41},{\mathsf{\Sigma }}_1,{\mathsf{\Psi }}_{42},{\mathsf{\Sigma }}_2$$

by Lemma 7, ${\left[S_3\right]}_{G^{‴}}\bigcap {\left[S_4\right]}_{G^{‴}}=\varnothing ,{\left[S_{31}\right]}_{G_1|S_{31}|S_{41}}\bigcap {\left[S_{41}\right]}_{G_1|S_{31}|S_{41}}=\varnothing ,{\left[S_{32}\right]}_{G_2|S_{32}|S_{42}}\bigcap {\left[S_{42}\right]}_{G_2|S_{32}|S_{42}}=\varnothing$. Then the proof of ${\mathcal{D}}_{G^{‴}}(S_3|S_4)$ is constructed by combing the proofs of ${\mathcal{D}}_{G^{\prime }}(S_1)$ and ${\mathcal{D}}_{G^{″}}(S_2)$ with $\frac{{\mathcal{D}}_{G^{\prime }}(S_1){\mathcal{D}}_{G^{″}}(S_2)}{{\mathcal{D}}_{G^{‴}}(S_3|S_4)}(COM).$

Case 5$\frac{G^{\prime }|G^{″}|G^{‴}}{G^{\prime }|G^{″}}(E{C}_{\mathsf{\Omega }})\in \tau$. Then $G^{\prime },G^{″}$ and $G^{‴}$ are closed and $G^{‴}$ is a copy of $G^{″}$ thus ${\mathcal{D}}_{G^{\prime }|G^{″}|G^{‴}}(G^{″})={\mathcal{D}}_{G^{\prime }|G^{″}|G^{‴}}(G^{‴})$ hence a proof of $\mathcal{D}(G^{\prime }|G^{″})$ is constructed by combining the proof of $\mathcal{D}(G^{\prime }|G^{″}|G^{‴})$ and $\frac{\mathcal{D}(G^{\prime }|G^{″}|G^{‴})}{\mathcal{D}(G^{\prime }|G^{″})}(E{C}^{*})$.  □

The following two lemmas are corollaries of Lemma 8.

Lemma 9.

If there exists a derivation of $G_0$ from $G_1,\cdots ,G_r$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$ then there exists a derivation of $\mathcal{D}(G_0)$ from $\mathcal{D}(G_1),\cdots ,\mathcal{D}(G_r)$ in $\mathbf{GL}$.

Lemma 10.

Let τ be a cut-free proof of $G_0$ in $\mathbf{GL}$ and ${\tau }^{*}$ be the proof of $G|G^{*}$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$ resulting from preprocessing of τ. Then ${⊢}_{\mathbf{GL}}\mathcal{D}(G|G^{*})$.

6. Extraction of Elimination Rules

In this section, we will investigate Construction 1 further to extract more derivations from ${\tau }^{*}$.

Any two sequents in a hypersequent seem independent of one another in the sense that they can only be contracted into one by $(EC)$ when it is applicable. Note that one-premise logical rules just modify one sequent of a hypersequent and two-premise rules associate a sequent in a hypersequent with one in a different hypersequent.

${\tau }^{*}$ (or any proof without $(E{C}_{\mathsf{\Omega }})$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$) has an essential property, which we call the distinguishability of ${\tau }^{*}$, i.e., any variables, formulas, sequents or hypersequents which occur at the node H of ${\tau }^{*}$ occur inevitably at $H^{\prime }<H$ in some forms.

Let $H\equiv G^{\prime }|S^{\prime }|S^{″}\in {\tau }^{*}$. If $S^{\prime }$ is equal to $S^{″}$ as two sequents then the case that ${\tau }_{H:S^{\prime }}^{*}$ is equal to ${\tau }_{H:S^{″}}^{*}$ as two derivations could possibly happen. This means that both $S^{\prime }$ and $S^{″}$ are the focus sequent of one node in ${\tau }^{*}$ when $G_{H:S^{\prime }}^{*}\ne S^{\prime }$ and $G_{H:S^{″}}^{*}\ne S^{″}$, which contradicts that each node has the unique focus sequent in any derivation. Thus we need to differentiate $S^{\prime }$ from $S^{″}$ for all $G^{\prime }|S^{\prime }|S^{″}\in {\tau }^{*}$.

Define $\overline{S^{\prime }}\in {\tau }^{*}$ such that $G^{\prime }|S^{\prime }|S^{″}⩽\overline{S^{\prime }}$, $S^{\prime }\in \overline{S^{\prime }}$ and $S^{\prime }$ is the principal sequent of $\overline{S^{\prime }}$. If $\overline{S^{\prime }}$ has the unique principal sequent, $N_{S^{\prime }}:=0$, otherwise $N_{S^{\prime }}:=1$ (or $N_{S^{\prime }}=2)$ to indicate that $S^{\prime }$ is one designated principal sequent (or accordingly $N_{S^{\prime }}=2$ for another) of such an application as $(COM),({\wedge }_{rw})$ or $({\vee }_{lw})$. Then we may regard $S^{\prime }$ as $(S^{\prime };\mathcal{P}(\overline{S^{\prime }}),N_{S^{\prime }})$. Thus $S^{\prime }$ is always different from $S^{″}$ by $\mathcal{P}(\overline{S^{\prime }})\ne \mathcal{P}(\overline{S^{″}})$ or, $\mathcal{P}(\overline{S^{\prime }})=\mathcal{P}(\overline{S^{″}})$ and $N_{S^{\prime }}\ne N_{S^{″}}$. We formulate it by the following construction.

Construction 3.

(Appendix A.5.2) A labeled tree ${\tau }^{**}$, which has the same tree structure as ${\tau }^{*}$, is constructed as follows.

(i) If S is a leaf ${\tau }^{*}$, define $\overline{S}=S$, $N_S=0$ and the node $\mathcal{P}(S)$ of ${\tau }^{**}$ is labeled by $(S;\mathcal{P}(\overline{S}),N_S)$;

(ii) If $\frac{G^{\prime }|S^{\prime }}{H\equiv G^{\prime }|S^{″}}(I)\in {\tau }^{*}$ and $\mathcal{P}(G^{\prime }|S^{\prime })$ be labeled by ${\mathcal{G}}^{\prime }|(S^{\prime };\mathcal{P}(\overline{S^{\prime }}),N_{S^{\prime }})$ in ${\tau }^{**}$. Then define $\overline{S^{″}}=H$, $N_{S^{″}}=0$ and the node $\mathcal{P}(H)$ of ${\tau }^{**}$ is labeled by ${\mathcal{G}}^{\prime }|(S^{″};\mathcal{P}(\overline{S^{″}}),N_{S^{″}})$;

(iii) If $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{H\equiv G^{\prime }|G^{″}|H^{\prime }}(II)\in {\tau }^{*}$, $\mathcal{P}(G^{\prime }|S^{\prime })$ and $\mathcal{P}(G^{″}|S^{″})$ be labeled by ${\mathcal{G}}^{\prime }|(S^{\prime };\mathcal{P}(\overline{S^{\prime }}),N_{S^{\prime }})$ and ${\mathcal{G}}^{″}|(S^{″};\mathcal{P}(\overline{S^{″}}),N_{S^{″}})$ in ${\tau }^{**}$, respectively. If $H^{\prime }=S_1|S_2$ then define $\overline{S_1}=\overline{S_2}=H$, $N_{S_1}=1$, $N_{S_2}=2$ and the node $\mathcal{P}(H)$ of ${\tau }^{**}$ is labeled by ${\mathcal{G}}^{\prime }|{\mathcal{G}}^{″}|(S_1;\mathcal{P}(\overline{S_1}),N_{S_1})|(S_2;\mathcal{P}(\overline{S_2}),N_{S_2})$. If $H^{\prime }=S_1$ then define $\overline{S_1}=H$, $N_{S_1}=0$ and $\mathcal{P}(H)$ is labeled by ${\mathcal{G}}^{\prime }|{\mathcal{G}}^{″}|(S_1;\mathcal{P}(\overline{S_1}),N_{S_1})$.

In the whole paper, we treat ${\tau }^{*}$ as ${\tau }^{**}$ without mention of ${\tau }^{**}$. Note that in preprocessing of $\tau$, some logical applications could also be converted to $(I{D}_{\mathsf{\Omega }})$ in Step 3 and we need fix the focus sequent at each node H and subsequently assign valid identification numbers to each $H^{\prime }<H$ by eigenvariable-labeling operation.

Proposition 3.

(i) $G^{\prime }|S^{\prime }|S^{″}\in {\tau }^{*}$ implies $\{S^{\prime }\}\bigcap \{S^{″}\}=\varnothing$; (ii) $H\in {\tau }^{*}$ and $H^{\prime }|H^{″}\subseteq H$ imply $H^{\prime }\bigcap H^{″}=\varnothing$; (iii) Let $H\in {\tau }^{*}$ and $S_i^c\in H$ then $H⩽H_i^c$ or $H_i^c⩽H$.

Proof. 

(iii) Let $S_i^c\in H$ then $S_i^c=S_{iu}^c$ for some $1⩽u⩽m_i$ by Notation 5. Thus $S_i^c\in H_i^c$ also by Notation 5. Hence $H⩽\overline{S_i^c}$ and $H_i^c⩽\overline{S_i^c}$ by Construction 3. Therefore $H⩽H_i^c$ or $H_i^c⩽H$.  □

Lemma 11.

Let $H\in {\tau }^{*}$ and $Th(H)=(H_0,\cdots ,H_n)$, where $H_0=H$, $H_n=G|G^{*}$, $G_k\subseteq H$ for $1⩽k⩽3$.

(i) If $G_3=G_1\bigcap G_2$ then ${⟨H_i⟩}_{H:G_3}={⟨H_i⟩}_{H:G_1}\bigcap {⟨H_i⟩}_{H:G_2}$ for all $0⩽i⩽n$;

(ii) If $G_3=G_1|G_2$ then ${⟨H_i⟩}_{H:G_3}={⟨H_i⟩}_{H:G_1}|{⟨H_i⟩}_{H:G_2}$ for all $0⩽i⩽n$.

Proof. 

The proof is by induction on i for $0⩽i<n$. Only (i) is proved as follows and (ii) by a similar procedure and omitted.

For the base step, ${⟨H_0⟩}_{H:G_3}={⟨H_0⟩}_{H:G_1}\bigcap {⟨H_0⟩}_{H:G_2}$ holds by ${⟨H_0⟩}_{H:G_1}=G_1$, ${⟨H_0⟩}_{H:G_2}=G_2$, ${⟨H_0⟩}_{H:G_3}=G_3$ and $G_3=G_1\bigcap G_2$.

For the induction step, suppose that ${⟨H_i⟩}_{H:G_3}={⟨H_i⟩}_{H:G_1}\bigcap {⟨H_i⟩}_{H:G_2}$ for some $0⩽i<n$. Only is the case of a one-premise rule given in the following and other cases are omitted.

Let $\frac{G^{\prime }|S^{\prime }}{G^{\prime }|S^{″}}(I)\in {\tau }^{*}$, $H_i=G^{\prime }|S^{\prime }$ and $H_{i+1}=G^{\prime }|S^{″}$.

Let $S^{\prime }\in {⟨H_i⟩}_{H:G_3}$. Then ${⟨H_{i+1}⟩}_{H:G_3}=({⟨H_i⟩}_{H:G_3}\backslash \{S^{\prime }\})|S^{″}$, ${⟨H_{i+1}⟩}_{H:G_1}=({⟨H_i⟩}_{H:G_1}\backslash \{S^{\prime }\})|S^{″}$ by $S^{\prime }\in {⟨H_i⟩}_{H:G_1}$ and

$${⟨H_{i+1}⟩}_{H:G_2}=({⟨H_i⟩}_{H:G_2}\backslash \{S^{\prime }\})|S^{″}\mathrm{by}{S}^{\prime }\in {⟨H_i⟩}_{H:G_2}.$$

Thus

$${⟨H_{i+1}⟩}_{H:G_3}={⟨H_{i+1}⟩}_{H:G_1}\bigcap {⟨H_{i+1}⟩}_{H:G_2}\mathrm{by}{⟨H_i⟩}_{H:G_3}={⟨H_i⟩}_{H:G_1}\bigcap {⟨H_i⟩}_{H:G_2}.$$

Let $S^{\prime }\notin {⟨H_i⟩}_{H:G_1}$ and $S^{\prime }\notin {⟨H_i⟩}_{H:G_2}$. Then ${⟨H_{i+1}⟩}_{H:G_1}={⟨H_i⟩}_{H:G_1}$,

$${⟨H_{i+1}⟩}_{H:G_2}={⟨H_i⟩}_{H:G_2}\mathrm{and}{⟨H_{i+1}⟩}_{H:G_3}={⟨H_i⟩}_{H:G_3}.$$

Thus

$${⟨H_{i+1}⟩}_{H:G_3}={⟨H_{i+1}⟩}_{H:G_1}\bigcap {⟨H_{i+1}⟩}_{H:G_2}\mathrm{by}{⟨H_i⟩}_{H:G_3}={⟨H_i⟩}_{H:G_1}\bigcap {⟨H_i⟩}_{H:G_2}.$$

Let $S^{\prime }\notin {⟨H_i⟩}_{H:G_1},S^{\prime }\in {⟨H_i⟩}_{H:G_2}$. Then ${⟨H_{i+1}⟩}_{H:G_1}={⟨H_i⟩}_{H:G_1}$,

$${⟨H_{i+1}⟩}_{H:G_3}={⟨H_i⟩}_{H:G_3}\mathrm{and}{⟨H_{i+1}⟩}_{H:G_2}=({⟨H_i⟩}_{H:G_2}\backslash \{S^{\prime }\})|S^{″}.$$

Thus

$${⟨H_{i+1}⟩}_{H:G_3}={⟨H_{i+1}⟩}_{H:G_1}\bigcap {⟨H_{i+1}⟩}_{H:G_2}\mathrm{by}{⟨H_i⟩}_{H:G_3}={⟨H_i⟩}_{H:G_1}\bigcap {⟨H_i⟩}_{H:G_2},S^{″}\notin {⟨H_{i+1}⟩}_{H:G_1}.$$

The case of $S^{\prime }\notin {⟨H_i⟩}_{H:G_2},S^{\prime }\in {⟨H_i⟩}_{H:G_1}$ is proved by a similar procedure and omitted.  □

Lemma 12.

(i) Let $G^{\prime }|S^{\prime }\in {\tau }^{*}$ then $G_{G^{\prime }|S^{\prime }:S^{\prime }}^{*}\bigcap G_{G^{\prime }|S^{\prime }:G^{\prime }}^{*}=\varnothing ,G_{G^{\prime }|S^{\prime }:G^{\prime }}^{*}|G_{G^{\prime }|S^{\prime }:S^{\prime }}^{*}=G|G^{*};$

(ii) $H\in {\tau }^{*}$, $H^{\prime }|H^{″}\subseteq H$ then $G_{H:H^{\prime }|H^{″}}^{*}=G_{H:H^{\prime }}^{*}|G_{H:H^{″}}^{*}$.

Proof. 

(i) and (ii) are immediately from Lemma 11.  □

Notation 6.

We write ${\tau }_{H_i^c:S_{i1}^c}^{*}$, $G_{H_i^c:S_{i1}^c}^{*}$ as ${\tau }_{S_{i1}^c}^{*}$, $G_{S_{i1}^c}^{*}$, respectively, for the sake of simplicity.

Lemma 13.

(i) $G_{S_{i1}^c}^{*}\subseteq G|G^{*}$;

(ii) ${\tau }_{S_{i1}^c}^{*}$ is a derivation of $G_{S_{i1}^c}^{*}$ from $S_{i1}^c$, which we denote by $\frac{\underline{S_{i1}^c}}{G_{S_{i1}^c}^{*}}⟨{\tau }_{S_{i1}^c}^{*}⟩$;

(iii) $G_{S_{iu}^c}^{*}=S_{iu}^c$ and ${\tau }_{S_{iu}^c}^{*}$ consists of a single node $S_{iu}^c$ for all $2⩽u⩽m_i$;

(iv) $v_l(G_{S_{i1}^c}^{*})\backslash v_l(S_{i1}^c)=v_r(G_{S_{i1}^c}^{*})\backslash v_r(S_{i1}^c)$;

(v) ${⟨H⟩}_{S_{i1}^c}\in {\tau }_{S_{i1}^c}^{*}$ implies $H⩽H_i^c$. Note that ${⟨H⟩}_{S_{i1}^c}$ is undefined for any $H>H_i^c$ or $H\parallel H_i^c$.

(vi) $S_j^c\in G_{S_{i1}^c}^{*}$ implies $H_i^c\nleqq H_j^c$.

Proof. 

Claims from (i) to (v) follow immediately from Construction 1 and Lemma 4.

(vi) Since $S_j^c\in G_{S_{i1}^c}^{*}\subseteq G|G^{*}$ then $S_j^c$ has the form $S_{ju}^c$ for some $u\ge 2$ by Notation 5. Then $G_{S_j^c}^{*}=S_j^c$ by (iii). Suppose that $H_i^c⩽H_j^c$. Then $S_j^c$ is transferred from $H_j^c$ downward to $H_i^c$ and in side-hypersequent of $H_i^c$ by Notation 5 and $G|G^{*}<H_i^c⩽H_j^c$. Thus $\{S_{i1}^c\}\bigcap \{S_j^c\}=\varnothing$ at $H_i^c$ since $S_{i1}^c$ is the unique focus sequent of $H_i^c$. Hence $S_j^c\notin G_{S_{i1}^c}^{*}$ by Lemma 11 and (iii), a contradiction therefore $H_i^c\nleqq H_j^c$.  □

Lemma 14.

Let $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{H\equiv G^{\prime }|G^{″}|H^{\prime }}(II)\in {\tau }^{*}$. (i) If $S_j^c\in G_{H:H^{\prime }}^{*}$ then $H_j^c⩽H$ or $H_j^c\parallel H$; (ii) If $S_j^c\in G_{H:G^{″}}^{*}$ then $H_j^c⩽H$ or $H_j^c\parallel G^{\prime }|S^{\prime }$.

Proof. 

(i) We impose a restriction on $(II)$ such that each sequent in $H^{\prime }$ is different from $S^{\prime }$ or $S^{″}$ otherwise we treat it as an $(EW)$-application. Since $S_j^c\in G_{H:H^{\prime }}^{*}\subseteq G|G^{*}$ then $S_j^c$ has the form $S_{ju}^c$ for some $u\ge 2$ by Notation 5. Thus $G_{S_j^c}^{*}=S_j^c$. Suppose that $H_j^c>H$. Then $S_j^c$ is transferred from $H_j^c$ downward to H. Thus $S_j^c\in H^{\prime }$ by $G_{S_j^c}^{*}=S_j^c\in G_{H:H^{\prime }}^{*}$ and Lemma 11. Hence $S_j^c=S^{\prime }$ or $S_j^c=S^{″}$, a contradiction with the restriction above. Therefore $H_j^c⩽H$ or $H_j^c\parallel H$.

(ii) Let $S_j^c\in G_{H:G^{″}}^{*}$. If $H_j^c>H$ then $S_j^c\in H$ by Proposition 2(i) and thus $S_j^c\in G^{″}$ by Lemma 11 and, hence $H_j^c\parallel G^{\prime }|S^{\prime }$ by $H_j^c⩾G^{″}|S^{″}$, $G^{\prime }|S^{\prime }\parallel G^{″}|S^{″}$. If $H_j^c\parallel H$ then $H_j^c\parallel G^{\prime }|S^{\prime }$ by $H⩽G^{\prime }|S^{\prime }$. Thus $H_j^c⩽H$ or $H_j^c\parallel G^{\prime }|S^{\prime }$.  □

Definition 21.

(i) By $H_i^c⇝H_j^c$ we mean that $S_{ju}^c\in G_{S_{i1}^c}^{*}$ for some $2⩽u⩽m_j$; (ii) By $H_i^c\leftrightsquigarrow H_j^c$ we mean that $H_i^c⇝H_j^c$ and $H_j^c⇝H_i^c$; (iii) $H_i^c{H}_j^c$ means that $S_{ju}^c\notin G_{S_{i1}^c}^{*}$ for all $2⩽u⩽m_j$.

Then Lemma 13(vi) shows that $H_i^c⇝H_j^c$ implies $H_i^c\nleqq H_j^c$.

Lemma 15.

Let $H_i^c\parallel H_j^c$, $H_i^c⇝H_j^c$, $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{G^{\prime }|G^{″}|H^{\prime }}(II)\in {\tau }^{*}$ such that $G^{\prime }|S^{\prime }⩽H_i^c$, $G^{″}|S^{″}⩽H_j^c$. Then $S^{\prime }\in {⟨G^{\prime }|S^{\prime }⟩}_{S_{i1}^c}$.

Proof. 

Suppose that $S^{\prime }\notin {⟨G^{\prime }|S^{\prime }⟩}_{S_{i1}^c}$. Then ${⟨G^{\prime }|S^{\prime }⟩}_{S_{i1}^c}\subseteq G^{\prime }$ by ${⟨G^{\prime }|S^{\prime }⟩}_{S_{i1}^c}\subseteq G^{\prime }|S^{\prime }$, ${⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{S_{i1}^c}={⟨G^{\prime }|S^{\prime }⟩}_{S_{i1}^c}$ by Construction 1. Thus ${⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{S_{i1}^c}\subseteq G^{\prime }$. Hence $G^{″}|H^{\prime }\bigcap {⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{S_{i1}^c}=\varnothing$ by Proposition 3(ii). Therefore $S_{ju}^c\notin G_{S_{i1}^c}^{*}$ for all $1⩽u⩽m_j$ by Lemma 11, i.e., $H_i^c{H}_j^c$, a contradiction and hence $S^{\prime }\in {⟨G^{\prime }|S^{\prime }⟩}_{S_{i1}^c}$.  □

Lemma 13(ii) shows that ${\tau }_{S_{i1}^c}^{*}$ is a derivation of $G_{S_{i1}^c}^{*}$ from one premise $S_{i1}^c$. We generalize it by introducing derivations from multiple premises in the following. In the remainder of this section, let $I=\{H_{i_1}^c,\cdots ,H_{i_m}^c\}\subseteq \{H_1^c,\cdots ,H_N^c\}$, $H_{i_k}^c\leftrightsquigarrow H_{i_q}^c$ for all $1⩽k<q⩽m$. Then $H_{i_k}^c\nleqq H_{i_q}^c$ and $H_{i_q}^c\nleqq H_{i_k}^c$ by Lemma 13(vi) thus $H_{i_k}^c\parallel H_{i_q}^c$ for all $1⩽k<q⩽m$.

Notation 7.

$H_I^V$ denotes the intersection node of $H_{i_1}^c,\cdots ,H_{i_m}^c$. We sometimes write the intersection node of $H_i^c$ and $H_j^c$ as $H_{ij}^V$. If $I=\{H_i^c\}$, $H_I^V:=H_i^c$, i.e., the intersection node of a single node is itself.

Let $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{G^{\prime }|G^{″}|H^{\prime }}(II)\in {\tau }^{*}$ such that $G^{\prime }|G^{″}|H^{\prime }=H_I^V$. Then I is divided into two subsets $I_l=\{H_{l_1}^c,\cdots ,H_{l_{m(l)}}^c\}$ and $I_r=\{H_{r_1}^c,\cdots ,H_{r_{m(r)}}^c\}$, which occur in the left subtree ${\tau }^{*}(G^{\prime }|S^{\prime })$ and right subtree ${\tau }^{*}(G^{″}|S^{″})$ of ${\tau }^{*}(G^{\prime }|G^{″}|H^{\prime })$, respectively.

Let $\mathcal{I}=\{S_{i_{1}1}^c,\cdots ,S_{i_{m}1}^c\}$, ${\mathcal{I}}_l=\{S_{l_{1}1}^c,\cdots ,S_{l_{m(l)}1}^c\}$, ${\mathcal{I}}_r=\{S_{r_{1}1}^c,\cdots ,S_{r_{m(r)}1}^c\}$ such that $\mathcal{I}={\mathcal{I}}_l\bigcup {\mathcal{I}}_r$. A derivation ${\tau }_{\mathcal{I}}^{*}$ of ${⟨G|G^{*}⟩}_{\mathcal{I}}$ from $S_{i_{1}1}^c,\cdots ,S_{i_{m}1}^c$ is constructed by induction on $|I|$. The base case of $\left|I\right|=1$ has been done by Construction 1. For the induction case, suppose that derivations ${\tau }_{{\mathcal{I}}_l}^{*}$ of ${⟨G|G^{*}⟩}_{{\mathcal{I}}_l}$ from $S_{l_{1}1}^c,\cdots ,S_{l_{m(l)}1}^c$ and ${\tau }_{{\mathcal{I}}_r}^{*}$ of ${⟨G|G^{*}⟩}_{{\mathcal{I}}_r}$ from $S_{r_{1}1}^c,\cdots ,S_{r_{m(r)}1}^c$ are constructed. Then ${\tau }_{\mathcal{I}}^{*}$ of ${⟨G|G^{*}⟩}_{\mathcal{I}}$ from $S_{i_{1}1}^c,\cdots ,S_{i_{m}1}^c$ is constructed as follows.

Construction 4.

(Appendix A.5.2) (i)

$${⟨H⟩}_{\mathcal{I}}:={⟨H⟩}_{{\mathcal{I}}_l}\mathrm{for}\mathrm{all}{G}^{\prime }|S^{\prime }⩽H⩽H_i^c\mathrm{for}\mathrm{some}{H}_i^c\in I_l,$$

$${⟨H⟩}_{\mathcal{I}}:={⟨H⟩}_{{\mathcal{I}}_r}\mathrm{for}\mathrm{all}{G}^{″}|S^{″}⩽H⩽H_i^c\mathrm{for}\mathrm{some}{H}_i^c\in I_r,$$

$${\tau }_{\mathcal{I}}^{*}({⟨G^{\prime }|S^{\prime }⟩}_{\mathcal{I}}):={\tau }_{{\mathcal{I}}_l}^{*}({⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_l}),{\tau }_{\mathcal{I}}^{*}({⟨G^{″}|S^{″}⟩}_{\mathcal{I}}):={\tau }_{{\mathcal{I}}_r}^{*}({⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_r});$$

(ii)

$${⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{\mathcal{I}}:={⟨G^{\prime }⟩}_{{\mathcal{I}}_l}|{⟨G^{″}⟩}_{{\mathcal{I}}_r}|H^{\prime }$$

and

$$\frac{{⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_l}{⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_r}}{{⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{\mathcal{I}}}(II)\in {\tau }_{\mathcal{I}}^{*};$$

(iii) Other nodes of ${\tau }_{\mathcal{I}}^{*}$ are built up by Construction 1(ii).

The following lemma is a generalization of Lemma 13.

Lemma 16.

Let $Th(H_{i_k}^c)=(H_{i_{k}0}^c,\cdots ,H_{i_k{n}_{i_k}}^c)$, where $1⩽k⩽m,H_{i_{k}0}^c=H_{i_k}^c$ and $H_{i_k{n}_{i_k}}^c=G|G^{*}$. Then, for all $0⩽u⩽n_{i_k}$,

(i)

$${⟨H_{i_{k}u}^c⟩}_{\mathcal{I}}=\bigcap \{{⟨H_{i_{k}u}^c⟩}_{S_{j1}^c}:H_j^c\in I,H_{i_{k}u}^c⩽H_j^c\};$$

(ii)

$$\frac{\underline{\{S_{j1}^c:H_j^c\in I,H_{i_{k}u}^c⩽H_j^c\}}}{{⟨H_{i_{k}u}^c⟩}_{\mathcal{I}}}⟨{\tau }_{\mathcal{I}}^{*}({⟨H_{i_{k}u}^c⟩}_{\mathcal{I}})⟩;$$

(iii)

$$v_l({⟨H_{i_{k}u}^c⟩}_{{}_{\mathcal{I}}})\backslash \bigcup \{v_l(S_{j1}^c):H_j^c\in I,H_{i_{k}u}^c⩽H_j^c\}=$$

$$v_r({⟨H_{i_{k}u}^c⟩}_{{}_{\mathcal{I}}})\backslash \bigcup \{v_r(S_{j1}^c):H_j^c\in I,H_{i_{k}u}^c⩽H_j^c\};$$

(iv) ${⟨H⟩}_{\mathcal{I}}\in {\tau }_{\mathcal{I}}^{*}$ if and only if $H⩽H_i^c$ for some $H_i^c\in I$. Note that ${⟨H⟩}_{\mathcal{I}}$ is undefined if $H>H_i^c$ or $H\parallel H_i^c$ for all $H_i^c\in I$.

Proof. 

(i) is proved by induction on $\left|I\right|$. For the base step, let $\left|I\right|=1$ then the claim holds clearly. For the induction step, let $\left|I\right|⩾2$ then $\left|I_l\right|⩾1$ and $\left|I_r\right|⩾1$. Then $S^{\prime }\in {⟨G^{\prime }|S^{\prime }⟩}_{S_{i1}^c}$ for all $H_i^c\in I_l$ by Lemma 15 and $H_i^c⇝H_j^c$ for all $H_j^c\in I_r$. ${⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_l}={\bigcap }_{H_i^c\in I_l}{⟨G^{\prime }|S^{\prime }⟩}_{S_{i1}^c}$ by the induction hypothesis then $S^{\prime }\in {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_l}$ thus ${⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{{\mathcal{I}}_l}={⟨G^{\prime }⟩}_{{\mathcal{I}}_l}|G^{″}|H^{\prime }$ by $G^{\prime }|S^{\prime }⩽H_{I_l}^V$.

${⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{{\mathcal{I}}_r}={⟨G^{″}⟩}_{{\mathcal{I}}_r}|G^{\prime }|H^{\prime }$ holds by a procedure similar to above then

$$\begin{array}{cc}\hfill {⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{\mathcal{I}}& ={⟨G^{\prime }⟩}_{{\mathcal{I}}_l}|{⟨G^{″}⟩}_{{\mathcal{I}}_r}|H^{\prime }\hfill \\ & =({⟨G^{\prime }⟩}_{{\mathcal{I}}_l}|G^{″}|H^{\prime })\bigcap ({⟨G^{″}⟩}_{{\mathcal{I}}_r}|G^{\prime }|H^{\prime })\hfill \\ & ={⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{{\mathcal{I}}_l}\bigcap {⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{{\mathcal{I}}_r}\hfill \end{array}$$

by ${⟨G^{\prime }⟩}_{{\mathcal{I}}_l}\subseteq G^{\prime }$ and ${⟨G^{″}⟩}_{{\mathcal{I}}_r}\subseteq G^{″}$. Other claims hold immediately from Construction 4.  □

Lemma 17.

(i) Let $G_{\mathcal{I}}^{*}$ denote ${⟨G|G^{*}⟩}_{\mathcal{I}}$ then $G_{\mathcal{I}}^{*}={\bigcap }_{H_i^c\in I}{G}_{S_{i1}^c}^{*}$;

(ii) $\frac{\underline{S_{i_{1}1}^c\cdots S_{i_{m}1}^c}}{G_{\mathcal{I}}^{*}}⟨{\tau }_{\mathcal{I}}^{*}⟩;$

(iii) $v_l(G_{\mathcal{I}}^{*})\backslash {\bigcup }_{H_j^c\in I}{v}_l(S_{j1}^c)=v_r(G_{\mathcal{I}}^{*})\backslash {\bigcup }_{H_j^c\in I}{v}_r(S_{j1}^c)$;

(iv) $S_j^c\in G_{\mathcal{I}}^{*}$ implies $H_i^c\nleqq H_j^c$ for all $H_i^c\in I$.

Proof. 

(i), (ii) and (iii) follow immediately from Lemma 16. (iv) holds by (i) and Lemma 13 (vi).  □

Lemma 17 (iv) shows that there exists no copy of $S_{i_k}^c$ in $G_{\mathcal{I}}^{*}$ for any $1⩽k⩽m$. Then we may regard them to be eliminated in ${\tau }_{\mathcal{I}}^{*}$. We then call ${\tau }_{\mathcal{I}}^{*}$ an elimination derivation.

Let ${\mathcal{I}}^{\prime }=\{S_{i_1{u}_1}^c,\cdots ,S_{i_m{u}_m}^c\}$ be another set of sequents to I such that $G^{\prime }\equiv S_{i_1{u}_1}^c|\cdots |S_{i_m{u}_m}^c$ is a copy of $G^{″}\equiv S_{i_{1}1}^c|\cdots |S_{i_{m}1}^c$. Then $G^{\prime }$ and $G^{″}$ are disjoint and there exist two bijections ${\sigma }_l:v_l(G^{\prime })\to v_l(G^{″})$ and ${\sigma }_r:v_r(G^{\prime })\to v_r(G^{″})$ such that ${\sigma }_r\circ {\sigma }_l(G^{\prime })=G^{″}$. By applying ${\sigma }_r\circ {\sigma }_l$ to ${\tau }_{\mathcal{I}}^{*}$, we construct a derivation from $S_{i_1{u}_1}^c,\cdots ,S_{i_m{u}_m}^c$ and denote it by ${\tau }_{{\mathcal{I}}^{\prime }}^{*}$ and its root by $G_{{\mathcal{I}}^{\prime }}^{*}$.

Let ${\mathbf{I}}^{\prime }=\{G_{b_1}|S_{i_1{u}_1}^c,\cdots ,G_{b_m}|S_{i_m{u}_m}^c\}$ be a set of hypersequents to I, where $G_{b_k}|S_{i_k{u}_k}^c$ be closed for all $1⩽k⩽m$. By applying ${\tau }_{{\mathcal{I}}^{\prime }}^{*}$ to $S_{i_1{u}_1}^c,\cdots ,S_{i_m{u}_m}^c$ in $G_{b_1}|S_{i_1{u}_1}^c,\cdots ,G_{b_m}|S_{i_m{u}_m}^c$, we construct a derivation from

$$G_{b_1}|S_{i_1{u}_1}^c,\cdots ,G_{b_m}|S_{i_m{u}_m}^c$$

and denote it by ${\tau }_{{\mathbf{I}}^{\prime }}^{*}$ and its root by $G_{{\mathbf{I}}^{\prime }}^{*}$. Then $G_{{\mathbf{I}}^{\prime }}^{*}={\{G_{b_k}\}}_{k=1}^m|G_{{\mathcal{I}}^{\prime }}^{*}$.

Definition 22.

We will use all ${\tau }_{{\mathbf{I}}^{\prime }}^{*}$ as rules of ${\mathbf{GL}}_{\mathsf{\Omega }}$ and call them elimination rules. Further, we call $S_{i_1{u}_1}^c,\cdots ,S_{i_m{u}_m}^c$ focus sequents and, all sequents in $G_{{\mathcal{I}}^{\prime }}^{*}$ principal sequents and, $G_{b_1},\cdots ,G_{b_m}$ side-hypersequents of ${\tau }_{{\mathbf{I}}^{\prime }}^{*}$.

Remark 2.

We regard Construction 1 as a procedure $\mathcal{F}$, whose inputs are ${\tau }^2,H,H^{\prime }$ and output ${\tau }_{H:H^{\prime }}^2$. With such a viewpoint, we write ${\tau }_{H:H^{\prime }}^2$ as ${\mathcal{F}}_{H:H^{\prime }}({\tau }^2)$. Then ${\tau }_{\mathcal{I}}^{*}$ can be constructed by iteratively applying $\mathcal{F}$ to ${\tau }^{*}$, i.e., ${\tau }_{\mathcal{I}}^{*}={\mathcal{F}}_{H_{i_m}^c:S_{i_{m}1}^c}(\cdots {\mathcal{F}}_{H_{i_1}^c:S_{i_{1}1}^c}({\tau }^{*})\cdots )$.

We replace locally each $\frac{G^{\prime }}{G^{\prime }}(I{D}_{\mathsf{\Omega }})$ in ${\tau }_{\mathcal{I}}^{*}$ with $G^{\prime }$ and denote the resulting derivation also by ${\tau }_{\mathcal{I}}^{*}$. Then each non-root node in ${\tau }_{\mathcal{I}}^{*}$ has the focus sequent.

Let $H\in {\tau }_{\mathcal{I}}^{*}$. Then there exists a unique node in ${\tau }^{*}$, which we denote by $\mathcal{O}(H)$ such that H comes from $\mathcal{O}(H)$ by Constructions 1 and 4. Then the focus sequent of $\mathcal{O}(H)$ in ${\tau }^{*}$ is the focus of H in ${\tau }_{\mathcal{I}}^{*}$ if H is a non-root node and, $\mathcal{O}(H)=H$ or $H\subseteq \mathcal{O}(H)$ as two hypersequents. Since the relative positions of any two nodes in ${\tau }^{*}$ are kept unchanged in constructing ${\tau }_{\mathcal{I}}^{*}$, $H_1{⩽}_{{\tau }_{\mathcal{I}}^{*}}{H}_2$ if and only if $\mathcal{O}(H_1){⩽}_{{\tau }^{*}}\mathcal{O}(H_2)$ for any $H_1,H_2\in {\tau }_{\mathcal{I}}^{*}$. Especially, $\mathcal{O}(S_{i_{k}1}^c)=H_{i_k}^c$ for $S_{i_{k}1}^c\in {\tau }_{\mathcal{I}}^{*}$.

Let $H\in {\tau }_{\mathcal{I}}^{*}$. Then $H^{\prime }\equiv {\sigma }_r\circ {\sigma }_l(H)\in {\tau }_{{\mathcal{I}}^{\prime }}^{*}$ and $H^{″}\equiv \{G_{b_k}:H{⩽}_{{\tau }_{\mathcal{I}}^{*}}{S}_{i_{k}1}^c\mathrm{and}1⩽k⩽m\}\mid H^{\prime }\in {\tau }_{{\mathbf{I}}^{\prime }}^{*}$. Define $\mathcal{O}(H^{\prime })=\mathcal{O}(H^{″})=\mathcal{O}(H)$. Then $\mathcal{O}(G_{{\mathbf{I}}^{\prime }}^{*})=G|G^{*}$ and $\mathcal{O}(G_{b_k}|S_{i_k{u}_k}^c)=H_{i_k}^c$ for all $G_{b_k}|S_{i_k{u}_k}^c\in {\tau }_{{\mathbf{I}}^{\prime }}^{*}$.

Since $G_{\mathcal{I}}^{*}={⟨G|G^{*}⟩}_{\mathcal{I}}\subseteq G|G^{*}$, then each $(pEC)$-sequent in $G_{\mathcal{I}}^{*}$ has the form $S_{jv}^c$ for some $1⩽j⩽N$, $2⩽v⩽m_j$ by Proposition 2(ii). Then we introduce the following definition.

Definition 23.

(i) By $S_j^c\in G_{\mathcal{I}}^{*}$ we means that there exists $H\in {\tau }_{\mathcal{I}}^{*}$ such that $S_j^c\in H$, $\mathcal{O}(H)=H_j^c$. So is $S_j^c\in G_{{\mathcal{I}}^{\prime }}^{*}$.

(ii) Let $S_j^c\in G_{\mathcal{I}}^{*}$. By $H_j^c{⩽}_{{\tau }_{\mathcal{I}}^{*}}{H}_i^c$ we means that there exist $H,H^{\prime }\in {\tau }_{\mathcal{I}}^{*}$ such that $S_j^c\in H$, $\mathcal{O}(H)=H_j^c,\mathcal{O}(H^{\prime })=H_i^c$ and $H_j^c{⩽}_{{\tau }^{*}}{H}_i^c$. We usually write ${⩽}_{{\tau }_{\mathcal{I}}^{*}}$ as ⩽.

7. Separation of One Branch

In the remainder of this paper, we assume that p occur at most one time for each sequent in $G_0$ as the one in the main theorem, $\tau$ be a cut-free proof of $G_0$ in $\mathbf{GL}$ and ${\tau }^{*}$ the proof of $G|G^{*}$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$ resulting from preprocessing of $\tau$. Then $\left|v_l(S)\right|+\left|v_r(S)\right|\le 1$ for all $S\in G$, which plays a key role in discussing the separation of branches.

Definition 24.

By $S^{\prime }{\in }_c{G}^{\prime }$ we mean that there exists some copy of $S^{\prime }$ in $G^{\prime }$. $G^{\prime }{\subseteq }_c{G}^{″}$ if $S^{\prime }{\in }_c{G}^{″}$ for all $S^{\prime }\in G^{\prime }$. $G^{\prime }{=}_c{G}^{″}$ if $G^{\prime }{\subseteq }_c{G}^{″}$ and $G^{″}{\subseteq }_c{G}^{\prime }$. Let $G_{11},\cdots ,G_{1m}$ be m copies of $G_1$ then we denote $G^{\prime }|G_{11}|\cdots |G_{1m}$ by $G^{\prime }|{\{G_{1u}\}}_{u=1}^m$ or $G^{\prime }|{\{G_1\}}^m$.

Definition 25.

Let $I=\{H_{i_1}^c,\cdots ,H_{i_m}^c\}\subseteq \{H_1^c,\cdots ,H_N^c\}$, $H_{i_k}^c\parallel H_{i_l}^c$ for all $1⩽k<l⩽m$. ${\lceil S_{i_k}^c\rceil }_I$ is called a branch of $H_{i_k}^c$ to I if it is a closed hypersequent such that

$(i){\lceil S_{i_k}^c\rceil }_I{\subseteq }_{c}G|G^{*},$

$(ii)S_{i_k}^c\in {\lceil S_{i_k}^c\rceil }_I,$

$(iii)S_j^c\in {\lceil S_{i_k}^c\rceil }_I$ implies $H_j^c⩽H_{i_k}^c$ or $H_j^c\parallel H_i^c$ for all $H_i^c\in I.$

Then (i) $S_{i_l}^c{\notin }_c{\lceil S_{i_k}^c\rceil }_I$ for all $1⩽k,l⩽m$, $k\ne l$; (ii) $S_j^c\in {\lceil S_{i_k}^c\rceil }_I$ and $H_j^c\nleqq H_{i_k}^c$ imply $H_j^c\notin I$.

In this section, let $I=\{H_i^c\}$, $\mathbf{I}=\{{\lceil S_i^c\rceil }_I\}$, we will give an algorithm to eliminate all $S_j^c\in {\lceil S_i^c\rceil }_I$ satisfying $H_j^c⩽H_i^c$.

Construction 5.

(Appendix A.3) A sequence of hypersequents $G_{\mathbf{I}}^{☆(q)}$ and their derivations ${\tau }_{\mathbf{I}}^{☆(q)}$ from ${\lceil S_i^c\rceil }_I$ for all $q⩾0$ are constructed inductively as follows.

For the base case, define $G_{\mathbf{I}}^{☆(0)}$ to be ${\lceil S_i^c\rceil }_I$ and, ${\tau }_{\mathbf{I}}^{☆(0)}$ be $\frac{\underline{}}{G_{\mathbf{I}}^{☆(0)}}$. For the induction case, suppose that ${\tau }_{\mathbf{I}}^{☆(q)}$ and $G_{\mathbf{I}}^{☆(q)}$ are constructed for some $0⩽q$. If there exists no $S_j^c\in G_{\mathbf{I}}^{☆(q)}$ such that $H_j^c⩽H_i^c$, then the procedure terminates and define $J_{\mathbf{I}}$ to be q; otherwise define $H_{i_q}^c$ such that $S_{i_q}^c\in G_{\mathbf{I}}^{☆(q)}$, $H_{i_q}^c⩽H_i^c$ and $H_j^c⩽H_{i_q}^c$ for all $S_j^c\in G_{\mathbf{I}}^{☆(q)},H_j^c⩽H_i^c$. Let $S_{i_{q}1}^c,\cdots ,S_{i_q{m}_q}^c$ be all copies of $S_{i_q}^c$ in $G_{\mathbf{I}}^{☆(q)}$ then define $G_{\mathbf{I}}^{☆(q+1)}=G_{\mathbf{I}}^{☆(q)}\backslash {\{S_{i_{q}u}^c\}}_{u=1}^{m_q}|{\{G_{S_{i_{q}u}^c}^{*}\}}_{u=1}^{m_q}$ and its derivation ${\tau }_{\mathbf{I}}^{☆(q+1)}$ is constructed by sequentially applying ${\tau }_{S_{i_{q}1}^c}^{*},\cdots ,{\tau }_{S_{i_q{m}_q}^c}^{*}$ to $S_{i_{q}1}^c,\cdots ,S_{i_q{m}_q}^c$ in $G_{\mathbf{I}}^{☆(q)}$, respectively. Notice that we assign new identification numbers to new occurrences of p in ${\tau }_{S_{i_{q}u}^c}^{*}$ for all $0⩽q⩽J_{\mathbf{I}}-1$, $1⩽u⩽m_q$.

Lemma 18.

(i) $H_{i_0}^c=H_i^c$ and $H_{i_{q+1}}^c<H_{i_q}^c$ for all $0⩽q⩽J_{\mathbf{I}}-2$;

(ii) $G_{\mathbf{I}}^{☆(q)}{\subseteq }_{c}G|G^{*}$ is closed for all $0⩽q⩽J_{\mathbf{I}}$;

(iii) $\frac{\underline{{\lceil S_i^c\rceil }_I}}{G_{\mathbf{I}}^{☆(q)}}⟨{\tau }_{\mathbf{I}}^{☆(q)}⟩$ for all $0⩽q⩽J_{\mathbf{I}}$, especially, $\frac{\underline{{\lceil S_i^c\rceil }_I}}{G_{\mathbf{I}}^{☆(J_{\mathbf{I}})}}⟨{\tau }_{\mathbf{I}}^{☆(J_{\mathbf{I}})}⟩$;

(iv) $S_j^c\in G_{\mathbf{I}}^{☆(J_{\mathbf{I}})}$ implies $H_j^c\parallel H_i^c$ and, $S_j^c\in G_{S_{i_{q}u}^c}^{*}$ for some ${\tau }_{G_b|S_{i_{q}u}^c}^{*}\in {\tau }_{\mathbf{I}}^{☆(J_{\mathbf{I}})}$ or $S_j^c\in {\lceil S_i^c\rceil }_I$, $H_j^c\nleqq H_i^c$, where $G_b=G_I^{☆(q)}\backslash {\{S_{i_{q}v}^c\}}_{v=1}^u|{\{G_{S_{i_{q}v}^c}^{*}\}}_{v=1}^{u-1}$, $G_b|S_{i_{q}u}^c$ is closed and $0⩽q⩽J_{\mathbf{I}}-1$, $1⩽u⩽m_q$.

Proof. 

(i) Since $S_i^c\in G_{\mathbf{I}}^{☆(0)}$ by $S_i^c\in {\lceil S_i^c\rceil }_I=G_{\mathbf{I}}^{☆(0)}$ and, $H_j^c⩽H_i^c$ for all $S_j^c\in G_{\mathbf{I}}^{☆(0)},H_j^c⩽H_i^c$ then $H_{i_0}^c=H_i^c$. If $S_{i_{q+1}}^c\in G_{\mathbf{I}}^{☆(q)}\backslash {\{S_{i_{q}u}^c\}}_{u=1}^{m_q}$ then $H_{i_{q+1}}^c⩽H_{i_q}^c$ by $S_{i_{q+1}}^c\in G_{\mathbf{I}}^{☆(q)}$, $H_{i_{q+1}}^c⩽H_i^c$ thus $H_{i_{q+1}}^c<H_{i_q}^c$ by all copies of $S_{i_q}^c$ in $G_{\mathbf{I}}^{☆(q)}$ being collected in ${\{S_{i_{q}u}^c\}}_{u=1}^{m_q}$. If $S_{i_{q+1}}^c\in {\{G_{S_{i_{q}u}^c}^{*}\}}_{u=1}^{m_q}$ then $H_{i_q}^c\nleqq H_{i_{q+1}}^c$ by Lemma 13(vi) thus $H_{i_{q+1}}^c<H_{i_q}^c$ by $H_{i_q}^c⩽H_i^c$, $H_{i_{q+1}}^c⩽H_i^c$. Then $H_{i_{q+1}}^c<H_{i_q}^c$ by $G_{\mathbf{I}}^{☆(q+1)}=G_{\mathbf{I}}^{☆(q)}\backslash {\{S_{i_{q}u}^c\}}_{u=1}^{m_q}|{\{G_{S_{i_{q}u}^c}^{*}\}}_{u=1}^{m_q}$. Note that $H_{i_{J_{\mathbf{I}}}}^c$ is undefined in Construction 5.

(ii) $v_l(G_{\mathbf{I}}^{☆(0)})=v_r(G_{\mathbf{I}}^{☆(0)}),G_{\mathbf{I}}^{☆(0)}{\subseteq }_{c}G|G^{*}$ by $G_{\mathbf{I}}^{☆(0)}={\lceil S_i^c\rceil }_I$. Suppose that $v_l(G_{\mathbf{I}}^{☆(q)})=v_r(G_{\mathbf{I}}^{☆(q)}),G_{\mathbf{I}}^{☆(q)}{\subseteq }_{c}G|G^{*}$ then $v_l(G_{\mathbf{I}}^{☆(q+1)})=v_r(G_{\mathbf{I}}^{☆(q+1)}),G_{\mathbf{I}}^{☆(q+1)}{\subseteq }_{c}G|G^{*}$ by $G_{\mathbf{I}}^{☆(q+1)}=G_{\mathbf{I}}^{☆(q)}\backslash {\{S_{i_{q}u}^c\}}_{u=1}^{m_q}|{\{G_{S_{i_{q}u}^c}^{*}\}}_{u=1}^{m_q}$, $v_l(G_{S_{i_{q}u}^c}^{*}\backslash \{S_{i_{q}u}^c\})=v_r(G_{S_{i_{q}u}^c}^{*}\backslash \{S_{i_{q}u}^c\})$ and $G_{S_{i_{q}u}^c}^{*}{\subseteq }_{c}G|G^{*}$ for all $1⩽u⩽m_q$.

(iii) ${\tau }_{\mathbf{I}}^{☆(0)}$ is $\frac{\underline{}}{G_{\mathbf{I}}^{☆(0)}}⟨{\tau }_{\mathbf{I}}^{☆(0)}⟩$. Given $\frac{\underline{{\lceil S_i^c\rceil }_I}}{G_{\mathbf{I}}^{☆(q)}}⟨{\tau }_{\mathbf{I}}^{☆(q)}⟩$ then $\frac{\underline{{\lceil S_i^c\rceil }_I}}{G_{\mathbf{I}}^{☆(q+1)}}⟨{\tau }_{\mathbf{I}}^{☆(q+1)}⟩$ is constructed by linking up the conclusion of previous derivation to the premise of its successor in the sequence of derivations

$$\frac{\underline{{\lceil S_i^c\rceil }_I}}{G_{\mathbf{I}}^{☆(q)}}⟨{\tau }_{\mathbf{I}}^{☆(q)}⟩,\frac{\underline{G_{\mathbf{I}}^{☆(q)}\backslash \{S_{i_{q}1}^c\}|S_{i_{q}1}^c}}{G_{\mathbf{I}}^{☆(q)}\backslash \{S_{i_{q}1}^c\}|G_{S_{i_{q}1}^c}^{*}}⟨{\tau }_{S_{i_{q}1}^c}^{*}⟩,\cdots ,\frac{\underline{G_{\mathbf{I}}^{☆(q)}\backslash {\{S_{i_{q}u}^c\}}_{u=1}^{m_q-1}|S_{i_q{m}_q}^c|{\{G_{S_{i_{q}u}^c}^{*}\}}_{u=1}^{m_q-1}}}{G_{\mathbf{I}}^{☆(q+1)}=G_{\mathbf{I}}^{☆(q)}\backslash {\{S_{i_{q}u}^c\}}_{u=1}^{m_q}|{\{G_{S_{i_{q}u}^c}^{*}\}}_{u=1}^{m_q}}⟨{\tau }_{S_{i_q{m}_q}^c}^{*}⟩,$$

as shown in Figure 14.

Figure 14. A derivation of $G_{\mathbf{I}}^{☆(q+1)}$ from $G_{\mathbf{I}}^{☆(q)}$.

(iv) Let $S_j^c\in G_{\mathbf{I}}^{☆(J_{\mathbf{I}})}$. Then $H_j^c\nleqq H_i^c$ by the definition of $J_{\mathbf{I}}$. If $S_j^c\in {\lceil S_i^c\rceil }_I$, then $H_j^c\parallel H_i^c$ by $H_j^c\nleqq H_i^c$ and the definition of ${\lceil S_i^c\rceil }_I$. Otherwise, by Construction 5, there exists some ${\tau }_{G_b|S_{i_{q}u}^c}^{*}$ in ${\tau }_{\mathbf{I}}^{☆(J_{\mathbf{I}})}$ such that $S_j^c\in G_{S_{i_{q}u}^c}^{*}.$ Then $H_{i_q}^c\nleqq H_j^c$ by Lemma 13(vi). Thus $H_i^c\nleqq H_j^c$ by $H_{i_q}^c⩽H_i^c$. Hence $H_j^c\parallel H_i^c$.  □

Lemma 18 shows that Construction 5 presents a derivation ${\tau }_{\mathbf{I}}^{☆(J_{\mathbf{I}})}$ of $G_{\mathbf{I}}^{☆(J_{\mathbf{I}})}$ from ${\lceil S_i^c\rceil }_I$ such that there does not exist $S_j^c\in G_{\mathbf{I}}^{☆(J_{\mathbf{I}})}$ satisfying $H_j^c⩽H_i^c$, i.e., all $S_j^c\in {\lceil S_i^c\rceil }_I$ satisfying $H_j^c⩽H_i^c$ are eliminated by Construction 5. We generalize this procedure as follows.

Construction 6.

Let $H\in {\tau }^{*}$, $H_1\subseteq H$ and $H_2{\subseteq }_{c}G|G^{*}$. Then $G_{H:H_l}^{☆(J_{H:H_l})}$ and its derivation ${\tau }_{H:H_l}^{☆(J_{H:H_l})}$ for $l=1,2$ are constructed by procedures similar to that of Construction 5 such that $H_j^c\nleqq H$ for all $S_j^c\in G_{H:H_l}^{☆(J_{H:H_l})}$, where $G_{H:H_1}^{☆(0)}:=G_{H:H_1}^{*}$, ${\tau }_{H:H_1}^{☆(0)}:={\tau }_{H:H_1}^{*}$, which are defined by Construction 1.

We sometimes write $J_{\mathbf{I}}$, $J_{H:H_l}$ as J for simplicity. Then the following lemma holds clearly.

Lemma 19.

(i) $\frac{\underline{H_l}}{G_{H:H_l}^{☆(J)}}⟨{\tau }_{H:H_l}^{☆(J)}⟩$, $H_j^c\nleqq H$ for all $S_j^c\in G_{H:H_l}^{☆(J)}$.

(ii) If $S_i^c\in H$ and $H_i^c>H$ then $G_{H:S_i^c}^{☆(J)}=S_i^c$.

(iii) If $S{\in }_{c}G$ or, $S{\in }_c{G}^{*}$ is a copy of $S_{i1}^c$ and $H_i^c\nleqq H$ then $G_{H:S}^{☆(J)}=S$.

(iv) Let $H^{\prime }|H^{″}\subseteq H\in {\tau }^{*}$. Then $G_{H:H^{\prime }|H^{″}}^{☆(J)}=G_{H:H^{\prime }}^{☆(J)}|G_{H:H^{″}}^{☆(J)}$ by suitable assignments of identification numbers to new occurrences of p in constructing ${\tau }_{H:H^{\prime }|H^{″}}^{☆(J)}$, ${\tau }_{H:H^{\prime }}^{☆(J)}$ and ${\tau }_{H:H^{″}}^{☆(J)}$.

(v) $G_{\mathbf{I}}^{☆(J)}=\bigcup \{G_{H_i^c:S_j^c}^{☆(J)}:S_j^c\in {\lceil S_i^c\rceil }_I,H_j^c⩽H_i^c\}|\bigcup \{S_j^c:S_j^c\in {\lceil S_i^c\rceil }_I,H_j^c\nleqq H_i^c\}|\bigcup \{S:S\in {\lceil S_i^c\rceil }_I,S{\in }_{c}G\}$.

Proof. 

Part (i) is proved by a procedure similar to that of Lemma 18(iii) and (iv), and omitted.

(ii) Since $S_{i1}^c$ is the focus sequent of $H_i^c$ then it is revised by some rule at the node lower than $H_i^c$. Thus $S_i^c\in H$ is some copy of $S_{i1}^c$ by $H_i^c>H$. Hence $S_i^c$ has the form $S_{iu}^c$ for some $u\ge 2$. Therefore it is transferred downward to $G|G^{*}$, i.e., $S_i^c\in G|G^{*}$. Then $G_{H:S_i^c}^{☆(0)}=G_{H:S_i^c}^{*}=S_i^c$. Since there exists no $S_j^c\in G_{H:S_j^c}^{☆(0)},H_j^c⩽H$ then $J=0$. Thus $G_{H:S_i^c}^{☆(J)}=S_i^c$.

(iii) is proved by a procedure similar to that of (ii) and omitted.

(iv) Since $H^{\prime }|H^{″}\subseteq H\in {\tau }^{*}$, then $H^{\prime }\bigcap H^{″}=\varnothing$ by Proposition 3. Thus $G_{H:H^{\prime }|H^{″}}^{☆(0)}=G_{H:H^{\prime }|H^{″}}^{*}=G_{H:H^{\prime }}^{*}|G_{H:H^{″}}^{*}=G_{H:H^{\prime }}^{☆(0)}|G_{H:H^{″}}^{☆(0)}$. Suppose that $G_{H:H^{\prime }|H^{″}}^{☆(q)}=G_{H:H^{\prime }}^{☆(q)}|G_{H:H^{″}}^{☆q)}$ for some $q\ge 0$. Then all copies ${\{S_{i_{q}u}^c\}}_{u=1}^{m_q}$ of $S_{i_q}^c$ in $G_{H:H^{\prime }|H^{″}}^{☆(q)}$ are divided two subsets ${\{S_{i_{q}u}^c\}}_{u=1}^{m_q}\bigcap G_{H:H^{\prime }}^{☆(q)}$ and ${\{S_{i_{q}u}^c\}}_{u=1}^{m_q}\bigcap G_{H:H^{″}}^{☆(q)}$. Thus we can construct $G_{H:H^{\prime }|H^{″}}^{☆(q+1)},G_{H:H^{\prime }}^{☆(q+1)}$ and $G_{H:H^{″}}^{☆(q+1)}$ simultaneously and assign the same identification numbers to new occurrences of p in $G_{H:H^{\prime }}^{☆(q+1)}$ and $G_{H:H^{″}}^{☆(q+1)}$ as the corresponding one in $G_{H:H^{\prime }|H^{″}}^{☆(q+1)}$. Hence $G_{H:H^{\prime }|H^{″}}^{☆(q+1)}=G_{H:H^{\prime }}^{☆(q+1)}|G_{H:H^{″}}^{☆(q+1)}$. Then $G_{H:H^{\prime }|H^{″}}^{☆(J)}=G_{H:H^{\prime }}^{☆(J)}|G_{H:H^{″}}^{☆(J)}$.

Note that the requirement is imposed only on one derivation that distinct occurrence of p has a distinct identification number. We permit $G_{H:H^{″}}^{☆(q+1)}=G_{H:H^{″}}^{☆(q)}$ or $G_{H:H^{\prime }}^{☆(q+1)}=G_{H:H^{\prime }}^{☆(q)}$ in the proof above, which has no essential effect on the proof of the claim.

(v) is immediately from (iv).  □

Lemma 19 (v) shows that $G_{\mathbf{I}}^{☆(J)}$ could be constructed by applying ${\tau }_{H_i^c:S_j^c}^{☆(J)}$ sequentially to each $S_j^c\in {\lceil S_i^c\rceil }_I$ satisfying $H_j^c⩽H_i^c$. Thus the requirement $H_{i_{q+1}}^c<H_{i_q}^c$ in Construction 5 is not necessary, but which make the termination of the procedure obvious.

Construction 7.

Apply $(E{C}_{\mathsf{\Omega }}^{*})$ to $G_{\mathbf{I}}^{☆(J)}$ and denote the resulting hypersequent by $G_{\mathbf{I}}^{☆}$ and its derivation by ${\tau }_{\mathbf{I}}^{☆}$. It is possible that $(E{C}_{\mathsf{\Omega }}^{*})$ is not applicable to $G_{\mathbf{I}}^{☆(J)}$ in which case we apply $⟨I{D}_{\mathsf{\Omega }}⟩$ to it for the regularity of the derivation.

Lemma 20.

(i) $\frac{\underline{{\lceil S_i^c\rceil }_I}}{G_{\mathbf{I}}^{☆}}⟨{\tau }_{\mathbf{I}}^{☆}⟩$, $G_{\mathbf{I}}^{☆}$ is closed and $H_j^c\parallel H_i^c$ for all $S_j^c\in G_{\mathbf{I}}^{☆}$;

(ii) ${\tau }_{\mathbf{I}}^{☆}$ is constructed by applying elimination rules, say, $\frac{\underline{G_b|S_{i_{q}u}^c}}{G_b|G_{S_{i_{q}u}^c}^{*}}⟨{\tau }_{G_b|S_{i_{q}u}^c}^{*}⟩$, and the fully constraint contraction rules, say, $\frac{\underline{G_2}}{G_1}⟨E{C}_{\mathsf{\Omega }}^{*}⟩$, where $H_{i_q}^c⩽H_i^c$, $G_b|S_{i_{q}u}^c$ is closed for $0⩽q⩽J-1$, $1⩽u⩽m_q$.

Proof. 

The proof follows immediately from Lemma 18.  □

Definition 26.

Let $G^{\prime }\in G_{\mathbf{I}}^{☆(J)}$, $H^{\prime }\subseteq G^{\prime }$ and $S^{\prime }\in H^{\prime }$.

(i) For any sequent-formula A of $S^{\prime }$, define $\widehat{A}$ to be the sequent S of $G_{\mathbf{I}}^{☆(J)}$ such that A is a sequent-formula of S or subformula of a sequent-formula of S.

(ii) Let $S^{\prime }$ be in the form $A_1,\cdots ,A_n\Rightarrow B_1,\cdots ,B_m$, define $\widehat{S^{\prime }}$ to be the hypersequent which consists of all distinct sequents among $\widehat{A_1},\cdots ,\widehat{A_n},\widehat{B_1},\cdots ,\widehat{B_m}$; (iii) Let $H^{\prime }$ be in the form $S_1|\cdots |S_m$, define $\widehat{H^{\prime }}$ to be $\widehat{S_1}|\cdots |\widehat{S_m}$.

(iv) We call $H^{\prime }$ to be separable if $\widehat{H^{\prime }}{\subseteq }_{c}G$ and, call it to be separated into $\widehat{H^{\prime }}$.

Note that ${\tau }_{\mathbf{I}}^{☆(J)}$ is a derivation without $(E{C}_{\mathsf{\Omega }})$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$. Then we can extract elimination derivations from it by Construction 1.

Notation 8.

Let $H^{\prime }\subseteq G^{\prime }\in {\tau }_{\mathbf{I}}^{☆(J)}$. ${\tau }_{\mathbf{I}\{{\mathrm{G}}^{\prime }:{\mathrm{H}}^{\prime }\}}^{☆(J)}$ denotes the derivation from $H^{\prime }$, which extracts from ${\tau }_{\mathbf{I}}^{☆(J)}$ by Construction 1, and denote its root by $G_{\mathbf{I}\{G^{\prime }:H^{\prime }\}}^{☆(J)}$.

The following two lemmas show that Constructions 5 and 6 force some sequents in ${\lceil S_i^c\rceil }_I$ or $H^{\prime }$ to be separable.

Lemma 21.

Let $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{H\equiv G^{\prime }|G^{″}|H^{\prime }}(II)\in {\tau }^{*}$. Then

(i) $H^{\prime }$ is separable in ${\tau }_{\mathrm{H}:{\mathrm{H}}^{\prime }}^{☆(J)}$.

(ii) If $\frac{G_b|{⟨G^{\prime }|S^{\prime }⟩}_{S_{i_{q}u}^c}{G}^{″}|S^{″}}{H_1\equiv G_b|{⟨G^{\prime }⟩}_{S_{i_{q}u}^c}|G^{″}|H^{\prime }}(II)\in {\tau }_{G_b|S_{i_{q}u}^c}^{*}\in {\tau }_{\mathbf{I}}^{☆}$, then $H^{\prime }$ is separable in ${\tau }_{\mathbf{I}}^{☆(J)}$ and there is a unique copy of $\widehat{S^{″}}|G_{\mathbf{I}\{H_1:G^{″}\}}^{☆(J)}$ in $G_{\mathbf{I}}^{☆}$.

Proof. 

(i) We write ${⩽}_{{\tau }_{H:H^{\prime }}^{☆(J)}}$ and ${⩽}_{{\tau }^{*}}$ respectively as ${⩽}_{☆}$ and ⩽ for simplicity. Since $G_{H:H^{\prime }}^{☆(J)}{\subseteq }_{c}G|G^{*}$, we divide it into two hypersequents $G_{H:H^{\prime }}^{0(J)}$ and $G_{H:H^{\prime }}^{*(J)}$ such that $G_{H:H^{\prime }}^{☆(J)}=G_{H:H^{\prime }}^{0(J)}|G_{H:H^{\prime }}^{*(J)},G_{H:H^{\prime }}^{0(J)}{\subseteq }_{c}G,$$G_{H:H^{\prime }}^{*(J)}{\subseteq }_c{G}^{*}$.

Let $S_j^c\in G_{H:H^{\prime }}^{*(J)}$ then $H_j^c\nleqq H$ by Construction 6. We prove that $H_j^c\parallel H^{\prime }$ in ${\tau }_{H:H^{\prime }}^{☆(J)}$ as follows. If $S_j^c\in G_{H:H^{\prime }}^{*}$ then $H_j^c||H^{\prime }$ in ${\tau }_{H:H^{\prime }}^{*}$ by Lemma 14(i), ${\tau }_{H:H^{\prime }}^{*}\in {\tau }_{H:H^{\prime }}^{☆(J)}$ and $H_j^c\nleqq H$. Thus we assume that $S_j^c{G}_{H:H^{\prime }}^{*}$ in the following.

Then, by Lemma 18(iv), there exists some ${\tau }_{G_b|S_i^c}^{*}$ in ${\tau }_{H:H^{\prime }}^{☆(J)}$ such that $H_i^c⩽H$, $S_j^c\in G_{S_i^c}^{*}$. Then $H_i^c\nleqq H_j^c$ by Lemma 13(vi). $H_j^c\nleqq H_i^c$ by $H_i^c⩽H$, $H_j^c\nleqq H$. Thus $H_i^c{\parallel }_{{\tau }^{*}}{H}_j^c$. Let $\frac{G_1|S_1{G}_2|S_2}{G_1|G_2|H_2}(II)\in {\tau }^{*}$, where $G_1|G_2|H_2=H_{ij}^V$, $G_1|S_1⩽H_i^c$, $G_2|S_2⩽H_j^c$. Then $S_1\in {⟨G_1|S_1⟩}_{S_i^c}$, $G_b|{⟨G_1|S_1⟩}_{S_i^c}\in {\tau }_{H:H^{\prime }}^{☆(J)}$, $G_2|S_2\in {\tau }_{H:H^{\prime }}^{☆(J)}$ by $S_j^c\in G_{S_i^c}^{*}\subseteq G_b|G_{S_i^c}^{*}\in {\tau }_{H:H^{\prime }}^{☆(J)}$. Thus $H_j^c{\parallel }_{☆}{H}^{\prime }$ by $G_b|{⟨G_1|S_1⟩}_{S_i^c}{⩽}_{☆}{G}_b|S_i^c{⩽}_{☆}{H}^{\prime }$, $G_2|S_2{⩽}_{☆}{H}_j^c$ and $G_b|{⟨G_1|S_1⟩}_{S_i^c}{\parallel }_{☆}{G}_2|S_2$.

Thus $H_j^c||H^{\prime }$ in ${\tau }_{H:H^{\prime }}^{☆(J)}$. Therefore $G_{H:H^{\prime }}^{*(J)}\bigcap \widehat{H^{\prime }}=\varnothing$. Then $\widehat{H^{\prime }}\subseteq G_{H:H^{\prime }}^{0(J)}{\subseteq }_{c}G$, i.e., $H^{\prime }$ is separable in ${\tau }_{\mathrm{H}:{\mathrm{H}}^{\prime }}^{☆(J)}$.

(ii) Clearly, $G_{\mathbf{I}\{{\mathrm{H}}_1:{\mathrm{G}}^{″}\mid {\mathrm{H}}^{\prime }\}}^{☆(J)}$ is a copy of $G_{H:G^{″}\mid H^{\prime }}^{☆(J)}$ and, ${\tau }_{\mathbf{I}\{{\mathrm{H}}_1:{\mathrm{G}}^{″}\mid {\mathrm{H}}^{\prime }\}}^{☆(J)}$ has no difference with ${\tau }_{H:G^{″}\mid H^{\prime }}^{☆(J)}$ except some applications of $(I{D}_{\mathsf{\Omega }})$ and identification numbers of some $p^{\prime }s$. Then $H^{\prime }$ is separated into $\widehat{H^{\prime }}$ in $G_{\mathbf{I}\{H_1:H^{\prime }\}}^{☆(J)}$ by the same reason as that of (i). Then $S^{\prime },S^{″}$ are separated into $\widehat{S^{\prime }}$ and $\widehat{S^{″}}$ in ${\tau }_{\mathbf{I}}^{☆(J)}$, respectively. Then $\widehat{S^{″}}|G_{\mathbf{I}\{H_1:G^{″}\}}^{☆(J)}\subseteq G_{\mathbf{I}}^{0(J)}|G_{\mathbf{I}}^{*(J)}$ is closed since $G^{″}|S^{″}$ is closed. Thus all copies of $\widehat{S^{″}}|G_{\mathbf{I}\{H_1:G^{″}\}}^{☆(J)}$ in ${\tau }_{\mathbf{I}}^{☆(J)}$ are contracted into one by $(E{C}_{\mathsf{\Omega }}^{*})$ in $G_{\mathbf{I}}^{☆}$.  □

Lemma 22.

(i) All copies of $S_i^c$ in ${\lceil S_i^c\rceil }_I$ are separable in ${\tau }_{\mathbf{I}}^{☆(J)}$.

(ii) Let $H\in {\tau }^{*}$, $H^{\prime }\subseteq H$, $H_j^c⩽H$ or $H_j^c\parallel H$ for all $S_j^c\in G_{H:H^{\prime }}^{*}$. Then $H^{\prime }$ is separable in ${\tau }_{H:H^{\prime }}^{☆(J)}$.

Proof. 

Parts (i) and (ii) are proved by a procedure similar to that of Lemma 21 and are omitted.  □

Definition 27.

The skeleton of ${\tau }_{\mathbf{I}}^{☆}$, which we denote by ${\overline{\tau }}_{\mathbf{I}}^{☆}$, is constructed by replacing all $\frac{\underline{G_b|S_{i_{q}u}^c}}{G_b|G_{S_{i_{q}u}^c}^{*}}⟨{\tau }_{G_b|S_{i_{q}u}^c}^{*}⟩\in {\tau }_{\mathbf{I}}^{☆}$ with $\frac{G_b|S_{i_{q}u}^c}{G_b|G_{S_{i_{q}u}^c}^{*}}({\tau }_{G_b|S_{i_{q}u}^c}^{*})$, i.e, $G_b|S_{i_{q}u}^c$ is the parent node of $G_b|G_{S_{i_{q}u}^c}^{*}$ in ${\overline{\tau }}_{\mathbf{I}}^{☆}$.

Lemma 23.

The parameter ${\overline{\tau }}_{\mathbf{I}}^{☆}$ is a linear structure with the lowest node $G_{\mathbf{I}}^{☆}$ and the highest ${\lceil S_i^c\rceil }_I$.

Proof. 

It holds by all ${\tau }_{G_b|S_{i_{q}u}^c}^{*}$ and $E{C}_{\mathsf{\Omega }}^{*}$ in ${\tau }_{\mathbf{I}}^{☆}$ being one-premise rules.  □

Definition 28.

We call Construction 5 together with 7 the separation algorithm of one branch and, Construction 6 the separation algorithm along H.

8. Separation Algorithm of Multiple Branches

In this section, let $I=\{H_{i_1}^c,\cdots ,H_{i_m}^c\}\subseteq \{H_1^c,\cdots ,H_N^c\}$ such that $H_{i_k}^c\parallel H_{i_l}^c$ for all $1⩽k<l⩽m$. We will generalize the separation algorithm of one branch to that of multiple branches. Roughly speaking, we give an algorithm to eliminate all $S_j^c\in G|G^{*}$ satisfying $H_j^c⩽H_{i_k}^c$ for some $H_{i_k}^c\in I$.

Definition 29.

$\overline{I}:=\{H_j^c:H_j^c⩽H_i^{c}forsome{H}_i^c\in I\}$.

Theorem 2.

$([\mathrm{A}.4,\mathrm{A}.5.4])$ Let $\mathbf{I}=\{{\lceil S_{i_1}^c\rceil }_I,\cdots ,{\lceil S_{i_m}^c\rceil }_I\}$. Then there exist one closed hypersequent $G_{\mathbf{I}}^{☆}{\subseteq }_{c}G|G^{*}$ and its derivation ${\tau }_{\mathbf{I}}^{☆}$ from ${\lceil S_{i_1}^c\rceil }_I$, …, ${\lceil S_{i_m}^c\rceil }_I$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$ such that

(i) ${\tau }_{\mathbf{I}}^{☆}$ is constructed by applying elimination rules, say,

$$\frac{\underline{G_{b_1}|S_{j_1}^c{G}_{b_2}|S_{j_2}^c\cdots G_{b_w}|S_{j_w}^c}}{G_{{\mathbf{I}}_{\mathbf{j}}}^{*}={\{G_{b_k}\}}_{k=1}^w|G_{{\mathcal{I}}_{\mathbf{j}}}^{*}}⟨{\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}⟩,$$

and the fully constraint contraction rules, say $\frac{\underline{G_2}}{G_1}⟨E{C}_{\mathsf{\Omega }}^{*}⟩$, where $1⩽w⩽m$, $H_{j_k}^c\leftrightsquigarrow H_{j_l}^c$ for all $1⩽k<l⩽w$, $I_{\mathbf{j}}=\{H_{j_1}^c,\cdots ,H_{j_w}^c\}\subseteq \overline{I}$, ${\mathcal{I}}_{\mathbf{j}}=\{S_{j_1}^c,\cdots ,S_{j_w}^c\}$, ${\mathbf{I}}_{\mathbf{j}}=\{G_{b_1}|S_{j_1}^c,\cdots ,G_{b_w}|S_{j_w}^c\}$ and $G_{b_k}|S_{j_k}^c$ is closed for all $1⩽k⩽w$. Then $H_i^c\nleqq H_j^c$ for all $S_j^c\in G_{{\mathcal{I}}_{\mathbf{j}}}^{*}$ and $H_i^c\in I$.

(ii) For all $H\in {\overline{\tau }}_{\mathbf{I}}^{☆}$,

$${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H):=\left\{\begin{array}{cc}G|G^{*}\hfill & Histherootof{\overline{\tau }}_{\mathbf{I}}^{☆}or{G}_{2}in\frac{\underline{G_2}}{G_1}⟨E{C}_{\mathsf{\Omega }}^{*}\mathrm{or}I{D}_{\mathsf{\Omega }}⟩\in {\overline{\tau }}_{\mathbf{I}}^{☆},\hfill \\ H_{j_k}^c\hfill & His{G}_{b_k}|S_{j_k}^{c}in{\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}\in {\overline{\tau }}_{\mathbf{I}}^{☆}forsome1⩽k⩽w,\hfill \end{array}\right.$$

where, ${\overline{\tau }}_{\mathbf{I}}^{☆}$ is the skeleton of ${\tau }_{\mathbf{I}}^{☆}$ which is defined as Definition 27. Then

${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(G_{{\mathbf{I}}_{\mathbf{j}}}^{*})⩽{\partial }_{{\tau }_{\mathbf{I}}^{☆}}(G_{b_k}|S_{j_k}^c)$ for some $1⩽k⩽w$ in ${\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}$.

(iii) Let $H\in {\overline{\tau }}_{\mathbf{I}}^{☆}$, $G|G^{*}<{\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H)⩽H_I^V$, then $G_{H_I^V:H}^{☆(J)}\in {\tau }_{\mathbf{I}}^{☆}$ and it is constructed by applying the separation algorithm along $H_I^V$ to H and, is an upper hypersequent of either $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$ if it is applicable, or $⟨I{D}_{\mathsf{\Omega }}⟩$ otherwise.

(iv) $S_j^c\in G_{\mathbf{I}}^{☆}$ implies $H_j^c\parallel H_i^c$ for all $H_i^c\in I$ and, $S_j^c\in G_{{\mathcal{I}}_{\mathbf{j}}}^{*}$ for some ${\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}\in {\tau }_{\mathbf{I}}^{☆}$ or $S_j^c\in {\lceil S_{i_k}^c\rceil }_I$ for some $H_{i_k}^c\in I$ satisfying $H_j^c\nleqq H_{i_k}^c$.

Note that in Claim (i), bold $\mathbf{j}$ in $I_{\mathbf{j}},{\mathcal{I}}_{\mathbf{j}}$ or ${\mathbf{I}}_{\mathbf{j}}$ indicates the w-tuple $(j_1,\cdots ,j_w)$ in $S_{j_1}^c,\cdots ,S_{j_w}^c$. Claim (iv) shows the final aim of Theorem 2, i.e., there exists no $S_j^c\in G_{\mathbf{I}}^{☆}$ such that $H_j^c⩽H_i^c$ for some $H_i^c\in I$. It is almost impossible to construct ${\tau }_{\mathbf{I}}^{☆}$ in a non-recursive way. Thus we use Claims (i)–(iii) in Theorem 2 to characterize the structure of ${\tau }_{\mathbf{I}}^{☆}$ in order to construct it recursively.

Proof. 

${\tau }_{\mathbf{I}}^{☆}$ is constructed by induction on $\left|I\right|$. For the base case, let $\left|I\right|=1$. Then ${\tau }_{\mathbf{I}}^{☆}$ is constructed by Construction 5 and 7. Here, Claim (i) holds by Lemma 20(ii), Lemma 18(i) and Lemma 13(vi), Claim (ii) by Lemma 18(i), (iii) is clear and (iv) by Lemma 18(iv).

For the induction case, let $\left|I\right|⩾2$. Let $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{G^{\prime }|G^{″}|H^{\prime }}(II)\in {\tau }^{*}$, where $G^{\prime }|G^{″}|H^{\prime }=H_I^V$. Then $\{H_{i_1}^c,\cdots ,H_{i_m}^c\}$ is divided into two subsets $I_l=\{H_{l_1}^c,\cdots ,H_{l_{m(l)}}^c\},I_r=\{H_{r_1}^c,\cdots ,H_{r_{m(r)}}^c\},$ which occur in the left subtree ${\tau }^{*}(G^{\prime }|S^{\prime })$ and right subtree ${\tau }^{*}(G^{″}|S^{″})$ of ${\tau }^{*}(H_I^V)$, respectively. Then $m(l)+m(r)=m$. Let ${\mathbf{I}}_l=\{{\lceil S_{l_1}^c\rceil }_I,\cdots ,{\lceil S_{l_{m(l)}}^c\rceil }_I\},{\mathbf{I}}_r=\{{\lceil S_{r_1}^c\rceil }_I,\cdots ,{\lceil S_{r_{m(r)}}^c\rceil }_I\}.$ Suppose that derivations ${\tau }_{{\mathbf{I}}_l}^{☆}$ of $G_{{\mathbf{I}}_l}^{☆}$ and ${\tau }_{{\mathbf{I}}_r}^{☆}$ of $G_{{\mathbf{I}}_r}^{☆}$ are constructed such that Claims from (i) to (iv) hold. There are three cases to be considered in the following.

Case 1.$S^{\prime }\notin {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_l}}$ for all ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$. Then ${\tau }_{\mathbf{I}}^{☆}:={\tau }_{{\mathbf{I}}_l}^{☆}$ and $G_{\mathbf{I}}^{☆}:=G_{{\mathbf{I}}_l}^{☆}$.

• For Claim (i), let ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$ and $S_j^c\in G_{{\mathcal{I}}_{{\mathbf{j}}_l}}^{*}$. By the induction hypothesis, $H_i^c\nleqq H_j^c$ for all $H_i^c\in I_l$. Since $S^{\prime }\notin {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_l}}$ then $G^{″}|H^{\prime }\bigcap {⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_l}}=\varnothing$. Thus $G_{H_I^V:G^{″}|H^{\prime }}^{*}\bigcap G_{{\mathcal{I}}_{{\mathbf{j}}_l}}^{*}=\varnothing$ by Lemmas 11 and 12. Then $S_j^c\notin G_{H_I^V:G^{″}|H^{\prime }}^{*}$. Thus $G^{″}|S^{″}\nleqq H_j^c$ by Proposition 2(i). Hence, for all $H_i^c\in I_r$, $H_i^c\nleqq H_j^c$ by $G^{″}|S^{″}⩽H_i^c$. Then $H_i^c\nleqq H_j^c$ for all $H_i^c\in I$. Claims (ii) and (iii) follow directly from the induction hypothesis.
• For Claim (iv), let $S_j^c\in G_{\mathbf{I}}^{☆}$. It follows from the induction hypothesis that $H_j^c\parallel H_i^c$ for all $H_i^c\in I_l$ and, $S_j^c\in G_{{\mathcal{I}}_{{\mathbf{j}}_l}}^{*}$ for some ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$ or $S_j^c\in {\lceil S_{l_k}^c\rceil }_I$ for some $H_{l_k}^c\in I_l,H_j^c\nleqq H_{l_k}^c$. Then $H_j^c\nleqq H_I^V$ by $H_j^c\parallel H_{l_1}^c,H_I^V<H_{l_1}^c$.

If $S_j^c\in {\lceil S_{l_k}^c\rceil }_I$ for some $H_{l_k}^c\in I_l,H_j^c\nleqq H_{l_k}^c$ then $H_j^c\parallel H_i^c$ for all $H_i^c\in I$ by the definition of branches to I. Thus we assume that $S_j^c\in G_{{\mathcal{I}}_{{\mathbf{j}}_l}}^{*}$ for some ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$ in the following. If $G^{\prime }|S^{\prime }⩽H_j^c$ then $H_j^c\parallel H_i^c$ for all $H_i^c\in I_r$ thus $H_j^c\parallel H_i^c$ for all $H_i^c\in I$. Thus let $G^{\prime }|S^{\prime }\nleqq H_j^c$ in the following. By the proof of Claim (i) above, $G^{″}|S^{″}\nleqq H_j^c$. Then $H_I^V\nless H_j^c$ by $G^{\prime }|S^{\prime }\nleqq H_j^c$ and $G^{″}|S^{″}\nleqq H_j^c$. Thus $H_j^c\parallel H_I^V$. Hence $H_j^c\parallel H_i^c$ for all $H_i^c\in I$.

Case 2.$S^{″}\notin {⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}$ for all ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}\in {\tau }_{{\mathbf{I}}_r}^{☆}$. Then ${\tau }_{\mathbf{I}}^{☆}:={\tau }_{{\mathbf{I}}_r}^{☆}$ and $G_{\mathbf{I}}^{☆}:=G_{{\mathbf{I}}_r}^{☆}$. This case is proved by a procedure similar to that of Case 1 and omitted.

Case 3.$S^{\prime }\in {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_l}}$ for some ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$ and $S^{″}\in {⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}^{☆}}$ for some ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}\in {\tau }_{{\mathbf{I}}_r}^{☆}$.

Given

$$\frac{\underline{G_{b_{r1}}|S_{j_{r1}}^c{G}_{b_{r2}}|S_{j_{r2}}^c\cdots G_{b_{rv}}|S_{j_{rv}}^c}}{G_r\equiv {\{G_{b_{rk}}\}}_{k=1}^v|G_{{\mathcal{I}}_{{\mathbf{j}}_r}}^{*}}⟨{\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}⟩\in {\tau }_{{\mathbf{I}}_r}^{☆}$$

such that $S^{″}\in {⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}$ and $H_{j_{rk}}^c>H_I^V$ for all $1⩽k⩽v$, where, $1⩽v⩽m(r)$, $G_{b_{rk}}|S_{j_{rk}}^c$ is closed for all $1⩽k⩽v$, $I_{{\mathbf{j}}_r}=\{H_{j_{r1}}^c,H_{j_{r2}}^c,\cdots ,H_{j_{rv}}^c\}\subseteq \overline{I_r},$ ${\mathcal{I}}_{{\mathbf{j}}_r}=\{S_{j_{r1}}^c,S_{j_{r2}}^c,\cdots ,S_{j_{rv}}^c\},$ ${\mathbf{I}}_{{\mathbf{j}}_r}=\{G_{b_{r1}}|S_{j_{r1}}^c,\cdots ,G_{b_{rv}}|S_{j_{rv}}^c\}.$ Then $H_{I_{{\mathbf{j}}_r}}^V⩾G^{″}|S^{″}$ by $I_{{\mathbf{j}}_r}\subseteq \overline{I_r}$ and $H_{j_{rk}}^c>H_I^V$ for all $1⩽k⩽v$. Thus $H_j^c⇝H_i^c$ for all $H_j^c\in I_{{\mathbf{j}}_r}$ and $H_i^c\in I_l$ by $S^{″}\in {⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}$ and Construction 4.

For each ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}\in {\tau }_{{\mathbf{I}}_r}^{☆}$ above, we construct a derivation ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ in which you may regard ${\tau }_{{\mathbf{I}}_l}^{☆}$ as a subroutine, and ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ as its input in the following stage 1. Then a derivation ${\tau }_{{\mathbf{I}}_r}^{☆}({\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}))$ is constructed by calling ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ in Stage 2, in which you may regard ${\tau }_{{\mathbf{I}}_r}^{☆}({\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}))$ as a routine and ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ as its subroutine.

Before proceeding to deal with Case 3, we present the following property of ${\tau }_{\mathbf{I}}^{☆}$ which are derived from Claims (i) ∼ (iv) and applicable to ${\tau }_{{\mathbf{I}}_l}^{☆}$ or ${\tau }_{{\mathbf{I}}_r}^{☆}$ under the induction hypothesis.

Notation 9.

Let

$$G_{†}:=\widehat{S^{″}}|G_{H_I^V:G^{″}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}and$$

$$G_{‡}:={\{G_{b_{rk}}\}}_{k=1}^v|\widehat{S^{″}}|G_{{}^{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}$$

be two close hypersequents, $G_{†}\subseteq H$ for some $H\in {\tau }_{{\mathbf{I}}_l}^{☆}$ and $G_{‡}\backslash {\{G_{b_{rk}}\}}_{k=1}^v\subseteq H$ for some $H\in {\tau }_{{\mathbf{I}}_r}^{☆}$.

Generally, $\widehat{S^{″}}\subseteq G_{†}$ is a copy of $\widehat{S^{″}}\subseteq G_{‡}$, i.e., eigenvariables in $\widehat{S^{″}}\subseteq G_{†}$ have different identification numbers with those in $\widehat{S^{″}}\subseteq G_{‡}$, so are $H^{\prime },G^{″},S^{\prime }$.

Lemma 24.

$S_j^c\in G_{†}$ implies $H_j^c\parallel G^{\prime }|S^{\prime }$.

Proof. 

Let $S_j^c\in G_{†}\subseteq G_{H_I^V:G^{″}|H^{\prime }}^{☆(J)}$. Then $H_j^c\nleqq H_I^V$ by Lemma 19(i). Thus $H_j^c>H_I^V$ or $H_j^c\parallel H_I^V$. If $H_j^c\parallel H_I^V$ then $H_j^c\parallel G^{\prime }|S^{\prime }$ by $H_I^V<G^{\prime }|S^{\prime }$ and Proposition 1 (ii). If $H_j^c>H_I^V$ then $S_j^c\in H_I^V$ by Proposition 2(i). Thus $S_j^c\in G^{″}$ by Lemma 11, Lemma 14(i). Hence $H_j^c\parallel G^{\prime }|S^{\prime }$ by $H_j^c⩾G^{″}|S^{″}$, $G^{\prime }|S^{\prime }\parallel G^{″}|S^{″}$.  □

Lemma 25.

(1) ${\overline{\tau }}_{\mathbf{I}}^{☆}$ is an m-ary tree and, ${\tau }_{\mathbf{I}}^{☆}$ is a binary tree;

(2) Let $H\in {\overline{\tau }}_{\mathbf{I}}^{☆}$ then ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H)⩽H_{i_k}^c$ for some $1⩽k⩽m$;

(3) Let $H\in {\overline{\tau }}_{\mathbf{I}}^{☆}$ then $H_I^V\nparallel {\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H)$;

(4) Let $w>1$ in ${\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}\in {\tau }_{\mathbf{I}}^{☆}$ then $H_I^V<H_{j_k}^c$ for all $1⩽k⩽w$.

(5) Let ${\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}\in {\tau }_{\mathbf{I}}^{☆}$, ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(G_{b_k}|S_{j_k}^c)⩽H_I^V$ for some $1⩽k⩽w$. Then $w=1$.

Proof. 

(1) is immediately from Claim (i). (2) holds by $G|G^{*}⩽H_{j_k}^c$ and $H_{j_k}^c⩽H_{i_k}^c$ for some $H_{i_k}^c\in I$ by $I_{\mathbf{j}}\subseteq \overline{I}$. (3) holds by Proposition 1(iii), (2) and $H_I^V⩽H_{i_k}^c$.

For (4), let $w>1$. Then $H_{j_1}^c\parallel H_{j_k}^c$ for each $2⩽k⩽w$, $H_{j_1}^c⩽H_{i_g}^c$ and $H_{j_k}^c⩽H_{i_h}^c$ for some $H_{i_g}^c,H_{i_h}^c\in I$ by (2). Thus $H_{j_1}^c\parallel H_{i_h}^c$ and $H_{j_k}^c\parallel H_{i_g}^c$ by Proposition 1(ii). Hence $H_{j_1}^c\nleqq H_{i_g{i}_h}^V$ by $H_{i_g{i}_h}^V<H_{i_h}^c$, and $H_{j_k}^c\nleqq H_{i_g{i}_h}^V$ by $H_{i_g{i}_h}^V<H_{i_g}^c$. Thus $H_I^V<H_{j_1}^c$ and $H_I^V<H_{j_k}^c$ by (3), $H_I^V⩽H_{j_1{j}_k}^V$. Hence $H_I^V<H_{j_k}^c$ for all $1⩽k⩽w$. (5) is from (4).  □

Lemma 26.

Let $\frac{\underline{H_{i,1}\cdots H_{i,w_i}}}{H_{i-1,1}}⟨{\tau }_{{\mathbf{I}}_{\mathbf{j}}(i)}^{*}⟩\in {\tau }_{\mathbf{I}}^{☆}$ for all $1⩽i⩽n$ such that ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{0,1})=G|G^{*}$ and ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{n,1})⩽H_I^V$. Then ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{i,1})⩽H_I^V$ and $w_i=1$ for all $1⩽i⩽n$.

Proof. 

The proof is by induction on n. Let $n=1$ then $w_1=1$ by Lemma 25(5) and ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{1,1})⩽H_I^V$. For the induction step, let ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{i,1})⩽H_I^V$ for some $1<i⩽n$ then $w_i=1$ by Lemma 25(5). Since $\frac{\underline{H_{i,1}\cdots H_{i,w_i}}}{H_{i-1,1}}⟨{\tau }_{{\mathbf{I}}_{\mathbf{j}}(i)}^{*}⟩\in {\tau }_{\mathbf{I}}^{☆}$ then ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{i-1,1})⩽{\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{i,k})$ for some $1⩽k⩽w_i$ by Claim (ii). Then ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{i-1,1})⩽{\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{i,1})⩽H_I^V$ by $w_i=1$. Thus $w_{i-1}=1$ by Lemma 25(5).  □

Definition 30.

Let $\frac{\underline{G_2}}{G_1}⟨E{C}_{\mathsf{\Omega }}^{*}⟩\in {\tau }_{\mathbf{I}}^{☆}$. The module of ${\tau }_{\mathbf{I}}^{☆}$ at $G_2$, which we denote by ${\tau }_{\mathbf{I}:G_2}^{☆}$, is defined as follows: (1) $G_2\in {\tau }_{\mathbf{I}:G_2}^{☆}$; (2) $\frac{\underline{H_1\cdots H_u}}{H_0}⟨{\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}⟩\in {\tau }_{\mathbf{I}:G_2}^{☆}$ if $H_0\in {\tau }_{\mathbf{I}:G_2}^{☆}$; (3) $H_1\notin {\tau }_{\mathbf{I}:G_2}^{☆}$ if $\frac{\underline{H_1}}{H_0}⟨E{C}_{\mathsf{\Omega }}^{*}⟩\in {\tau }_{\mathbf{I}}^{☆}$, $H_0\in {\tau }_{\mathbf{I}:G_2}^{☆}$.

Each node of ${\tau }_{\mathbf{I}:G_2}^{☆}$ is determined bottom-up, starting with $G_2$, whose root is $G_2$ and leaves may be branches, leaves of ${\tau }^{*}$ or lower hypersequents of $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$-applications. While each node of ${\tau }_{H:H^{\prime }}^{*}$ is determined top-down, starting with $H^{\prime }$, whose root is a subset of $G|G^{*}$ and leaves contain $H^{\prime }$ and some leaves of ${\tau }^{*}$.

Lemma 27.

(1) ${\tau }_{\mathbf{I}:G_2}^{☆}$ is a derivation without $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$.

(2) Let $H^{\prime }\in {\overline{\tau }}_{\mathbf{I}:G_2}^{☆}$ and ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H^{\prime })>H_I^V$. Then ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H)>H_I^V$ for all $H\in {\overline{\tau }}_{\mathbf{I}:G_2}^{☆}$ and $H⩾H^{\prime }$.

Proof. 

Part (1) is clear and (2) immediately follows from Lemma 26.  □

Now, we continue to deal with Case 3 in the following.

Stage 1 Construction of Subroutine ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}).$ Roughly speaking, ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ is constructed by replacing some nodes ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$ with ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}\bigcup {\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ in post-order. However, the ordinal postorder-traversal algorithm cannot be used to construct ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ because the tree structure of ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ is generally different from that of ${\tau }_{{\mathbf{I}}_l}^{☆}$ at some nodes $H\in {\tau }_{{\mathbf{I}}_l}^{☆}$ satisfying ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)<H_{{\mathbf{I}}_l}^V$. Thus we construct a sequence ${\tau }_{{\mathbf{I}}_l}^{☆(q)}$ of trees for all $q⩾0$ inductively as follows.

For the base case, we mark all $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$-applications in ${\tau }_{{\mathbf{I}}_l}^{☆}$ as unprocessed and define such marked derivation to be ${\tau }_{{\mathbf{I}}_l}^{☆(0)}$. For the induction case, let ${\tau }_{{\mathbf{I}}_l}^{☆(q)}$ be constructed. If all applications of $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$ in ${\tau }_{{\mathbf{I}}_l}^{☆(q)}$ are marked as processed, we firstly delete the root of the tree resulting from the procedure and then, apply $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$ to the root of the resulting derivation if it is applicable otherwise add an $⟨I{D}_{\mathsf{\Omega }}⟩$-application to it and finally, terminate the procedure. Otherwise we select one of the outermost unprocessed $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$-applications in ${\tau }_{{\mathbf{I}}_l}^{☆(q)}$, say, $\frac{\underline{G_{q+1}^{\circ \circ }}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$, and perform the following steps to construct ${\tau }_{{\mathbf{I}}_l}^{☆(q+1)}$ in which $\frac{\underline{G_{q+1}^{\circ \circ }}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ be revised as $\frac{\underline{G_{q+1}^{··}}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{·}$ such that

(a) ${\tau }_{{\mathbf{I}}_l}^{☆(q+1)}$ is constructed by locally revising ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$ and leaving other nodes of ${\tau }_{{\mathbf{I}}_l}^{☆(q)}$ unchanged, particularly including $G_{q+1}^{\circ }$;

(b) ${\tau }_{{\mathbf{I}}_l}^{☆(q+1)}(G_{q+1}^{··})$ is a derivation in ${\mathbf{GL}}_{\mathsf{\Omega }}$;

(c) $G_{q+1}^{··}=G_{q+1}^{\circ \circ }$ if $S^{\prime }\notin {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}$ for all ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}(G_{q+1}^{\circ \circ })$ otherwise

$G_{q+1}^{··}=G_{q+1}^{\circ \circ }\backslash G_{†}^{m_{q+1}}|G_{‡}^{m_{q+1}}$ for some $m_{q+1}⩾1$.

Remark 3.

By two superscripts ∘ and · in ${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ or ${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{·}$, we indicate the unprocessed state and processed state, respectively. This procedure determines an ordering for all $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$-applications in ${\tau }_{{\mathbf{I}}_l}^{☆}$ and the subscript $q+1$ indicates that it is the $q+1$-th application of $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$ in a post-order transversal of ${\tau }_{{\mathbf{I}}_l}^{☆}$. $G_{q+1}^{\circ \circ }$ and $G_{q+1}^{\circ }$ ($G_{q+1}^{··}$ and $G_{q+1}^{·}$) are the premise and conclusion of ${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ (${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{·}$), respectively.

Step 1 (Delete). Take the module ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$ out of ${\tau }_{{\mathbf{I}}_l}^{☆(q)}$. Since ${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ is the unique unprocessed $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$-applications in ${\tau }_{{\mathbf{I}}_l}^{☆(q)}(G_{q+1}^{\circ })$ by its choice criteria, ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$ is the same as ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆}$ by Claim (a). Thus it is a derivation. If ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩽H_I^V$ for all $H\in {\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$, delete all internal nodes of ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$. Otherwise there exists

$$\frac{\underline{G_{b_{l^{\prime }1}}|S_{j_{l^{\prime }1}}^c{G}_{b_{l^{\prime }2}}|S_{j_{l^{\prime }2}}^c\cdots G_{b_{l^{\prime }{u}^{\prime }}}|S_{j_{l^{\prime }{u}^{\prime }}}^c}}{G_{l^{\prime }}\equiv {\{G_{b_{l^{\prime }k}}\}}_{k=1}^{u^{\prime }}|G_{{\mathcal{I}}_{{\mathbf{j}}_{l^{\prime }}}}^{*}}⟨{\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{l^{\prime }}}}^{*}⟩\in {\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$$

such that ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(G_{b_{l^{\prime }k}}|S_{j_{l^{\prime }k}}^c)>H_I^V$ for all $1⩽k⩽u^{\prime }$ and ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(G_{l^{\prime }})⩽H_I^V$ by Lemma 27(2) and ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(G_{q+1}^{\circ \circ })=G|G^{*}⩽H_I^V$, then delete all $H\in {\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$, $G_{q+1}^{\circ \circ }⩽H<G_{l^{\prime }}$. We denote the structure resulting from the deletion operation above by ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$. Since ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(G_{l^{\prime }})⩽H_I^V$ then ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$ is a tree by Lemma 26. Thus it is also a derivation.

Step 2 (Update). For each $G_{q^{\prime }}^{\circ }\in {\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$ which satisfies $\frac{\underline{G_{q^{\prime }}^{··}}}{G_{q^{\prime }}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q^{\prime }}^{·}\in {\tau }_{I_l}^{☆(q)}$ and $S^{\prime }\in {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}$ for some ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}(G_{q^{\prime }}^{\circ \circ })$, we replace H with $H\backslash G_{†}|G_{‡}$ for each $H\in {\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$, $G_{l^{\prime }}⩽H⩽G_{q^{\prime }}^{\circ }$.

Since $\frac{\underline{G_{q^{\prime }}^{··}}}{G_{q^{\prime }}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q^{\prime }}^{·}\in {\tau }_{I_l}^{☆(q)}(G_{q+1}^{\circ \circ })$ and ${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ is the outermost unprocessed

$⟨E{C}_{\mathsf{\Omega }}^{*}⟩$-application in ${\tau }_{{\mathbf{I}}_l}^{☆(q)}$ then $q^{\prime }⩽q$ and ${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q^{\prime }}^{·}$ has been processed. Thus Claims (b) and (c) hold for ${\tau }_{{\mathbf{I}}_l}^{☆(q)}(G_{q^{\prime }}^{·})$ by the induction hypothesis. Then $\frac{\underline{G_{q^{\prime }}^{··}}}{G_{q^{\prime }}^{·}}$ is a valid $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$-application since $\frac{\underline{G_{q^{\prime }}^{\circ \circ }}}{G_{q^{\prime }}^{\circ }}$, $\frac{\underline{G_{†}^{m_{q^{\prime }}}}}{G_{†}}$ and $\frac{\underline{G_{‡}^{m_{q^{\prime }}}}}{G_{‡}}$ are valid, where $G_{q^{\prime }}^{··}=G_{q^{\prime }}^{\circ \circ }\backslash G_{†}^{m_{q^{\prime }}}|G_{‡}^{m_{q^{\prime }}}$, $G_{q^{\prime }}^{·}=G_{q^{\prime }}^{\circ }\backslash G_{†}|G_{‡}$.

Lemma 28.

Let $G_{l^{\prime }}<H⩽G_{q^{\prime }}^{\circ }$. Then ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩾G^{\prime }|S^{\prime }$.

Proof. 

Since $G_{l^{\prime }}<H$ then $G_{b_{l^{\prime }k}}|S_{j_{l^{\prime }k}}^c⩽H$ for some $1⩽k⩽u^{\prime }$. If ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩾H_{I_l}^V$ then ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩾G^{\prime }|S^{\prime }$. Otherwise all applications between $G_{l^{\prime }}$ and H are one-premise rules by Lemma 26. Then $H_{j_{l^{\prime }k}}^c⩽{\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)$ by Claim (ii). Thus ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩾G^{\prime }|S^{\prime }$ by $H_I^V<H_{j_{l^{\prime }k}}^c$, ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩽H_{l_{k^{\prime }}}^c$ for some $1⩽k^{\prime }⩽m(l)$ by Claim (i).  □

Since ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩾G^{\prime }|S^{\prime }$ by Lemma 28 and $H_j^c\parallel G^{\prime }|S^{\prime }$ for each $S_j^c\in G_{†}$ by Lemma 24, then $G_{†}\subseteq H$ as side-hypersequent of H. Thus this step updates the revision of $G_{q^{\prime }}^{··}$ downward to $G_{l^{\prime }}$.

Let $m^{\prime }$ be the number of $G_{q^{\prime }}^{\circ }$ satisfying the above conditions, ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$, $G_{l^{\prime }}$ and $G_{b_{l^{\prime }k}}|S_{j_{l^{\prime }k}}^c$ for all $1⩽k⩽u^{\prime }$ be updated as ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(2)}^{☆(q)}$, $G_{l^{″}}$, $G_{b_{l^{\prime }k}}^{\prime }|S_{j_{l^{\prime }k}}^c$, respectively. Then ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(2)}^{☆(q)}$ is a derivation and $G_{l^{″}}=G_{l^{\prime }}\backslash G_{†}^{m^{\prime }}|G_{‡}^{m^{\prime }}$.

Step 3 (Replace). All ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}}^{*}\in {\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(2)}^{☆(q)}$ are processed in post-order. If $H_i^c⇝H_j^c$ for all $H_i^c\in I_{{\mathbf{j}}_{{}_l}}$ and $H_j^c\in I_{{\mathbf{j}}_r}$ it proceeds by the following procedure otherwise it remains unchanged. Let ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}$ be in the form

$$\frac{\underline{G_{b_{l1}}|S_{j_{l1}}^c{G}_{b_{l2}}|S_{j_{l2}}^c\cdots G_{b_{lu}}|S_{j_{lu}}^c}}{G_l\equiv {\{G_{b_{lk}}\}}_{k=1}^u|G_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}^{*}}.$$

Then $H_{j_{lk}}^c⩾G^{\prime }|S^{\prime }$ for all $1⩽k⩽u$ by Lemma 28, $G_{b_{lk}}|S_{j_{lk}}^c>G_{l^{″}}$.

Firstly, replace ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}}^{*}$ with ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}\cup {\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$. We may rewrite the roots of ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}}^{*}$ and ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}\cup {\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ as

$$\begin{array}{cc}\hfill G_l& ={\{G_{b_{lk}}\}}_{k=1}^u|G_{H_I^V:{⟨G^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}}^{*}|G_{H_I^V:G^{″}|H^{\prime }}^{*}\mathrm{and}\hfill \\ \hfill G_{l,r}& \equiv {\{G_{b_{lk}}\}}_{k=1}^u|G_{H_I^V:{⟨G^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}}^{*}|{\{G_{b_{rk}}\}}_{k=1}^v|G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}|H^{\prime }}^{*},\hfill \end{array}$$

respectively.

Let $G_{l^{″}}<H⩽G_l$. By Lemma 28, ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩾G^{\prime }|S^{\prime }$. By Lemma 14, $H_j^c⩽H_I^V<G^{\prime }|S^{\prime }$ or $H_j^c\parallel G^{\prime }|S^{\prime }$ for all $S_j^c\in G_{H_I^V:G^{″}|H^{\prime }}^{*}$. Thus $G_{H_I^V:G^{″}|H^{\prime }}^{*}\subseteq H$. Secondly, we replace H with $H\backslash G_{H_I^V:G^{″}|H^{\prime }}^{*}|{\{G_{b_{rk}}\}}_{k=1}^v|G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}|H^{\prime }}^{*}$ for all $G_{l^{\prime }}⩽H⩽G_l$. Let $m^{″}$ be the number of ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(2)}^{\mathsf{\Omega }(q)}$ satisfying the replacement conditions above, ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(2)}^{☆(q)}$, $G_{l^{″}}$ and $G_{b_{l^{\prime }k}}^{\prime }|S_{j_{l^{\prime }k}}^c$ for all $1⩽k⩽u^{\prime }$ be updated as ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(3)}^{☆(q)}$, $G_{l^{‴}}$, $G_{b_{l^{\prime }k}}^{″}|S_{j_{l^{\prime }k}}^c$, respectively. Then ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(3)}^{☆(q)}$ is a derivation of $G_{l^{‴}}$ and $G_{l^{‴}}=G_{l^{″}}\backslash {\{G_{H_I^V:G^{″}|H^{\prime }}^{*}\}}^{m^{″}}|{\{{\{G_{b_{rk}}\}}_{k=1}^v|G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}|H^{\prime }}^{*}\}}^{m^{″}}.$

Step 4 (Separation along $H_I^V$). Apply the separation algorithm along $H_I^V$ to $G_{l^{‴}}$ and denote the resulting derivation by ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(4)}^{☆(q)}$ whose root is labeled by $G_{q+1}^{··}$. Then all $G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}|H^{\prime }}^{*}$ in $G_{l^{‴}}$ are transformed into $G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}|H^{\prime }}^{☆(J)}$ in ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(4)}^{\mathsf{\Omega }(q)}$. Since $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{H_I^V=G^{\prime }|G^{″}|H^{\prime }}(II)\in {\tau }^{*},$

$$\frac{{\{G_{b_{lk}}\}}_{k=1}^u|{⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}{\{G_{b_{rk}}\}}_{k=1}^v|{⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_r}}}}{{\{G_{b_{lk}}\}}_{k=1}^u|{\{G_{b_{rk}}\}}_{k=1}^v|{⟨G^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}|{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_r}}}|H^{\prime }}(II)\in {\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}\cup {\mathbf{I}}_{{\mathbf{j}}_{{}_r}}}^{*}\in {\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(3)}^{☆(q)},$$

$H^{\prime }$, $S^{\prime }$ and $S^{″}$ are separable in ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(4)}^{☆(q)}$ by a procedure similar to that of Lemma 21. Let $S^{\prime }$ and $S^{″}$ be separated into $\widehat{S^{\prime }}$ and $\widehat{S^{″}}$, respectively. By Claim (iii), $G_{H_I^V:G_{l^{\prime }}}^{☆(J)}=G_{q+1}^{\circ \circ }.$

$$\begin{array}{cc}\hfill G_{H_I^V:G_{l^{″}}}^{☆(J)}& =G_{q+1}^{\circ \circ }\backslash G_{†}^{m^{\prime }}|G_{‡}^{m^{\prime }}byLemma19(iv),\hfill \\ \hfill G_{q+1}^{··}& =G_{H_I^V:G_{l^{‴}}}^{☆(J)}\hfill \\ & =G_{H_I^V:G_{l^{″}}}^{☆(J)}\backslash {\{G_{H_I^V:G^{″}|H^{\prime }}^{☆(J)}\}}^{m^{″}}|{\{{\{G_{b_{rk}}\}}_{k=1}^v|G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}|H^{\prime }}^{☆(J)}\}}^{m^{″}}\hfill \\ & =G_{H_I^V:G_{l^{″}}}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}|G_{H_I^V:G^{″}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}{\}}^{m^{″}}|\hfill \\ & \{{\{G_{b_{rk}}\}}_{k=1}^v|\widehat{S^{\prime }}|\widehat{S^{″}}|G_{{}^{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}{\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}\}}^{m^{″}}\hfill \\ & =G_{H_I^V:G_{l^{″}}}^{☆(J)}\backslash G_{†}^{m^{″}}|G_{‡}^{m^{″}}\hfill \\ & =\{G_{q+1}^{\circ \circ }\backslash G_{†}^{m^{\prime }}|G_{‡}^{m^{\prime }}\}\backslash G_{†}^{m^{″}}|G_{‡}^{m^{″}}\hfill \\ & =G_{q+1}^{\circ \circ }\backslash G_{†}^{m^{\prime }+m^{″}}|G_{‡}^{m^{\prime }+m^{″}}\hfill \\ & =G_{q+1}^{\circ \circ }\backslash G_{†}^{m_{q+1}}|G_{‡}^{m_{q+1}}\hfill \end{array}$$

where $m_{q+1}:=m^{\prime }+m^{″}$.

Step 5 (Put back). Replace ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$ in ${\tau }_{{\mathbf{I}}_l}^{☆(q)}$ with ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(4)}^{☆(q)}$ and mark $\frac{\underline{G_{q+1}^{··}}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ as processed, i.e., revise ${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ as ${⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{·}$. Among leaves of ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }}^{☆(q)}$, all $G_{q^{\prime }}^{\circ }$ are updated as $G_{q^{\prime }}^{·}$ and others keep unchanged in ${\tau }_{{\mathbf{I}}_l:G_{q+1}^{\circ \circ }(4)}^{☆(q)}$. Then this replacement is feasible, especially, $G_{q+1}^{\circ \circ }$ be replaced with $G_{q+1}^{··}$. Define the tree resulting from Step 5 to be ${\tau }_{{\mathbf{I}}_l}^{☆(q+1)}$. Then Claims (a), (b) and (c) hold for $q+1$ by the above construction.

Finally, we construct a derivation of $G_{{\mathbf{I}}_l}^{☆}\backslash G_{†}|G_{‡}$ from ${\lceil S_{l_1}^c\rceil }_I,\cdots ,{\lceil S_{l_{m(l)}}^c\rceil }_I$, $G_{b_{r1}}|S_{j_{r1}}^c,\cdots ,$ $G_{b_{rv}}|S_{j_{rv}}^c$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$, which we denote by ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$.

Remark 4.

All elimination rules used in constructing ${\tau }_{{\mathbf{I}}_l}^{☆}$ are extracted from ${\tau }^{*}$. Since ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ is a derivation in ${\mathbf{GL}}_{\mathsf{\Omega }}$ without $(E{C}_{\mathsf{\Omega }})$, we may extract elimination rules from ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ which we may use to construct ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ by a procedure similar to that of constructing ${\tau }_{{\mathbf{I}}_l}^{☆}$ with minor revision at every node H that ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩽H_I^V$. Note that updates and replacements in Steps 2 and 3 are essentially inductive operations but we neglect it for simplicity.

We may also think of constructing ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ as grafting ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ in ${\tau }_{{\mathbf{I}}_l}^{☆}$ by adding ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ to some ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$. Since the rootstock ${\tau }_{{\mathbf{I}}_l}^{☆}$ of the grafting process is invariant in Stage 2, we encapsulate ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ as an rule in ${\mathbf{GL}}_{\mathsf{\Omega }}$ whose premises are $G_{b_{r1}}|S_{j_{r1}}^c,G_{b_{r2}}|S_{j_{r2}}^c,\cdots ,G_{b_{rv}}|S_{j_{rv}}^c$ and conclusion is $\widehat{S^{″}}|{\{G_{b_{rk}}\}}_{k=1}^v|G_{{}^{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}$, i.e.,

$$\frac{\underline{G_{b_{r1}}|S_{j_{r1}}^c{G}_{b_{r2}}|S_{j_{r2}}^c\cdots G_{b_{rv}}|S_{j_{rv}}^c}}{\widehat{S^{″}}|{\{G_{b_{rk}}\}}_{k=1}^v|G_{{}^{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}}⟨{\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})⟩,$$

where, $G_{{\mathbf{I}}_{l\backslash r}}^{☆}=G_{{\mathbf{I}}_l}^{☆}\backslash G_{†}$ is closed.

Stage 2. Construction of routine ${\tau }_{{\mathbf{I}}_r}^{☆}({\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}))$. A sequence ${\tau }_{{\mathbf{I}}_r}^{☆(q)}$ of trees for all $q⩾0$ is constructed inductively as follows. ${\tau }_{{\mathbf{I}}_r}^{☆(0)}$, ${\tau }_{{\mathbf{I}}_r}^{☆(q)}$, $\frac{\underline{G_{q+1}^{\circ \circ }}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ are defined as those of Stage 1. Then we perform the following steps to construct ${\tau }_{{\mathbf{I}}_r}^{☆(q+1)}$ in which $\frac{\underline{G_{q+1}^{\circ \circ }}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ be revised as $\frac{\underline{G_{q+1}^{··}}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{·}$ such that Claims (a) and (b) are same as those of Stage 1 and (c) $G_{q+1}^{··}=G_{q+1}^{\circ \circ }$ if $S^{″}\notin {⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_r}}^{({\mathbf{t}}_{{}_r})}}$ for all ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_{\mathbf{r}}}}}^{*}\in {\tau }_{{\mathbf{I}}_r}^{☆}(G_{q+1}^{\circ \circ })$ otherwise $G_{q+1}^{··}=G_{q+1}^{\circ \circ }\backslash {\{\widehat{S^{\prime }}|G_{H_I^V:G^{\prime }}^{☆(J)}\}}^{m_{q+1}}|{\{G_{{\mathbf{I}}_{l\backslash r}}^{☆}\}}^{m_{q+1}}$ for some $m_{q+1}⩾1$.

Step 1 (Delete). ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }}^{☆(q)}$ and ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$ are defined as before.

$$\frac{\underline{G_{b_{r^{\prime }1}}|S_{j_{r^{\prime }1}}^c{G}_{b_{r^{\prime }2}}|S_{j_{r^{\prime }2}}^c\cdots G_{b_{r^{\prime }{v}^{\prime }}}|S_{j_{r^{\prime }{v}^{\prime }}}^c}}{G_{r^{\prime }}\equiv {\{G_{b_{r^{\prime }k}}\}}_{k=1}^{v^{\prime }}|G_{{\mathcal{I}}_{{\mathbf{j}}_{r^{\prime }}}}^{*}}⟨{\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{r^{\prime }}}}^{*}⟩\in {\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }}^{☆(q)}$$

satisfies ${\partial }_{{\tau }_{{\mathbf{I}}_r}^{☆}}(G_{b_{r^{\prime }k}}|S_{j_{r^{\prime }k}}^c)>H_I^V$ for all $1⩽k⩽v^{\prime }$ and ${\partial }_{{\tau }_{{\mathbf{I}}_r}^{☆}}(G_{r^{\prime }})⩽H_I^V$.

Step 2 (Update). For all $G_{q^{\prime }}^{\circ }\in {\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$ which satisfy $\frac{\underline{G_{q^{\prime }}^{··}}}{G_{q^{\prime }}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q^{\prime }}^{·}\in {\tau }_{{\mathbf{I}}_r}^{☆(q)}$ and $S^{″}\in {⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_{{}_r}}}$ for some ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_r}}}^{*}\in {\tau }_{{\mathbf{I}}_r}^{☆}(G_{q^{\prime }}^{\circ \circ })$, we replace H with $H\backslash \{\widehat{S^{\prime }}|G_{H_I^V:G^{\prime }}^{☆(J)}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}$ for all $H\in {\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$, $G_{r^{\prime }}⩽H⩽G_{q^{\prime }}^{\circ }$. Then Claims (a) and (b) are proved by a procedure as before. Let $m^{\prime }$ be the number of $G_{q^{\prime }}^{·}$ satisfying the above conditions. ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(1)}^{☆(q)}$, $G_{r^{\prime }}$ and $G_{b_{r^{\prime }k}}|S_{j_{r^{\prime }k}}^c$ for all $1⩽k⩽v^{\prime }$ be updated as ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(2)}^{☆(q)}$, $G_{r^{″}}$, $G_{b_{r^{\prime }k}}^{\prime }|S_{j_{r^{\prime }k}}^c$, respectively. Then ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(2)}^{☆(q)}$ is a derivation and $G_{r^{″}}=G_{r^{\prime }}\backslash {\{\widehat{S^{\prime }}|G_{H_I^V:G^{\prime }}^{☆(J)}\}}^{m^{\prime }}|{\{G_{{\mathbf{I}}_{l\backslash r}}^{☆}\}}^{m^{\prime }}$.

Step 3 (Replace). All ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}\in {\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(2)}^{\mathsf{\Omega }(q)}$ are processed in post-order. If $H_i^c⇝H_j^c$ for all $H_i^c\in I_{{\mathbf{j}}_r}$ and $H_j^c\in I_l$ it proceeds by the following procedure otherwise it remains unchanged. Let ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ be in the form

$$\frac{\underline{G_{b_{r1}}|S_{j_{r1}}^c{G}_{b_{r2}}|S_{j_{r2}}^c\cdots G_{b_{rv}}|S_{j_{rv}}^c}}{G_r\equiv {\{G_{b_{rk}}\}}_{k=1}^v|G_{{\mathcal{I}}_{{\mathbf{j}}_r}}^{*}}.$$

Then there exists the unique $1⩽k^{\prime }⩽v^{\prime }$ such that $G_{r^{″}}<G_{b_{r^{\prime }{k}^{\prime }}}|S_{j_{r^{\prime }{k}^{\prime }}}^c⩽G_r$.

Firstly, we replace ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ with ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$. We may rewrite the roots of ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$, ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ as $G_r={\{G_{b_{rk}}\}}_{k=1}^v|G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{j_r}}}^{*}|G_{H_I^V:G^{\prime }|H^{\prime }}^{*},$ $G_{l\backslash r}\equiv {\{G_{b_{rk}}\}}_{k=1}^v|\widehat{S^{″}}|G_{{}^{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆},$ respectively.

Let $G_{r^{″}}<H⩽G_r$. Then ${\partial }_{{\tau }_{{\mathbf{I}}_r}^{☆}}(H)⩾G^{″}|S^{″}$ by Lemma 28. Thus $G_{H_I^V:G^{\prime }|H^{\prime }}^{☆(0)}\subseteq H,\{S_j^c:S_j^c\in G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{j_r}}}^{*},H_j^c⩾G^{″}|S^{″}\}=\{S_j^c:S_j^c\in G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{j_r}}}^{☆(J)},H_j^c⩾G^{″}|S^{″}\}.$ Define $G_H^{**}=\{S_j^c:S_j^c\in G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{j_r}}}^{*},S_j^c\mathrm{be}\mathrm{the}\mathrm{focus}\mathrm{sequent}\mathrm{of}\mathrm{some}{H}^{\prime }\in {\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(2)}^{☆(q)},H⩽H^{\prime }⩽G_r\}$.

Then we replace H with

$$H\backslash \{G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{j_r}}}^{*}\backslash G_H^{**}|G_{H_I^V:G^{\prime }|H^{\prime }}^{*}\}|\widehat{S^{″}}|\{G_{{}^{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}}^{☆(J)}\backslash G_H^{**}\}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}$$

for all $G_{b_{r^{\prime }{k}^{\prime }}}|S_{j_{r^{\prime }{k}^{\prime }}}^c⩽H⩽G_r$.

Let $m^{″}$ be the number of ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}\in {\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(2)}^{\mathsf{\Omega }(q)}$ satisfying the replacement conditions as above, ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(2)}^{☆(q)}$, $G_{r^{″}}$ and $G_{b_{r^{\prime }k}}^{\prime }|S_{j_{r^{\prime }k}}^c$ for all $1⩽k⩽v^{\prime }$ be updated as ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(3)}^{☆(q)}$, $G_{r^{‴}}$, $G_{b_{r^{\prime }k}}^{″}|S_{j_{r^{\prime }k}}^c$, respectively. Then ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(3)}^{☆(q)}$ is a derivation and $G_{r^{‴}}=G_{r^{″}}\backslash H_1^{m^{″}}|H_2^{m^{″}}$, where

$$\begin{array}{cc}\hfill H_0& =G_{G_{b_{r^{\prime }k}}^{\prime }|S_{j_{r^{\prime }k}}^c}^{**},\hfill \\ \hfill H_1& =G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{j_r}}}^{*}\backslash H_0|G_{H_I^V:G^{\prime }|H^{\prime }}^{*},\hfill \\ \hfill H_2& =\widehat{S^{″}}|G_{{}^{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}}^{☆(J)}\backslash H_0|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}.\hfill \end{array}$$

Step 4 (Separation along $H_I^V$). Apply the separation algorithm along $H_I^V$ to $G_{r^{‴}}$ and denote the resulting derivation by ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(4)}^{☆(q)}$ whose root is labeled by $G_{q+1}^{··}$.

By Claim (iii), $G_{H_I^V:G_{r^{\prime }}}^{☆(J)}=G_{q+1}^{\circ \circ }$.

$$\begin{array}{cc}\hfill G_{H_I^V:G_{r^{″}}}^{☆(J)}& =G_{q+1}^{\circ \circ }\backslash {\{G_{H_I^V:G^{\prime }}^{☆(J)}|\widehat{S^{\prime }}\}}^{m^{\prime }}|{\{G_{{\mathbf{I}}_{l\backslash r}}^{☆}\}}^{m^{\prime }},\hfill \\ \hfill G_{H_I^V:H_1}^{☆(J)}& =G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{j_r}}}^{☆(J)}\backslash G_{H_I^V:H_3}^{☆(J)}|G_{H_I^V:G^{\prime }|H^{\prime }}^{☆(J)},\hfill \\ \hfill G_{H_I^V:H_2}^{☆(J)}& =\widehat{S^{″}}|G_{{}^{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}}^{☆(J)}\backslash G_{H_I^V:H_3}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill G_{H_I^V:G_{r^{‴}}}^{☆(J)}& =G_{H_I^V:G_{r^{″}}}^{☆(J)}\backslash {\{G_{H_I^V:G^{\prime }|H^{\prime }}^{☆(J)}\}}^{m^{″}}|\{\widehat{S^{″}}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}{|G_{{\mathbf{I}}_{l\backslash r}}^{☆}\}}^{m^{″}}\hfill \\ & =G_{H_I^V:G_{r^{″}}}^{☆(J)}\backslash {\{G_{H_I^V:G^{\prime }}^{☆(J)}|\widehat{S^{\prime }}\}}^{m^{″}}|{\{G_{{\mathbf{I}}_{l\backslash r}}^{☆}\}}^{m^{″}}.\hfill \end{array}$$

Then

$$G_{q+1}^{··}=G_{H_I^V:G_{r^{‴}}}^{☆(J)}=G_{q+1}^{\circ \circ }\backslash {\{\widehat{S^{\prime }}|G_{H_I^V:G^{\prime }}^{☆(J)}\}}^{m_{q+1}}|{\{G_{{\mathbf{I}}_{l\backslash r}}^{☆}\}}^{m_{q+1}}$$

where $m_{q+1}:=m^{\prime }+m^{″}$.

Step 5 (Put back). Replace ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }}^{☆(q)}$ in ${\tau }_{{\mathbf{I}}_r}^{☆(q)}$ with ${\tau }_{{\mathbf{I}}_r:G_{q+1}^{\circ \circ }(4)}^{☆(q)}$ and revise $\frac{\underline{G_{q+1}^{··}}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{\circ }$ as $\frac{\underline{G_{q+1}^{··}}}{G_{q+1}^{\circ }}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_{q+1}^{·}$. Define the resulting tree from Step 5 to be ${\tau }_{{\mathbf{I}}_r}^{☆(q+1)}$ then Claims (a), (b) and (c) hold for $q+1$ by the above construction.

Finally, we construct a derivation of $G_{{\mathbf{I}}_r}^{☆}\backslash \{\widehat{S^{\prime }}|G_{H_I^V:G^{\prime }}^{☆(J)}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}$ from ${\lceil S_{i_1}^c\rceil }_I$, …, ${\lceil S_{i_m}^c\rceil }_I$ in ${\mathbf{GL}}_{\mathsf{\Omega }}$. Since the major operation of Stage 2 is to replace ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ with ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}^{({\mathbf{t}}_r)}}^{*})$ for all ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}\in {\tau }_{{\mathbf{I}}_r}^{☆}$ satisfying $S^{″}\in {⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}^{({\mathbf{t}}_r)}}$, then we denote the resulting derivation from Stage 2 by ${\tau }_{{\mathbf{I}}_r}^{☆}({\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}))$.

In the following, we prove that the claims from (i) to (iv) hold if ${\tau }_{\mathbf{I}}^{☆}:={\tau }_{{\mathbf{I}}_r}^{☆}({\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}))$ and $G_{\mathbf{I}}^{☆}:=G_{{\mathbf{I}}_r}^{☆}\backslash \{\widehat{S^{\prime }}|G_{H_I^V:G^{\prime }}^{☆(J)}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}$.

• For Claims (i) and (ii): Let $\frac{\underline{H_1\cdots H_w}}{H_0}⟨{\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}⟩\in {\tau }_{\mathbf{I}}^{☆}$ and $S_j^c\in G_{{\mathcal{I}}_{\mathbf{j}}}^{*}$. Then ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_k)\nleqq H_j^c$ for all $1⩽k⩽w$ by Lemma 17(iv).
  If ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{k^{\prime }})⩽H_I^V$ for some $1⩽k^{\prime }⩽w$, then $H_i^c\nleqq H_j^c$ for all $H_i^c\in I$ by ${\partial }_{{\tau }_{\mathbf{I}}^{☆}}(H_{k^{\prime }})⩽H_I^V⩽H_i^c$. Thus Claim (i) holds and Claim (ii) holds by Lemma 25(5) and Lemma 19(i). Note that Lemma 25(5) is independent of Claims from (ii) to (iv).
  Otherwise ${\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}$ is built up from ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}\in {\tau }_{{\mathbf{I}}_r}^{☆}$, ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}$ or ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}\cup {\mathbf{I}}_{{\mathbf{j}}_{{}_r}}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ by keeping their focus and principal sequents unchanged and making their side-hypersequents possibly to be modified, but which has no effect on discussing Claim (ii) and then Claim (ii) holds for ${\tau }_{\mathbf{I}}^{☆}$ by the induction hypothesis on Claim (ii) of ${\tau }_{{\mathbf{I}}_l}^{☆}$ or ${\tau }_{{\mathbf{I}}_r}^{☆}$.
  If ${\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}$ is from ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_{{}_l}}\cup {\mathbf{I}}_{{\mathbf{j}}_{{}_r}}}^{*}$ then $S^{\prime }\in {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_l}}$ and $S^{″}\in {⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}$ by the choice of ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}$ and ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ at Stage 1. By the induction hypothesis, $H_i^c\nleqq H_j^c$ for all $S_j^c\in G_{{\mathcal{I}}_{{\mathbf{j}}_l}}^{*},$ $H_i^c\in I_l$ and $H_i^c\nleqq H_j^c$ for all $S_j^c\in G_{{\mathcal{I}}_{{\mathbf{j}}_r}}^{*},$ $H_i^c\in I_r$. Then $H_i^c\nleqq H_j^c$ for all $S_j^c\in G_{{\mathcal{I}}_{\mathbf{j}}}^{*}=G_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}\cup {\mathcal{I}}_{{\mathbf{j}}_{{}_r}}}^{*}$, $H_i^c\in I$ by $G_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}\cup {\mathcal{I}}_{{\mathbf{j}}_{{}_r}}}^{*}=G_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}^{*}\bigcap G_{{\mathcal{I}}_{{\mathbf{j}}_{{}_r}}}^{*}$, $I=I_l\cup I_r$.
  If ${\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}$ is from ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}$ then $S^{\prime }\notin {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_l}}$ by Step 3 at Stage 1. Then ${⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_l}}\bigcap (G^{″}|H^{\prime })=\varnothing$. Thus $S_j^c\notin G_{H_I^V:G^{″}|H^{\prime }}^{*}$. Hence $G^{″}|S^{″}\nleqq H_j^c$. Therefore $H_i^c\nleqq H_j^c$ for all $H_i^c\in I_r$ by $G^{″}|S^{″}⩽H_i^c$. Thus $H_i^c\nleqq H_j^c$ for all $H_i^c\in I$ by $S_j^c\in G_{{\mathcal{I}}_{\mathbf{j}}}^{*}=G_{{\mathcal{I}}_{{\mathbf{j}}_{{}_l}}}^{*}$ and the induction hypothesis from ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$. The case of ${\tau }_{{\mathbf{I}}_{\mathbf{j}}}^{*}$ built up from ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ is proved by a procedure similar to above and omitted.
• Claim (iii) holds by Step 4 at Stages 1 and 2. Note that in the whole of Stage 1, we treat ${\{G_{b_{rk}}\}}_{k=1}^v$ as a side-hypersequent. But it is possible that there exists $S_j^c\in {\{G_{b_{rk}}\}}_{k=1}^v$ such that $H_j^c⩽H_I^V$. Since we have not applied the separation algorithm to ${\{G_{b_{rk}}\}}_{k=1}^v$ in Step 4 at Stage 1, then it could make Claim (iii) invalid. But it is not difficult to find that we just move the separation of such $S_j^c$ to Step 4 at Stage 2. Of course, we can move it to Step 4 at Stage 1, but which make the discussion complicated.
• For Claim (iv), we prove (1) $H_i^c\parallel H_j^c$ for all $S_j^c\in G_{{\mathbf{I}}_{l\backslash r}}^{☆}$ and $H_i^c\in I$, (2) $H_i^c\parallel H_j^c$ for all $S_j^c\in G_{{\mathbf{I}}_r}^{☆}\backslash \{\widehat{S^{\prime }}|G_{H_I^V:G^{\prime }}^{☆(J)}\}$ and $H_i^c\in I$. Only (1) is proved as follows and (2) by a similar procedure and omitted.

Let $S_j^c\in G_{{\mathbf{I}}_{l\backslash r}}^{☆}$. Then $S_j^c\in G_{{\mathbf{I}}_l}^{☆}$ and $S_j^c\notin \widehat{S^{″}}|G_{H_I^V:G^{″}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}$ by the definition of $G_{{\mathbf{I}}_{l\backslash r}}^{☆}$. By a procedure similar to that of Claim (iv) in Case 1, we get $H_j^c\nleqq H_I^V$ and assume that $S_j^c\in G_{{\mathcal{I}}_{{\mathbf{j}}_l}}^{*}$ for some ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}\in {\tau }_{{\mathbf{I}}_l}^{☆}$ and let $G^{\prime }|S^{\prime }\nleqq H_j^c$ in the following.

Suppose that $G^{″}|S^{″}⩽H_j^c$. Then $S_j^c\in G_{H_I^V:G^{″}}^{*}$ and $S^{\prime }\in {⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_{{\mathbf{j}}_l}}$ by $S_j^c\in G_{{\mathcal{I}}_{{\mathbf{j}}_l}}^{*}$. Hence $S_j^c\in G_{H_I^V:G^{″}}^{☆(J)}$ by $H_j^c⩾G^{″}|S^{″}>H_I^V$. Therefore $S_j^c\in \widehat{S^{″}}|G_{H_I^V:G^{″}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}$, a contradiction thus $G^{″}|S^{″}\nleqq H_j^c$. Then $H_I^V\nless H_j^c$ by $G^{\prime }|S^{\prime }\nleqq H_j^c$ and $G^{″}|S^{″}\nleqq H_j^c$. Thus $H_j^c\parallel H_I^V$. Hence $H_j^c\parallel H_i^c$ for all $H_i^c\in I$. This completes the proof of Theorem 2.  □

Definition 31.

The manipulation described in Theorem 2 is called a derivation-grafting operation.

9. The Proof of the Main Theorem

Recall that in the main theorem $G_0\equiv G^{\prime }|{\{{\mathsf{\Gamma }}_i,p\Rightarrow {\mathsf{\Delta }}_i\}}_{i=1\cdots n}|{\{{\mathsf{\Pi }}_j\Rightarrow p,{\mathsf{\Sigma }}_j\}}_{j=1\cdots m}.$

Lemma 29.

(i) If $G_2=G_0\backslash \{{\mathsf{\Gamma }}_1,p\Rightarrow {\mathsf{\Delta }}_1\}$ and ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_2)$ then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$;

$(i^{\prime })$ If $G_2=G_0\backslash \{{\mathsf{\Pi }}_1\Rightarrow p,{\mathsf{\Sigma }}_1\}$ and ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_2)$ then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$;

(ii) If $G_2=G_0|\{{\mathsf{\Gamma }}_1,p\Rightarrow {\mathsf{\Delta }}_1\}$ and ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_2)$ then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$;

$(i{i}^{\prime })$ If $G_2=G_0|\{{\mathsf{\Pi }}_1\Rightarrow p,{\mathsf{\Sigma }}_1\}$ and ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_2)$ then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$;

(iii) If $G_2=G_0\backslash \{{\mathsf{\Gamma }}_1,p\Rightarrow {\mathsf{\Delta }}_1\}|\{{\mathsf{\Gamma }}_1,\top \Rightarrow {\mathsf{\Delta }}_1\}$ and ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_2)$ then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$;

$(ii{i}^{\prime })$ If $G_2=G_0\backslash {\mathsf{\Pi }}_1\Rightarrow p,{\mathsf{\Sigma }}_1|{\mathsf{\Pi }}_1\Rightarrow \perp ,{\mathsf{\Sigma }}_1$ and ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_2)$ then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$.

Proof. 

(i) Since ${\mathcal{D}}_0(G_2)=G^{\prime }|{\{{\mathsf{\Gamma }}_i,{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_i,{\mathsf{\Sigma }}_j\}}_{i=2\cdots n;j=1\cdots m}\subseteq G^{\prime }|{\{{\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_1,{\mathsf{\Sigma }}_j\}}_{j=1\cdots m}|{\{{\mathsf{\Gamma }}_i,{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_i,{\mathsf{\Sigma }}_j\}}_{i=2\cdots n;j=1\cdots m}={\mathcal{D}}_0(G_0)$ then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$ holds. If $n=1$, we replace all p in ${\mathsf{\Pi }}_j\Rightarrow p,{\mathsf{\Sigma }}_j$ with ⊥. Then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$ holds by applying $(CUT)$ to ${\mathsf{\Gamma }}_1,\perp \Rightarrow {\mathsf{\Delta }}_1$ and $G^{\prime }|{\{{\mathsf{\Pi }}_j\Rightarrow \perp ,{\mathsf{\Sigma }}_j\}}_{j=1\cdots m}.$

(ii) Since ${\mathcal{D}}_0(G_2)=G^{\prime }|{\{{\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_1,{\mathsf{\Sigma }}_j\}}_{j=1\cdots m}|{\{{\mathsf{\Gamma }}_i,{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_i,{\mathsf{\Sigma }}_j\}}_{i=1\cdots n;j=1\cdots m}$ then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$ holds by applying $(E{C}^{*})$ to ${\mathcal{D}}_0(G_2)$.

(iii) Since ${\mathcal{D}}_0(G_2)=G^{\prime }|{\mathsf{\Gamma }}_1,\top \Rightarrow {\mathsf{\Delta }}_1|{\{{\mathsf{\Gamma }}_i,{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_i,{\mathsf{\Sigma }}_j\}}_{i=2\cdots n;j=1\cdots m}$ then ${⊢}_{\mathbf{GL}}{G}^{″}\equiv G^{\prime }|{\mathsf{\Gamma }}_1,{\mathsf{\Pi }}_1\Rightarrow {\mathsf{\Delta }}_1,{\mathsf{\Sigma }}_1|{\{{\mathsf{\Gamma }}_i,{\mathsf{\Pi }}_j\Rightarrow {\mathsf{\Delta }}_i,{\mathsf{\Sigma }}_j\}}_{i=2\cdots n;j=1\cdots m}$ holds by applying $(CUT)$ to ${\mathsf{\Gamma }}_1,\top \Rightarrow {\mathsf{\Delta }}_1$ in ${\mathcal{D}}_0(G_2)$ and ${\mathsf{\Pi }}_1\Rightarrow \top ,{\mathsf{\Sigma }}_1$. Thus ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$ holds by applying $(EW)$ to $G^{″}$.

$({\mathrm{i}}^{\prime }),({\mathrm{ii}}^{\prime })$ and $({\mathrm{iii}}^{\prime })$ are proved by a procedure respectively similar to those of (i), (ii) and (iii) and omitted.  □

Let $I=\{H_{i_1}^c,\cdots ,H_{i_m}^c\}\subseteq \{H_1^c,\cdots ,H_N^c\}$, $G_I$ denote a closed hypersequent such that $G_I{\subseteq }_{c}G|G^{*}$ and $H_j^c\parallel H_i^c$ for all $S_j^c\in G_I$ and $H_i^c\in I$.

Lemma 30.

There exists $G_I$ such that ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{G}_I$ for all $I\subseteq \{H_1^c,\cdots ,H_N^c\}$.

Proof. 

The proof is by induction on m. For the base step, let $m=0$, then $I=\varnothing$ and $G_I:=G|G^{*}$ and ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{G}_I$ by Lemma 5 (v).

For the induction step, suppose that $m⩾1$ and there exists $G_I$ such that ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{G}_I$ for all $\left|I\right|⩽m-1$. Then there exist $G_{I\backslash \{H_{i_k}^c\}}$ for all $1⩽k⩽m$ such that ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{G}_{I\backslash \{H_{i_k}^c\}}$ and $H_j^c\parallel H_i^c$ for all $S_j^c\in G_{I\backslash \{H_{i_k}^c\}}$ and $H_i^c\in I\backslash \{H_{i_k}^c\}$.

If $H_j^c\parallel H_{i_k}^c$ for all $S_j^c\in G_{I\backslash \{H_{i_k}^c\}}$ then $G_I:=G_{I\backslash \{H_{i_k}^c\}}$ and the claim holds clearly. Otherwise there exists $S_j^c\in G_{I\backslash \{H_{i_k}^c\}}$ such that $H_j^c⩽H_{i_k}^c$ or $H_j^c>H_{i_k}^c$ then we rewrite $G_{I\backslash \{H_{i_k}^c\}}$ as ${\lceil S_{i_k^{\prime }}^c\rceil }_{\{H_{i_k^{\prime }}^c\}\cup I\backslash \{H_{i_k}^c\}}$, where we define $H_{i_k^{\prime }}^c$ such that $S_{i_k^{\prime }}^c\in G_{I\backslash \{H_{i_k}^c\}}$ and, $S_j^c\in G_{I\backslash \{H_{i_k}^c\}}$ implies $H_j^c⩽H_{i_k^{\prime }}^c$ or $H_j^c\parallel H_i^c$ for all $H_i^c\in \{H_{i_k^{\prime }}^c\}\cup I\backslash \{H_{i_k}^c\}$. If we cannot define $G_I$ to be $G_{I\backslash \{H_{i_k}^c\}}$ for each $1⩽k⩽m$, let $I^{\prime }:=\{H_{i_1^{\prime }}^c,\cdots ,H_{i_m^{\prime }}^c\}$. Then $G_{I^{\prime }}$ is constructed by applying the separation algorithm of multiple branches (or one branch if $m=1$) to ${\lceil S_{i_1^{\prime }}^c\rceil }_{I^{\prime }},\cdots ,{\lceil S_{i_m^{\prime }}^c\rceil }_{I^{\prime }}$. Then ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{G}_{I^{\prime }}$ by ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{\lceil S_{i_1^{\prime }}^c\rceil }_{I^{\prime }},\cdots ,{⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{\lceil S_{i_m^{\prime }}^c\rceil }_{I^{\prime }}$, Theorem 2 (or Lemma 20(i) for one branch). Let $G_I:=G_{I^{\prime }}$ then ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{G}_I$ clearly.  □

The proof of Theorem 1:

Let $I=\{H_1^c,\cdots ,H_N^c\}$ in Lemma 30. Then there exists $G_I$ such that ${⊢}_{{\mathbf{GL}}_{\mathsf{\Omega }}}{G}_I$, $G_I{\subseteq }_{c}G|G^{*}$ and $H_j^c\parallel H_i^c$ for all $S_j^c\in G_I$ and $H_i^c\in I$. Then ${⊢}_{\mathbf{GL}}\mathcal{D}(G_I)$ by Lemma 8.

Suppose that $S_j^c\in G_I$. Then $H_j^c\parallel H_i^c$ for all $H_i^c\in I$. Thus $H_j^c\parallel H_j^c$ by $H_j^c\in I$, a contradiction with $H_j^c⩽H_j^c$ and hence there does not exist $S_j^c\in G_I$. Therefore $G_I{\subseteq }_{c}G$ by $G_I{\subseteq }_{c}G|G^{*}$.

By removing the identification number of each occurrence of p in G, we obtain the sub-hypersequent $G_2$ of $G_2|G_2^{*}$, which is the root of ${\tau }^4$ resulting from Step 4 in Section 4. Then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_2)$ by ${⊢}_{\mathbf{GL}}\mathcal{D}(G_I)$ and $G_I{\subseteq }_{c}G$. Since $G_2$ is constructed by adding or removing some ${\mathsf{\Gamma }}_i,p\Rightarrow {\mathsf{\Delta }}_i$ or ${\mathsf{\Pi }}_j\Rightarrow p,{\mathsf{\Sigma }}_j$ from $G_0$, or replacing ${\mathsf{\Gamma }}_i,p\Rightarrow {\mathsf{\Delta }}_i$ with ${\mathsf{\Gamma }}_i,\top \Rightarrow {\mathsf{\Delta }}_i$, or ${\mathsf{\Pi }}_j\Rightarrow p,{\mathsf{\Sigma }}_j$ with ${\mathsf{\Pi }}_j\Rightarrow \perp ,{\mathsf{\Sigma }}_j$, then ${⊢}_{\mathbf{GL}}{\mathcal{D}}_0(G_0)$ by Lemma 29. This completes the proof of the main theorem.  □

Theorem 3.

Density elimination holds for all $\mathbf{GL}$ in $\{\mathbf{GUL},\mathbf{GIUL},\mathbf{GMTL},\mathbf{GIMTL}\}.$

Proof. 

It follows immediately from the main theorem.  □

10. Final Remarks and Open Problems

Recently, we have generalized our method described in this paper to the non-commutative substructural logic ${\mathbf{GpsUL}}^{*}$ in [20]. This result shows that ${\mathbf{GpsUL}}^{*}$ is the logic of pseudo-uninorms and their residua and answered the question posed by Metcalfe, Olivetti, Gabbay and Tsinakis in [21,22].

It has often been the case in the past that metamathematical proofs of the standard completeness have the corresponding algebraic ones, and vise verse. In particular, Baldi and Terui [23] had given an algebraic proof of the standard completeness of UL. A natural problem is whether there is an algebraic proof corresponding to our proof-theoretic one. It seems difficult to obtain it by using the insights gained from the approach described in this paper because ideas and syntactic manipulations introduced here are complicated and specialized. In addition, Baldi and Terui [23] also mentioned some open problems. Whether our method could be applied to their problems is another research direction.

On 21 March 2014, I found the way to deal with the example in Section 3. Then I finished the one branch algorithm in Section 7 on the late April 2014. I devised the multi-branch algorithm in Section 8 on early November 2014. Since I submitted my paper to Transactions of the American Mathematical Society on 20 January 2015, it has been reviewed successively by Annals of Pure and Applied Logic, Fuzzy Sets and Systems and, the Journal of Logic and Computation. As a mathematician, the greatest anxiety is that his work has never been taken seriously by his academic circle during his career, but after his death, someone would say, sir, your proof is wrong.

Appendix A.1. Why Do We Adopt Avron-Style Hypersequent Calculi?

A hypersequent calculus is called Pottinger-style if its two-premise rules are in the form of $\frac{G|S^{\prime }G|S^{″}}{G|H^{\prime }}(II)$ and, Avron-style if in the form of $\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{G^{\prime }|G^{″}|H^{\prime }}(II)$. In the viewpoint of Avron-style systems, each application of two-premise rules contains implicitly applications of $(EC)$ in Pottinger-style systems, as shown in the following.

$$\begin{array}{|c|}\hline \frac{G|S^{\prime }G|S^{″}}{G|H^{\prime }}(II)\underset{inAvron-stylesystem}{\overset{correspondsto}{\to }}\frac{\frac{G|S^{\prime }G|S^{″}}{G|G|H^{\prime }}(II)}{G|H^{\prime }}(E{C}^{*})\\ \hline\end{array}$$

The choice of the underlying system of hypersequent calculus is vital to our purpose and it gives the background or arena. In Pottinger-style system, $G_0$ in Section 3 is proved without application of $(EC)$ as follows. But it seems helpless to prove that $H_0$ is a theorem of IUL.

$$\begin{array}{|c|}\hline \frac{\frac{C\Rightarrow C}{C\Rightarrow C|\Rightarrow p,B|B\Rightarrow p,\neg A\odot \neg A}\frac{\frac{B\Rightarrow B}{B\Rightarrow B|p,p\Rightarrow A\odot A}\frac{\frac{\frac{\frac{p\Rightarrow pA\Rightarrow A}{A\Rightarrow p|p\Rightarrow A}\frac{p\Rightarrow pA\Rightarrow A}{A\Rightarrow p|p\Rightarrow A}}{A\Rightarrow p|p,p\Rightarrow A\odot A}}{\Rightarrow p,\neg A|p,p\Rightarrow A\odot A}\frac{\frac{\frac{p\Rightarrow pA\Rightarrow A}{A\Rightarrow p|p\Rightarrow A}\frac{p\Rightarrow pA\Rightarrow A}{A\Rightarrow p|p\Rightarrow A}}{A\Rightarrow p|p,p\Rightarrow A\odot A}}{\Rightarrow p,\neg A|p,p\Rightarrow A\odot A}}{\Rightarrow p,p,\neg A\odot \neg A|p,p\Rightarrow A\odot A}}{\Rightarrow p,B|B\Rightarrow p,\neg A\odot \neg A|p,p\Rightarrow A\odot A}}{\Rightarrow p,B|B\Rightarrow p,\neg A\odot \neg A|p\Rightarrow C|C,p\Rightarrow A\odot A}\\ \hline\end{array}$$

The peculiarity of our method is not only to focus on controlling the role of the external contraction rule in the hypersequent calculus but also introduce other syntactic manipulations. For example, we label occurrences of the eigenvariable p introduced by an application of the density rule in order to be able to trace these occurrences from the leaves (axioms) of the derivation to the root (the derived hypersequent).

Appendix A.2. Why Do We Need the Constrained External Contraction Rule?

We use the example in Section 3 to answer this question. Firstly, we illustrate Notation 5 as follows. In Figure 4, let $S_{11}^c=A\Rightarrow p_2;S_{12}^c=A\Rightarrow p_1;S_{21}^c=A\Rightarrow p_4;S_{22}^c=A\Rightarrow p_3;S_{31}^c=p_1,p_2\Rightarrow A\odot A;$ $S_{32}^c=p_3,p_4\Rightarrow A\odot A;G_1^{\prime }=p_1,p_2\Rightarrow A\odot A;G_2^{\prime }=p_3,p_4\Rightarrow A\odot A;$ $G_3^{\prime }=A\Rightarrow p_1|\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|A\Rightarrow p_3.$ Then $H_i^c=G_i^{\prime }|S_{i1}^c|S_{i2}^c$ for $i=1,2,3$. $H_i^c$ are $(pEC)$-nodes and, $S_{i1}^c$ and $S_{i2}^c$ are $(pEC)$-sequents.

Let $G_{H_1^c:A\Rightarrow p_2}^{*}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A$. We denote the derivation ${\tau }_{H_1^c:A\Rightarrow p_2}^{*}$ of $G_{H_1^c:A\Rightarrow p_2}^{*}$ from $A\Rightarrow p_2$ by $\frac{\underline{A\Rightarrow p_2}}{G_{H_1^c:A\Rightarrow p_2}^{*}}⟨{\tau }_{H_1^c:A\Rightarrow p_2}^{*}⟩$. Since we focus on sequents in $G^{*}$ in the separation algorithm, we abbreviate $\frac{\underline{A\Rightarrow p_2}}{G_{H_1^c:A\Rightarrow p_2}^{*}}⟨{\tau }_{H_1^c:A\Rightarrow p_2}^{*}⟩$ to $\frac{\underline{S_{11}^c}}{S_{22}^c|S_{32}^c}⟨{\tau }_{S_{11}^c}^{*}⟩$ and further to $\frac{1}{2|3}⟨{\tau }_1^{*}⟩$. Then the separation algorithm ${\tau }_{H_1^c:G|G^{*}}^{☆}$ is abbreviated as

$$\begin{array}{|c|}\hline \frac{\frac{\frac{1|2|3}{2^{\prime }|3^{\prime }|2|3}⟨{\tau }_1^{*}⟩}{2^{\prime }|2}⟨{\tau }_3^{*},{\tau }_{3^{\prime }}^{*}⟩}{2}⟨E{C}_{\mathsf{\Omega }}⟩\\ \hline\end{array}$$

where $2^{\prime }$ and $3^{\prime }$ are abbreviations of $A\Rightarrow p_5$ and $p_5,p_6\Rightarrow A\odot A$, respectively. We also write $2^{\prime }$ and $3^{\prime }$ respectively as 2 and 3 for simplicity. Then the whole separation derivation is given as follows.

$$\begin{array}{|c|}\hline \frac{\frac{\frac{\frac{1|2|3}{2|3|2|3}⟨{\tau }_1^{*}⟩}{2|2}⟨{\tau }_3^{*},{\tau }_3^{*}⟩}{2}⟨E{C}_{\mathsf{\Omega }}⟩\frac{\frac{\frac{1|2|3}{1|1|3}⟨{\tau }_2^{*}⟩}{1|1}⟨{\tau }_3^{*}⟩}{1}⟨E{C}_{\mathsf{\Omega }}⟩}{\varnothing }⟨{\tau }_{\{1,2\}}^{*}⟩\\ \hline\end{array}$$

where ∅ is an abbreviation of $G^{″}$ in page 14 and means that all sequents in it are copies of sequents in $G_0$. Note that the simplified notations become intractable when we decide whether $⟨E{C}_{\mathsf{\Omega }}⟩$ is applicable to resulting hypersequents. If no application of $⟨E{C}_{\mathsf{\Omega }}⟩$ is used in it, all resulting hypersequents fall into the set $\{1|2|\underset{\underset{l}{︸}}{3|\cdots |3},2|2|\underset{\underset{m}{︸}}{3|\cdots |3},1|1|\underset{\underset{n}{︸}}{3|\cdots |3}:l\ge 0,m\ge 0,n\ge 0\}$ and ∅ is never obtained.

Appendix A.3. Why Do We Need the Separation of Branches?

In Figure 11, $p_1$ and $p_2$ in the premise of $\frac{\underline{p_1,p_2\Rightarrow A\odot A}}{p_1\Rightarrow C|C,p_2\Rightarrow A\odot A}⟨{\tau }_{S_{31}^c}^{*}⟩$ could be viewed as being tangled in one sequent $p_1,p_2\Rightarrow A\odot A$ but in the conclusion of $⟨{\tau }_{S_{31}^c}^{*}⟩$ they are separated into two sequents $p_1\Rightarrow C$ and $C,p_2\Rightarrow A\odot A$, which are copies of sequents in $G_0$. In Figure 5, $p_2$ in $A\Rightarrow p_2$ falls into $\Rightarrow p_2,B$ in the root of ${\tau }_{H_1^c:A\Rightarrow p_2}^{*}$ and $\Rightarrow p_2,B$ is a copy of a sequent in $G_0$. The same is true for $p_4$ in $A\Rightarrow p_4$ in Figure 8. But it’s not the case.

Lemma 13(vi) shows that in the elimination rule $\frac{\underline{S_{11}^c}}{G_{S_{11}^c}^{*}}⟨{\tau }_{S_{11}^c}^{*}⟩$, $S_j^c\in G_{S_{11}^c}^{*}$ implies $H_j^c<H_i^c$ or $H_j^c\parallel H_i^c$. If there exists no $S_j^c\in G_{S_{11}^c}^{*}$ such that $H_j^c<H_i^c$, then $S_j^c\in G_{S_{11}^c}^{*}$ implies $H_j^c\parallel H_i^c$ and, thus each occurrence of $p^{\prime }s$ in $S_{11}^c$ is fell into a unique sequent which is a copy of a sequent in $G_0$. Otherwise there exists $S_j^c\in G_{S_{11}^c}^{*}$ such that $H_j^c<H_i^c$, then we apply $⟨{\tau }_{S_j^c}^{*}⟩$ to $S_j^c$ in $G_{S_{11}^c}^{*}$ and the whole operations can be written as

$$\frac{\underline{\frac{\underline{S_{11}^c}}{G_{S_{11}^c}^{☆(0)}\equiv G_{S_{11}^c}^{*}\backslash \{S_j^c\}|S_j^c}⟨{\tau }_{S_{11}^c}^{*}⟩}}{G_{S_{11}^c}^{☆(1)}\equiv G_{S_{11}^c}^{*}\backslash \{S_j^c\}|G_{S_j^c}^{*}}⟨{\tau }_{S_j^c}^{*}⟩.$$

Repeatedly we can get $G_{S_{11}^c}^{☆(J)}$ such that $S_j^c\in G_{S_{11}^c}^{☆(J)}$ implies $H_j^c\parallel H_1^c$. Then each occurrence of $p^{\prime }s$ in $S_{11}^c$ is fell into a unique sequent in $G_{S_{11}^c}^{☆(J)}$ which is a copy of a sequent in $G_0$. In such case, we call occurrences of $p^{\prime }s$ in $S_{11}^c$ are separated in $G_{S_{11}^c}^{☆(J)}$ and call such a procedure the separation algorithm. It is the starting point of the separation algorithm. We introduce branches in order to tackle the case of multiple-premise separation derivations for which it is necessary to apply $(E{C}_{\mathsf{\Omega }})$ to the resulting hypersequents.

Appendix A.4. Some Questions about Theorem 2

In Theorem 2, ${\tau }_{\mathbf{I}}^{☆}$ is constructed by induction on the number $\left|I\right|$ of branches. As usual, we take the algorithm of $\left|I\right|-1$ branches as the induction hypothesis. Why do we take ${\tau }_{{\mathbf{I}}_l}^{☆}$ and ${\tau }_{{\mathbf{I}}_r}^{☆}$ as the induction hypothesises?

Roughly speaking, it degenerates the case of $\left|I\right|$ branches into the case of two branches in the following sense. The subtree ${\tau }^{*}(G^{″}|S^{″})$ of ${\tau }^{*}$ is as a whole contained in ${\tau }_{{\mathcal{I}}_{{\mathbf{j}}_l}}^{*}$ or not in it. Similarly, ${\tau }^{*}(G^{\prime }|S^{\prime })$ of ${\tau }^{*}$ is as a whole contained in ${\tau }_{{\mathcal{I}}_{{\mathbf{j}}_r}}^{*}$ or not in it. It is such a division of I into $I_l$ and $I_r$ that makes the whole algorithm possible.

Claim (i) of Theorem 2 asserts that $H_i^c\neg ⩽H_j^c$ for all $S_j^c\in G_{{\mathcal{I}}_{\mathbf{j}}}^{*}$ and $H_i^c\in I$. It guarantees that ${\tau }_{{\mathcal{I}}_{\mathbf{j}}}^{*}$ is not far from the final aim of Theorem 2 but roughly close to it if we define some complexity to calculate it. If $H_i^c⩽H_j^c$, the complexity of $G_{{\mathbf{I}}_{\mathbf{j}}}^{*}$ is more than or equal to that of ${⌈S_i^c⌉}_I$ under such a definition of complexity and thus such an application of ${\tau }_{{\mathcal{I}}_{\mathbf{j}}}^{*}$ is redundant at least. Claim (iii) of Theorem 2 guarantees the validity of the step 4 of Stages 1 and 2.

The tree structure of the skeleton of ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ can be obtained by deleting some node $H\in {\overline{\tau }}_{{\mathbf{I}}_l}^{☆}$ satisfying ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(H)⩽H_{\mathbf{I}}^V$. The same is true for ${\tau }_{\mathbf{I}}^{☆}$ if ${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})$ is treated as a rule or a subroutine whose premises are same as ones of ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$. However, it is incredibly difficult to imagine or describe the structure of ${\tau }_{\mathbf{I}}^{☆}$ if you want to expand it as a normal derivation, a binary tree.

All syntactic manipulations in constructing ${\tau }_{\mathbf{I}}^{☆}$ are performed on the skeletons of ${\tau }_{{\mathbf{I}}_{\mathbf{l}}}^{☆}$ or ${\tau }_{{\mathbf{I}}_{\mathbf{r}}}^{☆}$. The structure of the proof of Theorem 2 is depicted in Figure A1.

Figure A1. The structure of the proof of Theorem 2.

Appendix A.5. Illustrations of Notations and Algorithms

We use the example in Section 3 to illustrate some notations and algorithms in this paper.

Appendix A.5.1. Illustration of Two Cases of (COM) in the Proof of Lemma 8

Let $\frac{G^{\prime }{G}^{″}}{G^{‴}}(COM)$ be $\frac{p_1\Rightarrow p_{1}A\Rightarrow A}{A\Rightarrow p_1|p_1\Rightarrow A}(COM)$, where $G^{\prime }=S_1=p_1\Rightarrow p_1$; $G^{″}=S_2=A\Rightarrow A$; $S_3=A\Rightarrow p_1$; $S_4=p_1\Rightarrow A$ and $G^{‴}=S_3|S_4$. Then ${\left[S_3\right]}_{G^{‴}}={\left[S_4\right]}_{G^{‴}}$; ${\mathcal{D}}_{G^{\prime }}(S_1)=\Rightarrow t$; ${\mathcal{D}}_{G^{″}}(S_2)=A\Rightarrow A$; ${\mathcal{D}}_{G^{‴}}(S_3|S_4)=A\Rightarrow A$. Thus the proof of $\frac{\underline{{\mathcal{D}}_{G^{\prime }}(S_1){\mathcal{D}}_{G^{\prime }}(S_2)}}{{\mathcal{D}}_{G^{\prime }}(S_3|S_4)}$ is constructed by $\frac{\Rightarrow t\frac{A\Rightarrow A}{A,t\Rightarrow A}(t_l)}{A\Rightarrow A}(CUT)$.

Let $\frac{G^{\prime }{G}^{″}}{G^{‴}}(COM)$ be $\frac{B\Rightarrow B\left(\begin{array}{c}\Rightarrow p_2,p_4,\neg A\odot \neg A|p_1,p_2\Rightarrow A\odot A|\\ A\Rightarrow p_1|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A\end{array}\right)}{\left(\begin{array}{c}\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|A\Rightarrow p_1|\\ p_1,p_2\Rightarrow A\odot A|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A\end{array}\right)}(COM),$

$whereG’=S_1=B\Rightarrow B;G_2=p_1,p_2\Rightarrow A\odot A|A\Rightarrow p_1|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A$;

$S_2=\Rightarrow p_2,p_4,\neg A\odot \neg A$; $G^{″}=G_2|S_2$; $S_3=\Rightarrow p_2,B$; $S_4=B\Rightarrow p_4,\neg A\odot \neg A$ and $G^{‴}=G_2|S_3|S_4$. Then ${\mathcal{D}}_{G^{\prime }}(S_1)=B\Rightarrow B$; ${\mathcal{D}}_{G^{″}}(S_2)=A,A\Rightarrow A\odot A,\neg A\odot \neg A,A\odot A$; ${\mathcal{D}}_{G^{‴}}(S_3)=A\Rightarrow B,A\odot A$; ${\mathcal{D}}_{G^{‴}}(S_4)=A,B\Rightarrow A\odot A,\neg A\odot \neg A;{\mathcal{D}}_{G^{‴}}(S_3|S_4)={\mathcal{D}}_{G^{‴}}(S_4)|{\mathcal{D}}_{G^{‴}}(S_4)$.

Thus the proof of $\frac{\underline{{\mathcal{D}}_{G^{\prime }}(S_1){\mathcal{D}}_{G^{\prime }}(S_2)}}{{\mathcal{D}}_{G^{\prime }}(S_3|S_4)}$ is constructed by

$$\frac{B\Rightarrow BA,A\Rightarrow A\odot A,\neg A\odot \neg A,A\odot A}{A\Rightarrow B,A\odot A|A,B\Rightarrow A\odot A,\neg A\odot \neg A}(COM).$$

Appendix A.5.2. Illustration of Construction 3

Let ${\tau }^{*}$ be

$$\frac{\frac{\frac{H_8\equiv B\Rightarrow B{H}_9\equiv A\Rightarrow A}{H_4\equiv A\Rightarrow B|B\Rightarrow A}(COM)\frac{H_{10}\equiv B\Rightarrow B{H}_{11}\equiv A\Rightarrow A}{H_5\equiv A\Rightarrow B|B\Rightarrow A}(COM)}{H_2\equiv A\Rightarrow B|A\Rightarrow B|B,B\Rightarrow A\odot A}({\odot }_r)}{H_1\equiv A\Rightarrow B|\Rightarrow B,\neg A|B,B\Rightarrow A\odot A}({\neg }_r).$$

By Construction 3, ${\tau }^{**}$ is then given as follows.

$$\frac{\frac{\frac{(B\Rightarrow B;8,0)(A\Rightarrow A;9,0)}{(A\Rightarrow B;4,1)|(B\Rightarrow A;4,2)}(COM)\frac{(B\Rightarrow B;10,0)(A\Rightarrow A;11,0)}{(A\Rightarrow B;5,1)|(B\Rightarrow A;5,2)}(COM)}{(A\Rightarrow B;4,1)|(A\Rightarrow B;5,1)|(B,B\Rightarrow A\odot A;2,0)}({\odot }_r)}{(A\Rightarrow B;4,1)|(\Rightarrow B,\neg A;1,0)|(B,B\Rightarrow A\odot A;2,0)}({\neg }_r).$$

As an example, we calculate $\wp (H_8)$. Since $Th(H_8)=(H_8,H_4,H_2,H_1)$, then $b_3=1$, $b_2=b_1=b_0=0$ by Definition 10. Thus $\wp (H_8)=b_0{2}^0+b_1{2}^1+b_2{2}^2+b_3{2}^3=8.$

Note that we cannot distinguish the one from the other for two $A\Rightarrow B^{\prime }s$ in $H_2\in {\tau }^{*}$. If we divide $H_2$ into $H^{\prime }|H^{″}$, where $H^{\prime }\equiv A\Rightarrow B$ and $H^{″}\equiv A\Rightarrow B|B,B\Rightarrow A\odot A$, then $H^{\prime }\bigcap H^{″}=\{A\Rightarrow B\}$ in the conventional meaning of hypersequents. Thus only in the sense that we treat ${\tau }^{*}$ as ${\tau }^{**}$, the assertion that $H^{\prime }\bigcap H^{″}=\varnothing$ for any $H^{\prime }|H^{″}\subseteq H$ in Proposition 3 holds.

Appendix A.5.3. Illustration of Notation 7 and Construction 4

Let $I=\{H_1^c,H_2^c\},I_l=\{H_1^c\},I_r=\{H_2^c\},\mathcal{I}=\{S_{11}^c,S_{21}^c\},{\mathcal{I}}_l=\{S_{11}^c\},{\mathcal{I}}_r=\{S_{21}^c\},$

$$\frac{G^{\prime }|S^{\prime }{G}^{″}|S^{″}}{G^{\prime }|G^{″}|H^{\prime }}({\odot }_r)\in {\tau }^{*},$$

where $G^{\prime }|G^{″}|H^{\prime }=H_I^V;G^{\prime }\equiv A\Rightarrow p_1|p_1,p_2\Rightarrow A\odot A;S^{\prime }\equiv \Rightarrow p_2,\neg A;G^{″}\equiv A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A;S^{″}\equiv \Rightarrow p_4,\neg A;H^{\prime }\equiv \Rightarrow p_2,p_4,\neg A\odot \neg A$ (See Figure 4).

${⟨G^{\prime }|S^{\prime }⟩}_{{\mathcal{I}}_l}=\Rightarrow p_2,\neg A;{⟨G^{\prime }⟩}_{{\mathcal{I}}_l}=\varnothing ;{⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{{\mathcal{I}}_l}=A\Rightarrow p_3|\Rightarrow p_2,p_4,\neg A\odot \neg A|p_3,p_4\Rightarrow A\odot A;{⟨G|G^{*}⟩}_{{\mathcal{I}}_l}=G_{{\mathcal{I}}_l}^{*}=G_{S_{11}^c}^{*}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|A\Rightarrow p_3|p_3,p_4\Rightarrow A\odot A$ (See Figure 5).

${⟨G^{″}|S^{″}⟩}_{{\mathcal{I}}_r}=\Rightarrow p_4,\neg A;{⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{{\mathcal{I}}_r}=A\Rightarrow p_1|\Rightarrow p_2,p_4,\neg A\odot \neg A|p_1,p_2\Rightarrow A\odot A;$

${⟨G|G^{*}⟩}_{{\mathcal{I}}_r}=G_{{\mathcal{I}}_r}^{*}=G_{S_{21}^c}^{*}=A\Rightarrow p_1|\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A$ (See Figure 8).

${⟨G^{\prime }|G^{″}|H^{\prime }⟩}_{\mathcal{I}}=\Rightarrow p_2,p_4,\neg A\odot \neg A;{⟨G|G^{*}⟩}_{\mathcal{I}}=G_{\mathcal{I}}^{*}=G_{{}^{\{S_{11}^c,S_{21}^c\}}}^{*}=G_{{\mathcal{I}}_l}^{*}\bigcap G_{{\mathcal{I}}_r}^{*}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A$ (See Figure 10).

Appendix A.5.4. Illustration of Theorem 2

Note that sequents in $\left[\right]$ are principal sequents of elimination rules in the following. Let $I,I_r,I_l$ be the same as in Appendix A.5.3 and, $\mathbf{I}=\{{⌈S_1^c⌉}_I,{⌈S_2^c⌉}_I\},{\mathbf{I}}_l=\{{⌈S_1^c⌉}_I\},{\mathbf{I}}_r=\{{⌈S_2^c⌉}_I\},$

$${⌈S_1^c⌉}_I=G_{H_2^c:G|G^{*}}^{☆}=A\Rightarrow p_5|\Rightarrow p_6,B|B\Rightarrow p_8,\neg A\odot \neg A|p_5\Rightarrow C|$$

$$C,p_6\Rightarrow A\odot A|B\Rightarrow p_7,\neg A\odot \neg A|p_7\Rightarrow C|C,p_8\Rightarrow A\odot A,$$

$${⌈S_2^c⌉}_I=G_{H_1^c:G|G^{*}}^{☆}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|$$

$$A\Rightarrow p_3|\Rightarrow p_1,B|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A.$$

$${\tau }_{{\mathbf{I}}_l}^{☆}=\frac{\underline{\frac{\underline{\frac{\underline{{⌈S_1^c⌉}_I}}{G_{{\mathbf{I}}_l}^{☆(1)}}⟨{\tau }_{H_1^c:A\Rightarrow p_5}^{*}⟩}}{G_{{\mathbf{I}}_l}^{☆(2)}}⟨{\tau }_{H_3^c:p_9,p_{10}\Rightarrow A\odot A}^{*}⟩}}{G_{{\mathbf{I}}_l}^{☆}}⟨E{C}_{\mathsf{\Omega }}^{*}⟩,$$

where

$$G_{{\mathbf{I}}_l}^{☆(1)}=\left[\Rightarrow p_5,B|B\Rightarrow p_{10},\neg A\odot \neg A|A\Rightarrow p_9|p_{10},p_9\Rightarrow A\odot A\right]|\Rightarrow p_6,B|$$

$$B\Rightarrow p_8,\neg A\odot \neg A|p_5\Rightarrow C|C,p_6\Rightarrow A\odot A|B\Rightarrow p_7,\neg A\odot \neg A|$$

$$p_7\Rightarrow C|C,p_8\Rightarrow A\odot A,$$

$$G_{{\mathbf{I}}_l}^{☆(2)}=\Rightarrow p_5,B|B\Rightarrow p_{10},\neg A\odot \neg A|A\Rightarrow p_9|[p_9\Rightarrow C|C,p_{10}\Rightarrow A\odot A]|$$

$$\Rightarrow p_6,B|B\Rightarrow p_8,\neg A\odot \neg A|p_5\Rightarrow C|C,p_6\Rightarrow A\odot A|$$

$$B\Rightarrow p_7,\neg A\odot \neg A|p_7\Rightarrow C|C,p_8\Rightarrow A\odot A,$$

$$G_{{\mathbf{I}}_l}^{☆}=\Rightarrow p_5,B|A\Rightarrow p_9|p_9\Rightarrow C|\Rightarrow p_6,B|B\Rightarrow p_8,\neg A\odot \neg A|$$

$$p_5\Rightarrow C|C,p_6\Rightarrow A\odot A|B\Rightarrow p_7,\neg A\odot \neg A|p_7\Rightarrow C|C,p_8\Rightarrow A\odot A,$$

$$G_{H_I^V:G^{″}}^{☆(J)}=A\Rightarrow p_9|p_9\Rightarrow C|C,p_{10}\Rightarrow A\odot A;\widehat{S^{″}}=B\Rightarrow p_{10},\neg A\odot \neg A;\widehat{S^{\prime }}=\Rightarrow p_5,B;$$

$$G_{H_I^V:H^{\prime }}^{☆(J)}=G_{H_I^V:H^{\prime }}^{*}=\widehat{S^{\prime }}|\widehat{S^{″}};G_{†}=A\Rightarrow p_9|p_9\Rightarrow C|C,p_{10}\Rightarrow A\odot A|B\Rightarrow p_{10},\neg A\odot \neg A.$$

$${\tau }_{{\mathbf{I}}_r}^{☆}=\frac{\underline{\frac{\underline{{⌈S_2^c⌉}_I}}{G_{{\mathbf{I}}_r}^{☆(1)}}⟨{\tau }_{H_2^c:A\Rightarrow p_3}^{*}⟩}}{G_{{\mathbf{I}}_r}^{☆}}⟨E{C}_{\mathsf{\Omega }}^{*}⟩,$$

where

$$G_{{\mathbf{I}}_r}^{☆(1)}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|$$

$$\Rightarrow p_1,B|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A|[A\Rightarrow p_{11}|\Rightarrow p_{12},B|$$

$$B\Rightarrow p_3,\neg A\odot \neg A|p_{11}\Rightarrow C|C,p_{12}\Rightarrow A\odot A],$$

$$G_{{\mathbf{I}}_r}^{☆}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|$$

$$\Rightarrow p_1,B|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A|A\Rightarrow p_{11}|B\Rightarrow p_3,\neg A\odot \neg A|p_{11}\Rightarrow C.$$

Since there is only one elimination rule in ${\tau }_{{\mathbf{I}}_r}^{☆}$, the case we need to process is ${\tau }_{H_2^c:A\Rightarrow p_3}^{*}$, i.e.,

$${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}=\frac{\underline{{⌈S_2^c⌉}_I}}{G_{H_2^c:{⌈S_2^c⌉}_I}^{☆(1)}}⟨{\tau }_{H_2^c:A\Rightarrow p_3}^{*}⟩.$$

Then $v=1$, $S_{j_{r1}}^c=A\Rightarrow p_3$; $G_{b_{r1}}=\Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|$

$$C,p_2\Rightarrow A\odot A|\Rightarrow p_1,B|p_3\Rightarrow C|C,p_4\Rightarrow A\odot A\mathrm{in}{\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*}.$$

$${\tau }_{{\mathbf{I}}_l}^{☆(0)}=\frac{\underline{\frac{\underline{\frac{\underline{{⌈S_1^c⌉}_I}}{G_{{\mathbf{I}}_l}^{☆(1)}}⟨{\tau }_{H_1^c:A\Rightarrow p_5}^{*}⟩}}{G_{{\mathbf{I}}_l}^{☆(2)}}⟨{\tau }_{H_3^c:p_9,p_{10}\Rightarrow A\odot A}^{*}⟩}}{G_{{\mathbf{I}}_l}^{☆}}{⟨E{C}_{\mathsf{\Omega }}^{*}⟩}_1^{\circ },$$

where ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}({⌈S_1^c⌉}_I)=H_1^c$, ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(G_{{\mathbf{I}}_l}^{☆(1)})=H_3^c<H_I^V$, ${\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(G_{{\mathbf{I}}_l}^{☆(2)})={\partial }_{{\tau }_{{\mathbf{I}}_l}^{☆}}(G_{{\mathbf{I}}_l}^{☆})=G|G^{*}$, $G_1^{\circ \circ }=G_{{\mathbf{I}}_l}^{☆(2)}$, $G_1^{\circ }=G_{{\mathbf{I}}_l}^{☆}$.

$${\tau }_{{\mathbf{I}}_l:G_1^{\circ \circ }}^{☆(0)}=\frac{\underline{\frac{\underline{{⌈S_1^c⌉}_I}}{G_{{\mathbf{I}}_l}^{☆(1)}}⟨{\tau }_{H_1^c:A\Rightarrow p_5}^{*}⟩}}{G_{{\mathbf{I}}_l}^{☆(2)}}⟨{\tau }_{H_3^c:p_9,p_{10}\Rightarrow A\odot A}^{*}⟩,$$

$${\tau }_{{\mathbf{I}}_l:G_1^{\circ \circ }(1)}^{☆(0)}={\tau }_{{\mathbf{I}}_l:G_1^{\circ \circ }(2)}^{☆(0)}=\frac{\underline{{⌈S_1^c⌉}_I}}{G_{{\mathbf{I}}_l}^{☆(1)}}⟨{\tau }_{H_1^c:A\Rightarrow p_5}^{*}⟩.$$

Since there is only one elimination rule in ${\tau }_{{\mathbf{I}}_l:G_1^{\circ \circ }(2)}^{☆(0)}$, the case we need to process is ${\tau }_{H_1^c:A\Rightarrow p_5}^{*}$, i.e.,

$${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}=\frac{\underline{{⌈S_1^c⌉}_I}}{G_{{\mathbf{I}}_l}^{☆(1)}}⟨{\tau }_{H_1^c:A\Rightarrow p_5}^{*}⟩.$$

Then $u=1$, $S_{j_{l1}^{(t_{l1})}}^c=A\Rightarrow p_5$; $G_{b_{l1}}=\Rightarrow p_6,B|B\Rightarrow p_8,\neg A\odot \neg A|$

$$p_5\Rightarrow C|C,p_6\Rightarrow A\odot A|B\Rightarrow p_7,\neg A\odot \neg A|p_7\Rightarrow C|C,p_8\Rightarrow A\odot A\mathrm{in}{\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}.$$

${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}}^{*}$ is replaced with ${\tau }_{{\mathbf{I}}_{{\mathbf{j}}_l}\cup {\mathbf{I}}_{{\mathbf{j}}_r}}^{*}$ in Step 3 of Stage 1, i.e.,

$$\frac{\underline{{⌈S_1^c⌉}_I{⌈S_2^c⌉}_I}}{G_{l,r}}⟨{\tau }_{\{H_1^c:A\Rightarrow p_5,H_2^c:A\Rightarrow p_3\}}^{*}⟩={\tau }_{{\mathbf{I}}_l:G_1^{\circ \circ }(3)}^{☆(0)}={\tau }_{{\mathbf{I}}_l:G_1^{\circ \circ }(4)}^{☆(0)},$$

where

$$\begin{array}{ll}\hfill G_{l,r}=& \Rightarrow p_5,B|B\Rightarrow p_3,\neg A\odot \neg A|G_{b_{r1}}|G_{b_{l1}}=\hfill \\ & \Rightarrow p_2,B|B\Rightarrow p_4,\neg A\odot \neg A|p_1\Rightarrow C|C,p_2\Rightarrow A\odot A|\Rightarrow p_1,B|\hfill \\ \hfill p_3& \Rightarrow C|C,p_4\Rightarrow A\odot A|\Rightarrow p_6,B|B\Rightarrow p_8,\neg A\odot \neg A|\hfill \\ \hfill p_5& \Rightarrow C|C,p_6\Rightarrow A\odot A|B\Rightarrow p_7,\neg A\odot \neg A|p_7\Rightarrow C|\hfill \\ & \Rightarrow C,p_8\Rightarrow A\odot A|p_5,B|B\Rightarrow p_3,\neg A\odot \neg A\hfill \end{array}.$$

Replacing ${\tau }_{{\mathbf{I}}_l:G_1^{\circ \circ }}^{☆(0)}$ in ${\tau }_{{\mathbf{I}}_l}^{☆(0)}$ with ${\tau }_{{\mathbf{I}}_l:G_1^{\circ \circ }(4)}^{☆(0)}$, then deleting $G_{{\mathbf{I}}_l}^{☆}$ and after that applying $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$ to $G_{l,r}$ and keeping $G_{b_{r1}}$ unchanged, we get

$${\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})=\frac{\underline{\frac{\underline{{⌈S_1^c⌉}_I{⌈S_2^c⌉}_I}}{G_{l,r}}⟨{\tau }_{\{H_1^c:A\Rightarrow p_5,H_2^c:A\Rightarrow p_3\}}^{*}⟩}}{\widehat{S^{″}}|G_{b_{r1}}|G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}}⟨E{C}_{\mathsf{\Omega }}^{*}⟩,$$

where $G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}^{☆(J)}=G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}^{*}=\varnothing$; $\widehat{S^{\prime }}=\Rightarrow p_5,B$;

$$\widehat{S^{″}}=B\Rightarrow p_3,\neg A\odot \neg A;G_{‡}=G_{b_{r1}}|\widehat{S^{″}},G_{H_I^V:H^{\prime }}^{☆(J)}=G_{H_I^V:H^{\prime }}^{*}=\widehat{S^{\prime }}|\widehat{S^{″}};$$

$$G_{{\mathbf{I}}_{l\backslash r}}^{☆}=\Rightarrow p_5,B|\Rightarrow p_6,B|B\Rightarrow p_7,\neg A\odot \neg A|p_5\Rightarrow C|C,p_6\Rightarrow A\odot A|$$

$$p_7\Rightarrow C|C,p_8\Rightarrow A\odot A|B\Rightarrow p_8,\neg A\odot \neg A.$$

Stage 2${\tau }_{{\mathbf{I}}_r:G_1^{\circ \circ }}^{☆(0)}={\tau }_{{\mathbf{I}}_r:G_1^{\circ \circ }(1)}^{☆(0)}={\tau }_{{\mathbf{I}}_r:G_1^{\circ \circ }(2)}^{☆(0)}=\frac{\underline{{⌈S_2^c⌉}_I}}{G_{{\mathbf{I}}_r}^{☆(1)}}⟨{\tau }_{H_2^c:A\Rightarrow p_3}^{*}⟩,$

$${\tau }_{{\mathbf{I}}_r:G_1^{\circ \circ }(3)}^{☆(0)}={\tau }_{{\mathbf{I}}_r:G_1^{\circ \circ }(4)}^{☆(0)}=\frac{\underline{{⌈S_1^c⌉}_I{⌈S_2^c⌉}_I}}{\widehat{S^{″}}|G_{b_{r1}}|G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}}⟨{\tau }_{{\mathbf{I}}_l}^{☆}({\tau }_{{\mathbf{I}}_{{\mathbf{j}}_r}}^{*})⟩.$$

Replacing ${\tau }_{{\mathbf{I}}_r:G_1^{\circ \circ }}^{☆(0)}$ in ${\tau }_{{\mathbf{I}}_r}^{☆(0)}$ with ${\tau }_{{\mathbf{I}}_r:G_1^{\circ \circ }(4)}^{☆(0)}$, then deleting $G_{{\mathbf{I}}_r}^{☆}$ and after that applying $⟨E{C}_{\mathsf{\Omega }}^{*}⟩$ to $\widehat{S^{″}}|G_{b_{r1}}|G_{H_I^V:{⟨G^{″}⟩}_{{\mathcal{I}}_{{\mathbf{j}}_r}}}^{☆(J)}|G_{H_I^V:H^{\prime }}^{☆(J)}\backslash \{\widehat{S^{\prime }}|\widehat{S^{″}}\}|G_{{\mathbf{I}}_{l\backslash r}}^{☆}$, we get ${\tau }_{\mathbf{I}}^{☆}$.