A Generic Framework for Accountable Optimistic Fair Exchange Protocol †
Abstract
1. Introduction
1.1. Motivation
1.2. Contribution
1.3. Organisation of the Paper
2. Definitions and Security Models of Accountable Optimistic Fair Exchange Protocol
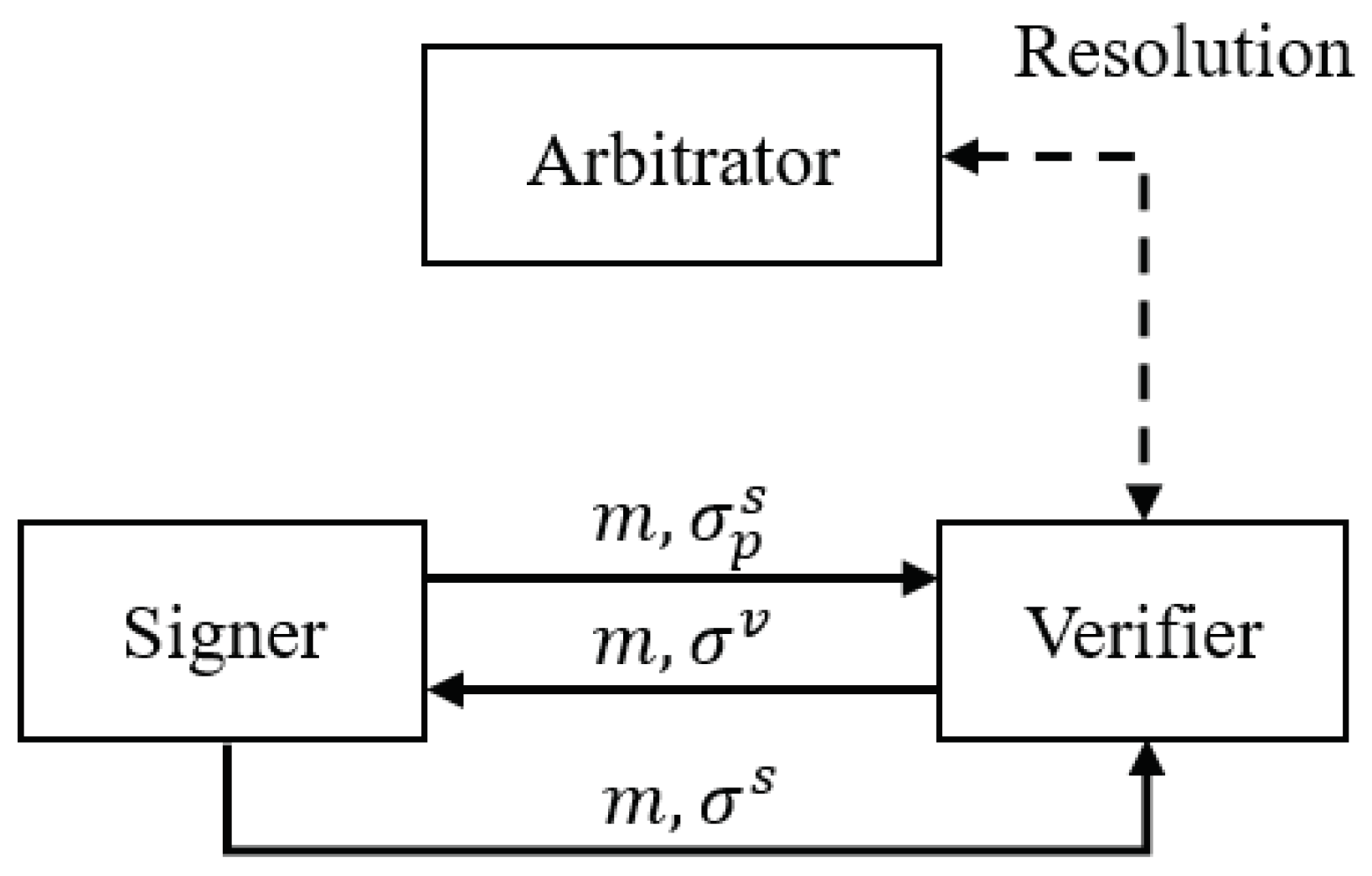
2.1. Accountable OFE Protocol
- : On input a security parameter , it outputs a public parameter .
- : On input , it generates an arbitrator’s public and private key pair ().
- : On input , it generates a user’s public and private key pair ().
- : On input a message m and ), it generates a partial signature .
- : On input (), it validates () and outputs if is valid on or otherwise.
- : On input (), it generates a full signature .
- : On input (), it validates () under () and outputs if is valid or otherwise.
- : On input (), it resolves by first checking its validity. If is valid on , it generates a full signature or outputs otherwise.
- : On input (), it generates an arbitrator proof that can claim or deny whether was generated by using .
- : On input (), it generates a user proof that can claim or deny whether was generated by using .
- : On input (), it first validates under . It then outputs if can prove is generated by the algorithm or if is generated by the algorithm . Otherwise, it outputs which indicates is invalid and it cannot be opened.
2.2. Accessible Oracles
- Partial Sign Oracle : On input , it runs and returns as a partial signature.
- Full Sign Oracle : On input , it runs and returns as a full signature.
- Resolution Oracle : On input , it runs and returns as a resolved signature.
- Arbitrator Prove Oracle : On input under , it runs and returns as an arbitrator proof.
- User Prove Oracle : On input under , it runs and returns as a user proof.
2.3. Security Properties
2.3.1. Resolution Ambiguity
- Phase 1: runs and . then passes to .
- Phase 2: can make queries to all oracles defined in Section 2.2. At the end, outputs a challenge message and partial signature pair with the restriction that .
- Phase 3: picks a random bit and generates a challenge signature . If , . Otherwise, .
- Phase 4: Once receives , can still continue to make queries to all oracles with the restriction that has never been queries to or . At the end, outputs the guess . wins the game if .
2.3.2. Accountability
- Type I: It is impossible for a dishonest signer to produce a full signature that can be proven as an output of the algorithm .
- -
- Phase 1: runs and . then passes to .
- -
- Phase 2: can make queries to all oracles defined in Section 2.2. At the end, chooses a challenge user’s public key and passes it to .
- -
- Phase 3: continues to make queries to and only as does not know .
- -
- Phase 4: outputs a challenge message and signature pair that is valid on and a proof with the restriction that is not generated from . wins the game if
Definition 2.An OFE protocol is -type I accountable if no PPT can have success probability more than ε in its game with at most queries to , queries to , queries to , queries to , and queries to in time t. - Type II: It is impossible for a dishonest arbitrator to resolve a full signature that can be proven as an output of the algorithm .
- -
- Phase 1: chooses a challenge arbitrator’s public key and passes it to .
- -
- Phase 2: can make queries to all oracles defined in Section 2.2 except and due to does not have the knowledge of .
- -
- Phase 3: outputs a valid on and a proof with the restriction that is not generated from . wins the game if and only if
Definition 3.An OFE protocol is -type II accountable if no PPT can have success probability more than ε in its game with at most queries to , queries to , and queries to in time t. - Type III: It is impossible for the signer and the arbitrator to both claim or deny a valid full signature .
- -
- Phase 1: runs . is then given to run both and .
- -
- Phase 2: outputs a valid on and two proofs . wins the game if and only if either one of the following statements holds:
- is both claimed by the signer and the arbitrator. Such that
- is both denied by the signer and the arbitrator. Such that
Definition 4.An OFE is -type III accountable if no PPT can have success probability more than ε in its game in time t.
2.3.3. Security against Signers
- Phase 1: runs and passes to .
- Phase 2: can make queries to .
- Phase 3: outputs a challenge message and partial signature pair on . wins the game if .
2.3.4. Security against Verifiers
- Phase 1: first runs and both and . is then given .
- Phase 2: can make queries to , , and .
- Phase 3: outputs a challenge message and signature pair on with the restriction that is not generated from or . wins the game if .
2.3.5. Security against Arbitrator
- Phase 1: runs and passes to .
- Phase 2: runs and sends to .
- Phase 3: can make queries to .
- Phase 4: outputs a challenge message and signature pair on with the restriction that has not been a query to . wins the game if .
2.3.6. Security in the Multi-User Setting and Chosen-Key Model
3. Preliminaries
3.1. Bilinear Pairings
- Bilinearity: for all , , and , we have .
- Non-degeneracy: if is a generator of and , then is a generator of , which also implies .
- Computability: there exists an efficient algorithm to compute for all and .
3.2. Ordinary Signature Scheme
- : On input security parameter , it outputs a public and private key pair .
- : On input a message and private key , it outputs an ordinary signature .
- : On input , it outputs if is valid and outputs otherwise.
Unforgeability
- Setup: runs , then is given .
- Queries: can query the Sign Oracle : On input a message m, it outputs a signature that is valid on .
- Output: At the end, is required to output a challenge message and signature pair that is valid on , with the restriction that has not been a query to before.
3.3. Convertible Undeniable Signature
- : On input a security parameter, , outputs a signer public and private key pair ().
- : On input a message and a signer private key, , outputs an undeniable signature .
- : An interactive protocol that runs between the signer and the verifier on common input . The signer uses to check the validity of , the output is a non-transferable proof that shows is valid/invalid on .
- : On input , it computes a selective token which can be used to publicly verify on .
- : On input , it outputs if is an invalid token on . It outputs if is a valid signature and outputs otherwise.
- If is valid on , then
- Or else, if is invalid on , then
3.3.1. Unforgeability
- Setup: runs , then is given .
- Queries: is allowed to make queries to the following oracles:
- -
- Sign Oracle : On input a message m, it outputs an undeniable signature that is valid on .
- -
- Confirmation/Disavowal Oracle : On input any message and signature pair , it runs the protocol with and outputs a non-transferable proof to show the validity of .
- -
- (For convertible schemes only) SConvert Oracle : On input a message and signature pair , it outputs a selective token .
- Output: At the end, is required to output a challenge message and undeniable signature pair , with the restriction that has not been a query to . If the scheme is convertible, must not have been queried to . wins the game if is valid on .
3.3.2. Anonymity
- Setup: first runs and and sends to .
- Queries I: Same as in Section 3.3.1.
- Output I: At some point, outputs a challenge message to request a challenge signature . If the scheme is deterministic, is restricted where it has not been submitted to during Queries I. responds by randomly choosing and generates a challenge signature that is valid on either or .
- Queries II: Once obtains , can continue making queries to the accessible oracles as in Queries I. If the scheme is deterministic, is restricted to be submitted to . An additional restriction is added where any in the equivalence class of is not allowed to submit to (and if the scheme is convertible).
- Output II: outputs a guess and wins the game if .
3.4. Ring Signature
- : On input , it outputs a public and private key pair .
- : On input a message, a private key, and a list of public keys where with n members, it outputs a ring signature .
- : On input , it outputs if is valid and output otherwise.
3.4.1. Unforgeability
- Setup: runs for n times to generate n public and private key pair , where n is the number of members. is given .
- Queries: can query the Sign Oracle : On input , where is a sub list of members within and e is a selected member. It then runs to produce a ring signature to .
- Output: At the end, is required to output a challenge message and ring signature pair on a challenge sub list of members with the restriction that has not been a query to before. wins the game if
3.4.2. Anonymity
- Setup: Same as in Section 3.4.1.
- Queries: Same as in Section 3.4.1.
- Output: At the end, is required to output a challenge message and a sub list of members and two distinct indices such that . then chooses randomly and computes a challenge ring signature . is given and is required to output a guess . wins the game if .
4. Generic Transformation
4.1. Generic Framework
- : On input the security parameter , it generates the public parameters needed for the ordinary signature, convertible undeniable signature, and ring signature scheme.
- : On input , it runs and to compute an arbitrator public and private key pair .
- : On input , it runs , , and to compute a user public and private key pair .
- : On input a message and a signer private key , it runs and outputs a partial signature .
- : On input , it can validate by running . It outputs if is valid and outputs otherwise.
- : On input . Let . It runs and , where and outputs a full signature .
- : On input , it can verify by running and , where . Therefore, if and are valid, this algorithm outputs and otherwise.
- : On input , it first checks the validity of by running . It outputs if is invalid. Otherwise, it continues to compute . It then runs and , where and outputs a full signature
- : On input , it first runs to check its validity and continue if and only if it is valid. Then it computes and runs and outputs a proof . Otherwise, it outputs .
- : On input , it first runs to check its validity and continue if and only if it is valid. Then it computes and runs and outputs a proof . Otherwise, it outputs .
- : On input , it first runs to check its validity and continue if and only if it is valid. Otherwise, it outputs . It computes and parses in the following cases:
- -
- If , it runs . If , it outputs which indicates is originally generated by the arbitrator using . Otherwise, it outputs . If the output is , it means is invalid.
- -
- Else if , it runs . If , it outputs which indicates is originally generated by the signer using . Otherwise, it outputs . If the output is , it means is invalid.
4.2. Security Analysis
4.2.1. Resolution Ambiguity
4.2.2. Type I Accountability
- Phase 1: On input to , sets and passes to .
- Phase 2: can make queries to its accessible oracles defined in Section 2.2. At the end, runs to generate users’ private and public key pairs. then passes a challenge public key to .
- Phase 3: can make queries to the following oracles:
- -
- Resolution Oracle : On input , requests from convertible undeniable signature scheme’s on input , where . then requests from ring signature scheme’s on input , where and is the selected public key position in . Note that is generated with respectively. Finally, returns a signature to .
- -
- Arbitrator Prove Oracle : On input , requests a selective token on from convertible undeniable signature scheme’s on input , where . then returns an arbitrator proof .
- Phase 4: outputs a challenge message and signature pair that is valid on and a proof with the restriction that is not generated from . Note that be can either by or by .
- Case 1: is generated by using , so and hold.
- Case 2: is generated by using , but is not sound. Hence, and .
4.2.3. Type II Accountability
- Phase 1: On input to , then passes to which then runs and passes to .
- Phase 2: can make queries to the following oracles for a selected :
- -
- Partial Sign Oracle : On input , requests a signature from ordinary signature scheme’s on input . then returns a partial signature .
- -
- Full Sign Oracle : On input , requests from convertible undeniable signature scheme’s on input , where . then requests from ring signature scheme’s on input , where and is the selected public key position in . Note that is generated with respectively.
- -
- User Prove Oracle : On input , requests a selective token on from convertible undeniable signature scheme’s on input , where . then returns a user proof .
- Phase 3: outputs a challenge message and signature pair that is valid on and a proof , with the restriction that is not generated from . Note that can either be the by or the by .
- Case 1: is generated by using , so and hold.
- Case 2: is generated by using , but is not sound. Therefore, and .
4.2.4. Type III Accountability
- Phase 1: On input to , then passes to which then runs and .
- Phase 2: outputs a challenge message and signature pair that is valid on and two proofs .
- A valid on but
- A valid on but ∧
4.2.5. Security against Signers
4.2.6. Security against Verifiers
- Phase 1: On input two challenge public key pairs to , first runs . then chooses and sets and . is given .
- Phase 2: can make queries to the following oracles:
- -
- Partial Sign Oracle : On input , returns to .
- -
- Full Sign Oracle : On input , requests from convertible undeniable signature scheme’s on input , where . then requests from ring signature scheme’s on input , where and is the selected public key position in . Note that is generated with respectively. Finally, returns a signature to .
- -
- Resolution Oracle : This oracle is similar to above, but is generated with respectively, where is from convertible undeniable signature scheme’s on input and is from ring signature scheme’s on input where and is the selected public key position in .
- Phase 3: outputs a challenge message and signature pair , where with the restriction that is not generated from or .
4.2.7. Security against Arbitrator
- Phase 1: On input a challenge public key to . first generates public parameters and passes to .
- Phase 2: then runs and sends to .
- Phase 3: can make queries to Partial Sign Oracle : On input , where requests a signature from ordinary signature scheme’s on input . returns a partial signature .
- Phase 4: outputs a challenge message and signature pair , where with the restriction that has not been queried to .
5. An Instantiation of Accountable Optimisitc Fair Exchange Protocol
5.1. Boneh et al.’s Short Signature Scheme
- : It randomly picks and computes . It then returns a public and private key pair .
- : On input a message and a private key , it returns an ordinary signature .
- : On input , it checks whether . It outputs if is valid and otherwise.
5.2. Li et al.’s Convertible Undeniable Signature Scheme
- : It randomly picks to compute and . It outputs a public and private key pair .
- : On input a message and private key , it computes an undeniable signature .
- : Given a message and signature pair , it can confirm or deny with the following designated verifier non-interactive zero knowledge proof of knowledge :or
- : On input , it computes a converter .
- : On input , it first verifies by checking whether or not. If is valid, then it proceeds to validate by checking whether holds or not.
5.3. Shim’s Ring Signature Scheme
- : For a user i, it randomly picks to compute . It outputs a public and private key pair .
- : Let be a list of users’ public keys with n members. On input a signer’s public and private key pair and a message , it first randomly chooses and computes for and . It then chooses a random salt and computes , whereFinally, it outputs a ring signature .
- : On input , where is a list of users’ public keys with n members. It first computes for . It then checks whether holds or not. If it holds, it outputs and otherwise.
5.4. The Derived Accountable Optimistic Fair Exchange Protocol
- : On input , it generates , where ,, are cyclic groups of prime order q, and are two generators, and is a bilinear map. Let , , and , where is the message space. Finally, it outputs .
- : On input , it runs , where and . Note that will be used for ring signature later. Lastly, it returns an arbitrator public and private key pair .
- : On input , it runs , where and . Note that will be used for ordinary signature and ring signature later. Lastly, it returns a user public and private key pair .
- : On input , it runs to compute an ordinary signature, . It outputs a partial signature .
- : On input , it runs to check the validity by comparing . It returns if the equation holds and otherwise.
- : On input , it runs and continues if and only if is valid. Let , it runs to generate a convertible undeniable signature, . It then runs to generate a ring signature, . Let , it randomly chooses and computes . It then chooses a random salt and computes :Finally, it outputs a full signature where .
- : On input , it first runs and continues if and only if is valid. It then runs to verify . Let , it then computes and . It then checks whether holds or not. If it holds, it outputs and otherwise.
- : On input , it runs and continues if and only if is valid. Let , it runs to compute a convertible undeniable signature, . It then runs to generate a ring signature, . Let , it first randomly chooses and computes . It then chooses a random salt and computes :Finally, it outputs a full signature where .
- : On input , it first runs and continues if and only if is valid. Let , it runs to compute a proof . Otherwise, it outputs
- : On input , it first runs and continues if and only if is valid. Let , it runs to compute a proof . Otherwise, it outputs
- : On input , it runs and continues if and only if is valid. Let , it runs to verify , where
- -
- If , it first checks the validity of by running and outputs if is invalid. Otherwise, it proceeds to validate by running . If the equation holds, it means was signed by the arbitrator and outputs , otherwise it outputs .
- -
- If , it first checks the validity of by running and outputs if is invalid. Otherwise, it proceeds to validate by running . If the equation holds, it means was signed by the signer and outputs , otherwise it outputs .
Security Analysis
- Resolution Ambiguity: This property requires that the underlying convertible undeniable signature and ring signature scheme satisfy anonymous. The derived protocol is resolution ambiguous which follows Lemma 1, such that the underlying Li et al.’s convertible undeniable signature scheme [31] is proven invisible based on One-more Decisional Co-Tripartite-Diffie-Hellman (1m-DCTDH) in the random oracle model, where it is also well known that the invisibility and anonymity are equivalent as proven by Galbraith and Mao [39]. Besides, the underlying Shim’s ring signature scheme is unconditionally anonymous as shown by the author [32].
- Accountability: This property requires that the underlying convertible undeniable signature scheme satisfies EUF-CMA and completeness and soundness. The derived protocol is accountable which follows Lemmas 2–4, such that the underlying Li et al.’s convertible undeniable signature scheme [31] achieves EUF-CMA based on Computational co-Diffie-Hellman (Co-CDH) in the random oracle model. The completeness and soundness of Li et al.’s scheme is unconditionally satisfied as shown by the author.
- Security against Signers: This property is unconditionally satisfied which follows Lemma 5 as the generic framework follows the same construction as in Huang et al. [19] and Ganjavi et al. [24], such that the arbitrator can always convert a partial signature into a full signature by generating a convertible undeniable signature and ring signature.
- Security against Verifiers: This property requires that the underlying convertible undeniable signature and ring signature scheme satisfy EUF-CMA and EUF-CSA respectively. The derived protocol is secure against verifiers which follows Lemma 6, such that the underlying Li et al.’s convertible undeniable signature scheme [31] and Shim’s ring signature scheme [32] are both proven EUF-CMA and EUF-CSA respectively based on Co-CDH in the random oracle model.
- Security against Arbitrator: This property requires that the underlying ordinary signature scheme satisfies EUF-CMA. The derived protocol is secure against arbitrator which follows Lemma 7, such that the underlying Boneh et al.’s ordinary signature [30] acheives EUF-CMA based on Co-CDH in the random oracle model.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bao, F.; Wang, G.; Zhou, J.; Zhu, H. Analysis and Improvement of Micali’s Fair Contract Signing Protocol. In Information Security and Privacy; Wang, H., Pieprzyk, J., Varadharajan, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 176–187. [Google Scholar]
- Ben-Or, M.; Goldreich, O.; Micali, S.; Rivest, R.L. A fair protocol for signing contracts. IEEE Trans. Inf. Theory 1990, 36, 40–46. [Google Scholar] [CrossRef]
- Park, J.M.; Chong, E.K.P.; Siegel, H.J. Constructing Fair-exchange Protocols for E-commerce via Distributed Computation of RSA Signatures. In Proceedings of the PODC ‘03 Twenty-Second Annual Symposium on Principles of Distributed Computing, Boston, MA, USA, 13–16 July 2003; ACM: New York, NY, USA, 2003; pp. 172–181. [Google Scholar] [CrossRef]
- Abadi, M.; Glew, N.; Horne, B.; Pinkas, B. Certified email with a light on-line trusted third party: Design and implementation. Int. World Wide Web Conf. 2002, 2, 387–395. [Google Scholar]
- Ateniese, G.; Nita-Rotaru, C. Stateless-Recipient Certified E-Mail System Based on Verifiable Encryption. In Topics in Cryptology—CT-RSA 2002; Preneel, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 182–199. [Google Scholar]
- Imamoto, K.; Sakurai, K. A Certified E-mail System with Receiver’s Selective Usage of Delivery Authority. In Progress in Cryptology—INDOCRYPT 2002; Menezes, A., Sarkar, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 326–338. [Google Scholar]
- AlOtaibi, A.; Aldabbas, H. A review of fair exchange protocols. Int. J. Comput. Netw. Commun. 2012, 4, 307. [Google Scholar] [CrossRef]
- Bahreman, A.; Tygar, J. Certified electronic mail. In Proceedings of the 1994 Network and Distributed System Security Symposium (NDSS 1994), New York, NY, USA, February 1994; pp. 3–19. [Google Scholar]
- Coffey, T.; Saidha, P.; Burrows, P. Analysing the Security of a Non-repudiation Communication Protocol with Mandatory Proof of Receipt. In Proceedings of the ISICT ‘03 1st International Symposium on Information and Communication Technologies, Dublin, Ireland, 24–26 September 2003; Trinity College Dublin: Dublin, Ireland, 2003; pp. 351–356. [Google Scholar]
- Cox, B.; Tygar, J.D.; Sirbu, M. NetBill Security and Transaction Protocol. In Proceedings of the USENIX Workshop on Electronic Commerce, New York, NY, USA, 11–12 July 1995; Volume 1. [Google Scholar]
- Deng, R.H.; Gong, L.; Lazar, A.A.; Wang, W. Practical protocols for certified electronic mail. J. Netw. Syst. Manag. 1996, 4, 279–297. [Google Scholar] [CrossRef]
- Asokan, N.; Schunter, M.; Waidner, M. Optimistic Protocols for Fair Exchange. In Proceedings of the CCS ‘97 4th ACM Conference on Computer and Communications Security, Zurich, Switzerland, 1–4 April 1997; ACM: New York, NY, USA, 1997; pp. 7–17. [Google Scholar] [CrossRef]
- Dodis, Y.; Reyzin, L. Breaking and Repairing Optimistic Fair Exchange from PODC 2003. In Proceedings of the DRM ‘03 3rd ACM Workshop on Digital Rights Management, Washington, DC, USA, 27 October 2003; ACM: New York, NY, USA, 2003; pp. 47–54. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, G.; Wong, D.S.; Susilo, W. Efficient Optimistic Fair Exchange Secure in the Multi-user Setting and Chosen-Key Model without Random Oracles. In Topics in Cryptology—CT-RSA 2008; Malkin, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 106–120. [Google Scholar]
- Huang, Q.; Yang, G.; Wong, D.S.; Susilo, W. Ambiguous Optimistic Fair Exchange. In Advances in Cryptology–ASIACRYPT 2008; Pieprzyk, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 74–89. [Google Scholar]
- Wang, Y.; Au, M.H.; Susilo, W. Perfect Ambiguous Optimistic Fair Exchange. In Information and Communications Security; Chim, T.W., Yuen, T.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 142–153. [Google Scholar]
- Huang, Q.; Wong, D.S.; Susilo, W. P2OFE: Privacy-Preserving Optimistic Fair Exchange of Digital Signatures. In Topics in Cryptology—CT-RSA 2014; Benaloh, J., Ed.; Springer: Cham, Switzerland, 2014; pp. 367–384. [Google Scholar]
- Guo, Q.; Cui, Y.; Zou, X.; Huang, Q. Generic Construction of Privacy-Preserving Optimistic Fair Exchange Protocols. J. Internet Serv. Inf. Secur. 2017, 7, 44–56. [Google Scholar]
- Huang, X.; Mu, Y.; Susilo, W.; Wu, W.; Zhou, J.; Deng, R.H. Preserving Transparency and Accountability in Optimistic Fair Exchange of Digital Signatures. IEEE Trans. Inf. Forensics Secur. 2011, 6, 498–512. [Google Scholar] [CrossRef]
- Bellare, M.; Rogaway, P. Random Oracles Are Practical: A Paradigm for Designing Efficient Protocols. In Proceedings of the CCS ‘93 1st ACM Conference on Computer and Communications Security, Fairfax, VA, USA, 3–5 November 1993; ACM: New York, NY, USA, 1993; pp. 62–73. [Google Scholar] [CrossRef]
- Bellare, M.; Goldreich, O. On Defining Proofs of Knowledge. In Advances in Cryptology—CRYPTO’ 92; Brickell, E.F., Ed.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 390–420. [Google Scholar]
- Fiat, A.; Shamir, A. How To Prove Yourself: Practical Solutions to Identification and Signature Problems. In Advances in Cryptology—CRYPTO’ 86; Odlyzko, A.M., Ed.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 186–194. [Google Scholar]
- Cramer, R.; Damgård, I.; Schoenmakers, B. Proofs of Partial Knowledge and Simplified Design of Witness Hiding Protocols. In Advances in Cryptology—CRYPTO ’94; Desmedt, Y.G., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 174–187. [Google Scholar]
- Ganjavi, R.; Asaar, M.R.; Salmasizadeh, M. A traceable optimistic fair exchange protocol. In Proceedings of the 2014 11th International ISC Conference on Information Security and Cryptology, Tehran, Iran, 3–4 September 2014; pp. 161–166. [Google Scholar] [CrossRef]
- Fujisaki, E.; Suzuki, K. Traceable Ring Signature. In Public Key Cryptography–PKC 2007; Okamoto, T., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 181–200. [Google Scholar]
- Fujisaki, E. Sub-linear Size Traceable Ring Signatures without Random Oracles. In Topics in Cryptology—CT-RSA 2011; Kiayias, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 393–415. [Google Scholar]
- Gu, K.; Wu, N. Constant Size Traceable Ring Signature Scheme without Random Oracles. Cryptology ePrint Archive, Report 2018/288, 2018. Available online: https://eprint.iacr.org/2018/288 (accessed on 6 June 2018).
- Hu, C.; Li, D. Forward-Secure Traceable Ring Signature. In Proceedings of the Eighth ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing (SNPD 2007), Qingdao, China, 30 July–1 August 2007; Volume 3, pp. 200–204. [Google Scholar] [CrossRef]
- Loh, J.C.; Heng, S.H.; Tan, S.Y. A Generic Framework for Accountable Optimistic Fair Exchange Protocol. In Lecture Notes in Computer Science, Proceeding of the 14th International Conference on Information Security Practice and Experience, Tokyo, Japan, 25–27 September 2018; Su, C., Kikuchi, H., Eds.; Springer: New York, NY, USA, 2018; Volume 11125, pp. 299–309. [Google Scholar]
- Boneh, D.; Lynn, B.; Shacham, H. Short Signatures from the Weil Pairing. In Advances in Cryptology—ASIACRYPT 2001; Boyd, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 514–532. [Google Scholar]
- Li, F.; Gao, W.; Wang, Y.; Wang, X. Short Convertible Undeniable Signature From Pairing. J. Softw. 2013, 8, 2983–2990. [Google Scholar] [CrossRef]
- Shim, K.A. An efficient ring signature scheme from pairings. Inf. Sci. 2015, 300, 63–69. [Google Scholar] [CrossRef]
- Dodis, Y.; Lee, P.J.; Yum, D.H. Optimistic Fair Exchange in a Multi-user Setting. In Public Key Cryptography—PKC 2007; Okamoto, T., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 118–133. [Google Scholar]
- Zhu, H.; Susilo, W.; Mu, Y. Multi-party Stand-Alone and Setup-Free Verifiably Committed Signatures. In Public Key Cryptography—PKC 2007; Okamoto, T., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 134–149. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-Based Encryption from the Weil Pairing. In Advances in Cryptology—CRYPTO 2001; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Goldwasser, S.; Micali, S.; Rivest, R.L. A Digital Signature Scheme Secure Against Adaptive Chosen-Message Attacks. SIAM J. Comput. 1988, 17, 281–308. [Google Scholar] [CrossRef]
- Chaum, D.; van Antwerpen, H. Undeniable Signatures. In Advances in Cryptology—CRYPTO’ 89 Proceedings; Brassard, G., Ed.; Springer: New York, NY, USA, 1990; pp. 212–216. [Google Scholar]
- Boyar, J.; Chaum, D.; Damgård, I.; Pedersen, T. Convertible Undeniable Signatures. In Advances in Cryptology-CRYPT0’ 90; Menezes, A.J., Vanstone, S.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 189–205. [Google Scholar]
- Galbraith, S.D.; Mao, W. Invisibility and Anonymity of Undeniable and Confirmer Signatures. In Topics in Cryptology—CT-RSA 2003; Joye, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 80–97. [Google Scholar]
- Huang, X.; Mu, Y.; Susilo, W.; Wu, W. Provably Secure Pairing-Based Convertible Undeniable Signature with Short Signature Length. In Pairing-Based Cryptography—Pairing 2007; Takagi, T., Okamoto, T., Okamoto, E., Okamoto, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 367–391. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Tauman, Y. How to Leak a Secret. In Advances in Cryptology—ASIACRYPT 2001; Boyd, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 552–565. [Google Scholar]
- Bender, A.; Katz, J.; Morselli, R. Ring Signatures: Stronger Definitions, and Constructions Without Random Oracles. In Theory of Cryptography; Halevi, S., Rabin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 60–79. [Google Scholar]
- Bender, A.; Katz, J.; Morselli, R. Ring Signatures: Stronger Definitions, and Constructions without Random Oracles. J. Cryptol. 2009, 22, 114–138. [Google Scholar] [CrossRef]
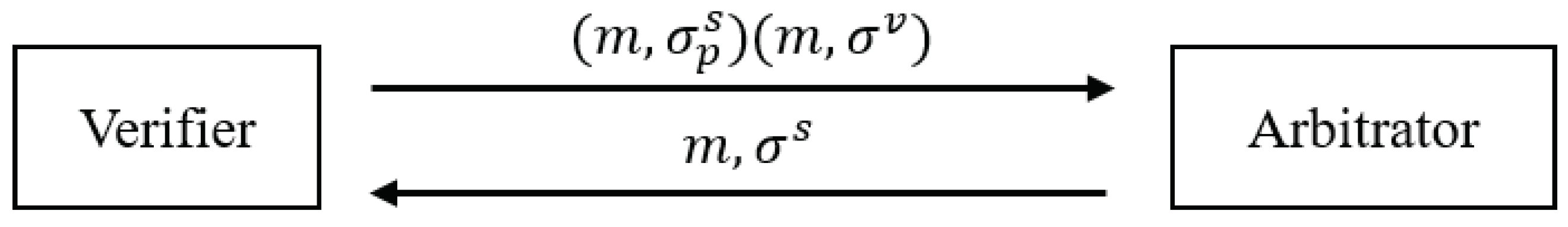
| Generic Framework | Partial Signature | Full Signature | Proof | Standard Model | Random Oracle Model |
|---|---|---|---|---|---|
| Huang et al. [19] | OS | ,US, | SPK | × | √ |
| r, -Signature | |||||
| Ganjavi et al. [24] | OS | , TRS | TRS | √ | √ |
| Proposed | OS | , CUS, RS | token | √ | √ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loh, J.-C.; Heng, S.-H.; Tan, S.-Y. A Generic Framework for Accountable Optimistic Fair Exchange Protocol. Symmetry 2019, 11, 285. https://doi.org/10.3390/sym11020285
Loh J-C, Heng S-H, Tan S-Y. A Generic Framework for Accountable Optimistic Fair Exchange Protocol. Symmetry. 2019; 11(2):285. https://doi.org/10.3390/sym11020285
Chicago/Turabian StyleLoh, Jia-Ch’ng, Swee-Huay Heng, and Syh-Yuan Tan. 2019. "A Generic Framework for Accountable Optimistic Fair Exchange Protocol" Symmetry 11, no. 2: 285. https://doi.org/10.3390/sym11020285
APA StyleLoh, J.-C., Heng, S.-H., & Tan, S.-Y. (2019). A Generic Framework for Accountable Optimistic Fair Exchange Protocol. Symmetry, 11(2), 285. https://doi.org/10.3390/sym11020285





