Abstract
Usually, the nodes’ interactions in many complex networks need a more accurate mapping than simple links. For instance, in social networks, it may be possible to consider different relationships between people. This implies the use of different layers where the nodes are preserved and the relationships are diverse, that is, multiplex networks or biplex networks, for two layers. One major issue in complex networks is the centrality, which aims to classify the most relevant elements in a given system. One of these classic measures of centrality is based on the PageRank classification vector used initially in the Google search engine to order web pages. The PageRank model may be understood as a two-layer network where one layer represents the topology of the network and the other layer is related to teleportation between the nodes. This approach may be extended to define a centrality index for multiplex networks based on the PageRank vector concept. On the other hand, the adapted PageRank algorithm (APA) centrality constitutes a model to obtain the importance of the nodes in a spatial network with the presence of data (both real and virtual). Following the idea of the two-layer approach for PageRank centrality, we can consider the APA centrality under the perspective of a two-layer network where, on the one hand, we keep maintaining the layer of the topological connections of the nodes and, on the other hand, we consider a data layer associated with the network. Following a similar reasoning, we are able to extend the APA model to spatial networks with different layers. The aim of this paper is to propose a centrality measure for biplex networks that extends the adapted PageRank algorithm centrality for spatial networks with data to the PageRank two-layer approach. Finally, we show an example where the ability to analyze data referring to a group of people from different aspects and using different sets of independent data are revealed.
1. Introduction
1.1. Literature Review
Network theory is an important tool for describing and analyzing complex systems throughout the social, biological, physical, information and engineering sciences [1]. Originally, almost all studies of networks employed an abstraction in which systems are represented as ordinary graphs [2]. Although this approach is naive in many respects, it has been extremely successful. For instance, it has been used to illustrate that many real networks possess a heavy-tailed degree distribution [3], exhibit the small-world property [4], contain nodes that play central roles [5] and/or have modular structures [6].
It has been recently recognized [7,8,9] that most complex systems are not simply formed by a simple network, but they are instead formed by multilayer networks. Multilayer networks include not just one but several layers (networks) characterizing interactions of different nature and connotation. Multiplex networks [10,11] are a special type of multilayer networks. They are formed by a set of nodes connected by different types of interactions. The term multiplex was defined to indicate the presence of more than one relationship between the same actors of a social network [12]. Each set of interactions of the same type determines a distinct layer (network) of the multiplex. Examples of multiplex networks are ubiquitous. Other major examples of multiplex networks range from transportation networks [13] to social [14], financial [15] and biological networks [16]. In transportation networks, different layers can represent different means of transportation while in scientific collaboration networks the different layers can represent several topics of the collaboration. Given the surge of interest in multiplex networks, recently several algorithms [17,18] have been proposed to assess the centrality of nodes in these multilayer structures.
On the other hand, when pairs of nodes can be connected through multiple links and in multiple layers, the ranking of nodes should necessarily reflect the importance of nodes in one layer as well as their importance in other interdependent layers. Our world is increasingly dependent on efficient ranking algorithms [19,20,21]. Currently the ranking of nodes in complex networks is used in a variety of different contexts [22], from finance to social, urban and biological networks. For instance, in the context of economical trade networks, formed by networks of countries and products, ranking algorithms [23] are recognized as an important tool to evaluate the economic development of countries.
Within the general problem of centrality in urban networks [24], the adapted PageRank algorithm (APA) proposed by [25] provides us a model to establish a ranking of nodes in spatial networks according to their importance in it. This centrality was originally proposed for urban networks, although it may be generalized to spatial networks or networks with data. It constitutes a centrality measure in urban networks with the main characteristic that it is able to consider the importance of data obtained from any source in the whole process of computing the centrality of the individual nodes. Starting from the basic idea of the PageRank vector concept [26], the matrix used for obtaining the classification of the nodes is constructed in a slightly different way as we will see later.
Centrality measures originally defined on single networks have been used extensively in some types of networks, as social, technological or biological. In multiplex networks these measures can be extended in different ways [27]. Generalizing centrality measures from monoplex networks to multilayer networks is not trivial. When ranking nodes in a multilayer or multiplex network, the key question to be addressed is how one should take into consideration all the different types of edges, not all of which have the same importance [17].
The Multiplex PageRank [28] evaluates the centrality of the nodes of multiplex networks and is based on the idea of biased random walks to define the Multiplex PageRank centrality measure in which the effects of the interplay between networks on the centrality of nodes are directly taken into account. Other centrality measures associate a different influence with the links of different layers that weights their contribution to the centrality of the nodes, as for example Multiplex Eigenvector Centralities [17], or Functional Multiplex PageRank [18], which takes into account the fact that different multilinks contribute differently to the centrality of each node and associates with each node a function. In [29], Solé–Ribalta et al. re-define the betweenness centrality measure to account for the inherent structure of multiplex networks and propose an algorithm to calculate it efficiently.
1.2. Main Contribution
The main objective of this paper is to propose a centrality measure for biplex networks that adapts the APA centrality for spatial networks with data to the PageRank two-layer approach.
The multiplex PageRank algorithm proposed by Halu et al. [28] measures the centrality of a node in a layer with the corresponding adjacency matrix using a random walker as in the usual PageRank biased by the PageRank of the nodes in the layer . So, Multiplex PageRank can be described in terms of the bias that one layer exerts on the random jumps that a surfer makes in another layer. Four versions of the centrality are presented depending on how layers affect each other or, alternatively, exert a bias upon the random walk.
The advantage of the model proposed for biplex networks is that since it is based on the APA centrality, the randomness in the jumps of the surfer is replaced by the influence of the data present in the network. Therefore, the model is able to study and analyze several relationships of a set of nodes by different layers, but it is also capable of measuring the influence of the data in the different layers of the network. Thus, it is not only taken into account the topology of the networks but also the data. In addition, the parameter initially associated to the PageRank model and exported to APA centrality can be used to assign the importance that each of these data layers has in the calculation of centrality. These characteristics summarizes the novelty and potential of this research work.
The potential of the applications to which this centrality can be applied should also be highlighted. Nowadays multilayers and multiplex networks are investigated in many fields, as were enumerated in Section 1.1. However, there are other potential applications not so well known but equally interesting where the centrality measure proposed in this research can be applied. One of these topics is the improvement in the recommender systems [30,31]. These systems were initially based on demographic, content-based and collaborative filtering although actually are incorporating social information. Another unknown topic of application is in Public Safety Networks [32,33] which have emerged as the key solution to a successful response to emergency and disaster events. In these systems each user is associated with some social, physical and mobility-related characteristics and attributes in a public safety network.
1.3. Structure of the Paper
This paper is organized as follows: Section 2 summarizes the methodology used in the paper: the basic characteristics of the APA centrality, as well as the biplex approach to the PageRank vector. Once these models are described, the new centrality is presented combining the APA centrality (based on data) and the biplex approach of PageRank vector. In Section 3, some results are presented with their interpretation. The discussion of the experimental results are performed in Section 4 and, finally, some conclusions are summarized.
2. Methodology
In practical applications, the computation of a global index to measure the importance to each node is a main task. If the system studied contains several types of relations between actors it is expected that the measures, in some way, consider the importance obtained from the different layers. A simple choice could be to combine the centrality of the nodes computed from the different layers independently according to some heuristic choice.
In this section, both the well-established methods and the proposed centrality for multiplex networks with data are described in detail.
2.1. The Adapted PageRank Algorithm (APA) Model
Let us establish some notation that will be used in the following. Let be a graph where and . The link belongs to the set if and only if there exists a link connecting node i to j. The adjacency matrix of is an matrix , where
The adapted PageRank algorithm (APA) proposed by Agryzkov et al. [25] provides us a model to establish a ranking of nodes in an urban network taking into account the data presented in it. This centrality was originally proposed for urban networks, although it may be generalized to spatial networks or networks with data. It constitutes a centrality measure for networks with the main characteristic being that it is able to consider the importance of data obtained from any source in the whole process of computing the centrality of the individual nodes. Starting from the basic idea of the PageRank vector concept, the construction of the matrix used for obtaining the classification of the nodes is modified.
In its original approach, PageRank was based on a model of a web surfer that probabilistically browses the web graph, starting at a node chosen at random according to a personalization vector whose components give us the probability of starting at node v. At each step, if the current node had outgoing links to other nodes, the surfer next browsed with probability one of those nodes (chosen uniformly at random), and with probability a node chosen at random according to the personalized vector. For the web graph, the most popular value of the dumping factor was . If the current node was a sink with no outgoing links, the surfer automatically chose the next node at random according to the personalized vector.
In the APA model, the data matrix was constructed following a similar reasoning from the original idea of the PageRank vector; a random walker can jump between connecting nodes following the local link given by the network or can jump between nodes (not directly connected) with the same probability, regardless the topological distance between them (number of nodes in the walk).
In the algorithm implemented to calculate the APA centrality (see [25], p. 2190), a new matrix is constructed from the adjacency matrix A, as
where represents the sum of the j-th column of the adjacency matrix.
Algebraically, may be obtained as
where is the degree matrix of the graph, that is, , for and , for . We refer to as the transition matrix, and it represents, by columns, the probability to navigate from a page to other. In the literature related to this topic the matrix is also denoted as P or , so , P or are the same matrix. Following the notation of Pedroche et al. [34] it will preferably be used P.
The transition matrix, has the following characteristics (see [25]):
- It is nonnegative.
- It is stochastic by columns.
- The highest eigenvalue of P is .
The key point of the model is the construction of the so-called data matrix D of size , with its n rows representing the n nodes of the network, and each of its k columns representing the attributes of the data object of the study. Specifically, an element is the value we attach to the data class at node i.
However, not all the characteristics of data may have the same relevance or influence in the question object of the analysis. Therefore, a vector is constructed, where the element that occupies the row i is the multiplicative factor associated with the property or characteristic . With this vector a weighting factor of the data is introduced, in order to work with the entire data set or a part of it.
Then, multiplying D and , may be obtained as
with .
The construction of vector allows us to associate to each node a value that represents the amount of data assigned to it. Thus, two different values are associated with every node; on the one hand, its degree, related to the topology and, on the other hand, the value of the data associated to it. For a more detailed description of how the data are associated to the nodes, see [25,35].
After normalizing , denoted as , it is possible to define the matrix as
where is a matrix in which all of its components in the i-th row are equal to . The parameter is fixed and it is related to the teleportation idea. The value that is traditionally used is .
In practice, vector is repeated (n times) in every column of the matrix V.
The matrix was used to compute the ranking vector for the network.
With these considerations, the APA algorithm proposed in [25] may be summarized by the Algorithm 1:
| Algorithm 1: (Adapted PageRank algorithm (APA)). Let be a primary graph representing a network with n nodes. |
|
The main feature of this algorithm is the construction of the data matrix D and the weighted vector . The matrix D allows us to represent numerically the dataset. Vector determines the importance of each of the factors or characteristics that have been measured by means of D.
The Perron–Frobenius theorem is of great importance in this problem, since it constitutes the theoretical base that ensures that there exists an eigenvector associated with the dominant eigenvalue , so that all its components are positive, which allows establishing an order or classification of these elements. In our case, due to the way in which P and V have been constructed, it can be seen that is a stochastic matrix by columns, which assures us of the spectral properties necessary for the Perron–Frobenius theorem to be fulfilled. Therefore, the existence and uniqueness of a dominant eigenvector with all its components positive is guaranteed. See [36,37] for further study of spectral and algebraic properties of the models based on PageRank.
Vector constitutes the adapted PageRank vector and provides a classification or ranking of the pages according to the connectivity criterion between them and the presence of data.
2.2. The Biplex Approach for Classic PageRank
Pedroche et al. [34] propose a two-layer approach for the classic PageRank classification vector based on the idea that we now briefly expose. The two-layer approach is to consider the PageRank classification of the nodes as a process divided into two clearly differentiated parts. The first part is related to the topology of the network, where the connections of the nodes are basically taken into account by means of their adjacency matrix. There is a second part regarding to the teleportation from one node to another, following a criterion of equiprobability.
They affirm that the PageRank classification for a graph G with personalized vector can be understood as the stationary distribution of a Markov chain that occurs in a network with two layers, which are:
- , physical layer, it is the network G.
- , teleportation layer, it is an all-to-all network, with weights given by the personalized vector.
Under this perspective, it is easy to construct a block matrix based on these two layers where each of the diagonal blocks is associated to a given layer. Therefore, we can construct
where defines a Markov chain in a network with two layers.
Due to the good spectral characteristics of (it is irreducible and primitive), they arrive to the conclusion that given a network with n nodes, whose adjacency matrix is A, the two-layer approach PageRank of A is the vector
where is the unique normalized and positive eigenvector of matrix given by the expression (4).
In [38], the authors propose a new centrality measure for complex networks with geo-located data based on the application of the two-layer PageRank approach to the APA centrality measure for spatial networks with data. They design an algorithm to evaluate this centrality and show the coherence of this measure regarding the original APA by calculating the correlation and the quantitative difference of both centralities using different network models. This coherence in the results obtained for the APA and the proposed centrality using the two-layer approach is absolutely mandatory in our objective to extend the two-layer approach for multiplex networks with data.
Therefore, the two-layer approach may be extended to the case of multiplex networks, where we have several networks with the same nodes and with different topologies and connections between nodes. Following the notation used by Pedroche et al. [34], let us consider a multiplex network with layers . Given a multiplex network with several layers, a multiplex PageRank centrality can be defined by associating to each layer a two-layer random walker with one the physical layer and a teleportation layer. In addition, transition between these layers must be allowed. The idea behind this process is the application of the two-layer approach to each layer of the multiplex network.
For now, let us consider our problem restricted to biplex networks , with layers whose adjacency matrices are , respectively. For convenience in the notation we will write , and instead of , and , respectively.
The authors (see, [34]) construct a general matrix as a new block matrix by associating to each layer a two-layer multiplex defined, for , as:
Reordering the blocks in such a way that the physical layers appear in the first block, the final matrix is
with , for row stochastic matrices and , for the personalized vectors.
It is straightforward to check that all the spectral properties of are essentially the same as the Google matrix in the PageRank model. Then, there exists an eigenvector
associated to the dominant eigenvalue . This vector is the key to obtain the classification vector representing the nodes centrality.
Consequently, summarizing the main characteristic of the biplex PageRank approach, considering a biplex network with n nodes, with two layers , and whose adjacency matrices are , it can be affirmed that the PageRank vector that classifies the nodes of this biplex network is the unique vector such as
with normalized.
2.3. Constructing the APABI Centrality by Applying the Two-Layer Approach
The idea of the treatment of the PageRank concept by means of two layers has a great sense within the idea of APA centrality, since the influence of the data in the network is measured separately in the original algorithm. Paying attention to the construction of given by (3), note that V is the matrix summarizing all the data information. But not only the application of this concept is interesting for our centrality, since may be also interesting to analyze the differences that occur between both techniques of calculating the importance of the nodes.
In this section, we describe how to adapt the APA centrality taking as a reference the two-layers technique, where a block matrix is used to distinguish the topology and the personalized vector.
The original APA centrality model, described in Section 2, presents some differences from the model described and implemented by Pedroche et al. [34], where the final matrix involved in the eigenvector computation is stochastic by rows. In our approach, the basis of the original APA model consists of the construction of a stochastic matrix by columns, where we reflect the topology of the network by the probability matrix P and the influence of the data, through the matrix V.
In order to build a block matrix, the same approach used in [34] may be reproduced. The first upper diagonal block contains the information referring to the network topology, while the lower diagonal block is associated to the collected data in the network and assigned to each node of it.
Taking as a reference the APA algorithm, the matrix used to compute the eigenvector associated to the dominant eigenvalue is given by
A new block matrix is constructed as
The idea that underlies the construction of the matrix by blocks given by (6) is to maintain the spectral properties of the original matrix , with the aim that the numerical algorithms for determining dominant eigenvalue and eigenvector are stable and fast. Note that we have doubled the size of the original matrix.
Following the same reasoning used in Section 3 to construct a model for biplex networks taking as a basis the classical PageRank vector, it is necessary to extend the two-layers APA approach given by the block matrix (6). Using the same notation, let us consider , with layers be a biplex network.
Reordering the blocks in such a way that the physical layers appear in the first block, the final matrix is given by
with , for column stochastic matrices and , for , the matrices containing the data information.
Note the differences between matrices (5) and (7). The matrix is stochastic by rows, however, in the APA centrality the basic matrix is stochastic by columns, so the definition of the matrix is determined by the need to maintain the spectral properties suitable for obtaining the proper vector of the centrality. These desirable spectral properties are ensured by the way in which has been built, being stochastic by columns, as well as irreducible.
Then, there exists an eigenvector
associated to the dominant eigenvalue . This vector is the key to obtain the classification vector representing the nodes centrality. Therefore, it can be obtained a unique vector
with a normalized vector.
In Figure 1, a schematic representation of the extended APA model for biplex networks has been represented. All the graphs share the same n nodes, although the relationships between them in the two layers and are different, which produces two different adjacency matrices and . Data are also different in each layer; consequently, two data matrices are constructed and .
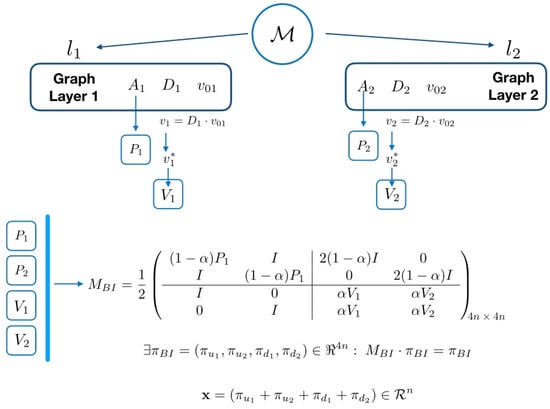
Figure 1.
Scheme of the adapted PageRank algorithm (APA) extended model for biplex networks.
The existence of the weighted vectors and allows us to determine those data that are the object of our interest, being able to discard those that do not present real interest for the study that is carried out.
The model presented in this section may be summarized by the Algorithm 2.
| Algorithm 2: (Adapted PageRank algorithm biplex (APABI)). Let , with layers and adjacency matrices be a biplex network with n nodes. |
|
Algorithm 2 summarizes the steps necessary to calculate a centrality measure that will be denoted as the adapted PageRank algorithm biplex (APABI). This measure provides us with a vector for classifying the nodes of the network according to their importance within a biplex network. This classification is obtained from the importance of the nodes in two networks where what changes are the associations between the nodes and the data associated with them. This classification is obtained from the importance of the nodes in two layers where the nodes are the same and what changes are the associations (links) between the nodes and the data associated with them.
Note that the matrix is built for biplex networks. However, it can be easily extended the same reasoning for a multiplex network with k layers , defining the adjacency matrices and a set of k data matrices . The matrix is extended to a multiplex network with k layers as
with
where , are diagonal matrices. More exactly, is formed by k blocks and is formed by k identity blocks I.
In the approach made so far in this section, we have considered the same value for the parameter in all the layers that make up the network. However, it could happen that the value was different in the different layers, as a consequence of the need to differentiate the importance that must be assigned to the data in each of the layers. That leads us to consider various , for each layer i. Note that this variant does not imply in any way modify the spectral properties of the matrices involved in the calculation of centrality. Consequently, matrix should be written now as
2.4. A Note about the Computational Cost
We discuss certain general aspects of the computational cost of the proposed model. It should be noted that if we look closely at Algorithm 2, the most expensive algebraic operations that are carried out are the product of a scalar by a matrix, the matrix-vector product and the calculation of the dominant eigenpair of matrix , given by the expression (8).
As it is well-known and can be seen in any linear algebra textbook, the product of a scalar by a square matrix of size n requires multiplications, while the product of two square matrices of size n requires a computational cost of . In our case, we need to make the product , for , where D is the data matrix of size and is a column vector of size n. Therefore, the computational cost of is of .
However, the most expensive part from the computational point of view is found in step 8 of the algorithm, in which, once the matrix is constructed, it is necessary to obtain its dominant eigenpair . The numerical problem of calculating the eigenvalues and eigenvectors of any matrix is very expensive, in general, if the matrix in question does not have a structure that simplifies its calculation in some way. In general, for matrices of low dimension (such as ), there are efficient methods for finding all the eigenvalues and eigenvectors. For example, the Householder–QL–Wilkinson modification of the given method is built into the EISPACK routines and is routinely used. The computation time for any of these methods grows as and the memory requirement grows as . For large matrices, a very commonly used algorithm is Lanczos, that is an adaptation of power methods to find the m most useful eigenvalues and eigenvectors of an Hermitian matrix. For a more detailed description of the numerical matrix eigenvalue problems, see [39].
Due to the way we have built the matrix following the original idea of the Google matrix used in the original PageRank combined with the two-layer PageRank approach, we have ensured that this matrix inherits the spectral properties of the original Google matrix in the original PageRank model. It is a stochastic matrix by columns of which we can affirm, using a variant of the Perron–Frobenius theorem, that its own dominant eigenvector associated to eigenvalue corresponds to the stationary distribution of the Markov chain by the column normalized matrix . This stationary vector verifies that
and may be obtained by using the well-known power iteration method, applying it until the convergence of the iterative process
for .
In addition, it should be noted that the use of the power method for the calculation of the dominant eigenvector is especially useful when applied to sparse matrices.
3. Results
In this section, an example of a biplex network is analyzed in detail in order to highlight the possibilities offered by disposing of a centrality measure that establishes a classification of the nodes in order of importance.
For this purpose, let us consider a graph of 20 nodes, where each node represents a physical person; specifically, a player from a football team. Around this group the example is developed.
With these 20 nodes, let us proceed to construct a network with two layers that relate the nodes in a different way, taking two datasets (one for each of the layers). The calculation of the APABI centrality on this biplex network will allow us to determine the importance of each member of the team and obtain a classification of them in order of importance.
First, a layer is constructed with the 20 nodes where the relationships between the members of the team are analyzed from the point of view of social or virtual relationships. Thus, an undirected graph is constructed with an adjacency matrix in which two nodes are joined by an edge if they are related or linked through a social network. The graph of social relations between the nodes is shown in Figure 2. The data that are considered in this layer associated with each node are related to the number of messages that each person receives from their teammates in a period of time.
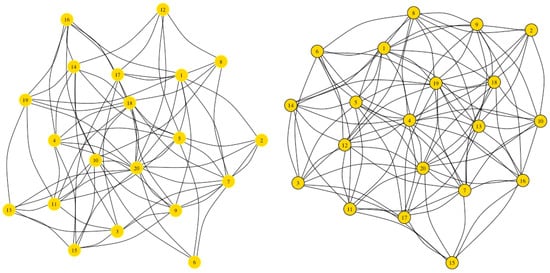
Figure 2.
Graphs of the first layer (left) and the second one (right).
Secondly, a second layer is constituted from the same 20 nodes of layer , but analyzing in how the players relate to each other within the game, that is, if they associate with each other in the game. Thus, two players who combine with each other or pass the ball with some assiduity during a match are connected by an edge. From these links, it is possible to build a new adjacency matrix associated with this layer, which we denote by . In most team sports with a ball, each player occupies a specific position in the field of play, covering a certain area. Players (nodes) that occupy closer positions associate or relate more easily with each other than with those who are further away. For example, a defender is associated more with a midfielder than with a forward. The graph of game relations between the nodes is shown in Figure 2.
Both the links and the data associated to each of the 20 nodes of the graph are summarized in Table 1. There, the second column specifies the social links of every node while in the four column the game links between them are detailed. So, for example, the table shows that node 1 (player labeled as 1) has social interactions with the nodes while presents strong interactions within the game with the nodes .

Table 1.
Data associated to the biplex network constructed from the team.
Datasets about the number of messages received during one day through social networks and the number of games that have played along the season are detailed in columns three and five, respectively. So, node 1 has received 15 messages in a day and has played 33 games in the season.
In this example, one of the advantages of working with biplex networks becomes manifest, such as the possibility of studying different relationships between the same set of nodes, analyzing the correlation between them. This example shows the advantage offered by adding what we can call a data layer in each of the multilayers of the network. We can assign the data that we consider appropriate to the specific relationships that we are representing by means of the corresponding graph. Thus, as can be seen in this example, in the layer where the social relations between the nodes are considered, we introduce the data corresponding to the number of received messages. However, in the second layer where game relations are represented, data are completely different, since now the number of games played are considered. Thus, each layer allows us to introduce one or more data sets related to the relationships of the nodes. This leads us to affirm that the inclusion of data in each of the layers enriches the nature of the problems that can be analyzed.
The objective in this example is to determine the most important or influential players within the team. For this task, two different aspects may be evaluated; on the one hand, the importance of the nodes from the point of view of the social relations that are established between them through messages, social networks, or any other virtual means. The nodes that have an intense social activity in the group create a very important union within the group, being very influential for other nodes. On the other hand, the importance of the nodes from the point of view of the game may be also evaluated, that is, which players are more important in the game, for their participation or quality. In other words, it is decisive to look for the leaders of the group, analyzing their importance from the social and technical point of view.
In order to determine the importance of the nodes of the biplex network of this example, the APABI centrality described in Section 2.3 has been calculated. Algorithm 2 has been executed using the information shown in Table 1. The numerical results shown in Table 2 are graphically displayed in Figure 3. This calculation gives us the importance of the nodes relating both layers. Figure 4 shows the final graph considering the information of two layers and the final result of the APABI centrality for each node, representing the size of each node according to its importance.

Table 2.
Adapted PageBreak algorithm (APA) centrality for layers and and APA biplex (APABI) centrality for biplex network.
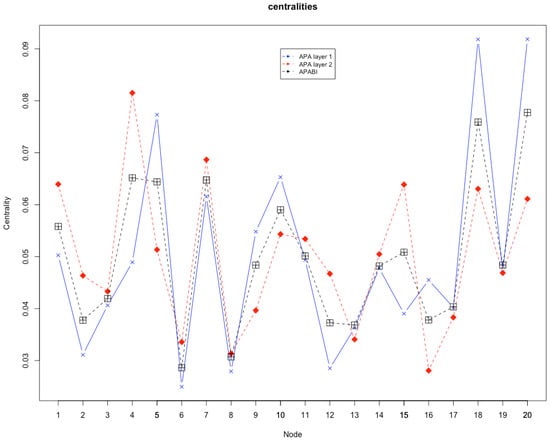
Figure 3.
Centralities shown in Table 2.
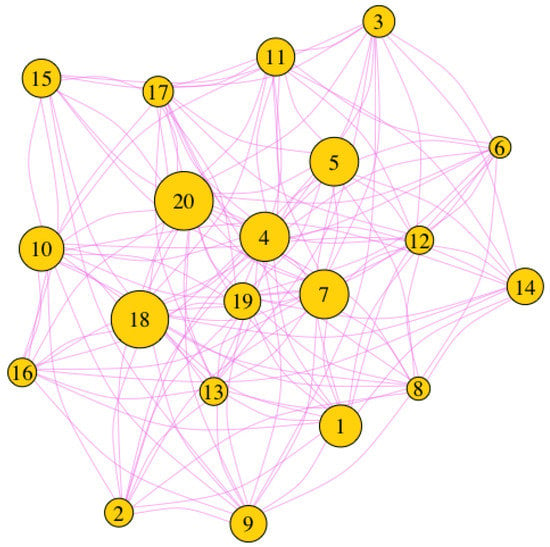
Figure 4.
Adapted PageRank algorithm biplex (APABI) centrality for the example object of this study.
The APABI centrality shows that the nodes that can be classified as the most important, the leaders within the group, are nodes 20 and 18, respectively. Note that node 20, which is the most important, is not the node that receives the most messages from its colleagues, being the node 18 is the one that receives the most messages from his teammates, but is second in the ranking.
Finally, it should be noted that, as discussed in Section 2.4, the use of the power method to calculate the stationary vector of the Markov chain that forms the stochastic matrix provides the numerical stability needed in the implemented algorithm.
We have performed several tests with randomly generated adjacency matrices of different sizes in a range from 10 to 10,000 and we have obtained stable results. Matrices of dimension exceeding cannot be stored in the central memory of most computers, except for sparse matrices. Consequently, the only matrix-arithmetic operation that is easily performed is a matrix-vector product. This makes possible to use this centrality algorithm for large matrices. In the scope of our research with urban network matrices, the sizes of the case studies are relatively large, with 2000–5000 nodes, approximately.
4. Discussion
In the discussion of the model presented and evaluated in the previous sections, let us pay attention to the example studied, the network of football team components. Results have been presented related to the proposed centrality measure APABI for a biplex network like this one.
We also consider that it may be relevant to calculate the nodes centrality in each of the layers, that is, separately and independently. In this way, it is possible to analyze the differences in the calculation of centrality in a single or multiplex networks, respectively, verifying if there is a certain correlation between the results obtained. We have calculated the APA centrality of the nodes in each of the layers. The numerical results obtained are shown in Table 2, where the numerical values of the centrality and the position of the nodes in the classification or ranking can be seen.
It should be noted that all the calculations have been made taking the value of the alpha parameter equal to . This means that we assign the same importance in the centrality computation to the connections of the nodes as to the data associated with them.
As it was already mentioned, the APABI centrality provides a classification of the nodes according to their importance in the biplex network studied. So, nodes 20 and 18 were the most important in the team. This can also be analyzed when the layers are considered independently.
The comparison between the APABI centrality and the APA centrality by independent layers offers us some remarkable facts. For instance, the most active nodes from the point of view of social networks are 20, 18, 10 and 5. The most important nodes from the point of view of the game are 4, 7, 1, 15. It is evident that there is no correlation between both relationships; leaders from the social point of view are not necessarily the most decisive players in the team’s game. Thus, the most participative player of the team, the one who most relates to the game with his teammates, is not socially the most active nor will he be the most influential individual within the group.
We appreciate that the most important nodes in a biplex network are nodes that maintain high positions in the two rankings obtained in each of the layers. The node 20 is the one that presents a greater importance from the social point of view, however, it is not among the first three nodes that have a greater participation in the team game. On the other hand, node 18 is not as socially active as node 20, although it has a greater degree of association with its teammates in the team game than the first one and has had a greater presence in the team games, specifically participating in more than 5 games. The numerical results show that this positive rating does not compensate the high social importance of node 20, although it should be highlighted that the difference in the centrality between both nodes is very small. It can be concluded that both nodes are the team leaders.
5. Conclusions
A measure of centrality for biplex networks (APABI) based on the APA centrality for spatial networks with data has been designed and implemented following the two-layers approach for PageRank model. The advantage of having a measure of centrality of this type is twofold; on the one hand, we can determine the importance of the nodes of a network when we study various relationships between the nodes. On the other hand, we can work with several data sets associated with the nodes themselves, without any connection or relationship between them.
This measure, initially proposed for two layers of topological relationships and data, can be easily extended to any set of layers and thus add the relationships between the nodes. Its use in the study of social networks can allow us to relate various aspects of the actors, as well as their interactions. These possibilities are shown in the example studied, where the social and professional relationships of a group of people that are part of a sports group are analyzed. The importance of each node (player) is analyzed both from the social and game aspects, respectively. From the proposed centrality we determine the most influential players in the team. It is observed how the most relevant nodes in each of the layers do not have to be the most important when analyzing the related data.
Author Contributions
All authors contributed equally to this work: conceptualization, methodology, formal analysis, investigation and writing—Original Draft preparation.
Funding
This research is partially supported by the Spanish Government, Ministerio de Economía y Competividad, grant number TIN2017-84821-P.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| APA | Adapted PageRank algorithm |
| APABI | Adapted PageRank algorithm biplex |
References
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Bollobas, B. Modern Graph Theory; Springer: Berlin, Germany, 1998. [Google Scholar]
- Caluset, A.; Shalizi, C.; Newman, M. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Porter, M. Small-world network. Scholarpedia 2012, 7, 1739. [Google Scholar] [CrossRef]
- Boccaleti, S.; Latora, V.; Moreno, Y.; Hwang, D. Complex networks: structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- De Domenico, M.; Granell, C.; Porter, M.; Arenas, A. The physics of spreading processes in multilayer networks. Nat. Phys. 2016, 12, 901–906. [Google Scholar] [CrossRef]
- De Domenico, M.; Solè-Ribalta, A.; Cozzo, E.; Kivelä, M.; Moreno, Y.; Porter, M.; Gómez, S.; Arenas, A. Mathematical formulation of multilayer networks. Phys. Rev. 2013, 3, 041022. [Google Scholar] [CrossRef]
- Kivela, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.; Moreno, Y.; Porter, M. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Cellai, D.; Bianconi, G. Multiplex networks with heterogeneous activities of the nodes. Phys. Rev. 2016, 93, 032302. [Google Scholar] [CrossRef]
- De Domenico, M.; Solè-Ribalta, A.; Gómez, S.; Arenas, A. Navigability of interconnected networks under random failures. Proc. Natl. Acad. Sci. USA 2014, 111, 8351–8356. [Google Scholar] [CrossRef]
- Padgett, J.; Ansell, C. Robust Action and the Rise of the Medici. Am. J. Sociol. 2016, 98, 1259–1319. [Google Scholar] [CrossRef]
- Cardillo, A.; Gómez-Gardeñes, A.; Zanin, M.; Romance, M.; Papo, D.; del Pozo, F.; Boccaletti, S. Emergence of network features from multiplexity. SIAM Rev. 2013, 3, 1–122. [Google Scholar] [CrossRef] [PubMed]
- De Domenico, M.; Lancichinetti, A.; Arenas, A.; Rosvall, M. Identifying modular flows on multilayer networks reveals highly overlapping organization in interconnected systems. Phys. Rev. X 2015, 5, 011027. [Google Scholar] [CrossRef]
- Battiston, S.; Caldarelli, G.; May, R.; Roukny, T.; Stiglitz, J. The price of complexity in financial networks. Proc. Natl. Acad. Sci. USA 2016, 113, 10031–10036. [Google Scholar] [CrossRef] [PubMed]
- Bentley, B.; Branicky, R.; Barnes, C.; Chew, Y.; Yemini, E.; Bullmore, E.; Vértes, P. The Multilayer Connectome of Caenorhabditis elegans. PLOS Comput. Biol. 2016, 12, e1005283. [Google Scholar] [CrossRef]
- Sola, L.; Romance, M.; Criado, R.; Flores, J.; Garcia del Amo, A.; Boccaletti, S. Eigenvector centrality of nodes in multiplex networks. Chaos 2013, 23, 033131. [Google Scholar] [CrossRef]
- Iacovacci, J.; Rahmede, C.; Arenas, A.; Bianconi, G. Functional Multiplex PageRank. arXiv, 2016; arXiv:1608.06328v2. [Google Scholar] [CrossRef]
- Bonacich, P. Power and centrality: A family of measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Bonacich, P. Simultaneous group and individual centrality. Soc. Netw. 1991, 13, 155–168. [Google Scholar] [CrossRef]
- Meiss, M.; Menczer, F.; Fortunato, S.; Flammini, A.; Vespignani, A. Ranking web sites with real user traffic. In Proceedings of the 2008 International Conference on Web Search and Data Mining (WSDM ’08), Palo Alto, CA, USA, 11–12 February 2008; pp. 65–76. [Google Scholar]
- Ghoshal, G.; Barabàsi, A.L. Ranking stability and super-stable nodes in complex networks. Nat. Commun. 2011, 2, 394. [Google Scholar] [CrossRef]
- Cristelli, M.; Gabrielli, A.; Tacchella, A.; Caldarelli, G.; Pietronero, L. Measuring the intangibles: A metrics for the economic complexity of countries and products. PLoS ONE 2013, 8, e70726. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Porta, S. Centrality measures in spatial networks of urban streets. Phys. Rev. E 2006, 73, 036125. [Google Scholar] [CrossRef] [PubMed]
- Agryzkov, T.; Oliver, J.; Tortosa, L.; Vicent, J. An algorithm for ranking the nodes of an urban network based on the concept of PageRank vector. Appl. Math. Comput. 2012, 219, 2186–2193. [Google Scholar] [CrossRef]
- Berkhin, P. A survey on PageRank computing. Internet Math. 2005, 2, 73–120. [Google Scholar] [CrossRef]
- Bianconi, G. Multilayer Networks. Structure and Functions; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Halu, A.; Mondragón, R.; Panzarasa, P.; Bianconi, G. Multiplex PageRank. PLoS ONE 2013, 8, e78293. [Google Scholar] [CrossRef] [PubMed]
- Solé-Ribalta, A.; De Domenico, M.; Gómez, S.; Arenas, A. Centrality Rankings in Multiplex Networks. In Proceedings of the 2014 ACM Conference on Web Science, Bloomington, IN, USA, 23–26 June 2014; ACM: New York, NY, USA, 2014; pp. 149–155. [Google Scholar] [CrossRef]
- Bobadilla, J.; Ortega, F.; Hernando, A.; Gutiérrez, A. Recommender systems survey. Knowl.-Based Syst. 2013, 46, 109–132. [Google Scholar] [CrossRef]
- Stai, E.; Kafetzoglou, S.; Tsiropoulou, E.E.; Papavassiliou, S. A Holistic Approach for Personalization, Relevance Feedback and Recommendation in Enriched Multimedia Content. Multimedia Tools Appl. 2018, 77, 283–326. [Google Scholar] [CrossRef]
- Rabieekenari, L.; Sayrafian, K.; Baras, J. Autonomous relocation strategies for cells on wheels in environments with prohibited areas. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Tsiropoulou, E.; Koukas, K.; Papavassiliou, S. A Socio-physical and Mobility-Aware Coalition Formation Mechanism in Public Safety Networks. EAI Endorsed Trans. Future Internet 2018, 4. [Google Scholar] [CrossRef]
- Pedroche, F.; Romance, M.; Criado, R. A biplex approach to PageRank centrality: From classic to multiplex networks. Chaos 2016, 26, 065301. [Google Scholar] [CrossRef]
- Agryzkov, T.; Tortosa, L.; Vicent, J.; Wilson, R. A centrality measure for urban networks based on the eigenvector centrality concept. Environ. Plan. B 2017, 291, 14–29. [Google Scholar] [CrossRef]
- Page, L.; Brin, S.; Motwani, R.; Winogrand, T. The Pagerank Citation Ranking: Bringing Order to the Web; Technical Report 1999-66; Stanford InfoLab: Stanford, CA, USA, 1999; Volume 66. [Google Scholar]
- Pedroche, F. Métodos de cálculo del vector PageRank. Bol. Soc. Esp. Mat. Apl. 2007, 39, 7–30. [Google Scholar]
- Agryzkov, T.; Pedroche, F.; Tortosa, L.; Vicent, J. Combining the Two-Layers PageRank Approach with the APA Centrality in Networks with Data. Int. J. Geo-Inform. 2018, 7. [Google Scholar] [CrossRef]
- Datta, B. Numerical Linear Algebra and Applications; Brooks/Cole Publishing Company: Pacific Grove, CA, USA, 1995. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).