Analysis of Open Source Operating System Evolution: A Perspective from Package Dependency Network Motif

Abstract

Complexity of open source operating systems constantly increase on account of their widespread application. It is increasingly difficult to understand the collaboration between components in the system. Extant research of open source operating system evolution is mainly achieved by Lehman’s law, which is conducted by analyzing characteristics such as line of the source code. Networks, which are utilized to demonstrate relationships among entities, is an adequate model for exploring cooperation of units that form a software system. Software network has become a research hotspot in the field of software engineering, leading to a new viewpoint for us to estimate evolution of open source operating systems. Motif, a connected subgraph that occurs frequently in a network, is extensively used in other scientific research such as bioscience to detect evolutionary rules. Thus, this paper constructs software package dependency network of open source software operating systems and investigates their evolutionary discipline from the perspective of the motif. Results of our experiments, which took Ubuntu Kylin as a study example, indicate a stable evolution of motif change as well as discovering structural defect in that system.

1. Introduction

The scale and complexity of open source operating systems are growing at an alarming rate with the rising complexity of application environments and demands of society. Moreover, that growth will continue as the system improves. The open source code characteristic of open source operating system determines that it has obvious dynamics and rapid development. Bug correction and addition of new functions make the operating system software iterate continuously, which results in continued and fast rise and change in its version number. Huge scale of operating system software, accompanied by the continuous upgrading of software system complexity, will also complicate software system elements’ interactions, cognition as well as the problems described by software. The combination of various factors has increased the complexity of open source operating system software beyond developers’ understanding, making them more difficult to comprehend and maintain.

Emergence of complex network theory has caught the attention of researchers in different fields. Using a network model to describe and characterize large-scale real systems is helpful to analyze the structural properties, dynamic behavior and evolutionary mechanism of the system. The structure of many biological systems, such as protein-interacting networks and metabolic networks, and engineering artifacts of human society such as the Internet and World Wide Web exhibit common statistical characteristics of “small world” and “scale-free”. Open source operating systems are comprised of elements of different granularity that interact with each other in various ways. They can be viewed from the perspective of a network, and the many reusable elements in the system can be regarded as nodes. The relationships between these nodes constitute a complex network of dependencies [1,2].

Current evolution of open source operating system is mainly analyzed by Lehman’s law [3]. Specifically, analysis of evolution of open source operating system is conducted by evaluating eight aspects of their source code including continuing change, increasing complexity, self-regulation, conservation of organizational stability, conservation of familiarity, continuing growth, declining quality and feedback system. At present, less attention has been given to the structural characteristics of open source operating system. However, structural analysis is of great significance in studying the principles of software evolution, system maintenance and reconstruction. Lacking explicit and direct support for structural changes, software systems can become complex and difficult to understand, leading to problems such as poor understandability and predictability in adapting to changing requirements. The emerging interdisciplinary study of network science and software engineering represented by complex network research provides a new research idea to study the evolution law of open source operating system structure from the perspective of network topology. Evolution rules of the software system in the process of version iteration can be observed according to the quality of the new version of the software caused by unique structural characteristics. According to information recording form the process of software evolution, software engineers may obtain a better understanding of software evolution, thus reducing unnecessary time and cost of manpower and material resources consumption as well as laying a foundation for better control and prediction of future software changes [4].

Researchers have conducted extensive empirical studies on the topological properties of a large number of real networks in different fields. Various network topology models are proposed from different aspects. Network topology is characterized by the average path length, clustering coefficient and degree distribution. However, traditional definitions such as clustering coefficient and vertex degree do not take into account structural characteristics of motifs in the network, which leads to a deficiency in the study of network topology and evolution rules.

A motif is a connected subgraph with a stable structure in a complex network, which is usually comprised of three or four nodes, among which there are stable cooperation and dependence relations. As the basic building block of a complex network, a motif is mainly utilized to analyze and study structural characteristics and formation mechanism of complex systems from the internal structure hierarchy. Thus, it is suitable for estimating structural features and evolution rules of complex systems. Since the theory was put forward, it has attracted wide attention in many fields of scientific research and has made remarkable achievements. In recent years, motif has been extensively used in research and development of life sciences, such as protein network, gene transcription network, neuron network, brain network and so on. The same applies to areas of social science research, such as networking, scientist collaboration networks, as well as engineering science research, such as the AS-level topology of the Internet [1,5,6,7].

The concept of motif was first proposed by [8]. The authors analyzed several kinds of real-world networks and found that networks with similar functions have the exact same motifs. Later, they brought up a concept to measure the importance of motif: Z-score [9]. All of [1,6]’s work have pointed out the significance of motif in the evolution of network topology. Reference [10] studied motif structure of the world trade network and described the structural characteristics of 13 three-node motifs and their importance in the network. Xu et al. put foreword a motif-preserving network representation learning algorithm, seeking to take account of network motif structure features when representing a network node vector in machine learning technology [2,3,6,7,8,10,11,12,13].

Frequent occurrence of network motif may indicate the patterns fostered by the growth and evolution of complex networks. To wit, it may be the evolutionary trend of networks. Hence, motif theory is of great significance in researching the formation mechanism of networks. Once there is a set of motifs in the software network, their incessant appearance may be an embodiment of commonly used modules in the software, reflecting a potential schema of cooperation and reuse of the software elements. However, at present, in the field of software engineering, there is little research on the software network motif, especially the open source operating system software package network motif, and it has not yet been applied in the process of version evolution analysis. Therefore, this paper investigates open source operating system evolution from the perspective of the package dependency network motif for the sake of discovering potential cooperation and reusing schema in software development [4,9,14,15,16,17,18,19,20]. Specifically, this manuscript makes three main contributions:

• It establishes software package dependency network for open-source operating system, which regarding packages as nodes and dependency relationships as edges among nodes.
• On account of software package dependency network, this paper employs Rand_ESU algorithm to detect motif structures.
• This paper takes Ubuntu Kylin Linux as a research object and explores motif evolution of the system.

The rest of this manuscript are organized as follows. Section 2 describes the establishment of an open source operating system package dependency network. Section 3 gives a detailed description of network motif and its detection algorithm. Section 4 presents experimental results of motif structures through the evolution of Ubuntu Kylin Linux as well as analyzing the internal rules. Finally, conclusions are provided in Section 5.

2. Package Dependency Network

2.1. Open Source Operating System Package

Current mainstream open source operating system organizes installable software units as software packages when releasing their distribution version. Releasers also provide corresponding software package management and distribution systems to manage numerous interdependent software packages, assisting users to obtain, install, delete or update their requisite software packages. A package, which is compressed binary archives, contains all the required data to describe its attributes and requirements referring to the environment in which they will be deployed in order to maintain a correct function. Namely, it includes program, data and associated configuration files of the published software, along with metadata describing the name, version and dependencies of that software package. Metadata accomplishes the following functions:

• They are used to create user accounts on a system.
• They help to set ownership and permissions of related files after installation of the system.
• They provide creation or modification of configuration files that are not actually contained in the .Rpm or .Deb file, which are two fundamental patterns of released software packages.
• They assist running shell commands as root, which has a super power of the system.
• They specify dependency of the current package.

2.2. Software Package Dependency Network

Open source operating systems contain divers’ typical data types, such as classes, functions, and software packages. Interaction of these internal structural units is a reflection of the dependency relationship. Structural units that complete basic tasks are constantly reused and they need to cooperate with each other to complete their own tasks as well as the functions of the whole software system. The purpose of software design and development is to establish an optimal or better dependency structure. Therefore, this paper constructs the open source operating system as a network model, taking software packages as the smallest structural unit for research, abstracting software packages as nodes, and dependencies between software packages as edges.

This paper defines an open source software package dependency network as G = (V, E), which is an unweighed directed graph. Concretely, V is a set of vertices; each vertex depicts a software package. E, edges set, denotes a collection of dependent relationship among software packages. An edge combines two dependent packages together. When there is a dependent relationship between v${}_i$ and v${}_j$, such as v${}_j$ depends on v${}_i$, there is an edge pointing from v${}_i$ to v${}_j$. In the physical sense, package represented by v${}_j$ is derived from package shown by v${}_i$. Edges in an open source software package dependency network are directed. Furthermore, the path between vertices in the network is fixed. That is to say, by removing of some edges, the relationships illustrated by those edges in the system become nonexistent, which may lead to failure of compilation and running.

The following Algorithm 1 is used by this paper to extract open source software package dependency network.

Algorithm 1 Framework of extracting package dependency network.

1:  for $i=1$ to n do

2:   initialize all vertices, vi ← package names

3:  end for

4:  for $i=1$ to n do

5:   for $j=1$ to $i-1$, $i-1$ to n do

6:    scan the dependencies list of vi

7:    add an edge when dependency exit between vi and vj

8:   end for

9:  end for

10:  delete redundant edges

11:  store the graph as a table

12:  visualization

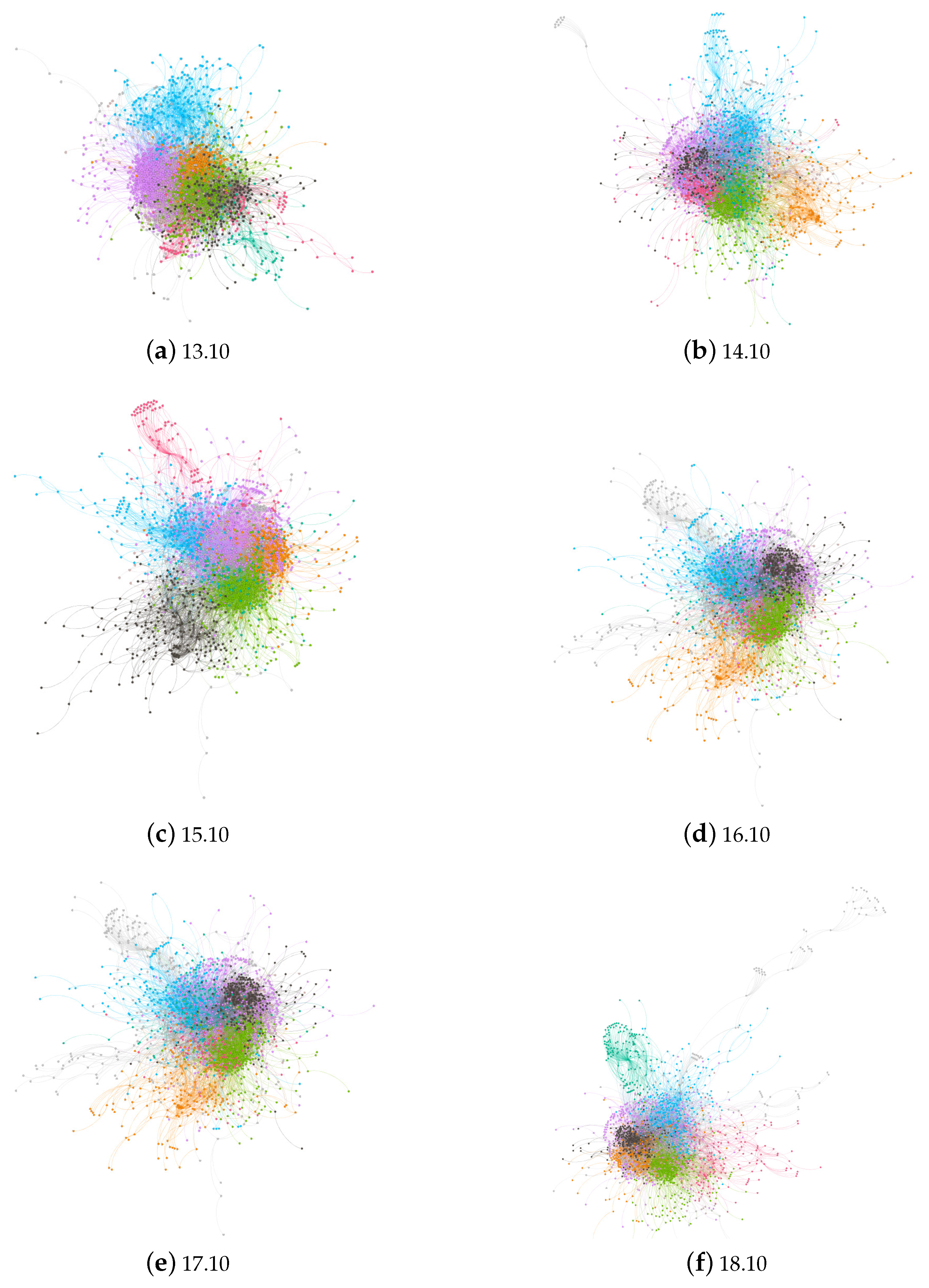
In this paper, six versions of Ubuntu Kylin operating system software dependency network are portrayed in our experiments. As a Chinese distribution of Ubuntu, distributor released their first distribution by 2013. From then on, six stable versions were produced. Thus, experiments of extracting package dependency network is conducted from official versions of 13–18. However, as time goes by, quantity and variety of installed software packages differ from one user to another on account of their own using habits. Therefore, all of our experiments are accomplished by using the original version of the system, videlicet, the original released version. Figure 1 summarizes holistic structures of six operating system software package dependency networks. Gpephi, which is an open-source tool, was utilized to realize visualization of all networks. All networks in Figure 1 are demonstrated in modularity and each color represents a unique module. Nodes inside a module are highly connected with each other while there are few connections among modules.

3. Network Motif and Its Detection

Although the structure of a complex network is complicated and changeable, the primary pattern and process of forming a network have certain rules. In recent years, researchers in the field of complexity science have analyzed many real systems and found that the emergence of multiple relationships in a network is not random. These structures form typical connection modes in a network, namely certain connections between structure units in a network repeatedly appear. Furthermore, these connection methods occur with disparate frequencies in different networks. That is to say, different categories of networks acquire distinct types of representative connection mode. In 2002, Reference [8] named this connected mode, which appears more often in real networks compared to in the random networks, as network motif. Network motif which can reveal the design principle of a complex network structure is considered as the fundamental building block of network.

3.1. Definition of Network Motif

The so-called network motif is a kind of repeated connected subgraph pattern in a network, and these subgraph patterns must satisfy the following conditions:

• The frequency of occurrence in the input network graph is significantly higher than that in a series of random network graphs generated from the input network and having the same degree sequence with it.
• The probability that the frequency of the subgraph in the random network corresponding to the input network is greater than the frequency of its occurrence in the input network is very small.
• The frequency of such connected subgraphs in the input network is not less than a certain lower limit value. Here, subgraphs of the same type refer to all isomorphic subgraphs.

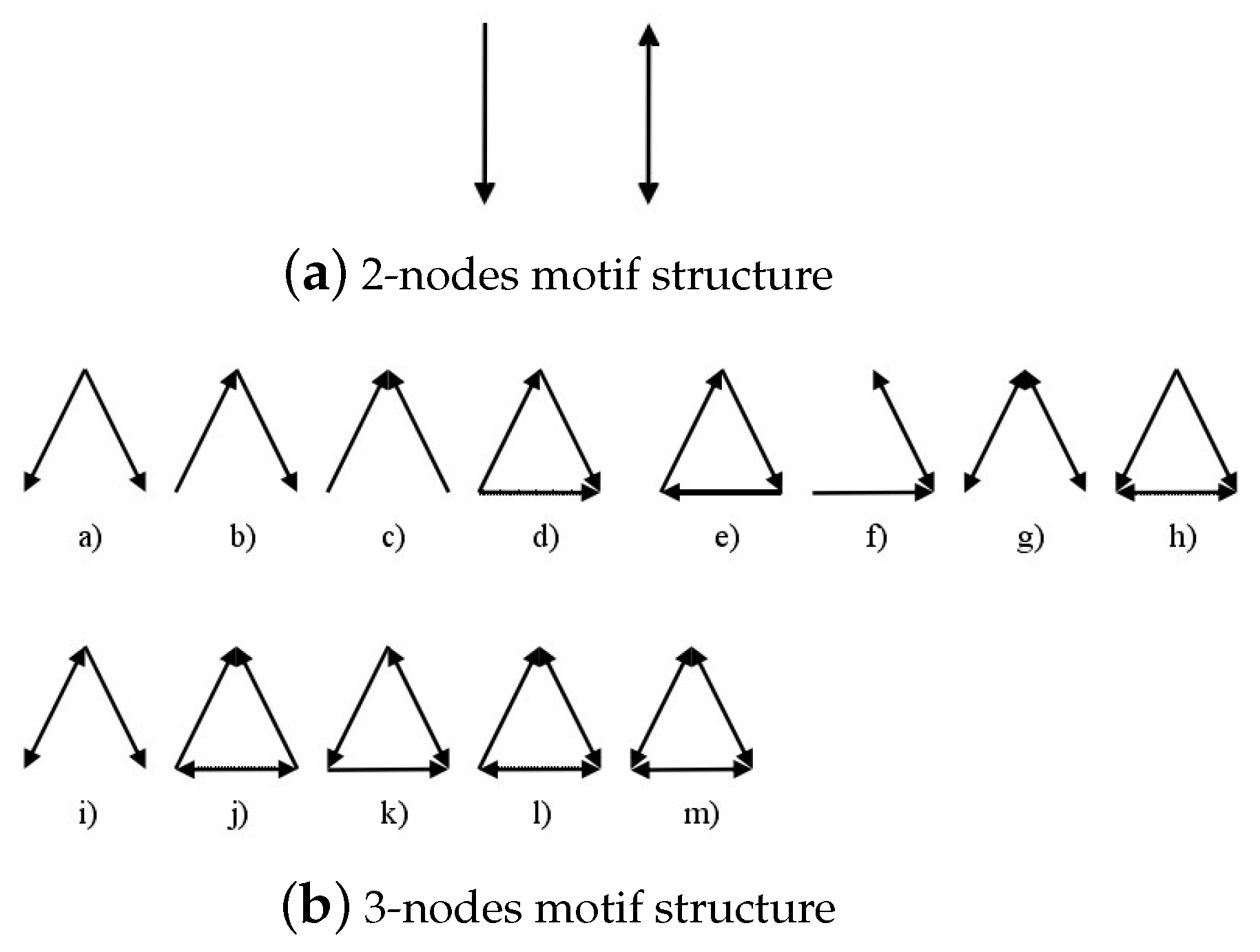
A connected graph is a graph in which nodes can reach each other. Theoretically, there are at most two kinds of relations between two nodes in a directed network, while three nodes can form 13 different connections. The connected subgraph of two nodes and three nodes are shown in Figure 2.

3.2. Detection Algorithm of Network Motif

Detection of a motif in a network includes two parts: the first one is statistic of subgraph in a random network, which is generated with the same scale and connection methods of the input network. The second part is the processing of graph isomorphism. General procedure to detect a motif is as follows:

• Label the nodes in the input network and generate a random network set.
• Search the labeled graph by traversal subgraph, and sample the subgraph according to a certain sampling method.
• Make isomorphic judgment and classification on the sampled subgraph. Record the frequency of the corresponding subgraphs and obtain the set of subgraphs.
• According to the frequency of each kind of subgraph, the appropriate significant judgement indicator is calculated to determine whether it is a motif.

3.2.1. Significant Judgment Method

According to previous description about motif and its detection, it is known that a motif is a series of connected subgraph in a real network that satisfies certain conditions, which are significant judgment indicators. A significant judgment method of motifs is a statistical method. Frequency of all kinds of possible subgraphs in the input network as well as a random network is counted to calculate a reasonable index value, and then make a corresponding judgment according to the index value. Z-score [9], P-value [9] and frequency of a motif [9] are three indicators utilized to determine a motif.

For a given subgraph V with n nodes, when regarding its frequency of occurrence in the actual network as n(V), the total time of occurrence of all subgraphs with n nodes as N, the frequency of occurrence of subgraph V is:

$$f\left(V\right)=\frac{n\left(V\right)}{N}$$

(1)

Once the subgraph is a motif of a network, its frequency is identified as frequency of a motif.

Significance level, which is represented by Z-score, refers to the quantitative extent to which the frequency of subgraphs in the real network is higher than that of a group of random networks. It is a necessary indicator to determine whether a subgraph is a motif. Z-score can be acquired through following equation.

$$\mathit{\text{Z-score}}=\frac{N_{real}-\langle N_{rand}\rangle }{std\left(\langle N_{rand}\rangle \right)}$$

(2)

$$\langle N_{rand}\rangle =\frac{{\sum }_{i=1}^n{N}_{i-rand}}{n}$$

(3)

$$std\left(\langle N_{rand}\rangle \right)=\sqrt{{\displaystyle \sum _{i=1}^n}\frac{{(N_{i-rand}-\langle N_{rand}\rangle )}^2}{n-1}}$$

(4)

where N${}_{real}$ represents the number of time the subgraph appears in the real network; N${}_{i-rand}$ is the time of the subgraph appearing in the ith randomized network; 〈N${}_{rand}$〉 demonstrates the average occurrence of a subgraph in n random networks; and std($\langle N_{rand}\rangle$) is the standard variance of a subgraph occurrence in n random networks.

P-value represents the probability that a subgraph is not significant. When the probability of a subgraph appearing in a real network smaller than that in a random network is less than a threshold. In this condition, this subgraph meets the judging criteria. Definition of P-value is as follows:

$$\mathit{\text{P-value}}=\frac{{\sum }_{i=1}^n{P}_i}{n}$$

(5)

If the number of occurrence of subgraphs in the ith random network is greater than or equal to that of the actual network, then P${}_i$ equals to 1, otherwise it will be set to 0.

In summary, a candidate subgraph cam be identified as a motif when it satisfies following conditions:

• P-value ≤ P
• Z-score ≥ D
• f(V) > U

P, D and U illustrate three threshold values, accordingly. The exact value used by [8], respectively, were $0.01$, 2, and 4. The number of random networks they selected was 1000.

3.2.2. Detection Algorithm

Two classical approaches are utilized to discover network motif, ESA [16] and Rand_ESU [16], which are on the basis of edge sampling and vertex sampling, respectively. As Rand_ESU makes up ESA’s defect of sampling bias, the probability of each subgraph node being accessed is the same. Hence, this paper employs Rand_ESU algorithm to explore software package dependency network’s motif. Detailed steps of this algorithm are described at Algorithms 2 and 3.

Algorithm 2 Framework of Enumerate Subgraphs: Rand_ESU.

Input: A Graph $G=(V,E)$ and an integer $1\le k\le \left|V\right|$

Output: All size-k subgraph in G

1:  for each vertex $v\in V$ do

2:   $V_{Extension}\leftarrow \{u\in N\left(\left\{v\right\}\right):u>v\}$

3:   with probability $p_d$ call ExtendSubgraphs($\left\{v\right\},V_{Extension},v$)

4:  end for

5:  return

Algorithm 3 Framework of Extend Subgraphs: ExtendSubgraphs.

Input: A Graph $G=(V,E)$ and an integer $1\le k\le \left|V\right|$

Output:  Size-k subgraph in G

1:  if $|V_{Subgrpah}|=k$ then

2:   output $G\left[V_{Subgrpah}\right]$

3:  end if

4:  while $V_{Extension}\ne NULL$ do

5:   remove and arbitrarily choose vertex $\omega$ from $V_{Extension}$

6:   $V_{Extension}^{\prime }\leftarrow V_{Extension}\bigcup \{u\in N_{gxcl}(\omega ,V_{Subgrpah}):u>v\}$

7:   with probability $p_d$ call ExtendSubgraphs($V_{Subgrpah}\bigcup \left\{\omega \right\},V_{Extension}^{\prime },v$)

8:  end while

9:  return

4. Results

For software reuse, developers often use the same design patterns, software artifacts, and subsystems that describe relationships between three or four objects to construct software systems with different functions. Therefore, we can study the local and global structural characteristics of a software system as well as the growth and evolution rules of the software system by investigating motifs with three or four nodes in a software network. In this paper, Rand_ESU algorithm is selected to perform motif detection of above six package dependency network of Ubuntu Kylin obtained in the previous section. This algorithm is quick and has the ability to detect more types of motifs. It is appropriate for detecting motifs of networks with diverse sizes. It was found that, despite the unique value of significant indicators, all six versions of Ubuntu Kylin operating system share the same motif structure. Figure 3 presents motif structures of all the dependency networks.

Table 1. Motif of version 13.10 software package dependency network.

ID	Frequency	Average Frequency	Standard Deviation	Z-Score	p-Value
6	92.815%	92.344%	0.00023674	19.86	0
38	1.2974%	0.76752%	0.00028327	18.705	0
46	0.017378%	0.00043124%	6.66 × 10−6	25.445	0
166	0.0045094%	0.0018502%	3.2985 × 10−6	8.0619	0

,

Table 2. Motif of version 14.10 software package dependency network.

ID	Frequency	Average Frequency	Standard Deviation	Z-Score	p-Value
6	94.142%	93.705%	0.00021961	19.902	0
38	1.1316%	0.65306%	0.00025559	18.723	0
46	0.01449%	0.0003343%	5.8019 × 10−6	24.397	0
166	0.0022178%	0.0011312%	2.0729 × 10−6	5.242	0

,

Table 3. Motif of version 15.10 software package dependency network.

ID	Frequency	Average Frequency	Standard Deviation	Z-Score	p-Value
6	93.846%	93.384%	0.00021671	21.36	0
38	1.1809%	0.66908%	0.00025403	20.149	0
46	0.014658%	0.00011946%	1.4697 × 10−6	98.921	0
166	0.0028834%	0.0011805%	2.1485 × 10−6	7.9264	0

,

Table 4. Motif of version 16.10 software package dependency network.

ID	Frequency	Average Frequency	Standard Deviation	Z-Score	p-Value
6	93.729%	93.259%	0.00015969	29.414	0
38	1.0851%	0.5749%	0.00018688	27.299	0
46	0.019033%	0.00017485%	1.9217 × 10−6	98.132	0
166	0.0022191%	0.00084671%	1.9515 × 10−6	7.0327	0

,

Table 5. Motif of version 17.10 software package dependency network.

ID	Frequency	Average Frequency	Standard Deviation	Z-Score	p-Value
6	93.911%	93.466%	0.000169969	26.2	0
38	1.0488%	0.56156%	0.00017915	27.198	0
46	0.018577%	0.0033692%	6.1828 × 10−5	2.4597	0
166	0.0019555%	0.00073805%	1.5201 × 10−6	8.0085	0

and

Table 6. Motif of version 18.10 software package dependency network.

ID	Frequency	Average Frequency	Standard Deviation	Z-Score	p-Value
6	93.271%	92.815%	0.00015638	29.166	0
38	1.0802%	0.57927%	0.00018556	26.995	0
46	0.018186%	3.8517 × 10−5%	7.6252 × 10−7	237.99	0
166	0.0024383%	0.0009276%	2.1076 × 10−6	7.16709	0

give the detailed information about their value of three significant judgment indicators.

As can be observed in the above six tables, motifs in the software package dependency networks of Ubuntu Kylin operating system have been relatively stable during version evolution process. Each version has four network motifs of the same type. Except version 17.10, four motifs of other versions seem to be of similar importance. It can be discovered from these motifs that the internal connection of the module also presents the phenomenon of preferred choice. Stable evolution of motifs demonstrates a robustness and stability of Ubuntu Kylin operating system evolution. However, through the estimation of motif mining, it is revealed that connected subgraphs with ring topology exist with a relatively higher proportion of 50%. Even the Z-score of these motifs in some versions are very high. It can be seen from the above description that the larger Z-score is, the more important the motif is in the network. Since ring structure in a network predicts a lower stability of the network, for the sake of improving system complexity and readability, loops should be prevented. Thus, developers must pay attention to the software packages that generate loops in the distribution. 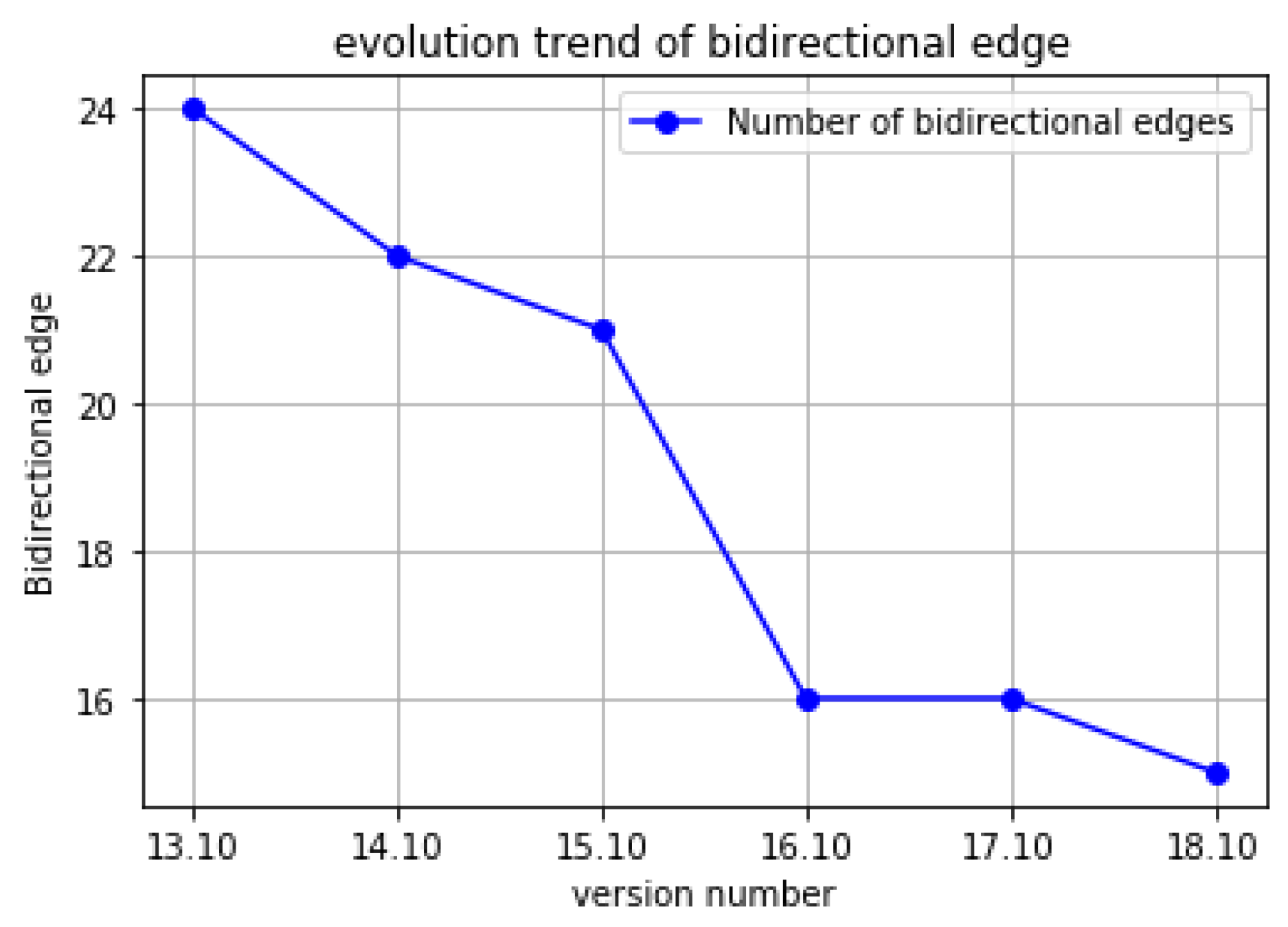Figure 4 depicts the number of bidirectional edges in the evolution of Ubuntu Kylin operating system.

It can be seen from the above figure that the bidirectional edges of the ring structure tend to decrease in the process of version evolution. However, there are still 15 pairs of edges that go both ways. Therefore, system developers must further decompose the dependencies of these software packages, which are unstable factors in the software structure.

Table 7. Packages that are interdependent with each other.

ID	Source Package	Target Package
1	gconf-service	gconf-service-backed
2	grub-pc	grub-gfxpayload-lists
3	libc6	libgcc1
4	perl-module	perl
5	python3-update-manager	python3-distupgrade

lists part of packages that interdependent with each other.

5. Conclusions

The traditional software structure measurement method has difficulty describing and measuring the change of the whole structure of a large software system. This paper describes the software architecture of open source operating system based on network architecture and explores its motif architecture. The stability of motif reflects the microstructure stability of the entire structure of the software system. Studying the stability of motif is helpful to understand the stability of the software network and its influencing factors. It provides strong support for testing the defects of structural design and ensuring the reliability of the system. Through experiments, the authors discovered that the software package dependency network motif of open source operating system is relatively stable in the process of version evolution. However, connected subgraphs with ring topology appear in higher proportion in the motif structure. System developers must further decompose the dependencies of these software packages to eliminate instability in the software structure.