Reliability Enhancement of Edge Computing Paradigm Using Agreement

Abstract

Driven by the vision of the Internet of Things (IoT), there has been a dramatic shift in mobile computing in recent years from centralized mobile cloud computing (MCC) to mobile edge computing (MEC). The main features of MECs are to promote mobile computing, network control, and storage to the edge of the network in order to achieve computationally intensive and latency-critical applications on resource-constrained mobile devices. Therefore, MEC is proposed to enable computing directly at the edge of the network, which can deliver new applications and services, especially for the IoT. In order to provide a highly flexible and reliable platform for the IoT, a MEC-based IoT platform (MIoT) is proposed in this study. Through the MIoT, the information asymmetrical symmetry between the consumer and producer can be reduced to a certain extent. Because of the IoT platform, fault tolerance is an important research topic. In order to deal with the impact of a faulty component, it is important to reach an agreement in the event of a failure before performing certain special tasks. For example, the initial time of all devices and the time stamp of all applications should be the same in a smart city before further processing. However, previous protocols for distributed computing were not sufficient for MIoT. Therefore, in this study, a new polynomial time and optimal algorithm is proposed to revisit the agreement problem. The algorithm makes all fault-free nodes decide on the same initial value with minimal rounds of message exchanges and tolerate the maximal number of allowable faulty components in the MIoT.

1. Introduction

The Internet of Things (IoT) paradigm is based on intelligent self-configuring nodes (things) that are interconnected in a dynamic and global network infrastructure. The IoT can provide many applications, including electronic commerce, smart home, smart city, and intelligent transportation system. The IoT has promoted interaction between people and smart cities, infrastructure, and services that improve the quality of life. It enables ubiquitous pervasive computing scenarios. The IoT typically features small, real-world things, limited storage and processing capabilities, and related issues related to reliability, performance, security, and privacy [1]. Since cloud computing (CC) has virtually unlimited capacity in terms of storage and processing power, most IoT issues are at least partially solved. Therefore, the IT paradigm that combines the two technologies of cloud and IoT can provide current and future Internet.

However, for various reasons, the CC paradigm cannot meet the low latency and jitter, environment awareness, and mobility support requirements that are important for several applications, such as vehicular networks and augmented reality [2]. In order to meet these requirements, various examples have emerged in recent years, such as MEC and MCC [3]. The common feature of these edge examples is the deployment of cloud-like capabilities at the edge of the network. The edge data center is owned and deployed by the infrastructure provider and implements a multi-tenant virtualization infrastructure. Any customer can use these data center services. In addition, although edge data centers can operate autonomously and cooperate with each other, they are not disconnected from the traditional cloud. It is thus possible to create a hierarchical multi-layered architecture interconnected by a network infrastructure.

MEC is a distributed paradigm that provides cloud-like services to the edge of the network. It uses cloud and edge resources and its own infrastructure. Essentially, the technology handles IoT data locally by utilizing a client or edge device in the vicinity of the user for extensive storage, communication, control, configuration, and management. This approach benefits from the proximity of edge devices to the sensors while exploiting the scalability of the demand for cloud resources [2].

Since the IoT greatly can provide encourages distributed system design and practices to support user-oriented service applications [4]. However, distributed systems have grown rapidly both in size and in number. In a distributed computing system, the nodes that are allocated to different locations or separate units are connected together so that they can be used together for greater advantages. In many cases, reaching a common agreement in the presence of faulty components is the central issue of fault-tolerant distributed computing, because many applications require such agreement [5,6]. For instance, the initial time and the time stamps of many applications and smart devices in the smart city system should be the same, including traffic light control components in the traffic automatic control system, switches and brightness adjusters in the street light management system, computers for intelligent self-driving vehicles, detection components of fire-disaster relief vehicles, etc. In addition, many applications of IoT provide convenience. However, for users, the system must provide better reliability [4]. Therefore, reliability is one of the most important aspects of the IoT. To ensure that an IoT environment is reliable, a mechanism to allow a set of nodes to reach an agreed value is necessary.

In order to provide a highly flexible and reliable platform of IoT, a MEC-based IoT platform (MIoT) is proposed in this study. In the MIoT, numerous nodes are interconnected. For achieving agreement on the same value in the MIoT, even if certain components fail, protocols are required so that systems can operate correctly. However, so far, no relevant research has tackled the agreement issue in the IoT platform based on cloud computing and MEC. Therefore, this is the first time that an algorithm has been proposed to make all fault-free nodes reach agreement underlying MIoT. In this study, the agreement problem is revisited with the assumption of node failure due to malicious faults in MIoT. The proposed algorithm, MEC-based Agreement Algorithm (MECAA) of MIoT, makes all fault-free nodes communicate with each other and collect the exchanged messages to decide an agreement value. Based on the agreement value, the algorithm makes all fault-free nodes reach agreement without the influence of malicious faulty nodes. Finally, we proved theoretically that the proposed algorithm can tolerate the maximum number of faulty components and using only the minimal rounds of message exchanges.

The rest of this paper is organized as follows. Section 2 will serve to introduce the proposed MIoT platform and the basic concepts of the agreement problem. Then, the proposed MECAA of MIoT will be brought up and illustrated in detail in Section 3. For simulation, a pseudo-code is also provided here. Section 4 gives an example of executing the proposed protocol. Section 5 is responsible proves the complexity of our new algorithm. Finally, Section 6 gives the conclusions of this research.

2. Related Works

Before the agreement problem of MIoT can be solved, the proposed topology of MIoT needs to be defined firstly. Two basic concepts are introduced and discussed in advance: the agreement problems and the failure types of faulty components.

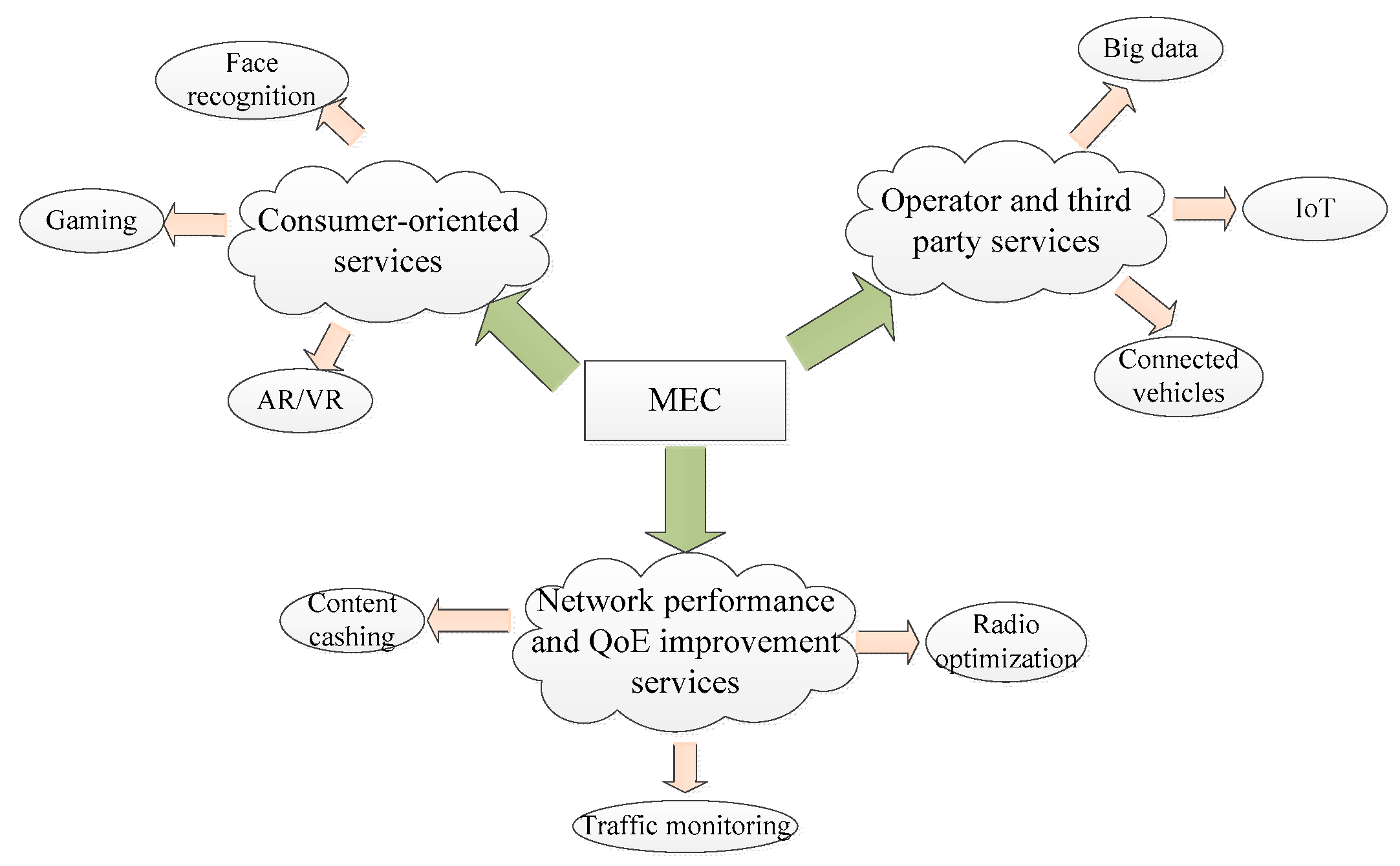
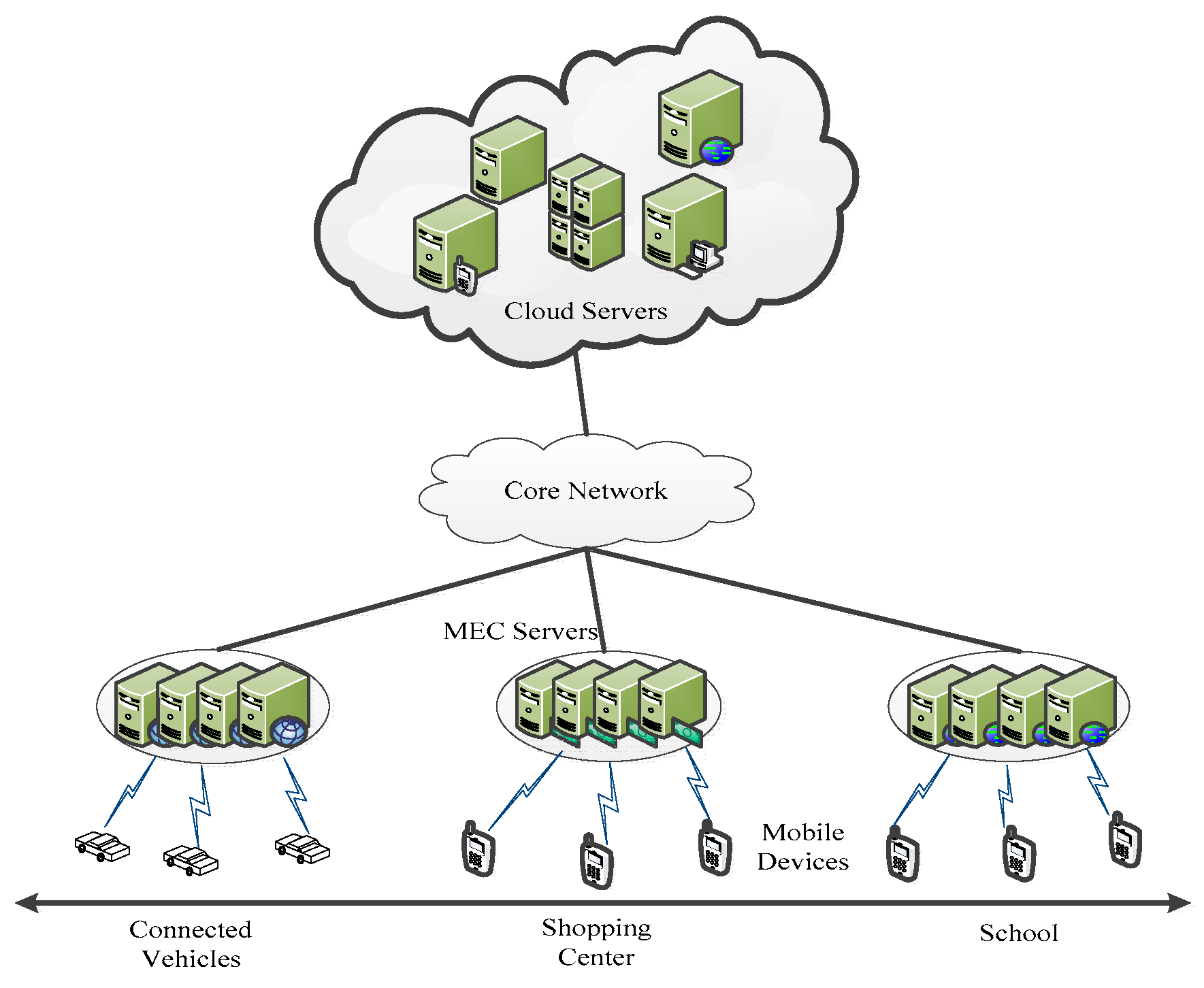
2.1. The Network Structure

The term MEC was first used in 2013 to describe the implementation of services at the network edge. At that time, IBM and Nokia Siemens Networks introduced a platform that could run applications on mobile base stations [7]. In recent years, user demand for data rates and quality of service (QoS) has grown exponentially. In addition, the development of mobile user devices such as smartphones or laptops and new mobile applications is rapidly advancing.

Moreover, high battery consumption still poses a significant obstacle, restricting the use of highly demanding applications [8]. This motivates development of the MCC concept, allowing CC for mobile users [9]. In MCC, user equipment (UE) can utilize powerful remote centralized CC and storage resources that are accessible through the mobile operator’s core network and the Internet. However, in terms of network topology, the MCC, because it is far away from the user, imposes a huge extra load on the radio and backhaul of the mobile network, and has a high latency due to the data being sent to a powerful server farm.

In order to solve the problem of long latency, the cloud services should be moved to the vicinity of the UEs, i.e., to the edge of the mobile network, such as edge computing [8]. Edge computing can be understood as a special case of MCC. However, in the conventional MCC, the cloud service is accessed through the Internet connection; in the case of edge computing, it is assumed that the computing/storage resources are near the UEs. Therefore, compared with MCC, MEC can provide significantly lower latencies and jitter. Moreover, while the MCC is a completely centralized approach, the farm of computers is usually placed in one or several locations, and edge computing should be deployed in a fully distributed manner. On the other hand, edge computing provides only limited computing and storage resources relative to MCC.

The MEC brings many benefits to all stakeholders such as mobile operators, service providers, and users. As described in [9], MEC can distinguish between three major categories of use cases, including consumer-oriented services, operator and third party services, and network performance and QoE (Quality of Experience) improvement services, depending on the subjects that can benefit from them. An example of the use cases and scenarios for the MEC is shown in Figure 1 [9].

A novel architecture of MEC is proposed by Roman et al. [3], as shown in Figure 2. There are three basic components to the architecture: (1) Edge devices include all types of mobile devices (UEs) connected to the Internet; (2) Edge cloud is the less resourceful cloud deployed in each of the mobile base station. Edge cloud is responsible for traditional network traffic control, including forwarding and filtering, as well as hosting a variety of mobile edge applications such as edge health care, smart tracking, and more; (3) Public cloud is the cloud infrastructure hosted in the Internet. The prime objectives of MEC are [3]:

(1)

Optimization of mobile resources by hosting compute intensive application at the edge network.

(2)

Optimization of the large data before sending to the cloud.

(3)

Enabling cloud services within the close proximity of mobile subscribers.

(4)

Providing context-aware services with the help of radio access network (RAN) information.

With the advancement and development of various information technologies, computing problems have become larger and more complex [4]. The CC environment allows users to access Internet applications more quickly. Most CC infrastructures include reliable services provided through data centers and are built on servers with different levels of virtualization technologies [10]. As long as users can access the network infrastructure, users can access these services. Commercial offerings must meet the quality of service requirements of customers, and typically offer service-level agreements [4]. Therefore, a distributed system must have high stability to handle instances where many users utilize a given environment. In this section, the proposed IoT platform is discussed.

In order to provide a highly flexible and reliable platform of IoT, a MEC-based IoT platform (MIoT) is proposed in this study. The topology of MIoT is shown in Figure 3. There are two layers in the MIoT: MEC-layer and CC-layer. The MEC-layer is constructed by a set of MEC clusters; each MEC cluster is composed of a large number of MEC servers (MEC nodes), responsible for the processing of specific information and judgments. The CC-layer is made up of many cloud nodes, which provide cloud users’ services. In the MIoT environment, through the combination of a large number of mobile devices (UEs), various types of data can be collected and a wide range of services can be provided.

In short, MIoT is proposed by the MEC, where data can be analyzed and processed by the MEC-layer instead of being centralized in the CC. By coordinating and managing the computing and storage resources at the edge of the network, more and more connected devices and the emerging needs of IoT can be processed by the MEC. When the technological requirements and constraints of the IoT applications are properly fulfilled, it is up to the platform designer to decide whether an endpoint should be served by the CC, the MEC, or an adequate combination of the two at any given time during the service lifetime. Based on the above characteristics, the MEC can serve as a suitable platform for providing key services and applications for the IoT, including connecting vehicles, smart cities, and shopping centers.

Recently, the Intelligent Transportation System (ITS) has become increasingly popular in many countries. When the traffic control system of ITS is constructed by MIoT, connecting vehicles are used to get the data required by the ITS [11]. The MEC-layer is used to capture the traffic status of each intersection. The CC-layer is used as a traffic control center. An example of the traffic control system constructed by MIoT is shown in Figure 4.

2.2. Agreement Problems

In an IoT environment, a mechanism to allow a given set of nodes to agree on a common value, such as the initial time and the time stamp, is necessary for a reliable smart city [12,13]. Such a unanimity problem is called an agreement problem [14]. It requires a number of independent nodes to reach agreement in cases where some of those nodes might be faulty. Namely, the goal of agreement is making the fault-free nodes reach a common value. There are three kinds of agreement issues, Byzantine agreement [6,15], consensus [16], and interaction consistency (IC) [17,18] (Wang et al., 2018). In our study, the consensus problem of the MEC-layer and the IC problem of the CC-layer in MIoT will be explored separately.

The consensus problem is defined by Meyer and Pradhan [16]. The solutions to the consensus problem are defined as protocols that achieve a consensus and use the minimum number of rounds of message exchanges to achieve the maximum number of allowable faulty nodes. In this study, the solution to the consensus problem involves the MEC-layer of MIoT. The idea is to make the fault-free MEC nodes in the MEC-layer of MIoT reach a consensus. Each MEC node of the MEC-layer chooses an initial value to start with, and they communicate with each other by exchanging messages. The MEC nodes are understood to have reached a consensus if the following conditions are satisfied [16]:

Consensus:	All fault-free MEC nodes agree on a common value.
Validity:	If the initial value of each fault-free MEC node ni is vi then all fault-free MEC nodes shall agree on the value vi.

A closely related sub-problem, the interactive consistency problem (IC problem) has been studied extensively [17,18] (Wang et al., 2018). In this study, the solution to the IC problem involves the CC-layer of MIoT. The idea of IC is to make the fault-free cloud nodes in the CC-layer reach interactive consistency. Each cloud node chooses an initial value and communicates with the others by exchanging messages. There is interactive consistency in that each cloud node i has its initial value v_i and agrees on a set of common values. Therefore, interactive consistency has been achieved if the following conditions are met [17,18]:

Consistency:	Each fault-free cloud node agrees on a set of common values V = [v1, v2, …, vn].
Validity:	If the initial value of fault-free cloud node i is vi, then the i-th value in the common vector V should be vi.

The IoT environment is an Internet-based development. It is a style of computing in which dynamically scalable and often virtualized resources are provided as a service over the Internet. Nevertheless, in an IoT environment, the connected topology is not very significant. In this study, the consensus problem is to be solved on the MEC-layer and the IC problem is to be solved on the CC-layer of the proposed MIoT platform. In addition, the proposed algorithm MECAA can use a minimum number of message exchanges and can tolerate a maximum number of allowable faulty components to make each fault-free node reach an agreement in cases of node failure. Due to agreement being a purely mathematical problem, the correctness of all previous research is proven by mathematical methods [14,15,16,17,18,19,20,21]. The proposed polynomial time algorithm is a static and exact algorithm; a mathematical proof is provided to illustrate the correctness and time complexity in this study. Theoretical analysis of algorithms for Byzantine Agreement can provide insight into their efficiency.

2.3. Failure Types

In a distributed system, the network components may not always work well. A node is said to be fault-free if it follows algorithm specifications during the execution of an algorithm; otherwise, the node is said to be faulty.

The symptoms of node failure can be classified into two categories. There are dormant faults and malicious faults [15]. Dormant faults of nodes include crashes and omissions. A crash fault occurs when the node is damaged. Omission faults occur when nodes cannot send or receive messages on time or at all. In the event of a malicious failure, the behavior of the faulty node is unpredictable and arbitrary. The message transmitted by the malicious faulty node is random or arbitrary. This is the most destructive type of failure and leads to the most serious problems. If the agreement problem can be resolved in the case of a malicious fault, then the agreement problem can also be resolved in other failure modes.

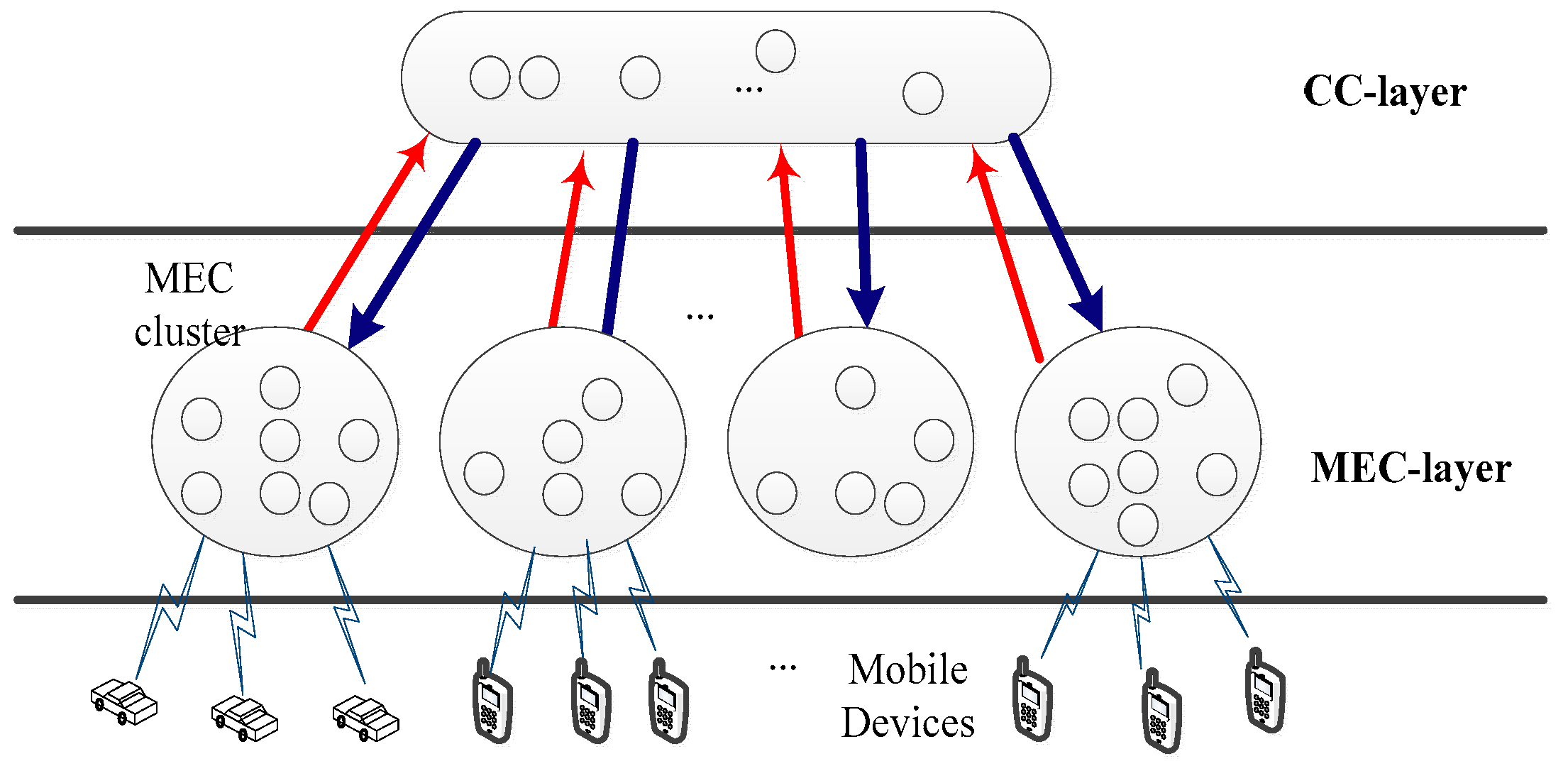
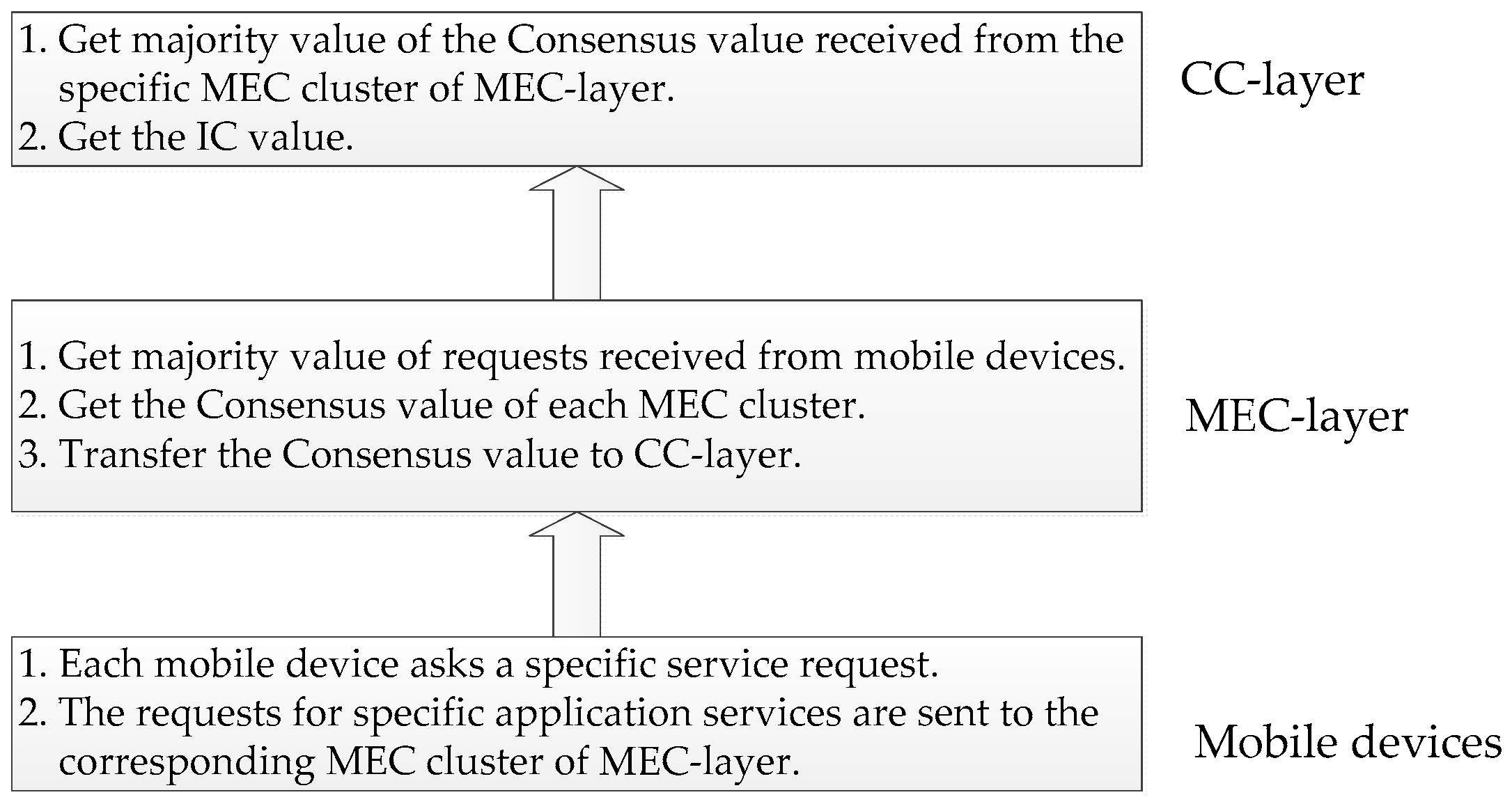
3. The Proposed Protocol

In this study, the agreement problem is discussed in the proposed MIoT platform; no delay of nodes or communication media is included in our discussion. Therefore, the nodes executing our new algorithm should receive messages from other nodes within a predictable period of time. If the message is not received on time, the message must have been influenced by faulty components.

In the agreement problem, the number of faulty components allowed is determined by the total number of nodes. In Lamport et al.’s algorithm [15], the constraint is n > 3f, where n is the number of nodes and f is the total number of allowable malicious faulty nodes in the distributed system.

In this research, MECAA is used to solve the agreement problem in MIoT with malicious fallible nodes. With consideration for efficient agreement, the UEs of MIoT is used to request the specific IoT application, the procedure Consensus is applied to the MEC nodes of the MEC-layer, and the procedure Interactive Consistency is applied to each cloud node in the CC-layer.

Therefore, the constraints of the MECAA are as follows.

• (Constraint of MEC-layer): n_Ej > ⌊(n_Ej − 1)/3⌋ + 2f_mEj where n_Ej is the number of MEC nodes and f_mEj is the total number of allowable malicious faulty MEC nodes in MEC cluster E_j of the MEC-layer. This constraint specifies the number of MEC nodes required in MEC cluster E_j.
• (Constraint of CC-layer): The (Constraint of CC-layer) is similar to the (Constraint of MEC-layer) in that n_C > ⌊(n_C − 1)/3⌋ + 2f_mC where n_C is the number of cloud nodes and f_mC is the total number of allowable malicious faulty cloud nodes in the CC-layer.

(Constraint of MEC-layer) specifies the number of MEC nodes in MEC cluster E_j of MEC-layer required; due to the unit of the MEC cluster E_j of MEC-layer is MEC node, so that an agreement can be achieved if n_Ej > ⌊(n_Ej − 1)/3⌋ + 2f_mEj. (Constraint of CC-layer) specifies the number of cloud nodes required in the CC-layer; due to the unit of the CC-layer being a cloud node, an agreement can be achieved if n_C > ⌊(n_C − 1)/3⌋ + 2f_mC.

In this study, MECAA is proposed to solve the agreement problem with fallible nodes underlying the MIoT platform. The proposed algorithm MECAA is divided into two parts based on the two layers of MIoT. The nodes of the MEC-layer execute procedure Consensus, and the nodes of the CC-layer execute procedure Interactive Consistency.

When UE makes a specific service request, the request for the specific application service is transferred to the corresponding MEC cluster of the MEC-layer. In procedure Consensus, the MEC node takes the majority value of the requests received from UEs firstly, and the majority value is used as the initial value (v_i) of MEC node to execute function Agreement. When the Consensus value of each MEC cluster is obtained, the value is represented as the result of a specific service. Finally, the Consensus value is transferred to the CC-layer. In procedure Interactive Consistency, the primary work of cloud nodes in the CC-layer is to collect the results of different specific services, and then the request vector of the interactive consistency can be obtained to provide an integrated service such as connecting vehicles, smart cities, and shopping centers. The progression steps of MECAA are shown in Figure 5.

MECAA is initiated by the UEs to ask for a specific application service. The nodes of MEC-layer need to execute procedure Consensus and the nodes of CC-layer need to execute procedure Interactive Consistency. In procedures Consensus and Interactive Consistency, the function Agreement will be called up. There are two steps of function Agreement, one is the Request Gathering Step, and the other is the Request Deciding Step. The parameters of Agreement include σ, v_s, and n_A, where σ is the required rounds, v_s is the initial value, and n_A is the number of nodes participating in the agreement. In order for all fault-free nodes to reach agreement, each node must collect enough exchanged messages from all other nodes if they are fault-free. As a result, exchanging the received values helps fault-free nodes to collect enough exchanged messages.

Fischer and Lynch proved that ⌊(n − 1)/3⌋ + 1 is the rounds of message exchanges sufficient to solve an agreement problem, where n is the number of nodes in the underlying network [17,18]. Based on the works of Fischer and Lynch, ⌊(n − 1)/3⌋ + 1 rounds of message exchanges are the lower bound for solving the agreement problem. Therefore, the required rounds σ is ⌊(n_Ej − 1)/3⌋ + 1 when MEC nodes execute the function Agreement of procedure Consensus, where n_Ej is the number of MEC nodes in MEC cluster E_j of MEC-layer and n_Ej > 3. Moreover, the required rounds σ is ⌊(n_C − 1)/3⌋ + 1 when cloud nodes execute the function Agreement of procedure Interactive Consistency, where n_C is the number of cloud nodes in the CC-layer and n_C > 3.

The received messages of Request Gathering Step are stored in a tree structure called the request-gathering tree (rg-tree), which is similar to that proposed by Bar-Noy et al. [19]. Each fault-free node maintains such an rg-tree during the execution of MECAA. In the first round of the Request Gathering Step, node i transmits its initial request to other nodes. However, that each receiver node can always identify the sender of a request is assumed. When a fault-free node receives the request sent from node i, it stores the received value, denoted as req(i), at the root of its rg-tree. In the second round, each node transmits the root value of its rg-tree to all other nodes. If node 1 sends request req(i) to node 2, then node 2 stores the received request, denoted as req(i1), in vertex i1 of its rg-tree. Similarly, if node 2 sends request req(i1) to node 1, the received request is named req(i12) and stored in vertex i12 of node 1’s rg-tree in the third round. Generally, request req(i12…n), stored in the vertex i12…n of a rg-tree, implies that the request just received was sent through the node i, the node 1,…, the node n; and the node n is the latest node to pass the request. When a request is transmitted through a node more than once, the name of the node will also be repeated. For instance, request req(11), stored in vertex 11, indicates that the request is sent to node 1, then to node 1 again; therefore, name 1 appears twice in vertex name 11. In summary, the root of rg-tree is always named i to denote that the stored request is sent from node i in the first round; the vertex of an rg-tree is labeled by a list of node names. The node name list contains the names of the nodes through which the stored request was transferred. Figure 6 shows an example of rg-tree.

In the Request Gathering Step of function Agreement, the vertices with repeated node names in each rg-tree will be deleted. Finally, all fault-free nodes use function VOTE to remove the faulty influence from faulty nodes to obtain the common value. When the function VOTE is applied to the root of each corresponding rg-tree, and then the common value VOTE(i) is obtained. The proposed algorithm MECAA is presented in

Table 1. The algorithm MECAA.

MEC Agreement Algorithm (MECAA)
Main
The requests for the application services are sent to the corresponding MEC cluster of MEC-layer by UEs. The MEC nodes of the MEC-layer execute procedure Consensus. The cloud nodes of the CC-layer execute procedure Interactive Consistency.
Procedure Consensus (for the MEC node eij in the MEC cluster Ej of MEC-layer, 1 ≤ i ≤ nEj where nEj is the number of MEC nodes in MEC cluster Ej of MEC-layer and nEj > 3)
The MEC node eij receives the requests sent from UEs. The received requests are taken as the majority. And the majority value is used as the initial value (vi) of eij when function Agreement is executed. Compute the number of rounds required, σ = ⌊(nEj − 1)/3⌋ + 1. Execute function Agreement(σ, vi, nEj), then the agreement vector of the specific application service requests is obtained. Take the majority value of the agreement vector, and then the Consensus value is obtained. The Consensus value is transferred to CC-layer.
Procedure Interactive Consistency (for the cloud node ci in the CC-layer, 1 ≤ j ≤ nC, where nC is the number of cloud nodes in the CC-layer and nC > 3)
The cloud node cj receives the Consensus values transferred from nodes in the MEC cluster Ej of MEC-layer. The received Consensus values from nodes in the MEC cluster Ej of MEC-layer are taken as the majority. And the majority value is used as the initial value (vj) of cj when function Agreement is executed. Compute the number of rounds required, σ = ⌊(nC − 1)/3⌋ + 1. Execute function Agreement(σ, vj, nC), then the agreement vector is obtained. The obtained vector is IC value.
Agreement(σ, vs, nA) (σ is the required rounds, vs is the initial value and nA is the number of nodes participating in the agreement)
Request Gathering Step:
If r = 1 then:	(1) Each node broadcasts its initial value vs to other nodes in the same cluster simultaneously. (2) Each node receives and stores the nA values sent from nA nodes of the same cluster in the corresponding root of its rg-tree.
For 2 < r ≤ σ, do:	(1) Each node transmits the values at level r−1 in its rg-tree to other nodes in the same cluster simultaneously. (2) Each receiver node stores the received values in the corresponding vertices at level r of its rg-tree.
Request Deciding Step:
Step 1:	Reorganize each rg-tree by deleting the vertices with repeated node names.
Step 2:	Using function VOTE with the root i of each node’s rg-tree and obtaining the common value VOTE(i).
VOTE(α)=	If the α is a leaf, then outputs the value α. If the majority value does not exist, then output the default value φ.

.

However, analysis of algorithms under varying parameters and practical constraints through computer simulation can be key to understanding the performance and trade-offs of theoretically well-performing algorithms [20]. In order to facilitate the simulation experiment, the pseudo code of the proposed MECAA is shown in

Table 2. Pseudo code of MECAA.

MECAP MECAA /* MEC Agreement Algorithm*/

{ for i = 1 to NUE /* NUE is the total number of UEs */ trans(req, Ej); end for j = 1 to NE /* NE is the total number of MEC clusters in MEC-layer */  Consensus(nEj, Ej)  Interactive Consistency(nC, Ej) end } Consensus(nEj, Ej) { for i = 1 to nEj    recv(req, Ej);    vi = majority(recv(req, Ej));    σ = ⌊(nEj − 1)/3⌋ + 1;    cv = Agreement(σ, vi, nEj);    trans(cv, Ej); end } Interactive Consistency(nC, Ej) { for j = 1 to nC    recv(cv, Ej);    vj = najority(recv(cv, Ej));    σ = ⌊(nC − 1)/3⌋ + 1;    IC = Agreement(σ, vj, nC); end }

Agreement(σ, vs, nA) /* σ is the required rounds, vs is the initial value and nA is the number of nodes participating in the agreement */ { int VOTE[nA]; /* Request Gathering Step */ for i = 1 to nA do  send(i, <vs>, nA);  rvst(i, nA, <vs>, rg-tree(root)); end for r = 2 to σ do  for i=1 to nA do  send(i, <val, r − 1>, nA);  rvst(i, nA, <val, r − 1>, re-tree(r)); end /* Request Deciding Step */ for i = 1 to nA do  new_rg-tree = retree(i, rg-tree);  VOTE(i) = vote_value(new_rg-tree); end return(VOTE); } vote_value(α) {  if (α is a leaf)   return(α);  else   if (tree_maj(α) = m) /* m is 0 or 1/    return(m);   else    return(φ);

. There are four parts of MECAA, including Consensus(n_Ej, E_j), Interactive Consistency(n_C, E_j), Agreement(σ, v_s, n_A), and vote_value(α). The functions involved in MECAA are listed as follows:

• trans(req, E_j): transfer the request of a specific application service to MEC cluster E_j.
• recv(req, E_j): receive the requests sent from UEs in the MEC cluster E_j.
• majority(recv(req, E_j)): take the majority of the received requests from UEs.
• recv(cv, E_j): receive the Consensus values transferred from nodes in the MEC cluster E_j.
• majority(recv(cv, E_j)): take the majority of the received Consensus values from nodes in the MEC cluster E_j.
• trans(cv, E_j): transfer the Consensus value of MEC cluster E_j to CC-layer.
• send(i, <v_s>, n_A): node i sends the initial value v_s to all n_A nodes in the same cluster.
• rvst(i, n_A, <v_s, >, rg-tree(root)): node i receives and stores the n_A <v_s, > sent from n_A nodes of same cluster in the corresponding root of its rg-tree.
• send(i, <val, r − 1>, n_A): node i sends the values at level r − 1 in its rg-tree to other n_A nodes in same cluster.
• rvst(i, n_A, <val, r − 1>, re-tree(r)): node i receives and stores the n_A <val, r − 1> sent from n_A nodes of same cluster in the corresponding vertices at level r of its rg-tree.
• retree(i, rg-tree): delete the vertices in node i’s rg-tree with repeated node names.
• vote_value(new_rg-tree): compute the function value at the root of the new_rg-tree.
• tree_maj(α): take the majority value of new_rg-tree.

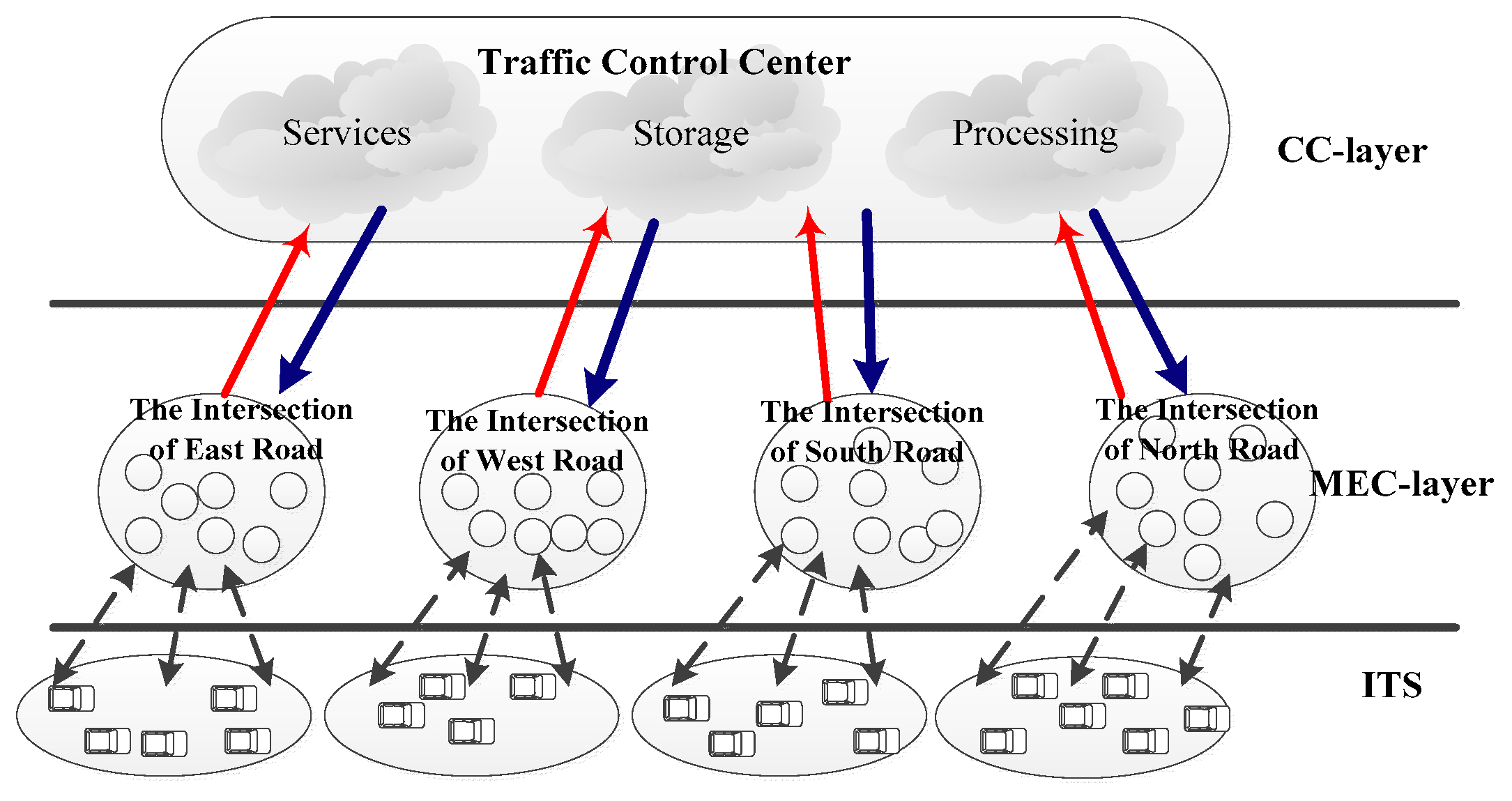
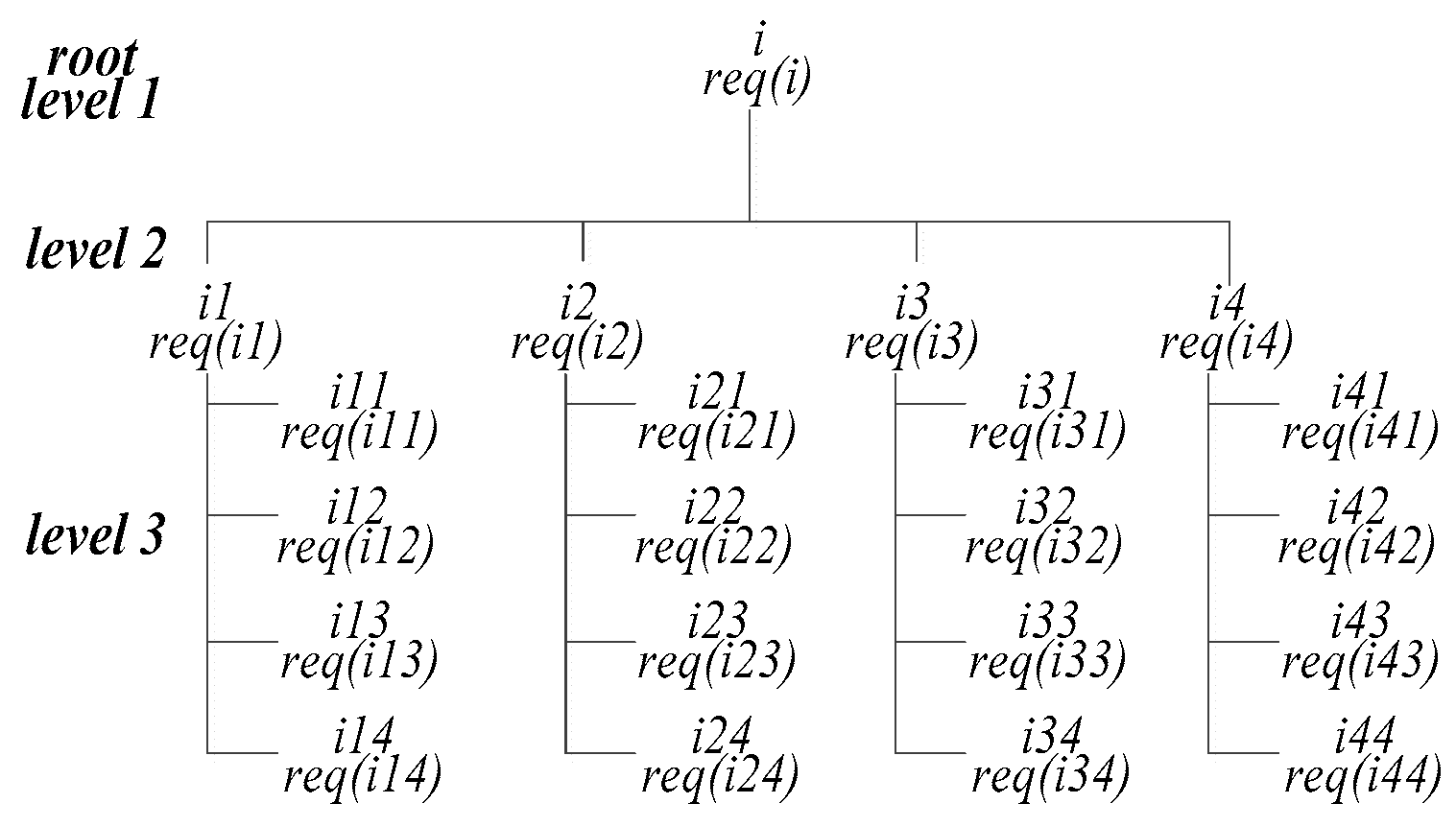
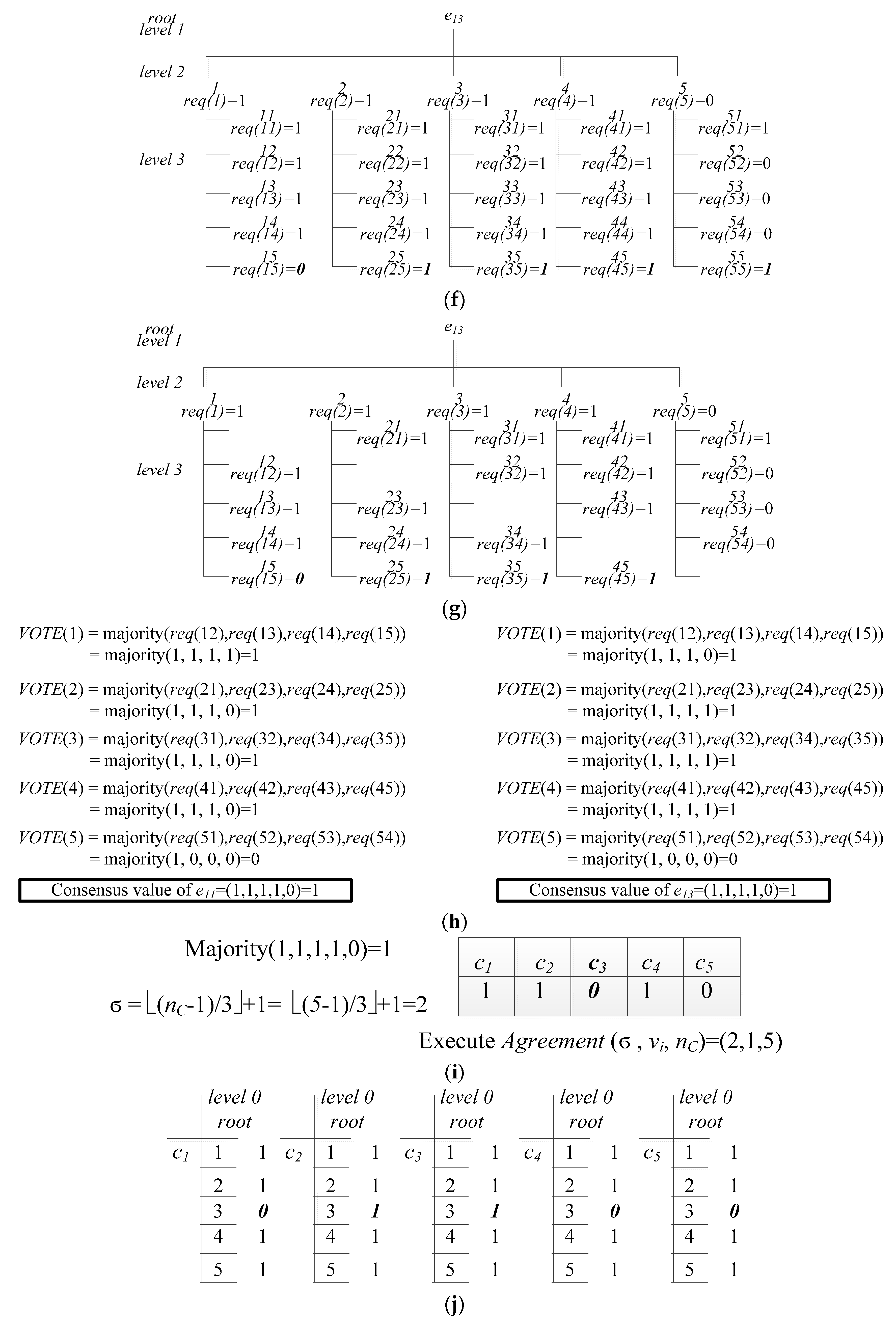
4. An Example of the Execution of MECAA

An example of executing MECAA, the application of connected vehicles by MIoT, is presented in Figure 7. Each vehicle (UE) asks for the service of traffic status. The request of each UE is shown in Figure 7a. And, the requests of UEs are transferred to MEC cluster E₁ of MEC-layer.

In procedure Consensus, each node in MEC cluster E₁ receives the requests transferred from UEs. The received requests are taken as the majority and the majority value is used as the initial value (v_i) of node in MEC cluster E₁ when function Agreement is executed. The initial value may be the initial time or the time stamp of the central traffic controller. Then, the number of rounds required, σ = ⌊(n_Ej − 1)/3⌋ + 1, is computed and function Agreement(σ, v_i, n_Ej) is executed. The initial value of each node in MEC cluster E₁ of MEC-layer is shown in Figure 7b.

For this example, two rounds (σ = ⌊(n_E1 − 1)/3⌋ + 1 = ⌊(5–1)/3⌋ + 1 = 2, where n_E1 is the number of nodes in MEC cluster E₁) are required to exchange the messages when Agreement is executed. In this example, there are five nodes in MEC cluster E₁ and MEC node e₁₅ is assumed in malicious fault. Figure 7b gives the initial value of each node in MEC cluster E₁. During the first round of Request Gathering Step, each node of MEC cluster E₁ transmits the initial value to all nodes of MEC cluster E₁ simultaneously, and stores the received n_E1 (=5) values in the corresponding root of each rg-tree, as shown in Figure 7c. In the second round, each node transmits the values in the root of the corresponding rg-tree to other nodes in MEC cluster E₁ simultaneously, and stores the received values in level 1 of the n_E1 (=5) corresponding rg-trees. The progression of nodes e₁₁ and e₁₃ during Request Gathering Step is shown in Figure 7d,f. Subsequently, in the Request Deciding Step, the rg-tree is reorganized by deleting those vertices with repeated node names. The corresponding rg-tree of nodes e₁₁ and e₁₃ is shown in Figure 7e,g. Then, function VOTE is applied on the rg-tree root of each node to take the majority value. The majority value of the agreement vector is taken, and the Consensus value is obtained. The Consensus value of nodes e₁₁ and e₁₃ is obtained and shown in Figure 7h. Finally, the Consensus value of each MEC cluster in the MEC-layer is transferred to the CC-layer.

In procedure Interactive Consistency, the cloud node in the CC-layer receives the Consensus value from nodes in the MEC cluster of MEC-layer. The received Consensus values from nodes in the MEC cluster are taken as the majority. The majority value is used as the initial value of the cloud node when function Agreement is executed. The initial value of each node in the CC-layer is shown in Figure 7i. For this example, two rounds (σ = ⌊(n_C − 1)/3⌋ + 1 + 1 = ⌊(5–1)/3⌋ + 1 = 2, where n_C is the number of nodes in the CC-layer) are required to execute Agreement. In this example, there are five nodes in the CC-layer and cloud node c₃ is assumed to have a malicious fault. Figure 7i is the initial value of each node in the CC-layer. During the first round of Request Gathering Step, each node of the CC-layer transmits the initial value to all nodes of the CC-layer and stores the received n_C (=5) values in the corresponding root of each rg-tree simultaneously, as shown in Figure 7j. In the second round, each node transmits the values in the root of the corresponding rg-tree to other nodes in the CC-layer simultaneously, and stores the received values in level 1 of the n_C (=5) corresponding rg-trees. The progression of nodes c₁ and c₄ during Request Gathering Step is shown in Figure 7k,m. Subsequently, in the Request Deciding Step, the rg-tree is reorganized and the corresponding rg-tree of nodes c₁ and c₄ is shown in Figure 7l,n. Then, function VOTE is applied on the rg-tree root of each node to take the majority value.

The majority value obtained through function Agreement is mapped to a traffic status. The IC value is a vector, and each element in the vector is the majority value obtained through Agreement function. Each element is used to present the request of a specific application. The IC value of nodes c₁ and c₄ is shown in Figure 7o. Eventually, an agreement is reached in MIoT. Finally, the service of traffic control system can be supported by each cloud node in the CC-layer.

5. The Complexity of MECAA

The following theorems are used to prove the complexity of MECAA, following the method of [21]. The complexity of MECAA is evaluated in terms of (1) the minimal number of rounds of message exchanges, and (2) the maximum number of allowable faulty nodes. Theorems 1 and 2 below will show that the optimal solution is reached.

Theorem 1.

The number of required rounds of message exchanges by MECAA is the minimum.

Proof: 

The total number of required rounds of message exchanges by MECAA can be discussed by two layers of MIoT.

(1)

MEC-layer: Because message passing is required only in the Request Gathering Step, the Request Gathering Step is time consuming. Dolev and Reischuk pointed out that ⌊(n–1)/3⌋ + 1 rounds are the minimum number of rounds to send sufficient messages to achieve agreement in an n-node fallible distributed system [21]. However, in the fallible MEC-layer, the MEC nodes maybe in malicious fault. In addition, each node in the fallible MEC-layer must exchange messages with other nodes. Therefore, a constraint on the minimum number of rounds can be applied to the study. In other words, in the MEC-layer, there are n_Ej nodes in the MEC cluster E_j; MECAA needs ⌊(n_Ej − 1)/3⌋ + 1 rounds to exchange messages. In an E-clusters MEC-layer, the nodes in each MEC cluster execute MECAA simultaneously, where E is the total number of clusters in the MEC-layer of MIoT. Therefore, the required rounds for executing MECAA by each node in all MEC clusters depend on the number of nodes in the MEC cluster.

(2)

CC-layer: As in the discussion of the number of message exchanges required in the MEC-layer. In the CC-layer, the research of Dolev and Reischuk can still be applied [21]. In the CC-layer, there are n_C nodes; MECAA needs ⌊(n_C − 1)/3⌋ + 1 rounds to exchange messages.

In short, number of required rounds of message exchanges by MECAA in MIoT is the minimum. □

Theorem 2.

The number of allowable faulty nodes by MECAA is the maximum.

Proof: 

The total number of allowable faulty nodes by MECAA is illustrated by the two layers of MIoT.

(1)

MEC-layer: Fischer and Lynch indicate the lower bound for agreement problem for node faults as f ≤ ⌊(n − 1)/3⌋, where f is the total number of allowable malicious faulty nodes and n is the total number of nodes in a distributed computing system [17]. Therefore, f ≤ ⌊(n − 1)/3⌋ in the study of Fischer and Lynch [17] can be applied to f_mEj ≤ ⌊(n_Ej − 1)/3⌋ in the MEC-layer, where f_mEj is the total number of allowable malicious faulty MEC nodes in MEC cluster E_j and n_Ej is the number of nodes in MEC cluster E_j. Then, T_FE = ${\displaystyle {\sum }_{j=1}^E{f}_{mEj}}$ where E is the total number of MEC clusters in the MEC-layer of MIoT, and T_FE is the total number of allowable faulty nodes in the MEC-layer.

(2)

CC-layer: The research results of Fischer and Lynch [17] can also be applied to the CC-layer. Therefore, f_mC is the total number of allowable faulty nodes in the CC-layer, and f_mC ≤ ⌊(n_C − 1)/3⌋ where n_C is the number of cloud nodes.

In summary, the maximum number of allowable faulty components by MECAA is T = T_FE + f_mC = ${\displaystyle {\sum }_{j=1}^E{f}_{mEj}}$ + ⌊(n_C-1)/3⌋. T is the maximum number of allowable faulty nodes in MIoT. □

As a result, MECAA takes the minimum number of rounds and tolerates the maximum number of faulty components to make fault-free nodes reach a common agreement. The optimality of the polynomial time algorithm is proven.

6. Conclusions

The last decade has seen cloud computing emerging as a new paradigm of computing. The vast resources available in the cloud can be leveraged to deliver elastic computing power and storage to support resource-constrained end-user devices. However, for various reasons, the cloud computing paradigm cannot meet the low latency and jitter, environment awareness, and mobility support requirements that are important for several applications.

The long propagation delay is the main drawback of cloud computing. Therefore, proximity access through the MEC is widely considered to be a key technology for implementing various next-generation IoT visions. The IoT can achieve innovations that improve quality of life, but will generate an unprecedented amount of data that is difficult for traditional systems to handle. So, the MEC is designed to overcome these limitations [4]. The main goal of the MEC study is to seamlessly integrate the two disciplines of wireless communications and mobile computing to form a new design of offloading computation technology.

MEC extends the cloud computing paradigm to the edge of the network, thus enabling a new breed of applications and services [19]. While MEC nodes provide localization, therefore enabling low latency and context awareness, the cloud provides global centralization. In this study, a highly flexible and reliable IoT platform MIoT is proposed. By using MIoT, the QoS for IoT application services can be improved.

The agreement problem is fundamental to a distributed system, and has been extensively studied. Network topology is an important issue related to consistency. However, MIoT is a new concept for distributed systems. It has encouraged distributed system design and practice to support user-oriented services. In this study, the agreement problem was redefined by the MECAA algorithm in the MIoT. The proposed algorithm ensures that all faulty nodes in the MIoT can reach an agreement value to cope with the influences of the faulty nodes by using the minimum number of message exchanges, while tolerating the maximum number of faulty nodes at any time. Our algorithm is the first to treat the agreement problem under an IoT platform based on cloud computing and MEC. In the future, an experimental evaluation will be conducted to compare the efficiency of the algorithm under different faulty nodes.