Abstract
In the countries of the former Eastern Bloc (Central and Eastern Europe) belonging to the European Union, a gradual elimination of the technological gap, greater expenditures, competitiveness and productivity can be noticed. In this context, analysis and forecast of the level of accessibility and use of ICT (information and communication technologies) by households in these countries has become interesting. It allows for the selection of digitally excluded regions, or those threatened with this phenomenon in the coming years (2018–2020). To carry out the analysis, a framework based on fuzzy numbers and the NEAT F-PROMETHEE (New Easy Approach To Fuzzy-PROMETHEE) method was developed. The potential of the fuzzy outranking approach taking into account the uncertainty of input data (criteria and preferences) has been demonstrated as an alternative to the IDI (ICT Development Index) methodology widely used in research on regional ICT development based on composite indices. Research has shown that Estonia is the leader in the area of ICT expansion among households, and in the next three years will definitely maintain its dominant position. Slovenia follows shortly after, followed by Latvia. At the end of the ranking were the countries with the largest percentage in Central and Eastern Europe of population excluded digitally or threatened with this phenomenon; these are: Poland, Slovakia, Bulgaria and, in last place, Romania. Within this framework, the robustness of the obtained rankings to change in the degree of uncertainty of preferences was also examined. It turned out that eliminating the uncertainty of preferences resulted in an increase in the uncertainty of the aggregate, fuzzy grades obtained at the output.
1. Introduction
Modern technologies, innovations, and, in particular, ICT (information and communication technologies) have had a significant impact on the functioning of households, their structure, organisation of professional and private life. The transfer of information and knowledge is able to take place, and distance ceases to be a communication obstacle [1,2]. The use of ICT has contributed to the growing interest in more flexible forms of employment and the establishment of cooperation with other market participants. Thanks to ICT, effective tools have been developed to activate unemployed or disabled people, resulting in increased social capital [3]. Solutions in the area of ICT have been used as a tool to reduce the scale of poverty [4,5,6].
More and more households are equipped with various types of information and communication technologies. This is due to an increase in affluence and awareness regarding the benefits of the dissemination of ICT, as well as the decreasing costs of access to these technologies. In [7,8,9], however, attention was drawn to the differences between the developed, developing and underdeveloped countries. In the case of countries belonging to the first group, a coherent ICT policy has meant that the majority of the population has access to broadband Internet and uses it in all spheres of their lives. However, in the case of countries classified into the other two groups, contact with ICT is usually possible within larger agglomerations, leading to inequality within the society as well as between countries and favouring the intensification of the digital divide phenomenon (also called digital exclusion) [10,11].
Intensive work is being done all the time to equalise the opportunities of ICT-using societies that live in culturally, mentally and economically diverse regions. In particular, these activities are visible in the countries belonging to the EU (European Union), because the members of the federation are both “old” EU countries and countries of Central and Eastern Europe, and the inequalities in ICT between these areas were significant not so long ago. However, as a result of ICT implementation and diffusion in the countries of the former Eastern Bloc, a gradual elimination of the technological gap, and greater expenditures, competitiveness and productivity [12] can be noticed.
The assessment of the level of accessibility and use of ICT in individual countries makes it possible to identify those regions that are affected by the phenomenon of digital divide and require support, and to apply specific measures. While the forecasting of the level of accessibility and use of ICT makes it possible to prevent the occurrence of this phenomenon by eliminating the anticipated factors that favour its emergence. Forecasts may also help in defining and evaluating the general direction of the information society development both in global and micro-regional terms.
One of the popular tools for monitoring progress towards a global information society is IDI (ICT Development Index) [13]. It has been developed by the United Nations International Telecommunication Union. IDI allows you to make comparisons between countries and over time in terms of the degree of access and use of ICT infrastructure and the skills of its users. The results of these comparisons may show disproportions in the spread of ICT in individual regions, as well as indicate areas affected by the digital divide. Nevertheless, IDI, due to the calculation procedures used in it, has some drawbacks. Namely, it uses weighted averages, which makes it a weak indicator for sustainability of individual development (IDI components). This means that the high value of one of the ICT development indicators can largely compensate for the low value of another indicator [14]. In turn, strong sustainability, based on low compensation between indicators, is a much more preferred approach in terms of scientific methodology than weak sustainability [15]. In addition, the IDI applies specific normalisation of individual development indicators to the scale [0,1]. This normalisation is based on the ratio of the value of a given indicator to its ideal (reference) value. However, there is a relatively frequent situation in which the value of a given indicator exceeds the reference value in the examined country. In this situation, the value of this indicator after normalisation is limited to 1 [13]. For example, if the value of the indicator “Secondary gross enrolment ratio” is greater than or equal to 100, regardless of whether the value is 100 or 200, after normalisation it will be 1. As a result, values of indicators higher than the reference values in individual countries are in a certain way limited, which affects the final IDI ranking and may cause this ranking to incorrectly reflect the level of ICT development in these regions.
To assess ICT development, social development and broadly understood sustainability, the MCDA (multi-criteria decision analysis) methods are more frequently used [16,17,18]. Some of MCDA methods, as compared to IDI, are characterised by stronger sustainability, and thus lower compensation of criteria/indicators. In addition, MCDA methods usually use other standardisation procedures, free from the disadvantages of standardisation used in the IDI. It should also be noted that the fuzzy MCDA methods make it possible to capture uncertainty in the decision problem [19], thanks to which they can be applied in broadly understood forecasting, including in the prediction of regional ICT development. One such method is the NEAT F-PROMETHEE (New Easy Approach To Fuzzy-PROMETHEE) [20] based on the classical PROMETHEE method (Preference Ranking Organisation Method for Enrichment Evaluations) [21,22]. This method can perform calculations on both fuzzy (uncertain) data and crisp (certain) data. As a result, it can be used to assess the current level of ICT development on the basis of complete, known and reliable data in crisp form. It should be noted that the NEAT F-PROMETHEE method applies a normalisation of the criteria (indicators) to the scale [0,1] based on the pairwise comparisons of alternatives, and thus the results and rankings obtained may vary depending on the considered set of alternatives (rank reversal paradox). Despite the fact that this is often considered a disadvantage, in practice, this paradox can be a positive phenomenon when comparing the level of ICT development of individual countries. It allows the specificity of the studied region and dependencies between individual countries to be taken into account. For example, the level of ICT development in developed Western European countries may influence the perception of the development level of the developing countries of Central and Eastern Europe. Therefore, a more numerous set of alternatives, including, for example, the countries of Western Europe and the countries of Central and Eastern Europe, may give different results than the smaller set, accounting for only Central and Eastern European countries, as the reference point and perspectives of the decision problem change. Moreover, by realising calculations on fuzzy data, NEAT F-PROMETHEE allows, to a large extent, the uncertainty and imprecision of both data and preferences to be taken into account, where this uncertainty is an inherent aspect of forecasting. An important feature of the NEAT F-PROMETHEE method is the fact that the results of calculations on crisp and fuzzy data are presented on the same scale, which makes it possible to compare them directly. Considering the above-mentioned aspects, the NEAT F-PROMETHEE method can be considered suitable for assessing and forecasting the ICT development in individual countries.
The aim of this article is to assess the level of regional ICT development and to develop a forecast of regional ICT development for the coming years for the countries of Central and Eastern Europe belonging to the European Union. Development in particular regions is characterised by access, use and ICT skills considered in the community composed of households (including natural persons). The comparative analysis of the obtained results of the assessment and forecasting may show the disproportions in the development of ICT in individual regions. Thus, the actual and predicted scale of the occurrence of the digital divide phenomenon between the researched societies may be revealed. The tool used to evaluate and forecast is the fuzzy MCDA method called NEAT F-PROMETHEE. The methodological contribution is the development of the evaluation and forecasting framework, based on fuzzy numbers and the NEAT F-PROMETHEE method. This framework takes into account the fuzzing, and hence uncertainty of: input data representing the values of ICT development indicators, preferences representing the advantages of one country over another in terms of a given indicator, and the time of occurrence of a given forecasted value.
Section 2 provides an overview of the literature indicating the relevance and high rank of the digital divide problem and the development of the information society and ICT in the world. Section 3 contains a description of the methodological framework and its individual constituent elements. The results of the conducted research, in the form of assessment of the level of ICT development and forecasts of ICT development of individual countries in the coming years, are presented in Section 4. The article ends with conclusions and indication of further directions of research.
2. Literature Review
Digital exclusion or digital divide is a term used to describe the difference between people and societies that have and do not have access to the latest technologies or do not keep up with technological novelties. Consequently, they do not achieve the benefits of digitalisation. In addition, it is constantly evolving and covers more and more areas of social life [23,24,25,26,27]. According to the OECD (Organisation for Economic Cooperation and Development) the term digital divide refers to “the gap between individuals, households, businesses and geographic areas at different socio-economic levels with regard both to their opportunities to access ICT and to their use of the Internet for a wide variety of activities” [28]. In the literature on the subject, you can read a lot of interesting publications on digital exclusion, which include, among others, discussing factors affecting the occurrence of this phenomenon, spatial comparison between different regions and various types of classifications, as well as valuable conclusions and recommendations addressed to decision-makers with proposals to reduce the existing digital divide.
Jahanmir and Cavadas [29] point out that despite the systematic research on the dissemination and introduction of digital innovations, little attention has been devoted to this subject in the literature. Among the determinants of delays in implementing digital innovations, the authors mentioned the following variables: approach to technology, negative opinions about technology, the image of the global brand, consumer innovation and profiles of the main user. In the study conclusions, they found that increasing the positive attitude of consumers to technology could more effectively accelerate the pace of digital innovation. However, understanding the factors that delay these activities will allow the development of technologies that will be faster to spread, accelerating the pace of introduction of digital innovations. Leaning [30], on the other hand, described the existence of a digital divide between countries and within countries, as well as social stratification in this area. Individual social groups, according to Leaning, have different opportunities and experiences in the case of digital technology. The author claims that today there are three main reasons for digital exclusion, among which he included: the ability of users to access computers and the Internet, user skills necessary to use the Internet and the specificity of use and the objectives imposed on digital media. A similar view is represented by Warren [31], who stated that the Internet provides users with obtaining information, enables the purchase of goods and services and promotes interpersonal interaction. He cited, in his opinion, the most common factors that affect digital exclusions: access to systems and equipment, ICT skills, and interest in content that is relevant and useful for given social groups.
Interesting research on digital exclusion among the users of mobile phones with a division into rich and poor countries was presented by James [32]. He used information that came from households. In his paper, He discussed the problems and socio-economic effects of using mobile phones. In turn, in the next publication [33], he characterised the phenomenon of digital readiness and digital divide as two ways to measure ICT performance.
An interesting article that proposes a procedure to compare the digital divide is the publication of Petrović et al. [34]. The authors, in order to implement the comparative analysis process, developed a method of multi-level elevation (ELECTRE MLO) based on the ELECTRE (ELimination Et Choice Translating REality) method family. The proposed approach, according to the authors, better presents the differences in access to digital technology. The activities focused on classifying countries into hierarchical performance levels and identifying relevant benchmarks. The empirical material came from 29 EBRD (European Bank for Reconstruction and Development) countries. For the purposes of this study, a set of 11 indicators was adopted that make up the IDI. Another methodological proposal is presented in the article by Coria et al. [35]. According to the authors, this is an innovative approach to the qualitative analysis and modelling of the digital divide phenomenon based on the example of one country, based on classification trees. The Quinlan algorithm was the inspiration, and is used to automatically generate classification trees. The studies used data from the Mexican census and housing. According to the authors, the methodology contributed to the creation of quantitative profiles that described the similarities and differences between the series of urban classes representing the percentage of Internet presence in households.
An intriguing article about the digital divide in the area of higher education is the work of Khalid et al. [36]. The authors identified factors that affect the shaping of this phenomenon, and divided them into three categories: social exclusion (low income, avoiding ICT as a standard, lack of motivation and commitment, and physical or mental disability), digital exclusion (no hardware or Internet services), and accessibility, including the division into rural and urban areas, as well as differences in the range of ICT skills and information literacy. On the other hand, an advanced approach to issues related to digital exclusion was presented in the publication by Scheerder et al. [37]. In their opinion, the digital division has three levels. The lowest is the binary access to the Internet, then there are the skills required to use the Internet. The digital division at the third (highest) level allows you to really see what the real use of the Internet is and identify the determinants of digital divide, which are largely limited to socio-demographic and socio-economic conditions.
An analysis of the digital gap between the countries of the European Union, carried out using multi-dimensional statistical methods, was presented by Cuervo and Menendez [38]. The results of these studies have significant historical value, because they concern the shaping of the phenomenon before the expansion of the federation. In turn, Polat [39] thoroughly analysed the subject of digital exclusion in his work on the example of Turkey. The author came to the conclusion that digital differences are linked to other social inequalities. In addition, high-budget solutions that are supposed to contribute to the reduction of these differences are supplanted by proposals that take into account the social basis of digital exclusion. In addition to all programs, there are, among others, older people, disabled people, women and rural residents who rarely use the Internet. The comparison of the development of the digital divide in 108 countries was carried out by Park et al. [40]. The authors focused on identifying factors that are conducive to a more creative global economy. Based on the research conducted, they concluded that the level of digital convergence that exists in the analysed countries can be divided into three groups, which are additionally internally differentiated. On the other hand, among factors influencing such a course of the phenomenon, they listed: GDP (gross domestic product) per capita, education rate of higher education, urban population indicator and share of trade in services in GDP. Cruz-Jesus et al. [41] provided a review of the research concerning international and internal digital divisions occurring in European Union countries, depending on the level of education of their inhabitants. The authors pay special attention to the study of the occurrence of internal inequalities in EU countries, which are noticeable even in digitally developed countries, such as Finland. Another interesting statement on digital exclusion was presented by Răileanu-Szeles [42]. This author analysed the panel data at the regional level and discussed the determinants of the digital divide in the European Union. The results of the conducted research indicated that a combination of effective regional and national funds could alleviate the regional digital divide in the EU. In the author’s opinion, stimulating economic growth, rising higher education, increasing R&D (research and development) spending and discouraging early leaving school are policy measures at the regional and national levels that effectively contribute to reducing the digital divide in the EU.
The Internet is a subject closely associated with ICT technologies. Kyriakidou et al. [43] wrote about the contribution of European countries to the spread of broadband Internet. They drew attention to the existence of a visible digital divide between countries and proposed a methodology for its measurement. The importance of mobile Internet access was stressed by Srinuan et al. [44] in their work. Thailand was used as an example in which its growth was recorded, thus contributing to overcoming the digital divide present in this country. The authors tried to identify the key factors that determine that an individual consumer has access to mobile Internet. The research shows that the price, availability and landline, age and living space are considered to be the strongest determinants of mobile Internet. Prieger [45] also drew attention to the important role of broadband Internet in the functioning of national economies and its impact on the personal lives of users. He also became interested in shaping this phenomenon in rural areas compared to urban areas. Empirical estimates of the availability and use of broadband in the United States showed that there were fewer fixed providers of the landlines and mobile phones in rural areas than in cities. Nevertheless, the availability of mobile broadband Internet helps bridge the gap in fixed broadband access. The author observed that the uneven use of broadband Internet between rural and urban households is proportionately greater in the case of low-income households. Fascinating, extensive research on the use of modern technology was conducted by Pick and Nishida [46]. Empirical material covered the main regions of the world. The obtained results indicated that different sets of factors were decisive for particular continents. In the case of the entire world, for broadband Internet subscribers, this set included higher education and innovative ability. There was also a different spatial division into developed and developing countries, along with related digital disproportions.
Chipeva et al. [47] presented a more individual approach to the digital divide, related to behavioural patterns on technology endorsement. They analysed individual ICT acceptance through a conceptual model combining UTAUT2 (Unified Theory of Acceptance and Use of Technology 2) with personality traits and income in two European Union countries: Bulgaria and Portugal. The authors state that openness is a significant predictor of behavioural intention, and for usage behaviour the important personality predictors include openness, extraversion and agreeableness. Significant country differences were revealed by their multi-group. In Portugal, the effect of hedonic motivation on behavioural intention and the effect of behavioural intention on usage are stronger, while in Bulgaria the effect of performance expectancy, habit, agreeableness, and neuroticism on behavioural intention and the effect of age on usage prevailed. In turn, Rockmann et al. [48] noticed that the unequal use of digital resources resulted in social disparities. They analysed the role that the prior workplace experiences of retired seniors have on exploratory IT behaviour. Their results showed how the digital divide ultimately leads to unequal health knowledge. It should be noted that earlier, in 2012, van Dijk [49] showed that the digital divide, regarded as effects of unequal access (mainly as a result of digital skills and different usage, and to a lesser extent, motivation and physical access) cause unequal participation in society. He considered this issue against the explanatory background of resources and appropriation theory, as well as materialist and relational theory. Haselhorst [50] points out that computer literacy is becoming an increasingly important skill in middle schools, high schools and for the workforce. School and district administrators must realise that, even with numerous financial problems in low-income areas, digital curricula are an ethical priority.
The analysis of these publications shows the importance of the problem of digital exclusion and ICT development. The study of this problem on a regional or even global scale, make it possible to determine the degree of evolution of the information society and indicate the disproportions of its development between countries. The deepening of ICT issues can be a source of valuable information for business needs, which will, for example, determine the conduct of online marketing campaigns, or condition the entry of new suppliers of ICT technologies in a given country. The ex-ante study of ICT development highlights, for example, much more interesting (more valuable cognitively) issues than ex-post study, because it can respond in advance to threats related to barriers to ICT development or take action in the ICT market more quickly. Forecasts regarding the development of ICT perform several significant functions, including supporting decision-making processes, simulating actions that favour their implementation, and counteracting the occurrence of unfavourable events. Forecasts also have an important information function. Nevertheless, forecasting development is a problem with relatively high uncertainty, although it formulates the most probable picture of it. Therefore, for this type of prediction, it is necessary to use methods and tools that successfully cope with the occurrence of uncertainty and impreciseness of data relating to the future use of ICT.
3. Materials and Methods
3.1. Methodological Framework
The developed methodological framework aims at forecasting the level of regional development of ICT in a group of households (natural persons) and studying the differences of this development between individual countries referred to as the digital divide. Because the forecast refers to the future, it is usually uncertain. Therefore, it is important that the framework makes it possible to capture the uncertainty of forecasts, where this uncertainty may refer to a forecasted value of ICT development at the regional level as well as the predominance of one country over another until the occurrence of this value. In addition, it is important to refer the forecast to the current state, which should therefore also be examined.
Therefore, the framework includes the following activities:
- obtaining partial historical data on the level of regional ICT development,
- defining the current level of ICT development in the countries studied,
- generating forecasts for individual ICT development indicators,
- blurring these forecasts,
- calculating the aggregate ICT development forecast for each of the countries studied.
In the case of historical data on the level of regional ICT development, it is important that these data are reliable and of adequate quality. This has a significant impact on the quality of the forecast itself, because in the case of unreliable data, the forecast could also be unreliable. Similarly, if the data were incomplete or subjective, this would have consequences in the form of poor forecast quality. Moreover, the data should include various ICT development indicators, so that it can be shown to what extent technologies or ICT elements shape the development of the information society in a given country, as well as the level of accessibility and applicability of ICT and the skills to use them. For the above reasons, the framework was based on reports of the ITU (International Telecommunication Union), and in particular on ICT development indicators constituting components of the IDI framework [13]. To ensure comparability of the rankings obtained under the IDI framework, it was necessary to use the same set of indicators.
The determination of the current status is aimed at establishing a reference point for the obtained forecast, with the latest available data (from 2017). It is important that the current level of ICT development in the regions is tested reliably. For this reason, the IDI defects indicated in the introduction should be eliminated, i.e., the high degree of compensation of indicators (strictly related to weak sustainability) and the controversial way of normalising ICT indicators. Therefore, to determine the current state of ICT development in the countries studied, it was decided to use the PROMETHEE method (in practice, it was NEAT F-PROMETHEE, to which crisp/certain data were given) in the form of performance table.
Generating forecasts for individual ICT indicators is necessary due to the predictive nature of the framework. Forecasts are determined separately for each indicator, which makes it possible to predict the future level of a given indicator, regardless of the others. At the outset, based on historical data, the change dynamics of a given indicator are determined. Then, predictions are generated based on the last known value of the indicator. We decided to use chain indices to generate forecasts, and the forecasts covered the next three years (2018–2020).
The framework takes into account the fact that forecasts are usually imprecise and uncertain. To capture the uncertainty of the forecast values of ICT development indicators, they are transformed into a fuzzy form [51]. This is accomplished by aggregating the forecasted crisp values of the ICT development indicator from three years (2018–2020) to one fuzzy number. This approach, apart from capturing the uncertainty related to the projected value, also shows to capture the imprecision referring to the time when the forecasted value should occur (period of 2018–2020). The fuzzy projected values of each ICT development indicator for individual countries form the so-called fuzzy performance table, which is the entrance for the NEAT F-PROMETHEE method.
The task of the NEAT F-PROMETHEE method is to aggregate the predicted values of individual indicators in the overall assessment of the countries studied and to determine their ranking. This method takes into account the uncertainty of preferences, and, in other words, the uncertainty of the advantage of one of the countries over another. Additionally, NEAT F-PROMETHEE gives the possibility of a wide analysis of the obtained solution, e.g., in terms of robustness to changes in the degree of uncertainty of preferences. Furthermore, the use of NEAT F-PROMETHEE provides the opportunity to directly compare the current status and the forecast obtained due to the use of the same methodology to determine both values and present them on a common scale.
The developed framework is presented in Figure 1, and its elements are described in more detail in Section 3.2 and Section 3.3.
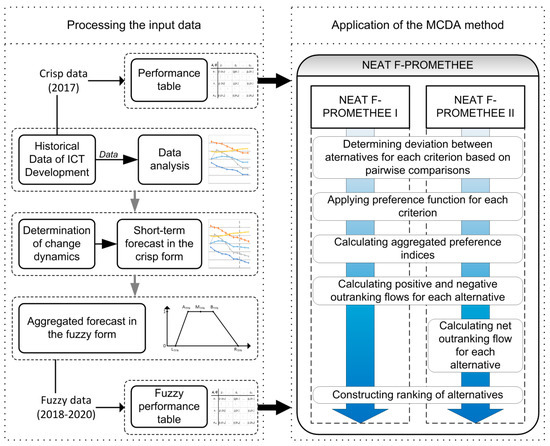
Figure 1.
Methodological framework.
3.2. Processing of Input Data
3.2.1. Data Sources
The empirical material containing information on the availability and use of ICT in households in 2011–2017 came from 11 operational EBRD (European Bank for Reconstruction and Development) countries located in Central and Eastern Europe. ERBD is an international financial institution that promotes the development of the private sector in countries implementing the principles of multi-party democracy, pluralism and market economy. These activities are aimed at accelerating the necessary structural changes in the countries carrying out the transformation. As part of affiliation to EBDR, countries participate in projects and exchange of experience, among others, concerning the development of ICT.
The research used a set of indicators published in the ITU reports [13]. On their basis, ITU calculates and publishes the ICT Development Index. This is used by international organisations to assess the level of ICT development. The ICT Development Index is a tool by means of which, for example, governments, operators, development agencies, researchers can measure the digital divide and compare the ICT involvement in each country. The construction of the ICT development index, included in the composite indicators, is based on 11 variables characterising ICT, grouped into three clusters containing information on access, use and skills. The index being discussed includes the following indicators (their weights are in brackets):
- Access indicators (ICT access, ):
- ○
- Fixed-telephone subscriptions per 100 inhabitants (FTL, ),
- ○
- Mobile-cellular subscriptions per 100 inhabitants (MCS, ),
- ○
- International Internet bandwidth Bit/s per Internet user (IIB, ),
- ○
- Percentage of households with computer (PHC, ),
- ○
- Percentage of households with Internet (PHI, ).
- Use indicators (ICT use, ):
- ○
- Percentage of individuals using the Internet (IU, ),
- ○
- Fixed-broadband subscriptions per 100 inhabitants (FBB, ),
- ○
- Active mobile-broadband subscriptions per 100 inhabitants (MBB, ).
- Skills indicators (ICT skills, ):
- ○
- Secondary gross enrolment ratio (SGE, ),
- ○
- Tertiary gross enrolment ratio (TGE, ),
- ○
- Mean years of schooling (MYS, ), which was introduced to ICT development index in 2014 (until 2013, Adult literacy rate—ALR was used). Therefore, the forecast for the MYS indicator was made on the basis of four-year data (2014–2017).
The study also used a ready-made set of weights available in reports [13]. The weight values for the indicators and sub-indicators included in the IDI were weighted on the basis of the PCA (Principal Components Analysis) results obtained in 2009 [52]. In the research methodology used by ITU, PCA was used to investigate the latent nature of the data. Before applying PCA, Barlett’s test of sphericity was performed to determine if the initially selected indicators were correlated. The fact that a correlation existed for some of the indicators confirmed by the test indicated the necessity of PCA. PCA relies on testing the correlation matrix and extraction of major components. The results derived from PCA include three main elements: eigenvalues, the percent (%) of variance explained in each component, and the rotated component loadings. Eigenvalues represent the relative importance of the components; components with high eigenvalues and which explain the maximum variance are retained. A more detailed description of the analysis can be found in Annex 1 to the 2009 report “Measuring the Information Society—The ICT Development Index” [52].
3.2.2. Chain Indices
To characterise the dynamics of changes in ICT level in households in the countries surveyed over the years 2011–2017, individual indices of chain dynamics were used [53], which were calculated in accordance with the Formula (1):
where: yu—level of the phenomenon during the studied period, yu-1—level of the phenomenon in the period preceding the studied period.
In this way, information on the development of indicators in a given year in relation to their level from the immediately preceding period was obtained. The determined chain indices were used to calculate the geometric mean, which using one number allows to express the dynamics of changes occurring in the analysed time interval. The geometric mean () was calculated as the r-1 root of the product of r-1 chain indices [54] according to the Formula (2):
The next step was to use the obtained results of the average pace of changes in time for individual variables to determine short-term forecasts. It was assumed that the average rate of change of the phenomenon in the forecasted period k (k = 1, 2, 3, …) would not change. Forecasts were built using Formula (3):
where: —level of the phenomenon in the period , —level of the phenomenon in the last period [55].
3.2.3. Generating Fuzzy Numbers
For each of the 11 ICT development indicators and for each country studies, the forecast values for 2018–2020 were aggregated in the form of trapezoidal fuzzy numbers. To build fuzzy numbers, in the beginning, a standard deviation from the forecast values for 2018–2020 was determined, according to Formula (4):
Next, the average value of the indicator for 2018–2020 was calculated according to Formula (5):
The left and right values of support of the fuzzy number were determined based on Formulas (6) and (7):
In turn, the left and right values of the kernel of the fuzzy number were determined based on the standard deviation, according to Formulas (8) and (9):
As a result, for each indicator and for each country studied, a trapezoid fuzzy number was obtained, aggregating the values of forecasts for 2018–2020. The general structure of the fuzzy numbers obtained is shown in Figure 2.
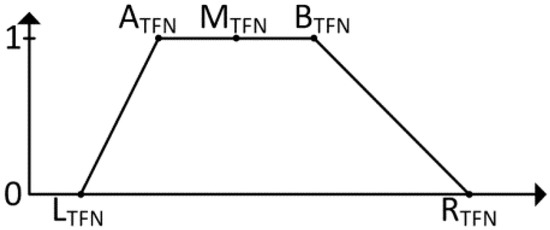
Figure 2.
The structure of trapezoid fuzzy numbers aggregating forecasts for 2018–2020.
The fuzzy numbers obtained in the above way were used to determine the forecasted ranking of countries in terms of the use of information and communication technologies with respect to the coming years. The construction of the ranking was carried out using the NEAT F-PROMETHEE method.
3.3. NEAT F-PROMETHEE Method
The NEAT F-PROMETHEE [20] method is a development of the classic PROMETHEE [56] method into a form able to operate on fuzzy numbers. Thanks to this, it makes it possible to capture both the uncertainty of preferences, as well as the uncertainty of input data, i.e., the weights of criteria and the assessment of alternatives in terms of individual criteria. The weights of criteria and assessment of alternatives can be expressed on quantitative and qualitative scales in the form of linguistic values. The method itself is characterised by low complexity, and thanks to its use of trapezoid fuzzy numbers, it is easy to use and allows a simple interpretation of the obtained results. In addition, it reduces the inaccuracies in calculations resulting from the use of fuzzy numbers, which results in more precise results than other implementations of Fuzzy PROMETHEE. It has two options that give a partial and total order of alternatives. These variants correspond to the PROMETHEE I and PROMETHEE II methods. The NEAT F-PROMETHEE method is used to consider discrete fuzzy decision problems in which the m-element set of fuzzy alternatives and the n-element set of criteria are included.
The NEAT F-PROMETHEE I variant consists of five, and the NEAT F-PROMETHEE II version of six stages:
- determination of fuzzy deviation between the alternatives for individual criteria and pairwise comparisons,
- application of the preference function for each criterion,
- calculation of aggregate preference indices,
- calculation of positive and negative out ranking flows for each alternative,
- calculation of net outranking flow for each alternative (only NEAT F-PROMETHEE II),
- construction of the ranking of alternatives.
In the first stage, for each pair of alternatives, a fuzzy deviation is determined using Formula (10):
where is the fuzzy value of the alternative in terms of the j=1...n criterion.
The second stage involves mapping the trapezoid fuzzy number to the form of . Mapping takes place using the selected preference function F, which in general is represented by Formula (11):
However, the NEAT F-PROMETHEE method assumes that the mapping process should be verified and possibly corrected, thanks to which the error of approximation resulting from the application of trapezoid fuzzy numbers is reduced. In addition, the thresholds of indifference (), preference (), or the parameter of the Gaussian function () may be used in the mapping process. In the NEAT F-PROMETHEE method, the crisp threshold values are used, in order to avoid dividing two trapezoid fuzzy numbers, which would result in inaccuracies in the calculation and loss of information. In this stage, the following preference functions may be applied: usual criterion, U-shape criterion, V-shape criterion, level criterion, V-shape criterion with indifference area, and Gaussian criterion. The mathematical forms of preference functions and their corrections are represented by Formulas (12)–(23).
The usual criterion:
The U-shaped criterion:
The V-shaped criterion:
The level criterion:
The V-shaped criterion with an area of indifference:
The Gaussian criterion:
The third step is the aggregation of criterion preferences for each pair of alternatives, in accordance with Formula (24):
where is the weight of the j-th criterion, whereby . The criteria weights are normalised to one, to be sure that . Therefore, at the beginning, weights can be defined as fuzzy numbers , and their defuzzification may be required at this stage. In the NEAT F-PROMETHEE method, the defuzzification of weights is performed using the centroid method, as shown in Formula (25):
In the fourth step, fuzzy, positive and negative outranking flows are calculated for each alternative, according to Formulas (26) and (27):
The fifth stage, implemented only in the case of NEAT F-PROMETHEE II, is the calculation of net outranking flow for each alternative. This is done using Formula (28):
The last stage is building a ranking of alternatives. In the case of NEAT F-PROMETHEE I, the ranking is constructed on the basis of positive () and negative () outranking flows, and in the case of NEAT F-PROMETHEE II, the net outranking flows are used to construct the ranking (). In the first variant of the NEAT F-PROMETHEE method, the defuzzification of fuzzy values and is necessary, according to Formulas (29) and (30):
Then, a partial order of alternatives is generated:
- the preference of alternative over takes place when and , while at least one of the inequalities must be strong,
- indifference between alternatives occurs when and ,
- incomparability between alternatives takes place when and , or when and .
Similarly, in the second variant of the method, the value is defuzzified according to Formula (31):
The NEAT F-PROMETHEE II method makes it possible to determine the total order of alternatives:
- the alternative preference of over takes place when ,
- indifference between alternatives occurs when .
4. Results
4.1. Processing of Input Data
At the outset of the research, historical values of IDI indicators from 2010 to 2017 for individual countries were acquired. Table 1 presents the values of the FTL indicator in subsequent years, while the values of other indicators are included in Appendix A.

Table 1.
Values of the FTL indicators in 2010–2017.
The next stage of the research was to determine the dynamics of changes in each indicator in 2011–2017 and the average dynamics of changes in those years. The average change dynamics was also the forecasted dynamics for the period 2018–2020. On this basis, the forecasted values of IDI indicators were calculated. The dynamics of changes for subsequent years was determined based on Formula (1). To calculate the average dynamics in 2011–2017, Formula (2) was used, and the forecasted values of ratios for 2018–2020 were determined using Formula (3). The dynamics of changes and forecasted future values of the FTL indicator are presented in Table 2. Analogical data for other indicators are included in Appendix B.

Table 2.
Change dynamics and forecast of the FTL indicator values.
On the basis of forecasted values of each indicator for 2018–2020, aggregated values of forecasts in the form of trapezoid fuzzy numbers were calculated in accordance with Formulas (4)–(9). Fuzzy numbers obtained from the FTL indicator, representing the aggregate forecast of the value of this indicator for 2018–2020, are presented in Table 3. Fuzzy numbers generated for other indicators are included in Appendix C.

Table 3.
Forecasted value of the FTL indicator for 2018–2020, aggregated to a single fuzzy number .
Table 4 and Table 5 acted as input sources for the NEAT F-PROMETHEE method. The data processed in the above manner is included in the fuzzy performance table presented in Table 5, which was the basis for determining the aggregate forecast of ICT development in individual countries. Table 4 includes the assessment of individual indicators for the surveyed countries in 2017. The data presented in Table 4 comprises a performance table, which is the basis for examining the current level of ICT development in individual countries.

Table 4.
The values of individual IDI indicators in 2017.

Table 5.
Fuzzy performance table.
4.2. Evaluation and Forecast of Regional ICT Development Using the NEAT F-PROMETHEE Method
Application of the NEAT F-PROMETHEE method initially required defining the preference model, i.e., defining the weights of criteria, functions and directions of preferences and threshold values. For each criterion, the V-shaped preference function was used, and the preference direction for each criterion was the maximum. The criteria weights were taken directly from IDI [13]. Preference threshold value (p) was defined as twice the standard deviation determined separately for data from 2017 (current state survey) and the value for each country (forecast for 2018–2020). The preference model used in the study is presented in Table 6.

Table 6.
Model of preferences for the NEAT F-PROMETHEE method.
As a result of the application of the NEAT F-PROMETHEE method, on the basis of the performance table (Table 4), outranking flow values were determined and rankings of countries showing their current ICT development state. These rankings are presented in Table 7, which also includes the order of the countries considered according to the IDI ranking from 2017 [13]. The ranking is also the ranking of the NEAT F-PROMETHEE II method.

Table 7.
The outranking flow values and rankings of the regional ICT development for 2017.
Comparing the ranking of NEAT F-PROMETHEE II (Rank ) and ranking of IDI, it is easy to notice that they differ to some extent. These differences are mainly caused by the specific type of normalisation mentioned in the introduction, used in IDI. This normalisation causes average and above average values of a given indicator in IDI to be just as well rewarded (it is enough for it to be at the reference level). Therefore, the high values of a given indicator are greatly limited in the standardisation process. Differences between the PROMETHEE and IDI rankings also result from the fact that PROMETHEE, unlike IDI, takes into account preference uncertainty (preference threshold is used) and relationships between the surveyed countries (pairwise comparisons are used). Nevertheless, in both rankings, Estonia, Slovenia and Latvia are considered to be the most developed countries in terms of ICT level in households, and Romania is considered to be the least developed country.
The NEAT F-PROMETHEE I ranking was built on the basis of partial rankings (Rank , Rank ), and is presented in Figure 3. This ranking confirms the dominant position of Estonia, as well as Slovenia, Latvia and Lithuania, and the lowest positions of Bulgaria and Romania in terms of current ICT development. In turn, Hungary and the Czech Republic, the Czech Republic and Poland, and Croatia, Poland and Slovakia were considered incomparable.
Figure 3.
Ranking of the regional ICT development in 2017, based on the NEAT F-PROMETHEE I method.
After analysing the current situation, the forecast of ICT development in households of particular countries was set for the period of 2018–2020. At the outset, the fuzzy values in Table 8 were obtained for each country based on the fuzzy performance table presented in Table 5.

Table 8.
Forecasted outranking flow fuzzy values.
After the defuzzification of values presented in Table 8, the crisp values were obtained, which form the basis for determining the forecasted NEAT F-PROMETHEE I and II rankings. The defuzzified values of outranking flows and the rankings generated on their basis are presented in Table 9.

Table 9.
Forecasted crisp values of outranking flows.
The ranking is also the ranking of the NEAT F-PROMETHEE II method. Figure 4 shows the ranking of NEAT F-PROMETHEE II, together with the representation of forecasted fuzzy and crisp outranking flows values.
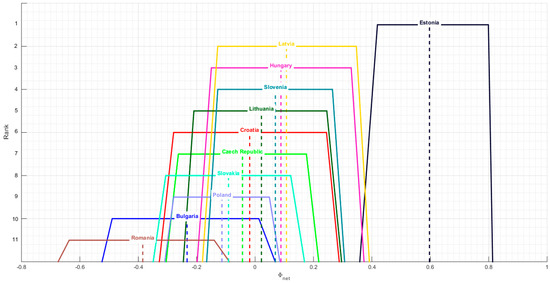
Figure 4.
Forecasted ranking of regional ICT development for the period 2018–2020, based on the NEAT F-PROMETHEE II method.
The analysis of Table 9 and Figure 4 shows that Estonia will be the country that will dominate the analysed countries in the future in terms of ICT development. Its advantage over other countries in the forecasted period is so great that there is only a minimal chance for Estonia to be overtaken by Latvia and Hungary, which is confirmed in Figure 4. The next countries in the ranking obtained similar forecasted values for ICT development and trapezoids representing their predicted fuzzy assessment overlap, meaning that their mutual order in the forecasted period may change. This observation is less relevant for Bulgaria and Romania, which are in the last positions in the ranking.
The forecasted ranking of NEAT F-PROMETHEE I was built on the basis of partial rankings (Rank , Rank ), and it is presented in Figure 5. This ranking confirms the dominant position of Estonia in the developed forecast and indicates the advantage of Hungary, Latvia and Slovenia over other countries.

Figure 5.
Forecasted ranking of regional ICT development for the period 2018–2020, based on the NEAT F-PROMETHEE I method.
Comparison of the ranking and values presented in Table 7 (current state) with the ranking and values included in Table 9 (forecast for the period 2018–2020) makes it possible to determine the dynamics of ICT development in particular countries in the near future. Changes in the rankings are presented in Figure 6. This comparison shows that Estonia will continue to grow dynamically, maintaining its dominant position among Central and Eastern European countries in the use of ICT in households. The most dynamic development is expected for Hungary, which should advance from the 6th position in 2017 to the 3rd place in the near future, moving ahead of countries such as the Czech Republic, Lithuania and Slovakia. Latvia, Croatia and Slovakia are expected to be promoted by one position, and declines in the ICT ranking are forecasted for Slovenia, Lithuania, the Czech Republic and Poland.
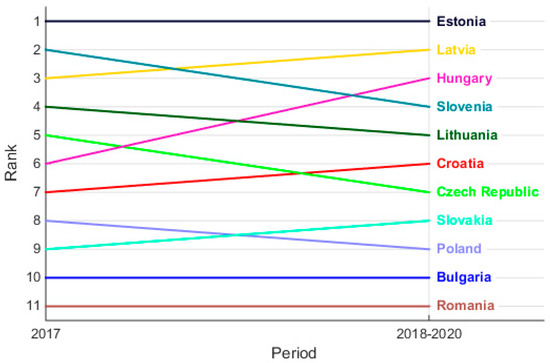
Figure 6.
Changes in NEAT F-PROMETHEE II rankings for 2017 and 2018–2020.
4.3. Testing the Resilience of Rankings to Changes in the Degree of Uncertainty of Preferences
To test the robustness of the obtained rankings to changes in the degree of uncertainty of preferences, additionally, the test was repeated with the use of the so-called usual criterion; that is, for situations where preferences are certain, the preference threshold is not used. From the current status study for 2017, the rankings presented in Table 10 were obtained. By analysing the partial rankings (Rank and Rank ), it is easy to notice that NEAT F-PROMETHEE I and II rankings are the same, which results from the usual criterion.

Table 10.
Values of outranking flows and rankings of the regional ICT development for 2017 obtained using the usual criterion.
The application of certain preferences does not change the four top (Estonia, Slovenia, Latvia, Lithuania) or the two final positions (Bulgaria and Romania) in the ranking of NEAT F-PROMETHEE II. Hungary and Poland also maintain their position in this ranking. In turn, the Czech Republic drops from position 5 to 7, Croatia from position 7 to 9, and Slovakia moves up from position 9 to 5 (compare with Table 7). Compared to the NEAT F-PROMETHEE I ranking established using preference thresholds, the ranking generated on the basis of the usual criterion achieved full comparability of countries, with Hungary predominating over the Czech Republic, the Czech Republic over Poland, and Poland over Croatia. The position of Slovakia, which dominates over Hungary, the Czech Republic, Poland and Croatia, has also changed significantly (compared with Figure 3).
The application of certain preferences for the forecasted values of ICT indicators for 2018–2020 made it possible to obtain the forecasted rankings presented in Table 11. Figure 7, in addition, presents a graphic representation of forecasted fuzzy and crisp outranking flows values.

Table 11.
Crisp outranking flows values, forecast for 2018–2020 using the usual criterion.
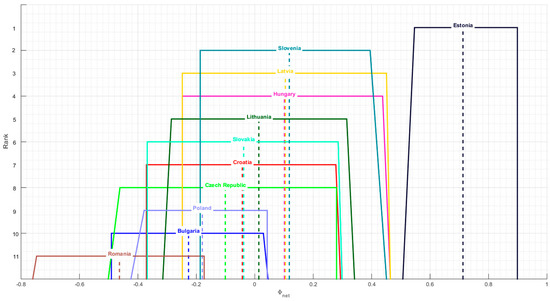
Figure 7.
Forecasted ranking of regional ICT development for the period 2018–2020, based on the NEAT F-PROMETHEE II method, obtained using the usual criterion.
Similar to the calculations for 2017, it is also easy to notice that the NEAT F-PROMETHEE I and II rankings are the same in the case of the forecast for 2018–2020. In comparison to the forecasted NEAT F-PROMETHEE II ranking, obtained with the use of uncertain preferences, Table 11 shows changes in the following positions: 2–4 and 6–8. The sequence of countries in the NEAT F-PROMETHEE I ranking has also changed. These changes result from the fact that the uncertain preferences in the rankings presented in Table 11 are not taken into account. The effect of not considering the uncertainty of preferences is particularly noticeable when comparing Figure 4 and Figure 7. Trapezoid fuzzy numbers, representing the assessment of individual countries, shown in Figure 4 have more inclined shoulders, but at the same time have narrower kernels than the trapezoid fuzzy numbers in Figure 7. This, paradoxically, means that with the elimination of uncertainty of preferences, the uncertainty of the aggregated assessments of countries has increased. Therefore, it should be noted that the use of fuzzy and uncertain preferences together with uncertain and fuzzy input ratings in the case of forecasts is a more appropriate action than the use of certain preferences and uncertain ratings.
5. Conclusions
The phenomenon of digital exclusion may give rise to several dilemmas. In the conducted research, it was necessary to obtain answers to further questions. How to measure them? What are the appropriate parameters? Where does this happen? What is its scope, or how big is the digital divide? In which regions is its level critical, or will be in future? What regions are or will be threatened by this phenomenon? An incentive to further research on digital exclusion may be the search for answers to other questions: What are its causes? What are the effects in the short and long-term? What should be done to alleviate them?
Souter [57] analysed this issue from a broader perspective, and stated that digital divides are hard to bridge by digital policies alone. First, they’re rooted in structural inequalities, second, although access and usage in developing countries are growing fast, the other side of the divide is always moving further distant. One of Souter’s postulates is that we should concentrate on overall development strategies concerned with reducing poverty, inequality and educational disadvantage that will have most effect on bridging digital divides within societies. The digital divide cannot be completely eliminated because it is also a constant pursuit of innovations introduced in richer societies. From this it follows that we should not slow down the processes of its levelling.
The article assesses the level of regional ICT development in households living in Central and Eastern European countries belonging to the European Union and a forecast of this phenomenon for the coming years (2018–2020) was prepared. The ICT development has been identified with the concept of technological expansion in a specific region. The aspect of innovation and the level of advancement of ICT was omitted due to maintaining the comparability of the obtained rankings with IDI. The ICT development is characterised by indicators specifying the percentage of its users, broken down into access, use and ICT skills. The obtained research results can be interpreted as follows: the higher the relative level of ICT development in a given country, the smaller the number of households (natural persons) excluded digitally.
The comparative analysis of the obtained results of the current state and forecasts of ICT development in the examined countries of Central and Eastern Europe confirmed that the intensive expansion of this technology has not only created many opportunities for social and economic development, but also introduced divisions and inequalities perceived as digital exclusion. In 2017, with regard to the society of Estonia, in which the highest level of ICT development was noted, Romania, Bulgaria, Slovakia and Poland were digitally included in the countries with the largest percentage of the excluded population. The results of fuzzy forecasts showed that this trend for these countries will continue in the period 2018–2020. A slight change may only affect Poland and Slovakia, which will exchange their position with respect to one another in the ranking (Figure 6). Important management information is the answer to the question about countries in which this negative phenomenon will increase. The forecasts indicated that the upward trend in the threat of digital exclusion was clearly marked in the Czech Republic, Slovenia and, to a lesser extent, in Lithuania. These results could be an impulse to verify the anticipated threat state and diagnose its causes.
The framework developed for the needs of evaluation and forecasting based on fuzzy numbers as opposed to the IDI methodology did not limit the ranges of values used for the entry of indicators (criteria) of ICT, it made it possible to take into account the uncertainty of preferences (preference thresholds were used) and dependencies between the studied countries (pairwise comparisons were used). These differences caused the rankings of the Central and Eastern European countries for 2017 obtained by using both methods to be partly different from each other (Table 7). The changes did not include: Estonia, Slovenia and Latvia, occupying the same order on the podium in both studies, or Romania, which remained in the last place.
A comparative study of the robustness of the obtained rankings to changes in the uncertainty of preferences using the NEAT F-PROMETHEE method proved that taking into account certain preferences together with uncertain (fuzzy) forecasts of indicators is less beneficial than using uncertain preferences and indicators. The failure to take into account the uncertainty of preferences (exclusion of preference thresholds) resulted in increasing the uncertainty of the aggregated, fuzzy estimates obtained at the output (see the trapezoids in Figure 4 and Figure 7).
Summing up, the framework developed for the evaluation and forecasting of the framework based on the fuzzy NEAT F-PROMETHEE method allowed to take into account the uncertainty of input data, which is particularly burdened with the forecast values of the ICT development indicators. At the same time, it gave the opportunity to express the uncertainty of preferences, representing the advantage of one country over another in terms of a given indicator.
During the research, some possible areas were identified in which the framework could be developed. The development could include new elements, making it possible to carry out a broader analysis of the obtained fuzzy solution to a decision problem. First of all, it would be interesting to prepare a development of the GAIA (Geometrical Analysis for Interactive Assistance) analysis [56] for fuzzy numbers, which, in consequence, would allow the analysis of the fuzzy decision problem from a descriptive perspective. Moreover, further research ought to deal with the development of an ontology [58] for sustainability decision problems where there is uncertainty of input data relating to the performance of alternatives, weights of criteria and the decision-maker’s preferences. Presenting the fuzzy decision problem dealing with sustainability in the form of an ontology would make it possible to infer new knowledge [59,60] from the decision model. Yet another interesting research challenge would be to prepare global sensitivity and uncertainty analyses (GSUA) that can highlight the uncertainty, sensitivity and complexity of the model/data and indicate potential management strategies in relation to the modelled patterns. GSUA typically assigns probability distribution functions to all model factors and propagate that into model outputs. Thus, GSUA informs about the dynamics of the processes investigated. It is also very important for management purposes, for instance for defining one systemic indicator [61,62].
Author Contributions
P.Z. developed methodological, research and application assumptions of the article and wrote Section 3.1, Section 3.2.3, Section 3.3 and Section 4.2. J.B. elaborated the procedure of forecast and fuzzy aggregation, performed data processing and wrote Section 2, Section 3.2.1, Section 3.2.2 and Section 5. The following sections were prepared and written jointly by both authors: 1, 4.1, 4.3. Both authors reviewed the paper. All authors have read and approved the final manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Values of Indicators in 2010–2017

Table A1.
Values of the MCS indicators in 2010–2017.
Table A1.
Values of the MCS indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 136.1 | 140.7 | 148.1 | 145.2 | 132.4 | 129.3 | 127.2 | 127.2 |
| Croatia | 111.9 | 116.4 | 115.4 | 114.5 | 104.4 | 103.8 | 104.1 | 104.1 |
| Czech Republic | 121.7 | 121.6 | 126.8 | 131.3 | 129.5 | 115.6 | 115.5 | 115.5 |
| Estonia | 123.2 | 139.0 | 160.4 | 159.7 | 160.7 | 148.7 | 148.7 | 148.7 |
| Hungary | 120.3 | 117.3 | 116.1 | 116.4 | 118.1 | 118.9 | 119.1 | 119.1 |
| Latvia | 102.4 | 102.9 | 112.1 | 136.6 | 116.8 | 127.5 | 131.2 | 131.2 |
| Lithuania | 147.2 | 151.3 | 165.1 | 151.3 | 141.9 | 139.5 | 140.7 | 140.7 |
| Poland | 122.7 | 128.5 | 141.5 | 150.0 | 148.9 | 142.7 | 146.2 | 146.2 |
| Romania | 113.6 | 109.2 | 105.0 | 105.6 | 105.9 | 107.1 | 106.4 | 106.4 |
| Slovakia | 108.5 | 109.3 | 111.9 | 113.9 | 116.9 | 122.3 | 128.0 | 128.0 |
| Slovenia | 104.5 | 106.6 | 108.4 | 110.2 | 112.1 | 113.2 | 114.6 | 114.6 |

Table A2.
Values of the IIB indicators in 2010–2017.
Table A2.
Values of the IIB indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 136.1 | 140.7 | 148.1 | 145.2 | 132.4 | 129.3 | 127.2 | 127.2 |
| Croatia | 111.9 | 116.4 | 115.4 | 114.5 | 104.4 | 103.8 | 104.1 | 104.1 |
| Czech Republic | 121.7 | 121.6 | 126.8 | 131.3 | 129.5 | 115.6 | 115.5 | 115.5 |
| Estonia | 123.2 | 139.0 | 160.4 | 159.7 | 160.7 | 148.7 | 148.7 | 148.7 |
| Hungary | 120.3 | 117.3 | 116.1 | 116.4 | 118.1 | 118.9 | 119.1 | 119.1 |
| Latvia | 102.4 | 102.9 | 112.1 | 136.6 | 116.8 | 127.5 | 131.2 | 131.2 |
| Lithuania | 147.2 | 151.3 | 165.1 | 151.3 | 141.9 | 139.5 | 140.7 | 140.7 |
| Poland | 122.7 | 128.5 | 141.5 | 150.0 | 148.9 | 142.7 | 146.2 | 146.2 |
| Romania | 113.6 | 109.2 | 105.0 | 105.6 | 105.9 | 107.1 | 106.4 | 106.4 |
| Slovakia | 108.5 | 109.3 | 111.9 | 113.9 | 116.9 | 122.3 | 128.0 | 128.0 |
| Slovenia | 104.5 | 106.6 | 108.4 | 110.2 | 112.1 | 113.2 | 114.6 | 114.6 |

Table A3.
Values of the PHC indicators in 2010–2017.
Table A3.
Values of the PHC indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 35.1 | 38.0 | 52.3 | 54.9 | 57.9 | 59.0 | 60.2 | 60.2 |
| Croatia | 60.0 | 64.0 | 68.0 | 66.3 | 70.1 | 76.8 | 79.5 | 79.5 |
| Czech Republic | 64.1 | 69.0 | 67.3 | 73.9 | 78.5 | 73.1 | 75.6 | 75.6 |
| Estonia | 69.2 | 75.3 | 75.5 | 80.0 | 82.5 | 87.9 | 89.6 | 89.6 |
| Hungary | 66.4 | 71.8 | 71.4 | 73.1 | 74.0 | 75.0 | 76.4 | 76.4 |
| Latvia | 62.8 | 64.5 | 69.5 | 71.7 | 73.5 | 76.1 | 78.0 | 78.0 |
| Lithuania | 59.2 | 63.1 | 63.6 | 65.9 | 66.8 | 67.6 | 70.5 | 70.5 |
| Poland | 69.0 | 73.0 | 73.4 | 74.7 | 77.7 | 77.9 | 80.1 | 80.1 |
| Romania | 47.9 | 52.9 | 56.7 | 61.2 | 63.8 | 68.7 | 74.0 | 74.0 |
| Slovakia | 72.2 | 79.4 | 78.8 | 80.1 | 80.5 | 80.5 | 80.9 | 81.0 |
| Slovenia | 70.5 | 75.1 | 76.1 | 76.4 | 77.1 | 77.8 | 78.1 | 78.1 |

Table A4.
Values of the PHI indicators in 2010–2017.
Table A4.
Values of the PHI indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 33.1 | 45.0 | 50.9 | 53.7 | 56.7 | 59.1 | 63.5 | 63.5 |
| Croatia | 56.5 | 61.4 | 66.4 | 64.6 | 68.4 | 76.7 | 77.2 | 77.3 |
| Czech Republic | 60.5 | 66.6 | 65.4 | 72.6 | 78.0 | 73.1 | 76.1 | 76.1 |
| Estonia | 67.8 | 70.8 | 75.0 | 80.3 | 82.9 | 87.7 | 86.2 | 86.2 |
| Hungary | 60.5 | 65.2 | 68.6 | 71.5 | 75.1 | 75.6 | 78.6 | 78.6 |
| Latvia | 59.8 | 63.6 | 68.7 | 71.6 | 73.4 | 76.0 | 77.3 | 77.3 |
| Lithuania | 60.6 | 61.8 | 61.6 | 64.7 | 66.0 | 68.3 | 71.7 | 71.8 |
| Poland | 63.4 | 66.6 | 70.5 | 71.9 | 74.8 | 75.8 | 80.4 | 80.5 |
| Romania | 42.2 | 47.4 | 53.8 | 58.1 | 60.5 | 67.7 | 72.4 | 72.4 |
| Slovakia | 67.5 | 70.8 | 75.4 | 77.9 | 78.4 | 79.5 | 80.5 | 80.5 |
| Slovenia | 68.1 | 72.6 | 73.9 | 75.6 | 76.8 | 77.6 | 78.4 | 78.4 |

Table A5.
Values of the IU indicators in 2010–2017.
Table A5.
Values of the IU indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 46.2 | 51.0 | 51.9 | 53.1 | 55.5 | 56.7 | 59.8 | 59.8 |
| Croatia | 60.3 | 70.7 | 61.9 | 66.7 | 68.6 | 69.8 | 72.7 | 72.7 |
| Czech Republic | 68.8 | 73.0 | 73.4 | 74.1 | 79.7 | 75.7 | 76.5 | 76.5 |
| Estonia | 74.1 | 76.5 | 78.4 | 80.0 | 84.2 | 88.4 | 87.2 | 87.2 |
| Hungary | 53.0 | 59.0 | 70.6 | 72.6 | 76.1 | 72.8 | 79.3 | 79.3 |
| Latvia | 68.4 | 71.7 | 73.1 | 75.2 | 75.8 | 79.2 | 79.9 | 79.9 |
| Lithuania | 62.1 | 65.1 | 67.2 | 68.5 | 72.1 | 71.4 | 74.4 | 74.4 |
| Poland | 62.3 | 64.9 | 62.3 | 62.8 | 66.6 | 68.0 | 73.3 | 73.3 |
| Romania | 39.9 | 44.0 | 45.9 | 49.8 | 54.1 | 55.8 | 59.5 | 59.5 |
| Slovakia | 75.7 | 74.4 | 76.7 | 77.9 | 80.0 | 77.6 | 80.5 | 80.5 |
| Slovenia | 70.0 | 72.0 | 68.3 | 72.7 | 71.6 | 73.1 | 75.5 | 75.5 |

Table A6.
Values of the FBB indicators in 2010–2017.
Table A6.
Values of the FBB indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 14.5 | 15.5 | 17.9 | 19.0 | 20.7 | 22.7 | 23.3 | 23.3 |
| Croatia | 18.3 | 19.5 | 20.7 | 21.5 | 23.0 | 23.2 | 24.6 | 24.6 |
| Czech Republic | 14.5 | 15.7 | 16.4 | 17.0 | 27.9 | 27.3 | 27.7 | 27.7 |
| Estonia | 25.1 | 27.1 | 25.5 | 26.5 | 28.9 | 30.0 | 31.1 | 31.1 |
| Hungary | 20.6 | 22.2 | 22.9 | 24.1 | 26.0 | 27.4 | 28.5 | 28.5 |
| Latvia | 19.3 | 20.4 | 23.3 | 24.7 | 24.7 | 24.8 | 25.6 | 25.6 |
| Lithuania | 20.6 | 22.1 | 21.1 | 22.0 | 26.7 | 27.8 | 28.7 | 28.7 |
| Poland | 13.0 | 14.4 | 15.6 | 15.6 | 18.9 | 19.0 | 19.2 | 19.2 |
| Romania | 14.0 | 15.4 | 16.1 | 17.3 | 18.6 | 19.8 | 20.7 | 20.7 |
| Slovakia | 12.7 | 13.6 | 14.7 | 15.5 | 21.8 | 23.3 | 24.5 | 24.5 |
| Slovenia | 23.7 | 24.8 | 24.3 | 25.0 | 26.8 | 27.4 | 28.3 | 28.3 |

Table A7.
Values of the MBB indicators in 2010–2017.
Table A7.
Values of the MBB indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 8.0 | 14.5 | 48.5 | 58.6 | 66.4 | 81.3 | 88.4 | 88.4 |
| Croatia | 7.5 | 6.6 | 53.9 | 66.1 | 68.5 | 73.1 | 79.7 | 79.7 |
| Czech Republic | 34.1 | 43.1 | 52.1 | 54.4 | 66.7 | 72.0 | 76.0 | 76.0 |
| Estonia | 24.0 | 42.0 | 76.9 | 78.9 | 117.0 | 112.9 | 125.0 | 125.0 |
| Hungary | 7.8 | 13.2 | 24.2 | 27.5 | 34.0 | 39.8 | 44.5 | 44.5 |
| Latvia | 27.5 | 37.6 | 58.2 | 61.2 | 61.2 | 67.0 | 77.0 | 77.0 |
| Lithuania | 14.2 | 17.2 | 41.4 | 53.8 | 70.2 | 67.6 | 76.8 | 76.8 |
| Poland | 50.0 | 48.4 | 63.6 | 59.5 | 55.7 | 57.4 | 58.9 | 58.9 |
| Romania | 10.7 | 14.1 | 27.0 | 37.7 | 49.3 | 63.7 | 73.7 | 73.7 |
| Slovakia | 20.7 | 31.9 | 39.7 | 54.9 | 59.5 | 67.5 | 78.7 | 78.7 |
| Slovenia | 24.4 | 29.3 | 36.7 | 42.1 | 46.7 | 52.0 | 62.3 | 62.3 |

Table A8.
Values of the GSE indicators in 2010–2017.
Table A8.
Values of the GSE indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 88.0 | 88.0 | 93.1 | 93.1 | 100.9 | 100.9 | 99.0 | 99.0 |
| Croatia | 95.3 | 95.3 | 98.4 | 98.4 | 98.4 | 98.4 | 99.0 | 99.0 |
| Czech Republic | 90.4 | 90.4 | 96.6 | 96.6 | 104.4 | 104.4 | 105.1 | 105.1 |
| Estonia | 103.6 | 103.6 | 107.1 | 107.1 | 108.6 | 108.6 | 115.2 | 115.2 |
| Hungary | 98.3 | 98.3 | 101.6 | 101.6 | 108.2 | 108.2 | 105.2 | 105.2 |
| Latvia | 95.2 | 95.2 | 97.7 | 97.7 | 110.5 | 110.5 | 115.4 | 115.4 |
| Lithuania | 98.0 | 98.0 | 105.9 | 105.9 | 105.4 | 105.4 | 106.8 | 106.8 |
| Poland | 97.0 | 97.0 | 97.7 | 97.7 | 108.7 | 108.7 | 108.7 | 108.7 |
| Romania | 95.1 | 95.1 | 95.0 | 95.0 | 97.9 | 97.9 | 92.3 | 92.3 |
| Slovakia | 89.4 | 89.4 | 93.9 | 93.9 | 91.8 | 91.8 | 91.9 | 91.9 |
| Slovenia | 97.1 | 97.1 | 97.6 | 97.6 | 110.9 | 110.9 | 110.7 | 110.7 |

Table A9.
Values of the GTE indicators in 2010–2017.
Table A9.
Values of the GTE indicators in 2010–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 53.0 | 53.0 | 62.7 | 62.7 | 70.8 | 70.8 | 73.9 | 73.9 |
| Croatia | 49.2 | 49.2 | 61.6 | 61.6 | 61.6 | 61.6 | 69.5 | 69.5 |
| Czech Republic | 60.7 | 60.7 | 64.2 | 64.2 | 65.4 | 65.4 | 66.0 | 66.0 |
| Estonia | 62.7 | 62.7 | 76.7 | 76.7 | 72.9 | 72.9 | 69.6 | 69.6 |
| Hungary | 61.7 | 61.7 | 59.6 | 59.6 | 57.0 | 57.0 | 50.9 | 50.9 |
| Latvia | 60.1 | 60.1 | 65.1 | 65.1 | 67.0 | 67.0 | 67.0 | 67.0 |
| Lithuania | 77.4 | 77.4 | 73.9 | 73.9 | 72.0 | 72.0 | 68.5 | 68.5 |
| Poland | 70.5 | 70.5 | 73.2 | 73.2 | 71.2 | 71.2 | 71.2 | 71.2 |
| Romania | 63.8 | 63.8 | 51.6 | 51.6 | 52.2 | 52.2 | 53.2 | 53.2 |
| Slovakia | 54.2 | 54.2 | 55.1 | 55.1 | 54.4 | 54.4 | 52.9 | 52.9 |
| Slovenia | 86.9 | 86.9 | 86.0 | 86.0 | 85.2 | 85.2 | 82.9 | 82.9 |

Table A10.
Values of the MYS indicators in 2014–2017.
Table A10.
Values of the MYS indicators in 2014–2017.
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | - | - | - | - | 10.6 | 10.6 | 10.8 | 10.8 |
| Croatia | - | - | - | - | 11.0 | 11.0 | 11.2 | 11.2 |
| Czech Republic | - | - | - | - | 12.3 | 12.3 | 12.3 | 12.3 |
| Estonia | - | - | - | - | 12.5 | 12.5 | 12.5 | 12.5 |
| Hungary | - | - | - | - | 11.6 | 11.6 | 12.0 | 12.0 |
| Latvia | - | - | - | - | 11.5 | 11.5 | 11.7 | 11.7 |
| Lithuania | - | - | - | - | 12.7 | 12.7 | 12.7 | 12.7 |
| Poland | - | - | - | - | 11.9 | 11.9 | 11.9 | 11.9 |
| Romania | - | - | - | - | 10.6 | 10.6 | 10.8 | 10.8 |
| Slovakia | - | - | - | - | 12.1 | 12.1 | 12.2 | 12.2 |
| Slovenia | - | - | - | - | 12.1 | 12.1 | 12.1 | 12.1 |
Appendix B. Change Dynamics in 2011–2017 and Forecast of Indicators in 2018–2020

Table A11.
Change dynamics and forecast of the MCS indicator values.
Table A11.
Change dynamics and forecast of the MCS indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.03 | 1.05 | 0.98 | 0.91 | 0.98 | 0.98 | 1.00 | 0.99 | 126.01 | 124.80 | 123.61 |
| Croatia | 1.04 | 0.99 | 0.99 | 0.91 | 0.99 | 1.00 | 1.00 | 0.99 | 103.04 | 101.99 | 100.94 |
| Czech Republic | 1.00 | 1.04 | 1.04 | 0.99 | 0.89 | 1.00 | 1.00 | 0.99 | 114.61 | 113.75 | 112.90 |
| Estonia | 1.13 | 1.15 | 1.00 | 1.01 | 0.93 | 1.00 | 1.00 | 1.03 | 152.73 | 156.88 | 161.15 |
| Hungary | 0.98 | 0.99 | 1.00 | 1.01 | 1.01 | 1.00 | 1.00 | 1.00 | 118.94 | 118.77 | 118.60 |
| Latvia | 1.00 | 1.09 | 1.22 | 0.86 | 1.09 | 1.03 | 1.00 | 1.04 | 135.88 | 140.77 | 145.84 |
| Lithuania | 1.03 | 1.09 | 0.92 | 0.94 | 0.98 | 1.01 | 1.00 | 0.99 | 139.81 | 138.91 | 138.02 |
| Poland | 1.05 | 1.10 | 1.06 | 0.99 | 0.96 | 1.02 | 1.00 | 1.03 | 149.92 | 153.72 | 157.62 |
| Romania | 0.96 | 0.96 | 1.01 | 1.00 | 1.01 | 0.99 | 1.00 | 0.99 | 105.44 | 104.47 | 103.50 |
| Slovakia | 1.01 | 1.02 | 1.02 | 1.03 | 1.05 | 1.05 | 1.00 | 1.02 | 131.05 | 134.18 | 137.38 |
| Slovenia | 1.02 | 1.02 | 1.02 | 1.02 | 1.01 | 1.01 | 1.00 | 1.01 | 116.07 | 117.61 | 119.16 |

Table A12.
Change dynamics and forecast of the IIB indicator values.
Table A12.
Change dynamics and forecast of the IIB indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.03 | 1.38 | 1.18 | 1.26 | 1.13 | 1.15 | 1.00 | 1.15 | 203104.53 | 234557.56 | 270881.45 |
| Croatia | 0.96 | 1.88 | 1.08 | 1.43 | 0.98 | 2.09 | 1.00 | 1.28 | 152660.03 | 195919.13 | 251436.51 |
| Czech Republic | 1.32 | 1.12 | 1.09 | 1.00 | 1.45 | 1.12 | 1.00 | 1.15 | 207235.08 | 237671.20 | 272577.40 |
| Estonia | 1.05 | 1.09 | 1.09 | 0.98 | 6.07 | 1.21 | 1.00 | 1.37 | 289019.37 | 396267.11 | 543311.74 |
| Hungary | 1.00 | 1.28 | 1.59 | 1.49 | 0.36 | 11.48 | 1.00 | 1.44 | 222260.59 | 319192.59 | 458398.44 |
| Latvia | 1.44 | 1.33 | 1.14 | 1.38 | 0.23 | 11.57 | 1.00 | 1.34 | 331501.43 | 445514.74 | 598740.67 |
| Lithuania | 1.27 | 1.34 | 1.29 | 1.26 | 1.11 | 1.43 | 1.00 | 1.23 | 245140.53 | 302641.83 | 373630.90 |
| Poland | 1.07 | 1.36 | 1.34 | 1.10 | 0.97 | 1.06 | 1.00 | 1.12 | 93277.12 | 104451.00 | 116963.43 |
| Romania | 1.69 | 1.10 | 1.09 | 0.86 | 1.24 | 1.07 | 1.00 | 1.13 | 175170.43 | 197309.34 | 222246.27 |
| Slovakia | 1.02 | 0.97 | 0.98 | 1.27 | 2.77 | 1.27 | 1.00 | 1.23 | 64542.17 | 79573.10 | 98104.50 |
| Slovenia | 0.97 | 1.42 | 1.58 | 0.79 | 1.54 | 1.28 | 1.00 | 1.19 | 284834.13 | 339220.27 | 403990.88 |

Table A13.
Change dynamics and forecast of the PHC indicator values.
Table A13.
Change dynamics and forecast of the PHC indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.08 | 1.38 | 1.05 | 1.05 | 1.02 | 1.02 | 1.00 | 1.08 | 65.05 | 70.26 | 75.89 |
| Croatia | 1.07 | 1.06 | 0.98 | 1.06 | 1.10 | 1.04 | 1.00 | 1.04 | 82.70 | 86.09 | 89.61 |
| Czech Republic | 1.08 | 0.98 | 1.10 | 1.06 | 0.93 | 1.03 | 1.00 | 1.02 | 77.37 | 79.21 | 81.09 |
| Estonia | 1.09 | 1.00 | 1.06 | 1.03 | 1.07 | 1.02 | 1.00 | 1.04 | 92.95 | 96.44 | 100.06 |
| Hungary | 1.08 | 0.99 | 1.02 | 1.01 | 1.01 | 1.02 | 1.00 | 1.02 | 77.95 | 79.52 | 81.13 |
| Latvia | 1.03 | 1.08 | 1.03 | 1.03 | 1.04 | 1.02 | 1.00 | 1.03 | 80.48 | 83.01 | 85.62 |
| Lithuania | 1.07 | 1.01 | 1.04 | 1.01 | 1.01 | 1.04 | 1.00 | 1.03 | 72.23 | 74.05 | 75.92 |
| Poland | 1.06 | 1.01 | 1.02 | 1.04 | 1.00 | 1.03 | 1.00 | 1.02 | 81.83 | 83.59 | 85.39 |
| Romania | 1.10 | 1.07 | 1.08 | 1.04 | 1.08 | 1.08 | 1.00 | 1.06 | 78.70 | 83.73 | 89.09 |
| Slovakia | 1.10 | 0.99 | 1.02 | 1.00 | 1.00 | 1.00 | 1.00 | 1.02 | 82.28 | 83.64 | 85.02 |
| Slovenia | 1.07 | 1.01 | 1.00 | 1.01 | 1.01 | 1.00 | 1.00 | 1.01 | 79.19 | 80.35 | 81.53 |

Table A14.
Change dynamics and forecast of the PHI indicator values.
Table A14.
Change dynamics and forecast of the PHI indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.36 | 1.13 | 1.06 | 1.06 | 1.04 | 1.07 | 1.00 | 1.10 | 69.74 | 76.55 | 84.03 |
| Croatia | 1.09 | 1.08 | 0.97 | 1.06 | 1.12 | 1.01 | 1.00 | 1.05 | 80.78 | 84.47 | 88.33 |
| Czech Republic | 1.10 | 0.98 | 1.11 | 1.07 | 0.94 | 1.04 | 1.00 | 1.03 | 78.60 | 81.21 | 83.91 |
| Estonia | 1.04 | 1.06 | 1.07 | 1.03 | 1.06 | 0.98 | 1.00 | 1.03 | 89.20 | 92.31 | 95.53 |
| Hungary | 1.08 | 1.05 | 1.04 | 1.05 | 1.01 | 1.04 | 1.00 | 1.04 | 81.62 | 84.73 | 87.96 |
| Latvia | 1.06 | 1.08 | 1.04 | 1.03 | 1.04 | 1.02 | 1.00 | 1.04 | 80.19 | 83.18 | 86.29 |
| Lithuania | 1.02 | 1.00 | 1.05 | 1.02 | 1.03 | 1.05 | 1.00 | 1.02 | 73.50 | 75.30 | 77.14 |
| Poland | 1.05 | 1.06 | 1.02 | 1.04 | 1.01 | 1.06 | 1.00 | 1.03 | 83.23 | 86.12 | 89.10 |
| Romania | 1.12 | 1.14 | 1.08 | 1.04 | 1.12 | 1.07 | 1.00 | 1.08 | 78.20 | 84.47 | 91.24 |
| Slovakia | 1.05 | 1.06 | 1.03 | 1.01 | 1.01 | 1.01 | 1.00 | 1.03 | 82.57 | 84.68 | 86.84 |
| Slovenia | 1.07 | 1.02 | 1.02 | 1.02 | 1.01 | 1.01 | 1.00 | 1.02 | 80.02 | 81.65 | 83.31 |

Table A15.
Change dynamics and forecast of the IU indicator values.
Table A15.
Change dynamics and forecast of the IU indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.10 | 1.02 | 1.02 | 1.05 | 1.02 | 1.05 | 1.00 | 1.04 | 62.08 | 64.42 | 66.84 |
| Croatia | 1.17 | 0.88 | 1.08 | 1.03 | 1.02 | 1.04 | 1.00 | 1.03 | 74.67 | 76.69 | 78.77 |
| Czech Republic | 1.06 | 1.01 | 1.01 | 1.08 | 0.95 | 1.01 | 1.00 | 1.02 | 77.65 | 78.83 | 80.03 |
| Estonia | 1.03 | 1.02 | 1.02 | 1.05 | 1.05 | 0.99 | 1.00 | 1.02 | 89.30 | 91.41 | 93.56 |
| Hungary | 1.11 | 1.20 | 1.03 | 1.05 | 0.96 | 1.09 | 1.00 | 1.06 | 83.95 | 88.92 | 94.18 |
| Latvia | 1.05 | 1.02 | 1.03 | 1.01 | 1.04 | 1.01 | 1.00 | 1.02 | 81.68 | 83.51 | 85.39 |
| Lithuania | 1.05 | 1.03 | 1.02 | 1.05 | 0.99 | 1.04 | 1.00 | 1.03 | 76.32 | 78.32 | 80.36 |
| Poland | 1.04 | 0.96 | 1.01 | 1.06 | 1.02 | 1.08 | 1.00 | 1.02 | 75.02 | 76.79 | 78.59 |
| Romania | 1.10 | 1.04 | 1.08 | 1.09 | 1.03 | 1.07 | 1.00 | 1.06 | 63.00 | 66.70 | 70.61 |
| Slovakia | 0.98 | 1.03 | 1.02 | 1.03 | 0.97 | 1.04 | 1.00 | 1.01 | 81.19 | 81.90 | 82.62 |
| Slovenia | 1.03 | 0.95 | 1.06 | 0.98 | 1.02 | 1.03 | 1.00 | 1.01 | 76.32 | 77.15 | 77.99 |

Table A16.
Change dynamics and forecast of the FBB indicator values.
Table A16.
Change dynamics and forecast of the FBB indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.07 | 1.15 | 1.06 | 1.09 | 1.10 | 1.03 | 1.00 | 1.07 | 24.87 | 26.61 | 28.46 |
| Croatia | 1.07 | 1.06 | 1.04 | 1.07 | 1.01 | 1.06 | 1.00 | 1.04 | 25.69 | 26.80 | 27.96 |
| Czech Republic | 1.08 | 1.04 | 1.04 | 1.64 | 0.98 | 1.01 | 1.00 | 1.10 | 30.32 | 33.25 | 36.46 |
| Estonia | 1.08 | 0.94 | 1.04 | 1.09 | 1.04 | 1.04 | 1.00 | 1.03 | 32.03 | 33.02 | 34.05 |
| Hungary | 1.08 | 1.03 | 1.05 | 1.08 | 1.05 | 1.04 | 1.00 | 1.05 | 29.80 | 31.21 | 32.69 |
| Latvia | 1.06 | 1.14 | 1.06 | 1.00 | 1.00 | 1.03 | 1.00 | 1.04 | 26.70 | 27.81 | 28.96 |
| Lithuania | 1.07 | 0.95 | 1.04 | 1.21 | 1.04 | 1.03 | 1.00 | 1.05 | 30.09 | 31.55 | 33.08 |
| Poland | 1.11 | 1.08 | 1.00 | 1.21 | 1.01 | 1.01 | 1.00 | 1.06 | 20.32 | 21.49 | 22.73 |
| Romania | 1.10 | 1.05 | 1.07 | 1.08 | 1.06 | 1.05 | 1.00 | 1.06 | 21.87 | 23.12 | 24.44 |
| Slovakia | 1.07 | 1.08 | 1.05 | 1.41 | 1.07 | 1.05 | 1.00 | 1.10 | 26.87 | 29.51 | 32.41 |
| Slovenia | 1.05 | 0.98 | 1.03 | 1.07 | 1.02 | 1.03 | 1.00 | 1.03 | 28.97 | 29.70 | 30.46 |

Table A17.
Change dynamics and forecast of the MBB indicator values.
Table A17.
Change dynamics and forecast of the MBB indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.81 | 3.34 | 1.21 | 1.13 | 1.22 | 1.09 | 1.00 | 1.41 | 124.56 | 175.56 | 247.44 |
| Croatia | 0.88 | 8.17 | 1.23 | 1.04 | 1.07 | 1.09 | 1.00 | 1.40 | 111.77 | 156.67 | 219.61 |
| Czech Republic | 1.26 | 1.21 | 1.04 | 1.23 | 1.08 | 1.06 | 1.00 | 1.12 | 85.24 | 95.59 | 107.19 |
| Estonia | 1.75 | 1.83 | 1.03 | 1.48 | 0.96 | 1.11 | 1.00 | 1.27 | 158.28 | 200.36 | 253.64 |
| Hungary | 1.69 | 1.83 | 1.14 | 1.24 | 1.17 | 1.12 | 1.00 | 1.28 | 57.01 | 73.10 | 93.74 |
| Latvia | 1.37 | 1.55 | 1.05 | 1.00 | 1.09 | 1.15 | 1.00 | 1.16 | 89.17 | 103.30 | 119.67 |
| Lithuania | 1.21 | 2.41 | 1.30 | 1.30 | 0.96 | 1.14 | 1.00 | 1.27 | 97.74 | 124.40 | 158.32 |
| Poland | 0.97 | 1.31 | 0.94 | 0.94 | 1.03 | 1.03 | 1.00 | 1.02 | 60.26 | 61.68 | 63.14 |
| Romania | 1.32 | 1.91 | 1.40 | 1.31 | 1.29 | 1.16 | 1.00 | 1.32 | 97.12 | 127.96 | 168.58 |
| Slovakia | 1.54 | 1.24 | 1.38 | 1.08 | 1.13 | 1.17 | 1.00 | 1.21 | 95.30 | 115.34 | 139.59 |
| Slovenia | 1.20 | 1.25 | 1.15 | 1.11 | 1.11 | 1.20 | 1.00 | 1.14 | 71.17 | 81.37 | 93.02 |

Table A18.
Change dynamics and forecast of the GSE indicator values.
Table A18.
Change dynamics and forecast of the GSE indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.00 | 1.06 | 1.00 | 1.08 | 1.00 | 0.98 | 1.00 | 1.02 | 100.70 | 102.41 | 104.16 |
| Croatia | 1.00 | 1.03 | 1.00 | 1.00 | 1.00 | 1.01 | 1.00 | 1.01 | 99.54 | 100.08 | 100.63 |
| Czech Republic | 1.00 | 1.07 | 1.00 | 1.08 | 1.00 | 1.01 | 1.00 | 1.02 | 107.42 | 109.76 | 112.16 |
| Estonia | 1.00 | 1.03 | 1.00 | 1.01 | 1.00 | 1.06 | 1.00 | 1.02 | 116.94 | 118.72 | 120.53 |
| Hungary | 1.00 | 1.03 | 1.00 | 1.06 | 1.00 | 0.97 | 1.00 | 1.01 | 106.22 | 107.26 | 108.30 |
| Latvia | 1.00 | 1.03 | 1.00 | 1.13 | 1.00 | 1.04 | 1.00 | 1.03 | 118.57 | 121.87 | 125.26 |
| Lithuania | 1.00 | 1.08 | 1.00 | 1.00 | 1.00 | 1.01 | 1.00 | 1.01 | 108.14 | 109.48 | 110.84 |
| Poland | 1.00 | 1.01 | 1.00 | 1.11 | 1.00 | 1.00 | 1.00 | 1.02 | 110.48 | 112.29 | 114.14 |
| Romania | 1.00 | 1.00 | 1.00 | 1.03 | 1.00 | 0.94 | 1.00 | 1.00 | 91.85 | 91.45 | 91.05 |
| Slovakia | 1.00 | 1.05 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 92.29 | 92.65 | 93.02 |
| Slovenia | 1.00 | 1.01 | 1.00 | 1.14 | 1.00 | 1.00 | 1.00 | 1.02 | 112.76 | 114.88 | 117.05 |

Table A19.
Change dynamics and forecast of the GTE indicator values.
Table A19.
Change dynamics and forecast of the GTE indicator values.
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.00 | 1.18 | 1.00 | 1.13 | 1.00 | 1.04 | 1.00 | 1.05 | 77.53 | 81.31 | 85.26 |
| Croatia | 1.00 | 1.25 | 1.00 | 1.00 | 1.00 | 1.13 | 1.00 | 1.05 | 73.06 | 76.77 | 80.66 |
| Czech Republic | 1.00 | 1.06 | 1.00 | 1.02 | 1.00 | 1.01 | 1.00 | 1.01 | 66.82 | 67.62 | 68.44 |
| Estonia | 1.00 | 1.22 | 1.00 | 0.95 | 1.00 | 0.95 | 1.00 | 1.01 | 70.59 | 71.64 | 72.71 |
| Hungary | 1.00 | 0.97 | 1.00 | 0.96 | 1.00 | 0.89 | 1.00 | 0.97 | 49.48 | 48.13 | 46.82 |
| Latvia | 1.00 | 1.08 | 1.00 | 1.03 | 1.00 | 1.00 | 1.00 | 1.02 | 68.09 | 69.17 | 70.25 |
| Lithuania | 1.00 | 0.95 | 1.00 | 0.97 | 1.00 | 0.95 | 1.00 | 0.98 | 67.35 | 66.19 | 65.05 |
| Poland | 1.00 | 1.04 | 1.00 | 0.97 | 1.00 | 1.00 | 1.00 | 1.00 | 71.25 | 71.35 | 71.44 |
| Romania | 1.00 | 0.81 | 1.00 | 1.01 | 1.00 | 1.02 | 1.00 | 0.97 | 51.86 | 50.53 | 49.24 |
| Slovakia | 1.00 | 1.02 | 1.00 | 0.99 | 1.00 | 0.97 | 1.00 | 1.00 | 52.74 | 52.56 | 52.38 |
| Slovenia | 1.00 | 0.99 | 1.00 | 0.99 | 1.00 | 0.97 | 1.00 | 0.99 | 82.38 | 81.83 | 81.28 |

Table A20.
Change dynamics and forecast of the MYS indicator values.
Table A20.
Change dynamics and forecast of the MYS indicator values.
| Country | Change Dynamics in 2015–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | - | - | - | - | 1.00 | 1.02 | 1.00 | 1.01 | 10.87 | 10.94 | 11.00 |
| Croatia | - | - | - | - | 1.00 | 1.02 | 1.00 | 1.01 | 11.27 | 11.34 | 11.40 |
| Czech Republic | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 12.30 | 12.30 | 12.30 |
| Estonia | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 12.50 | 12.50 | 12.50 |
| Hungary | - | - | - | - | 1.00 | 1.03 | 1.00 | 1.01 | 12.14 | 12.27 | 12.41 |
| Latvia | - | - | - | - | 1.00 | 1.02 | 1.00 | 1.01 | 11.77 | 11.84 | 11.90 |
| Lithuania | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 12.70 | 12.70 | 12.70 |
| Poland | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 11.90 | 11.90 | 11.90 |
| Romania | - | - | - | - | 1.00 | 1.02 | 1.00 | 1.01 | 10.87 | 10.94 | 11.00 |
| Slovakia | - | - | - | - | 1.00 | 1.01 | 1.00 | 1.00 | 12.23 | 12.27 | 12.30 |
| Slovenia | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 12.10 | 12.10 | 12.10 |
Appendix C. Forecasted Values of Indicators Aggregated to Fuzzy Numbers

Table A21.
Forecasted value of the MCS indicator for 2018–2020, aggregated to a single fuzzy number .
Table A21.
Forecasted value of the MCS indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 123.61 | 123.83 | 125.79 | 126.01 | 124.81 | 0.98 |
| Croatia | 100.94 | 101.13 | 102.85 | 103.04 | 101.99 | 0.86 |
| Czech Republic | 112.90 | 113.05 | 114.45 | 114.61 | 113.75 | 0.70 |
| Estonia | 152.73 | 153.48 | 160.36 | 161.15 | 156.92 | 3.44 |
| Hungary | 118.60 | 118.63 | 118.91 | 118.94 | 118.77 | 0.14 |
| Latvia | 135.88 | 136.77 | 144.90 | 145.84 | 140.83 | 4.07 |
| Lithuania | 138.02 | 138.18 | 139.64 | 139.81 | 138.91 | 0.73 |
| Poland | 149.92 | 150.61 | 156.90 | 157.62 | 153.75 | 3.14 |
| Romania | 103.50 | 103.67 | 105.26 | 105.44 | 104.47 | 0.79 |
| Slovakia | 131.05 | 131.62 | 136.79 | 137.38 | 134.20 | 2.59 |
| Slovenia | 116.07 | 116.35 | 118.88 | 119.16 | 117.62 | 1.26 |

Table A22.
Forecasted value of the IIB indicator for 2018–2020, aggregated to a single fuzzy number .
Table A22.
Forecasted value of the IIB indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 203104.53 | 208487.56 | 263874.80 | 270881.45 | 236181.18 | 27693.62 |
| Croatia | 152660.03 | 159576.52 | 240433.93 | 251436.51 | 200005.22 | 40428.70 |
| Czech Republic | 207235.08 | 212464.54 | 265857.91 | 272577.40 | 239161.23 | 26696.69 |
| Estonia | 289019.37 | 305295.40 | 513770.08 | 543311.74 | 409532.74 | 104237.34 |
| Hungary | 222260.59 | 236367.44 | 430200.31 | 458398.44 | 333283.87 | 96916.44 |
| Latvia | 331501.43 | 349094.86 | 568076.37 | 598740.67 | 458585.61 | 109490.76 |
| Lithuania | 245140.53 | 254585.54 | 359689.98 | 373630.90 | 307137.76 | 52552.22 |
| Poland | 93277.12 | 95222.14 | 114572.22 | 116963.43 | 104897.18 | 9675.04 |
| Romania | 175170.43 | 179012.06 | 217471.96 | 222246.27 | 198242.01 | 19229.95 |
| Slovakia | 64542.17 | 67013.34 | 94466.50 | 98104.50 | 80739.92 | 13726.58 |
| Slovenia | 284834.13 | 293974.69 | 391388.83 | 403990.88 | 342681.76 | 48707.07 |

Table A23.
Forecasted value of the PHC indicator for 2018–2020, aggregated to a single fuzzy number .
Table A23.
Forecasted value of the PHC indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 65.05 | 65.97 | 74.83 | 75.89 | 70.40 | 4.43 |
| Croatia | 82.70 | 83.31 | 88.95 | 89.61 | 86.13 | 2.82 |
| Czech Republic | 77.37 | 77.70 | 80.74 | 81.09 | 79.22 | 1.52 |
| Estonia | 92.95 | 93.58 | 99.38 | 100.06 | 96.48 | 2.90 |
| Hungary | 77.95 | 78.23 | 80.84 | 81.13 | 79.54 | 1.30 |
| Latvia | 80.48 | 80.94 | 85.14 | 85.62 | 83.04 | 2.10 |
| Lithuania | 72.23 | 72.57 | 75.57 | 75.92 | 74.07 | 1.50 |
| Poland | 81.83 | 82.15 | 85.05 | 85.39 | 83.60 | 1.45 |
| Romania | 78.70 | 79.59 | 88.09 | 89.09 | 83.84 | 4.25 |
| Slovakia | 82.28 | 82.53 | 84.76 | 85.02 | 83.65 | 1.12 |
| Slovenia | 79.19 | 79.40 | 81.31 | 81.53 | 80.36 | 0.95 |

Table A24.
Forecasted value of the PHI indicator for 2018–2020, aggregated to a single fuzzy number .
Table A24.
Forecasted value of the PHI indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 69.74 | 70.94 | 82.61 | 84.03 | 76.78 | 5.83 |
| Croatia | 80.78 | 81.44 | 87.61 | 88.33 | 84.53 | 3.08 |
| Czech Republic | 78.60 | 79.07 | 83.41 | 83.91 | 81.24 | 2.17 |
| Estonia | 89.20 | 89.76 | 94.93 | 95.53 | 92.34 | 2.58 |
| Hungary | 81.62 | 82.18 | 87.36 | 87.96 | 84.77 | 2.59 |
| Latvia | 80.19 | 80.73 | 85.71 | 86.29 | 83.22 | 2.49 |
| Lithuania | 73.50 | 73.83 | 76.80 | 77.14 | 75.31 | 1.48 |
| Poland | 83.23 | 83.76 | 88.54 | 89.10 | 86.15 | 2.39 |
| Romania | 78.20 | 79.32 | 89.97 | 91.24 | 84.64 | 5.33 |
| Slovakia | 82.57 | 82.96 | 86.44 | 86.84 | 84.70 | 1.74 |
| Slovenia | 80.02 | 80.31 | 83.00 | 83.31 | 81.66 | 1.34 |

Table A25.
Forecasted value of the IU indicator for 2018–2020, aggregated to a single fuzzy number .
Table A25.
Forecasted value of the IU indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 62.08 | 62.50 | 66.39 | 66.84 | 64.45 | 1.94 |
| Croatia | 74.67 | 75.04 | 78.38 | 78.77 | 76.71 | 1.67 |
| Czech Republic | 77.65 | 77.86 | 79.81 | 80.03 | 78.83 | 0.97 |
| Estonia | 89.30 | 89.68 | 93.16 | 93.56 | 91.42 | 1.74 |
| Hungary | 83.95 | 84.84 | 93.19 | 94.18 | 89.02 | 4.18 |
| Latvia | 81.68 | 82.02 | 85.04 | 85.39 | 83.53 | 1.51 |
| Lithuania | 76.32 | 76.68 | 79.98 | 80.36 | 78.33 | 1.65 |
| Poland | 75.02 | 75.34 | 78.26 | 78.59 | 76.80 | 1.46 |
| Romania | 63.00 | 63.66 | 69.88 | 70.61 | 66.77 | 3.11 |
| Slovakia | 81.19 | 81.32 | 82.49 | 82.62 | 81.90 | 0.58 |
| Slovenia | 76.32 | 76.47 | 77.83 | 77.99 | 77.15 | 0.68 |

Table A26.
Forecasted value of the FBB indicator for 2018–2020, aggregated to a single fuzzy number .
Table A26.
Forecasted value of the FBB indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 24.87 | 25.18 | 28.12 | 28.46 | 26.65 | 1.47 |
| Croatia | 25.69 | 25.89 | 27.74 | 27.96 | 26.81 | 0.93 |
| Czech Republic | 30.32 | 30.84 | 35.85 | 36.46 | 33.34 | 2.51 |
| Estonia | 32.03 | 32.21 | 33.86 | 34.05 | 33.03 | 0.82 |
| Hungary | 29.80 | 30.06 | 32.41 | 32.69 | 31.24 | 1.18 |
| Latvia | 26.70 | 26.90 | 28.74 | 28.96 | 27.82 | 0.92 |
| Lithuania | 30.09 | 30.35 | 32.80 | 33.08 | 31.58 | 1.22 |
| Poland | 20.32 | 20.53 | 22.49 | 22.73 | 21.51 | 0.98 |
| Romania | 21.87 | 22.09 | 24.19 | 24.44 | 23.14 | 1.05 |
| Slovakia | 26.87 | 27.34 | 31.86 | 32.41 | 29.60 | 2.26 |
| Slovenia | 28.97 | 29.10 | 30.32 | 30.46 | 29.71 | 0.61 |

Table A27.
Forecasted value of the MBB indicator for 2018–2020, aggregated to a single fuzzy number .
Table A27.
Forecasted value of the MBB indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 124.56 | 132.12 | 232.93 | 247.44 | 182.52 | 50.40 |
| Croatia | 111.77 | 118.46 | 206.92 | 219.61 | 162.69 | 44.23 |
| Czech Republic | 85.24 | 87.04 | 104.97 | 107.19 | 96.01 | 8.96 |
| Estonia | 158.28 | 165.07 | 243.11 | 253.64 | 204.09 | 39.02 |
| Hungary | 57.01 | 59.58 | 89.65 | 93.74 | 74.62 | 15.03 |
| Latvia | 89.17 | 91.59 | 116.51 | 119.67 | 104.05 | 12.46 |
| Lithuania | 97.74 | 102.03 | 151.61 | 158.32 | 126.82 | 24.79 |
| Poland | 60.26 | 60.52 | 62.87 | 63.14 | 61.69 | 1.18 |
| Romania | 97.12 | 101.96 | 160.49 | 168.58 | 131.22 | 29.26 |
| Slovakia | 95.30 | 98.63 | 134.85 | 139.59 | 116.74 | 18.11 |
| Slovenia | 71.17 | 72.93 | 90.78 | 93.02 | 81.85 | 8.92 |

Table A28.
Forecasted value of the GSE indicator for 2018–2020, aggregated to a single fuzzy number .
Table A28.
Forecasted value of the GSE indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 100.70 | 101.02 | 103.83 | 104.16 | 102.42 | 1.41 |
| Croatia | 99.54 | 99.64 | 100.53 | 100.63 | 100.08 | 0.44 |
| Czech Republic | 107.42 | 107.85 | 111.71 | 112.16 | 109.78 | 1.93 |
| Estonia | 116.94 | 117.26 | 120.20 | 120.53 | 118.73 | 1.47 |
| Hungary | 106.22 | 106.41 | 108.11 | 108.30 | 107.26 | 0.85 |
| Latvia | 118.57 | 119.17 | 124.63 | 125.26 | 121.90 | 2.73 |
| Lithuania | 108.14 | 108.39 | 110.59 | 110.84 | 109.49 | 1.10 |
| Poland | 110.48 | 110.81 | 113.80 | 114.14 | 112.30 | 1.49 |
| Romania | 91.05 | 91.13 | 91.78 | 91.85 | 91.45 | 0.32 |
| Slovakia | 92.29 | 92.35 | 92.95 | 93.02 | 92.65 | 0.30 |
| Slovenia | 112.76 | 113.14 | 116.65 | 117.05 | 114.90 | 1.75 |

Table A29.
Forecasted value of the GTE indicator for 2018-2020, aggregated to a single fuzzy number .
Table A29.
Forecasted value of the GTE indicator for 2018-2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 77.53 | 78.21 | 84.52 | 85.26 | 81.37 | 3.16 |
| Croatia | 73.06 | 73.73 | 79.93 | 80.66 | 76.83 | 3.10 |
| Czech Republic | 66.82 | 66.96 | 68.29 | 68.44 | 67.63 | 0.66 |
| Estonia | 70.59 | 70.78 | 72.51 | 72.71 | 71.65 | 0.87 |
| Hungary | 46.82 | 47.06 | 49.23 | 49.48 | 48.14 | 1.08 |
| Latvia | 68.09 | 68.29 | 70.05 | 70.25 | 69.17 | 0.88 |
| Lithuania | 65.05 | 65.25 | 67.13 | 67.35 | 66.19 | 0.94 |
| Poland | 71.25 | 71.27 | 71.43 | 71.44 | 71.35 | 0.08 |
| Romania | 49.24 | 49.48 | 51.61 | 51.86 | 50.54 | 1.07 |
| Slovakia | 52.38 | 52.41 | 52.71 | 52.74 | 52.56 | 0.15 |
| Slovenia | 81.28 | 81.38 | 82.28 | 82.38 | 81.83 | 0.45 |

Table A30.
Forecasted value of the MYS indicator for 2018–2020, aggregated to a single fuzzy number .
Table A30.
Forecasted value of the MYS indicator for 2018–2020, aggregated to a single fuzzy number .
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 10.87 | 10.88 | 10.99 | 11.00 | 10.94 | 0.06 |
| Croatia | 11.27 | 11.28 | 11.39 | 11.40 | 11.34 | 0.06 |
| Czech Republic | 12.30 | 12.30 | 12.30 | 12.30 | 12.30 | 0.00 |
| Estonia | 12.50 | 12.50 | 12.50 | 12.50 | 12.50 | 0.00 |
| Hungary | 12.14 | 12.16 | 12.39 | 12.41 | 12.27 | 0.11 |
| Latvia | 11.77 | 11.78 | 11.89 | 11.90 | 11.84 | 0.06 |
| Lithuania | 12.70 | 12.70 | 12.70 | 12.70 | 12.70 | 0.00 |
| Poland | 11.90 | 11.90 | 11.90 | 11.90 | 11.90 | 0.00 |
| Romania | 10.87 | 10.88 | 10.99 | 11.00 | 10.94 | 0.06 |
| Slovakia | 12.23 | 12.24 | 12.29 | 12.30 | 12.27 | 0.03 |
| Slovenia | 12.10 | 12.10 | 12.10 | 12.10 | 12.10 | 0.00 |
References
- Cairncross, F. The Death of Distance 2.0: How the Communications Revolution Will Change Our Lives, 2nd ed.; Texere Publishing: London, UK, 2001; ISBN 978-1-58799-089-2. [Google Scholar]
- Redding, S.; Venables, A.J. Economic geography and international inequality. J. Int. Econ. 2004, 62, 53–82. [Google Scholar] [CrossRef]
- Bank, I.-A.D.; Chong, A. Development Connections: Unveiling the Impact of New Information Technologies, 2011th ed.; Palgrave Macmillan: New York, NY, USA, 2011; ISBN 978-0-230-11194-3. [Google Scholar]
- Forestier, E.; Grace, J.; Kenny, C. Can information and communication technologies be pro-poor? Telecommun. Policy 2002, 26, 623–646. [Google Scholar] [CrossRef]
- Graham, C. Strengthening Institutional Capacity in Poor Countries. Reducing Global Poverty; Brookings Institution: Washington, DC, USA, 2002. [Google Scholar]
- Cecchini, S.; Scott, C. Can information and communications technology applications contribute to poverty reduction? Lessons from rural India. Inf. Technol. Dev. 2003, 10, 73–84. [Google Scholar] [CrossRef]
- Pick, J.B.; Azari, R. Global digital divide: Influence of socioeconomic, governmental, and accessibility factors on information technology. Inf. Technol. Dev. 2008, 14, 91–115. [Google Scholar] [CrossRef]
- Barney, D. The Network Society, 1st ed.; Polity: Cambridge, UK, 2004; ISBN 978-0-7456-2668-0. [Google Scholar]
- Castells, M. The Internet Galaxy: Reflections on the Internet, Business, and Society, 1st ed.; Oxford University Press: Oxford, UK, 2003; ISBN 978-0-19-925577-1. [Google Scholar]
- Hüsing, T.; Selhofer, H. The digital divide index—A measure of social inequalities in the adoption of ICT. In Proceedings of the Paper to IST 2002 Conference, Copenhagen, Denmark, 4–6 November 2002; pp. 1273–1286. [Google Scholar]
- Fuchs, C.; Horak, E. Informational Capitalism and the Digital Divide in Africa. Masaryk Univ. J. Law Technol. 2008, 1, 11–32. [Google Scholar]
- Kubielas, S.; Olender-Skorek, M. ICT modernization in Central and Eastern Europe: a Schumpeterian catching up perspective. Int. Econ. Econ. Policy 2014, 11, 115–136. [Google Scholar] [CrossRef]
- ITU Measuring the Information Society Reports 2010–2017. Available online: https://www.itu.int/en/ITU-D/Statistics/Pages/publications/mis2017.aspx (accessed on 22 August 2018).
- Ziemba, P.; Wątróbski, J.; Zioło, M.; Karczmarczyk, A. Using the PROSA Method in Offshore Wind Farm Location Problems. Energies 2017, 10, 1755. [Google Scholar] [CrossRef]
- Pelenc, J.; Ballet, J.; Dedeurwaerdere, T. Weak Sustainability versus Strong Sustainability; Brief for GSDR United Nations: Fontainebleau, France, 2015. [Google Scholar]
- Becker, J.; Becker, A.; Sulikowski, P.; Zdziebko, T. ANP-based analysis of ICT usage in Central European enterprises. Procedia Comput. Sci. 2018, 126, 2173–2183. [Google Scholar] [CrossRef]
- White, L.; Lee, G.J. Operational research and sustainable development: Tackling the social dimension. Eur. J. Oper. Res. 2009, 193, 683–692. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; González-Pachón, J.; Romero, C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res. 2017, 258, 607–616. [Google Scholar] [CrossRef]
- Ziemba, P.; Jankowski, J.; Wątróbski, J. Online Comparison System with Certain and Uncertain Criteria Based on Multi-criteria Decision Analysis Method. In Proceedings of the Computational Collective Intelligence, Nicosia, Cyprus, 27–29 September 2017; Nguyen, N.T., Papadopoulos, G.A., Jędrzejowicz, P., Trawiński, B., Vossen, G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 579–589. [Google Scholar]
- Ziemba, P. NEAT F-PROMETHEE—A new fuzzy multiple criteria decision making method based on the adjustment of mapping trapezoidal fuzzy numbers. Expert Syst. Appl. 2018, 110, 363–380. [Google Scholar] [CrossRef]
- Ziemba, P.; Jankowski, J.; Wątróbski, J. Dynamic Decision Support in the Internet Marketing Management. In Transactions on Computational Collective Intelligence XXIX; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; pp. 39–68. ISBN 978-3-319-90286-9. [Google Scholar]
- Ziemba, P.; Wątróbski, J.; Karczmarczyk, A.; Jankowski, J.; Wolski, W. Integrated approach to e-commerce websites evaluation with the use of surveys and eye tracking based experiments. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, Czech Republic, 3–6 September 2017; pp. 1019–1030. [Google Scholar]
- Campbell, D. Can the digital divide be contained? Int. Labour Review 2001, 140, 119–141. [Google Scholar] [CrossRef]
- Norris, P. Digital Divide: Civic Engagement, Information Poverty and the Internet World-Wide; Cambridge University Press: Cambridge, UK, 2001; Volume 5, ISBN 978-0-521-00223-3. [Google Scholar]
- Warschauer, M. Technology and Social Inclusion: Rethinking the Digital Divide; The MIT Press: Cambridge, MA, USA, 2004; ISBN 978-0-262-73173-7. [Google Scholar]
- Gumpert, G.; Drucker, S. The Perfections of Sustainability and Imperfections in the Digital Community: Paradoxes of Connection and Disconnection. In Proceedings of the Digital Cities III, Information Technologies for Social Capital: Cross-Cultural Perspectives, Amsterdam, The Netherlands, 18–19 September 2003; van den Besselaar, P., Koizumi, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 369–379. [Google Scholar]
- White, D.S.; Gunasekaran, A.; Shea, T.P.; Ariguzo, G.C. Mapping the global digital divide. Int. J. Bus. Inf. Syst. 2011, 7, 207–219. [Google Scholar] [CrossRef]
- OECD. Understanding the Digital Divide; Organization for Economic Cooperation and Development (OECD): Paris, France, 2001. [Google Scholar]
- Jahanmir, S.F.; Cavadas, J. Factors affecting late adoption of digital innovations. J. Bus. Res. 2018, 88, 337–343. [Google Scholar] [CrossRef]
- Leaning, M. Chapter One—Integrating Media and Information Literacy. In Media and Information Literacy; Leaning, M., Ed.; Chandos Publishing: Cambridge, UK, 2017; pp. 3–14. ISBN 978-0-08-100170-7. [Google Scholar]
- Warren, M. The digital vicious cycle: Links between social disadvantage and digital exclusion in rural areas. Telecommun. Policy 2007, 31, 374–388. [Google Scholar] [CrossRef]
- James, J. Sharing mobile phones in developing countries: Implications for the digital divide. Technol. Forecast. Soc. Chang. 2011, 78, 729–735. [Google Scholar] [CrossRef]
- James, J. The ICT Development Index and the digital divide: How are they related? Technol. Forecast. Soc. Chang. 2012, 79, 587–594. [Google Scholar] [CrossRef]
- Petrović, M.; Bojković, N.; Anić, I.; Petrović, D. Benchmarking the digital divide using a multi-level outranking framework: Evidence from EBRD countries of operation. Gov. Inf. Q. 2012, 29, 597–607. [Google Scholar] [CrossRef]
- Coria, S.R.; Mondragón-Becerra, R.; Pérez-Meza, M.; Ramírez-Vásquez, S.K.; Martínez-Peláez, R.; Barragán-López, D.; Ávila-Barrón, O.R. CT4RDD: Classification trees for research on digital divide. Expert Syst. Appl. 2013, 40, 5779–5786. [Google Scholar] [CrossRef]
- Khalid, M.S.; Pedersen, M.J.L. Digital Exclusion in Higher Education Contexts: A Systematic Literature Review. Procedia Soc. Behav. Sci. 2016, 228, 614–621. [Google Scholar] [CrossRef]
- Scheerder, A.; van Deursen, A.; van Dijk, J. Determinants of Internet skills, uses and outcomes. A systematic review of the second- and third-level digital divide. Telemat. Inform. 2017, 34, 1607–1624. [Google Scholar] [CrossRef]
- Vicente Cuervo, M.R.; López Menéndez, A.J. A multivariate framework for the analysis of the digital divide: Evidence for the European Union-15. Inf. Manag. 2006, 43, 756–766. [Google Scholar] [CrossRef]
- Polat, R.K. Digital exclusion in Turkey: A policy perspective. Gov. Inf. Q. 2012, 29, 589–596. [Google Scholar] [CrossRef]
- Park, S.R.; Choi, D.Y.; Hong, P. Club convergence and factors of digital divide across countries. Technol. Forecast. Soc. Chang. 2015, 96, 92–100. [Google Scholar] [CrossRef]
- Cruz-Jesus, F.; Vicente, M.R.; Bacao, F.; Oliveira, T. The education-related digital divide: An analysis for the EU-28. Comput. Hum. Behav. 2016, 56, 72–82. [Google Scholar] [CrossRef]
- Szeles, M.R. New insights from a multilevel approach to the regional digital divide in the European Union. Telecommun. Policy 2018, 42, 452–463. [Google Scholar] [CrossRef]
- Kyriakidou, V.; Michalakelis, C.; Sphicopoulos, T. Digital divide gap convergence in Europe. Technol. Soc. 2011, 33, 265–270. [Google Scholar] [CrossRef]
- Srinuan, C.; Srinuan, P.; Bohlin, E. An analysis of mobile Internet access in Thailand: Implications for bridging the digital divide. Telemat. Inform. 2012, 29, 254–262. [Google Scholar] [CrossRef]
- Prieger, J.E. The broadband digital divide and the economic benefits of mobile broadband for rural areas. Telecommun. Policy 2013, 37, 483–502. [Google Scholar] [CrossRef]
- Pick, J.B.; Nishida, T. Digital divides in the world and its regions: A spatial and multivariate analysis of technological utilization. Technol. Forecast. Soc. Chang. 2015, 91, 1–17. [Google Scholar] [CrossRef]
- Chipeva, P.; Cruz-Jesus, F.; Oliveira, T.; Irani, Z. Digital divide at individual level: Evidence for Eastern and Western European countries. Gov. Inf. Q. 2018, 35, 460–479. [Google Scholar] [CrossRef]
- Rockmann, R.; Gewald, H.; Haug, M. Equal Access for Everyone? A Digital Divide Cascade for Retired Senior Citizens; ECIS: Portsmouth, UK, 2018. [Google Scholar]
- Van Dijk, J.A.G.M. The Evolution of the Digital Divide. Stand Alone 2012, 15, 57–75. [Google Scholar]
- Haselhorst, P. Bridging the Digital Divide. Available online: https://www.digitalethics.org/essays/bridging-digital-divide (accessed on 13 January 2019).
- Wątróbski, J.; Jankowski, J.; Ziemba, P. Multistage performance modelling in digital marketing management. Econ. Sociol. 2016, 9, 101–125. [Google Scholar] [CrossRef] [PubMed]
- ITU Measuring the Information Society Report 2009. Available online: https://www.itu.int/en/ITU-D/Statistics/Pages/publications/mis2009.aspx (accessed on 3 September 2018).
- Eurostat Glossary: Chain Index. Available online: http://ec.europa.eu/eurostat/statistics-explained/index.php/Glossary:Chain_index (accessed on 22 August 2018).
- Crawley, M.J. The R Book, 2nd ed.; A John Wiley & Sons: Silwood Park, UK, 2012; ISBN 978-0-470-97392-9. [Google Scholar]
- Sobczyk, M. Statystyka. Podstawy Teoretyczne, Przykłady—Zadania; Wyd. UMCS: Lublin, Poland, 1998. [Google Scholar]
- Brans, J.-P.; De Smet, Y. PROMETHEE Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Greco, S., Ehrgott, M., Figueira, J.R., Eds.; International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2016; pp. 187–219. ISBN 978-1-4939-3094-4. [Google Scholar]
- Souter, D. Inside the Information Society: How the Digital Divide has Changed. Available online: https://www.apc.org/en/blog/inside-information-society-how-digital-divide-has-changed (accessed on 13 January 2019).
- Ziemba, P.; Jankowski, J.; Wątróbski, J.; Becker, J. Knowledge Management in Website Quality Evaluation Domain. In Proceedings of the Computational Collective Intelligence, Madrid, Spain, 21–23 September 2015; Núñez, M., Nguyen, N.T., Camacho, D., Trawiński, B., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 75–85. [Google Scholar]
- Ziemba, P.; Jankowski, J.; Wątróbski, J.; Wolski, W.; Becker, J. Integration of domain ontologies in the repository of website evaluation methods. In Proceedings of the 2015 Federated Conference on Computer Science and Information Systems (FedCSIS), Lodz, Poland, 13–16 September 2015; pp. 1585–1595. [Google Scholar]
- Ziemba, P.; Wątróbski, J.; Jankowski, J.; Wolski, W. Construction and Restructuring of the Knowledge Repository of Website Evaluation Methods. In Information Technology for Management; Ziemba, E., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 29–52. [Google Scholar]
- Convertino, M.; Muñoz-Carpena, R.; Chu-Agor, M.L.; Kiker, G.A.; Linkov, I. Untangling drivers of species distributions: Global sensitivity and uncertainty analyses of MaxEnt. Environ. Model. Softw. 2014, 51, 296–309. [Google Scholar] [CrossRef]
- Convertino, M.; Muñoz-Carpena, R.; Kiker, G.A.; Perz, S.G. Design of optimal ecosystem monitoring networks: hotspot detection and biodiversity patterns. Stoch. Environ. Res. Risk Assess. 2015, 29, 1085–1101. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).