Hermite-Type Collocation Methods to Solve Volterra Integral Equations with Highly Oscillatory Bessel Kernels

Abstract

In this paper, we present two kinds of Hermite-type collocation methods for linear Volterra integral equations of the second kind with highly oscillatory Bessel kernels. One method is direct Hermite collocation method, which used direct two-points Hermite interpolation in the whole interval. The other one is piecewise Hermite collocation method, which used a two-points Hermite interpolation in each subinterval. These two methods can calculate the approximate value of function value and derivative value simultaneously. Both methods are constructed easily and implemented well by the fast computation of highly oscillatory integrals involving Bessel functions. Under some conditions, the asymptotic convergence order with respect to oscillatory factor of these two methods are established, which are higher than the existing results. Some numerical experiments are included to show efficiency of these two methods.

1. Introduction

Volterra integral equations arise from many mathematical problems in engineering and physics [1,2,3]. For example, the numerical solution of a scalar retarded potential integral equation posted on an infinite flat surface,

$${\int }_{{\mathbb{R}}^2}\frac{u(x^{\prime },t-|x^{\prime }-x|)}{|x^{\prime }-x|}d{x}^{\prime }=a(x,t)on{\mathbb{R}}^2\times (0,T),$$

where u and a satisfy the causality condition $u\equiv 0$, $a\equiv 0$ for all $t\le 0$. The continuous Fourier transform (CFT) of a function $g\in L^2({\mathbb{R}}^2)$ is $\tilde{g}\in L^2({\mathbb{R}}^2)$ defined by $\tilde{g}(\overrightarrow{\omega })={\int }_{{\mathbb{R}}^2}g(x)e^{-ix\overrightarrow{\omega }}dx$. When $a(·,t),u(·,t)\in L^2({\mathbb{R}}^2)$ for $t\in (0,T)$, by taking CFT, Davies and Duncan [2] reformulated it as the following Volterra integral equation of the first kind with highly oscillatory Bessel kernel,

$$2\pi {\int }_0^t\tilde{u}(\overrightarrow{\omega },t-R)J_0(\omega R)dR=\tilde{a}(\overrightarrow{\omega },t),for\overrightarrow{\omega }\in {\mathbb{R}}^2,t\in (0,T),$$

(1)

where $J_m(x)$ is the first-kind Bessel function of order m, which is the solution of the Bessel equation $\frac{d^{2}y}{d{x}^2}+\frac{1}{x}\frac{dy}{dx}+(1-\frac{m^2}{x^2})y=0$. In 2005, for the study of the problem of the electromagnetic scattering from a large cavity, G. Bao and W. W. Sun [1] reformulated (1) as a Volterra integral equation with Cauchy singular and highly oscillatory Hankel kernel.

The Bessel kernel of the above Equation (1) has a parameter $\omega$. Obviously, when $\omega \gg 1$, the Bessel kernel function becomes highly oscillatory. When resort to numerical solutions of Equation (1), the computation of integrals involved Bessel kernel functions is inevitable. However, the classical quadrature rules, such as Newton-Cotes rule, Clenshaw-Curtis rule or Gauss rule, are failed to calculate this kind of integral. Hence, adopting suitable quadrature rules for the corresponding highly oscillatory integrals plays an important role in obtaining the numerical solution.

The function $J_0(\omega (x-t))$ satisfies the condition of Theorem 2.1.8 ([4], p. 64). Upon differentiation with respect to x, the first-kind Volterra integral Equation (1) can be rewritten as the second-kind Volterra integral equations. In this paper, we treat the following Volterra integral equation of the second kind with highly oscillatory Bessel kernel

$$u(x)-{\int }_0^x{J}_m(\omega (x-t))u(t)dt=f(x),x\in [0,1],t\in I:=[0,x],$$

(2)

where $u(x)$ is an unknown function, $f(x)$ is a given smooth function, $J_m$ is the Bessel function of the first kind of order $m\ge 0$ and the frequency $\omega$ is a parameter. When $\omega \gg 1$, the Bessel kernel function is highly oscillatory, and this makes solving Equation (2) a challenging problem.

In recent years, there has been tremendous interest in developing methods for solving highly oscillatory Volterra integral equation, such as discontinuous Galerkin method [5], Filon-type method [6,7], collocation method [4,8,9], collocation boundary value method [10,11], collocation method on uniform mesh [12], collocation method on graded mesh [13].

Xiang and Brunner [14] presented three methods: direct Filon method, piecewise constant collocation method and piecewise linear collocation method for the equation,

$$u(x)-{\int }_0^x{J}_m(\omega (x-t))\frac{u(t)}{{(x-t)}^{\alpha }}dt=f(x),x\in [0,1],t\in I:=[0,x],0\le \alpha <1,f(x)\in C^1[0,1].$$

Based on the asymptotic analysis of the solution, they gave corresponding convergence rates in terms of the frequency for these methods. For the case of the $\alpha =0,f\in C^2[0,1]$, Fang et al. [15] showed that the optimal convergence with respect to the $\omega$ are $O({\omega }^{-2}),O({\omega }^{-3/2}),O({\omega }^{-2})$ respectively. These three methods, same as other existing methods, are constructed by original integral equation or its equivalent equation. Since only the function value in start point is used, which leads to low error precision. In this paper, we present two kinds of Hermite-type collocation methods by combining original integral equation and its differential equation. The new methods will use the values of function and derivative function in start point, which gets higher error precision than that of the above three methods.

The rest of the paper is organized as follows. In Section 2, we present two efficient methods for Equation (2): direct Hermite collocation method and piecewise Hermite collocation method. We show the error bound with respect to the frequency $\omega$ in Section 3. In Section 4, several numerical examples are included to verify the results of theoretical analysis. It is observed from numerical experiments that these methods have higher accuracy as compared with the Direct Filon method in [14].

2. Hermite-Type Collocation Methods

2.1. Direct Hermite Collocation Method (Algorithm 1)

Differentiate both sides of Equation (2),

$$\begin{array}{c}\hfill u^{\prime }(x)-J_m(0)u(x)-{\int }_0^x(J_m{(\omega (x-t))}^{\prime }u(t)dt=f^{\prime }(x).\end{array}$$

(3)

Since

$$\begin{array}{c}\hfill (J_m{(\omega (x-t))}^{\prime }=\left\{\begin{array}{c}\frac{\omega }{2}(-J_{m+1}(\omega (x-t))+J_{m-1}(\omega (x-t))),m>0,\hfill \\ -\omega J_1(\omega (x-t)),m=0,\hfill \end{array}\right.\end{array}$$

(4)

it follows that for the case $m=0$,

$$u^{\prime }(x)-J_0(0)u(x)+\omega {\int }_0^x(J_1(\omega (x-t))u(t)dt=f^{\prime }(x),$$

(5)

and for $m>0$,

$$u^{\prime }(x)-J_m(0)u(x)+\frac{\omega }{2}{\int }_0^x(J_{m+1}(\omega (x-t))-J_{m-1}(\omega (x-t)))u(t)dt=f^{\prime }(x).$$

(6)

Let us denote the Hermite interpolant polynomial between $u(0)$ and $u(x_j)$ by

$$u_h(x)=H_{0j}u(0)+H_{1j}u(x_j)+H_{2j}{u}^{\prime }(0)+H_{3j}{u}^{\prime }(x_j),$$

where the polynomials

$$\begin{array}{cc}\hfill H_{0j}=& \left(1+\frac{2x}{x_j}\right){\left(\frac{x-x_j}{x_j}\right)}^2,H_{1j}=\left(1+2\frac{x-x_j}{-x_j}\right){\left(\frac{x}{x_j}\right)}^2,\hfill \\ \hfill H_{2j}=& x{\left(\frac{x-x_j}{-x_j}\right)}^2,H_{3j}=(x-x_j){\left(\frac{x}{x_j}\right)}^2,\hfill \end{array}$$

mean the fundamental polynomials with respect to the nodes 0 and $x_j$. Then the collocation systems follow

$$\begin{array}{c}{u}_j^d-{\int }_0^{x_j}{J}_m(\omega (x_j-t))(H_{0j}{u}_0+H_{1j}{u}_j^d+H_{2j}{u}_0^{\prime }+H_{3j}{u}_j^{\prime d})dt=f_j,\hfill \end{array}$$

(7)

$$\begin{array}{c}{u}_j^{\prime d}-J_m(0)u_j^d+\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t))(H_{0j}{u}_0+H_{1j}{u}_j^d+H_{2j}{u}_0^{\prime }+H_{3j}{u}_j^{\prime d})dt=f_j^{\prime },\hfill \end{array}$$

(8)

where $u_j^d$ denotes an approximation of $u(x_j)$, $u_j^{\prime d}$ denotes an approximation of $u^{\prime }(x_j)$. That is

$$\begin{array}{c}(1-I(1,j,m))u_j^d-I(3,j,m)u_j^{\prime d}=f_j+I(0,j,m)u_0+I(2,j,m)u_0^{\prime },\hfill \end{array}$$

(9)

$$\begin{array}{c}\left(-J_m(0)+\frac{\omega }{2}\left(I(1,j,m+1)-I(1,j,m-1)\right)\right)u_j^d+\left(1+\frac{\omega }{2}\left(I(3,j,m+1)-I(3,j,m-1)\right)\right)u_j^{\prime d}\hfill \\ =f_j^{\prime }-\frac{\omega }{2}(I(0,j,m+1)-I(0,j,m-1))u_0-\frac{\omega }{2}(I(2,j,m+1)-I(2,j,m-1))u_0^{\prime }.\hfill \end{array}$$

(10)

Solving these systems, we get direct Hermite appromximate schemes for $m=0$,

$$\begin{array}{c}\hfill u_j^d=\frac{(f_j+I(0,j,0)u_0+I(2,j,0)u_0^{\prime })(1+\omega I(3,j,1))+(f_j^{\prime }-\omega I(0,j,1)u_0-\omega I(2,j,1)u_0^{\prime })I(3,j,0)}{(1-I(1,j,0))(1+\omega I(3,j,1))+I(3,j,0)(-1+\omega I(1,j,1))},\end{array}$$

(11)

$$\begin{array}{c}\hfill u_j^{{}^{\prime }d}=\frac{(f_j+I(0,j,0)u_0+I(2,j,0)u_0^{\prime })(1-\omega I(1,j,1))+(f_j^{\prime }-\omega I(0,j,1)u_0-\omega I(2,j,1)u_0^{\prime })(1-I(1,j,0))}{-I(3,j,0)(1-\omega I(1,j,1))+(1+\omega I(3,j,0))(1-I(1,j,0))},\end{array}$$

(12)

for $m>0$,

$$\begin{array}{c}\hfill u_j^d=\frac{b_1{a}_{22}-b_2{a}_{12}}{a_{11}{a}_{22}-a_{21}{a}_{12}},u_j^{{}^{\prime }d}=\frac{a_{11}{b}_2-a_{21}{b}_1}{a_{11}{a}_{22}-a_{21}{a}_{12}},\end{array}$$

(13)

where

$$\begin{array}{c}{a}_{11}=1-I(1,j,m),a_{12}=-I(3,j,m),a_{21}=-J_m(0)+\frac{\omega }{2}(I(1,j,m+1)-I(1,j,m-1)),\hfill \\ a_{22}=1+\frac{\omega }{2}(I(3,j,m+1)-I(3,j,m-1)),b_1=f_j+I(0,j,m)u_0+I(2,j,m)u_0^{\prime },\hfill \\ b_2=f_j^{\prime }-\frac{\omega }{2}(I(0,j,m+1)-I(0,j,m-1))u_0-\frac{\omega }{2}(I(2,j,m+1)-I(2,j,m-1))u_0^{\prime }.\hfill \end{array}$$

$I(k,j,m)$ denotes the moment

$$I(k,j,m)={\int }_0^{x_j}{H}_{kj}{J}_m(\omega (x_j-t))dtk=0,1,2,3.$$

The specific calculation formula follows

$$\begin{array}{cc}\hfill I(0,j,m)=& \frac{3}{x_j^2}L(2,m,\omega ,x_j)-\frac{2}{x_j^3}L(3,m,\omega ,x_j),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill I(1,j,m)=& L(0,m,\omega ,x_j)-\frac{3}{x_j^2}L(2,m,\omega ,x_j)+\frac{2}{x_j^3}L(3,m,\omega ,x_j),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill I(2,j,m)=& \frac{1}{x_j}L(2,m,\omega ,x_j)-\frac{1}{x_j^2}L(3,m,\omega ,x_j),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill I(3,j,m)=& -L(1,m,\omega ,x_j)+\frac{2}{x_j}L(2,m,\omega ,x_j)-\frac{1}{x_j^2}L(3,m,\omega ,x_j).\hfill \end{array}$$

(17)

The moments ${\displaystyle L[\mu ,m,\omega ,a]={\int }_0^a{t}^{\mu }{J}_m(\omega t)dt}$ can be efficiently calculated by

$$L[\mu ,m,\omega ,a]=\frac{2^{\mu }\Gamma \left(\frac{m+\mu +1}{2}\right)}{a^2{\omega }^{\mu +1}\Gamma \left(\frac{m-\mu +1}{2}\right)}+\frac{(m+\mu -1)J_m(\omega a)s_{\mu -1,m-1}^{(2)}(\omega a)-J_{m-1}(\omega a)s_{\mu ,m}^{(2)}(\omega a)}{a{\omega }^{\mu }},$$

(18)

where $\Gamma (x)={\int }_0^{\infty }{e}^{-t}{t}^{x-1}dt$ denotes the Gamma function and $s_{\mu ,\nu }^{(2)}(z)$ denotes the Lommel function of the second kind [16,17]. Once $\omega$ is large, the Lommel function can be efficiently approximated by truncating

$$s_{\mu ,\nu }^{(2)}(z)=z^{\mu -1}[1-\frac{{(\mu -1)}^2-{\nu }^2}{z^2}+\dots +{(-1)}^p\frac{[{(\mu -1)}^2-{\nu }^2]\dots [{(\mu -2p+1)}^2-{\nu }^2]}{z^{2p}}]+O(z^{\mu -2p-2})$$

(19)

Algorithm 1: direct Hermite collocation method.

1. Compute$L[i,m,\omega ,x_j],i=0,1,2,3$ by (18); 2. Compute $I(k,j,m),k=0,1,2,3$ by (14)–(17); 3. Compute $u_j^d$ and $u_j^{\prime d}$ by (13).

2.2. Piecewise Hermite Collocation Method

To obtain higher-order approximations, a direct improvement of the direct Hermite collocation method is the composite Hermite collocation method, which is so-called piecewise Hermite collocation method (Algorithm 2), that is split the interval into several bins and apply the formula over each bin independently of the other.

Without loss of generality, suppose that $I_{\Delta }=\{x_j=j\ast h:j=0,1,\cdots ,N\}$ is a uniform nodal point and $\widehat{u}(x)$ is an approximation of $u(x)$ such that $\widehat{u}(x)|[x_{j-1},x_j]$ is the Hermite interpolant polynomial between $u(x_{j-1})$ and $u(x_j)$ for $j=1,\dots ,N$.

Let us define

$$\widehat{u}(x)={\widehat{H}}_{0j}u(x_{j-1})+{\widehat{H}}_{1j}u(x_j)+{\widehat{H}}_{2j}{u}^{\prime }(x_{j-1})+{\widehat{H}}_{3j}{u}^{\prime }(x_j),$$

where the polynomials

$$\begin{array}{ccc}{\widehat{H}}_{0j}& =\hfill & \left(1+2\frac{x-x_{j-1}}{x_j-x_{j-1}}\right){\left(\frac{x-x_j}{x_j-x_{j-1}}\right)}^2=\left(1+2\frac{x-x_{j-1}}{h}\right){\left(\frac{x-x_j}{h}\right)}^2,\hfill \\ {\widehat{H}}_{1j}& =\hfill & \left(1+2\frac{x_j-x}{x_j-x_{j-1}}\right){\left(\frac{x-x_{j-1}}{x_j-x_{j-1}}\right)}^2=\left(1+2\frac{x_j-x}{h}\right){\left(\frac{x-x_{j-1}}{h}\right)}^2,\hfill \\ {\widehat{H}}_{2j}& =\hfill & (x-x_{j-1}){\left(\frac{x-x_j}{x_j-x_{j-1}}\right)}^2=(x-x_{j-1}){\left(\frac{x-x_j}{h}\right)}^2,{\widehat{H}}_{3j}=(x-x_j){\left(\frac{x-x_{j-1}}{x_j-x_{j-1}}\right)}^2=(x-x_j){\left(\frac{x-x_{j-1}}{h}\right)}^2\hfill \end{array}$$

denote the fundamental polynomials with respect to the nodes $x_{j-1}$ and $x_j$. Then the collocation systems follow

$$\begin{array}{c}{u}_j-\sum _{i=1}^{j-1}{\int }_{x_{i-1}}^{x_i}{J}_m(\omega (x_j-t)){\widehat{u}}_i(t)dt-{\int }_{x_{j-1}}^{x_j}{J}_m(\omega (x_j-t)){\widehat{u}}_j(t)dt=f_j,\hfill \end{array}$$

(20)

$$\begin{array}{c}{u}_j^{\prime }-J_m(0)u_j+\frac{\omega }{2}\sum _{i=1}^{j-1}{\int }_{x_{i-1}}^{x_i}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t))\ast {\widehat{u}}_i(t)dt\hfill \\ +\frac{\omega }{2}{\int }_{x_{j-1}}^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t))\ast {\widehat{u}}_j(t)dt=f_j^{\prime }.\hfill \end{array}$$

(21)

This leads to the piecewise Hermite collocation method

$$\begin{array}{c}\left[\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\end{array}\right]\left[\begin{array}{c}{u}_j\\ u_j^{\prime }\end{array}\right]=\left[\begin{array}{c}{r}_1\\ r_2\end{array}\right],\end{array}$$

(22)

where

$$\begin{array}{cc}\hfill b_{11}=& 1-A_{jj1m},b_{12}=-A_{jj3m},b_{21}=-J_m(0)+\frac{\omega }{2}(A_{jj1(m+1)}-A_{jj1(m-1)}),\hfill \\ \hfill b_{22}=& 1+\frac{\omega }{2}(A_{jj3(m+1)}-A_{jj3(m-1)}),\hfill \\ \hfill r_1=& f_j+\sum _{i=1}^{j-1}(A_{ij0m}{u}_{i-1}+A_{ij1m}{u}_i+A_{ij2m}{u}_{i-1}^{\prime }+A_{ij3m}{u}_i^{\prime })+A_{jj0m}{u}_{j-1}+A_{jj2m}{u}_{j-1}^{\prime },\hfill \\ \hfill r_2=& f_j^{\prime }-\frac{\omega }{2}\sum _{i=1}^{j-1}(A_{ij0(m+1)}-A_{ij0(m-1)})u_{i-1}+(A_{ij1(m+1)}-A_{ij1(m-1)})u_i\hfill \\ & +(A_{ij2(m+1)}-A_{ij2(m-1)})u_{i-1}^{\prime }+(A_{ij3(m+1)}-A_{ij3(m-1)})u_i^{\prime }\hfill \\ & -\frac{\omega }{2}\left((A_{jj0(m+1)}-A_{jj0(m-1)})u_{j-1}+(A_{jj2(m+1)}-A_{jj2(m-1)})u_{j-1}^{\prime }\right),\hfill \end{array}$$

(23)

$A_{ijkm}$ denotes the moment

$$A_{ijkm}={\int }_{x_{i-1}}^{x_i}{\widehat{H}}_{ki}{J}_m(\omega (x_j-t))dtk=0,1,2,3.$$

The specific calculation formula is following that

$$\begin{array}{cc}\hfill A_{ij0m}=& \left(L(0,m,\omega ,(j-i+1)h)-L(0,m,\omega ,(j-i)h)\right)(2j-2i+3){(j-i)}^2\hfill \\ & -\left(L(1,m,\omega ,(j-i+1)h)-L(1,m,\omega ,(j-i)h)\right)(j-i+1)(j-i)6/h\hfill \\ & +\left(L(2,m,\omega ,(j-i+1)h)-L(2,m,\omega ,(j-i)h)\right)3(2j-2i+1)/h^2\hfill \\ & -\left(L(3,m,\omega ,(j-i+1)h)-L(3,m,\omega ,(j-i)h)\right)2/h^3,\hfill \\ \hfill A_{ij1m}=& \left(L(0,m,\omega ,(j-i+1)h)-L(0,m,\omega ,(j-i)h)\right){(j-i+1)}^2(-2j+2i+1)\hfill \\ & +\left(L(1,m,\omega ,(j-i+1)h)-L(1,m,\omega ,(j-i)h)\right)(j-i+1)(j-i)6/h\hfill \\ & -\left(L(2,m,\omega ,(j-i+1)h)-L(2,m,\omega ,(j-i)h)\right)3(2j-2i+1)/h^2\hfill \\ & +\left(L(3,m,\omega ,(j-i+1)h)-L(3,m,\omega ,(j-i)h)\right)2/h^3,\hfill \\ \hfill A_{ij2m}=& \left(L(0,m,\omega ,(j-i+1)h)-L(0,m,\omega ,(j-i)h)\right)(j-i+1){(j-i)}^{2}h\hfill \\ & -\left(L(1,m,\omega ,(j-i+1)h)-L(1,m,\omega ,(j-i)h)\right)(3j-3i+2)(j-i)\hfill \\ & +\left(L(2,m,\omega ,(j-i+1)h)-L(2,m,\omega ,(j-i)h)\right)(3j-3i+1)/h\hfill \\ & -\left(L(3,m,\omega ,(j-i+1)h)-L(3,m,\omega ,(j-i)h)\right)/h^2,\hfill \\ \hfill A_{ij3m}=& \left(L(0,m,\omega ,(j-i+1)h)-L(0,m,\omega ,(j-i)h)\right){(j-i+1)}^2(j-i)h\hfill \\ & -\left(L(1,m,\omega ,(j-i+1)h)-L(1,m,\omega ,(j-i)h)\right)(j-i+1)(3j-3i+1)\hfill \\ & +\left(L(2,m,\omega ,(j-i+1)h)-L(2,m,\omega ,(j-i)h)\right)(3j-3i+2)/h\hfill \\ & -\left(L(3,m,\omega ,(j-i+1)h)-L(3,m,\omega ,(j-i)h)\right)/h^2.\hfill \end{array}$$

(24)

Algorithm 2: piecewise Hermite collocation method.

1. Compute$L[i,m,\omega ,x_j],i=0,1,2,3$ by (18); 2. Compute $A_{ijkm},k=0,1,2,3$ by (24); 3. Compute $u_j$ and $u_j^{\prime }$ by (22).

3. Error Analyses

Firstly, we introduce some useful lemmas, which will be used to prove theorems for the later analyses.

Lemma 1

([15], Lemma 1). For any integers $\mu ,\nu \ge 0$ and $x\in (0,1],$ the following integral

$$\begin{array}{c}\hfill \omega {\int }_0^x{J}_{\mu }(\omega t)J_{\nu }(\omega (x-t))dt\end{array}$$

(25)

is uniformly bounded with respect to $\omega >0.$

Lemma 2

([15], Lemma 2). Suppose $g_{\omega }(t)\in C[0,1]$ and $g_{\omega }(t)=O(1)$ as $\omega \to \infty .$ Then for any $v>0$ and $x\in (0,1],$ it is true that the integral

$${\int }_0^x\frac{g_{\omega }(t)J_{\nu }(\omega t)}{t}dt$$

(26)

is uniformly bounded with respect to $\omega >0.$

Lemma 3

([18], Lemma 2.1). For any $\omega \gg 1$, $m\ge 0$ and $h_{\omega }(t)$ satisfies

• ${\displaystyle {\int }_0^1|h_{\omega }^{\prime }(s)|ds}$ is integrable;
• ${\displaystyle {\int }_0^1|h_{\omega }^{\prime }(s)|ds}$ and $h_{\omega }(t)$ are bounded in $\omega \in (0,\infty ]$ for fixed $t,$ respectively,

it is true that

$$\left|{\int }_0^1{h}_{\omega }(t)t^k{J}_m(\omega t)dt\right|\le \left\{\begin{array}{cc}{K}_1{\omega }^{-1-k},\hfill & -1<k<\frac{1}{2},\hfill \\ K_2{\omega }^{-3/2},\hfill & k\ge \frac{1}{2},\hfill \end{array}\right.$$

(27)

where the constants $K_1$ and $K_2$ are independent of ω.

Let $\mathcal{A}:C(I)\to C(I)$ denote the linear Volterra integral operator defined by

$$(\mathcal{A}u)(t):={\int }_0^x{J}_m(\omega (x-t))u(t)dt,x\in [0,1],t\in I:=[0,x],$$

and $\mathcal{I}$ denote identity operator. Then Equation (2) can be reformulated more compactly as

$$\left(\mathcal{I}-\mathcal{A}\right)u=f.$$

(28)

To get the expression of (1)–(3) order derivatives of the solution of (2), we first discuss the relation between the integral operator $\mathcal{A}$ and the differential operator D.

Theorem 1.

Assume $f\in C^3[0,1]$. The Volterra operator ${\mathcal{A}}^n:=C(I)\to C(I)$ defined by $({\mathcal{A}}^{n}u)(x):={\int }_0^x{K}_n(t,x)u(t)dt,n\ge 1$, where $K_n(t,x)$ are the iterated kernels. Then the solution of (2) satisfies

$$\begin{array}{cc}\hfill u=& \sum _{j=0}^{\infty }{\mathcal{A}}^{j}f,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill Du=& \sum _{j=0}^{\infty }\left(f(0){\mathcal{A}}^{j-1}r+{\mathcal{A}}^{j}Df\right),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill D^{2}u=& \sum _{j=0}^{\infty }\left(f(0)r(0){\mathcal{A}}^{j-2}r+f(0){\mathcal{A}}^{j-1}Dr+f^{\prime }(0){\mathcal{A}}^{j-1}r+{\mathcal{A}}^j{D}^{2}f\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill D^{3}u=& \sum _{j=0}^{\infty }(f(0)r(0)\left(r(0){\mathcal{A}}^{j-3}r+{\mathcal{A}}^{j-2}Dr\right)+f(0)\left(r^{\prime }(0){\mathcal{A}}^{j-2}r+{\mathcal{A}}^{j-1}{D}^{2}r\right)\hfill \\ & +f^{\prime }(0)\left(r(0){\mathcal{A}}^{j-2}r+{\mathcal{A}}^{j-1}Dr\right)+\left(f^{″}(0){\mathcal{A}}^{j-1}r+{\mathcal{A}}^j{D}^{3}f\right)).\hfill \end{array}$$

(32)

where, $r(x)=J_m(\omega x)$ and ${\mathcal{A}}^j=0$ if $j<0.$ Moreover, we have both of ${\parallel Du\parallel }_{\infty }$, ${∥D^{2}u-f(0)Dr-D^{2}f∥}_{\infty }$ and $\parallel D^{3}u-f(0)r(0)Dr-f(0)D^{2}r-f^{\prime }(0)Dr-D^3{f\parallel }_{\infty }$ are uniformly bounded with respect to $\omega .$

Proof. 

$$\begin{array}{c}\hfill {\mathcal{A}}^{j}f={\int }_0^x{J}_m(\omega (x-s_1)){\int }_0^{s_1}{J}_m(\omega (s_1-s_2))\dots {\int }_0^{s_{j-1}}{J}_m(\omega (s_{j-1}-s))f(s)dsd{s}_{j-1}\dots d{s}_1.\end{array}$$

(33)

Let $s_1^{\prime }=x-s_1,s_2^{\prime }=s_1-s_2,\dots ,s_{j-1}^{\prime }=s_{j-2}-s_{j-1},s^{\prime }=s_{j-1}-s,$ it follows that

$$\begin{array}{c}\hfill {\mathcal{A}}^{j}f={\int }_0^x{J}_m(\omega s_1^{\prime }){\int }_0^{x-s_1^{\prime }}{J}_m(\omega s_2^{\prime })\dots {\int }_0^{x-{\sum }_{k=1}^{j-1}{s}_k^{\prime }}{J}_m(\omega s^{\prime })f\left(x-\sum _{k=1}^{j-1}{s}_k^{\prime }-s^{\prime }\right)d{s}^{\prime }d{s}_{j-1}^{\prime }\dots d{s}_1^{\prime }.\end{array}$$

(34)

Then

$$\begin{array}{cc}\hfill D{\mathcal{A}}^{j}f& =f(0){\int }_0^x{J}_m(\omega s_1^{\prime }){\int }_0^{x-s_1^{\prime }}{J}_m(\omega s_2^{\prime })\dots {\int }_0^{x-{\sum }_{k=1}^{j-2}{s}_k^{\prime }}{J}_m(\omega s_{j-1}^{\prime })J_m\left(\omega (x-\sum _{k=1}^{j-1}{s}_k^{\prime })\right)d{s}_{j-1}^{\prime }\dots d{s}_1^{\prime }\hfill \\ & +{\int }_0^x{J}_m(\omega s_1^{\prime }){\int }_0^{x-s_1^{\prime }}{J}_m(\omega s_2^{\prime })\dots {\int }_0^{x-{\sum }_{k=1}^{j-1}{s}_k^{\prime }}{J}_m(\omega s^{\prime })f^{\prime }\left(x-\sum _{k=1}^{j-1}{s}_k^{\prime }-s^{\prime }\right)d{s}^{\prime }d{s}_{j-1}^{\prime }\dots d{s}_1^{\prime }\hfill \\ & =f(0){\mathcal{A}}^{j-1}r+{\mathcal{A}}^{j}Df.\hfill \end{array}$$

(35)

Since

$$u=\sum _{j=0}^{\infty }{\mathcal{A}}^{j}f,$$

(36)

this series is uniformly absolutely convergent, therefore we can differentiate it term by term

$$\begin{array}{c}\hfill Du=\sum _{j=0}^{\infty }\left(f(0){\mathcal{A}}^{j-1}r+{\mathcal{A}}^{j}Df\right),\end{array}$$

$$\begin{array}{c}\hfill D^{2}u=\sum _{j=0}^{\infty }\left(f(0)r(0){\mathcal{A}}^{j-2}r+f(0){\mathcal{A}}^{j-1}Dr+f^{\prime }(0){\mathcal{A}}^{j-1}r+{\mathcal{A}}^j{D}^{2}f\right),\end{array}$$

$$\begin{array}{cc}\hfill D^{3}u=& \sum _{j=0}^{\infty }(f(0)r(0)(r(0){\mathcal{A}}^{j-3}r+{\mathcal{A}}^{j-2}Dr)+f(0)(r^{\prime }(0){\mathcal{A}}^{j-2}r+{\mathcal{A}}^{j-1}{D}^{2}r)\hfill \\ & +f^{\prime }(0)(r(0){\mathcal{A}}^{j-2}r+{\mathcal{A}}^{j-1}Dr)+(f^{″}(0){\mathcal{A}}^{j-1}r+{\mathcal{A}}^j{D}^{3}f)),\hfill \end{array}$$

where ${\mathcal{A}}^j=0$ if $j<0$. □

If we define

$$\parallel {\mathcal{A}}^j\parallel :=sup\frac{\parallel {\mathcal{A}}^j{\varphi \parallel }_{\infty }}{{\parallel \varphi \parallel }_{\infty }}=\underset{x\in I}{max}{\int }_0^x|K_j(x,s)|ds$$

and recall that $\parallel {\mathcal{A}}^j{\varphi \parallel }_{\infty }\le \parallel {\mathcal{A}}^j{\parallel \parallel \varphi \parallel }_{\infty }$, we find

Remark 1.

$$\parallel {\mathcal{A}}^j\parallel \le max\{|J_m(\omega (x-s))|:(x,s)\in I\times (0,x)\}/j!\le 1/j!,$$

$$\begin{array}{cc}\hfill \parallel Du\parallel \le & \sum _{j=0}^{\infty }\left(f(0)\parallel {\mathcal{A}}^{j-1}\parallel \parallel r\parallel +\parallel {\mathcal{A}}^j\parallel \parallel Df\parallel \right),\hfill \\ \hfill ∥D^{2}u-f(0)\sum _{j=0}^{\infty }{\mathcal{A}}^{j-1}Dr∥\le & \sum _{j=0}^{\infty }\left(f(0)r(0)\parallel {\mathcal{A}}^{j-2}\parallel \parallel r\parallel +f^{\prime }(0)\parallel {\mathcal{A}}^{j-1}\parallel \parallel r\parallel +\parallel {\mathcal{A}}^j\parallel \parallel D^{2}f\parallel \right),\hfill \end{array}$$

$$\begin{array}{c}\hfill \parallel D^{3}u-\sum _{j=0}^{\infty }(f(0)r(0){\mathcal{A}}^{j-2}Dr-f(0){\mathcal{A}}^{j-1}{D}^{2}r-f^{\prime }(0){\mathcal{A}}^{j-1}Dr)\le \sum _{j=0}^{\infty }(|f(0)r^2(0)|\parallel {\mathcal{A}}^{j-3}\parallel \parallel r\parallel \\ \hfill +|f(0)r^{\prime }(0)|\parallel {\mathcal{A}}^{j-2}\parallel \parallel r\parallel +f^{\prime }(0)r(0)|\parallel {\mathcal{A}}^{j-2}\parallel \parallel r\parallel +|f^{″}(0)|\parallel {\mathcal{A}}^{j-1}\parallel \parallel r\parallel +\parallel {\mathcal{A}}^j\parallel \parallel D^{3}f\parallel ,\end{array}$$

then, we have ${\parallel Du\parallel }_{\infty }$, ${∥D^{2}u-f(0)Dr-D^{2}f∥}_{\infty }$ and $\parallel D^{3}u-f(0)r(0)Dr-f(0)D^{2}r-f^{\prime }(0)Dr-D^3{f\parallel }_{\infty }$ are uniform bounded with respect to $\omega$.

Theorem 2.

Assuming $f\in C^3[0,1],$ the pointwise error of the direct Hermite collocation method for (2) satisfies

$$\begin{array}{c}|u(x_i)-u_i^d|=\left\{\begin{array}{c}O({\omega }^{-3}),f(0)=0\hfill \\ O({\omega }^{-2}),f(0)\ne 0\hfill \end{array}\right.\omega \to \infty ,i=1,2,3,\dots ,N.\hfill \end{array}$$

(37)

$$\begin{array}{c}|u^{\prime }(x_i)-u_i^{\prime d}|=\left\{\begin{array}{c}O({\omega }^{-2}),f(0)=0\hfill \\ O({\omega }^{-1}),f(0)\ne 0\hfill \end{array}\right.\omega \to \infty ,i=1,2,3,\dots ,N.\hfill \end{array}$$

(38)

Proof. 

We only prove a situation $m>0$. For the case $m=0$, the proof method is similar.

By the definition of the direct Hermite collocation method, for any $x_i\in I_N$, it follows that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}E(x_j)-{\int }_0^{x_j}{J}_m(\omega (x_j-t))E(t)dt=0,\hfill \\ E^{\prime }(x_j)-J_m(0)E(t)+\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))E(t)dt=0,\hfill \end{array}\right.\end{array}$$

(39)

where $E(x)=u(x)-u_h(x)$ be the error function. Interpolating E(x) at $x=0$ and $x=x_j$, we have

$$E(x)=H_{1j}E(x_j)+H_{3j}{E}^{\prime }(x_j)+R(x),$$

(40)

where $R(x)$ denotes the remainder of the Hermite interpolation. As we know $E(x)$ satisfies that $E(0)=E^{\prime }(0)=0$. Substituting (40) into (39), we are led to

$$\begin{array}{c}\hfill \left\{\begin{array}{c}E(x_j)-{\int }_0^{x_j}{J}_m(\omega (x_j-t))(H_{1j}E(x_j)+H_{3j}{E}^{\prime }(x_j)+R(t))dt=0,\hfill \\ E^{\prime }(x_j)-J_m(0)E(t)\hfill \\ +\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))(H_{1j}E(x_j)+H_{3j}{E}^{\prime }(x_j)+R(t))dt=0.\hfill \end{array}\right.\end{array}$$

(41)

That is

$$\left\{\begin{array}{c}(1-{\int }_0^{x_j}{J}_m(\omega (x_j-t))H_{1j}dt)E(x_j)-{\int }_0^{x_j}{J}_m(\omega (x_j-t))H_{3j}dt{E}^{\prime }(x_j)={\int }_0^{x_j}{J}_m(\omega (x_j-t)R(t)dt\hfill \\ \left(-J_m(0)+\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))H_{1j}dt\right)E(x_j)\hfill \\ +\left(1+\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))H_{3j}dt\right)E^{\prime }(x_j)\hfill \\ =-\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))R(t)dt.\hfill \end{array}\right.$$

(42)

Therefore, the error $E(x_j)$ can be computed by

$$E(x_j)=\frac{Q_1}{Q_3},E^{\prime }(x_j)=\frac{Q_2}{Q_3},$$

(43)

where

$$\begin{array}{c}\hfill Q_1={\int }_0^{x_j}{J}_m(\omega (x_j-t))R(t)dt\ast \left(1+\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))H_{3j}dt\right)\\ \hfill -{\int }_0^{x_j}{J}_m(\omega (x_j-t))H_{3j}dt\ast \frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))R(t)dt\\ \hfill Q_2={\int }_0^{x_j}{J}_m(\omega (x_j-t))R(t)dt\ast \left(J_m(0)-\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))H_{1j}dt\right)\\ \hfill -\left(1-{\int }_0^{x_j}{J}_m(\omega (x_j-t))H_{1j}dt\right)\ast \frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))R(t)dt\\ \hfill Q_3=\left(1-{\int }_0^{x_j}{J}_m(\omega (x_j-t))H_{1j}dt\right)\ast \left(1+\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))H_{3j}dt\right)\\ \hfill -{\int }_0^{x_j}{J}_m(\omega (x_j-t))H_{3j}dt\ast \left(J_m(0)-\frac{\omega }{2}{\int }_0^{x_j}(J_{m+1}(\omega (x_j-t))-J_{m-1}(\omega (x_j-t)))H_{1j}dt\right).\end{array}$$

Defining $R(x_j-t)=S(t)$, then $S(0)=S^{\prime }(0)=S(x_j)=S^{\prime }(x_j)$. From Lemma 1 to Lemma 3, we can easily get $Q_3=O(1)$ with respect to $\omega$. What shall we do is prove that

$${\int }_0^{x_j}{J}_m(\omega s)S(s)ds=\left\{\begin{array}{c}O({\omega }^{-3}),f(0)=0\hfill \\ O({\omega }^{-2}),f(0)\ne 0\hfill \end{array}\right..$$

Using integration by parts twice, we get

$$\begin{array}{cc}\hfill {\int }_0^{x_j}{J}_m(\omega s)S(s)ds& ={\int }_0^{x_j}S(s)d\frac{s^{m+1}{J}_{m+1}(\omega s)}{\omega s^{m+1}}\hfill \\ & =\frac{1}{{\omega }^2}{\int }_0^{x_j}\left(S^{″}(s)-(2m+3)\frac{S^{\prime }(s)}{s}+(m+1)(m+3)\frac{S(s)}{s^2}\right)J_{m+2}(\omega s)ds.\hfill \end{array}$$

Denote

$$J={\int }_0^{x_j}\left(S^{″}(s)-(2m+3)\frac{S^{\prime }(s)}{s}+(m+1)(m+3)\frac{S(s)}{s^2}\right)J_{m+2}(\omega s)ds.$$

So, we only need to prove that $J=\left\{\begin{array}{c}O({\omega }^{-1})f(0)=0\hfill \\ O(1)f(0)\ne 0\hfill \end{array}\right..$

In the following, we show that the convergence degree of J with respect to $\omega$.

Letting

$$F(s)=S^{″}(s)-(2m+3)\frac{S^{\prime }(s)}{s}+(m+1)(m+3)\frac{S(s)}{s^2},$$

then we have

$$F(0)=S^{″}(0)-(2m+3)S^{″}(0)+(m+1)(m+3)\frac{S^{″}(0)}{2},$$

$$\begin{array}{cc}\hfill J& ={\int }_0^{x_j}F(s)J_{m+2}(\omega s)ds\hfill \\ & ={\int }_0^{x_j}(F(s)-F(0))J_{m+2}(\omega s)ds+{\int }_0^{x_j}F(0)J_{m+2}(\omega s)ds\hfill \\ & =\frac{1}{\omega }\left(J_{m+3}{(\omega s)(F(s)-F(0))|}_{s=0}^{s=x_j}-{\int }_0^{x_j}(F^{\prime }(s)-(m+3)\frac{F(s)-F(0)}{s})J_{m+3}(\omega s)ds\right)\hfill \\ & +F(0){\int }_0^{x_j}{J}_{m+2}(\omega s)ds.\hfill \end{array}$$

Observing that

$$\begin{array}{cc}\hfill F^{\prime }(s)& =S^{‴}(s)-(2m+3)\frac{S^{″}(s)s-S^{\prime }(s)}{s^2}+(m+1)(m+3)\left(\frac{S^{\prime }(s)}{s^2}-\frac{2S(s)}{s^3}\right),\hfill \\ \hfill \frac{F(s)-F(0)}{s}& =\frac{S^{″}(s)s-S^{\prime }(0)}{s}-(2m+3)\left(\frac{S^{\prime }(s)}{s}-S^{″}(0)\right)+(m+1)(m+3)\left(\frac{S^{\prime }(s)}{s^2}-\frac{S^{″}(0)}{2}\right).\hfill \end{array}$$

Notice that

$$\begin{array}{cc}\hfill S^{‴}(s)& =u^{‴}(s)-u_h^{‴}(s)\hfill \\ & =u^{‴}(s)+c_1·u_0^{\prime }+c_2·u_j^{\prime },\hfill \end{array}$$

where $c_1$ and $c_2$ are some constants independent of $\omega$. For $u_h(x)$ is cubic polynomial, we can easily show that $u_h^{‴}(s)=O(1)$ with respect to $\omega .$ According to Theorem 1 it follows that $\parallel D^{3}u-f(0)r(0)Dr-f(0)D^{2}r-f^{\prime }(0)Dr-D^3{f\parallel }_{\infty }.$ Together with Lemma 3 we can easily get

$${\int }_0^{x_j}(u^{‴}(s)-f(0)r(0)Dr-f(0)D^{2}r-f^{\prime }(0)Dr-D^{3}f)J_m(\omega (x_j-s)ds=\left\{\begin{array}{c}O(1),f(0)=0,\hfill \\ O(\omega ),f(0)\ne 0.\hfill \end{array}\right.$$

That is

$${\int }_0^{x_j}{S}^{‴}(s)J_m(\omega (x_j-s))ds=\left\{\begin{array}{c}O(1),f(0)=0,\hfill \\ O(\omega ),f(0)\ne 0.\hfill \end{array}\right.$$

Then

$$J=\left\{\begin{array}{c}O({\omega }^{-1}),f(0)=0,\hfill \\ O(1),f(0)\ne 0.\hfill \end{array}\right.$$

Therefore, we can get

$$\begin{array}{c}|u(x_i)-u_i^d|=\left\{\begin{array}{c}O({\omega }^{-3}),f(0)=0\hfill \\ O({\omega }^{-2}),f(0)\ne 0\hfill \end{array}\right.\omega \to \infty ,i=1,2,3,\dots ,N.\hfill \end{array}$$

(44)

$$\begin{array}{c}|u^{\prime }(x_i)-u_i^{\prime d}|=\left\{\begin{array}{c}O({\omega }^{-2}),f(0)=0\hfill \\ O({\omega }^{-1}),f(0)\ne 0\hfill \end{array}\right.\omega \to \infty ,i=1,2,3,\dots ,N.\hfill \end{array}$$

(45)

 □

Theorem 3.

Assuming $f\in C^3(I),$ the error of the piecewise Hermite collocation method for (2) satisfies

$$\begin{array}{c}|u(x_i)-u_i|=\left\{\begin{array}{c}O({\omega }^{-3}h),f(0)=0\hfill \\ O({\omega }^{-2}h),f(0)\ne 0\hfill \end{array}\right.\omega \to \infty ,i=1,2,3,\dots ,N.\hfill \end{array}$$

(46)

$$\begin{array}{c}|u^{\prime }(x_i)-u_i^{\prime }|=\left\{\begin{array}{c}O({\omega }^{-2}h),f(0)=0\hfill \\ O({\omega }^{-1}h),f(0)\ne 0\hfill \end{array}\right.\omega \to \infty ,i=1,2,3,\dots ,N.\hfill \end{array}$$

(47)

Proof. 

For the piecewise Hermite collocation method, $u(x_j)$ satisfies

$$u(x_j)-\sum _{k=1}^{j-1}{\int }_{x_{k-1}}^{x_k}{J}_m(\omega (x_j-t))u(t)dt-{\int }_{x_{j-1}}^{x_j}{J}_m(\omega (x_j-t))u(t)dt=f(x_j).$$

(48)

Combining the above equation with

$$u_j-\sum _{k=1}^{j-1}{\int }_{x_{k-1}}^{x_k}{J}_m(\omega (x_j-t)){\widehat{u}}_k(t)dt-{\int }_{x_{j-1}}^{x_j}{J}_m(\omega (x_j-t)){\widehat{u}}_j(t)dt=f(x_j),$$

(49)

we get

$${\epsilon }_j=\frac{{\sum }_{k=1}^{j-1}{\epsilon }_k{\int }_{x_{k-1}}^{x_k}{J}_m(\omega (x_j-t))dt+{\sum }_{k=1}^j{\int }_{x_{k-1}}^{x_k}{J}_m(\omega (x_j-t))r_k(t)dt}{1-{\int }_0^{x_1}{J}_m(\omega t)dt},$$

(50)

where ${\epsilon }_j=u(x_j)-u_j,j=1,2,\cdots ,N$ and $r_k(t)=(u(t)-{\widehat{u}}_k(t)){|}_t\in [x_{k-1},x_k]$. An argument similar to the one used in Theorem 2 shows that

$$\frac{{\sum }_{k=1}^j{\int }_{x_{k-1}}^{x_k}{J}_m(\omega (x_j-t))r_k(t)dt}{1-{\int }_0^{x_1}{J}_m(\omega t)dt}=\left\{\begin{array}{c}O({\omega }^{-3}h),f(0)=0\hfill \\ O({\omega }^{-2}h),f(0)\ne 0\hfill \end{array}\right.,$$

(51)

the desired result is then found by employing the generalized discrete Gronwall inequality ([4], p. 95). Similarly, one can derive the convergence order of $|u^{\prime }(x_i)-u_i^{\prime }|$. □

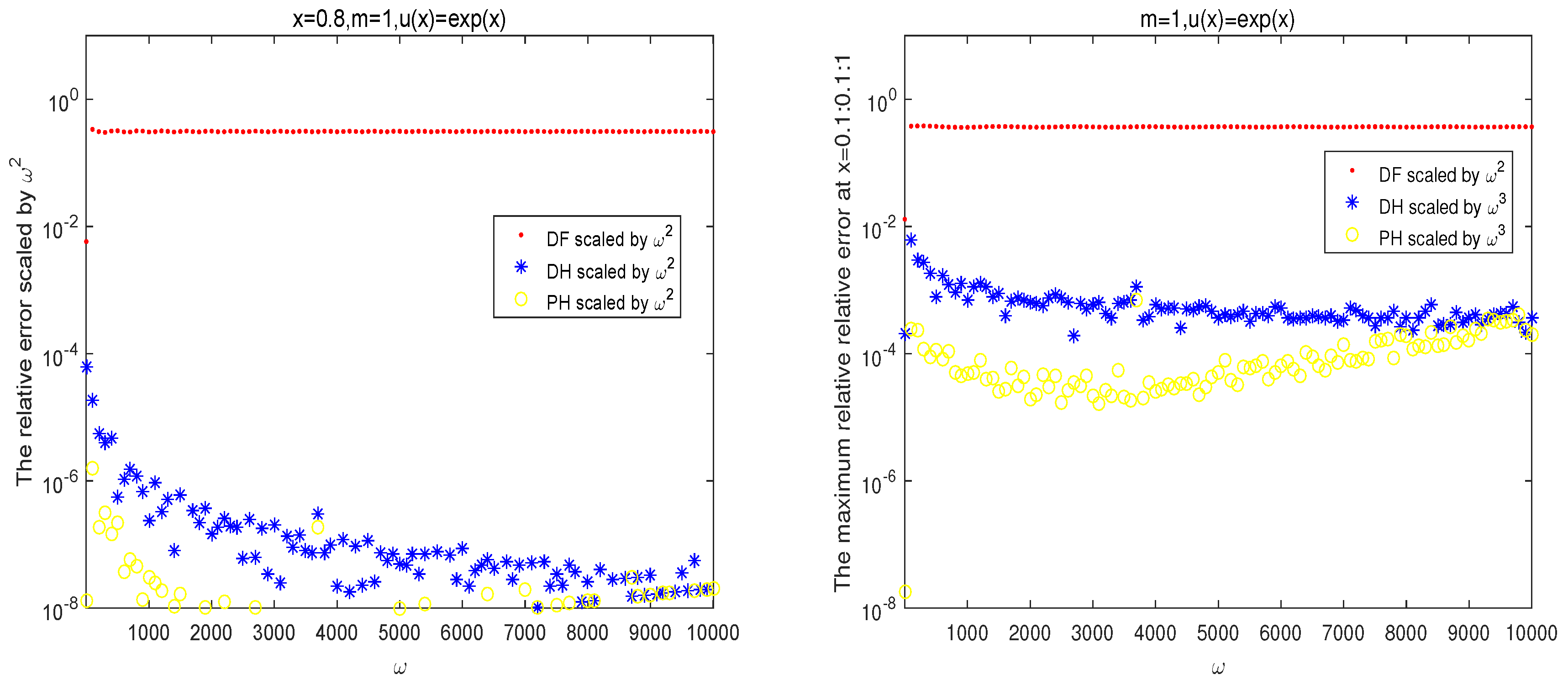
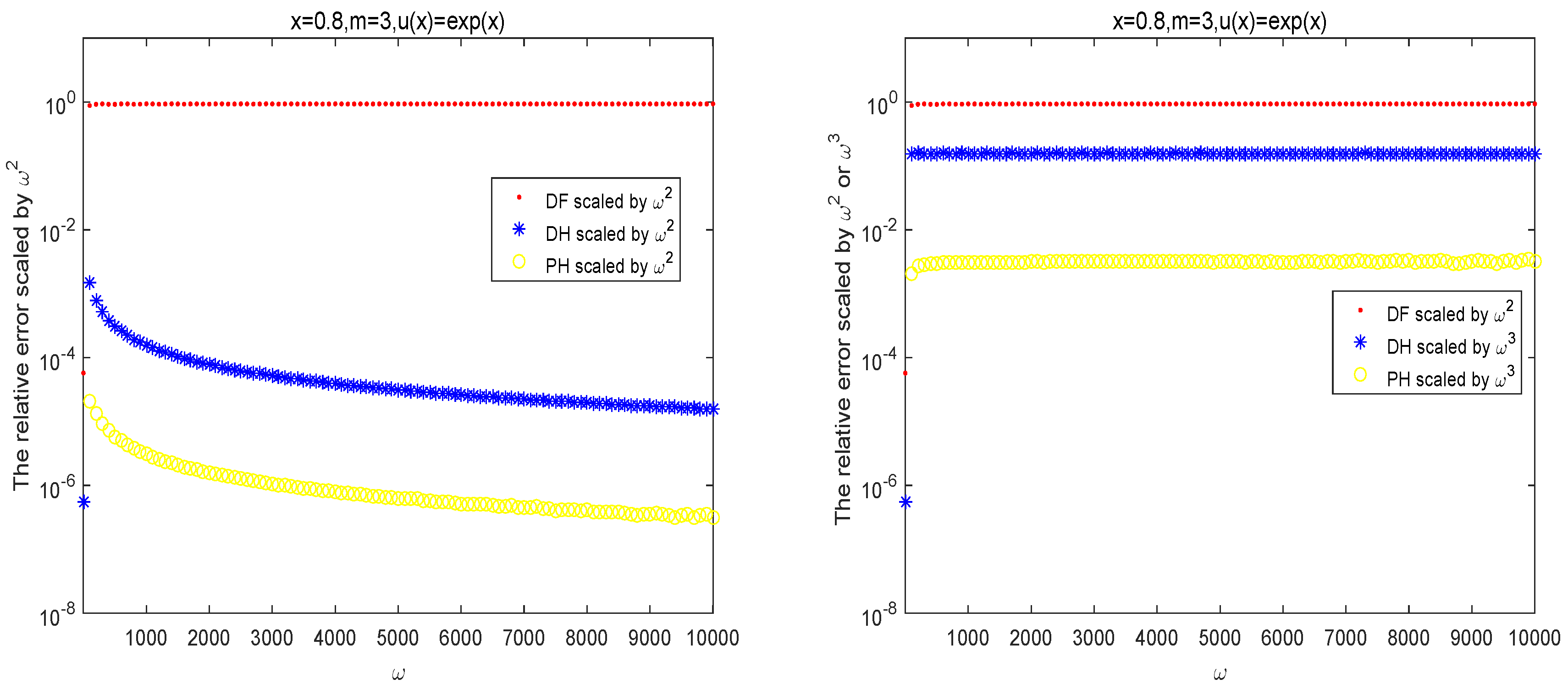
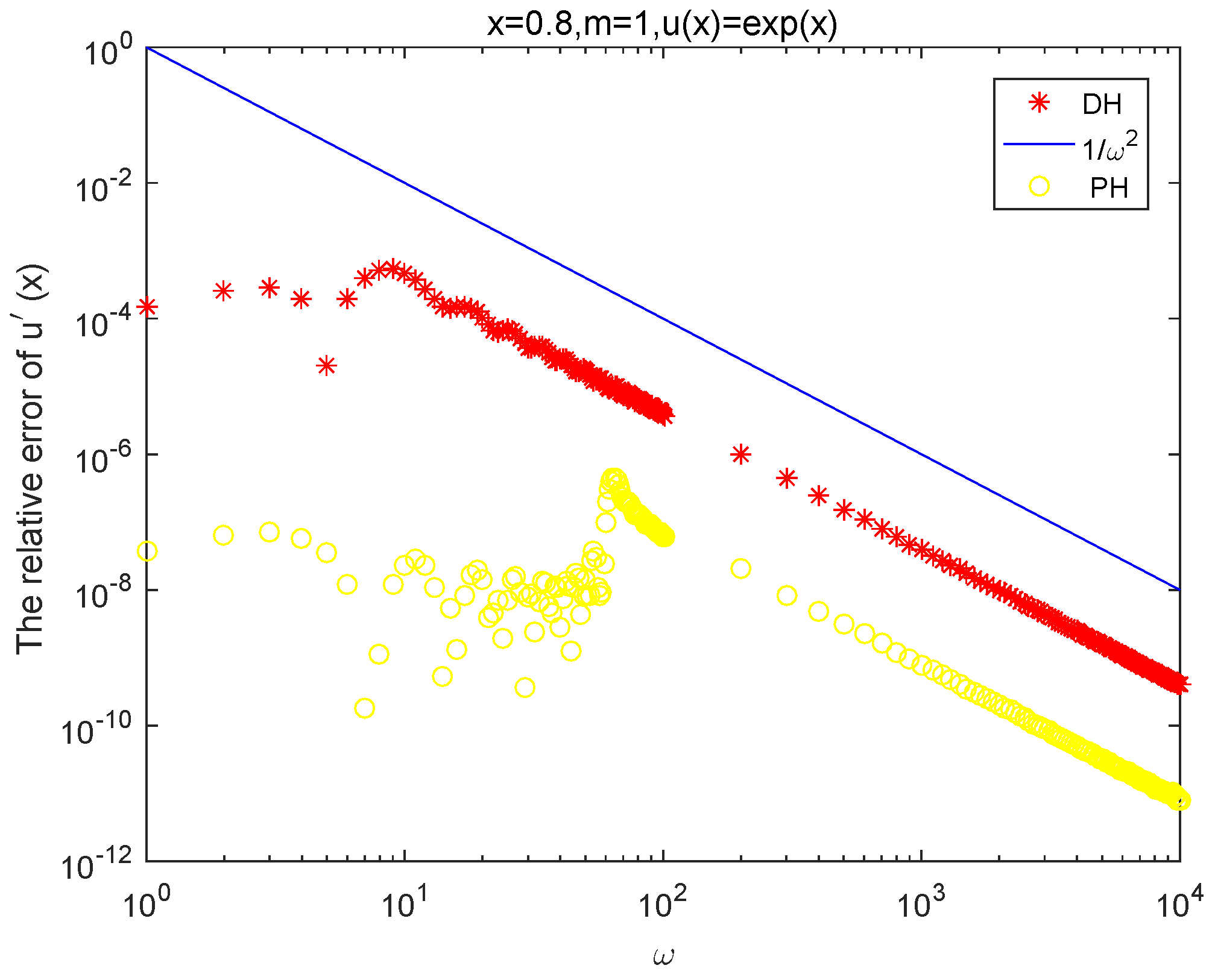
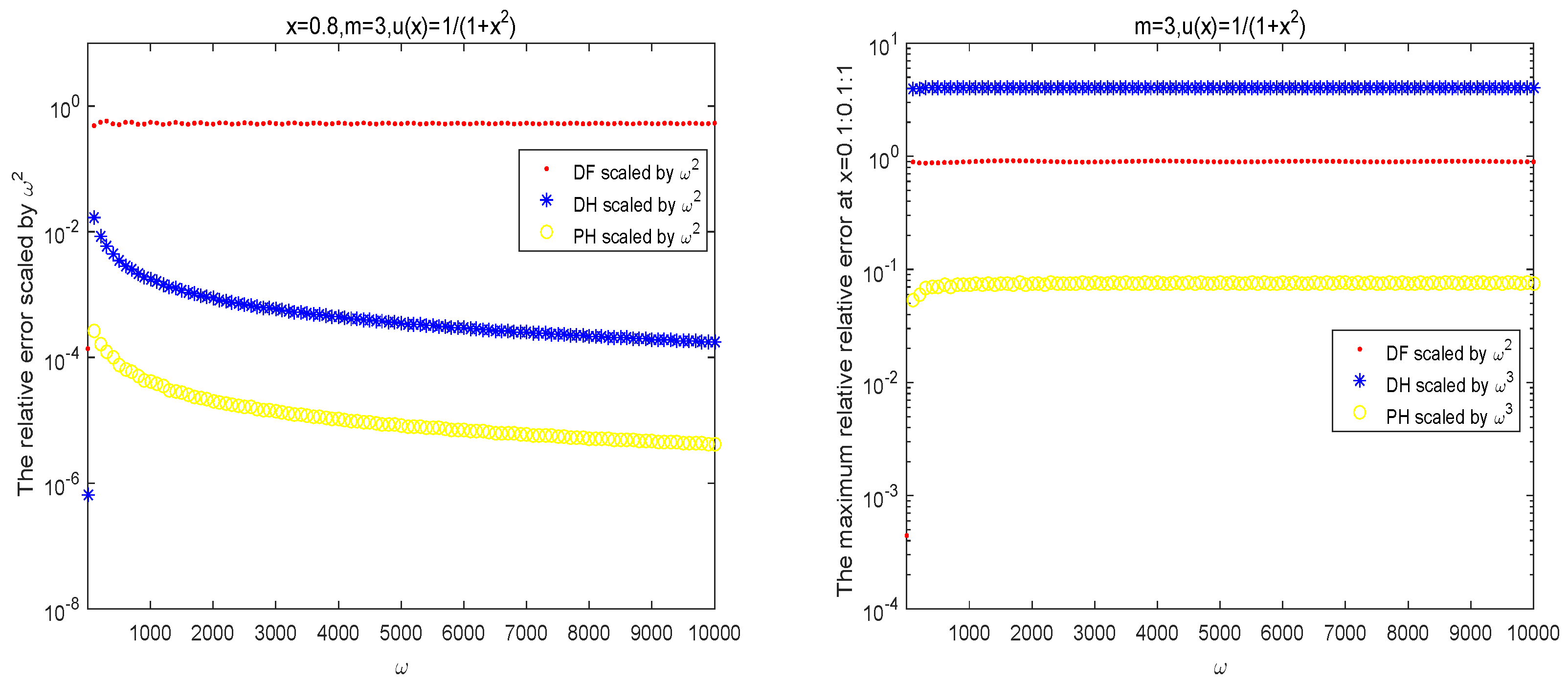
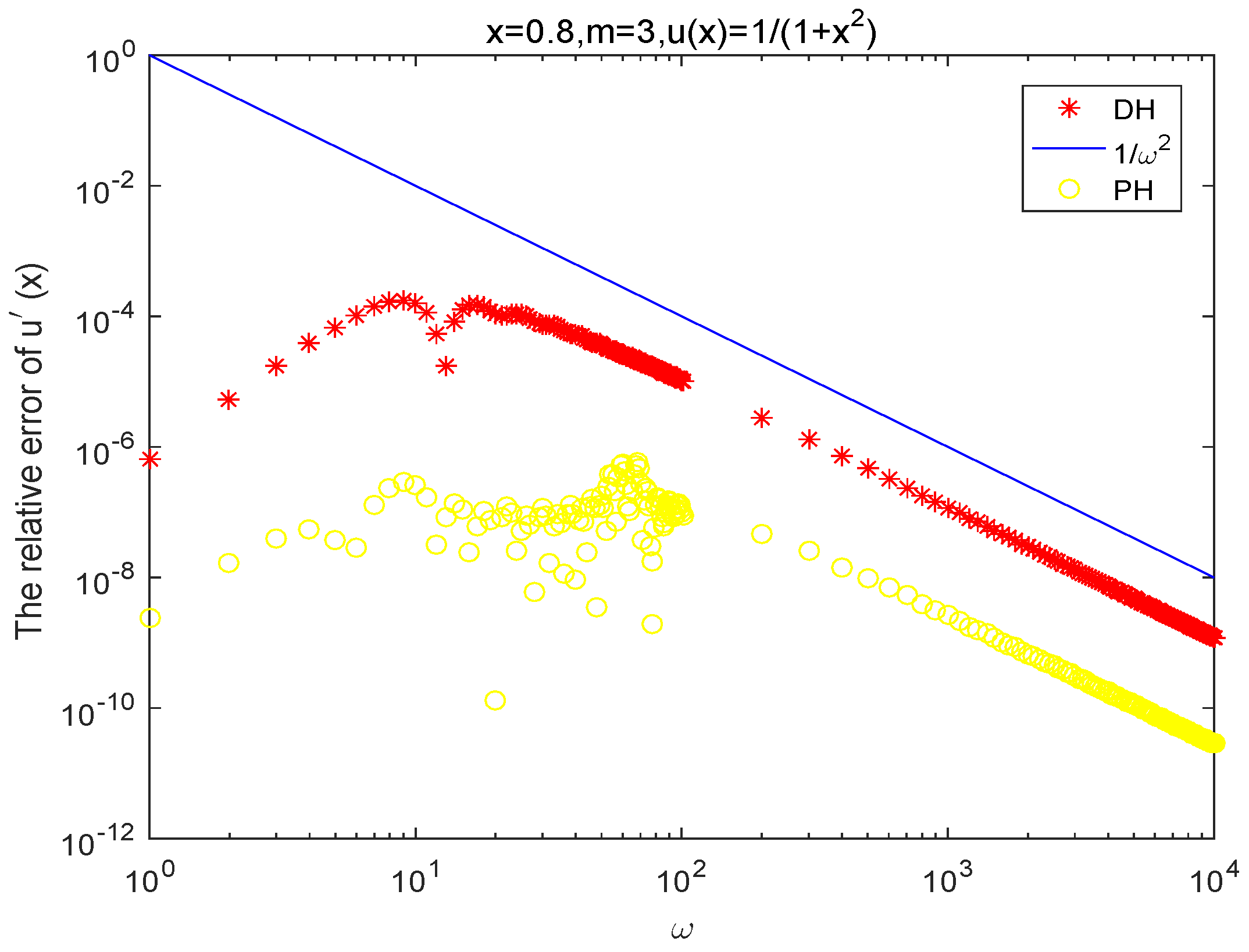
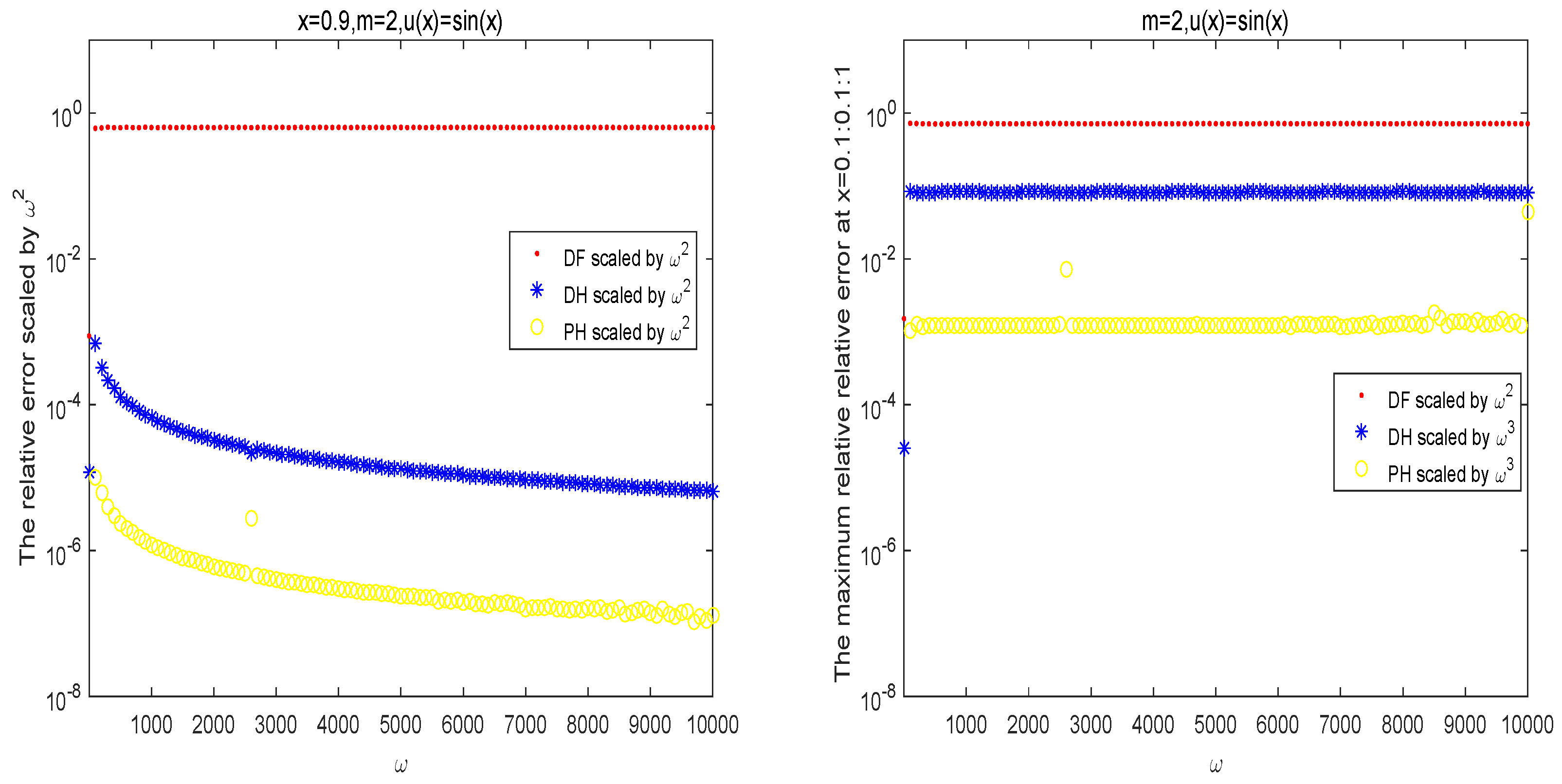
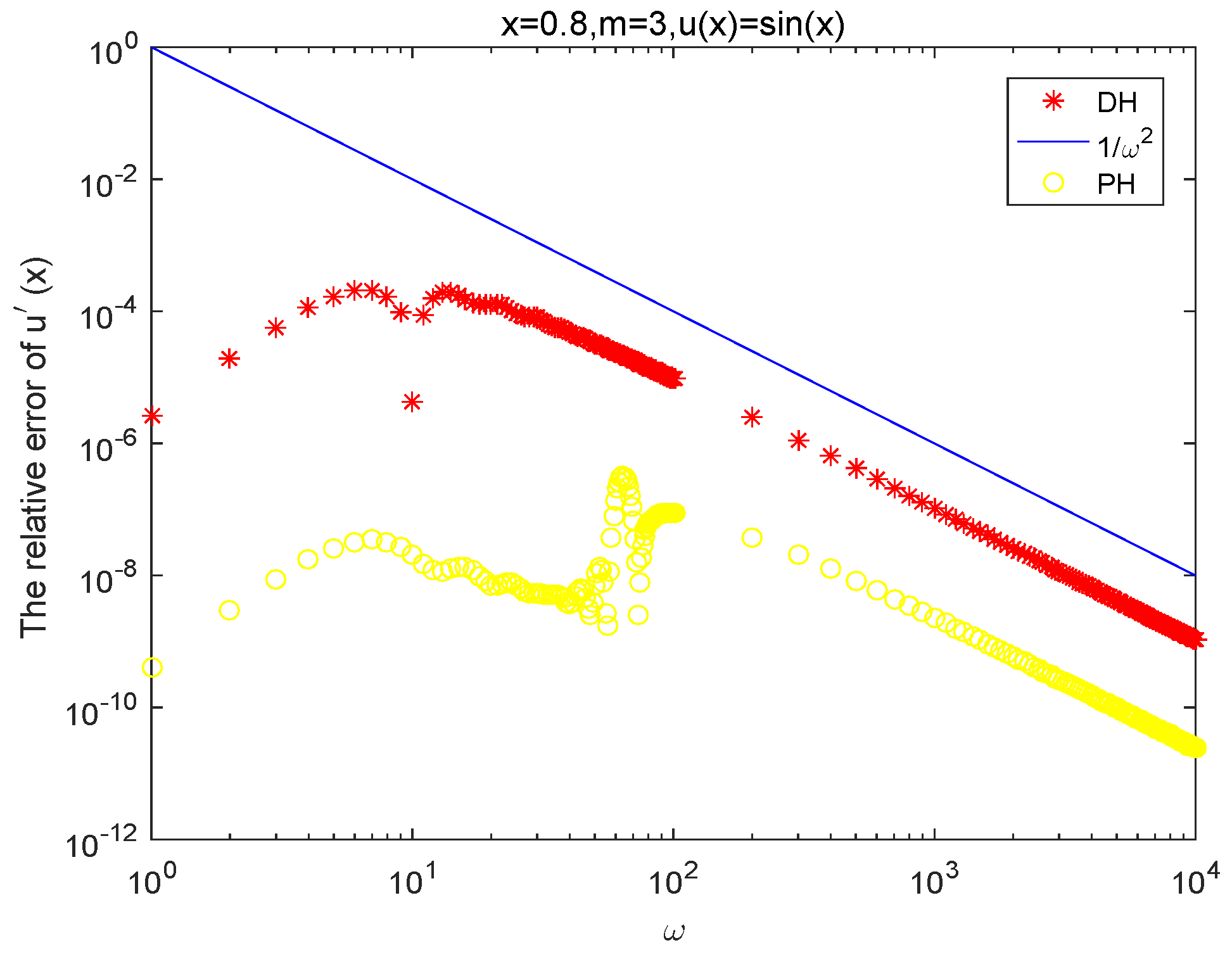
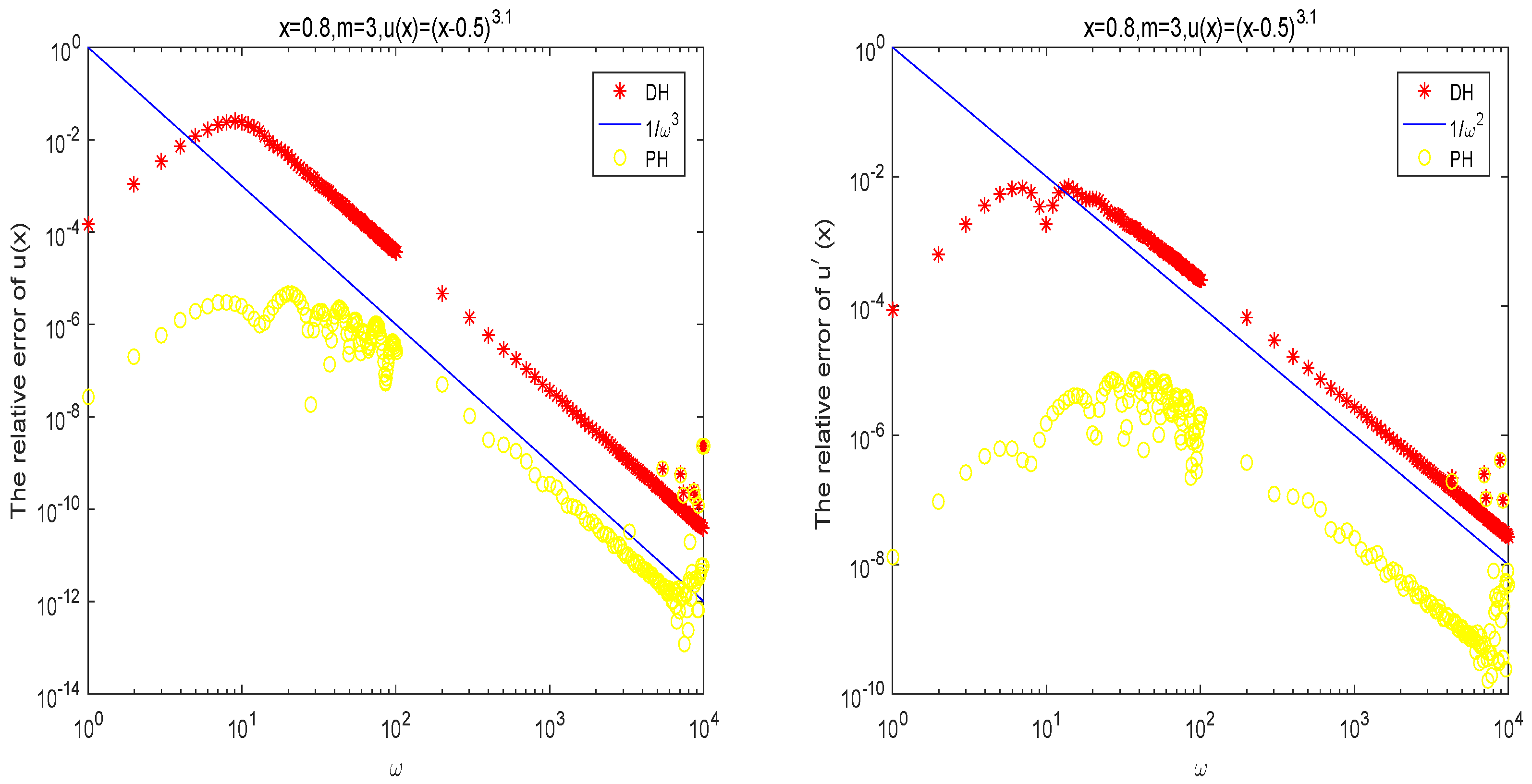
4. Numerical Examples

From Section 4, we can see that direct Hermite collocation method and piecewise Hermite collocation method are very efficient for solving the second-kind Volterra integral equation with highly oscillatory Bessel kernel. They possess the property that the higher oscillation, the higher accuracy. In this section, based on the Formulas (11), (13) and (22), we present some preliminary numerical experiments to verify the result of theoretical analysis. The experiments are performed on a 1.86 GHz PC with 2 GB of RAM. We are using the R2016a version of the Matlab system. The following Direct Filon method (DF) is presented in paper [14].

Example 1.

Consider the following equation

$$\begin{array}{c}\hfill u(x)-{\int }_0^x{J}_m(\omega (x-t))u(t)dt=f(x)withx\in I=[0,1],\end{array}$$

(52)

where $f(x)=e^x-{\int }_0^x{J}_m(\omega (x-t))e^{t}dt$. The analytic solution is $u(x)=e^x$.

In

Table 1. Relative errors of $u(x)$ in N–point approximations to the Example 1 by the DF method, the piecewise linear method (PL), the direct Hermite method(DH) and the piecewise Hermite collocation method(PH). The step is 0.1 for piecewise method and the test point is 0.8.

$\mathit{\omega }\backslash \mathit{Method}$	$\mathit{DF}$	$\mathit{PL}$	$\mathit{DH}$	$\mathit{PH}$
10	$6.85\times {10}^{-3}$	$6.86\times {10}^{-5}$	$8.80\times {10}^{-5}$	$1.14\times {10}^{-8}$
100	$8.89\times {10}^{-5}$	$1.06\times {10}^{-5}$	$1.56\times {10}^{-7}$	$2.08\times {10}^{-9}$
1000	$9.38\times {10}^{-7}$	$1.31\times {10}^{-7}$	$1.56\times {10}^{-10}$	$3.08\times {10}^{-12}$
$10,000$	$9.36\times {10}^{-9}$	$1.46\times {10}^{-9}$	$1.57\times {10}^{-13}$	$3.39\times {10}^{-15}$

, we compare the relative error of $u(x)$ from the DF method, piecewise linear collocation method, direct Hermite collocation, and piecewise Hermite collocation method. In

Table 2. Relative errors of $u(x)$ in N–point approximations to the Example 1 by the PL method and the piecewise Hermite collocation method(PH). where $\omega =1000$ and the test point is 0.8.

$\mathit{Method}\backslash \mathit{h}$	$0.2$	$0.1$	$0.05$	$0.01$
$PL$	$2.71\times {10}^{-7}$	$1.31\times {10}^{-7}$	$5.69\times {10}^{-8}$	$1.10\times {10}^{-8}$
$PH$	$1.21\times {10}^{-11}$	$3.08\times {10}^{-12}$	$7.44\times {10}^{-13}$	$1.03\times {10}^{-14}$

, for fixed $\omega$, we compare the relative error of $u(x)$ from the piecewise linear collocation method and piecewise Hermite collocation method when the steps are different. In Figure 1, Figure 2 and Figure 3, we can see the convergence rate with respect to $\omega$ of these methods.

Example 2.

Consider the following equation,

$$\begin{array}{c}\hfill u(x)-{\int }_0^x{J}_3(\omega (x-t))u(t)dt=f(x)withx\in I=[0,1],\end{array}$$

(53)

where $f(x)=\frac{1}{1+x^2}-{\int }_0^x{J}_3(\omega (x-t))\frac{1}{1+t^2}dt$. The analytic solution is $u(x)=\frac{1}{1+x^2}$.

We can see the numerical solutions from the

Table 3. Relative errors of $u(x)$ in N–point approximations to the Example 2 by the DF method, the PL method, the DH method, and the piecewise Hermite collocation method (PH). The step is 0.1 for piecewise method and the test point is 0.8.

$\mathit{\omega }\backslash \mathit{Method}$	$\mathit{DF}$	$\mathit{PL}$	$\mathit{DH}$	$\mathit{PH}$
10	$1.13\times {10}^{-2}$	$6.83\times {10}^{-5}$	$4.34\times {10}^{-4}$	$2.22\times {10}^{-7}$
100	$5.10\times {10}^{-5}$	$7.23\times {10}^{-6}$	$1.68\times {10}^{-6}$	$2.53\times {10}^{-8}$
1000	$5.12\times {10}^{-7}$	$6.77\times {10}^{-8}$	$1.75\times {10}^{-9}$	$4.11\times {10}^{-11}$
$10,000$	$5.32\times {10}^{-9}$	$9.68\times {10}^{-10}$	$1.75\times {10}^{-12}$	$4.21\times {10}^{-14}$

and

Table 4. Relative errors of $u(x)$ in N–point approximations to the Example 2 by the PL method and the piecewise Hermite collocation method (PH). where $\omega =10,000$ and the test point is 0.8.

$\mathit{Method}\backslash \mathit{h}$	$0.2$	$0.1$	$0.05$	$0.01$
$PL$	$1.64\times {10}^{-9}$	$9.68\times {10}^{-10}$	$4.91\times {10}^{-10}$	$8.78\times {10}^{-11}$
$PH$	$1.85\times {10}^{-13}$	$4.21\times {10}^{-14}$	$1.00\times {10}^{-14}$	0

and Figure 4 and Figure 5.

Example 3.

Consider the following equation,

$$\begin{array}{c}\hfill u(x)-{\int }_0^x{J}_m(\omega (x-t))u(t)dt=f(x)withx\in I=[0,1],\end{array}$$

(54)

where $f(x)=sin(x)-{\int }_0^x{J}_2(\omega (x-t))sin(t)dt$. The analytic solution is $u(x)=sin(x)$.

Results of these calculations are given in

Table 5. Relative errors of $u(x)$ in N–point approximations to the Example 3 by the DF method and the PL method and the DH method, and the piecewise Hermite collocation method (PH). The step is 0.1 for piecewise method and the test point is 0.9.

$\mathit{\omega }\backslash \mathit{Method}$	$\mathit{DF}$	$\mathit{PL}$	$\mathit{DH}$	$\mathit{PH}$
10	$5.02\times {10}^{-3}$	$7.35\times {10}^{-5}$	$7.88\times {10}^{-5}$	$1.23\times {10}^{-8}$
100	$6.31\times {10}^{-5}$	$6.83\times {10}^{-6}$	$7.01\times {10}^{-8}$	$1.03\times {10}^{-9}$
1000	$6.38\times {10}^{-7}$	$8.92\times {10}^{-8}$	$6.62\times {10}^{-11}$	$1.20\times {10}^{-12}$
$10,000$	$6.35\times {10}^{-9}$	$9.88\times {10}^{-10}$	$6.56\times {10}^{-14}$	$1.28\times {10}^{-15}$

and Figure 6 and Figure 7.

Example 4.

Consider the following equation,

$$\begin{array}{c}\hfill u(x)-{\int }_0^x{J}_3(\omega (x-t))u(t)dt=f(x)withx\in I=[0,1],\end{array}$$

(55)

where $f(x)={(x-0.5)}^{3.1}-{\int }_0^x{J}_3(\omega (x-t)){(t-0.5)}^{3.1}dt$. The analytic solution is $u(x)={(x-0.5)}^{3.1}$.

We can see the numerical solutions from the Figure 8.

From above examples, as can be seen, there is a good agreement between the present result and the exact solution. The Hermite-type collocation methods are better than DF method and PL collocation method. For Hermite-type collocation methods, the higher oscillation, the higher accuracy. For fixed frequency, the error is decrease with the increase of nodes.

5. Conclusions

Collocation methods are efficient in solving Volterra integral equation with highly oscillatory kernel. In this paper, we present two collocation methods: DH collocation method and piecewise Hermite collocation method. The first conclusion to be drawn from the numerical evidence presented earlier is that Hermite-type collocation methods are higher efficient than existent collocation methods. Both methods can calculate the approximate value of function value and derivative value simultaneously. Finally, while we have considered only the case of Bessel kernel in this paper, the Hermite-type collocation methods can be extended to Fourier kernel.

In the future work, we will study better methods to solve the Volterra integral equations with different kernel and Fredholm integral equations.