Model of Threats to Computer Network Software

Abstract

This article highlights the issue of identifying information security threats to computer networks. The aim of the study is to increase the number of identified threats. Firstly, it was carried out the analysis of computer network models used to identify threats, as well as in approaches to building computer network threat models. The shortcomings that need to be corrected are highlighted. On the basis of the mathematical apparatus of attributive metagraphs, a computer network model is developed that allows to describe the software components of computer networks and all possible connections between them. On the basis of elementary operations on metagraphs, a model of threats to the security of computer network software is developed, which allows compiling lists of threats to the integrity and confidentiality of computer network software. These lists include more threats in comparison with the considered analogues.

1. Introduction

The problem of ensuring the security of computer networks has not lost its relevance from the moment of their appearance and wide distribution to the present day. Thus, according to a study by Positive Technologies, in 2018, as part of an external penetration testing, the network perimeter of 92 percent of companies was breached [1]. Along with this, technologies are constantly evolving. New types of threats appear [2], and the security of computer networks is evolving into the security of the Internet of Things [3,4,5,6].

An essential step in the process of providing security is to identify a list of relevant threats. However, before determining the relevance, it is necessary to compile the most extensive list of threats [7], in other words, to identify threats.

Network security issues are relevant for both large companies and small organizations [8]. At the same time, it is obvious that the resources that can be allocated for security will differ. This affects not only the possible costs of technical equipment, but also the qualifications of the specialists which the organization can hire. The professional level, as well as the subjective opinion of an expert when using existing approaches to building lists of threats to information systems, significantly affects the result.

An urgent task is to develop an effective methodology for compiling a list of threats to information security, the use of which will minimize the impact of the professional level and subjective opinion of an expert. This study is part of the development of a comprehensive approach to assessing the security of the information systems conducted in Tomsk University of Control Systems and Radioelectronics [9].

This paper addresses the issue of identifying security threats to computer network software. The aim of the study is to increase the number of identified threats. At the same time, issues of determining the relevance of threats and further risk analysis remain outside the scope of this work. To achieve this goal it is necessary:

• To analyze the current state of the subject area: computer network models and approaches to building threat models used in compiling lists of threats.
• To develop a computer network model that allows to describe the structure of the system at a level of detail enough to compile a list of threats.
• To develop a computer network threat model that takes into account the maximum possible number of threats.

With computer networks we mean local area networks, which are a system that provides data exchange between subnets, network nodes, and the software installed on them.

2. Related Work

There are many approaches to building a threat model. In [10] it is indicated that in threat modeling, there are techniques that center on attackers, assets, or software. It includes the STRIDE threat model [11], attack trees originally presented by B. Schneier, attack libraries, and privacy tools. In [12] authors deal with the threat classification problem and its motivation. They categorize threat classification approaches into two main classes: methods based on attacks techniques and methods based on threats impacts.

It should be clarified that the concepts of threat classification and threat modeling in the context of different works may differ. Classification is understood as a ride to gain an understanding of the characteristics and nature of known threats [12]. Threat modeling involves determining a list of threats to the security of the system or information used to further risk assessment and building a protection system [13].

Moreover, threat classification methods are used in threat modeling, which is justified. If there is a classification, it is easier for a specialist to navigate in the whole variety of existing threats. This approach to threat modeling is called high-level. On the other hand, using only classifications, it is difficult to obtain a detailed list of threats on the basis of which it is possible to build the structure of a protection system. Examples of such approaches can be considered in [11] and [14].

Low-level approaches are those that describe threats in detail. Such approaches may be based on the use of the list of attacks [15,16,17,18,19] or the list of attack scenarios [20]. Some approaches come down to analyzing the exploitation of vulnerabilities in the system [21,22,23].

In [24] a classification of threats is proposed that has signs of a high-level and low-level approach. The work is aimed at describing the threat’s class impact instead of a threat impact as a threat varies over time. However, for its effective application in practice, there is not enough formalization.

The problem with many approaches is the lack of formalization, which leads to their ambiguous interpretation and subjectivity of the resulting list of threats. There are works that use the mathematical apparatus of graph theory, but they are aimed at formalizing the description of attacks, not threats themselves [25,26,27]. Some works are aimed at the description of attackers and does not allow to determine the list of threats [28].

Separately, it is necessary to mention the databases of threats, attacks, and vulnerabilities that are often used in practice when building threat models, such as the ATT&CK Matrix [29] and Information Security Threat Databank of FSTEC of Russia [30]. In connection with the specifics of the study [30], a detailed comparison of the results of the work was carried out with a list of threats mentioned in it.

In the analysis of approaches to building models of threats to the security of information systems and, in particular, computer networks, the following shortcomings were identified:

• Some threat models contain elements of the attacker model, or the attacker model directly influences the formation of the list of threats.
• In one threat model at one level there may be a generalized description of threats, as well as a description of special cases.
• There is no division into threats aimed at the system and threats aimed at the information.
• The building of threat lists is based on the subjective opinion of an information security specialist.

The key disadvantage of all models is that none of them explicitly describes threats to the information system. All attention is paid to the security threats to information processed in the information system.

Each of the considered models can take into account certain threats that are not described in another.

Furthermore, in many of the considered models there is no mathematical formalization, that is, threats are presented through verbal descriptions. The sequence of identification of threats to the system under consideration is given by general instructions, without a step-by-step description of the actions. This often leads to the fact that experts can interpret the same technique differently, moreover, experts often do not have a direct relationship with the organization, which introduces additional inaccuracies in the formation of a threat model.

Another drawback of existing approaches is the lack of justification for the classification of threats and consequently the lack of justification for the completeness of the proposed classification.

As a result of the analysis of approaches to building computer network models [31,32,33,34,35], we can conclude that, with their help, it is impossible to describe in detail what the objects in the information system are (that is, describe their parameters), as well as describe how they interact with each other. In order to more fully describe the threats to the information security of a computer network, the model of the computer network should satisfy the following requirements. It is necessary to take into account:

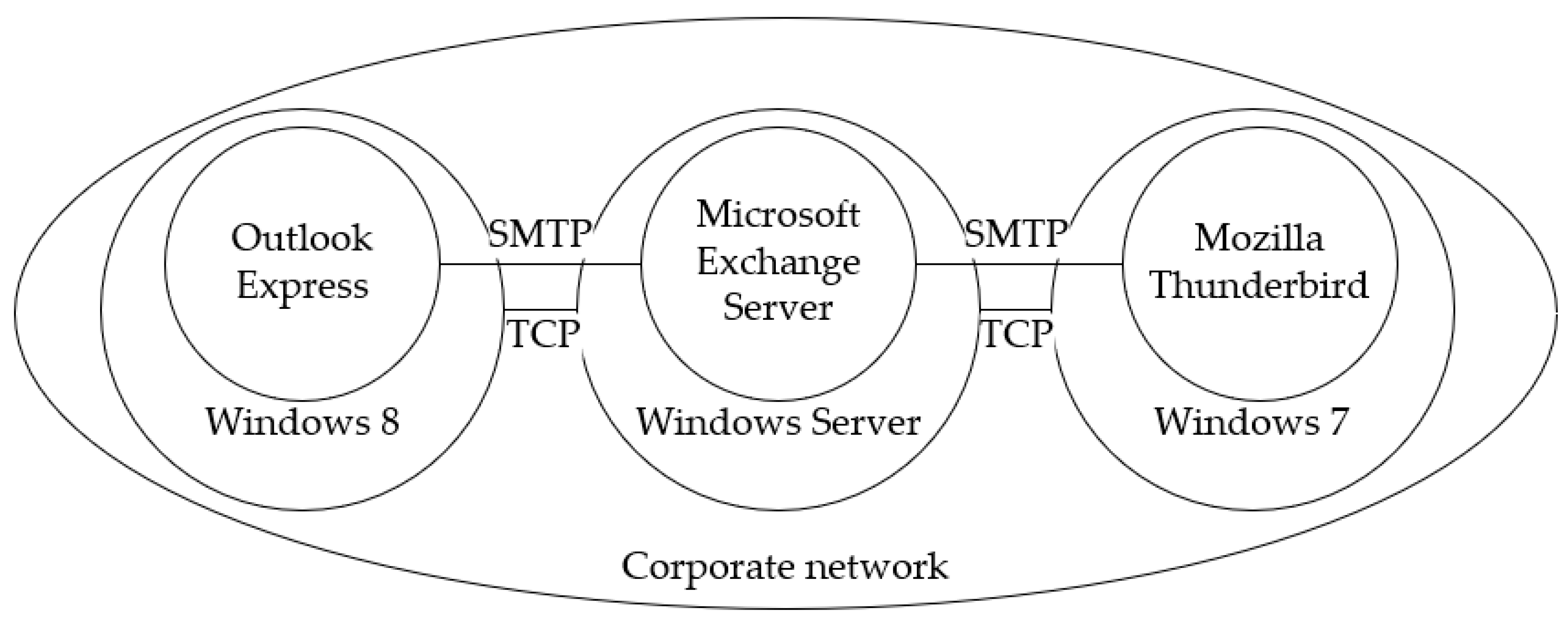
• The hierarchy of computer network software.
• The possibility of the existence of several connections between two elements.
• The elements and the connections between them have parameters.

3. Proposed Approach

3.1. Computer Network Model

A computer network model based on attributive metagraphs allows to describe the software components of computer networks and all possible connections between them. The study considers only the software elements of computer networks (computer network software components and applications) and the links between them. The software in this case includes the application, system, and network software. A similar approach to the classification of system elements was applied in [36]. Links are implied not only between elements located at the same level, but also by indicating the nesting of one element in another. That is, application software operates in operating systems, which are system software. In turn, operating systems operate within the framework of local area networks (or subnets) implemented through network software. Thus, three levels of computer network software are distinguished. For convenience, the levels are designated as the application level, the operating system level, and the network level.

As a mathematical apparatus for the implementation of the model, attributive metagraphs were chosen [37]. The metagraph contains and coordinates among itself two main properties of the system: unity (a set of interlinked elements) and divisibility (each element of the system is also a system). In this regard, subsystems can be distinguished from the system. This allows to focus on the system or its subsystem if necessary.

The attributive metagraph nested at n levels of depth is represented as an ordered pair:

$$G=\left(X,E\right),$$

(1)

where G is the attributive metagraph nested at n levels of depth; $X=\left\{x_i\right\},i=\overline{1,n}$ is nonempty finite set of vertices; $E=\left\{e_k\right\},k=\overline{1,m}$ is nonempty finite set of edges.

Each edge of an n-dimensional graph connects two subsets of the set of vertices:

$$e_k=\left(V_i,W_i\right),$$

(2)

where $V_i,W_i\subseteq X;V_i{\displaystyle \cup }{W}_i\ne \varnothing$; $i$ is nesting level.

There are also functions that indicate the nesting of vertices and edges of a metagraph:

$$f_1^l:g_1^l\left(x_1^l,e_1^l\right)\to x_2^p,f_2^p:g_2^p\left(x_2^p,e_2^p\right)\to x_3^m,\dots ,f_{n-1}^t:g_{n-1}^t\left(x_{n-1}^t,e_{n-1}^t\right)\to x_n,$$

(3)

where $l, p, r, \dots ,t$ is number of vertices and edges at the appropriate level.

The vertices and edges of the attribute metagraph are characterized by many attributes:

$$x_i=\left\{at{r}_j\right\},$$

(4)

$$e_k=\left\{at{r}_h\right\},$$

(5)

where $x_i$ is a vertex of the metagraph, $x_i\in X$; $e_i$ is an edge of the metagraph, $e_i\in E$; $at{r}_j$ and $at{r}_h$ are attributes of vertices and edges, respectively.

Thus, the elements of the computer network applications and the connections between the elements are represented by the following symmetric sets:

• $X_1=\left\{x_1^k\right\}$, $k=\overline{1,q}$ is a set of applications;
• $X_2=\left\{x_2^l\right\}$, $l=\overline{1,r}$ is a set of operating systems;
• $X_3=\left\{x_3^m\right\}$, $m=\overline{1,s}$ is a set of networks;
• $E_1=\left\{e_1^n\right\}$, $n=\overline{1,t}$ is a set of links between applications, defined over a set $X_1$;
• $E_2=\left\{e_2^o\right\}$, $o=\overline{1,u}$ is a set of links between operating systems, defined over a set $X_2$;
• $E_3=\left\{e_3^p\right\}$, $p=\overline{1,v}$ is a set of links between networks, defined over a set $X_3$.

The entire computer network can be represented as the following attributive metagraph, or the ordered sequence of six values:

$$G=\left(X_1,X_2,X_3,E_1,E_2,E_3\right).$$

(6)

Moreover, there are functions that indicate the occurrence of applications in operating systems and operating systems in networks:

$$f_1^w:g_1^w\left(x_1^k,e_1^n\right)\to x_2^l,$$

(7)

where $x_1^k$ is an element of the set of applications; $e_1^n$ is an element of the set of links between applications; $x_2^l$ is an element of the set of operating systems.

$$f_2^y:g_2^y\left(x_2^l,e_2^o\right)\to x_3^m,$$

(8)

where $x_2^l$ is an element of the set of operating systems; $e_2^o$ is an element of the set of links between operating systems; $x_3^m$ is an element of the set of networks.

The vertex is characterized by a set of attributes:

$$x_i^b=\left\{at{r}_a\right\},$$

(9)

where $i=\overline{1,3}$ is the level of nesting of the vertex; $b$ is the vertex number at a corresponding level $i$; $at{r}_a$ are the attributes of the vertex (number, line, etc.).

The edge is characterized by a set of attributes:

$$e_i^h=\{x_i^s,x_i^e,\left\{at{r}_z\right\}\},$$

(10)

where $x_i^s$, $x_i^e$ are vertices connected by the edge; $i=\overline{1,3}$ is the level of nesting of the edge; $at{r}_z$ are the attributes of the edge (number, line, etc.).

Table 1. Attributes.

Elements	Attributes
Element of set $X_1$ (applications)	Application name Application version Number of the port used by the application
Element of set $X_2$ (operating systems)	OS name OS version IP-address used by the OS
Element of set $X_3$ (networks)	Network name Protocols in the network (OSI model network layer) Routing table IP-address and network mask
Element of set $E_1$ (links between applications)	OSI model application layer (session, presentation)
Element of set $E_2$ (links between operating systems)	Protocols of the OSI model transport layer
Element of set $E_3$ (links between networks)	Protocols of the OSI model network layer

shows the potential attributes of the elements of the sets in question.

In addition, a rule is introduced that a link between two elements at the i-th level exists if and only if a link exists between all elements located at higher levels to which objects of the i-th level belong. This means that applications installed on different operating systems are interlinked only if the corresponding operating systems are also interlinked. Similarly, operating systems in different networks can be interlinked only if such networks are interlinked as well.

With using the developed model, it is possible at the design stage of the system structure to take the characteristics of the elements and the relationships between them into account for requirements for the functions of information security tools.

The following is an example of using the model to describe a computer network. A small computer network consists of three computers, one of which has a mail server, and two mail clients. Since we consider only software, computers are represented by operating systems. To provide an example, not all communications between operating systems and software are provided. A graphical representation of the metagraph describing this network is presented in Figure 1.

In terms of the proposed model, a computer network will be described as follows:

$$G=\left(X_1,X_2,X_3,E_1,E_2\right).$$

(11)

Set $X_1$ represents a list of software, set $X_2$ represents a list of operating systems and set $X_3$ a list of computer networks. Sets $E_1$ and $E_2$ contain lists of relationships between software and operating systems. Next, is an example:

$$X_1=\left\{Outloo{k}_1^1,Exchang{e}_1^2,Thunderbir{d}_1^3\right\},$$

(12)

$$E_2=\left\{TC{P}_2^1,TC{P}_2^2\right\}.$$

(13)

The functions indicating the nesting of software in operating systems will be as follows:

$$f_1^1:g_1^1\left(Outloo{k}_1^1\right)\to Windows{8}_2^1.$$

(14)

Other nesting functions looks similar.

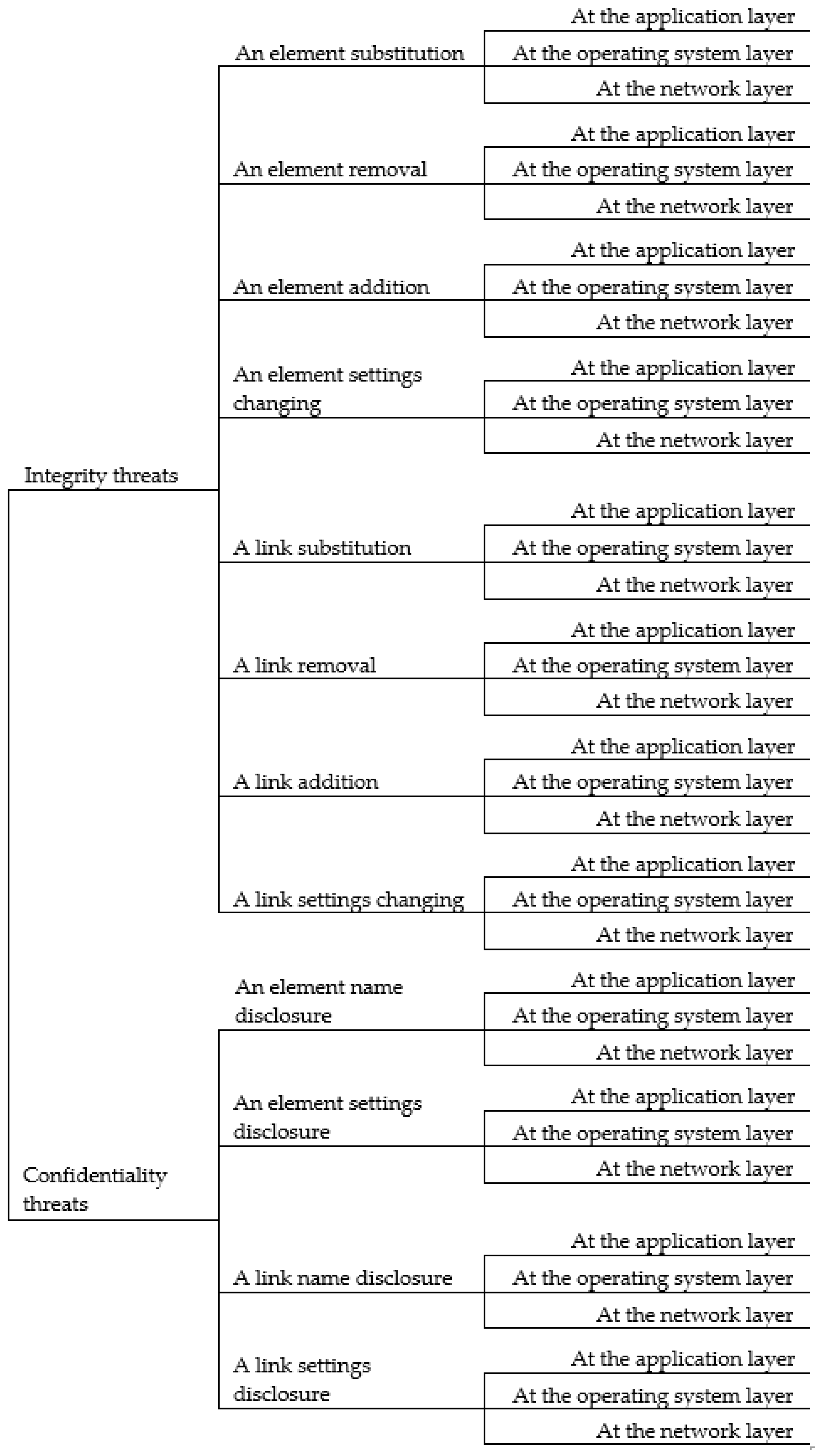
3.2. Model of Threats

The proposed approach to the classification of threats and the developed threats model are based on elementary operations on metagraphs [37]. As shown earlier, a computer network is considered as a structure of interacting elements (vertices of the graph) and the links between them (edges of the graph). Threats are understood as an unauthorized change in the structure of a computer network (graph).

At this stage, it is necessary to indicate that the study considers only threats to the security of the system, not the information. At the same time, the classification of threats by violated properties is taken as the basis: confidentiality, integrity, and availability. The threats to the availability of the system are not considered, since when combining the lists of threats to the security of information and of the system, these threats will coincide. Thus, threats to the integrity and confidentiality of computer network software are considered.

The basic operations on attributive metagraphs include adding a vertex or an edge, removing a vertex or an edge and changing a vertex or edge attribute [38].

Based on this, the following classes of threats to the integrity of a computer network are proposed:

• Threats of an element substitution—$C_{s1X}$
• Threats of a link substitution—$C_{s1E}$
• Threats of an element removal—$C_{s2X}$
• Threats of a link removal—$C_{s2E}$
• Threats of an element addition—$C_{s3X}$
• Threats of a link addition—$C_{s3E}$
• Threats of an element settings changing—$C_{s4X}$
• Threats of a link settings changing—$C_{s4E}$

The threat of an element or link removal is characterized by the removal of a vertex or edge from the set $X_i$ or $E_j$, respectively. Thus, for a set of applications, it is characterized as follows:

$$G^{\prime }=\left(X_1\backslash x_1^k,X_2,X_3,E_1,E_2,E_3\right),$$

(15)

where $X_1$ is a set of applications; $x_1^k$ is a remote application and $x_1^k\in X_1$.

The threat of an element or link addition is characterized by the adding of a vertex or edge from the set $X_i$ or $E_j$, respectively. Thus, for a set of applications, it is characterized as follows:

$$G^{\prime }=\left(X_1{\displaystyle \cup }{x}_1^{q+1},X_2,X_3,E_1,E_2,E_3\right),$$

(16)

where $x_1^{q+1}$ is an added application.

The threat of an element or link substitution is characterized by removing a vertex or an edge from the set $X_i$ or $E_j$, respectively, and adding a vertex or an edge instead of the deleted one, i.e., for a set of applications, this is described by the sequence of Equations (15) and (16):

$$G^{\prime }=\left(X_1\backslash x_1^k,X_2,X_3,E_1,E_2,E_3\right),$$

(17)

$$G^{″}=\left(X_1{\displaystyle \cup }{x}_1^{k\prime },X_2,X_3,E_1,E_2,E_3\right).$$

(18)

The threat of an element or link settings changing is carried out by changing an attribute of a vertex or an edge:

$$at{r}_a:=at{r}_a^{\prime }.$$

(19)

The following threat classes are proposed as a classification of computer network confidentiality threats:

• Threats of an element name disclosure—$K_{s1X}$
• Threats of a link name disclosure—$K_{s1E}$
• Threats of an element settings disclosure—$K_{s2X}$
• Threats of a link settings disclosure—$K_{s2E}$

In graph theory, the confidentiality threats of a computer network are described as the intersection of sets of protected elements, information about which should be hidden, with sets of well-known elements. Hence, the threat of disclosure (leakage) of information about the name of the application is characterized by the intersection of the set $X_1$ with the set $J_1$:

$$G^{\prime }=\left(X_1{\displaystyle \cap }{J}_1,X_2,X_3,E_1,E_2,E_3\right),$$

(20)

where $X_1{\displaystyle \cap }{J}_1=\left\{x_1^k|x_1^k\in X_1\wedge x_1^k\in J_1\right\}$; $x_1^k$ is an element belonging to the set $X_1$; $X_1$ is set of applications that needs to be protected; $J_1$ is set of applications whose elements are well-known.

The result of the study is a computer network threat model that integrates classes of threats $K_S$ and $C_S$:

$$T_S=K_S{\displaystyle \cup }{C}_S,$$

(21)

where $K_S$ is threats to the confidentiality of computer network elements; $C_S$ is threats to the integrity of computer network elements.

At the same time, each of the 12 presented threat classes contains three types of threats: threats at the application layer, threats at the operating system layer, and threats at the network layer. In total, 36 types of threats to the information security of computer network software are obtained. The final threat classification is presented in Figure 2.

On the basis of the use of basic operations on attribute metagraphs to determine the threat classes, it becomes possible to make an assumption about the completeness of the proposed classification of security threats to computer network software.

4. Discussion

The following is a comparison of the types of threats identified in this paper with those in [36], which uses a similar approach to the classification of system elements. In [36], four levels of system elements are distinguished: the physical layer, network layer, operating system (OS) layer, and application layer. The physical layer in connection with the limitations established in this paper is not considered in the comparison. The following threats are listed as threats to the software:

• Network layer: the availability of equipment is isolated, network traffic is intercepted, network traffic is modified.
• OS layer: malicious software is installed, the stability of system processes and services is violated, information resources are impacted.
• Application layer: applications are disabled, information resources of applications are impacted, the operations of applications are modified.

Some of these threats are explicitly threats to information, and therefore are not considered in the comparison. The result of the comparison is shown in

Table 2. Comparison of threats from [36] with the types of threats of the author’s threat model.

Threat Classes	Computer Network Software Layers
	Application	OS	Network
$K_{s1X}$
$K_{s1E}$
$K_{s2X}$
$K_{s2E}$
$C_{s1X}$	+	+
$C_{s1E}$
$C_{s2X}$	+		+
$C_{s2E}$			+
$C_{s3X}$	+
$C_{s3E}$
$C_{s4X}$
$C_{s4E}$

. The intersections of the lines with the threat classes of the author’s model with the columns in which the software levels of the computer network are indicated the identified types of threats. The marked cell means that in [36] security threats to the system related to this type were found. The unmarked cell means that no threats that could be attributed to this type were detected.

The information presented in the table shows that the proposed model describes a significantly larger number of types of threats than the considered counterpart. However, the approach in [36] allows the specialist to add other threats to the review, which makes the comparison incorrect. For a detailed comparison, we selected a list of threats from the Security Threat Databank of FSTEC of Russia [30].

In the course of the comparison, all 213 information security threats from [30] were classified by exposed object. Since the data bank defines threats as violating the confidentiality, integrity, and availability of information, it is difficult to identify threats to the information system among them. Threats were attributed to threats to the system in the case of a clear indication in the description of the threat that it violates any of the properties of the system. Threats in the description of which meant a violation of the properties of information due to gaining access to the system were considered as threats of information. As a result, 68 threats to the security of the information system were identified. All these threats were correlated with the threat types identified during the development of the threat model.

The generalized comparison result is presented in

Table 3. Comparison of threats from [30] with the types of threats of the author’s threat model.

Threat Classes	Computer Network Software Layers
	Application	OS	Network
$K_{s1X}$		+
$K_{s1E}$		+	+
$K_{s2X}$	+	+	+
$K_{s2E}$		+	+
$C_{s1X}$	+	+	+
$C_{s1E}$	+
$C_{s2X}$	+	+	+
$C_{s2E}$		+
$C_{s3X}$	+	+
$C_{s3E}$	+	+
$C_{s4X}$	+	+	+
$C_{s4E}$	+	+

. The marked cell in [30] means that security threats to the system related to this type were found. The unmarked cell means that no threats that could be attributed to this type were detected.

On the basis of the comparison results, it was found that the proposed approach to building a threat model allows information protection specialists to consider, when building an information protection system, 11 more types of information security threats than when using [30]. In total, according to the author’s classification, 36 types of threats to the confidentiality and integrity of the system were identified, 25 of them were presented in [30].

One of the earliest versions of the approach proposed in this work was used to compile a list of threats to an automated system for commercial accounting of energy resources [39]. As a result, a list of 70 threats to the integrity of the system was compiled. Threats were considered at the software and hardware levels for the three main types of system elements and connections between them. The list obtained using the author’s methodology and models turned out to be 18 percent more than that previously compiled by customer experts (59 threats to the integrity of the system).

It should be noted that formalization also has some disadvantages. Firstly, the complexity of formalized models can narrow the circle of people who can apply this model. Secondly, compiling threat lists using the developed formalized models may require a specialist to take a lot of time, especially for large computer networks that include dozens and hundreds of elements. However, both mentioned disadvantages will not matter if the proposed models are implemented in a software tool. The formalization of models allows to algorithmize the process of compiling lists of threats. Currently, the concept of a software tool is being developed. It is assumed that the specialist’s task will be to compile a computer network model by specifying lists of elements and the relationships between them. Furthermore, a list of threats will be compiled automatically.

5. Conclusions

The analysis of the current state of the subject area—computer network models used to identify threats, as well as approaches to building computer network threat models—is carried out:

On the basis of the mathematical apparatus of attributive metagraphs, a computer network model was developed that allows to describe computer network software components (application, system, and network software) and all possible connections between them (network protocols, drivers, etc.).

Based on elementary operations on metagraphs, a model of threats to the security of computer network software was developed, which allows compiling complete lists of threats to the integrity and confidentiality of computer network software.

The relevance of threats is not considered in the framework of this work, however, it should be noted that the addition of one threat, for which it is necessary to introduce protection mechanisms, is already sufficient reason to consider an expanded list of threats.