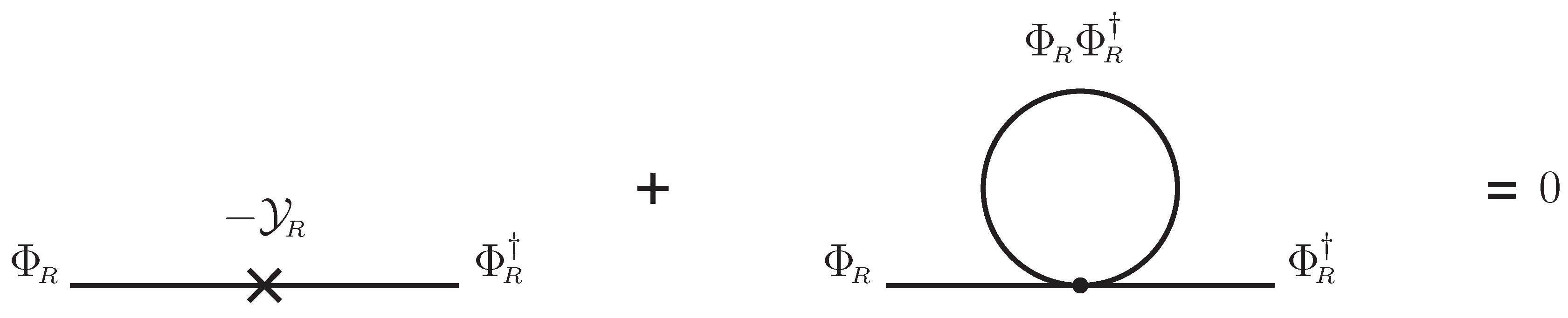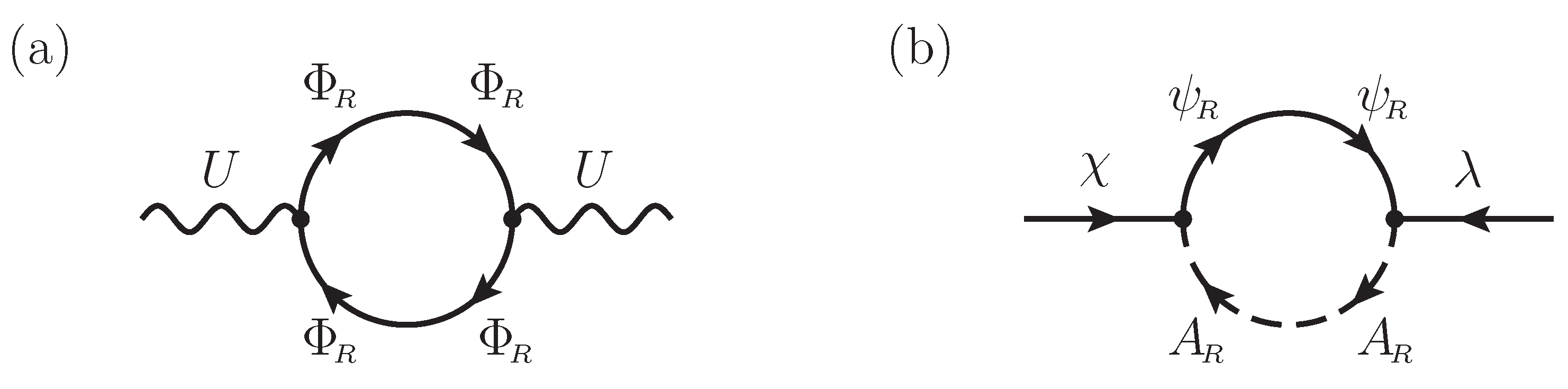Supersymmetric NJL-Type Model for a Real Superfield Composite

Abstract

The Nambu–Jona-Lasinio (NJL) model is a classic theory for the strong dynamics of composite fields and symmetry breaking. Supersymmetric versions of the NJL-type models are certainly of interest too. Particularly, the case with a composite (Higgs) chiral superfield formed by two (quark) chiral superfields has received much attention. Here, we propose a prototype model with a four-chiral-superfield interaction, giving a real superfield composite. It has a spin-one composite vector field with properties being somewhat similar to a massive gauge boson of spontaneously broken gauge symmetry. As such, it is like the first supersymmetric analog to non-supersymmetric models with spin-one composites. The key formulation developed here is the picture of quantum effective action as a superfield functional with parameters like constant superfields, having explicit supersymmetric and Grassmann number dependent supersymmetry breaking parts. Following the standard non-perturbative analysis for NJL-type models, the gap equation analysis shows plausible signature of dynamical supersymmetry breaking which is worth more serious analysis. With an extra superfield model Lagrangian included, comparison between the models and their non-supersymmetric counterparts is discussed, illustrating the notion of supersymmetrization is nontrivial in the setting.

1. Introduction

The Nambu–Jona-Lasinio (NJL) model [1,2] is a classic model with a strong four-fermion interaction, which gives rise to a dynamical composite (scalar) bosonic field as the analog of the Cooper pair. The composite scalar usually bears a nonzero vacuum expectation value (VEV) which causes dynamical symmetry breaking and the generation of (Dirac) fermion mass. There have been many attempts to construct viable models of which the Higgs doublet can be identified as such a two-fermion composite [3,4,5,6,7,8]. See [9] for a theoretical and phenomenological review of the approach focusing on physics related to the idea of “top quark condensate”.

Composite spin-one boson may also be resulted in a model of the kind. Such spin-one field (multiplet) as bifermion composite typically behaves much like the massive gauge bosons from models of spontaneously broken gauge symmetry [10]. In a more recent study [11], a similar model with the spin-one boson as composite of scalar bosonic rather than fermionic fields is also discussed.

On the other hand, the first investigation into supersymmetric model of composite fields via NJL mechanism was conducted in the early eighties [12,13]. The four-fermion interaction was replaced by a six-dimension four-chiral-superfield interaction in the Kähler potential. A new chiral superfield as a composite of two chiral superfields can be obtained. The model is as much an exact analog of the non-supersymmetric one as possible. However, the notion of supersymmetrization in the setting actually leaves room for alternative construction [14]. Applications of the model with dimension-six interaction to spontaneous electroweak symmetry breaking have also caught much phenomenological attention [15,16]. The model is now highly disfavored phenomenologically, if not completely ruled out while the (holomorphic) alternative with a dimension-five interaction may survive better [17]. Other applications or extended analyses of the NJL mechanism in spontaneous symmetry breaking models, within the chiral superfield composite from dimension-six interaction setting, see [18,19,20].

In a re-examination of the supersymmetric Nambu–Jona-Lasinio (SNJL) model, in general, our group found many interesting features in variants of the model in the alternative supersymmetrization. The new holomorphic model has a dimension-five four-chiral-superfield interaction in the superpotential [14,17,21]. The interaction gives rise to a chiral superfield as a composite of two chiral superfields, with the scalar being a bi-scalar composite. A model with two such composite chiral superfields bearing symmetry breaking VEVs can give a supersymmetric Standard Model with both Higgs doublets being (different) squark composites [17,21]. Nevertheless, input soft supersymmetry breaking masses are needed. On the theoretical side, the basic framework works as well for a model starting with a single chiral superfield, instead of a Dirac pair, with generation of Majorana mass. The case of a Dirac pair admits both masses of Majorana and Dirac type depending on input soft masses [22].

NJL-type models in the superfield setting still provide more interesting possibilities. In the literature the studies of supersymmetric NJL-type models focus on the formation of composite chiral superfields. However, a real superfield can also be dynamically generated as a composite of two chiral superfields. We report a new prototype model with a real superfield composite from a dimension-six four-chiral-superfield interaction. The real superfield contains a spin-one component, which is really a combination of bi-scalar and bifermion parts. No input soft supersymmetry breaking masses are assumed and the model Lagrangian is fully supersymmetric. It may be seen, in a way, as a supersymmetric version of the ones analyzed in [11]. The latter considered the case of a composite spin-one vector field formed by fermionic and bosonic fields separately. Our model here is the simplest supersymmetric model of the kind, with a composite spin-one field. It is interesting to compare the models in [11] with ours. Though there are interesting differences, it may be the closest analog one can have.

The composite real superfield of our model contains scalar and auxiliary scalar components which may bear nonzero VEVs. The part for the scalar would give supersymmetric wave function renormalization, whereas that of the auxiliary scalar component(s) may actually give soft supersymmetry breaking masses. We present the standard superfield gap equation analysis and non-perturbative effective theory description. To the extent that the $1/N_c$ type approximation does give the correct qualitative feature there, the nontrivial solutions to the gap equation for the soft masses indicates dynamical supersymmetry breaking. Whether the latter can be obtained with the very simple model structure is a question warrants further analysis.

In Ref. [21], we introduced the powerful analysis of formulating the quantum effective action as a superfield functional with parameters like constant superfields, having explicit supersymmetric and Grassmann number dependent supersymmetry breaking parts. A superfield diagram, like the proper self-energy diagram in the gap equation, therefore also including the supersymmetry breaking parts. We further develop the formulation here with the superfield parameter for the wave function renormalization factor seen as naturally having supersymmetry breaking parts corresponding to soft masses. The kind of formulation considered was initiated by Miller’s very successful treatment of the mass parameters and propagators [23,24] in the early eighties, but did not apparently develop much otherwise. It is our opinion that complete formulations of various superfield theories along the basic theme should be of great interest. The formulation plays a key role in our earlier works [21,22] as well as here.

In Section 2, we present the model Lagrangian with a single chiral superfield, and the effective theory in terms of component fields including the composite. In Section 3, we demonstrate the basic analyses. The advocated superfield formulation is given and used to obtain the superfield gap equation. That is matched to an effective potential analysis for the Lagrangian with the composite, deriving the component field gap equations as the tadpole equations. Section 4 is devoted to analysis of the nontrivial solutions, as well as the existence of the massless fermionic mode. In Section 5, we discuss the kinetic and mass terms of the physical degrees of freedom in the model. Some of them become dynamic due to the contribution of loop diagrams. A careful comparison on important features of the model, together with another model Lagrangian, with the non-supersymmetric analog of the examples from Suzuki [11] can be found in the last section. Again we see that the notion of supersymmetrization is somewhat nontrivial. For example, direct supersymmetrization of Suzuki’s simplest fermion or scalar model is not the same one though a chiral superfield has both fermion and scalar parts. Our main model here is more like a supersymmetrization of the fermion model as compared to the alternative model Lagrangian as supersymmetrization of the scalar one.

2. The Model Lagrangian

We focus on the simplest supersymmetric NJL model to acquire a superfield composite containing a spin-one component. We consider a model of single chiral superfield multiplet, for example in the fundamental representation of $SU\left(N_c\right)$, with a four-superfield interaction. The Lagrangian is similar to that of the ordinary supersymmetric NJL model [12,13], but with an alternative color index contraction, namely,

$$\mathcal{L}=\int d^4\theta \left[\overline{\Phi }\Phi -\frac{g_o^2}{2}(\overline{\Phi }\Phi )(\overline{\Phi }\Phi )\right],$$

(1)

where $\overline{\Phi }\Phi \equiv {\overline{\Phi }}_a{\Phi }^a$ with a being the color index, therefore ${\Phi }^a$ belongs to the $N_c$-dimensional fundamental representation of $SU\left(N_c\right)$, and ${\overline{\Phi }}_a$ then the anti-fundamental representation. As a chiral superfield, each ${\Phi }^a$ is of course a scalar field on the chiral superspace of unit mass dimension, with standard spin zero and half components, given here explicitly by $\Phi (x^{\mu },\theta )=A\left(x^{\mu }\right)+\sqrt{2}\theta \psi \left(x^{\mu }\right)+\theta \theta F\left(x^{\mu }\right)$, where A is a scalar field, $\psi$ a two-spinor, and F the auxiliary component (we follow notation and convention in [25]). The coupling of the four-superfield interaction is written as $g_o^2$ for convenience. It has mass dimension $-2$, the same as the original NJL model with a four-fermion coupling, which is also included as a component of the four-superfield interaction. The latter is the only nontrivial term characterizing the model Lagrangian, in addition to the standard kinetic term as given above. The model Lagrangian contains only the kinetic term and a dimension-six interaction. It gives superfield content with the biggest symmetry possible, namely, the global symmetry of $SU\left(N_c\right)$, the $U{\left(1\right)}_{\Phi }$ and a $U{\left(1\right)}_R$. In the component considerations, the two $U\left(1\right)$ symmetries can be seen as essentially a $U{\left(1\right)}_A$ and a $U{\left(1\right)}_f$ (i.e., $\psi$-number). Adding a superpotential would reduce the symmetry, and any perturbative superpotential would be quite irrelevant to the key feature of which our analysis is after anyway. We further introduce an auxiliary real superfield U, and add

$${\mathcal{L}}_s=\int d^4\theta \frac{1}{2}{(\mu U+g_o\overline{\Phi }\Phi )}^2$$

(2)

to the Lagrangian. $\mu$ is a real and positive mass parameter (for $g_o^2>0$). The equation of motion for U, from $\mathcal{L}+{\mathcal{L}}_s$, gives

$$U=-\frac{g_o}{\mu }\overline{\Phi }\Phi ,$$

(3)

showing it as a superfield composite of $\overline{\Phi }$ and $\Phi$. Obviously, from Equations (2) and (3), the model with $\mathcal{L}+{\mathcal{L}}_s$ is equivalent to that of $\mathcal{L}$ alone, at least at the classical level. The approach is standard to the NJL-type model analysis. Rigorous derivation of the two Lagrangians as given equivalent quantum (super) field theories can be obtained from a path integral analysis as for example presented in [11]. The gist of the analysis is that the auxiliary composite, U here, with the absence of a kinetic term can be integrated out as essentially a Gaussian, reducing the new Lagrangian (more exactly as like ${\mathcal{L}}_{eff}$ below) back to the original. While an explicit illustration of that for SNJL theories seems to be unavailable, there looks like no reason for the kind of simple chiral superfield models not to fit in well with that [26]. Expanding the term in ${\mathcal{L}}_s$, the four-superfield interaction is cancelled in the full Lagrangian as

$${\mathcal{L}}_{eff}\equiv \mathcal{L}+{\mathcal{L}}_s=\int d^4\theta \left[\overline{\Phi }\Phi +\frac{{\mu }^2}{2}{U}^2+\mu g_{o}U\overline{\Phi }\Phi \right].$$

(4)

The effective Lagrangian is considered to give an alternative description of the physics with the composite U, which would become dynamical at low energy upon renormalization.

The real superfield U can be seen as two parts, as illustrated by the component expansion $U(x,\theta ,\overline{\theta })=\frac{C\left(x\right)}{\mu }+\sqrt{2}\theta \frac{\chi \left(x\right)}{\mu }+\sqrt{2}\overline{\theta }\frac{\overline{\chi }\left(x\right)}{\mu }+\theta \theta \frac{N\left(x\right)}{\mu }+\overline{\theta }\overline{\theta }\frac{N^{*}\left(x\right)}{\mu }+\sqrt{2}\theta {\sigma }^{\mu }\overline{\theta }{v}_{\mu }\left(x\right)+\sqrt{2}\theta \theta \overline{\theta }\overline{\lambda }\left(x\right)+\sqrt{2}\overline{\theta }\overline{\theta }\theta \lambda \left(x\right)+\theta \theta \overline{\theta }\overline{\theta }D\left(x\right)$, where the components C, $\chi$, and N belong to the first part, which has the content like a chiral superfield with real C. The $\mu$ factor is put to have the right mass dimensions. The rest is like the content of a superfield for the usual gauge field supermultiplet, with D and $v_{\mu }$ being real. Note that even if U contains a vector component, its couplings differ from that of the usually studied “vector superfield”, which is a gauge field supermultiplet. In addition, the supersymmetric mass term for U in Equation (4) can be compatible only with a broken gauge symmetry.

By expanding $\Phi$ into its components $A\left(x\right),\psi \left(x\right)$, and $F\left(x\right)$ [25], we can write down the composition conditions for all the components in U. Specifically, we have for the scalar and spin-one component fields,

$$\begin{array}{cc}\hfill C\left(x\right)& =-g_o{A}^{*}A\hfill \\ \hfill v_{\mu }\left(x\right)& =\frac{g_o}{\sqrt{2}\mu }\left[-i{A}^{*}{\partial }_{\mu }A+i\left({\partial }_{\mu }{A}^{*}\right)A-\overline{\psi }{\overline{\sigma }}_{\mu }\psi \right].\hfill \end{array}$$

(5)

One can see that C is a composite of two scalar fields A, while $v_{\mu }\left(x\right)$ is a combination of bi-scalar and bifermion composites. However, to verify the formation of composite real superfield U, we should look into the standard non-perturbative analysis for NJL-type models, and seek for nontrivial solutions to the corresponding gap equations.

The effective Lagrangian is given in component fields as

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{eff}& =& (1+g_{o}C)\left[A^{*}\square A+i\left({\partial }_{\mu }\overline{\psi }\right){\overline{\sigma }}^{\mu }\psi +F^{*}F\right]+\mu CD-\mu \chi \lambda -\mu \overline{\chi }\overline{\lambda }+N{N}^{*}-\frac{{\mu }^2}{2}{v}^{\nu }{v}_{\nu }\hfill \\ & & -\mu g_o\psi \lambda A^{*}-\mu g_o\overline{\psi }\overline{\lambda }A+\mu g_{o}D{A}^{*}A-i\frac{g_o}{2}\overline{\psi }{\overline{\sigma }}^{\mu }\chi {\partial }_{\mu }A+i\frac{g_o}{2}\left({\partial }_{\mu }\overline{\psi }\right){\overline{\sigma }}^{\mu }\chi A-g_o\chi \psi F^{*}+g_{o}NA{F}^{*}\hfill \\ & & +i\frac{g_o}{2}\overline{\chi }{\overline{\sigma }}^{\mu }\psi {\partial }_{\mu }{A}^{*}-i\frac{g_o}{2}{A}^{*}\overline{\chi }{\overline{\sigma }}^{\mu }{\partial }_{\mu }\psi -g_o\overline{\chi }\overline{\psi }F+g_o{N}^{*}{A}^{*}F\hfill \\ & & -\frac{\mu g_o}{\sqrt{2}}{\eta }^{\mu \nu }{v}_{\mu }i{A}^{*}{\partial }_{\nu }A+\frac{\mu g_o}{\sqrt{2}}{\eta }^{\mu \nu }{v}_{\mu }i\left({\partial }_{\nu }{A}^{*}\right)A-\frac{\mu g_o}{\sqrt{2}}{\eta }^{\mu \nu }{v}_{\mu }\overline{\psi }{\overline{\sigma }}_{\nu }\psi .\hfill \end{array}$$

(6)

Following the standard NJL analysis, we consider nonzero VEV for the composite scalar C from non-perturbative dynamics of the original model Lagrangian. Obviously, a $〈C〉\equiv c$ corresponds to a wave function renormalization factor $1+g_o〈C〉$ for $\Phi$ or its components. The contribution can be also seen as a correction to the kinetic term directly from the four-superfield interaction.

3. NJL Analysis and the Gap Equations

To implement the superfield NJL analysis on the original Lagrangian $\mathcal{L}$ in a fully consistent manner, the best way is to take the approach of considering superfield functionals, which take values like constant superfields admitting supersymmetry breaking parts, as formulated in [21]. It is an extension of what Miller did for the mass parameters in his superfield propagator analysis [23,24], to the full superfield theory. All parameters and quantities such as the amplitude of the proper self-energy diagram are to be treated as like a constant superfield with Grassmann number dependent parts. Lorentz symmetry forbids nonzero fermionic components (e.g., the $\theta$ component of a chiral parameter/quantity), while soft supersymmetry breaking parts like a ${\theta }^2$ component would be admissible.

For the model at hand, we consider a non-perturbative composite/condensate from the two superfield product of $\overline{\Phi }\Phi$ firstly from an analysis of superfield Lagrangian (1). The product corresponds to a real superfield, and the condensate as a parameter is a non-chiral quantity. Therefore, we introduce it as $\mathcal{Y}=y-{\tilde{\eta }}_o{\theta }^2-{\tilde{\eta }}_o^{*}{\overline{\theta }}^2-{\tilde{m}}_o^2{\theta }^2{\overline{\theta }}^2$. The parameter is exactly in correspondence, in the present model, with the (Dirac) mass parameter $\mathcal{M}=m-\eta {\theta }^2$ for the model with chiral superfield composites [21]. The $\mathcal{Y}\overline{\Phi }\Phi$ should then be added to and subtracted from the Lagrangian (1), as the first step of self-consistent Hartree approximation [27,28]. In this way, the Lagrangian is split as $\mathcal{L}={\mathcal{L}}_o+{\mathcal{L}}_{int}$, where

$$\begin{array}{cc}\hfill {\mathcal{L}}_o& =\int d^4\theta \overline{\Phi }\Phi (1+\mathcal{Y})\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{int}& =\int d^4\theta \left[-\mathcal{Y}\overline{\Phi }\Phi -\frac{g_o^2}{2}\overline{\Phi }\Phi \overline{\Phi }\Phi \right].\hfill \end{array}$$

(8)

Apparently, a nonzero y contributes to wave function renormalization ${\Phi }_R\equiv \sqrt{Z}\Phi =\sqrt{1+y}\Phi$, whereas the other parts of $\mathcal{Y}$ correspond to soft masses. For simplicity of the analysis, we assume ${\tilde{\eta }}_o=0$. One can choose to present the gap equation analysis in terms of the renormalized superfield ${\Phi }_R$ and couplings, with more direct physical interpretations. The quantum effective action is then given by

$$\begin{array}{ccc}\hfill \Gamma & =& \int d^4\theta \left[{\overline{\Phi }}_R{\Phi }_R(1-{\tilde{m}}^2{\theta }^2{\overline{\theta }}^2)-{\mathcal{Y}}_R{\overline{\Phi }}_R{\Phi }_R-\frac{g^2}{2}{\overline{\Phi }}_R{\Phi }_R{\overline{\Phi }}_R{\Phi }_R+{\Sigma }_{{\Phi }_R{\Phi }_R^{†}}{\overline{\Phi }}_R{\Phi }_R+\cdots \right],\hfill \end{array}$$

(9)

with now renormalized $g^2$, ${\Phi }_R$, ${\mathcal{Y}}_R\equiv \frac{\mathcal{Y}}{Z}$ and therefore also ${\tilde{m}}^2$. ${\Sigma }_{{\Phi }_R{\Phi }_R^{†}}$ is the two-point proper vertex from quantum correction. The superfield gap equation is thus given by

$$\begin{array}{c}\hfill -{\mathcal{Y}}_R+{\left.{\Sigma }_{{\Phi }_R{\Phi }_R^{†}}^{\left(loop\right)}(p;{\theta }^2{\overline{\theta }}^2)\right|}_{on\text{-}shell}=0,\end{array}$$

(10)

which can be expressed diagrammatically as Figure 1. In accordance with the standard NJL analysis, the one-loop contribution from the four-superfield interaction to ${\Sigma }_{{\Phi }_R{\Phi }_R^{†}}(p;{\theta }^2{\overline{\theta }}^2)$, in the presence of ${\mathcal{Y}}_R$ in the superfield propagator, is used. More clearly, it is essentially an approximation of $1/N_c$ type, with $N_c$ being the number of color to which $\Phi$ is a multiplet in the fundamental representation.

Performing a supergraph calculation directly, we get

$$\begin{array}{c}{\left.{\Sigma }_{{\Phi }_R{\Phi }_R^{†}}^{\left(loop\right)}(p;{\theta }^2{\overline{\theta }}^2)\right|}_{on\text{-}shell}=-g^2{N}_c{\int }^E\frac{d^{4}k}{{\left(2\pi \right)}^4}\left[\frac{1}{k^2}-\frac{{\tilde{m}}^2}{k^2(k^2+{\tilde{m}}^2)}\left(1-k^2{\theta }^2{\overline{\theta }}^2+4k_a{\sigma }_{\alpha \dot{\alpha }}^a{\theta }^{\alpha }{\overline{\theta }}^{\dot{\alpha }}\right)\right].\hfill \end{array}$$

(11)

Note that the $4k_a{\sigma }_{\alpha \dot{\alpha }}^a{\theta }^{\alpha }{\overline{\theta }}^{\dot{\alpha }}$ term vanishes upon integration. Through a careful inspection of the supergraph diagram, one can see that nontrivial ${\theta }^2$ and ${\overline{\theta }}^2$ parts would be resulted if the assumption of vanishing ${\tilde{\eta }}_o$ in $\mathcal{Y}$ is not taken, giving a nonzero value for the corresponding part of the superfield propagator. We will take that up in an upcoming analysis.

Alternatively, we perform an analysis on effective Lagrangian (4) in component fields, i.e., assuming the composite formation. Corresponding to the wave function renormalization from $〈C〉\equiv c$, we replace the fields $A,\psi ,F$ and coupling $g_o$ by renormalized ones as

$$\begin{array}{cc}\hfill & A\to \frac{A_R}{\sqrt{1+g_{o}c}},\psi \to \frac{{\psi }_R}{\sqrt{1+g_{o}c}},F\to \frac{F_R}{\sqrt{1+g_{o}c}},\frac{g_o}{1+g_{o}c}\to g,\hfill \end{array}$$

(12)

in the Lagrangian (6). In addition, the composite component fields N and D may also develop nonzero VEVs. They are responsible for the generation of soft supersymmetry breaking masses for $\overline{\Phi }\Phi$. For simplicity, we analyze here the simple scenario considering only the development of $〈D〉$, and unavoidable $〈C〉$, in correspondence with the superfield analysis.

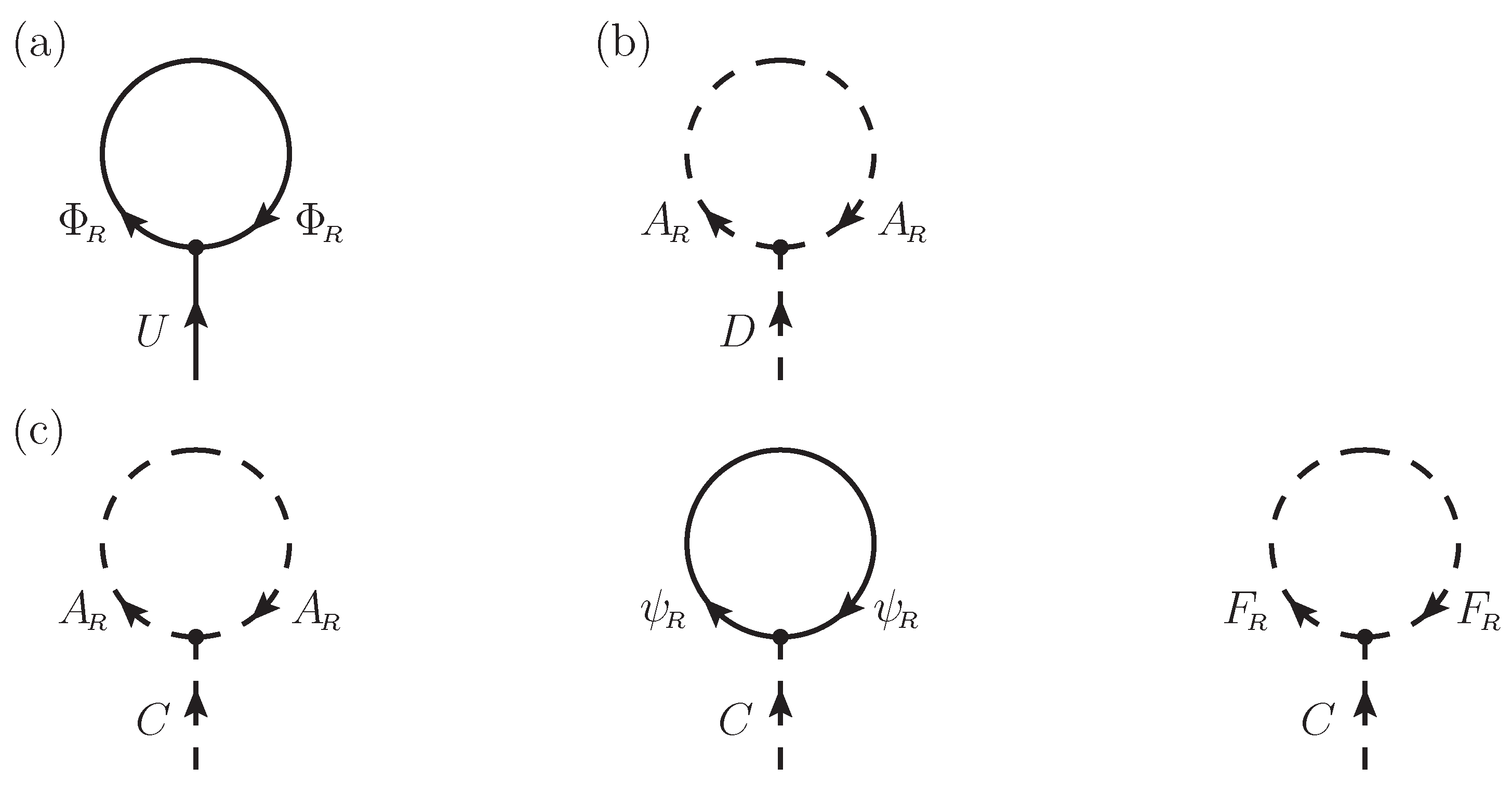
Here, we perform an effective potential analysis based on the Weinberg tadpole method [29] with the effective Lagrangian in component form. Vanishing tadpole conditions can be obtained for the scalar potential $V(C,N,D)$ up to one-loop level. The related tadpole diagrams are shown in Figure 2. If C and D fields can develop nonzero VEVs, the two tadpole equations corresponding to D-tadpole and C-tadpole are, respectively,

$$\begin{array}{cc}\hfill c& =-g{N}_c{\int }^E\frac{d^{4}k}{{\left(2\pi \right)}^4}\frac{1}{k^2+{\tilde{m}}^2}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\tilde{m}}^2& =g^2{N}_c{\int }^E\frac{d^{4}k}{{\left(2\pi \right)}^4}\frac{{\tilde{m}}^2}{k^2+{\tilde{m}}^2},\hfill \end{array}$$

(14)

where we have defined ${\tilde{m}}^2=-\mu g〈D〉$. The Euclidean momentum loop integral is to be evaluated with a cutoff $\Lambda$.

It is interesting to see that the tadpole equations are directly equivalent to the superfield gap equation mentioned above. The supersymmetric part and ${\theta }^2{\overline{\theta }}^2$ part of the superfield gap equation correspond to tadpole Equations (13) and (14), respectively, with $\frac{y}{1+y}=gc$. The ${\theta }^2$ and ${\overline{\theta }}^2$ parts are matched to $〈N〉$ in $〈U〉$, and are zero in our setting. In terms of the superfield, the potential minimum condition is given by

$$\begin{array}{c}{\mu }^2〈U〉+U_{tadpole}=0⟹\mu g〈U〉=-g^2{I}_{{\Phi }_R{\Phi }_R^{†}}^{\left(loop\right)}\hfill \end{array}$$

(15)

where $I_{{\Phi }_R{\Phi }_R^{†}}^{\left(loop\right)}$ is the momentum integral of the ${\Phi }_R{\Phi }_R^{†}$ propagator loop (cf. the first diagram in Figure 2). Note that from the original Lagrangian with two-superfield composite assumed, we can obtain $-g^2〈\left({\Phi }_R{\Phi }_R^{†}\right)〉={\mathcal{Y}}_R$, which is equivalent to $\mu g〈U〉={\mathcal{Y}}_R={\left.{\Sigma }_{{\Phi }_R{\Phi }_R^{†}}^{\left(loop\right)}(p;{\theta }^2{\overline{\theta }}^2)\right|}_{on\text{-}shell}=-g^2{I}_{{\Phi }_R{\Phi }_R^{†}}^{\left(loop\right)}$. The same loop integral is of course involved in both the gap equation picture and the effective potential analysis. The results here are in direct matching with the corresponding discussion for the NJL case presented in [13], though for a superfield theory instead. The component field effective potential analysis, and therefore serves as a double-check of the superfield gap equation analysis.

4. Solutions to the Gap Equation

Let us check for nontrivial solutions to the gap equation as given in component form. Equation (13) directly expresses the result for the wave function renormalization of the superfield $\Phi$. The simple result hides its nontrivial nature as c is really $\frac{y}{g(1+y)}$ with y being the NJL contribution to the $\Phi$ kinetic term, for which we are looking for the nontrivial solution. It is the use of renormalized parameters that turns the part of gap equation into the simple form, which actually says the trivial $y=0$ cannot be admissible. Recall that c is the VEV of the scalar component of composite U as $C=-g{A}_R^{*}{A}_R$, therefore effectively a two-field condensate. Evaluating the integral in Equation (13), we have

$$\begin{array}{c}\hfill c=-g{N}_c{I}_F\left({\tilde{m}}^2\right)=-\frac{g{N}_c}{16{\pi }^2}\left({\Lambda }^2-{\tilde{m}}^{2}ln\frac{{\Lambda }^2+{\tilde{m}}^2}{{\tilde{m}}^2}\right),\end{array}$$

(16)

where $I_F\left({\tilde{m}}^2\right)={\int }^E\frac{d^{4}k}{{\left(2\pi \right)}^4}\frac{1}{k^2+{\tilde{m}}^2}$. One can see that depending on the coupling g and cutoff $\Lambda$, a nonzero c always exists, revealing its unavoidable nature as a correction to the kinetic term by the four-superfield interaction. In particular, we would have $c=-\frac{g{N}_c{\Lambda }^2}{16{\pi }^2}$ for vanishing ${\tilde{m}}^2$ (i.e., $〈D〉=0$).

The ${\theta }^2{\overline{\theta }}^2$ component of the gap equation as in Equation (14) is responsible for the generation of soft supersymmetry breaking mass ${\tilde{m}}^2$. In terms of the effective theory, it involves the VEV of the D-term of U. Interestingly, it is the same as the gap equation in the basic NJL model with the soft mass ${\tilde{m}}^2$ replacing the Dirac fermionic mass, if we take $\frac{g^2}{2}$ as the four-fermion coupling [13].

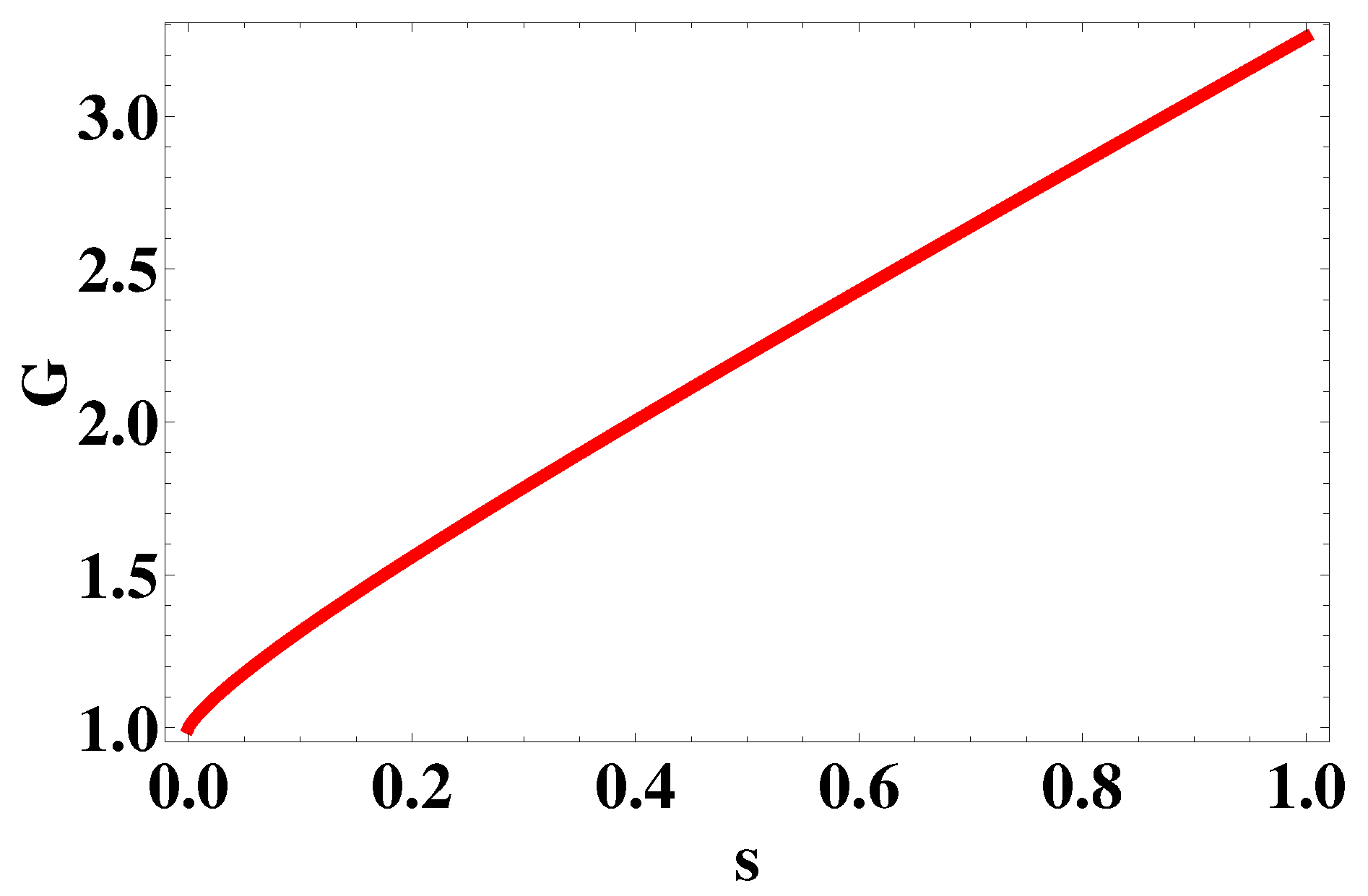
In the spirit of the NJL approach, nontrivial solution for ${\tilde{m}}^2$ would give dynamical generation of soft supersymmetry breaking mass. One can rewrite the equation with the explicit integral expression, in dimensionless variables, as

$$\frac{1}{G}=1-sln\left[1+\frac{1}{s}\right],$$

(17)

where $G=\frac{g^2{N}_c{\Lambda }^2}{16{\pi }^2}$, and $s=\frac{{\tilde{m}}^2}{{\Lambda }^2}$. Numerically, we found that nontrivial solutions for the soft mass ($0<s<1$) can be resulted for a large enough coupling $G>1$, as illustrated in Figure 3. All that look exactly in line with basic NJL model features, except that the symmetry involved here is the somewhat more tricky supersymmetry.

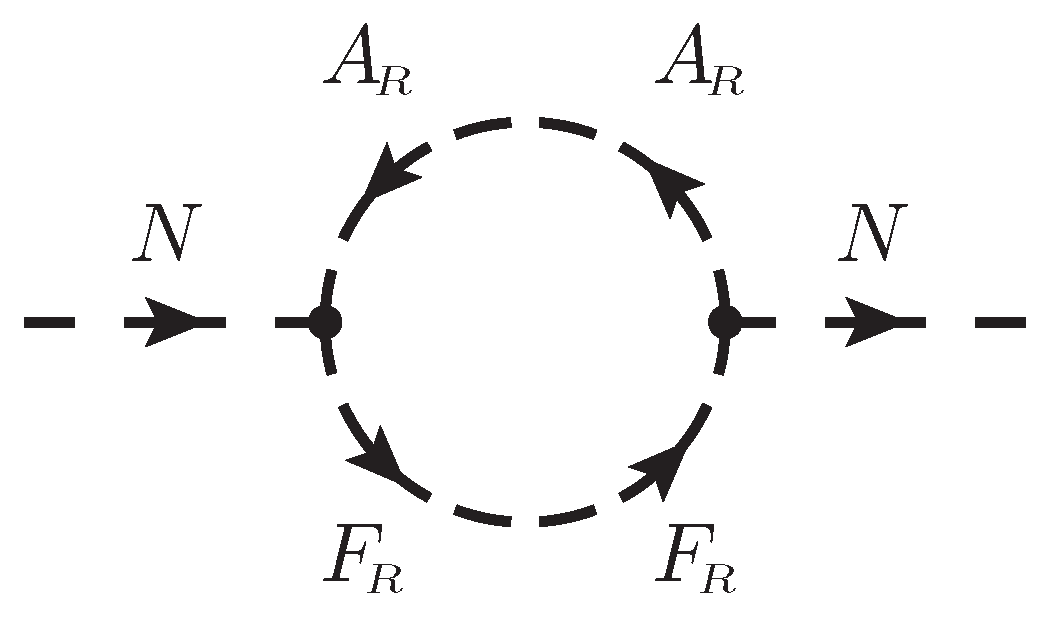
Corresponding to the dynamical generation of soft mass, supersymmetry would be broken. One consistency check is the existence of the massless Goldstino state. Analytically, the required analysis is the “quark-loop” corrected two-point function for the composite superfield U, as shown in Figure 4. The loop contribution is also expected to generate a kinetic term to turn U into a dynamic one. Here, we need only the part for the fermionic components. There are two fermionic components in U—the $\chi$ and $\lambda$, with the tree-level Dirac mass term $\mu \chi \lambda$. Note that the Lagrangian contains a $U{\left(1\right)}_R$ symmetry, with N, $\chi$ and $\lambda$ having $U{\left(1\right)}_R$ charges −2, −1, and +1, respectively, whereas $\Phi =A+\sqrt{2}\theta \psi +{\theta }^{2}F$ carries charge 1. With $〈N〉=0$, the $U{\left(1\right)}_R$ symmetry is maintained, which protects against any generation of $\chi \chi$ or $\lambda \lambda$ (Majorana) mass term. In the loop correction to two-point function for U, we have one component diagram contributing to the fermion mass matrix as in Figure 4. It gives a $\chi \lambda$ mass as

$$-{\Sigma }_{\chi \lambda }=-\mu g^2{N}_c{I}_F\left({\tilde{m}}^2\right).$$

(18)

Comparing to Equation (14), which has to be satisfied with nontrivial ${\tilde{m}}^2$ for the case at hand, one can see that the loop generated mass is exactly $-\mu$, which cancels the tree-level mass term. All the elements of the fermion mass matrix are then zero. There is no other piece of contribution to $\chi$ or $\lambda$ masses. There can be the Goldstino state among them, the one to be eaten up by the gravitino, which would then be massive. There are well-known no-go theorems against spontaneous supersymmetry breaking in the literature which may lead to serious doubts about what seems otherwise to be the plausible supersymmetry breaking features of our model (from the $1/N_c$ approximation). We will discuss the tricky issues related in the final section. A bottom line is the no-go theorems cannot be shown to apply to our case.

5. Kinetic and Mass Terms for the Composite Fields

Along with the generation of the real superfield composite, it is important to see if all of its components have sensible kinetic terms. For $\chi$ and $\lambda$, we have chirality-conserving self-energy diagrams as illustrated in Figure 5, which give rise to kinetic terms as $ip·\overline{\sigma }\Xi$ with

$$\begin{array}{cc}\hfill {\Xi }_{\chi \chi }& =-g^2{N}_c{I}_F\left({\tilde{m}}^2\right)+2g^2{N}_c{\tilde{m}}^2{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)=-1+2g^2{N}_c{\tilde{m}}^2{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)\hfill \\ \hfill {\Xi }_{\lambda \lambda }& =-2{\mu }^2{g}^2{N}_c{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2),\hfill \end{array}$$

(19)

where $I_{nF}$ denote integrals of n Feynman propagators with the mass-squared parameters as given, and we have applied the gap equation to simplify the ${\Xi }_{\chi \chi }$ result.

For the spin one component, we have a tree level mass term $-\frac{{\mu }^2}{2}{v}^{\nu }{v}_{\nu }$ in the Lagrangian, and loop diagrams as in Figure 6. They sum to give the kinetic term

$$\begin{array}{cc}\hfill {\Sigma }_{v\left(p\right)}& =-\frac{{\mu }^2{g}^2{N}_c}{6}{p}^2\left[I_{2F}(0,0)+\frac{1}{4}{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)\right]\hfill \end{array}$$

(20)

and a mass term

$$\begin{array}{cc}\hfill -{\Sigma }_{v\left(m\right)}& =\frac{{\mu }^2}{2}-\frac{{\mu }^2{g}^2{N}_c}{4}\left[-{\tilde{m}}^2{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)+I_F\left({\tilde{m}}^2\right)\right]\hfill \\ \hfill & =\frac{{\mu }^2}{4}\left[1+g^2{N}_c{\tilde{m}}^2{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)\right],\hfill \end{array}$$

(21)

all of the proper sign. Absorbing the non-canonical magnitude of the kinetic term into a field renormalization would give the rescaled mass term of the renormalized spin-one field.

For the spin zero bosonic components we have a tree level quadratic term $N{N}^{*}$ in the Lagrangian, as well as one diagram contributing to the two-point function of $N{N}^{*}$ as in Figure 7, which gives the amplitude as

$${\Sigma }_N=-g^2{N}_c{I}_F\left({\tilde{m}}^2\right).$$

(22)

After applying the gap equation, ${\Sigma }_N$ gives −1, which cancels the tree level $N{N}^{*}$ term. Obviously, there is no kinetic term for $N{N}^{*}$ from the loop contribution, indicating that N is purely an auxiliary field.

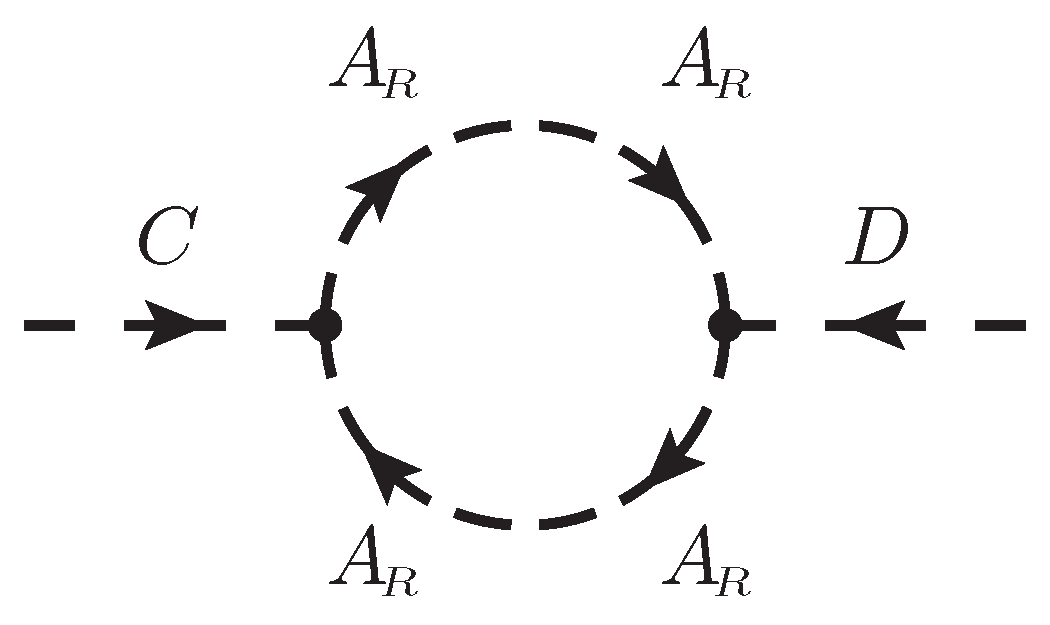
We have also a tree level $\mu CD$ term in the Lagrangian, as well as one diagram contributing to $CD$ two-point function as in Figure 8. They give the kinetic and mass terms in the Lagrangian for $CD$ as

$$\begin{array}{cc}\hfill {\Sigma }_{CD}& =\mu -\mu g^2{N}_c\left[I_F\left({\tilde{m}}^2\right)-{\tilde{m}}^2{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)\right]+p^2\mu g^2{N}_c{\tilde{m}}^2{I}_{34}({\tilde{m}}^2,{\tilde{m}}^2)\hfill \\ \hfill & =\mu g^2{N}_c{\tilde{m}}^2{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)+p^2\mu g^2{N}_c{\tilde{m}}^2{I}_{34}({\tilde{m}}^2,{\tilde{m}}^2).\hfill \end{array}$$

(23)

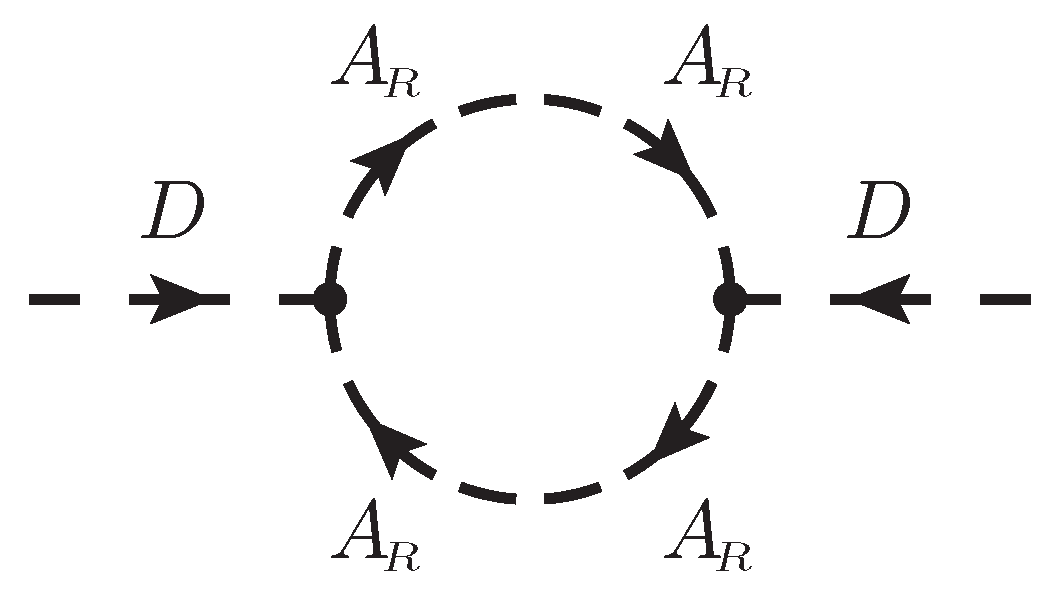
Here, we have introduced $I_{34}(m_a^2,m_b^2)\equiv 3I_{3F}(m_a^2,m_b^2,m_b^2)-4m_b^2{I}_{4F}(m_a^2,m_b^2,m_b^2,m_b^2)$ for convenience. Furthermore, there are loop diagrams as in Figure 9 giving

$$\begin{array}{cc}\hfill {\Sigma }_{CC}& =\frac{1}{2}{g}^2{N}_c\left[-2{\tilde{m}}^2{I}_F\left({\tilde{m}}^2\right)+{\tilde{m}}^4{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)\right]\hfill \\ \hfill & =\frac{1}{2}\left[-2{\tilde{m}}^2+g^2{N}_c{\tilde{m}}^4{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)\right]+p^2\frac{1}{2}{g}^2{N}_c{\tilde{m}}^4{I}_{34}({\tilde{m}}^2,{\tilde{m}}^2),\hfill \end{array}$$

(24)

and there is also a loop diagram as in Figure 10, which gives

$$\begin{array}{c}\hfill {\Sigma }_{DD}=\frac{{\mu }^2{g}^2{N}_c}{2}{I}_{2F}({\tilde{m}}^2,{\tilde{m}}^2)+p^2\frac{{\mu }^2{g}^2{N}_c}{2}{I}_{34}({\tilde{m}}^2,{\tilde{m}}^2).\end{array}$$

(25)

C and D mixes, and we can write their “kinetic terms” in matrix form on the diagonal basis as

$$\begin{array}{cc}\hfill & p^2\frac{1}{2}{g}^2{N}_c{\mu }^2{I}_{34}\left(\begin{array}{cc}\frac{{\tilde{m}}^2}{\mu }C+D& C-\frac{{\tilde{m}}^2}{\mu }D\end{array}\right)\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}\frac{{\tilde{m}}^2}{\mu }C+D\\ C-\frac{{\tilde{m}}^2}{\mu }D\end{array}\right).\hfill \end{array}$$

(26)

One can see that only one linear combination of C and D is dynamic, whereas the orthogonal combination is purely auxiliary. Therefore, we have a canonically normalized dynamic real scalar field as given by $C^{\prime }=\sqrt{{\mu }^2{g}^2{N}_c{I}_{34}}\left(\frac{{\tilde{m}}^2}{\mu }C+D\right)$. The orthogonal real scalar $D^{\prime }=\sqrt{{\mu }^2{g}^2{N}_c{I}_{34}}\left(C-\frac{{\tilde{m}}^2}{\mu }D\right)$ is the auxiliary one. The $C^{\prime }$ mass-squared is then given by $\frac{I_{2F}}{I_{34}}(1+\Delta )$, with $\Delta =-\frac{2{\tilde{m}}^6}{{\mu }^2({\mu }^2+{\tilde{m}}^4)g^2{I}_{2F}}$.

In conclusion, in the model with the apparently supersymmetry breaking vacuum, the propagating components in the composite superfield U include one real scalar $C^{\prime }=\sqrt{{\mu }^2{g}^2{N}_c{I}_{34}}\left(\frac{{\tilde{m}}^2}{\mu }C+D\right)$, two Weyl fermions $\chi$, and $\lambda$, as well as a spin one field $v^{\mu }$. All their kinetic terms are properly behaved (note our metric convention as $g_{\mu \nu }=diag(-1,1,1,1)$, and $I_{nF}$ as well as $I_{34}$ are all positive in the energy scale below the cut-off). $\chi$ or $\lambda$ may correspond to the massless Goldstino mode for supersymmetry breaking solution, which would then be eaten by the gravitino. $C^{\prime }$ and $v^{\mu }$ have masses at roughly the same scale. Moreover, the elementary field A gets its mass from the term $\mu gD{A}^{*}A$ in the Lagrangian once D develops VEV through non-perturbative effects described here, and $\psi$ remains massless. A and $\psi$ as dynamic components of the original superfield $\Phi$ have the kinetic terms undergoing a wave function renormalization, from the scalar VEV of $\mu g_{o}U$ in Equation (4). Amplitude of the VEV contribution as obtained from our gap equation analysis is given by $g_{o}c=-0.5$. It is very substantial, as expected by its non-perturbative nature and actually negative, but the $\Phi$, or A and $\psi$, renormalization remains sensible. Therefore, there is no indication at all of anything improper in our analysis of the possible supersymmetry breaking solution here.

6. Discussions and Conclusions

The original model Lagrangian in component fields:

$$\begin{array}{cc}\hfill \mathcal{L}=& i{\partial }_{\mu }\overline{\psi }{\overline{\sigma }}^{\mu }\psi -{\partial }^{\mu }{A}^{*}{\partial }_{\mu }A+F^{*}F-\frac{g^2}{2}{|2FA-\psi \psi |}^2\hfill \\ \hfill & +2g^2{A}^{*}A{\partial }^{\mu }{A}^{*}{\partial }_{\mu }A-2g^{2}i{\partial }_{\mu }\overline{\psi }{\overline{\sigma }}^{\mu }\psi A^{*}A-2g^{2}i\overline{\psi }{\overline{\sigma }}^{\mu }\psi A{\partial }_{\mu }{A}^{*}.\hfill \end{array}$$

(27)

From the equation of motion for $F^{*}$, we get

$$F=-\frac{g^2\psi \psi A^{*}}{1-2g^2{\left|A\right|}^2}.$$

(28)

The fractional form of F indicates that the Lagrangian with F eliminated would have unconventional interaction terms. Naively, the scalar potential is given by

$$-V_s=F^{*}F-2g^2{A}^{*}A{F}^{*}F.$$

(29)

Eliminating F gives

$$V_s=\frac{-g^4\psi \psi \overline{\psi }\overline{\psi }{\left|A\right|}^2}{1-2g^2{\left|A\right|}^2},$$

(30)

which contains no pure scalar part. It is a strong hint of a bifermion condensate which fits in the general NJL picture. If the multi-fermion condensate cannot be generated, the scalar potential is purely zero everywhere, therefore very unstable towards quantum corrections. Nevertheless, the potential actually blows up for $1-2g^2{\left|A\right|}^2$ being zero. While that can be kept from happening within the cutoff scale when the coupling is weak, strong coupling would causes serious problem. That is an indication of nontrivial non-perturbative dynamics. As discussed above, the introduction of the dynamic composite gives the model a sensible vacuum.

Our analysis along the standard NJL approach shows both supersymmetry preserving and supersymmetry breaking solutions. Therefore, the four-superfield interaction may serve as a source of supersymmetry breaking. The kind of analysis, though essentially a $1/N_c$ approximation, is commonly believed to give a qualitatively correct result for NJL models, in favor of the symmetry breaking solution for coupling beyond the critical value. Unfortunately, we do not have a more definite answer about the supersymmetry breaking issue here. If the issue can be clarified through further analysis, it would be of great interest. In the literature on the supersymmetric Standard Model (SSM), four-superfield interactions of the form $-g_s^2{\overline{\Phi }}_s{\Phi }_s\overline{\Phi }\Phi$ with the spurion superfield ${\Phi }_s$ bearing a supersymmetry breaking VEV has often been taken to communicate supersymmetry breaking to a SSM superfield $\Phi$, generating the soft masses. If the supersymmetry breaking discussed in our model here really works, one can have a similar scenario, only with the $〈{\left.{\overline{\Phi }}_s{\Phi }_s\right|}_D〉$ coming from the dynamically induced two-superfield condensate instead of individual $〈{\left.{\Phi }_s\right|}_F〉$. Neither extra supersymmetry breaking sector, nor additional messenger superfield is needed.

There are well known no-go theorems against spontaneous supersymmetry breaking. However, no matter in the famous paper by S. Weinberg [30], or the first proof presented by M. T. Grisaru, W. Siegel and M. Rocek [31], only perturbative non-renormalization theorems were discussed, as also pointed out for example in Ref. [32], “non-renormalization theorems may be violated by non-perturbative effects”. Although there have been other analyses indicating the general difficulty to get spontaneous supersymmetry breaking, to our knowledge, there is no solid analysis on the issue that applies to our model and establish the invalidity of our plausible supersymmetry breaking scenario. Considering the supersymmetry breaking structure in our model to those more conventional ones, our model, in the effective Lagrangian picture, may can be seen similar to the Fayet-Iliopoulos case, with a potential linear in the D-term, and a non-zero VEV coming from the dynamically induced two-superfield condensate via the non-perturbative effects.

We are not making any solid claim in the paper that the model sure gives dynamical supersymmetry breaking, but only that the NJL analysis as a $1/N_c$ approximation suggests that. Due to reasons explained above, in our opinion, whether our model breaks supersymmetry dynamically is still an open question, and needs further investigation. However, if that supersymmetry breaking with soft mass generation really works, phenomenological application of the model as a basic part of a background model giving rise to the supersymmetric standard model would be of great interest.

It is interesting to compare our model here with the corresponding non-supersymmetric models. The basic NJL mechanism has four-fermion interaction giving rise to a scalar composite. A Dirac pair, though massless, is the usual starting ingredient. Supersymmetrization is actually nontrivial as particularly discussed in [14], due to the fact that a dimension-six interaction term of four chiral superfields in place of the four-fermion term would have to be a Kähler potential term, while the Yukawa interaction term for the composite scalar has to be a superpotential term. There is also the issue that the natural fermionic field(s) should be chiral, instead of a Dirac four-spinor as a vectorlike pair. That leads to the two supersymmetrization pictures which allows the holomorphic alternative [21]. The latter has the scalar composite forming from scalar ingredients. For the case with spin-one composite, interestingly, Suzuki has presented models with fermion and scalar ingredients [11]. A chiral superfield contains both the scalar and fermion components. An interesting question is if the simplest versions of the fermion and scalar models can actually be parts of the same supersymmetric model. We answer this in the negative below, and illustrate the interesting issues involved.

A spin-one composite of course has to transform as a Minkowski four-vector. A natural good choice for such a field combination for a simple fermionic model would be the current for the $U{\left(1\right)}_f$ for the fermion number, i.e., $j_{\mu }=\overline{\Psi }{\gamma }_{\mu }\Psi$ for a Dirac multiplet $\Psi$. The fact that the current–current interaction $j_{\mu }{j}^{\mu }$ having no derivative in $\Psi$ means that putting in the interaction does not change the $U{\left(1\right)}_f$ current. Therefore, one has a working model. The spin-one composite $v_{\mu }$ being proportional to the conserved $j_{\mu }$ keeps it a tightly-bound state which apart from having a non-gauge-invariant mass, resembles much a gauge boson [10,11]. In particular, the couplings for the $v_{\mu }$ in the effective theory are exactly those of a gauge boson, of the $U{\left(1\right)}_f$ symmetry. A Dirac fermion is composed of two chiral fermions. The current–current interaction can be expressed by chiral fermions in the form of $\left({\overline{\psi }}_i{\overline{\sigma }}_{\mu }{\psi }^i\right)\left({\overline{\psi }}_j{\overline{\sigma }}^{\mu }{\psi }^j\right)=-2{\overline{\psi }}_i{\overline{\psi }}_j{\psi }^i{\psi }^j$. With the two chiral fermion identified, $\overline{\psi }\overline{\psi }\psi \psi$ is just the four-fermion interaction which is a component of the $\overline{\Phi }\Phi \overline{\Phi }\Phi$ term in our superfield model Lagrangian. We need two chiral superfields to fully supersymmetrize the Dirac fermion model, which would only be a simple extension of our model. Nevertheless, the single superfield, or in the non-supersymmetric case single chiral fermion model, is the simplest one.

We have shown that the fermionic part of our four-superfield interaction gives half of the current–current interaction of a fermion. However, on the superfield setting, a chiral fermion comes along with its supersymmetric partner as a scalar. Therefore, a superfield interaction term gives rise to component field terms involving both. In fact, Equation (5) gives our spin-one vector boson $v_{\mu }$ as a sum of both a boson and a chiral fermion parts. The $U{\left(1\right)}_f$ is really a $U{\left(1\right)}_{\Phi }$ under which the scalar A is also charged. The bosonic part of $v_{\mu }$ in the form of $j_{\mu }^s=-i{A}^{*}{\partial }_{\mu }A+h.c.$ corresponds to the $U{\left(1\right)}_A$ of a pure scalar model having only field derivative in the kinetic term. However, $j_{\mu }^s$ involves ${\partial }_{\mu }A$, therefore adding a $j_{\mu }^s{j}^{s\mu }$ interaction change the nature of the $U{\left(1\right)}_A$ current. Any spin-one composite from such an interaction would not corresponds to the conserved current [11]. The author of the latter paper gives an alternative interaction in the form $-\frac{g^2}{2}{j}_{\mu }^s{j}^{s\mu }{[1+2g^2{A}^{†}A]}^{-1}$, (we have translated the notation to match ours here for easy comparison; A being an $SU\left(N_c\right)$ multiplet in the fundamental representation) with the spin-one composite keeping the status as (proportional to) the conserved $U{\left(1\right)}_A$ current, and therefore a tightly bound state. Besides the $U{\left(1\right)}_{\Phi }$ symmetry, the superfield model also has the $U{\left(1\right)}_R$ symmetry, mentioned above. The product of the two is equivalent to that of $U{\left(1\right)}_f$ and $U{\left(1\right)}_A$. Any linear combination of the two currents is therefore a conserved current. Explicitly, the currents for our superfield model are given by

$$\begin{array}{cc}\hfill j_s^{\mu }& =(-A{\partial }^{\mu }{A}^{*}+A^{*}{\partial }_{\mu }A)(1-2g^2{A}^{*}A)+i\overline{\psi }{\overline{\sigma }}^{\mu }\psi \left(2g^2{A}^{*}A\right),\hfill \\ \hfill j_f^{\mu }& =-i\overline{\psi }{\overline{\sigma }}^{\mu }\psi (1-2g^2{A}^{*}A).\hfill \end{array}$$

(31)

It is clear that our composite spin-one does not correspond to any of the conserved currents. Therefore, it is not the kind of tightly bounded state as in the case of the non-supersymmetric models in [11].

Recall that our model in the effective theory description does not have the right coupling structure required for the composite behaving like a gauge boson. The necessary $U^2\overline{\Phi }\Phi$ term is missing. It is interesting to note another model Lagrangian which looks like a supersymmetrization of the Suzuki scalar model above and have naturally the kind of right interactions for the composite spin-one to the original chiral superfield in the form of a gauge field:

$$\begin{array}{c}\hfill \mathcal{L}=\int d^4\theta \left[\overline{\Phi }\Phi -\frac{g^2}{2}\frac{\overline{\Phi }\Phi \overline{\Phi }\Phi }{1+n{g}^2\overline{\Phi }\Phi }\right],\end{array}$$

(32)

which has the effective theory as

$$\begin{array}{cc}\hfill {\mathcal{L}}_{eff}& =\int d^4\theta \left[\overline{\Phi }\Phi \left(1+\mu gU+\frac{n{\mu }^2{g}^2}{2}{U}^2\right)+\frac{{\mu }^2}{2}{U}^2\right],\hfill \end{array}$$

(33)

with the composite

$$\begin{array}{cc}\hfill U& =-\frac{g\overline{\Phi }\Phi }{\mu (1+n{g}^2\overline{\Phi }\Phi )};\hfill \end{array}$$

(34)

where ${\mathcal{L}}_{eff}=\mathcal{L}+\int d^4\theta \frac{1}{2}(1+n{g}^2\overline{\Phi }\Phi ){\left[\mu U+\frac{g\overline{\Phi }\Phi }{1+n{g}^2\overline{\Phi }\Phi }\right]}^2$ [an extra $2{\delta }^4\left(0\right)ln(1+n{g}^2\overline{\Phi }\Phi )$ skipped here and above.] We put a parameter n above for a purpose below, while $n=1$ is the case of interest which gives the correct “gauge”-coupling form of the spin-one component $v^{\mu }$ in U to $\Phi$ or its A and $\psi$ components; the coupling constant being $\frac{\mu g}{\sqrt{2}}$. For the spin-one component in U, we have actually the result

$$\begin{array}{cc}\hfill v^{\mu }& =-\frac{ig(A^{*}{\partial }^{\mu }A-A{\partial }^{\mu }{A}^{*})}{\sqrt{2}\mu {(1+g^2{A}^{*}A)}^2}-\frac{g(1-g^2{A}^{*}A)}{\sqrt{2}\mu {(1+g^2{A}^{*}A)}^3}\overline{\psi }{\overline{\sigma }}^{\mu }\psi .\hfill \end{array}$$

(35)

Note that there are nontrivial contributions at higher order of ${(1+g^2{A}^{*}A)}^{-1}$ from the $\theta$- and $\overline{\theta }$- dependent components of $(1+g^2\overline{\Phi }\Phi )$. Now, even taking only the scalar part above, it is not the same as the spin-one of the Suzuki model which reads $v^{\mu }=\frac{ig(A^{*}{\partial }^{\mu }A-A{\partial }^{\mu }{A}^{*})}{\mu (1+2g^2{A}^{*}A)}$. The latter has $n=2$ instead of 1 in the factor in the denominator, which is only to the first power; “gauge” coupling constant is actually $\mu g$, $\mu$ being the spin-one mass in both cases. The conserved currents for the superfield model have, however, the results have even higher powers of the ${(1+g^2{A}^{*}A)}^{-1}$ factor. Explicitly,

$$\begin{array}{cc}\hfill j_s^{\mu }=& \frac{A^{*}{\partial }^{\mu }A-A{\partial }^{\mu }{A}^{*}}{2{(1+g^2{A}^{*}A)}^3}[2+2g^2{A}^{*}A+3g^4{\left(A^{*}A\right)}^2+g^6{\left(A^{*}A\right)}^3]+\frac{i\overline{\psi }{\overline{\sigma }}^{\mu }\psi }{{(1+g^2{A}^{*}A)}^4}[2g^2{A}^{*}A-g^4{\left(A^{*}A\right)}^2]\hfill \\ \hfill j_f^{\mu }=& -\frac{i\overline{\psi }{\overline{\sigma }}^{\mu }\psi }{2{(1+g^2{A}^{*}A)}^3}\left[2+2g^2{A}^{*}A+3g^4{\left(A^{*}A\right)}^2+g^6{\left(A^{*}A\right)}^3\right].\hfill \end{array}$$

(36)

So, we have exhibited supersymmetric versions of four-chiral-superfield interaction giving rise to a composite real superfield bearing a spin-one component, including one example where the spin-one boson couples to the components of the chiral superfield in the form of a gauge coupling. The model, like others, has a mass term for the spin-one, therefore at most may correspond to gauge boson of broken gauge symmetry. The latter is the same as the non-supersymmetric models. A feature we fail to reproduce is such a spin-one mode which is tightly-bounded, like the non-supersymmetric models, in which the spin-one matches with a conserved current of the original model Lagrangian. The interesting question of if such a supersymmetric model with a spin-zero couples like a gauge boson is possible remains open. The study illustrates again that the notion of supersymmetrization of NJL-type models is quite nontrivial. Basic model features typically cannot be all maintained when the original fermion or scalar field is replaced by a chiral superfield.

In conclusion, we have presented here a supersymmetric model with a new kind of NJL-type composite, namely a real superfield. Most interesting component of the latter is a spin-one boson $v^{\mu }$ somewhat similar to a massive gauge boson, with its ‘gaugino’ partner. Up to the $1/N_c$ type of approximation as in standard NJL analysis, it looks like the real superfield composite may develop nontrivial VEV giving to dynamical supersymmetry breaking. We compared the model, together with one having a more complicated interaction in the fractional form, with models that look like their non-supersymmetric counterparts. The key formulation which facilitates the superfield calculations is the picture of quantum effective action as a superfield functional with parameters like constant superfields, having explicit supersymmetric and Grassmann number dependent supersymmetry breaking parts. We consider only the simple case of a singlet composite $U\sim {\overline{\Phi }}_a{\Phi }^a$. It can also be in the adjoint representation, as studied in the non-supersymmetric case. Phenomenological application of the kind of models also worth explorations.