1. Introduction
The increasing complexity of devices being developed and physical processes occurring in them make a mathematical simulation very important, in particular, because a full-scale simulation is more expensive than a mathematical simulation. Moreover, a lot of conductors create various crosstalk noises and parasitic couplings which complicate the process of diagnosing radio-electronic equipment (REE) because of the necessity to take into account all couplings between conductors [
1]. It is important for the diagnostics to be carried out at the designing stage and be aimed at detecting possible vulnerabilities of printed circuit boards (PCB), for example, detecting the places with an excess of voltage or current amplitudes [
2,
3]. Timely and accurate application of a mathematical simulation would exclude the influence of electromagnetic interference (EMI) on high sensitive equipment during its operation [
4], as well as decrease the consequences of intentional EMI which make the REE inoperative [
5,
6]. Ultra-wideband pulses, power ultrashort pulses [
7], and electrostatic discharge (ESD) [
8] can be referred to as such excitations. Due to this fact, it is necessary to take into account both useful and interference signals during the PCB diagnostics. Moreover, it is particularly important in the field of aerospace because a fault that appears in one of the parts of aircraft equipment can cause the loss of an aircraft [
9,
10]. For example, the new method of hardware-in-the-loop simulation for an aircraft electric power system has been presented in [
11] and the use a new fault diagnostic method by multi sensor fusion for testing spacecraft control system sensors has been proposed in [
12]. In addition, the noises (crosstalk) generated by the useful signals, the powerful intentional electromagnetic pulses of nanosecond and subnanosecond ranges, are dangerous because they are capable of penetrating into various electronic equipment and disabling them. This is important for supporting the uninterrupted operation of critical systems, for example, to assess the situation of electromagnetic terrorism manifestations that have powerful electromagnetic effects on the electrical network, or to protect special technical buildings from external electromagnetic effects. The propagation of such signals in multiconductor transmission lines has been well studied, however, the features of the ultrashort pulse propagation along the conductors with a high density of PCB interconnects are not clearly understood and can lead to their uncontrolled propagation, whereby it is important to provide the control of signal propagation along the entire length of the conductors.
The way to determine the propagation path of noise using the source modulation technique was reviewed in [
2], which considered the key parameters and the main properties of the noise source modulation technique (NSMT) based on the amount and the type of modulation of the noise at the victim location. The experiment was performed under ideal conditions, in which two cables had the same common-mode currents, but only one of them was a noise propagating path for the victim. By comparing the propagation path index with the measured insertion loss between the cables and receiving antennas, the NSMT was proved to determine the noise propagation path. Quantifying EMI was examined in [
3], namely a methodology for determining and quantifying radiation for practical design guidelines. Due to tight EMC standards, it becomes increasingly important to diagnose the radiation hot spot in the radiation process before applying attenuation measures. The researchers implemented the analysis of characteristic mode together with the integral equation based numerical method in order to identify the hot spots for EMI radiation. Several numerical examples were applied to benchmark the proposed approach. An analysis in time domain and simulation of crosstalk noise reduction for high-speed digital circuits by a guard trace with an open stub between coupled striplines was carried out in [
13]. In order to mitigate the interference of crosstalk noise in PCBs or packages the grounded guard traces were utilized. The study included a discussion on how the guard trace with inserted coupled striplines with an open stub affects the crosstalk noise. A design curve for the geometric parameters of coupled striplines inserted guard trace stub was constructed based on the proposed method. The maximum reduction in crosstalk noise in the presented examples exceeded 50%. A new method for the fast-transient analysis of large linear chains using stable high-order methods was presented in [
14]. A new algorithm based on the A-stable and L-stable high-speed integration methods in the time domain for simulating large linear circuits was presented. The proposed method took advantage of the mathematical description of the circuits found in these cases in a special form to significantly reduce computational costs. Several variants of schemes were presented to demonstrate the acceleration achieved by the proposed algorithm.
The optimization by means of different methods based on collective intelligence to different application areas has been widely used. For example, a genetic algorithm (GA) with real number encoding was used for structural damage detection based on vibration data in [
15]. The objective function was minimized by directly comparing the changes in the measurements before and after damage. Three different criteria were considered, namely, the frequency changes, the mode shape changes, and their combination. All the damaged elements could be detected accurately by genetic algorithm, as seen from the numerical results, even when the analytical model was not accurate. A particle swarm optimization algorithm was used for the quantization thresholds in [
16]. The authors considered decentralized detection of an unknown signal corrupted by zero-mean unimodal noise via wireless sensor networks. The asymptotic performance analysis of the multi-bit Rao test was provided and exploited to propose a (signal independent) quantizer design approach by maximizing the noncentrality parameter of the test statistic distribution. Numerical results were provided to show the effectiveness of the Rao test in comparison to generalized likelihood ratio test and the boost in performance obtained by (multiple) threshold optimization. A GA was used for mobile robot localization using ultrasonic sensors in [
17]. The researchers investigated an ultrasonic sensor localization system for autonomous mobile robot navigation in an indoor semi-structured environment. They developed a self-localization module which has been integrated successfully in a more complex navigation system. A method for the joint optimization of radio and computing resources for multichannel mobile computing was proposed by [
18]. This study, considered a multiple-input multiple-output (MIMO) multicell system where several mobile users ask for computation offloading to an ordinary cloud server. The resulting optimization problem was nonconvex. Nevertheless, in the case of a single user, researchers were able to calculate the main optimal solution in closed form. In the more challenging scenario with an increasing number of users, they suggested an iterative algorithm, which was based on a novel successive convex approximation approach, converging to a local optimal solution of the original nonconvex task. Numerical results showed that the proposed approach excelled the other optimization methods. The projection matrix was optimized for sparse signals in structured interference in [
19]. The researchers considered the problem of estimating a signal which has been corrupted with structured noise and proposed an approach for the design optimization of the projection matrix, in which the objective was not only to decrease the amount of data to be processed but also to eliminate the undesired signal components. As a result, they reduced the computation time and the error on the estimation of the unknown parameters of the sparse model, with respect to the uncompressed data. The joint optimization of data and energy transfer in multiuser MIMO systems was performed in [
20]. The researchers presented a method to solve the nonconvex optimization task that appeared when constructing the transmit covariance matrices in multiuser MIMO broadcast networks with implementation of simultaneous wireless information and power transfer. Two different approaches were applied to reformulate the (nonconvex) multiobjective problem. In order to solve the resulting formulations, the researchers proposed using the majorization-minimization approach. A method for optimizing the received signal strength (RSS) using the Gauss method was presented in [
21]. The optimal RSS threshold was found through minimizing the best achievable localization root mean square error formulated with the aid of fundamental lower bound analysis. The resulting optimal RSS threshold enabled enhanced performance of new fashioned low-cost and low-complex proximity report-based positioning algorithms. A synthesis of a control system based on multicriteria optimization using a GA was presented in [
22] in which an approach for the parametric synthesis of the automatic control system (ACS) was suggested. The approach used the genetic algorithm that carries out an approximation of Pareto-optimal solution sets and it was shown that their approach obtained a reasonable solution in a shorter time and with less computational costs than other methods. In [
23] optimization was considered using a GA, optimization by the particle swarm method and optimization by the firefly algorithm when designing antennas, and demonstrated the application of the evolutionary optimization methods with multiple objectives to the microstrip antennas constructing. Impedance matching and gain improvement were optimized over a predefined frequency range, resulting in a very small and compact 12 mm x 21 mm ultra-wideband antenna which was fabricated and measured. For radio-electronic equipment optimization the most popular are GAs and evolution strategies (ES) [
24]. For example, a new algorithm for optimizing a direct eye diagram for an arbitrary transmission line using a finite impulse response (FIR) filter was proposed in [
25] in which a new design algorithm, which directly optimizes the eye diagram using the FIR filter as transmitter pre-emphasis, was proposed to counteract the intersymbol interference in the high-speed data transmission. In order to minimize the resistance of electrical contact, a method for controlling the location of microcontacts based on a GA was proposed in [
26]. In this study, the positioning and sizing optimization of microcontact spots were investigated in relation to minimizing the ECR. The optimal solutions were obtained by a novel method of a real-coded genetic-algorithm implemented with a subpopulation-based selection method and a normal distribution probability-based crossover. A method for analyzing and optimizing signal integrity for complex circuits with multiple inputs and outputs based on the analysis of S-parameter data was proposed in [
27]. The proposed data mining approach considered both the interconnect structure and the stimulated pattern of a MIMO system, which can carry out thoughtful analysis and optimization with high efficiency. The decentralized dynamic optimization of voltage management in the power supply network was investigated in [
28]. By simulating the network dynamics using an autoregressive process and considering time-varying resource constraints, the researchers provided an error bound in tracking the instantaneous optimal solution to the quadratic error objective. The design of the circuit of the delay lines using a GA to minimize crosstalk noise was investigated in [
29]. The paper highlighted a development of a design methodology of delay line layout for minimizing crosstalk with the use of a GA for optimization. The GA required a large number of function evaluations, and efficient calculation of crosstalk was proposed together with a new approach of generating random line, making offsprings, and mutation. Different optimum results have been obtained for different objectives and compared.
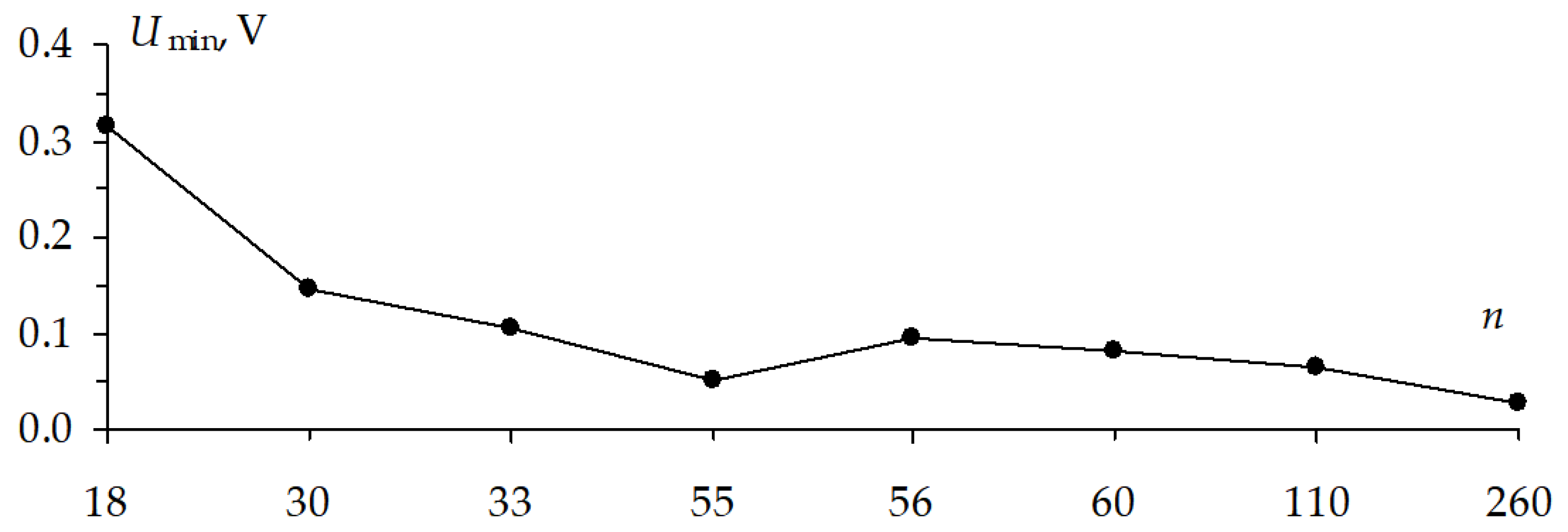
The quasi-static approach is widely used for analyzing PCB interconnects, because the accuracy of the circuit analysis is often unacceptable, while the electromagnetic analysis often involves large computational costs. The investigations of techniques for detecting and localizing signal extreme points have been performed for single and coupled [
30,
31] transmission lines, and for a PCB bus of a spacecraft autonomous navigation system (ANS) [
32,
33], also with the use of a GA [
34,
35]. The voltage maximum exceeding the signal amplitude at the input by 1.14 times is detected in the meander line with two turns. The voltage maximum, twice as big as the signal amplitude at the input, is detected in the microstrip cross section. The voltage maximum exceeding the steady state level by 18% is detected in the PCB bus of a spacecraft autonomous navigation system. The voltage maximums exceeding the steady state level by 36% and 38% are revealed in the PCB bus by using the GA for optimization. The voltage maximum exceeding the steady state level by 20% is detected in the PCB bus by using the ES optimization.
However, an approach combining the opportunity to perform the diagnostics for detecting and localizing signal extreme points and the optimization of obtained results has not been developed. Therefore, the purpose of this paper is to develop the approach and to demonstrate some recently obtained and new results of applying this approach in detecting and localizing extreme points of useful and interference signals which are necessary for REE diagnostics.
The paper is organized as following. In
Section 2, a brief theory is presented. In
Section 3, a description of the proposed approach for detecting and localizing signal extreme points is presented. In
Section 4, block diagrams of the developed algorithms for the approach are shown. The results of the investigation of coupled transmission lines are presented in
Section 5. In
Section 6, the results of the investigation of the spacecraft ANS bus are considered. In
Section 7, the results of the GA for optimization are shown. In
Section 8, the results of the GA for optimization are shown.
Section 9 is the conclusions.
2. Theory
The theoretical bases and algorithms for calculating quasi-static responses along each conductor of each multiconductor transmission line (MCTL) section connected to the multiconductor network were developed earlier and presented in [
30]. But it seems to be important to show them again for a full understanding of the approach.
Frequency domain equations are used for calculating voltage and current responses in an MCTL section:
where S
V and S
I are the matrices of modal voltages and currents; E0 and ED are the diagonal matrices E0 = diag(exp(–
x), …, exp(–
x)) and ED = diag(exp(–
∙(
l–
x)), …, exp(–
(
l–
x)));
is the propagation constant for the
k-th MCTL section;
Nk is a number of conductors in the
k-th MCTL section;
l is the length of MCTL section; and
x is the coordinate along the MCTL section (the number of
x is defined by
nTLS parameter). The calculation of S
V, S
I, and
E(
x) is described in [
36]. C1 and C2 are constant vectors calculated as:
where E(
l) = diag(exp(–
l), exp(–
l), … exp(–
l)); V(0) and V(
l) are vectors describing the voltage at the ends of the MCTL section, determined after solving the equation for the circuit with
n MCTL sections with lumped elements at the ends:
where
s =
jω, where ω is angular frequency; W and H are matrices of order
A ×
A describing the lumped memory and memoryless elements of the network, respectively (
A is the number of parameters, which are calculated by the modified node potential method);
with entries
{0, 1}, where
{1, …,
Nk},
{1, …, 2
Nk} with one nonzero value in each column, is the selector matrix that maps the terminal currents of the
k-th MCTL section;
is the conductance matrix of the
k-th MCTL section; V is the vector of the node voltage waveforms; and E is a constant vector with the entries determined by the independent voltage and current sources.
The description of the response calculation algorithm is presented in [
36]. By applying the forward fast Fourier transformation (FFT), the original excitation in the time domain is transformed into the frequency domain. Then, calculations of Equations (1) to (4) are carried out. Then, by applying the inverse FFT, the obtained result is transformed into the time domain.
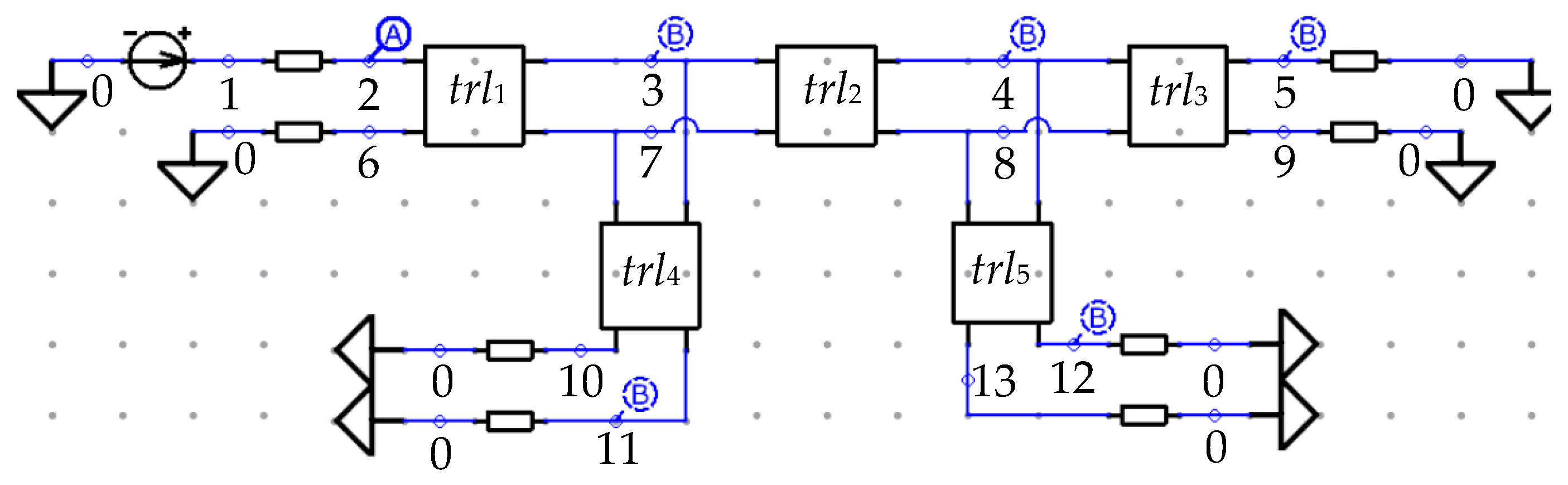
3. Proposed Approach for Signal Extreme Points Detection and Localization
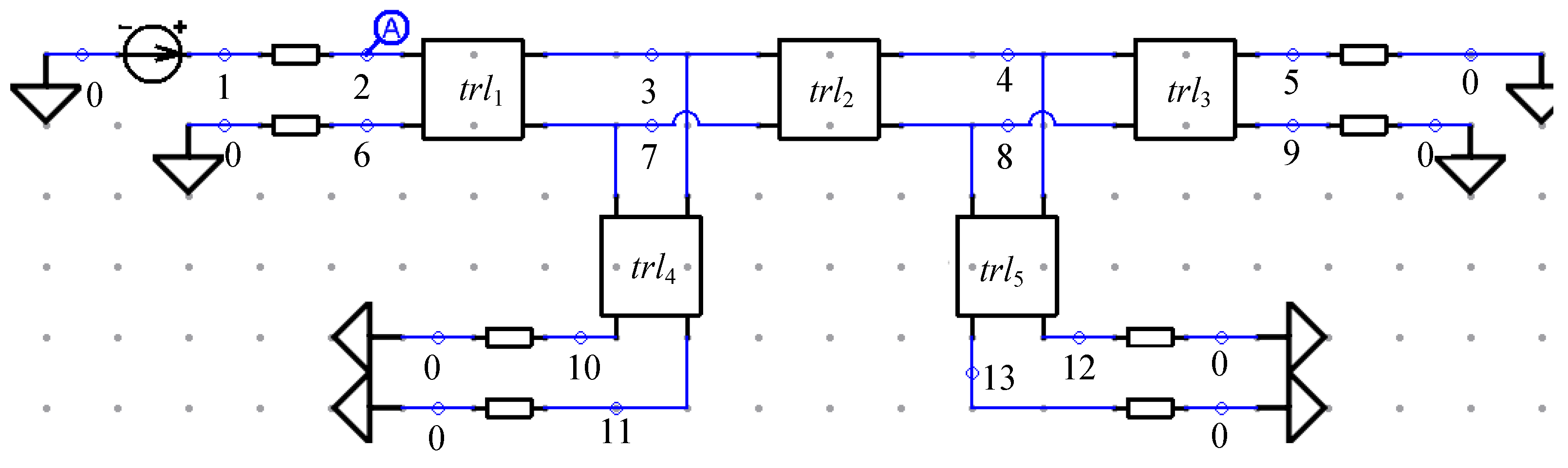
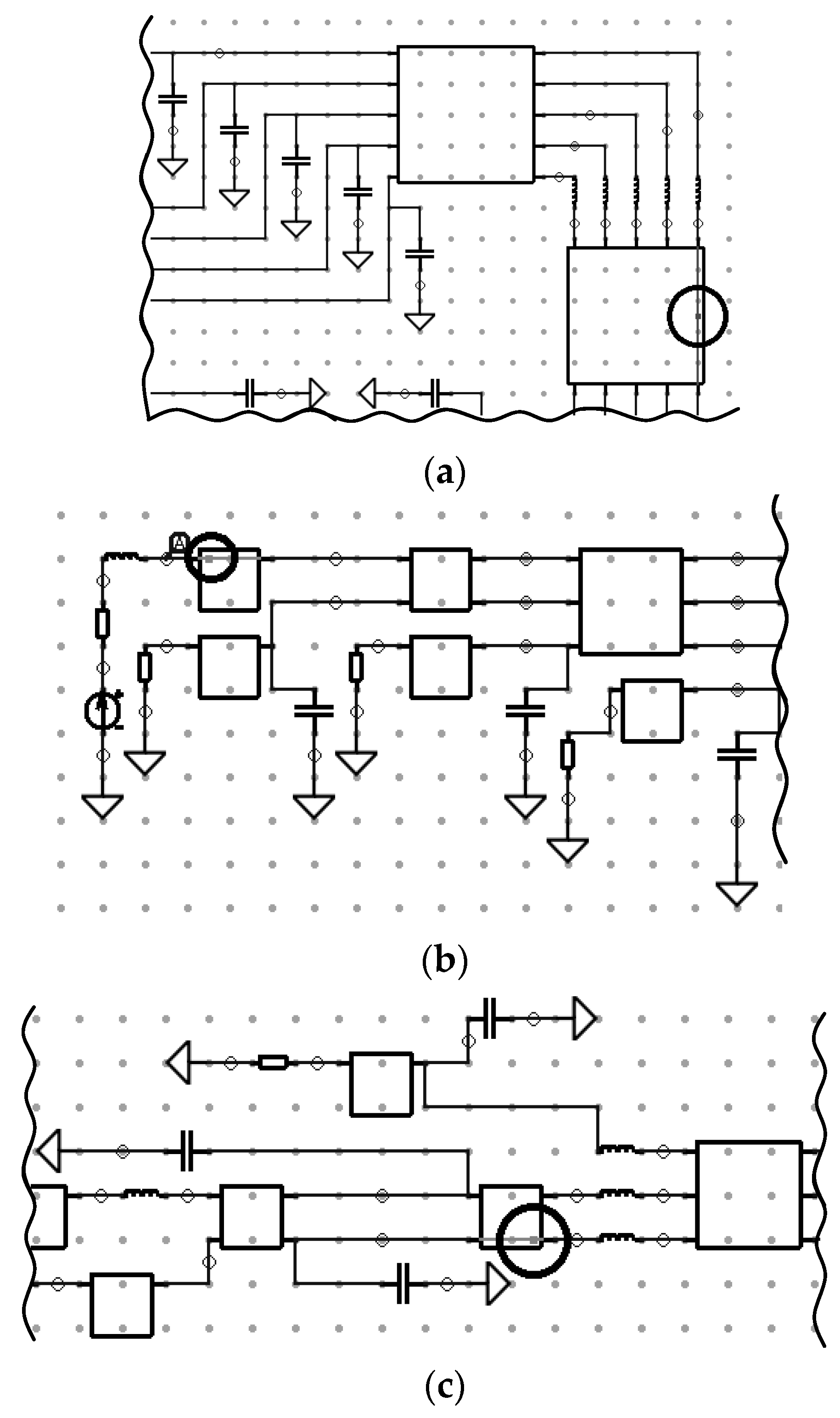
On the basis of the theory presented in Equations (1) to (4), an approach for signal extreme points detection and localization was developed. The description of the approach is presented further. First, an REE developer should make a correct circuit diagram of a structure under development. Then, he should choose a fragment in one of the conductors of the structure to be diagnosed. The diagnostics is aimed at checking whether the amplitudes of a propagating signal exceed the maximum agreed value or how the signal waveform is transformed during the propagation. The chosen fragment can consist of several segments of transmission lines or can be chosen over the whole conductor. In addition, the fragment can be located at any conductor of the structure (the developer can perform the diagnostics of the active or passive conductors to analyze the signal or crosstalk waveforms propagation respectively).
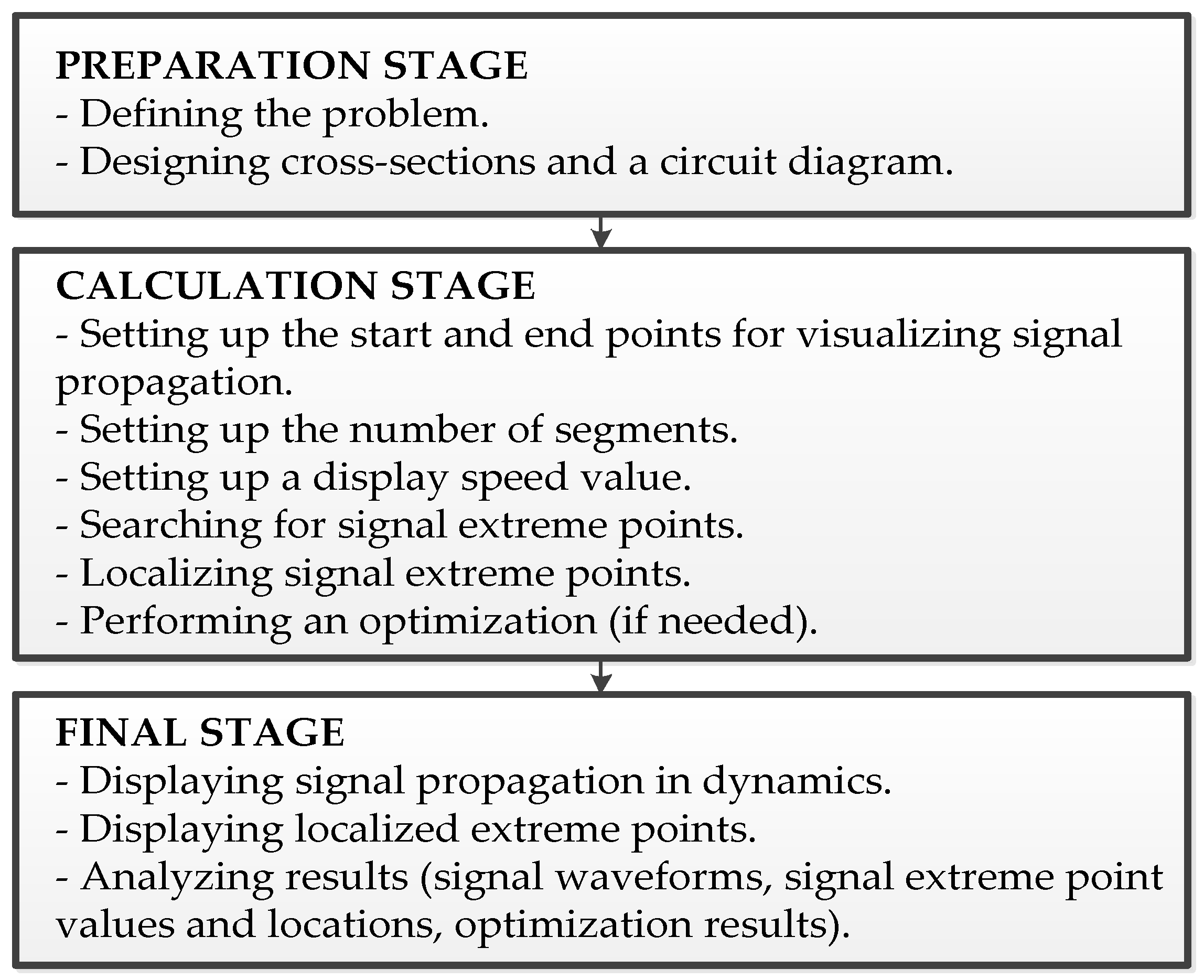
Thus, the proposed approach includes the following stages:
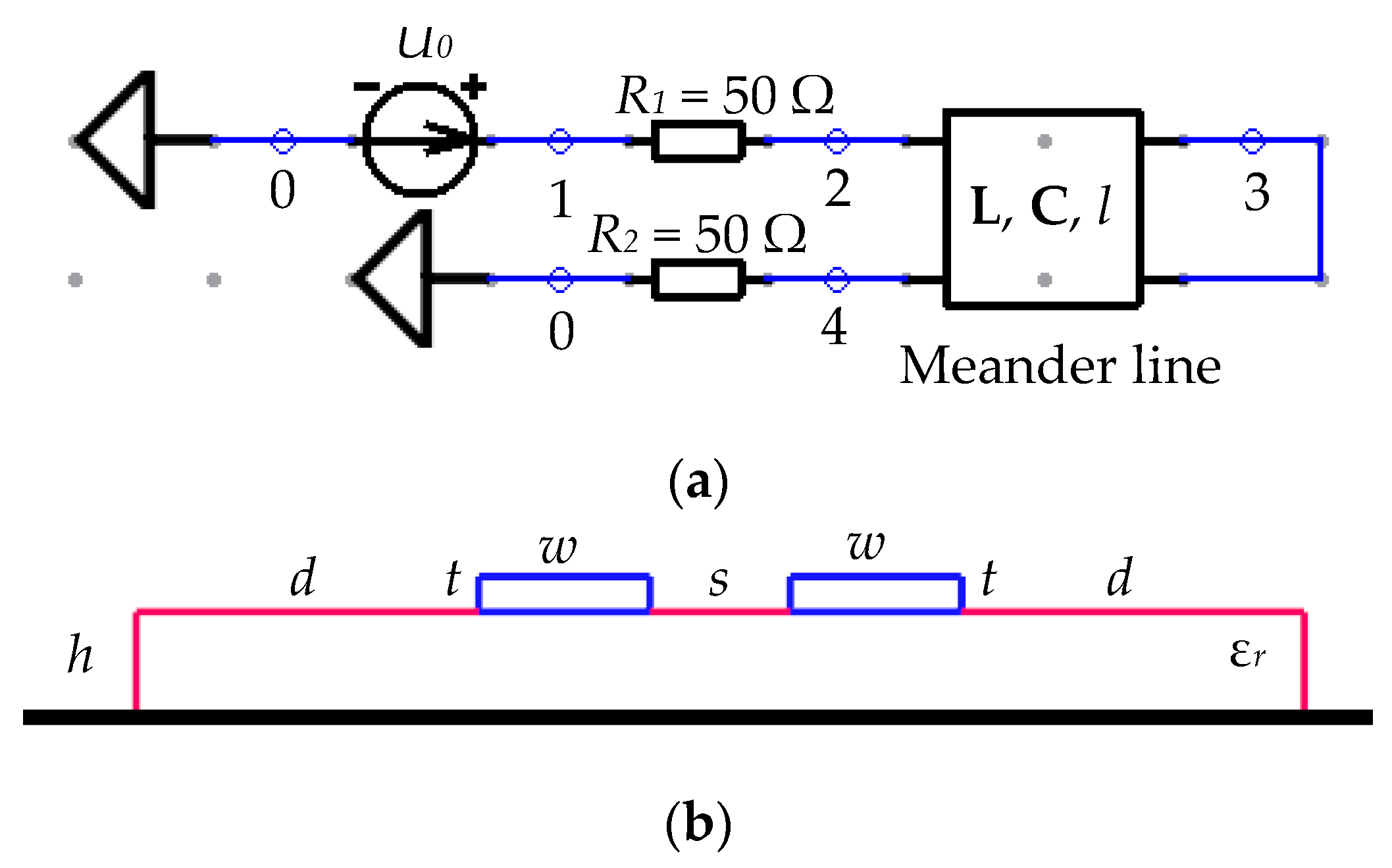
Preparation stage Formulating a problem to be solved, the aim, and expected results. Designing cross sections and a circuit diagram of REE (taking into account all galvanic connections between circuit diagram components), adding all parameters of active and reactive components (for a transmission line section, the per unit length coefficient matrices of electromagnetic (L) and electrostatic (C) induction, conductivities (G), and resistances (R); for the excitation signal source, the type of a signal and its parameters).
Calculation stage Setting up the start and end points of the pulse propagation, the number of a segment along each MCTL section, and the speed of displaying. Calculating signal waveforms. Detecting and localizing signal extreme points. Performing optimization to obtain an optimal solution.
Final stage Analyzing the obtained results, i.e., signal waveforms, whose propagation along each conductor of each MCTL is displayed in dynamics; detected signal extreme points; localization of these points in the circuit diagram.
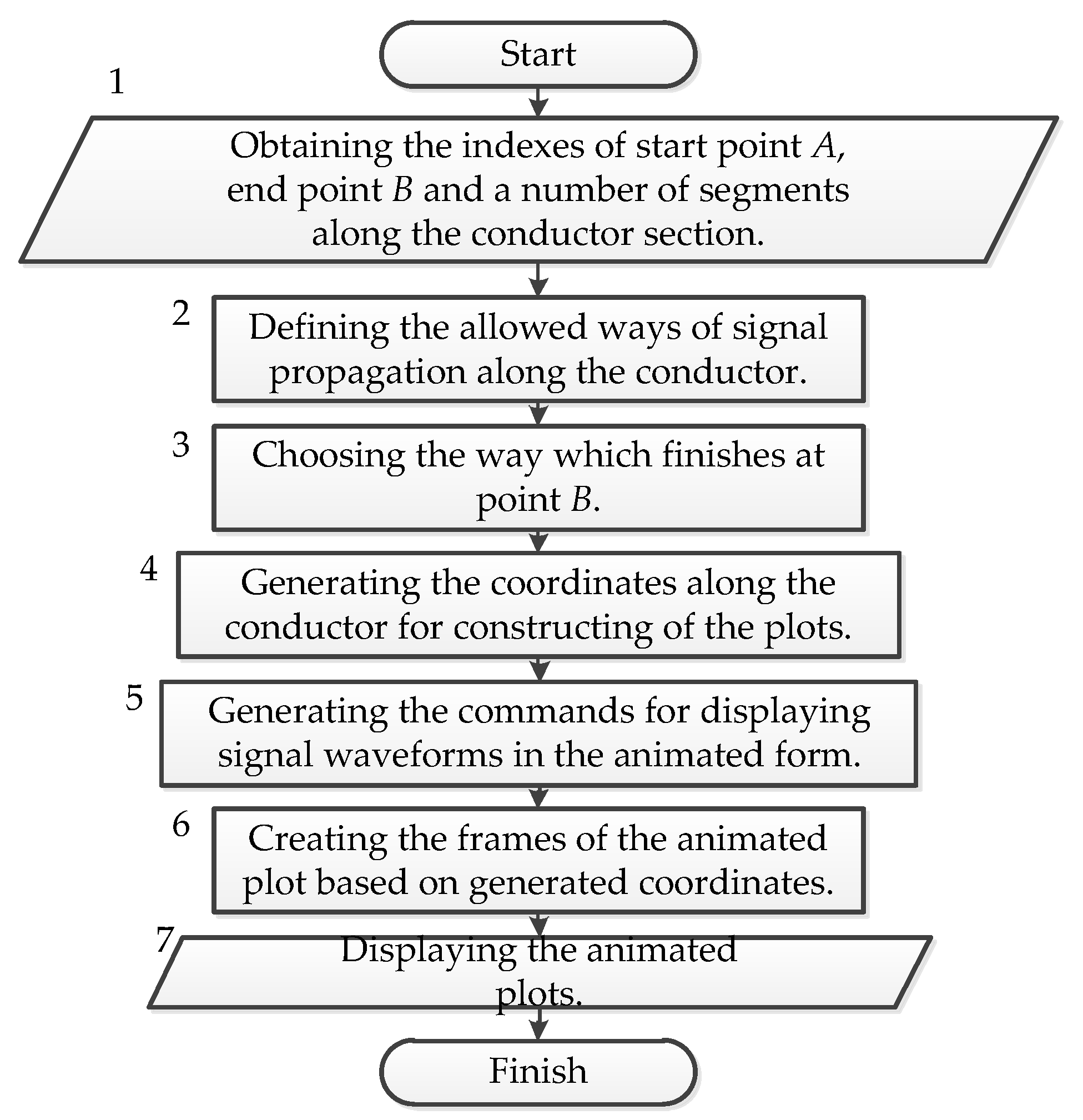
Let us consider the calculation and final stages in detail. In the calculation stage, to choose the fragment of the conductor (or the whole conductor) that consists of several MCTL sections, the developer should set the start and end points in the circuit diagram. The diagnostics and visualization of the signal propagation will be done along this fragment. Each MCTL section is divided into a number of segments which are set by the developer. The signal waveform is calculated in each segment of each MCTL section. The response (signal waveforms) calculation algorithm differs from the algorithm described in [
36] primarily in the fact that it uses segment coordinates instead of a node number. As a result, the system stores voltage or current values calculated in each segment of each conductor section. Then, the signal propagation way along the chosen conductor is defined taking into account all galvanic connections between MCTL sections (in other words a successive display of the signal waveforms calculated in each MCTL segment). The speed of the display is also defined by the developer. Then, the search for signal extreme points is carried out in each segment. It should be mentioned that we need to find not all extreme points but the global (relative to all segments) maximum and minimum only. The numbers of the segment and the MCTL section are assigned to the global maximum or minimum. These numbers are then used for localizing the extreme points. Moreover, there is an opportunity to apply the GA for optimization in this stage, for example, if a user needs to define such excitation pulse duration at which the maximum value of the signal amplitude along the conductor will be the highest.
In the final stage, dynamic visualization of the signal propagation along the conductor is performed. The developer can control the visualization as follows: stop the animation, display the signal waveform in the previous and next segment, and continue the animation. The developer can also push a button with an extreme point to display the signal waveforms with the global extreme point (maximum or minimum). These results are displayed in another window of the program. At the same time, the segments with the calculated signal waveforms are displayed as points in the circuit diagram (according to the signal waveform animation). The animation in the circuit diagram stops when the signal extreme point is displayed, and therefore one can see the place where the extreme point is located. Thus, the developer can perform the diagnostics aimed at checking what global extreme voltages or currents have been detected, where they are localized, and how the signal waveforms have been transformed during its propagation along the conductor. A block diagram of the proposed approach is presented in
Figure 1.
8. Use of Evolution Strategies
However, despite the popularity of GAs in various scientific spheres, other optimization methods are also used [
42]. Therefore, it is useful to consider how the task of detecting and localizing the signal extreme points in an ANS PCB bus can be solved by an another method of optimization, for example, an evolution strategy (ES). The ESs have a parameter of initial solution (IS) in contrast to GAs, and it is useful to study the effect of the IS of ESs on the signal extreme point in a preset point of the ANS PCB bus when detecting the worst-case effects.
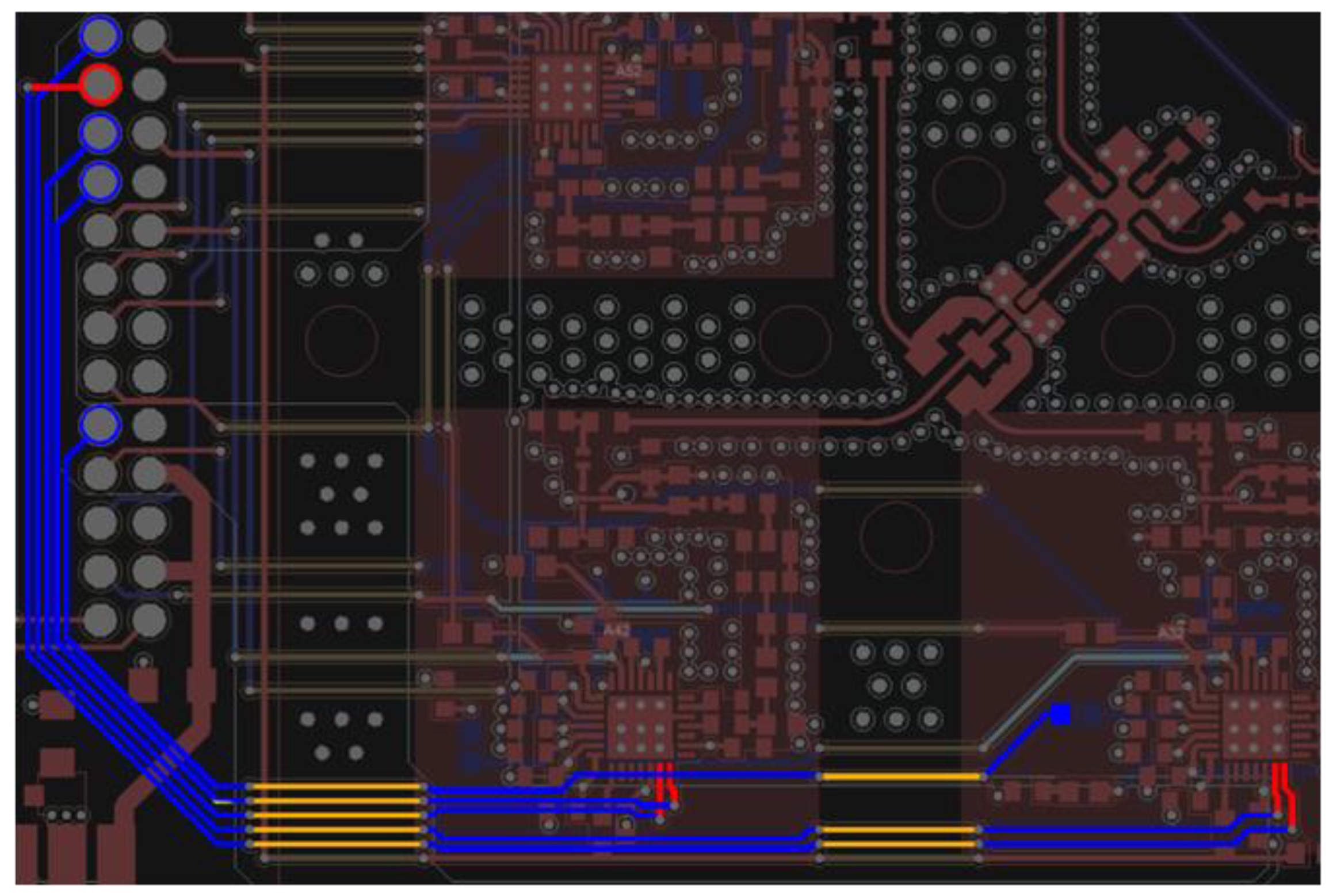
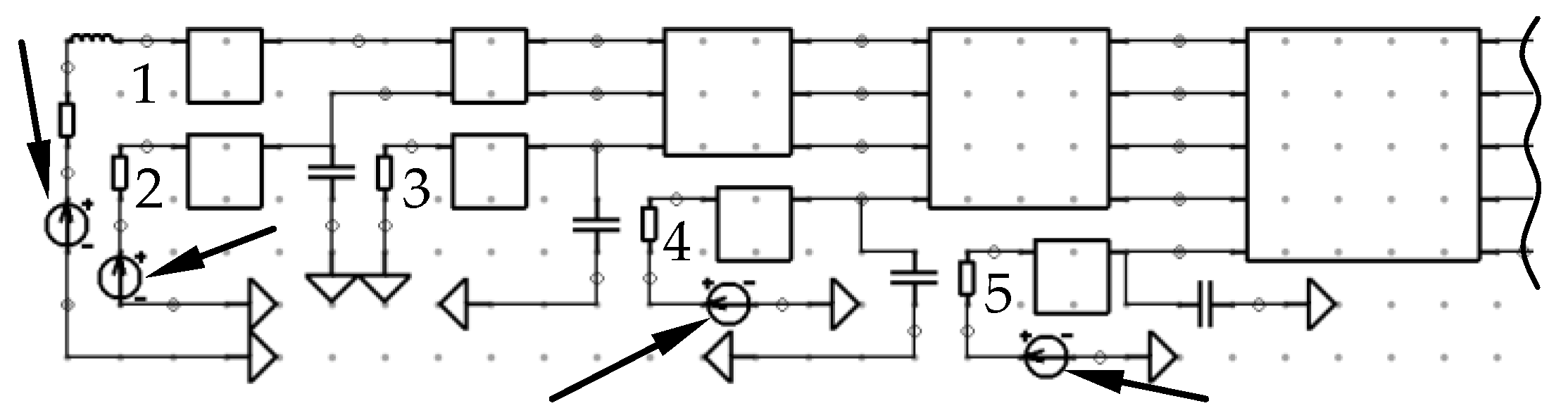
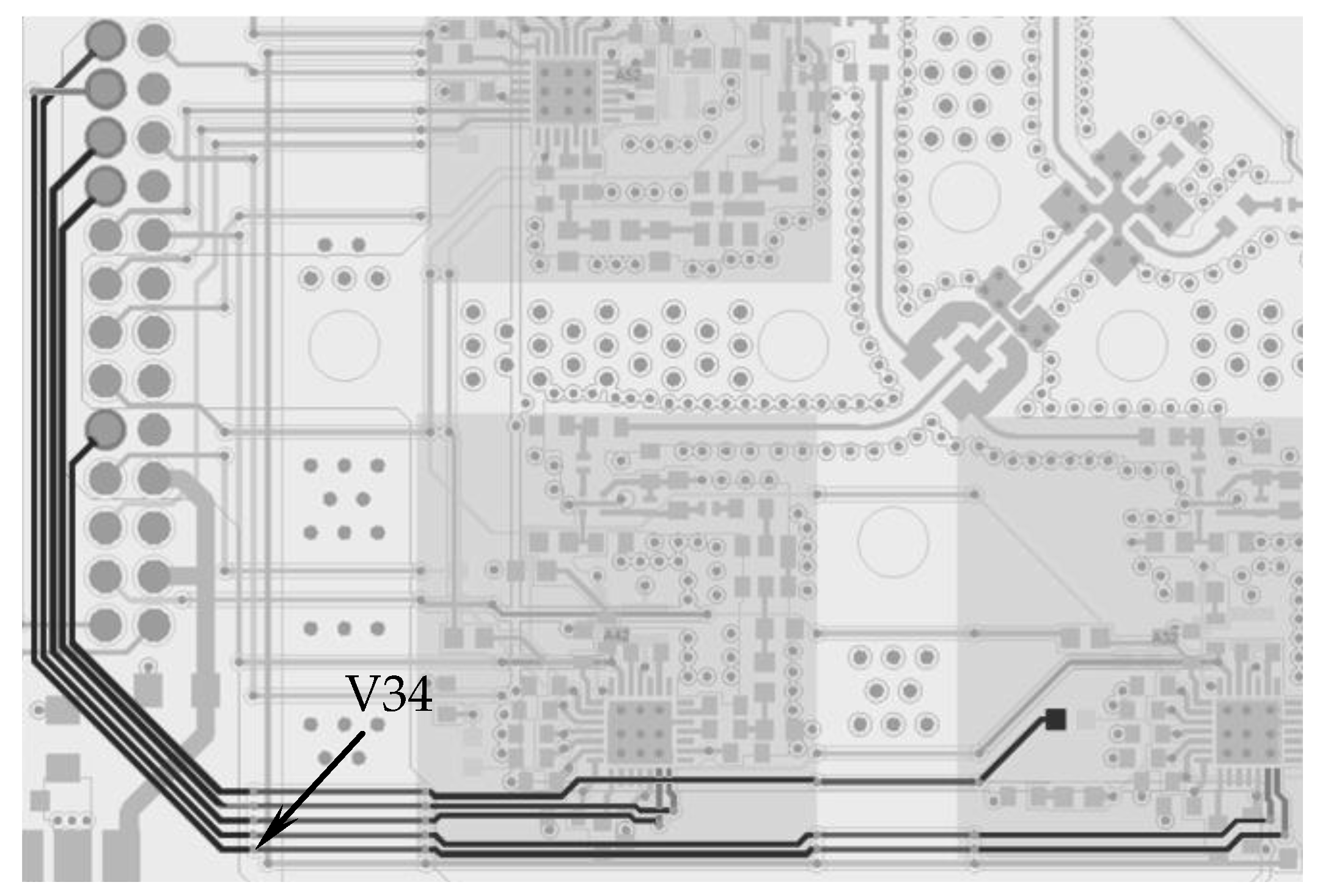
The goal of this study is to investigate the use of an ES and the IS influence when detecting the worst-case effects of the ultrashort pulse propagation in the PCB bus of a spacecraft ANS. The PCB fragment with the preset point is shown in
Figure 33.
The ES algorithm in general view can be formulated as [
43]:
- (1)
The initialization of a population …, with the use of μ parent chromosomes.
- (2)
The generation of λ offspring forming the offspring population …, where each offspring is generated by the following steps:
- (3)
Select (randomly) ρ parents from Pμ (if ρ = μ take all parental individuals instead).
- (4)
Recombine the ρ selected parents to form a recombinant individual r.
- (5)
Mutate the strategy parameter set s of the recombinant r.
- (6)
Mutate the objective parameter set, y, of the recombinant, r, using the mutated strategy parameter set to control the statistical properties of the object parameter mutation.
- (7)
The selection of a new parent population (using deterministic truncation selection) from either the offspring population (this is referred to as comma-selection, usually denoted as “(μ, λ) selection”), or the offspring and parent Pμ population (this is referred to as plus-selection, usually denoted as “(μ + λ) selection”).
- (8)
Go to 2 until the termination criterion is fulfilled.
The barecmaes2.py module [
43] was used with TALGAT software to perform optimization. The optimization was applied to the whole ultrashort pulse in order to get the highest extreme value of the voltage in the V34 node (shown in
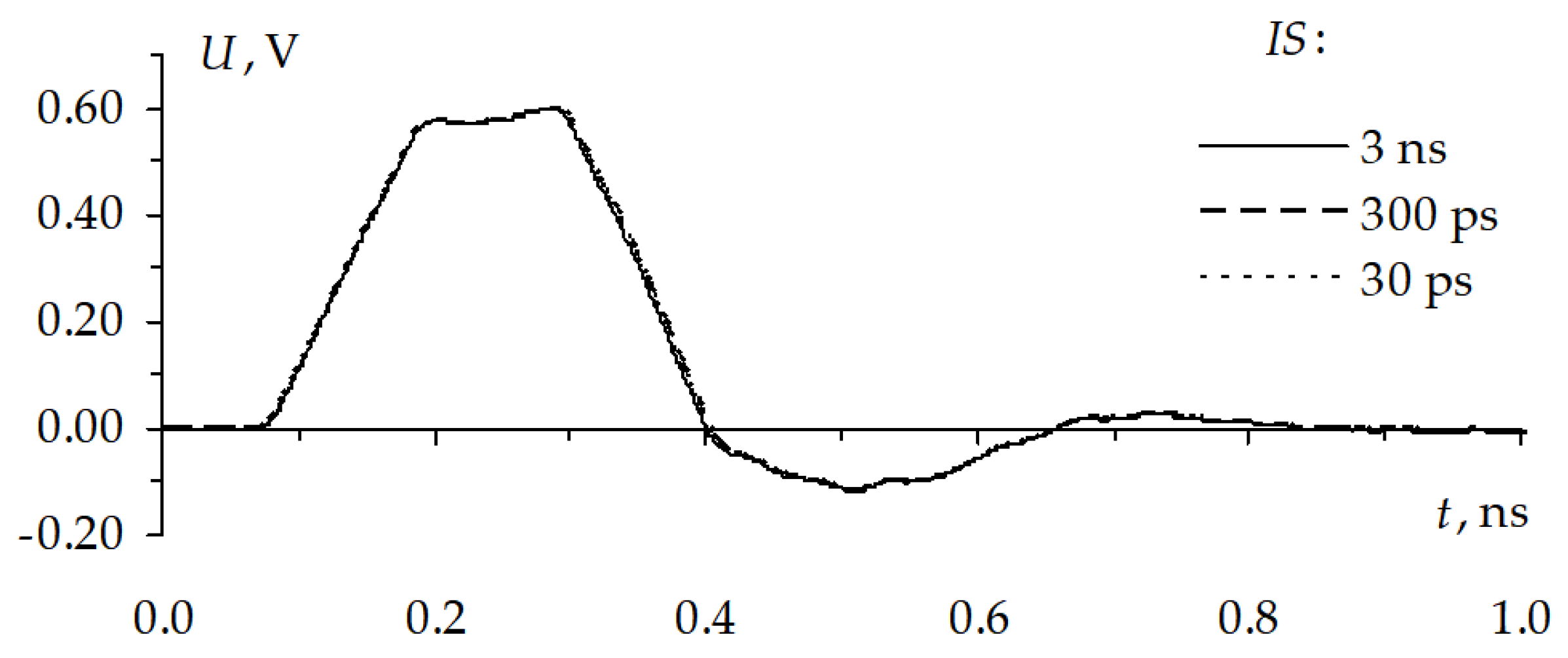
Figure 33). The sigma of the ES algorithm was 10 ps. The ES was launched ten times for each IS (3 ns, 300 ps, and 30 ps). The goal of the optimization was to get such duration values of the ultrashoprt pulse at which the extreme value of the voltage in the V34 node would be the highest.
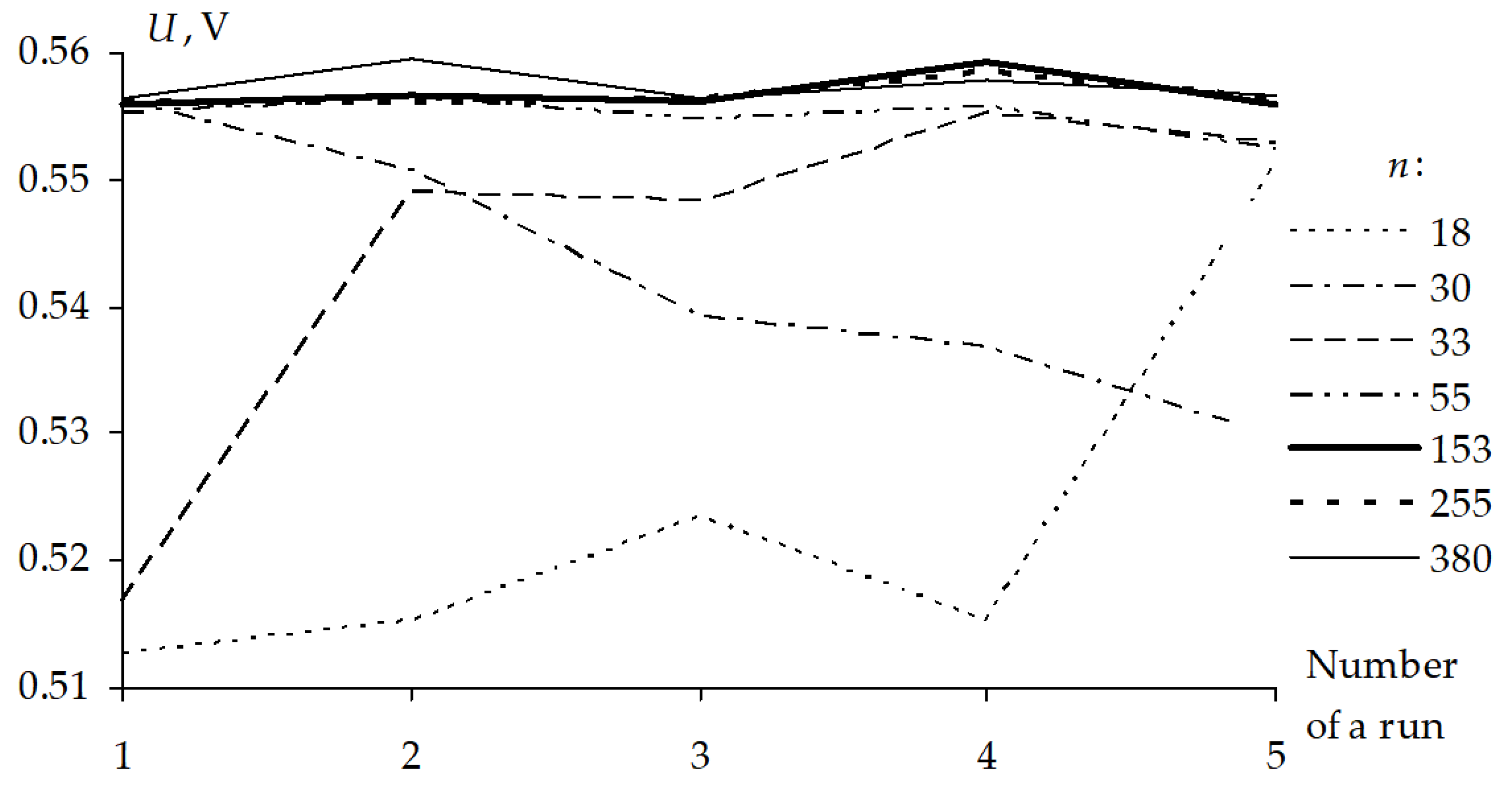
The results of the ES operation are the following: the peak voltages (
Umax) in the preset point (for ten ES runs) and the best solutions with different ISs of the ES are shown in
Table 7. (Cells with the highest
Umax for each IS are colored in yellow.) The signal waveforms calculated with IS = 3, 0.3, 0.03 ns for the highest
Umax are shown in
Figure 34.
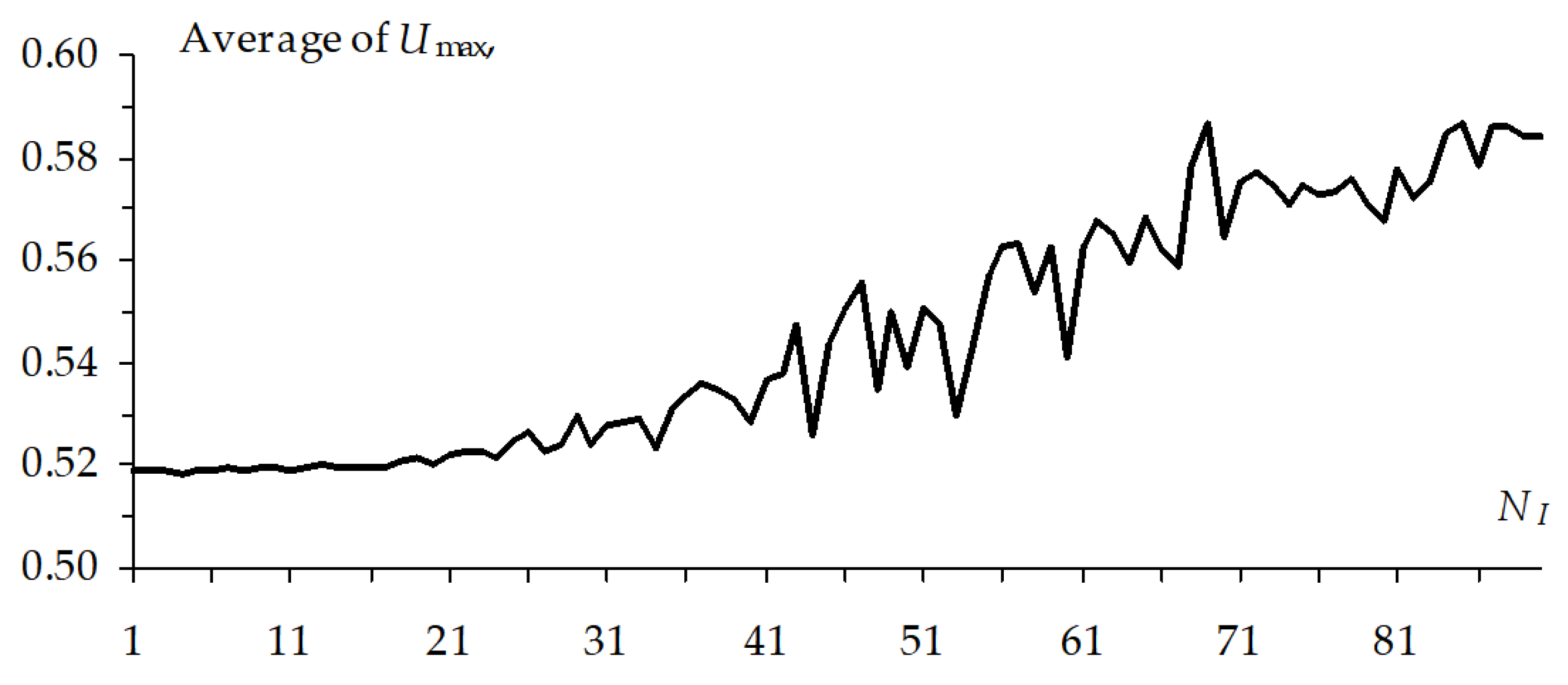
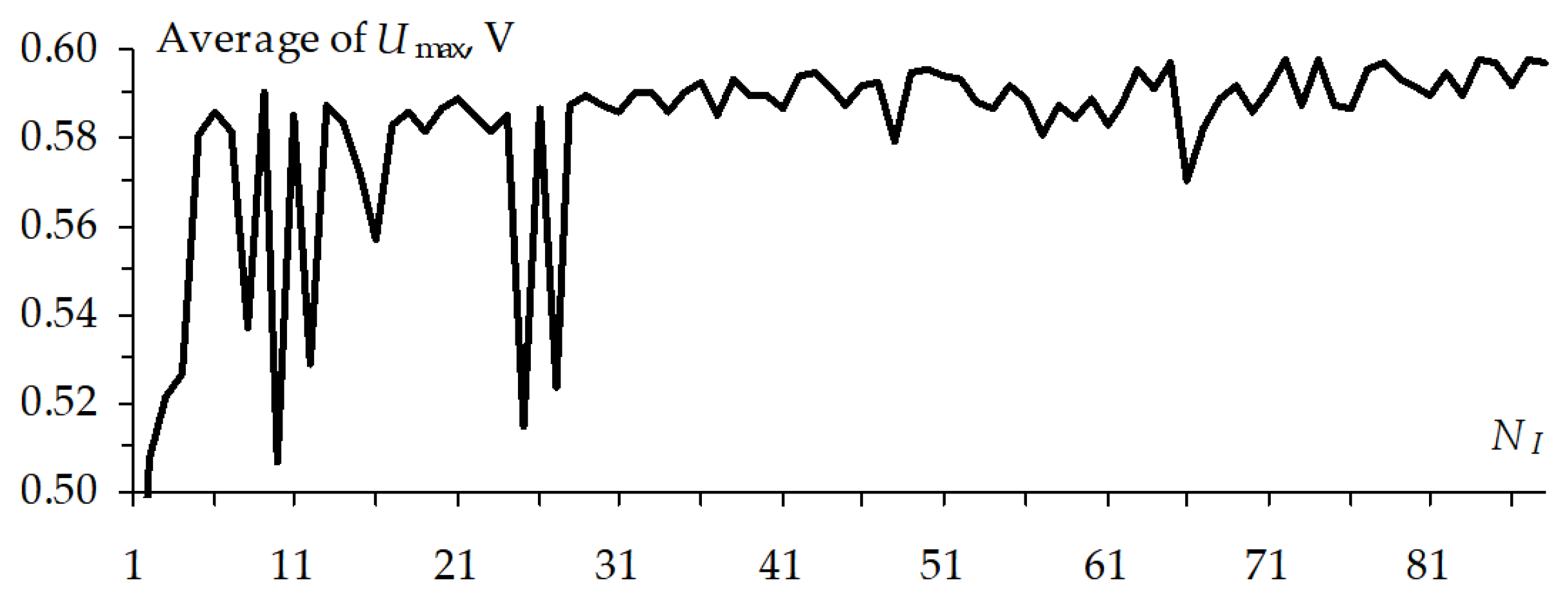
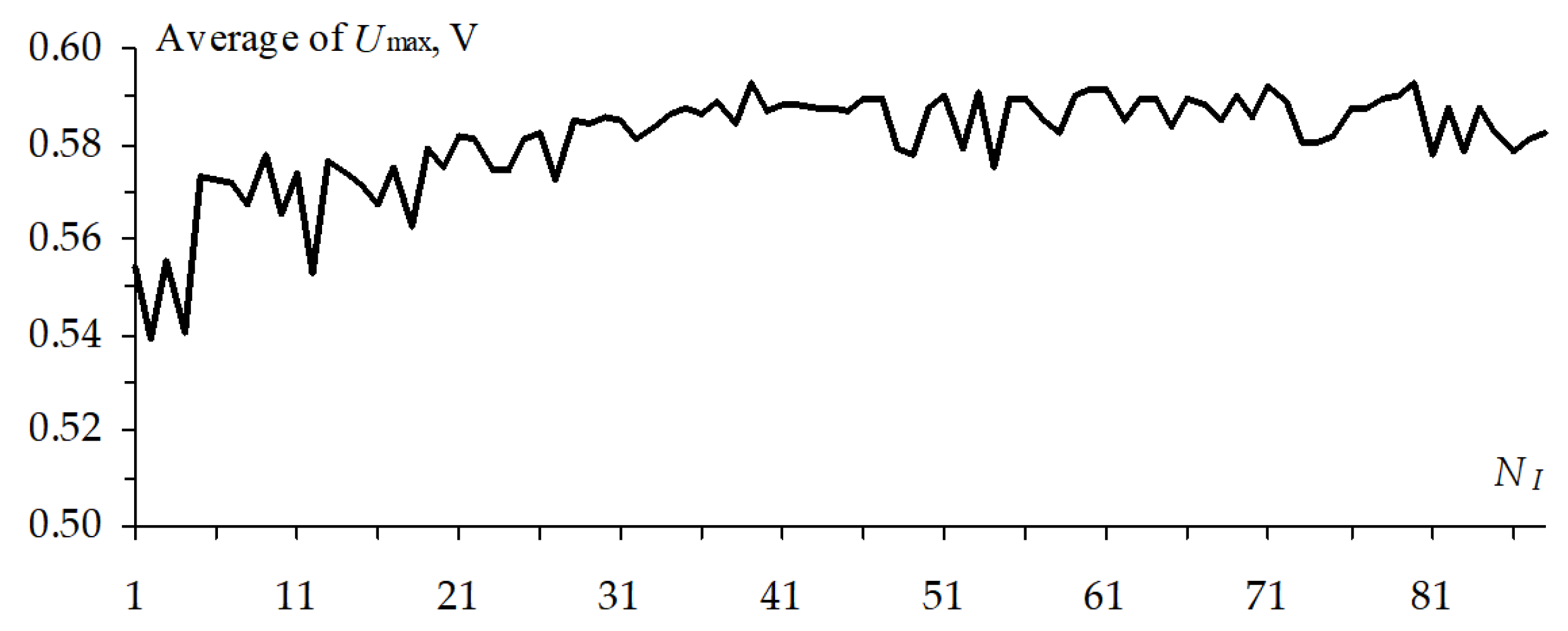
The
Umax arithmetic averages (of 10 runs) for IS = 3, 0.3, 0.03 ns in their dependence on the ES iteration number (
NI) are shown in
Figure 35,
Figure 36 and
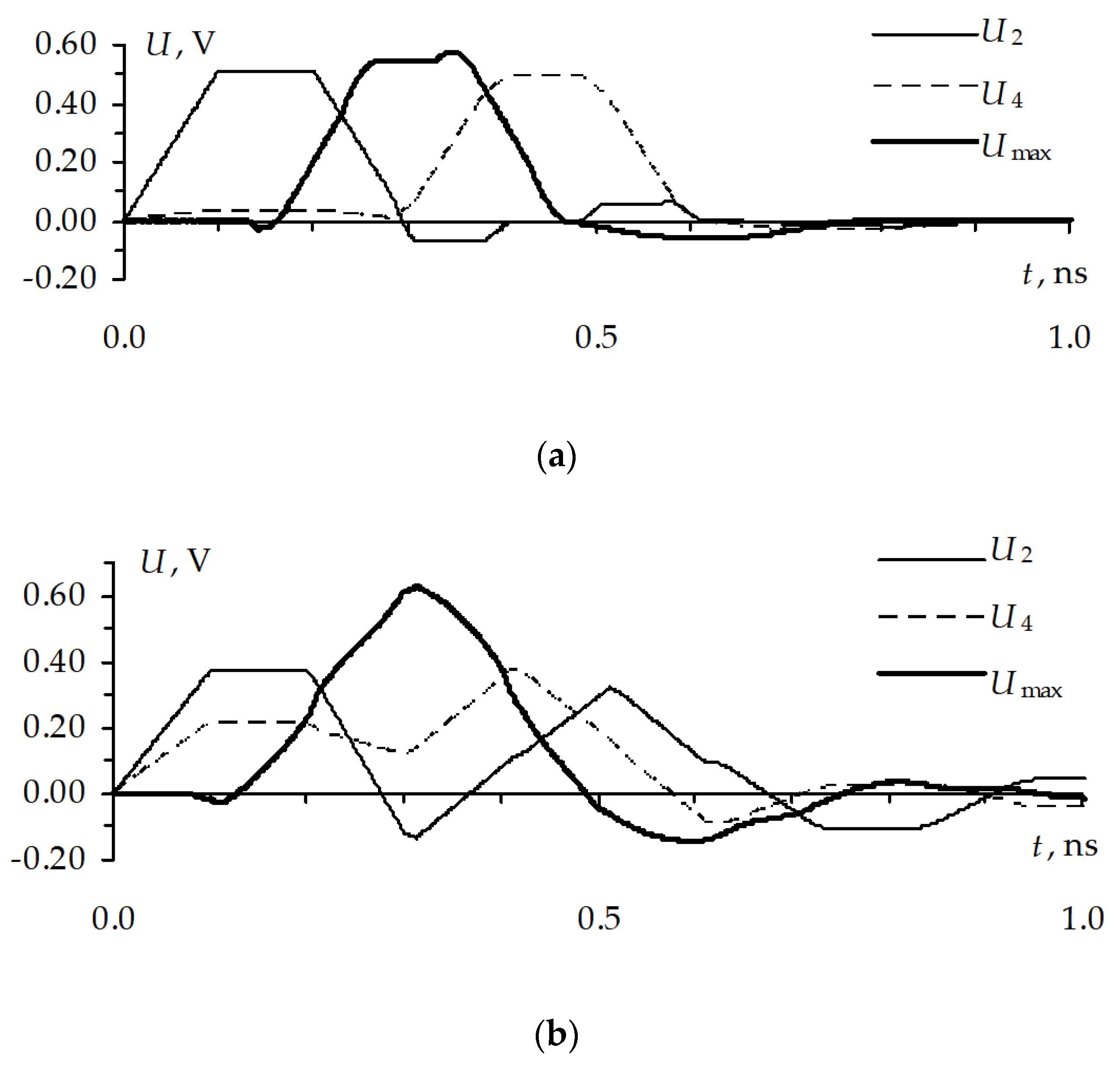
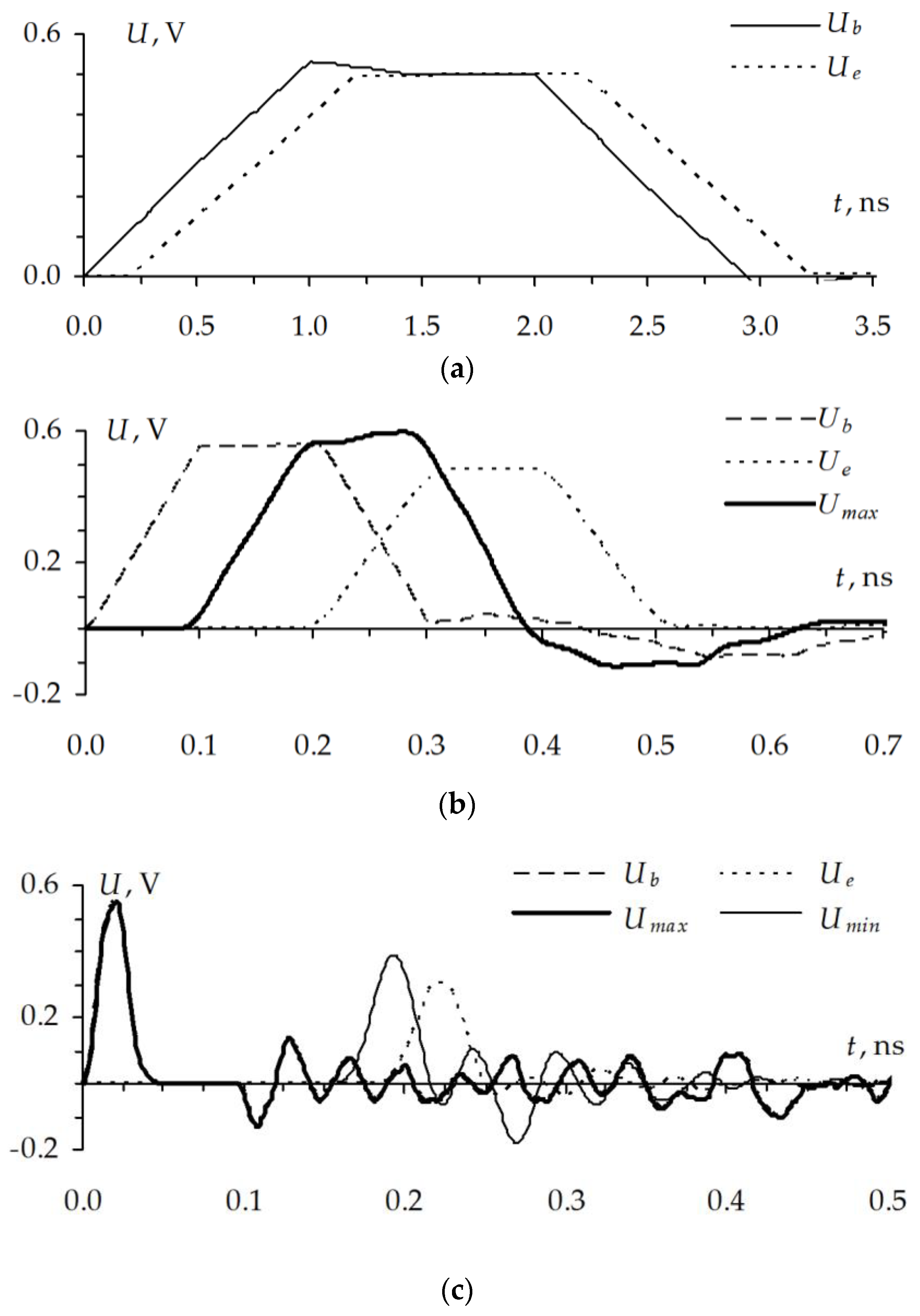
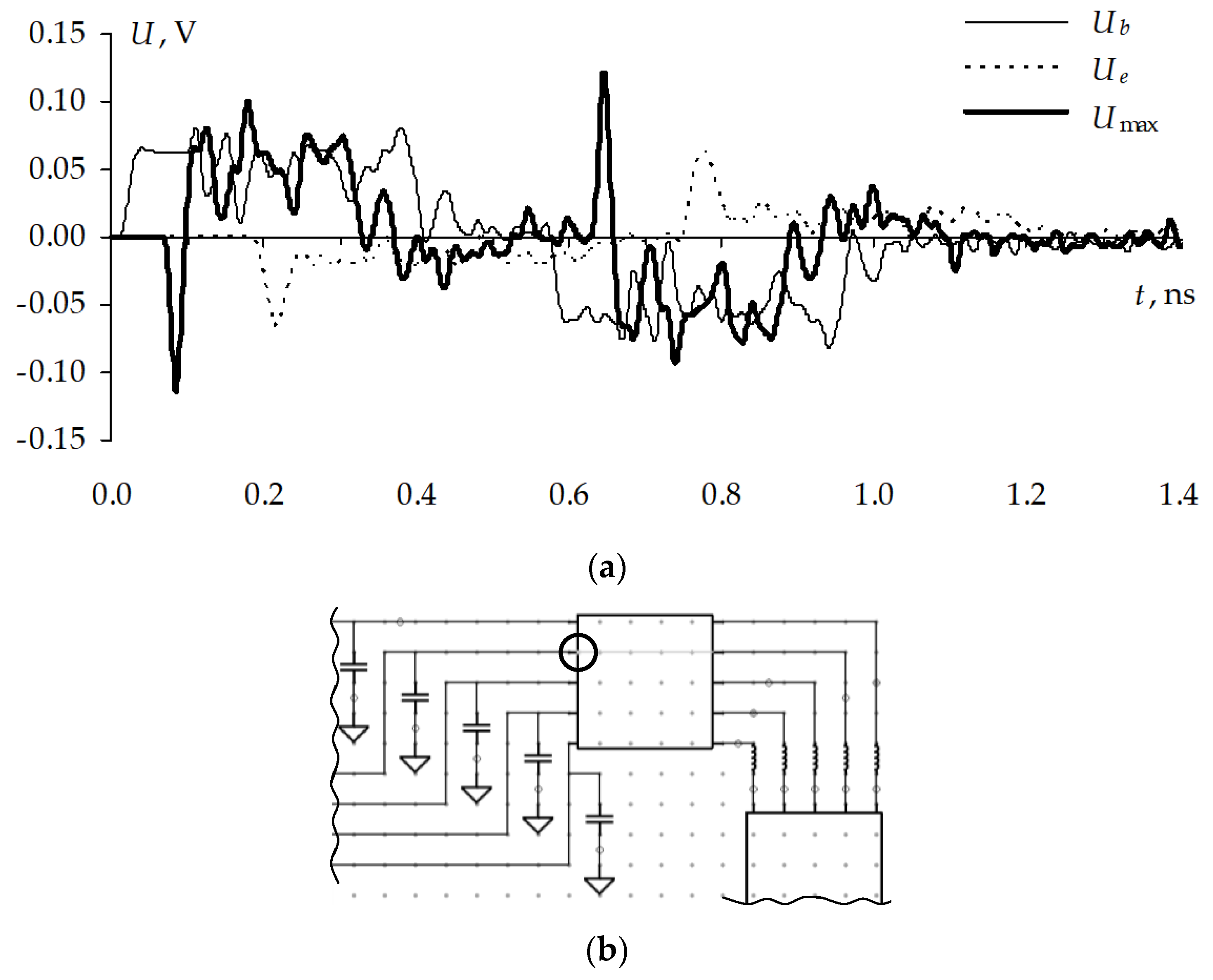
Figure 37, respectively. It is necessary to check the appearing of signal peaks along the whole conductor with the use of excitation parameters which have been obtained as a result of the optimization. The voltage waveforms along the active conductor are shown in
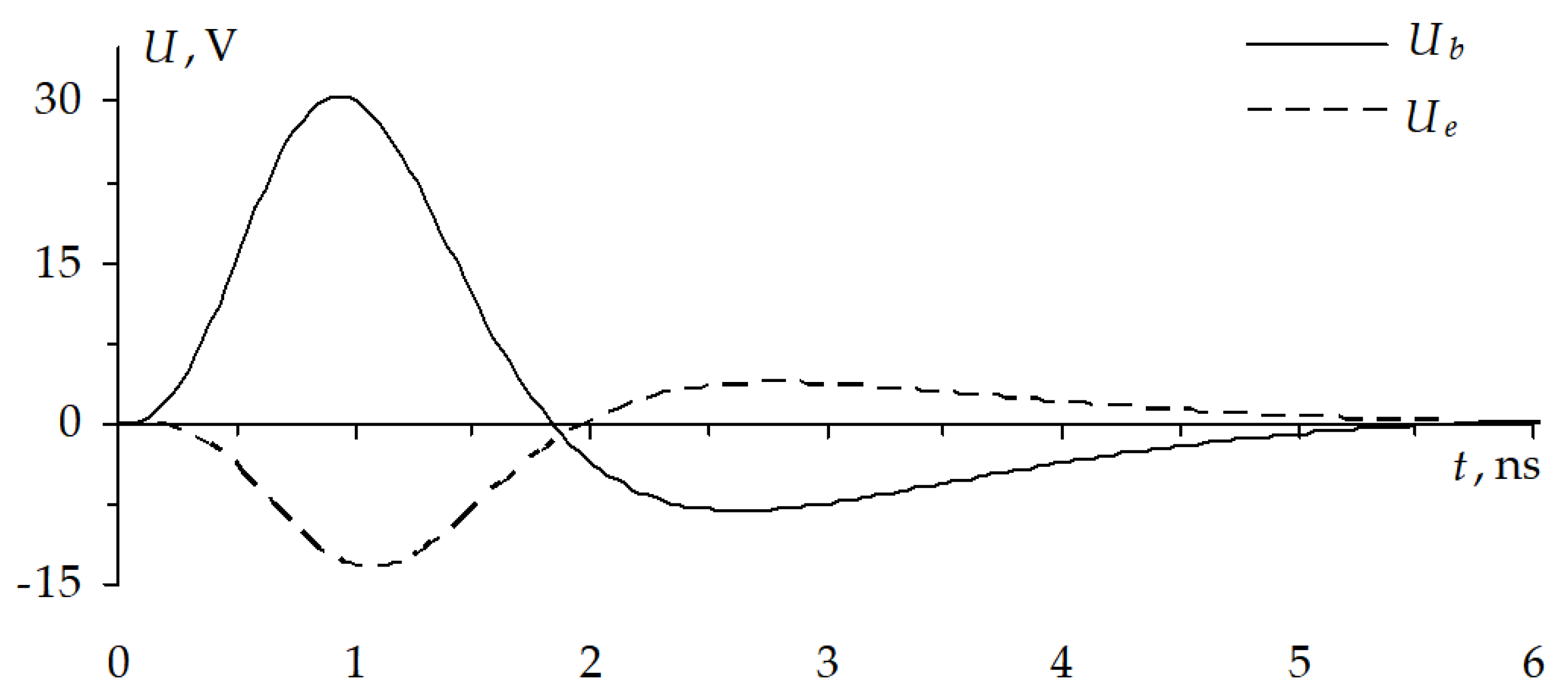
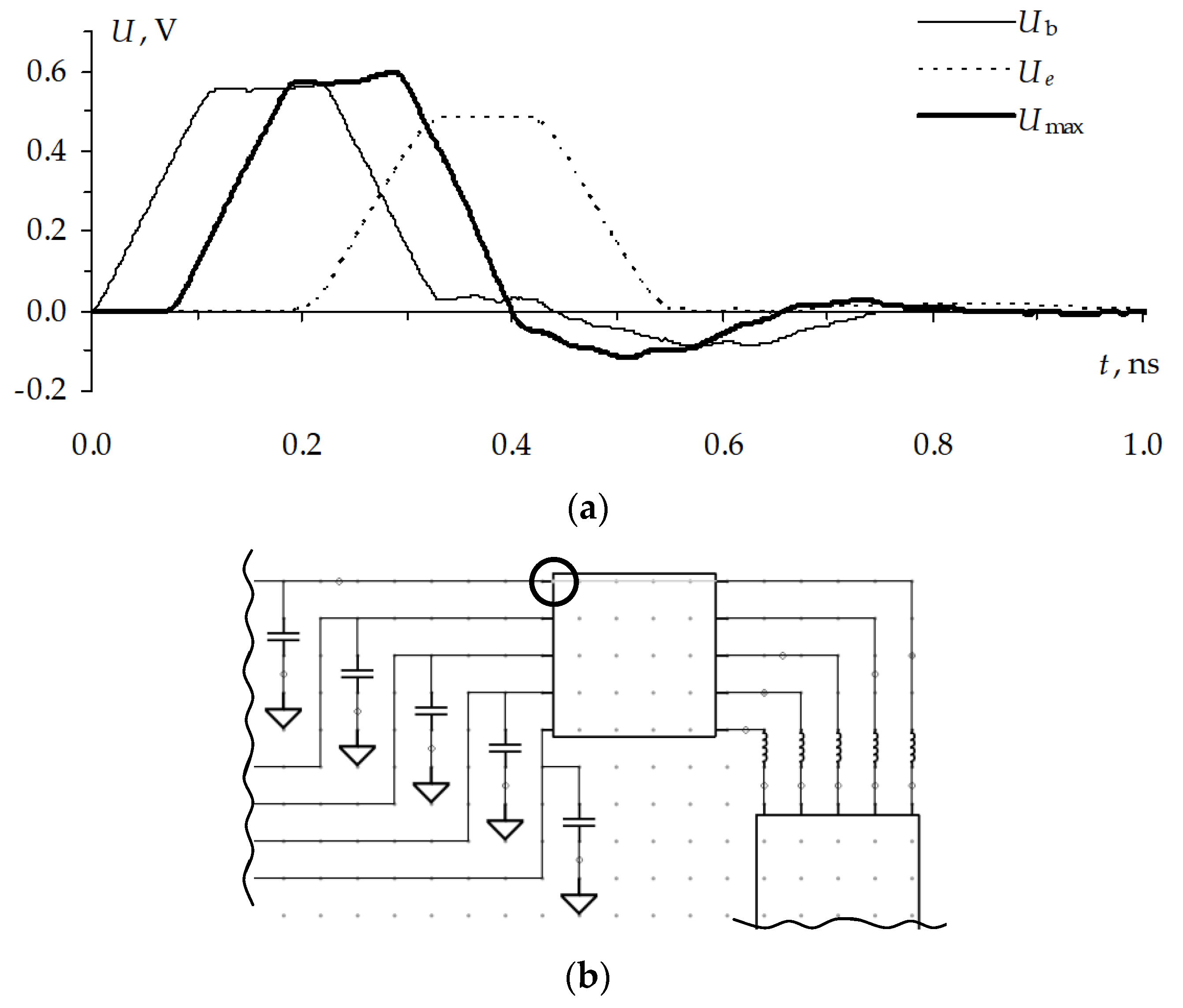
Figure 38a, where the waveforms are the following:
Ub, at the input;
Ue, at the end; and
Umax, with the highest peak voltage. The voltage maximum localization is shown in
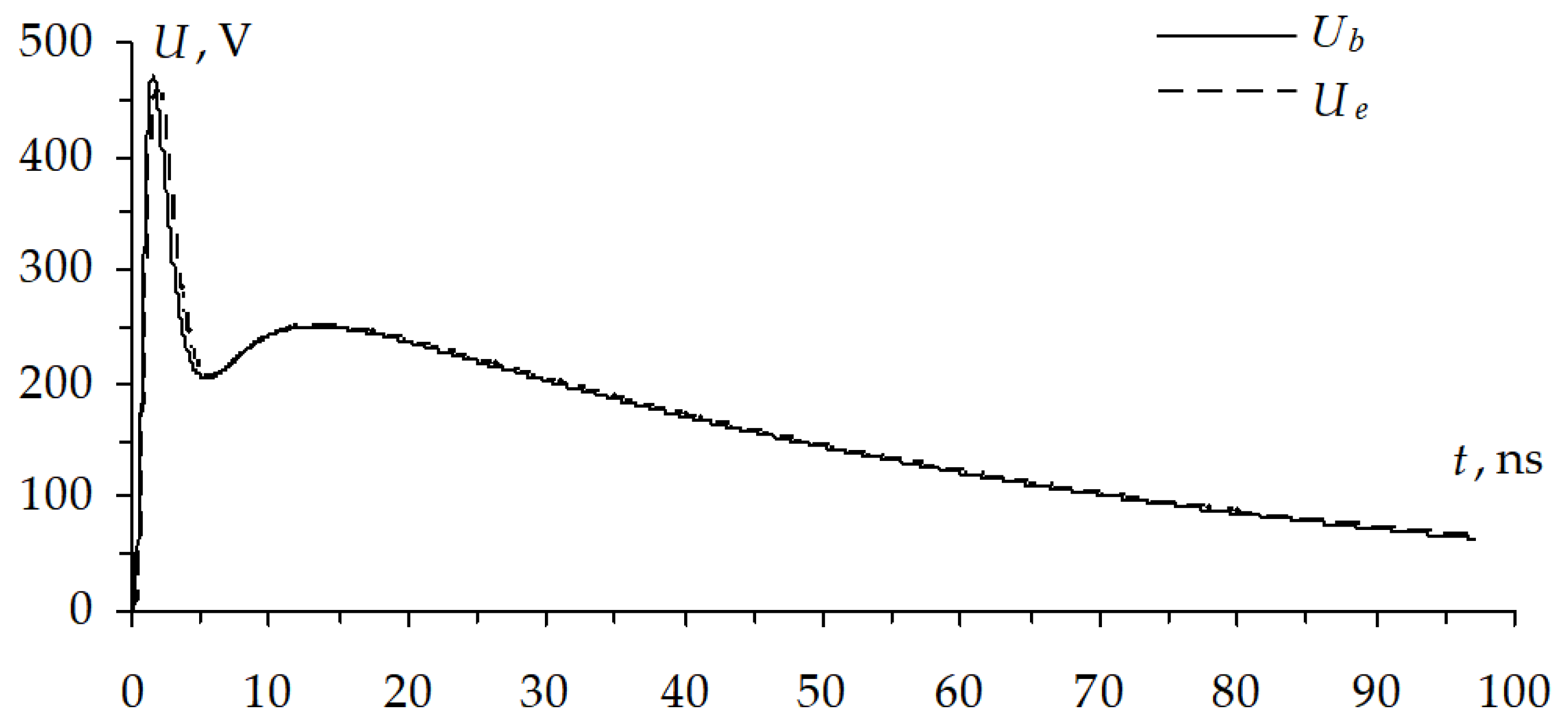
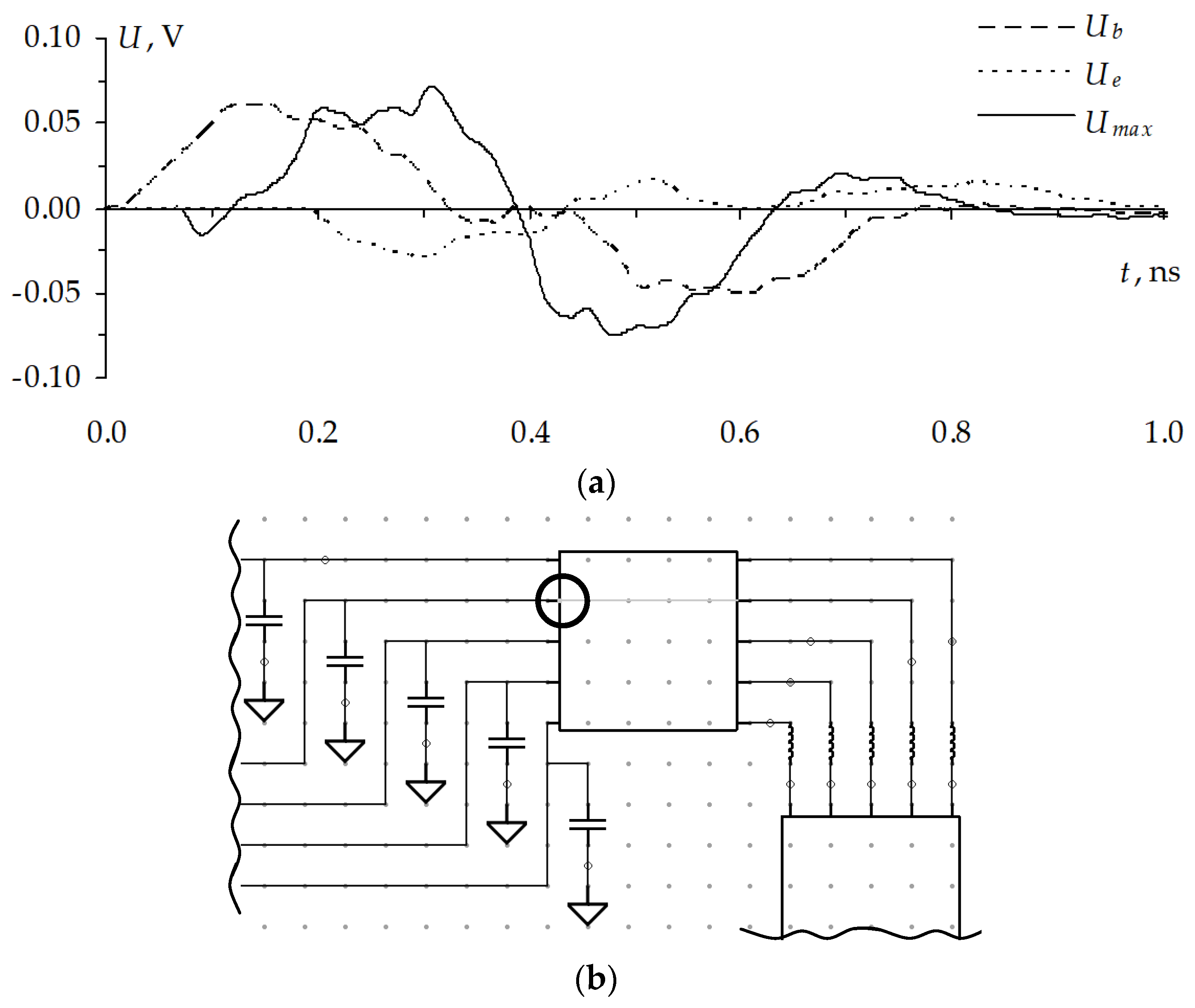
Figure 38b. The voltage waveforms calculated along the passive (nearest to active) conductor with the highest amplitude of the crosstalk and its maximum localization are presented in
Figure 39.
Consider the results of the optimization presented in
Table 7. They show that all
Umax values are very similar and differ in the fourth decimal place. The same situation is observed with the best solutions obtained after each ES cycle – the differences are near 5 ps. The highest
Umax is obtained in the first ES run for all ISs. The small differences in the obtained results hardly change the voltage waveforms calculated in the V34 node. As we can see from
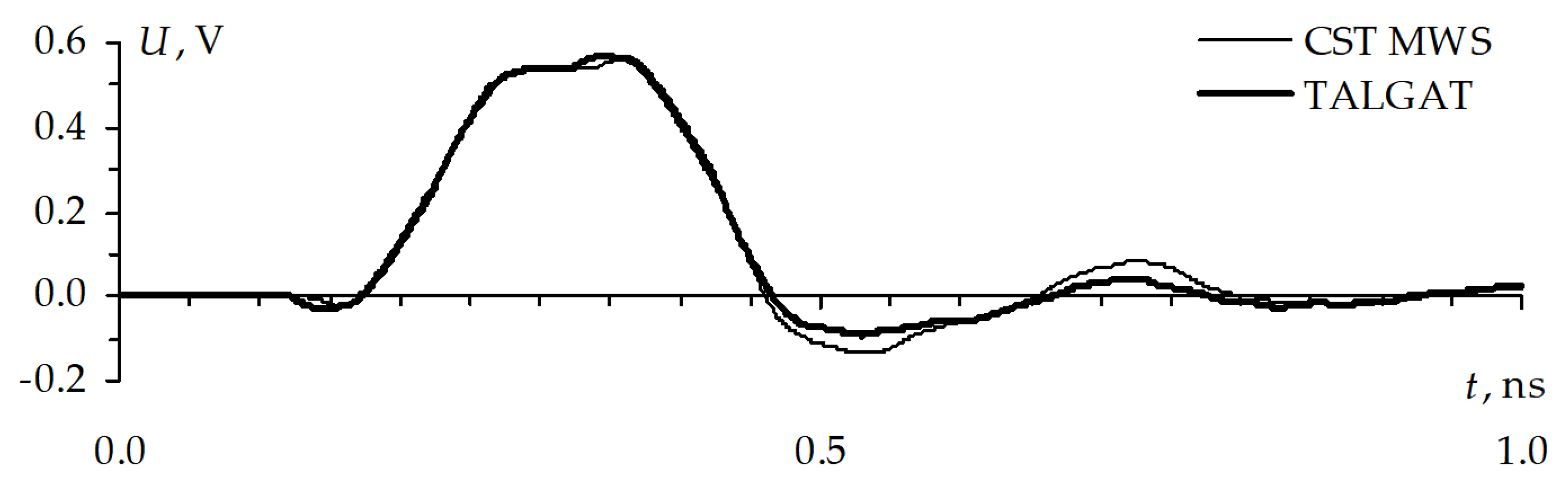
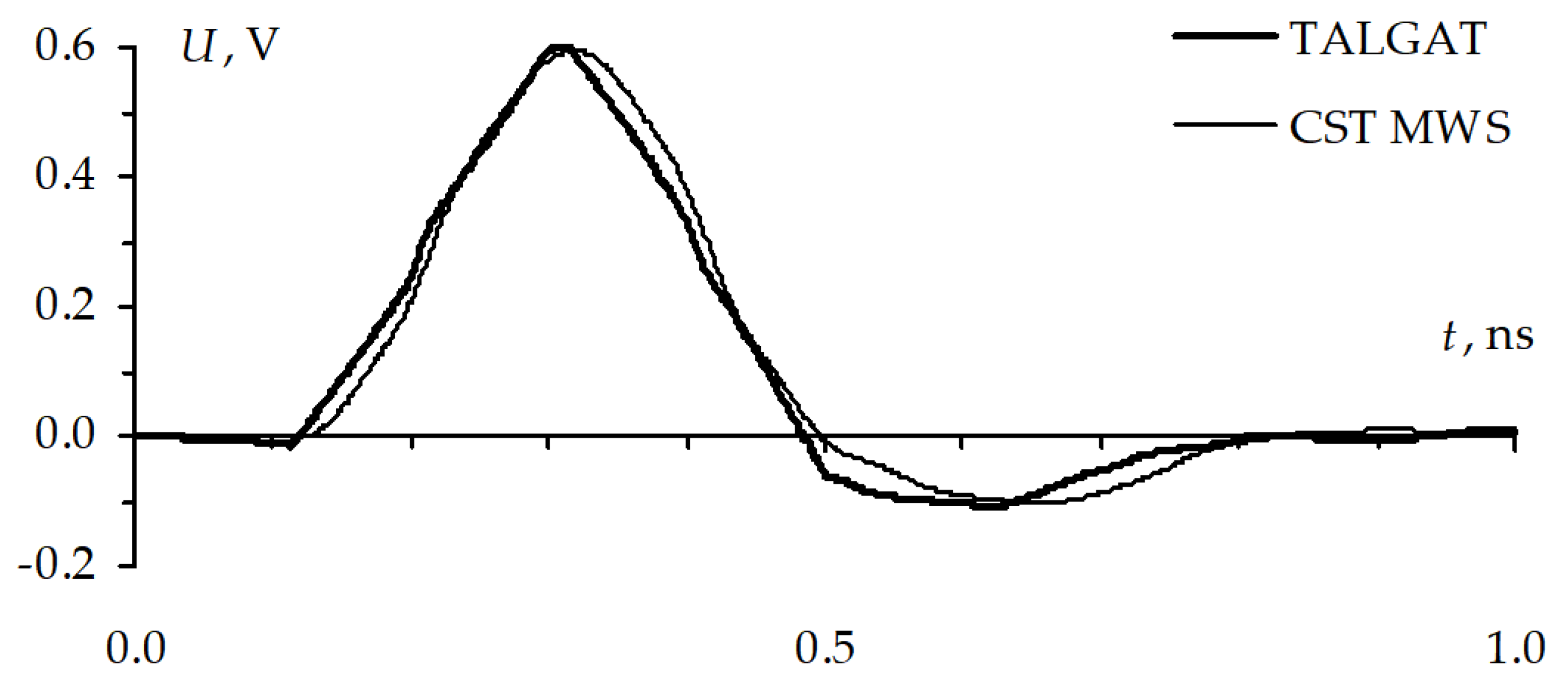
Figure 34, the signal waveforms coincide.
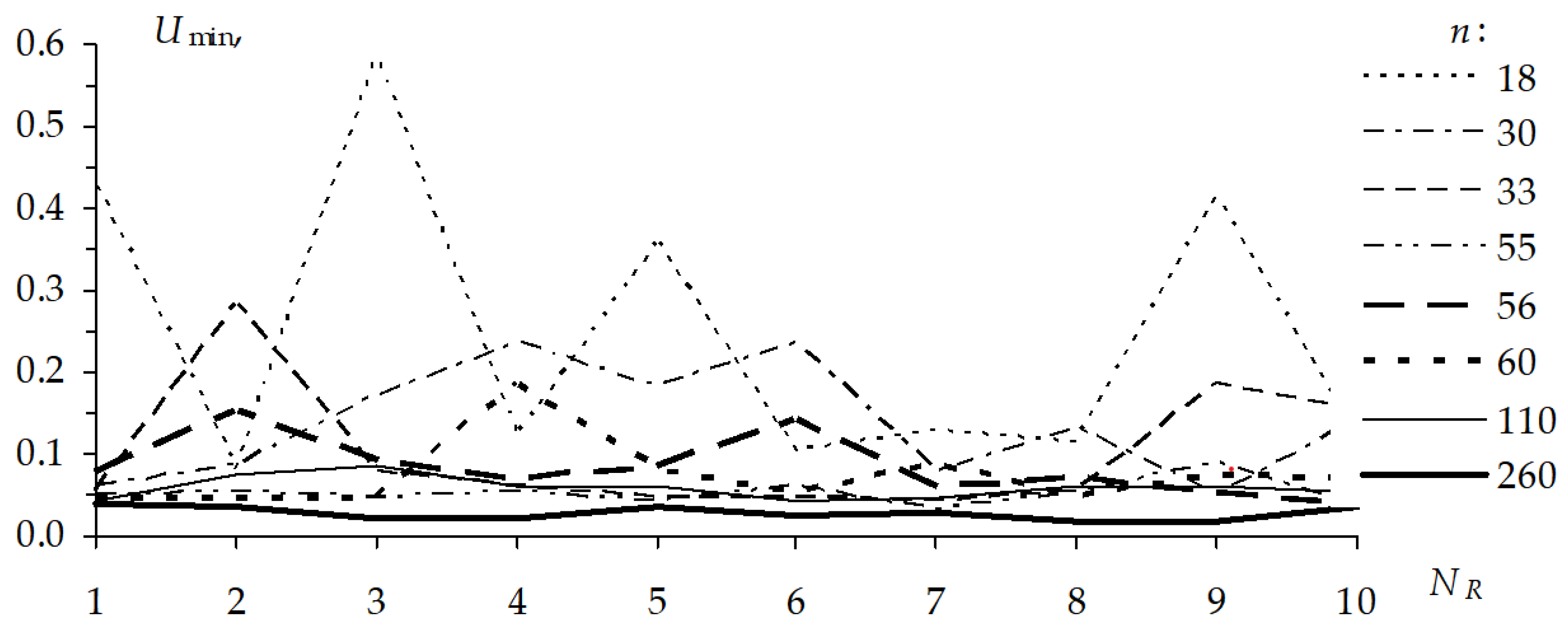
Consider the
Umax arithmetic average for each IS. The strongest change of
Umax is observed when IS = 300 ps, starting from 0.5 V (
Figure 36). However, after 30th calculation, it becomes almost the highest and other changes are within the bounds of 30 mV. Before the 30th calculation, the
Umax change has strong spikes, which are possibly caused by a strong mutation of an offspring. When IS = 3 ns (
Figure 35), the
Umax arithmetic average has a smooth rising character without strong spikes (in the range up to 30 mV) and starting at 0.52 V it reaches the maximum value in the 69th calculation, and when IS = 30 ps (
Figure 37), the
Umax changes the least of all and starting at 0.55 mV it reaches the maximum in the 39th calculation.
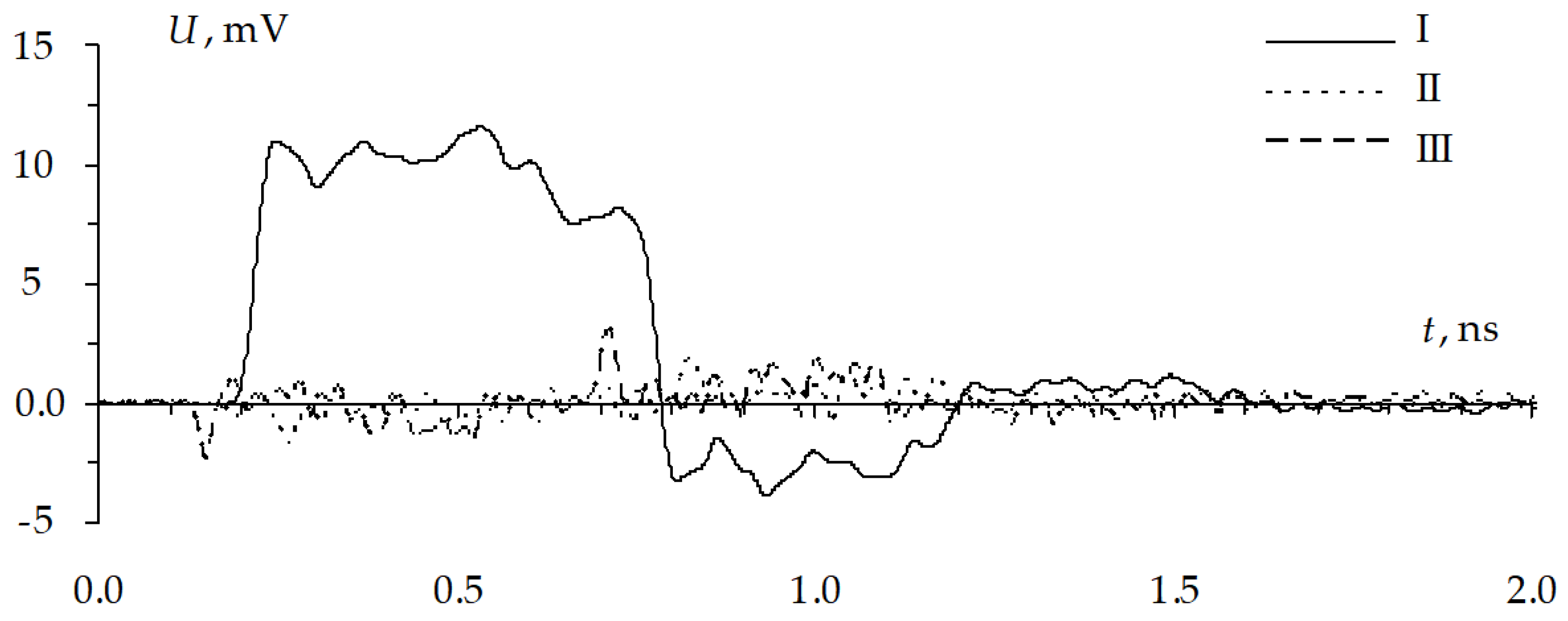
Consider the voltage waveforms with the localized maximums. The maximum is localized in segment 1 of the same MCTL section both in the active (
Figure 38) and passive (
Figure 39) conductors. The ultrashort pulse maximum in the active conductor is 598 mV, which is 20% higher than at the steady state level. The maximum in the passive conductor is 70 mV, which is 14% of the steady state level in the active conductor.
This investigation shows the importance of using ES for optimization for detecting and localizing signal extreme points under the excitation of the ultrashort pulse with various durations. The highest peak level of the active conductor (20% higher than at the steady state level) and the crosstalk of 14% of the steady state level are detected for 325 ps ultrashort pulse. It is also shown that if the IS changes towards the best solution, it does not influence the optimization result.