Abstract
Statistical analysis of the results of minisodar measurements of vertical profiles of wind velocity components in a 5–200 m layer of the atmosphere shows that this problem belongs to the class of robust nonparametric problems of mathematical statistics. In this work, a new consecutive nonparametric method of adaptive pendular truncation is suggested for outlier detection and selection in sodar data. The method is implemented in a censoring algorithm. The efficiency of the suggested algorithm is tested in numerical experiments. The algorithm has been used to calculate statistical characteristics of wind velocity components, including vertical profiles of the first four moments, the correlation coefficient, and the autocorrelation and structure functions of wind velocity components. The results obtained are compared with classical sample estimates.
1. Introduction
Sodars or acoustic radars are widely used all over the world to investigate the atmospheric boundary layer (ABL) [1,2,3,4,5]. The principle of their operation is based on sound scattering by small-scale atmospheric turbulent inhomogeneities. Possessing high spatiotemporal resolution and being capable of obtaining data in real time around the clock, they are unique instruments for ABL monitoring. Three-component Doppler monostatic sodars, based on effects of sound backscattering and Doppler frequency shift of the transmitted signal due to scatterer motion, identify the thermal structure of the atmosphere, and measure vertical profiles of wind velocity components. Depending on the working frequency, sodars are subdivided into conventional ones with working frequencies in the range 1–2 kHz, 50–1000 m sounding altitudes, and 20–30 m vertical resolution, and minisodars with working frequencies in the range 3–6 kHz, 5–200 m sounding altitudes, and 5–20 m vertical resolution. In recent decades, a trend toward the development and application of high-frequency compact minisodars equipped with phased antenna arrays has been observed.
Sodars allow one to obtain long time series of continuous observations of atmospheric parameters with high spatial resolution to several meters and high temporal resolution (statistically reliable profiles of the wind velocity and turbulence characteristics are obtained with averaging, as a rule, from 10 to 30 min) and to analyze their spatiotemporal dynamics.
However, processing of sodar wind velocity measurements in the ABL reveals some problems associated with the determination of the Doppler frequencies of echo signals, and hence, the wind velocity components [3,4] are caused by signal fluctuations and taking measurements in the presence of background noise and reflections from local objects [3,4]. The large volume of measurements, the presence of various outliers in the measured Doppler frequencies, and difficulties of selection of parametric models (due to nonparametricity of the problems being solved) exclude manual fitting of the results obtained to the well-known parametric models and require the application of robust nonparametric methods of statistics [6,7,8].
Experimenters have long been familiar with the problem of anomalous observations (outliers) in data samples. The bearing on outliers is twofold. On the one hand, outliers may significantly distort results of the investigation and the process of decision-making and hence must be removed using various robust procedures [7,8]. On the other hand, the outlier itself can represent the most valuable result of the investigation—a new physical property. In this case, outliers carry information, and it is necessary not only to detect, but also to select the outliers.
In this regard, the problem of outlier detection and selection in data processing has been a focus of attention of experimenters for a long time and it remains urgent from both a theoretical and a practical point of view. There are a number of reviews, for example in References [9,10,11] where an extensive bibliography of works on this subject is presented. Hereafter, an outlier is understood to be any observation whose statistical or geometric characteristics differ from the main group (class or cluster) of observations [7,8,9,10,11,12,13,14,15,16,17,18]. This definition is qualitative in character, and when solving particular problems, what statistical or geometric parameters determine the anomalous observation is usually indicated. The problems of outlier detection and selection for one-dimensional problems were initially considered as remote extreme observation in a sample with a normal distribution. In this case, a number of parametric criteria were proposed, including the Grubbs criteria [12] and their generalizations (the Tietjen–Moore, Rosner, and Ferguson criteria) [13,14,15]. Further research [16] has shown that these criteria are unstable when the distributions deviate from normal ones. This has caused a certain amount of skepticism about their application. Efforts toward the creation of a nonparametric criterion in the classical sense have not been successful. The typical technique used in this situation and widely used in practice is the application of robust truncation procedures for experimental data processing [19]. The full complexity of synthesis and application of the robust truncation procedures is due to the fact that there is no a priori information on the outlier fraction and location. In this case, the problem is reduced to semiparametric or semi-nonparametric classes of problems of robust statistics [6,8].
A shift of emphasis to problems of multidimensional statistics and random processes, for example, to problems of detection of outliers in correlation analysis and regression analysis and problems of detection of the change point of a random process, has revealed a number of difficulties and has resulted in the development of new research directions [9,10,11,17,18]. In this case, the problem of detection of outliers in the form of remote multidimensional observations (objects or patterns) reduces to problems of pattern recognition and the development of adaptive algorithms [9,17]. For example, the problem of detection of outliers changing the form (symmetry) of the distribution of the main group of observations should be mentioned. The most important direction of research here is associated with problems of correlation analysis and regression analysis. Among these problems, the simplest one is the problem of the estimation of the correlation coefficient. Classical estimators of the correlation coefficients and correlation matrices are very sensitive to the occurrence of specific outliers that can substantially change the sample correlation coefficient [18].
In the present work, based on a new approach to processing data of acoustic sounding in the ABL, the diurnal dynamics of the vertical profiles of the first four moments of wind velocity components (their mean value, variance, skewness, and kurtosis) are analyzed together with their correlation coefficient and structure functions. The variance is an important statistical characteristic of the wind velocity field. The skewness is a measure of the lack of distribution symmetry; it measures the relative size of the two tails of the wind velocity distribution function. It should be mentioned that, for normal distributions, it is equal to zero. The kurtosis is a measure of the combined sizes of the two tails of the distribution. It measures the amount of probability in the tails. These characteristics of the wind velocity field determine its dynamics and are used to construct mathematical models of the atmospheric boundary layer and to make weather forecasts. On the basis of the empirical influence-and-sensitivity function [7,8], an iterative nonparametric procedure is suggested that allows one to rank sample values of applicants for outliers. For formal substantiation of the procedure, the assumption of continuity and econd-order stationarity of the sensitivity function is required [7,8]. Thus, the new consecutive nonparametric method of adaptive pendular truncation (APT) for outlier detection and selection is used for data processing. The method is implemented in the algorithm of pendular truncation of sample values based on sorting of the empirical influence functions. On the basis of this algorithm, it is convenient to construct adaptive robust estimates based on operations of sample truncation without a preliminary analysis of distribution symmetries and tail behavior [7].
2. Procedure of Outlier Detection and Selection
2.1. Adaptive Pendular Truncation Algorithm
Let be a sample of size N of independent, identically-distributed random variables with unknown distribution F(x), where is Tukey’s model of outliers, is the reference aprioristic distribution, is the outlier distribution, is the outlier fraction, and is the number of outliers in the sample. We assume that , and are absolutely continuous unimodal distributions with densities , and , respectively.
The standard problem of detection and selection of outliers remote from the center of the distribution reduces to the problem of testing of hypotheses:
Let us consider an anomaly measure based on the functional
where is the known function, and introduce a sample , with variable size. According to the anomaly measure, we transform the sample observations to the form
Let us sort the variables , , and consider the consecutive procedure of detection of applicants for outliers. The outliers according to the anomaly measure T are represented by extreme ordinal statistics . The observation corresponding to is an applicant for outlier status; therefore, we remove it from the sample . As a result, we obtain the sample of size (n − 1). This procedure of detection of applicants for outlier status is repeated for . The sample observations thus removed are not outliers; they are only applicants for outliers. To determine which of them are outliers, an additional decision making procedure is required.
Let us introduce the statistic
where
Since and , it follows that and, hence, the statistic 0 < Ln ≤ 1 is a monotonically decreasing function of n.
Let us find average values of the statistics , , and :
where . Let us consider the first-order differences of :
and find the average value of the difference :
As follows from Equation (10), the first-order differences in the presence of k outliers are, on average, constant at the level , and in the absence of outliers (), they are, on average, constant at the level , where . At the point , the function jumps on average by .
Let us consider the second-order differences . They are on average equal to zero, and at the point , a delta-shaped spike of the function is observed.
The special features in the behavior of the statistics , , and indicated above allow us to construct a consecutive procedure of adaptive pendular truncation (APT) for outlier detection and selection based on the empirical influence and sensitivity functions [7,8] that generalizes the adaptive pendular truncation algorithm (APTA) [20].
2.2. Adaptive Pendular Truncation Algorithm
For the sample , , we perform the following procedures:
- Calculate ,
- Calculate ,
- Sort the variables , ,
- Calculate ,
- Calculate ,
- Find the first-order differences ,
- Find the second-order differences ,
- Remove the observation corresponding to from the sample,
- Execute the above cycle from item 1 to item 9 for .
We note that the APTA is nonparametric, that is, the result of its execution is independent of the form of the distribution and automatically finds on which side of the center the applicant for the outlier status is located.
Generalization of the Algorithm
As the anomaly measure and the transformation described by Equation (1), the functionals , , and can be used, where is a continuous function with bounded variation, is a parameter, and is an estimate of the parameter .
3. Simulation
To test the efficiency of the APT algorithm, we performed a number of computer-based numerical experiments.
3.1. Remote Outliers
Let us consider an example of remote outliers. Asymmetric outliers for distributions of the same type were generated with the location parameter set equal to seven. The sample size was N = 100. The outlier fraction was . Five symmetric (fourth-order generalized normal distribution, normal distribution, and Laplace distribution) and asymmetric distributions (Weibull distribution and exponential distribution) with different tails were chosen. The scaling parameters of all of the distributions were chosen so that their quantile level 0.99 coincided with quantile level 0.99 of the standard normal distribution.
Figure 1 and Figure 2 show the results of numerical simulation. Here, curves 1 are for the fourth-order generalized normal distribution, curves 2 are for the normal distribution, curves 3 are for the Weibull distribution, curves 4 are for the Laplace distribution, and curves 5 are for the exponential distribution.
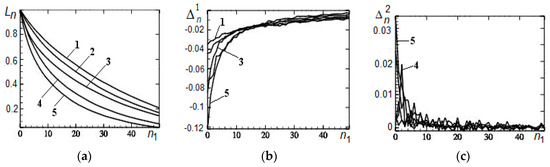
Figure 1.
Results of the application of the adaptive pendular truncation algorithm to distributions without outliers: (a) Dependence of the statistic on the number n1 of truncated observations, (b) dependence of the statistic on the number of truncated observations, and (c) dependence of the statistic on the number of truncated observations.
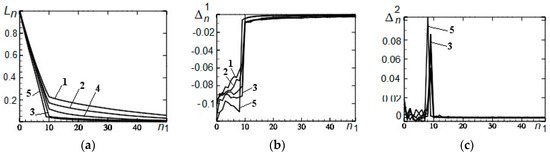
Figure 2.
Results of application of the adaptive pendular truncation algorithm to distributions with asymmetric outliers: (a) Dependence of the statistic on the number of truncated observations, (b) dependence of the statistic on the number of truncated observations, and (c) dependence of the statistic on the number of truncated observations.
Analysis of the results of the application of the algorithm to distributions without outliers (Figure 1) shows that the empirical influence function is continuous for all symmetric and asymmetric distributions (Figure 1a). Figure 1c demonstrates that for distributions with heavy tails (exponential (5) and Laplace (4)), delta-shaped spikes are observed for single observations. Here, it is appropriate to recall R. Hubert’s remark that small truncation always brings more good than harm [21].
Figure 2 shows results of application of the algorithm to distributions with asymmetric outliers. From Figure 2a, it can be seen that the empirical influence function has a point of discontinuity of the first kind and is a continuous function to the left of it with the distribution F and to the right of it with the distribution for all symmetric and asymmetric distribution models. Figure 2b confirms conclusions (10) and the presence of the change point of the process . In Figure 2c, delta-shaped spikes of characterizing the outlier fraction are observed.
3.2. Asymmetry
Let be a sample from an independent identically-distributed random variable that obeys an unknown distribution of the form
where is the aprioristic unimodal distribution symmetric about , is the distribution of outliers, , and is the outlier fraction; accordingly, . Consider the anomaly measure having the form
Figure 3 shows changes of the form of the standard normal distribution density with remote and internal outliers.
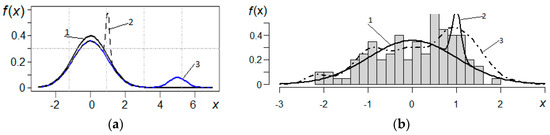
Figure 3.
Nonparametric estimates of the distribution density (a) in the presence of internal and remote outliers and (b) in the presence of internal outliers.
Consider transformation (1.1) of sample values to the form
where is the Rosenblatt–Parzen nonparametric kernel density estimator [22]:
is the bandwidth parameter, and is the kernel function. The standard normal distribution density (curve 1), the standard normal distribution density with internal outliers (curve 2), the Rosenblatt–Parzen density estimator (curve 3), and the histogram (N = 100 and ) are shown in Figure 3.
In the adaptive pendular truncation algorithm presented in Section 2.2, we now replace item 3 by the new item.
3. Sort variables for .
Figure 4 shows the simulation results.
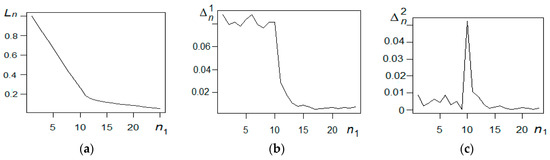
Figure 4.
Results of application of the adaptive pendular algorithm to truncation of internal outliers: (a) Dependence of the statistic Ln on the number of truncated observations, (b) dependence of the statistic on the number of truncated observations, and (c) dependence of the statistic on the number of truncated observations.
The delta-shaped spike in Figure 4c testifies to the presence of 10 outliers.
3.3. Correlation
Let be a sample from the two-dimensional distribution , where is the reference distribution with correlation coefficient , is the distribution of outliers with the correlation coefficient , and is the outlier fraction. Since the classical estimate of the sample correlation coefficient is non-robust, different robust estimates of the correlation coefficient are suggested in robust statistics [18]. Here, we consider the following transformation of the sample:
where , , , and . As a model of the outliers, we consider Tukey’s model of a bivariate normal distribution
where , , is the bivariate normal distribution with average values and and variances and , correlation coefficient , and outlier fraction .
Let us apply the consecutive APT procedure. In all our experiments, the reference sample was generated from the distribution with 10% fraction of the outliers (ε = 0.1). Samples with distributions and (ε = 0.1 and N = 20 = 18 + 2 outliers) were also generated. We found that the sample correlation coefficient without outliers was RS = 0.93, and the sample correlation coefficient with outliers was RS = 0.42. The independence criterion based on the statistic at the significance level for the critical value demonstrates that with outliers, , and the zero hypothesis is accepted; without outliers, , and the zero hypothesis is rejected.
The outliers seriously worsen the situation. Without outliers, RS = 0.91, and the criterion unambiguously rejects the zero hypothesis, but in the presence of two outliers, RS decreased by more than twice, down to RS = 0.42, and the criterion unambiguously accepts the zero hypothesis. Figure 5 shows the results of application of the APT algorithm for N = 18 + 2 outliers depending on the number of truncated observations n1. From Figure 5c, it can be seen that the algorithm detects and selects 2 outliers.
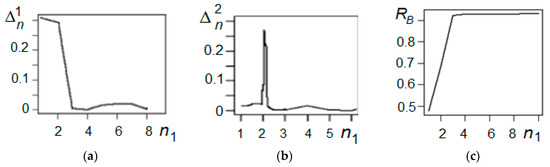
Figure 5.
Results of application of the algorithm of adaptive pendular truncation of outliers to correlation analysis: (a) Dependence of the statistic on the number of truncated observations, (b) dependence of the statistic on the number of truncated observations, and (c) dependence of the statistic of the sample correlation coefficient RS on the number of truncated observations.
4. Statistical Analysis of Vertical Profiles of Wind Velocity Components from Results of Minisodar Measurements using the Pendular Truncation Algorithm
The pendular truncation algorithm was used to process results of measurements of vertical profiles of wind velocity components with an AV4000 Doppler minisodar. The working frequency of the sodar was 4900 Hz, its pulse duration was 60 ms, and its pulse repetition period was 4 s. Radiation was successively transmitted in three directions—vertical and at angles of 14° to the vertical in two mutually orthogonal planes. The radial components of the wind velocity were calculated from the Doppler shifts of the echo signal frequencies in the three receiving minisodar channels. They were then recalculated to the orthogonal wind velocity components, and one vertical profile of the wind velocity vector was retrieved for each sounding cycle.
Data of measurements of wind velocity components in 40 strobes of vertical extent 5 m each at altitudes of 5–200 m were processed. To analyze the spatiotemporal variations of the first four moments of wind velocity components in the ABL, results of morning measurements were processed. Series from N = 150 profiles (sample size) were processed, which provided a 10 min data averaging period.
Statistical analysis of the results of minisodar measurements of vertical profiles of wind velocity components at altitudes of 5–200 m showed that this problem belongs to the class of robust nonparametric problems of mathematical statistics [6,19]. Using the APT algorithm, outliers were excluded from the samples, and the truncated estimates of the first four moments of the wind velocity components were calculated. Figure 6, Figure 7 and Figure 8 illustrate the vertical profiles of the first four moments of the wind velocity components, including their average values Vi, in m/s (a), variances σi2, in m2/s2 (b), skewnesses Ki sc (c), and kurtoses Ki kurt (d), where i = x, y, z.
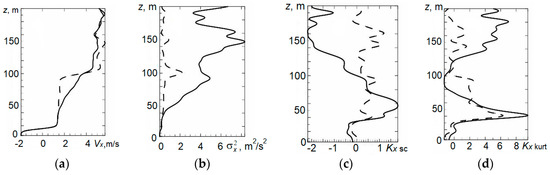
Figure 6.
Vertical profiles of four moments of the x-component of the wind velocity retrieved from minisodar measurements in the morning (from 07:00 till 07:10, local time) using the standard minisodar data processing algorithm [23] (solid curves) and the adaptive pendular truncation algorithm (dashed curves): (a) Average Vx values, in m/s; (b) variances, in m2/s2; (c) skewnesses; and (d) kurtoses.
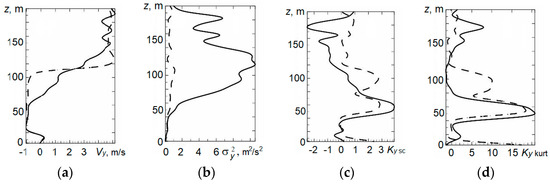
Figure 7.
Vertical profiles of four moments of the y-component of the wind velocity retrieved from minisodar measurements in the morning (from 07:00 till 07:10, local time) using the standard minisodar data processing algorithm [23] (solid curves) and the adaptive pendular truncation algorithm (dashed curves): (a) Average values, in m/s; (b) variances, in m2/s2; (c) skewnesses; and (d) kurtoses.
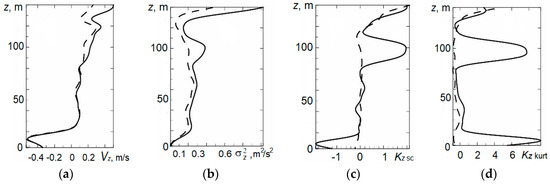
Figure 8.
Vertical profiles of four moments of the z-component of the wind velocity retrieved from minisodar measurements in the morning (from 07:00 till 07:10, local time) using the standard minisodar data processing algorithm [23] (solid curves) and the adaptive pendular truncation algorithm (dashed curves): (a) Average values, in m/s, (b) variances, in m2/s2, (c) skewnesses, and (d) kurtoses.
From Figure 6, Figure 7 and Figure 8, it can be seen that the application of the APT algorithm changes the average values of the wind velocity components and decreases the variances, which demonstrates its efficiency. The forms of the distributions of sample values of the wind velocity components differ from the symmetric and normal ones even for the vertical wind velocity component, although at small altitudes, the distribution of the vertical wind velocity component is close to normal. At higher altitudes, significant air-flows are observed.
Using the APT algorithm, censoring of the samples was performed to obtain estimates of the autocorrelation and structure functions. As an example, Figure 9 show the dependences of the autocorrelation function ρ(τ) of the x-component of the wind velocity on the lag τ retrieved from minisodar measurements at the indicated altitudes in the morning, and Figure 10 show the corresponding dependences of the structure functions St(τ) in m2/s2. The red curves here show the results of calculations for the full sample, and the black curves show the results of calculations for the truncated sample using the APTA.
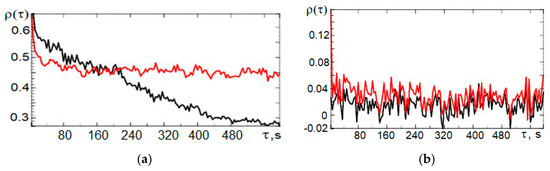
Figure 9.
Dependences of the autocorrelation functions retrieved using the APTA from the data of minisodar measurements of the x-component of the wind velocity at altitudes of 45 m (a) and 180 m (b) from 08:00 till 08:10, local time, on the lag τ.
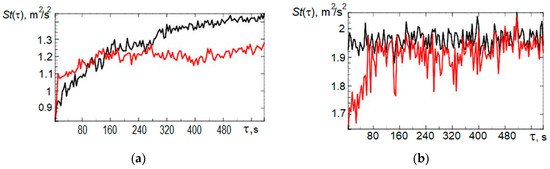
Figure 10.
Dependences of the structure functions of the x-component of the wind velocity retrieved using the APTA from the data of minisodar measurements at altitudes of 35 m (a) and 175 m (b) from 08:00 till 08:10, local time, on the lag τ.
As expected, the correlation at the altitude z = 45 m (Figure 9a) decreases with increasing lag, and for the censored sample, it decreases monotonically and faster, whereas for the full sample, the process becomes nonstationary already at lags exceeding 1–2 min. The process proceeds even faster at an altitude of 180 m (Figure 9b), where Vx for individual sounding cycles (individual vertical profiles) becomes uncorrelated. Here, the influence of atmospheric turbulence and noise becomes pronounced.
The structure function at an altitude of 35 m (Figure 10a) behaves in the classical manner, and even better for the censored sample. Here, the inflection point of the dependence is observed at 160–280 s with its subsequent saturation. At an altitude of 175 m (Figure 10b), the structure function acquires large values, and for the censored samples, it remains on average unchanged with the lag. It is natural to suggest that the results of measurements with increasing sounding altitude are more strongly influenced by noise that has an uncorrelated character [3,4] and lead to the occurrence of false outliers.
5. Conclusions
In the present work, the nonparametric consecutive pendular algorithm of censoring intended for the detection and selection of outliers of various origins in the observation samples has been studied. Results of numerical simulation with different outliers demonstrated the high efficiency of the APT algorithm. The application of the APT algorithm to processing of measurements of vertical profiles of wind velocity components obtained with a Doppler minisodar revealed significant asymmetric outliers of wind velocity components that lead to biased estimates of their moments and structure functions. Therefore, the application of the algorithm of sodar data processing is expedient, especially at low signal-to-noise ratios. In addition, it should be noted that the application of symmetric censoring at the level [19] did not remove asymmetric outliers and bias of the estimates, but decreased the efficiency of the estimates.
Author Contributions
Conceptualization, N.K., V.S., L.S., and O.C.; Methodology, N.K., V.S., L.S., and O.C.; Validation, N.K., V.S., L.S., and O.C.; Formal Analysis, N.K., V.S., L.S., and O.C.; Investigation, N.K., V.S., L.S., and O.C.; Data Curation, N.K., V.S., L.S., and O.C.; Writing—Original Draft Preparation, N.K., V.S., L.S., and O.C.; Writing—Review & Editing, N.K., V.S., L.S., and O.C.; Visualization, N.K., V.S., L.S., and O.C.; Supervision, N.K., V.S., L.S., and O.C.; Project Administration, N.K., V.S., L.S., and O.C.; Funding Acquisition, N.K., V.S., L.S., and O.C.
Funding
The results were obtained with financial support from the Ministry of Science and Higher Education of the Russian Federation (Project No. 5.3279.2017/4.6) and from the Siberian Branch of the Russian Academy of Sciences (Project of Basic Research No. IX.138.2.5).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Singal, S.P. Acoustic Remote-Sensing Applications; Springer-Verlag: Berlin, Germany, 1997; p. 585. [Google Scholar]
- Kallistratova, M.A.; Kon, A.I. Radioacoustic Sounding of the Atmosphere; Nauka: Moscow, Russia, 1985; p. 197. (In Russian) [Google Scholar]
- Krasnenko, N.P. Acoustic Sounding of the Atmosphere; Nauka: Novosibirsk, Russia, 1986; p. 168. (In Russian) [Google Scholar]
- Krasnenko, N.P. Acoustic Sounding of the Atmospheric Boundary Layer; Vodolei: Tomsk, Russia, 2001; p. 279. (In Russian) [Google Scholar]
- Bradley, S. Atmospheric Acoustic Remote Sensing: Principles and Applications; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2007; p. 296. [Google Scholar]
- Simakhin, V.A.; Cherepanov, O.S.; Shamanaeva, L.G. Spatiotemporal dynamics of the wind velocity from minisodar measurement data. Russ. Phys. J. 2015, 58, 176–181. [Google Scholar] [CrossRef]
- Hampel, F.; Ronchetti, E.; Rausseu, P.; Shtael, V. Robustness in Statistics. Approach Based on Influence Functions; MIR: Moscow, Russia, 1989; p. 512, (Russian translation). [Google Scholar]
- Shulenin, V.P. Methods of Mathematical Statistics; Publishing House of Scientific and Technology Literature: Tomsk, Russia, 2016; p. 260. (In Russian) [Google Scholar]
- Muthukrishnan, R.; Poonkuzhali, G. A comprehensive survey on outlier detection methods. Am. -Eurasian J. Sci. Res. 2017, 12, 161–171. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 1–83. [Google Scholar] [CrossRef]
- Hodge, V.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Grubbs, F.E. Sample criteria for testing outlying observations. Ann. Math. Stat. 1950, 21, 27–58. [Google Scholar] [CrossRef]
- Tietjen, G.L.; Moore, R.H. Some Grubbs-type statistics for the detection of several outliers. Technometrics 1972, 14, 583–597. [Google Scholar] [CrossRef]
- Rosner, B. On the detection of many outliers. Technometrics 1975, 17, 221–227. [Google Scholar] [CrossRef]
- Ferguson, T.S. On the rejection of outliers. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20–30 July 1961; Volume 1, pp. 253–287. [Google Scholar]
- Orlov, A.I. Instability of parametric methods of rejection of sharply allocated observations. Zavod. Lab. 1992, 7, 40–42. (In Russian) [Google Scholar]
- Rocke, D.M.; Woodruff, D.L. Identification of outliers in multivariate data. J. Am. Stat. Assoc. 2012, 91, 1047–1061. [Google Scholar] [CrossRef]
- Shevlyakov, G.L.; Vilchevski, N.O. Robustness in Data Analysis: Criteria and Methods; VSP: Utrecht, The Netherlands, 2002; p. 315. [Google Scholar]
- Fedorov, V.A. Measurements with the “Volna-3” sodar of the parameters of radial components of wind velocity vector. Atmos. Ocean. Opt. 2003, 16, 151–155. [Google Scholar]
- Simakhin, V.A.; Cherepanov, O.S. Detection and selection of signal outliers. In Proceedings of the XIX International Symposium “Atmospheric and Oceanic Optics. Atmospheric Physics”, Barnaul, Russia, 1–3 July 2013; pp. С221–С224. (In Russian). [Google Scholar]
- Huber, P.J. Robust Statistics; Willey: New York, NY, USA, 1981; p. 308. [Google Scholar]
- Simakhin, V.A. Robust Nonparametric Estimates; Lambert Academic Publishing: Saarbrücken, Germany, 2011; p. 292. [Google Scholar]
- Krasnenko, N.P.; Tarasenkov, M.V.; Shamanaeva, L.G. Spatiotemporal dynamics of the wind velocity from data of sodar measurements. Russ. Phys. J. 2014, 57, 1539–1546. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).