Symmetry Analysis, Explicit Solutions, and Conservation Laws of a Sixth-Order Nonlinear Ramani Equation

Abstract

In this work, we study the completely integrable sixth-order nonlinear Ramani equation. By applying the Lie symmetry analysis technique, the Lie point symmetries and the optimal system of one-dimensional sub-algebras of the equation are derived. The optimal system is further used to derive the symmetry reductions and exact solutions. In conjunction with the Riccati Bernoulli sub-ODE (RBSO), we construct the travelling wave solutions of the equation by solving the ordinary differential equations (ODEs) obtained from the symmetry reduction. We show that the equation is nonlinearly self-adjoint and construct the conservation laws (CL) associated with the Lie symmetries by invoking the conservation theorem due to Ibragimov. Some figures are shown to show the physical interpretations of the acquired results.

1. Introduction

It is well-known that the majority of real-world physical phenomena are modeled by mathematical equations, especially partial differential equations (PDEs). These phenomena include the problems from fluid mechanics, elasticity, plasma physics and optical fibers, general relativity, gas dynamics, thermodynamics, and so on [1]. In order to understand the understanding of such physical phenomena, it is vital to look for the exact solutions of the PDEs. In the last few decades, many scientists and mathematicians have extensively studied the dynamic behaviors of several PDEs [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24] using different concepts. Symmetry analyses have been used to study the PDEs [2,3,4,5,6]. It has been found that some new solutions to PDEs can be obtained from the old ones through symmetry transformations [2]. On the other hand, conservation laws (CLs) are very important in the study of PDEs. CLs are important in determining the integrability of PDEs [2].

As an important integrable nonlinear model, the integrable sixth-order nonlinear Ramani equation [10,11,12,13,14,15,16]

$$-5{\psi }_{tt}+45{{\psi }_x}^2{\psi }_{xx}+15{\psi }_{xx}{\psi }_{xxx}-5\left(3{\psi }_x{\psi }_{xt}+3{\psi }_t{\psi }_{xx}+{\psi }_{xxxt}\right)+15{\psi }_x{\psi }_{xxxx}+{\psi }_{xxxxxx}=0$$

(1)

has attracted much attention in soliton theory in recent years. The equation was first proposed in reference [10]. The equation was obtained as a five-reduction of the bilinear Kadomtsev–Petviashvili (BKP) equation [11]. It has been shown that the Ramani equation possesses bilinear Bäcklund transformation and CL [12]. In reference [13], the truncated singular expansion scheme was applied to construct the Bäcklund self-transformation and Lax pairs for Equation (1). In reference [14], the Lax pairs and Bäcklund transformation were applied to study the equation. An extension of Equation (1), called the coupled Ramani equation, was extensively studied in references [15,16,17,18].

To our knowledge, a Lie symmetry analysis of Equation (1) has not been completed. The main aim of this work is to derive the Lie point symmetries [2,4], the optimal system of one-dimensional sub-algebras, invariant solutions, and the CL of the equation by invoking the conservation theorem due to Ibragimov [7,8]. The invariant solutions are derived by solving the ordinary differential equations (ODEs) obtained from the symmetry reduction process using the Riccati Bernoulli sub-ODE (RBSO) [19].

1.1. Lie Symmetry Analysis of Equation (1)

In this part, we construct the vector fields of Equation (1). The associated vector field of Equation (1) is given by

$$X=\xi (x,t,\psi ){\partial }_x+\eta (x,t,\psi ){\partial }_t+\varphi (x,t,\psi ){\partial }_{\psi },$$

(2)

where the coefficient functions $\xi (x,t,\psi ),\eta (x,t,\psi ),\varphi (x,t,\psi )$ are the infinitesimals. The one-parameter Lie group is represented by

$$\begin{array}{c}\hfill \overline{x}=x+ϵ\xi (x,t,\psi )+O\left({ϵ}^2\right),\\ \hfill \overline{t}=t+ϵ\eta (x,t,\psi )+O\left({ϵ}^2\right),\\ \hfill \overline{\psi }=\psi +ϵ\varphi (x,t,\psi )+O\left({ϵ}^2\right),\end{array}$$

where $ϵ$ represents a group parameter. If the vector field in Equation (2) generates a point symmetry of Equation (1), then X should satisfy the invariance condition given by

$${\left.P_r^{6}X\left(\mathsf{\Delta }\right)\right|}_{\mathsf{\Delta }=0}=0,$$

(3)

where $P_r^6$ is the sixth-order prolongation of $\mathsf{\Gamma }$ [2], and

$$\mathsf{\Delta }=-5{\psi }_{tt}+45{{\psi }_x}^2{\psi }_{xx}+15{\psi }_{xx}{\psi }_{xxx}-5\left(3{\psi }_x{\psi }_{xt}+3{\psi }_t{\psi }_{xx}+{\psi }_{xxxt}\right)+15{\psi }_x{\psi }_{xxxx}+{\psi }_{xxxxxx}=0.$$

(4)

Putting Equation (4) into Equation (3) together with the sixth-order prolongation, we obtain a set of determining equations of linear PDEs. From solving the system of linear PDEs, we obtain the infinitesimals $\xi$, $\varphi$, and $\eta$, given by

$$\begin{array}{c}\hfill \xi =C_1+x{C}_2,\\ \hfill \eta =3t{C}_2+C_4,\\ \hfill \varphi =-\psi C_2+C_3,\end{array}$$

where $C_1$, $C_2,$ $C_3$ and $C_4$ are constants. The symmetries of Equation (1) are spanned by the vector fields given by

$$X_1=\frac{\partial }{\partial x},$$

(5)

$$X_2=\frac{\partial }{\partial \psi },$$

(6)

$$X_3=\frac{\partial }{\partial t},$$

(7)

$$X_4=3t\frac{\partial }{\partial t}-\psi \frac{\partial }{\partial \psi }+x\frac{\partial }{\partial x}.$$

(8)

1.2. Optimal System of Algebras

In this part, we derive the optimal system of sub-algebras [4] of the vector fields in Equations (5)–(8). To do this, we begin by noting that each $X_i(i=1,2,3,4)$ yields an adjoint representation $Ad\left(exp\left(ϵX_i\right)\right)X_j$, defined by [4]

$$Ad\left(exp\left(ϵX_i\right)\right)X_j=X_j-ϵ[X_i,X_j]+\frac{1}{2}{ϵ}^2[X_i,[X_i,X_j]]-\dots ,$$

where $[X_i,X_j]$ represents the commutator

$$X_i{X}_j-X_j{X}_i.$$

There is a need to figure out the invariants of the adjoint, because they pose restrictions on the element

$$X=\sum _{i=1}^4{c}_i{X}_i.$$

A real valued function $\eta :\mathfrak{g}⟶\mathbb{R}$ given by $\eta \left(X\right)=\varphi (c_1,\dots ,c_4)$ for $\varphi$ is invariant $\forall X\ne 0,$ $X\in \mathfrak{g},$

$$\eta \left(Ad\left(exp\left(ϵX_i\right)\right)X_1\right)=\eta \left(X\right),i=1,\dots ,4.$$

The adjoint representation group is spanned by the Lie algebra ${\mathfrak{g}}^A$, which is spanned by the following expression

$${\mathsf{\Delta }}_i=c_{ij}^k{e}^j\frac{\partial }{\partial e^k},i=1,\dots ,4,$$

where $c_{ij}^k$ are constants obtained from Table 1. Thus, one can obtain

$${\mathsf{\Delta }}_1\eta \left(X\right)=c_4\frac{\partial \eta \left(X\right)}{\partial c_1}=0,$$

(9)

$${\mathsf{\Delta }}_2\eta \left(X\right)=c_4\frac{\partial \eta \left(X\right)}{\partial c_2}=0,$$

(10)

$${\mathsf{\Delta }}_3\eta \left(X\right)=3c_4\frac{\partial \eta \left(X\right)}{\partial c_3}=0,$$

(11)

$${\mathsf{\Delta }}_4\eta \left(X\right)=c_1\frac{\partial \eta \left(X\right)}{\partial c_1}-c_2\frac{\partial \eta \left(X\right)}{\partial c_2}+3c_3\frac{\partial \eta \left(X\right)}{\partial c_3}=0.$$

(12)

Table 1. Commutator of vector fields in Equations (5)–(8).

Cumm	${\mathit{X}}_{\mathbf{1}}$	${\mathit{X}}_{\mathbf{2}}$	${\mathit{X}}_3$	${\mathit{X}}_{\mathbf{4}}$
$X_1$	0	0	0	$X_1$
$X_2$	0	0	0	−$X_2$
$X_3$	0	0	0	3 $X_3$
$X_4$	$-X_1$	$X_2$	$-3X_3$	0

In addition, we can have

$$X=\sum _{i=1}^4{c}_i{X}_i=Ad\left(exp\left(\alpha X_i\right)\right)oAd\left(exp\left(\beta X_i\right)\right)X,i=1,\dots ,4.$$

From Equations (9)–(12) and Table 1 and Table 2, we derive the following optimal system of Lie algebras:

$$[X_1,\alpha X_3+X_1,X_3,X_4].$$

(13)

Table 2. Adjoint representation of the vector fields in Equations (5)–(8).

Adj	${\mathit{X}}_{\mathbf{1}}$	${\mathit{X}}_{\mathbf{2}}$	${\mathit{X}}_{\mathbf{3}}$	${\mathit{X}}_{\mathbf{4}}$
$X_1$	$X_1$	$X_2$	$X_3$	$-ϵX_1+X_4$
$X_2$	$X_2$	$X_2$	$X_3$	$ϵX_2+X_4$
$X_3$	$X_1$	$X_2$	$X_3$	$-3ϵX_3+X_4$
$X_4$	$X_1{e}^{ϵ}$	$X_2{e}^{-ϵ}$	$X_3{e}^{3ϵ}$	$X_4$

1.3. Similarity Reductions and Exact Solutions

In this part, we use the derived optimal system of Lie algebras in Equation (13) to investigate the solutions of Equation (1). To achieve this, one needs to solve the characteristic equations denoted by

$$\begin{array}{c}\hfill \frac{dx}{\xi (x,t,\psi )}=\frac{dt}{\eta (x,t,\psi )}=\frac{d\psi }{\varphi (x,t,\psi )}.\end{array}$$

1.3.1. Symmetry Reduction with the Vector Field $X_1$

For the reduction by the vector field $X_1=\frac{\partial }{\partial x}$, we acquire the similarity variables $\psi (x,t)=\mathcal{F}\left(t\right)$ with $\mathcal{F}\left(t\right)$ satisfying the ODE:

$${\mathcal{F}}^{″}=0.$$

(14)

The solution of Equation (1) after solving Equation (14) is given by

$$\psi (x,t)=c_{1}t+c_2.$$

1.3.2. Symmetry Reduction with the Vector Field $X_2$

For the reduction by the vector field $\alpha X_3+X_1=\alpha \frac{\partial }{\partial t}+\frac{\partial }{\partial x}$, we acquire the similarity variables $\psi (x,t)=\mathcal{F}\left(\zeta \right),$ where $\zeta =t-\alpha x.$ The function $\mathcal{F}\left(\zeta \right)$ satisfies the following ODE:

$$5{\mathcal{F}}^{″}\left(1+6{\alpha }^2{\mathcal{F}}^{\prime }-9{\alpha }^4{\mathcal{F}}^{\prime 2}+3{\alpha }^5{\mathcal{F}}^{‴}\right)+5{\alpha }^3\left(-1+3{\alpha }^2{\mathcal{F}}^{\prime }\right){\mathcal{F}}^{″″}-{\alpha }^6{\mathcal{F}}^{‴‴}=0.$$

(15)

1.3.3. Symmetry Reduction with the Vector Field $X_3$

For the reduction by the vector field $X_3=\frac{\partial }{\partial t}$ , we get the similarity variables $\psi (x,t)=\mathcal{F}\left(x\right),$ where $\mathcal{F}\left(x\right)$ satisfies the following ODE:

$$-45{\mathcal{F}}^{\prime 2}{\mathcal{F}}^{\prime \prime }-15{\mathcal{F}}^{\prime \prime }{\mathcal{F}}^{‴}-15{\mathcal{F}}^{\prime }{\mathcal{F}}^{‴\prime }-{\mathcal{F}}^{‴‴}=0.$$

1.3.4. Symmetry Reduction with the Vector Field $X_4$

For the reduction by the vector field $X_4=3t\frac{\partial }{\partial t}-\psi \frac{\partial }{\partial \psi }+x\frac{\partial }{\partial x}$, we get the similarity variables $\psi (x,t)=\frac{\mathcal{F}\left(\zeta \right)}{x},$ where $\zeta =\frac{t}{x^3}.$ $\mathcal{F}\left(\zeta \right)$ thus satisfies the following ODE:

$$\begin{array}{c}\hfill -720\mathcal{F}+540{\mathcal{F}}^2-90{\mathcal{F}}^3-600{\mathcal{F}}^{\prime }-59760\zeta {\mathcal{F}}^{\prime }+90\mathcal{F}{\mathcal{F}}^{\prime }+18360\zeta \mathcal{F}{\mathcal{F}}^{\prime }-\\ \hfill 1350\zeta {\mathcal{F}}^2{\mathcal{F}}^{\prime }+450\zeta {\mathcal{F}}^{\prime 2}+67500{\zeta }^2{\mathcal{F}}^{\prime 2}-5670{\zeta }^2\mathcal{F}{\mathcal{F}}^{\prime 2}-7290{\zeta }^3{\mathcal{F}}^{\prime 3}+\\ \hfill 5{\mathcal{F}}^{″}-1920\zeta {\mathcal{F}}^{″}-272520{\zeta }^2{\mathcal{F}}^{″}+45\zeta \mathcal{F}{\mathcal{F}}^{″}+30240{\zeta }^2\mathcal{F}{\mathcal{F}}^{″}-\\ \hfill 405{\zeta }^2{\mathcal{F}}^2{\mathcal{F}}^{″}+270{\zeta }^2{\mathcal{F}}^{\prime }{\mathcal{F}}^{″}+127980{\zeta }^3{\mathcal{F}}^{\prime }{\mathcal{F}}^{″}-2430{\zeta }^3\mathcal{F}{\mathcal{F}}^{\prime }{\mathcal{F}}^{″}-\\ \hfill 3645{\zeta }^4{\mathcal{F}}^{\prime 2}{\mathcal{F}}^{″}+18225{\zeta }^4{\mathcal{F}}^{″2}-1080{\zeta }^2{\mathcal{F}}^{‴}-298080{\zeta }^3{\mathcal{F}}^{‴}+\\ \hfill 12150{\zeta }^3\mathcal{F}{\mathcal{F}}^{‴}+41310{\zeta }^4{\mathcal{F}}^{\prime }{\mathcal{F}}^{‴}+3645{\zeta }^5{\mathcal{F}}^{″}{\mathcal{F}}^{‴}-135{\zeta }^3{\mathcal{F}}^{″″}-\\ \hfill 112590{\zeta }^4{\mathcal{F}}^{″″}+1215{\zeta }^4\mathcal{F}{\mathcal{F}}^{″″}+3645{\zeta }^5{\mathcal{F}}^{\prime }{\mathcal{F}}^{″″}-16038{\zeta }^5{\mathcal{F}}^{\left(5\right)}-\\ \hfill 729{\zeta }^6{\mathcal{F}}^{\left(6\right)}=0.\end{array}$$

1.3.5. Invariant Solutions of Equation (15)

Equation (15) is a sixth-order nonlinear ODE. We apply the RBSO technique [19] to derive its solutions. In what follows, we provide the description of the RBSO method.

Consider the PDE given by

$$\begin{array}{c}\hfill P(\psi ,{\psi }_t,{\psi }_x,{\psi }_{tt},{\psi }_{xx},{\psi }_{xt},\dots )=0,\end{array}$$

(16)

where $\psi =\psi (x,t)$.

Step 1: 

By introducing the transformation

$$\psi (x,t)=\mathcal{F}\left(\zeta \right),\zeta =k(x\pm \alpha t),$$

Equation (16) is transformed to the following ODE

$$\begin{array}{c}\hfill P(\mathcal{F},{\mathcal{F}}^{\prime },{\mathcal{F}}^{″},\dots )=0,\end{array}$$

(17)

with ${\mathcal{F}}^{\prime }\left(\zeta \right)=\frac{du}{d\zeta }$.

Step 2: 

Suppose the solution of Equation (17) is the solution of the RBE

$${\mathcal{F}}^{\prime }=b\mathcal{F}+a{\mathcal{F}}^{2-m}+c{\mathcal{F}}^m,$$

(18)

with $a,$ $b,$ $c,$ and m being arbitrary constants. By integrating Equation (18), we acquire

$${\mathcal{F}}^{″}={\mathcal{F}}^{-1-2m}\left(a{\mathcal{F}}^2+c{\mathcal{F}}^{2m}+b{\mathcal{F}}^{1+m}\right)(-a(-2+\left.m){\mathcal{F}}^2+cm{\mathcal{F}}^{2m}+b{\mathcal{F}}^{1+m}\right),$$

$$\begin{array}{c}\hfill {\mathcal{F}}^{‴}={\mathcal{F}}^{-2(1+m)}\left(b\mathcal{F}+a{\mathcal{F}}^{2-m}+c{\mathcal{F}}^m\right)\left(a^2(-2+m)(-3+\right.\\ \hfill 2m){\mathcal{F}}^4+c^{2}m(-1+2m){\mathcal{F}}^{4m}+ab(-3+\\ \hfill m)(-2+m){\mathcal{F}}^{3+m}+\left(b^2+2ac\right){\mathcal{F}}^{2+2m}+\\ \hfill \left.bcm(1+m){\mathcal{F}}^{1+3m}\right),\dots \end{array}$$

Remark 1.

When $m=0$ and $ac\ne 0$, Equation (18) is called the Riccati equation. When $m\ne 1,$ $c=0$ and $a\ne 0$, Equation (18) gives the Bernoulli equation. Equation (18) is called the Riccati–Bernoulli equation to avoid introducing new terminology.

Equation (18) has the following solutions:

Case 1: 

If $m=1$, then we have

$$\mathcal{F}\left(\zeta \right)=C{e}^{(b+a+c)\zeta }.$$

(19)

Case 2: 

If $m\ne 1$, $b=0$, and $c=0$, then we have

$$\mathcal{F}\left(\zeta \right)={\left(a(m-1)(\zeta +C)\right)}^{\frac{1}{m-1}}.$$

(20)

Case 3: 

If $b\ne 0$, $c=0$ and $m\ne 1$, then we have

$$\mathcal{F}\left(\zeta \right)={\left(C{e}^{\left(b\right(m-1\left)\zeta \right)}-\frac{a}{b}\right)}^{\frac{1}{m-1}}.$$

(21)

Case 4: 

If $m\ne 1$, $a\ne 0$ and $b^2-4ac<0$, then we have

$$\mathcal{F}\left(\zeta \right)={\left(-\frac{b}{2a}+\frac{\sqrt{4ac-b^2}}{2a}\tan \left[\frac{(1-m)\sqrt{4ac-b^2}}{2}(\zeta +C)\right]\right)}^{\frac{1}{1-m}},$$

(22)

and

$$\mathcal{F}\left(\zeta \right)={\left(-\frac{b}{2a}-\frac{\sqrt{4ac-b^2}}{2a}\cot \left[\frac{(1-m)\sqrt{4ac-b^2}}{2}(\zeta +C)\right]\right)}^{\frac{1}{1-m}}.$$

(23)

Case 5: 

If $m\ne 1$, $a\ne 0$ and $b^2-4ac>0$, then we have

$$\mathcal{F}\left(\zeta \right)={\left(-\frac{b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\tan \mathrm{h}\left[\frac{(1-m)\sqrt{b^2-4ac}}{2}(\zeta +C)\right]\right)}^{\frac{1}{1-m}},$$

(24)

and

$$\mathcal{F}\left(\zeta \right)={\left(-\frac{b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\cot \mathrm{h}\left[\frac{(1-m)\sqrt{b^2-4ac}}{2}(\zeta +C)\right]\right)}^{\frac{1}{1-m}}.$$

(25)

Case 6: 

If $m\ne 1$, $a\ne 0$ and $b^2-4ac=0$, then we have

$$\mathcal{F}\left(\zeta \right)={\left(\frac{1}{a(m-1)(\zeta +C)}-\frac{a}{b}\right)}^{\frac{1}{1-m}}.$$

(26)

Here, C is a constant.

Step 3: 

By putting the derivatives of $\mathcal{F}$ into Equation (17), one can obtain algebraic expressions involving $\mathcal{F}$ and other parameters. By choosing the value of m according to the steps described above, comparing the coefficients of ${\mathcal{F}}^i,i=(1,2,\dots ,0$, performing all the necessary algebraic computations, and utilizing Equations (19)–(26), the solutions of Equation (16) may be derived.

To solve Equation (15) using the RBSO technique, we substitute Equation (18) along with the 2$\mathrm{nd},$ 3$\mathrm{rd},$ 4th and 6th derivatives into Equation (15) and set $m=0$ in the resulting algebraic expression to get

$$\begin{array}{c}\hfill -bc\left(-5+5b^2{\alpha }^3+b^4{\alpha }^6+c^2{\alpha }^4\left(45-150a\alpha +136a^2{\alpha }^2\right)+2c{\alpha }^2(-15+\right.\\ \hfill \left.\left.20a\alpha -15b^2{\alpha }^3+26a{b}^2{\alpha }^4\right)\right)+\left(-b^6{\alpha }^6+b^4\left(-5{\alpha }^3+60c{\alpha }^5-114ac{\alpha }^6\right)+\right.\\ \hfill 2ac\left(5+10c{\alpha }^2(3-4a\alpha )+c^2{\alpha }^4\left(-45+150a\alpha -136a^2{\alpha }^2\right)\right)-5b^2(-1+\\ \hfill \left.\left.2c{\alpha }^2(-6+11a\alpha )+9c^2{\alpha }^4\left(3-14a\alpha +16a^2{\alpha }^2\right)\right)\right)\mathcal{F}-b\left(616a^3{c}^2{\alpha }^6-\right.\\ \hfill 35b^2{\alpha }^2\left(2-9c{\alpha }^2+2b^2{\alpha }^3\right)+2a^{2}c{\alpha }^3\left(50-285c{\alpha }^2+196b^2{\alpha }^3\right)+a(-5+\\ \hfill \left.\left.25b^2{\alpha }^3+135c^2{\alpha }^4+21b^4{\alpha }^6-10c{\alpha }^2\left(6+29b^2{\alpha }^3\right)\right)\right){\mathcal{F}}^2+\left(-45b^4{\alpha }^4-\right.\\ \hfill 1232a^4{c}^2{\alpha }^6+4a^{3}c{\alpha }^3\left(-50+285c{\alpha }^2-896b^2{\alpha }^3\right)+30a{b}^2{\alpha }^2\left(4-18c{\alpha }^2+\right.\\ \hfill \left.\left.13b^2{\alpha }^3\right)-2a^2\left(-5+125b^2{\alpha }^3+135c^2{\alpha }^4+301b^4{\alpha }^6-60c\left({\alpha }^2+24b^2{\alpha }^5\right)\right)\right){\mathcal{F}}^3-\\ \hfill 75ab{\alpha }^2(-1+2a\alpha )\left(-3b^2{\alpha }^2+28a^{2}c{\alpha }^3+a\left(2-9c{\alpha }^2+14b^2{\alpha }^3\right)\right){\mathcal{F}}^4-\\ \hfill 5a^2{\alpha }^2(-1+2a\alpha )\left(-27b^2{\alpha }^2+56a^{2}c{\alpha }^3+2a\left(2-9c{\alpha }^2+56b^2{\alpha }^3\right)\right){\mathcal{F}}^5-\\ \hfill 1315a^{3}b{\alpha }^4\left(1-6a\alpha +8a^2{\alpha }^2\right){\mathcal{F}}^6-90a^4{\alpha }^4\left(1-6a\alpha +8a^2{\alpha }^2\right){\mathcal{F}}^7=0.\end{array}$$

(27)

By collecting the terms of ${\mathcal{F}}^i(i=0,1\dots ,7)$ in Equation (27) and performing all the necessary algebraic computations, we get

Constants:

$$\begin{array}{c}\hfill -bc(-5+5b^2{\alpha }^3+b^4{\alpha }^6+c^2{\alpha }^4(45-150a\alpha +\\ \hfill 136a^2{\alpha }^2)+2c{\alpha }^2(-15+20a\alpha -15b^2{\alpha }^3+26a{b}^2{\alpha }^4))=0,\end{array}$$

(28)

${\mathcal{F}}^1$:

$$\begin{array}{c}\hfill (-b^6{\alpha }^6+b^4(-5{\alpha }^3+60c{\alpha }^5-114ac{\alpha }^6)+2ac(5+10c{\alpha }^2(3-4a\alpha )+\\ \hfill c^2{\alpha }^4(-45+150a\alpha -136a^2{\alpha }^2))-5b^2(-1+2c{\alpha }^2(-6+11a\alpha )+\\ \hfill 9c^2{\alpha }^4(3-14a\alpha +16a^2{\alpha }^2)\left)\right),\end{array}$$

(29)

${\mathcal{F}}^2$:

$$\begin{array}{c}\hfill -3b(616a^3{c}^2{\alpha }^6-5b^2{\alpha }^2(2-9c{\alpha }^2+2b^2{\alpha }^3)+2a^{2}c{\alpha }^3(50-285c{\alpha }^2+\\ \hfill 196b^2{\alpha }^3)+a(-5+25b^2{\alpha }^3+135c^2{\alpha }^4+21b^4{\alpha }^6-10c{\alpha }^2(6+29b^2{\alpha }^3))=0,\end{array}$$

(30)

${\mathcal{F}}^3$:

$$\begin{array}{c}\hfill (-45b^4{\alpha }^4-1232a^4{c}^2{\alpha }^6+4a^{3}c{\alpha }^3(-50+285c{\alpha }^2-896b^2{\alpha }^3)+\\ \hfill 30a{b}^2{\alpha }^2(4-18c{\alpha }^2+13b^2{\alpha }^3)-2a^2(-5+125b^2{\alpha }^3+135c^2{\alpha }^4+\\ \hfill 301b^4{\alpha }^6-60c({\alpha }^2+24b^2{\alpha }^5))=0,\end{array}$$

(31)

${\mathcal{F}}^4$:

$$\begin{array}{c}\hfill -75ab{\alpha }^2(-1+2a\alpha )\left(-3b^2{\alpha }^2+28a^{2}c{\alpha }^3+a\left(2-9c{\alpha }^2+14b^2{\alpha }^3\right)\right)=0,\end{array}$$

(32)

${\mathcal{F}}^5$:

$$\begin{array}{c}\hfill -15a^2{\alpha }^2(-1+2a\alpha )\left(-27b^2{\alpha }^2+56a^{2}c{\alpha }^3+2a\left(2-9c{\alpha }^2+56b^2{\alpha }^3\right)\right)=0,\end{array}$$

(33)

${\mathcal{F}}^6$:

$$\begin{array}{c}\hfill -315a^{3}b{\alpha }^4\left(1-6a\alpha +8a^2{\alpha }^2\right)=0,\end{array}$$

(34)

${\mathcal{F}}^7$:

$$\begin{array}{c}\hfill -90a^4{\alpha }^4\left(1-6a\alpha +8a^2{\alpha }^2\right)=0.\end{array}$$

(35)

From solving Equations (28)–(35), we acquire the following family of parameter values:

Family 1: When

$$c=0,a=\frac{1}{2\alpha },b=\frac{1}{\alpha }\sqrt{\frac{-5+3\sqrt{5}}{2\alpha }},$$

(36)

we have cases and solutions given by

Case A: If $\alpha >0,$ we acquire the kink-type solution given by

$$\psi (x,t)=-\frac{1}{2}\sqrt{\frac{-10+6\sqrt{5}}{\alpha }}\left\{1+tanh\left[\frac{1}{2\alpha }\sqrt{\frac{-5+3\sqrt{5}}{2\alpha }}(C+t-x\alpha )\right]\right\},$$

(37)

and the singular solution

$$\psi (x,t)=-\frac{1}{2}\sqrt{\frac{-10+6\sqrt{5}}{\alpha }}\left\{1+coth\left[\frac{1}{2\alpha }\sqrt{\frac{-5+3\sqrt{5}}{2\alpha }}(C+t-x\alpha )\right]\right\}.$$

(38)

Case B: If $\alpha <0,$ we acquire the following periodic traveling wave solutions

$$\psi (x,t)=-\sqrt{\frac{-5+3\sqrt{5}}{2\alpha }}+\sqrt{\frac{5-3\sqrt{5}}{2\alpha }}tan\left[\frac{1}{2}\sqrt{\frac{5-3\sqrt{5}}{2\alpha }}(C+t-x\alpha )\right],$$

and

$$\psi (x,t)=-\sqrt{\frac{-5+3\sqrt{5}}{2\alpha }}-\sqrt{\frac{5-3\sqrt{5}}{2\alpha }}cot\left[\frac{1}{2}\sqrt{\frac{5-3\sqrt{5}}{2\alpha }}(C+t-x\alpha )\right].$$

Case C: From substituting the parameters in Equation (36) into Equation (21), we obtain the following exact solution of Equation (1):

$$\begin{array}{c}\hfill \psi (x,t)={\left\{C{e}^{\frac{1}{\alpha }\sqrt{\frac{-5+3\sqrt{5}}{2\alpha }}(-t+x\alpha )}-\alpha \sqrt{\frac{1}{-10+6\sqrt{5}}}\right\}}^{-1}.\end{array}$$

(39)

Family 2: When

$$a=\frac{1}{2\alpha },c=\frac{1}{4}\left\{\frac{3\sqrt{5}}{{\alpha }^2}+\frac{5}{{\alpha }^2}+2b^2\alpha \right\},$$

we acquire the periodic traveling wave solutions represented by

$$\begin{array}{c}\hfill \psi (x,t)=-b\alpha +\frac{1}{\sqrt{2}}\sqrt{\frac{5+3\sqrt{5}}{\alpha }}tan\left[\frac{1}{2\alpha }\sqrt{\frac{5+3\sqrt{5}}{\alpha }}(C+t-x\alpha )\right],\end{array}$$

(40)

and

$$\begin{array}{c}\hfill \psi (x,t)=-\frac{1}{2}\alpha \left\{2b+\frac{1}{\alpha }\sqrt{\frac{10+6\sqrt{5}}{\alpha }}cot\left[\frac{1}{2\alpha }\sqrt{\frac{5+3\sqrt{5}}{2\alpha }}(C+t-x\alpha )\right]\right\}.\end{array}$$

(41)

2. Conservation Laws

In this part, we derive the nonlinear self-adjointness of Equation (1) for the purpose of constructing the CL. We begin by considering the following theorem from references [7,8]:

Theorem 1.

The system of $\overline{m}$ differential equations,

$$F_{\overline{\alpha }}(\overline{x},\psi ,{\psi }_{\left(1\right)},\dots ,{\psi }_s)=0,\overline{\alpha }=1,\dots ,m,$$

(42)

with m dependent variables $\psi =({\psi }^1,\dots ,{\psi }^m)$ has an adjoint equation

$$F_{\overline{\alpha }}^{*}(\overline{x},\psi ,{\psi }_{\left(1\right)},\dots ,{\psi }_s)=\frac{\delta \left({\upsilon }^{\overline{\beta }}{F}_{\overline{\beta }}\right)}{\delta {\psi }^{\overline{\alpha }}},\alpha =1,\dots ,m,$$

(43)

where

$$\frac{\delta }{\delta {\psi }^{\overline{\alpha }}}=\frac{\partial }{\partial {\psi }^{\overline{\alpha }}}+\sum _{s=0}^{\infty }{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial }{\partial {\psi }_{i_1\dots i_s}^{\overline{\alpha }}}.$$

The formal Lagrangian $\mathcal{L}$ for Equation (42) is given by

$$\mathcal{L}=\sum _{\overline{\beta }=1}^m{\upsilon }^{\overline{\beta }}{F}_{\overline{\beta }}(\overline{x},\psi ,{\psi }_{\left(1\right)},\dots ,{\psi }_s),$$

(44)

where ${\upsilon }^{\overline{\beta }}={\upsilon }^{\overline{\beta }}(\overline{x},t)$ is a nonlocal dependent variable.

The formal Lagrangian Equation (44) for Equation (1) is written as

$$\begin{array}{c}\hfill \mathcal{L}=\upsilon (x,t)\left(5{\psi }_{tt}-45{{\psi }_x}^2{\psi }_{xx}-15{\psi }_{xx}{\psi }_{xxx}+5\left(3{\psi }_x{\psi }_{xt}+3{\psi }_t{\psi }_{xx}+{\psi }_{xxxt}\right)-15{\psi }_x{\psi }_{xxxx}-{\psi }_{xxxxxx}\right),\end{array}$$

(45)

where $\upsilon =\upsilon (x,t)$ is a nonlocal variable. Subsequently, we derive the adjoint of Equation (1) as

$$\begin{array}{c}\hfill F^{*}=5{\upsilon }_{tt}+30{\upsilon }_x{\psi }_{xt}+15{\psi }_t{\upsilon }_{xx}-45{{\psi }_x}^2{\upsilon }_{xx}-45{\psi }_{xx}{\upsilon }_{xxx}-60{\upsilon }_{xx}{\psi }_{xxx}+\\ \hfill 5{\upsilon }_{xxxt}+15{\psi }_x\left({\upsilon }_{xt}-6{\upsilon }_x{\psi }_{xx}-{\upsilon }_{xxxx}\right)-30{\upsilon }_x{\psi }_{xxxx}-{\upsilon }_{xxxxxx}=0.\end{array}$$

(46)

Theorem 2.

Equation (42) is nonlinear self-adjoint if it becomes equivalent to its adjoint Equation (43) upon the substitution

$${\upsilon }^{\overline{\alpha }}={\varphi }^{\overline{\alpha }}(\overline{x},\psi ),\overline{\alpha }=1,2,\dots ,\overline{m},$$

such that

$$\varphi (\overline{x},\psi )\ne 0.$$

(47)

Equation (47) means that not all components of ${\varphi }^{\overline{\alpha }}(\overline{x},\psi )$ of ϕ vanish.

Theorem 3.

Equation (1) is nonlinear self-adjoint if υ in Equation (46) is given by

$$\begin{array}{c}\hfill \upsilon =c_1+t{c}_2.\end{array}$$

(48)

Proof. 

Let

$$\begin{array}{c}\hfill \upsilon =\varphi (x,t,\psi ).\end{array}$$

(49)

By putting Equation (49) into the adjoint Equation (46), we acquire

$$\begin{array}{c}\hfill -15{\varphi }_{\psi \psi }=0,-10{\varphi }_{\psi \psi }=0,-6{\varphi }_{\psi \psi }=0,5{\varphi }_{\psi \psi }=0,15{\varphi }_{\psi \psi }=0,\\ \hfill -60{\varphi }_{\psi \psi \psi }=0,-15{\varphi }_{\psi \psi \psi }=0,15{\varphi }_{\psi \psi \psi }=0,-45{\varphi }_{\psi \psi \psi \psi }=0,\\ \hfill -20{\varphi }_{\psi \psi \psi \psi }=0,5{\varphi }_{\psi \psi \psi \psi }=0,-15{\varphi }_{\psi \psi \psi \psi \psi }=0,-{\varphi }_{\psi \psi \psi \psi \psi \psi }=0,\\ \hfill -6{\varphi }_{x\psi }=0,15{\varphi }_{x\psi }=0,15{\varphi }_{x\psi \psi }=0,-30\left({\varphi }_{\psi }+{\varphi }_{x\psi \psi }\right)=0,\\ \hfill 30\left({\varphi }_{\psi }+{\varphi }_{x\psi \psi }\right)=0,-15\left(6{\varphi }_{\psi }+4{\varphi }_{x\psi \psi }\right)=0,-180{\varphi }_{\psi \psi }-\\ \hfill 90{\varphi }_{x\psi \psi \psi }=0,-120{\varphi }_{\psi \psi }-60{\varphi }_{x\psi \psi \psi }=0,15\left(2{\varphi }_{\psi \psi }+{\varphi }_{x\psi \psi \psi }\right)=0,\\ \hfill -15\left(9{\varphi }_{\psi \psi \psi }+4{\varphi }_{x\psi \psi \psi \psi }\right)=0,-3\left(5{\varphi }_{\psi \psi \psi \psi }+2{\varphi }_{x\psi \psi \psi \psi \psi }\right)=0,\\ \hfill -30{\varphi }_x-15{\varphi }_{xx\psi }=0,30{\varphi }_x+15{\varphi }_{xx\psi }=0,-180{\varphi }_{x\psi }-60{\varphi }_{xx\psi \psi }=0,\\ \hfill -45\left(3{\varphi }_{x\psi }+{\varphi }_{xx\psi \psi }\right)=0,45{\varphi }_{x\psi }+15{\varphi }_{xx\psi \psi }=0,-45\left(2{\varphi }_{\psi }+7{\varphi }_{x\psi \psi }+\right.\\ \hfill \left.2{\varphi }_{xx\psi \psi \psi }\right)=0,-45{\varphi }_{\psi \psi }-60{\varphi }_{x\psi \psi \psi }-15{\varphi }_{xx\psi \psi \psi \psi }=0,5{\varphi }_{t\psi }-\\ \hfill 60{\varphi }_{xx}-20{\varphi }_{xxx\psi }=0,10{\varphi }_{t\psi }+15{\varphi }_{xx}+5{\varphi }_{xxx\psi }=0,15{\varphi }_{t\psi \psi }-\\ \hfill 90{\varphi }_x-225{\varphi }_{xx\psi }-60{\varphi }_{xxx\psi \psi }=0,5{\varphi }_{t\psi \psi \psi }-90{\varphi }_{x\psi }-0{\varphi }_{xx\psi \psi }-\\ \hfill 920{\varphi }_{xxx\psi \psi \psi }=0,15{\varphi }_{xt\psi }-45{\varphi }_{xxx}-15{\varphi }_{xxxx\psi }=0,15{\varphi }_{t\psi }+\\ \hfill 15{\varphi }_{xt\psi \psi }-45{\varphi }_{xx}-60{\varphi }_{xxx\psi }-15{\varphi }_{xxxx\psi \psi }=0,15{\varphi }_{xt}+15{\varphi }_{xxt\psi }-\\ \hfill 15{\varphi }_{xxxx}-6{\varphi }_{xxxxx\psi }=0,5{\varphi }_{tt}+5{\varphi }_{xxxt}-{\varphi }_{xxxxxx}=0. \square \end{array}$$

(50)

Using the Mathematica package called SYM [24], we obtain the solution of Equation (50) as

$$\begin{array}{c}\hfill \varphi =c_1+t{c}_2.\end{array}$$

□

Theorem 4.

Any infinitesimal symmetry (Lie point, Bäcklund, nonlocal)

$$X={\xi }^i(\overline{x},\psi ,{\psi }_{\left(1\right)},\dots )\frac{\partial }{\partial {\overline{x}}^i}+{\eta }^{\overline{\alpha }}(\overline{x},\psi ,{\psi }_{\left(1\right)},\dots )\frac{\partial }{\partial {\psi }^{\overline{\alpha }}}$$

of Equation (42) leads to a CL $D_i\left(T^i\right)=0$, constructed by the formula

$$\begin{array}{c}\hfill T^i={\xi }^i\mathcal{L}+W^{\overline{\alpha }}\left[\frac{\partial \mathcal{L}}{\partial {\psi }_i^{\overline{\alpha }}}-D_j\left(\frac{\partial \mathcal{L}}{\partial {\psi }_{ij}^{\overline{\alpha }}}\right)+D_j{D}_k\left(\frac{\partial \mathcal{L}}{\partial {\psi }_{ijk}^{\overline{\alpha }}}\right)-\dots \right]\\ \hfill +D_j\left(W^{\overline{\alpha }}\right)\left[\frac{\partial \mathcal{L}}{\partial {\psi }_{ij}^{\overline{\alpha }}}-D_k\left(\frac{\partial \mathcal{L}}{\partial {\psi }_{ijk}^{\overline{\alpha }}}\right)+\dots \right]+D_j{D}_k\left(W^{\overline{\alpha }}\right)\left[\frac{\partial \mathcal{L}}{\partial {\psi }_{ijk}^{\overline{\alpha }}}-\dots \right],\end{array}$$

(51)

where $W^{\overline{\alpha }}={\eta }^{\overline{\alpha }}-{\xi }^j{\psi }_j^{\overline{\alpha }}$ and $T^i$ are the conserved vectors.

Equation (1) is nonlinear self-adjoint with the substitution Equation (48). We now use this fact to construct the conserved vectors. As a special case, we choose $c_1=c_2=1$ in Equation (48) to get

$$\upsilon (x,t)=(1+t).$$

(52)

By putting Equation (52) into Equation (45), we acquire

$$\begin{array}{c}\hfill {\mathcal{L}}^{*}=(1+t)(5{\psi }_{tt}-45{{\psi }_x}^2{\psi }_{xx}-15{\psi }_{xx}{\psi }_{xxx}+5(3{\psi }_x{\psi }_{xt}+3{\psi }_t{\psi }_{xx}+{\psi }_{xxxt})-\\ \hfill 15{\psi }_x{\psi }_{xxxx}-{\psi }_{xxxxxx}).\end{array}$$

We now use each one of the symmetries Equations (9)–(12) and the conservation formula Equation (51) to obtain the following conserved vectors:

• The generator $X_1={\partial }_x$ determines the conserved vector:

  $$\begin{array}{c}{\mathbf{T}}_{\mathbf{1}}^{\mathbf{x}}=\frac{5}{4}\left(4(1+t){\psi }_{tt}+6{{\psi }_x}^2+12(1+t){\psi }_x{\psi }_{xt}+{\psi }_{xxx}+(1+t){\psi }_{xxxt}\right),\hfill \\ {\mathbf{T}}_{\mathbf{1}}^{\mathbf{t}}=-\frac{5}{4}\left(4{\psi }_x\left(-1+3(1+t){\psi }_{xx}\right)+(1+t)\left(4{\psi }_{xt}+{\psi }_{xxxx}\right)\right).\hfill \end{array}$$
• The generator $X_2={\partial }_{\psi }$ determines the conserved vector:

  $$\begin{array}{c}{\mathbf{T}}_{\mathbf{2}}^{\mathbf{x}}=-\frac{15}{2}\left({\psi }_x+(1+t){\psi }_{xt}\right),\hfill \\ {\mathbf{T}}_{\mathbf{2}}^{\mathbf{t}}=-5+\frac{15}{2}(1+t){\psi }_{xx}.\hfill \end{array}$$
• The generator $X_3={\partial }_t$ determines the conserved vector:

  $$\begin{array}{c}{\mathbf{T}}_{\mathbf{3}}^{\mathbf{x}}=\frac{1}{2}\left(15{\psi }_t\left({\psi }_x-t{\psi }_{xt}\right)+t\left(-15{\psi }_{tt}{\psi }_x+90{{\psi }_x}^2{\psi }_{xt}+30{\psi }_{xt}{\psi }_{xxx}+30{\psi }_x{\psi }_{xxxt}+2{\psi }_{xxxxxt}\right)\right),\hfill \\ {\mathbf{T}}_{\mathbf{3}}^{\mathbf{t}}=-45t{{\psi }_x}^2{\psi }_{xx}+\frac{5}{2}{\psi }_t\left(2+3t{\psi }_{xx}\right)+5{\psi }_{xxx}-15t{\psi }_{xx}{u}_{xxx}+\frac{15}{2}t{\psi }_x\left({\psi }_{xt}-2{\psi }_{xxxx}\right)-t{\psi }_{xxxxxx}.\hfill \end{array}$$
• The generator $X_4=3t{\partial }_t-\psi {\partial }_{\psi }+x{\partial }_x$ determines the conserved vector:

  $$\begin{array}{c}{\mathbf{T}}_{\mathbf{4}}^{\mathbf{x}}=\frac{1}{4}\left(30\left(\psi +3t{\psi }_t+x{\psi }_x\right)\left({\psi }_x+(1+t){\psi }_{xt}\right)-30(1+t){\psi }_x\left(4{\psi }_t+3t{\psi }_{tt}+x{\psi }_{xt}\right)+\right.\hfill \\ 60(1+t)\left(2{\psi }_x+3t{\psi }_{xt}+x{\psi }_{xx}\right)\left(-{\psi }_t+3{{\psi }_x}^2+{\psi }_{xxx}\right)+5\left(3{\psi }_{xx}+3t{\psi }_{xxt}+\right.\hfill \\ \left.x{\psi }_{xxx}\right)-15(1+t)\left(6{\psi }_{xxt}+3t{\psi }_{xxtt}+x{\psi }_{xxxt}\right)+60(1+t){\psi }_x\left(4{\psi }_{xxx}+\right.\hfill \\ \left.3t{\psi }_{xxxt}+x{\psi }_{xxxx}\right)+4(1+t)x\left(5{\psi }_{tt}+5\left(-9{{\psi }_x}^2{\psi }_{xx}+3{\psi }_{xx}\left({\psi }_t-{\psi }_{xxx}\right)+\right.\right.\hfill \\ \left.\left.{\psi }_{xxxt}+3{\psi }_x\left({\psi }_{xt}-{\psi }_{xxxx}\right)\right)-{\psi }_{xxxxxx}\right)+4(1+t)\left(6{\psi }_{xxxxx}+\right.\hfill \\ \left.\left.3t{u}_{xxxxxt}+x{\psi }_{xxxxxx}\right)\right),\hfill \\ {\mathbf{T}}_{\mathbf{4}}^{\mathbf{t}}=\frac{1}{4}\left(10\psi \left(2-3(1+t){\psi }_{xx}\right)+10{\psi }_t\left(-2(4+t)+9t(1+t){\psi }_{xx}\right)+\right.\hfill \\ 10\left(-6(1+t){{\psi }_x}^2\left(1+9t{\psi }_{xx}\right)+{\psi }_x\left(2x+9t(1+t){\psi }_{xt}-6(1+t)x{\psi }_{xx}\right)-\right.\hfill \\ \left.2(1+t)\left(x{\psi }_{xt}+\left(1+9t{\psi }_{xx}\right){\psi }_{xxx}\right)\right)+45t(1+t){\psi }_{xxxt}-\hfill \\ \left.5(1+t)\left(x+36t{\psi }_x\right){\psi }_{xxxx}-12t(1+t){\psi }_{xxxxxx}\right).\hfill \end{array}$$

3. Conclusions

In this paper we obtained travelling wave solutions of the sixth-order nonlinear Ramani equation. The symmetries were used to reduce the equation to ODEs. The RBSO scheme was used to derive the traveling wave solutions of the equation by first solving the ODEs. These traveling wave solutions included kink-type, singular, and exponential function solutions. Furthermore we derived the CL of the equation using the conservation theorem due to Ibragimov. Some interesting figures showing the physical meaning of the obtained results have been shown in Figure 1, Figure 2 and Figure 3.

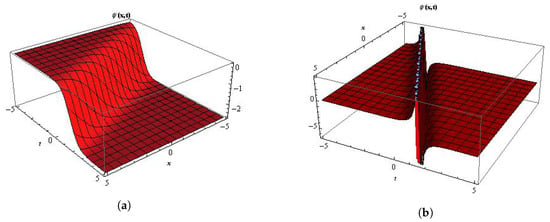
Figure 1. (a) The 3D surface of the kink-type solution Equation (37) and (b) the singular solution to Equation (38) by setting $\alpha =0.7,C=1$. These solutions have several physical applications in a Bloch wall between two magnetic domains in a ferromagnetic. The solitary waves propagate without change in the dynamics of the amplitude and width. It can be observed that the solitary waves move along the 3D axis with positive phase velocity and a constant period. The amplitude and phase of the solitary waves do not change during the evolution.

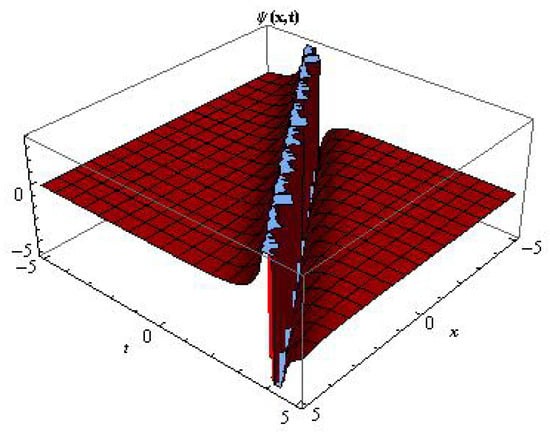
Figure 2. The 3D surface of the exponential function solution to Equation (39) by setting $\alpha =0.7,C=1$.

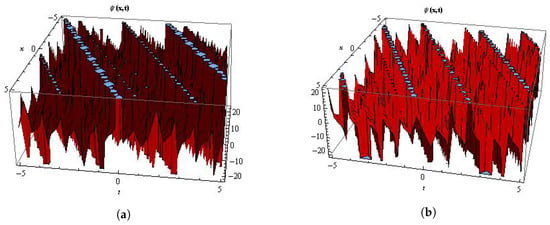
Figure 3. (a) The 3D surface of the periodic singular solutions to Equation (40) and (b) Equation (41) by setting $\alpha =0.5,C=0.2,b=0.5$. These solutions have a low frequency and with several applications in surface waves.These solitary waves also propagate without change in the dynamics of the amplitude, but the width varies due to the periodic oscillation. The phase of the solitary waves change during the evolution process. It can be observed that the periodic solitary waves also move along the 3D axis with phase velocity in a periodic pattern constant period.