A Robust Distributed Big Data Clustering-based on Adaptive Density Partitioning using Apache Spark
Abstract
1. Introduction
1.1. Preliminaries Literature Review and Related Works
1.2. Clustering by Fast Search and Find of Density Peaks (CDP)
2. Preliminaries of the Proposed Method
2.1. Adaptive Density Estimation
2.2. Bayesian Locality Sensitive Hashing (BALSH)
2.3. Ordered Weighted Averaging Distance Function
2.4. Gene Expression Clustering
3. Proposed Method
3.1. Distributed Similarity Calculation Using Adaptive Cut-off Threshold
3.2. Distributed Bayesian Locality Sensitive Hashing (BALSH)
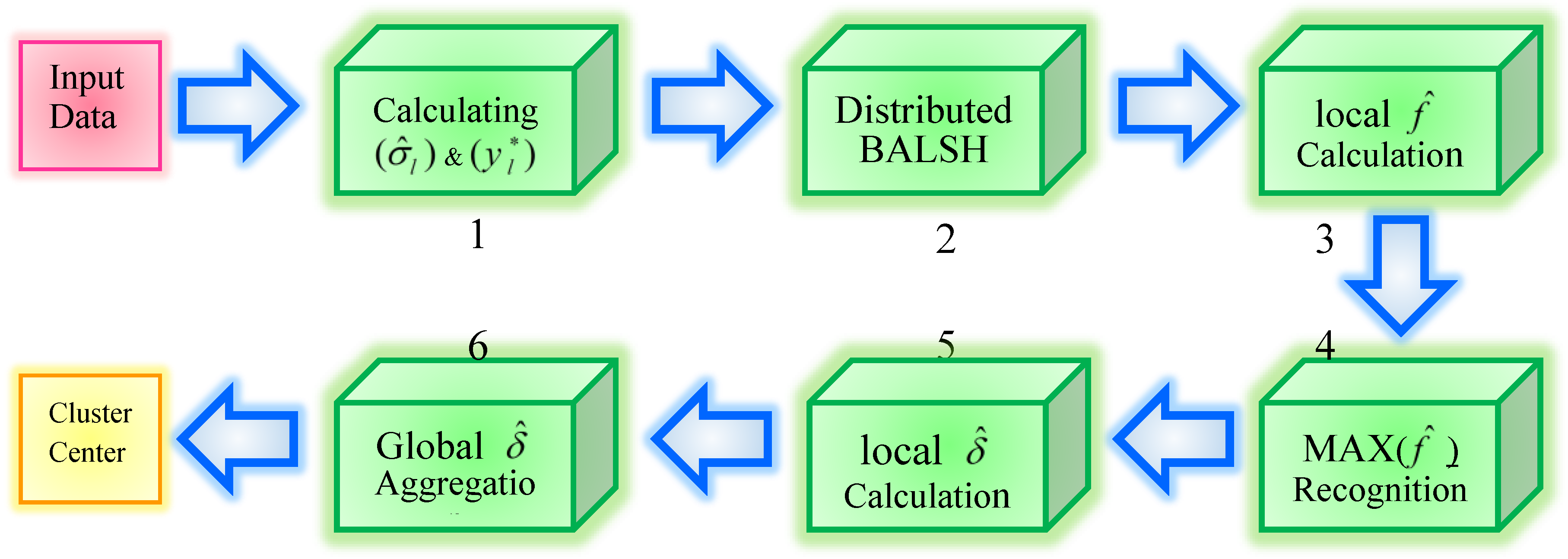
4. Design and Implementation
5. Experimental Results
5.1. Datasets
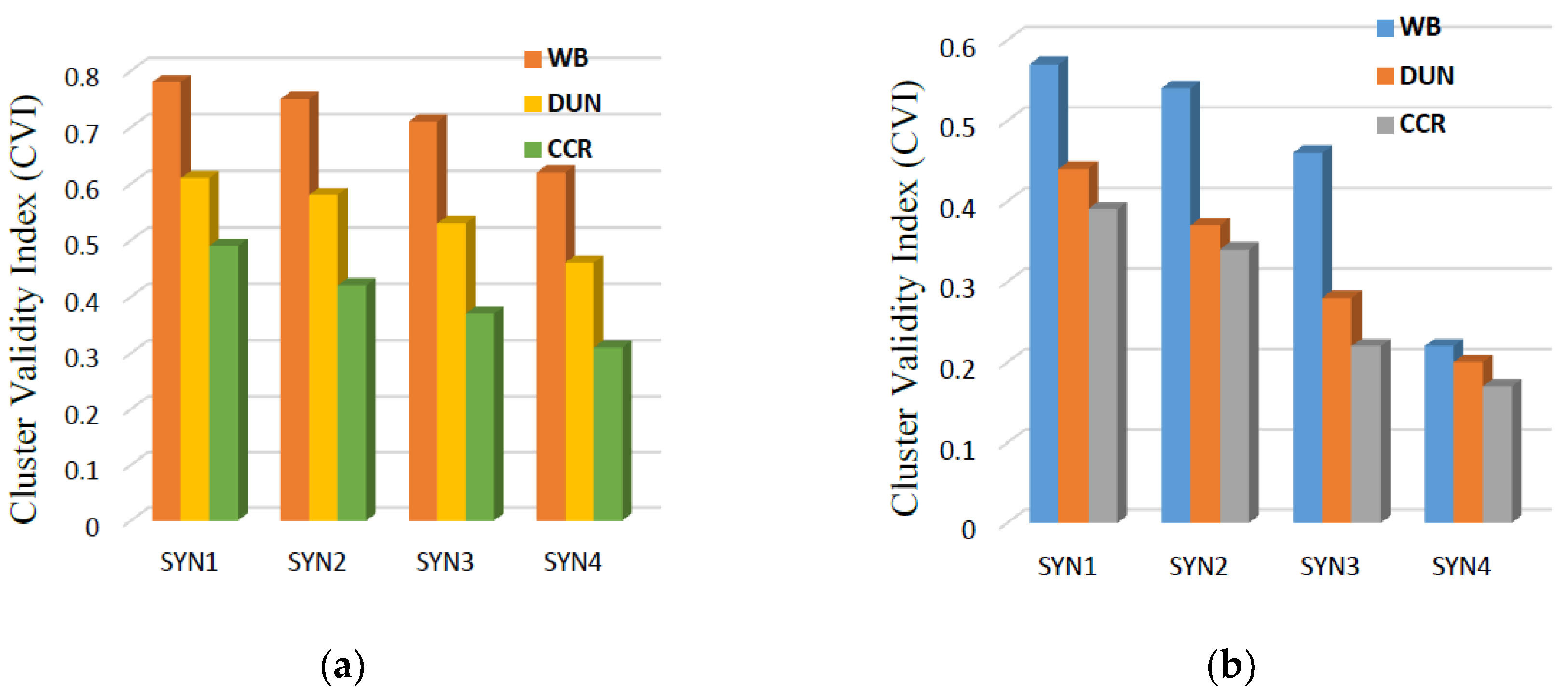
5.2. Cluster Validity Index
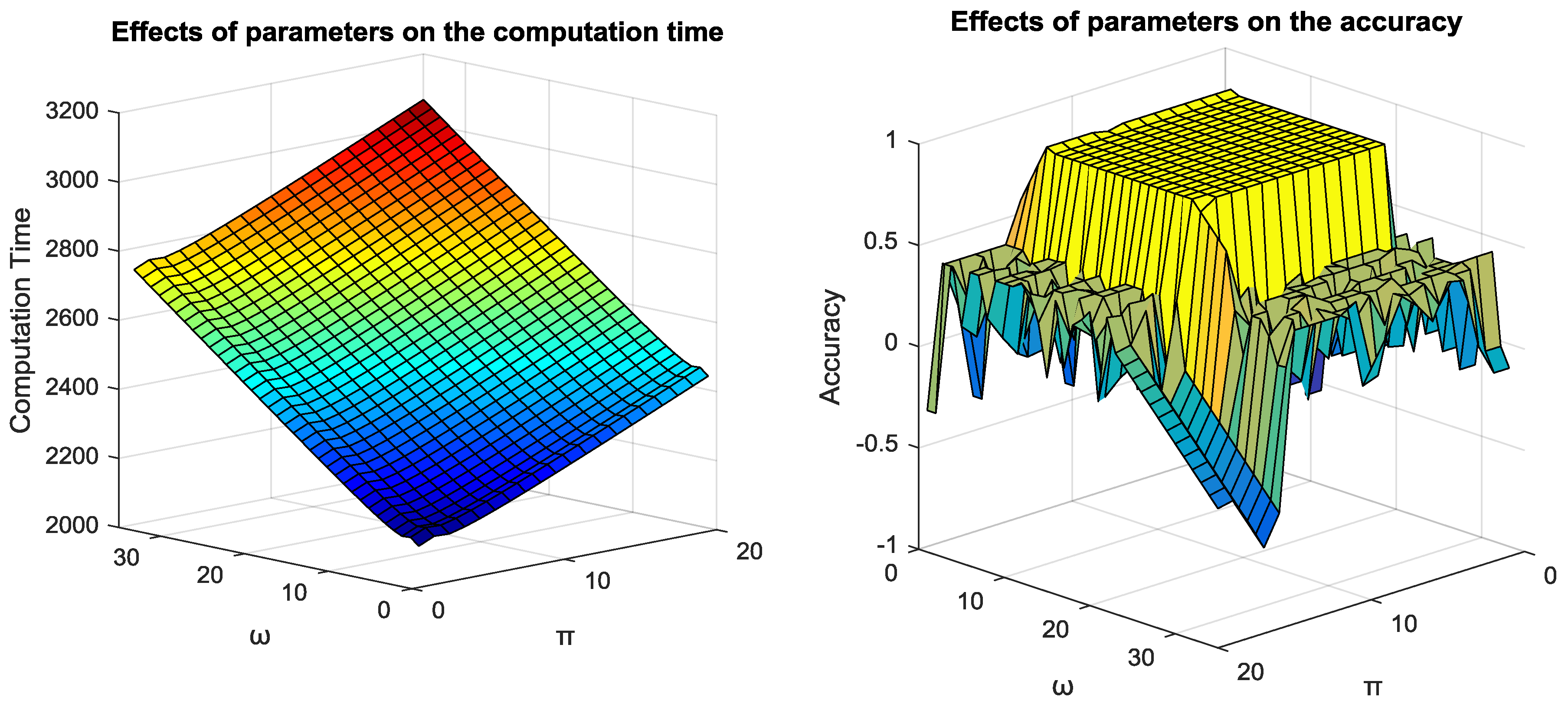
5.3. Parameter Tuning
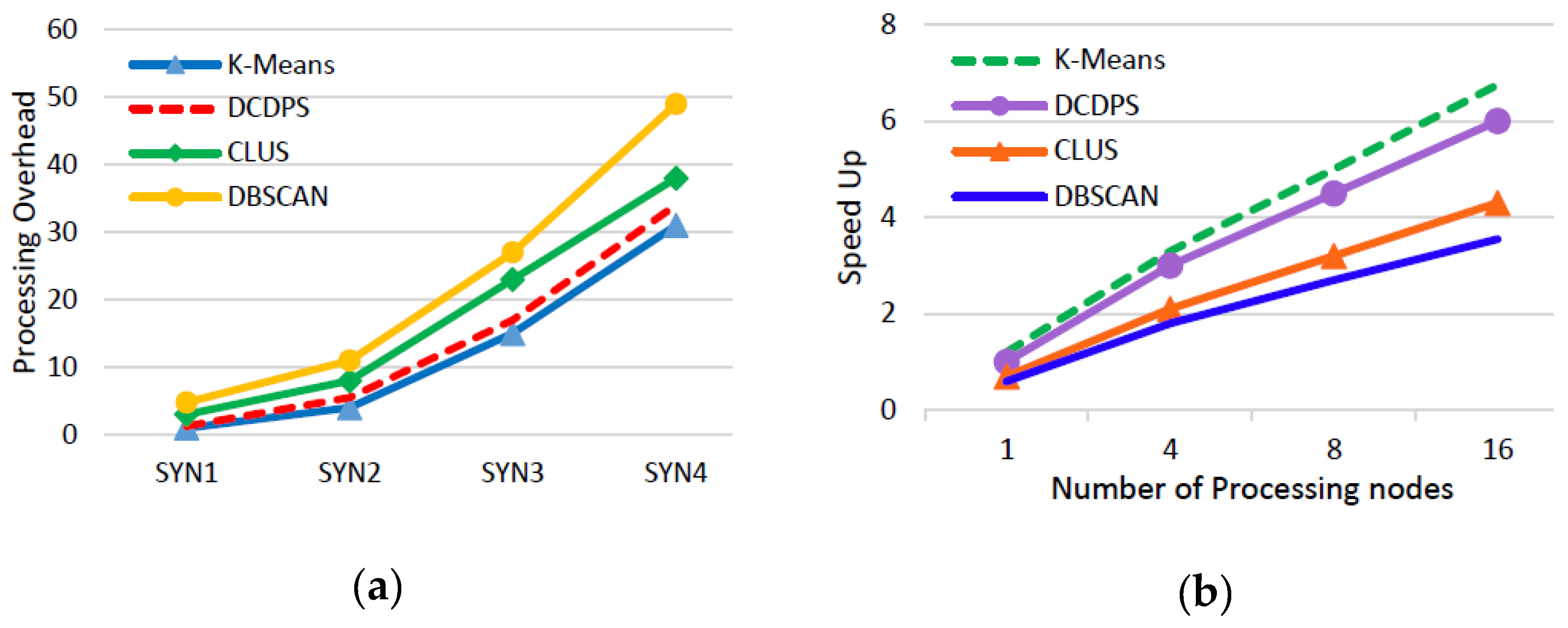
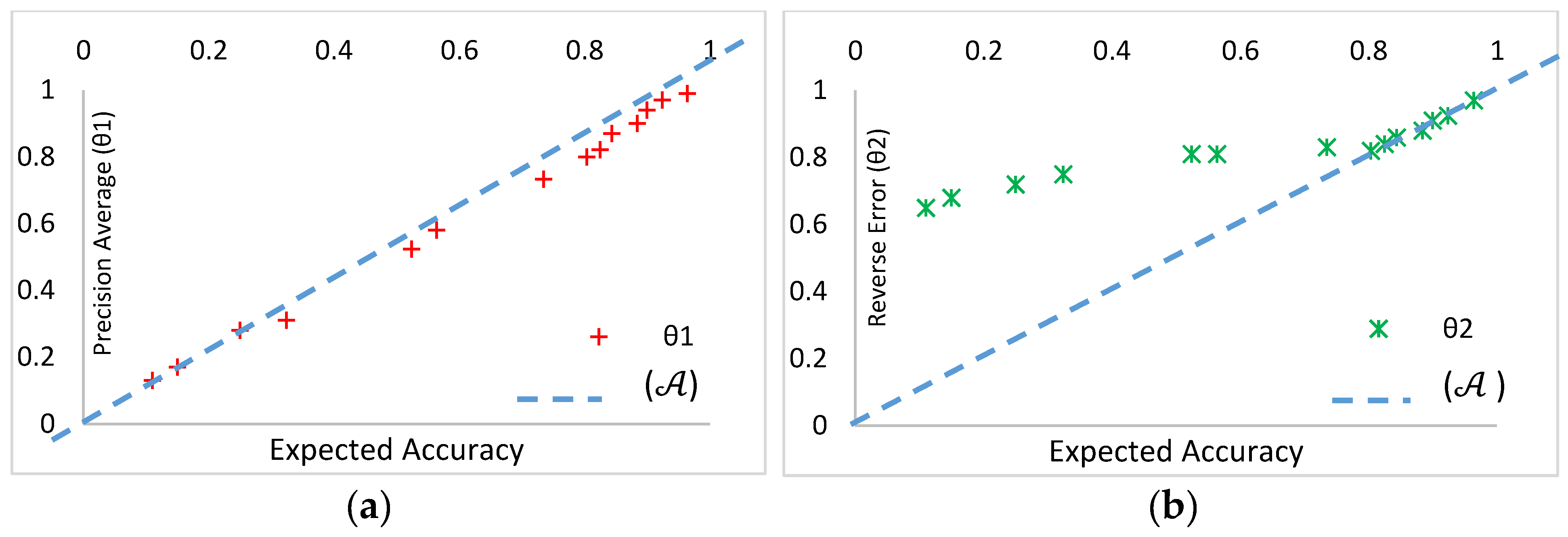
5.4. Results
6. Discussion
7. Conclusions
Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aggarwal, C.C.; Reddy, C.K. DATA CLUSTERING Algorithms and Applications; Chapman and Hall/CRC: London, UK, 2013. [Google Scholar]
- Mirkin, B. Clustering for Data Mining: A Data Recovery Approach, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C.T. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef]
- Basanta-Val, P. An efficient industrial big-data engine. IEEE Trans. Ind. Inform. 2018, 14, 1361–1369. [Google Scholar] [CrossRef]
- Lv, Z.; Song, H.; Basanta-Val, P.; Steed, A.; Jo, M. Next-generation big data analytics: State of the art, challenges, and future research topics. IEEE Trans. Ind. Inform. 2017, 13, 1891–1899. [Google Scholar] [CrossRef]
- Stoica, I. Trends and challenges in big data processing. Proc. VLDB Endow. 2016, 9, 1619. [Google Scholar] [CrossRef]
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J.; et al. Apache Spark: A unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Meng, X.; Bradley, J.; Yavuz, B.; Sparks, E.; Venkataraman, S.; Liu, D.; Freeman, J.; Tsai, D.B.; Amde, M.; Owen, S.; et al. Mllib: Machine learning in apache spark. J. Mach. Learn. Res. 2016, 17, 1235–1241. [Google Scholar]
- Shoro, A.G.; Soomro, T.R. Big data analysis: Apache spark perspective. Glob. J. Comput. Sci. Technol. 2015. Available online: https://computerresearch.org/index.php/computer/article/view/1137 (accessed on 13 August 2015).
- Wang, K.; Khan, M.M.H. Performance prediction for apache spark platform. In Proceedings of the 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems, New York, NY, USA, 24–26 August 2015. [Google Scholar]
- Singh, P.; Meshram, P.A. Meshram, Survey of density based clustering algorithms and its variants. In Proceedings of the 2017 International Conference on Inventive Computing and Informatics (ICICI), Coimbatore, India, 23–24 November 2017; pp. 920–926. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD-96, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Cordova, I.; Moh, T.S. Dbscan on resilient distributed datasets. In Proceedings of the 2015 International Conference on High Performance Computing & Simulation (HPCS), Amsterdam, The Netherlands, 20–24 July 2015; pp. 531–540. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Li, Z.; Tang, Y. Comparative density peaks clustering. Expert Syst. Appl. 2018, 95, 236–247. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Madan, S.; Dana, K.J. Modified balanced iterative reducing and clustering using hierarchies (m-BIRCH) for visual clustering. Pattern Anal. Appl. 2016, 19, 1023–1040. [Google Scholar] [CrossRef]
- McNicholas, P.D. Model-based clustering. J. Classif. 2016, 33, 331–373. [Google Scholar] [CrossRef]
- Kriegel, H.P.; Kröger, P.; Sander, J.; Zimek, A. Density-based clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 231–240. [Google Scholar] [CrossRef]
- Zerhari, B.; Lahcen, A.A.; Mouline, S. Big data clustering: Algorithms and challenges. In Proceedings of the International Conference on Big Data, Cloud and Applications, Tetuan, Morocco, 25–26 May 2015. [Google Scholar]
- Khondoker, M.R. Big Data Clustering, 2018. Wiley StatsRef: Statistics Reference Online. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/9781118445112.stat07978 (accessed on 13 August 2018).
- Fahad, A.; Alshatri, N.; Tari, Z.; Alamri, A.; Khalil, I.; Zomaya, A.Y.; Foufou, S.; Bouras, A. A survey of clustering algorithms for big data: Taxonomy and empirical analysis. IEEE Trans. Emerg. Top. Comput. 2014, 2, 267–279. [Google Scholar] [CrossRef]
- He, Y.; Tan, H.; Luo, W.; Feng, S.; Fan, J. MR-DBSCAN: A scalable MapReduce-based DBSCAN algorithm for heavily skewed data. Front. Comput. Sci. 2014, 8, 83–99. [Google Scholar] [CrossRef]
- Kim, Y.; Shim, K.; Kim, M.S.; Lee, J.S. DBCURE-MR: An efficient density-based clustering algorithm for large data using MapReduce. Inf. Syst. 2014, 42, 15–35. [Google Scholar] [CrossRef]
- Jin, C.; Liu, R.; Chen, Z.; Hendrix, W.; Agrawal, A.; Choudhary, A. A scalable hierarchical clustering algorithm using spark. In Proceedings of the 2015 IEEE First International Conference on Big Data Computing Service and Applications, Redwood City, CA, USA, 30 March–2 April 2015; pp. 418–426. [Google Scholar]
- Zhu, B.; Mara, A.; Mozo, A. CLUS: Parallel subspace clustering algorithm on spark. In Proceedings of the East European Conference on Advances in Databases and Information Systems, Poitiers, France, 8–11 September 2015; pp. 175–185. [Google Scholar]
- Han, D.; Agrawal, A.; Liao, W.K.; Choudhary, A. A Fast DBSCAN Algorithm with Spark Implementation. Big Data Eng. Appl. 2018, 44, 173–192. [Google Scholar]
- Blomstedt, P.; Dutta, R.; Seth, S.; Brazma, A.; Kaski, S. Modelling-based experiment retrieval: A case study with gene expression clustering. Bioinformatics 2016, 32, 1388–1394. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Hu, X.; He, T.; Jiang, X. Hessian regularization based symmetric nonnegative matrix factorization for clustering gene expression and microbiome data. Methods 2016, 111, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Alok, A.K.; Saha, S.; Ekbal, A. Semi-supervised clustering for gene-expression data in multiobjective optimization framework. Int. J. Mach. Learn. Cybern. 2017, 8, 421–439. [Google Scholar] [CrossRef]
- Maji, P.; Paul, S. Rough-Fuzzy Clustering for Grouping Functionally Similar Genes from Microarray Data. IEEE/ACM Trans. Comput. Biol. Bioinforma. 2013, 10, 286–299. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.F.; Xu, Y. Fast clustering using adaptive density peak detection. Stat. Methods Med. Res. 2017, 26, 2800–2811. [Google Scholar] [CrossRef] [PubMed]
- McInnes, L.; Healy, J.; Astels, S. hdbscan: Hierarchical density based clustering. J. Open Source Softw. 2017, 2, 205. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation For Statistics And Data Analysis; Routledge: New York, NY, USA, 2018. [Google Scholar]
- Hosseini, B.; Kiani, K. FWCMR: A scalable and robust fuzzy weighted clustering based on MapReduce with application to microarray gene expression. Expert Syst. Appl. 2018, 91, 198–210. [Google Scholar] [CrossRef]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, And Visualization, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wand, M.P.; Jones, M.C. Kernel Smoothing; Chapman & Hall/CRC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Agarwal, G.G.; Studden, W.J. Asymptotic integrated mean square error using least squares and bias minimizing splines. Ann. Stat. 1980, 8, 1307–1325. [Google Scholar] [CrossRef]
- Zhao, K.; Lu, H.; Mei, J. Locality Preserving Hashing. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, Québec, Canada, 27–31 July 2014; pp. 2874–2881. [Google Scholar]
- Chakrabarti, A.; Satuluri, V.; Srivathsan, A.; Parthasarathy, S. A Bayesian Perspective on Locality Sensitive Hashing with Extensions for Kernel Methods. ACM Trans. Knowl. Discov. Data 2015, 10, 19. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Marra, M. Ordered weighted averaging operators 1988–2014: A citation-based literature survey. Int. J. Intell. Syst. 2014, 29, 994–1014. [Google Scholar] [CrossRef]
- Masciari, E.; Mazzeo, G.M.; Zaniolo, C. Analysing microarray expression data through effective clustering. Inf. Sci. 2014, 262, 32–45. [Google Scholar] [CrossRef]
- Vlamos, P. GeNeDis 2016: Computational Biology and Bioinformatics; Springer Nature: Cham, Switzerland, 2017. [Google Scholar]
- Yu, Z.; Li, T.; Horng, S.J.; Pan, Y.; Wang, H.; Jing, Y. An Iterative Locally Auto-Weighted Least Squares Method for Microarray Missing Value Estimation. IEEE Trans. Nanobioscience 2017, 16, 21–33. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, T.; Sebe, N.; Shen, H.T. A survey on learning to hash. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 769–790. [Google Scholar] [CrossRef] [PubMed]
- Chi, L.; Zhu, X. Hashing techniques: A survey and taxonomy. ACM Comput. Surv. 2017, 50, 11. [Google Scholar] [CrossRef]
- Amazon Elastic Compute Cloud, (Amazon EC2). Available online: https://aws.amazon.com/ec2/ (accessed on 13 July 2018).
- Instance Types of Amazon Elastic Compute Cloud, Amazon EC2 Instance Types. Available online: https://aws.amazon.com/ec2/instance-types/#burst (accessed on 13 July 2018).
- Shirkhorshidi, A.S.; Aghabozorgi, S.; Wah, T.Y.; Herawan, T. Big Data Clustering: A Review. In Proceedings of the International Conference on Computational Science and Its Applications, Guimarães, Portugal, 30 June–3 July 2014; pp. 707–720. [Google Scholar]
- Raghavachari, N.; Garcia-Reyero, N. Gene Expression Analysis: Methods and Protocols; Springer: New York, NY, USA, 2018. [Google Scholar]
- Woo, Y.; Affourtit, J.; Daigle, S.; Viale, A.; Johnson, K.; Naggert, J.; Churchill, G. A comparison of cDNA, oligonucleotide, and Affymetrix GeneChip gene expression microarray platforms. J. Biomol. Tech. JBT 2004, 15, 276. [Google Scholar] [PubMed]
- Kristiansson, E.; Österlund, T.; Gunnarsson, L.; Arne, G.; Larsson, D.J.; Nerman, O. A novel method for cross-species gene expression analysis. BMC Bioinform. 2013, 14, 70. [Google Scholar] [CrossRef] [PubMed]
- Maulik, U.; Mukhopadhyay, A.; Bandyopadhyay, S. Combining pareto-optimal clusters using supervised learning for identifying co-expressed genes. BMC Bioinform. 2009, 10, 27. [Google Scholar] [CrossRef] [PubMed]
- Yeap, W.C.; Loo, J.M.; Wong, Y.C.; Kulaveerasingam, H. Evaluation of suitable reference genes for qRT-PCR gene expression normalization in reproductive, vegetative tissues and during fruit development in oil palm. Plant Cell Tissue Organ Cult. 2014, 116, 55–66. [Google Scholar] [CrossRef]
- Stisen, A.; Blunck, H.; Bhattacharya, S.; Prentow, T.S.; Kjærgaard, M.B.; Dey, A.; Sonne, T.; Jensen, M.M. Smart devices are different: Assessing and mitigatingmobile sensing heterogeneities for activity recognition. In Proceedings of the 13th ACM Conference on Embedded Networked Sensor Systems, Seoul, South Korea, 1–4 November 2015; pp. 127–140. [Google Scholar]
- Stisen, A.; Blunck, H. Heterogeneity Activity Recognition Data Set. UCI Mach. Learn. Repos. 2015. Available online: https://archive.ics.uci.edu/ml/datasets/Heterogeneity+Activity+Recognition (accessed on 13 August 2015).
- Dobbins, C.; Rawassizadeh, R. Towards Clustering of Mobile and Smartwatch Accelerometer Data for Physical Activity Recognition. Informatics 2018, 5, 29. [Google Scholar] [CrossRef]
- Kafle, S.; Dou, D. A heterogeneous clustering approach for Human Activity Recognition. In Proceedings of the International Conference on Big Data Analytics and Knowledge Discovery, Porto, Portugal, 6–8 September 2016; pp. 68–81. [Google Scholar]
- Hebrail, G. Individual household electric power consumption Data Set. UCI Mach. Learn. Repos. 2012. Available online: https://archive.ics.uci.edu/ml/datasets/Individual+household+electric+power+consumption (accessed on 13 August 2012).
- Chang, C.J.; Li, D.C.; Dai, W.L.; Chen, C.C. A latent information function to extend domain attributes to improve the accuracy of small-data-set forecasting. Neurocomputing 2014, 129, 343–349. [Google Scholar] [CrossRef]
- Zhao, Q.; Fränti, P. WB-index: A sum-of-squares based index for cluster validity. Data Knowl. Eng. 2014, 92, 77–89. [Google Scholar] [CrossRef]
- Rathore, P.; Ghafoori, Z.; Bezdek, J.C. Approximating Dunn’s Cluster Validity Indices for Partitions of Big Data. IEEE Trans. Cybern. 2018, 99, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.; Lee, H.; Kang, P. Integrating cluster validity indices based on data envelopment analysis. Appl. Soft Comput. 2018, 64, 94–108. [Google Scholar] [CrossRef]
- Chou, C.H.; Hsieh, Y.Z.; Su, M.C. A New Measure of Cluster Validity Using Line Symmetry. J. Inf. Sci. Eng. 2014, 30, 443–461. [Google Scholar]
- Shi, J.; Qiu, Y.; Minhas, U.F.; Jiao, L.; Wang, C.; Reinwald, B.; Özcan, F. Clash of the titans: Mapreduce vs. spark for large scale data analytics. Proc. VLDB Endow. 2015, 8, 2110–2121. [Google Scholar] [CrossRef]
- Gopalani, S.; Arora, R. Comparing apache spark and map reduce with performance analysis using K-means. Int. J. Comput. Appl. 2015, 113, 1–4. [Google Scholar] [CrossRef]



| DUN | CCR | SYM | ||
|---|---|---|---|---|
| 0.51 | 0.57 | 0.61 | 0.70 | |
| 0.59 | 0.63 | 0.69 | 0.75 | |
| 0.53 | 0.61 | 0.64 | 0.73 | |
| 0.64 | 0.67 | 0.72 | 0.79 | |
| 0.69 | 0.72 | 0.73 | 0.82 |
| DUN | CCR | SYM | ||
|---|---|---|---|---|
| 04 | 0.53 | 0.53 | 0.72 | |
| 0.81 | 0.57 | 0.61 | 0.79 | |
| 0.77 | 0.55 | 0.56 | 0.75 | |
| 0.82 | 0.58 | 0.65 | 0.78 | |
| 0.82 | 07 | 0.71 | 0.82 |
| Method | WB | DUN | CCR | SYM |
|---|---|---|---|---|
| 0.57 | 0.48 | 0.55 | 0.75 | |
| 0.64 | 0.54 | 0.63 | 0.82 | |
| 0.59 | 0.50 | 0.59 | 0.76 | |
| 0.61 | 0.54 | 0.64 | 0.85 | |
| 0.69 | 0.60 | 0.67 | 0.87 |
| Method | WB | DUN | CCR | SYM |
|---|---|---|---|---|
| 0.74 | 0.64 | 0.66 | 0.76 | |
| 0.78 | 0.65 | 0.68 | 0.78 | |
| 0.81 | 0.67 | 0.70 | 0.82 | |
| 0.82 | 0.66 | 0.69 | 0.83 | |
| 0.82 | 0.67 | 0.71 | 0.82 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, B.; Kiani, K. A Robust Distributed Big Data Clustering-based on Adaptive Density Partitioning using Apache Spark. Symmetry 2018, 10, 342. https://doi.org/10.3390/sym10080342
Hosseini B, Kiani K. A Robust Distributed Big Data Clustering-based on Adaptive Density Partitioning using Apache Spark. Symmetry. 2018; 10(8):342. https://doi.org/10.3390/sym10080342
Chicago/Turabian StyleHosseini, Behrooz, and Kourosh Kiani. 2018. "A Robust Distributed Big Data Clustering-based on Adaptive Density Partitioning using Apache Spark" Symmetry 10, no. 8: 342. https://doi.org/10.3390/sym10080342
APA StyleHosseini, B., & Kiani, K. (2018). A Robust Distributed Big Data Clustering-based on Adaptive Density Partitioning using Apache Spark. Symmetry, 10(8), 342. https://doi.org/10.3390/sym10080342





