Abstract
Secret image sharing (SIS) with small-sized shadow images has many benefits, such as saving storage space, improving transmission time, and achieving information hiding. When adjacent pixel values in an image are similar to each other, the secret image will be leaked when all random factors of an SIS scheme are utilized for achieving small sizes of shadow images. Most of the studies in this area suffer from an inevitable problem: auxiliary encryption is crucial in ensuring the security of those schemes. In this paper, an SIS scheme with small-sized shadow images based on the Chinese remainder theorem (CRT) is proposed. The size of shadow images can be reduced to nearly of the original secret image. By adding random bits to binary representations of the random factors in the CRT, auxiliary encryption is not necessary for this scheme. Additionally, reasonable modifications of the random factors make it possible to incorporate all advantages of the CRT as well, including a () threshold, lossless recovery, and low computation complexity. Analyses and experiments are provided to demonstrate the effectiveness of the proposed scheme.
1. Introduction
The security of important information transmitted over insecure communication channels is attracting increasing attention. In particular, the transmission of images has become commonplace, so image security is becoming a higher concern. Previous literature has mainly focused on three aspects, including image encryption, image steganography, and secret image sharing (SIS). Image encryption was subject to the earliest research, and more advanced cryptographic methods are developing. Image steganography is the art of hiding secret information into an innocent-looking cover image. However both of these techniques create only one file to hold all secrets, which may lead to the failure of communication if this one item is lost or damaged. On the other hand, if duplicates are used to overcome this weakness, the danger of exposing the secret image increases. SIS [1,2] is a solution to the above risks.
In fact, SIS is the expansion of secret sharing (SS) of an image. At the very beginning, SS was a key safeguarding scheme put forward by Blakley [3] and Shamir [4] independently. It divided a block of data into n pieces, and any k or more pieces could reconstruct the original data, while any or fewer pieces left it undetermined. This kind of scheme is called the threshold. It is successful in guaranteeing the security of keys. However, with secret images, the number of bytes becomes much larger, and the pixel value is bounded in a specific range (for example, 0–255 for gray-scale images). In this case, using the SS scheme directly may waste a lot of storage space and computation time. So Thien and Lin [5] extended Shamir’s SS scheme to deal with digital images in 2002, which was the first threshold secret image sharing (abbreviated as –PSIS) scheme. It is particularly noteworthy that smaller shadow images were generated in their scheme by utilizing all k coefficients of Shamir’s polynomial to share the secret image, so that the size of each shadow image was reduced to of the original size. Inspired by their research, the advantages of smaller shadows have begun to attract interest in this area. These are pointed out as below:
- Saving storage space and transmission time. If each shadow image is the same size as the original secret image, the cost of the storage space and transmission time will be n times or at least k times in a threshold scheme. If the shadow image size is reduced to , the same amount of data is needed in the recovery process. For example, to share 1 GB images using an SIS scheme for a threshold, 5 GB data are generated, and 4 GB is required in the recovery process for the scheme with the same size of shadow images. Meanwhile, only 1 GB shadow images are sufficient for reconstruction in Thien and Lin’s –PSIS scheme, which has smaller shadow images.
- Easier process for image hiding. The shadow images produced by SIS are usually noise-like, which tend to attract more attention from an adversary or warden. So, image hiding after sharing is desired in storage and transmission for better security. Many image hiding methods [6,7] require that the embedded image should be at least 1/2 (or even 1/4) smaller than the size of the cover image. In such cases, it is more valuable to have smaller shadow images in a secret image sharing scheme.
Consequently, many studies have been devoted to researching the properties of small shadow images. As we all know, a lossy experiment was implemented in Thien and Lin’s –PSIS scheme, in which all pixel values more than 250 of the secret image were truncated to less than 251. Therefore, if the pixel value is 251–255, at least 1 bit or at most 3 bits will be changed. In order to minimize the number of modified bits, a cyclical shift was done in Kanso and Ghebleh’s study [8]. For each pixel value more than 250 in the secret image, they cyclically shifted the 8-bit binary representation of it one position to the right, so that only the most significant bit needed to be set to 0 for truncation. It reduced the difference between the secret image and the recovered image. The other properties of Thien and Lin’s scheme remained unchanged. A serious flaw, referring to the computational security, in Thien and Lin’s –PSIS scheme was also inherited: fewer than k shadow images might reveal the secret image. More details of the problem were analyzed in Yan et al.’s research [9]. This drawback has been pointed out by many researchers. Most of them intended to solve it by advanced encryption. For example, Guo et al. [10] applied Advanced Encryption Standard (AES) encryption before the sharing process instead of a simple permutation. Then, they shared the encrypted secret image using Thien and Lin’s –PSIS scheme. Finally, the shadows were composed of shadow images and additional keys. The study patched up the computational security defect by using AES encryption before the sharing process. As a result, the security of their scheme depended upon the security of AES. The additional encryption cost more storage space and more computational time. Furthermore, because the size of the shadows in Guo et al.’s scheme was of the secret image plus a short key length, Zhou et al. [11] made a minor improvement. They also used a stronger encryption algorithm, rather than a simple permutation, to generate the encrypted secret image. Then, they subdivided the original image and encrypted image into super blocks, and used XOR operations to embed the key into the encrypted image. At last, they obtained the same-sized shadow images with Thien and Lin’s –PSIS scheme. It seemed to eliminate the obvious additional key. In fact, the key of auxiliary encryption must be recovered before reconstruction of the secret image. Some other studies also tried to solve the computation security problem by adopting more advanced encryption algorithms. Ahmadian et al.’s study [12] was a variation of Thien and Lin’s scheme, too. It used a slightly modified version of All-or-Nothing Transform (SI-AONT) to replace permutation of the secret image for the first step. Then, an information dispersal algorithm based on systematic Reed–Solomon coding was used to generate n shadow images, instead of Shamir’s polynomial. The security of this scheme was also guaranteed by SI-AONT transformation and not the sharing algorithm itself. For sharing a color image with small shadow images, Liu et al. [13] made an attempt. They applied compressed sensing (CS) to the –PSIS scheme before the sharing phase to complete compression and encryption of the secret color image. Next, the compressed and encrypted secret color image was shared using traditional Thien and Lin’s –PSIS scheme. Thus, the reduction of shadow size resulted from compressed sensing(CS). Though their scheme had error-resilient capability, the recovery image was lossy, and computation time was longer. All these properties were due to the additional compression method of CS.
In summary, former SIS schemes with small shadow images were mainly based on –PSIS. They experienced an inevitable weakness, which is that fewer than k shadow images might reveal the secret image if all coefficients are used to share the secret. So, permutation, encryption, or compression has become an integral step before sharing for these schemes. Additionally, the security of SIS with a small shadow size seems to necessarily rely on the strength and safeguarding of the auxiliary key. Also, the recovery image is lossy when p is 251 in these schemes. Finally, computation is more time-consuming due to more complex encryption and decryption algorithms and Lagrange interpolation in the recovery phase.
Compared to Shamir’s original polynomial-based SS, which needs Lagrange interpolation as a fundamental step in the recovery phase, the Chinese remainder theory -based SS has attracted some researchers’ attention for its low computation complexity. The first SS scheme based on the CRT for a threshold was put forward by Mignotte [14] in 1982. However, SIS literature based on the has had little concern for the reduction of shadow image size so far. In Hua et al.’s research [15], they applied Mignotte’s method to implement a threshold scheme with small shadow size. Because there is a lack of random factors in Mignotte’s expression, very complex arithmetic compression coding was used in the scheme before the sharing process to disrupt the similarity of adjacent pixel values in an image. Similar to the above –PSIS schemes, the reduction of shadow size in this scheme was caused by pre-compression too. The security and reduction of shadow images of Hua et al.’s scheme also relied on auxiliary encryption. As a matter of fact, the lack of random factors in Mignotte’s method was solved by Asmuth and Bloom [16] early in 1983. They introduced a big random integer as the random factor to share the secret image directly. The effectiveness was verified in Ulutas et al.’s research [17]. However, the size of the shadow images generated in the study was the same as the original secret image. Investigation has shown that studies focusing on the reduction of shadow image size based on Asmuth Bloom’s method are scarce to this day.
In short, former SIS schemes with small shadow sizes were mainly built on additional permutation, encryption, or compression of the secret image before the sharing process. As a result, security and reduction were guaranteed by additional operations and not the sharing procedure itself.
In this paper, a scheme with a small shadow size based on the is proposed. It utilizes a scheme named –CRTSIS [18], which was developed from Asmuth Bloom’s method. The advantages of the –CRTSIS scheme are the threshold, lossless recovery, and low recovery computation complexity, while the size of the shadow images are the same as the original secret image. To further reduce the size of the shadow images under the proposed scheme, several approaches are carried out. Similar to the –PSIS scheme, all random elements in –CRTSIS are utilized to share the secret image. First, the secret image is translated to binary data. Second, the bits of binary data are taken out in sequence as random element values. In order to get a lossless recovery image, is performed to ensure the value of the coefficient is in the right range, so that 1 bit is dropped per operation of rounding down. Additionally, optional random binary bits are added in each binary sequence to enhance the security of the proposed scheme. These operations subsequently cause randomness. At last, the secret image is divided into small shadow images, which are close to of original size in some cases. Thus the proposed scheme not only reduces the size of shadow images but also eliminates auxiliary encryption. Proper modifications also preserve the positive features of the , including threshold, lossless recovery, and low recovery computation complexity.
The rest of this paper is organized as follows. Section 2 introduces some basic requirements for the proposed scheme. In Section 3, the proposed scheme is presented in detail. Analyses and improvements are given in Section 4. Section 5 displays several examples of experiments to verify our method. Finally, Section 6 concludes this paper.
2. Preliminaries
In this section, some useful background is presented before introducing the proposed scheme, and the main parameters and constraints of –CRTSIS [18] are elaborated briefly.
Asmuth Bloom’s SS scheme, which is the basic theory of –CRTSIS, is presented first. The sharing process is carried out as follows:
Step 1. Choose a set of integers subject to
- .
- for .
where , .
Step 2. Let x denote the secret data, satisfying . Then, , where A is a random integer subject to . It yields A being in .
Step 3. For , is the shadow of the secret data x.
The recovery process aims to solve the following linear congruence equations, which has the only solution for any k shadows:
The solution is where , , and Consequently, the secret data can be recovered as .
Afterward, SIS based on Asmuth Bloom’s SS scheme was implemented in Ulutas et al.’s research [17]. It mapped the pixel values x (corresponding to the secret data), which is larger than p, in the right range and divided the span of A into two intervals corresponding to different pixel values x. Since the pixel values of a gray image are in the range , it leads to the changes in the first two steps in Asmuth Blooms’s scheme:
Step 1. The boundary value p is further clarified as to satisfy the constraints.
Step 2. According to different pixel values of x, the big integer y is computed differently. If , , A is a random integer in , while , , A is randomly picked from integral range . Here, t is a new boundary of two intervals.
Because of the two situations of x in the sharing phase, a comparison is also made in the recovery phase. Let , if , , else . Then, x is the recovered pixel value of the secret image.
Subsequently, –CRTSIS [18] enhanced the performance of the above scheme. It ensures the threshold, together with lossless reconstruction, by computing the boundary values more specifically.
1. In Step 1, the chosen integers are limited to , which is also subject to the original constraints.
2. In Step 2, the boundary values are narrowed and specified. First, the range of A is reduced from to . Second, the segmentation value t is computed as the median . Thus, the sharing phase can be carried out clearly, in line with the strict parameters. If , , A is in , else , A is in .
The reconstructed phase of –CRTSIS is the same as Ulutas et al.’s scheme [17], with two accessorial public parameters p and T.
The –CRTSIS overall acquires the following advantages:
- Lossless recovery. It is well known that in Thien and Lin’s scheme [5], only a lossy experiment was realized. In their experiment, the prime number p was set as 251, so that all the coefficients of Shamir’s polynomial needed to be truncated to less than 251 for reconstructing the secret image successfully. Apparently, the recovery image of Thien and Lin’s –PSIS scheme would be lossy. Although they also provided a lossless method, lack of realization for the solution is not optimal. The previous studies focusing on reducing the size of shadow images were mainly devoted to enhancing the security of the –PSIS scheme, but they did not pay much attention to obtaining a lossless result. In the –CRTSIS scheme, a lossless recovery image can be gained directly without any more complex operations or auxiliary encryptions. Thus, the proposed scheme based on –CRTSIS can obtain a lossless recovered image.
- Low computation complexity. As stated above, Lagrange interpolation is a fundamental step in the recovery phase of Shamir’s polynomial-based schemes. It requires operations to decrypt each pixel of the secret image. For the , only modular operations are needed in reconstruction [16]. This will show a clear priority for dealing with many secret images and large images.
A shortcoming of the –CRTSIS scheme which can be improved is that the size of shadow images is the same as the original secret image. The following Sections of this paper are devoted to solving this problem.
3. The Proposed –CRTSIS with Small Shadow Size
In this section, the proposed SIS scheme with small-sized shadow images based on –CRTSIS is demonstrated in detail. The model of this scheme is shown in Section 3.1. The sharing and recovery algorithms are described in Section 3.2.
3.1. The Proposed Model
The model of the proposed scheme is shown in Figure 1. It is composed of two parts, including the sharing and recovery process. More details of the two processes are described as follows.
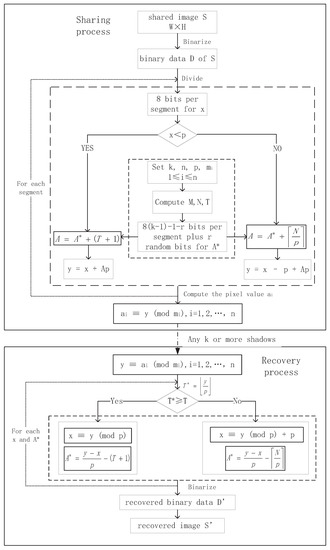
Figure 1.
The model of –CRTSIS (Chinese remainder theorem secret image sharing) with small shadow size.
Sharing process. The secret image is first transformed into a string of binary data D. Then, 8 bits of the string are selected as the value x. Next, x is compared with the unique integer p to generate y. The number of bits used to express coefficient A is , composed of r random bits and bits picked from the binary string D strictly after the former 8 bits, which is proved in Section 4. For n privacy modular integers of , the remainders are the pixel values of the shadow images corresponding to , respectively.
Recovery process. When k or more shadow images are collected, the unique solution y can be derived from Equation (1). The critical value is then computed by
to compare with the public boundary T. Two results of the comparison correspond to the terms of x and y in the sharing process. A couple of x and A would be binarized in sequence for one loop until all pixels of shadow images have been computed. Finally, the recovered binary data is converted to the reconstructed secret image .
3.2. Algorithms
The sharing and recovery algorithms are described in Algorithms 1 and 2, respectively, in this subsection. The inputs, outputs, and each step are elaborated in detail.
| Algorithm 1 The sharing process of –CRTSIS with small shadow size |
|
For Algorithms 1 and 2, we remark that:
- In Step 1 of Algorithm 1, p, which should be as small as possible [18], is fixed at 128 or 131 in our scheme. It is verified that 131, (which is a prime to guarantee the recoverability), is a better value.
- Compared to the original –CRTSIS, N is another public parameter in our scheme for the demand of recovering A in Step 3 of Algorithm 2.
- In Step 3 of Algorithm 1, the number of bits needed to represent the integer A is . This number is equal in the two situations, which are or . This is proved in Section 4.1.
- In Step 5 of Algorithm 1 and Step 3 of Algorithm 2, there is a translation of A to generate y or recover the secret binary data. Because in the original –CRTSIS scheme, when , and when . Yet, for a binary string of bits, the decimal value is in . So, it needs an add operation to move the value of the binary string to the right interval of A in the sharing process, and a minus operation to move back in the recovery process.
- In our scheme, the random coefficient A consists of r random bits and bits picked up from the binary data of the secret image. Accounting for the fact that adjacent pixels in an image are often continuous, the r random bits are utilized to enhance the randomness of integer A. The range of r is . The bigger r is, the more secure our scheme is. For natural images, performs well, and for images with lots of consecutive pixels, is adequate. With the increase of r, the size of the shadow images is enlarged, which is even the same as the original secret image when k = 2 and r = 7. This is exhibited in Section 5.3.
| Algorithm 2 The recovery process of –CRTSIS with small shadow size |
|
4. Performance Analysis
A secret image sharing scheme based on –CRTSIS with small shadow size is proposed in this paper. There are two aspects to be analyzed in this section. One is a reduction of the shadow image size, the other is the security of this scheme.
4.1. Reduction of Shadow Image Size
Reduction of shadow image size in our scheme is . It is proved through the following three theorems step by step.
Theorem 1.
The bits to represent A are equal for two intervals, which are and .
It is known that A is random in . T, which is the boundary of two intervals, is computed as the median.
Thus, two intervals are and corresponding to and , respectively. For A which is used to share the secret image pixels in our scheme, and pixel values that start from 0, the two intervals are transferred to and .
Thus, the length of these two intervals are:
When ,
When ,
It proves . Thus, Theorem 1 is proved.
Theorem 2.
For lossless reconstruction, A has a capacity of bits.
It was computed in Theorem 1 that the length of A is . Here, we prove the maximum number of bits that can be contained in A is .
For the constraint of the integers , p is as small as possible while is as large as possible, thus, is close to 2. It means that and will not affect the number of bits. The last small constant 1 also can be dropped. Thus, the computation is simplified as
Then
In order to get lossless recovery image, the max number of bits that can be contained in A is .
Theorem 3.
Reduction of shadow image size is for our lossless scheme.
As proved in Theorem 2, the maximum number of bits contained in A is fixed as . In our sharing process described in Section 3, x contains another 8 bits data of the secret image. Thus, 1 pixel, which is 8 bits of a shadow image, corresponds to bits of the secret image. Moreover, r random bits are added to them to enhance the security of our scheme, thus, the reduction ratio can be computed as
Consequently, the reduction of shadow image size in our scheme is .
4.2. Analysis of Security
In this subsection, the security of our scheme is proved by theoretical analysis. It includes both the randomness of the shadow images and satisfaction of the threshold.
Lemma 1.
There are no leakages in shadow images generated by the proposed scheme.
Proof.
As illustrated in Section 3.2, a pixel value is determined by y and , where is fixed early. Because when , and when , variations can only be x or A. x is a pixel value varied according to the secret image. A is a big integer expressed by bits which are composed of r random bits and bits selected from the secret image. In order to keep the value of A variation as large as possible, r random bits are arranged at high positions of bits.
Accounting for the range of x in two conditions, x and in two expressions are both in actually. For , bits of binary data is in the range of . Due to , can cover all possible values in . As a result, the pixel value of shadow images is approximately random in . However, the randomness is related to the secret image and the number of random bits in A. It has great performance for natural images and can be enhanced by increasing r random bits, which is displayed in Section 5.
Thus, Lemma 1 is proved to be met. ☐
Lemma 2.
The secret image can be recovered losslessly by any k or more shadow images in the proposed scheme.
Proof.
Due to or , and p is fixed at the sharing process, the recovered pixel value x is thus only determined by y. According to the CRT, when k or more shadow images are collected, there exists only solution y modulo , since . Then, x is gained by Step 3 in Algorithm 2. The secret image is shared and recovered as a string of binary data without any truncation. Thus, the recovered image is lossless.
Lemma 2 is proved. ☐
Lemma 3.
No clue of the secret image is given by any or fewer shadow images in the proposed scheme.
Proof.
When shadow images are collected, there is one solution modulo , where . Nevertheless, the true solution is , which is different from absolutely. Since , and , there are also other solutions in , which are for the collected equations in Equation (1). Thus, no clue of the secret image is given by any or fewer shadow images. ☐
5. Experiments and Comparisons
In this section, experiments are described to verify the effectiveness of the proposed scheme and prove the theoretic analysis in Section 4. Comparisons of Thien and Lin’s –PSIS without pre-encryption and our scheme are listed in Section 5.2. Finally, further discussions are given to enhance the security of our scheme by increasing the random bits r.
5.1. Experiments
In this subsection, and threshold experiments are presented, which are provided to verify that our scheme can satisfy the threshold. It indicates that our scheme has the general threshold. It takes as an example for random bits added in A, which is good enough for ordinary natural images.
In Figure 2, results of a threshold is utilized to demonstrate the effectiveness of the threshold in our scheme, with . Figure 2a is the original secret image S with pixels. Figure 2b–d are noise-like shadow images with the small size of pixels, which is . Figure 2e is an example of the image recovered by two shadow images, which is less than the threshold . It is a bit different from the noise-like image but has no leakage of visual information of the secret image. The security of shadow images and recovery images is further analyzed through their histograms in Figure 3.

Figure 2.
An experimental example of the proposed scheme for threshold. (a) The original secret image S (); (b–d) shadow images corresponding to (); (e) recovery image from shadow images with ; (f) recovery image S’ by all three shadow images.
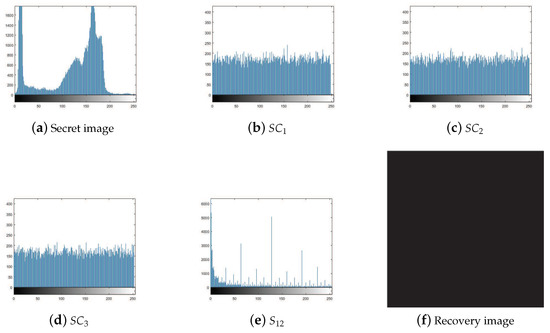
Figure 3 displays the histograms of the experimental results shown in Figure 2. Histograms in Figure 3b–d indicate that the pixels of the shadow images are indeed distributed randomly. The histogram of the recovery image, which is reconstructed by two shadow images, is not similar to the original secret image (shown in Figure 3a) at all. It means that there is no leakage of the secret image when shadow images are collected below the threshold. Also, our scheme is a lossless recovery method, as verified by the difference image, which is all black, shown in Figure 3f.
In Figure 4, the experimental results are not listed completely. Figure 4a,b are the original secret image and its histogram. Figure 4c is an example of the shadow images with , and Figure 4d is its histogram. Figure 4e,g,i are the instances of recovery images corresponding to , and Figure 4f,h,j are their histograms, respectively. Figure 4k,l show the difference between the recovery image and the secret image when more than the threshold shadow images are collected. Figure 4c,d shows that the pixels of shadow images in our scheme are entirely random. Figure 4e–j verifies the threshold of our scheme, which means that there is no leakage when less than k shadows are collected, and the secret image can be reconstructed losslessly when k or more than k shadows are gained.
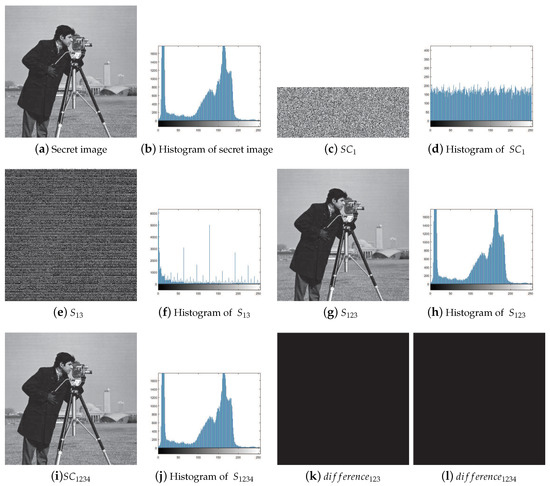
Figure 4.
An experimental example of the proposed scheme for threshold. (a) Original secret image S (); (b) histogram of (a); (c) a shadow image corresponding to (); (d) histogram of (c); (e) recovery image of shadow images with ; (f) histogram of (e); (g) recovery image of shadow images with ; (h) histogram of (g); (i) recovery image S’ by all four shadow images; (j) histogram of (i); (k) difference between (g) and (a); (l) difference between (i) and (a).
The two above experiments prove that our scheme based on –CRTSIS with small shadow size is feasible and secure.
5.2. Comparisons
A threshold experiment is presented in this subsection, which is used to compare with the experimental results shown in Thien and Lin’s scheme [5].
Thien and Lin’s –PSIS scheme was based on Shamir’s SS, which shared the secret data by using a degree polynomial, as shown in Equation (2), in which p is a prime to guarantee the recoverability.
However, there are two disadvantages in Thien and Lin’s –PSIS: In Shamir’s original algorithm, only is used to embed the secret message, while are random integers. In this way, shadow images are generated with the same size as the original secret image. To reduce the size of each shadow image, all coefficients in Equation (12) are utilized for sharing in Thien and Lin’s –PSIS. It means that are all pixel values selected from the secret image S. The size of the generated shadow images are thus of the original secret image. For the reason that adjacent pixel values in the same image may be consecutive, when all coefficients of the polynomial are replaced by pixel values of the secret image, it diminishes the randomness of the integers. As a result, pre-permutation is essential for Thien and Lin’s scheme.
Additionally, should be limited to , since in Equation (12). However, the gray-scaling image has 256 gray levels from 0 to 255. Therefore, pixel values more than 250 are all truncated to less than 251. Consequently, the recovery image in Thien and Lin’s scheme is a lossy result. Although the recovered images by this technique look similar to the secret images, they cannot satisfy the requirement of lossless recovery in certain application scenarios.
A lossless solution was also advised in their paper. It split the pixel values of more than 250 to two partitions, first 250, then . Thus, the size of shadow images will vary a lot according to the statistics of the secret image pixels. Nevertheless, the lossless experimental result was not displayed for the complex solution.
The two disadvantages of Thien and Lin’s scheme is presented in Figure 5. It can be seen that significant parts of the secret image are revealed in the four shadow images (Figure 5e–h) without pre-permutation, and lossy pixels exist in the recovery image indeed when pixel values are more than 250 in the original secret image. The differences are shown in Figure 5d, where the white parts are different pixels between the recovery image and the secret image.

Figure 5.
Thien and Lin’s scheme without pre-permutation for threshold. (a) Original secret image S (); (b) an example of recovery image S’ by 2 shadows; (c) recovery image S’ by 4 shadows; (d) difference between (c) and (a); (e–h) 4 shadow images ().
In our scheme, the only random factor, which is the big integer A in the linear congruence equations, is also used to share the secret image. Firstly, the pixel values of the secret image are multiplied in groups to express A. Secondly, is done to A to get lossless reconstruction, so that a shift occurs for each loop. For a further step, r random bits are added in A to enhance the security of the proposed scheme. Above all, noise-like shadows can be generated by our scheme without pre-encryption, which is shown in Figure 6. Also, no truncations are manufactured in our scheme, so no lossy pixels are produced in our scheme either. The compared image is also shown in Figure 6d with all black pixels.

Figure 6.
The proposed scheme for threshold. (a) Original secret image S (); (b) an example of recovery image S’ by 2 shadows; (c) recovery image S’ by 4 shadows; (d) difference between (c) and (a); (e–h) 4 shadow images ().
5.3. Discussion
As mentioned in the algorithms of the proposed scheme in Section 3.2, the randomness of coefficient A is enhanced by increasing the number of random bits r in A. The range of r is . The bigger r is, the more secure our scheme is. In Section 5.1, the experimental results with are elaborated. This is sufficient for natural images when r is small. However, if the secret image has lots of continuous pixel values, it needs more random bits to guarantee the security of the method.
Figure 7 is a secret image with lots of continuous pixels. Though the shadow images are still noise-like in Figure 7b, the outline of the secret image may be revealed a little when less than the threshold for shadows are collected when , as shown in Figure 7c. The problem can be solved by increasing random bits of A. As shown in Figure 7e, there is no leakage for the same parameters as Figure 7c, except . Nevertheless, security is strengthened as the size of shadow images is enlarged from to . Furthermore, when and , there will be no reduction of the size of the shadow images for .

Figure 7.
Experimental results of the continuous image for threshold. (a) The original secret image S (); (b) a shadow image corresponding to when , with size of ; (c) recovery image of shadows with when ; (d) a shadow image corresponding to when , with size of ; (e) recovery image of shadows with when ; (f) difference between recovery image S’ and secret image S when .
Based on the above analyses and discussions, the priorities of our scheme can be concluded as follows.
- Reduction of shadow images. In the proposed scheme, x and A in the formula of the are all used to share the secret image. As illustrated in Section 4.1, reduction of shadow image size is .
- No pre-encryption. The number of bits contained in A is . There is always 1 bit dropped and r random bits added in one sharing step. The two operations guarantee the randomness of our scheme. Consequently, the security of the scheme relies on the sharing scheme itself and not additional encryption.
- Imperceptibility. Every single shadow image is noise-like, for the pixel values are approximately uniform in distribution. Any or fewer shadows give no clue about the secret image.
- Losslessness. Our scheme is built on a lossless –CRTSIS method, and the number of bits used to share is limited to the floor of A. Consequently, the reconstruction of secret image S is lossless.
- Low computation complexity. Compared to operations needed in the recovery phase of the polynomial-based scheme due to Lagrange interpolations, it requires only operations of modular method based on –CRTSIS [16].
6. Conclusions
In this paper, we proposed a secret image sharing scheme with small-sized shadow images. Compared to previous research in this area, the proposed scheme exhibits many positive features. On the one hand, our scheme successfully reduces the size of the shadow images using the CRT, which has been paid less attention in previous studies. By using the CRT for SIS, it avoids the computational complexity problem caused by Lagrange interpolation in the recovery phase of the –PSIS scheme. On the other hand, by using –CRTSIS and controlling the value of random factors in CRT representations, our scheme can gain a lossless recovery image. Most important of all, sufficient reduction of shadow images is implemented by adding random bits into binary representations of random factors in the CRT. Consequently, there is no auxiliary encryption required in our scheme, which avoids the risk of attacks on additional keys. It has been proved that our scheme is effective enough for natural images, even the images with lots of continuous pixel values.
Furthermore, our scheme can achieve nearly of the original secret image size (when ) for natural images. Even for images with lots of continuous pixel values, our scheme is effective enough by increasing the number of random bits, although the size of the shadow images is a bit larger than . For binary images, the results are yet unsatisfactory. In order to guarantee security, pre-encryption may be necessary. This topic should be studied in future work.
Author Contributions
Conceptualization, J.C. and X.Y.; Data curation, L.L., X.Z. and L.T.; Formal analysis, J.C.; Funding acquisition, X.Y. and K.L.; Methodology, X.Y. and K.L.; Supervision, K.L.; Validation, J.C. and L.L.; Writing—Original Draft, J.C.; and Writing—Review and Editing, J.C., K.L. and X.Y.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Numbers: 61602491) and the Key Program of the National University of Defense Technology (Grant Number: ZK-17-02-07).
Acknowledgments
The authors are thankful to the reviewers for their comments and suggestions to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, P.; Liu, Z.; Yang, C.N. A construction method of (t, k, n)-essential secret image sharing scheme. 2018, 65, 210–220. [Google Scholar]
- Liu, X.; Wang, S.; Yan, X.; Zhang, W. Random grid-based threshold visual secret sharing with improved visual quality and lossless recovery ability. Multimed. Tools Appl. 2017. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the IEEE National Computer Conference, Chicago, IL, USA, 6–8 November 1979; IEEE Computer Society: New York, USA, 1979; pp. 313–317. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Thien, C.C.; Lin, J.C. Secret image sharing. Comput. Graph. 2002, 26, 765–770. [Google Scholar] [CrossRef]
- Wu, D.C.; Tsai, W.H. Spatial-domain image hiding using image differencing. IEEE Proc. Vis. Image Signal Process. 2002, 147, 29–37. [Google Scholar] [CrossRef]
- Chae, J.J.; Mukherjee, D.; Manjunath, B.S. A Robust Data Hiding Technique Using Multidimensional Lattices. In Proceedings of the IEEE International Forum on Research and Technology Advances in Digital Libraries, 1998 (ADL 98), Santa Barbara, CA, USA, 22–24 April 1998; p. 319. [Google Scholar]
- Kanso, A.; Ghebleh, M. An efficient (t, n)–threshold secret image sharing scheme. Multimed. Tools Appl. 2017, 76, 16369–16388. [Google Scholar] [CrossRef]
- Yan, X.; Lu, Y.; Liu, L.; Wan, S.; Ding, W.; Liu, H. Security Analysis of Secret Image Sharing. In Data Science, Proceedings of the Third International Conference of Pioneering Computer Scientists, Engineers and Educators (ICPCSEE 2017), Changsha, China, 22–24 September 2017; Proceedings Part I; Zou, B., Li, M., Wang, H., Song, X., Xie, W., Lu, Z., Eds.; Springer: Singapore, 2017; pp. 305–316. [Google Scholar] [CrossRef]
- Guo, T.; Liu, F.; Wu, C.K.; Yang, C.N.; Wang, W.; Ren, Y.W. Threshold Secret Image Sharing. In Proceedings of the 15th International Conference on Information and Communications Security, Beijing, China, 20–22 November 2013; pp. 404–412. [Google Scholar]
- Zhou, Z.; Yang, C.N.; Cao, Y. Secret Image Sharing based on Encrypted Pixels. IEEE Access 2018, 6, 15021–15025. [Google Scholar] [CrossRef]
- Ahmadian, A.M.; Amirmazlaghani, M. Computationally secure secret image sharing. In Proceedings of the 2017 Iranian Conference on the Electrical Engineering, Tehran, Iran, 2–4 May 2017; pp. 2217–2222. [Google Scholar]
- Liu, L.; Wang, A.H.; Chang, C.C.; Li, Z.H.; Liu, J.B. A lossy secret color image sharing scheme with small shadows and error-resilient capability. J. Inf. Hiding Multimed. Signal Process. 2015, 6, 246–253. [Google Scholar]
- Mignotte, M. How to Share a Secret. In Proceedings of the Conference on Cryptography, Berlin, Germany, 29 March–2 April 1982; pp. 371–375. [Google Scholar]
- Hua, W.; Liao, X. A secret image sharing scheme based on piecewise linear chaotic map and Chinese remainder theorem. Multimed. Tools Appl. 2017, 76, 7087–7103. [Google Scholar] [CrossRef]
- Asmuth, C.; Bloom, J. A modular approach to key safeguarding. IEEE Trans. Inf. Theory 1983, 30, 208–210. [Google Scholar] [CrossRef]
- Ulutas, M.; Nabiyev, V.V.; Ulutas, G. A new secret image sharing technique based on Asmuth Bloom’s scheme. In Proceedings of the International Conference on Application of Information and Communication Technologies (AICT 2009), Baku, Azerbaijan, 14–16 October 2009; pp. 1–5. [Google Scholar]
- Yan, X.; Lu, Y.; Liu, L.; Wan, S.; Ding, W.; Liu, H. Chinese Remainder Theorem-Based Secret Image Sharing for (k, n) Threshold. In Cloud Computing and Security, Proceedings of the Third International Conference ICCCS 2017, Nanjing, China, 16–18 June 2017; Revised Selected Papers, Part II; Sun, X., Chao, H.C., You, X., Bertino, E., Eds.; Springer: Cham, Switzerland, 2017; pp. 433–440. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).