Abstract
Electric multiple unit (EMU) trains’ high-level maintenance planning is a discrete problem in mathematics. The high-level maintenance process of the EMU trains consumes plenty of time. When the process is undertaken during peak periods of the passenger flow, the transportation demand may not be fully satisfied due to the insufficient supply of trains. In contrast, if the process is undergone in advance, extra costs will be incurred. Based on the practical requirements of high-level maintenance, a 0–1 programming model is proposed. To simplify the description of the model, candidate sets of delivery dates, i.e., time windows, are generated according to the historical data and maintenance regulations. The constraints of the model include maintenance regulations, the passenger transportation demand, and capacities of workshop. The objective function is to minimize the mileage losses of all EMU trains. Moreover, a modified particle swarm algorithm is developed for solving the problem. Finally, a real-world case study of Shanghai Railway is conducted to demonstrate the proposed method. Computational results indicate that the (approximate) optimal solution can be obtained successfully by our method and the proposed method significantly reduces the solution time to 500 s.
1. Introduction
In China, high-speed railway has become a priority option for the long trip due to its convenience and comfortableness, and it account for 60% of rail total passenger traffic. It has long been a difficult problem for the China Railway (CR) that supply enough available Electric Multiple Unit (EMU) trains in tourist rush seasons to fulfill heavy transportation tasks. The EMU trains are the unique vehicles running on the China high-speed railway. In addition, they have a high purchase cost and complicated maintenance regulations. Therefore, the problem becomes much worse.
The gigh-level maintenance planning (HMP) is an important part of the operation and maintenance management for the EMU trains, which covers the third-level maintenance, the fourth-level maintenance and the fifth-level maintenance. Due to the complex regular preventive maintenance, uneven distribution of passenger flow, limited maintenance capacity of workshop and several weeks for maintenance service time, the EMU trains’ HMP needs to be scheduled in advance, of which the planning horizon lasts for a natural year or more. The HMP’s aim is to provide enough available EMU trains for the long peak period of the passenger flow (such as the Spring Festival and the summer holiday) under the conditions of limited maintenance resources and the regular preventive maintenance policy. The HMP is a prerequisite for the EMU operational plan, the second-level maintenance plan, the job shop scheduling at workshop, and the outsourcing plan for high-level maintenance workloads (see Figure 1).
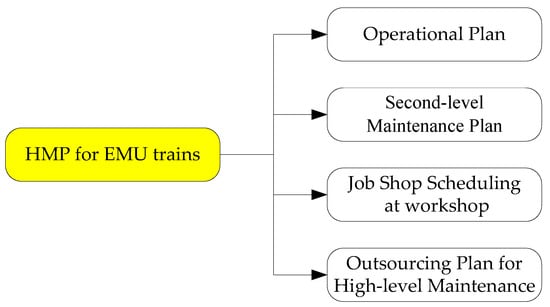
Figure 1.
The position of high-level maintenance plan (HMP) in the operation and maintenance management system for the electric multiple unit (EMU) trains.
In the CR system, according to the maintenance regulations [1], the EMU trains that have been put into operation in the first period will undergo the high-level maintenance (HM) procedures together in the next few years. When lots of EMU trains are sent to workshop in tourist rush season, it will lead to the travel needs of passengers cannot be met. Not only the operating income but also the traveler satisfaction level on high-speed railway transportation will decrease. Meanwhile, it will increase the maintenance costs when the HM procedures are undergone in advance. Due to the limited capacities of workshops, the maintenance service time will be prolonged when plenty of EMU trains undergo the maintenance procedures together. Therefore, to scientifically formulate the HMP that meets the travel demands and reduces maintenance cost as much as possible is a complicated combinatorial optimization problem that needs to be solved in the field of high-speed railway operation.
For the maintenance system, Stuchly et al. [2] and Rezvanizaniani et al. [3] developed a condition based maintenance management system, Shimada [4] introduced the accident prevention maintenance system, and Cheng and Tsao [5] proposed a preventive and corrective maintenances system. These maintenance systems can reduce the maintenance costs and improve the utilization efficiency of EMU train.
Many experts and scholars study the first-level and the second-level maintenances. Maróti and Kroon [6,7] proposed that adjust the operation schedule ahead of time to ensure the maintenance procedures can be undertook in time. Tsuji et al. [8] developed a novel approach based on ant colony optimization and Wang et al. [9] designed an algorithm based column generation to solve the EMU train maintenance plan problem. Giacco et al. [10] integrated the rolling stock circulation problem and short-term maintenance planning, and a mixed-integer linear-programming formulation was proposed.
In other fields, scheduled maintenance planning problems also have been researched. Ziarati et al. [11], Lingaya et al. [12], and Wang et al. [13] studied the locomotive operation and maintenance. Moudania and Félix [14] and Mehmet and Bilge [15] developed the aircraft operation and maintenance. Budai et al. [16] researched the long-term planning of railway maintenance works. In addition, Grigoriev et al. [17] tried to find the length of maintenance plan to minimize the total operation costs.
There are a few relevant literatures available for the EMU trains HMP problem. Lin et al. [18] designed a state function to show the state of EMU train on each day during the planning horizon, and a non-linear 0–1 programming model and its solution strategy was proposed. Wu et al. [19] proposed a time-state network to optimize the EMU trains HMP problem. Li et al. [20] presented a forecast method to estimate the maintenance quantity of the EMU trains in future.
Compared to the existing researches, a 0–1 programming model and solution strategy were proposed. In the mathematic model, all necessary regulations and practical constraints were considered.
The remainder of this paper is organized as follows. The problem description of HMP in the CR system is presented in Section 2. In Section 3, a 0–1 programming model is proposed, and then the solution algorithm on the basis of particle swarm algorithm is designed in Section 4. An empirical case is provided to verify the effectiveness of the model and the algorithm in Section 5. The last section gives some conclusions and the possible areas of further research.
2. HMP Problem at CR
The HMP, a typical discrete system, is a tactical plan that determines when the EMU trains to undergo the high-level maintenance. The length of the planning horizon lasts for about one year. Each train undergoes the high-level maintenance at most once during the planning horizon because of the interval between two adjacent HM processes is longer than the span of planning horizon; the order of the maintenance level for a train is the third-level, the fourth-level, the third-level, the fifth level, the third-level and so on until they are scrapped [1]. Therefore, the level of the high-level maintenance can be deduced beforehand according to the records and regulations of maintenance. According to the maintenance regulations, each train has a time window during which the train can be delivered to workshop on any day. The lower bound of the time window is the earliest date on which a train can be delivered to workshop while the upper bound is the latest date. The detailed problem descriptions can be referred to Lin et al. [18] and Wu et al. [19]. Here, we focus on the generation steps of the time window.
The estimated time of arrival (eta) of the HM can be easily calculated [20]. In this process, the average daily operating mileage is used to describe the daily usage of EMU trains before HM procedures. The notations used in the generation process of the time window are listed in Table 1.

Table 1.
Notations used in the generation process of the time window.
The time window of the start time for the HM can be generated as follows.
Step 1. Take an EMU train from , and calculate the eta of HM [20];
Step 2. According to and , determine the offset range of the operating mileage for the EMU train : [,];
Step 3. Calculate the offset range of the time window for the EMU train : [,];
Step 4. Determine the time window of the EMU train : [,], and set , ;
Step 5. If , turn to Step 6, otherwise turn to Step 1;
Step 6. Set , over.
The EMU train’s time window is continuous if we set the “day” as the minimum time unit. In this way, the time window can be presented by a time interval.
In addition, the HMP aims to ensure that there are enough well-conditioned trains to meet the passenger transport demand. We set a maximum HM rate to guarantee it. The HM rate is the ratio of the number of trains in HM state to the fleet size.
3. Mathematical Model of the HMP Problem
In this section, we propose a 0–1 programming model for the HMP problem. The constraints of the model include the maintenance interval, the passenger transportation demand, and the capacity of workshop. The objective function is to minimize the mileage losses of all EMU trains.
3.1. Notations
The all notations that used in the model are listed in Table 2.

Table 2.
Notations used in the model.
3.2. Optimization Objective
The objective function of the mathematical model is to maximize the service efficiency of the EMU trains, i.e., to minimize the unutilized mileage. In this way, the objective function can be presented as follows.
3.3. Constraints Analysis
According to Section 2, each train can choose one and only one delivery date during the time window. This is the uniqueness constraint.
Any time out of the time window for the train cannot be selected.
The is a variable according to travel demand which should be guaranteed. Theoretically, the value of is different for each day during the planning horizon. To describe this requirement, a set of constraints established as follows.
Because of the various itineraries, the number of the trains with the specific type in the HM state must be less than the given threshold value on the -th day. Constraints in this respect can be expressed as follows.
The number of trains in each level of the HM state should not be exceeded the capacity of workshops. A set of constraints can be listed as follows.
Meanwhile, restricted by the limited resources, only a few trains are permitted to enter the workshop over several days. This situation can be described in the form of mathematical inequalities as follows.
In addition, the logical relationships between those three sets of decision variables are presented as follows.
Finally, all of the decision variables are binary variables.
3.4. Model Construction
On the basis of above analysis, a 0–1 programming model for the EMU train HMP problem is proposed as follows.
We can see from the HMP model that the number of all decision variables equals to that is the product of two factors: the time span of the planning horizon and the number of trains. But the search space will reach according to the model. It is too complicated to be solved by using CPLEX or Gurobi within a reasonable time. Thus, a meta-heuristic solution strategy based on the particle swarm optimization (PSO) algorithm is designed to address this problem.
4. Modified Particle Swarm Optimization Algorithm
PSO algorithm is a population based stochastic optimization technique motivated by social behavior of organisms. PSO algorithm has the advantage of fast convergence speed and high accuracy solution and it is easy to be applied in most areas [21], which makes it attract great attention from researchers. The algorithm can also be used in solving the combinatorial optimization problem [22,23]. In this section, we present a modified particle swarm optimization (MPSO) algorithm to solve the HMP model based on analysis and preprocess.
4.1. Processing of Model Constraints
The constraint conditions of the HMP model need to be processed before applying the MPSO algorithm. Constraints (2), (3), (8)–(12) are the logical relationships, and they can be observed by the specific encoding rules (see the latter section), while the others can be removed by the penalty function method. For the value of the penalty factor, it is necessary to combine the actual application of the EMU trains and the strength of the constraint. Among the Inequations (4)–(7), the Inequation (7) has the strongest constraint and the Inequation (4) has the weakest constraint. The relationship of the penalty coefficient is . The optimization model can be presented as follows.
s.t. (2), (3), (8)–(12).
4.2. General Particle Swarm Optimization Algorithm
In general PSO algorithm, the basic update equations of the velocity and position of the particles are as follows:
where and denote the velocity and the position, respectively, for particle in the iteration. denotes the best position in the history for particle by the end of the iteration; denotes the best position in the history for all of the particles by the end of the iteration. denotes the inertia weight; denotes the self-learning factor; denotes the social learning factor; and are the random numbers in [0, 1].
4.3. MPSO and Solution Strategy
4.3.1. Inertia Weight
In order to make the particles have a better search ability in the early stage of evolution and have a better development ability in the later stage of the evolution, the linear time-varying inertia weight is adopted in this paper. The inertia weight can be calculated as follows.
where denotes the inertia weight at the r-th iteration. and denotes the maximum inertia weight and the minimum inertia weight, respectively. And denotes the maximum number of the evolution iterations.
4.3.2. Learning Factor
In the same way, in order to make the particles strengthen the global search ability in the early stage and converge to the global optimum in the later period, we decrease the self-learning factor and increase the social learning factor continuously during the process of optimization. The calculation formulae are as follows.
where and denote the self-learning factor and the social learning factor in the iteration. and denote the initial value and the final value for the self-learning factor; and denote the initial value and the final value for the social learning factor; they are the constants.
4.3.3. Update Equations
The particle continuously updates its position in the search space at an unfixed speed. The velocity represents the variation of position in magnitude and direction like the definition in classical physics, and it has the same dimension as the position. Let denote the corresponding fitness value of . Let denote the corresponding fitness value of . The fitness value can be calculated by the formula (13). The update equations of the position and velocity for the particle are as follows.
where and are the random numbers in [0,1].
Each dimension of the velocity of a particle is limited to an interval [−, ], and if it is out of the interval, we set the boundary value of the interval as the actual velocity component. Similarly, the components of the position vector are limited to the time window for each train. Let denote the fitness value for .
4.3.4. Encoding Rules and Initial Solution
It is a crucial step to make the particle of the MPSO and the solution of a certain problem correspond with each other. We use a particle to represent an overall HMP for all of the EMU trains. According to Equations (2) and (3), we set the dimensionality of a particle to . The value of each dimension represents the start time of the HM for the corresponding EMU train. The detailed description is shown in Figure 2 with the help of schematic diagram.
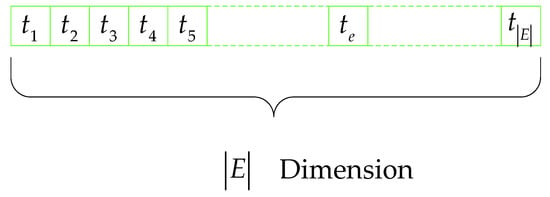
Figure 2.
Encoding Rules (a particle).
In Figure 2, denotes the start time of the HM for the EMU train. Therefore, = 1 when the value of is determined, and the in equals to . Because of the maintenance level and the type of each train can be ensured in advance, the value of and for the train is known. Then, the value of and can be determined accordingly, i.e., = 1 (); = 1 (). In this way, the Constraints (2), (3), (8)–(12) are well handled.
The initial solution can be generated by selecting the start time of the HM during the time window for each train. The selection is stochastic in this process.
4.4. Algorithm Steps
Step 1. Generate the time window for all of the EMU trains that need to be maintained during the planning horizon, turn to Step 2.
Step 2. Initialization. Assign values to related parameters including the size of particle swarm , , , , , , , and . Generate the initial solution according to Section 4.3.1, and generate the initial velocity randomly. Set , turn to Step 3.
Step 3. Calculate the fitness value of each particle, turn to Step 4.
Step 4. Compare the fitness values of with . If < , then = , = . Turn to Step 5.
Step 5. Compare the fitness values of () with . If < , then = , = . Turn to Step 6.
Step 6. Update , and according to Formulas (16)–(18), turn to Step 7.
Step 7. Update and according to Formulas (19) and (20). If any dimension in out of [−, ], we set the boundary value of the interval as an actual value. If any dimension in out of [, ], we set the boundary value of the time window as an actual value, turn to Step 8.
Step 8. . If or = ( > 200), turn to Step 9; otherwise, turn to Step 3.
Step 9. Make feasible according to the HMP model, and output and . Over.
5. Case Study
In this section, we implement the proposed method to solve a practice problem. The detailed description of the case can be found in the literature [20]. The proposed model is solved by the commercial optimization solver, e.g., Gurobi, as well as the MPSO algorithm. The exact method is coded in Python 2.7 and implemented within Spyder 3.1.4 and the MPSO algorithm is implemented in C++. All the computational experiments are conducted on the computer with Intel Core i5-6200U CPU and 8 GB RAM.
According to the literature [20], some parameters are valued as follows. = 115, = 60, = 533. To protect data confidentiality, we can only generate the time window in advance for each train and use an ID number replace the train. The initial conditions of trains when = 0, which include the train ID, type, the average daily operating mileage, the time window, the maintenance level and the maintenance service time, are listed in Table 3.

Table 3.
Initial conditions of all trains.
From Table 3, it can be seen that there are 60 EMU trains will undergo HM procedures during the planning period. Among them, there are 101 candidate dates at most, and the minimum values are only 36 candidate dates.
During the planning horizon, the HM rate is valued as follows:
All of these trains undergo the HM procedures in the factory. The maximal capacity is ten, i.e., . Meanwhile, the receiving capability per day for a factory is limited, e.g., ; = = = = = = = = = 1. According to the demand, = = 4, = 10 (). Therefore, the Formula (13) can be converted to the following form.
In addition, the values of other parameters are as follows. = 0.001, = 100, = 500, = 800, = 1000; = 1000, = 1.2, = 0.8, = 2.5, = 0.5, = 0.5, = 2.5, = (-+1)/2 = 1000.
Based on the data given above, the HMP model is solved by the proposed algorithm. The program runs for 500 s. The returned optimal fitness value is 3,213,121. The curve of the optimal fitness value in the iterative process is depicted in Figure 3.
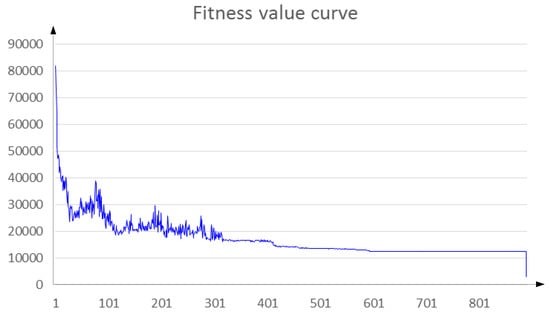
Figure 3.
The optimal fitness value curve.
As can be seen in Figure 3, in the first 300 iterations, the algorithm has a strong search capability, which can effectively avoid the occurrence of the premature phenomena; and from about the 300th to the 690th iteration, the development ability of the algorithm is strengthened, which is helpful to search the optimal solution; the fitness value remains the same in the last 200 iterations, indicating that the (approximate) optimal solution for the HMP problem has been generated. The (approximate) optimal solution is listed in Table 4, and the first column is the train’s ID; the second column is the start date of HM procedures denoted by .

Table 4.
Optimal solution.
We present the daily HM rates from the (approximate) optimal solution, and compare those with the predefined maintenance rate thresholds (see Figure 4).
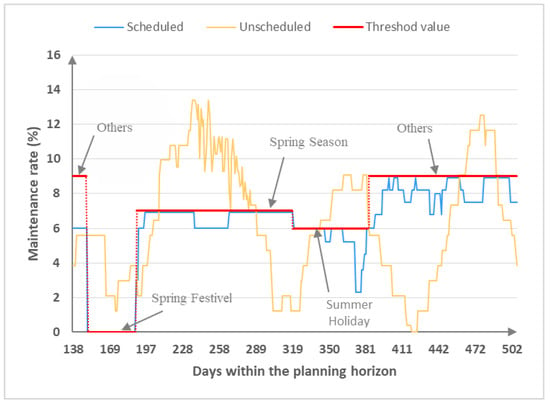
Figure 4.
The distribution of the high-level maintenance rate in 2017.
From Figure 4, we can see that the HM rate of the optimal solution remains below the threshold in each period. Therefore, the proposed HMP model and the algorithm can meet the travel demands. However, the HM rate from the unscheduled solution fluctuates sharply.
In addition, to compare the performance of the proposed algorithm, we solve the HMP model by the Gurobi solver because the HMP model is linear. The detailed numerical comparison results of two solution methods, i.e., the Gurobi and the MPSO algorithm, are shown in Table 5.

Table 5.
Numerical comparison results.
We can conclude that our proposed approach is efficient and effective from Table 5. This result demonstrates that the proposed algorithm is more efficient than the commercial optimization solver with reducing 84.31% in the solution time consumption.
6. Conclusions
This paper researches the electric multiple unit train’s HMP problem. A 0–1 integer programming model and a modified particle swarm optimization algorithm are proposed. The objective function of the model is to minimize the unutilized mileage for all trains, and the model considers the necessary regulations and practical constraints, including passenger transport demand, workshop maintenance capacity, and maintenance regulations. A real-world instance demonstrates that the proposed method can efficaciously obtain the (approximate) optimal solution (see Table 4), and the solution strategy significantly reduces the solution time to 500 s (see Table 5). This result also demonstrates that the proposed algorithm is more efficient than the commercial optimization solver with reducing 84.31% in the solution time consumption. Optimize the workshop’s overhaul process to shorten the maintenance service time is needed in future research.
Author Contributions
The authors contributed equally to this work.
Acknowledgments
This work was supported by the National Railway Administration of the People’s Republic of China under the Grant Number KF2017-015, and the China Railway (formerly Ministry of Railways) under the Grant Number 2015X004-C. We would like to thank Lirong Diao of State Intellectual Property Office of the P.R.C. and Yinan Zhao of Beijing Jiaotong University for her valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- China Railway. User Manual for EMU Operation and Maintenance Procedures, 1st ed.; Railway Publishing House: Beijing, China, 2013. [Google Scholar]
- Stuchly, V.; Grencik, J.; Poprocky, R. Railway vehicle maintenance and information systems. WIT Trans. Built Environ. 2000, 50, 885–894. [Google Scholar]
- Rezvanizanianil, S.M.; Valibeiglool, M.; Asgharil, M.; Barabady, J.; Kumar, U. Reliability centered maintenance for rolling stock: A case study in coaches’ wheel sets of passenger trains of Iranian railway. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 8–11 December 2008; pp. 516–520. [Google Scholar]
- Shimada, N. Rolling stock maintenance for safe and stable transport. Jpn. Railw. Eng. 2006, 46, 4–7. [Google Scholar]
- Cheng, Y.H.; Tsao, H.L. Rolling stock maintenance strategy selection, spares parts’ estimation, and replacements’ interval calculation. Int. J. Prod. Econ. 2010, 128, 404–412. [Google Scholar] [CrossRef]
- Maróti, G.; Kroon, L. Maintenance routing for train units: The transition model. Transp. Sci. 2005, 39, 518–525. [Google Scholar] [CrossRef]
- Maróti, G.; Kroon, L. Maintenance routing for train units: The interchange model. Comput. Oper. Res. 2007, 34, 1121–1140. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kuroda, M.; Imoto, Y. Rolling stock planning for passenger trains based on ant colony optimization. Trans. Jpn. Soc. Mech. Eng. Part C 2010, 76, 397–406. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Miao, J.R. Column generation algorithms based optimization method for maintenance scheduling of multiple units. China Railw. Sci. 2010, 31, 115–120. [Google Scholar]
- Giacco, G.L.; D’Ariano, A.; Pacciarelli, D. Rolling stock rostering optimization under maintenance constraints. J. Intell. Transp. Syst. 2014, 18, 95–105. [Google Scholar] [CrossRef]
- Ziaratia, K.; Soumisa, F.; Desrosiers, J.; Gélinas, S.; Saintonge, A. Locomotive assignment with heterogeneous consists at CN North America. Eur. J. Oper. Res. 1997, 97, 281–292. [Google Scholar] [CrossRef]
- Lingaya, N.; Cordeau, J.F.; Desaulniers, G.; Desrosiers, J.; Soumis, F. Operational car assignment at VIA Rail Canada. Transp. Res. B Meth. 2002, 36, 755–778. [Google Scholar] [CrossRef]
- Wang, L.; Ma, J.J.; Lin, B.L.; Chen, L.; Wen, X.H. Method for optimization of freight locomotive scheduling and routing problem. J. China Railw. Soc. 2014, 36, 7–15. [Google Scholar] [CrossRef]
- Moudania, W.E.; Félix, M.C. A dynamic approach for aircraft assignment and maintenance scheduling by airlines. J. Air Transp. Manag. 2000, 6, 233–237. [Google Scholar] [CrossRef]
- Mehmet, B.; Bilge, Ü. Operational aircraft maintenance routing problem with remaining time consideration. Eur. J. Oper. Res. 2014, 235, 315–328. [Google Scholar] [CrossRef]
- Budai, G.; Huisman, D.; Dekker, R. Scheduling preventive railway maintenance activities. J. Oper. Res. Soc. 2006, 57, 1035–1044. [Google Scholar] [CrossRef]
- Grigoriev, A.; Klundert, J.V.D.; Spieksma, F.C.R. Modeling and solving the periodic maintenance problem. Eur. J. Oper. Res. 2006, 172, 783–797. [Google Scholar] [CrossRef]
- Lin, B.L.; Lin, R.X. An Approach to the high-level maintenance planning for EMU trains based on simulated annealing. arXiv. 2017. Available online: https://arxiv.org/abs/1704.02752 (accessed on 10 April 2017).
- Wu, J.P.; Lin, B.L.; Wang, J.X.; Liu, S.Q. A network-based method for the EMU train high-level maintenance planning problem. Appl. Sci. 2018, 8, 2. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.J.; Jia, Z.K. Forecast method of annual senior over haul amount for EMU. J. Transp. Eng. 2013, 13, 102–107. [Google Scholar]
- Wang, D.W.; Wang, J.W.; Wang, H.F.; Zhang, R.Y; Guo, Z. Intelligent Optimization Method; High Education Press: Beijing, China, 2007; pp. 217–259. [Google Scholar]
- Li, J.; Lin, B.L.; Wang, Z.K.; Chen, L.; Wang, J.X. A pragmatic optimization method for motor train set assignment and maintenance scheduling problem. Discrete Dyn. Nat. Soc. 2016, 3, 1–13. [Google Scholar] [CrossRef]
- Wang, J.X.; Lin, B.L.; Jin, J.C. Optimizing the shunting schedule of electric multiple units depot using an enhanced particle swarm optimization algorithm. Comput. Intell. Neurosci. 2016, 1, 1–11. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).