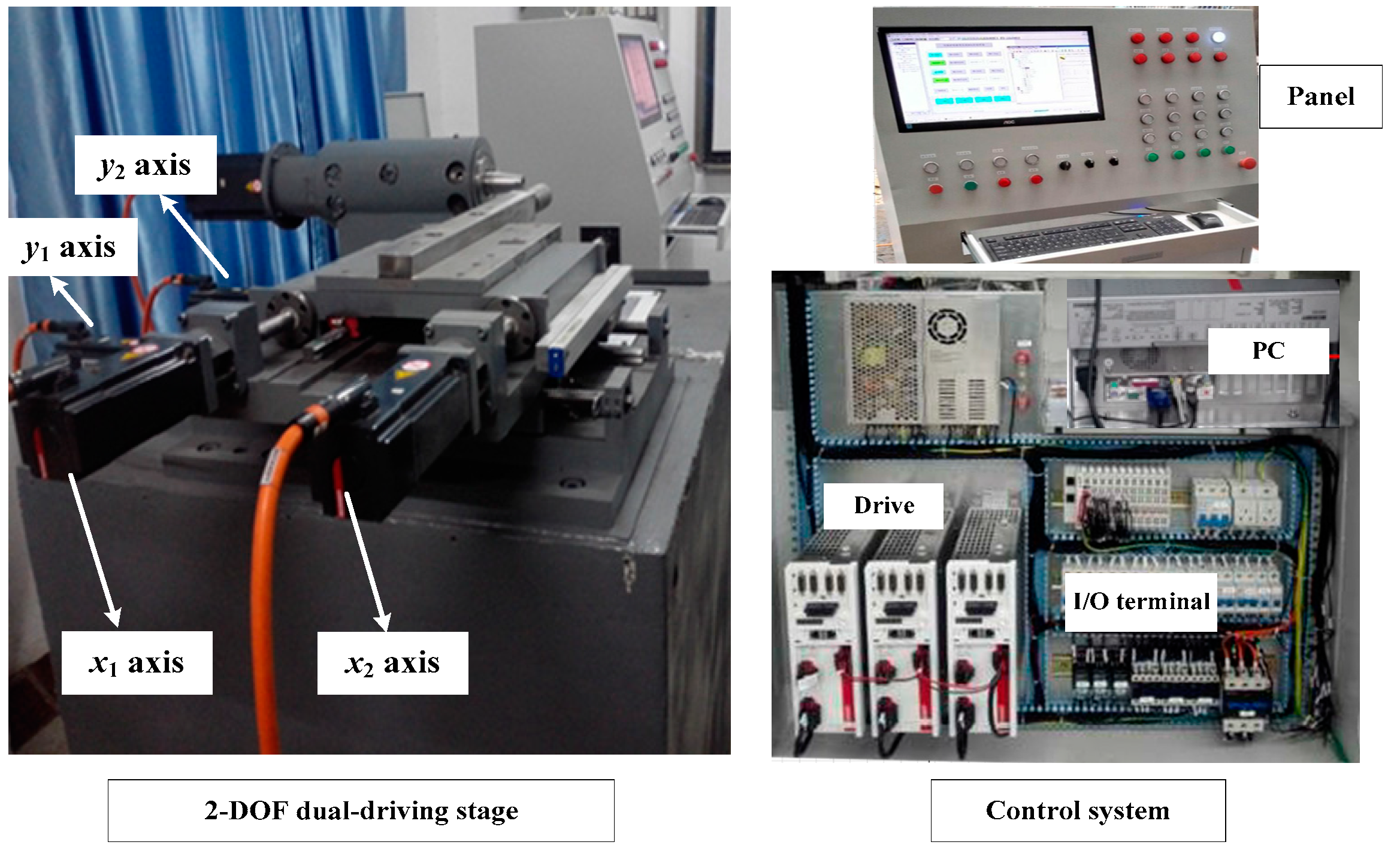
1. Introduction
With the increasing demand for higher precision and greater productivity, modern manufacturing techniques have been in rapid development. Many advanced manufacturing machines such as gantry machine, computer numerical control (CNC) engraving machine, coordinate measurement machine and robotic arms are required to have multi-axis synchronous or coordinated motion [
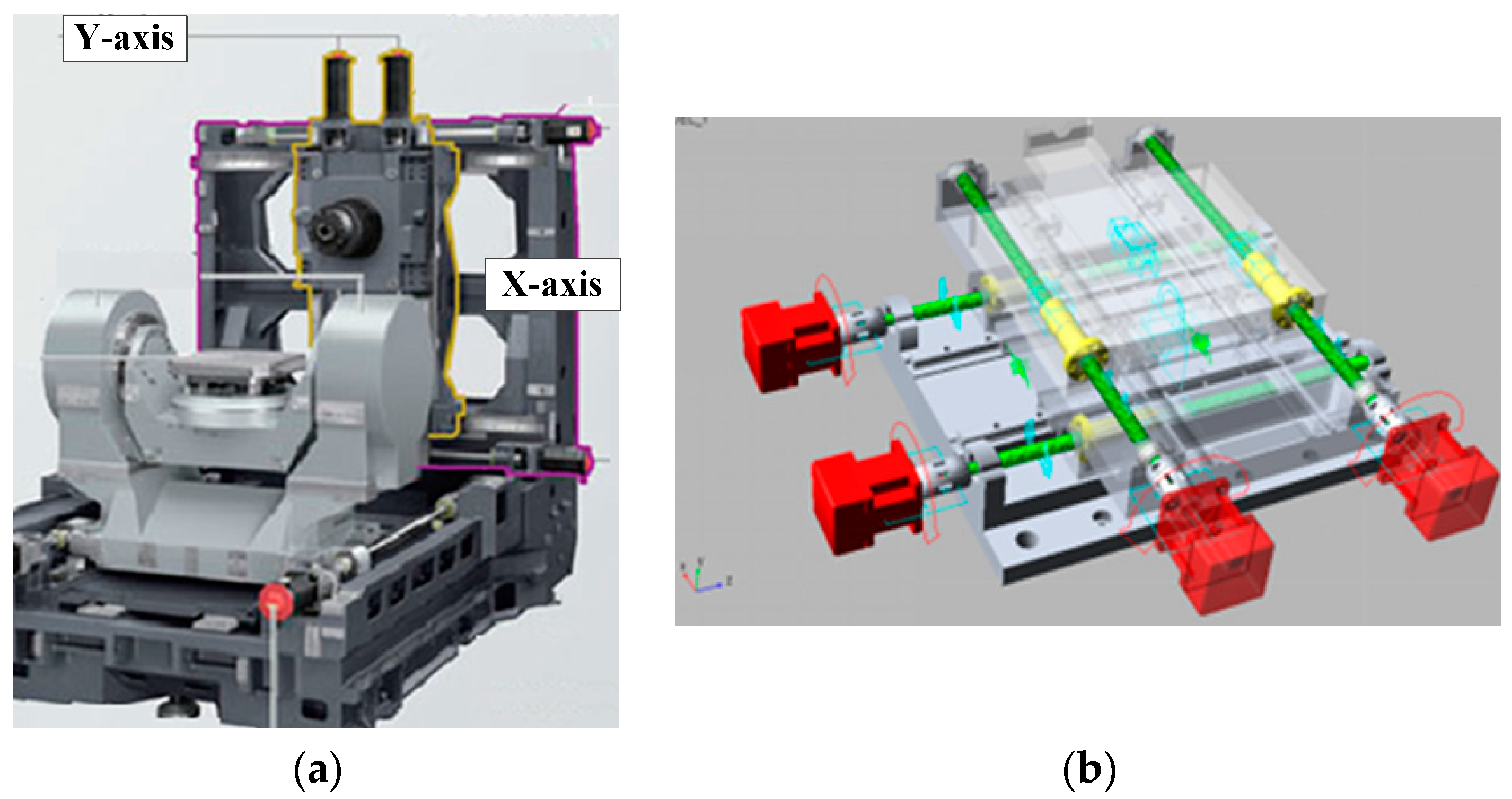
1]. In the configuration of the two-degree-of-freedom (2-DOF) dual-driving feed stage, dual ball-screws and motors are mounted parallel to each other in each feed direction of a planar motion. Since the joint force is provided by double motors and screws, the dual-driving structure can significantly increase the feed rigidity and overall thrust. An innovative industrial implication of 2-DOF dual-driving feed stage is proposed by Mori Seiki [
2]. The stage which is moved by dual motors in its systematic configuration can generate higher acceleration and precision, as shown in
Figure 1.
However, the dual-driving synchronous feed mechanism has also brought some additional concerns. Although the dual axes have the same mechanical structure, the synchronous error is unavoidable due to the unbalanced forces, characteristics diversities, and mechanical coupling of dual axes [
3,
4]. In addition, the damage may even occur when significant desynchronization takes place. The normal industrial motion control is usually performed by widening the bandwidth and improving the resistance capacity against disturbance independently on the single axis, which cannot guarantee the synchronization performance of dual axes. To overcome the drawback, the appropriate control scheme along with the dynamic characteristics analysis is required to satisfy the tracking and synchronization accuracy as the dual-driving stage traces a complex trajectory [
5].
Many researches have explored the errors modelling and compensation methods of machine tools. Some scholars provide the methodology for the estimation of the geometrical errors of the multi-axis machine, based on the Denavit and Hartenberg’s formulation. In this method, the elemental error in each joint has been defined for a multitasking machine and calculated by homogenous matrix [
6,
7]. These error modelling methods are often used in the serial multi-axis machine tool, and can be helpful to the research for error compensation in the dual-driving feed system.
As for the synchronous control, the most recent tandem approach is mechanical rigid coupling. Both axes are joint feeds based on the mechanical line-shaft or connection rods [
8]. However, the performance of mechanical rigid synchronization is heavily dependent on the machining and assembly accuracy and has a poor flexibility when the structure or application changed for its complex structure.
With the development of electrical technology, the master-slave control which follows the tandem structure becomes a potential solution. In master-slave control, the position or velocity signal of the master motor is used as reference command to the slave. For its convenient application, the master-slave control has been adopted widely in industry, such as FANUC Ltd. and speed/torque coupling control in SIEMENS [
9,
10]. In addition, the electronic virtual main shaft control has been developed to eliminate the unbalanced problem based on the master-slave theory [
11]. Nevertheless, the tandem structure generates an unavoidable delay between the dual axes and the load disturbance imposed on the slave axis cannot be fed back to the master, which leads to a poor dynamic synchronization performance.
The cross-coupled control was initially proposed for contour processes and has been extended by many scholars. In cross-coupled control, each axis has its own reference command and feedback. This arrangement allows reflecting any load disturbances presented in both axes by using the additional signal as an additional tracking signal via weighted gains [
12,
13]. However, cross-coupled control is achieved by a synchronous controller. The controller will calculate the position error of dual axis in the closed-loop, which fundamentally makes the dual axis follow and move against each other in high frequency, which is defined by the controller and sampling rate. The following process of dual-driving axes inevitably generates an oscillation of the dual-driving system [
14,
15].
Traditional algorithms such as P, PI, and PID or more robust ones such as adaptive and H-infinity controller can be used in combination with the master-slave and cross-coupled control structure [
16,
17]. The sliding mode control (SMC) is particularly suited to dual-driving systems for its lesser sensitivity to the external disturbances and modeling accuracy. The fuzzy neural network SMC system is proposed to achieve both tracking accuracy and synchronous motion control for dual linear motor motion control system. The fuzzy logic control is presented in some researches to eliminate the unknown dynamics, and the adaptive fuzzy SMC is also proposed to achieve a better performance [
18,
19]. Compared to normal SMC, the terminal sliding mode control (TSMC) guarantees state convergence to sliding surface in finite time. Therefore, the TSMC is suitable for high synchronization performance dual-driving applications [
20]. In our previous work, the cross-coupled fuzzy SMC scheme was designed, while the flexible mechanical driver body model was not taken into consideration [
21].
Many researches have been provided to analyze the forces and disturbances in processing [
22,
23]. Some scholars designed the data acquisition system to simultaneously record the cutting forces and cutting tool positions [
24]. However, to control the dual-driving system, the transmission system is usually developed by the simplified screw transmission ratio, and the mechanical coupling is ignored [
6,
9,
10,
11,
12]. Some scholars studied the dynamic modelling in order to deal with the mechanical coupling disturbance that exists in various dual-driving stages. However, the model usually only takes into account the mass and inertia of the components, and ignores the flexible deformation and vibration of the transmission-mechanism [
13,
14]. Considering the system identification test to obtain the dynamic characteristics of the dual-driving mechanical structure, some scholars develop the lumped parameter model for ball screw system, and design the acceleration feedforward controller based on the transfer function of the overall drive system. The screw system is taken as a rigid body, and the coupling effect due to mechanical linking can be identified as a first-order inertial transfer function [
25,
26], which degrades the accuracy of the dynamic model.
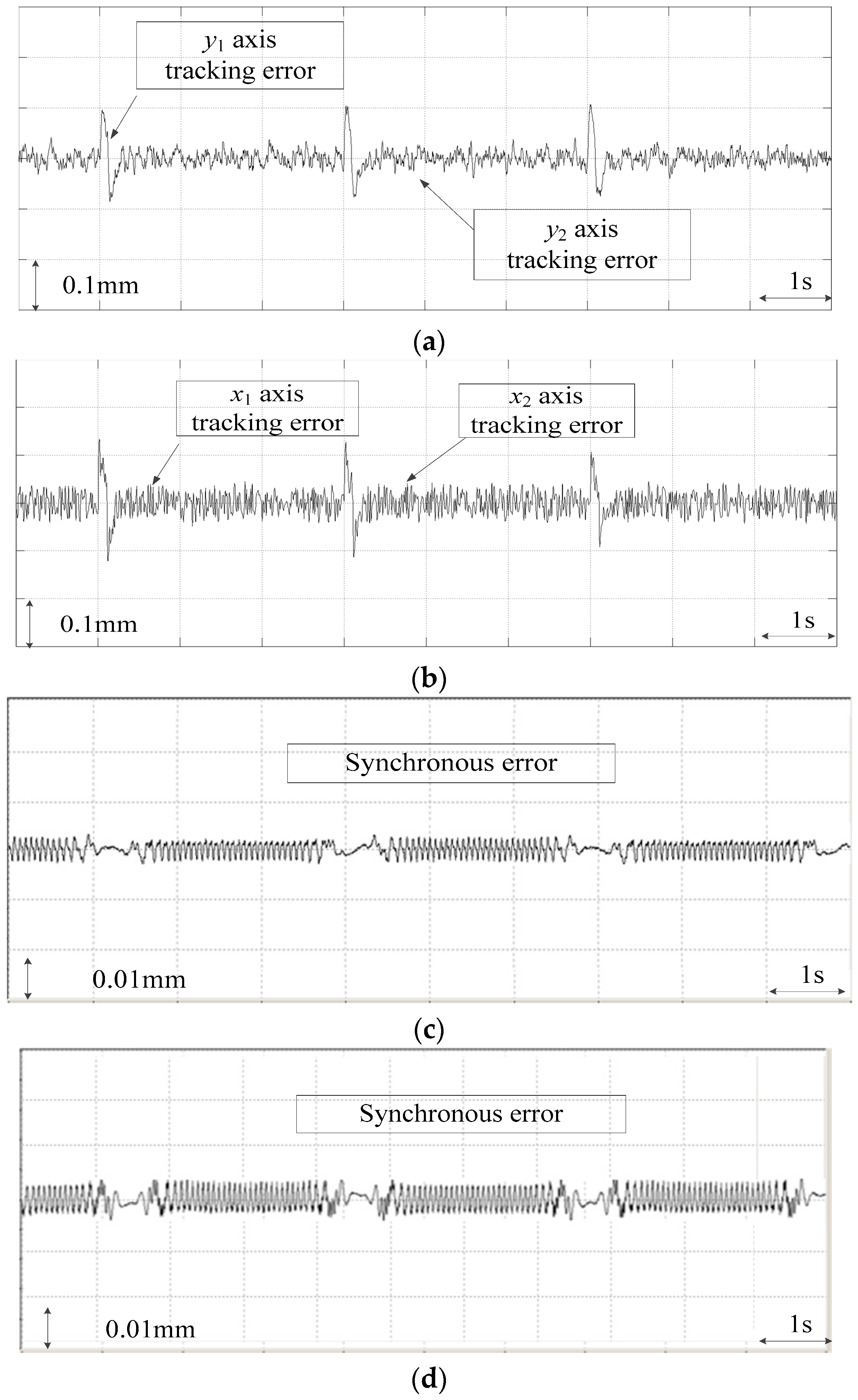
Hence, there are two main problems restricting the development of the dual-driving feed system. Firstly, the synchronization precision is affected by the diversities of system characteristics, transmission features, and vibration. Secondly, the mechanical-coupling can give rise to the desynchronization or even mechanism damage in industry application. Especially in the sudden change of acceleration, the mismatch disturbances between the unbalanced driving force and dynamic characteristics of dual axes will cause a fluctuation of synchronous error. Hence, the characteristics diversity, flexible deformation, and mechanical coupling should be taken into account for dynamic modeling. Based on it, the strategy of the synchronous control should be robust against the coupling between two drives and penalize synchronous errors that are generated due to disturbances, as well as parameter diversities, when performing the TSMC and observer design.
This paper is organized as follows:
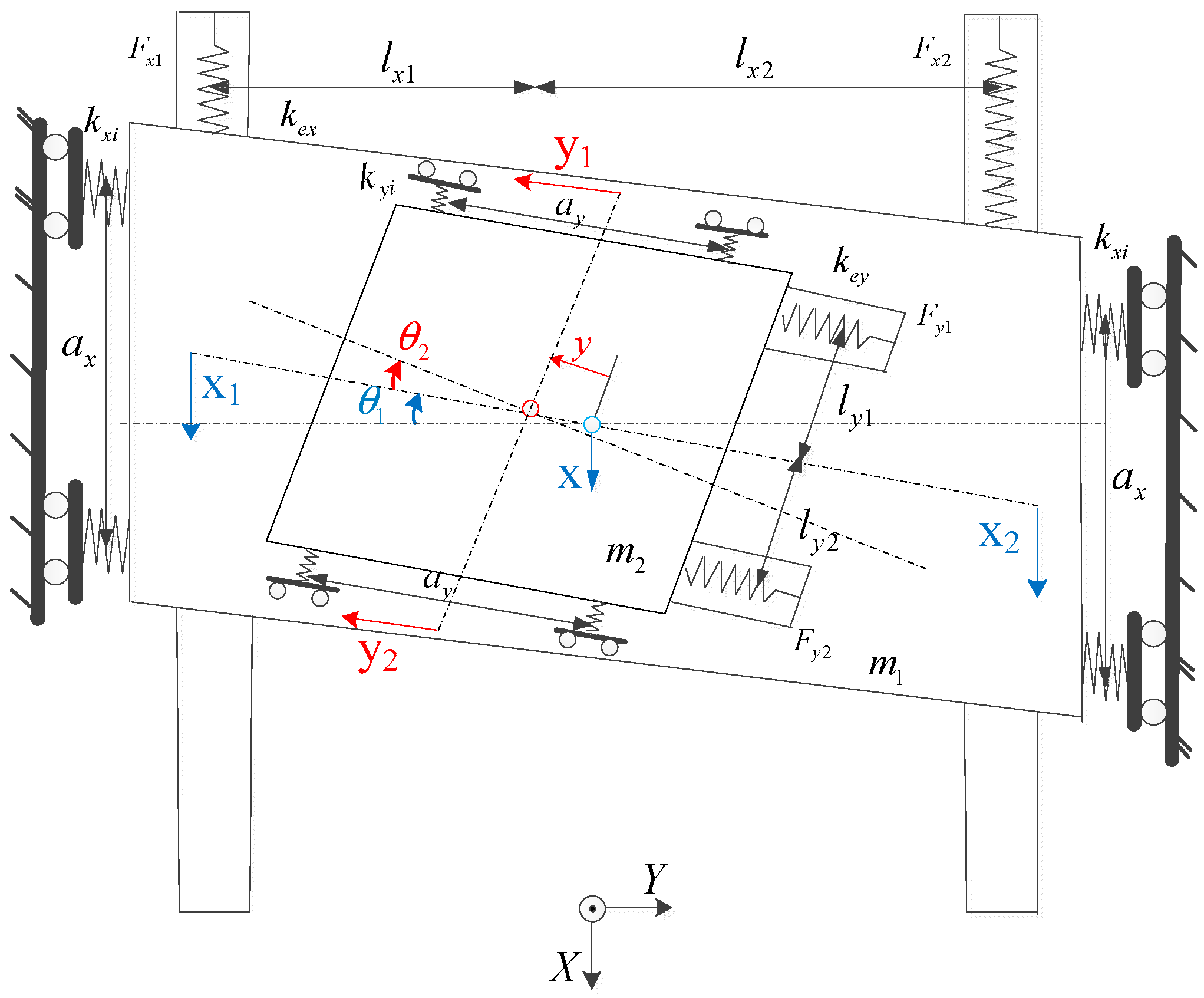
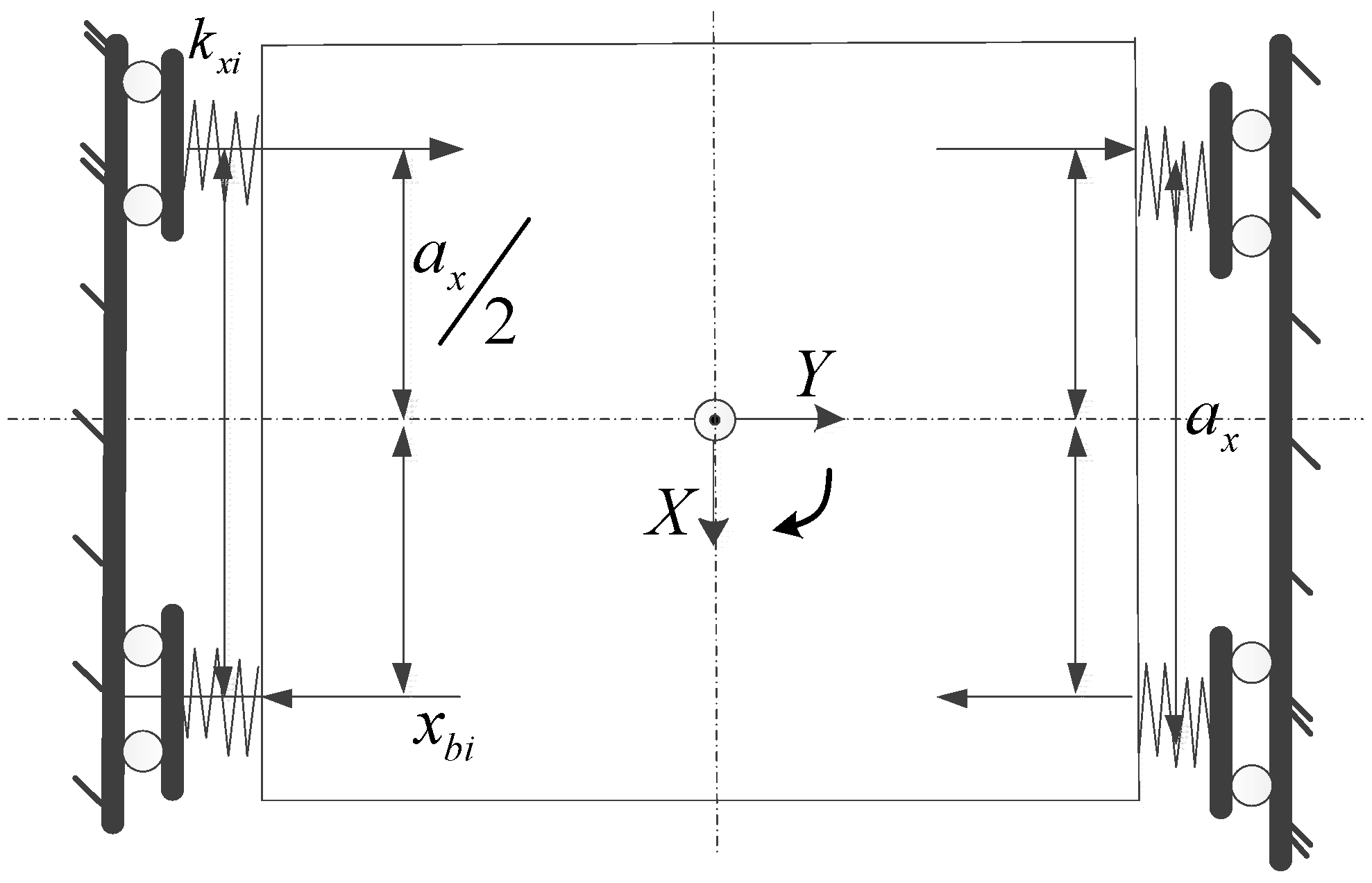
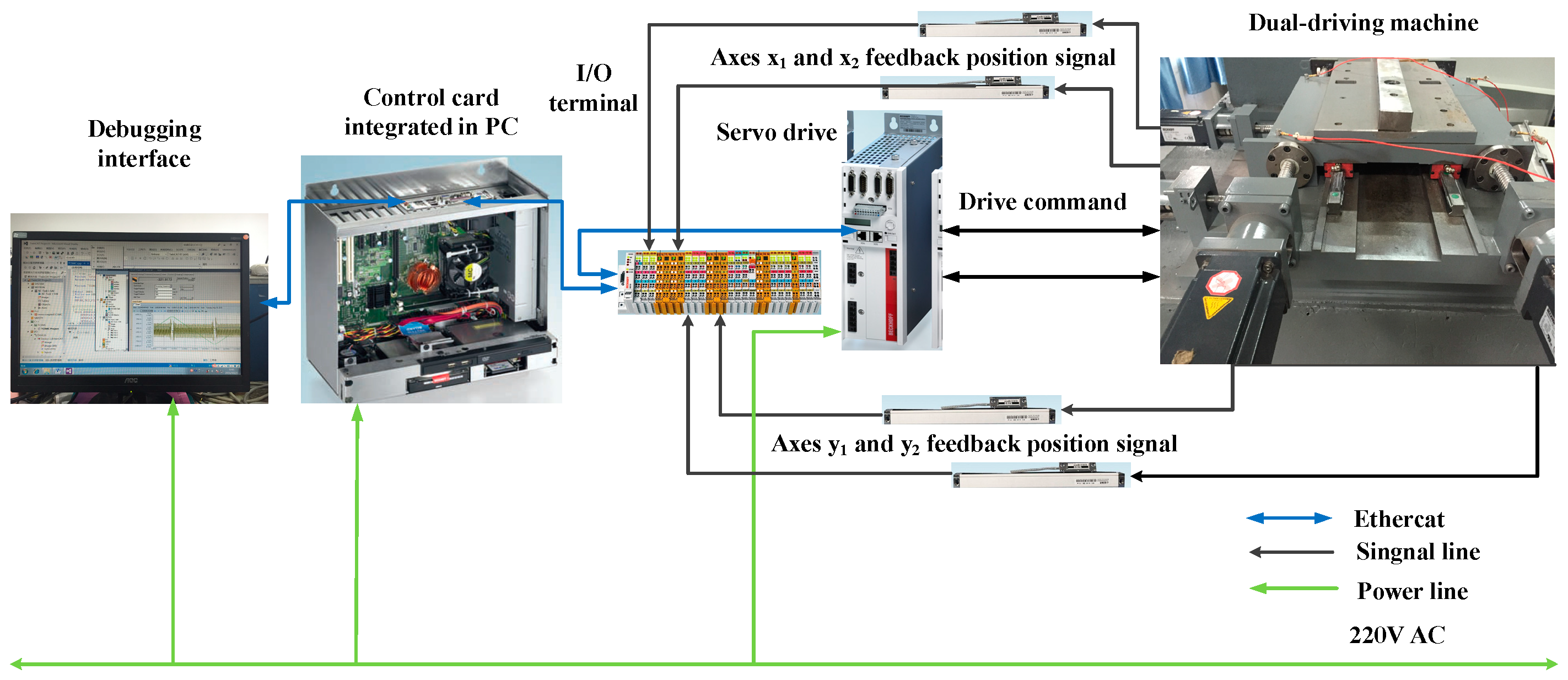
Section 2 presents the modelling and analysis of the 2-DOF dual-driving feed stage. The dynamics model is verified by the modal test.
Section 3 proposes the dynamic model-based TSMC, and the disturbance and state observer is developed to deal with the mechanical coupling disturbance. Then, the Lyapunov stability analysis of the proposed synchronous control scheme is provided to guarantee closed-loop tracking stability. In
Section 4, the tracking and synchronization performance of the proposed 2-DOF dynamic model-based TSMC with observer control scheme is compared with the other two synchronous control schemes by experiment. The experimental results show the effectiveness of the proposed control scheme. Conclusions are drawn in
Section 5.
3. Two-Degree-Of-Freedom Dynamic Model-Based Sliding Mode Control
The 2-DOF dynamic model-based TSMC is proposed in this section. The diagram of the control scheme is shown in
Figure 7.
3.1. Terminal Sliding Mode Control Design
In the practical scenario, the displacements of each axis
,
,
, and
are measurable. The state variables are defined as
,
; and the measurement variables are
,
. Thus the dynamic model of the 2-DOF dual-driving gantry stage can be rearranged as
Considering the parameters variation and unknown dynamics of the gantry position stage, (17) can be rewritten as
where
is the lumped uncertainty,
,
,
,
, and
. In (18), the mechanical coupling is modeled as disturbances.
For the 2-DOF dual-driving feed system, in each feed direction, the control scheme can be separated in two components at the same time: The first one is to eliminate the tracking error according to a given position signal; and the second one is to preserve the synchronous position with the other motor. According to the hybrid question, in this paper, the individual SMC with an extra cross-coupled synchronous controller is proposed to handle with the dual-driving hybrid error simultaneously to eliminate the complementary synchronous error and achieve the quick and accurate tracking of the given position signal.
As for the single axis, the position tracking error can be described as follows
The second derivative of (21) can be found as
where
and
are the reference position command in X and Y directions,
and
are the actual displacements of
ith axis in X and Y direction,
and
are the errors between actual displacements and reference positions of the
ith axis in X and Y directions.
The synchronous errors between dual axes in X and Y directions can be expressed as
The control objective of the 2-DOF feed stage is to guarantee the tracking error and the synchronous error to be zero simultaneously. The individual SMC is adopted as a class of nonlinear control approach in the drive dynamics, to eliminate the tracking errors
and
. What is more, to eliminate the synchronous error, a synchronous controller should be designed to generate the relationship between the input
and the actual synchronous error
, caused by displacement
and
. Then the comprehensive error can be rewritten as
For its advantages of being completely insensitive to system parameter variations and modeling inaccuracies, SMC is particularly suited for a nonlinear system. A SMC is designed based on the dual-driving model, the control objective is to generate a robust sliding mode controller to force the actual motion position to track the given bounded desired reference trajectory, this can guarantee the comprehensive error converges asymptotically to zero.
Sliding surface is the first step to design a sliding mode controller, the terminal sliding variable is defined as
where
is the sliding surface constant to be designed, which should be a positive constant like a transmission gain to determine the convergence speed of the dynamic error on the sliding surface.
and
are odd integers satisfying
.
Taking the derivative of (25), we have
Considering the stability of the overall system using the proposed TSMC, defining the following Lyapunov function
Take the derivative of (27), one can obtain
Evaluating the derivative of the Lyaponov function along the dynamics of the system in (28), we have
The negative sufficient condition of (29) can be designed as
where
.
Considering the 2-DOF dynamic model as shown in (17), the model-based TSMC control law can be designed as follows
Since
is the bounded total force which satisfies
, where
. Considering the definition of sliding surface function, the estimation of error
can be derived as
Then the Lyapunov function can be found as
Apparently, is negative semidefinite.
3.2. Disturbance Observer and State Observer Design
As can be seen from model (12)–(15), the disturbance is composed of disturbances and coupled force of 2-DOF dual-driving axes. In the conventional sliding mode control, the switching parameter is required to be larger than the bound of the disturbance . Therefore, if is estimated and compensated by a disturbance observer in the TSMC, a small switching parameter can be designed and can reduce the risk of chattering.
The following disturbance estimation error is defined, which penalizes deviation of errors from the sliding surface.
where
and
, because
is required in the calculation of
,
can be induced.
Since the disturbance observer is postulated to penalize deviation of error dynamics from the sliding surface, therefore, the disturbance observer can be designed as
can be assumed because the dynamics of the disturbance observer are much higher than the actual disturbance with interested frequency components. The dynamics of the disturbance estimation error can be expressed as
Moreover, the dynamic expression of the state observer can be modeled by system model (17)
The estimation error of state variables is defined as
Replacing the state variables given in (18)–(20), the dynamics of the state observer are obtained
where
.
The error dynamics of the observer (36) and (39) can be combined as
where
, and
.
The following Lyapunov function is chosen to derive stability of the observer
where
is a positive definite matrix, and
P1 and
P2 are the parameters that need to be designed. The derivative of the Lyapunov function can be given as [
29]
The parameters are designed to guarantee the convergence of the observers, which means the Lyapunov function of observer need to be a negative definite matrix. Hence, the parameters can be obtained by solving the linear matrix inequality (LMI)
For solving the LMI, (43) can be rewritten as
Therefore, the main idea behind the design of the proposed model-based TSMC scheme is that the control variables are errors calculated by the dynamic model instead of linear errors measured by the grating scale. Moreover, the disturbances due to the mechanical coupling of 2-DOF dual-driving feed stage can be compensated by the disturbance and state observer, while the effect associated with the acceleration and force of the stage is compensated by the TSMC control.