1. Introduction
Data hiding is a technology that can imperceptibly embed secret data into the carrier (e.g., text, sound, images, videos) to obtain the stego-carrier. After being transmitted in the communication channel, the receiver can extract the secret data accurately from the stego-carrier using the extraction algorithm. Due to the imperceptibility characteristic, stego-carriers can avoid attracting malicious attackers during transmission, which in some terms is superior to cryptographic encryption, another communications security technology. In practical applications, data hiding is widely used in the fields of medical images, copyright protection, military secrets, forensic evidence and anonymous communications [
1,
2]. Meanwhile, with the rapid development and the wide use of digital images, data hiding in images has attracted increasing attention from researchers in recent decades [
3]. In addition, some researchers further studied this field and proposed several reversible data hiding methods in which the cover image can be recovered losslessly after the secret data was extracted [
4,
5,
6]. The performance of data hiding technology is measured mainly by embedding capacity (EC) and the image quality after embedding.
The existing data hiding techniques are conducted mainly in three domains, i.e., the frequency domain, the compression domain, and the spatial domain. In the frequency domain, the cover image is first transformed to the discrete cosine transform (DCT) coefficients [
4,
7] or the discrete wavelet transformation (DWT) coefficients [
8,
9], in which the secret data is embedded. Since only a small quantity of the coefficients can be used for embedding, the embedding capacity cannot meet the requirements for most of the applications in practicality. In the compression domain, the cover image is first compressed to vacate space for embedding. Several researchers have proposed data hiding schemes based on vector quantization (VQ) compression [
10,
11,
12,
13], which can achieve larger embedding capacities; however, this capacity is at the expense of the distortion of the cover image.
In terms of the spatial domain, schemes can be roughly categorized into three types: the least significant bit (LSB) substitution [
14,
15,
16], the exploiting modification direction (EMD) [
17,
18,
19], and the magic matrix based (MMB) schemes [
20,
21,
22,
23,
24,
25,
26]. Among them, LSB is the most commonly used scheme and was first proposed by Bender et al. in 1996 [
3]. The original LSB scheme directly replaces the LSBs of each pixel with the secret bits. Later on, Wang et al. [
14] proposed an optimal LSB substitution to improve the image quality and developed a genetic algorithm to solve the huge computation problem. The algorithm of LSB replacement is quite simple; however, the hiding data can be easily detected [
16]. In order to avoid being attacked by malicious users, Mielikainen [
15] improved the LSB matching method and pairwisely embedded data by modifying their parity. The embedding capacities of [
14,
15] are both 1 bit per pixel (bpp). Zhang and Wang [
17] fully exploited the directions of modification so as to embed one secret
-ary digit into a vector with
pixels by changing at most one LSB of one pixel. The method, called EMD, can achieve a large embedding capacity with less distortion. In 2010, Kim et al. [
18] proposed two methods called 2-EMD and EMD-2, which can achieve a larger capacity than the original EMD method presented in [
13] with similar distortion. Particularly in EMD-2, Kim et al., embedded one
-ary digit into a vector of
pixels by flipping at most LSBs of 2 pixels, where
when
,
when
. Moreover, the two methods can be generalized to
n-EMD and EMD-
n, where
. Later on, Liu et al. [
19] further improved the embedding capacity by combining the EMD and the Chinese remainder theorem.
Unlike the aforementioned methods, several novel schemes based on MMB have been proposed in the past few years. In 2008, Chang et al. [
20] proposed a novel data hiding scheme using Sudoku, which considers a pixel pair as the coordinate of a Sudoku matrix to specify the value to embed one 9-ary digit into each pixel pair. The embedding capacity is 1.5 bpp. Hong et al. [
21] improved the method in [
20] by searching embedding positions based on the nearest Euclidean distance to achieve higher image quality. To enhance the security, a Sudoku-based wet paper hiding scheme was presented by Wang et al. [
22]. In 2014, Chang et al. [
23] put forward a novel TSB scheme, in which a secret 8-ary digit is embedded into each pixel pair with the guidance of the turtle shell. The scheme in [
23] can maintain a large embedding capacity (1.5 bpp) with less distortion. In 2016, Liu et al. [
24] produced an extra location table to achieve a larger embedding capacity of 2 bpp. Then, in 2017, for better image quality and the security of the hidden data, Jim et al. [
25] proposed a new method using particle swarm optimization to minimize the distortion. In the same year, Liu et al. [
26] extended the turtle shell matrix to different matrix models to meet diverse requirements of embedding capacity and image quality. The scheme in [
26] can maintain a good image quality with an average peak signal-to-noise ratio (PSNR) of 41.87 when the embedding capacity is high, up to 2.5 bpp.
In this paper, we introduce an extra attribute of a 4-ary digit, namely type, to each element of the turtle shell matrix, and then proposed a two-layer turtle shell matrix based (TTSMB) scheme. The first layer is a type of 4-ary digit represented by two bits, and the second layer is the value of an 8-ary digit represented by three bits. Similar to TSB schemes, each pixel pair, considered the coordinate of the turtle shell matrix, can specify only one element in matrix. Therefore, for each pixel pair, five bits can be embedded by the two-layer turtle shell matrix, and the embedding capacity can reach 2.5 bpp. Meanwhile, the experimental results proved that the stego-image kept a high visual quality.
In
Section 2, the related work of the original TSB scheme proposed by Chang et al. is introduced.
Section 3 gives a detailed depiction of the proposed scheme, followed by an analysis of experimental results in
Section 4. Finally, conclusions are made in
Section 5.
2. Chang et al.’s Scheme
Chang et al. [
23] first put forward the concept of the turtle shell matrix in the field of data hiding. The turtle shell matrix is a magic matrix on which you arbitrarily draw a turtle shell that contains eight digits from 0 to 7. Based on the characteristics, a pixel pair, which is considered the coordinate of the matrix, can specify an 8-ary digit. The following section gives a brief review of Chang et al.’s scheme.
2.1. Construction of the Turtle Shell Matrix
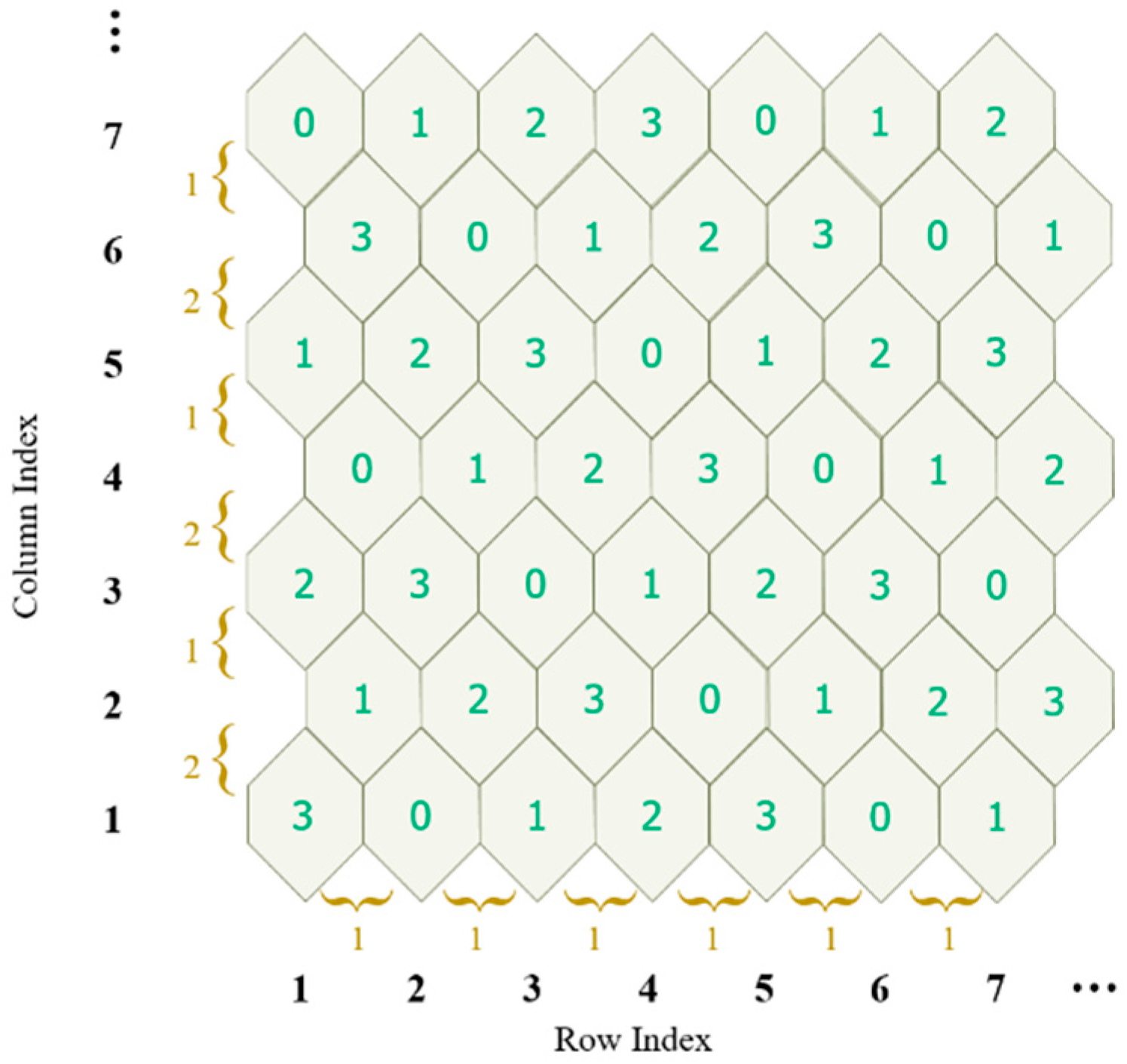
The turtle shell is defined as a hexagon containing eight different digits from 0 to 7, including two digits inside the hexagon, called back digits, and six digits on the edges of the hexagon, called the edge digits. As shown in
Figure 1, a turtle shell matrix sized 256 × 256 is constructed for data embedding. The construction rules are as follows: first, the values of elements in the same row change according to the gradient ascent/descent with a magnitude of “1”; second, the values of elements in the same column change according to the gradient ascent/descent with an alternate magnitude of “2” and “3”.
Once the data hider constructs a turtle shell matrix, he/she can embed the secret data into the cover image to obtain the stego-image according to the matrix. With the stego-image and the matrix, the receiver can accurately extract the secret data. Since the construction of the turtle shell matrix follows certain rules, there is no need to send the whole matrix to the receiver. Instead, only the value with the coordinate (0, 0) and the construction rules need to be shared with the receiver. For easy explanation, the shared information is called the construction information. With the construction information, the receiver can construct the exact matrix. The embedding and extraction procedures are depicted in detail in the following section.
2.2. Data Embedding and Data Extraction
Assume that a secret binary stream is embedded into a cover image with size of according to the turtle shell matrix . The embedding procedure of Chang et al.’s method is described as follows:
Step 1: Convert the secret binary stream into a sequence of octal digits , where is the number of octal digits.
Step 2: Divide the cover image into non-overlapping pixel pairs , where . Consider as the coordinate of matrix to specify the value .
Step 3: Embed one octal digit into each pixel pair. The algorithm can be categorized into two cases.
Case 1: , which means that the current pixel pair exactly corresponds to the secret octal digit; therefore, do nothing and go to Step 4.
Case 2: , which means the current pixel pair cannot correspond to the secret octal digit; therefore, find the closest that equals to , and then replace with in the cover image to embed the octal digit . Find the closest according to the following rules:
Rule 1: If is a back digit, then find in the current turtle shell.
Rule 2: If is an edge digit, then find the closest in the involved turtle shells.
Rule 3: If is not included in any turtle shell, then find the closest in the 3 × 3 sub-block where is located.
Step 4: Repeat Step 3 to embed the next octal digit into the follow-up pixel pair until all the secret data is embedded.
Finally, the stego-image is obtained.
At the procedure of the data extraction, with the construction information, the receiver constructs the turtle shell matrix . According to stego-image and the turtle shell matrix, the secret data can be easily extracted by mapping the stego pixel pairs to the elements of the turtle shell matrix, the values of which are exactly the secret data.
2.3. Example of Data Embedding and Data Extraction
To better understand the process, an example of the embedding and extraction procedure of Chang et al.’s scheme is given in this section.
Table 1 gives different cases of data embedding.
Case 1:
The to-be-embedded binary data 100 are first converted into an octal digit 4, the value of which is just equal to the value specified by the original pixel pair, viz.,
in
Figure 2. Then, embed the secret data by doing nothing, since the stego pixel pair still is (2,4).
Case 2:.
Rule 1: The element that the original pixel pair (2,7) specifies, , is a back digit. The to-be-embedded binary data 110 is converted to an octal digit 6. Find the satisfactory element in the turtle shell that the original pixel pair located, which is . Then, replace the original pixel pair with the stego pixel pair (2,8) in the cover image.
Rule 2: The element that the original pixel pair (5,3) specifies,
, is an edge digit. Find the closest satisfactory pair in the involved turtle shells, which is
, to embed the converted octal digital 0, as shown in
Figure 2. Thus, replace the original pixel pair with the stego pixel pair (6,4) in the cover image.
Rule 3: The element that the original pixel pair (2,0) specifies, , is not involved in any turtle shell. Find the closest satisfactory pair in the 3 × 3 sub-block, which is to carry the converted octal digit 5. Thus, replace the original pixel pair with the stego pixel pair (3,1) in the cover image.
On the receiver side, the turtle shell matrix (as shown in
Figure 2) is first constructed according to the construction rules. Then, the stego-image is divided into non-overlapping pixel pairs. Take the stego pixel pair (2,4) for example. The element value ‘4’ is extracted by mapping the coordinate (2,4) in the turtle shell matrix. Finally, the value ‘4’ is converted into binary data ‘100’, which is the secret data.
3. Proposed Scheme
3.1. Construction of the Two-Layer Matrix
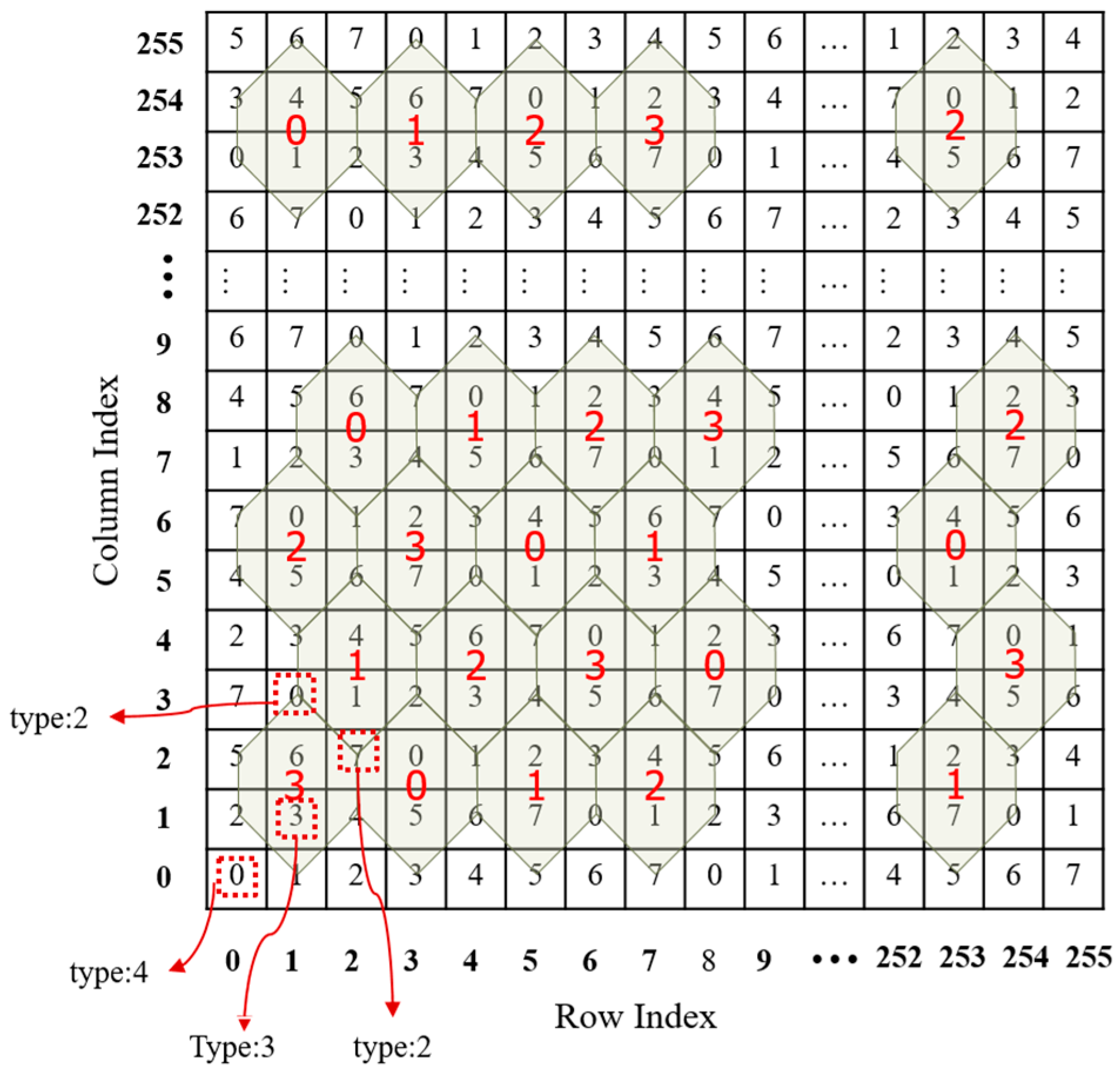
Observing the turtle shell matrix
, we can say that, to some extent, it is composed with turtle shells sized 127 × 127. In the proposed scheme, we assign a 4-ary digit, referred to as type, to each turtle shell, as shown in
Figure 3. For ease of description, the type matrix of the turtle shell is denoted as
. The type matrix is constructed following the rules: first, the values of type in the same row change according to the gradient ascent/descent with a magnitude of “1”; second, the values of the elements in the same column change according to the gradient ascent/descent with an alternate magnitude of “2” and “1”.
Figure 3 shows an example of a type matrix for turtle shell.
To go further, we assign an extra attribute, type, to each
, which is denoted as
. The algorithm for calculating
can be described as follows: conduct an exclusive operation on all involved turtle shell types. If there are no involved turtle shells, then set a value of ‘4’. The algorithm can be summarized into four cases, as shown in
Figure 4.
Case 1: No involved turtle shells, e.g., , and the type of such element is set as 4, e.g., .
Case 2: Only one turtle shell involved, e.g., . The type of such element is set as the type of the turtle shell, e.g., .
Case 3: Two turtle shells involved, e.g., . Then, the type of such element is the result of an operation exclusive of binary representations of the corresponding types of two turtle shells, e.g., .
Case 4: Three turtle shells involved, e.g., . The type of such element is the result of an operation exclusive of binary representations of the corresponding types of three turtle shells, e.g., .
According to the calculation algorithm, each
in the turtle shell matrix
is assigned to a corresponding type
. In other words, a two-layer turtle shell matrix is generated. The first layer is the value matrix of elements, viz.,
. The second layer is the type matrix of elements, viz.,
.
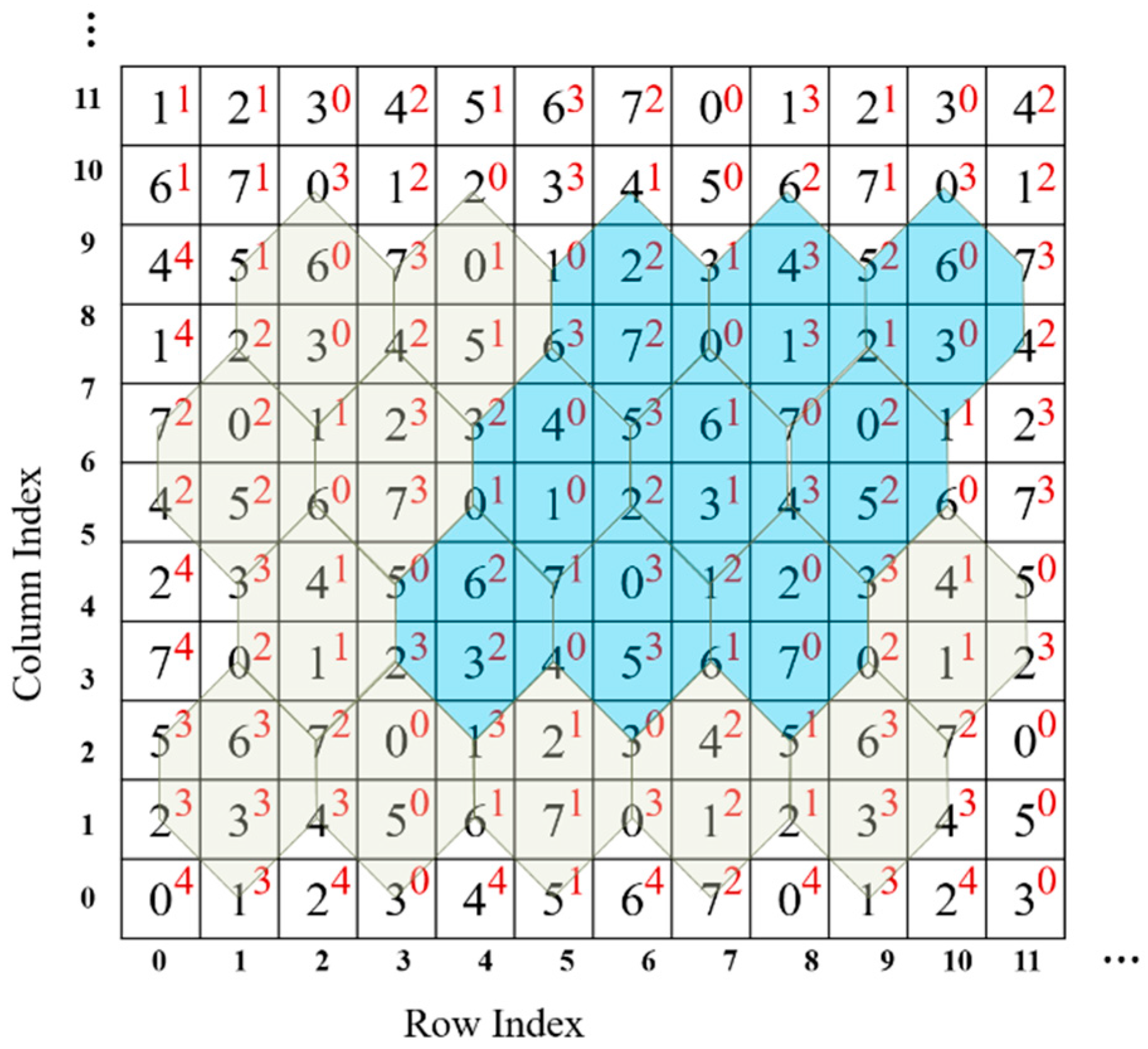
Figure 5 shows part of a two-layer turtle shell matrix. Digits in black are the values of elements, and digits in red are the values of a corresponding type. The statistical results confirm that all combinations of type and value, in other words, the
mappings (
), can be found in any parallelogram district consisting of nine turtle shells. Turtle shells in blue in
Figure 5 show an example. In this case, we can exploit the type matrix
as well as
to hide data. Consequently, a TTSMB data hiding scheme is proposed in this paper.
On the data hider side, he/she constructs a two-layer turtle shell matrix, and then embeds every five bits into each pixel pair. As in the TSB scheme, the construction information is shared with the receiver. With the construction information, the receiver reconstructs the two-layer matrix and extracts the secret data from the stego-image using the matrix. The difference is that the construction information in TTSMB includes extra information of the second layer. Since the construction of the second layer matrix (i.e., the type matrix) can be calculated according to the above-mentioned algorithm, the construction information of the second layer includes the value with the coordinate (0,0) in , the construction rules of , and the algorithm for generating type matrix . The procedures for data embedding and extraction are described in detail in the following sections.
3.2. Data Embedding and Data Extraction Procedures
Here, two procedures are described, respectively, one is data embedding procedure and the other is data extraction procedure to present the core concept of our proposed scheme.
Data embedding procedure
Figure 6 shows the flowchart of data embedding. Firstly, the cover image is divided into non-overlapping pixel pairs and the binary secret stream is divided into sub-streams with five bits, which are further converted into 4-ary digits and octal digits. Then, embed a 4-ary digit and an octal digit into each pixel pair using the constructed two-layer matrix. Lastly, we get the stego-image after all the secret data are embedded. The detail is described as below.
Input: A cover image sized , the binary secret stream with length .
Output: A stego-image .
Step 1: Generate a two-layer turtle shell matrix. First, construct a turtle shell matrix
according to the rules described in
Section 2. Second, a corresponding type matrix
is calculated according to the algorithm depicted in the
Section 3.1.
Step 2: Divide the cover image into non-overlapping pixel pairs , where . Consider as the coordinate of matrix to specify the value with the corresponding type .
Step 3: Divide into sub-streams with five bits, where . For each sub-stream, covert the first two bits into a 4-ary digit and the last three bits into an octal digit .
Step 4: Embed each sub-stream
into one pixel pair
according to the following rule: Find the closest element
, where
and
, by spiral scanning from the
, as shown in
Figure 7. Replace
with
in the cover image to embed the sub-stream
consisting of
and
.
Step 5: Repeat Step 4 until all the sub-streams are embedded.
Finally, the stego-image is obtained.
Data extraction procedure
Input: A stego-image sized , the construction information.
Output: The secret binary stream .
Step 1: Reconstruct the two-layer turtle shell matrix ( and ) using the shared construction information in the same way as described in the data embedding procedure.
Step 2: Divide the stego-image into non-overlapping pixel pairs , where .
Step 3: Extract the hidden secret data by mapping each pixel pair to the two-layer turtle shell matrix ( and ), that is and , which are in 4-ary and octal format, respectively.
Step 4: Convert the values of these two digits (i.e., and ) into binary bits, and then combine them to form the sub-stream of secret data.
Step 5: Finally, combine all the sub-streams to form the secret binary stream when all the sub-streams are extracted.
3.3. Example of Data Embedding and Data Extraction
For better understanding, an example of TTSMB data embedding and data extraction is given in this section.
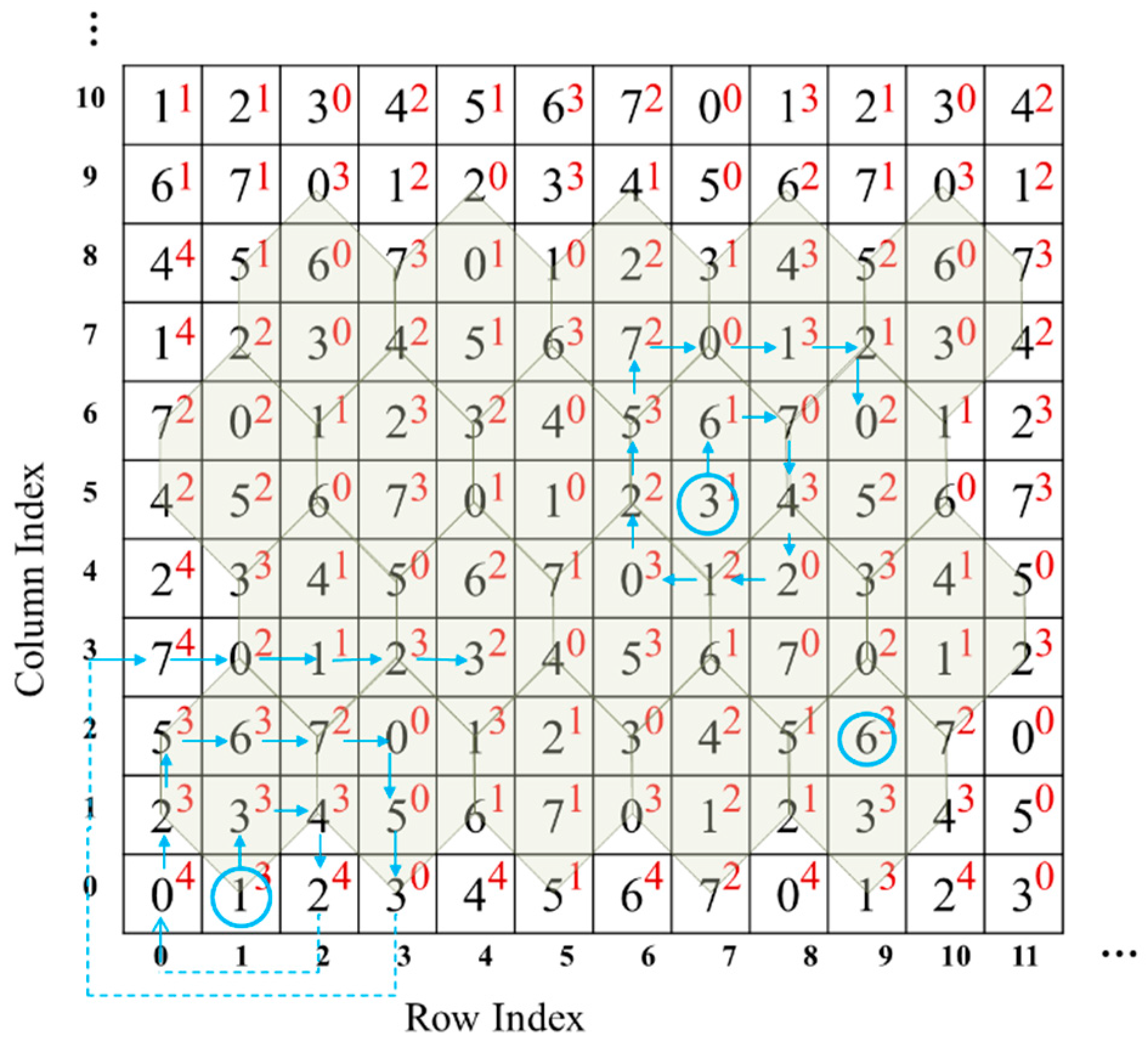
Table 2 gives an example of data embedding. The corresponding two-layer turtle shell matrix is shown in
Figure 7. For the first original pixel pair (9,2), the to-be-embedded bit stream is 11,110. The bit stream 11,110 is firstly converted to two digits, 3 and 6. Since
and
(as shown in
Figure 7), there is no need to change the original pixel pair, which itself just specifies the secret data. Thus, the stego pixel pair still is (9,2). For the second original pixel pair (7,5), the to-be-embedded bit stream is 10,000, which is converted to 2 and 0. Find the closest satisfactory element by spiral scanning the surrounding elements, i.e., (9,6) where
and
. Then, change the original pixel pair to (9,6) in the cover image. Conduct the same operation on the third original pixel pair. The only special circumstance that needs to be mentioned is that, when scanning to the edge of the matrix, extend outward to form a spiral, as shown at the bottom-left corner in
Figure 7.
On the receiver side, the two-layer turtle shell (as shown in
Figure 7) is first constructed using the shared construction information. Then, the stego-image is divided into non-overlapping pixel pairs, from which every five bits can be extracted. Take the stego pixel pair (9,2), for example. The values of the mapping elements
and
, viz., ‘3’ and ‘6’, are extracted. Then, ‘3’ and ‘6’ are converted into binary data ‘11’ and ‘110’, respectively. Finally, we get the combined secret data ’11,110’.
4. Experimental Results
Experiments were conducted to verify the performance of the proposed scheme. Six test grayscale images, ‘Lena’, ‘Airplane’, ‘Boat’, ‘Baboon’, ‘Peppers’, and ‘Sailboat’, were used from the University of Southern California-Signal and Image Processing Institute (USC-SIPI) image database [
27]. The sizes of the six test images were 512 × 512 shown in
Figure 8. The binary secret stream
was randomly generated. In addition,
Figure 9a–f are the corresponding stego-images with maximum embedding capacity (EC) of 2.5 bpp. The results show that, for all the test images, the stego-images remain high quality with a PSNR not lower than 47 dB. For a cover image sized
, EC and PSNR can be calculated by Equations (1) and (2), respectively. The higher
PSNR indicates the better image quality:
where
is the number of embedding bits, and the mean square error (MSE) is defined as Equation (3):
Herein, and are the original pixel values and the stego pixel values, respectively.
Comparisons with four previous TSB schemes are made in
Table 3. It can be observed that the proposed scheme obviously outperforms the other four in terms of the embedding capacity and image quality. To be more detailed, the embedding capacity of the proposed scheme (i.e., 2.5 bpp) is much higher than that of [
23] (i.e., 1.5 bpp), just with a slight decrease of PSNR. The image quality of the proposed scheme is better than that of [
24,
25], even with a higher embedding capacity. That is, with an embedding capacity of 2 bpp, the average PSNRs are 45.55 dB and 45.57 dB for [
24,
25], respectively. With an embedding capacity of 2.5 bpp, the average PSNR is 47.12 dB in the proposed scheme. Though [
26] can achieve a high embedding capacity as can the proposed scheme, viz. 2.5 bpp, there is a remarkable improvement of the image quality in the proposed scheme, with an average PSNR of 47.12 dB versus 41.87 dB.
From
Table 3, we can also find that, for all the five TSB based schemes including the proposed scheme, in the condition of a certain EC, the PSNRs of all the test images keep steady on the whole. The reason for the phenomenon is that the changing magnitude of pixels during the embedding procedure is determined by the constructed turtle shell matrix and the embedding algorithm, in other words, the image quality of stego-image is irrelevant to the cover image. Therefore, we can draw a remark: PSNR of the proposed scheme always keeps around 47.12 dB and higher than the other four TSB schemes, regardless of the content of test images.
Comparisons between other non-TSB schemes are made in this paper as well. As shown in
Table 4, the embedding capacities of other non-TSB schemes are no more than 1.6 bpp (i.e., 1 bpp for EMD [
17], 1.37 bpp for EMD-2 [
18], 1.5 bpp for [
20], 1.585 bpp for [
21]), which is much lower than that of the proposed scheme (i.e., 2.5 bpp). Moreover, the image quality of the proposed scheme outperforms that of [
20,
21], even with the larger embedding capacity (i.e., 1.6 bpp for the proposed scheme vs. 1.5 bpp and 1.585 bpp for [
20,
21], respectively). From both
Table 3 and
Table 4, we can also infer that TSB schemes perform better than EMB- and Sudoku-based schemes in terms of image quality and embedding capacity, which boils down to the property that eight digits (0–7) can be found within a turtle shell, result in the maximum changing magnitude is “2” during the embedding procedure.
In addition to PSNR, structural similarity Index (SSIM) is also used as image quality evaluation criteria. PSNR measures the difference between two images based on the estimated absolute errors, and SSIM considers image perceptual degradation in structural information. The SSIM index is calculated on the blocks of an image. Assuming there are two blocks,
and
, of common size,
, the SSIM index can be calculated according to Equation (4), and
. The larger the SSIM index is, the higher the similarity is. If
, then the two images are the same.
with:
, are the average of and , respectively;
, are the variance of and , respectively;
is the covariance of and ;
are two variables to stabilize the division with weak denominator;
is the dynamic range of the pixel-values; and
and by default.
Table 5 shows a comparison of SSIM between the proposed scheme and [
26]. It is obvious to see the absolute advantage of the proposed scheme; that is, for all the test images, the SSIM of the proposed scheme is higher than that of [
26] when embedding the maximum capacity of secret data (2.5 bpp). Additionally, an average SSIM of 0.03 improvement is obtained.