MetrIntSimil—An Accurate and Robust Metric for Comparison of Similarity in Intelligence of Any Number of Cooperative Multiagent Systems
Abstract
:1. Introduction
2. Measuring the Machine Intelligence Quotient
2.1. Intelligent Cooperative Multiagent Systems
2.2. Metrics for Measuring the Machine Intelligence
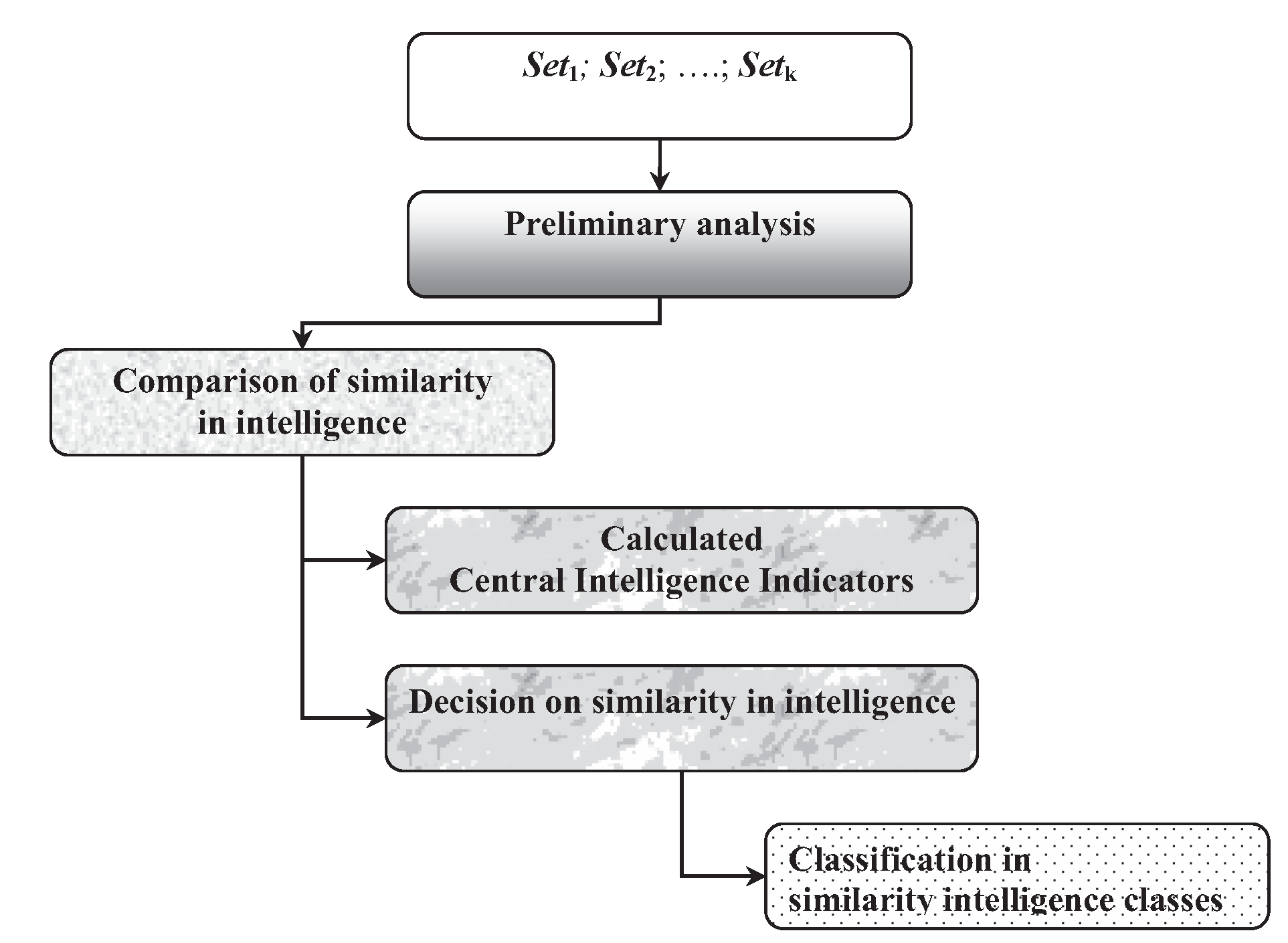
3. Description of the MetrIntSimil Metric
4. Measuring the Intelligence of More CMASs—A Case Study on Solving the Symmetric TSP
4.1. Symmetric Travelling Salesman Problem Solving
4.2. CMASs That Operate by Mimicking Biological Ants
4.3. The Experimental Setup
5. Discussion and Comparison of the MetrIntSimil Metric
6. Theory of Multiple Intelligences in Machines: The Next Research Works
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guillaud, A.; Troadec, H.; Benzinou, A.; Bihan, J.L.; Rodin, V. Multiagent System for Edge Detection and Continuity Perception on Fish Otolith Images. EURASIP J. Appl. Signal Process. 2002, 7, 746–753. [Google Scholar] [CrossRef]
- Iantovics, L.B. A New Intelligent Mobile Multiagent System. In Proceedings of the IEEE-SOFA 2005, Szeged, Hungary and Arad, Romania, 27–30 August 2005; pp. 153–159. [Google Scholar]
- Iantovics, L.B.; Zamfirescu, C.B. ERMS: An Evolutionary Reorganizing Multiagent System. Innov. Comput. Inf. Control 2013, 9, 1171–1188. [Google Scholar]
- Stoean, C.; Stoean, R. Support Vector Machines and Evolutionary Algorithms for Classification; Intelligent Systems Reference Library; Springer International Publishing: Cham, Switzerland, 2014; Volume 69, pp. 570–573. [Google Scholar]
- Chen, M.H.; Wang, L.; Sun, S.W.; Wang, J.; Xia, C.Y. Evolution of cooperation in the spatial public goods game with adaptive reputation assortment. Phys. Lett. A 2016, 380, 40–47. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Wang, J.; Sun, S.; Xia, C. Inferring the reputation enhances the cooperation in the public goods game on interdependent lattices. Appl. Math. Comput. 2017, 293, 18–29. [Google Scholar] [CrossRef]
- Yang, K.; Galis, A.; Guo, X.; Liu, D. Rule-Driven Mobile Intelligent Agents for Real-Time Configuration of IP Networks. In International Conference on Knowledge-Based Intelligent Information and Engineering Systems; Palade, V., Howlett, R.J., Jain, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2773, pp. 921–928. [Google Scholar]
- Van Jan, L. (Ed.) Algorithms and Complexity. In Handbook of Theoretical Computer Science; Elsevier: Amsterdam, The Netherlands, 1998; Volume A. [Google Scholar]
- Crisan, G.C.; Nechita, E.; Palade, V. On the Effect of Adding Nodes to TSP Instances: An Empirical Analysis. In Advances in Combining Intelligent Methods; Hatzilygeroudis, I., Palade, V., Prentzas, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 116, pp. 25–45. [Google Scholar]
- Karp, R.M. Reducibility among Combinatorial Problems. In Complexity of Computer Computations; Miller, R.E., Thatcher, J.W., Eds.; Plenum Press: New York, NY, USA, 1972; pp. 85–103. [Google Scholar]
- Grotschel, M.; Padberg, M.W. On the Symmetric Travelling Salesman Problem: Theory and Computation. In Optimization and Operations Research; Henn, R., Korte, B., Oettli, W., Eds.; Springer: Berlin/Heidelberg, Germany, 1978; Volume 157. [Google Scholar]
- Zhang, Y.; Wang, H.; Zhang, Y.; Chen, Y. Best-Worst Ant System. In Proceedings of the 3rd International Conference on Advanced Computer Control (ICACC), Harbin, China, 18–20 January 2011; pp. 392–395. [Google Scholar]
- Cordon, O.; de Viana, I.F.; Herrera, F. Analysis of the Best-Worst Ant System and Its Variants on the QAP. In International Workshop on Ant Algorithms; Dorigo, M., Di Caro, G., Sampels, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2463. [Google Scholar]
- Prakasam, A.; Savarimuthu, N. Metaheuristic algorithms and probabilistic behaviour: A comprehensive analysis of Ant Colony Optimization and its variants. Artif. Intell. Rev. 2016, 45, 97–130. [Google Scholar] [CrossRef]
- Stutzlem, T.; Hoos, H.H. Max-Min Ant System. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed Optimization by Ant Colonies. In Actes de la Premiere Conference Europeenne sur la vie Artificielle; Elsevier: Paris, France, 1991; pp. 134–142. [Google Scholar]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 1992. [Google Scholar]
- Lin, Y.; Duan, X.; Zhao, C.; Xu, L. Systems Science Methodological Approaches; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Xu, L. The Contribution of Systems Science to Information Systems Research. Syst. Res. Behav. Sci. 2000, 17, 105–116. [Google Scholar] [CrossRef]
- Langley, P.; Laird, J.E.; Rogers, S. Cognitive architectures: Research issues and challenges. Cogn. Syst. Res. 2009, 10, 141–160. [Google Scholar] [CrossRef]
- Tang, C.; Xu, L.; Feng, S. An Agent-Based Geographical Information System. Knowl. Based Syst. 2001, 14, 233–242. [Google Scholar] [CrossRef]
- Dreżewski, R.; Doroz, K. An Agent-Based Co-Evolutionary Multi-Objective Algorithm for Portfolio Optimization. Symmetry 2017, 9, 168. [Google Scholar] [CrossRef]
- Wang, D.; Ren, H.; Shao, F. Distributed Newton Methods for Strictly Convex Consensus Optimization Problems in Multi-Agent Networks. Symmetry 2017, 9, 163. [Google Scholar] [CrossRef]
- West, D.; Dellana, S. Diversity of ability and cognitive style for group decision processes. Inf. Sci. 2009, 179, 542–558. [Google Scholar] [CrossRef]
- Zamfirescu, C.B.; Duta, L.; Iantovics, L.B. On investigating the cognitive complexity of designing the group decision process. Stud. Inform. Control 2010, 19, 263–270. [Google Scholar] [CrossRef]
- Iantovics, L.B.; Rotar, C. A Novel Metric for Comparing the Intelligence of Two Swarm Multiagent Systems. J. Artif. Intell. 2016, 9, 39–44. [Google Scholar] [CrossRef]
- Besold, T.; Hernández-Orallo, J.; Schmid, U. Can Machine Intelligence be Measured in the Same Way as Human intelligence? Künstl. Intell. 2015, 29, 291–297. [Google Scholar] [CrossRef]
- Kannan, B.; Parker, L.E. Metrics for quantifying system performance in intelligent, fault-tolerant multi-robot teams. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 951–958. [Google Scholar]
- Park, H.J.; Kim, B.K.; Lim, K.Y. Measuring the machine intelligence quotient (MIQ) of human-machine cooperative systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2001, 31, 89–96. [Google Scholar] [CrossRef]
- Schreiner, K. Measuring IS: Toward a US standard. IEEE Intell. Syst. Their Appl. 2000, 15, 19–21. [Google Scholar] [CrossRef]
- Arik, S.; Iantovics, L.B.; Szilagyi, S.M. OutIntSys—A Novel Method for the Detection of the Most Intelligent Cooperative Multiagent Systems. In Proceedings of the 24th International Conference on Neural Information Processing, Guangzhou, China, 14–18 November 2017; Volume 10637, pp. 31–40. [Google Scholar]
- Wallace, C.S.; Dowe, D.L. Minimum message length and Kolmogorov complexity. Comput. J. 1999, 42, 270–283. [Google Scholar] [CrossRef]
- Wallace, C.S. Statistical and Inductive Inference by Minimum Message Length; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Dowe, D.L. MML, hybrid Bayesian network graphical models, statistical consistency, invariance and uniqueness. In Handbook of the Philosophy of Science; Bandyopadhyay, P.S., Forster, M.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 7, pp. 901–982. [Google Scholar]
- Dowe, D.L.; Hajek, A.R. A computational extension to the Turing Test. In Proceedings of the 4th Conference of the Australasian Cognitive Science Society, Melbourne, Australia, 28 November–1 December 2013. [Google Scholar]
- Dowe, D.L.; Hajek, A.R. A non-behavioural, computational extension to the Turing Test. In Proceedings of the International Conference on Computational Intelligence and Multimedia Application, Gippsland, Australia, 7–10 February 1998; pp. 101–106. [Google Scholar]
- Wallace, C.S.; Boulton, D.M. An information measure for classification. Comput. J. 1968, 11, 185–194. [Google Scholar] [CrossRef]
- Sterret, S.G. Turing on the Integration of Human and Machine Intelligence. In Philosophical Explorations of the Legacy of Alan Turing; Floyd, J., Bokulich, A., Eds.; Springer: Cham, Switzerland, 2017; Volume 324, pp. 323–338. [Google Scholar]
- Ferrucci, D.; Levas, A.; Bagchi, S.; Gondek, D.; Mueller, E.T. Watson: Beyond Jeopardy! Artificial Intelligence 2013, 199, 93–105. [Google Scholar] [CrossRef]
- Legg, S.; Hutter, M. A Formal Measure of Machine Intelligence. In Proceedings of the 15th Annual Machine Learning Conference of Belgium and The Netherlands (Benelearn 2006), Ghent, Belgium, 11–12 May 2006; pp. 73–80. [Google Scholar]
- Hibbard, B. Measuring Agent Intelligence via Hierarchies of Environments. In Artificial General Intelligence AGI 2011; Schmidhuber, J., Thórisson, K.R., Looks, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6830, pp. 303–308. [Google Scholar]
- Anthon, A.; Jannett, T.C. Measuring machine intelligence of an agent-based distributed sensor network system. In Advances and Innovations in Systems, Computing Sciences and Software Engineering; Elleithy, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 531–535. [Google Scholar]
- Hernandez-Orallo, J.; Dowe, D.L. Measuring universal intelligence: Towards an anytime intelligence test. Artif. Intell. 2010, 174, 1508–1539. [Google Scholar] [CrossRef]
- Iantovics, L.B.; Emmert-Streib, F.; Arik, S. MetrIntMeas a novel metric for measuring the intelligence of a swarm of cooperating agents. Cogn. Syst. Res. 2017, 45, 17–29. [Google Scholar] [CrossRef]
- Winklerova, Z. Maturity of the Particle Swarm as a Metric for Measuring the Collective Intelligence of the Swarm. In Advances in Swarm Intelligence, ICSI 2013; Tan, Y., Shi, Y., Mo, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7928, pp. 40–54. [Google Scholar]
- Iantovics, L.B.; Rotar, C.; Niazi, M.A. MetrIntPair—A Novel Accurate Metric for the Comparison of Two Cooperative Multiagent Systems Intelligence Based on Paired Intelligence Measurements. Int. J. Intelli. Syst. 2018, 33, 463–486. [Google Scholar] [CrossRef]
- Liu, F.; Shi, Y.; Liu, Y. Intelligence quotient and intelligence grade of artificial intelligence. Ann. Data Sci. 2017, 4, 179–191. [Google Scholar] [CrossRef]
- Detterman, D.K. A challenge to Watson. Intelligence 2011, 39, 77–78. [Google Scholar] [CrossRef]
- Sanghi, P.; Dowe, D.L. A computer program capable of passing I.Q. tests. In Proceedings of the Joint International Conference on Cognitive Science, 4th ICCS International Conference on Cognitive Science and 7th ASCS Australasian Society for Cognitive Science (ICCS/ASCS-2003), Sydney, Australia, 13–17 July 2003; pp. 570–575. [Google Scholar]
- Campbell, M.; Hoane, A.J.; Hsu, F. Deep Blue. Artif. Intell. 2002, 134, 57–83. [Google Scholar] [CrossRef]
- Iantovics, L.B.; Rotar, C.; Nechita, E. A novel robust metric for comparing the intelligence of two cooperative multiagent systems. Procedia Comput. Sci. 2016, 96, 637–644. [Google Scholar] [CrossRef]
- Chakravarti, I.M.; Laha, R.G.; Roy, J. Handbook of Methods of Applied Statistics; John Wiley and Sons: Hoboken, NJ, USA, 1967; Volume I, pp. 392–394. [Google Scholar]
- Lilliefors, H. On the Kolmogorov–Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Lilliefors, H. On the Kolmogorov–Smirnov test for the exponential distribution with mean unknown. J. Am. Stat. Assoc. 1969, 64, 387–389. [Google Scholar] [CrossRef]
- Dallal, G.E.; Wilkinson, L. An analytic approximation to the distribution of Lilliefors’s test statistic for normality. Am. Stat. 1986, 40, 294–296. [Google Scholar]
- Markowski, C.A.; Markowski, E.P. Conditions for the Effectiveness of a Preliminary Test of Variance. Am. Stat. 1990, 44, 322–326. [Google Scholar]
- Bartlett, M.S. Properties of sufficiency and statistical tests. Proc. R. Soc. Lond. A 1937, 160, 268–282. [Google Scholar] [CrossRef]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods, 8th ed.; Iowa State University Press: Iowa, IA, USA, 1989. [Google Scholar]
- Ross, S.M. Peirce’s Criterion for the Elimination of Suspect Experimental Data. J. Eng. Technol. 2003, 2, 1–12. [Google Scholar]
- Zerbet, A.; Nikulin, M. A new statistics for detecting outliers in exponential case. Commun. Stat. Theory Methods 2003, 32, 573–583. [Google Scholar] [CrossRef]
- Stigler, S.M. Mathematical statistics in the early states. Ann. Stat. 1978, 6, 239–265. [Google Scholar] [CrossRef]
- Dean, R.B.; Dixon, W.J. Simplified Statistics for Small Numbers of Observations. Anal. Chem. 1951, 23, 636–638. [Google Scholar] [CrossRef]
- Barnett, V.; Lewis, T. Evolution by gene duplication. In Outliers in Statistical Data, 3rd ed.; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Motulsky, H. GraphPad InStat Version 3. In The InStat Guide to Choosing and Interpreting Statistical Tests; GraphPad Software, Inc.: La Jolla, CA, USA, 2003. [Google Scholar]
- Fisher, R.A. On the “Probable Error” of a Coefficient of Correlation Deduced from a Small Sample. Metron 1921, 1, 3–32. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple comparisons using rank sums. Technometrics 1964, 6, 241–252. [Google Scholar] [CrossRef]
- Tukey, J. Comparing Individual Means in the Analysis of Variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef] [PubMed]
- Sosnoff, J.J.; Heffernan, K.S.; Jae, S.Y.; Fernhall, B. Aging, hypertension and physiological tremor: The contribution of the cardioballistic impulse to tremorgenesis in older adults. J. Neurol. Sci. 2013, 326, 68–74. [Google Scholar]
- Lee, J.Y.; Shin, S.Y.; Park, T.H.; Zhang, B.T. Solving traveling salesman problems with DNA molecules encoding numerical values. Biosystems 2004, 78, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A.; Fischer, F.; Jager, G.; Keilwagen, J.; Molitor, P.; Grosse, I. Computational Recognition of RNA Splice Sites by Exact Algorithms for the Quadratic Traveling Salesman Problem. Computation 2015, 3, 285–298. [Google Scholar] [CrossRef]
- Kim, E.; Lee, M.; Gatton, T.M.; Lee, J.; Zang, Y. An Evolution Based Biosensor Receptor DNA Sequence Generation Algorithm. Sensors 2010, 10, 330–341. [Google Scholar] [CrossRef] [PubMed]
- Boctor, F.F.; Laporte, G.; Renaud, J. Heuristics for the traveling purchaser problem. Comput. Oper. Res. 2003, 30, 491–504. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Dantzig, G.; Fulkerson, D.; Johnson, S. Solution of a large scale traveling salesman problem. Oper. Res. 1954, 2, 393–410. [Google Scholar] [CrossRef]
- Ouaarab, A.; Ahiod, B.; Yang, X.S. Discrete cuckoo search algorithm for the travelling salesman problem, Neural Comput. Appl. 2014, 24, 1659. [Google Scholar]
- Huang, Z.G.; Wang, L.G.; Xu, Z.; Cui, J.J. An efficient two-step iterative method for solving a class of complex symmetric linear systems. Comput. Math. Appl. 2018, in press. [Google Scholar] [CrossRef]
- Koczy, L.T.; Foldesi, P.; Tuu-Szabo, B. Enhanced discrete bacterial memetic evolutionary algorithm—An efficacious metaheuristic for the traveling salesman optimization. Inf. Sci. 2017, in press. [Google Scholar] [CrossRef]
- Jonker, R.; Volgenant, T. Transforming asymmetric into symmetric traveling salesman problems. Oper. Res. Lett. 1983, 2, 161–163. [Google Scholar] [CrossRef]
- Arthanari, T.S.; Usha, M. An alternate formulation of the symmetric traveling salesman problem and its properties. Discret. Appl. Math. 2000, 98, 173–190. [Google Scholar] [CrossRef]
- Smith, T.H.C.; Meyer, T.W.S.; Thompson, G.L. Lower bounds for the symmetric travelling salesman problem from Lagrangean relaxations. Discret. Appl. Math. 1990, 26, 209–217. [Google Scholar] [CrossRef]
- Holldobler, B.; Wilson, E.O. The Ants; Harvard University Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Higashi, S.; Yamauchi, K. Influence of a Supercolonial Ant Formica(Formica) yessensis Forel on the Distribution of Other Ants in Ishikari Coast. Jpn. J. Ecol. 1979, 29, 257–264. [Google Scholar]
- Giraud, T.; Pedersen, J.S.; Keller, L. Evolution of supercolonies: The Argentine ants of southern Europe. Proc. Natl. Acad. Sci. USA 2002, 99, 6075–6079. [Google Scholar] [CrossRef] [PubMed]
- Sim, Y.B.; Lee, S.G.; Lee, S. Function-Oriented Networking and On-Demand Routing System in Network Using Ant Colony Optimization Algorithm. Symmetry 2017, 9, 272. [Google Scholar] [CrossRef]
- Crisan, G.C.; Pintea, C.M.; Palade, V. Emergency Management Using Geographic Information Systems: Application to the first Romanian Traveling Salesman Problem Instance. Knowl. Inf. Syst. 2017, 50, 265–285. [Google Scholar] [CrossRef]
- Everitt, B. The Cambridge Dictionary of Statistics; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Marusteri, M.; Bacarea, V. Comparing groups for statistical differences: How to choose the right statistical test? Biochem. Med. 2010, 20, 15–32. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Fay, M.P.; Proschan, M.A. Wilcoxon–Mann–Whitney or t-test? On assumptions for hypothesis tests and multiple interpretations of decision rules. Stat. Surv. 2010, 4, 1–39. [Google Scholar] [CrossRef] [PubMed]
- McDonald, J.H. Handbook of Biological Statistics, 3rd ed.; Sparky House Publishing: Baltimore, MD, USA, 2014. [Google Scholar]
- Fagerland, M.W.; Sandvik, L. The Wilcoxon-Mann-Whitney Test under scrutiny. Stat. Med. 2009, 28, 1487–1497. [Google Scholar] [CrossRef] [PubMed]
- Slavin, R. Educational Psychology Theory and Practice, 9th ed.; Allyn and Bacon: Boston, MA, USA, 2009; p. 117. [Google Scholar]
- Gardner, H. Frames of Mind: The Theory of Multiple Intelligences, 3rd ed.; Basic Books: New York, NY, USA, 2011. [Google Scholar]
- Visser, B.A.; Ashton, M.C.; Vernon, P.A. g and the measurement of Multiple Intelligences: A response to Gardner. Intelligence 2006, 34, 507–510. [Google Scholar] [CrossRef]
- Bell, E.A.; Boehnke, P.; Harrison, T.M.; Mao, W.L. Potentially biogenic carbon preserved in a 4.1 billion year-old zircon. Proc. Natl. Acad. Sci. USA 2015, 112, 14518–14521. [Google Scholar] [CrossRef] [PubMed]

| … | |||
|---|---|---|---|
| … | |||
| … | |||
| … | … | … | … |
| … | |||
| of | of | … | of |
| Type of Data and Distribution | Normalizing Transformation |
|---|---|
| Set comes from Poisson distribution | Square root of Set |
| Set comes from Binomial distribution | Arcsine of square root of Set |
| Set comes from Lognormal distribution | Log (Set) |
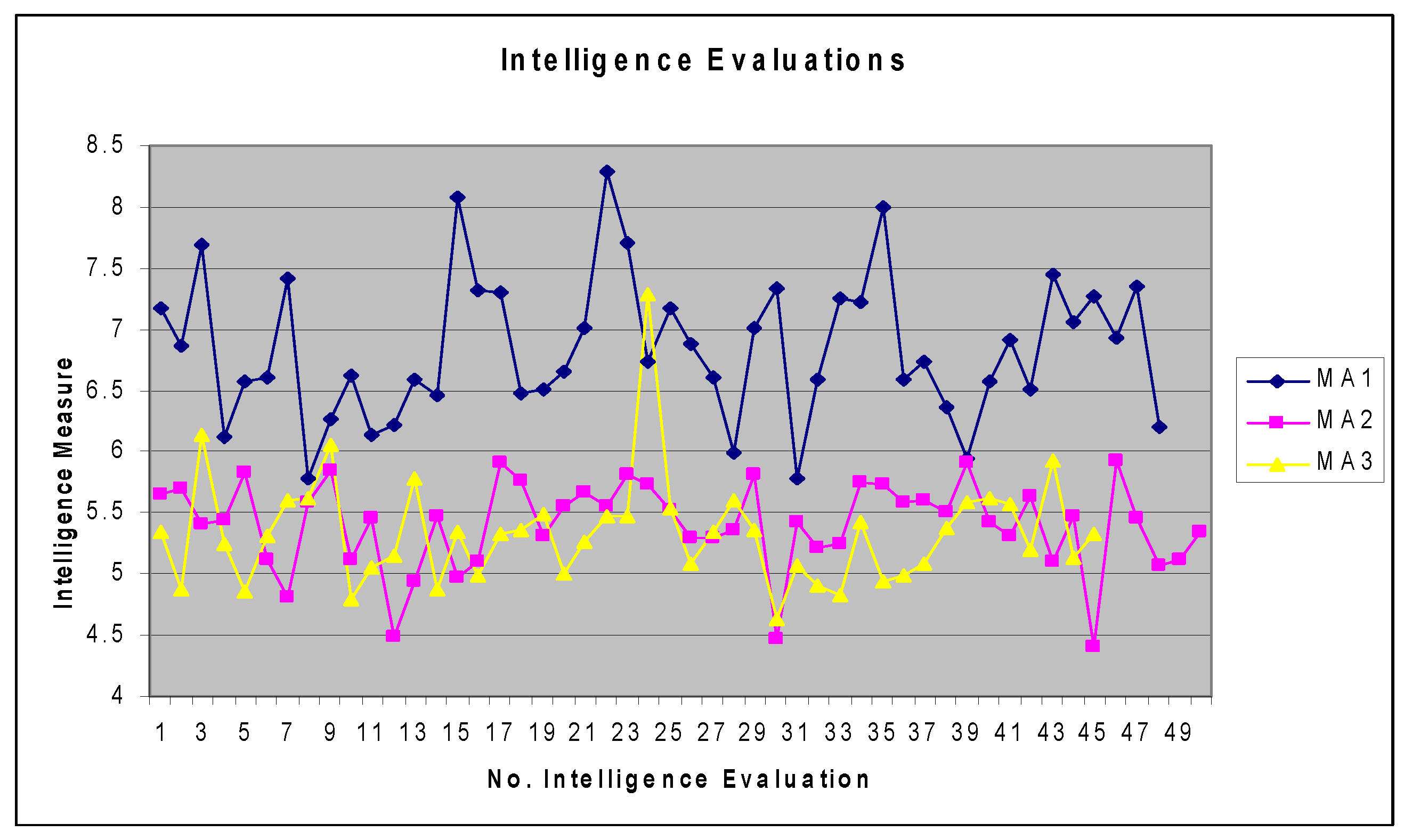
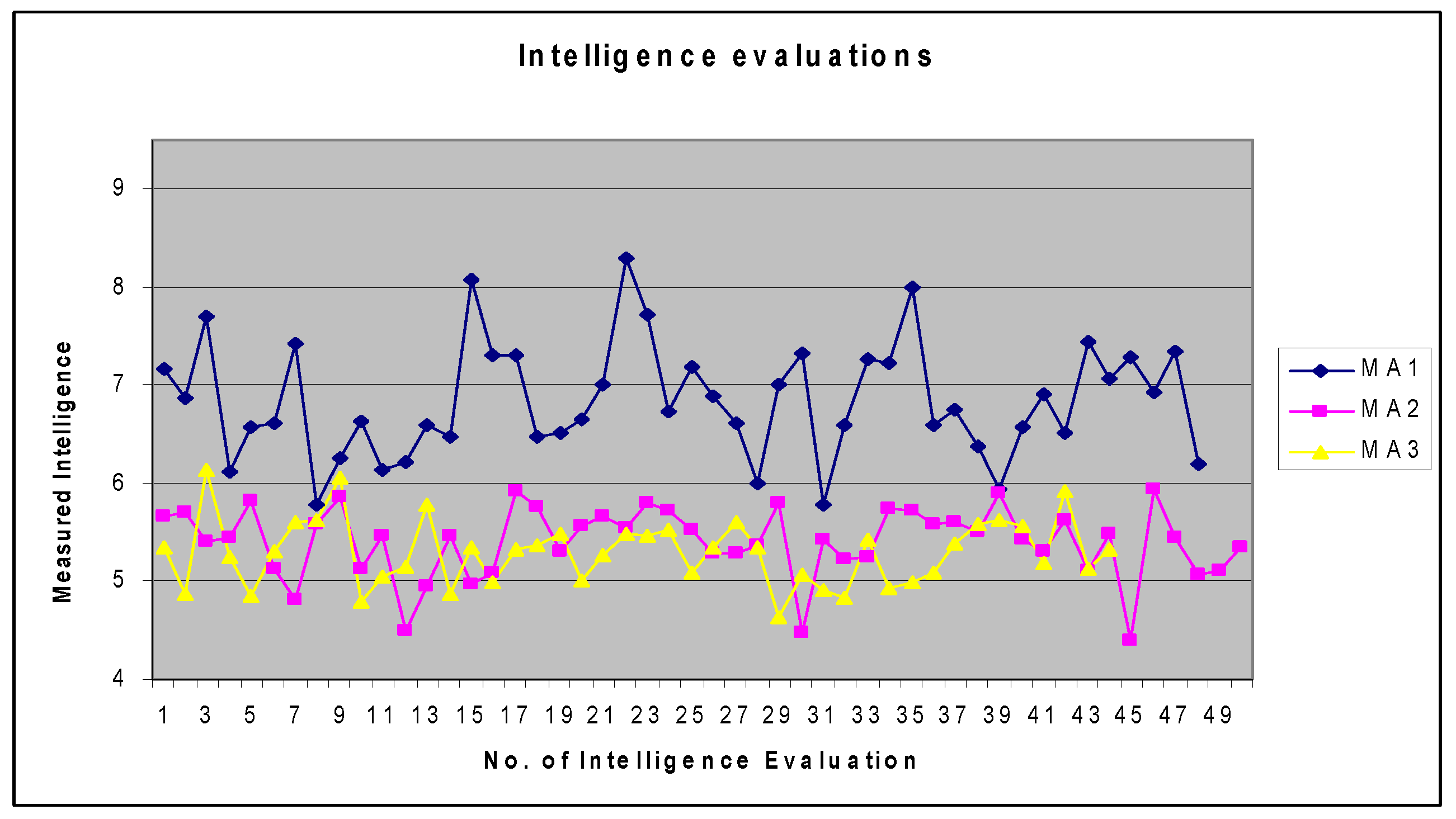
| 7.172; 6.864; 7.691; 6.12; | 5.657;5.706; 5.409; 5.442; | 5.342; 4.868; 6.134; 5.251; |
| 6.572; 6.612; 7.413; 5.786; | 5.826; 5.123; 4.81; 5.579; | 4.85; 5.307; 5.605; 5.624; |
| 6.262; 6.626; 6.135; 6.217; | 5.853; 5.121; 5.459; 4.492; | 6.053; 4.788; 5.055; 5.153; |
| 6.586; 6.467; 8.084; 7.313; | 4.944; 5.466; 4.978; 5.095; | 5.779; 4.87; 5.339; 4.992; |
| 7.295; 6.473; 6.516; 6.657; | 5.917; 5.76; 5.315; 5.558; | 5.322; 5.363; 5.493; 5.004; |
| 7.009; 8.297; 7.714; 6.729; | 5.661; 5.546; 5.809; 5.729; | 5.261; 5.476; 5.469; 7.278*; |
| 7.177; 6.887; 6.612; 5.99; | 5.519; 5.288; 5.293; 5.365; | 5.53; 5.084; 5.337; 5.595; |
| 7.007; 7.333; 5.78; 6.585; | 5.806; 4.465; 5.427; 5.217; | 5.352; 4.631; 5.068; 4.911; |
| 7.257; 7.225; 8.005; 6.592; | 5.244; 5.741; 5.724; 5.579; | 4.831; 5.431; 4.933; 4.987; |
| 6.741; 6.37; 5.944; 6.573; | 5.599; 5.506; 5.907; 5.421; | 5.092; 5.377; 5.589; 5.623; |
| 6.911; 6.513; 7.447; 7.066; | 5.312; 5.632; 5.101; 5.476; | 5.563; 5.195; 5.926; 5.136; |
| 7.277; 6.924; 7.343; 6.204 | 4.405; 5.932; 5.454; 5.065; | 5.325; |
| 5.111; 5.345 |
| Type of Analysis | * | |||
|---|---|---|---|---|
| Mean | 6.841104 | 5.40378 | 5.3376 | 5.2935 |
| SD/Variance | 0.5861/0.3435 | 0.3647/0.133 | 0.4471/0.1999 | 0.3392/0.1151 |
| Sample size | 48 | 50 | 45 | 44 |
| SEM | 0.08460 | 0.05158 | 0.06666 | 0.05113 |
| [LCI95%, UCI95%] | [6.671, 7.011] | [5.3, 5.508] | [5.203, 5.472] | [5.19, 5.397] |
| Lowest/Highest | 5.780/8.297 | 4.405/5.932 | 4.631/7.278 | 4.631/6.134 |
| Median | 6.735 | 5.454 | 5.325 | 5.324 |
| CV | ≈8.5673 | ≈6.7499 | ≈8.3764 | ≈6.4079 |
| K-S Stat/p-value | 0.1024/>0.1 | 0.1057/>0.1 | 0.1498/0.0128 | 0.07404/>0.1 |
| Lill Stat/p-value | 0.102/0.2 | 0.106/0.2 | 0.15/0.013 | 0.074/0.2 |
| Normality passed | YES | YES | NO | YES |
| Compared CMASs | p-Value | Mean Rank Difference | Interpretation of the Result |
|---|---|---|---|
| vs. | <0.001 | 64.909 | and * |
| vs. | <0.001 | 76.241 | and * |
| vs. | >0.05 | 11.331 | and ** |
| Comparison criterion | MetrIntComp | MetrIntSimil |
|---|---|---|
| Principle | * | * |
| Applicability | @ | @ |
| Computations | + | + |
| Number of compared CMASs | 2 | Any number |
| Properties | Universality, Robustness | Universality, Robustness, Accuracy |
| Variability in intelligence | Treated | Treated |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iantovics, L.B.; Dehmer, M.; Emmert-Streib, F. MetrIntSimil—An Accurate and Robust Metric for Comparison of Similarity in Intelligence of Any Number of Cooperative Multiagent Systems. Symmetry 2018, 10, 48. https://doi.org/10.3390/sym10020048
Iantovics LB, Dehmer M, Emmert-Streib F. MetrIntSimil—An Accurate and Robust Metric for Comparison of Similarity in Intelligence of Any Number of Cooperative Multiagent Systems. Symmetry. 2018; 10(2):48. https://doi.org/10.3390/sym10020048
Chicago/Turabian StyleIantovics, Laszlo Barna, Matthias Dehmer, and Frank Emmert-Streib. 2018. "MetrIntSimil—An Accurate and Robust Metric for Comparison of Similarity in Intelligence of Any Number of Cooperative Multiagent Systems" Symmetry 10, no. 2: 48. https://doi.org/10.3390/sym10020048
APA StyleIantovics, L. B., Dehmer, M., & Emmert-Streib, F. (2018). MetrIntSimil—An Accurate and Robust Metric for Comparison of Similarity in Intelligence of Any Number of Cooperative Multiagent Systems. Symmetry, 10(2), 48. https://doi.org/10.3390/sym10020048







