A Hybrid MCDM Technique for Risk Management in Construction Projects
Abstract
:1. Introduction
- Categorise and describe proper risk issues concerning various socio-economic, technical, and geo-political based sectors correlated to construction projects.
- Develop a logical structure incorporating a D-CFPR based ANP model for risk prioritisation during construction.
- Identify and prioritise risk response factors in the construction industry based on the D-MABAC methodology.
2. Risks in Construction Projects
2.1. An Overview
2.2. Previous Studies on Risk Assessment in Construction Projects
3. Preliminaries
3.1. Dempster–Shafer (D–S) Evidence Theory
3.2. D Numbers Theory
- Firstly, D numbers with nonexclusive hypothesis in each element of the frame of discernment is more applicable for linguistic assessment.
- Secondly, in an evidence theory, a normal BPA must be complete, implying that the sum of all focal length elements in BPA is 1. D numbers allows the experts to input incomplete and uncertain information to the framework resulting in an incomplete BPA, thus releasing the completeness constraint. Thus, if the information is said to be complete, and for the information is said to be incomplete.
4. Methodology
4.1. D-CFPR: D Numbers Extended CFPR
- For the elements satisfying
- ○
- If then
- ○
- If then .
- When
- ○
- If then
- ○
- If then .
- when
- ○
- If ,
- ○
- If then .
- First, sum up each row of the matrix and determine the row number with maximum value.
- Then, assuming the obtained row number is k, delete the k-th row and k-th column in the matrix.
- Replicate the two procedures above until the matrix is empty.
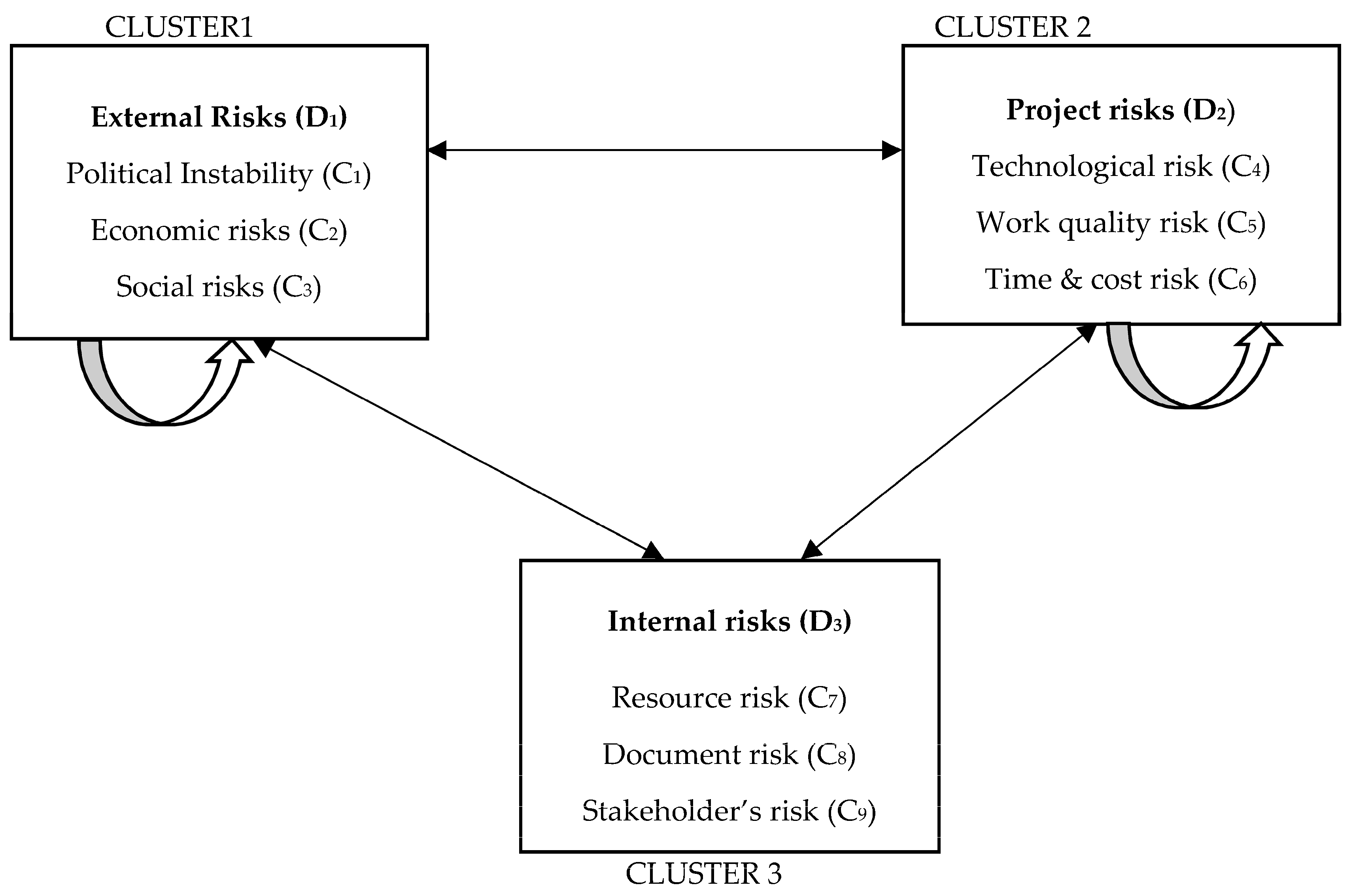
4.2. Evaluating the Risk Criteria Weight Using D-ANP
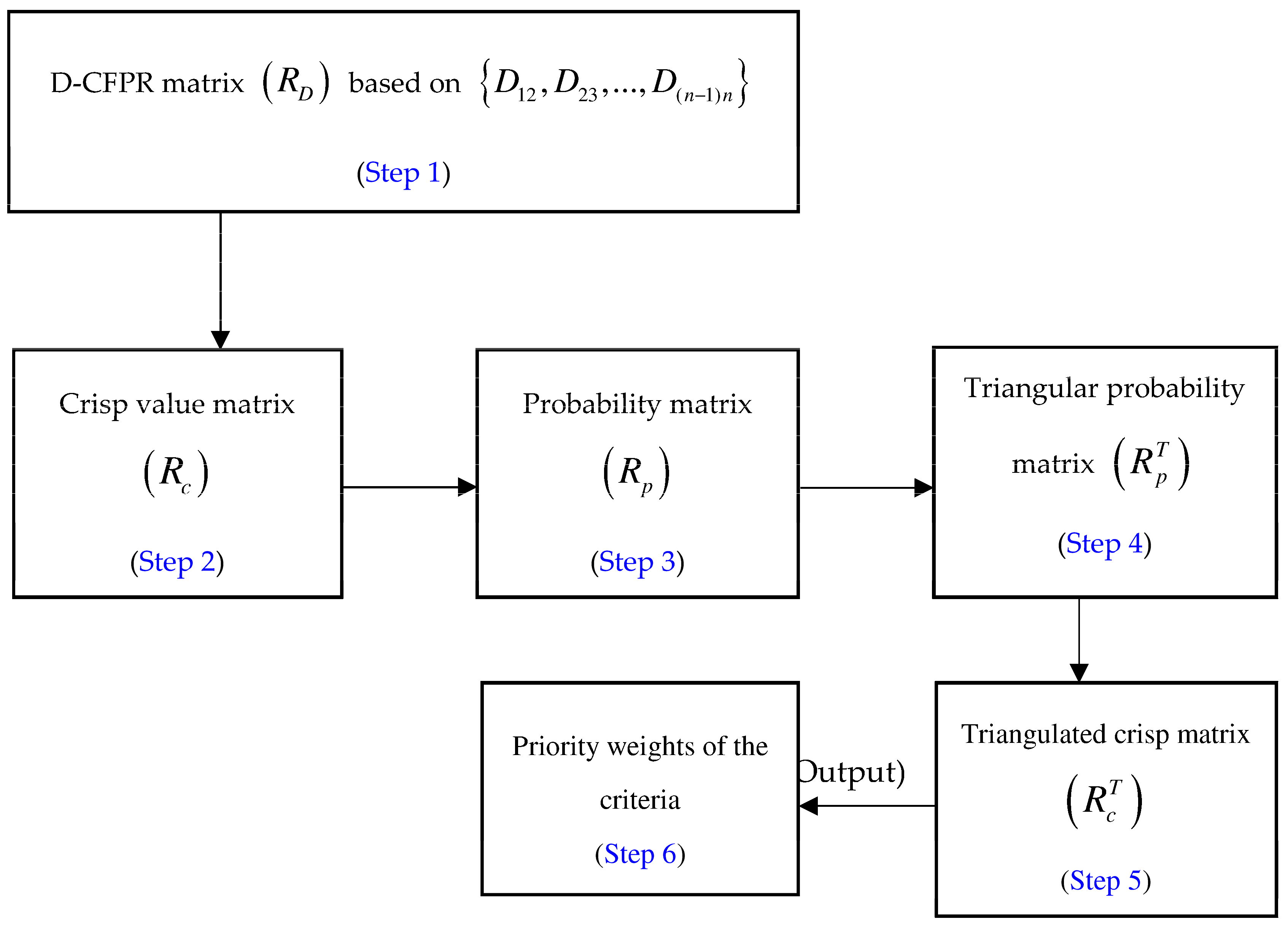
- In the first step, the D-CFPR matrix , is constructed for n criteria, by considering the system as an input using Equations (9)–(12).
- The D-CFPR matrix formed , is converted to a crisp matrix , using the integration representation of D number, shown in Equation (13).
- The probability matrix is then constructed based on the derived crisp matrix using Equation (14), and it satisfies a set of rules in Step 3 of Section 4.1.
- In the next step, using Equation (15), triangularisation is applied to the probability matrix using local information that contains the preference relations of pairwise criteria.
- Lastly, applying Equations (16)–(19), the crisp based triangular matrix , is obtained, and relative priority weights of each criteria , based on clusters (dimensions) are calculated, thereby checking its inconsistency as per Equation (21).
4.3. D-MABAC for Ranking Alternatives
5. Numerical Example: Risk Assessment in a Construction Project
5.1. Identification of Construction Projects Risk Indicators and Their Mitigation Strategies
5.2. Calculating Risk Based Criteria Weight Using D-ANP Framework
5.3. Determination of Final Alternative Ranking by D-MABAC
6. Results and Discussion
6.1. Comparison of Alternative Ranking Using Different MCDM Methods
6.2. Sensitivity Analysis
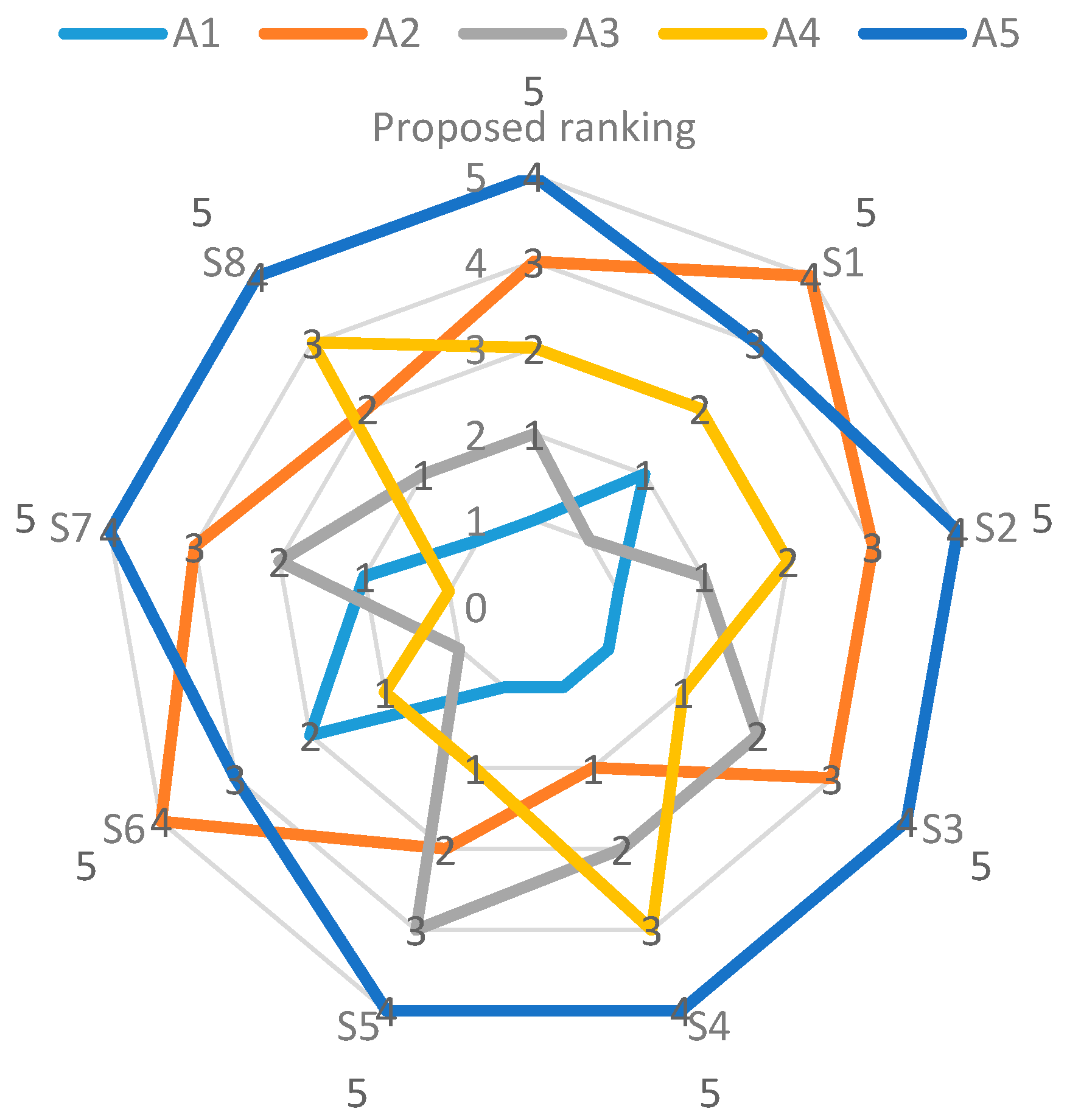
- Analysis of the alternative ranking through eight scenarios (Table 18) showed that alternative A1 retained its rank in five scenarios (best-ranked alternative), while, in the remaining two scenarios , it was ranked second, and third in scenario .
- The worst-ranked alternative A5 retained its rank in six scenarios , while in two scenarios , it was ranked second worst. Therefore, changing the criteria weights through different scenarios resulted in changes to the ranks of the remaining alternatives.
- In addition, from Table 17 and Table 18, it is clear that prioritising criteria C9 has less of an effect on ranking position of alternatives. However, prioritising criteria set {C4, C6, and C7} in scenario S7, {C2, C6, and C8} in scenario S1, along with {C4, C6, and C8} in scenario S6, all altered the positions of risk response alternatives .
- The prioritising of criteria weight in scenarios has no effect on ranking of best or worst risk response alternative A1 and A5, respectively, but it does have an effect on the ranking of the second best risk response alternative A2.
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Akintoye, A.S.; MacLeod, M.J. Risk analysis and management in construction. Int. J. Proj. Manag. 1997, 15, 31–38. [Google Scholar] [CrossRef]
- Schatteman, D. Methodology for integrated risk management and proactive scheduling of construction projects. J. Constr. Eng. Manag. 2008, 134, 885–893. [Google Scholar] [CrossRef]
- Skorupka, D. Identification and initial risk assessment of construction projects in Poland. J. Manag. Eng. 2008, 24, 120–127. [Google Scholar] [CrossRef]
- Wang, S.; Dulaimi, M.; Aguria, M. Risk management framework for construction projects in developing countries. Constr. Manag. Econ. 2004, 22, 237–252. [Google Scholar] [CrossRef]
- Abdelgawad, M.; Fayek, A. Risk Management in the construction industry using combined fuzzy FMEA and fuzzy AHP. J. Constr. Eng. Manag. 2010, 10, 1028–1036. [Google Scholar] [CrossRef]
- Mhetre, K.; Konnur, B.A.; Landage, A.B. Risk Management in construction industry. Int. J. Eng. Res. 2016, 5, 153–155. [Google Scholar]
- Ribeiro, M.I.F.; Ferreira, F.A.F.; Jalali, M.S.; Meidutė-Kavaliauskienė, I. A fuzzy knowledge-based framework for risk assessment of residential real estate investments. Technol. Econ. Dev. Econ. 2017, 23, 140–156. [Google Scholar] [CrossRef]
- Ribeiro, C.; Ribeiro, A.R.; Maia, A.S.; Tiritan, M.E. Occurrence of Chiral Bioactive Compounds in the Aquatic Environment: A Review. Symmetry 2017, 9, 215. [Google Scholar] [CrossRef]
- Iqbal, S.; Choudhry, R.; Holschemacher, K.; Ali, A.; Tamošaitienė, J. Risk management in construction projects. Technol. Econ. Dev. Econ. 2015, 21, 65–78. [Google Scholar] [CrossRef]
- Hwang, B.-G.; Zhao, X.; Yu, G.S. Risk identification and allocation in underground rail construction joint ventures: Contractors’ perspective. J. Civ. Eng. Manag. 2016, 22, 758–767. [Google Scholar] [CrossRef]
- Butaci, C.; Dzitac, S.; Dzitac, I.; Bologa, G. Prudent decisions to estimate the risk of loss in insurance. Technol. Econ. Dev. Econ. 2017, 23, 428–440. [Google Scholar] [CrossRef]
- Pak, D.; Han, C.; Hong, W.-T. Iterative Speedup by Utilizing Symmetric Data in Pricing Options with Two Risky Assets. Symmetry 2017, 9, 12. [Google Scholar] [CrossRef]
- Ravanshadnia, M.; Rajaie, H. Semi-Ideal Bidding via a Fuzzy TOPSIS Project Evaluation Framework in Risky Environments. J. Civ. Eng. Manag. 2013, 19 (Suppl. 1), S106–S115. [Google Scholar] [CrossRef]
- Ebrat, M.; Ghodsi, R. Construction project risk assessment by using adaptive-network-based fuzzy inference system: An Empirical Study. KSCE J. Civ. Eng. 2014, 18, 1213–1227. [Google Scholar] [CrossRef]
- Taylan, O.; Bafail, A.; Abdulaal, R.; Kabli, M. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Dziadosz, A.; Rejment, M. Risk analysis in construction project-chosen Methods. Procedia Eng. 2015, 122, 258–265. [Google Scholar] [CrossRef]
- Schieg, M. Risk management in construction project management. J. Bus. Econ. Manag. 2006, 7, 77–83. [Google Scholar]
- Serpella, A.F.; Ferrada, X.; Howard, R.; Rubio, L. Risk management in construction projects: A knowledge-based approach. Procedia-Soc. Behav. Sci. 2014, 119, 653–662. [Google Scholar] [CrossRef]
- Santos, R.; Jungles, A. Risk level assessment in construction projects using the schedule performance index. J. Constr. Eng. 2016, 2016, 5238416. [Google Scholar] [CrossRef]
- Sadeghi, N.; Fayek, A.; Pedrycz, W. Fuzzy Monte Carlo simulation and risk assessment in construction. Comput.-Aided Civ. Infrastruct. Eng. 2010, 25, 238–252. [Google Scholar] [CrossRef]
- Nieto-Morote, A.; Ruz-Vila, F. A fuzzy approach to construction project risk assessment. Int. J. Proj. Manag. 2011, 29, 220–231. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y. Bridge condition assessment using D numbers. Sci. World J. 2014, 2014, 358057. [Google Scholar] [CrossRef] [PubMed]
- Zavadskas, E.K.; Turskis, Z.; Tamošaitienė, J. Risk assessment of construction projects. J. Civ. Eng. Manag. 2010, 16, 33–46. [Google Scholar] [CrossRef]
- Vafadarnikjoo, A.; Mobin, M.; Firouzabadi, S. An intuitionistic fuzzy-based DEMATEL to rank risks of construction projects. In Proceedings of the 2016 International Conference on Industrial Engineering and Operations Management, Detroit, MI, USA, 23–25 September 2016; pp. 1366–1377. [Google Scholar]
- Mohammadi, A.; Tavakolan, M. Construction project risk assessment using combined fuzzy and FMEA. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting, Edmonton, AB, Canada, 24–28 June 2013; pp. 232–237. [Google Scholar]
- Hashemi, S.; Karimi, A.; Tavana, M. An integrated green supplier selection approach with analytic network process and improved grey relational analysis. Int. J. Prod. Econ. 2015, 159, 178–191. [Google Scholar] [CrossRef]
- Ahmadi, M.; Behzadian, K.; Ardeshir, A.; Kapelan, Z. Comprehensive risk management using fuzzy FMEA and MCDA technique in highway construction projects. J. Civ. Eng. Manag. 2016, 23, 300–310. [Google Scholar] [CrossRef]
- Shin, D.; Shin, Y.; Kim, G. Comparison of risk assessment for a nuclear power plant construction project based on analytic hierarchy process and fuzzy analytic hierarchy process. J. Build. Const. Plan. Res. 2016, 4, 157–171. [Google Scholar] [CrossRef]
- Dehdasht, G.; Zin, R.M.; Ferwati, M.S.; Abdullahi, M.M.; Keyvanfar, A.; McCaffer, R. DEMATEL-ANP risk assessment in oil and gas construction projects. Sustainability 2017, 9, 1420. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F.; Luque, M. Some issues on consistency of fuzzy preference relations. Eur. J. Oper. Res. 2004, 154, 98–109. [Google Scholar] [CrossRef]
- Chen, Y.H.; Chao, R.J. Supplier selection using consistent fuzzy preference relations. Expert Syst. Appl. 2012, 39, 3233–3240. [Google Scholar] [CrossRef]
- Hosseini, L.; Tavakkoli-Moghaddam, R.; Vahdani, B.; Mousavi, S.; Kia, R. Using the analytical network process to select the best strategy for reducing risks in a supply chain. J. Eng. 2013, 2013, 355628. [Google Scholar] [CrossRef]
- Hesamamiri, R.; Mahdavi Mazdeh, M.; Bourouni, A. Knowledge-based strategy selection: A hybrid model and its implementation. VINE J. Inf. Knowl. Manag. Syst. 2016, 46, 21–44. [Google Scholar] [CrossRef]
- Deng, X.; Lu, X.; Chan, F.; Sadiq, R.; Mahadevan, S.; Deng, Y. D-CFPR: D numbers extended consistent fuzzy preference relations. Knowl.-Based Syst. 2015, 73, 61–68. [Google Scholar] [CrossRef]
- Zhang, X.; Deng, Y.; Chan, F.; Adamatzky, A.; Mahadevan, S. Supplier selection based on evidence theory and analytic network process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 230, 562–573. [Google Scholar] [CrossRef]
- Deng, Y.D. Numbers: Theory and applications. J. Inf. Comput. Sci. 2012, 9, 2421–2428. [Google Scholar]
- Han, X.; Chen, X. D-VIKOR method for medicine provider selection. In Proceedings of the IEEE Seventh International Joint Conference on Computational Sciences and Optimization (CSO), Beijing, China, 4–6 July 2014; pp. 419–423. [Google Scholar]
- Liu, H.; You, J.; Fan, X.; Lin, Q. Failure mode and effects analysis using D numbers and grey relational projection method. Expert Syst. Appl. 2014, 41, 4670–4679. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Supplier selection using AHP methodology extended by D numbers. Expert Syst. Appl. 2014, 41, 156–167. [Google Scholar] [CrossRef]
- Fan, G.; Zhong, D.; Yan, F.; Yue, P. A hybrid fuzzy evaluation method for curtain grouting efficiency assessment based on an AHP method extended by D numbers. Expert Syst. Appl. 2015, 44, 289–303. [Google Scholar] [CrossRef]
- Fei, L.; Hu, Y.; Xiao, F.; Chen, L.; Deng, Y. A modified TOPSIS method based on D numbers and its application in human resources selection. Math. Probl. Eng. 2016, 2016, 6145196. [Google Scholar] [CrossRef]
- Zuo, Q.; Qin, X.; Tian, Y.; Wei, D. A multi-attribute decision making for investment decision based on D numbers methods. Sci. Res. 2016, 6, 765–775. [Google Scholar] [CrossRef]
- Renault, B.; Agumba, J. Risk management in the construction industry: A new literature review. MATEC Web Conf. 2016, 66. [Google Scholar] [CrossRef]
- Pamucar, D.; Cirovic, G. The selection of transport and handling resources in logistics centers using Multi-Attribute Border Approximation area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Pythagorean fuzzy Choquet integral based MABAC method for multiple attribute group decision making. Int. J. Intell. Syst. 2016, 31, 989–1020. [Google Scholar] [CrossRef]
- Yu, S.; Wang, J.; Wang, J. An interval type-2 fuzzy likelihood-based MABAC approach and its application in selecting hotels on a tourism website. Int. J. Fuzzy Syst. 2016, 9, 47–61. [Google Scholar] [CrossRef]
- Xue, Y.; You, J.; Lai, X.; Liu, H. An interval-valued intuitionistic fuzzy MABAC approach for material selection with incomplete weight information. Appl. Soft Comput. 2016, 38, 703–713. [Google Scholar] [CrossRef]
- Bozanic, D.; Pamucar, D.; Karovic, S. Use of the fuzzy AHP-MABAC hybrid model in ranking potential locations for preparing laying-up positions. Mil. Tech. Cour. 2016, 64, 705–729. [Google Scholar] [CrossRef]
- Salah, A.; Moselhi, O. Risk identification and assessment for engineering procurement construction management projects using fuzzy set theory. Can. J. Civ. Eng. 2016, 43, 429–442. [Google Scholar] [CrossRef]
- Lyons, T.; Skitmore, M. Project risk management in the Queensland engineering construction industry: A survey. Int. J. Proj. Manag. 2004, 22, 51–61. [Google Scholar] [CrossRef]
- Baloi, P.; Price, A. Modelling global risk factors affecting construction cost performance. Int. J. Proj. Manag. 2003, 21, 261–269. [Google Scholar] [CrossRef]
- Jafarnejad, A.; Ebrahimi, M.; Abbaszadeh, M.; Abtahi, S. Risk management in supply chain using consistent fuzzy preference relations. Int. J. Acad. Res. Bus. Soc. Sci. 2014, 4, 77–89. [Google Scholar]
- Tah, J.H.M.; Carr, V. A proposal for construction project risk assessment using fuzzy logic. Constr. Manag. Econ. 2000, 18, 491–500. [Google Scholar] [CrossRef]
- Wen, G. Construction project risk evaluation based on rough sets and artificial neural networks. In Proceedings of the 2010. IEEE Sixth International Conference on Natural Computation (ICNC), Yantai, China, 10–12 August 2010; pp. 1624–1628. [Google Scholar]
- Fouladgar, M.M.; Yazdani-Chamzini, A.; Zavadskas, E.K. Risk evaluation of tunneling projects. Arch. Civ. Mech. Eng. 2012, 12, 1–12. [Google Scholar] [CrossRef]
- Taroun, A.; Yang, J. A DST-based approach for construction project risk analysis. J. Opt. Res. Soc. 2013, 64, 1221–1230. [Google Scholar] [CrossRef]
- Kao, C.H.; Huang, C.H.; Hsu, M.S.C.; Tsai, I.H. Success factors for Taiwanese contractors collaborating with local Chinese contractors in construction projects. J. Bus. Econ. Manag. 2016, 17, 1007–1021. [Google Scholar] [CrossRef]
- Burcar Dunovic, I.; Radujkovic, M.; Vukomanovic, M. Internal and external risk based assessment and evaluation for the large infrastructure projects. J. Civ. Eng. Manag. 2016, 22, 673–682. [Google Scholar] [CrossRef]
- Yousefi, V.; Yakhchali, S.H.; Khanzadi, M.; Mehrabanfar, E.; Saparauskas, J. Proposing a neural network model to predict time and cost claims in construction projects. J. Civ. Eng. Manag. 2016, 22, 967–978. [Google Scholar] [CrossRef]
- Valipour, A.; Yahaya, N.; Noor, N.M.; Mardini, N.; Antucheviciene, J. A new hybrid fuzzy cybernetic analytic network process model to identify shared risks in PPP projects. Int. J. Strateg. Prop. Manag. 2016, 20, 409–426. [Google Scholar] [CrossRef]
- Ulubeyli, S.; Kazaz, A. Fuzzy multi-criteria decision making model for subcontractor selection in international construction projects. Technol. Econ. Dev. Econ. 2016, 22, 210–234. [Google Scholar] [CrossRef]
- Rajakallio, K.; Ristimaki, M.; Andelin, M.; Junnila, S. Business model renewal in context of integrated solutions delivery: A network perspective. Int. J. Strateg. Prop. Manag. 2017, 21, 72–86. [Google Scholar] [CrossRef]
- Valipour, A.; Yahaya, N.; Noor, N.M.; Antucheviciene, J.; Tamošaitienė, J. Hybrid SWARA-COPRAS method for risk assessment in deep foundation excavation project: An Iranian case study. J. Civ. Eng. Manag. 2017, 23, 524–532. [Google Scholar] [CrossRef]
- Khanzadi, M.; Turskis, Z.; Amiri, G.G.; Chalekaee, A. A model of discrete zero-sum two-person matrix games with grey numbers to solve dispute resolution problems in construction. J. Civ. Eng. Manag. 2017, 23, 824–835. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A new combinative distance-based assessment (CODAS) method for multi-criteria decision-making. Econ. Comput. Econ. Cybern. Stud. Res. 2016, 50, 25–44. [Google Scholar]
- Jiang, W.; Zhuang, M.; Qin, X.; Tang, Y. Conflicting evidence combination based on uncertainty measure and distance of evidence. Springer Plus 2016, 5, 12–17. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Hu, Y.; Zhang, Q.; Deng, Y. A novel distance function of D numbers and its application in product engineering. Eng. Appl. Artif. Intell. 2015, 47, 61–67. [Google Scholar] [CrossRef]
- Jiang, W.; Zhan, J.; Zhou, D.; Li, X. A method to determine generalized basic probability assignment in the open world. Math. Probl. Eng. 2016, 2016, 3878634. [Google Scholar] [CrossRef]
- Zhou, X.; Shi, Y.; Deng, X.; Deng, Y. D-DEMATEL: A new method to identify critical success factors in emergency management. Saf. Sci. 2017, 91, 93–104. [Google Scholar] [CrossRef]
- Zhou, D.; Tang, Y.; Jiang, W. An improved belief entropy and its application in decision-making. Complexity 2017, 2017, 4359195. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Environmental impact based on D numbers. Expert Syst. Appl. 2014, 41, 635–643. [Google Scholar] [CrossRef]
- Bozanic, D.; Pamucar, D.; Karovic, S. Application the MABAC method in support of decision-making on the use of force in defensive operation. Tehnika Menadžment 2016, 6, 129–135. [Google Scholar] [CrossRef]
- Lin, J.H.; Yang, C.J. Applying analytic network process to the selection of construction projects. Open J. Soc. Sci. 2016, 4, 41–47. [Google Scholar] [CrossRef]
- Forbes, D.; Smith, S.; Horner, M. Tools for selecting appropriate risk management techniques in the built environment. Constr. Manag. Econ. 2008, 26, 1241–1250. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Vasiljević, M.; Stojić, G.; Korica, S. Novel Integrated Multi-Criteria Model for Supplier Selection: Case Study Construction Company. Symmetry 2017, 9, 279. [Google Scholar] [CrossRef]
| Characteristics | Frequency | Percentage (%) | |
|---|---|---|---|
| Age group | 21–31 | 2 | 20 |
| 31–39 | 4 | 40 | |
| 39–45 | 3 | 30 | |
| 45–58 | 1 | 10 | |
| Gender | Female | 4 | 40 |
| Male | 6 | 60 | |
| Level of Education | Bachelor’s degree | 4 | 40 |
| Master’s degree | 5 | 50 | |
| Higher | 1 | 10 | |
| Role of respondents | Chief personal officer | 1 | 10 |
| Manager or general manager | 2 | 20 | |
| Staff or assistant manager | 1 | 10 | |
| Project risks analyst | 2 | 20 | |
| Purchasing manager | 1 | 10 | |
| Construction site engineer | 3 | 30 | |
| Years of experience in construction sector | Above 15 years | 2 | 20 |
| 10 years~15 years | 4 | 40 | |
| 5 years~10 years | 3 | 30 | |
| Less than 5 years | 1 | 10 | |
| Total available number | 10 |
| Risk Indicators in Project Based Construction Management | References |
|---|---|
| Environmental risk; political, social and economic risk; contractual agreement risk; financial risk; construction risk; project design risk; market risk. | [1] |
| Safety risk, quality risk, environmental risk, political risk, project site risk, project complexity risk. | [53] |
| Quality risks, personnel risks, cost risks, deadline risks, strategic decision risks, external risks. | [17] |
| Operational risk, economic risk, political risk, financial risk, legal risk, currency and inflation risk, corruption risk, tendering procedures. | [3] |
| Political risks, economic risk, social risk, weather risk, cost, quality risk, technical risk, construction risk, resources risk, project member risk, information risk, construction site risks. | [23] |
| Resources risk, inexperience of project members, lack of motivational approach, design errors risk, efficiency risk, technical risk, quality risk. | [21] |
| Inflation risk, Payment security risk, Programme overrun risk, subcontractor pricing risk. | [56] |
| Political risk, economic risk, natural risk, legal risk, contractor risk, financial risk, management risk, equipment risk, designer risk. | [25] |
| Management risk, project risk, design risk, financial risk, operational risk, external risk. | [14] |
| Information risk, cost risks, lack of coordination, project schedule risk, lack of professional planning, legal dispute risk. | [15] |
| Designing risk, time risk, budget risk, labour risk, political risk. | [16] |
| Design risk, payment delay risk, funding risk, quality risk, labour dispute risks, natural disaster risk, exchange rate fluctuation risk, political instability, site condition risks, insurance inadequacy risk. | [9] |
| Technical risks, organisational risks, socio-political risks, environmental risks, financial risks. | [6] |
| Inflation (economic) risk, environmental and geological risk, design risk, construction delay risk, inadequate managerial skills risk, resource risk. | [29] |
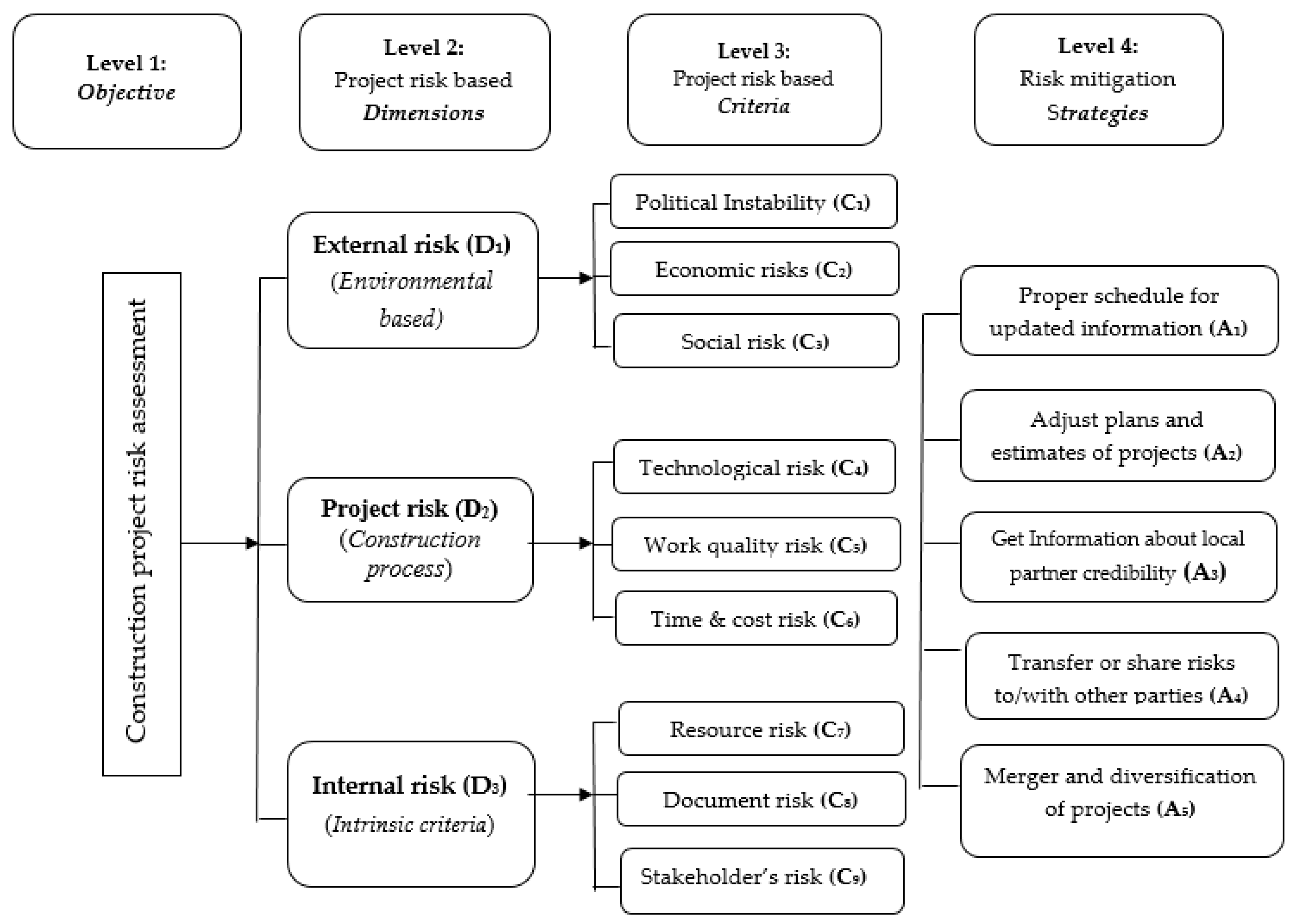
| Risk Dimension | Risk Criteria * | Brief Descriptions of Causes of the Mentioned Criteria Risks |
|---|---|---|
| External risks (D1) | Political instability (C1) | Frequent changes in government due to disputes among political parties, change in law due to local government’s unpredictable new regulations, needless influence by local government on court proceedings regarding project disputes. |
| Economic risk (C2) | Fluctuation in currency exchange rate, unpredictable inflation due to immature banking systems, payment delays due to poor funding for project, inadequate forecasting about market demand. | |
| Social risk (C3) | Racial tension and differences in work culture and language between foreign and local partners. | |
| Project risk (D2) | Technological risk (C4) | Risk of insufficient technology, improper design, unexpected design changes; inadequate site investigation; change in construction procedures and insufficient resource availability. |
| Work quality risk (C5) | Corruption, including bribery, at sites; obsolete technology and practices by the local partner; low local workforce labor productivity due to poor skills or inadequate supervision; improper quality control; local partner tolerance of defects and inferior quality. | |
| Time and cost risk (C6) | Delays due to disputes with contractors, natural disasters, and lack of availability of utilities; risk of labor disputes and strikes; insufficient cash flow, improper measurements, ill planned schedules, and delays in payment; lack of proper benchmarking and monitoring of construction activities. | |
| Internal risks (D3) | Resource risk (C7) | Difficulty in hiring suitable skilled employees; risk of defective material from suppliers; risk of labor, materials, and equipment availability; poor competence and productivity of labor *. |
| Documents and information risk (C8) | Intellectual property protection risk from former local employees, partners, and third parties; corporate fraud including unexpected increases in turnover, unexpected resignations of financial advisers, intentional or unintentional negligence by auditors, bankers, or creditors. | |
| Stakeholder’s risk (C9) | Local partner’s creditworthiness: Information on local partner’s accounts lucidity, financial soundness, foreign exchange liquidity, staff reliability. Termination of joint ventures (JV): unfair dividends, e.g., assets, shares, and benefits, to foreign firms by local partner upon termination of JV contract. |
| Alternative (s) | Preventive Management Techniques | References |
|---|---|---|
| A1 | Proper scheduling for getting updated project information. | [9] |
| A2 | Adjust plans for scope of work and estimates to counter risk implications. | [2] |
| A3 | Get information about local partner’s credibility from present and past business partners. | [4] |
| A4 | Transfer or share risks to/with other parties. | [6] |
| A5 | Merger and diversification of projects. | [23] |
| External Risk (D1) | Project Risk (D2) | Internal Risk (D3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | ||
| External risk (D1) | C1 | 0.000 | 0.576 | 0.589 | 0.315 | 0.386 | 0.373 | 0.332 | 0.353 | 0.395 |
| C2 | 0.525 | 0.000 | 0.411 | 0.357 | 0.351 | 0.347 | 0.336 | 0.321 | 0.327 | |
| C3 | 0.475 | 0.424 | 0.000 | 0.327 | 0.264 | 0.280 | 0.332 | 0.326 | 0.278 | |
| Project risk (D2) | C4 | 0.288 | 0.355 | 0.354 | 0.000 | 0.461 | 0.510 | 0.348 | 0.346 | 0.340 |
| C5 | 0.416 | 0.320 | 0.338 | 0.481 | 0.000 | 0.490 | 0.334 | 0.361 | 0.363 | |
| C6 | 0.296 | 0.326 | 0.308 | 0.519 | 0.539 | 0.000 | 0.318 | 0.293 | 0.298 | |
| Internal risk (D3) | C7 | 0.332 | 0.324 | 0.357 | 0.364 | 0.313 | 0.370 | 0.000 | 1.000 | 1.000 |
| C8 | 0.351 | 0.369 | 0.351 | 0.343 | 0.371 | 0.351 | 1.000 | 0.000 | 1.000 | |
| C9 | 0.316 | 0.308 | 0.292 | 0.293 | 0.315 | 0.279 | 1.000 | 1.000 | 0.000 | |
| Dimensions | |||
|---|---|---|---|
| External Risk | Project Risk | Internal Risk | |
| External risk | 1 | 0.518 | 0.503 |
| Project risk | 0.537 | 1 | 0.496 |
| Internal risk | 0.462 | 0.482 | 1 |
| External Risk | Project Risk | Internal Risk | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | ||
| External risk | C1 | 0.000 | 0.576 | 0.589 | 0.163 | 0.200 | 0.193 | 0.167 | 0.178 | 0.199 |
| C2 | 0.525 | 0.000 | 0.411 | 0.185 | 0.182 | 0.180 | 0.169 | 0.162 | 0.165 | |
| C3 | 0.475 | 0.424 | 0.000 | 0.170 | 0.137 | 0.145 | 0.167 | 0.164 | 0.140 | |
| Project risk | C4 | 0.155 | 0.191 | 0.191 | 0.000 | 0.461 | 0.510 | 0.173 | 0.172 | 0.169 |
| C5 | 0.223 | 0.172 | 0.182 | 0.481 | 0.000 | 0.490 | 0.166 | 0.179 | 0.180 | |
| C6 | 0.159 | 0.175 | 0.165 | 0.519 | 0.539 | 0.000 | 0.158 | 0.146 | 0.148 | |
| Internal risk | C7 | 0.154 | 0.150 | 0.165 | 0.176 | 0.151 | 0.178 | 0.000 | 1.000 | 1.000 |
| C8 | 0.162 | 0.171 | 0.162 | 0.165 | 0.179 | 0.169 | 1.000 | 0.000 | 1.000 | |
| C9 | 0.146 | 0.142 | 0.135 | 0.141 | 0.152 | 0.134 | 1.000 | 1.000 | 0.000 | |
| External Risk | Project Risk | Internal Risk | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | ||
| External risk | C1 | 0.000 | 0.288 | 0.294 | 0.082 | 0.100 | 0.097 | 0.056 | 0.059 | 0.066 |
| C2 | 0.263 | 0.000 | 0.206 | 0.093 | 0.091 | 0.090 | 0.056 | 0.054 | 0.055 | |
| C3 | 0.238 | 0.212 | 0.000 | 0.085 | 0.068 | 0.073 | 0.056 | 0.055 | 0.047 | |
| Project risk | C4 | 0.078 | 0.095 | 0.095 | 0.000 | 0.231 | 0.255 | 0.058 | 0.057 | 0.056 |
| C5 | 0.112 | 0.086 | 0.091 | 0.241 | 0.000 | 0.245 | 0.055 | 0.060 | 0.060 | |
| C6 | 0.079 | 0.088 | 0.083 | 0.260 | 0.270 | 0.000 | 0.053 | 0.049 | 0.049 | |
| Internal risk | C7 | 0.077 | 0.075 | 0.083 | 0.088 | 0.075 | 0.089 | 0.000 | 0.333 | 0.333 |
| C8 | 0.081 | 0.085 | 0.081 | 0.083 | 0.090 | 0.085 | 0.333 | 0.000 | 0.333 | |
| C9 | 0.073 | 0.071 | 0.068 | 0.071 | 0.076 | 0.067 | 0.333 | 0.333 | 0.000 | |
| External Risk | Project Risk | Disruption Risk | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | ||
| External risk | C1 | 0.1062 | 0.1062 | 0.1062 | 0.1062 | 0.1062 | 0.1062 | 0.1062 | 0.1062 | 0.1062 |
| C2 | 0.0958 | 0.0958 | 0.0958 | 0.0958 | 0.0958 | 0.0958 | 0.0958 | 0.0958 | 0.0958 | |
| C3 | 0.0894 | 0.0894 | 0.0894 | 0.0894 | 0.0894 | 0.0894 | 0.0894 | 0.0894 | 0.0894 | |
| Project risk | C4 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | 0.0972 |
| C5 | 0.0996 | 0.0996 | 0.0996 | 0.0996 | 0.0996 | 0.0996 | 0.0996 | 0.0996 | 0.0996 | |
| C6 | 0.0971 | 0.0971 | 0.0971 | 0.0971 | 0.0971 | 0.0971 | 0.0971 | 0.0971 | 0.0971 | |
| Internal risk | C7 | 0.1392 | 0.1392 | 0.1392 | 0.1392 | 0.1392 | 0.1392 | 0.1392 | 0.1392 | 0.1392 |
| C8 | 0.1406 | 0.1406 | 0.1406 | 0.1406 | 0.1406 | 0.1406 | 0.1406 | 0.1406 | 0.1406 | |
| C9 | 0.1349 | 0.1349 | 0.1349 | 0.1349 | 0.1349 | 0.1349 | 0.1349 | 0.1349 | 0.1349 | |
| Dimensions | Risk Criteria | Ranking |
|---|---|---|
| External risk (D1) | Political instability (C1) | 4 |
| Economic risk (C2) | 8 | |
| Social risk (C3) | 9 | |
| Project risk (D2) | Technological risk (C4) | 6 |
| Work quality risk (C5) | 5 | |
| Time and cost risk (C6) | 7 | |
| Internal risk (D3) | Resource risk (C7) | 2 |
| Document and information risk (C8) | 1 | |
| Stakeholder’s risk (C9) | 3 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| A1 | (0.62, 0.5) | (0.72, 0.4), (0.48, 0.6) | (0.53, 0.4) | (0.58, 0.5) | (0.72, 0.6) | (0.48, 0.6), (0.64, 0.4) | (0.66, 0.6) | (0.38, 0.9) | (0.84, 0.2) |
| A2 | (0.68, 0.4) | (0.44, 0.8) | (0.64, 0.6), (0.32, 0.3) | (0.44,.9) | (0.82, 0.9) | (0.88, 0.6) | (0.56, 0.8) | (0.92, 0.8) | (0.69, 0.4) |
| A3 | (0.54, 0.8), (0.68, 0.2) | (0.68, 0.3) | (0.47, 0.9) | (0.78, 0.8) | (0.38, 0.7), (0.59, 0.3) | (0.68, 0.5) | (0.29, 0.6), (0.39, 0.4) | (0.28, 0.6) | (0.34, 0.6) |
| A4 | (0.72, 0.9) | (0.49, 0.7) | (0.78, 0.4) | (0.86, 0.4) | (0.88, 0.4) | (0.47, 0.7) | (0.64, 0.2) | (0.62, 1) | (0.56, 0.7) |
| A5 | (0.48, 1) | (0.56, 0.9) | (0.82, 0.7) | (0.36, 1) | (0.78, 0.7) | (0.59, 0.9) | (0.78, 0.7) | (0.68, 0.3), (0.49, 0.6) | (0.44, 0.8) |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.8989 | 0 | 1 | 1 | 0.7927 | 0 | 0.3589 | 0.5846 | 1 |
| A2 | 1 | 0.6022 | 0.2597 | 0.6826 | 0 | 0.0744 | 0.2344 | 0 | 0.5179 |
| A3 | 0.2128 | 1 | 0.4171 | 0 | 0.7642 | 0.9488 | 0.5167 | 0.8427 | 0.8393 |
| A4 | 0 | 0.6263 | 0.7238 | 0.8383 | 1 | 1 | 1 | 1 | 0 |
| A5 | 0.4468 | 0.1935 | 0 | 0.7904 | 0.4974 | 0.0605 | 0 | 0.3531 | 0.1786 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.2017 | 0.1916 | 0.1788 | 0.1944 | 0.1786 | 0.0971 | 0.1892 | 0.2381 | 0.2698 |
| A2 | 0.2124 | 0.1304 | 0.1126 | 0.1636 | 0.0996 | 0.1043 | 0.1718 | 0.1406 | 0.2048 |
| A3 | 0.1288 | 0.1641 | 0.1267 | 0.0972 | 0.1757 | 0.1892 | 0.2111 | 0.2812 | 0.2481 |
| A4 | 0.1062 | 0.1324 | 0.1541 | 0.1787 | 0.1992 | 0.1942 | 0.2784 | 0.1693 | 0.1349 |
| A5 | 0.1537 | 0.0958 | 0.0894 | 0.1740 | 0.1491 | 0.1030 | 0.1392 | 0.1995 | 0.1590 |
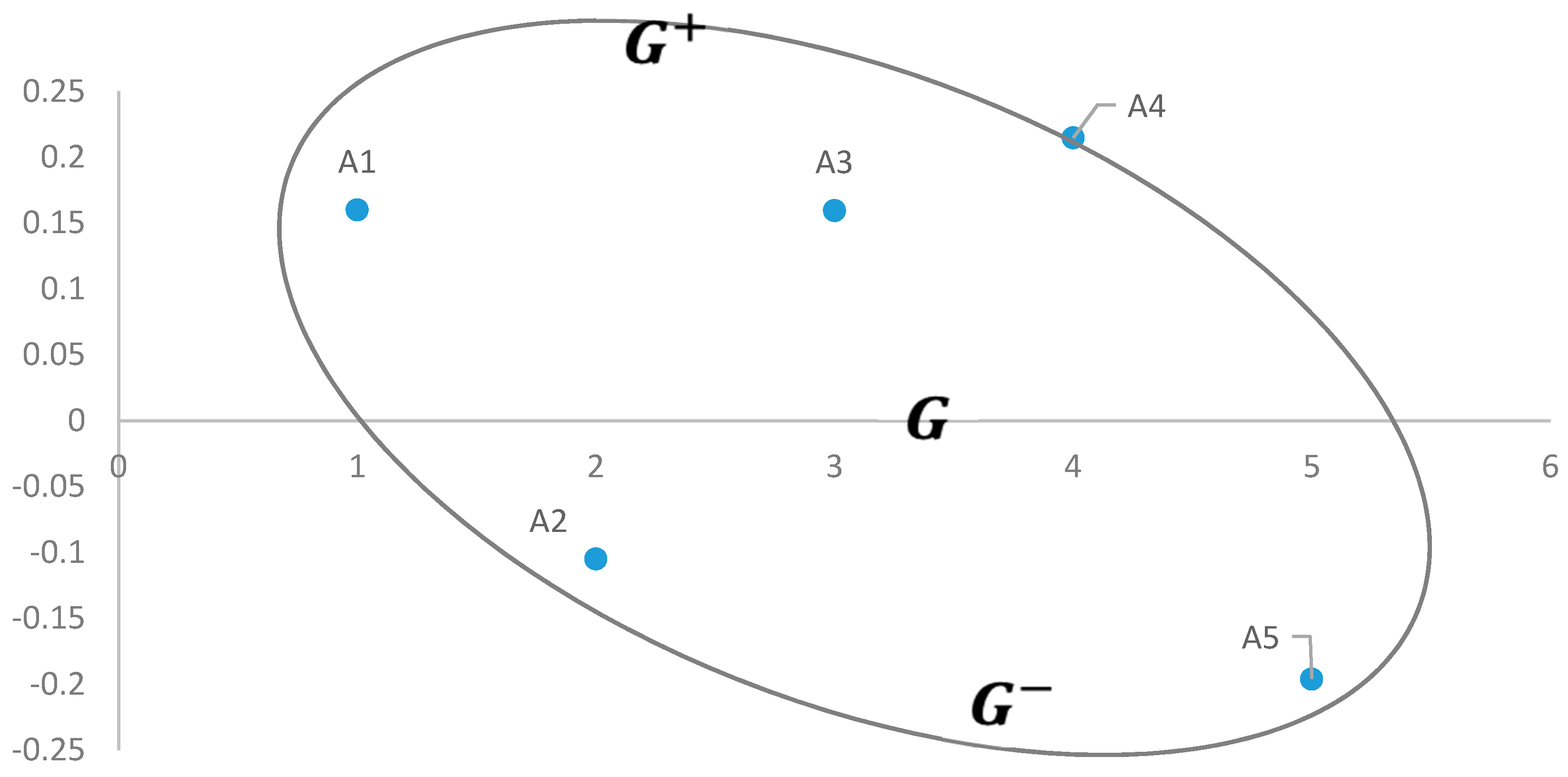
| Alternative Risk Responses | Q | Rank | |
|---|---|---|---|
| Risk response (A1) | Proper scheduling for getting updated project information. | 0.2830 | 1 |
| Risk response (A2) | Adjust plans for scope of work and estimates to counter risk implications. | −0.1161 | 4 |
| Risk response (A3) | Get information about local partner’s credibility from its present and past business partners. | 0.1660 | 2 |
| Risk response (A4) | Transfer or share risks to/with other parties. | 0.0913 | 3 |
| Risk response (A5) | Merger and diversification of projects. | −0.1935 | 5 |
| Alternative Risk Responses | D-MABAC | D-TOPSIS | D-COPRAS | D-ARAS |
|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 |
| A2 | 4 | 4 | 4 | 4 |
| A3 | 2 | 2 | 2 | 2 |
| A4 | 3 | 3 | 3 | 3 |
| A5 | 5 | 5 | 5 | 5 |
| Spearman’s Coefficient | D-MABAC | D-TOPSIS | D-COPRAS | D-ARAS |
|---|---|---|---|---|
| - | 1.000 | 1.000 | 1.000 |
| Scenarios * | ||||||||
|---|---|---|---|---|---|---|---|---|
| Criteria | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
| C1 | 0.0113 | 0.1482 | 0.0226 | 0.2674 | 0.1944 | 0.0795 | 0.0081 | 0.1602 |
| C2 | 0.1578 | 0.1121 | 0.1204 | 0.1178 | 0.0914 | 0.0632 | 0.0962 | 0.0537 |
| C3 | 0.0576 | 0.1789 | 0.2946 | 0.0001 | 0.1853 | 0.0577 | 0.0308 | 0.1054 |
| C4 | 0.0904 | 0.1118 | 0.2655 | 0.1556 | 0.2219 | 0.0519 | 0.2032 | 0.0958 |
| C5 | 0.1172 | 0.0033 | 0.0478 | 0.0598 | 0.0603 | 0.0703 | 0.0875 | 0.1805 |
| C6 | 0.2016 | 0.0233 | 0.0496 | 0.0631 | 0.0322 | 0.3311 | 0.1958 | 0.0218 |
| C7 | 0.0894 | 0.1663 | 0.0352 | 0.0937 | 0.056 | 0.0055 | 0.1485 | 0.0223 |
| C8 | 0.2103 | 0.0933 | 0.003 | 0.0276 | 0.0871 | 0.332 | 0.1191 | 0.0539 |
| C9 | 0.0645 | 0.1628 | 0.1613 | 0.215 | 0.0714 | 0.0089 | 0.1107 | 0.3063 |
| Alternative Risk Responses | Scenarios | |||||||
|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | |
| A1 | 2 | 1 | 1 | 1 | 1 | 3 | 2 | 1 |
| A2 | 5 | 4 | 4 | 2 | 3 | 5 | 4 | 3 |
| A3 | 1 | 2 | 3 | 3 | 4 | 1 | 3 | 2 |
| A4 | 3 | 3 | 2 | 4 | 2 | 2 | 1 | 4 |
| A5 | 4 | 5 | 5 | 5 | 5 | 4 | 5 | 5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, K.; Zavadskas, E.K.; Tamošaitienė, J.; Adhikary, K.; Kar, S. A Hybrid MCDM Technique for Risk Management in Construction Projects. Symmetry 2018, 10, 46. https://doi.org/10.3390/sym10020046
Chatterjee K, Zavadskas EK, Tamošaitienė J, Adhikary K, Kar S. A Hybrid MCDM Technique for Risk Management in Construction Projects. Symmetry. 2018; 10(2):46. https://doi.org/10.3390/sym10020046
Chicago/Turabian StyleChatterjee, Kajal, Edmundas Kazimieras Zavadskas, Jolanta Tamošaitienė, Krishnendu Adhikary, and Samarjit Kar. 2018. "A Hybrid MCDM Technique for Risk Management in Construction Projects" Symmetry 10, no. 2: 46. https://doi.org/10.3390/sym10020046
APA StyleChatterjee, K., Zavadskas, E. K., Tamošaitienė, J., Adhikary, K., & Kar, S. (2018). A Hybrid MCDM Technique for Risk Management in Construction Projects. Symmetry, 10(2), 46. https://doi.org/10.3390/sym10020046







