Abstract
In this paper, an efficient data hiding method that embeds data into absolute moment block truncation coding (AMBTC) codes is proposed. The AMBTC method represents image blocks by trios, and each trio consists of two quantization levels and an asymmetrically distributed bitmap. However, the asymmetric phenomena of bitmaps cause large degradation in image quality during data embedment. With the help of reference tables filled with symmetrical patterns, the proposed method exploits a symmetry adjustment model to modify the quantization levels in those smooth blocks to achieve the smallest distortion. If the block is complex, a lossless embedding method is performed to carry one additional bit. A sophisticated division switching mechanism is also proposed to modify a block from smooth to complex if the solution to the minimal distortion cannot be found. The payload can be adjusted by varying the threshold, or by embedding more bits into the quantization levels. The experiments indicate that the proposed work provides the best stego image quality under various payloads when comparing to the related prior works.
1. Introduction
Data hiding is a technique that embeds data into an innocent cover media for secret communication [1]. The digital images are often used as the cover objects to convey messages because they are easily available and provide rich redundancies for data embedment. When images are chosen as the carriers, the images used for embedding messages are called cover images, while the embedded images are called stego images [2]. The hiding capacity, stego image quality, and un-detectability are the most important issues for a data hiding method in images. A large hiding capacity allows an image to carry more data, while a higher image quality means that the distortion of the stego image is smaller. The un-detectability allows the stego image to resist the statistical detection by the steganalyzers [3,4,5].
According to the recoverability of the cover image, data-hiding methods can be classified into lossy [6,7,8,9,10,11,12,13,14] and lossless [15,16,17]. The least significant bit (LSB) matching [18] is one of the well-known lossy methods. Some recently proposed state-of-the-art approaches, such as the highly undetectable steganography (HUGO) [11], wavelet obtained weights (WOW) [12], and universal wavelet relative distortion (UNIWARD) [13,14], also belong to lossy methods. The HUGO approach is the pioneer of the modern content-adaptive data hiding methods in which the embedding distortion is formulated and minimized. The WOW method utilizes wavelet filter banks to measure the embedding distortion. The schemes based on UNIWARD have excellent performance and can be addressed by both the spatial and frequency domains. These methods are considered more efficient than many prior works, and the embedment of their method is only based on some convolution products, which require insignificant computation cost.
The lossy methods embed more data than those lossless ones and also provide a very acceptable image quality. However, methods of this type distort the cover images permanently. As a result, the cover image cannot be recovered from its stego version. On the other hand, the lossless data hiding methods have the capability to restore the cover image after data extraction and thus they have wide applications. For example, [17] employs a lossless data hiding scheme using integer wavelet transform to embed data into encrypted images. Nevertheless, the payload and stego image quality offered by the lossless methods are often considerably lower than that of lossy ones.
Data hiding methods can be applied to images in spatial domain [6,7,8,9,10,11,12,13,14,15] or compress domain [19,20,21,22,23,24,25,26,27,28]. The spatial domain data hiding methods embed data by slightly altering the pixel values. Since the modern steganalyzers based on rich models [29], deep learnings [30], or combinations of these approaches [31] are now capable of detecting the presence of embedment of this type to a large extent, an ideal spatial domain data hiding method should be designed such that the cover and stego images are statistically indistinguishable. To avoid the statistical trace, some novel coverless data hiding methods based on based on scale invariant feature transform and bag of feature [32], or based on binary numbers and transformed by Chinese characters [33] are proposed. The compress domain data hiding method embeds data by modifying the compressed codes. Because most of the data hiding methods exploit the redundancies in images to embed data, and the redundancies are considerably eliminated when images are compressed, a compress domain data hiding method often provides smaller payload than those of spatial domain methods. Moreover, since the pixel correlations are destroyed significantly in compress domain, a data hiding method in this domain often requires elaborate computation such as image processing or machine learning algorithms to achieve the goal of data embedment. However, since images are often stored or transmitted in their compressed format, the compressed domain data hiding methods thus attract researchers to investigate new techniques in various compress domains. A number of compressed domain data hiding methods based on vector quantization (VQ) [19,20,21], joint photographic experts group (JPEG) [22], and absolute moment block truncation coding (AMBTC) [23,24,25,26,27,28] compressed images are proposed. Compared to VQ and JPEG, AMBTC requires less computing cost but achieves acceptable image quality. Therefore, it is very suitable for applications with limited power consumption such as portable digital devices. Due to the increasing demands of low-cost data hiding methods in computation for portable devices, several data hiding methods for AMBTC codes are proposed.
The AMBTC compression method was proposed by Mitchell [34] in 1984. AMBTC partitions an image into blocks, and each block is independently compressed to obtain a trio that represents the compressed code. Each trio consists two quantization levels and a bitmap. Chuang and Chang [23] proposed a data hiding method to embed data using direct bitmap replacement. If the difference between the two quantization levels is small, the bitmap modification insignificantly affects the visual quality of the decoded block. As a result, this method replaces the bitmap by secret data to achieve the embedment. Chen et al. [24] use the order of two quantization levels to losslessly embed data into AMBTC codes. Since the swapped quantization levels and the flipped bitmap also reconstruct an identical AMBTC block, Chen et al.’s method not only effectively embeds data but also produces a stego BTC image that is identical to the original AMBTC image. Inspired by Chen et al.’s works, Hong et al. [25] proposed a hybrid AMBTC data hiding method to achieve lossy or lossless data embedment. In their method, the number of different bits between the to-be-embedded bits and bitmap is examined. If more than half the number of the bit values is different, the two quantization levels are reversely recorded to reduce the distortion.
Ou and Sun [26] proposed another efficient data hiding method for AMBTC codes based on quantization level modification. Ou and Sun observed that the replacement of bitmap with secret data while keeping the quantization levels unchanged might introduce larger distortion. As a result, they find an optimal modification to the quantization levels to ensure the distortion is the smallest. In 2016, Bai and Chang [27] proposed a two-phase method to embed data into AMBTC codes by using matrix encoding with high payload. In this method, the (7, 4) Hamming code is performed on the quantization levels and their differences to embed data bits in the first phase, and then performed on the bitmap to embed more bits in the second phase. In 2017, Huang et al. [28] also proposed an efficient method to embed data both in bitmap and quantization levels. Unlike Ou and Sun’s method, Huang et al.’s method exploits the difference between the quantization levels to embed data with great performance. Since the differences are subtly adjusted to carry additional data, the introduced distortion is confined and thus the embedding performance is greater than that of Ou and Sun’s method.
In this paper, we proposed an efficient data hiding method dedicated to the AMBTC compressed codes with the guidance of a reference table. The proposed method classified AMBTC blocks into smooth and complex. The bitmaps are replaced by secret data in those smooth blocks, and the quantization levels are searched in a reference table and modified to carry data bits in a way that the decoded AMBTC block has the smallest distortion. If the block is complex, a data bit can be losslessly embedded using Chen et al.’s method. The payload can be increased by adjusting a threshold, or by embedding more bits into the quantization levels. Since the embedded information can be easily removed as the values of trios are slightly altered while providing a high image quality, the proposed method can be adopted as a fragile watermarking technique used for image authentication.
2. Related Works
In this section, we briefly introduce the AMBTC compression and the pixel pair matching embedding technique. Huang et al.’s data hiding method based on AMBTC compressed images is also presented in this section.
2.1. AMBTC Compression Technique
To compress an original image O using AMBTC, O is firstly partitioned into N non-overlapping blocks of size . For each block , the mean value is calculated. Let be the pixel in . The lower and upper quantization levels and can be obtained by averaging those pixels satisfying and , respectively. A bitmap of size is employed to record which quantization levels should be used at the decoding stage. Let be the k-th bit in . If , then is set. Otherwise, . AMBTC uses the trio to represent the compressed code of block . As a result, the compressed codes of image O consist the trios . To decode an AMBTC trio , the bits recorded in are scanned. Let be the decoded AMBTC block using trio and be the k-th pixel of . If , then is set. Otherwise, . All the blocks are decoded using the same procedure, and the decoded AMBTC image is reconstructed.
The examples of encoding and decoding of the AMBTC compression technique are given as follows. Let (52 53 37 47; 48 48 38 43; 41 51 50 42; 48 47 50 48) be the image block to be encoded, where semicolons represent end of row. The mean value can be calculated. Averaging the pixels with value smaller than and rounding the result to the nearest integer, we have . Similarly, is obtained. The bitmap = (1101; 1100; 0110; 1111) can then be constructed. As a result, the compressed trio of is = (40, 49, (1101; 1100; 0110; 1111)). To decode the compressed trio, replace 0 and 1 in with 40 and 49, respectively, we have (49 49 40 49; 49 49 40 40; 40 49 49 40; 49 49 49 49).
2.2. Adaptive Pixel Pair Matching Technique
Pixel Pair Matching (PPM) [7] is a technique that embeds digits in -ary notational system into pixel pairs by matching the secret digits with entities in a reference table. The reference table is a table that fills with digits ranging from 0 to . Let be the entity located at the x-th column and the y-th row of the reference table . Figure 1 shows the schematic diagram of the PPM technique.
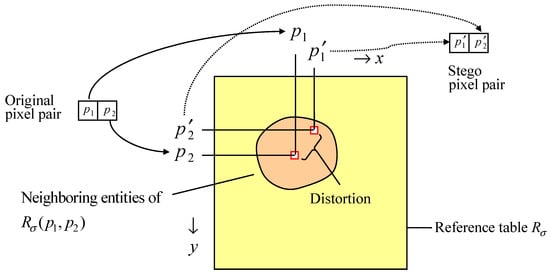
Figure 1.
Schematic illustration of the pixel pair matching (PPM)-based embedding methods.
To embed secret digits in notational system, the cover image is partitioned into blocks, and each block consists of a pixel pair. Let be the secret digit in -ary notational system to be embedded into the i-th pixel pair . Firstly, the neighboring entities of are searched to find a coordinate satisfying and the Euclidean distance between and is the smallest. The original pixel pair is then replaced by the stego pixel pair . Each pixel pair is embedded with a secret digit using the same procedure until all the secret digits are embedded. To extract the embedded secret, pixel pairs in the stego image are sequentially visited as in the embedding phase. The embedded digit in the i-th pixel pair can be easily extracted by referencing the entity located at , i.e., .
The design of the reference table greatly affects the embedding performance of the PPM-based method. A well-designed reference table should satisfy the condition that the MSE of the replacement of by all possible should be the smallest. The adaptive PPM (APPM) method proposed in [7] gives the optimal solution to construct the reference table for concealing digits with -ary notational system, where the reference table is filled with the digits by using the equation
where is a constant. For example, when = 4, 8, 16, 32, and 64, = 2, 3, 6, 7, and 14, respectively. We use a brief example to show the procedures of embedding and extraction of the APPM method. Let , , and the secret digits in 16-ary notational system to be embedded is . The reference table can be constructed using Equation (1). Figure 2 shows a fraction of the reference table.
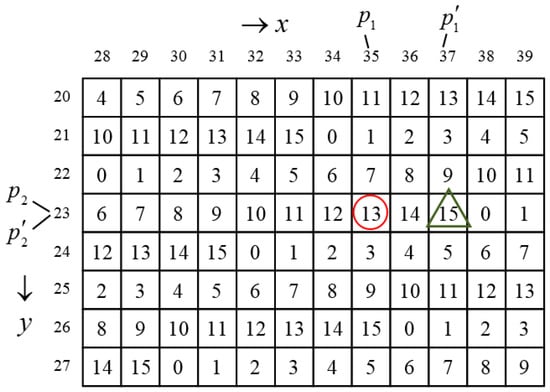
Figure 2.
Example of data embedding and extraction.
Because and has the nearest distance to for all , we have and . To extract the embedded digits, since we know and , we thus obtain .
2.3. Huang et al.’s Method
Huang et al. [28] proposed a data hiding method based on AMBTC in 2017. In their method, AMBTC blocks are classified into smooth and complex. The quantization levels of both smooth and complex blocks are used to carry data, while only the bitmaps of the smooth blocks are used to embed data. To embed data, the trios are scanned. Let be the difference between and , i.e., . If , where T is a predefined threshold, the block is classified as a smooth one. In this case, the bitmap is replaced by bits secret data . The two quantization levels and are also modified for carrying secret bits in a way that the binary representation of the difference is the secret bits. To do this, let D be the decimal value of secret bits. If , the difference between and has to be decreased such that the decreased difference , where and represent the modified values of and , respectively. This can be done by shifting by and shifting by , where . In [28], and are set. The schematic diagram of the shifting of and are shown in Figure 3.
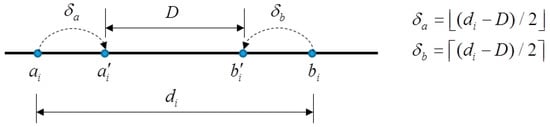
Figure 3.
Schematic diagram of the shifting of and for a smooth block.
With the concept described above, Huang et al. use the following equations to perform the modification of quantization levels for carrying secret bits:
On the other hand, if the scanned block is complex, i.e., , and are also modified to carry bits according to the equation given below:
where is the remainder between and T. For a complex block, because and , still hold. Huang et al. exploits this fact to embed one additional bit. That is, if the to-be-embedded bit is 12, the values of and are swapped and bitmap is set, where is the flipped version of . Otherwise, and are kept unchanged and set .
The data extraction procedures in Huang et al.’s method are quite straight forward. If , the scanned block is smooth and thus bits can be extracted from , and the other bits can be extracted from the two quantization levels, where represents the binary representation of x. Here we use a simple example to illustrate the embedment in the quantization levels. Suppose , , , and the to-be-embedded bits are 102. Because , the block is complex, and we have , . According to Equation (4), because , we have , . To extract the embedded bits, which is the binary representation of , we calculate . Because , the embedded bits are 102.
3. Proposed Method
Most of the prior works based on the AMBTC compressed images embed data by replacing the bitmap of trios with secret data. However, these methods do not fully exploit the adjustment of quantization levels for carrying additional data bits while minimizing the distortion. Ou and Sun’s method [26] gives an optimal modification to the quantization levels to ensure the distortion after the bitmap replacement is minimal. However, the quantization level modification is based on the original image blocks. The optimized quantization levels can be obtained only if the original image block is known. Besides this, the quantization levels in this method are not used to carry data bit. As a result, the embedding capacity is limited. Huang et al.’s method [28] subtly embeds additional data bits into the difference of the quantization levels. However, they provide no solution to deal with the overflow and underflow problems, and these problems occur frequently, as the threshold is large.
The proposed method fully exploits the modification of quantization levels to achieve a better embedding efficiency. A threshold is used in the proposed method to classify blocks into smooth and complex ones. For smooth blocks, the bitmap in each trio is replaced by secret messages, while the two quantization levels are adjusted in a way that the stego block has the smallest distortion. Moreover, the adjusted quantization levels can be further modified to embed additional data bits using the APPM technique [7]. For complex blocks, a data bit is losslessly embedded by switching the recording order of quantization levels while flipping the bitmap. The payload is adjustable by varying the threshold or by choosing a larger notational system. A division-switching mechanism is also adopted to solve the case when the constraints in the optimization problems cannot be satisfied. The detailed techniques used in the proposed method are given in the following subsection.
3.1. Optimal Quantization Level Adjustment
The proposed method uses a threshold T to classify blocks into smooth and complex. If the difference between and is smaller or equal to T, i.e., , the block is a smooth one, Otherwise, the block is classified as complex. The bitmap of a smooth block is employed to carry secret data by replacing with . The distortion due to the bitmap replacement will inevitably occur. Nevertheless, the quantization levels can be adjusted such that the distortion is the smallest. Let and be the decoded AMBTC block using the trio and , respectively. The quantization levels that minimize the distortion can be found by minimizing the mean square error (MSE) between and . Since and are 8-bit integers, the minimization problem can be formulated as:
Minimize:
Subject to:
Let denote the solution to Equation (6). Suppose and represent the percentage of the unchanged bits and flipped bits when replacing with , respectively. Therefore, the squared error caused by replacing with can be formulated as
The minimal distortion of SE can be found by setting the partial derivative of Equation (7) with respect to a and b to zero and solving the resultant equations, we have
Because , we assume where is a constant and . Therefore, Equation (8) can be rewritten as and . Since and , the conditions and always hold. Therefore, the second constraint in Equation (6) can be reduced to and , and thus the third constraint automatically holds. Because and can be obtained once and are known, and can be directly calculated by rounding the results of Equation (8).
3.2. Embedment Using APPM
The solution to Equation (6) gives a minimum distortion when bitmap is replaced by the secret data . However, and themselves do not carry any data. We observe that the slight modification to the optimized quantization levels can carry additional data bits, and the APPM technique gives the smallest distortion when modifying a pair of quantization levels to for concealing a digit in notational system [7]. Therefore, the proposed method adopts APPM to embed an additional secret digit in notational system into the optimized quantization levels, as formulated as
Minimize:
Subject to:
where is the reference table used for embedding digits in notational system. The solution and to Equation (9) can be easily solved by locating the neighboring entities of with value in the reference table , and then select the one satisfying and is the minimum.
3.3. Division-Switching Technique
In rare cases that the solution cannot be found because of no quantization levels and both satisfying and , we simply modify the original quantization levels and to and such that and the MSE between and is the smallest. This operation can be formulated as an optimization problem:
Minimize:
Subject to:
Once the solution and have been determined, one data bit can be embedded into this block. On the decoder side, because , the decoder knows the visited block is complex and thus the embedded data bit can be successfully extracted. The embedding and extraction of complex block will be discussed in the next subsection.
3.4. Lossless Embedment Technique
If , the block is classified as complex and the modification of quantization levels or bitmap will produce significant distortion. Nevertheless, a data bit can still be embedded losslessly using the method proposed in [24]. To losslessly embed a data bit into the trio , if the to-be-embedded bit is 02, the trio is unmodified. If the to-be-embedded bit is 12, the trio is modified to , where is the flipped version of . Note that the decoded blocks and are identical. As a result, the embedment in the complex blocks results in no distortion but contribute one bit to payload per block.
Figure 4a,b show the distribution of embedment using APPM (Section 3.2, marked by blue cross marks), division-switching (Section 3.3, marked by red circle marks), and the lossless embedment techniques proposed in this section (marked by black dots) using the parameters and , respectively. As seen from Figure 4a, when a large and a small T is set, the embedment using the division-switching technique sparsely distributed. However, when T slightly increases to 5, none of the division-switching technique is applied, and more blocks are classified as smooth ones. This is reasonable because when T is small, the first and third constraints in Equation (9) are more difficult to satisfy. As a result, the division-switching technique will be applied more often than larger T.
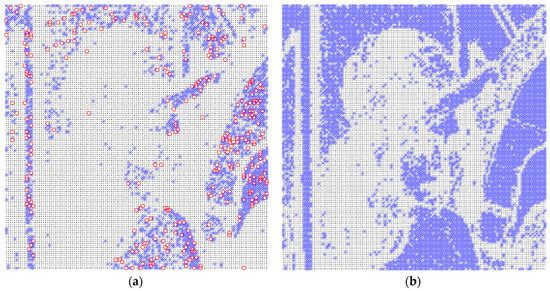
Figure 4.
Distribution of the proposed embedding techniques. (a) ; (b) .
3.5. Embedding Procedures
For a given payload and a notational system , the proposed method firstly finds a minimum threshold T such that all the payload can be embedded. Let and be the number of smooth and complex blocks, respectively. Since the proposed method embeds bits into smooth blocks and embeds one bit into complex block, therefore, the smallest T can be determined such that
Once the smallest T has been determined, the following procedures are employed to embed the secret data:
Input: AMBTC codes , secret data S, block size , and .
Output: AMBTC stego codes , threshold T.
- Step 1:
- Use Equation (11) to determine the smallest threshold T.
- Step 2:
- Scan the AMBTC trios .
- Step 3:
- If , the scanned trio is smooth. The following three steps are performed to embed bits into the scanned trio:
- (1)
- Extract bits from S, and replace with .
- (2)
- Adjust the quantization pair to by solving the Equation (6) given in Section 3.1.
- (3)
- Extract bits from S, convert the extracted bits to a digit in notational system, and perform the APPM embedding technique to embed into the quantization pair by solving Equation (9). In case the solution cannot be found, return the previously extracted to S, modify to according to the Equation (10), and go to Step 4 for embedding one additional bit.
- Step 4:
- If , the scanned trio is complex. Extract one bit from S and losslessly embed the extracted bit, as described in Section 3.4.
- Step 5:
- Steps 2–4 are repeated until all bits in S are embedded.
The embedding procedures are briefly illustrated in Figure 5. The final stego codes are denoted by . The parameters , m, and T are recorded as the keys for data extraction, and use a secret channel to transmit them to the receiver side.
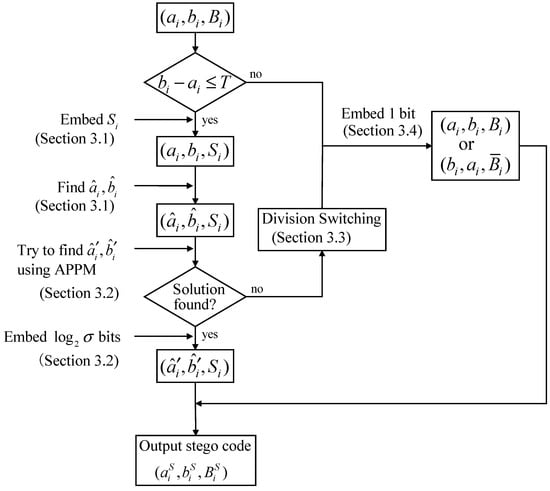
Figure 5.
Schematic illustration of the embedding procedures.
3.6. Extraction Procedures
Once the receiver has the stego codes and the keys m, , and T, the secret data can be extracted using the following procedures:
Input: AMBTC stego codes , , , and block size .
Output: Secret data S.
- Step 1:
- Scan the stego codes sequentially.
- Step 2:
- If , extract bits from the bitmap. Other bits can be extracted by obtaining first, and then convert to its binary representation.
- Step 3:
- If , one bit is embedded in this block. If , a bit 02 is extracted. If , a bit 12 is extracted.
- Step 4:
- Repeat Steps 2–4 until all the embedded data are extracted.
3.7. A Simple Example
The following is an example to show the procedures of embedding and extraction of the proposed method. For simplicity, the determination of threshold and the division-switching technique introduced in Section 3.3 are not demonstrated in this example. Suppose two AMBTC trios are to be embedded with secret data 0010001001100000101112. The two trios and the corresponding AMBTC block are shown in Figure 6a–c, respectively. Let and be the embedding parameters used, and the required reference table is shown in Figure 2. In this example, the bitmap is capable of carrying 16 bits while the pair of quantization levels are able to carry bits.
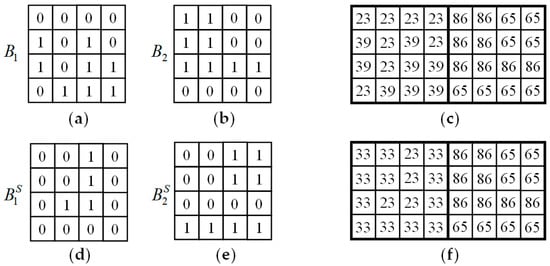
Figure 6.
Examples of the proposed method. (a) ; (b) ; (c) AMBTC compressed block; (d) ; (e) ; (f) Stego image block.
For the first trio, because , we embed 16 bits into the bitmap by replacing with the first 16 bits 00100010011000002 of S. Since the bitmap is replaced, a pair of quantization levels has to find such that the distortion due to the bitmap replacement is the smallest. and can be obtained by solving Equation (6) with few calculations. Now, and can be modified to carry four additional bits. Extract the 17-th to 20-th bits 10112 from S and convert it to the 16-ary notational system, we have . Because the coordinate (33, 23) is the nearest coordinate to (31, 23) satisfying and , we have and . As a result, the final stego trio for the first AMBTC block is . For the second block, because , one bit can be embedded into this block losslessly. Because the 21-th bit is 12, swapping the value of and , and flipping the bitmap of , we have the stego code . The final stego trios and the corresponding stego AMBTC block are shown in Figure 6d–f.
To extract the embedded bits, because , 16 bits are embedded in the bitmap and four bits are embedded in the quantization pair. Extract the 16 bits from the bitmap , we have 00100010011000002. Moreover, because , four bits 10112 can be extracted. For the second block, since and , a bit 12 is extracted. Concatenate these extracted bits, the embedded secret data 0010001001100000101112 can then be successfully extracted.
4. Experimental Results
In this section, several experiments are conducted to show the performance of the proposed method. Eight test images shown in Figure 7, including Lena, Jet, Tiffany, Peppers, Tank, Boat, House, and Baboon, were used in the experiment. These test images are 8-bit of size , which can be obtained from the USC-SIPI image database [35].

Figure 7.
Eight test images. (a) Lena; (b) Jet; (c) Tiffany; (d) Peppers; (e) Tank; (f) Boat; (g) House; (h) Baboon.
These test images were compressed to obtain the AMBTC codes with block size , and then the embedding performance was tested on these compressed codes. The secret data were simulated using a pseudo random number generator, and the peak signal-to-noise ratio (PSNR) metric is employed to evaluate the image quality, which is defined by
where M is the total number of pixels in the image, and , are the pixel values of the reference image and the to-be-measured image, respectively. A higher PSNR shows that the measured image quality is visually closer to the reference image.
It should be noted that in the following subsections, the image quality of the stego AMBTC compressed images was measured by referencing the original images. Table 1 shows the image qualities of the AMBTC compressed images when comparing to the original images. Once the data are embedded into the AMBTC codes, the PSNR of the stego AMBTC images should be smaller than the ones listed in this table.

Table 1.
Image quality (in dB) of the absolute moment block truncation coding (AMBTC) compressed images.
4.1. Performance of the Proposed Method
In this section, we compare the embedding performance of the proposed method when the parameter is chosen to be 2, 4, 8, 16, or 64, respectively. The results of the test images Lena and Baboon are shown in Figure 8, where the curves are plotted by varying the threshold for a given payload. In this figure, the legend denotes the optimized quantization levels are used to obtain the PSNR but they are not used to carry data. It is interesting to note that the decrease in PSNR of the Lena image at low payload is smaller than that of the Baboon image. This is because the Lena image possesses more smooth blocks than complex ones, and at low payload, only part of the smooth blocks are used for carrying bits, and other blocks are used to carry one bit losslessly. As a result, the decrease in PSNR is insignificant when comparing the Baboon image, where smooth blocks are far less than those in the Lena image.
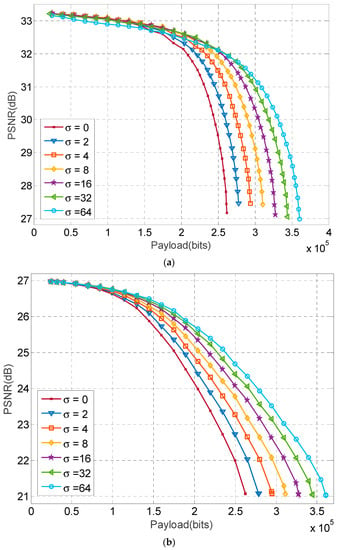
Figure 8.
Performance comparison of various . (a) Lena image; (b) Baboon image.
Figure 8 also shows that for the Lena image at a small payload, a smaller provides a slightly higher image quality. On the contrary, a larger at large payload offers significantly better image quality than smaller ones. For example, when the payload is 160,000 bits for the Lena image, the PSNR at 2, 4, 8, 16, 32, and 64 are 32.79, 32.85, 32.86, 32.88, 32.82, and 32.69 dB respectively. However, when the payload is increased to 260,000 bits, the PSNR at 2, 4, 8, 16, 32, and 64 are 29.98, 30.99, 31.56, 31.88, 31.96, and 31.94 dB respectively. Complex images such as Baboon at large payload have similar trends. The better embedding performance at high payload is due to the utilization of quantization levels for data embedment. Although Figure 8 only shows the comparison results of two test images, the similar results are obtained in other test images. The results suggest that the best can be selected for a given payload to minimize the image distortion in the proposed method. In real applications with a given payload , the best that result in the highest PSNR can be calculated by substituting various into using Equation (11) to find minimum thresholds T and subsequently obtain various PSNRs. The and T that result in the highest PSNR are selected as the parameter for data embedment.
4.2. Comparison with Previous Schemes
In this section, the embedding performance of the proposed method is compared with other recently published methods, including Huang et al.’s [28], Ou and Sun’s [26], Hong et al.’s [25], and Chuang et al.’s [23] methods. In Huang et al.’s method, threshold values are set to 2, 4, 8, and 16, respectively, to accommodate the given payload. In Ou and Sun’s method, the lossless embedding is also implemented to achieve the best performance. In Hong et al.’s and Chuang et al.’s methods, a threshold is used to control the payload such that the image distortion is the smallest. In the proposed method, the parameter that results in the best image quality is selected for data embedment. Figure 9a–c show the performance comparison of the Lena, Boat, and Baboon images, respectively, and Figure 9d is the averaged payload–PSNR curves of the eight test images.
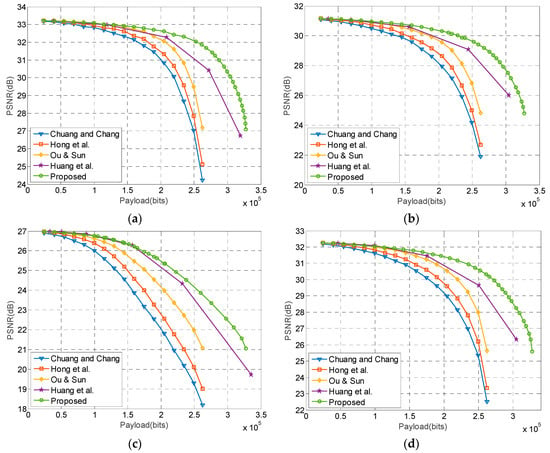
Figure 9.
Performance comparison of the related works. (a) Lena; (b) Boat; (c) Baboon; (d) Averaged results.
Figure 9 shows that the Chuang and Chang’s method has the lowest image quality because this method embeds data simply by bitmap replacement. Hong et al.’s method performs better than Chuang and Chang’s method because the quantization levels are modified according to the number of different bits between secret data and bitmap. Ou and Sun’s method gives an optimal modification to the quantization levels to minimize distortion. However, the aforementioned methods do not utilize the quantization levels to carry data bits, and thus the payload is limited to . Huang’s method effectively embeds data into quantization levels while keeping the distortion low. As a result, the method achieves a better performance over prior works. Nevertheless, the proposed method provides the best embedding result for various payloads, especially at high payloads. The increased PSNR is due in part to the proposed method efficiently embedding data bits into quantization levels using APPM, and due part to the embedding parameters can be selected to minimize the distortion.
It is interesting to note that although Huang et al.’s method offers a good embedding performance, their method provides no mechanism to deal with the overflow and underflow problems. As a result, if the threshold is large, or the image itself possesses any saturated pixel (pixels valued 0 or 255), the embedded data cannot be extracted correctly due to the occurrence of overflow/underflow. Figure 10a–c show the overflowed pixels (represented by black cross marks) of the Tiffany image using Huang et al.’s method when the threshold is set to 4, 8, and 16, respectively. As a comparison with Figure 10c, we also show the embedding result of the proposed method when approximately the same payload is embedded.
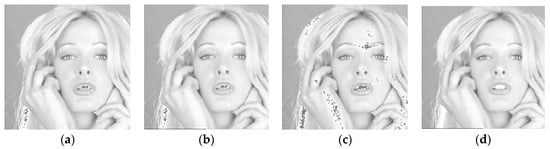
Figure 10.
Stego AMBTC images. (a–c) Huang et al.’s method; (d) The proposed method. (a) T = 4, 136,647 bits 35.30 dB; (b) T = 8, 219,721 bits 34.19 dB; (c) T = 16, 283,145 bits 31.54 dB; (d) T = 16, 283,125 bits 33.53 dB ().
As shown in Figure 10a–c, since the Tiffany image contains a considerable number of saturated pixels, the number of overflowed pixels increases as the threshold increases. On the contrary, the proposed method subtly employs the quantization levels to carry additional data bits, and provides mechanisms to avoid pixel from overflow or underflow. Therefore, the proposed method achieves an excellent performance while the embedded data can be successfully extracted.
In addition to the eight test images, we also perform the test on 200 images randomly selected from [36]. These images are 8-bit of size . Because the maximum payload of Chuang and Chang’s, Hong et al.’s, and Ou and Sun’s methods are 262,144 bits, we test the performance on two payloads: 200,000, and 262,144 bits. The results are sorted in ascending order according to PSNR values of Chuang and Chang’s method, as shown in Figure 11. The results show that the proposed method offers the best image quality among these five methods for most of the test images. Moreover, it is quite obvious that the increase in PSNR of the proposed method is more significant than other methods when bits. This is due to the subtle APPM usage on the quantization levels for carrying additional data bits. Note that the increase in PSNR of proposed method at bits is not so obvious at high PSNR (from 35 to 45 dB). This is because these high-PSNR images contain a significant number of flat blocks, which is relatively favorable to those methods only using bitmap replacement for embedment. Nevertheless, the proposed method still offers a comparable image quality for most flat images. We perform the test on another set of randomly selected images, which also shows similar results, indicating that the proposed method indeed offers a better performance than the recently published state-of-the-art works.
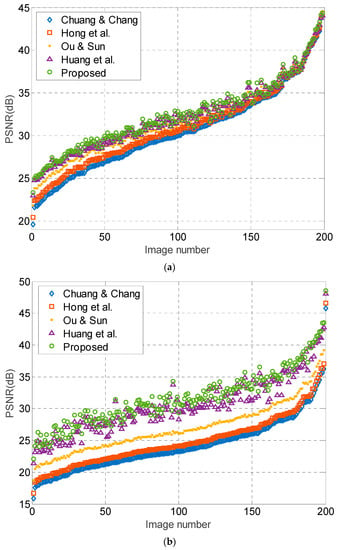
Figure 11.
Performance comparison of 200 test images. (a) PSNR comparisons at payload = 200,000 bits; (b) PSNR comparison at payload = 262,144 bits.
Notice that in the proposed method, the embedded digit in the i-th block is extracted via , and thus any modification to or will cause incorrect data extraction. Therefore, the embedded information is fragile and sensitive to the alteration of the marked AMBTC trios. Meanwhile, because the proposed method provides an excellent image quality with adjustable payload, it can be utilized as a fragile watermarking technique for the purpose of authentication of the AMBTC codes.
5. Conclusions
In this paper, we propose a novel data hiding method based on AMBTC compressed images. The proposed method embeds data into the bitmap if the block is smooth, and the quantization levels are adjusted to minimize the distortion while carrying additional bits. For those complex blocks, one data bit is embedded losslessly. Since the proposed method effectively exploits the quantization levels for data embedment using the APPM technique, the distortion can be effectively minimized and the payload is adjustable. Besides this, the proposed embedding method will never cause the overflow or underflow problems. The results show that the proposed method offers better image quality than previous schemes at high payload, and provides a comparable or better image quality at low payload. Since the proposed work efficiently embeds data into the AMBTC codes with least distortion, the method can be exploited in other applications such as authentication of AMBTC codes. The future work of this study is to incorporate the proposed technique to develop a new AMBTC authentication method with adjustable fault tolerance.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zielińska, E.; Mazurczyk, W.; Szczypiorski, K. Trends in steganography. Commun. ACM 2014, 57, 86–95. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.S.; Chen, J. Reversible data hiding using delaunay triangulation and selective embedment. Inf. Sci. 2015, 308, 140–154. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, X.; Sun, X.; Liu, Q.; Xiong, N. Steganalysis of LSB matching using differences between nonadjacent pixels. Multimed. Tools Appl. 2016, 75, 1947–1962. [Google Scholar] [CrossRef]
- Holub, V.; Fridrich, J. Random projections of residuals for digital image steganalysis. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1996–2006. [Google Scholar] [CrossRef]
- Holub, V.; Fridrich, J. Low-complexity features for JPEG steganalysis using undecimated DCT. IEEE Trans. Inf. Forensics Secur. 2015, 10, 219–228. [Google Scholar] [CrossRef]
- Liao, X.; Qin, Z.; Ding, L. Data embedding in digital images using critical functions. Signal Process. Image Commun. 2017, 58, 146–156. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.S. A novel data embedding method using adaptive pixel pair matching. IEEE Trans. Inf. Forensics Secur. 2012, 7, 176–184. [Google Scholar] [CrossRef]
- Muhammad, K.; Ahmad, J.; Rehman, N.U.; Jan, Z.; Sajjad, M. CISSKA-LSB: Color image steganography using stego key-directed adaptive LSB substitution method. Multimed. Tools Appl. 2017, 76, 8597–8626. [Google Scholar] [CrossRef]
- Liao, X.; Guo, S.; Yin, J.; Wang, H.; Li, X.; Sangaiah, A.K. New cubic reference table based image steganography. Multimed. Tools Appl. 2017. [Google Scholar] [CrossRef]
- Chen, W.S.; Wu, K.C.; Wang, C.M. A novel message embedding algorithm using the optimal weighted modulus. Inf. Sci. 2017, 388–389, 17–36. [Google Scholar] [CrossRef]
- Pevný, T.; Filler, T.; Bas, P. Using high-dimensional image models to perform highly undetectable steganography. In Proceedings of the 12th International Workshop on Information Hiding, Calgary, AB, Canada, 28–30 June 2010; Lecture Notes in Computer Science. Volume 6387, pp. 161–177. [Google Scholar]
- Holub, V.; Fridrich, J. Designing steganographic distortion using directional filters. In Proceedings of the IEEE International Workshop on Information Forensics and Security (WIFS), Tenerife, Spain, 2–5 December 2012; pp. 234–239. [Google Scholar] [CrossRef]
- Holub, V.; Fridrich, J.; Denemark, T. Universal distortion function for steganography in an arbitrary domain. EURASIP J. Inf. Secur. 2014. [Google Scholar] [CrossRef]
- Holub, V.; Fridrich, J. Digital image steganography using universal distortion. In Proceedings of the First ACM Workshop on Information Hiding and Multimedia Security, Montpellier, France, 17–19 June 2013; pp. 59–68. [Google Scholar]
- Hong, W.; Ma, Y.; Wu, H.C.; Chen, T.S. An efficient reversible data hiding method for AMBTC compressed images. Multimed. Tools Appl. 2017, 76, 5441–5460. [Google Scholar] [CrossRef]
- Hong, W.; Chen, M.; Chen, T.S. An efficient reversible image authentication method using improved PVO and LSB substitution techniques. Signal Process. Image Commun. 2017, 58, 111–122. [Google Scholar] [CrossRef]
- Xiong, L.; Xu, Z.; Shi, Y.Q. An integer wavelet transform based scheme for reversible data hiding in encrypted images. Multidimens. Syst. Signal Process. 2017. [Google Scholar] [CrossRef]
- Fridrich, J. Steganography in Digital Media: Principles, Algorithms, and Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Qin, C.; Hu, Y.C. Reversible data hiding in VQ index table with lossless coding and adaptive switching mechanism. Signal Process. 2016, 129, 48–55. [Google Scholar] [CrossRef]
- Manohar, K.; Kieu, T.D. An SMVQ-based reversible data hiding technique exploiting side match distortion. Multimed. Tools Appl. 2017. [Google Scholar] [CrossRef]
- Chang, C.C.; Nguyen, T.S.; Lin, M.C.; Lin, C.C. A novel data-hiding and compression scheme based on block classification of SMVQ indices. Dig. Signal Process. 2016, 51, 142–155. [Google Scholar] [CrossRef]
- Parah, S.A.; Sheikh, J.A.; Loan, N.A.; Bhat, G.M. Robust and blind watermarking technique in DCT domain using inter-block coefficient differencing. Dig. Signal Process. 2016, 53, 11–24. [Google Scholar] [CrossRef]
- Chuang, J.C.; Chang, C.C. Using a simple and fast image compression algorithm to hide secret information. Int. J. Comput. Appl. 2006, 28, 329–333. [Google Scholar]
- Chen, J.; Hong, W.; Chen, T.S.; Shiu, C.W. Steganography for BTC compressed images using no distortion technique. Imaging Sci. J. 2010, 58, 177–185. [Google Scholar] [CrossRef]
- Hong, W.; Chen, J.; Chen, T.S.; Shiu, C.W. Steganography for block truncation coding compressed images using hybrid embedding scheme. Int. J. Innov. Comput. Inf. Control 2011, 7, 733–743. [Google Scholar]
- Ou, D.; Sun, W. High payload image steganography with minimum distortion based on absolute moment block truncation coding. Multimed. Tools Appl. 2015, 74, 9117–9139. [Google Scholar] [CrossRef]
- Bai, J.; Chang, C.C. A high payload steganographic scheme for compressed images with hamming code. Int. J. Netw. Secur. 2016, 18, 1122–1129. [Google Scholar]
- Huang, Y.H.; Chang, C.C.; Chen, Y.H. Hybrid secret hiding schemes based on absolute moment block truncation coding. Multimed. Tools Appl. 2017, 76, 6159–6174. [Google Scholar] [CrossRef]
- Kodovský, J.; Fridrich, J.; Holub, V. Ensemble classifiers for steganalysis of digital media. IEEE Trans. Inf. Forensics Secur. 2012, 7, 432–444. [Google Scholar] [CrossRef]
- Xu, X.; Sun, Y.; Tang, G.; Chen, S.; Zhao, J. Deep learning on spatial rich model for steganalysis. In Proceedings of the International Workshop on Digital Watermarking, Magdeburg, Germany, 23–25 August 2017. [Google Scholar] [CrossRef]
- Couchot, J.F.; Couturier, R.; Salomon, M. Improving blind steganalysis in spatial domain using a criterion to choose the appropriate steganalyzer between CNN and SRM + EC. In Proceedings of the International Conference on ICT Systems Security and Privacy Protection, Rome, Italy, 29–31 May 2017. [Google Scholar] [CrossRef]
- Yuan, C.; Xia, Z.; Sun, X. Coverless image steganography based on SIFT and BOF. J. Internet Technol. 2017, 18, 435–442. [Google Scholar]
- Chen, X.; Chen, S.; Wu, Y. Coverless information hiding method based on the Chinese character encoding. J. Internet Technol. 2017, 18, 313–320. [Google Scholar]
- Lema, M.; Mitchell, O. Absolute moment block truncation coding and its application to color image. IEEE Trans. Commun. 1984, 32, 1148–1157. [Google Scholar] [CrossRef]
- The USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/ (accessed on 30 December 2017).
- BOWS-2 Image Database. Available online: http://bows2.ec-lille.fr/ (accessed on 30 December 2017).
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).