Separable Reversible Data Hiding in Encrypted Signals with Public Key Cryptography

Abstract

We propose separable reversible data hiding in an encrypted signal with public key cryptography. In our separable framework, the image owner encrypts the original image by using a public key. On receipt of the encrypted signal, the data-hider embeds data in it by using a data-hiding key. The image decryption and data extraction are independent and separable at the receiver side. Even though the receiver, who has only the data-hiding key, does not learn about the decrypted content, he can extract data from the received marked encrypted signal. However, the receiver who has only the private key cannot extract the embedded data, but he can directly decrypt the received marked encrypted signal to obtain the original image without any error. Compared with other schemes using a cipher stream to encrypt the image, the proposed scheme is more appropriate for cloud services without degrading the security level.

1. Introduction

With the ease of editing and the Internet distribution for digital media, copyright protection and the prevention of malicious tampering are important and challenging topics. Data hiding has been proposed to alleviate these concerns, which involves hiding data in media for various applications, such as copyright protection, image authentication, and access control. However, hiding data inevitably damages the content, though the distortion is imperceptible to human eyes. In some scenarios, such as encrypted data and medical images, any distortion is not tolerable. Hence, reversible data hiding (RDH) presents a solution to the problem of how to embed, in a lossless manner, data into the digital media such that the media can be completely recovered after data extraction.

The image owner may not believe the cloud service providers, which disposed the owner to encrypt the image before sending it to the cloud. However, traditional image processing is usually used before encryption or after decryption. Hence, the ability to directly process the encrypted signal while keeping the plain text unrevealed is desired. Therefore, reversible data hiding in encrypted signals provides privacy preserving services, where the data-hider can hide additional data in the encrypted signal for some applications such as authentication or annotation.

In 2011, Zhang [1] presented a reversible data hiding method in encrypted images. He encrypted the original image by using an exclusive or (XOR) operation with a cipher stream. He flipped least significant bits (LSBs) of selected encrypted pixels to hide the additional data. After data extraction, he used the spatial correlation to recover the original image. The resulting error rate of data extraction was decreased by Hong et al. [2]. They considered the pixel correlations in neighboring blocks and used the side-match scheme to improve the accuracy of data extraction. To improve the hiding capacity, Zhang et al. [3] chose half of the fourth LSB as the space to carry the data to be embedded. Different from encrypted images, Qian et al. 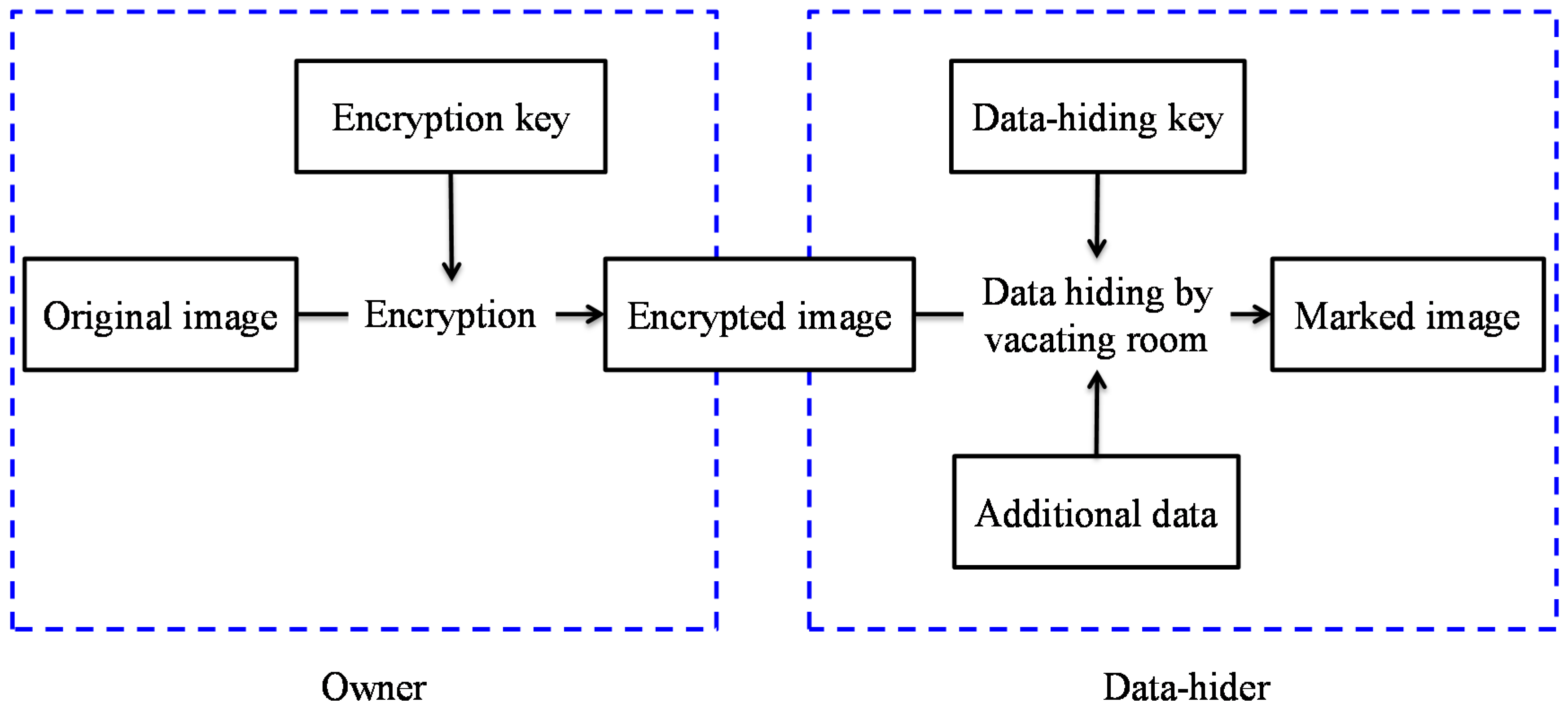[4] embedded data into the Joint Photographic Experts Group (JPEG) encrypted stream. These schemes tried to directly vacate room after encryption (VRAE) in order to embed data, as shown in Figure 1. However, it is difficult to find extra hiding space after encryption when the encrypted image achieves maximum entropy. Thus, the VRAE schemes may result in small payloads and some error rates introduced by data extraction.

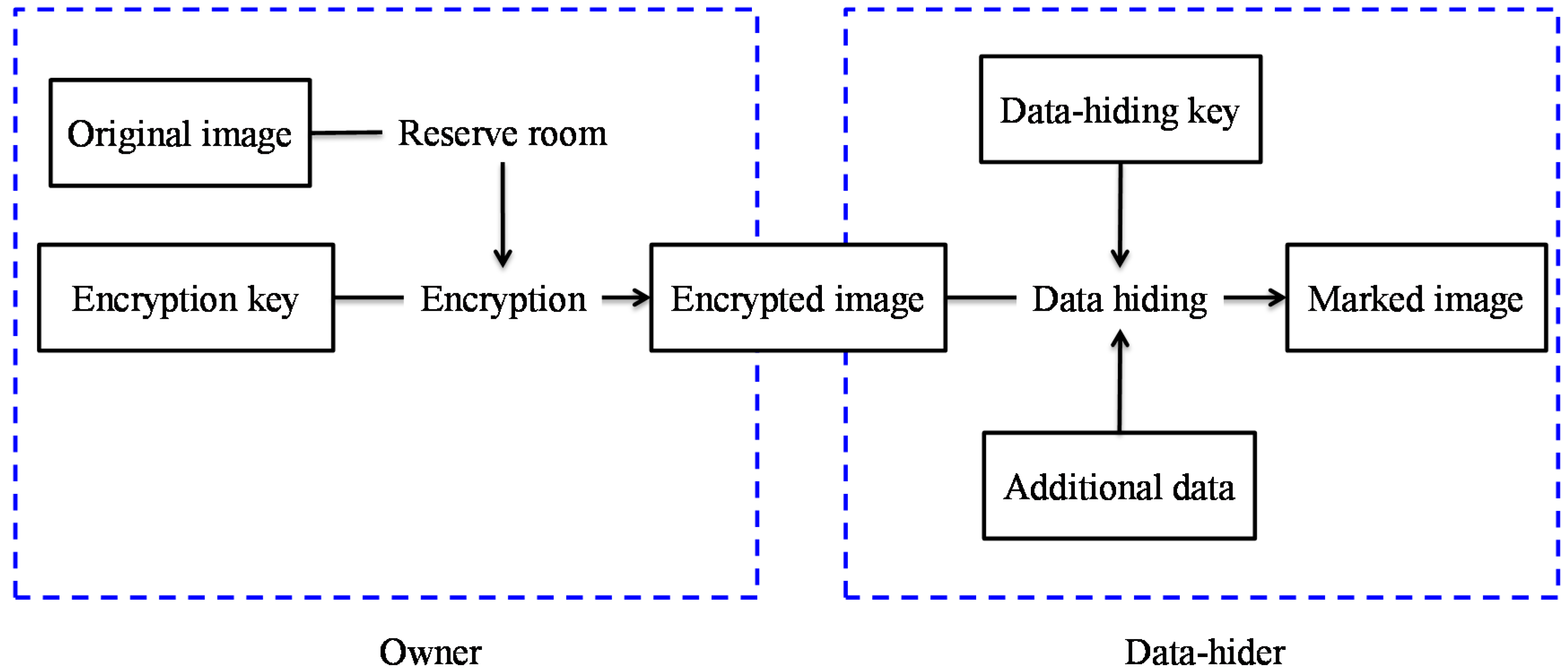
To overcome these drawbacks, Ma et al. [5] reserved room before encryption (RRBE) to hide data later, as illustrated in Figure 2. They emptied out LSBs of some pixels before encryption, and used an RDH scheme to embed these LSBs into other pixels. Zhang et al. [6] estimated some pixels before encryption to embed data in these estimating errors. To take advantage of the correlation between neighbor pixels, Cao et al. 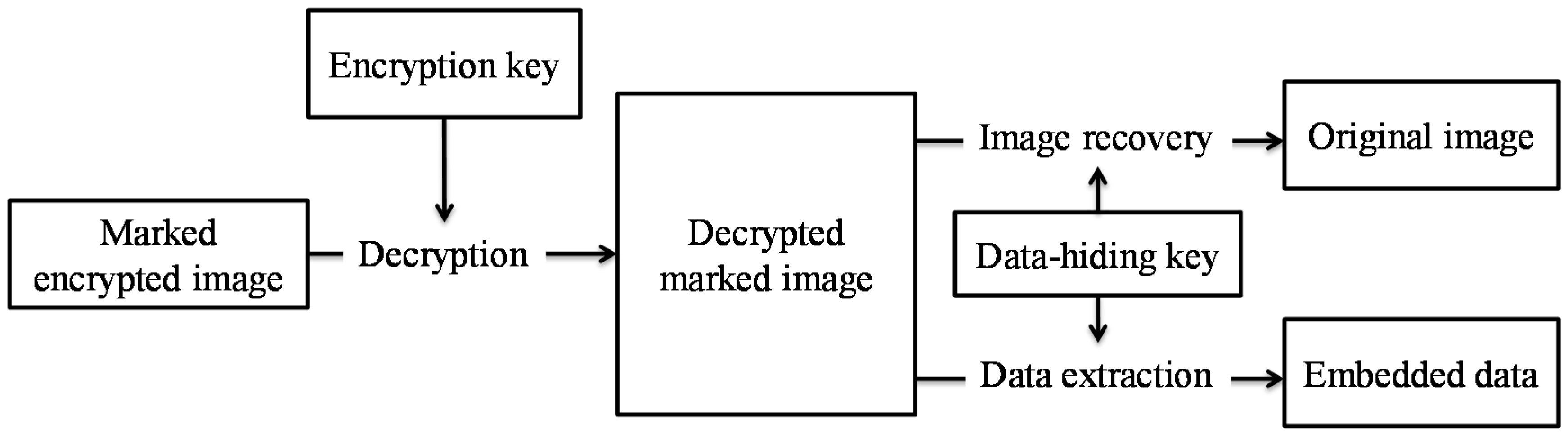[7] considered the patch-level sparse representation and used sparse coding to hide the data. At the receiver side of above schemes, the image decryption and data extraction have to be processed together. The original image content needs to be revealed before data extraction in order to retrieve the embedded data, as shown in Figure 3. However, in some scenarios, the owner does not want the receiver who has no encryption key to know the original content.

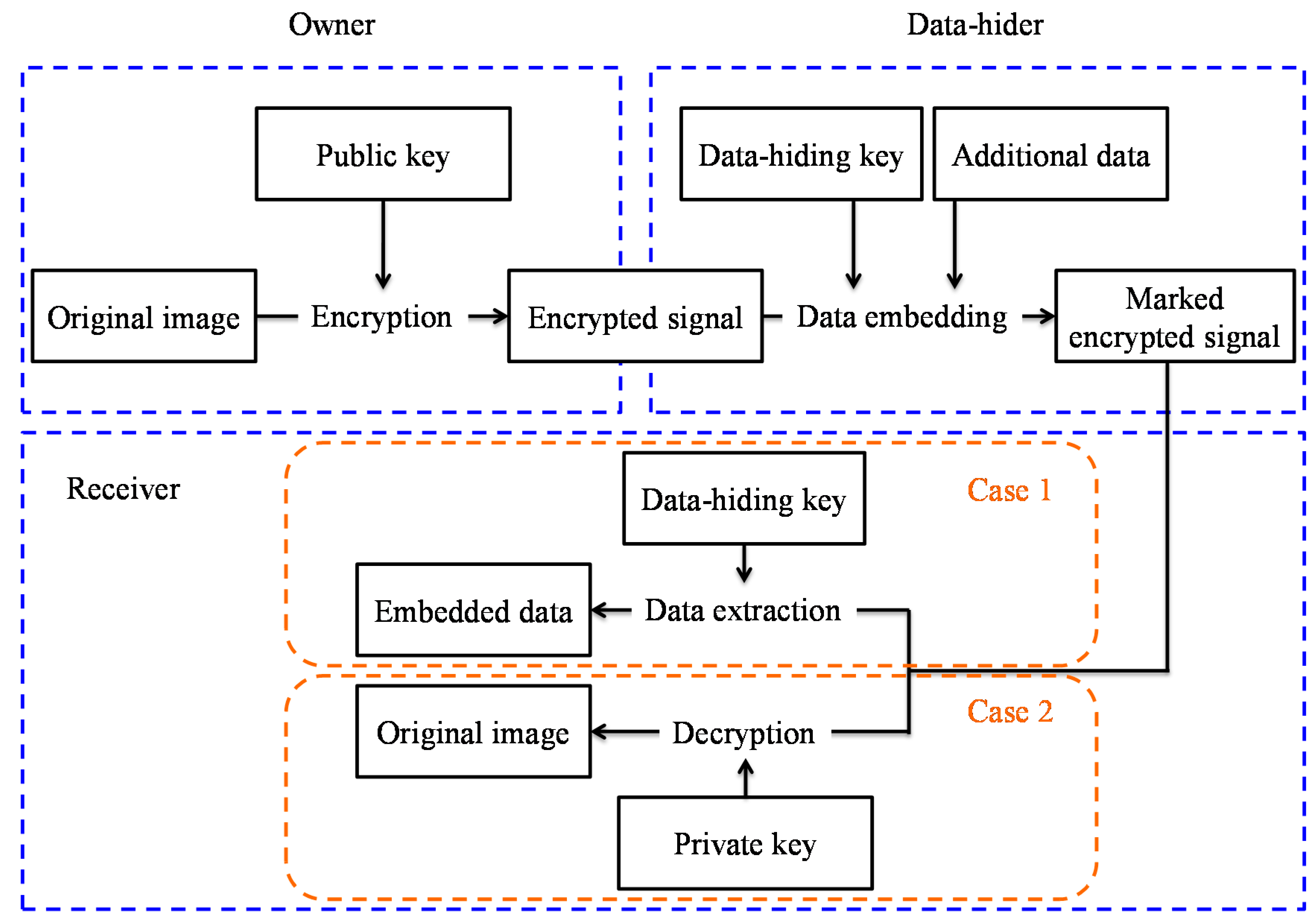
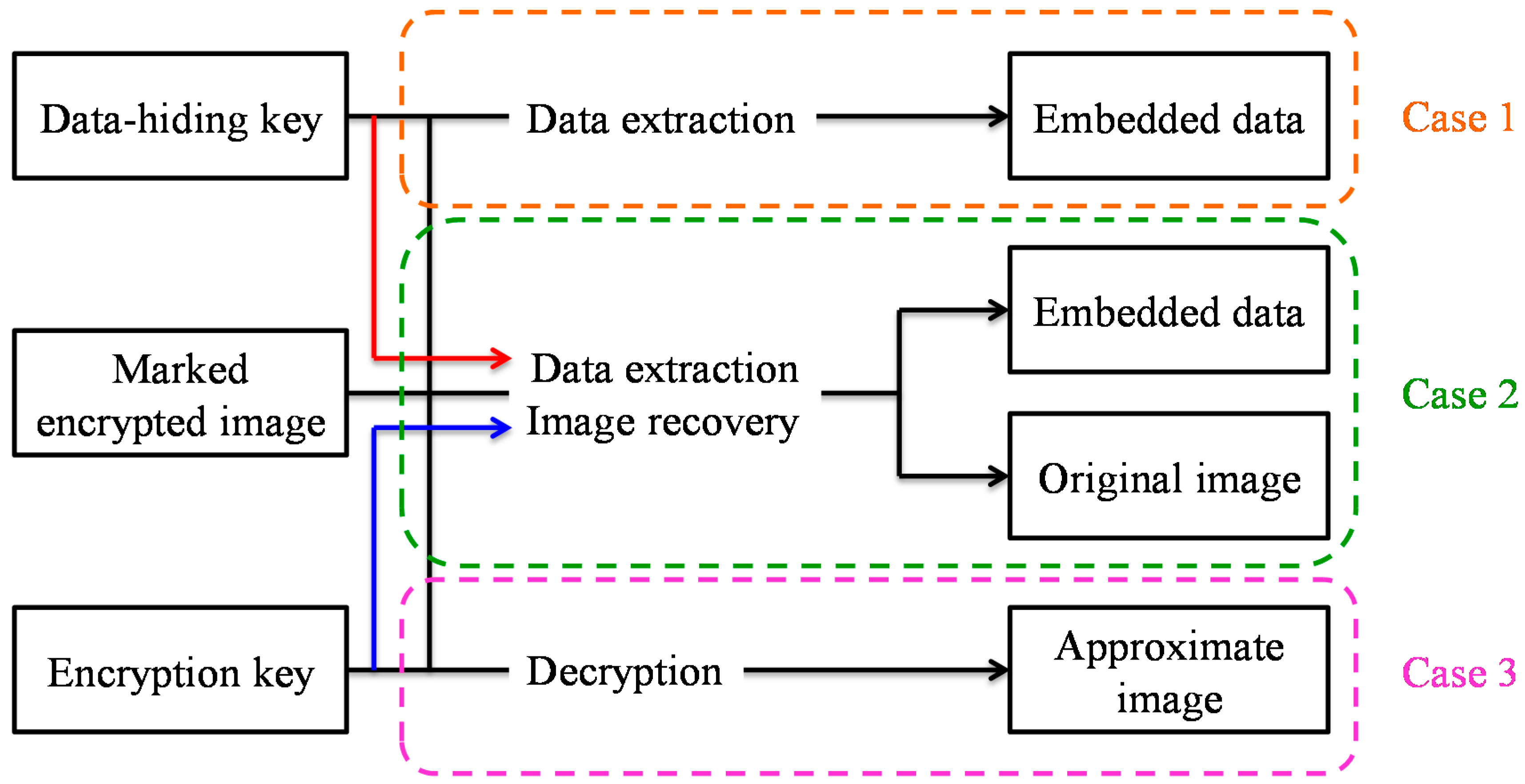
Thus, Zhang [8] presented a separable framework for RDH in encrypted image. Before transmitting the original image to the data-hider, the image owner firstly encrypted it with an encryption key. The data-hider embedded data in the received encrypted image by using the VRAE or RRBE framework with a data-hiding key. As shown in Figure 4, there are three cases occurring at the receiver side. In case 1, the receiver can use a data-hiding key to directly extract the data from the marked encrypted image without the knowledge of the original content. In case 2, only when the receiver has both a data-hiding key and an encryption key can he extract the embedded data and restore the image to its original form. In case 3, the receiver cannot extract the embedded data, but can decrypt the marked image and obtain an approximate image close to the original image. Wu and Sun [9] used the prediction error to propose a joint RDH and a separable RDH schemes in encrypted images. Xiao and Chen [10] left some space in the image for embedding data later to achieve separability. The quality of the decrypted image is improved by Liao et al. [11] using compressive sensing and discrete Fourier transform (DFT). Qian and Zhang [12] compressed some bits from the encrypted image to find room for hiding. In 2017, Wu et al. [13] proposed a separable RDH scheme for palette images. They used palette colors to build color triples, and embedded those indices into the encrypted image.

The above-mentioned methods embed the additional data into encrypted images by using symmetric cryptography. However, in some applications, the transmission of a secret key via a secure channel is impractical. Chen et al. [14] proposed a RDH method for encrypted signal with public key cryptosystem. They used Paillier encryption [15] to encrypt an image, and embedded data into adjacent encrypted pixels. Zhang et al. [16] proposed a combined RDH for images encrypted with public-key cryptosystem according to the homomorphic property.

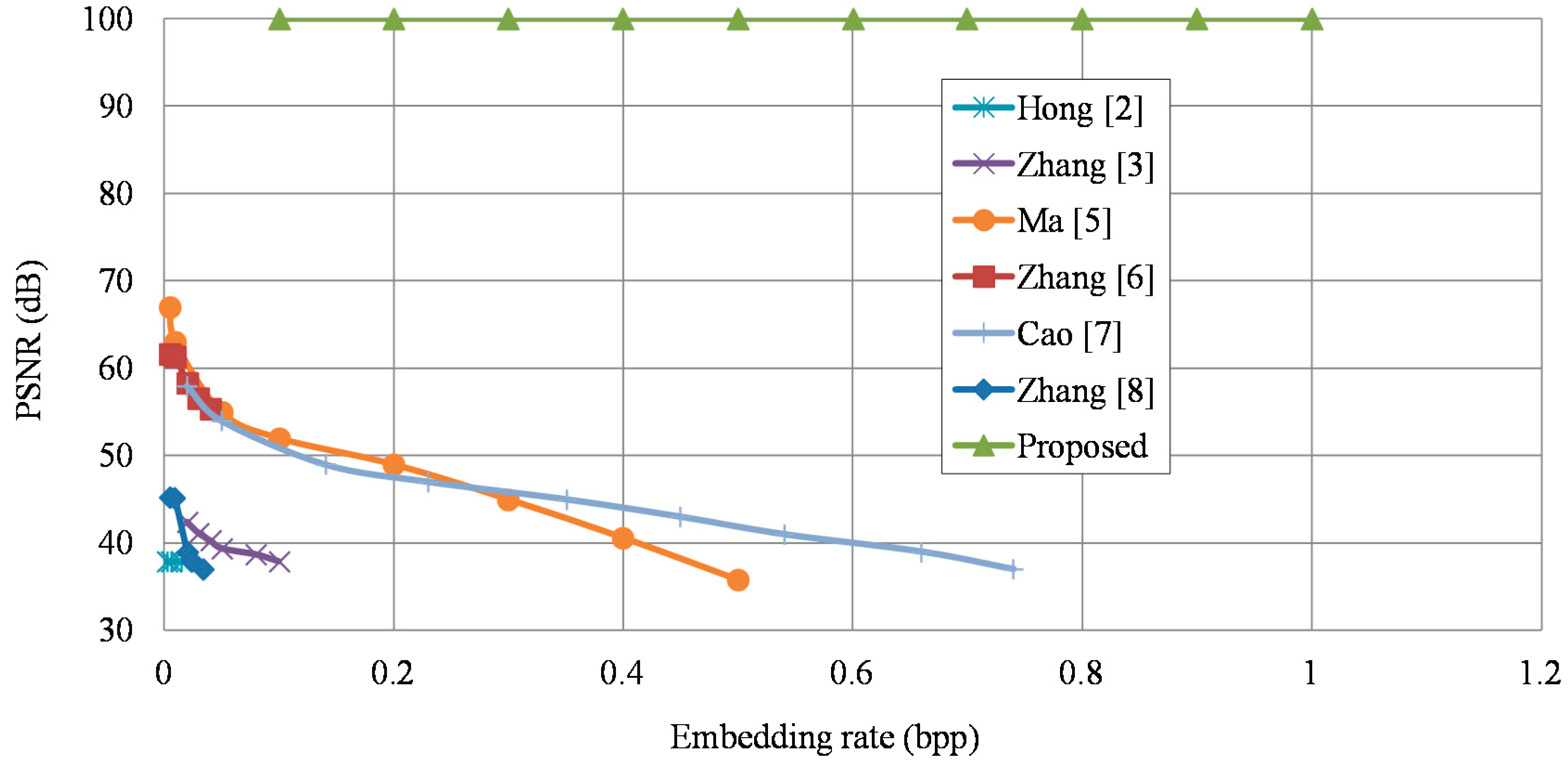
In this paper, we present a separable RDH in encrypted signals with public key cryptography. The original image is encrypted by Paillier encryption with a public key. After that, the data-hider directly hides the additional data in the encrypted signal with a data-hiding key. In our separable framework, there are two cases occurring at the receiver side. The receiver who has only the data-hiding key can directly extract the embedded data from the received marked encrypted signal without prior knowledge of the original content. However, the receiver who has only the private key can directly decrypt the received marked encrypted signal to obtain the original image without loss, but cannot retrieve the embedded data. The proposed method ensures that the image decryption and data extraction are separable at the receiver side. Moreover, compared with the image encrypted with a cipher stream, the proposed scheme is more applicable in the cloud without degrading the security level.

The paper is organized as follows: In Section 2, we describe the Paillier homomorphic cryptosystem. The proposed separable RDH scheme in encrypted signals is introduced in Section 3, where we also describe the procedures for extracting the embedded data and recovering the original image. The proposed method is experimentally validated in Section 4. Finally, the paper is concluded in Section 5.

2. Paillier Cryptosystem

The Paillier cryptosystem [15], whose security is under the RSA strong assumption, is a probabilistic asymmetric cryptography. Based on the additive homomorphic property, Paillier encryption is extensively used for privacy-preserving applications. The cryptosystem is depicted below. For key generation, the sender randomly chooses two large primes p and q, where gcd(pq, (p–1)(q–1)) = 1, and the sender calculates n = pq, λ = l cm (p – 1, q – 1), and selects a random integer g ∈ ${\mathbb{Z}}_{n^2}^{\ast }$ where gcd(L(g^λ mod n²), n) = 1, and $L\left(x\right)=\frac{x-1}{n}$. Finally, (n, g) is the public key and (λ) is the private key.

Given a message m ∈ ${\mathbb{Z}}_n^{\ast }$, the sender randomly chooses integer r ∈ ${\mathbb{Z}}_n^{\ast }$, and then computes the ciphertext of m:

c = E_pk (m, r) = g^m rⁿ mod n²,

(1)

where E is the encryption function and pk is the public key.

The receiver can decrypt the ciphertext with private key:

$$m=D_{sk}\left(c\right)=\frac{L\left(c^{\lambda }\mathrm{mod}{n}^2\right)}{L\left(g^{\lambda }\mathrm{mod}{n}^2\right)}\mathrm{mod}n,$$

(2)

where D is the decryption function and sk is the private key.

The additive homomorphic properties are held by Paillier encryption. Given two encryption functions E_pk (m₁, r₁) and E_pk (m₂, r₂), the two functions are additively homomorphic on ${\mathbb{Z}}_n$:

$$E_{pk}\left(m_1, r_1\right)E_{pk}\left(m_2, r_2\right)=g^{m_1+m_2}{\left(r_1{r}_2\right)}^n\mathrm{mod}{n}^2=E_{pk}\left(m_1+m_2,r_1{r}_2\right).$$

Thus:

D_sk (E_pk (m₁, r₁) × E_pk (m₂, r₂)) = m₁ + m₂.

(3)

Additionally, this brings about the following properties:

D_sk (E_pk (m₁, r₁)^k) = km₁,

D_sk (E_pk (m₁, r₁) × g^m2 mod n²) = m₁ + m₂,

$$D_{sk}\left(E_{pk}{\left(m_1,r_1\right)}^{m_2} \mathrm{mod} n^2\right)=m_1{m}_2.$$

These additively homomorphic identities are known to be appropriate for designing proxy signatures, electronic voting, watermarking, and authentication.

3. Proposed Scheme

The proposed scheme consists of image encryption, data embedding, data extraction, and image recovery. Figure 5 shows the framework of the proposed scheme. The image owner uses a public key to encrypt the original image to generate an encrypted signal. After receiving the encrypted signal, the data-hider is able to directly hide data in it with a data-hiding key. At the receiver side, the image recovery and data extraction are independent. The receiver can easily retrieve the embedded data from the received marked encrypted signal with only the data-hiding key. When the receiver has only the private key, he can directly decrypt the received marked encrypted signal regardless of data extraction to perfectly recover the original image rather than an approximate image.

3.1. Image Encryption

Suppose that the original image is an 8-bit grayscale image of W × H pixels, and the pixel value x_{i, j} denotes the grayscale value at the coordinate of (i, j), where 1 ≤ i ≤ H, 1 ≤ j ≤ W, and 0 ≤ x_{i, j} ≤ 255. The detailed procedure is listed below.

Step 1.

For each pixel x_{i, j}, convert x_{i, j} to x¹_{i, j} and x²_{i, j}, where x_{i, j} = x¹_{i, j} + x²_{i, j}.

Step 2.

Choose a random integer r₁ ∈ ${\mathbb{Z}}_n^{\ast }$, and then computes the encryption function E_pk (x¹_{i, j}, r₁) with a public key by Equation (1).

Step 3.

Choose a random integer r₂ ∈ ${\mathbb{Z}}_n^{\ast }$, and then computes the encryption function E_pk (x²_{i, j}, r₂) with a public key by Equation (1) so as to meet that E_pk (x¹_{i, j}, r₁) ≠ E_pk (x²_{i, j}, r₂).

Step 4.

All the encrypted units comprise the encrypted signal.

3.2. Data Embedding

The following algorithm describes how to embed data into the received encrypted signal. Suppose that the received encrypted signal with size of W × H × 2 ×$(\lfloor {\log }_2^{n^2}\rfloor +1)$ bits consists of encrypted units EU_i = (EU¹_i, EU²_i), where 1 ≤ i ≤ W × H.

Step 1.

Construct a non-repeat random embedding sequence using the data-hiding key.

Step 2.

Embed a secret bit into an encrypted unit EU_i according to the embedding sequence. If the secret bit is 1 and EU¹_i < EU²_i, EU¹_i swaps EU²_i.

Step 3.

If the secret bit is 0 and EU¹_i > EU²_i, EU¹_i swaps EU²_i.

Step 4.

Generate a marked encrypted signal when all bits are embedded.

3.3. Data Extraction

Suppose that the received marked encrypted signal with size of W × H × 2 ×$(\lfloor {\log }_2^{n^2}\rfloor +1)$ bits consists of marked encrypted units MEU_i = (MEU¹_i, MEU²_i), where 1 ≤ i ≤ W × H. If the receiver has only a data-hiding key, the data extraction procedure is listed below.

Step 1.

Step 1. Construct a non-repeat random embedding sequence using the data-hiding key.

Step 2.

Extract a secret bit from a marked encrypted unit MEU_i according to the embedding sequence. If MEU¹_i > MEU²_i, the extracted bit is 1.

Step 3.

If MEU¹_i < MEU²_i, the extracted bit is 0.

Step 4.

Obtain the embedded data when all the bits are extracted.

3.4. Image Recovery

Suppose that the received marked encrypted signal with size of W × H × 2 ×$(\lfloor {\log }_2^{n^2}\rfloor +1)$ bits consists of marked encrypted units MEU_i = (MEU¹_i, MEU²_i), where 1 ≤ i ≤ W × H. We assume that the receiver has only a private key. The image recovery procedure is listed below.

Step 1.

Decrypt the marked encrypted unit MEU_i using the private key by:

D_sk ((MEU¹_i × MEU²_i) mod n²) = x¹_{i, j} + x²_{i, j} = x_{i, j}.

(4)

Step 2.

Recover the original image when all marked encrypted units are decrypted.

An example of the proposed method is given. Consider the original pixel with value x_{i, j} = x¹_{i, j} + x²_{i, j} = 100 + 68 = 168, and set the secret bit as 0, two primes as p = 17 and q = 19. Thus, (323, 324) is the public key, and (144) is the private key. Compute the encrypted unit EU_i = (EU¹_i, EU²_i) = (E_pk (100, 7), E_pk (68, 11)) = (74,871, 34,549). In the data embedding phase, because the secret bit is 0 and EU¹_i > EU²_i, EU¹_i swaps EU²_i. Therefore, the marked encrypted unit MEU_i = (EU²_i, EU¹_i) = (34,549, 74,871). At the receiver side, the receiver who has only data-hiding key can extract secret bit 0 because MEU¹_i < MEU²_i. However, if the receiver has only a private key, he can decrypt the marked encrypted unit MEU_i to obtain the original pixel by computing D_sk ((MEU¹_i × MEU²_i) mod n²) = D_sk ((34,549 × 74,871) mod 323²) = D_sk (89,282) = 168.

4. Experimental Results

We used the test image Lena sized 512 × 512 pixels as the original image in the experiments. Different images do not affect the performance of the proposed method.

Table 1. The embedding rate and PSNR of directly decrypted image for Lena.

Original Image	Embedding Rate (bpp)	PSNR (dB)
Lena	1	+∞

lists the embedding rate and PSNR of the directly decrypted Lena image. In this experiment, a total of 512 × 512 = 262,144 bits are hidden in each encrypted unit. As a result, the corresponding embedding rate is 1 bit per pixel (bpp), whatever the kind of images are selected as the original image. Note that the +∞ denotes that the original image is perfectly recovered without any loss.

Figure 6 compares the embedding rate and image quality for Lena with other schemes [2,3,5,6,7,8]. In our scheme, the directly decrypted image without data extraction is the same as the original one. Hence, the associated PSNR of decrypted image is +∞ dB regardless of the embedding rate. Other schemes [2,3,5,6,7,8] degraded the visual image quality of the decrypted image due to the embedding distortion. They cannot restore the original image with only the encryption key. Clearly, the performance of the proposed method is significantly better than that of schemes [2,3,5,6,7,8].

Table 2. Characteristics of various schemes [2,3,5,6,7,8].

Scheme	Encryption	Receiver	Embedding Rate	Expansion
Hong [2]	Stream cipher	Non-separable	0.015	No
Zhang [3]	Stream cipher	Separable	0.17	No
Ma [5]	Stream cipher	Separable	0.5	No
Zhang [6]	Symmetric key	Separable	0.04	No
Cao [7]	Stream cipher	Separable	0.74	No
Zhang [8]	Stream cipher	Separable	0.034	No
Proposed	Public key	Separable	1	Yes

summarizes the comparison of characteristics of the considered schemes [2,3,5,6,7,8]. We note that in our scheme, asymmetric cryptography is adopted for image encryption. Therefore, data expansion exists in the encrypted signal. However, based on additive homomorphic properties, the proposed scheme is able to be further applied to multimedia without infringing the privacy.

5. Conclusions

This paper proposes a separate RDH method for images encrypted by public key cryptography. The two ciphertext values are exchanged with each other for embedding the additional data. Based on additive homomorphic properties, we can directly extract the embedded data from the encrypted domain without knowing the original content. Moreover, perfect image recovery can be directly processed without prior data extraction. Since the content privacy can be securely preserved by Paillier encryption, the proposed scheme is appropriate for cloud services without degrading the security level.