1. Introduction
The rapid developments of computer and network technologies led to an explosion in the transmission of digital information over the Internet. The digital information mostly contains sensitive and confidential contents that can be intercepted or tampered with during transmission. Therefore, ensuring secure information communication has become a very important issue. There are two main approaches to achieve this goal. One approach is cryptography [
1], in which the message is encrypted with a secret key and only the holder of the secret key can decrypt the cipher text to recover the original message. RSA public-key cryptosystem using a pair of keys is the most widely used cryptography. A public key is paired with a private key that is known only to the expected message receiver. The sender encrypts a message with the public key and only the receiver who has the paired private key can decrypt it. Unfortunately, disclosure of the message may happen if the private key leaks. The other approach for information security is data hiding, and this has attracted a lot of attention over the past few years [
2,
3,
4,
5].
Data hiding [
2,
3] is an efficient technique that conceals secret data into a medium. The differences in the image before and after concealing data are so tiny that it is impossible for an observer to visually perceive the presence of hidden data. A good data hiding scheme should both maintain good image quality and preserve sufficient embedding capacity. However, it is difficult to satisfy the two requirements at the same time in most cases. It is generally true that the image distortion increases when the embedding capacity increases; on the other hand, the image quality is enhanced at the cost of the embedding capacity. Therefore, how to achieve a satisfactory balance between the image quality and the embedding capacity has become a technically challenging topic and many researchers have proposed various data hiding methods [
4,
5,
6] focusing on this topic.
Data hiding for digital images is basically developed in three domains—the spatial domain, the frequency domain and the compression domain. In the frequency domain, the cover image is transformed into frequency coefficients via various discrete transform functions such as discrete Fourier transform (DFT), discrete cosine transform (DCT), and discrete wavelet transform (DWT). The primary property of frequency domain data is that low frequency coefficients contain more important information, whereas in high frequency areas, information is less significant. Thus, the matrix of frequency coefficients are divided into non-overlapping blocks and the secret data will be embedded in those blocks. For data hiding in compression domain, the frequently used compression technologies include vector quantization (VQ), block truncation coding (BTC) and joint photographic experts group (JPEG). A milestone in the history of spatial domain-based data hiding is the method of least-significant-bit (LSB) replacement [
2]. LSB method is very simple as it just replaces the LSBs in a cover image with secret bits to produce a stego image. The embedding capacity is satisfactory along with a good image quality, but it is very vulnerable to statistical analysis of the stego image. Westfeld and Pfitzmann [
3] found that the statistics for the frequencies of neighboring pixel value pairs in the stego image can easily detect the presence of hidden data. To resist statistical attack, LSB matching [
4] was introduced. It improves the way of modifying the cover image such that the value of the cover pixel is either randomly increased or decreased by one in case the LSB of the cover pixel is not identical to the secret bit. Later, Mielikainen [
5] exploited the direction of modification to the cover pixels for the first time to enhance the LSB matching scheme. A cover pixel pair is used as a minimal unit to embed two consecutive secret bits according to a binary function. This scheme outweighs LSB matching in terms of security and image quality degradation while keeping the same embedding capacity. However, Zhang and Wang [
6] pointed out that Mielikainen’s scheme [
5] does not fully exploit the modification directions, and they presented a novel data hiding scheme called the exploiting modification direction (EMD) scheme. The EMD scheme first converts binary secret data into a (2
m + 1)-ary stream of secret digits, and then uses a group of
m adjacent pixels to carry one secret digit. Only one pixel value in the group is +1 or −1 according to a new extraction function, thereby achieving very good image quality. The weakness of the EMD scheme is that the embedding capacity decreases drastically if the number of pixels in a group increases.
In recent years, many data hiding schemes that are inspired by the concept of EMD have been proposed to increase the embedding capacity [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21]. Lee et al.’s scheme [
7] employed a pixel segmentation strategy to provide a larger payload than that of EMD, but this suffers from worse image quality. Chang et al. [
8] introduced a novel scheme based on EMD and Sudoku solutions. Each cover pixel pair conceals one secret digit in the nonary numeral system by the reference matrix according to a selected Sudoku solution. The scheme can achieve a higher embedding capacity of 1.5 bits per pixel (bpp) and a very good image quality. Moreover, the scheme is more secure than the EMD method since it is very difficult to determine which Sudoku solution is selected from a large number of possible solutions. To minimize the image distortions, Hong et al. [
9] proposed a new scheme that searches embeddable positions using the nearest Euclidean distance, leading to a better image quality than that of Chang et al.’s scheme [
8] under the same embedding capacity. In 2010, Kim et al. [
10] introduced an EMD-2 scheme that changes the values of at most two pixels in a group. Experimental results showed that EMD-2 is superior to EMD in larger payloads with similar image distortions. In 2014, Chang et al. [
11] proposed a novel data hiding scheme originating from EMD and turtle shell structure. The binary secret stream can be embedded directly in such a way that three secret bits are embedded in a pair of consecutive cover pixels with the guidance of a reference matrix based on turtle shells. Experimental results revealed that this scheme has a higher embedding capacity than EMD and Kim et al.’s scheme [
10]. Also, it outperforms EMD, Chang et al.’s scheme [
8] and Hong et al.’s scheme [
9] in better image quality under the same embedding capacity. Later, Liu et al. [
12] improved Chang et al.’s scheme [
11] by constructing a location table from the turtle shell-based reference matrix to guide the modification of cover pixel pairs. This scheme achieves very good image quality above 45 dB and is better than Chang et al.’s scheme [
11] with higher embedding capacity.
Recently, Kuo et al. proposed a series of EMD-type schemes [
15,
16,
17] to further improve the EMD method. In order to increase the embedding capacity, a generalized EMD (GEMD) scheme was introduced in [
16]. Unlike the EMD, the GEMD does not require the conversion of the binary secret data before embedding so as to accelerate the embedding speed. The GEMD scheme maintains better embedding capacity than EMD under different pixel group sizes. Later, a modified signed digit (MSD) scheme [
17] for data hiding was proposed that restricts the number of modified pixels to
when the group size is m, while all group pixels may be changed in GEMD. Unfortunately, MSD sacrifices the embedding capacity to obtain better image quality than GEMD. Recently, Kuo et al. [
18] proposed a new EMD-type scheme called binary power EMD (BPEMD) in which both the coefficient and modulus of the extraction function are binary power. Experimental results reveal that BPEMD has higher embedding capacity than EMD and MSD and withstands well-known attacks.
In order to further increase the embedding capacity, we propose an EMD-type data hiding scheme based on Chinese remainder theorem (CRT) [
22]. CRT can make a solution to determine an integer by the given system of simultaneous congruencies in number theory. Nowadays, CRT is used extensively in secret sharing and other applications of information security [
22,
23,
24]. Fortunately, we also find that CRT is very suitable for data hiding. To the best of our knowledge, no EMD-type schemes employing CRT has been proposed. In this paper, for the first time, we propose a high capacity data hiding scheme from the combination of CRT and a new extraction function. The characteristics of the proposed scheme are listed below:
It is the first EMD-type data hiding scheme that uses CRT as its main building block. The cover image is divided into non-overlapping m-pixel groups for embedding data. According to the CRT and a new extraction function, the ith cover pixel in a group can directly embed binary secret bits;
The coefficients of the constructed extraction function are pairwise coprime integers and the modulus is the product of the coefficients, which is different from the extraction functions of previous EMD-type schemes. Therefore, for data extraction, the embedded secret data is first computed by the extraction function and then retrieved by a modular operation according to the CRT. This two layer embedding strategy can further increase the security;
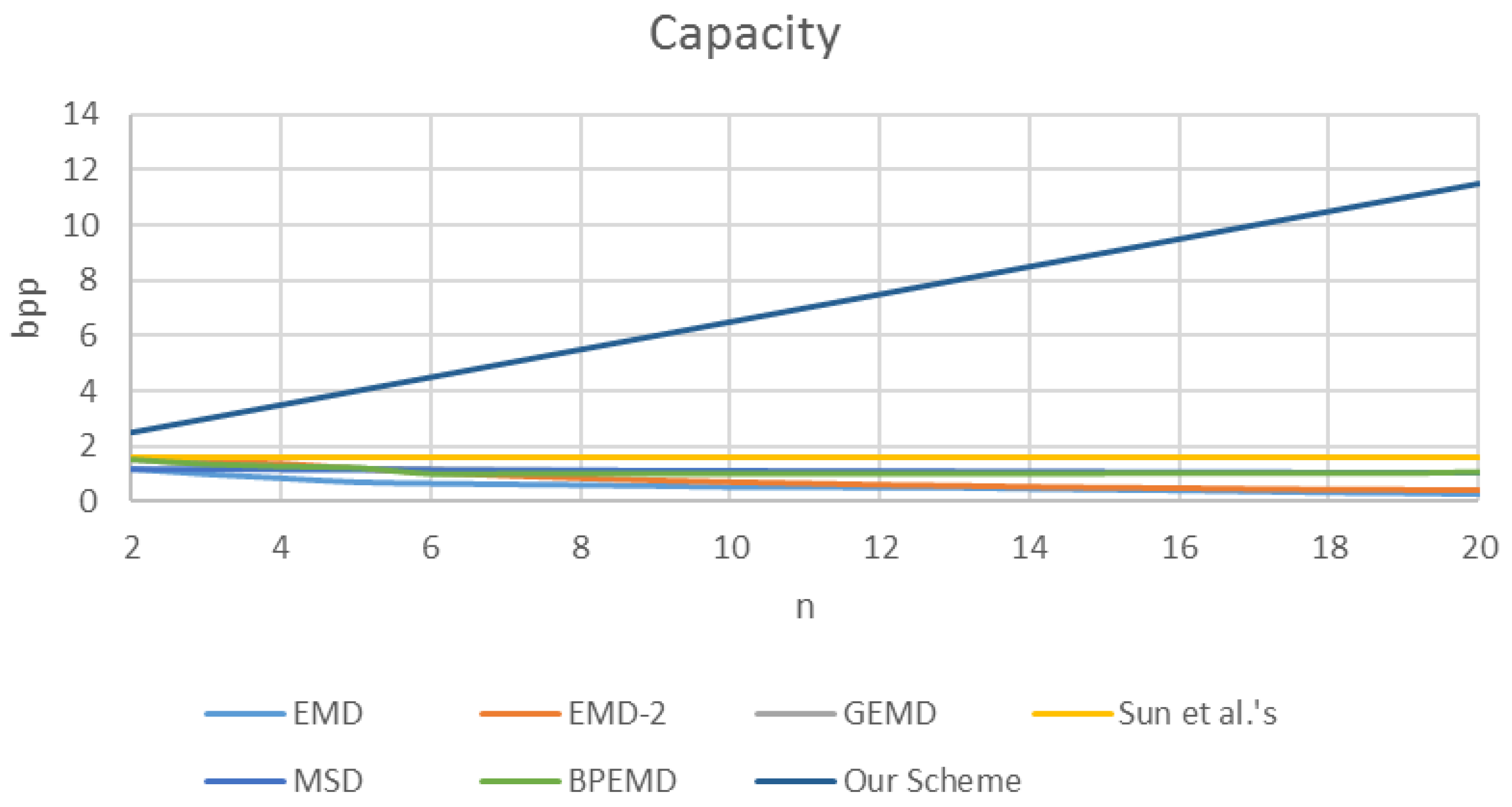
The embedding capacity of the proposed scheme is significantly high while guaranteeing good image quality. In particular, the embedding capacity can maintain at least 2.5 bpp and increase when the number of cover pixels in a group increases.
The rest of the paper is organized as follows.
Section 2 briefly reviews typical EMD-type data hiding schemes and basic knowledge about CRT.
Section 3 describes our proposed data hiding scheme. Experimental results are provided in
Section 4, and conclusions are given in
Section 5.
2. Preliminaries
In this section, we first give a review of typical EMD-type data hiding schemes, such as EMD [
6], GEMD [
16] and BPEMD [
18]. Then, we introduce essential knowledge about CRT since it is the most important building element of our proposed scheme.
2.1. EMD Data Hiding Scheme
The EMD scheme proposed by Zhang and Wang [
6] embeds one secret digit in a (2
m + 1)-ary numeral system into m cover pixels, among which at most one pixel is +1 or −1. Let a vector
denote a group of
m pixel values and
in an
m-dimensional space corresponds to a value of an extraction function
, which is computed by the following equation as a weighed sum modulo
:
According to the extraction function
, the EMD embedding algorithm (Algorithm 1) is shown as follows:
| Algorithm 1 EMD Embedding Algorithm [6]. |
Input: cover image and binary secret data stream
Output: stego image - Step 1.
Convert binary secret data stream to a (2 m + 1)-ary stream . First, is divided into a sequence of segments with l bits. Then, each l-bit segment is converted to r digits in a (2 m + 1)-ary numeral system, where
- Step 2.
Divide the cover image into non-overlapping groups, each of which consists of m adjacent pixels. - Step 3.
Obtain an m-pixel group from and one digit from . - Step 4.
Compute by Equation (1) and obtain the difference . - Step 5.
If , set for , where is the stego pixel. If and , set and for and . If and , set and for and . - Step 6.
Repeat Steps 3–5 until all secret data is embedded.
|
For the extraction, we retrieve all m-pixel group from the stego image , and then compute for each group. Obviously, is one digit in the (2m + 1)-ary secret stream . Finally, is converted back to the binary secret stream . Here, we give an example to illustrate how to embed secret data using the EMD scheme.
Example 1. Given three grayscale pixels of a cover image and a binary secret data stream , embed into the above three-pixel group using EMD when .
First, compute one digit . Then, compute . Thus, the difference is obtained. Because , we set , and in the stego image. To extract the hidden data, we just compute .
2.2. GEMD Data Hiding Scheme
From the EMD scheme, we can infer that its largest embedding capacity is achieved at 1.16 bpp when there are two pixels in a group. The embedding capacity decreases drastically if the size of the pixel group increases. To enhance the embedding capacity, Kuo and Wang [
16] proposed the GEMD scheme. GEMD has two main contributions: (1) it does not require the conversion of the binary secret data to a specified numeral stream before embedding; and (2) its embedding capacity stays greater than 1 bpp when the size of pixel group increases. A new extraction function
is introduced in GEMD as follows:
According to the extraction function
, the GEMD embedding algorithm (Algorithm 2) is shown below:
| Algorithm 2 GEMD Embedding Algorithm [16]. |
Input: cover image and binary secret data stream
Output: stego image - Step 1.
Divide the cover image into non-overlapping groups, each of which consists of m adjacent pixels. - Step 2.
Obtain an m-pixel group from . - Step 3.
Read (m + 1) secret bits from and obtain the corresponding -ary secret data . - Step 4.
Compute by Equation (3) and obtain the difference . - Step 5.
If , set , and for , where is the stego pixel, and then go to Step 8; else if , go to Step 6; else go to Step 7. - Step 6.
Transform to -bit data . For to do If ( and ) then ; else if ( and ) then ; else . End For. Go to Step 8. - Step 7.
Compute and then transform to -bit data . For to do If ( and ) then ; else if ( and ) then ; else . End For. - Step 8.
Go to Step 2 until all secret data is embedded.
|
Similar to the EMD scheme, the GEMD scheme extracts the secret data by computing the extraction function using stego pixels as its inputs. To make a clear comparison between GEMD and EMD, we still take Example 1 to demonstrate the embedding and extracting processes using GEMD when .
In the embedding process of GEMD, first, obtain -ary secret data . Then, compute . Thus, the difference is obtained. Because , transform to . According to Step 6, we set , and in the stego image. To extract the hidden data, we just compute .
2.3. BPEMD Data Hiding Scheme
Unlike the aforementioned EMD-type schemes, both the coefficient and modulus of the extraction function are binary power in the BPEMD scheme (Algorithm 3) [
18]. Since the multiplication of binary numbers implemented by shifting bits is faster than that of numbers in other radices, BPEMD can speed up the embedding process. Experimental results show that embedding capacity of BPEMD is quite similar to that of GEMD but higher than that of EMD and MSD. The extraction function
in BPEMD is shown below:
| Algorithm 3 BPGEMD Embedding Algorithm [18]. |
Input: cover image and binary secret data stream
Output: stego image - Step 1.
Divide the cover image into non-overlapping groups, each of which consists of m adjacent pixels. - Step 2.
Obtain an m-pixel group from . - Step 3.
Read (m + 1) secret bits from and obtain the corresponding -ary secret data . - Step 4.
Compute by Equation (4) and obtain the difference . - Step 5.
If , set and for , where is the stego pixel, and then go to Step 8; else if , go to Step 6; else go to Step 7. - Step 6.
Transform to -bit data . For to do . Go to Step 8. - Step 7.
Compute and then transform to m-bit data . For to do . - Step 8.
Go to Step 2 until all secret data is embedded.
|
From the embedding algorithm of BPEMD, it can be implied that can be modified by , whereas for can be modified by . Obviously, the secret data can be extracted easily by calculating the extraction function with stego pixels as its inputs. Here, we also use Example 1 to explain the BPGEMD scheme with .
For the embedding, after obtaining 16-ary secret data , we compute . Thus, the difference is obtained. Because , we compute and then transform it to . According to Step 7, we set , and in the stego image. To extract the hidden data, we just compute .
2.4. Chinese Remainder Theorem
The CRT [
22,
23,
24], resulting from Bézout’s Lemma [
25], is an approach to determine an integer in a specific range by the given system of simultaneous congruencies in number theory. CRT is used as a main building block in our proposed scheme and described as follows. Given
positive, pairwise coprime integers,
, and
positive integers,
, for
, a system of equations can be established for determining an integer
X:
Therefore, the unique solution X in is computed by CRT as where and
3. Proposed CRT-Based Scheme for Data Hiding
In this section, we propose a novel EMD-type data hiding scheme based on CRT called CRT-EMD. In the proposed scheme, the cover image is divided into non-overlapping
m-pixel groups. According to the CRT and a new extraction function, the
ith cover pixel in a group can directly embed
secret bits so as to achieve high embedding capacity. In particular, the feasibility of data embedding by our proposed scheme is addressed in
Section 3.1. In
Section 3.2 and
Section 3.3, we elaborate the embedding and extracting processes of the proposed scheme, respectively.
3.1. Feasibility Study
In our proposed data hiding scheme, an extraction function which is quite different from those of previous EMD-type schemes is constructed as follows:
where
is an
m-pixel group in the cover image and
are
positive, pairwise coprime integers with
for
. Denote the
-ary value of
secret bits carried by
as
, where
. Now the key issue is whether it is feasible to modify
for embedding
while minimizing the image distortion. In this subsection, we will analyze the feasibility of the above issue by using CRT.
Let
and thus the value of
is obviously in the range of
. Assume there is an integer
also in the range of
. Then, we can establish the following equations:
and easily compute the value of
by CRT. Therefore, if we can change
to
through modifying
, the secret data
can successfully be embedded in
. Let
and the modification on
be
(
). Therefore, we must prove
to ensure that
can be modified to
.
In the following, we apply Bézout’s Lemma (also called Bézout’s identity) [
25], a famous theorem in number theory, to prove Equation (7). Bézout’s Lemma is described as follows:
Bézout’s Lemma [25]. Let and be nonzero integers and denote as their greatest common divisor. Then there exist two integers and such thatwhere is a multiple of .
It should be noticed that the integer pair
is not unique. When one pair of solution
has been computed, all pairs can be obtained by
where
k is an arbitrary integer. Let a pair of solutions
that minimize the value of
be called
minimal solution. Bézout’s Lemma has an attractive property that it is very easy to determine the minimal solution. In fact, exactly two pairs of all the solutions satisfy
and
. The extended Euclidean algorithm [
25] always produces one of the above two pairs from which the minimal solution can be obtained immediately.
Lemma 1 [25]. Let and be coprime integers and be a nonzero integer. Then there exist two integers and such that Proof. Since the integers and are coprime, their greatest common divisor is “1”. According to Bézout’s Lemma, we can infer that . Therefore, Lemma 1 is a special case of Bézout’s Lemma when and are coprime integers. ☐
Both Bézout’s Lemma and Lemma 1 can be extended to more than two integers as follows:
Lemma 2 [25]. Let be nonzero integers and denote as their greatest common divisor. Then there exist integers such thatwhere is a multiple of . Lemma 3 [25]. Let be pairwise coprime integers and be a nonzero integer. Then there exist integers such that Now we present a very important theorem regarding our proposed scheme.
Theorem 1. In the CRT-EMD data hiding scheme, there exist integers, , satisfying (Equation (7)). In addition, a minimal solution that minimizes the value of can be obtained.
Proof. According to the CRT-EMD scheme, there are two integers and in the same range of , where and is computed by CRT through Equation (6). Let and the modification on the cover pixel be (). Since are positive, pairwise coprime integers, we can hold that by Lemma 3. Especially, we set when . Moreover, a minimal solution that minimizes the value of can be obtained easily by the extended Euclidean algorithm as stated previously in Bézout’s Lemma. This lemma indicates that the minimal image distortion can be achieved by employing the minimal solution. In other words, the issue to embed the secret data into the cover pixel while minimizing the image distortion is feasible by the CRT-EMD scheme. ☐
3.2. The Embedding Process
Detailed description of the embedding process is provided in the following algorithm (Algorithm 4).
| Algorithm 4 CRT-EMD Embedding Algorithm. |
Input: cover image and binary secret data stream
Output: stego image - Step 1.
Divide the cover image into non-overlapping m-pixel groups. - Step 2.
Select positive, pairwise coprime integers, , where for . - Step 3.
Obtain an m-pixel group from . - Step 4.
For to do Read secret bits from ; Obtain the -ary value of these bits. End For. - Step 5.
Compute by Equation (5). - Step 6.
Compute an integer by CRT. First, establish Equation (6) by using and . Finally, is computed by CRT as where and - Step 7.
Compute the difference . - Step 8.
Let the modification on be () and find the minimal solution for Equation (7). - Step 9.
Compute the stego pixel for . - Step 10.
Go to Step 3 until all secret data is embedded.
|
From the above embedding process, it can be observed that the CRT-EMD scheme has a very high embedding capacity since secret bits can be directly embedded into the ith cover pixel in a group. Now let us give a clear explanation for the embedding process of the CRT-EMD scheme.
Given two grayscale pixels of a cover image and a binary secret data stream , we will show how to embed into the above two-pixel group using CRT-EMD when . Because , the cover image is divided into non-overlapping groups for embedding, each contains 2 pixels. Accordingly, the binary secret stream is divided into a 2-bit segment and 3-bit segment , in which and . Then, we select two coprime integers and and compute by Equation (5) (See Step 5). After that, we establish two equations and and compute by CRT. We then find the minimal solution for the equation according to Step 8. Thus, we obtain stego pixels and .
3.3. The Extracting Process
Detailed steps of the extracting process are provided in the following algorithm (Algorithm 5).
| Algorithm 5 CRT-EMD Extracting Algorithm. |
Input: stego image and a sequence of integers
Output: binary secret data stream - Step 1.
Divide the cover image into non-overlapping m-pixel groups. - Step 2.
Obtain an m-pixel group from . - Step 3.
Compute by Equation (5). - Step 4.
Compute and convert to -bit binary data for . - Step 5.
Go to Step 2 until all stego pixel groups have been processed. The binary secret data stream is exactly retrieved by concatenating all binary data.
|
The extracting process implies that the extraction function constructed in the CRT-EMD scheme is different from those in previous EMD-type schemes. The secret data is computed directly by the extraction function in existing schemes. In contrast, the value computed by the extraction function in Step 3 of CRT-EMD is not the embedded secret data but just an intermediate. Then, the secret data is obtained by . This two layer embedding strategy can further increase the security. To extract the hidden data in the stego pixel pair , we first compute , and then obtain secret data and .