Abstract
Simulation of cutting is essential for many applications such as virtual surgical training. Most existing methods use the same triangle mesh for both visualization and collision handling, although the requirements for them in the interactive simulation are different. We introduce visual-collision binding between high-resolution visual meshes and low-resolution collision meshes, and thus extend the spatially reduced framework to support cutting. There are two phases in our framework: pre-processing and simulation. In the pre-processing phase, the fvisual-collision binding is built based on the computation of geodesic paths. In the simulation phase, the cutting paths are detected on the collision triangles and then mapped to local 2D coordinates systems in which the intersections between visual mesh and the cutting paths are calculated. Both collision and visual meshes are then re-meshed locally. The visual-collision binding is updated after cutting, based on which the collision-simulation and visual-simulation embedding are updated locally. Experimental results show that our cutting method is an efficient and flexible tool for interactive cutting simulation.
1. Introduction
Simulation of thin deformable objects has many applications in computer graphics, such as virtual surgical training. The cutting simulation is an essential part in these applications. For example, in a typical knee arthroscopy procedure, the surgeon needs to press the meniscus to identify the torn part before cutting and re-examines the meniscus after that. The simulation of this procedure involves at least three important models: (1) visual models for the rendering of surface of the meniscus; (2) collision detection models to handle the interaction between surgical tool and the meniscus, as well as the interaction between the meniscus and the cartilages; and (3) mechanical models to simulate the deformation of the meniscus. The cutting simulation affects all the three models, and thus affects the performance of the whole simulation.
In the past decades, although many methods have been proposed, the simulation of interactive cutting of deformable objects remains an important research issue. This is due to the computational complexity and numerical stability of cutting, especially in the applications that require an interactive rate. Most of the existing methods use the same mesh as visual and collision meshes. In [1], a spatially reduced framework was proven to be very robust and efficient for handling the collision detection and response of thin deformable objects. In this framework, the whole model is composed of three meshes with different resolutions: (1) high-resolution triangle mesh for visualization; (2) coarse resolution triangle mesh for collision; and (3) another low-resolution volumetric mesh for simulation. However, they did not provide a cutting scheme in this framework. It is difficult to update the collision and visual meshes consistently when the resolutions of them are different. If the cutting is performed on visual and collision meshes separately, it may happen that, while the high-resolution visual mesh has been cut, the low-resolution collision mesh has not. As a result, these two meshes become inconsistent. To overcome this issue, we introduce the binding between the visual and collision meshes (visual-collision binding). The cutting operation is performed only on the collision mesh, from which the visual mesh and the simulation mesh are updated, respectively.
The paper is organized as follows. We review related works in Section 2. An overview of our framework is presented in Section 3. The detailed methods are described in Section 4. In Section 5, we test and evaluate our cutting method with three different examples following the conclusions made in Section 6.
2. Related Works
Simulation of cutting involves simulation of deformable bodies, collision detection and response, as well as topological operations of mesh. Numerous methods have been proposed in the past decades. An excellent review can be found in [2], while we only cite the most related works.
2.1. Simulation of Deformable Bodies
Since the time of publication of [3], the simulation of deformable bodies remains an important research topic. The most popular methods are Mass-Spring [4], Finite Element Method (FEM) [5], and position based methods [6,7]. Our framework is independent of these simulation methods. We choose Co-rotational linear FEM for our experiments [8], since it is one of the most widely used methods in surgical training simulation. The integration of our framework with the other simulation methods will be our future works.
2.2. Collision Handling for Thin Deformable Bodies
Collision detection is essential for many applications, and a good review can be found in [9]. Our framework is compatible with most of the existing collision detection methods. Spillman et al. [1] proposed a spatially reduced framework, in which a high-resolution triangles mesh was used for rendering, a coarse resolution triangle mesh with radii was used for the collision handling, and a coarse volumetric mesh was used for the simulation. The robustness and efficiency for the collision handling of this framework have been proven by extensive example. However, the cutting simulation of this framework was left as a future work. We extend this framework by adding visual-collision binding to handle cutting.
2.3. Cutting for Deformable Objects
There are three models for a deformable body: visual, collision and simulation models. We categorize the existing cutting methods according to the relation of these models.
2.3.1. Cutting of Conformal Mesh
Many cutting frameworks use one conformal mesh for visualization, collision and simulation. Tetrahedral meshes are commonly used. The simulation of deformation is run on tetrahedral meshes while the outside faces of the meshes are used for visualization. The collision can be handled by the boundary triangles or the tetrahedral meshes. The cutting operation is performed on the tetrahedral meshes, while the visual collision mesh is updated accordingly. Many methods have been proposed, including element removal [10], element refinement [11,12], face-splits [13,14,15], node snapping [16], and their combinations [17,18]. The advantages of conformal mesh are that the cutting needs only to be considered on the tetrahedral mesh, and thus the complexity of updating the embedding between different meshes can be avoided. The drawbacks of using conformal tetrahedral meshes are that the resolution of visualization and collision has to be aligned with the resolution of simulation of deformation. Increasing the resolution of any of the three models directly leads to the resolution increments of the other two models.
2.3.2. Cutting of Multi-Resolution Mesh
The multi-resolution simulation framework has been adopted by many researchers. Tetrahedral meshes were used as simulation meshes in [19,20,21]. The virtual node method proposed in [19] generated a well-shaped tetrahedron for each material branch. Although arbitrary cut [20] and Graphics Processing Unit (GPU)-accelerated simulation [21] can be supported by this method, the connectivity analysis of tetrahedrons is not very efficient. In our work, hexahedral meshes are adopted for the simulation, for their regular structures. In addition, these works used the same triangle mesh for both visualization and collision, while our work supports different resolutions of visual and collision meshes in cutting simulation.
The idea of composite finite elements (CFEs) was introduced into the computer graphics community by Nesme et al. [22]. In this simulation framework, a high-resolution visual mesh is embedded into a fine hexahedral mesh, which is also embedded into a coarse hexahedral mesh. Branch analysis is performed so that, for each material component, a hexahedron is duplicated and assigned. Jeřábková et al. [23] simulated the cutting by element removal of the fine hexahedron and the dynamic branch analysis. Although interactive cutting rate could be achieved, the visual quality and mechanical accuracy were limited due to the element removal operation.
Based on the octree structure, Dick et al. [24] connected coarse hexahedral mesh to fine hexahedral mesh. The cutting was simulated by disconnecting the links between fine hexahedral elements. Wu et al. [25] improved the generation of visual mesh by the dual contour method. They also developed a method for the collision detection and response for this model [26]. The performance was further improved by Jia et al. [27] with Central Processing Unit (CPU)–GPU mixed implementation. Therefore, this model supports not only interactive cutting, but also efficient collision handling. However, both the cutting operation and the collision detection were relied upon the octree structure. In our cutting simulation, the cut is introduced on the triangles of the collision mesh, and the visual-collision binding is independent from the simulation mesh.
Seiler et al. [28] proposed a threefold model for the simulation of deformable objects. In this model, a high-resolution surface mesh was used for rendering, a mid-resolution tetrahedral mesh was used for collision detection and response, and a coarse resolution hierarchical hexahedral mesh was used for deformation. Later on, they developed a cutting method for this model [29] that was also applied in a data-driven simulation [30]. The cutting operation was simulated by the removal of tetrahedrons that were intersected by the blade volume. Efficient cutting simulation was achieved by this method. However, the resolution of the tetrahedral mesh should have been large enough to represent the shape of the cutting blade, due to the non-split operation they adopted for the cutting. This compromised the ability of tuning the resolution of collision of this model. The tetrahedral mesh was no longer used for the collision detection and response in their cutting simulation, and only served as a material graph. The collision handling was not discussed, and left for a future work. In our cutting simulation, the split operation on the triangles of the collision mesh is utilized, instead of the element removal. Therefore, the resolution of our collision mesh is not limited by the geometry of the cutting blade.
A few cutting methods in the framework of position based dynamics (PBD) was proposed recently. Pan et al. [31] combined a surface mesh with inner meatballs, while Berndt et al. [7] further discussed the haptic, electrocautery, and skinning in the cutting simulation. Although efficient cutting has been achieved, PBD is generally not designed for the surgical simulation due to its accuracy issue. Manteaux et al. [32] developed a method to interactively cut a thin sheet in detail, the deformation of which is driven by the frame based simulation. Their method can only cut thin sheets, while our method supports the cutting simulation of thin deformable volumetric objects.
A multi-model framework is supported by the Simulation Open Framework Architecture (SOFA) [33], which allows the deformation of an object with different resolutions for the visualization, collision and simulation. The flexible architecture and extensive components provided by SOFA make it very suitable for testing new algorithms. Therefore, we implement our cutting method based on SOFA. At the same time, since the cutting of multi-resolution model is not directly provided by SOFA currently, our implementation enriches its cutting components.
3. Research Hypothesis and Overview
Our framework is composed of three different models for visualization, collision, and simulation (see Figure 1). A high-resolution triangular mesh is used for the rendering, while a coarse triangular mesh with a certain thickness is used to represent the inner part of thin objects. Finally, a coarse hexahedral mesh is used for the simulation. The collision detection and response computation are handled by the collision mesh, while the force is mapped to the hexahedral mesh. The resolution of the hexahedral mesh should be close to the resolution of the collision mesh, since lower resolution could not resolve all the forces from the collision detection, while a higher resolution would waste the computational time. The physically based simulation is performed on the hexahedral mesh, and the deformation is mapped to both the collision and the visual meshes.
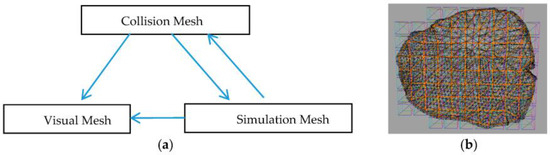
Figure 1.
Framework of the cutting simulation. (a) three different meshes and their relations; (b) an example of a steak model in wireframe mode. A low-resolution triangle mesh is used as a collision mesh (orange), a high-resolution triangle mesh is used for visualization (black), while a low-resolution hexahedral mesh is used as a simulation mesh. The hexahedra are visualized by different colors on their faces.
Our research hypothesis is that, by adding the visual-collision binding, the thin deformable volumetric objects with different resolutions can be cut consistently and interactively. Our cutting framework is composed of two phases: pre-processing and simulation phase. Before the simulation, the visual mesh is bound to the collision mesh by using the geodesic paths on the visual mesh and triangle splitting.
In the simulation phase, the cutting is performed on the collision mesh. Then, the hexahedral mesh adapts to the cutting by duplicating the elements. The relation between these models is updated, including the embedding between the collision and simulation meshes (collision-simulation embedding), the embedding between the visual and the simulation meshes (visual-simulation embedding), and the visual-collision binding, respectively. Our cutting simulation includes the following steps:
- Cutting of collision mesh. The cutting blade is intersected with the collision mesh. The triangles are split along the path of the blade.
- Cutting of visual mesh. Based on the visual-collision binding, the visual mesh is cut in the rest configuration using local 2D coordinates. Then, the visual-collision binding is updated.
- Simulation mesh adapting to the cut. The branches of the collision mesh contained in the elements of the simulation mesh are analyzed. The elements are duplicated for each branch. The collision-simulation embedding is updated.
- Updating the visual-simulation embedding. According to the visual-collision binding, the visual-simulation embedding is updated.
4. Method
Our cutting framework includes two phases: pre-processing and simulation. The pre-processing phase is run before the simulation, and the processing time is not critical. In the pre-processing phase, we build the visual-collision binding. In the simulation mesh, we locally cut the collision and visual meshes and update the binding.
4.1. Pre-Processing Phase
Given a visual mesh of a thin volumetric object, we build the collision mesh interactively using 3dsMax. Automatic generation of a reduced collision mesh will be done in our future work. As long as the collision mesh is built, the visual-collision binding will be calculated automatically. To keep the consistency in the cutting operation, we need to bind the fine visual mesh to the coarse collision mesh such that, when a triangle on the collision mesh is split by the cutting trajectory, the visual triangles bound to the collision triangle will be cut by the same cutting path. A visual vertex is either bound to the vertex, the edge or the triangle of collision mesh.
4.1.1. Bind Visual Vertices to Collision Vertices
For each vertex of the collision mesh, we search it to find the closest visual vertices (see Figure 2). If the vertex is on the border of the collision mesh, we find the closest vertex on the visual mesh with respect to this vertex. If the vertex is inside the collision mesh, we find the closest vertex along the normal built on this vertex to both sides of the visual mesh. Since the number of the visual vertices is larger than the number of the collision vertices, after this step, every collision vertices have their bound visual vertices. A necessary constraint here is that one visual vertex cannot be bound to two collision vertices.

Figure 2.
Visual vertices are bound to collision vertices. The visual mesh is black, while the orange one is the collision mesh. The red vertices are collision vertices, the blue vertices are visual vertices, and the green lines indicate their connections. Each collision vertex on the border is paired with one visual vertex. Each inside collision vertex is paired with two visual vertices: one is on the positive normal direction while another one is on the negative normal direction.
4.1.2. Calculate Geodesic Paths between the Bound Visual Vertices
For each edge of the collision mesh, its two end vertices are paired with the visual vertices, respectively. Since each collision edge is a straight line, i.e., the shortest path between two collision vertices, we want to find the shortest path between its two paired visual vertices. An ideal choice for this purpose is the geodesic path, since it is the shortest path on the surface between two vertices. We calculate the geodesic paths between these vertices on the visual mesh, according to the edges of the collision mesh (see Figure 3). There are many existing methods for the calculation of a geodesic path. We use the method proposed by Xin et al. [34], since it calculates the exact geodesic path that guarantees the non-intersection between each path. Although all these geodesic paths do not intersect with each other, they may have common points.
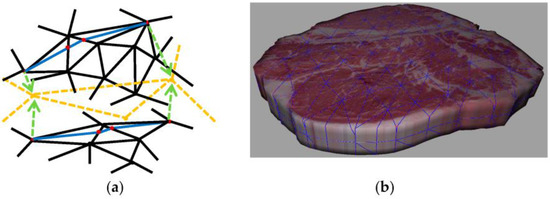
Figure 3.
Geodesic paths are calculated between the visual vertices that are bound to collision vertices. (a) the orange lines are the edges on the collision mesh, while blue lines are its relevant geodesic paths. The red points are the intersections between the geodesic paths and the visual mesh. The green arrows indicate the binding direction. Each collision edge is related with one or two geodesic paths; (b) the geodesic paths for all the collision edges are visualized on top of the original visual mesh.
4.1.3. Re-Meshing of the Visual Mesh
With reference to Figure 4, we add new visual vertices along all the geodesic paths. Then, we split the triangles that are intersected by these new visual vertices and re-mesh the whole visual mesh. The result is a new surface mesh that is geometrically identical to the original visual mesh. All the visual vertices on the paths are bound to the edges on the collision mesh, respectively. The visual mesh is divided into several regions with respect to the triangles on the collision mesh (collision triangles). For all the visual vertices that have not yet been assigned to the collision vertices and edges, we assign them to the collision triangles. This is achieved by the local Depth First Search (DFS) algorithm based on the topology of visual mesh. After this step, all the visual vertices are bound to either vertices or edges or triangles on the collision mesh (see Figure 5).
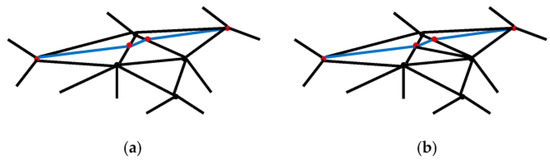
Figure 4.
The visual triangles intersected by the geodesic paths are split. (a) some of the visual triangles are intersected by the geodesic paths. The light blue lines are geodesic paths, while the red points are the intersections points between the geodesic paths and the visual edges; (b) all the visual triangles intersected by the geodesic paths are split, and a new visual mesh is generated.
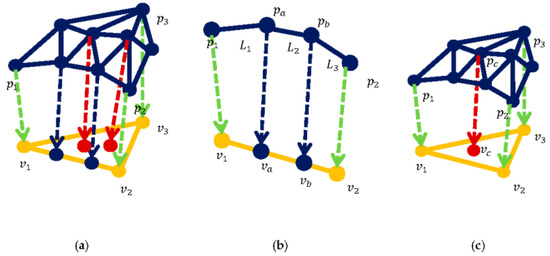
Figure 5.
All the visual vertices are bound to the collision triangles. (a) the orange triangle is the collision triangle, while the blue triangles are visual triangles. The arrows indicate the binding direction: green for the visual vertices bound to the collision vertices, blue for the visual vertices bound to the collision edges, and red for the visual vertices bound to the collision triangles; (b) the calculation of the binding parameters for the visual vertices bound to the collision edges; (c) visual vertex is bound to on the collision triangle.
4.1.4. Assigning Local Parameters to the Visual Vertices
We assign local parameters to all the visual vertices. For each visual vertex that is bound to a collision edge, we assign its parameter by their accumulated length, which can reflect the distances between the neighboring vertices. With reference to Figure 5b, suppose visual vertices and are bound to the collision vertices and , respectively, and and are bound to the collision edge (, ). Let , and be the lengths of the visual edges (, ) in the reference configuration (, ) and (, ). Then, the binding parameters for and are (, ) and (, ), respectively. With the above parameters, we can calculate the projected points of as , and of as . For each visual vertex that is bound to a collision triangle, we parameterize it by the mean value coordinates [35], since this parameterization has a good quality and is widely used in many geometric applications. With reference to Figure 5c, suppose visual vertex is bound to the collision triangle (, , ). Let (a, b, c) be the binding parameter of , then the projected point of it can be calculated by
Since each visual vertex that is bound to the collision vertex is shared by its one-ring surrounding collision triangles, the parameter of this visual vertex is defined by the specific collision triangle. For examples, in Figure 6, the parameter of in the triangle (, , ) is (1,0,0) while the parameter of in the triangle (, , ) is (0, 0, 1). Similarly, since each visual vertex that is bound to the collision edge is shared by two collision triangles, the parameter of this visual vertex is then defined by the specific collision triangle. With reference to Figure 6, suppose v is a projected point on the edge (, ) with the parameter (a, b). Then, for the collision triangle (, , ), the parameter of v is (a, 0, b), while for the collision triangle (, , ), the parameter of v is (a, b, 0). Thus, the local parameters of the visual vertices that are bound to the collision edges will be defined in the simulation phase according to the specific collision triangle. Therefore, for each given collision triangle, the coordinates of the visual vertices bound to it can be uniformly written as in Formula (1), no matter what visual vertices are bound to the collision vertices, edges, or triangles. In the above, we only discussed the visual vertices in the positive normal direction (positive visual vertices) of the collision triangles. It can be handled similarly for all the visual vertices in the negative normal direction (negative visual vertices) of the collision triangles. In Figure 7, we visualize the parameterization on top of the collision triangle. All the parameters are needed to be calculated only once at the pre-processing phase. In the simulation phase, the parameters of the new visual vertices can be interpolated or transformed from the parameters of the original visual vertices.
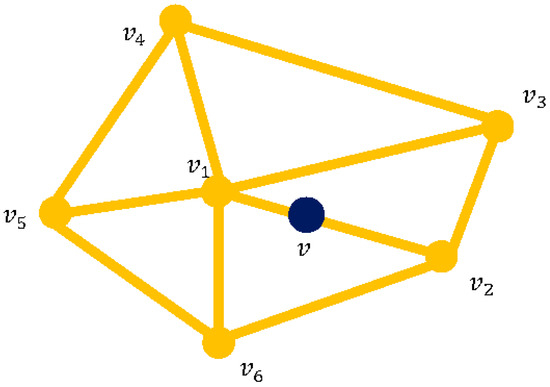
Figure 6.
The definition of local parameters for the visual vertices bound to collision edges. Visual vertex v is bound to collision edge (, ), its parameters in collision triangle (, , ) and (, , ) are different.
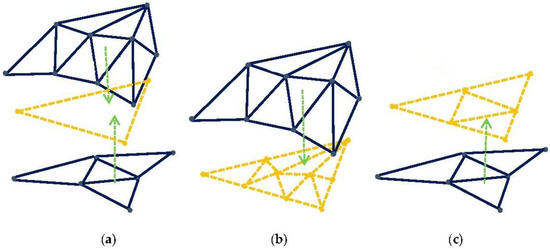
Figure 7.
Local parameterization of the visual vertices. (a) blue visual vertices are bound to the orange collision triangle, including the visual vertices on the positive and negative normal directions of this triangle. The green arrows indicate the binding direction; (b) each visual vertex on the positive normal direction is parameterized. The parameterization is visualized by overlapping with the collision triangle; (c) each visual vertex on the negative normal direction is parameterized.
4.2. Simulation Phase
4.2.1. Cutting the Collision Mesh and Updating the Collision-Simulation Embedding
We perform cutting of the collision mesh by the method of elements splitting that is similar to works [13,14,15]. We detect the intersection between the triangles of swiping blade and the edges of the collision mesh. If two edges of the collision triangle intersect with the blade, the triangle will be split into three triangles (see Figure 8).
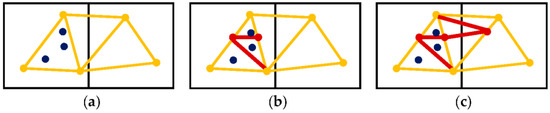
Figure 8.
The process of cutting the collision mesh. The hexahedra are illustrated in 2D as the quadrangles with black edges; the orange edges are the collision edges; the orange points are the collision vertices; the red points and lines are the cutting points and paths respectfully; the dark blue points are the visual vertices bound to the collision triangle. (a) the mesh before cut; (b) a triangle is cut by two intersection points and split into three triangles. Since the first hexahedron still has only one branch, the hexahedron remains unchanged; (c) the second triangle is cut. The first hexahedron needs to be duplicated because it has two branches.
After cutting of the collision mesh, we apply a method that is similar to the method published in [23,32] to update the hexahedral mesh to adapt to the cut (see Figure 9). We perform elements analysis on the relevant hexahedra. The hexahedral mesh is adapted to the cut by duplicating the elements of the hexahedra, such that, for each branch within the original hexahedron, a copy of the hexahedron is made. The hexahedra are connected according to the branch analysis, which is performed based on the topology of the new collision mesh. Since the cutting is locally performed, the branch analysis is also performed locally on a few hexahedra.
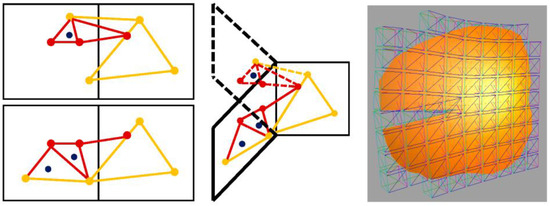
Figure 9.
Duplication of the hexahedron. The red points and lines are the new added collision vertices and edges as the result of the cut. (a) duplication of the hexahedron such that each copy has one branch of the collision vertices; (b) each copy of the hexahedron is connected with its surrounding hexahedra according to the topology of the collision mesh; and (c) snapshot of simulation of cutting the collision mesh.
4.2.2. Cutting the Visual Mesh
Based on the visual-collision binding that we built on the pre-processing phase, the cutting of the visual mesh is performed in the rest configuration of the collision mesh (see Figure 10 and Figure 11). With reference to Figure 10a, suppose , and are the coordinates in the rest configuration, and they are bound to the collision vertices , and , respectively. Now that a cut is introduced to this collision triangle (, , ) (see Figure 10b), vertices , and define a plane. We assign 2D coordinates to these vertices in such a way that it keeps the angles between the edges (, ), (, ) and (, ). We also keep the lengths between the above three vertices (see Figure 11a). Then, we transform all the visual vertices onto this plane and get their 2D coordinates. This is achieved by Formula (1) since all the binding parameters of the visual vertices have already been assigned in the pre-processing phase. Two cut points on the collision triangle are also transformed in the same way (see Figure 11b). The intersection points between the cut path and the visual edges are then calculated by their 2D coordinates on this plane. With reference to Figure 11c, we apply a standard method [36] to compute the intersection points between the cutting lines and the visual edges. All the parameters of the intersection points are then calculated by interpolating from the parameters of the end points of the edge. For examples, in Figure 11c, suppose and are two of the transformed visual vertices. After the computation of intersections, we get the parameters (, ) for the intersected point such that . Then, we get an intersected point on the visual mesh by (see Figure 10d or Figure 11c). After that, all the new visual points are added to the original visual mesh. The visual triangles that are intersected by these new visual edges are split and re-meshed (see Figure 10e). Therefore, we get a new visual mesh after cut.
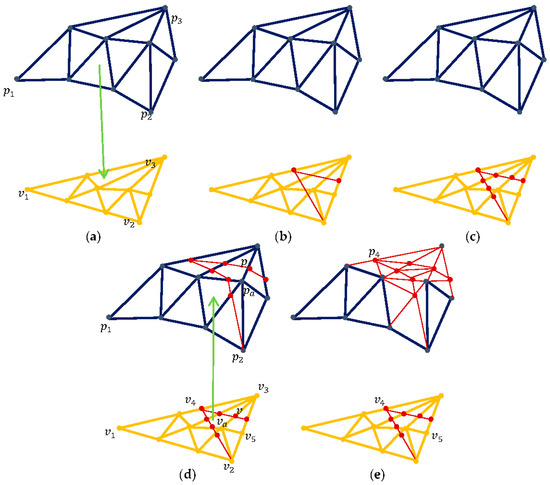
Figure 10.
The process of cutting the visual mesh. The dark blue points are the visual points; while the orange points are their parameters on the collision triangle in rest configuration. (a) the visual vertices have already been bound to the collision triangle in the pre-processing phase. The green arrow shows the binding direction; (b) the collision triangle is cut by the blade surface; (c) the intersection points are calculated; (d) new visual vertices are added according to the intersection points on the collision triangle. The green arrow shows the mapping direction; (e) The visual triangles are re-meshed to adapt to the new visual vertices.
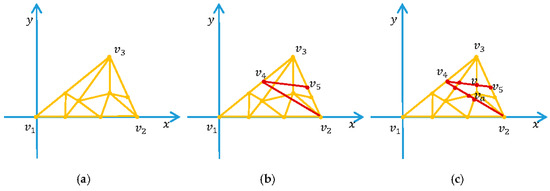
Figure 11.
Calculation of the intersection points on the plane defined by the collision triangle in the rest configuration. The orange points are the parameters of the visual vertices, while the red points are the intersection points. (a) the 2D coordinates are assigned for the visual vertices bound to the collision triangle that is cut; (b) the cut points are transformed to the rest configuration and assigned 2D coordinates; (c) the intersection points are calculated.
4.2.3. Updating the Visual-Collision Binding
After the cutting, we need to update the visual-collision binding for all the new collision triangles. With reference to Figure 11b, suppose the original collision triangle (, , ) is split into three new collision triangles (, , ), (, , ) and (, , ). For the binding of these collision vertices, we take , for example (see Figure 10e). The new added visual vertex is bound to it. The updating of its binding parameter is not necessary, since the parameter is only defined by the specific collision triangle. For the binding of the intersection points, we take , for example, (see Figure 10d). Its relevant new added visual vertex is bound to the collision edge (, ), the binding parameter of which is calculated by the accumulated length as in the pre-processing phase. For the binding of the original visual vertices that are bound to the collision triangle (see Figure 10d or Figure 11c), we take for example. Here, we already know the binding parameter of with respect to the collision triangle (, , ). Let this parameter be (, , ). We want to calculate the binding parameters of with respect to the collision triangle (, , ). Let this parameter be (, , ). We also know the binding parameters of the visual vertices , and with respect to the collision triangle (, , ). Thus, we know the 3 × 3 matrix , such as:
Therefore, we have
However, we do not know which new collision triangle is bound to. Thus, for , we calculate (, , ) for all the three new collision triangles by Formula 2. We bind to the collision triangle such as , and . Finally, all the visual vertices are bound to the new collision triangles, respectively.
4.2.4. Handling the Cut Surface Mesh
After cutting of the visual mesh, we need to generate the cut surface mesh to keep the visual look of the objects as a water-tight surface. Since the visual mesh in our simulation will not be used for collision handling and simulation, the quality of the cut surface mesh is not very important and even ill-shaped triangles can be accepted. Therefore, there are many ways to generate the cut surface mesh for our simulation. For each cut collision edge, we generate the cut surface by connecting the positive and negative visual vertices bound to this edge (see Figure 12). In [31], the cut surface is generated by down-sampling the related visual vertices in order to lower the data size of the new mesh. We up-sample the related visual vertices since the visual mesh in our simulation will not be involved in collision handling. This can be achieved by merging the parameters of positive and negative visual vertices that are bound to the cut collision edge. With reference to Figure 12b, suppose the parameters for , and are (0.7, 0.3), (0.2, 0.8) and (0.4, 0.6), respectively. After the up-sampling, the parameters for and remain unchanged, while the parameters for , and are (0.4, 0.6), (0.7, 0.3) and (0.2, 0.8), respectively. After the generation, the cut surface vertices are then bound to the cut collision edge, and their binding parameters are assigned according to the relevant positive and negative visual vertices. With reference to Figure 12c, for example, cut surface vertices , , and are assigned the same parameter (0.7, 0.3) according to the parameter of .
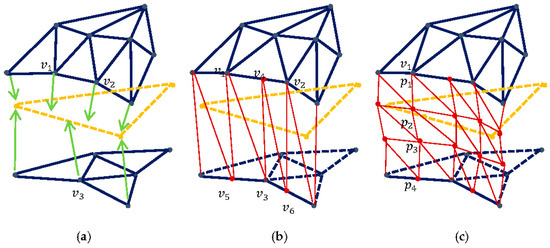
Figure 12.
Generating the cut surface mesh. The dark blue points are the visual vertices; the orange triangle is the collision triangle; the green arrows show the binding directions; the red points are the cut surface vertices. (a) before the generation, the positive and negative visual vertices are bound to the cut collision edge; (b) up-sampling the positive and negative visual vertices and connecting these vertices to form a cut surface; (c) different resolutions of cut surface can be generated by adding different resolutions of in-between visual vertices.
If the collision edges are cut again (see Figure 13), the cut surface is cut simply by comparing the parameters between the cut surface vertices and the cut points on the collision edge. The cut surface mesh is cut and separated by introducing new vertices according to the parameter of the cut points. All these new vertices are then bound to the new collision edges, respectively. Since the calculation of the interactions between the cut path and the cut surface mesh is not required, high-resolution cut surface mesh is supported by our cutting simulation.
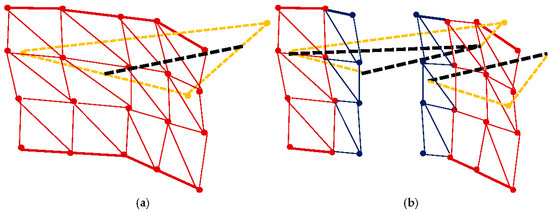
Figure 13.
Cutting of the surface mesh. (a) the orange triangle is the collision triangle, while the black dash line is the cut path on it. The red mesh is the cut surface mesh; (b) the blue points are the new added vertices on the cut surface.
4.2.5. Updating the Visual-Simulation Embedding
Once the collision-simulation embedding and visual-collision binding have been built, the visual-simulation embedding can be built accordingly. For each new triangle generated by cutting, we find the hexahedra containing their three vertices. Then, for all the visual and cut surface vertices bound to this triangle, we find and calculate the barycentric coordinates with these containing hexahedra. With reference to Figure 9, the green points represent visual vertices bound to the collision triangles. After the cutting, all these visual vertices are to be re-bound to new collision triangles and then re-embedded to the hexahedra according to the collision-simulation embedding.
5. Experimental Results
In this section, we test our framework on three different models and present the detailed experimental results. All the examples are run on a desktop PC equipped with Intel i7-4770 (Intel, Singapore) 3.40 GHz, 16 GB of RAM, and NVIDIA GeForce GTX 750Ti (NVIDIA Corporation, Singapore). All the simulations are implemented on the software platform called SOFA [33]. We use co-rotational linear FEM on hexahedral meshes as simulation meshes. The link to the accompanying videos of the examples can be found in the supplementary materials.
5.1. Cutting of a Steak
The first example is the cutting of a steak. The visual mesh of the steak is used as a de-facto standard test provided by SOFA for testing elastic object deformations and used by authors of several papers [22,31,33,37]. With reference to Figure 1b, the visual mesh of the steak has 2641 vertices and 5278 triangles. The simulation is run on the hexahedral mesh with 190 degree of freedoms (DOFs) and 76 hexahedra. We couple the above visual and simulation mesh with two collision meshes of different resolutions. Figure 14 shows the collision and hexahedral meshes, as well as the visual collision binding, respectively. Figure 15 shows the cutting of a steak with different collision meshes. For the real-time record of the interactive cutting of the steaks with different collision meshes, we refer the readers to the accompanying videos. Table 1 collects the performance data of the implementation of the pre-processing phase. The average preprocessing time of these two models are 5.1 s for model No. 1 and 10.2 s for model No. 2. This is because the bigger collision mesh requires more computation time to obtain the geodesic paths. Since the preprocessing is run before the simulation loop, time is not important. In our implementation, we only do the preprocessing once and then store the data, which will be loaded before every simulation. Table 2 collects the performance data of the implementation of the simulation phase. In the simulation, the time for cutting of model No. 1 is generally longer than the time for model No. 2. This is because model No. 1 has a coarser collision mesh, and thus has more visual points mapped to each collision triangle. More visual points to handle for each cut require more time. The time for intersection detections and for visual and collision re-meshing increases slightly, while the time for updating the binding increases significantly.
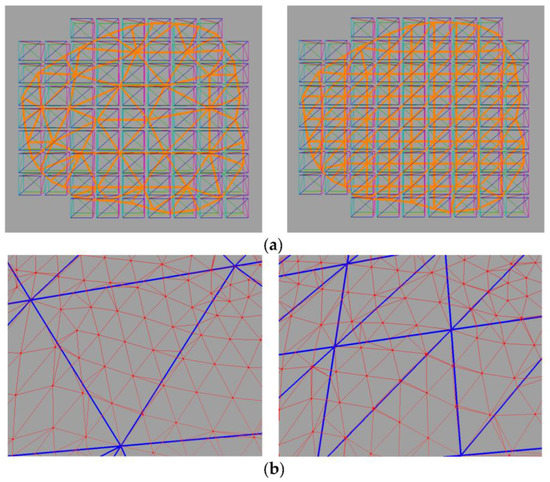
Figure 14.
Collision meshes with different resolutions and the visual collision binding after pre-processing. (a) the orange meshes are the collision meshes. From left to right, the resolution of collision is increased while the resolutions of visual and simulation meshes are fixed; (b) the close-up view of visual collision binding for different collision meshes, respectively, after the pre-processing.
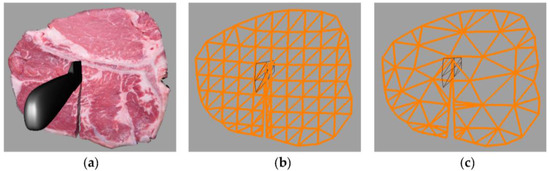
Figure 15.
Cutting of a steak with different collision meshes. (a) the visual mesh after cut; (b) the collision mesh after cut. There are 85 vertices and 137 triangles for the collision mesh of this model; (c) there are 50 vertices and 67 triangles for the collision mesh of this model.

Table 1.
Performance of the pre-process phase of cutting a steak.

Table 2.
Performance of the simulation phase of cutting a steak.
Since the cutting introduces new vertices for both visual, collision and simulation meshes, it will generally increase the simulation time. To better analyze the performance of our cutting method, we record the changes in six consecutive cuts of the No. 2 model. Figure 16a shows the numbers of vertices of visual, collision and simulation meshes, while Figure 16b shows the numbers of elements. We cannot see a clear difference of the simulation time between the first and the last cuts (however, the time is definitely less than 1 ms). Although the number of vertices and triangles of the visual mesh increases significantly, the number of vertices and elements of collision and simulation meshes grows very slow.
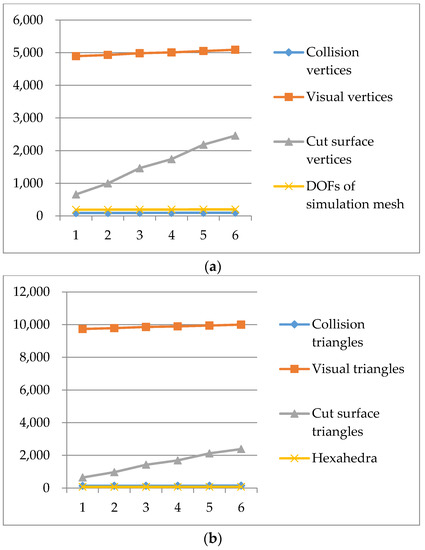
Figure 16.
The numbers of vertices and elements in six consecutive cuts. (a) the number of vertices; (b) the number of elements.
It is clear that the number of collision vertices and triangles affect the performance of the most of the collision algorithms. The very same steak model was also used in [31,37], where the same triangle mesh was used for both visualization and collision in their cutting simulation, while in our simulation the resolutions of visual and collision meshes are of different levels of magnitude. Since the authors of [31,37] did not provide the data of their collision meshes during cutting, we compare with the best scenario they could get, i.e., when the collision mesh remains unchanged. With reference to Figure 17, it is clear that the resolutions of collision meshes used in the previous cited works are of a different level of magnitude.
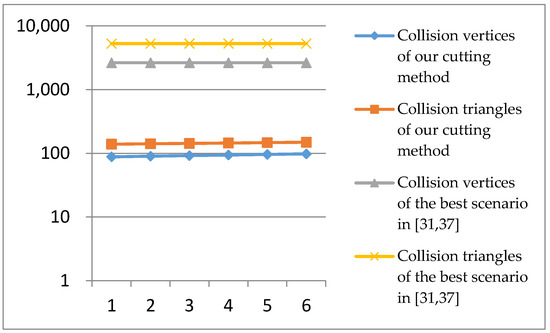
Figure 17.
Comparison of the number of collision vertices and triangles in our method with the best scenario, which could be found in [31,37]. Data is displayed in logarithmic scale of 10.
It is difficult to compare precisely with the cutting method of Wu et al. [26], since different models were used. The collision detection of their method relies on an octree structure, while our collision handling is independent from the simulation mesh. Their collision vertices are generated by down-sampling every 8th points of the visual mesh. In this way, only collision points can be utilized, while, in our simulation, all the collision points, edges and triangles are available. Furthermore, there was no discussion on how well the collision vertices approximate the visual ones by this down-sampling method. Jia et al. [27] has pointed out the difference between the down-sampling and the full simulation at the thin regions of the models, while, in our method, once a collision mesh with good approximation property is built before the simulation, the approximation will be maintained after each cut since the new collision points generated by the cut are the interpolations from the collision points before cut. This can also be seen in the next example. Their method supports general objects, while our method only supports thin volumetric object. This is a clear disadvantage of our method, and the generalization to support all objects will be our future work.
5.2. Cutting of a Thin Object
Thin objects, such as a thin sheet, are also supported by our framework. In the second example, we cut the thin sheet. In the first experiment, we fix the resolutions of the collision and simulation meshes, and then test our cutting method with the visual meshes of different resolutions. There are 65 vertices and 104 triangles in the collision mesh, while there are 200 vertices and 81 hexahedra in the simulation mesh. Figure 18 shows the cutting process of the thin sheet. For all the models, Figure 19 lists the visual collision binding after the preprocessing, and the visual mesh overlapped with the collision mesh before and after cutting. We refer the readers to the accompanying videos for the interactive cutting of different models of the thin sheet. Table 3 collects the performance data of the pre-processing phase of these models. These data are similar to the data in the previous example. The preprocessing time increases largely with the increase of the resolutions of the visual mesh. Table 4 collects the performance data of the simulation phase. The time to test intersections and re-meshing the collision and visual meshes increases slightly, while the time for updating the visual-simulation and collision-simulation embedding increases significantly. While the resolution of its visual triangles of model No. 4 is over the magnitude of 100 K, it still can be cut interactively. This indicates that our framework is very flexible with respect to different computation powers. For example, just like in many computer games, for the cutting simulation, we can provide different configurations of mesh resolutions for different computers. Although the simulations with all the models can be run in real time, updating of the collision-simulation and visual-simulation embedding is the bottleneck of our implementation.

Figure 18.
Simulation of cutting a thin sheet. (a) the visual and simulation meshes before cutting; (b) the visual and simulation meshes after cutting; (c) the collision and simulation meshes after cutting; (d) the visual, collision and simulation meshes after cutting.

Figure 19.
The visual mesh overlapped with the collision mesh before and after cutting. From left to right, the resolution of the visual mesh is increased while the resolution of the collision mesh remains unchanged. (a) the close-up view of the visual and collision bindings after the pre-processing; (b) the collision mesh is overlapped with the visual mesh before cutting; (c) the collision mesh is overlapped with the visual mesh after cutting.

Table 3.
Performance of the pre-processing phase in the first experiment of cutting a thin sheet.

Table 4.
Performance of the simulation phase in the first experiment of cutting a thin sheet.
In the second experiment of this example, we fix the resolution of visual mesh and then test our cutting method with the collision meshes of different resolutions. There are 3425 vertices and 6656 triangles in the visual mesh, while there are 200 vertices and 81 hexahedra in the simulation mesh. Four different collision meshes are used. We refer the readers to the accompanying videos for more information. Figure 20 lists the visual and collision meshes after cutting. Table 5 collects the performance data of the pre-processing phase of these models. The resolutions of the collision mesh increase from model No. 1 to model No. 3. No pre-processing phase is required for the fourth model, since it uses the same mesh for both the visualization and collision handling. Table 6 collects the performance data of the simulation phase. The average time for each cut of these models decrease slightly from model No. 1 to model No. 3. All the models can run in real time when there are no collisions with the environments. However, once the collisions are introduced, all the simulation times increase rapidly. From model No. 1 to model No. 4, the simulation times increase, following the increment of the resolutions of the collision mesh. The first two models can still run in real time, model No. 3 can run interactively at 21.7 frames per second (FPS), and model No. 4 only has 7.5 FPS. These data prove the flexibility of our cutting method that, when the resolution of visual mesh is fixed, different resolutions of collision mesh can be chosen to meet the requirements of the simulation.

Figure 20.
All the four models are cut and collide with the same environments. From left to right, the resolution of the collision mesh is increased. (a) visual meshes; (b) collision meshes.

Table 5.
Performance of the pre-processing phase in the second experiment of cutting a thin sheet.

Table 6.
Performance of the simulation phase in the second experiment of cutting a thin sheet.
5.3. Meniscus Lesion Handling in a Prototype Simulator
We have applied our cutting method in a feasibility study on knee arthroscopy surgery training simulation (see Figure 21). For the setup of our prototype simulator, a 3D printed knee model and two haptic devices were used. One device is used for controlling the camera, while another one for controlling the surgical tool. The meniscus is a vulnerable thin crescent-shaped soft tissue located within the knee between the bones. In a typical procedure of handling meniscus lesion, the surgeons punch out the torn tissue, and then contour the edge of the meniscus with a shaver. Figure 21 shows the cutting of the meniscus in our simulator compared to the snapshots from real surgical videos with the similar angle of views. The readers are also referred to the accompanying videos for more information. With reference to Figure 22, the meniscus model is composed of the visual mesh with 2882 vertices and 5760 triangles, the collision mesh with 105 vertices and 160 triangles, as well as the simulation mesh with 120 vertices and 42 hexahedra. The pre-processing time is about 12.7 s. There are about 64 visual vertices and 76 visual triangles for each collision triangle after the pre-processing phase. Figure 23 shows the cutting process. Each punch of the meniscus is composed of the cuts of a few collision triangles (see Figure 23b). For each punch, the average total cut time is 48.2 ms, the time for cutting collision and visual mesh and updating collision-visual binding is about 6.2 ms, the time for updating visual-simulation and collision-simulation embedding is 32.8 ms, while the time for adding the cut surface is about 8.1 ms. The time for each simulation step is about 6.5 ms, while the average number of frames per second is 162.
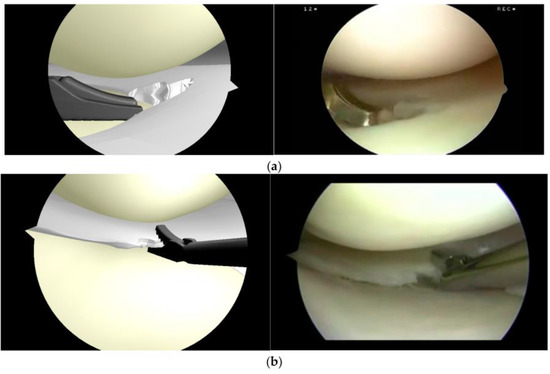
Figure 21.
The simulation of punching out the torn parts of a meniscus. The left images are our simulations while the right ones are the snapshots from real surgical videos. (a) the meniscus after several punches; (b) the meniscus after several punches on some other area.
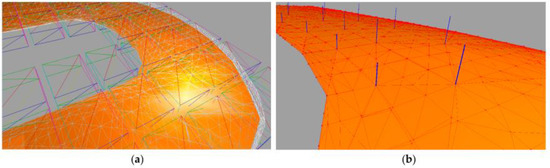
Figure 22.
The meniscus model. (a) the visual, collision and simulation meshes before cutting. The white wireframe mesh is the visual mesh, the orange mesh is the collision mesh, and the hexahedral mesh is the simulation mesh; (b) the close-up view of the visual and collision bindings after the pre-processing. The red points and lines are the visual vertices and edges bound to the collision mesh respectfully. The blue lines show the links between the collision vertices and their paired visual vertices.
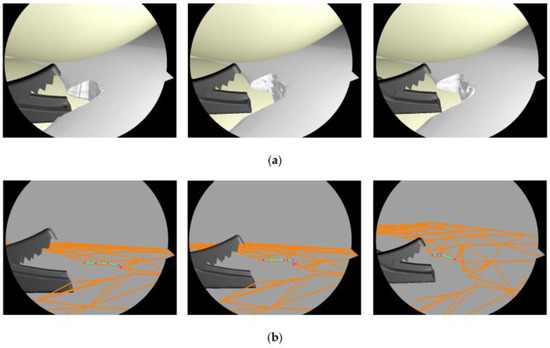
Figure 23.
The cutting process of the meniscus. (a) the visual mesh of meniscus after each punch; (b) the relevant collision mesh of the meniscus. The blue lines are the cutting paths, while the red points are the intersection points between the cutting triangles of the scissor and the collision edges of the meniscus.
Figure 24 shows the contouring process in our simulation. To simulate the contouring operation, we need to generate jagged surface on the edge of the meniscus in the punching simulation (see Figure 23a). This is achieved by introducing random numbers at the cut surface mesh generating section. Then, we activate the model of a shaver and turn on the shaving mode in our simulation. In the shaving mode, we will not cut the collision triangles when the shaver collides with them. Instead, we monitor the intersected parameters on the collision edges. Since the cut surface mesh was bound to these collision edges in the previous steps, we smooth the cut surface around the intersected parameters. During the contouring process, the meniscus is getting deformed when the shaver pushes on it, just as the behavior of the meniscus in the real surgery.

Figure 24.
Contouring the edge of the meniscus. The red circle highlights the edge of the meniscus before and after contouring.
In this example, the most related work that can be used as a benchmark is [29]. However, its authors did not provide the data of their models, thus it is difficult to make a precise comparison. The authors simulated punching of the meniscus by element removal, while we simulate it by cutting the collision triangles. They reported 86 ms for a total cut time of a punch, while the total cut time in our method is 48.2 ms. However, it is an unfair comparison since their paper was published in 2011, and the meniscus model used is different from ours. Anyway, a clear advantage of our method is the updating of the collision mesh, just as the example of cutting a steak. In [29], there is no mentioning of the collision, while our method separates the resolution of the visual and collision meshes. Furthermore, to the best of our knowledge, we did not find any simulation of contouring the edge of meniscus in all the existing simulators. In the examples of [29] and the released demos of the commercial simulator in [38], they both generate smooth cut surface, which leaves no room for the contouring operation.
6. Conclusions
We have introduced the visual-collision binding into cutting simulation, by which the framework described in [1] was extended. Several new techniques have been developed to support the interactive cutting of deformable thin objects in our framework. A high-resolution visual mesh is bound to a low-resolution mesh by the calculation of geodesic paths. With the visual-collision binding built in the pre-processing phase, high-resolution visual mesh is cut efficiently in a local 2D coordinates system in the simulation phase. After the cutting, the visual-collision binding, visual-simulation and collision-simulation embedding are updated locally. Experimental results show that thin deformable objects can be cut interactively with different resolution of visual, collision and simulation meshes. Compared to the works that use the same mesh for visualization and collision, the resolution of the collision mesh in our method can be tuned to different magnitudes. Compared to the methods that generate collision points by down-sampling the visual mesh, our method can provide the collision points, edges, and triangles with the same approximation property as the original collision mesh. In addition, our framework also supports the simulation of contouring the edge of a meniscus.
Although the cutting with interactive rates has been achieved, the implementation of our framework has not been optimized yet. In future, we will improve the implementation. The visual-collision binding is independent from the simulation meshes. We only tested it with the co-rotational FEM on the hexahedral meshes, which have drawbacks on the boundary alignment. In the future, we will test our method with the tetrahedral meshes and different simulation methods. Self-collision is not considered in our simulation currently, which will be addressed in the future work. In addition, we will extend our works to the general deformable objects.
Supplementary Materials
The following are available online at http://dx.doi.org/10.21979/N9/CN9V0Y, Video S1: videos_cutThin, videos_curvedCut, videos_sepaCut, Model S1: models_cutThin, Code S1: codes_cutThin.
Acknowledgments
We thank anonymous reviewers for their thoughtful and meaningful comments. This project is supported by the Ministry of Education of Singapore Grant MOE2011-T2-1-006.
Author Contributions
The contributions of all of the authors are the same. All of them have worked together to develop the present manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spillmann, J.; Harders, M. Robust Interactive Collision Handling between Tools and Thin Volumetric Objects. IEEE Trans. Vis. Comput. Graph. 2012, 18, 1241–1254. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Westermann, R.; Dick, C. A Survey of Physically Based Simulation of Cuts in Deformable Bodies. Comput. Graph. Forum 2015, 18, 161–187. [Google Scholar] [CrossRef]
- Terzopoulos, D.; Platt, J.; Barr, A.; Fleischer, K. Elastically deformable models. ACM Siggraph Comput. Graph. 1987, 21, 205–214. [Google Scholar] [CrossRef]
- Maciej, K.; Hiroshi, N. Mass spring models with adjustable Poisson’s ratio. Vis. Comput. 2017, 33, 283–291. [Google Scholar]
- Yeung, Y.H.; Crouch, J.; Pothen, A. Interactively Cutting and Constraining Vertices in Meshes Using Augmented Matrices. ACM Trans. Graph. 2016, 35, 1–17. [Google Scholar] [CrossRef]
- Fihai, F.; Florica, M. Position based simulation of solids with accurate contact handling. Comput. Graph. 2017, 69, 12–23. [Google Scholar]
- Berndt, I.; Torchelsen, R.; Maciel, A. Efficient Surgical Cutting with Position-Based Dynamics. IEEE Comput. Graph. Appl. 2017, 38, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Sifakis, E.; Barbic, J. FEM simulation of 3D deformable solids: A practitioner’s guide to theory, discretization and model reduction. In Proceedings of the ACM SIGGRAPH 2012 Courses, Los Angeles, CA, USA, 5–9 August 2012; ACM: New York, NY, USA, 2012; pp. 1–50. [Google Scholar]
- Teschner, M.; Kimmerle, S.; Heidelberger, B. Collision Detection for Deformable Objects. Comput. Graph. Forum 2005, 24, 61–81. [Google Scholar] [CrossRef]
- Cotin, S.; Delingette, H.; Ayache, N. A hybrid elastic model for real-time cutting, deformations, and force feedback for surgery training and simulation. Vis. Comput. 2000, 16, 437–452. [Google Scholar] [CrossRef]
- Courtecuisse, H.; Allard, J.; Kerfriden, P. Real-time simulation of contact and cutting of heterogeneous soft-tissues. Med. Image Anal. 2014, 18, 394–410. [Google Scholar] [CrossRef] [PubMed]
- Bielser, D.; Maiwald, V.A.; Gross, M.H. Interactive Cuts through 3-Dimensional Soft Tissue. Comput. Graph. Forum 1999, 18, 31–38. [Google Scholar] [CrossRef]
- Nienhuys, H.W.; Frank van der Stappen, A. A Surgery Simulation Supporting Cuts and Finite Element Deformation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention—MICCAI 2001, Utrecht, The Netherlands, 14–17 October 2001; Niessen, W., Viergever, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 145–152. [Google Scholar]
- Muller, M.; Gross, M. Interactive virtual materials. Proc. Graph. Interface 2004, 2004, 239–246. [Google Scholar]
- Lindblad, A.; Turkiyyah, G. A physically-based framework for real-time haptic cutting and interaction with 3D continuum models. In Proceedings of the 2007 ACM Symposium on Solid and Physical Modeling, Beijing, China, 4–6 June 2007; ACM: Beijing, China, 2007; pp. 421–429. [Google Scholar]
- Lim, Y.J.; Jin, W.; De, S. On Some Recent Advances in Multimodal Surgery Simulation: A Hybrid Approach to Surgical Cutting and the Use of Video Images for Enhanced Realism. Presence 2007, 16, 563–583. [Google Scholar] [CrossRef]
- Steiemann, D.; Harders, M.; Gross, M.; Szekely, G. Hybrid Cutting of Deformable Solids. In Proceedings of the Virtual Reality Conference, Alexandria, VA, USA, 25–29 March 2006; Volume 2006, pp. 35–42. [Google Scholar]
- Paulus, C.J.; Untereiner, L.; Courtecuisse, H.; Cotin, S. Virtual cutting of deformable objects based on efficient topological operations. Vis. Comput. 2015, 31, 831–841. [Google Scholar] [CrossRef]
- Molno, N.; Bao, Z.; Fedkiw, R. A virtual node algorithm for changing mesh topology during simulation. ACM Trans. Graph. 2004, 23, 385–392. [Google Scholar] [CrossRef]
- Sifakis, E.; Der, K.G.; Fedkiw, R. Arbitrary cutting of deformable tetrahedralized objects. In Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 2–4 August 2007; Eurographics Association: San Diego, CA, USA, 2007; pp. 73–80. [Google Scholar]
- Jia, S.; Zhang, W.; Yu, X. CPU–GPU mixed implementation of virtual node method for real-time interactive cutting of deformable objects using OpenCL. Int. J. Comput. Assist. Radiol. Surg. 2015, 10, 1477–1491. [Google Scholar] [CrossRef] [PubMed]
- Nesme, M.; Kry, P.G.; Jerábková, L.; Faure, F. Preserving topology and elasticity for embedded deformable models. ACM Trans. Graph. 2009, 28, 1–9. [Google Scholar] [CrossRef]
- Jeřábková, L.; Bousquet, G.; Barbier, S.; Faure, F. Volumetric modeling and interactive cutting of deformable bodies. Prog. Biophys. Mol. Biol. 2010, 103, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Dick, C.; Georgii, J.; Westermann, R. A Hexahedral Multigrid Approach for Simulating Cuts in Deformable Objects. IEEE Trans. Vis. Comput. Graph. 2011, 17, 1663–1675. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Dick, C.; Westermann, R. Interactive High-Resolution Boundary Surfaces for Deformable Bodies with Changing Topology. In Proceedings of the Workshop on Virtual Reality Interaction and Physical Simulation, Lyon, France, 5–6 December 2011; The Eurographics Association: Lyon, France, 2011; pp. 29–38. [Google Scholar]
- Wu, J.; Dick, C.; Westermann, R. Efficient Collision Detection for Composite Finite Element Simulation of Cuts in Deformable Bodies. Vis. Comput. 2013, 29, 739–749. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, W.; Yu, X. CPU–GPU Parallel Framework for Real-Time Interactive Cutting of Adaptive Octree-Based Deformable Objects. Comput. Graph. Forum 2017, in press. [Google Scholar] [CrossRef]
- Seiler, M.; Spillmann, J.; Harders, M. A Threefold Representation for the Adaptive Simulation of Embedded Deformable Objects in Contact. J. WSCG 2010, 18, 89–96. [Google Scholar]
- Seiler, M.; Steinemann, D.; Spillmann, J.; Harders, M. Robust interactive cutting based on an adaptive octree simulation mesh. Vis. Comput. 2011, 27, 519–529. [Google Scholar] [CrossRef]
- Seiler, M.; Spillmann, J.; Harders, M. Data-Driven Simulation of Detailed Surface Deformations for Surgery Training Simulators. IEEE Trans. Vis. Comput. Graph. 2014, 20, 1379–1391. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Yan, S.; Qin, H. Real-time dissection of organs via hybrid coupling of geometric metaballs and physics-centric mesh-free method. Vis. Comput. 2016, 32, 1–12. [Google Scholar] [CrossRef]
- Manteaux, P.L.; Sun, W.L.; Faure, F. Interactive detailed cutting of thin sheets. In Proceedings of the 8th ACM SIGGRAPH Conference on Motion in Games, Paris, France, 16–18 November 2015; ACM: Paris, France, 2015; pp. 125–132. [Google Scholar]
- Faure, F.; Duriez, C.; Delingette, H.; Allard, J.; Gilles, B.; Marchesseau, S.; Talbot, H.; Courtecuisse, H.; Bousquet, G.; Peterlik, I.; et al. SOFA: A Multi-Model Framework for Interactive Physical Simulation. In Soft Tissue Biomechanical Modeling for Computer Assisted Surgery; Payan, Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 283–321. [Google Scholar]
- Xin, S.Q.; Wang, G.J. Improving Chen and Han’s algorithm on the discrete geodesic problem. ACM Trans. Graph. 2009, 28, 104. [Google Scholar] [CrossRef]
- Floater, M.S. Mean value coordinates. Comput. Aided Geom. Des. 2003, 20, 19–27. [Google Scholar] [CrossRef]
- Schneider, P.J.; Eberly, D.H. Intersection In 2D. In Geometric Tools for Computer Graphics; Morgan Kaufmann: San Francisco, CA, USA, 2007; pp. 241–284. [Google Scholar]
- Yang, C.; Li, S.; Wang, L. Real-time physical deformation and cutting of heterogeneous objects via hybrid coupling of meshless approach and finite element method. Comput. Anim. Virtual Worlds 2014, 25, 423–435. [Google Scholar] [CrossRef]
- Virtamed ArthroS. Available online: https://www.virtamed.com/en/medical-training-simulators/arthros/ (accessed on 17 November 2017).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).