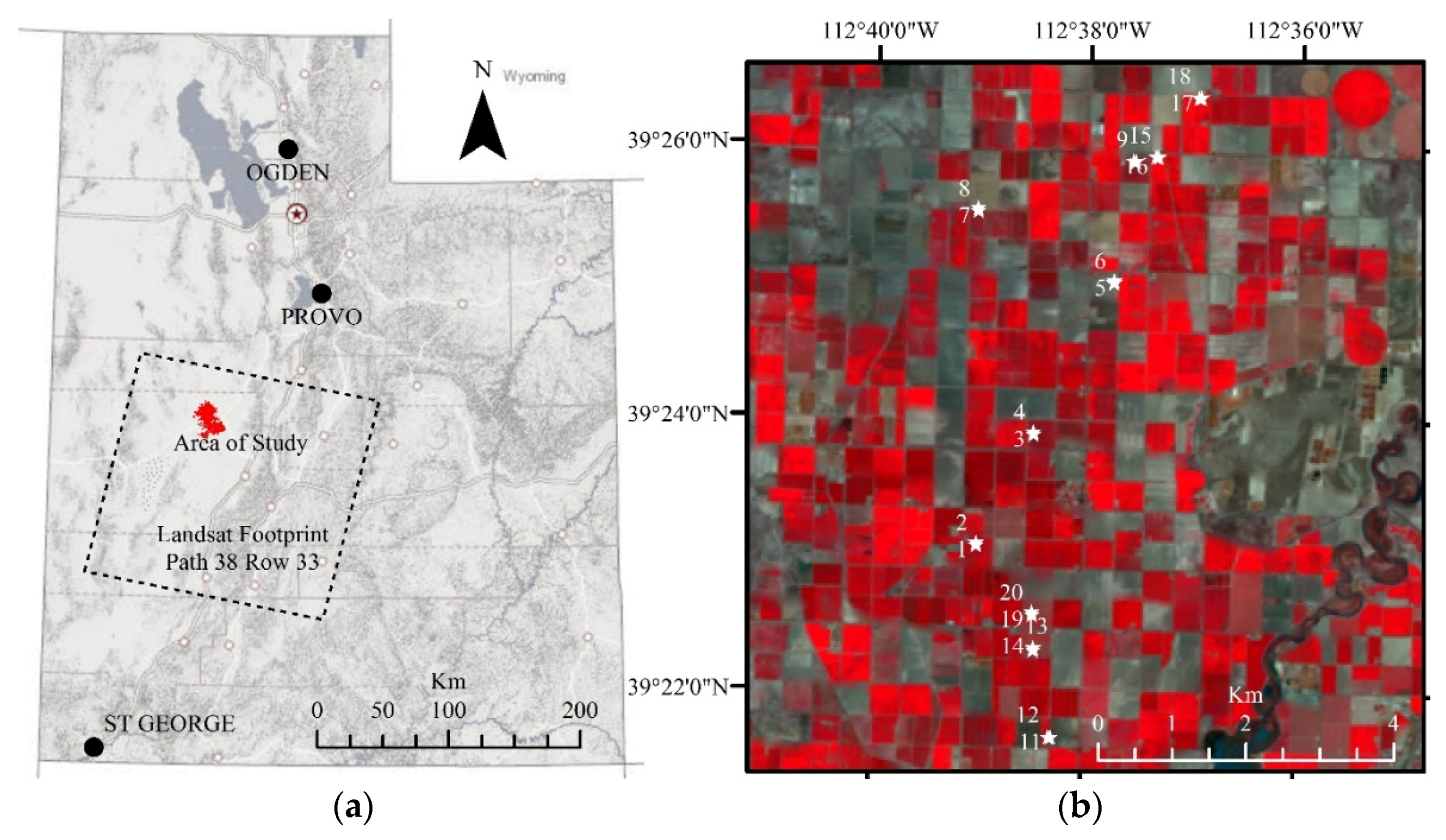
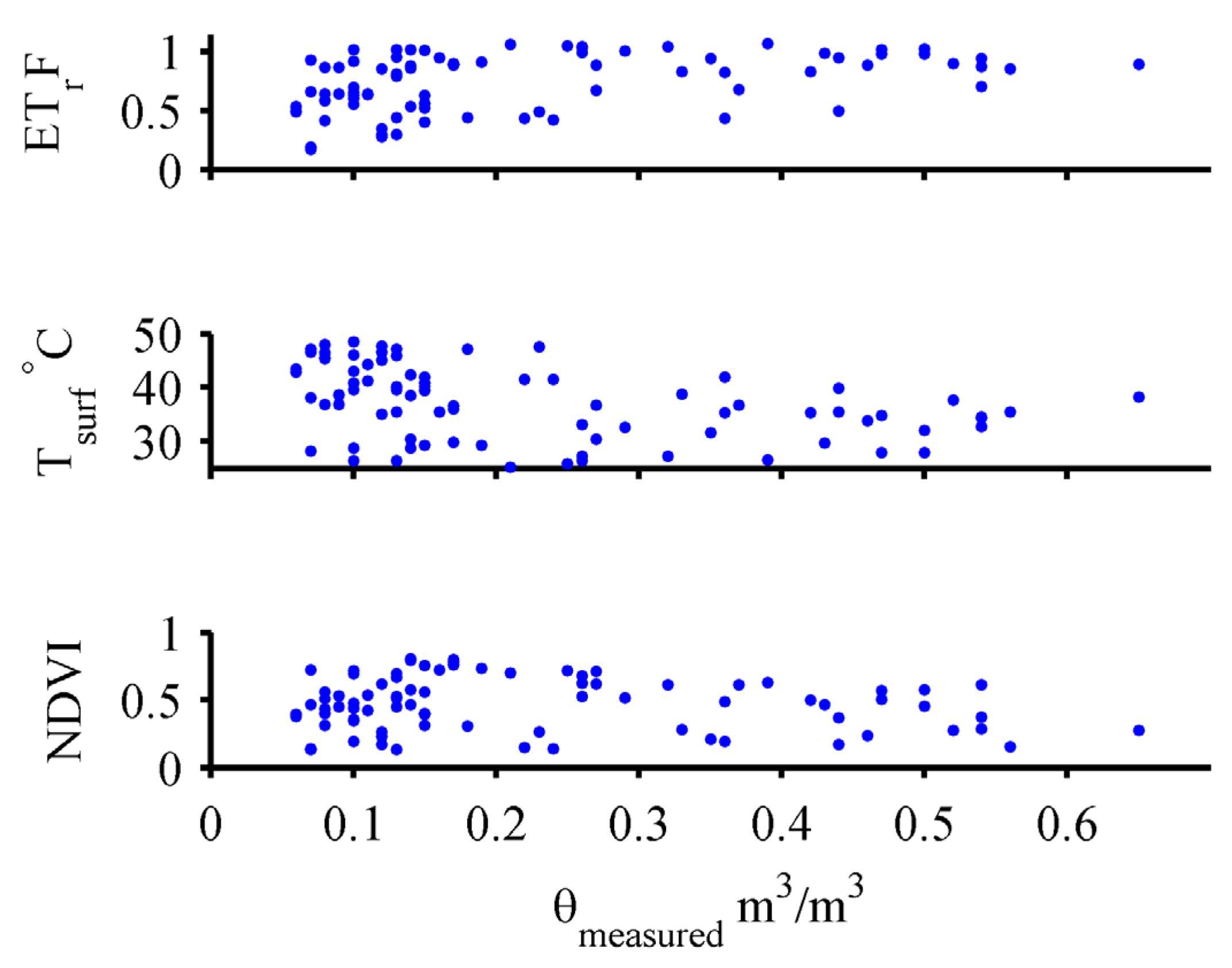
2.1. Soil Moisture Measurement and Estimation
Soil moisture plays a key role in a number of water and energy processes that affect weather, vegetation, and global chemical cycles [
22]. Additionally, spatial distribution of soil moisture is required for determining hydrological processes, including land–atmospheric interactions, rainfall-runoff response, and erosion processes [
23]. In agriculture, estimation of soil moisture content is important for irrigation scheduling, water management, crop growth, yield forecast modeling, forest dynamics, partitioning of sensible, and latent heat fluxes (
i.e., Bowen Ratio), and surface-atmospheric interactions, among others [
7]. Soil moisture is especially important in precision farming because soil moisture content information for any location within or across fields can provide a clear understanding of current soil water condition; thus, producers/irrigators can more effectively direct their sub-field or zonal water management efforts.
The study of soil moisture in agriculture divides the soil profile into two zones: the surface zone, which covers the first five centimeters (two inches) of soil, and the root zone soil moisture (held in the upper 200 cm of soil) [
7,
9]. This differentiation is based on the influence of external factors to each zone. The surface zone becomes a physical interface between the atmosphere and the soil water content, which regulates the rate of soil water evaporation. The root zone is strongly influenced by the initial water content and water fluxes from the phreatic water underneath. Surface soil moisture is physically related to the root zone through diffusion processes [
7].
In general, soil moisture measurements can be described as point measurements, which can be acquired using gravimetric, nuclear, electromagnetic, tensiometric, and hygrometric techniques or embedded sensors, such as time- and frequency-domain reflectometry (TDRs and FDRs) [
7]. These measurements are the most accurate, given the close contact of the sensor to the water-holding medium (soil), and are considered ground truth. Nevertheless, these measurements are restricted in spatial coverage to a small distance from where the sensor is placed. Therefore, installation of a large or dense sensor network would be necessary to monitor large field areas, with the associated inconveniences of operation and maintenance costs, especially in intensively mechanized fields.
Over the past decades, remote sensing technology has shown encouraging results for spatial estimation of soil moisture. Methods applicable on vegetation-covered surfaces have been limited to two basic wavelength bands: thermal infrared and microwave. The use of each band has its special advantages and disadvantages, which often allow the two bands to complement one another.
Microwave techniques, which rely on the large effect of water content on the soil dielectric constant, have the advantage of a wide dynamic range in signal between wet and dry soils. Remote sensing measurements in the microwave region can give useful information about soil moisture, due to the strong contrast between the dielectric constant of dry soil and water (four and 80, respectively) and its effect on microwave emission [
24,
25,
26]. The Soil Moisture Active Passive Satellite Program (SMAP) launched in 2015 was designed to provide direct estimation of surface soil moisture (Product Level 4 Surface and Root Soil Moisture L4_SM) at a resolution of 9 km/pixel by merging active radar information from SMAP with a land surface model [
27,
28]. Nevertheless, due to its spatial resolution, SMAP and other microwave satellites do not provide information at adequate scales (farm, subfield, ~30m/pixel), thus limiting their application to subbasin and larger scales.
Thermal infrared observation of soil moisture has the advantage of requiring a significantly more modest sensing system. A study of irrigated wheat [
29] concluded that useful qualitative soil moisture information could be obtained from vegetation canopy temperature measurements where the soil was completely obscured. In addition, [
30] showed that soil moisture can be most accurately estimated by thermal infrared information in dry or marginal agricultural areas where drought is a frequent threat.
In addition to infrared thermal and microwave sensing, other documented research efforts have estimated surface and root soil moisture using optical remote sensing imagery. [
31,
32,
33] present a relationship between root zone soil moisture conditions and the evaporative fraction (crop coefficient) as a product of the Surface Energy Balance Algorithm for Land (SEBAL), using Landsat and MODIS as sources of remotely-sensed data, as long as soil texture is adequately mapped. [
6,
20,
21] found relationships between surface soil moisture and remote sensing indices and products (such as NDVI; SAVI; LAI), surface temperature, meteorological parameters (precipitation, air temperature), and soil water holding capacity. [
34,
35] found that Landsat reflectance band ratios and cap-tasseled transformations were non-linearly related to surface soil moisture. Vegetation and soil water content have been found to be related to Landsat Normalized Burn Ratio (NBR) [
36], as well as surface albedo [
37] and energy balance components [
38].
Finally, physically-based models for soil moisture estimation, also called land surface models [
25,
39], relate soil water content and surface fluxes. [
20] lists some of these land surface models, which include the Soil-Plant-Atmosphere-Water model [
40,
41], US Department of Agriculture Hydrograph Laboratory [
42,
43], Sacramento Soil Moisture Accounting Model [
44], and soil vegetation atmosphere transfer schemes [
45]. However, the difficulty associated with measuring physical parameters required by these models serves as an impediment for their intensive use in agricultural management [
20]. Research on land surface models has confirmed that soil moisture varies both in space and time because of spatial and temporal variations in precipitation, weather patterns, soil, topographic features, and vegetation characteristics [
39,
46]. Additionally, there is an inherent feedback process between atmosphere and surface soil moisture [
9]. Near-surface atmospheric conditions (for example, humidity and temperature) affect the magnitude and direction of surface fluxes as soil moisture, while surface energy and hydrological fluxes affect atmospheric conditions at the surface. Land surface models have identified wind speed, roughness, and biomass as the three more important parameters that have a uniformly large effect on all of the potential signatures and would, therefore, need to be taken into account in any selected soil moisture algorithm [
30]. For issues of soil moisture scaling, the confounding effects of atmospheric stability, soil properties, vegetation, and topography also need to be considered. Results from these land surface models suggest that it may be possible to combine some simple parameters relating root zone soil moisture, surface runoff, groundwater discharge, the surface energy budget equation, and the effective evaporation efficiency control to describe the equilibrium state of a land surface scheme [
9]. However, issues related to interactions among multiple processes, nonlinearities, and feedbacks across land surfaces, along with relationships among single-sensor measurement, statistical averages, and the definition of spatial heterogeneity within pixels, are yet to be solved.
2.2. The Mapping Evapotranspiration at High Resolution with Internalized Calibration Model (METRIC) Model
The Mapping EvapoTranspiration at high Resolution with Internalized Calibration (METRIC) model is an algorithm developed by [
47] to estimate actual evapotranspiration (ET) for agricultural lands using aerial or satellite imagery that includes a thermal band. METRIC has been validated extensively using the Landsat satellite platform [
3], and continued research and development of applications demonstrate its validity. One main characteristic of METRIC is its specific design for arid, desert areas, such as the Western US and coastal locations in the world where water availability is restricted and improved water management is necessary. METRIC is based on the Surface Energy Balance (SEB) equation [
48,
49], the formulation of which is as follows Equation (1):
where R
n is net radiation at the surface; G is the soil heat flux; H is the sensible heat flux to the air; and LE is the latent heat flux (or actual evapotranspiration: the energy used to evaporate water). Every component of the SEB equation is expressed in Watts/m
2. ET models such as METRIC, SEBAL, and others, make use of the SEB equation to estimate actual evapotranspiration (LE) by solving for the other three components of Equation (1) [
3]. The METRIC model solves for each of the parameters of the SEB equation with the following procedure:
R
n Equation (2) is computed for each pixel using albedo (α) and transmittances computed from short wavebands (Landsat first to fifth and seventh reflectance bands, or ρ
1:ρ
5 and ρ
7), using broadband emissivity (ε
0) computed from the thermal band (Landsat sixth band).
where R
s↓, R
L↑, and R
L↓ are the incoming shortwave, emitted outgoing longwave, and the incoming longwave radiation, respectively (W/m
2) [
48,
50].
Soil heat flux (G, Equation (3)) is predicted using leaf area index (LAI) and surface temperature (T
s), along with the R
n estimates [
51]:
Sensible heat (H, Equation (4)) is calculated from several factors: a single wind speed measurement at the ground, air density (ρ
air), air specific heat (c
p), estimated aerodynamic resistance to heat transport (r
ah), and surface-to-air temperature differences (dT) predicted from thermal infrared radiances.
All computations are made specific to each pixel in the image. Iterative predictions of H are improved using atmospheric stability corrections based on Monin-Obukhov similarity [
51]. Endpoints for H within a satellite image are bounded by known evaporative conditions at key reference (anchor) points [
50]. These reference points include pixels having little or no evaporation (the “hot pixel”) and maximum evapotranspiration (the “cold pixel”). Evapotranspiration is calculated from LE by dividing by the latent heat of vaporization. Further details of the METRIC algorithm are presented in [
3,
47,
50].
2.3. The Relevance Vector Machine
The relevance vector machine (RVM) is a Bayesian learning approach for supervised learning regression and classification tasks developed by [
52] and posteriorly enhanced by [
53]. The RVM is a nonlinear model based on a Bayesian probabilistic treatment to determine a descriptive function based on existing information. The RVM has been extensively used in hydrological, water resources, and Earth image processing [
6,
15,
18,
19,
54,
55], with excellent results.
The development of an RVM model for regression tasks is based on a training set of input vectors
with corresponding targets
. For this training subset, the RVM develops a model of dependency of targets
t on the inputs
x, thus achieving accurate predictions of
t for previously unseen values of
x [
52]. The general form of the RVM function is presented in Equations (5) and (6):
where
w is the model “weights” and
Φ(x) is a basis function where
Φ=[φ
1… φ
M] is the N * M “design” matrix whose columns comprise the complete set of M “basic vectors”,
y or y
n is the RVM predictand, and ε
n is the difference or residual [
53]. The main feature of the RVM is the target function
y Equation (5), which attempts to minimize the difference
ε with respect to
t Equation (6).
Two main assumptions are made to implement the Bayesian probabilistic approach in the RVM: the distribution probability of
t, p(t
n|x
n) is Gaussian distributed, N(t
n|y
n,σ
2), as is the difference
ε, N(0,σ
2). Using these two assumptions, the likelihood of the set
{x, t} can be written as:
To avoid overfitting issues when solving for
w and σ, usually by maximum likelihood methods [
56], a common approach is to impose on them constraints based on an assumed “prior” Gaussian probability distribution Equation (8):
with
α being a vector of Q hyperparameters, individually related to each weight value. From Bayes’ rule, the “posterior” probability over all unknown parameters over the set is:
The first part of Equation (9) can be expressed as p(
w|t, α,σ
2) ∼ N(
m, Σ), where the mean
m and the covariance
Σ are given by:
and
A = diag(
α). Solving for
m and
Σ involves finding the hyperparameters (
α and σ
2) that maximize the second term in Equation (9):
Assuming uniform hyperpriors (thus ignoring p(
α) and p(σ
2)), it is possible to maximize the evidence or likelihood function (the first term in Equation (12)):
Replacing Equations (7) and (8) while solving the integrand gives:
where:
A fast marginal likelihood optimization algorithm is used to obtain the optimal set of hyperparameters α
opt and σ
opt2 (which affects the estimation of
m and
Σ). This optimization algorithm uses an efficient sequential addition and deletion of candidate basis functions described by [
53]. Thus, the basis functions from the training set that are associated with non-zero weights (not deleted during optimization) are called “relevance vectors”.
Given a previously unseen input vector
x′, the predictive distribution for the corresponding target t and the prediction confidence σ
2(
x′) can be computed as:
Therefore, the estimate for
t (
y) for an unseen input data
x′ is:
and the confidence in the prediction
y is determined by the variance of this distribution σ
2(
x′) given by:
This predictive variance is the sum of variances associated with both the noise of the data and the uncertainty (error bar) in the prediction of the weight parameters. The theory behind RVM, its mathematical formulation, likelihood maximization, and optimization procedure are discussed in detail in [
52,
53,
56,
57,
58].