An In-Depth Statistical Analysis of the Pearson Type III Distribution Behavior in Modeling Extreme and Rare Events
Abstract
1. Introduction
- (a)
- arising from the limited length of available recorded data;
- (b)
- associated with parameter estimation;
- (c)
- concerning uncertainties in predicted quantile values.
- -
- choosing the best model (the best statistical distribution according to different parameter estimation methods and certain hydrological and statistical characteristics, a holistic approach being necessary);
- -
- highlighting the errors of the forecasted values, by presenting the behavior of the distribution chosen as the best model, depending on the length of the available data correlated with the statistical peculiarities of the analyzed data.
- (1)
- The presentation of the main statistical–mathematical elements for the estimation of the three parameters of the distribution, related to the five estimation methods, by presenting new and/or improved relationships, so as to facilitate an easy use of the Pearson III distribution;
- (2)
- The presentation of the influence of the variability of the available data lengths (maximum observed annual data) on the behavior of the Pearson III distribution curve in different statistical-mathematical scenarios (theoretical statistical indicators that reflect the entire possible range of hydrological conditions: variability, torrentiality, asymmetry, etc.);
- (3)
- An analysis regarding the stability and robustness of the distribution depending on the parameter estimation method, rigorous criteria being offered in choosing the best parameter estimation method;
- (4)
- A comparative analysis between the most robust estimation method and the approach specific to technical hydrology in Romania, but also specific to other regions that use the same approach.
2. Methods
2.1. Probability Density Function and Cumulative Distribution Function
2.2. Quantile Function
2.3. Parameter Estimation
2.3.1. Method of Ordinary Method (MOM)
2.3.2. Linear Moments (L-Moments)
- (a)
- For uniform variation on a logarithmic scale, the function’s argument was logarithmized, and a polynomial function was used;
- (b)
- For non-uniform logarithmic variation, a rational function—the ratio of two polynomials—was applied, sometimes simplifying to a polynomial.
2.3.3. High-Order Linear Moments (First Level LH-Moments)
2.3.4. Maximum Likelihood Estimation (MLE)
- -
- Objective function:
- -
- Logarithm of the objective function:
2.3.5. Least Squares Method (LSM)
2.4. The Theoretical Framework Regarding the Influence of the Analyzed Data Lengths on the Behavior of the Pearson III Distribution
3. Case Studies
3.1. Description of the Analyzed Rivers Morphometric Information
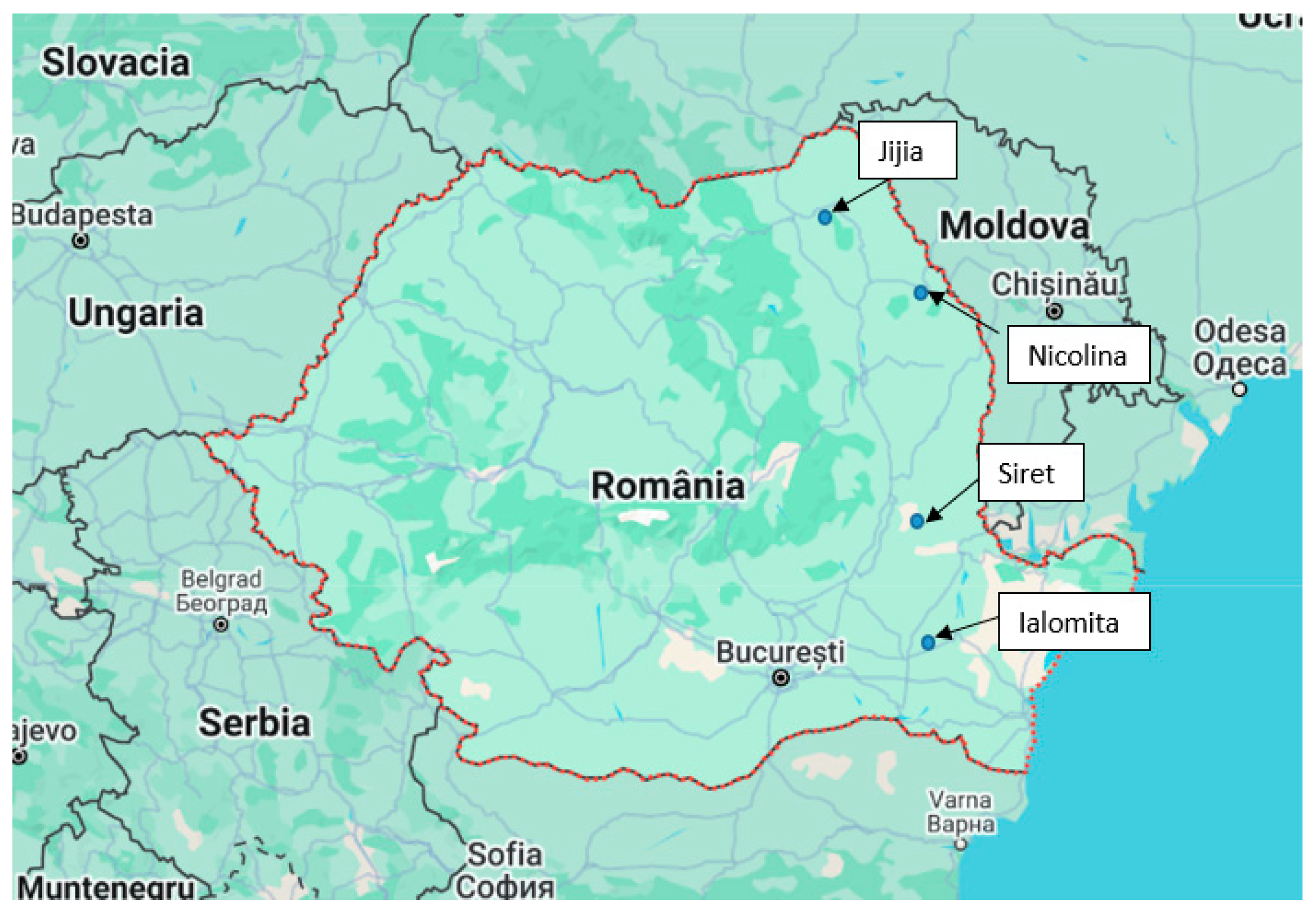
3.1.1. Ialomita River
3.1.2. Siret River
3.1.3. Jijia and Nicolina Rivers
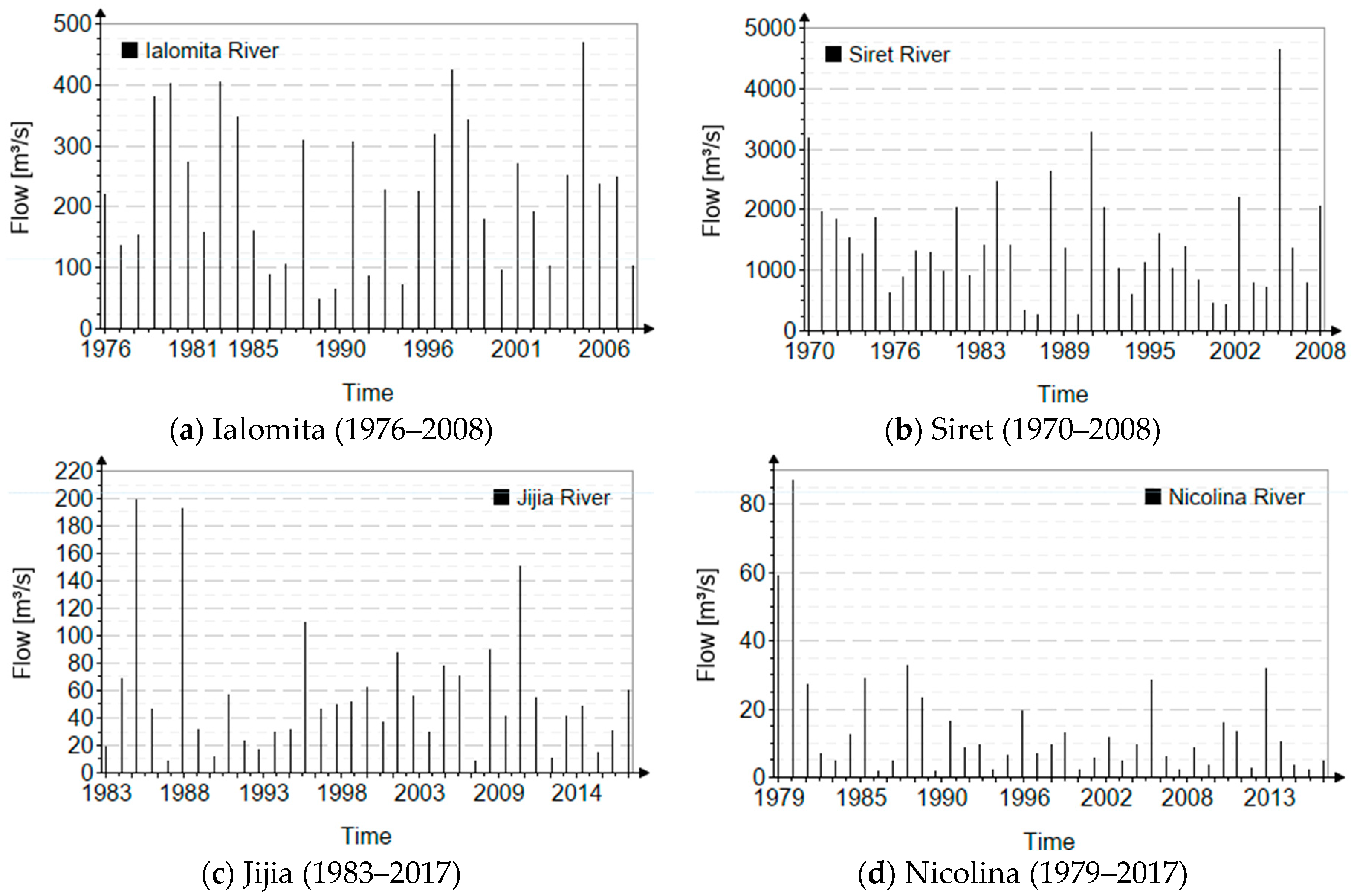
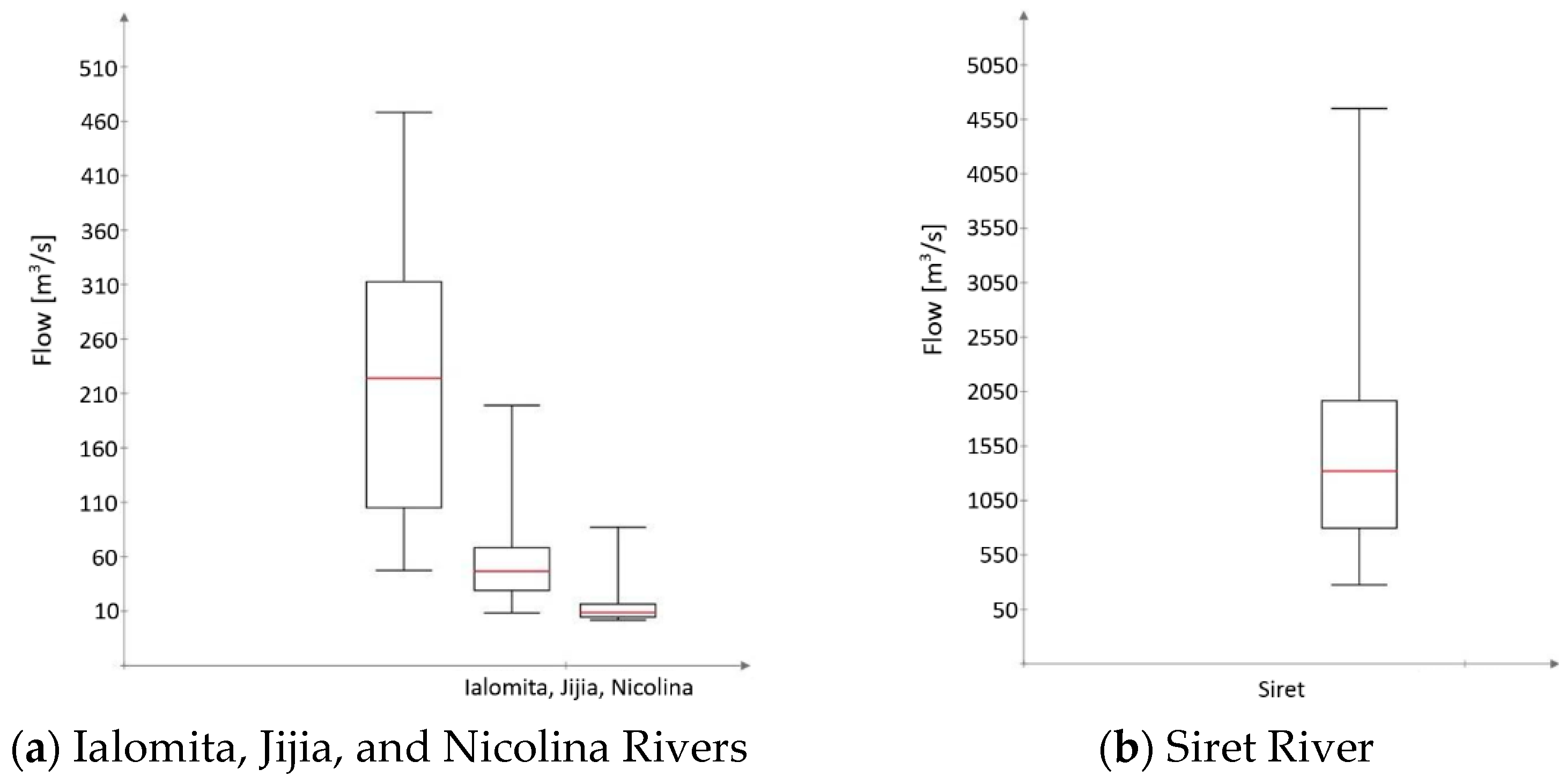
3.2. Time Series of Maximum Annual Flows
4. Results and Discussions
- (1)
- It is recommended to abandon the MOM, especially to use it while using the artificial choice of skewness. In this way, the strong subjective character that currently dominates the frequency analysis of maximum flows is eliminated. This also presents the disadvantage of some important theoretical biases, especially for short data series;
- (2)
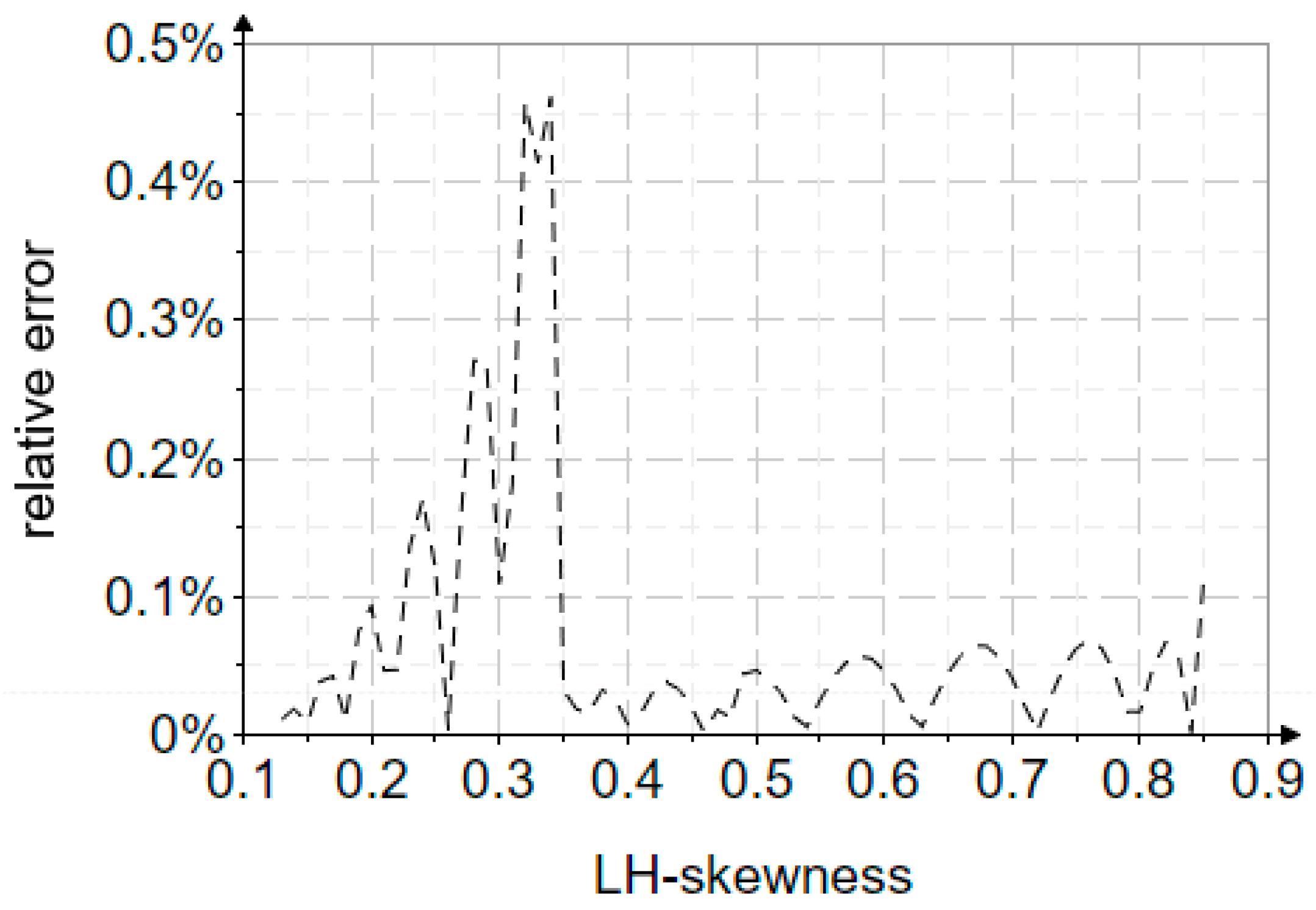
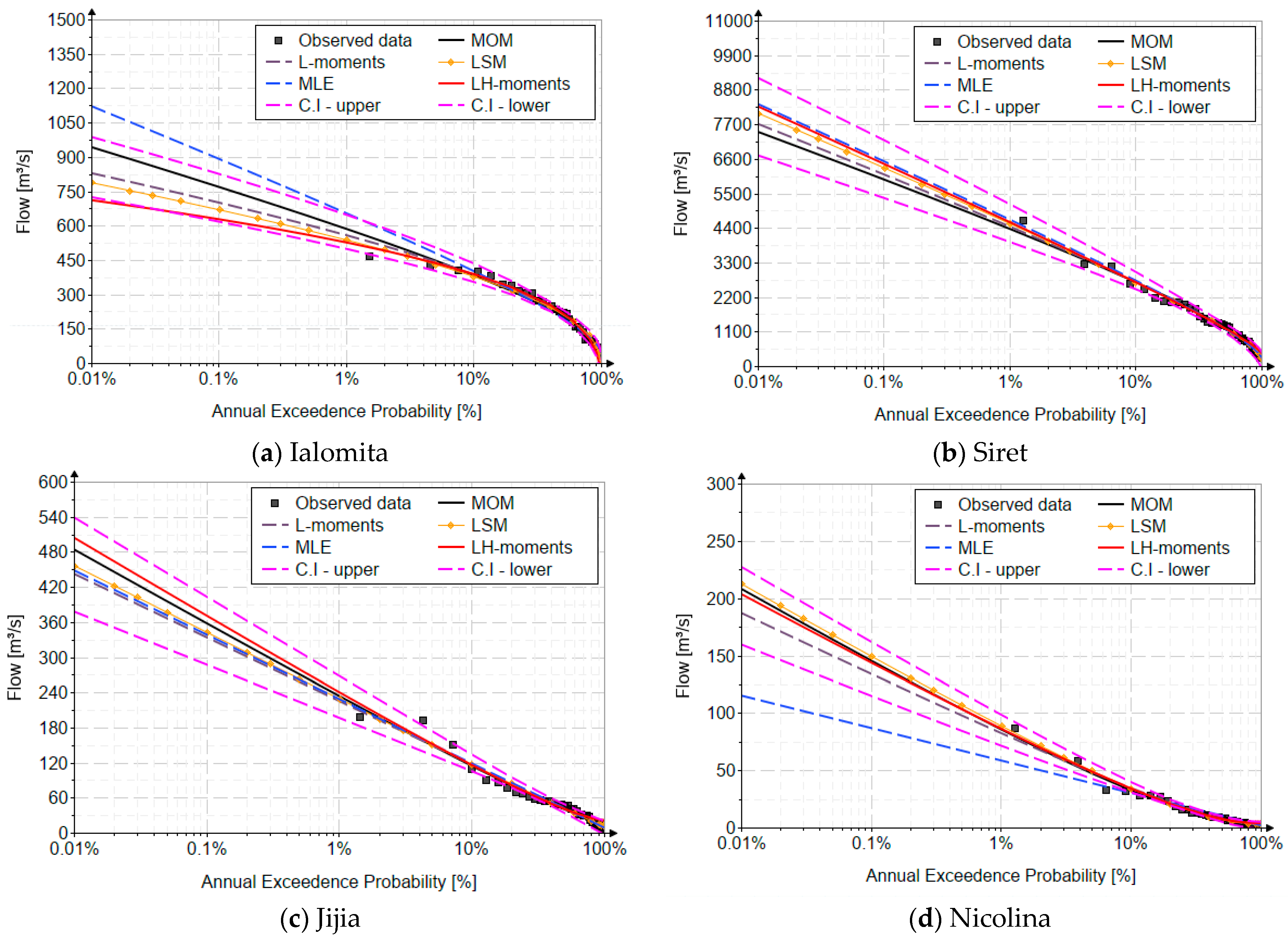
- It is recommended to use the PE3 distribution using the L-moments method, and only after a pre-selection stage based on the L-skewness and L-kurtosis values and interdependence diagrams. It is very important that, in the second stage, the biases of the distribution depending on the length of the observed data should be highlighted. For example, a short data series (25 years) for Nicolina resulted in biases of up to 31% for the 0.01% quantile. Longer series (50–80 years) reduced biases significantly, with errors under 5% for the Ialomita and Siret Rivers. Draw the confidence interval that includes these theoretical uncertainties.
5. Conclusions
6. Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FFA | flood frequency analysis |
| MOM | the method of ordinary moments |
| L-moments | the method of linear moments |
| LH-moments | the higher-order linear moments |
| expected value; arithmetic mean | |
| standard deviation | |
| coefficient of variation | |
| coefficient of skewness; skewness | |
| coefficient of kurtosis; kurtosis | |
| linear moments | |
| coefficient of variation based on the L-moments method | |
| coefficient of skewness based on the L-moments method | |
| coefficient of kurtosis based on the L-moments method | |
| central moments (with MOM) | |
| Gamma.INV | returns the inverse cumulative probability distribution for the Gamma distribution. In Mathcad Prime 6, this has the expression: In R, this has the expression: In Python, |
Appendix A. The Frequency Factors
Appendix B. The Coefficients of Approximate Functions
| p [%] | a | b | c | d | e |
|---|---|---|---|---|---|
| 0.01 | 3.686550 | 2.281056 | 0.013205 | −0.013575 | 0.000803 |
| 0.1 | 3.070699 | 1.507230 | −0.033443 | −0.006751 | 0.000475 |
| 0.5 | 2.562916 | 0.991395 | −0.058405 | −0.002505 | 0.000277 |
| 1 | 2.315597 | 0.777929 | −0.066149 | −0.000805 | 0.000200 |
| 2 | 2.044704 | 0.571450 | −0.071458 | 0.000860 | 0.000127 |
| 3 | 1.872511 | 0.454755 | −0.073224 | 0.001854 | 0.000085 |
| 5 | 1.637225 | 0.313358 | −0.073871 | 0.003209 | 0.000026 |
| 10 | 1.273993 | 0.135936 | −0.071982 | 0.005620 | −0.000095 |
| 20 | 0.832988 | −0.014687 | −0.066714 | 0.009667 | −0.000384 |
| 30 | 0.517983 | −0.091708 | −0.054094 | 0.011752 | −0.000631 |
| 40 | 0.254280 | −0.149822 | −0.027557 | 0.010103 | −0.000665 |
| 50 | 0.011164 | −0.196026 | 0.010608 | 0.004788 | −0.000449 |
| 60 | −0.233431 | −0.219943 | 0.052175 | −0.002735 | −0.000052 |
| 70 | −0.501809 | −0.203095 | 0.086693 | −0.010514 | 0.000416 |
| 80 | −0.826925 | −0.115902 | 0.101447 | −0.016375 | 0.000831 |
| 90 | −1.292445 | 0.118758 | 0.069412 | −0.016337 | 0.000986 |
| 95 | −1.681344 | 0.390422 | 0.002582 | −0.009442 | 0.000734 |
| p [%] | a | b | c |
|---|---|---|---|
| 0.01 | 6.5887103 | 23.4428109 | 16.3451916 |
| 0.1 | 5.4766362 | 15.550908 | 9.0973213 |
| 0.5 | 4.5657126 | 10.2188263 | 4.7799626 |
| 1 | 4.1236633 | 7.9914789 | 3.1782715 |
| 2 | 3.6405222 | 5.8225468 | 1.7747976 |
| 3 | 3.3339368 | 4.5887346 | 1.0633868 |
| 5 | 2.9156637 | 3.0827323 | 0.3030661 |
| 10 | 2.271564 | 1.1610927 | −0.4339022 |
| 20 | 1.4916395 | −0.5255067 | −0.7232427 |
| 30 | 0.9293178 | −1.3084367 | −0.6123297 |
| 40 | 0.4488931 | −1.6907365 | −0.367109 |
| 50 | −0.0000983 | −1.8093098 | −0.0613219 |
| 60 | −0.4490487 | −1.6969142 | 0.2698602 |
| 70 | −0.9293476 | −1.3202017 | 0.5929909 |
| 80 | −1.4914544 | −0.5409791 | 0.8375167 |
| 90 | −2.2711199 | 1.1488238 | 0.71406 |
| 95 | −2.9152375 | 3.0846318 | −0.0297187 |
| p [%] | a | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|
| 0.01 | 138.4454 | −2465.1403 | 17,892.3121 | −63,752.6912 | 120,214.5111 | −114,563.9925 | 43,558.7960 |
| 0.1 | 52.6867 | −889.8140 | 6536.4462 | −23,385.6306 | 44,343.2094 | −42,529.1934 | 16,305.2083 |
| 0.5 | 8.5283 | −84.4050 | 710.0442 | −2635.3321 | 5249.2959 | −5311.1613 | 2175.4185 |
| 1 | −2.6280 | 115.7398 | −752.6486 | 2601.1523 | −4681.3181 | 4213.7614 | −1475.0655 |
| 2 | −6.4948 | 179.9173 | −1244.9649 | 4403.9528 | −8196.9042 | 7690.8402 | −2858.8140 |
| 3 | −4.9899 | 146.9756 | −1028.6089 | 3668.7798 | −6898.5532 | 6550.0621 | −2473.1341 |
| 5 | −0.3988 | 54.1598 | −384.5506 | 1408.4120 | −2727.0609 | 2675.4512 | −1052.8528 |
| 10 | 3.5216 | −33.0494 | 230.5684 | −804.8975 | 1478.4454 | −1366.3202 | 491.2543 |
| 20 | 0.6022 | 2.4211 | −26.1560 | 73.8725 | −93.8615 | 27.9077 | 16.2937 |
| 30 | −0.4434 | 8.8140 | −79.7955 | 288.7791 | −549.5813 | 515.7971 | −185.8401 |
| 40 | −0.5276 | −1.5686 | −6.0962 | 38.2458 | −109.5742 | 142.8124 | −65.6908 |
| 50 | −0.8662 | −7.3388 | 41.8998 | −140.8366 | 240.5612 | −191.2167 | 56.2460 |
| 60 | −1.6664 | −5.0086 | 35.7882 | −134.5152 | 262.9802 | −242.9896 | 84.4331 |
| 70 | −2.7716 | 1.9929 | −2.3618 | −7.3744 | 48.9529 | −71.1804 | 31.7503 |
| 80 | −3.9611 | 8.1831 | −33.0043 | 110.2760 | −184.7844 | 147.2649 | −45.4138 |
| 90 | −5.1185 | 6.7527 | 1.2190 | 17.2169 | −89.7448 | 117.2605 | −49.4125 |
| 95 | −5.8786 | 0.3138 | 79.04519 | −250.3293 | 338.36417 | −214.3331 | 51.2532 |
Appendix C. General Relations for Determining Linear Moments
- : the first linear moment (the arithmetic mean)
- : second linear moment
- : third linear moment
- : fourth linear moment
- : represents L-CV (coefficient of L-variation)
- : represents L-Cs (L-skewness)
- : represents L-Ck (L-kurtozis)
References
- Montanari, A.; Merz, B.; Blöschl, G. HESS Opinions: The Sword of Damocles of the Impossible Flood. Hydrol. Earth Syst. Sci. 2024, 28, 2603–2615. [Google Scholar] [CrossRef]
- Bulletin 17B Guidelines for Determining Flood Flow Frequency; Hydrology Subcommittee, Interagency Advisory Committee on Water Data; U.S. Department of the Interior, U.S. Geological Survey, Office of Water Data Coordination: Reston, VA, USA, 1981.
- Bulletin 17C Guidelines for Determining Flood Flow Frequency; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 2017.
- World Meteorological Organization. (WMO-No.100) 2018 Guide to Climatological Practices; WMO: Geneva, Switzerland, 2018. [Google Scholar]
- EM 1110-2-1415 Hydrologic Frequency Analysis, Engineering and Design; Department of the Army U.S. Army Corps of Engineers: Washington, DC, USA, 1993.
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press LLC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Gubareva, T.S.; Gartsman, B.I. Estimating Distribution Parameters of Extreme Hydrometeorological Characteristics by L-Moment Method. Water Resour. 2010, 37, 437–445. [Google Scholar] [CrossRef]
- Anghel, C.G. Revisiting the Use of the Gumbel Distribution: A Comprehensive Statistical Analysis Regarding Modeling Extremes and Rare Events. Mathematics 2024, 12, 2466. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-moments: Analysis and Estimation of Distributions using Linear, Combinations of Order Statistics. J. R. Statist. Soc. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Citakoglu, H.; Demir, V.; Haktanir, T. L-MOMENTLER YÖNTEMİYLE KARADENİZ’E DÖKÜLEN AKARSULARA AİT YILLIK ANLIK MAKSİMUM AKIM DEĞERLERİNİN BÖLGESEL FREKANS ANALİZİ. Ömer Halisdemir Üniversitesi Mühendislik Bilim. Derg. 2017, 6, 571–580. [Google Scholar] [CrossRef][Green Version]
- Diaconu, C.; Serban, P. Syntheses and Hydrological Regionalization; Technical Publishing House: Bucharest, Romania, 1994. [Google Scholar]
- STAS 4068/1962; Maximum Water Discharges and Volumes, Determination of Maximum Water Discharges and Volumes of Watercourses. The Romanian Standardization Institute: Bucharest, Romania, 1962.
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; MCGraw-Hill, Inc.: New York, NY, USA, 1988; ISBN 007-010810-2. [Google Scholar]
- Mandru, R.; Ioanitoaia, H. Ameliorative Hydrology; Agro-Silvica Publishing House: Bucharest, Romania, 1962. [Google Scholar]
- Bejenaru, G.; Castravet, T.; Dilan, V. Hydrological Calculations; Print Caro Publishing House: Chisinau, Moldova, 2020. [Google Scholar]
- Teodorescu, I.; Filotti, A.; Chiriac, V.; Ceausescu, V.; Florescu, A. Water Management; Ceres Publishing House: Bucharest, Romania, 1973. [Google Scholar]
- Ciupak, M.; Ozga-Zieliński, B.; Tokarczyk, T.; Adamowski, J. A Probabilistic Model for Maximum Rainfall Frequency Analysis. Water 2021, 13, 2688. [Google Scholar] [CrossRef]
- Nwaogazie, I.L.; Sam, M.G. Probability and non-probability rainfall intensity-duration-frequency modeling for port-harcourt metropolis, Nigeria. Int. J. Hydro. 2019, 3, 66–75. [Google Scholar] [CrossRef]
- Ye, L.; Hanson, L.S.; Ding, P.; Wang, D.; Vogel, R.M. The probability distribution of daily precipitation at the point and catchment scales in the United States. Hydrol. Earth Syst. Sci. 2018, 22, 6519–6531. [Google Scholar] [CrossRef]
- World Meteorological Organization. (WMO-No.1029) 2008 Manual on Low-Flow Estimation and Prediction; Operational Hydrology Report No. 50; WHO: Geneva, Switzerland, 2008. [Google Scholar]
- Institute of Hydrology. (IH) 1992 Low Flow Estimation in the United Kingdom; Report No. 108; Hobbs the Printers Ltd.: Hampshire, UK, 1992. [Google Scholar]
- UNESCO. Methods of Computation of Low Streamflow, Studies and Reports in Hydrology; UNESCO: Paris, France, 1982; ISBN 92-102013-7. [Google Scholar]
- Loganathan, G.V.; Kuo, C.Y.; McCormick, T.C. Frequency Analysis of Low Flow. Nord. Hydrol. 1985, 16, 105–128. [Google Scholar] [CrossRef][Green Version]
- Matalas, N.C. Probability Distribution of Low Flows. Statistical Studies in Hydrology; Geological Survey, United States Government Printing Office: Washington, DC, USA, 1963.
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability Weighted Moments: Definition and Relation to Parameters of Several Distributions Expressable in Inverse Form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy-Based Parameter Estimation in Hydrology; Springer Science + Business Media: Dordrecht, The Netherlands, 1998; ISBN 978-90-481-5089-2/978-94-017-1431-0. [Google Scholar] [CrossRef]
- Md Sharwar, M.; Park, B.-J.; Jeong, B.-Y.; Park, J.-S. LH-Moments of Some Distributions Useful in Hydrology. Commun. Stat. Appl. Methods 2009, 16, 647–658. [Google Scholar]
- Wang, Q.J. LH moments for statistical analysis of extreme events. Water Resour. Res. 1997, 33, 2841–2848. [Google Scholar] [CrossRef]
- Domma, F.; Condino, F. Use of the Beta-Dagum and Beta-Singh-Maddala distributions for modeling hydrologic data. Stoch. Environ. Res. Risk Assess. 2017, 31, 799–813. [Google Scholar] [CrossRef]
- Houghton, J.C. Birth of a parent: The Wakeby distribution for modeling flood flows. Water Resour. Res. 1978, 14, 1105–1109. [Google Scholar] [CrossRef]
- Wang, Q.J. Approximate Goodness-of-Fit Tests of fitted generalized extreme value distributions using LH moments. Water Resour. Res. 1998, 34, 3497–3502. [Google Scholar] [CrossRef]
- Meshgi, A.; Khalili, D. Comprehensive evaluation of regional flood frequency analysis by L- and LH-moments. II. Development of LH-moments parameters for the generalized Pareto and generalized logistic distributions. Stoch. Environ. Res. Risk Assess. 2009, 23, 137–152. [Google Scholar] [CrossRef]
- Meshgi, A.; Khalili, D. Comprehensive evaluation of regional flood frequency analysis by L- and LH-moments. I. A re-visit to regional homogeneity. Stoch. Environ. Res. Risk Assess. 2009, 23, 119–135. [Google Scholar] [CrossRef]
- Bhuyan, A.; Borah, M.; Kumar, R. Regional Flood Frequency Analysis of North-Bank of the River Brahmaputra by Using LH-Moments. Water Resour. Manag. 2010, 24, 1779–1790. [Google Scholar] [CrossRef]
- Nouri Gheidari, M.H. Comparisons of the L- and LH-moments in the selection of the best distribution for regional flood frequency analysis in Lake Urmia Basin. Civ. Eng. Environ. Syst. 2013, 30, 72–84. [Google Scholar] [CrossRef]
- Deka, S.; Borah, M.; Kakaty, S.C. Statistical analysis of annual maximum rainfall in North-East India: An application of LH-moments. Theory Appl. Climatol. 2011, 104, 111–122. [Google Scholar] [CrossRef]
- Zakaria, Z.; Suleiman, J.; Mohamad, M. Rainfall frequency analysis using LH2212moments approach: A case of Kemaman Station, Malaysia. Int. J. Eng. Technol. 2018, 7, 107–110. [Google Scholar] [CrossRef]
- Bora, D.; Borah, M.; Bhuyan, A. Regional analysis of maximum rainfall using L-moment and LH-moment: A comparative case study for the northeast India. Mausam 2017, 68, 451–462. [Google Scholar] [CrossRef]
- Anghel, C.G.; Ilinca, C. Predicting Flood Frequency with the LH-Moments Method: A Case Study of Prigor River, Romania. Water 2023, 15, 2077. [Google Scholar] [CrossRef]
- Anghel, C.; Craciun, C.; Cornea, D.; Ilinca, C. Exploring the Applicability and Insights of the Pearson Type III Distribution in Flood Frequency Analysis. Rev. Romana De Ing. Civila/Rom. J. Civ. Eng. 2024, 15, 256–268. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Applied Mathematics Series; United States Department of Commerce, National Bureau of Standards: New York, NY, USA; Dover Publications: Washington, DC, USA, 1983; Volume 55, ISBN 978-0-486-61272-0.
- Crooks, G.E. Field Guide to Continuous Probability Distributions; Berkeley Institute for Theoretical Science: Berkeley, CA, USA, 2019. [Google Scholar]
- Voda, V.G. New Statistical Models in Durability Analysis; Academy Pubication House: Bucharest, Romania, 1980. (In Romanian) [Google Scholar]
- Polosin, V.G. Information entropy of the generalized beta distribution. ITM Web. Conf. 2024, 59, 02009. [Google Scholar] [CrossRef]
- Polosin, V.G. Shape measures of generalized beta distributions. J. Phys. Conf. Ser. 2021, 2094, 022009. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P. Generalized Beta Distribution of the Second Kind for Flood Frequency Analysis. Entropy 2017, 19, 254. [Google Scholar] [CrossRef]
- STAS 4068/2-87; Annual Probabilities of Maximum Flows and Volumes Under Normal and Special Operating Conditions. The Romanian Standardization Institute: Bucharest, Romania, 1987.
- STAS 4273-83; Hydrotechnical Constructions, Classification in the Importance Class. The Romanian Standardization Institute: Bucharest, Romania, 1983.
- The Romanian Water Classification Atlas, Part I–Morpho-Hydrographic Data on the Surface Hydrographic Network; Ministry of the Environment: Bucharest, Romania, 1992.
- Machiwal, D.; Jha, M. Hydrologic Time Series Analysis: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Khajehali, M.; Safavi, H.R.; Nikoo, M.R.; Najafi, M.R.; Alizadeh-Sh, R. A copula-based multivariate flood frequency analysis under climate change effects. Sci. Rep. 2025, 15, 146. [Google Scholar] [CrossRef]
- Anaraki, M.V.; Farzin, S.; Mousavi, S.F.; Karami, H. Uncertainty Analysis of Climate Change Impacts on Flood Frequency by Using Hybrid Machine Learning Methods. Water Resour. Manag. 2021, 35, 199–223. [Google Scholar] [CrossRef]
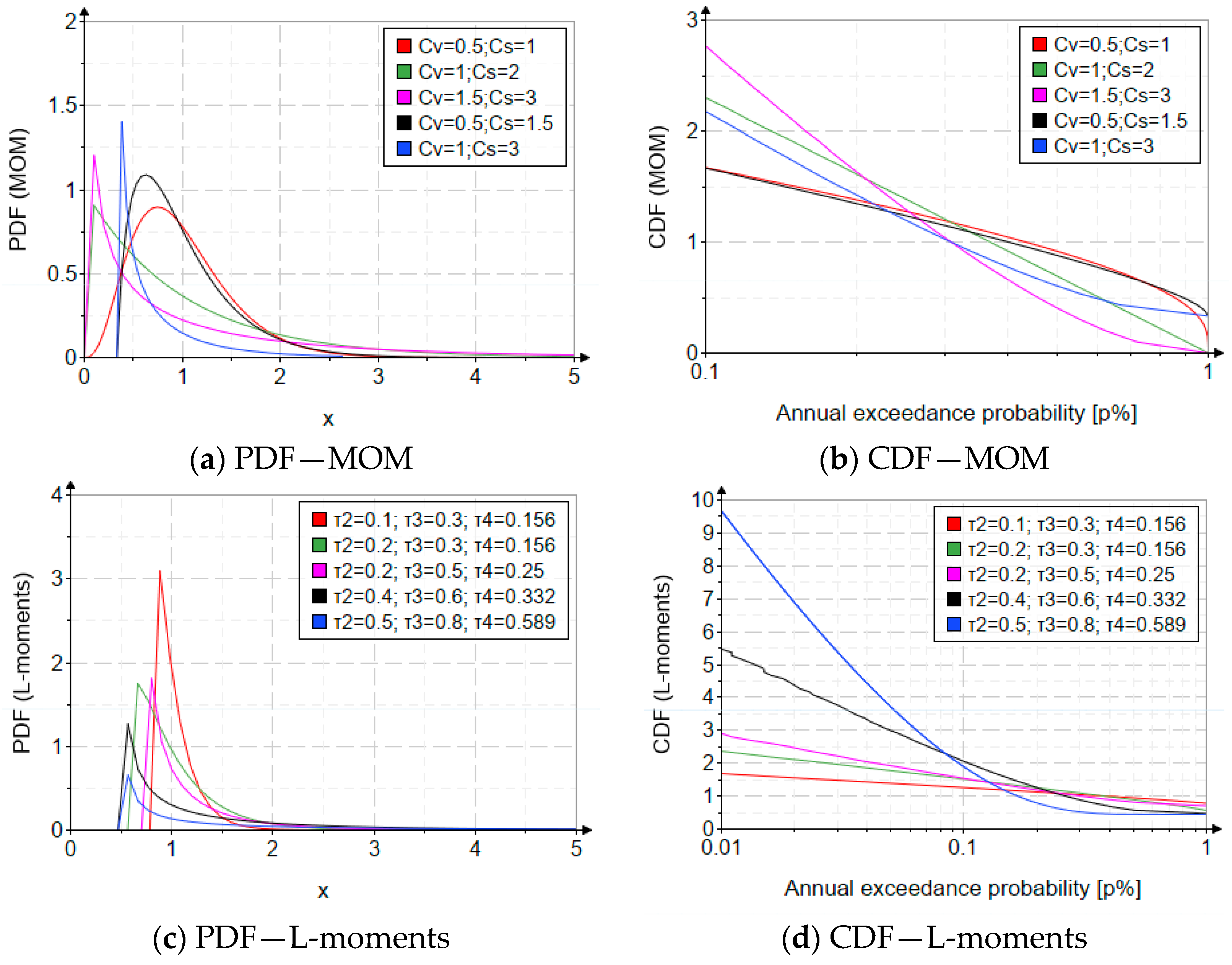
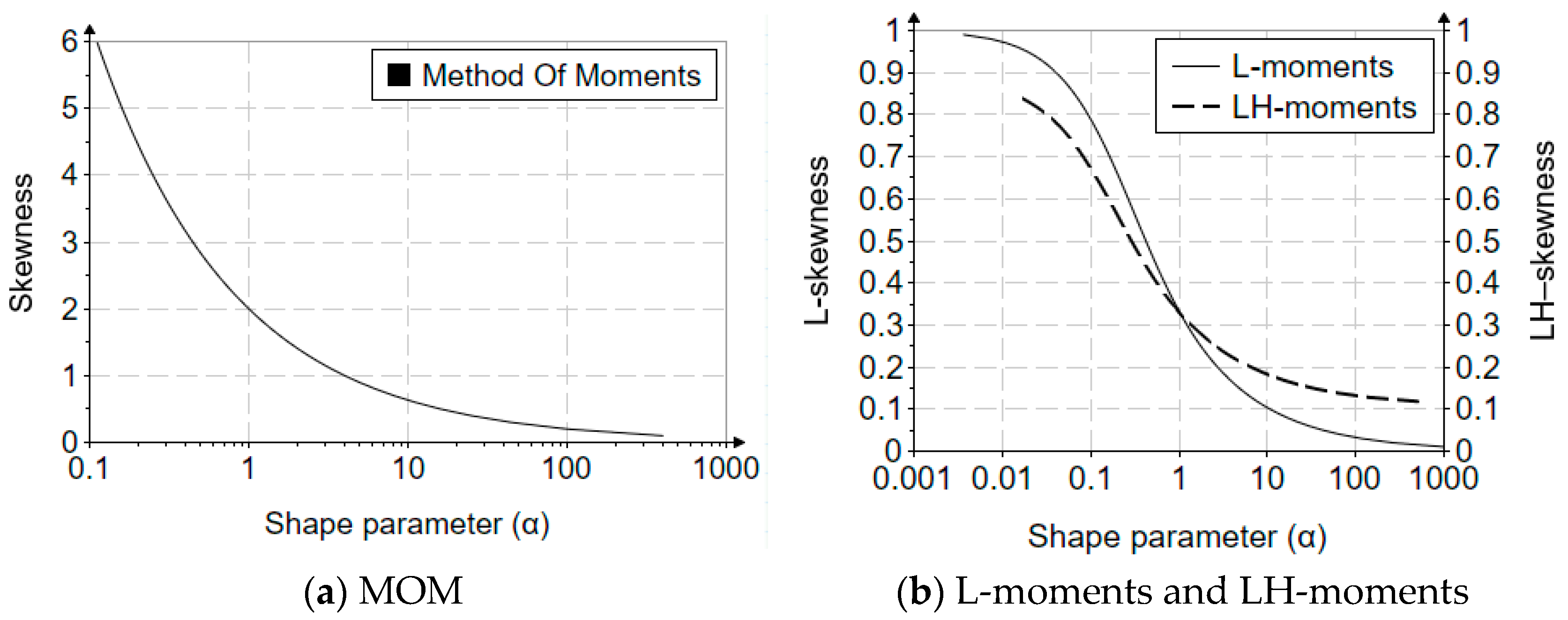

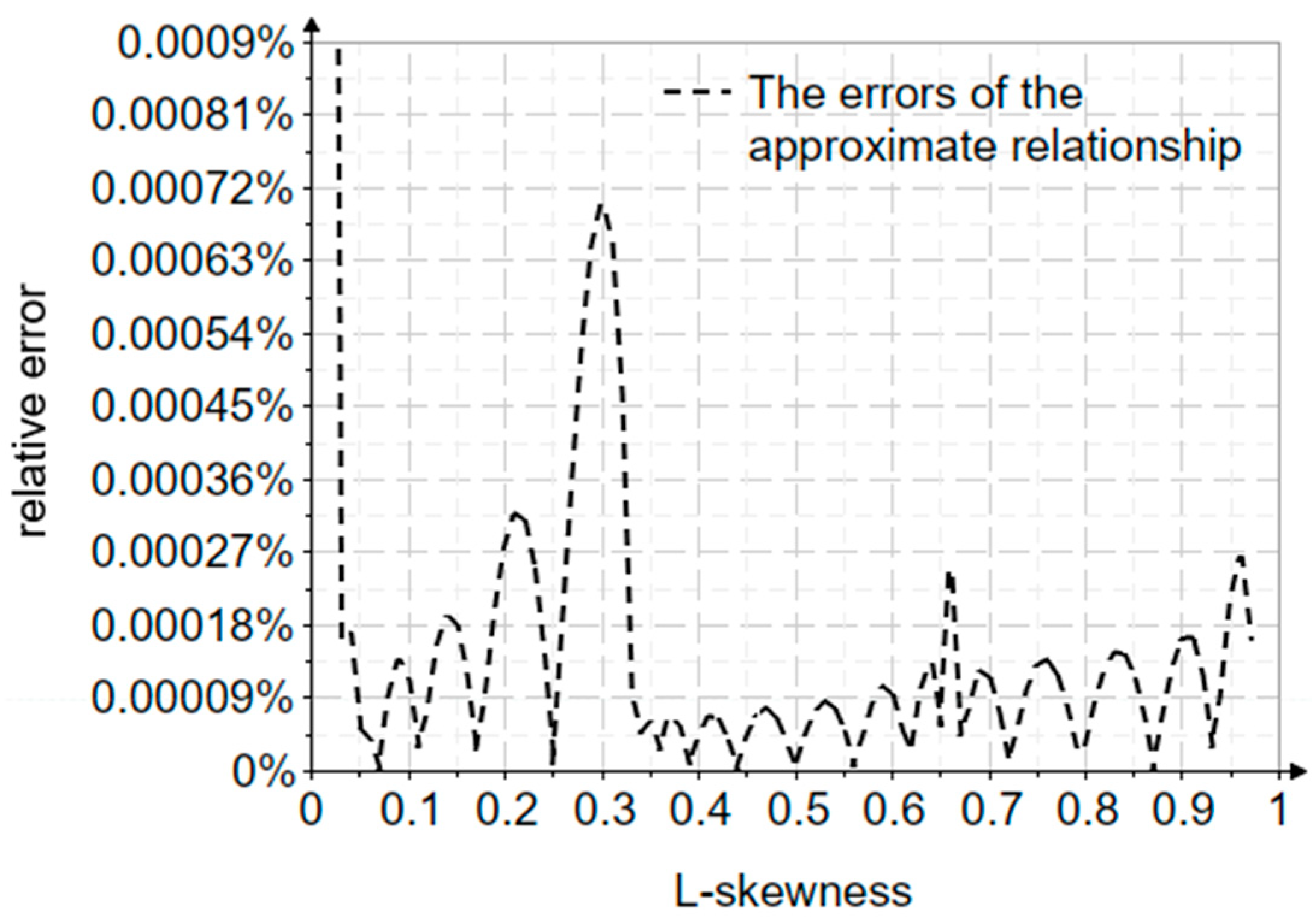
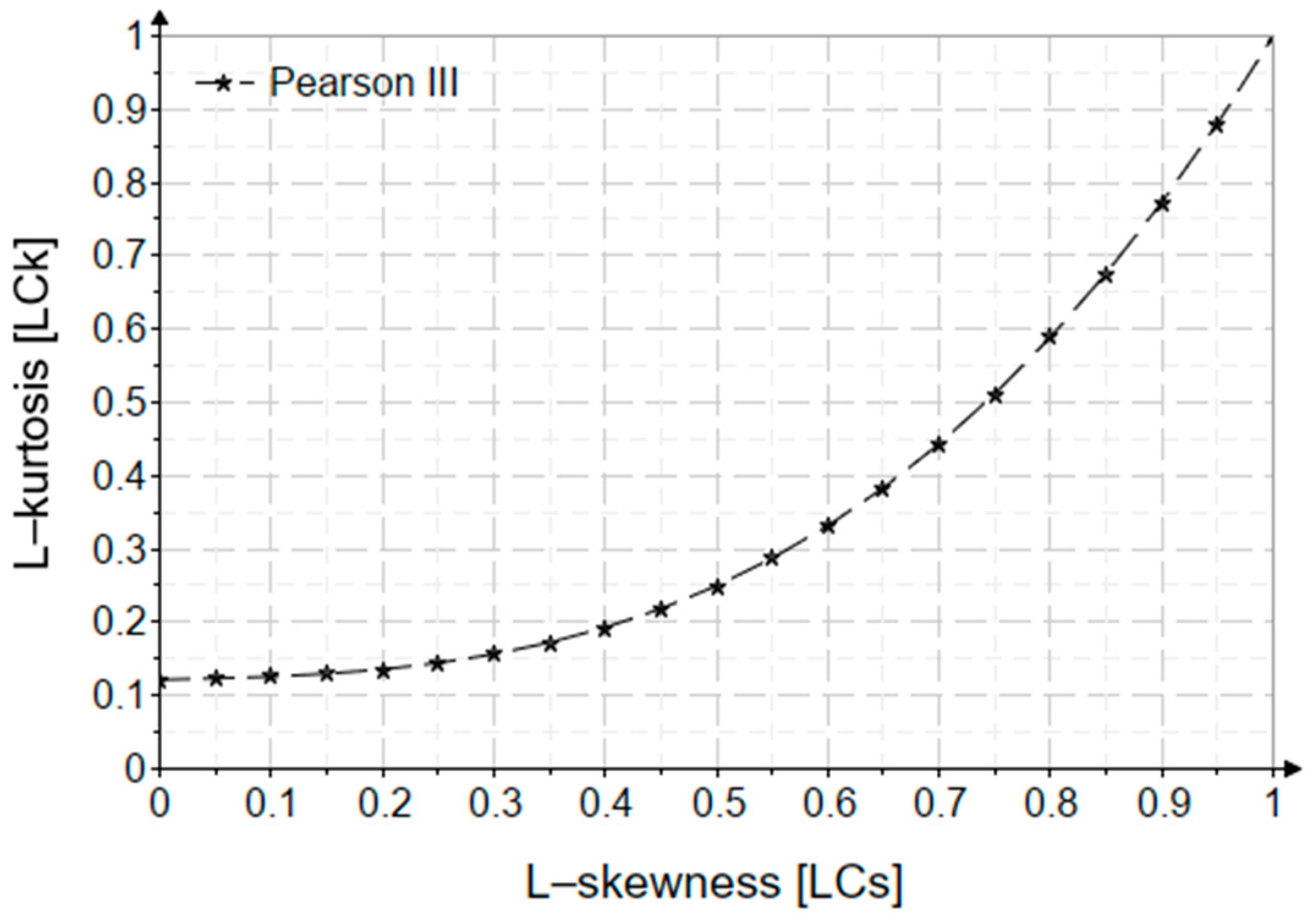


| Nr. Crt. | New Elements |
|---|---|
| 1 | New relationships for estimating the shape parameter for the L-moments method. |
| 2 | New relationships for estimating the shape parameter for the LH-moments method. |
| 3 | The flexibility of the density function, using the L-moments approach. |
| 4 | Variation graphs of the shape, scale, and position parameters for a wide range of values of the coefficient of variation and skewness. |
| 5 | New relationships for estimating the frequency factor for the MOM (including widening the range of annual exceedance probabilities). |
| 6 | New relationships for estimating the frequency factor for the L-moments method (including widening the range of annual exceedance probabilities). |
| 7 | New relationships for estimating the frequency factor for the LH-moments method (including widening the range of annual exceedance probabilities). |
| 8 | The Pearson III distribution’s theoretical biases, both for parameters and quantiles, for an extended field of statistical indicators particular to the L-moments and MOM approaches. |
| 9 | A comparative analysis to determine the optimal empirical probability for both the distribution and the parameter estimation method. |
| 10 | Rigorous recommendations regarding the applicability of this distribution. |
| Statistical indicators—MOM | |||||
| Parameters | ; | ; | ; | ; | ; |
| 4 | 1 | 0.444 | 1.778 | 0.444 | |
| 0.25 | 1 | 2.25 | 0.38 | 1.5 | |
| 0 | 0 | 0 | 0.333 | 0.333 | |
| Statistical indicators—L-moments | |||||
| Parameters | ; | ; | ; | ; | ; |
| 1.233 | 1.233 | 0.422 | 0.266 | 0.093 | |
| 0.176 | 0.352 | 0.708 | 1.998 | 6.013 | |
| 0.783 | 0.565 | 0.701 | 0.468 | 0.438 | |
| Record Length | Parameters | Quantiles | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.01% | 0.10% | 0.50% | 1% | ||||||
| 1000 | 4 | 0.5 | 1 | 1 | 3.978 | 3.266 | 2.744 | 2.511 | |
| 0.25 | |||||||||
| 0 | |||||||||
| 80 | 4.896 | 0.497 | 0.904 | 0.999 | 3.85 | 3.182 | 2.69 | 2.469 | |
| 0.225 | |||||||||
| −0.101 | |||||||||
| 50 | 5.272 | 0.496 | 0.871 | 0.998 | 3.804 | 3.151 | 2.67 | 2.454 | |
| 0.216 | |||||||||
| −0.14 | |||||||||
| 25 | 6.142 | 0.494 | 0.807 | 0.996 | 3.712 | 3.09 | 2.63 | 2.421 | |
| 0.199 | |||||||||
| −0.224 | |||||||||
| Record Length | Parameters | Quantiles | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.01% | 0.10% | 0.50% | 1% | ||||||
| 1000 | 1.778 | 0.5 | 1.5 | 1 | 4.546 | 3.617 | 2.955 | 2.665 | |
| 0.375 | |||||||||
| 0.333 | |||||||||
| 80 | 2.229 | 0.495 | 1.34 | 0.998 | 4.324 | 3.475 | 2.865 | 2.597 | |
| 0.331 | |||||||||
| 0.26 | |||||||||
| 50 | 2.408 | 0.493 | 1.289 | 0.997 | 4.249 | 3.426 | 2.834 | 2.573 | |
| 0.317 | |||||||||
| 0.234 | |||||||||
| 25 | 2.81 | 0.489 | 1.193 | 0.994 | 4.103 | 3.33 | 2.771 | 2.523 | |
| 0.29 | |||||||||
| 0.18 | |||||||||
| Record Length | Parameters | Quantiles | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.01% | 0.1% | 0.5% | 1% | ||||||
| 1000 | 1 | 0.5 | 2 | 1 | 5.105 | 3.954 | 3.149 | 2.803 | |
| 0.5 | |||||||||
| 0.5 | |||||||||
| 80 | 1.295 | 0.492 | 1.757 | 0.998 | 4.763 | 3.739 | 3.017 | 2.704 | |
| 0.431 | |||||||||
| 0.439 | |||||||||
| 50 | 1.406 | 0.489 | 1.687 | 0.997 | 4.654 | 3.669 | 2.973 | 2.67 | |
| 0.411 | |||||||||
| 0.419 | |||||||||
| 25 | 1.65 | 0.481 | 1.557 | 0.993 | 4.446 | 3.533 | 2.884 | 2.601 | |
| 0.372 | |||||||||
| 0.379 | |||||||||
| Record Length | Parameters | Quantiles | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.01% | 0.10% | 0.50% | 1% | |||||||
| 1000 | 10.71 | 1 | 0.182 | 0.1 | 0.126 | 2.564 | 2.224 | 1.969 | 1.852 | |
| 0.094 | ||||||||||
| −0.009 | ||||||||||
| 80 | 10.69 | 1 | 0.173 | 0.10009 | 0.129 | 2.575 | 2.233 | 1.976 | 1.858 | |
| 0.095 | ||||||||||
| −0.016 | ||||||||||
| 50 | 10.68 | 0.999 | 0.174 | 0.10014 | 0.131 | 2.582 | 2.238 | 1.98 | 1.861 | |
| 0.095 | ||||||||||
| −0.02 | ||||||||||
| 25 | 10.65 | 0.998 | 0.176 | 0.10027 | 0.134 | 2.598 | 2.251 | 1.989 | 1.869 | |
| 0.097 | ||||||||||
| −0.03 | ||||||||||
| Record Length | Parameters | Quantiles | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.01% | 0.1% | 0.5% | 1% | |||||||
| 1000 | 0.422 | 1 | 0.67 | 0.5 | 0.25 | 17.21 | 12.17 | 8.732 | 7.29 | |
| 2.373 | ||||||||||
| −0.001 | ||||||||||
| 80 | 0.410 | 0.991 | 0.675 | 0.50523 | 0.254 | 17.38 | 12.27 | 8.786 | 7.325 | |
| 2.411 | ||||||||||
| −0.002 | ||||||||||
| 50 | 0.410 | 0.985 | 0.678 | 0.50827 | 0.257 | 17.48 | 12.32 | 8.817 | 7.346 | |
| 2.433 | ||||||||||
| −0.002 | ||||||||||
| 25 | 0.39 | 0.971 | 0.687 | 0.5161 | 0.263 | 17.74 | 12.48 | 8.898 | 7.399 | |
| 2.492 | ||||||||||
| −0.004 | ||||||||||
| Record Length | Parameters | Quantiles | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.01% | 0.1% | 0.5% | 1% | |||||||
| 1000 | 0.041 | 1 | 0.949 | 0.9 | 0.773 | 109 | 63.08 | 34.36 | 23.52 | |
| 24.6 | ||||||||||
| −0.001 | ||||||||||
| 80 | 0.04 | 0.92 | 0.956 | 0.91246 | 0.799 | 112.9 | 64.18 | 33.99 | 22.74 | |
| 26.373 | ||||||||||
| −0.00131 | ||||||||||
| 50 | 0.03 | 0.877 | 0.96 | 0.91945 | 0.814 | 115.7 | 65.03 | 33.81 | 22.27 | |
| 27.452 | ||||||||||
| −0.0013 | ||||||||||
| 25 | 0.02 | 0.771 | 0.969 | 0.93653 | 0.85 | 124.7 | 67.79 | 33.28 | 20.87 | |
| 31.299 | ||||||||||
| −0.00137 | ||||||||||
| Multiplication Coefficient, | Coefficient of Variation, | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.3 | 0.5 | 0.7 | 0.9 | 1.1 | 1.3 | 1.5 | 1.7 | 2 | |
| Record length, n = 80 | ||||||||||
| 2 | 0.3 | 1.7 | 3.2 | 4.9 | 6.6 | 8.3 | 10 | 12 | 14 | 16 |
| 3 | 0.4 | 2.5 | 4.9 | 7.5 | 10 | 13 | 16 | 19 | 21 | 25 |
| 4 | 0.6 | 3.4 | 6.7 | 10 | 14 | 18 | 21 | 25 | 28 | 33 |
| Record length, n = 50 | ||||||||||
| 2 | 0.5 | 2.3 | 4.4 | 6.5 | 8.7 | 11 | 13 | 15 | 18 | 21 |
| 3 | 0.6 | 3.4 | 6.5 | 9.8 | 13 | 17 | 20 | 23 | 26 | 31 |
| 4 | 0.9 | 4.5 | 8.8 | 14 | 18 | 23 | 27 | 31 | 35 | 41 |
| Record length, n = 25 | ||||||||||
| 2 | 0.7 | 3.6 | 6.7 | 9.8 | 13 | 16 | 19 | 22 | 25 | 29 |
| 3 | 1.0 | 5.2 | 9.7 | 14 | 19 | 24 | 28 | 33 | 37 | 42 |
| 4 | 1.4 | 6.8 | 13 | 19 | 26 | 31 | 37 | 42 | 47 | 54 |
| L-Skewness, | Coefficient of L-Variation, | ||||
|---|---|---|---|---|---|
| 0.1 | 0.3 | 0.5 | 0.7 | 0.9 | |
| Record length, n = 80 | |||||
| 0 | −0.38 | −0.58 | −0.65 | −0.68 | −0.70 |
| 0.2 | −0.44 | −0.63 | −0.68 | −0.71 | −0.73 |
| 0.4 | −0.65 | −0.85 | −0.90 | −0.93 | −0.94 |
| 0.6 | −0.99 | −1.18 | −1.23 | −1.25 | −1.26 |
| 0.8 | −1.85 | −2.04 | −2.08 | −2.10 | −2.11 |
| 0.9 | −3.53 | −3.73 | −3.77 | −3.79 | −3.80 |
| Record length, n = 50 | |||||
| 0 | −0.505 | −0.773 | −0.865 | −0.911 | −0.939 |
| 0.2 | −0.582 | −0.836 | −0.916 | −0.955 | −0.978 |
| 0.4 | −0.879 | −1.14 | −1.212 | −1.246 | −1.265 |
| 0.6 | −1.352 | −1.612 | −1.677 | −1.706 | −1.723 |
| 0.8 | −2.583 | −2.846 | −2.906 | −2.932 | −2.947 |
| 0.9 | −5.057 | −5.344 | −5.406 | −5.433 | −5.448 |
| Record length, n = 25 | |||||
| 0 | −1.283 | −1.964 | −2.198 | −2.316 | −2.387 |
| 0.2 | −1.465 | −2.105 | −2.306 | −2.405 | −2.463 |
| 0.4 | −2.261 | −2.9 | −3.116 | −3.203 | −3.253 |
| 0.6 | −3.751 | −4.475 | −4.655 | −4.736 | −4.783 |
| 0.8 | −8.018 | −8.837 | −9.021 | −9.102 | −9.148 |
| 0.9 | −18.09 | −19.119 | −19.339 | −19.435 | −19.489 |
| River | Length [km] | Average Stream Slope [‰] | Sinuosity Coefficient [−] | Average Altitude, [m] | Catchments Area, [km2] |
|---|---|---|---|---|---|
| Ialomita | 417 | 1.5 | 1.88 | 327 | 10,350 |
| Siret | 559 | 1.7 | 1.86 | 515 | 42,890 |
| Jijia | 275 | 1.0 | 1.45 | 152 | 5757 |
| Nicolina | 20 | 16 | 1.37 | 138 | 177 |
| River | Number of Records (n) | Hydrometric Station | MOM | |||
|---|---|---|---|---|---|---|
| [−] | [m3/s] | [−] | [−] | |||
| Ialomita | 33 | Tandarei | 2 | 224 | 0.527 | 0.33 |
| Siret | 39 | Lungoci | 2 | 1443 | 0.634 | 1.41 |
| Jijia | 35 | Vladeni | 3 | 56.1 | 0.824 | 1.85 |
| Nicolina | 39 | Iasi | 3 | 14.1 | 1.193 | 2.80 |
| River | L-Moments Method | LH-Moments Method | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [m3/s] | [m3/s] | [m3/s] | [m3/s] | [−] | [−] | [−] | [m3/s] | [m3/s] | [m3/s] | [m3/s] | [−] | [−] | [−] | |
| Ialomita | 224 | 68.6 | 6.13 | 1.69 | 0.306 | 0.089 | 0.025 | 293 | 56.1 | 5.22 | 2.30 | 0.191 | 0.093 | 0.041 |
| Siret | 1443 | 490 | 112 | 90.6 | 0.339 | 0.228 | 0.185 | 1932 | 451 | 135 | 89.9 | 0.233 | 0.299 | 0.199 |
| Jijia | 56.1 | 23.2 | 7.86 | 6.01 | 0.414 | 0.338 | 0.259 | 79.4 | 23.3 | 9.25 | 6.13 | 0.294 | 0.396 | 0.263 |
| Nicolina | 14.1 | 7.55 | 3.60 | 2.22 | 0.536 | 0.477 | 0.294 | 21.6 | 8.36 | 3.88 | 2.34 | 0.386 | 0.464 | 0.280 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anghel, C.-G.; Ianculescu, D. An In-Depth Statistical Analysis of the Pearson Type III Distribution Behavior in Modeling Extreme and Rare Events. Water 2025, 17, 1539. https://doi.org/10.3390/w17101539
Anghel C-G, Ianculescu D. An In-Depth Statistical Analysis of the Pearson Type III Distribution Behavior in Modeling Extreme and Rare Events. Water. 2025; 17(10):1539. https://doi.org/10.3390/w17101539
Chicago/Turabian StyleAnghel, Cristian-Gabriel, and Dan Ianculescu. 2025. "An In-Depth Statistical Analysis of the Pearson Type III Distribution Behavior in Modeling Extreme and Rare Events" Water 17, no. 10: 1539. https://doi.org/10.3390/w17101539
APA StyleAnghel, C.-G., & Ianculescu, D. (2025). An In-Depth Statistical Analysis of the Pearson Type III Distribution Behavior in Modeling Extreme and Rare Events. Water, 17(10), 1539. https://doi.org/10.3390/w17101539







