Differentiated Optimization Policies for Water–Energy–Food Resilience Security: Empirical Evidence Based on Shanxi Province and the GWR Model
Abstract
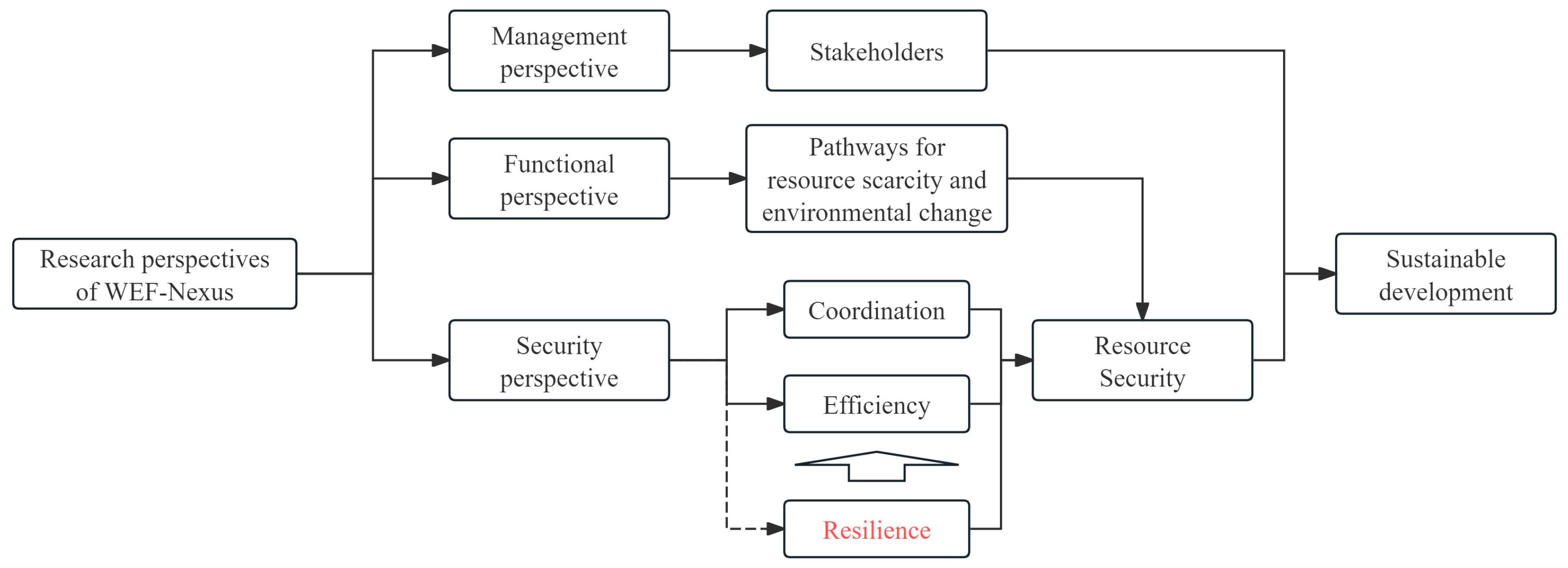
1. Introduction
2. Research Area and Data Sources
2.1. Overview of the Research Area
2.2. Data Sources and Processing
3. Description of Research Variables
3.1. Core Variables
3.2. Influencing Factor Variables
4. Method
4.1. Global Spatial Autocorrelation Analysis
4.2. Geographically Weighted Regression (GWR) Model
4.2.1. Description of the GWR Model
4.2.2. Screening of Explanatory Variables (Based on Exploratory Regression Method)
4.2.3. Construction of the GWR Model
4.3. Nature Breaks Method
5. Results and Analysis
5.1. Global Spatial Autocorrelation Test Results and Analysis
5.2. Results and Analysis of the Regression Parameters
5.2.1. Robustness Test of the Model
5.2.2. Analysis of the Effect of Data Fitting for Variables
5.2.3. Analysis of the Optimization Degree of the Model
5.3. Results and Analysis of GWR Model Regression (Year 2022)
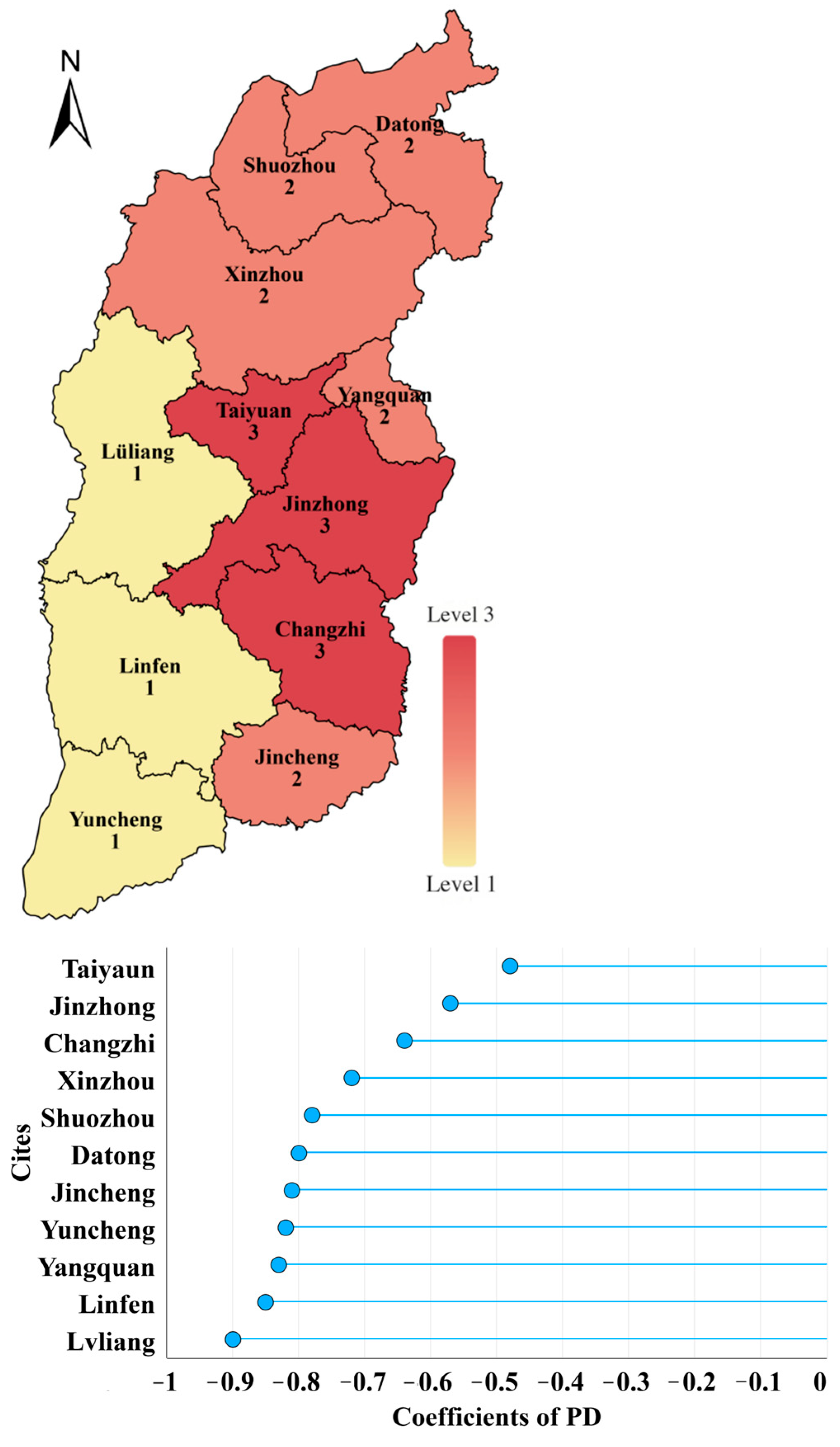
5.3.1. Analysis of Regional Differences in Population Density (PD) Regression Coefficients
5.3.2. Analysis of Regional Differences in Technology Innovation (TI) Regression Coefficients
5.3.3. Analysis of Regional Differences in Industrial Structure (IS) Regression Coefficients
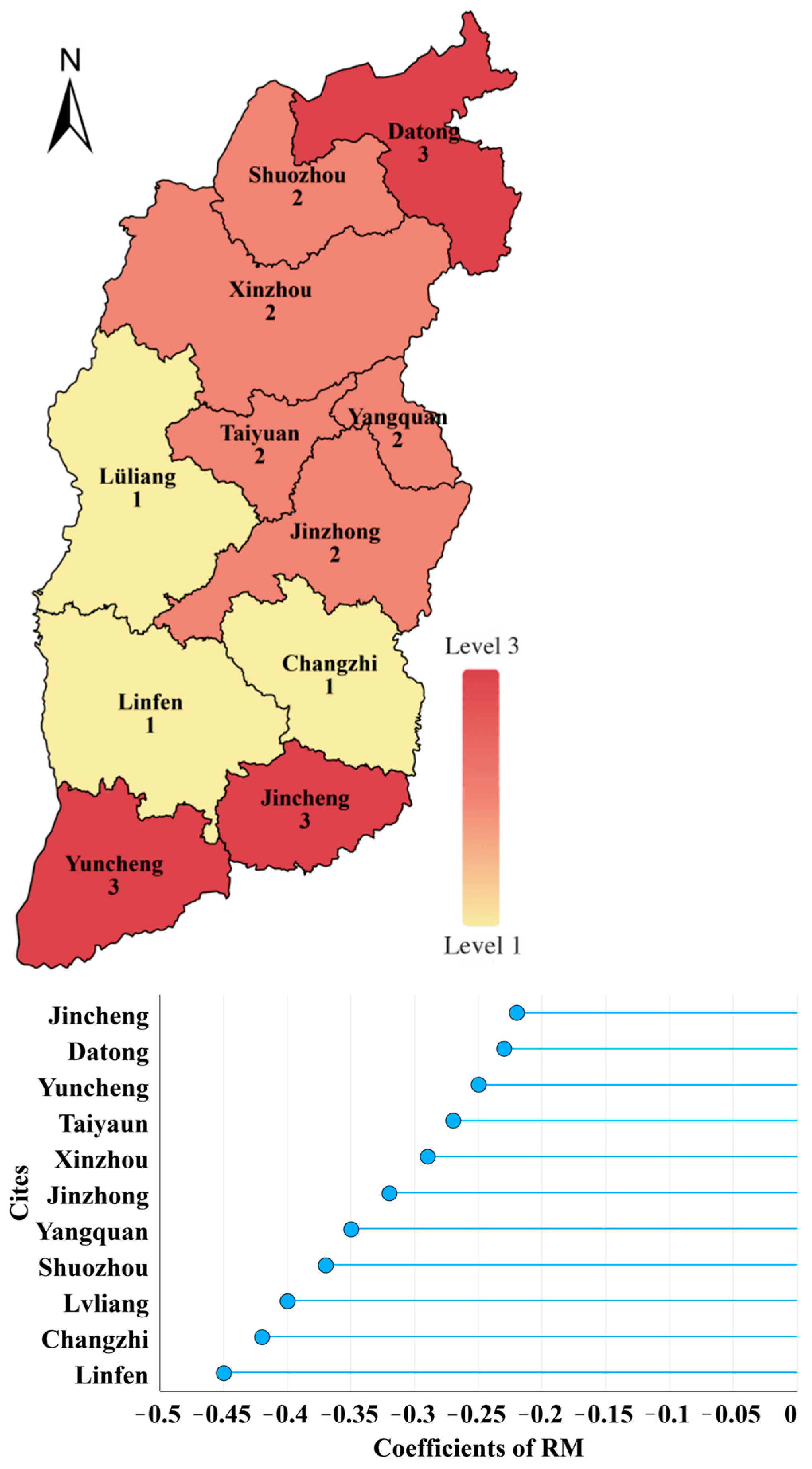
5.3.4. Analysis of Regional Differences in the RM Regression Coefficients
6. Suggestions
6.1. Differentiated Optimization Policies
6.2. Prioritization of Policies Across Cities
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoff, H. Understanding the nexus. In Proceedings of the Background Paper for the Bonn 2011 Conference: The Water Energy and Food Security Nexus, Stockholm, Sweden, 16–18 November 2011. [Google Scholar]
- Gai, D.H.B.; Shittu, E.; Ethan Yang, Y.; Li, H.-Y. A comprehensive review of the nexus of food, energy, and water systems: What the models tell us. J. Water Resour. Plan. Manag. 2022, 148, 04022031. [Google Scholar] [CrossRef]
- Javan, K.; Altaee, A.; BaniHashemi, S.; Darestani, M.; Zhou, J.; Pignatta, G. A review of interconnected challenges in the water–energy–food nexus: Urban pollution perspective towards sustainable development. Sci. Total Environ. 2024, 912, 169319. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Zhang, W.; Chen, W.; Chen, B. Land–water–energy nexus in agricultural management for greenhouse gas mitigation. Appl. Energy 2020, 265, 114796. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, X.; Peng, H.; Skitmore, M.; Bai, X.; Zheng, Z. The energy-food-water nexus: Water footprint of Henan-Hubei-Hunan in China. Renew. Sustain. Energy Rev. 2021, 135, 110417. [Google Scholar] [CrossRef]
- Zhou, Y.; Wei, B.; Zhang, R.; Li, H. Evolution of water–energy–food–climate study: Current status and future prospects. J. Water Clim. Change 2022, 13, 463–481. [Google Scholar] [CrossRef]
- Srigiri, S.R.; Dombrowsky, I. Analysing the water-energy-food nexus from a polycentric governance perspective: Conceptual and methodological framework. Front. Environ. Sci. 2022, 10, 725116. [Google Scholar] [CrossRef]
- Fleischmann, J.; Blechinger, P.; Ribbe, L.; Nauditt, A.; El Achkar, J.H.; Tiwari, K.; Kuleape, R.; Platzer, W. OWEFE—Open modeling framework for integrated water, energy, food, and environment systems. Environ. Res. Infrastruct. Sustain. 2023, 3, 015006. [Google Scholar] [CrossRef]
- Naderi, M.M.; Mirchi, A.; Bavani, A.R.M.; Goharian, E.; Madani, K. System dynamics simulation of regional water supply and demand using a food-energy-water nexus approach: Application to Qazvin Plain, Iran. J. Environ. Manag. 2021, 280, 111843. [Google Scholar] [CrossRef]
- Li, W.; Jiang, S.; Zhao, Y.; Li, H.; Zhu, Y.; He, G.; Xu, Y.; Shang, Y. A copula-based security risk evaluation and probability calculation for water-energy-food nexus. Sci. Total Environ. 2023, 856, 159236. [Google Scholar] [CrossRef]
- Wang, S.; Yang, J.; Wang, A.; Liu, T.; Du, S.; Liang, S. Coordinated analysis and evaluation of water–energy–food coupling: A case study of the Yellow River basin in Shandong Province, China. Ecol. Indic. 2023, 148, 110138. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, J.; Shu, K. The coupling and coordination assessment of food-water-energy systems in China based on sustainable development goals. Sustain. Prod. Consum. 2023, 35, 338–348. [Google Scholar] [CrossRef]
- Qi, Y.; Farnoosh, A.; Lin, L.; Liu, H. Coupling coordination analysis of China’s provincial water-energy-food nexus. Environ. Sci. Pollut. Res. 2022, 29, 23303–23313. [Google Scholar] [CrossRef]
- Yin, D.; Yu, H.; Lu, Y.; Zhang, J.; Li, G.; Li, X. A comprehensive evaluation framework of water-energy-food system coupling coordination in the Yellow River Basin, China. Chin. Geogr. Sci. 2023, 33, 333–350. [Google Scholar] [CrossRef]
- Sun, C.; Yan, X.; Zhao, L. Coupling efficiency measurement and spatial correlation characteristic of water–energy–food nexus in China. Resour. Conserv. Recycl. 2021, 164, 105151. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, W. Simulation study on the different policies of Jiangsu Province for a dynamic balance of water resources under the water–energy–food nexus. Water 2020, 12, 1666. [Google Scholar] [CrossRef]
- Mu, Y.-Q.; Wu, Y.-J.; Tian, P.; WANG, Y.-Q.; Jin, G. The adaptability of “water-energy-food” system and urban green transformation in the middle reaches of the Yangtze River Economic Zone. J. Nat. Resour. 2024, 39, 2140–2154. [Google Scholar] [CrossRef]
- Li, G.J.; Huang, D.; Li, Y.L. Water-energy-food nexus: New perspective on regional sustainable development. J. Cent. Univ. Financ. Econ. 2016, 12, 76–90. [Google Scholar]
- Núñez-López, J.M.; Rubio-Castro, E.; Ponce-Ortega, J.M. Involving resilience in optimizing the water-energy-food nexus at macroscopic level. Process Saf. Environ. Prot. 2021, 147, 259–273. [Google Scholar] [CrossRef]
- Ioannou, A.E.; Laspidou, C.S. Resilience analysis framework for a water–energy–food nexus system under climate change. Front. Environ. Sci. 2022, 10, 820125. [Google Scholar] [CrossRef]
- Huang, R.; Liu, H. Evaluation and External Driving Factors Analysis of Water–Energy–Food Resilience Security—Based on Spatial Durbin Model and Four Provinces Along the Yellow River. Sustainability 2024, 16, 10126. [Google Scholar] [CrossRef]
- Herrera-Franco, G.; Bollmann, H.A.; Lofhagen, J.C.P.; Bravo-Montero, L.; Carrión-Mero, P. Approach on water-energy-food (WEF) nexus and climate change: A tool in decision-making processes. Environ. Dev. 2023, 46, 100858. [Google Scholar] [CrossRef]
- Chen, S.; Nie, R.; Ding, Y.; Gao, K. Research progress and application exploration of energy system resilience. Sci. Technol. Manag. Res. 2020, 40, 233–242. [Google Scholar]
- Zhou, T. New risks and new logics of energy security: From the perspective of system resilience concurrently discussing problem of energy security and strategic thinking under the new logic in China. J. Technol. Econ. 2023, 42, 1–10. [Google Scholar]
- Gang, L.; Di, K.; Ming, H.; Liutao, L.; Laixi, H. Spatial-Temporal Characteristics and Driving Factors of Collaborative Security of Water-Energy-Food Linkage System in the Yellow River Basin. Geogr. Geogr. Inf. Sci. 2024, 40, 84. [Google Scholar]
- Abulibdeh, A.; Zaidan, E. Managing the water-energy-food nexus on an integrated geographical scale. Environ. Dev. 2020, 33, 100498. [Google Scholar] [CrossRef]
- Kurian, M.; Ardakanian, R. Governing the Nexus; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Conway, D.; Van Garderen, E.A.; Deryng, D.; Dorling, S.; Krueger, T.; Landman, W.; Lankford, B.; Lebek, K.; Osborn, T.; Ringler, C. Climate and southern Africa’s water–energy–food nexus. Nat. Clim. Change 2015, 5, 837–846. [Google Scholar] [CrossRef]
- Bahri, M. Analysis of the water, energy, food and land nexus using the system archetypes: A case study in the Jatiluhur reservoir, West Java, Indonesia. Sci. Total Environ. 2020, 716, 137025. [Google Scholar] [CrossRef]
- Niva, V.; Cai, J.; Taka, M.; Kummu, M.; Varis, O. China’s sustainable water-energy-food nexus by 2030: Impacts of urbanization on sectoral water demand. J. Clean. Prod. 2020, 251, 119755. [Google Scholar] [CrossRef]
- Jones, J.L.; White, D.D. Understanding barriers to collaborative governance for the food-energy-water nexus: The case of Phoenix, Arizona. Environ. Sci. Policy 2022, 127, 111–119. [Google Scholar] [CrossRef]
- Liu, L.; Chen, J.; Wang, C. Spatiotemporal evolution and trend prediction of regional water–energy–food–ecology system vulnerability: A case study of the Yangtze River Economic Belt, China. Environ. Geochem. Health 2023, 45, 9621–9638. [Google Scholar] [CrossRef]
- Zhao, Z.M.; Cao, Y.Q.; Chang, Z.D. Coupling coordination analysis of ecological carrying capacity of water and land resources in nine provinces along the Yellow River. Water Resour. Prot. 2023, 39, 121–129. [Google Scholar]
- Li, C.; Zhang, S. Chinese provincial water-energy-food coupling coordination degree and influencing factors research. China Popul. Resour. Env. 2020, 30, 120–128. [Google Scholar]
- Zhou, Y.; Yang, Y.; Song, Z.; He, Z.; Xia, S.; Ren, Y. Dynamic transition mechanism analysis of the impact of energy development on urbanization in Central Asia. J. Geogr. Sci. 2020, 30, 1825–1848. [Google Scholar] [CrossRef]
- Liu, Y.; Ou, C.; Li, Y.; Zhang, L.; He, J. Regularity of rural settlement changes driven by rapid urbanization in North China over the three decades. Sci. Bull. 2023, 68, 2115–2124. [Google Scholar] [CrossRef]
- Saray, M.H.; Baubekova, A.; Gohari, A.; Eslamian, S.S.; Klove, B.; Haghighi, A.T. Optimization of Water-Energy-Food Nexus considering CO2 emissions from cropland: A case study in northwest Iran. Appl. Energy 2022, 307, 118236. [Google Scholar] [CrossRef]
- Springmann, M.; Clark, M.; Mason-D’Croz, D.; Wiebe, K.; Bodirsky, B.L.; Lassaletta, L.; De Vries, W.; Vermeulen, S.J.; Herrero, M.; Carlson, K.M. Options for keeping the food system within environmental limits. Nature 2018, 562, 519–525. [Google Scholar] [CrossRef]
- Bruns, A.; Meisch, S.; Ahmed, A.; Meissner, R.; Romero-Lankao, P. Nexus disrupted: Lived realities and the water-energy-food nexus from an infrastructure perspective. Geoforum 2022, 133, 79–88. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Liu, Y.; Liu, H. Impacts and effects of government regulation on farmers’ responses to drought: A case study of North China Plain. J. Geogr. Sci. 2017, 27, 1481–1498. [Google Scholar] [CrossRef]
- Sharifi, A.; Yamagata, Y. Principles and criteria for assessing urban energy resilience: A literature review. Renew. Sustain. Energy Rev. 2016, 60, 1654–1677. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Xie, L.-H.; Xiao, J.-H. Government procurement, digital economy development and industrial structure upgrading. Contemp. Financ. Econ. 2024, 43–55. [Google Scholar]
- Hua, E.; Han, X.; Bai, Y.; Engel, B.A.; Li, X.; Sun, S.; Wang, Y. Synergy of water use in water-energy-food nexus from a symbiosis perspective: A case study in China. Energy 2023, 283, 129164. [Google Scholar] [CrossRef]
- Petrariu, R.; Constantin, M.; Dinu, M.; Pătărlăgeanu, S.R.; Deaconu, M.E. Water, energy, food, waste nexus: Between synergy and trade-offs in Romania based on entrepreneurship and economic performance. Energies 2021, 14, 5172. [Google Scholar] [CrossRef]
- Bai, J.; Liu, Y. Can outward foreign direct investment improve the resource misallocation of China. China Ind. Econ 2018, 1, 60–78. [Google Scholar]
- Lv, Q.; Liu, H.; Yang, D.; Liu, H. Effects of urbanization on freight transport carbon emissions in China: Common characteristics and regional disparity. J. Clean. Prod. 2019, 211, 481–489. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wang, S.; Fang, C.; Ma, H.; Wang, Y.; Qin, J. Spatial differences and multi-mechanism of carbon footprint based on GWR model in provincial China. J. Geogr. Sci. 2014, 24, 612–630. [Google Scholar] [CrossRef]
- de Smith, M.J.; Goodchild, M.F.; Longley, P. Geospatial Analysis: A Comprehensive Guide to Principles, Techniques and Software Tools, 6th ed.; The Winchelsea Press: Leicester, UK, 2018. [Google Scholar]
- Yu, H.; Fotheringham, A.S.; Li, Z.; Oshan, T.; Wolf, L.J. On the measurement of bias in geographically weighted regression models. Spat. Stat. 2020, 38, 100453. [Google Scholar] [CrossRef]
- Chen, F.; Mei, C.-L. Scale-adaptive estimation of mixed geographically weighted regression models. Econ. Model. 2021, 94, 737–747. [Google Scholar] [CrossRef]
- Wang, K.; Liu, J.; Xia, J.; Wang, Z.; Meng, Y.; Chen, H.; Mao, G.; Ye, B. Understanding the impacts of climate change and socio-economic development through food-energy-water nexus: A case study of mekong river delta. Resour. Conserv. Recycl. 2021, 167, 105390. [Google Scholar] [CrossRef]
- Rasul, G.; Sharma, B. The nexus approach to water–energy–food security: An option for adaptation to climate change. Clim. Policy 2016, 16, 682–702. [Google Scholar] [CrossRef]
- Pastor, A.V.; Palazzo, A.; Havlik, P.; Biemans, H.; Wada, Y.; Obersteiner, M.; Kabat, P.; Ludwig, F. The global nexus of food–trade–water sustaining environmental flows by 2050. Nat. Sustain. 2019, 2, 499–507. [Google Scholar] [CrossRef]
- Allouche, J.; Middleton, C.; Gyawal, D. Nexus Nirvana or Nexus Nullity? A Dynamic Approach to Security and Sustainability in the Water–Energy–Food Nexus; STEPS Working Paper No. 63; STEPS Centre: Brighton, UK, 2014. [Google Scholar]
- Shannak, S.d.; Mabrey, D.; Vittorio, M. Moving from theory to practice in the water–energy–food nexus: An evaluation of existing models and frameworks. Water-Energy Nexus 2018, 1, 17–25. [Google Scholar] [CrossRef]
- Hussein, H.; Ezbakhe, F. The water–employment–migration nexus: Buzzword or useful framework? Dev. Policy Rev. 2023, 41, e12676. [Google Scholar] [CrossRef]





| Year City | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
|---|---|---|---|---|---|---|---|---|---|---|
| Taiyuan | 0.505 | 0.502 | 0.520 | 0.504 | 0.502 | 0.522 | 0543 | 0.572 | 0.591 | 0.600 |
| Datong | 0.330 | 0.349 | 0.361 | 0.304 | 0.319 | 0.330 | 0.354 | 0.364 | 0.374 | 0.384 |
| Yangquan | 0.395 | 0.383 | 0.434 | 0.382 | 0.401 | 0.412 | 0.409 | 0.442 | 0.454 | 0.460 |
| Changzhi | 0.397 | 0.373 | 0.418 | 0.414 | 0.383 | 0.390 | 0.396 | 0.440 | 0.442 | 0.479 |
| Jincheng | 0.417 | 0.413 | 0.477 | 0.427 | 0.408 | 0.427 | 0.458 | 0.456 | 0.486 | 0.490 |
| Shuozhou | 0.372 | 0.378 | 0.414 | 0.336 | 0.406 | 0.428 | 0.438 | 0.459 | 0.465 | 0.468 |
| Jinzhong | 0.417 | 0.364 | 0.453 | 0.435 | 0.414 | 0.420 | 0.437 | 0.460 | 0.502 | 0.511 |
| Yuncheng | 0.343 | 0.338 | 0.354 | 0.362 | 0.353 | 0.359 | 0.372 | 0.385 | 0.391 | 0.396 |
| Xinzhou | 0.426 | 0.426 | 0.432 | 0.435 | 0.452 | 0.453 | 0.424 | 0.460 | 0.466 | 0.471 |
| Linfen | 0.401 | 0.351 | 0.355 | 0.374 | 0.351 | 0.344 | 0.327 | 0.346 | 0.361 | 0.364 |
| Lvliang | 0.243 | 0.248 | 0.323 | 0.347 | 0.321 | 0.317 | 0.346 | 0.349 | 0.355 | 0.357 |
| Indicators | Data Sources |
|---|---|
| Invention patent applications authorized per 10,000 people | The China Urban Statistical Yearbook |
| Total regional grade highway mileage | |
| Total regional employment | |
| Environment protection expenditure | |
| Total regional population | The Shanxi Statistical Yearbook |
| Total regional land area | |
| Total regional urban population | |
| Total regional public expenditure | |
| Value of the tertiary industry and secondary industry | |
| Value of the people employed tertiary industry and secondary industry | |
| Amount of freight transported at the end of the year | The statistical yearbooks of the prefecture-level cities in Shanxi Province |
| Regional gross domestic product | |
| Retail sales of consumer goods per capita | The Shanxi Statistical Yearbook and the statistical yearbooks of the prefecture-level cities in Shanxi Province |
| Parameter Names | Meanings |
|---|---|
| R2 | Measures the acceptability of the model’s goodness-of-fit. |
| p-criticality value | Measures whether each explanatory variable is significant under t-tests. |
| VIF boundary value | Measures the presence of multicollinearity across the explanatory variables. |
| Jarque–Bera p-value | A measure of whether the regression residuals of the model remain spatially autocorrelated. |
| Year | 2014 | 2015 | 2016 | 2017 | 2018 |
| Moran’s I | −0.021 | −0.007 | 0.013 * | 0.024 * | 0.019 ** |
| Z value | 0.430 | 0.604 | 1.977 | 1.982 | 2.352 |
| p value | 0.427 | 0.783 | 0.071 | 0.079 | 0.011 |
| Year | 2019 | 2020 | 2021 | 2022 | 2023 |
| Moran’s I | −0.012 | 0.023 ** | 0.029 ** | 0.041 *** | 0.043 *** |
| Z value | 0.482 | 2.104 | 2.227 | 2.390 | 3.213 |
| p value | 0.630 | 0.041 | 0.026 | 0.001 | 0.004 |
| Year | Bandwidth | AIC | Sigma | Residual Squares | R2 | Jarque–Bera p-Value | VIF |
|---|---|---|---|---|---|---|---|
| 2014 | 869,376.36 | −98.64 | 0.0546 | 0.0876 | 0.54 | 0.6231 | 1.42 |
| 2015 | 1,367,290.04 | −78.16 | 0.0692 | 0.0813 | 0.52 | 0.5904 | 1.26 |
| 2016 | 12,736,278.59× | −83.23 | 0.0747× | 0.0794 | 0.64 | 0.6033 | 1.26 |
| 2017 | 12,736,278.59× | −99.65 | 0.0561 | 0.1460× | 0.63 | 0.6015 | 1.33 |
| 2018 | 12,736,278.59× | −107.46 | 0.0512 | 0.1324 | 0.64 | 0.6994 | 1.41 |
| 2019 | 844,656.31 | −105.43 | 0.0634 | 0.1338 | 0.49× | 0.7085 | 1.40 |
| 2020 | 1,723,217.34 | −111.27× | 0.0478 | 0.0795 | 0.66√ | 0.7433 | 1.29 |
| 2021 | 786,803.15√ | −107.54 | 0.0520 | 0.0863 | 0.63 | 0.5978 | 1.26 |
| 2022 | 1,768,734.20 | −78.13√ | 0.0436√ | 0.0778√ | 0.63 | 0.6967 | 1.24 |
| 2023 | 12,367,632.83 | −96.23 | 0.0683 | 0.1231 | 0.64 | 0.7206 | 1.23 |
| Variable City | PD (Negative) | TI (Positive) | IS (Positive) | RM (Negative) | Policy Priorities |
|---|---|---|---|---|---|
| Taiyuan | 11 | 1 | 6 | 8 | TI > IS > RM > PD |
| Datong | 6 | 9 | 2 | 10 | IS > PD > TI > RM |
| Yangquan | 3 | 8 | 4 | 5 | PD > IS > RM > TI |
| Changzhi | 9 | 3 | 8 | 2 | RM > TI > IS > PD |
| Jincheng | 5 | 4 | 9 | 11 | TI > PD > IS > RM |
| Shuozhou | 7 | 7 | 3 | 4 | IS > RM > PD,TI |
| Jinzhong | 10 | 2 | 7 | 6 | TI > RM > IS > PD |
| Yuncheng | 4 | 6 | 11 | 9 | PD > TI > RM > IS |
| Xinzhou | 8 | 5 | 5 | 7 | TI,IS > PD > RM |
| Linfen | 2 | 11 | 10 | 1 | RM > PD > IS > TI |
| Lvliang | 1 | 10 | 1 | 3 | PD,IS > RM > TI |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Han, Y. Differentiated Optimization Policies for Water–Energy–Food Resilience Security: Empirical Evidence Based on Shanxi Province and the GWR Model. Water 2025, 17, 1540. https://doi.org/10.3390/w17101540
Huang R, Han Y. Differentiated Optimization Policies for Water–Energy–Food Resilience Security: Empirical Evidence Based on Shanxi Province and the GWR Model. Water. 2025; 17(10):1540. https://doi.org/10.3390/w17101540
Chicago/Turabian StyleHuang, Ruopeng, and Yue Han. 2025. "Differentiated Optimization Policies for Water–Energy–Food Resilience Security: Empirical Evidence Based on Shanxi Province and the GWR Model" Water 17, no. 10: 1540. https://doi.org/10.3390/w17101540
APA StyleHuang, R., & Han, Y. (2025). Differentiated Optimization Policies for Water–Energy–Food Resilience Security: Empirical Evidence Based on Shanxi Province and the GWR Model. Water, 17(10), 1540. https://doi.org/10.3390/w17101540






