Estimating Evapotranspiration from Commonly Occurring Urban Plant Species Using Porometry and Canopy Stomatal Conductance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Location
2.2. Obtaining ET from Mass Losses
2.3. Using Porometry to Obtain Canopy Stomatal Conductance and ET
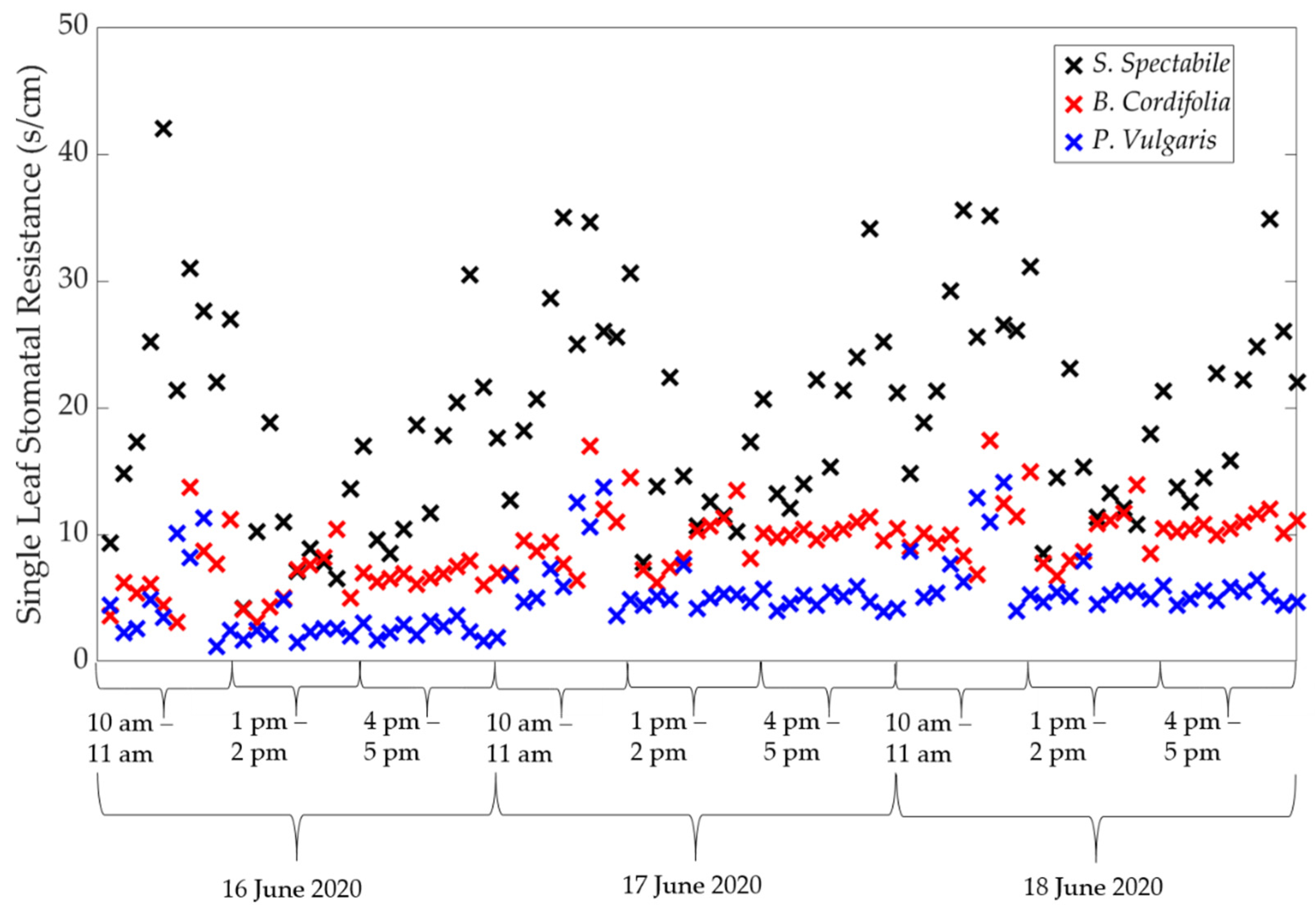
2.3.1. The Porometer
2.3.2. Calculating Single Leaf ET
2.3.3. Scaling Single Leaf ET to Canopy ET
3. Results and Discussion
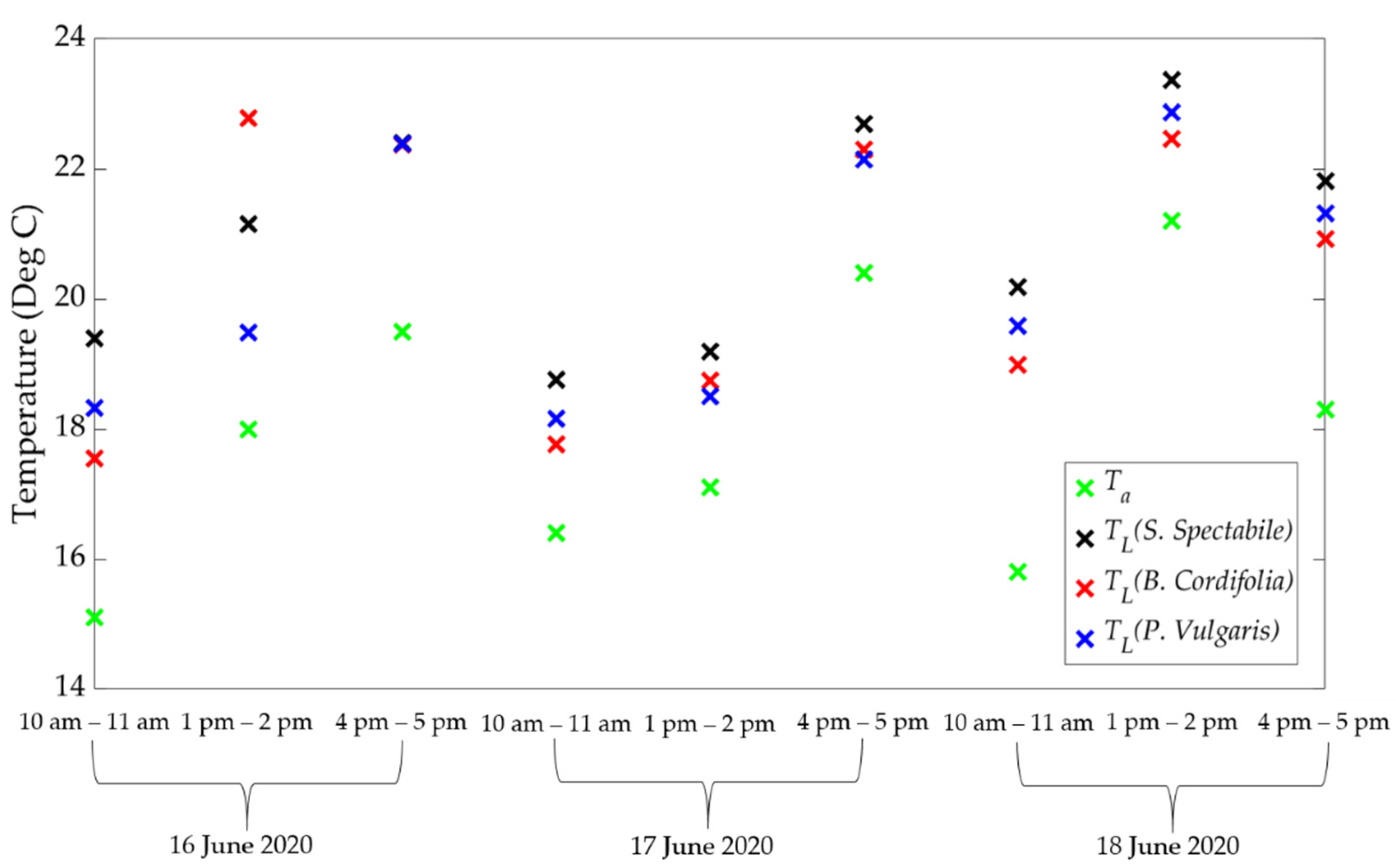
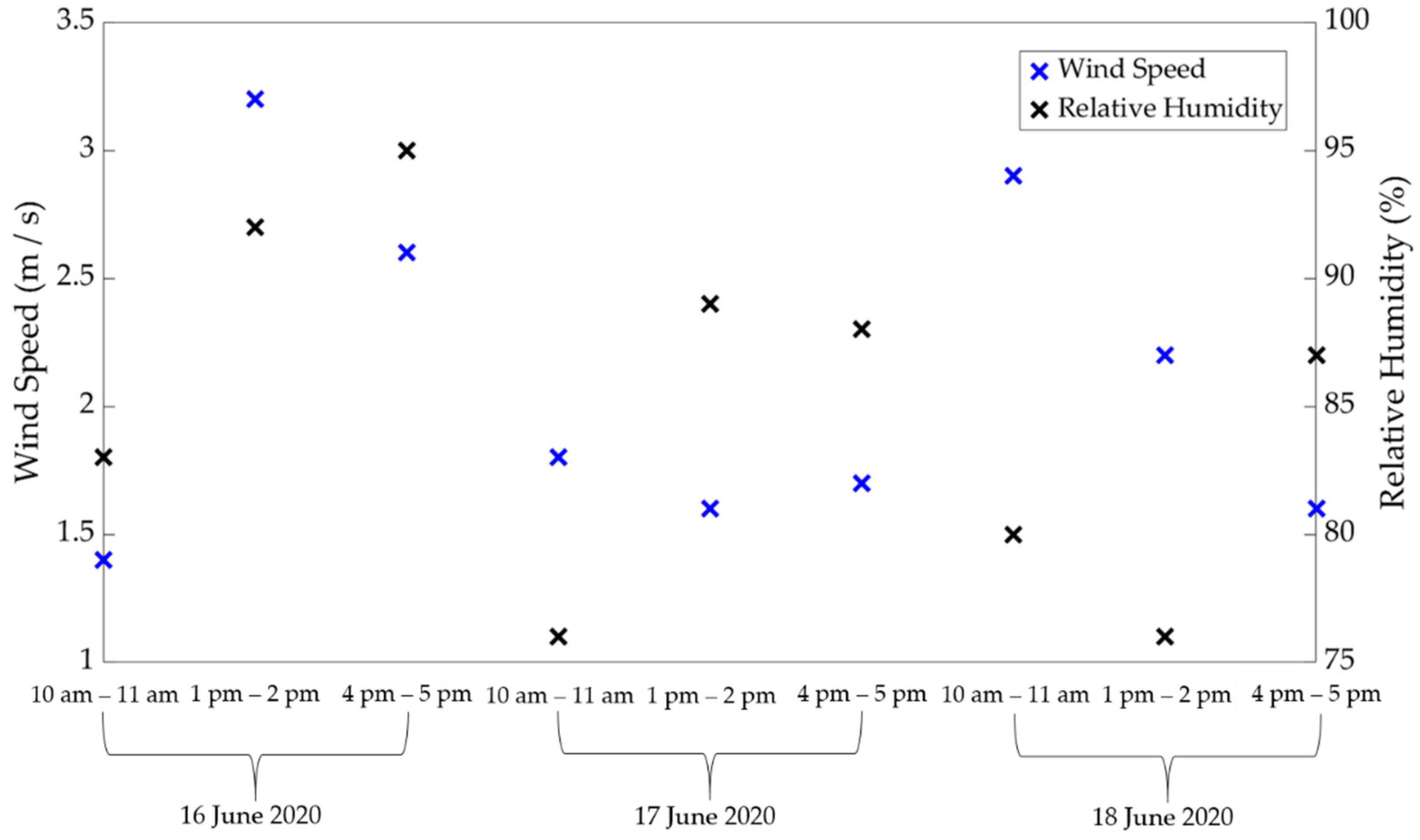
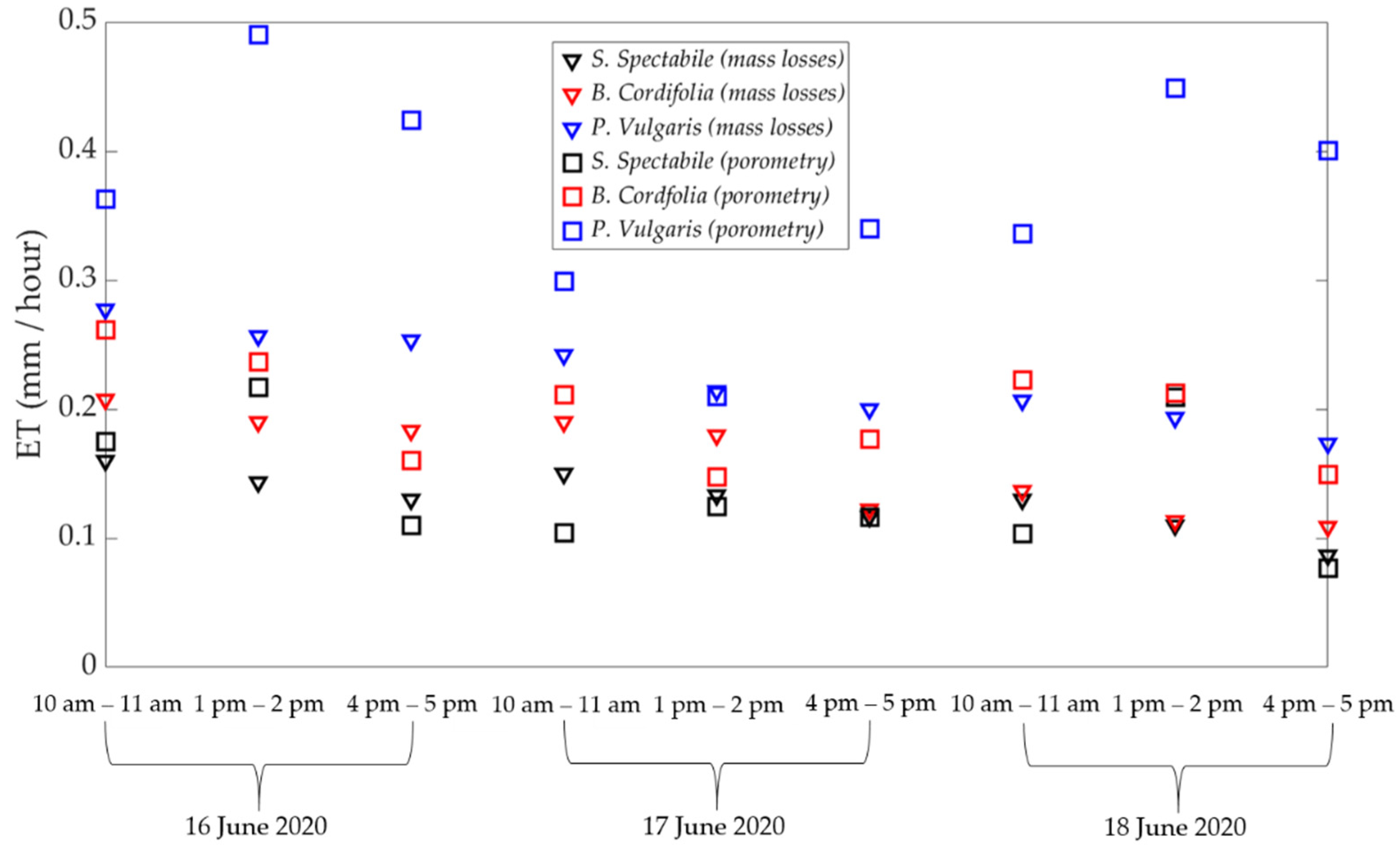
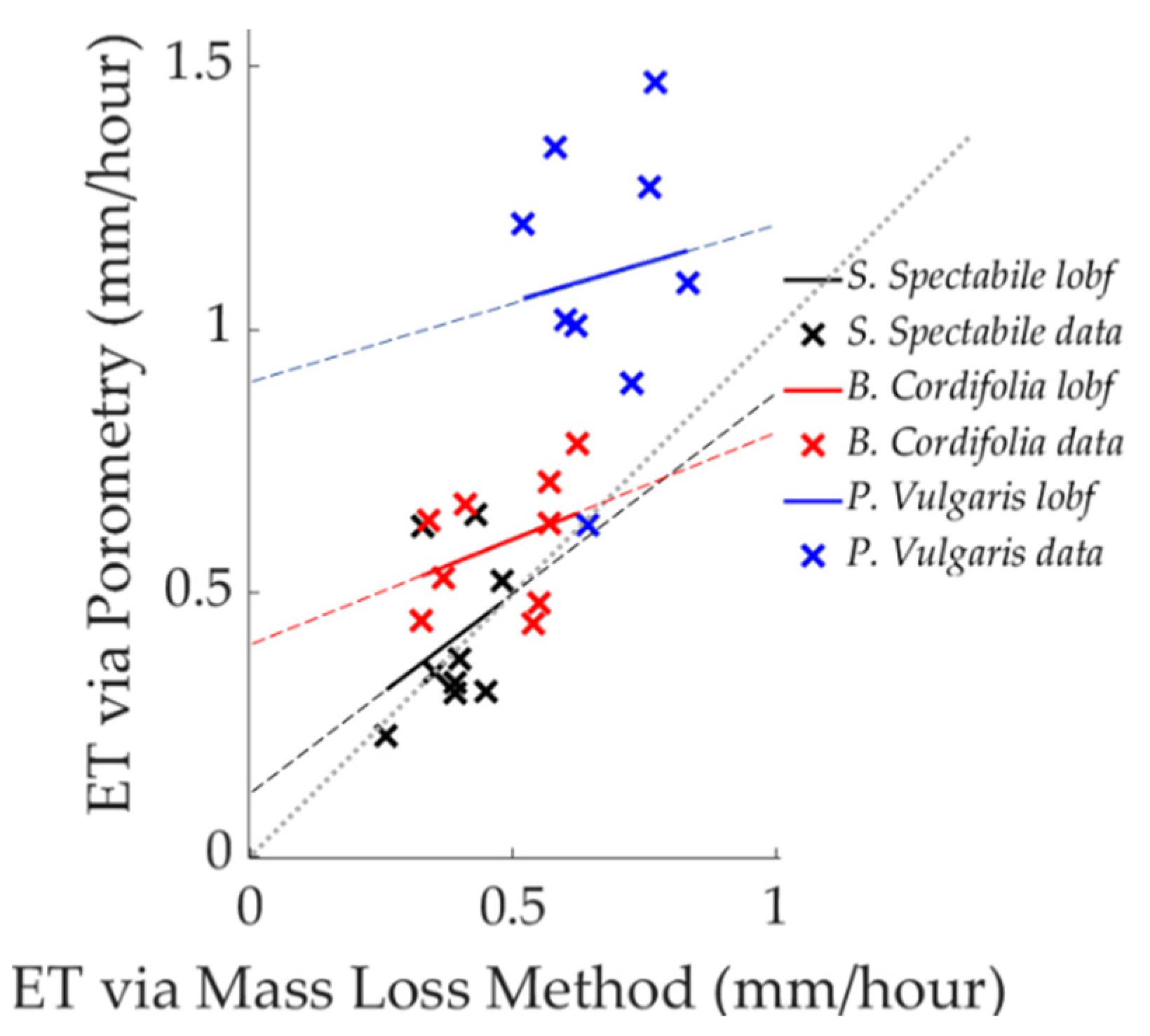
3.1. Comparison of Estimated ET between Porometric and Mass-Loss Measurements
3.2. Uncertainty in Analysis
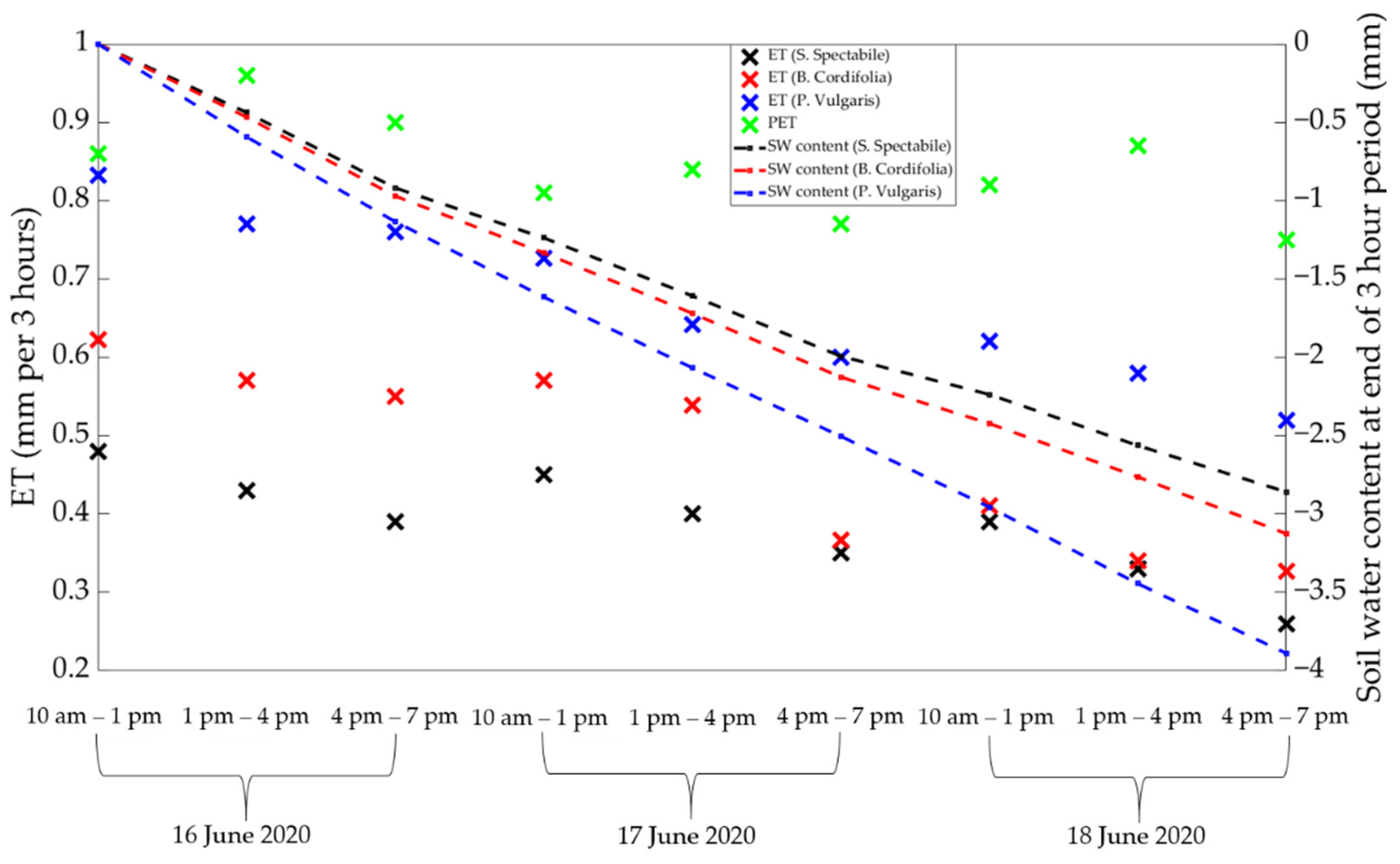
3.3. Considering Potential Evapotranspiration (PET) to Understand Decaying ET Rates
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Paschalis, A.; Mijic, A. Planning London’s green spaces in an integrated water management approach to enhance future resilience in urban stormwater control. J. Hydrol. 2021, 597, 126126. [Google Scholar] [CrossRef]
- Woods-Ballard, B.; Kellagher, R.; Martin, P.; Jefferies, C.; Bray, R.; Shaffer, P. The SuDS Manual (C697); CIRIA (Construction Industry Research and Information Association): London, UK, 2007; ISBN 978-0-86017-759-3. [Google Scholar]
- Levermore, G.; Parkinson, J.; Lee, K.; Laycock, P.; Lindley, S. The increasing trend of the urban heat island intensity. Urban Clim. 2018, 24, 360–368. [Google Scholar] [CrossRef]
- Gimenez-Maranges, M.; Breuste, J.; Hof, A. Sustainable Drainage Systems for transitioning to sustainable urban flood management in the European Union: A review. J. Clean. Prod. 2020, 255, 120191. [Google Scholar] [CrossRef]
- Castro, A.S.; Goldenfum, J.A.; da Silveira, A.L.; DallAgnol, A.L.; Loebens, L.; Demarco, C.F.; Leandro, D.; Nadaleti, W.C.; Quadro, M.S. The analysis of green roof’s runoff volumes and its water quality in an experimental study in Porto Alegre, Southern Brazil. Environ. Sci. Pollut. Res. 2020, 27, 9520–9534. [Google Scholar] [CrossRef] [PubMed]
- Sahnoune, S.; Benhassine, N. Quantifying the Impact of Green-Roofs on Urban Heat Island Mitigation. Int. J. Environ. Sci. Dev. 2017, 8, 116–123. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.; Jensen, M. Evaporation, Evapotranspiration, and Irrigation Water Requirements; American Society of Civil Engineers: Reston, VA, USA, 2016; ISBN 978-0-87262-763-5. [Google Scholar]
- Huryna, H.; Pokorný, J. The role of water and vegetation in the distribution of solar energy and local climate: A review. Folia Geobot. 2016, 51, 191–208. [Google Scholar] [CrossRef]
- Stovin, V.; Vesuviano, G.; Kasmin, H. The hydrological performance of a green roof test bed under UK climatic conditions. J. Hydrol. 2012, 414–415, 148–161. [Google Scholar] [CrossRef]
- Stovin, V.; Poë, S.; Berretta, C. A modelling study of long term green roof retention performance. J. Environ. Manag. 2013, 131, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Berretta, C.; Poë, S.; Stovin, V. Moisture content behaviour in extensive green roofs during dry periods: The influence of vegetation and substrate characteristics. J. Hydrol. 2014, 511, 374–386. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. ISBN 92-5-104219-5. [Google Scholar]
- Wang, T.; Melton, F.S.; Pôças, I.; Johnson, L.F.; Thao, T.; Post, K.; Cassel-Sharma, F. Evaluation of crop coefficient and evapotranspiration data for sugar beets from landsat surface reflectances using micrometeorological measurements and weighing lysimetry. Agric. Water Manag. 2021, 244, 106533. [Google Scholar] [CrossRef]
- Luo, C.; Wang, Z.; Sauer, T.; Helmers, M.; Horton, R. Portable canopy chamber measurements of evapotranspiration in corn, soybean, and reconstructed prairie. Agric. Water Manag. 2018, 198, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Shuttleworth, W.J. Evaporation. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw Hill: New York, NY, USA, 1993; pp. 4.1–4.53. [Google Scholar]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops—An energy combination theory. Quart. J. Roy Meteorol. Soc. 1985, 111, 839–853. [Google Scholar] [CrossRef]
- Thomas, B.; Murphy, D.; Murray, B. Encyclopedia of Applied Plant Sciences, 2nd ed.; Gro-Reg. Amsterdam Etc.; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 9780123948083. [Google Scholar]
- Wu, X.; Xu, Y.; Shi, J.; Zuo, Q.; Zhang, T.; Wang, L. Estimating stomatal conductance and evapotranspiration of winter wheat using a soil-plant water relations-based stress index. Agric. For. Meteorol. 2021, 303, 108393. [Google Scholar] [CrossRef]
- Spinelli, G.; Snyder, R.; Sanden, B.; Gilbert, M.; Shackel, K. Low and variable atmospheric coupling in irrigated Almond (Prunus dulcis) canopies indicates a limited influence of stomata on orchard evapotranspiration. Agric. Water Manag. 2018, 196, 57–65. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, B.; Chang, X.; Yang, Q.; Yang, Y.; Liu, Z.; Cleverly, J.; Eamus, D. Evapotranspiration partitioning, stomatal conductance, and components of the water balance: A special case of a desert ecosystem in China. J. Hydrol. 2016, 538, 374–386. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review. Eur. J. Agron. 2000, 13, 125–153. [Google Scholar] [CrossRef]
- Forschungsgesellschaft Landschaftsentwickung Landschaftsbau. Guidelines for the Planning, Construction and Maintenance of Green Roofing; Landscape Development and Landscaping Research Society: Bonn, Germany, 2018. [Google Scholar]
- Kirkham, M. Principles of Soil and Plant Water Relations; Academic Press: Oxford, UK, 2014; pp. 101–115. ISBN 9780124200784. [Google Scholar]
- Smith, W.; Roy, J.; Hinckley, T. Ecophysiology of Coniferous Forests; Elsevier Science: Saint Louis, MO, USA, 2014; pp. 255–308. ISBN 9780080925936. [Google Scholar]
- Verstraeten, W.; Veroustraete, F.; Feyen, J. Assessment of Evapotranspiration and Soil Moisture Content across Different Scales of Observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef] [Green Version]
- Enderle, J.; Bronzino, J. Introduction to Biomedical Engineering; Elsevier/Academic Press: Amsterdam, The Netherlands, 2012; pp. 359–445. ISBN 9780080961217. [Google Scholar]
- Pearcy, R.; Ehleringer, J.; Mooney, H.; Rundel, P. Plant Physiological Ecology, 1st ed.; Springer: Dordrecht, The Netherlands, 2000; pp. 137–160. ISBN 978-3-030-29639-1. [Google Scholar]
- Urban Flows Sheffield Live [Internet]. 2021. Available online: https://sheffield-portal.urbanflows.ac.uk/uflobin/ufportal/ (accessed on 19 June 2020).
- Singh, M.; Singh, K.; Singh, J. Indirect method for measurement of leaf area and leaf area index of soilless cucumber crop. Adv. Plants Agric. Res. 2018, 8, 188–191. [Google Scholar] [CrossRef] [Green Version]
- Wallace, J.; Roberts, J.; Sivakumar, M. The estimation of transpiration from sparse dryland millet using stomatal conductance and vegetation area indices. Agric. For. Meteorol. 1990, 51, 35–49. [Google Scholar] [CrossRef] [Green Version]
- Leuning, R.; Kelliher, F.; Pury, D.; Schulze, E. Leaf nitrogen, photosynthesis, conductance and transpiration: Scaling from leaves to canopies. Plant Cell Environ. 1995, 18, 1183–1200. [Google Scholar] [CrossRef]
- Ding, R.; Kang, S.; Du, T.; Hao, X.; Zhang, Y. Scaling Up Stomatal Conductance from Leaf to Canopy Using a Dual-Leaf Model for Estimating Crop Evapotranspiration. PLoS ONE 2014, 9, e95584. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, K.; Sun, Z.; Zhao, F.; Yang, T.; Tian, Z.; Lai, J.; Long, B.; Li, S. Remotely sensed canopy resistance model for analyzing the stomatal behavior of environmentally-stressed winter wheat. ISPRS J. Photogramm. Remote Sens. 2020, 168, 197–207. [Google Scholar] [CrossRef]
- Stovin, V.; Poë, S.; De-Ville, S.; Berretta, C. The influence of substrate and vegetation configuration on green roof hydrological performance. Ecol. Eng. 2015, 85, 159–172. [Google Scholar] [CrossRef] [Green Version]
- Hillel, D.; Hatfield, J. Encyclopedia of Soils in the Environment; Elsevier/Academic Press: Oxford, UK, 2005; pp. 502–506. ISBN 9780123485304. [Google Scholar]
- Zhao, L.; Xia, J.; Xu, C.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration estimation methods in hydrological models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]


| Plant 1, Sedum spectabile | Plant 2, Bergenia cordfolia | Plant 3, Primula vulgaris |
|---|---|---|
| Small ‘succulent species’ leaf type. Drought tolerant. Evergreen, flowering plant. Dense canopy. Expected low ET. | Medium sized broad shape leaf. Requires regular irrigation. Evergreen, flowering plant. Dense canopy. Expected medium ET. | Large, long broad shaped leaf. Requires regular irrigation. Evergreen, flowering plant. Sprawling canopy. Expected high ET. |
| LAI | Plant Species | ||
|---|---|---|---|
| Sedum spectabile | Bergenia cordifolia | Primula vulgaris | |
| LAImid | 7.3 | 6.9 | 5.9 |
| LAIold | 0.4 | 1.4 | 0.6 |
| LAIyng | 1.5 | 0.7 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askari, S.H.; De-Ville, S.; Hathway, E.A.; Stovin, V. Estimating Evapotranspiration from Commonly Occurring Urban Plant Species Using Porometry and Canopy Stomatal Conductance. Water 2021, 13, 2262. https://doi.org/10.3390/w13162262
Askari SH, De-Ville S, Hathway EA, Stovin V. Estimating Evapotranspiration from Commonly Occurring Urban Plant Species Using Porometry and Canopy Stomatal Conductance. Water. 2021; 13(16):2262. https://doi.org/10.3390/w13162262
Chicago/Turabian StyleAskari, Syed Hamza, Simon De-Ville, Elizabeth Abigail Hathway, and Virginia Stovin. 2021. "Estimating Evapotranspiration from Commonly Occurring Urban Plant Species Using Porometry and Canopy Stomatal Conductance" Water 13, no. 16: 2262. https://doi.org/10.3390/w13162262
APA StyleAskari, S. H., De-Ville, S., Hathway, E. A., & Stovin, V. (2021). Estimating Evapotranspiration from Commonly Occurring Urban Plant Species Using Porometry and Canopy Stomatal Conductance. Water, 13(16), 2262. https://doi.org/10.3390/w13162262






