Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy)
Abstract
1. Introduction
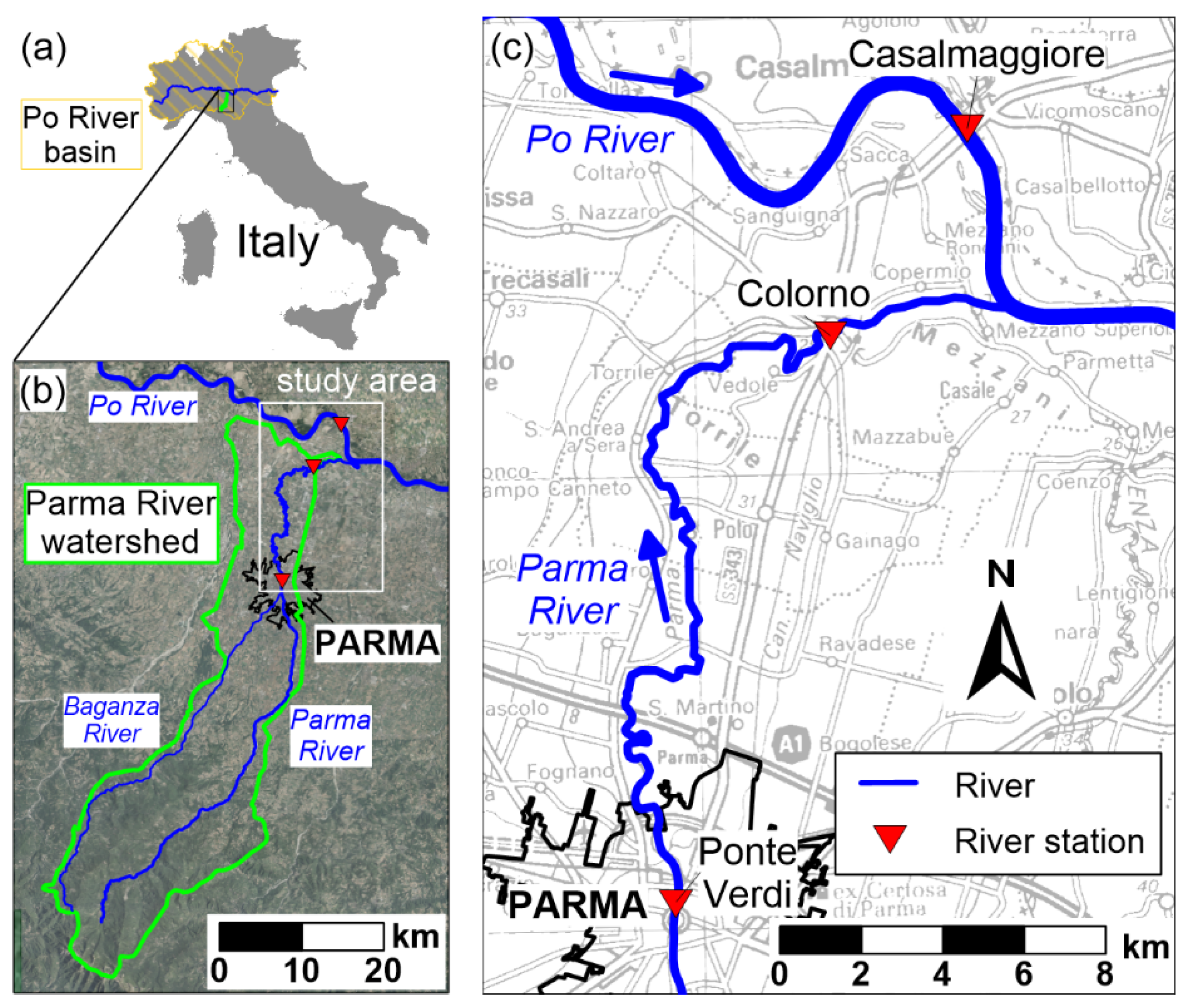
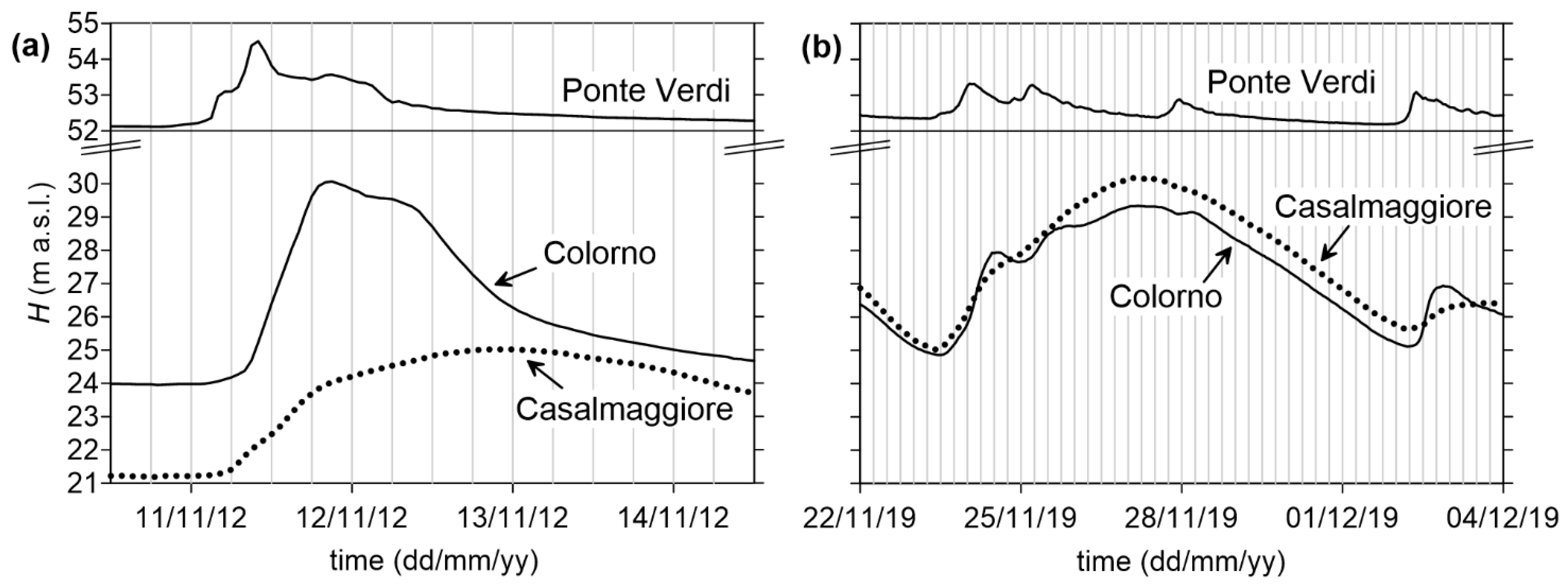
2. Case Study and Problem Statement
3. Materials and Methods
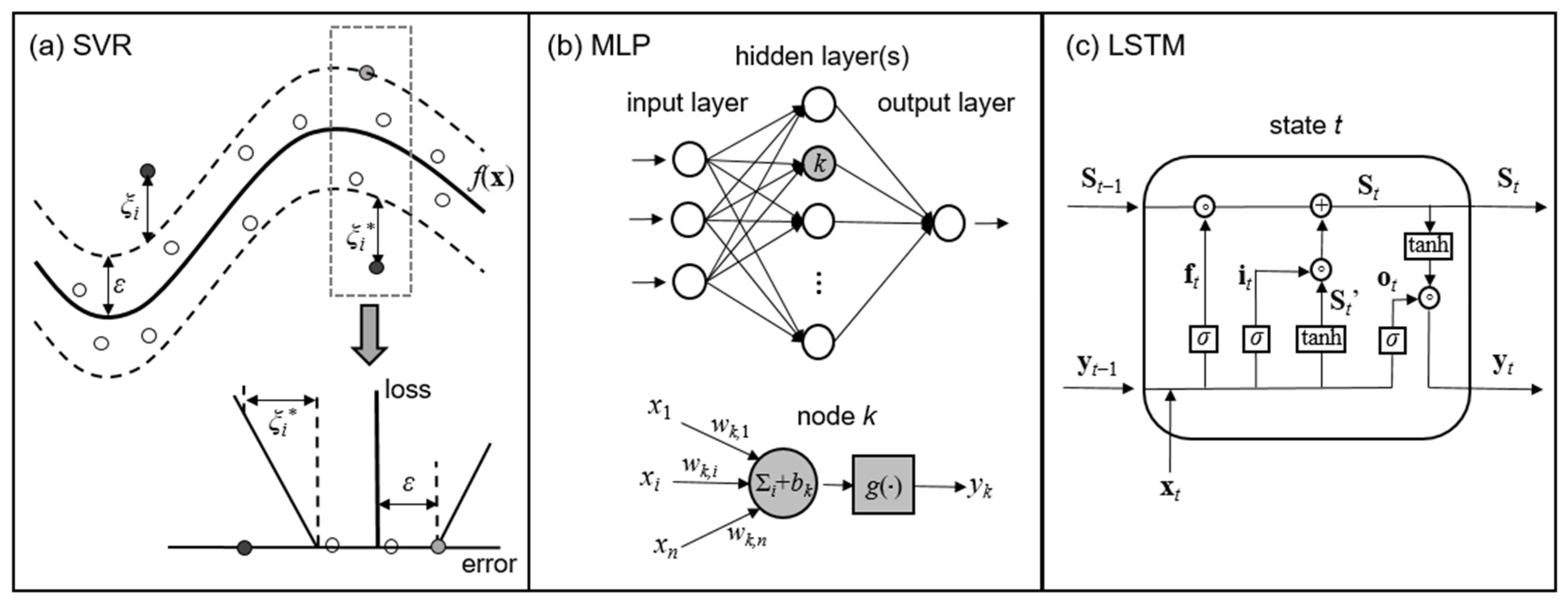
3.1. Machine Learning (ML) Models
3.1.1. Support Vector Regression (SVR)
3.1.2. MultiLayer Perceptron (MLP)
3.1.3. Long Short-Term Memory (LSTM)
3.1.4. Metrics for Model Evaluation
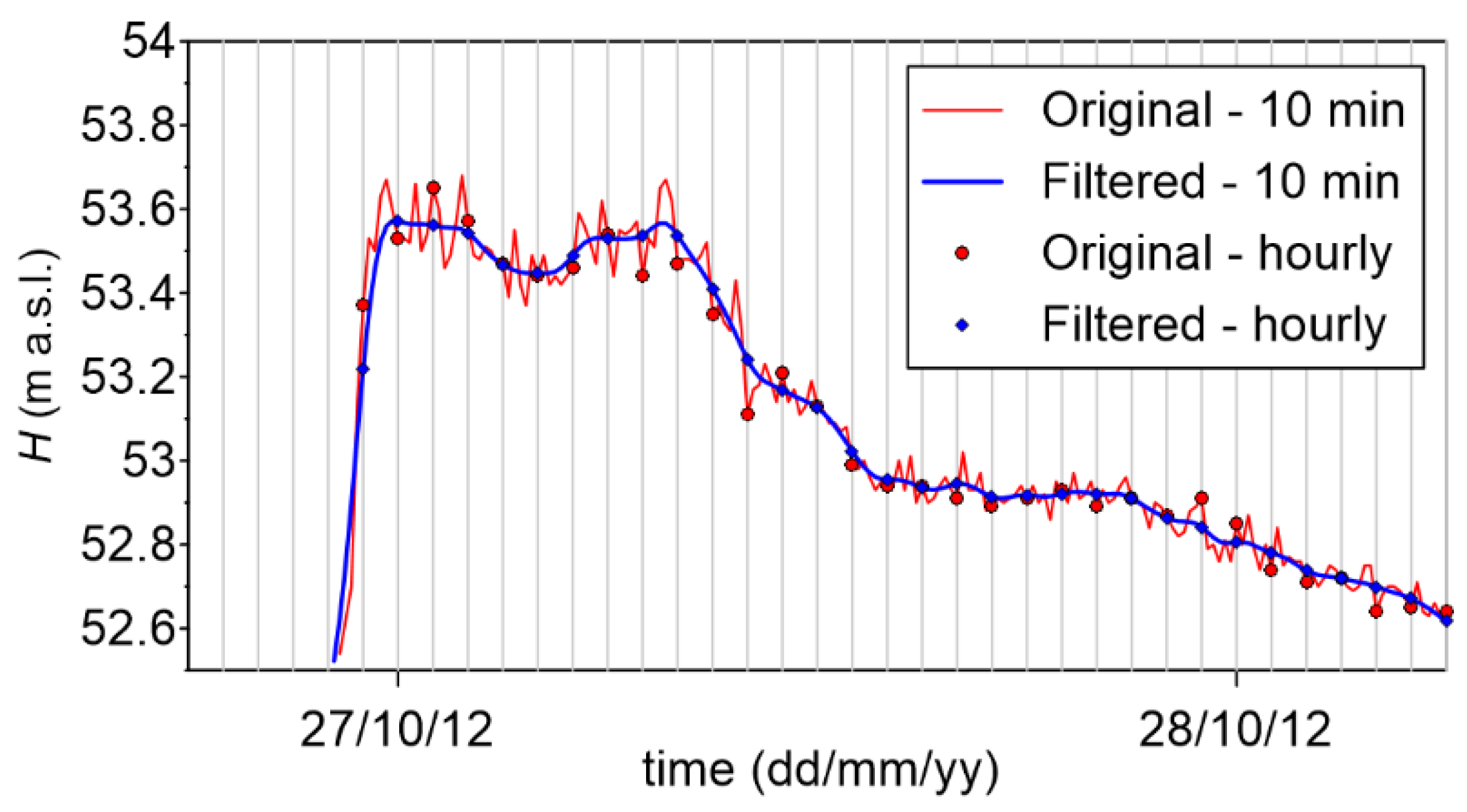
3.2. Availability of Data
3.3. Model Setup
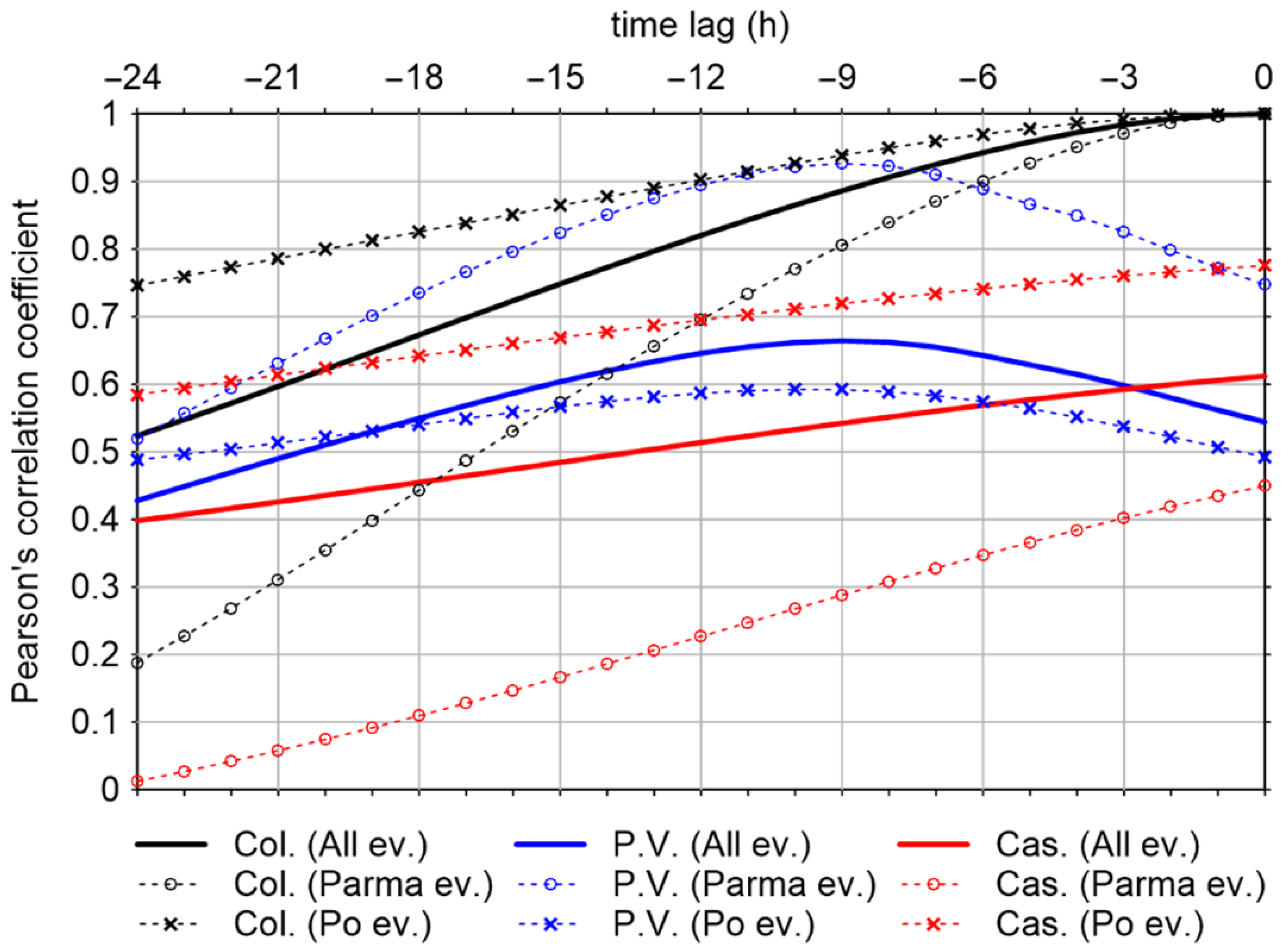
3.3.1. Input Selection
- HP.V.(t − 11),…, HP.V.(t − 1), HP.V.(t);
- HCas.(t − 11),…, HCas.(t − 1), HCas.(t);
- HCol.(t − 11),…, HCol.(t − 1), HCol.(t).
3.3.2. Training Process
3.3.3. Model Structure Definition
4. Results and Discussion
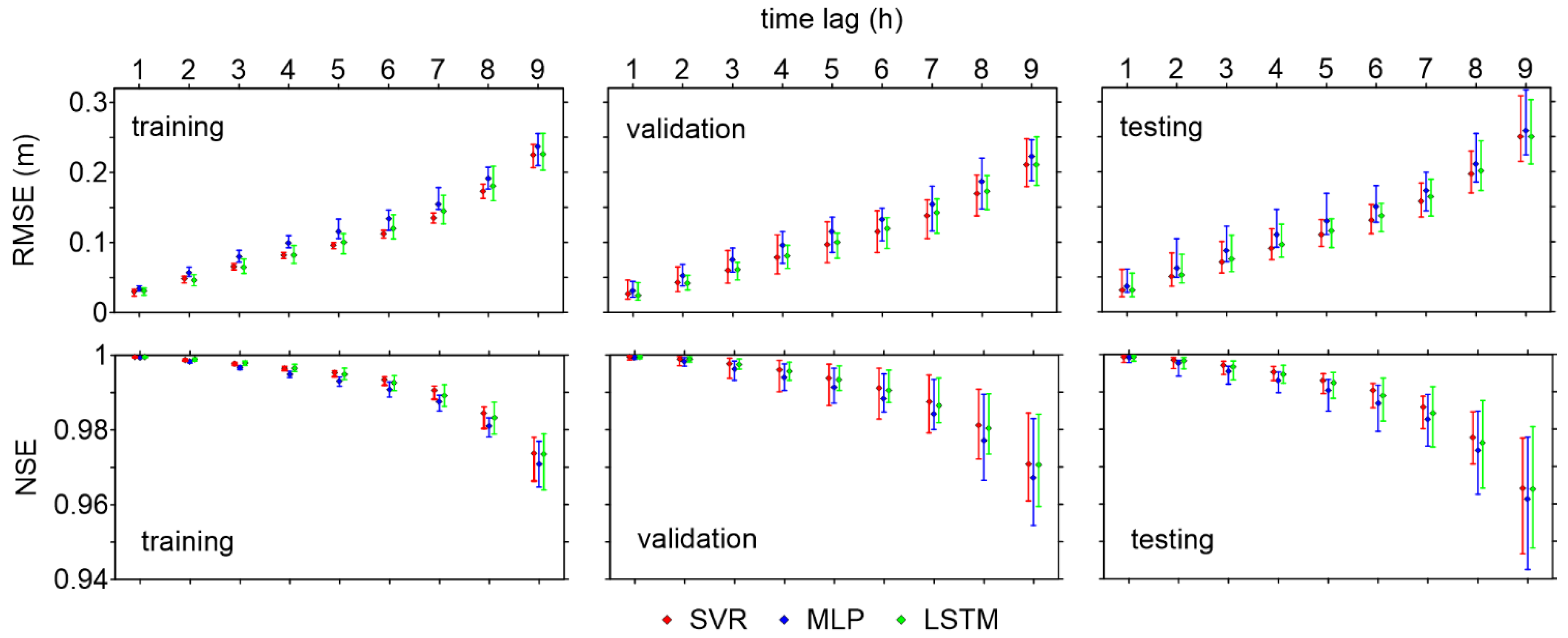
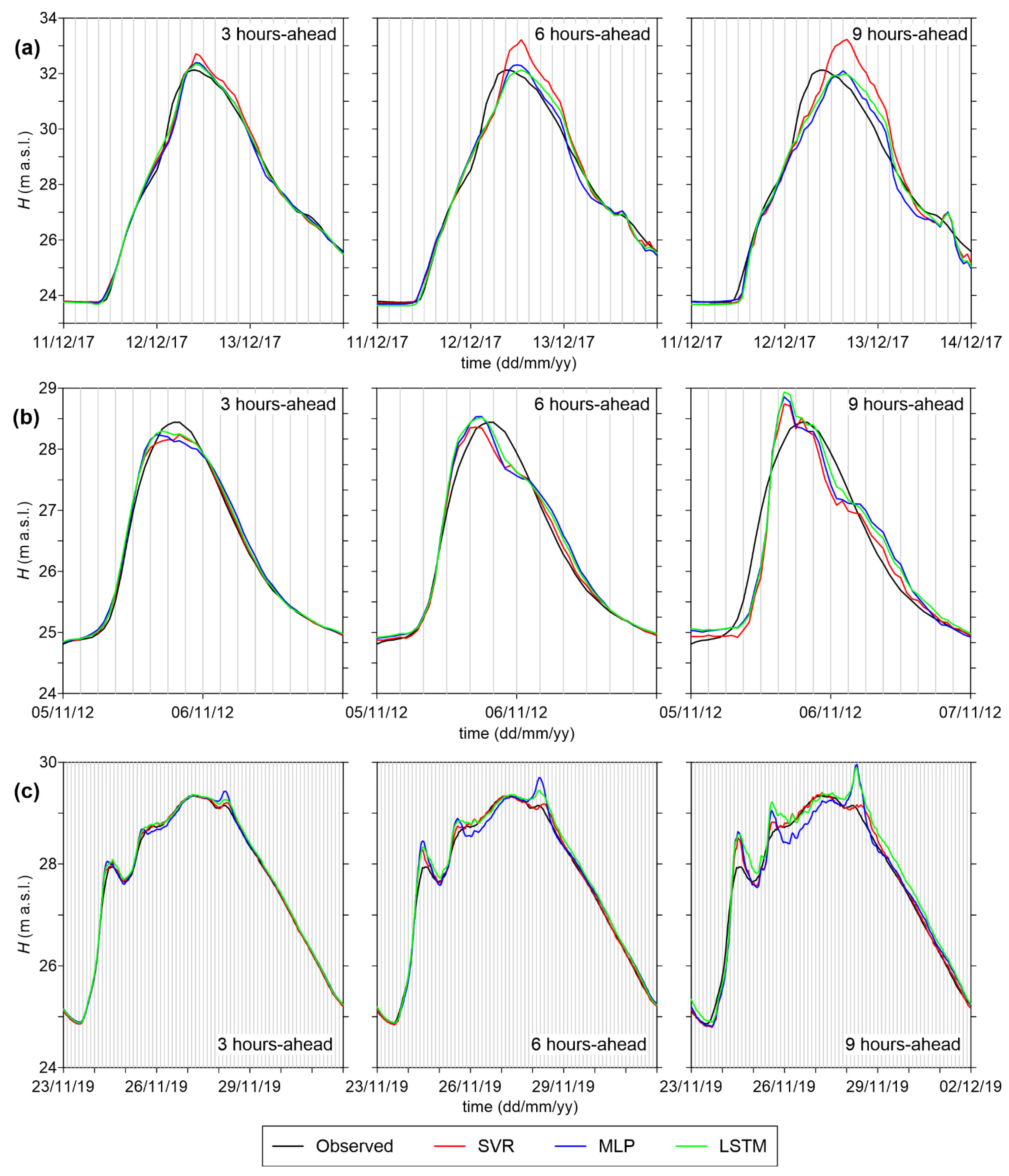
4.1. Comparison of Models’ Performance
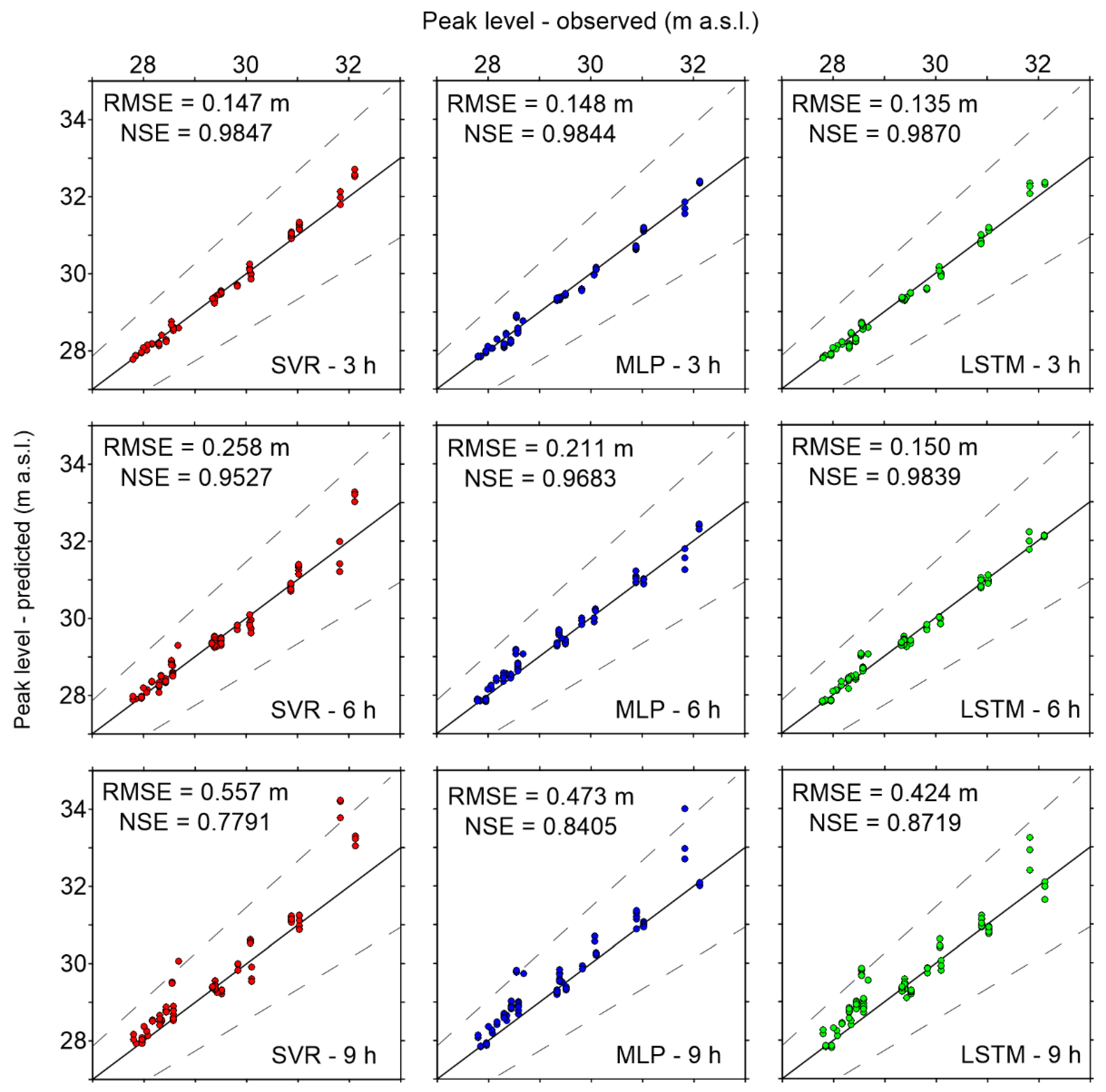
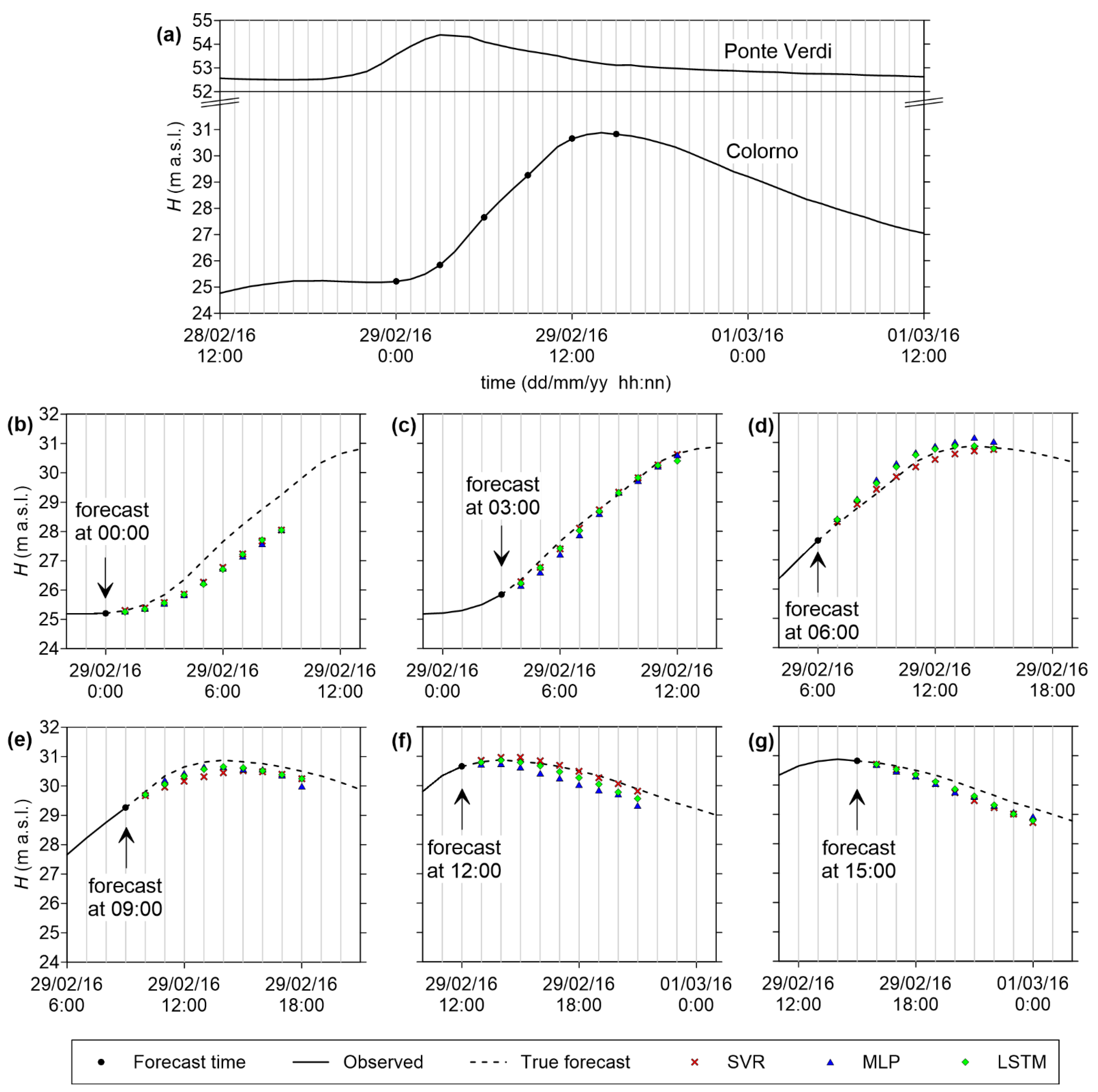
4.2. Predictive Validity
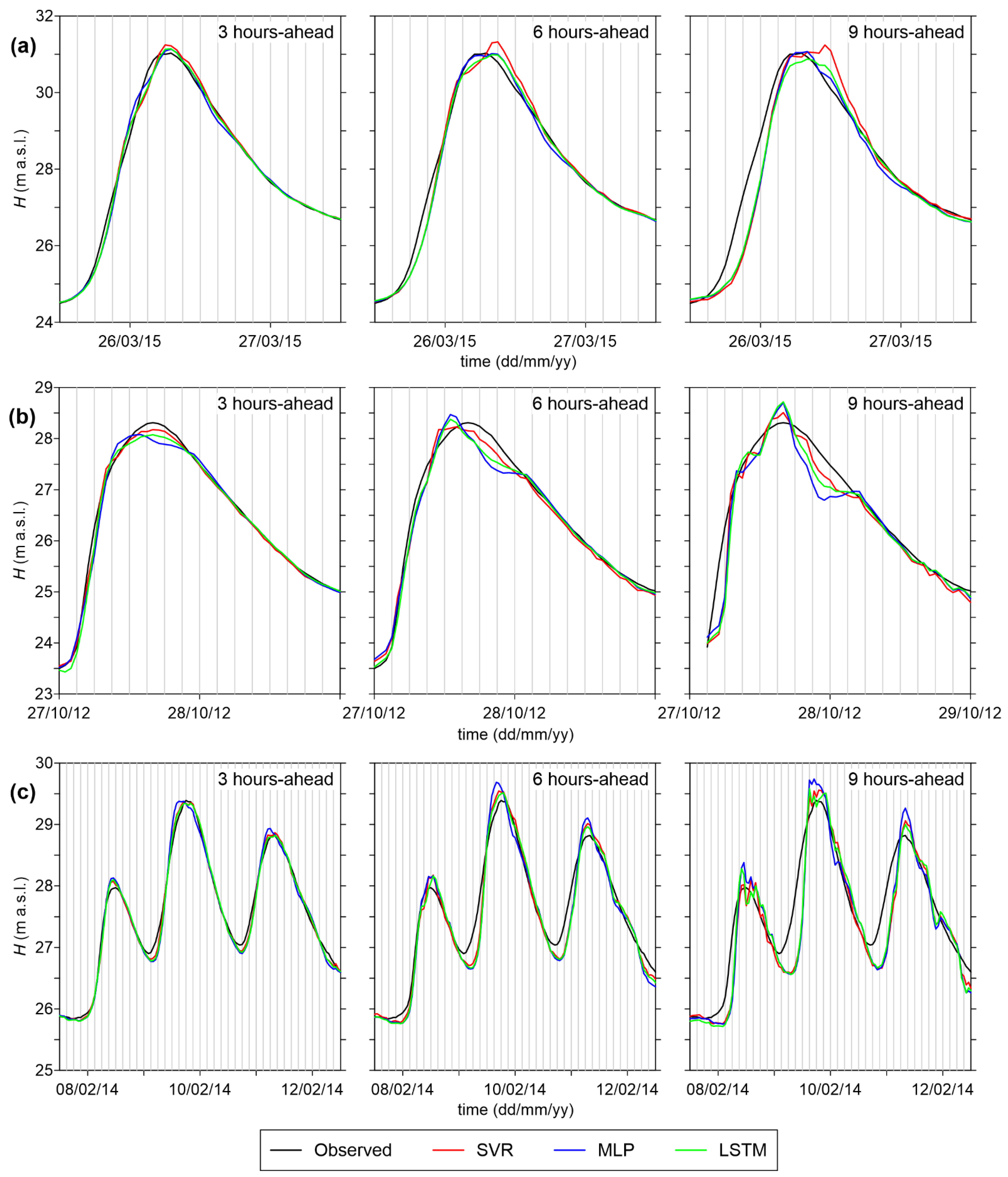
4.3. Example of Application
4.4. Computational Times
5. Conclusions
- In general, all models are able to provide sufficiently accurate stage forecasts up to 6 h ahead (RMSE < 15 cm, and NSE > 0.99), while prediction errors increase for longer lead times. The error on the peak levels also becomes very large for 9 h-ahead forecasts;
- SVR is characterized by the best RMSE values, and also by the shortest computational time. However, its accuracy on the peak levels is lower than those of the other models, especially for intermediate (6 h) and long (9 h) lead times;
- MLP presents the largest errors among the three models considered here, but the analysis of its predictive validity shows that it can still be considered suitable for practical purposes;
- LSTM performs similarly to SVR regarding the goodness-of-fit measures for the testing dataset, but it appears much more accurate in predicting the peak levels. Hence, despite the longer computational times required for the training phase, this ML model can be considered the best candidate for setting up a robust operational model for real-time flood forecasting.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jongman, B.; Ward, P.J.; Aerts, J.C.J.H. Global exposure to river and coastal flooding: Long term trends and changes. Glob. Environ. Chang. 2012, 22, 823–835. [Google Scholar] [CrossRef]
- Liu, C.; Guo, L.; Ye, L.; Zhang, S.; Zhao, Y.; Song, T. A review of advances in China’s flash flood early-warning system. Nat. Hazards 2018, 92, 619–634. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Matta, E.; Cominola, A.; Xia, X.; Zhang, Q.; Liang, Q.; Hinkelmann, R. Neurocomputing in surface water hydrology and hydraulics: A review of two decades retrospective, current status and future prospects. J. Hydrol. 2020, 588, 125085. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Dawson, C.; Wilby, R.L. Hydrological modelling using artificial neural networks. Prog. Phys. Geogr. Earth Environ. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- Talei, A.; Chua, L.H. Influence of lag time on event-based rainfall-runoff modeling using the data driven approach. J. Hydrol. 2012, 438-439, 223–233. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.; He, J.; Sudheer, K.; Tay, J.-H. Potential application of wavelet neural network ensemble to forecast streamflow for flood management. J. Hydrol. 2016, 536, 161–173. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; De Marinis, G. Support vector regression for rainfall-runoff modeling in urban drainage: A comparison with the EPA’s storm water management model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Choi, C.; Kim, J.; Han, H.; Han, D.; Kim, H.S. Development of water level prediction models using machine learning in wetlands: A case study of Upo Wetland in South Korea. Water 2019, 12, 93. [Google Scholar] [CrossRef]
- Nourani, V.; Kisi, Ö.; Komasi, M. Two hybrid artificial intelligence approaches for modeling rainfall-runoff process. J. Hydrol. 2011, 402, 41–59. [Google Scholar] [CrossRef]
- Chidthong, Y.; Tanaka, H.; Supharatid, S. Developing a hybrid multi-model for peak flood forecasting. Hydrol. Process. 2009, 23, 1725–1738. [Google Scholar] [CrossRef]
- Wang, J.-H.; Lin, G.-F.; Chang, M.-J.; Huang, I.-H.; Chen, Y.-R. Real-time water-level forecasting using dilated causal convolutional neural networks. Water Resour. Manag. 2019, 33, 3759–3780. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Neal, J.; Pender, G. A deep convolutional neural network model for rapid prediction of fluvial flood inundation. J. Hydrol. 2020, 590, 125481. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Lee, W.-K.; Resdi, T.A.T. Simultaneous hydrological prediction at multiple gauging stations using the NARX network for Kemaman catchment, Terengganu, Malaysia. Hydrol. Sci. J. 2016, 61, 2930–2945. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, H.I.; Han, K.Y.; Hong, W.H. Flood evacuation routes based on spatiotemporal inundation risk assessment. Water 2020, 12, 2271. [Google Scholar] [CrossRef]
- Song, T.; Ding, W.; Wu, J.; Liu, H.; Zhou, H.; Chu, J. Flash flood forecasting based on long short-term memory networks. Water 2020, 12, 109. [Google Scholar] [CrossRef]
- Fahimi, F.; Yaseen, Z.; El-Shafie, A. Application of soft computing based hybrid models in hydrological variables modeling: A comprehensive review. Theor. Appl. Clim. 2016, 128, 875–903. [Google Scholar] [CrossRef]
- Campolo, M.; Andreussi, P.; Soldati, A. River flood forecasting with a neural network model. Water Resour. Res. 1999, 35, 1191–1197. [Google Scholar] [CrossRef]
- Kia, M.B.; Pirasteh, S.; Pradhan, B.; Mahmud, A.R.; Sulaiman, W.N.A.; Moradi, A. An artificial neural network model for flood simulation using GIS: Johor River basin, Malaysia. Environ. Earth Sci. 2012, 67, 251–264. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Kourgialas, N.N.; Dokou, Z.; Karatzas, G.P. Statistical analysis and ANN modeling for predicting hydrological extremes under climate change scenarios: The example of a small Mediterranean agro-watershed. J. Environ. Manag. 2015, 154, 86–101. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Liu, H.; Wei, G.; Song, T.; Zhang, C.; Zhou, H. Flash flood forecasting using support vector regression model in a small mountainous catchment. Water 2019, 11, 1327. [Google Scholar] [CrossRef]
- Darras, T.; Estupina, V.B.; Kong-A-Siou, L.; Vayssade, B.; Johannet, A.; Pistre, S. Identification of spatial and temporal contributions of rainfalls to flash floods using neural network modelling: Case study on the Lez Basin (southern France). Hydrol. Earth Syst. Sci. 2015, 19, 4397–4410. [Google Scholar] [CrossRef]
- Khatibi, R.; Ghorbani, M.A.; Kashani, M.H.; Kisi, O. Comparison of three artificial intelligence techniques for discharge routing. J. Hydrol. 2011, 403, 201–212. [Google Scholar] [CrossRef]
- Tayfur, G.; Singh, V.P.; Moramarco, T.; Barbetta, S. Flood hydrograph prediction using machine learning methods. Water 2018, 10, 968. [Google Scholar] [CrossRef]
- Bermúdez, M.; Cea, L.; Puertas, J. A rapid flood inundation model for hazard mapping based on least squares support vector machine regression. J. Flood Risk Manag. 2019, 12, 12522. [Google Scholar] [CrossRef]
- Berkhahn, S.; Fuchs, L.; Neuweiler, I. An ensemble neural network model for real-time prediction of urban floods. J. Hydrol. 2019, 575, 743–754. [Google Scholar] [CrossRef]
- Chang, F.-J.; Liang, J.-M.; Chen, Y.-C. Flood forecasting using radial basis function neural networks. IEEE Trans. Syst. Man Cybern. Part. C Appl. Rev 2001, 31, 530–535. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a long short-term memory based encoder-decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Yilmaz, A.G.; Muttil, N. Runoff estimation by machine learning methods and application to the Euphrates Basin in Turkey. J. Hydrol. Eng. 2014, 19, 1015–1025. [Google Scholar] [CrossRef]
- Yu, P.-S.; Chen, S.-T.; Chang, I.-F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chen, P.-A.; Lu, Y.-R.; Huang, E.; Chang, K.-Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Rangan, D.M.; Ramasastri, K.S. Short-term flood forecasting with a neurofuzzy model. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- See, L.; Openshaw, S. Applying soft computing approaches to river level forecasting. Hydrol. Sci. J. 1999, 44, 763–778. [Google Scholar] [CrossRef]
- Hsu, M.-H.; Lin, S.-H.; Fu, J.-C.; Chung, S.-F.; Chen, A.S. Longitudinal stage profiles forecasting in rivers for flash floods. J. Hydrol. 2010, 388, 426–437. [Google Scholar] [CrossRef]
- Sung, J.Y.; Lee, J.; Chung, I.-M.; Heo, J.-H. Hourly water level forecasting at tributary affected by main river condition. Water 2017, 9, 644. [Google Scholar] [CrossRef]
- Leahy, P.; Kiely, G.; Corcoran, G. Structural optimisation and input selection of an artificial neural network for river level prediction. J. Hydrol. 2008, 355, 192–201. [Google Scholar] [CrossRef]
- Panda, R.K.; Pramanik, N.; Bala, B. Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model. Comput. Geosci. 2010, 36, 735–745. [Google Scholar] [CrossRef]
- Haykin, S.O. Neural Networks and Learning Machines, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Monaghan, J. Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics—A Meshfree Particle Method; World Scientific Publishing: Singapore, 2003. [Google Scholar]
| Type of Event | N° Events | Duration (Days) | Peak Level (m a.s.l.) | Criteria for Selection |
|---|---|---|---|---|
| Group 1: Large floods on the Parma River | 4 | 6–7 | 30.88–32.12 | Peak above the highest alert threshold (30.7 m a.s.l.) |
| Group 2: Po River floods | 16 | 6–29 | 26.99–30.10 | Events with backwater from the Po River |
| Group 3: Medium floods on the Parma River | 12 | 4–20 | 27.80–30.07 | Peak above the first alert threshold (27.7 m a.s.l.) |
| Group 4: Small floods on the Parma River | 15 | 4–11 | 26.73–27.68 | Peak above 26.7 m a.s.l. (i.e., 1 m below the first alert threshold) |
| Type of Event | Training Events | Validation Events | Testing Events |
|---|---|---|---|
| Group 1 | 3 | 0 | 1 |
| Group 2 | 10 | 3 | 3 |
| Group 3 | 8 | 2 | 2 |
| Group 4 | 11 | 2 | 2 |
| Total | 32 | 7 | 8 |
| Time Lag | Model | Training | Validation | Testing | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | CC | NSE | RMSE | MAE | CC | NSE | RMSE | MAE | CC | NSE | ||
| 3 h | SVR | 0.066 | 0.031 | 0.9978 | 0.9989 | 0.060 | 0.033 | 0.9976 | 0.9988 | 0.072 | 0.036 | 0.9971 | 0.9986 |
| MLP | 0.080 | 0.044 | 0.9967 | 0.9984 | 0.075 | 0.043 | 0.9963 | 0.9982 | 0.088 | 0.047 | 0.9956 | 0.9979 | |
| LSTM | 0.065 | 0.036 | 0.9979 | 0.9990 | 0.061 | 0.035 | 0.9976 | 0.9988 | 0.075 | 0.039 | 0.9967 | 0.9984 | |
| 6 h | SVR | 0.112 | 0.058 | 0.9935 | 0.9968 | 0.115 | 0.066 | 0.9912 | 0.9957 | 0.131 | 0.070 | 0.9904 | 0.9953 |
| MLP | 0.134 | 0.081 | 0.9907 | 0.9954 | 0.133 | 0.083 | 0.9884 | 0.9942 | 0.151 | 0.089 | 0.9870 | 0.9937 | |
| LSTM | 0.120 | 0.072 | 0.9926 | 0.9964 | 0.120 | 0.073 | 0.9905 | 0.9953 | 0.138 | 0.080 | 0.9891 | 0.9948 | |
| 9 h | SVR | 0.225 | 0.108 | 0.9737 | 0.9870 | 0.211 | 0.117 | 0.9707 | 0.9859 | 0.250 | 0.126 | 0.9642 | 0.9827 |
| MLP | 0.238 | 0.135 | 0.9709 | 0.9855 | 0.223 | 0.139 | 0.9672 | 0.9836 | 0.259 | 0.149 | 0.9613 | 0.9809 | |
| LSTM | 0.226 | 0.129 | 0.9735 | 0.9869 | 0.211 | 0.129 | 0.9707 | 0.9854 | 0.250 | 0.144 | 0.9640 | 0.9826 | |
| Time Lag | Model | Training | Validation | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (m) | NSE | MAPE | RMSE (m) | NSE | MAPE | RMSE (m) | NSE | MAPE | ||
| 3 h | SVR | 0.084 | 0.9958 | 0.98% | 0.101 | 0.9805 | 1.28% | 0.147 | 0.9847 | 1.46% |
| MLP | 0.132 | 0.9898 | 1.55% | 0.141 | 0.9619 | 1.63% | 0.148 | 0.9844 | 1.69% | |
| LSTM | 0.103 | 0.9938 | 1.15% | 0.115 | 0.9744 | 1.40% | 0.135 | 0.9870 | 1.48% | |
| 6 h | SVR | 0.121 | 0.9914 | 1.51% | 0.145 | 0.9596 | 1.65% | 0.258 | 0.9527 | 2.11% |
| MLP | 0.187 | 0.9793 | 2.32% | 0.229 | 0.8994 | 2.67% | 0.211 | 0.9683 | 2.45% | |
| LSTM | 0.153 | 0.9861 | 1.74% | 0.173 | 0.9424 | 1.76% | 0.150 | 0.9839 | 1.64% | |
| 9 h | SVR | 0.437 | 0.8874 | 4.27% | 0.395 | 0.6994 | 4.40% | 0.557 | 0.7791 | 4.74% |
| MLP | 0.425 | 0.8938 | 4.88% | 0.461 | 0.5911 | 5.23% | 0.473 | 0.8405 | 4.91% | |
| LSTM | 0.385 | 0.9128 | 4.47% | 0.427 | 0.6497 | 4.53% | 0.424 | 0.8719 | 4.66% | |
| Model | Training Time (s) (Single Model) | Training Time (s) (Ensemble 10 Models) | Prediction Time (s) |
|---|---|---|---|
| SVR | 7.8 | - | 1.1 |
| MLP | 23.8 | 245.7 | 11.5 |
| LSTM | 120.7 | 1230.8 | 67.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dazzi, S.; Vacondio, R.; Mignosa, P. Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy). Water 2021, 13, 1612. https://doi.org/10.3390/w13121612
Dazzi S, Vacondio R, Mignosa P. Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy). Water. 2021; 13(12):1612. https://doi.org/10.3390/w13121612
Chicago/Turabian StyleDazzi, Susanna, Renato Vacondio, and Paolo Mignosa. 2021. "Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy)" Water 13, no. 12: 1612. https://doi.org/10.3390/w13121612
APA StyleDazzi, S., Vacondio, R., & Mignosa, P. (2021). Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy). Water, 13(12), 1612. https://doi.org/10.3390/w13121612








