An Empirical Seasonal Rainfall Forecasting Model for the Northeast Region of Brazil
Abstract
1. Introduction
2. Materials and Methods
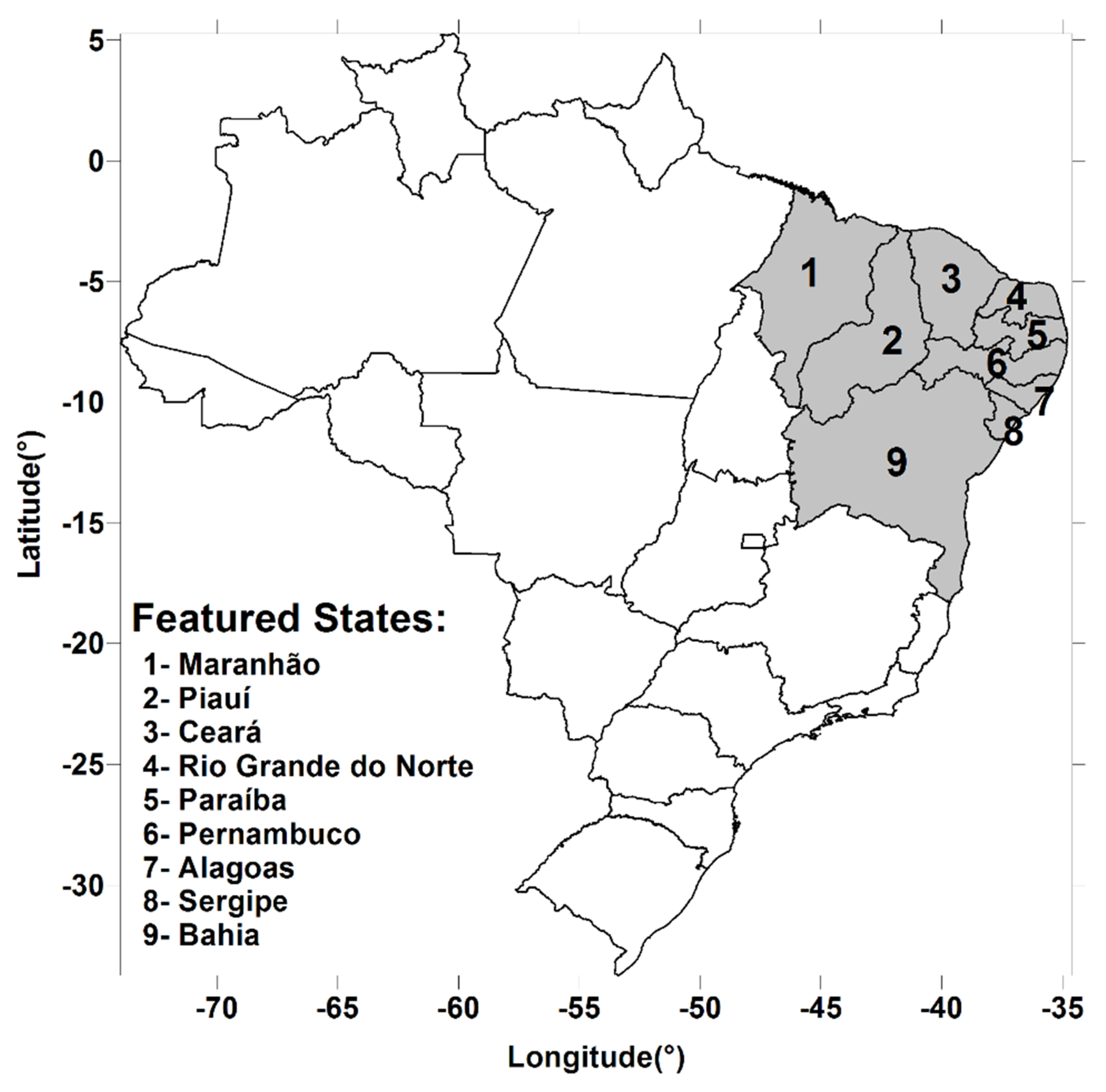
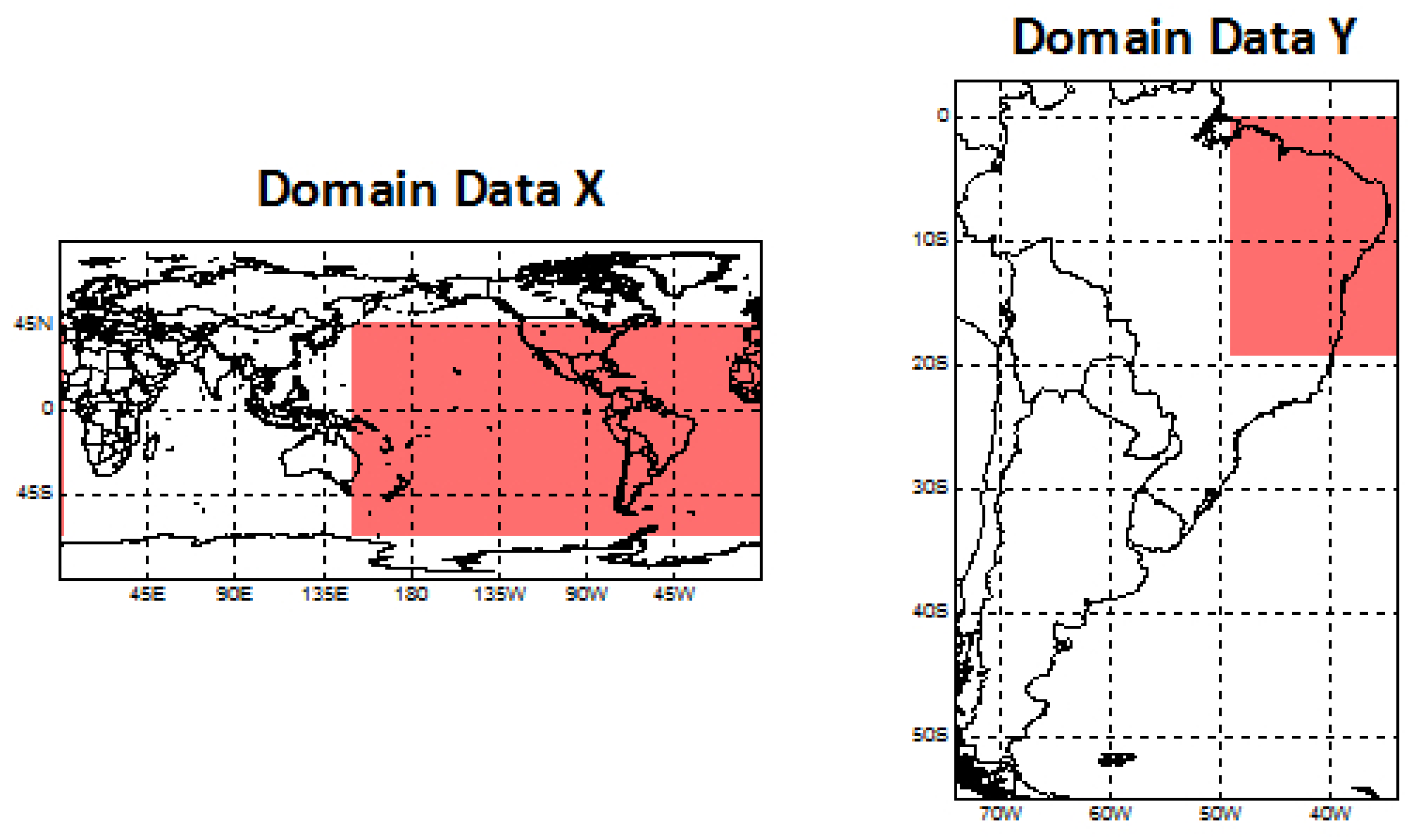
2.1. Data and Region of Study
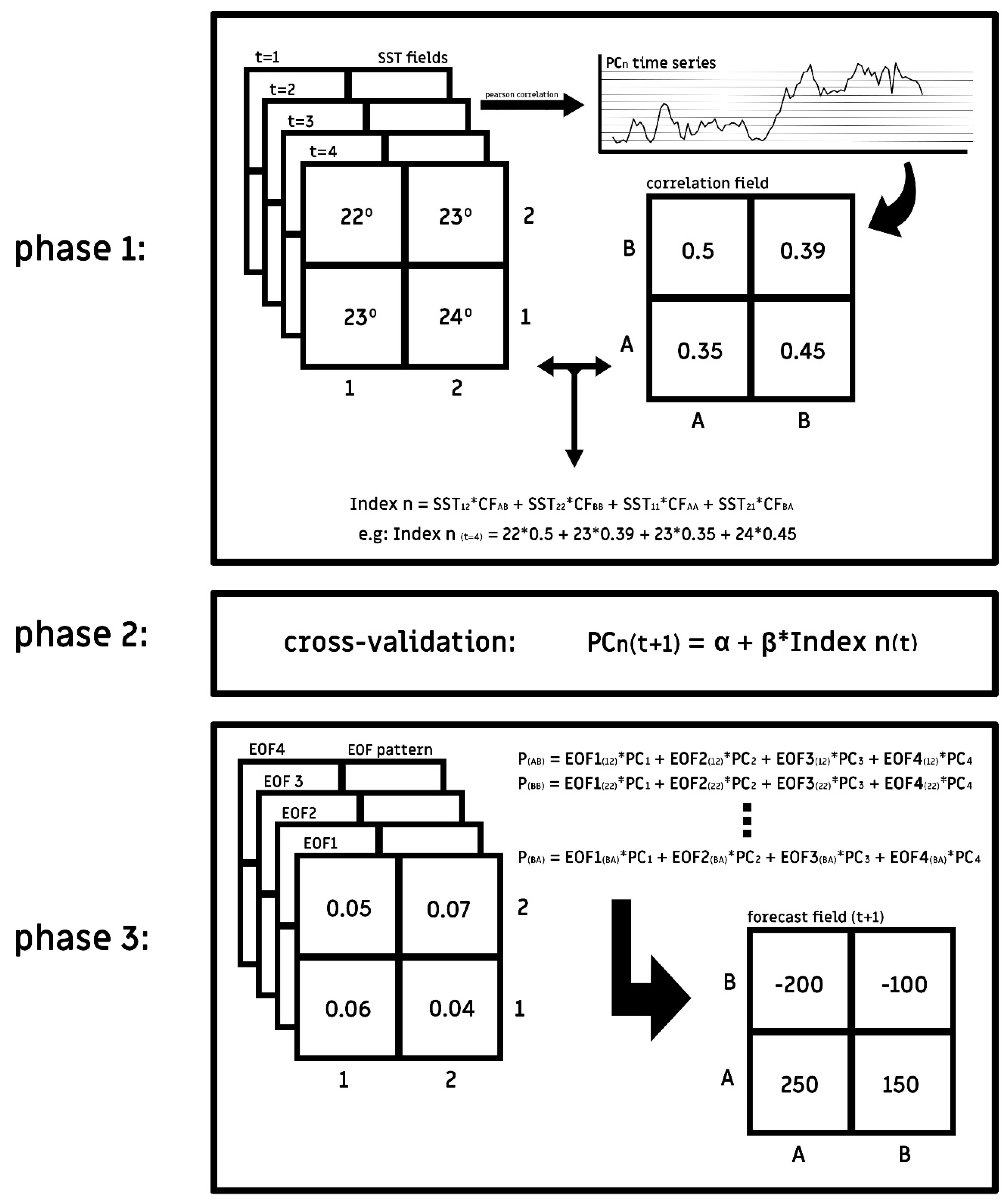
2.2. Description of the Empirical Model
2.3. North American Multi-Model Ensemble (NMME)
2.4. Model Downscaling Using the Climate Predictability Tool
2.5. Deterministic and Probabilistic Assessment
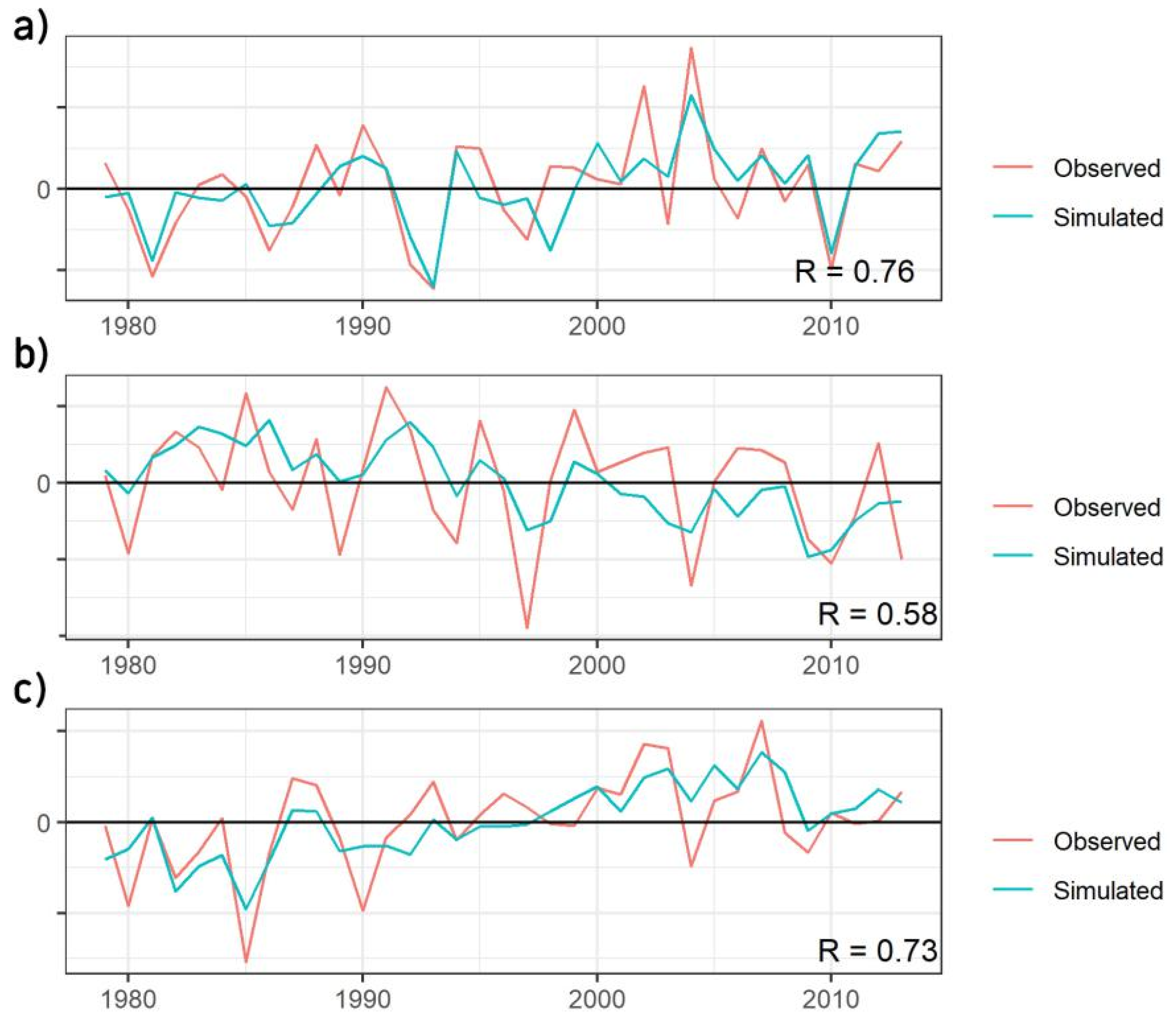
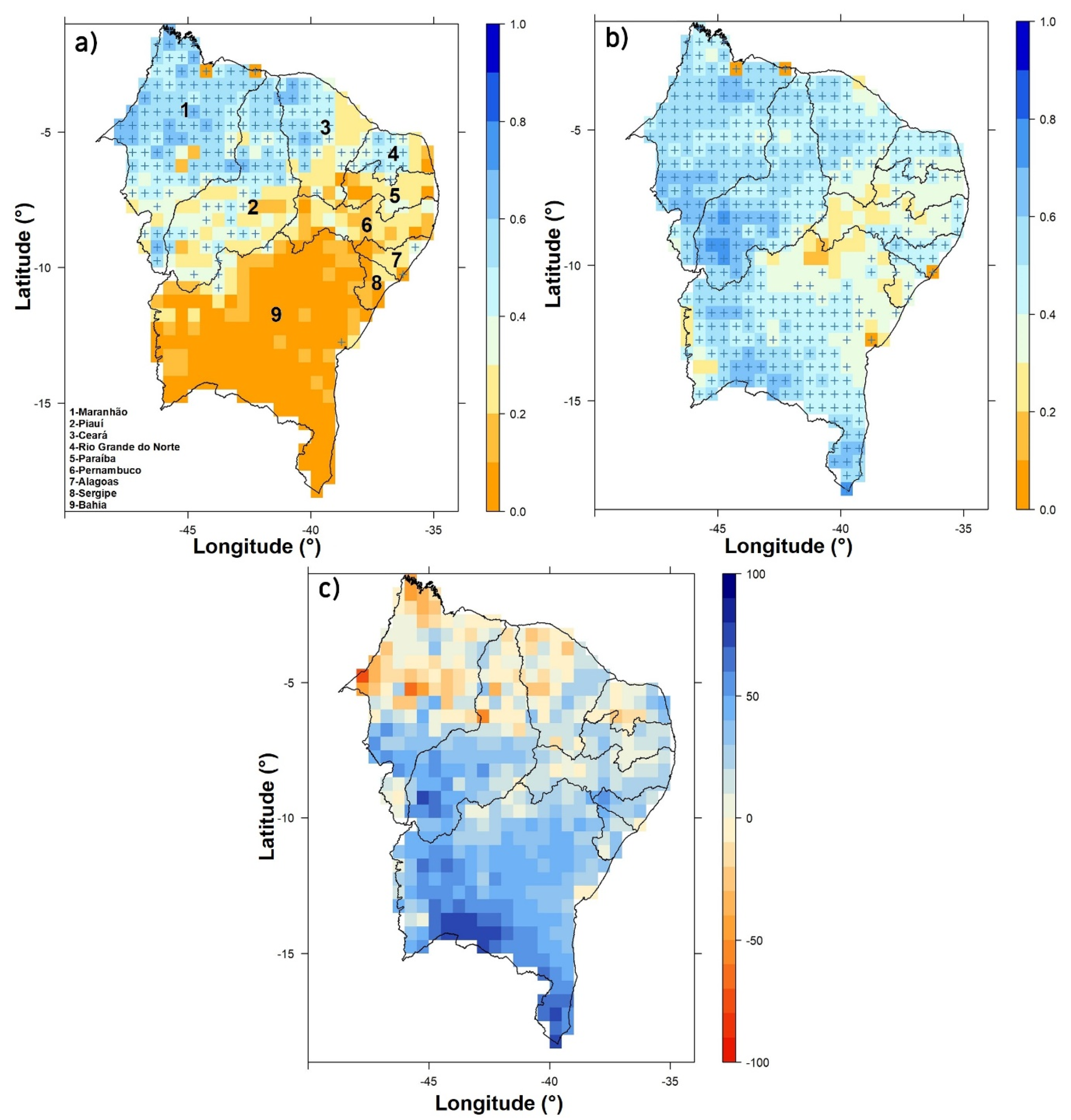
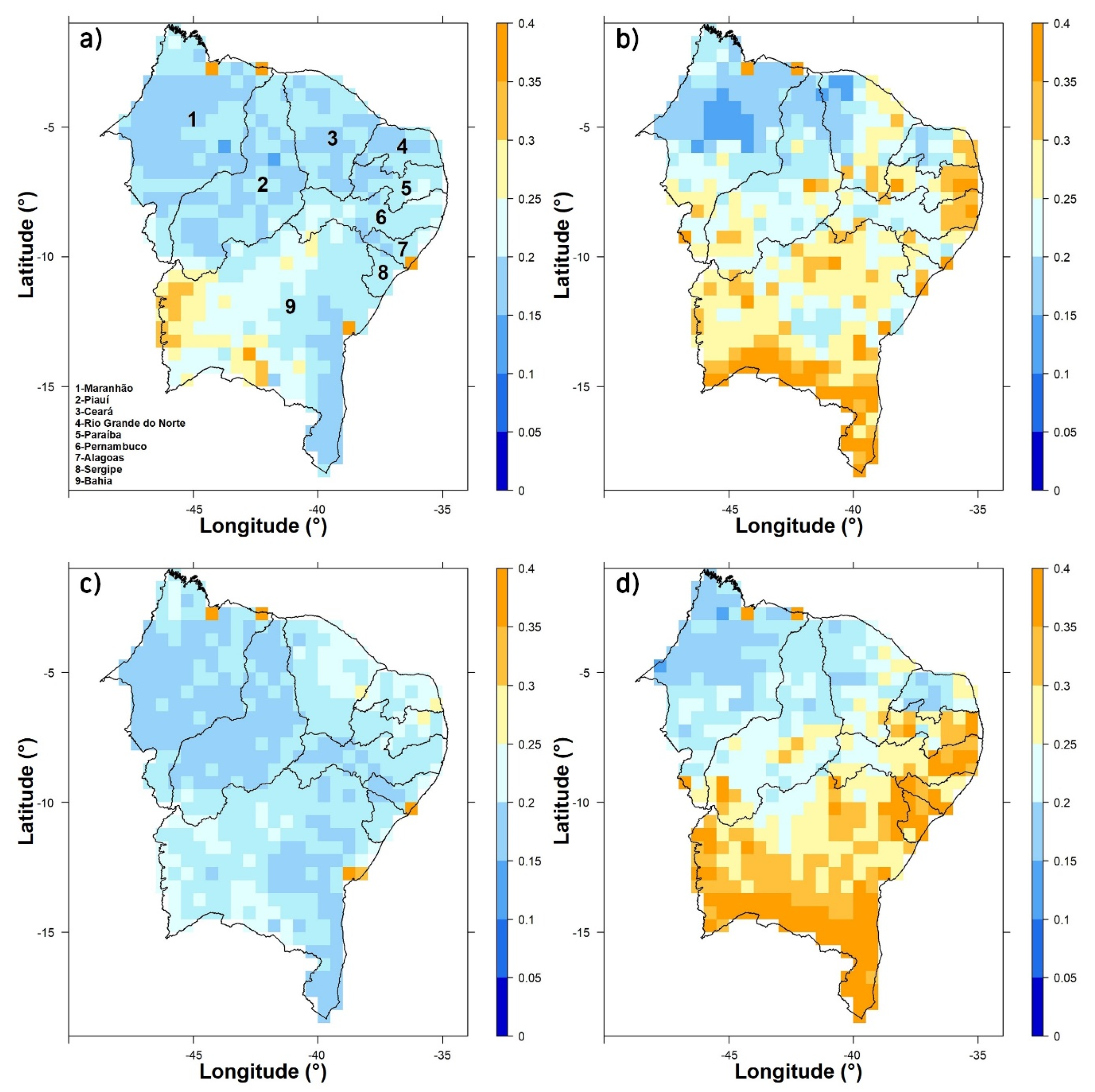
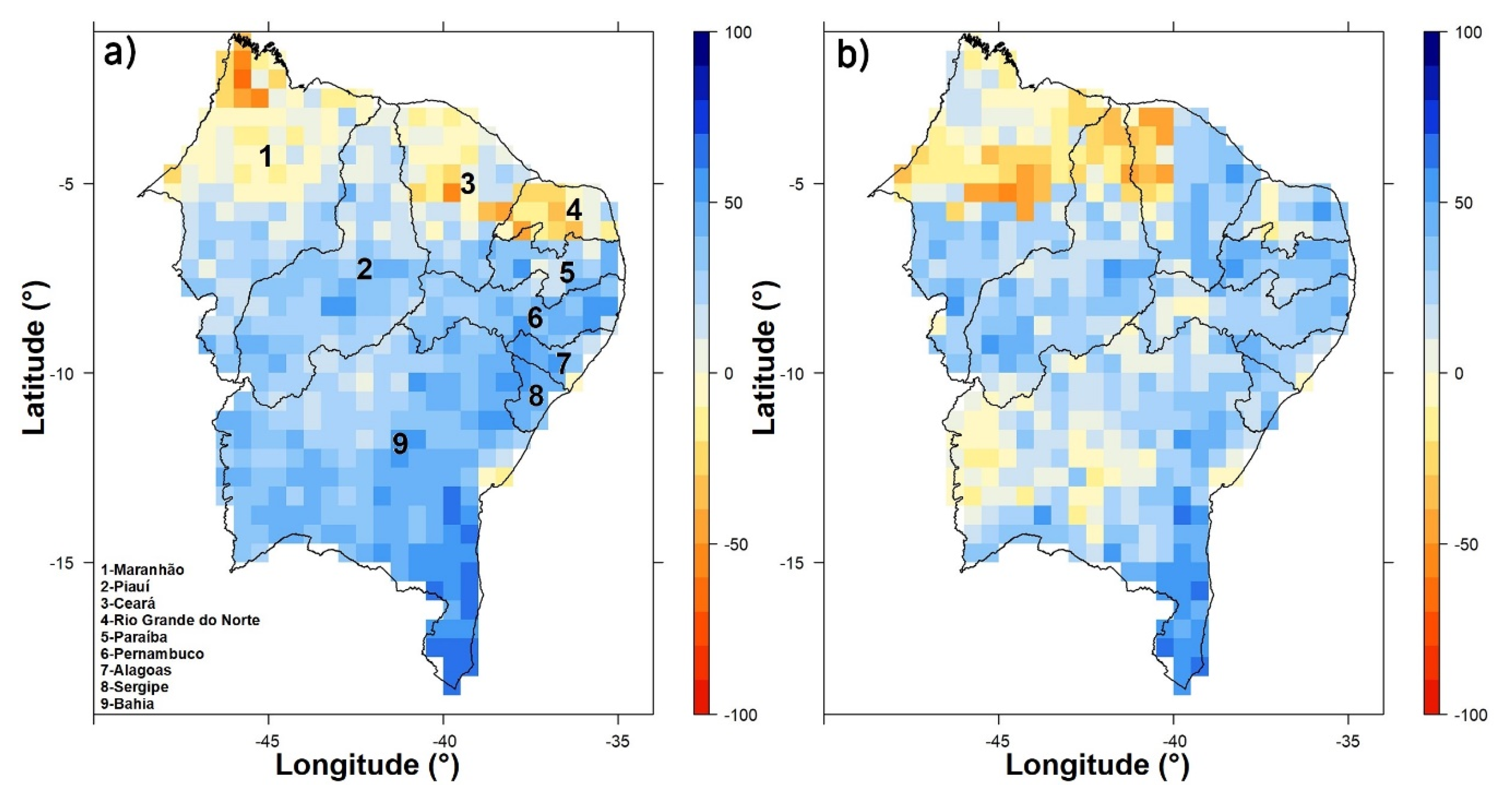
3. Results and Discussion
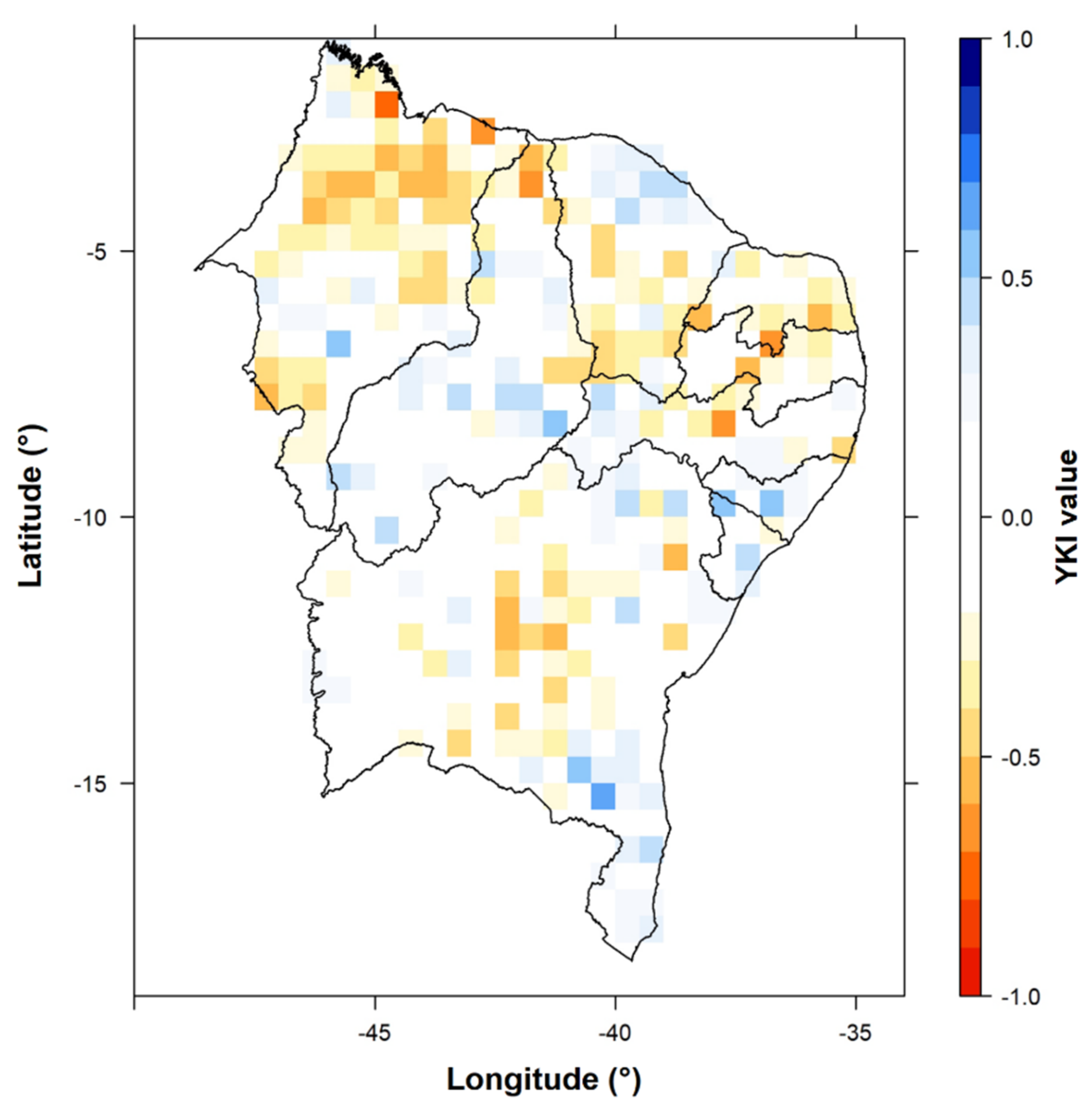
3.1. Precipitation and Teleconnection Patterns
3.2. Forecasting Patterns of Precipitation Anomalies
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dool, H.V.D. Empirical Methods in Short-Term Climate Prediction; Oxford University Press (OUP): Oxford, UK, 2006. [Google Scholar]
- Rasmusson, E.M.; Wallace, J.M. Meteorological Aspects of the El Nino/Southern Oscillation. Science 1983, 222, 1195–1202. [Google Scholar] [CrossRef]
- Karoly, D.F. Trend and Teleconnection Patterns in the Climatology of Extratropical Cyclones over the Southern Hemisphere. Palmen Memorial Symposium on Extratropical Cyclones; American Meteorological Society: Boston, MA, USA, 1988. [Google Scholar]
- Gagnon, A.S.; Smoyer-Tomic, K.E.; Bush, A.B. The El Niño Southern Oscillation and malaria epidemics in South America. Int. J. Biometeorol. 2002, 46, 81–89. [Google Scholar] [CrossRef]
- Min, S.-K.; Cai, W.; Whetton, P. Influence of climate variability on seasonal extremes over Australia. J. Geophys. Res. Atmos. 2013, 118, 643–654. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific Interdecadal Climate Oscillation with Impacts on Salmon Production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Chang, P.; Ji, L.; Li, H. A decadal climate variation in the tropical Atlantic Ocean from thermodynamic air-sea interactions. Nat. Cell Biol. 1997, 385, 516–518. [Google Scholar] [CrossRef]
- Delworth, T.L.; Zeng, F.; Vecchi, G.A.; Yang, X.; Zhang, L.; Zhang, R. The North Atlantic Oscillation as a driver of rapid climate change in the Northern Hemisphere. Nat. Geosci. 2016, 9, 509–512. [Google Scholar] [CrossRef]
- Hammer, G.; Hansen, J.; Phillips, J.; Mjelde, J.; Hill, H.; Love, A.; Potgieter, A. Advances in application of climate prediction in agriculture. Agric. Syst. 2001, 70, 515–553. [Google Scholar] [CrossRef]
- Edwards, P.N. History of climate modelling. Wires Clim. Chang. 2011, 2, 128–139. [Google Scholar] [CrossRef]
- Peña, M.; Chen, L.G.; van den Dool, H. Intraseasonal to Interannual Climate Variability and Prediction. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Wood, A., Cloke, H., Schaake, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Reboita, M.S.; Dias, C.G.; Dutra, L.M.M.; Rocha, R.P.; Llopart, M. Previsão Climática Sazonal para o Brasil Obtida Através de Modelos Climáticos Globais e Regional. Rev. Bras. Meteorol. 2018, 33, 207–224. [Google Scholar] [CrossRef]
- Hertig, E.; Maraun, D.; Bartholy, J.; Pongracz, R.; Vrac, M.; Mares, I.; Gutiérrez, J.M.; Wibig, J.; Casanueva, A.; Soares, P.M.M. Comparison of statistical downscaling methods with respect to extreme events over Europe: Validation results from the perfect predictor experiment of the COST Action VALUE. Int. J. Clim. 2018, 39, 3846–3867. [Google Scholar] [CrossRef]
- Rückamp, M.; Goelzer, H.; Humbert, A. Sensitivity of Greenland ice sheet projections to spatial resolution in higher-order simulations: The Alfred Wegener Institute (AWI) contribution to ISMIP6 Greenland using the Ice-sheet and Sea-level System Model (ISSM). Cryosphere 2020, 14, 3309–3327. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.K. Do Statistical Pattern Corrections Improve Seasonal Climate Predictions in the North American Multimodel Ensemble Models? J. Clim. 2017, 30, 8335–8355. [Google Scholar] [CrossRef]
- Hewitson, B.C.; Crane, R.G. Consensus between GCM climate change projections with empirical downscaling: Precipitation downscaling over South Africa. Int. J. Clim. 2006, 26, 1315–1337. [Google Scholar] [CrossRef]
- Ratnam, J.V.; Doi, T.; Behera, S. Dynamical Downscaling of SINTEX-F2v CGCM Seasonal Retrospective Austral Summer Forecasts over Australia. J. Clim. 2017, 30, 3219–3235. [Google Scholar] [CrossRef]
- Kaspar-Ott, I.; Hertig, E.; Kaspar, S.; Pollinger, F.; Ring, C.; Paeth, H.; Jacobeit, J. Weights for general circulation models from CMIP3/CMIP5 in a statistical downscaling framework and the impact on future Mediterranean precipitation. Int. J. Clim. 2019, 39, 3639–3654. [Google Scholar] [CrossRef]
- Han, Z.; Shi, Y.; Wu, J.; Xu, Y.; Zhou, B. Combined Dynamical and Statistical Downscaling for High-Resolution Projections of Multiple Climate Variables in the Beijing–Tianjin–Hebei Region of China. J. Appl. Meteorol. Clim. 2019, 58, 2387–2403. [Google Scholar] [CrossRef]
- Ozturk, T.; Altinsoy, H.; Türkeş, M.; Kurnaz, M.; Kurnaz, L. Simulation of temperature and precipitation climatology for the Central Asia CORDEX domain using RegCM 4.0. Clim. Res. 2012, 52, 63–76. [Google Scholar] [CrossRef]
- Giorgi, F.; Gutowski, W.J. Regional Dynamical Downscaling and the CORDEX Initiative. Annu. Rev. Environ. Resour. 2015, 40, 467–490. [Google Scholar] [CrossRef]
- Bhatla, R.; Ghosh, S.; Mandal, B.; Mall, R.; Sharma, K. Simulation of Indian summer monsoon onset with different parameterization convection schemes of RegCM-4.3. Atmos. Res. 2016, 176–177, 10–18. [Google Scholar] [CrossRef]
- Manzanas, R.; Gutiérrez, J.M.; Fernández, J.; Van Meijgaard, E.; Calmanti, S.; Magariño, M.E.; Cofiño, A.S.; Herrera, A. Dynamical and statistical downscaling of seasonal temperature forecasts in europe: Added value for sectorial applications. Clim. Serv. 2018, 9, 72–85. [Google Scholar] [CrossRef]
- Nikulin, G.; Lennard, C.; Dosio, A.; Kjellström, E.; Chen, Y.; Hänsler, A.; Kupiainen, M.; Laprise, R.; Mariotti, L.; Maule, C.F.; et al. The effects of 1.5 and 2 degrees of global warming on Africa in the CORDEX ensemble. Environ. Res. Lett. 2018, 13, 065003. [Google Scholar] [CrossRef]
- Giorgi, F. Thirty Years of Regional Climate Modeling: Where Are We and Where Are We Going next? J. Geophys. Res. Atmos. 2019, 124, 5696–5723. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Navarro, A.; Moreno, R.; Sánchez, J.L.; García-Ortega, E. Regional climate models: 30 years of dynamical downscaling. Atmos. Res. 2020, 235, 104785. [Google Scholar] [CrossRef]
- Imada, Y.; Kanae, S.; Kimoto, M.; Watanabe, M.; Ishii, M. Predictability of Persistent Thailand Rainfall during the Mature Monsoon Season in 2011 Using Statistical Downscaling of CGCM Seasonal Prediction. Mon. Weather Rev. 2015, 143, 1166–1178. [Google Scholar] [CrossRef]
- Chu, J.-L.; Kang, H.; Tam, C.-Y.; Park, C.-K.; Chen, C.-T. Seasonal forecast for local precipitation over northern Taiwan using statistical downscaling. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Kang, I.-S.; Lee, J.-Y.; Park, C.-K. Potential Predictability of Summer Mean Precipitation in a Dynamical Seasonal Prediction System with Systematic Error Correction. J. Clim. 2004, 17, 834–844. [Google Scholar] [CrossRef]
- Kang, H.; An, K.-H.; Park, C.-K.; Solis, A.L.S.; Stitthichivapak, K. Multimodel output statistical downscaling prediction of precipitation in the Philippines and Thailand. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Xing, W.; Wang, B.; Yim, S.-Y. Long-Lead Seasonal Prediction of China Summer Rainfall Using an EOF–PLS Regression-Based Methodology. J. Clim. 2016, 29, 1783–1796. [Google Scholar] [CrossRef]
- Madadgar, S.; AghaKouchak, A.; Shukla, S.; Wood, A.W.; Cheng, L.; Hsu, K.; Svoboda, M. A Hybrid Statistical-Dynamical Drought Prediction Framework: Application to the Southwestern United States. Water Resour. Res. 2016, 52, 5095–5110. [Google Scholar] [CrossRef]
- Liu, L.; Ning, L.; Liu, J.; Yan, M.; Sun, W. Prediction of summer extreme precipitation over the middle and lower reaches of the Yangtze River basin. Int. J. Clim. 2019, 39, 375–383. [Google Scholar] [CrossRef]
- Júnior, R.L.D.R.; Silva, F.D.D.S.; Costa, R.L.; Gomes, H.B.; Herdies, D.L.; Silva, V.D.P.R.D.; Xavier, A.C. Analysis of the Space–Temporal Trends of Wet Conditions in the Different Rainy Seasons of Brazilian Northeast by Quantile Regression and Bootstrap Test. Geosciences 2019, 9, 457. [Google Scholar] [CrossRef]
- Júnior, R.L.D.R.; Silva, F.D.D.S.; Costa, R.L.; Gomes, H.B.; Pinto, D.D.C.; Herdies, D.L. Bivariate Assessment of Drought Return Periods and Frequency in Brazilian Northeast Using Joint Distribution by Copula Method. Geosciences 2020, 10, 135. [Google Scholar] [CrossRef]
- Silva, V.B.S.; Kousky, V.E.; Silva, F.D.S.; Salvador, M.A.; Aravequia, J.A. The 2012 severe drought over Northeast Brazil. Bull. Am. Meteorol. Soc. 2013, 94, 162. [Google Scholar]
- Rodrigues, R.R.; Haarsma, R.J.; Campos, E.J.D.; Ambrizzi, T. The Impacts of Inter–El Niño Variability on the Tropical Atlantic and Northeast Brazil Climate. J. Clim. 2011, 24, 3402–3422. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; Stephenson, D.B.; Balmaseda, M.; Doblas-Reyes, F.J.; Van Oldenborgh, G.J.; Doblas-Reyes, F. Toward an Integrated Seasonal Forecasting System for South America. J. Clim. 2006, 19, 3704–3721. [Google Scholar] [CrossRef]
- Osman, M.; Vera, C.; Doblas-Reyes, F. Predictability of the tropospheric circulation in the Southern Hemisphere from CHFP models. Clim. Dyn. 2016, 46, 2423–2434. [Google Scholar] [CrossRef]
- Reboita, M.S.; da Rocha, R.P.; de Souza, M.R.; Llopart, M. Extratropical cyclones over the southwestern South Atlantic Ocean: HadGEM2-ES and RegCM4 projections. Int. J. Climatol. 2018, 38, 2866–2879. [Google Scholar] [CrossRef]
- Alves, J.M.B.; Costa, A.A.; Sombra, S.S.; Campos, J.N.B.; Souza Filho, F.A.; Martins, E.S.P.R.; Silva, E.M.; Santos, A.C.S.; Barbosa, H.A.; Melcíades, W.L.B.; et al. Um Estudo Inter-Comparativo de Previsão Sazonal Estatística-Dinâmica de Precipitação para o Nordeste do Brasil. Rev. Bras. Meteorol. 2007, 24, 20–29. [Google Scholar]
- Lucio, P.S.; Silva, F.D.D.S.; Fortes, L.T.G.; Dos Santos, L.A.R.; Ferreira, D.B.; Salvador, M.D.A.; Balbino, H.T.; Sarmanho, G.F.; Dos Santos, L.S.F.C.; Lucas, E.W.M.; et al. Um modelo estocástico combinado de previsão sazonal para a precipitação no Brasil. Rev. Bras. Meteorol. 2010, 25, 70–87. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; Stephenson, D.B.; Doblas-Reyes, F.J.; Balmaseda, M. The skill of empirical and combined/calibrated coupled multi-model South American seasonal predictions during ENSO. Adv. Geosci. 2006, 6, 51–55. [Google Scholar] [CrossRef]
- Lemos, M.C.; Finan, T.J.; Fox, R.W.; Nelson, D.R.; Tucker, J. The Use of Seasonal Climate Forecasting in Policymaking: Lessons from Northeast Brazil. Clim. Chang. 2002, 55, 479–507. [Google Scholar] [CrossRef]
- Kirtman, B.P.; Min, D.; Infanti, J.M.; Kinter, J.L.; Paolino, D.A.; Zhang, Q.; Van Den Dool, H.; Saha, S.; Mendez, M.P.; Becker, E.; et al. The North American multimodel ensemble: Phase-1 seasonal-to-interannual prediction; phase-2 toward developing intraseasonal prediction. Bull. Am. Meteorol. Soc. 2014, 95, 585–601. [Google Scholar] [CrossRef]
- Santos e Silva, C.M.; Lucio, P.S.; Spyrides, M.H.C. Distribuição espacial da precipitação sobre o Rio Grande do Norte: Estimativas via satélites e medidas por pluviômetros. Rev. Bras. Meteorol. 2012, 27, 337–346. [Google Scholar] [CrossRef]
- Wang, B.; Lee, J.Y.; Kang, I.S.; Shukla, J.; Hameed, S.N.; Park, C.K. Coupled predictability of seasonal tropical precipitation. CLIVAR Exch. 2007, 12, 17–18. [Google Scholar]
- Xing, W.; Wang, B.; Yim, S.-Y. Peak-summer East Asian rainfall predictability and prediction part I: Southeast Asia. Clim. Dyn. 2014, 47, 1–13. [Google Scholar] [CrossRef]
- Yim, S.-Y.; Wang, B.; Xing, W. Prediction of early summer rainfall over South China by a physical-empirical model. Clim. Dyn. 2014, 43, 1883–1891. [Google Scholar] [CrossRef]
- Wang, B.; Lee, J.-Y.; Xiang, B. Asian summer monsoon rainfall predictability: A predictable mode analysis. Clim. Dyn. 2015, 44, 61–74. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in The Atmospheric Sciences, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Bolinger, R.A.; Gronewold, A.D.; Kompoltowicz, K.; Fry, L.M. Application of the NMME in the Development of a New Regional Seasonal Climate Forecast Tool. Bull. Am. Meteorol. Soc. 2017, 98, 555–564. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Zhang, S.; Harrison, M.J.; Rosati, A.; Wittenberg, A. System Design and Evaluation of Coupled Ensemble Data Assimilation for Global Oceanic Climate Studies. Mon. Weather Rev. 2007, 135, 3541–3564. [Google Scholar] [CrossRef]
- Jia, L.; Yang, X.; Vecchi, G.; Gudgel, R.G.; Delworth, T.; Rosati, A.; Stern, W.F.; Wittenberg, A.T.; Krishnamurthy, L.; Zhang, S.; et al. Improved Seasonal Prediction of Temperature and Precipitation over Land in a High-Resolution GFDL Climate Model. J. Clim. 2015, 28, 2044–2062. [Google Scholar] [CrossRef]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.; Lawrence, D.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model Version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Vernieres, G.; Rienecker, M.M.; Kovach, R.; Keppenne, C. The GEOS-iODAS: Description and Evaluation; Tech. Rep. TM-2012-104606; NASA, National Aeronautics and Space Administration Goddard Space Flight Center: Greenbelt, MD, USA, 2012.
- Borovikov, A.; Cullather, R.; Kovach, R.; Marshak, J.; Vernieres, G.; Vikhliaev, Y.; Zhao, B.; Li, Z. GEOS-5 seasonal forecast system. Clim. Dyn. 2017, 53, 7335–7361. [Google Scholar] [CrossRef]
- Merryfield, W.J.; Lee, W.-S.; Boer, G.J.; Kharin, V.V.; Scinocca, J.F.; Flato, G.M.; Ajayamohan, R.S.; Fyfe, J.C.; Tang, Y.; Polavarapu, S. The Canadian Seasonal to Interannual Prediction System. Part I: Models and Initialization. Mon. Weather Rev. 2013, 141, 2910–2945. [Google Scholar] [CrossRef]
- Becker, E.; Dool, H.V.D.; Zhang, Q. Predictability and Forecast Skill in NMME. J. Clim. 2014, 27, 5891–5906. [Google Scholar] [CrossRef]
- Mo, K.C.; Lettenmaier, D.P. Objective Drought Classification Using Multiple Land Surface Models. J. Hydrometeorol. 2014, 15, 990–1010. [Google Scholar] [CrossRef]
- Mo, K.C.; Lyon, B. Global Meteorological Drought Prediction Using the North American Multi-Model Ensemble. J. Hydrometeorol. 2015, 16, 1409–1424. [Google Scholar] [CrossRef]
- Wood, E.F.; Schubert, S.D.; Wood, A.; Peters-Lidard, C.D.; Mo, K.C.; Mariotti, A.; Pulwarty, R.S. Prospects for Advancing Drought Understanding, Monitoring, and Prediction. J. Hydrometeorol. 2015, 16, 1636–1657. [Google Scholar] [CrossRef]
- Thiaw, W.M.; Kumar, V.B. NOAA’s African Desk: Twenty Years of Developing Capacity in Weather and Climate Forecasting in Africa. Bull. Am. Meteorol. Soc. 2015, 96, 737–753. [Google Scholar] [CrossRef]
- Ma, F.; Yuan, X.; Ye, A. Seasonal drought predictability and forecast skill over China. J. Geophys. Res. Atmos. 2015, 120, 8264–8275. [Google Scholar] [CrossRef]
- Tian, D.; Martinez, C.J.; Graham, W.D.; Hwang, S. Statistical Downscaling Multimodel Forecasts for Seasonal Precipitation and Surface Temperature over the Southeastern United States. J. Clim. 2014, 27, 8384–8411. [Google Scholar] [CrossRef]
- Climate Predictability Tool version 15.5.10; Mason, S.J., Tippett, M.K., Eds.; Columbia University Academic Commons: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Esquivel, A.; Llanos-Herrera, L.; Agudelo, D.; Prager, S.D.; Fernandes, K.; Rojas, A.; Valencia, J.J.; Ramirez-Villegas, J. Predictability of seasonal precipitation across major crop growing areas in Colombia. Clim. Serv. 2018, 12, 36–47. [Google Scholar] [CrossRef]
- Hossain, M.Z.; Azad, M.A.K.; Karmakar, S.; Mondal, M.N.I.; Das, M.; Rahman, M.M.; Haque, M.A. Assessment of Better Prediction of Seasonal Rainfall by Climate Predictability Tool Using Global Sea Surface Temperature in Bangladesh. Asian J. Adv. Res. Rep. 2019, 4, 1–13. [Google Scholar] [CrossRef]
- Barnett, T.P.; Preisendorfer, R. Origins and Levels of Monthly and Seasonal Forecast Skill for United States Surface Air Temperatures Determined by Canonical Correlation Analysis. Mon. Weather Rev. 1987, 115, 1825–1850. [Google Scholar] [CrossRef]
- Barnston, A.G. Linear Statistical Short-Term Climate Predictive Skill in the Northern Hemisphere. J. Clim. 1994, 7, 1513–1564. [Google Scholar] [CrossRef]
- Johansson, Å.; Barnston, A.; Saha, S.; van den Dool, H. On the Level and Origin of Seasonal Forecast Skill in Northern Europe. J. Atmos. Sci. 1998, 55, 103–127. [Google Scholar] [CrossRef]
- Moura, A.D.; Shukla, J. On the Dynamics of Droughts in Northeast Brazil: Observations, Theory and Numerical Experiments with a General Circulation Model. J. Atmos. Sci. 1981, 38, 2653–2675. [Google Scholar] [CrossRef]
- Chiang, J.C.H.; Kushnir, Y.; Zebiak, S.E. Interdecadal changes in eastern Pacific ITCZ variability and its influence on the Atlantic ITCZ. Geophys. Res. Lett. 2000, 27, 3687–3690. [Google Scholar] [CrossRef]
- Hounsou-Gbo, G.A.; Servain, J.; Araujo, M.; Martins, E.S.; Bourlès, B.; Caniaux, G. Oceanic Indices for Forecasting Seasonal Rainfall over the Northern Part of Brazilian Northeast. Am. J. Clim. Chang. 2016, 05, 261–274. [Google Scholar] [CrossRef]
- Kayano, M.T.; Andreoli, R.V. Relationships between rainfall anomalies over northeastern Brazil and the El Niño–Southern Oscillation. J. Geophys. Res. Space Phys. 2006, 111, 13101. [Google Scholar] [CrossRef]
- Nobre, C.A.; Molion, L.C.B. The Climatology of Droughts and Drought Prediction. In Impacts of Climatic Variations on Agriculture. Volume 2: Assessements in Semi-Arid Regions; Parry, M.P., Carter, T.R., Konijn, N.T., Eds.; D. Reidel Pub. Co.: Dordrecht, The Netherlands, 1988; 764p. [Google Scholar]
- Chaves, R.R.; Cavalcanti, I.F.A. Atmospheric Circulation Features Associated with Rainfall Variability over Southern Northeast Brazil. Mon. Weather Rev. 2001, 129, 2614–2626. [Google Scholar] [CrossRef]
- Rodrigues, R.R.; McPhaden, M.J. Why did the 2011-2012 La Niña cause a severe drought in the Brazilian Northeast? Geophys. Res. Lett. 2014, 41, 1012–1018. [Google Scholar] [CrossRef]
- Andreoli, R.V.; Kayano, M.T. A importância relativa do atlântico tropical sul e pacífico leste na variabilidade de precipitação do Nordeste do Brasil. Rev. Bras. Meteorol. 2007, 22, 63–74. [Google Scholar] [CrossRef]
- Uvo, C.B.; Repelli, C.A.; Zebiak, S.E.; Kushnir, Y. The Relationships between Tropical Pacific and Atlantic SST and Northeast Brazil Monthly Precipitation. J. Clim. 1998, 11, 551–562. [Google Scholar] [CrossRef]
- Molion, L.C.B.; Bernardo, S.O. Uma revisão da dinâmica das chuvas no Nordeste Brasileiro. Rev. Bras. Meteorol. 2002, 17, 1–10. [Google Scholar]
- Walker, G.T. Ceará (Brazil) famines and the general air movement. Beitr. Phys. Frein. Atmosph. 1928, 14, 88–93. [Google Scholar]
- Alvarez, M.S.; Vera, C.; Kiladis, G.N.; Liebmann, B. Influence of the Madden Julian Oscillation on precipitation and surface air temperature in South America. Clim. Dyn. 2016, 46, 245–262. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R. The Pacific Decadal Oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Andreoli, R.V.; Kayano, M.T. Multi-scale variability of the sea surface temperature in the Tropical Atlantic. J. Geophys. Res. 2004, 109, 1–12. [Google Scholar] [CrossRef]
- Oliveira, P.T.; e Silva, C.M.S.; Lima, K.C. Climatology and trend analysis of extreme precipitation in subregions of Northeast Brazil. Theor. Appl. Clim. 2017, 130, 77–90. [Google Scholar] [CrossRef]
- Müller, G.V.; Ambrizzi, T. Teleconnection patterns and Rossby wave propagation associated to generalized frosts over southern South America. Clim. Dyn. 2007, 29, 633–645. [Google Scholar] [CrossRef]
- Gomes, H.B.; Ambrizzi, T.; Herdies, D.L.; Hodges, K.; Da Silva, B.F.P. Easterly Wave Disturbances over Northeast Brazil: An Observational Analysis. Adv. Meteorol. 2015, 2015, 176238. [Google Scholar] [CrossRef]
- Fedorova, N.; Levit, V.; da Cruz, C.D. On Frontal Zone Analysis in the Tropical Region of the Northeast Brazil. Pure Appl. Geophys. 2016, 173, 1403–1421. [Google Scholar] [CrossRef]
- Costa, D.D.; Uvo, C.B.; Da Paz, A.R.; Carvalho, F.O.; Fragoso, C.R., Jr. Long-term relationships between climate oscillation and basin-scale hydrological variability during rainy season in eastern Northeast Brazil. Hydrol. Sci. J. 2018, 63, 1636–1652. [Google Scholar] [CrossRef]
- Zhang, Z.; Uotila, P.; Stössel, A.; Vihma, T.; Liu, H.; Zhong, Y. Seasonal southern hemisphere multi-variable reflection of the southern annular mode in atmosphere and ocean reanalyses. Clim. Dyn. 2018, 50, 1451–1470. [Google Scholar] [CrossRef]
- Visbeck, M. A Station-Based Southern Annular Mode Index from 1884 to 2005. J. Clim. 2009, 22, 940–950. [Google Scholar] [CrossRef]
- Namias, J. Influence of northern hemisphere general circulation on drought in northeast Brazil. Tellus 1972, 24, 336–343. [Google Scholar] [CrossRef]
- Gomes, H.B.; Ambrizzi, T.; Da Silva, B.F.P.; Hodges, K.; Dias, P.L.S.; Herdies, D.; Silva, M.C.L.; Gomes, H.B. Climatology of easterly wave disturbances over the tropical South Atlantic. Clim. Dyn. 2019, 53, 1393–1411. [Google Scholar] [CrossRef]
- Saurral, R.I.; Doblas-Reyes, F.J.; García-Serrano, J. Observed modes of sea surface temperature variability in the South Pacific region. Clim. Dyn. 2018, 50, 1129–1143. [Google Scholar] [CrossRef]
- Salinger, M.J.; Renwick, J.A.; Mullan, A.B. Interdecadal Pacific Oscillation and South Pacific climate. Int. J. Clim. 2001, 21, 1705–1721. [Google Scholar] [CrossRef]
- Henley, B.J.; Gergis, J.; Karoly, D.J.; Power, S.B.; Kennedy, J.J.; Folland, C.K. A Tripole Index for the Interdecadal Pacific Oscillation. Clim. Dyn. 2015, 45, 3077–3090. [Google Scholar] [CrossRef]
- Figueroa, S.N.; Bonatti, J.P.; Kubota, P.Y.; Grell, G.A.; Morrison, H.; Barros, S.R.M.; Fernandez, J.P.R.; Ramirez, E.; Siqueira, L.; Luzia, G.; et al. The Brazilian Global Atmospheric Model (BAM): Performance for Tropical Rainfall Forecasting and Sensitivity to Convective Scheme and Horizontal Resolution. Weather Forecast. 2016, 31, 1547–1572. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Rocha Júnior, R.L.; Cavalcante Pinto, D.D.; dos Santos Silva, F.D.; Gomes, H.B.; Barros Gomes, H.; Costa, R.L.; Santos Pereira, M.P.; Peña, M.; dos Santos Coelho, C.A.; Herdies, D.L. An Empirical Seasonal Rainfall Forecasting Model for the Northeast Region of Brazil. Water 2021, 13, 1613. https://doi.org/10.3390/w13121613
da Rocha Júnior RL, Cavalcante Pinto DD, dos Santos Silva FD, Gomes HB, Barros Gomes H, Costa RL, Santos Pereira MP, Peña M, dos Santos Coelho CA, Herdies DL. An Empirical Seasonal Rainfall Forecasting Model for the Northeast Region of Brazil. Water. 2021; 13(12):1613. https://doi.org/10.3390/w13121613
Chicago/Turabian Styleda Rocha Júnior, Rodrigo Lins, David Duarte Cavalcante Pinto, Fabrício Daniel dos Santos Silva, Heliofábio Barros Gomes, Helber Barros Gomes, Rafaela Lisboa Costa, Marcos Paulo Santos Pereira, Malaquías Peña, Caio Augusto dos Santos Coelho, and Dirceu Luís Herdies. 2021. "An Empirical Seasonal Rainfall Forecasting Model for the Northeast Region of Brazil" Water 13, no. 12: 1613. https://doi.org/10.3390/w13121613
APA Styleda Rocha Júnior, R. L., Cavalcante Pinto, D. D., dos Santos Silva, F. D., Gomes, H. B., Barros Gomes, H., Costa, R. L., Santos Pereira, M. P., Peña, M., dos Santos Coelho, C. A., & Herdies, D. L. (2021). An Empirical Seasonal Rainfall Forecasting Model for the Northeast Region of Brazil. Water, 13(12), 1613. https://doi.org/10.3390/w13121613









