Inline Pumped Storage Hydropower towards Smart and Flexible Energy Recovery in Water Networks
Abstract
1. Introduction
2. Electromechanical Equipment
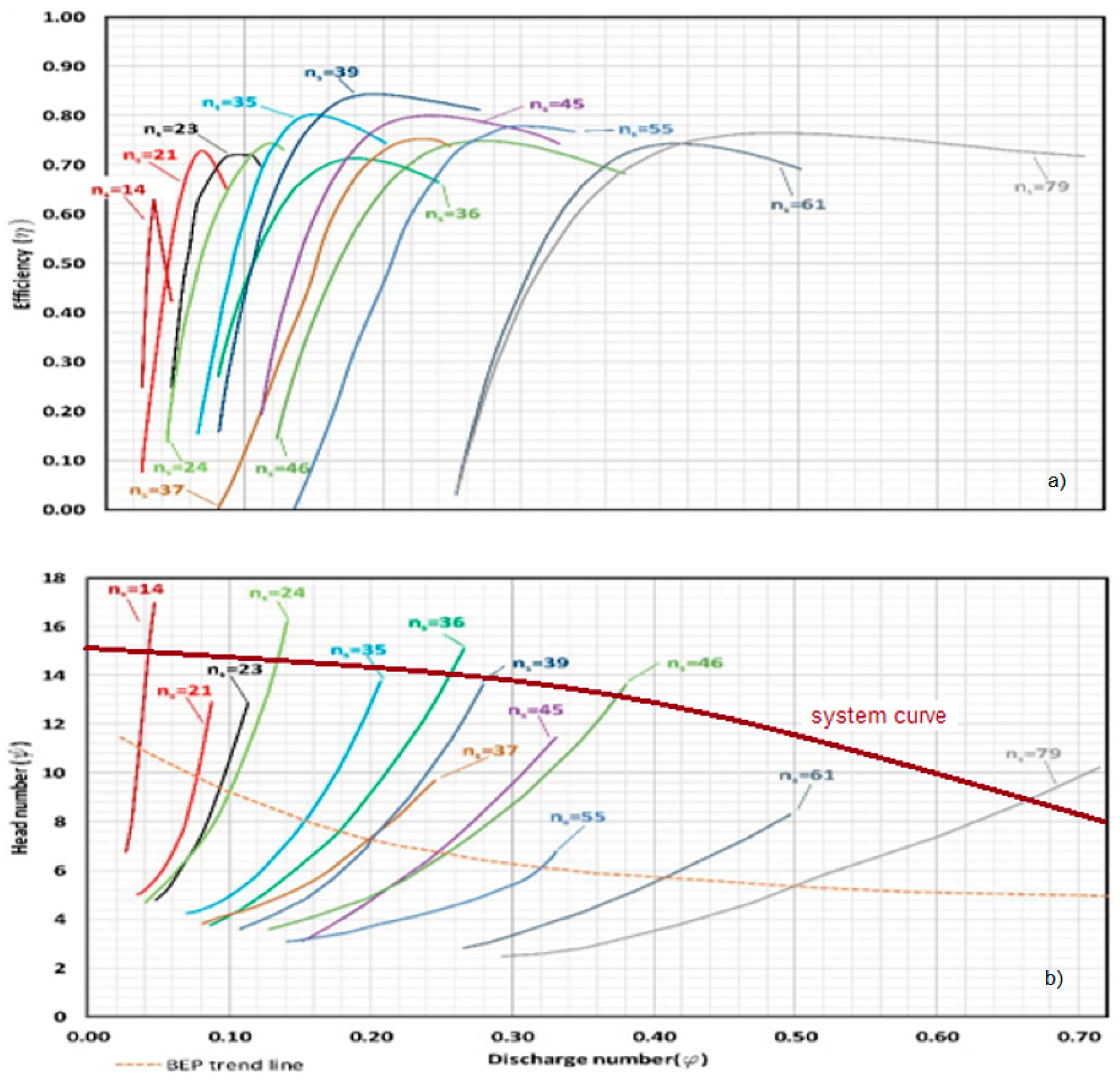
2.1. Pump Characteristics
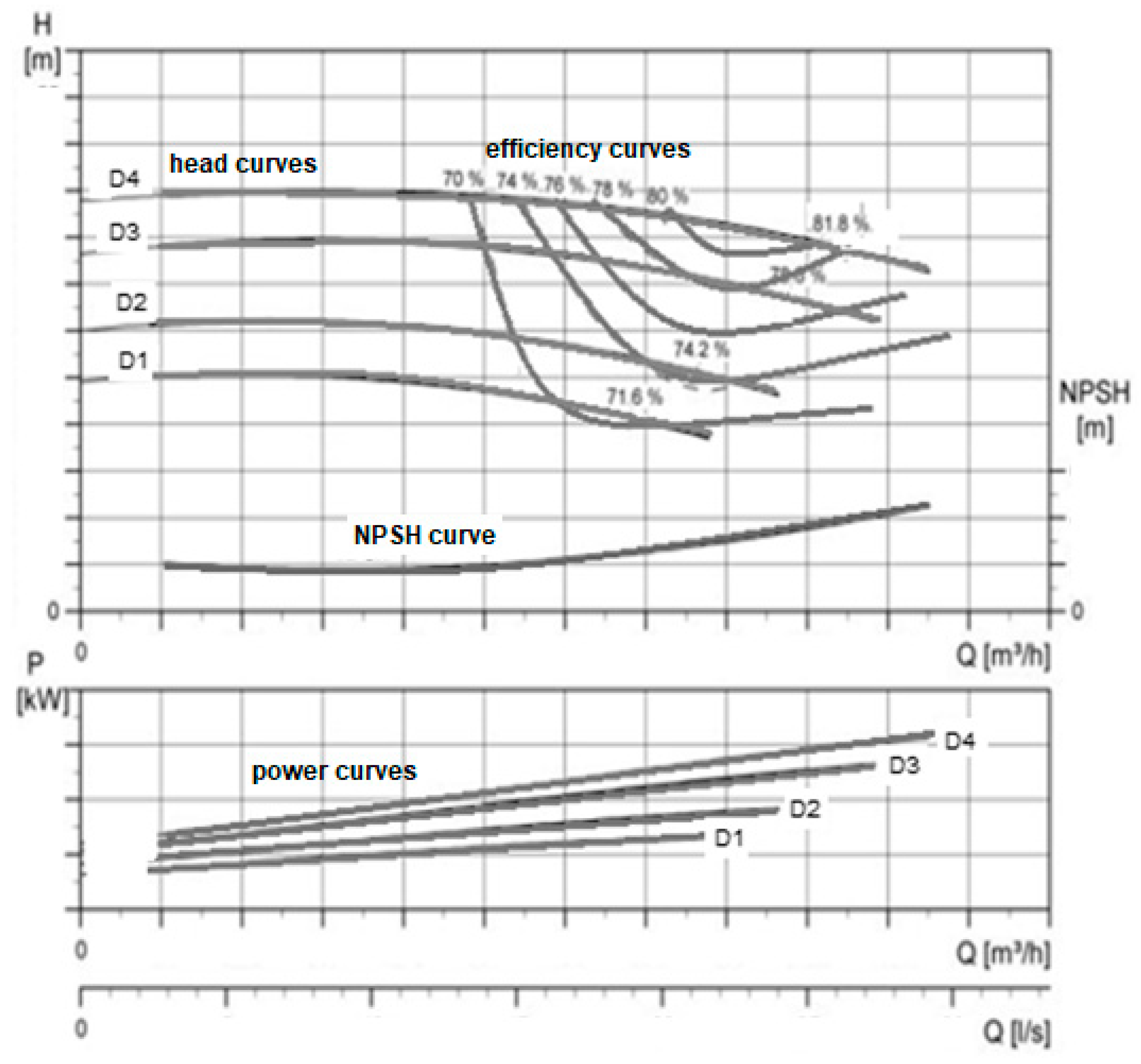
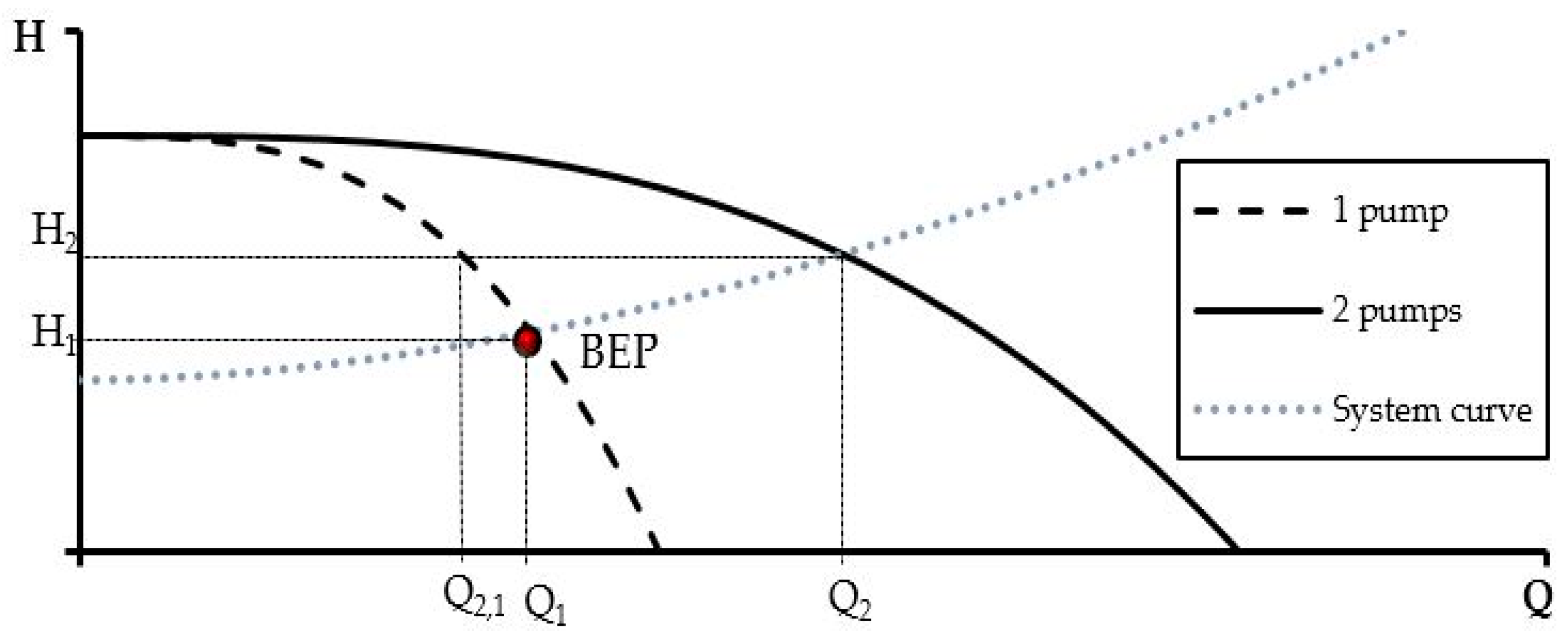
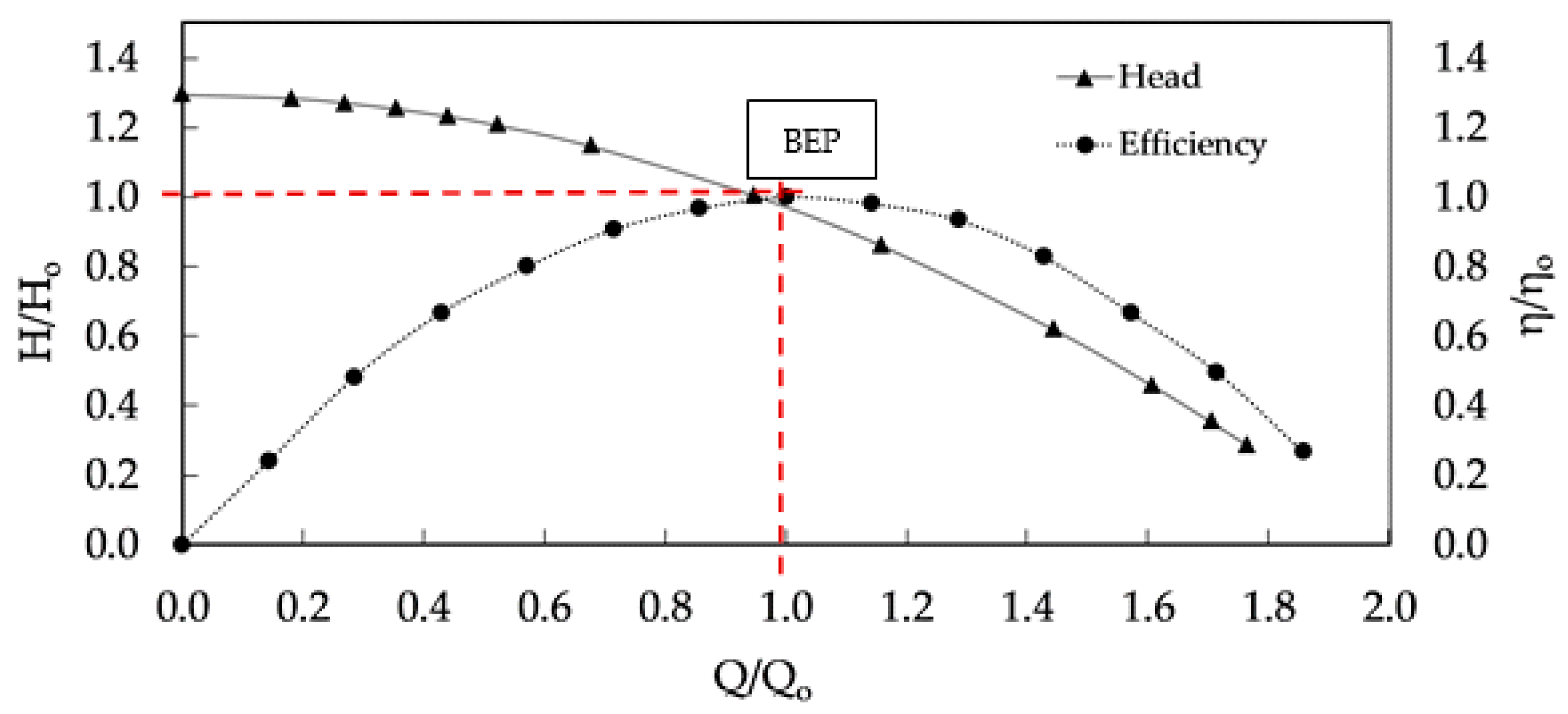
2.1.1. Characteristic Curves and Operational Point
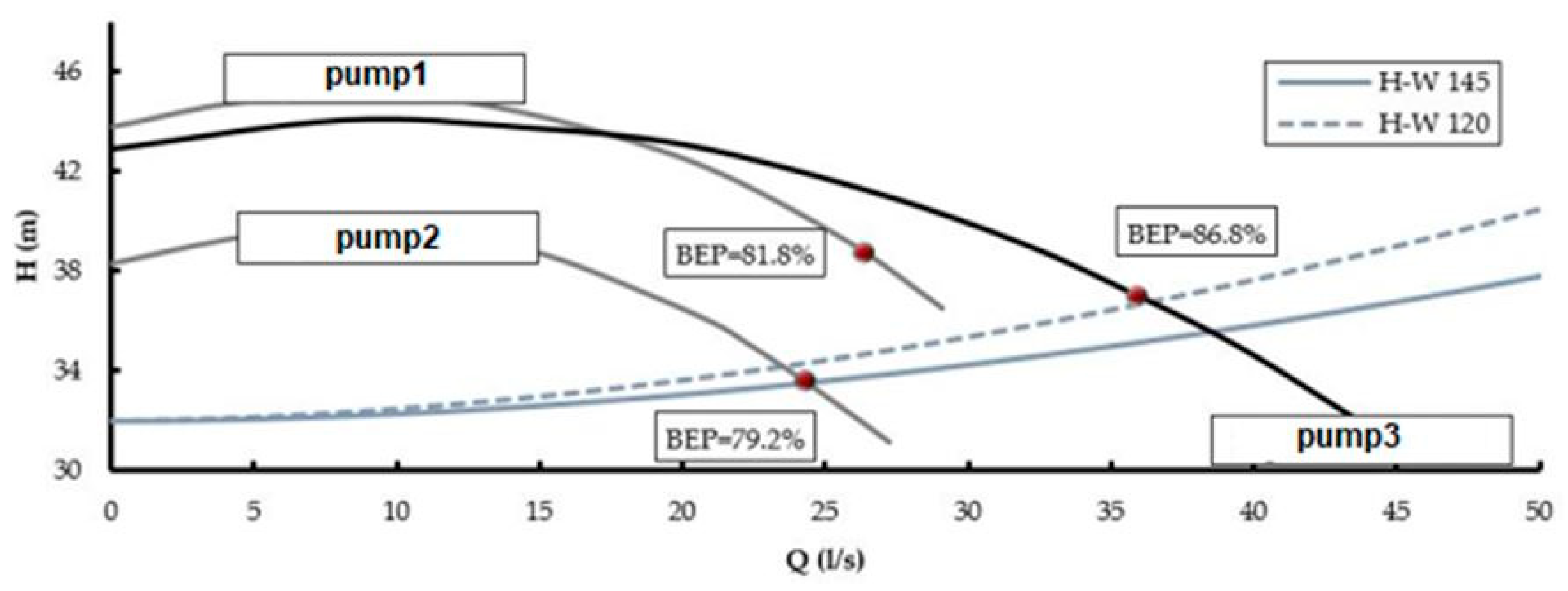
2.1.2. Selection of a Pump
- Pump 1 is not appropriate since it would operate with flow rates not recommended by the manufacturer;
- Pump 2 has a flow rate near to the average daily demand, increasing its probability of becoming obsolete if the demand is intensified or if the flow is reduced due to a pipe roughness increase over time. The maximum efficiency is also inferior to the pump 3 and, if equipped with a VSD, the possible speed range is minor given its inferior heads.
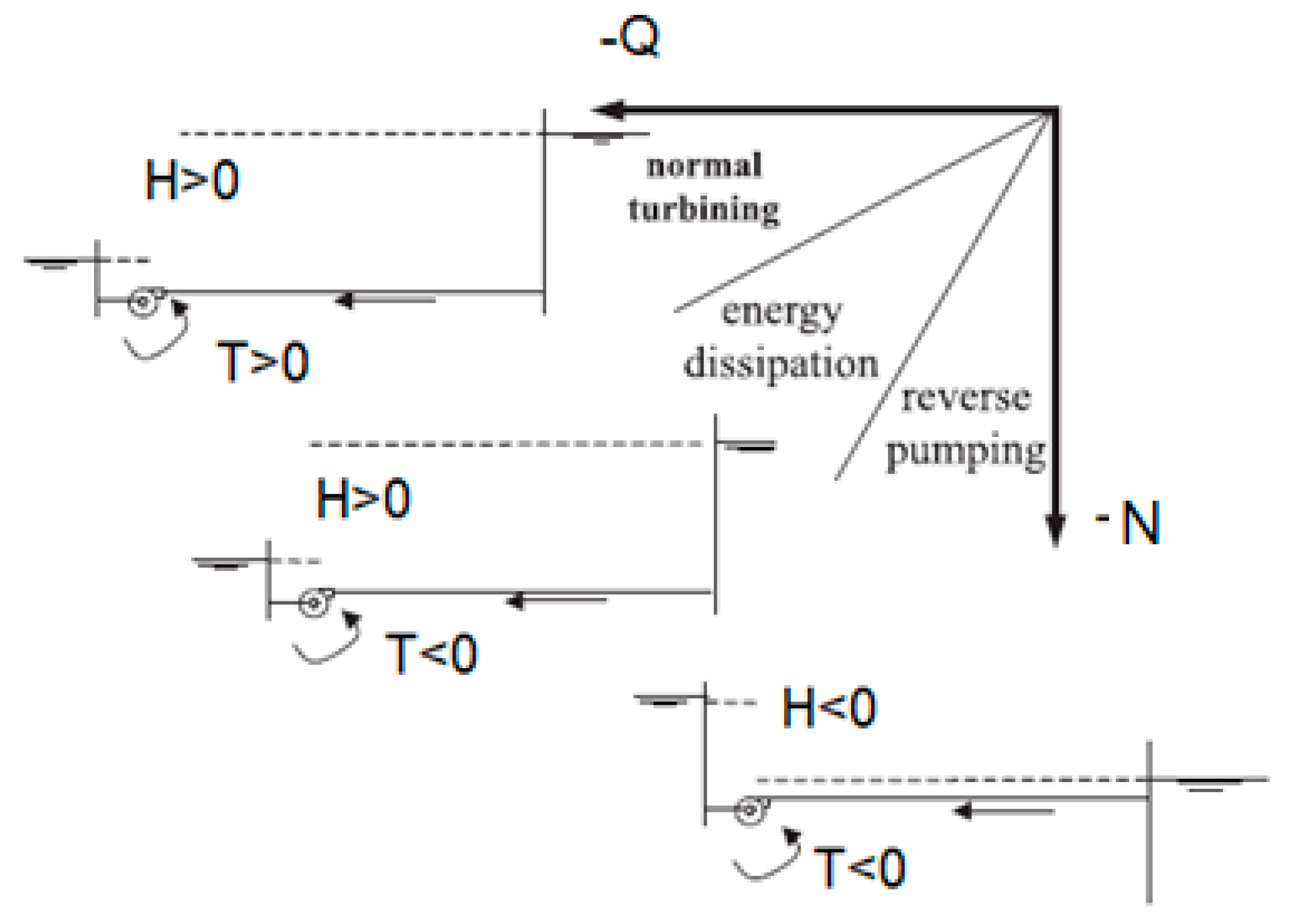
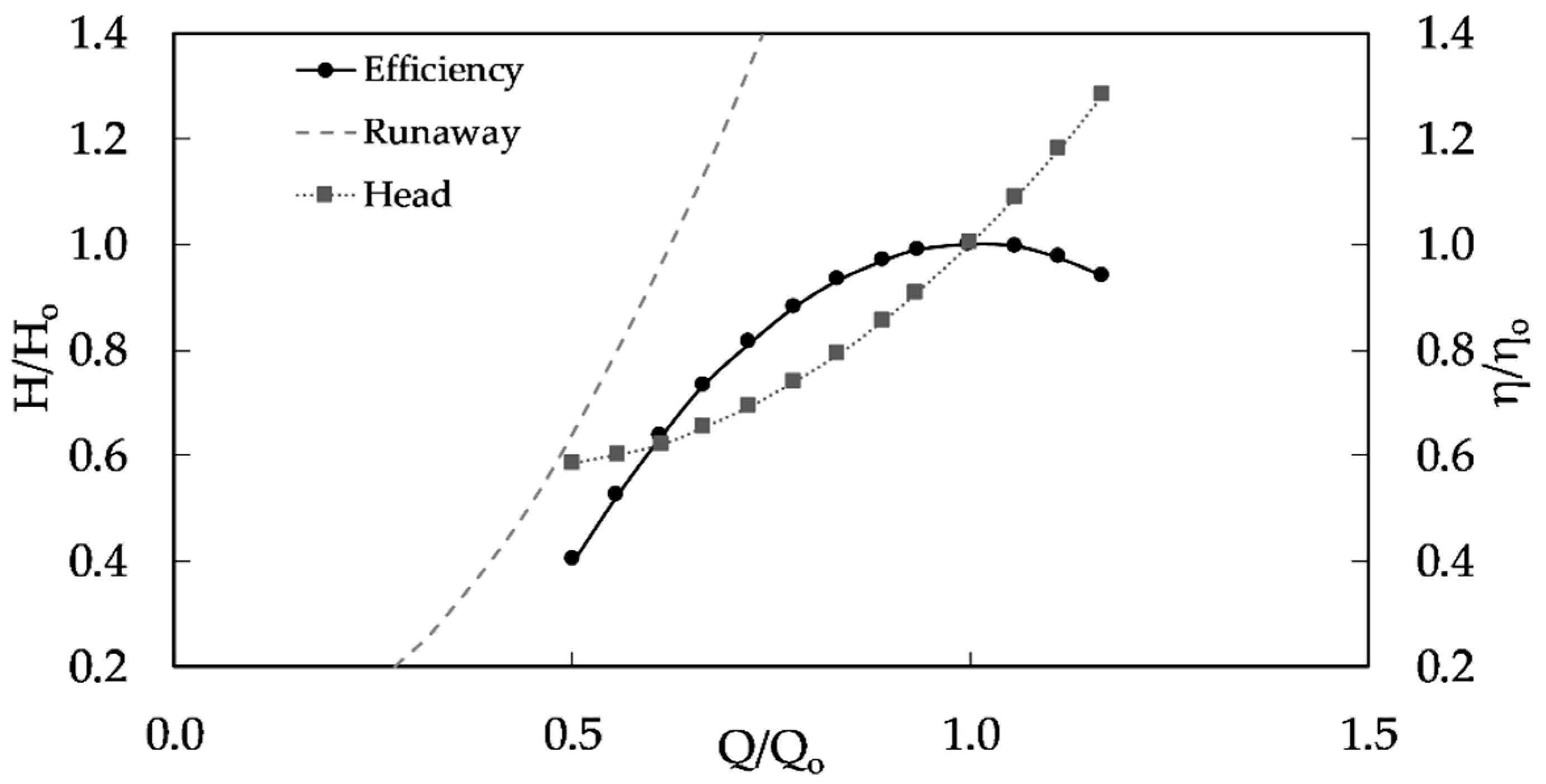
2.2. Pump as Turbine Curves
3. Methodology
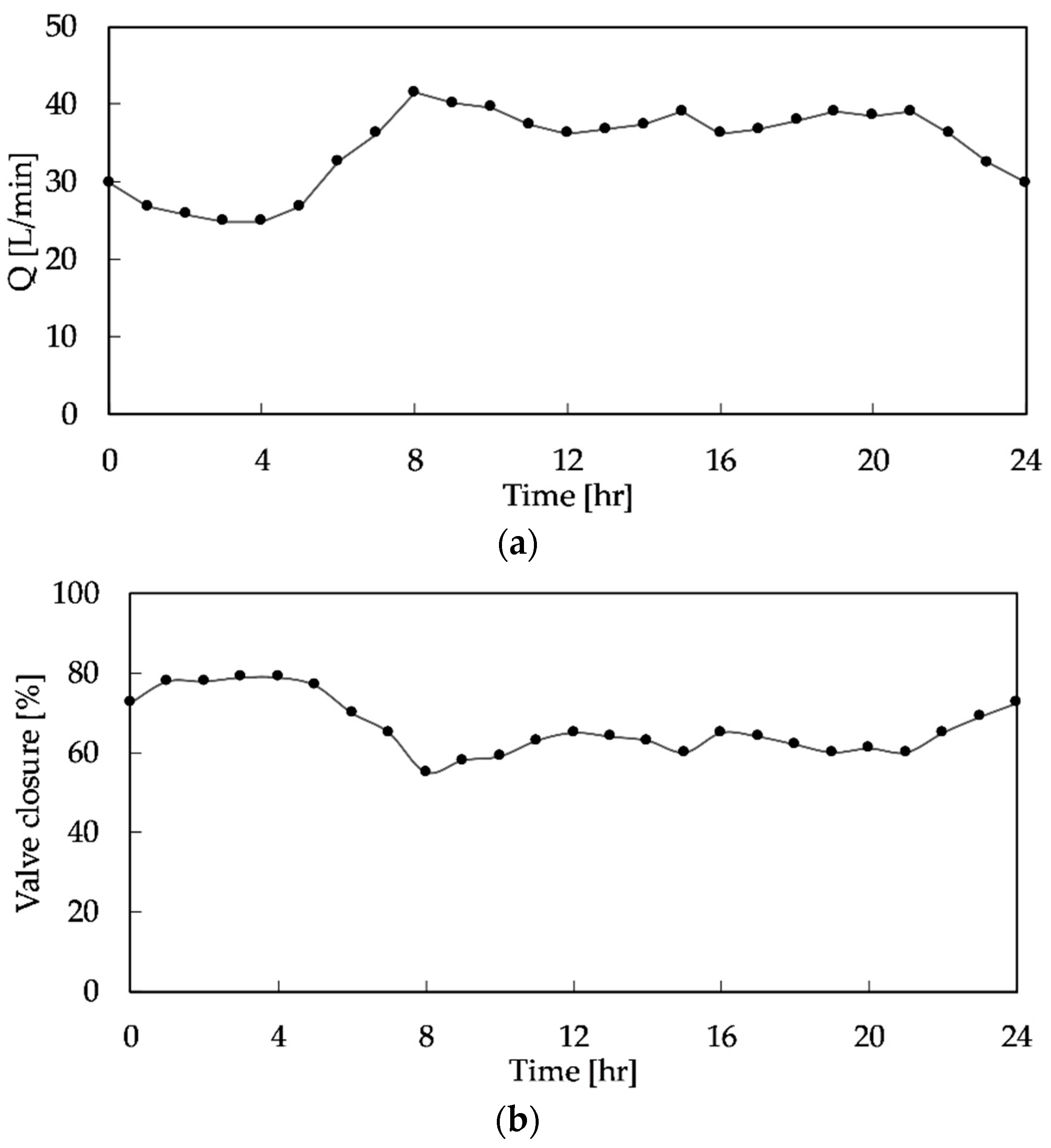
3.1. Base Pumping System (BPS) and Experimental Results
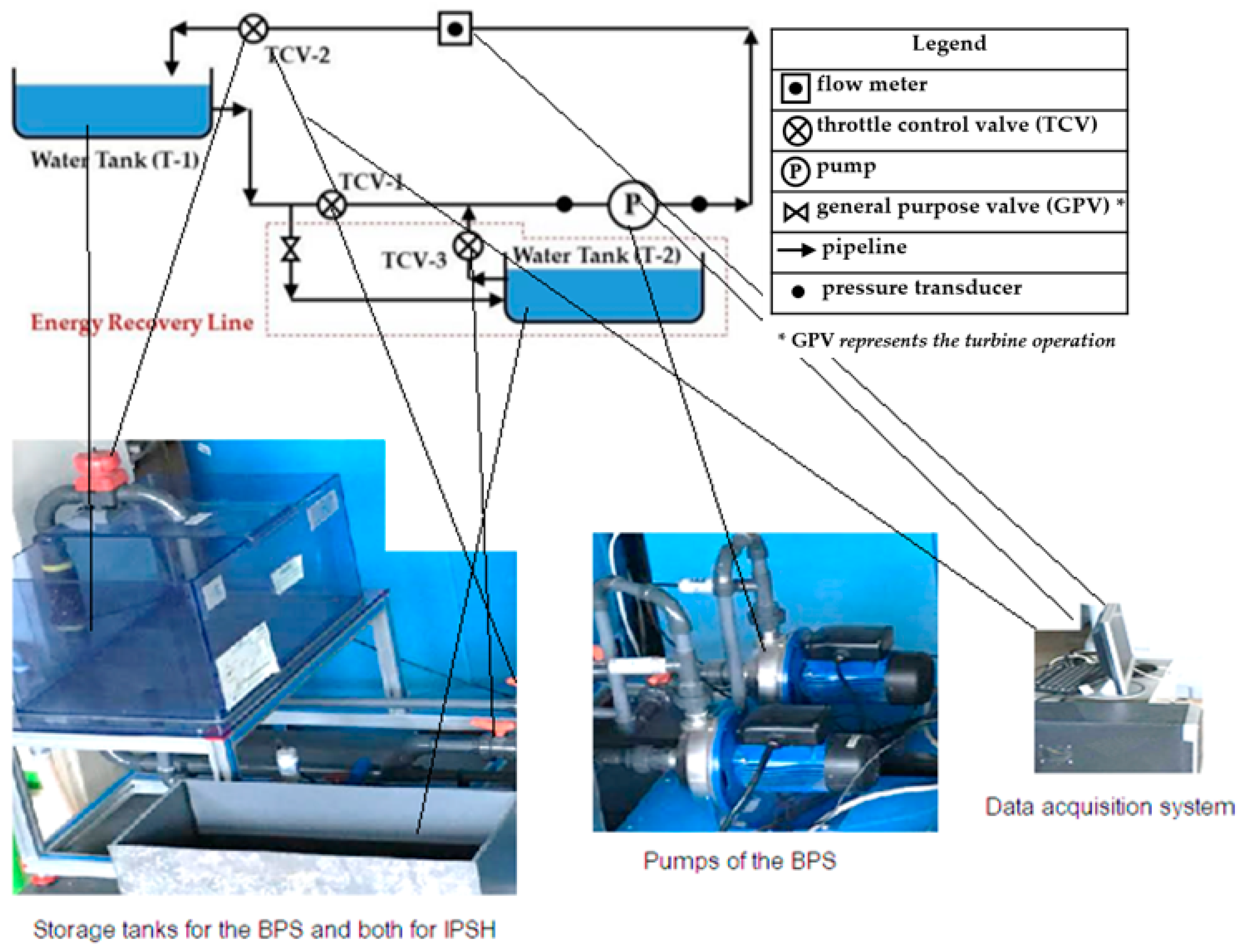
3.1.1. System Configuration
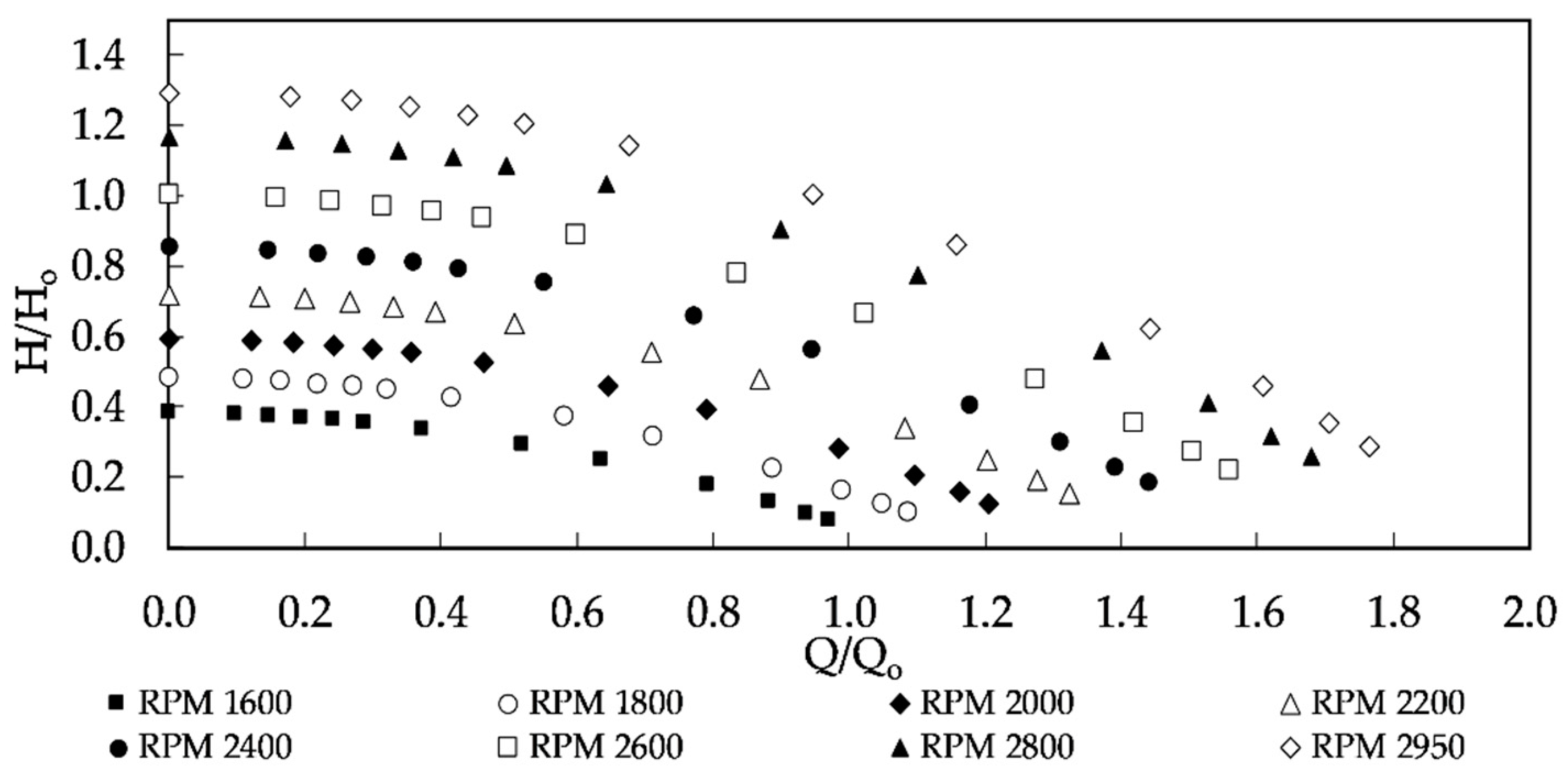
3.1.2. Experimental Results
3.2. Model Calibration
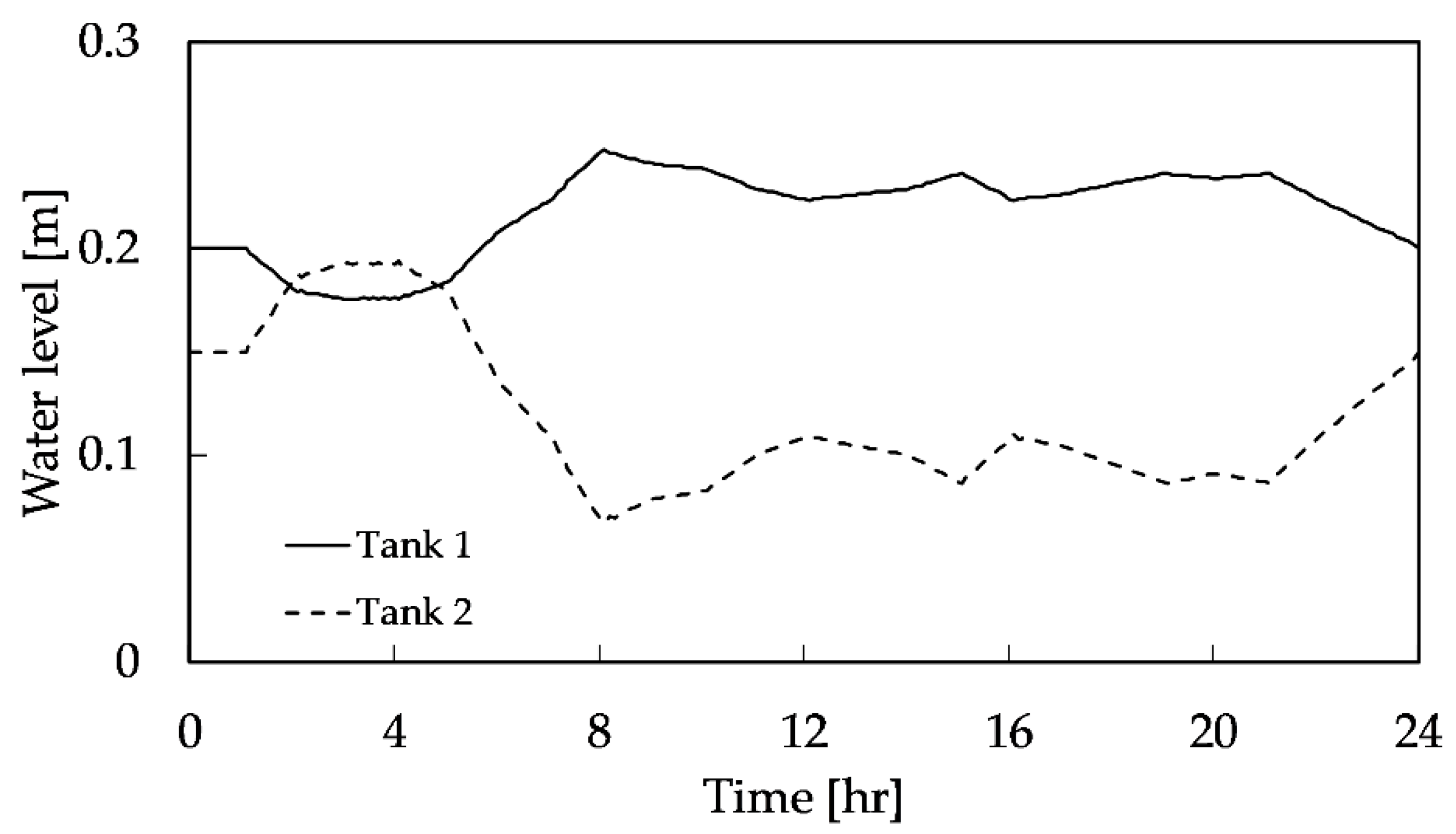
3.3. Pumping System Operation
3.4. Inline Pumped-Storage Hydropower (IPSH)
4. Dimensional Analysis and Discussion
5. Conclusions
- Characteristic curves of turbomachines in pump and turbine mode were defined for the best selection which conducts the best energy solution, avoiding eventual induced operating instabilities.
- An inline pumped-storage hydropower (IPSH) solution was defined and adapted from a base pumping system (BPS) in some existing water infrastructures of small to large scales, while not requiring significant changes and investments based on a by-pass and a lower tank upstream the pumping station.
- The energy generation using the gravitational flow appears to be an economic advantage in the definition of the energy recovery solution, as demonstrated through the achieved power.
- Depending on the type of demand (i.e., a constant flow between tanks or a variable demand pattern with water level compensation), the application shows a smart pressure and flow control in an energy recovery solution, replacing classical flow control valves.
- Based on similarity laws for the hydraulic system and the turbomachinery between pumps and turbines, a scaling-up approach for larger hydro energy converters was developed showing promising results.
- The smart approach based on a controlled recovery energy solution, which would be dissipated and the increasing of the system flexibility by a new bottom tank allowing two types of flow conditions (i.e., pump and turbine modes), can significantly improve the energy efficiency in the water sector, allowing us to better face the associated existent energy costs (e.g., pumping, treatment plants, water leakage, expansion and reparation of infrastructures and water bill for costumers).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| D | turbomachinery diameter [m] |
| H | head [m] |
| L | length [m] |
| rotational speed [rpm] | |
| specific speed of the pump | |
| specific speed of the turbine | |
| P | power [kW] |
| Q | flow rate [L/min] or [m3/s] |
| t | time [s] |
| V | flow velocity [m/s] |
| Indices | |
| h | hydraulic |
| int | interpolated value |
| mod | model |
| M | mechanical |
| pro | prototype |
| R | rated or best efficiency point |
| T | related to turbine |
| Greek letters | |
| specific weight [N/m3] | |
| efficiency | |
| head number | |
| flow rate number | |
| Abbreviations | |
| BPS | base pumping system |
| IPSH | inline pumped-storage hydropower |
| MHP | micro-hydropower |
| PAT | pump as turbine |
| WDN | water distribution network |
| WSS | water supply system |
References
- UN General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development. 21 October 2015. A/RES/70/1. Available online: refworld.org/docid/57b6e3e44.html (accessed on 14 February 2020).
- IEA (International Energy Agency). Renewables: Market Analysis and Forecast from 2019 to 2024, Paris. 2019. Available online: iea.org/reports/renewables-2019 (accessed on 13 February 2020).
- Ramos, J.S.; Ramos, H.M. Solar powered pumps to supply water for rural or isolated zones: A case study. Energy Sustain. Dev. 2009, 13, 151–158. [Google Scholar] [CrossRef]
- Ramos, J.S.; Ramos, H.M. Sustainable application of renewable sources in water pumping systems: Optimised energy system configuration. Energy Policy 2009, 37, 633–643. [Google Scholar] [CrossRef]
- Hoes, O.A.C.; Meijer, L.J.J.; Van der Ent, R.J.; Van de Giesen, N.C. Systematic high-resolution assessment of global hydropower potential. PLoS ONE 2017, 12. [Google Scholar] [CrossRef]
- Dadfar, A.; Besharat, M.; Ramos, H.M. Storage ponds application for flood control, hydropower generation and water supply. Int. Rev. Civ. Eng. 2019, 10. [Google Scholar] [CrossRef]
- Kougias, I.; Aggidis, G.; Avellan, F.; Deniz, S.; Lundin, U.; Moro, A.; Muntean, S.; Novara, D.; Pérez-Díaz, J.I.; Quaranta, E.; et al. Analysis of emerging technologies in the hydropower sector. Renew. Sustain. Energy Rev. 2019, 113. [Google Scholar] [CrossRef]
- Besharat, M.; Dadfar, A.; Viseu, M.T.; Brunone, B.; Ramos, H.M. Transient-flow induced compressed air energy storage (TI-CAES) system towards new energy concept. Water 2020, 12, 601. [Google Scholar] [CrossRef]
- Ramos, H.M.; Zilhao, M.; López-Jiménez, P.A.; Pérez-Sánchez, M. Sustainable water-energy nexus in the optimization of the BBC golf-course using renewable energies. Urban Water J. 2019, 16, 215–224. [Google Scholar] [CrossRef]
- Samora, I.; Hasmatuchi, V.; Münch-Allign, C.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Experimental characterization of a five blade tubular propeller turbine for pipe inline installation. Renew. Energy 2016, 95, 36–366. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H.M.; Mello, M.; Rodriguez-Diaz, J.A.; Morillo, J.G.; Kemi Adeyeye, K.; Coughlan, P.; Gallagher, J.; McNabola, A. Reducing the Energy Dependency of Water Networks in Irrigation, Public Drinking Water, and Process Industry: REDAWN Project. Proceedings 2018, 2, 681. [Google Scholar] [CrossRef]
- Samora, I.; Manso, P.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Energy Recovery Using Micro-Hydropower Technology in Water Supply Systems: The Case Study of the City of Fribourg. Water 2016, 8, 344. [Google Scholar] [CrossRef]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower Potential in Water Distribution Networks: Pressure Control by PATs. Water Resour. Manag. 2014, 29, 699–714. [Google Scholar] [CrossRef]
- Gallagher, J.; Harris, I.M.; Packwood, A.J.; McNabola, A.; Williams, A.P. Strategic assessment of energy recovery sites in the water industry for UK and Ireland: Setting technical and economic constraints through spatial mapping. Renew. Energy 2015, 81, 808–815. [Google Scholar] [CrossRef]
- Qian, Z.; Wang, F.; Guo, Z.; Lu, J. Performance evaluation of an axial-flow pump with adjustable guide vanes in turbine mode. Renew. Energy 2016, 99, 1146–1152. [Google Scholar] [CrossRef]
- Carravetta, A.; Derakhshan Houreh, S.; Ramos, H.M. Pumps as Turbines; Springer Tracts in Mechanical Engineering; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Vieira, F.; Helena, M.; Ramos, H.M. Optimization of operational planning for wind/hydro hybrid water supply systems. Renew. Energy 2009, 34, 928–936. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy Recovery in Existing Water Networks: Towards Greater Sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Glielmo, L.; Marini, G.; Raffaele, Z. Use of hydraulically operated PRVs for pressure regulation and power generation in water distribution networks. J. Water Resour. Plann. Manag. 2020, 146. [Google Scholar] [CrossRef]
- Postacchini, M.; Darvini, G.; Finizio, F.; Pelagalli, L.; Soldini, L.; Di Giuseppe, E. Hydropower Generation Through Pump as Turbine: Experimental Study and Potential Application to Small-Scale WDN. Water 2020, 12, 958. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Glielmo, L.; Marini, G.; Verrilli, F. Real time control of a PRV in water distribution networks for pressure regulation: Theoretical framework and laboratory experiments. J. Water Resour. Plann. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Creaco, E.; Campisano, A.; Fontana, N.; Marini, G.; Page, P.R.; Walski, T. Real time control of water distribution networks: A state-of-the-art review. Water Res. 2019, 161. [Google Scholar] [CrossRef]
- Puleo, V.; Fontanazza, C.M.; Notaro, V.; De Marchis, M.; Freni, G.; La Loggia, G. Pumps as turbines (PATs) in water distribution networks affected by intermittent service. J. Hydroinform. 2013. [Google Scholar] [CrossRef]
- Alberizzi, J.C.; Renzi, M.; Righetti, M.; Pisaturo, G.R.; Rossi, M. Speed and Pressure Controls of Pumps-as-Turbines Installed in Branch of Water-Distribution Network Subjected to Highly Variable Flow Rates. Energies 2019, 12, 4738. [Google Scholar] [CrossRef]
- Chacón, M.C.; Rodríguez Díaz, J.A.; Morillo, J.G.; McNabola, A. Hydropower energy recovery in irrigation networks: Validation of a methodology for flow prediction and pump as turbine selection. Renew. Energy 2020, 147, 1728–1738. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; López-Jiménez, P.A.; Ramos, H.M. PATs selection towards sustainability in irrigation networks: Simulated annealing as a water management tool. Renew. Energy 2018, 116, 234–249. [Google Scholar] [CrossRef]
- Morillo, J.G.; McNabola, A.; Camacho, E.; Montesinos, P.; Rodríguez Díaz, J.A. Hydro-power energy recovery in pressurized irrigation networks: A case study of an Irrigation District in the South of Spain. Agric. Water Manag. 2018, 204, 17–27. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Modeling Irrigation Networks for the Quantification of Potential Energy Recovering: A Case Study. Water 2016, 8, 234. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, A.J.; Ramos, H.M.; López-Jiménez, P.A. Optimization Strategy for Improving the Energy Efficiency of Irrigation Systems by Micro Hydropower: Practical Application. Water 2017, 9, 799. [Google Scholar] [CrossRef]
- Besharat, M.; Tarinejad, R.; Aalami, M.T.; Ramos, H.M. Study of a compressed air vessel for controlling the pressure surge in water networks: CFD and experimental analysis. Water Resour. Manag. 2016, 30, 2687–2702. [Google Scholar] [CrossRef]
- Pottie, D.L.F.; Ferreira, R.A.M.; Maia, T.A.C.; Porto, M.P. An alternative sequence of operation for Pumped-Hydro Compressed Air Energy Storage (PH-CAES) systems. Energy 2019. [Google Scholar] [CrossRef]
- Odukomaiya, A.; Abu-Heiba, A.; Graham, S.; Momen, A.M. Experimental and analytical evaluation of a hydro-pneumatic compressed-air Ground-Level Integrated Diverse Energy Storage (GLIDES) system. Appl. Energy 2018, 221, 75–85. [Google Scholar] [CrossRef]
- Ramos, H.; Borga, A. Pumps as turbines: An unconventional solution to energy production. Urban Water 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Ramos, H.; Borga, A. Pumps yielding power. Dam Eng. Water Power Dam Constr. 2000, 10, 197–217. [Google Scholar]
- Fontanella, S.; Fecarotta, O.; Molino, B.; Cozzolino, L.; Della Morte, R. A Performance Prediction Model for Pumps as Turbines (PATs). Water 2020, 12, 1175. [Google Scholar] [CrossRef]
- Chaker, M.A.; Triki, A. Investigating the branching redesign strategy for surge control in pressurized steel piping systems. Int. J. Pres. Ves. Pip. 2020, 180, 104044. [Google Scholar] [CrossRef]
- Kapelan, Z. Calibration of Water Distribution System Hydraulic Models. Ph.D. Thesis, University of Exeter, Exeter, UK, 2010. [Google Scholar]
- Wylie, E.; Streeter, V.; Suo, L.F. Fluid Transient in Systems; Prentice-Hall: Englewood, NJ, USA, 1993. [Google Scholar]
- Ramos, H.M. Simulação e Controlo de Transitórios Hidráulicos em Pequenos Aproveitamentos Hidroelétricos. Ph.D. Thesis, Civil Engineering, Instituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal, 1995. (In Portuguese). [Google Scholar]
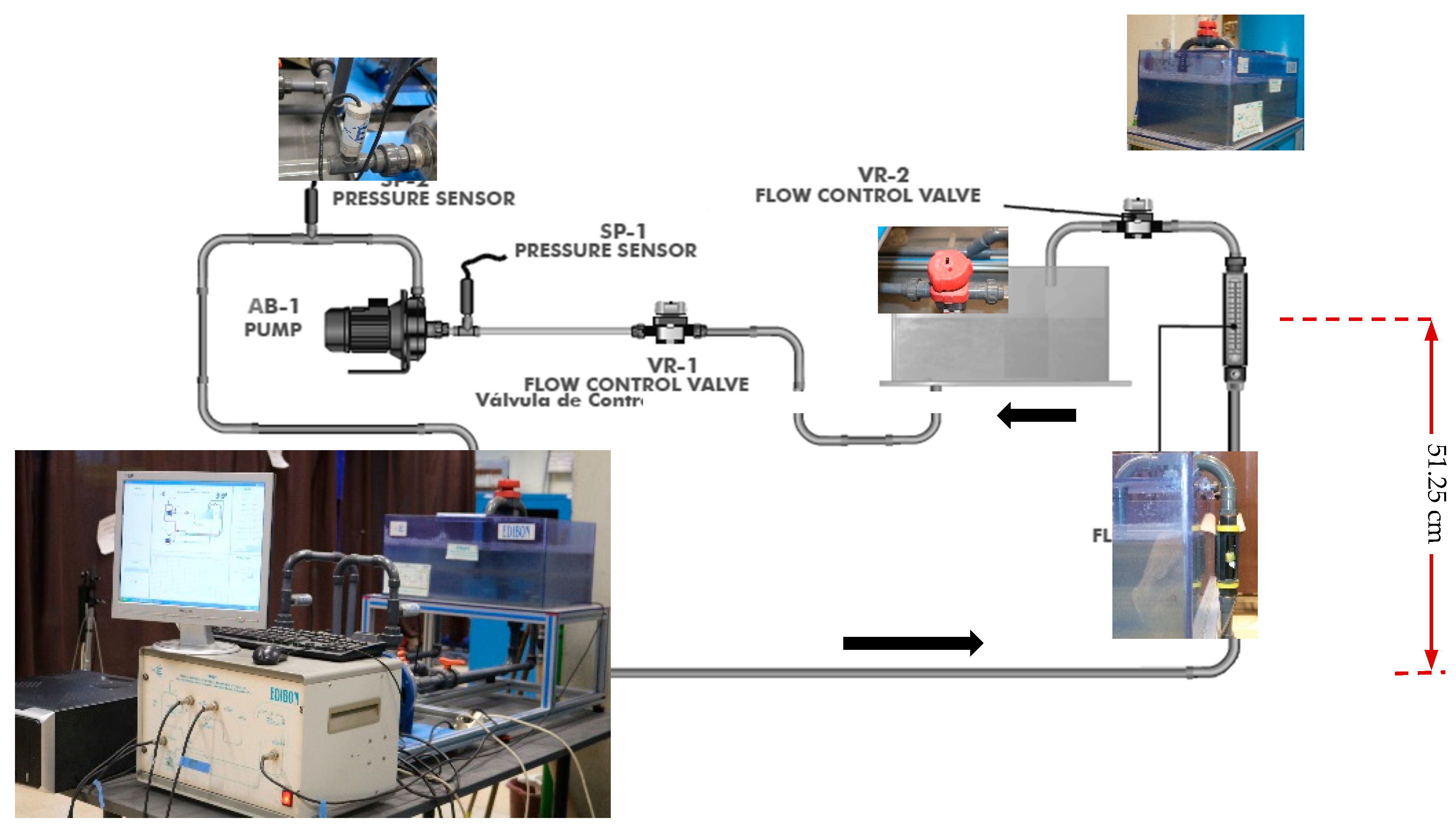
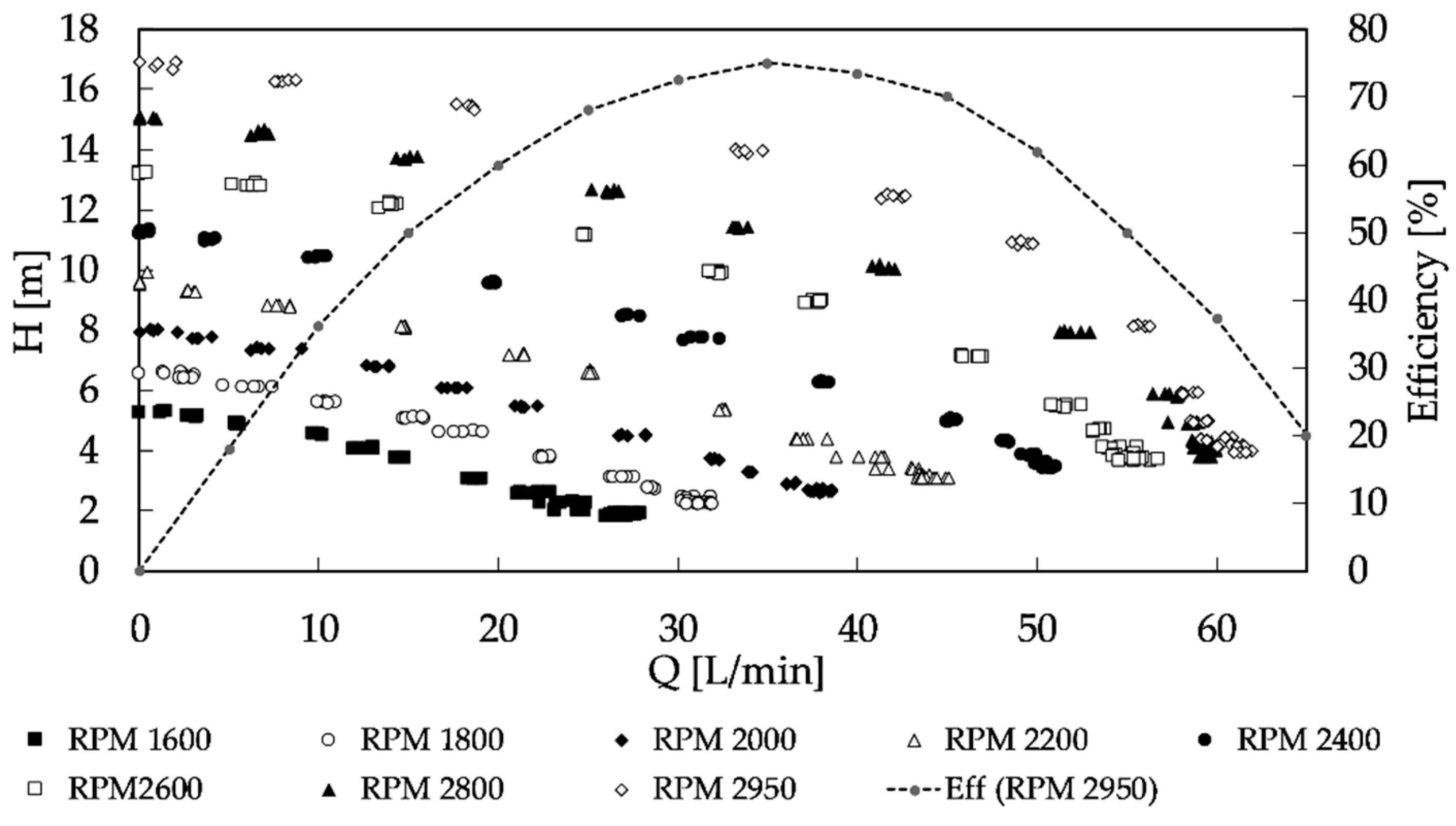
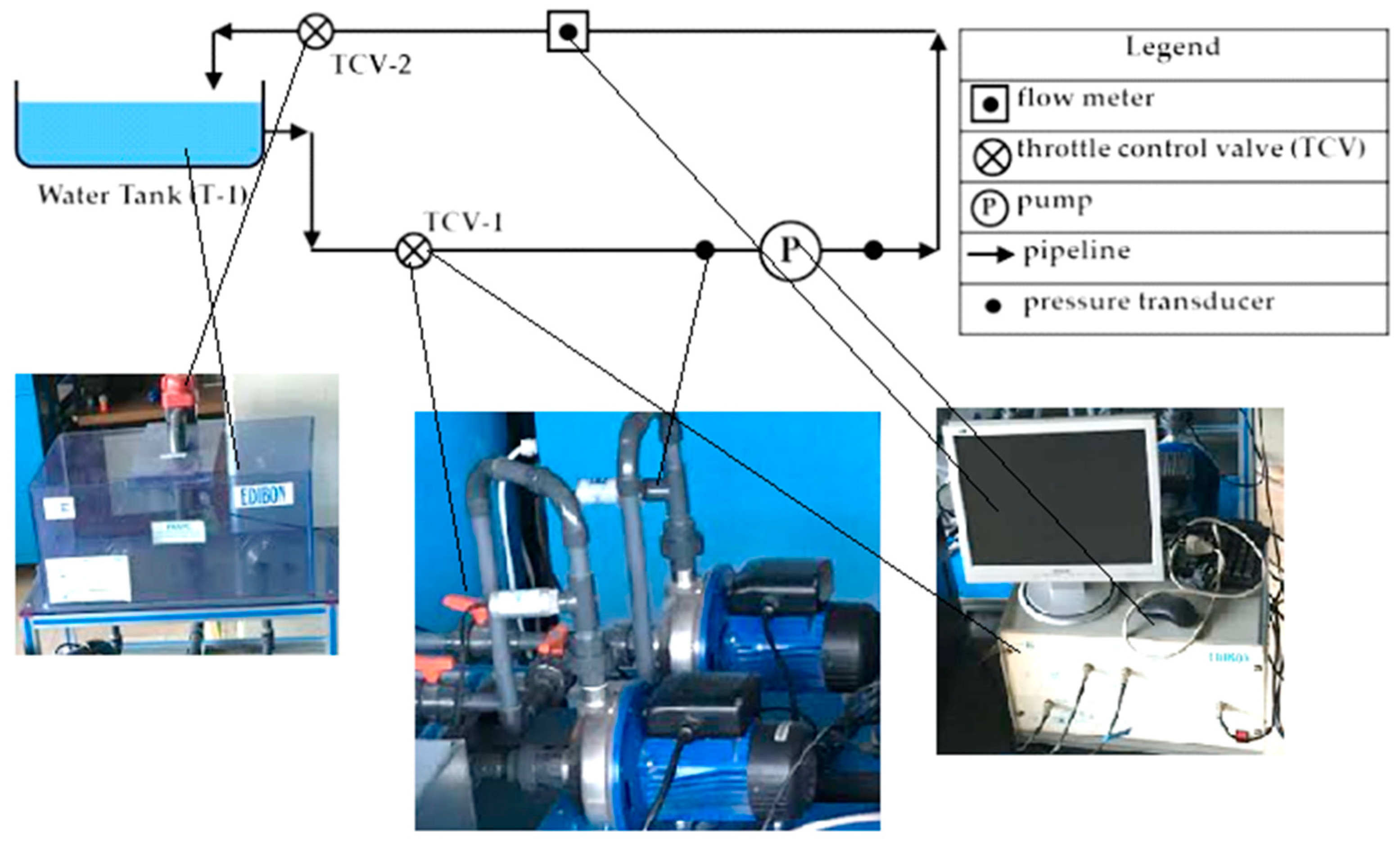


| Parameters | Measuring Range |
|---|---|
| Pump head [m] | 1.8 to 16.92 |
| Flowmeter Rate [L/min] | 0 to 61.98 |
| Rotational speed of the pump [rpm] | 1600 to 2950 |
| Opening valve VR2 [%] | 0 to 100 |
| Variable Parameters | Tested Values |
|---|---|
| VR-2 closure percentage [%] | 4.16, 6.25, 8.33, 10.41, 12.5, 16.66, 25, 33.33, 50, 66.60, 83.33, 100 |
| Pump rotational speed, N [rpm] | 1600, 1800, 2000, 2200, 2400, 2600, 2800, 2950 |
| Parameter | Value |
|---|---|
| Flow rate [L/min] | 35 |
| Head [m] | 13.5 |
| Efficiency [%] | 75 |
| Rotational speed [rpm] | 2950 |
| Specific speed (Equation (2)) | 10.05 |
| Parameter Unit | Hydraulic System | Turbine Impeller | Turbine Affinity Laws | |||
|---|---|---|---|---|---|---|
| Q | V | D | NT | HT | PT | |
| [m3/s] | [m/s] | [mm] | [rpm] | [m] | [kW] | |
| Model | 0.60 × 10−3 | 0.99 | 25 | 2170 | 10.64 | 0.052 |
| 1/20 | 1.04 | 4.42 | 500 | 470 | 200 | 1532 |
| 1/50 | 10.31 | 6.99 | 1250 | 298 | 503 | 41,657 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, H.M.; Dadfar, A.; Besharat, M.; Adeyeye, K. Inline Pumped Storage Hydropower towards Smart and Flexible Energy Recovery in Water Networks. Water 2020, 12, 2224. https://doi.org/10.3390/w12082224
Ramos HM, Dadfar A, Besharat M, Adeyeye K. Inline Pumped Storage Hydropower towards Smart and Flexible Energy Recovery in Water Networks. Water. 2020; 12(8):2224. https://doi.org/10.3390/w12082224
Chicago/Turabian StyleRamos, Helena M., Avin Dadfar, Mohsen Besharat, and Kemi Adeyeye. 2020. "Inline Pumped Storage Hydropower towards Smart and Flexible Energy Recovery in Water Networks" Water 12, no. 8: 2224. https://doi.org/10.3390/w12082224
APA StyleRamos, H. M., Dadfar, A., Besharat, M., & Adeyeye, K. (2020). Inline Pumped Storage Hydropower towards Smart and Flexible Energy Recovery in Water Networks. Water, 12(8), 2224. https://doi.org/10.3390/w12082224







