A New Mass-Conservative, Two-Dimensional, Semi-Implicit Numerical Scheme for the Solution of the Navier-Stokes Equations in Gravel Bed Rivers with Erodible Fine Sediments
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Model
2.1.1. Governing Equations
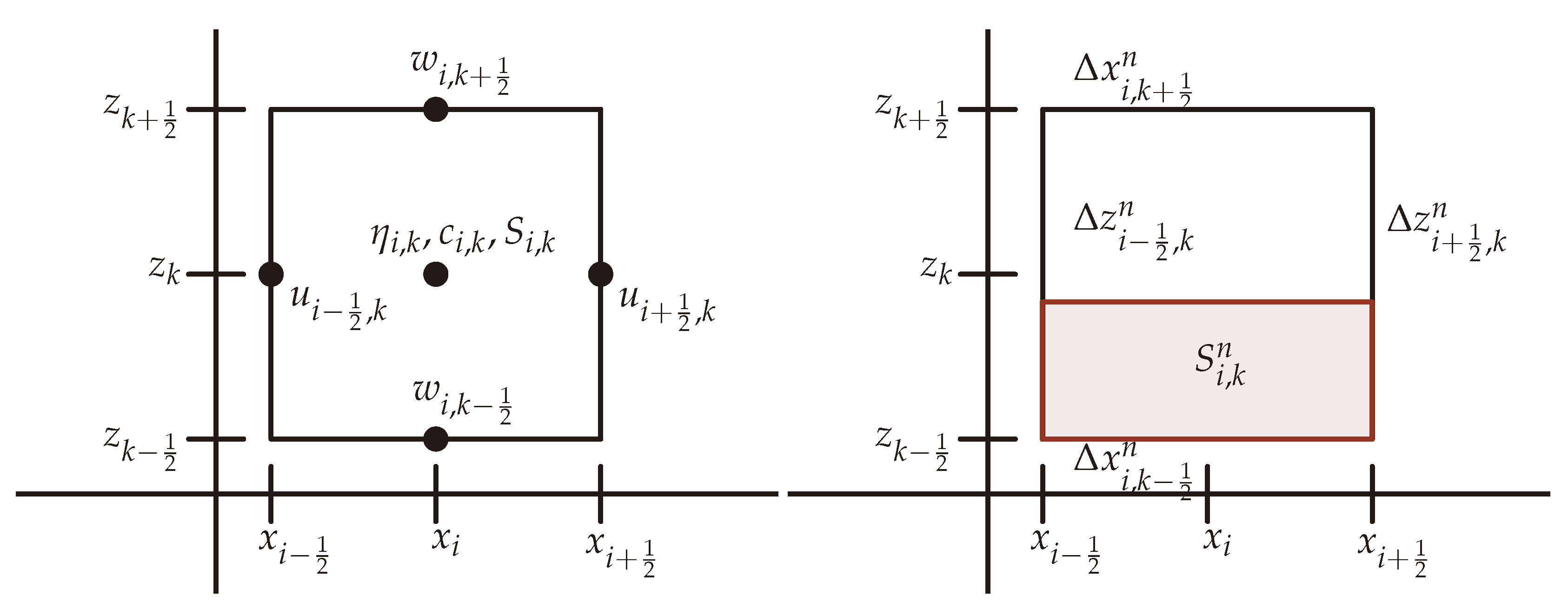
2.1.2. Staggered Mesh
2.1.3. Numerical Method
2.1.4. Crank-Nicholson Time Discretization
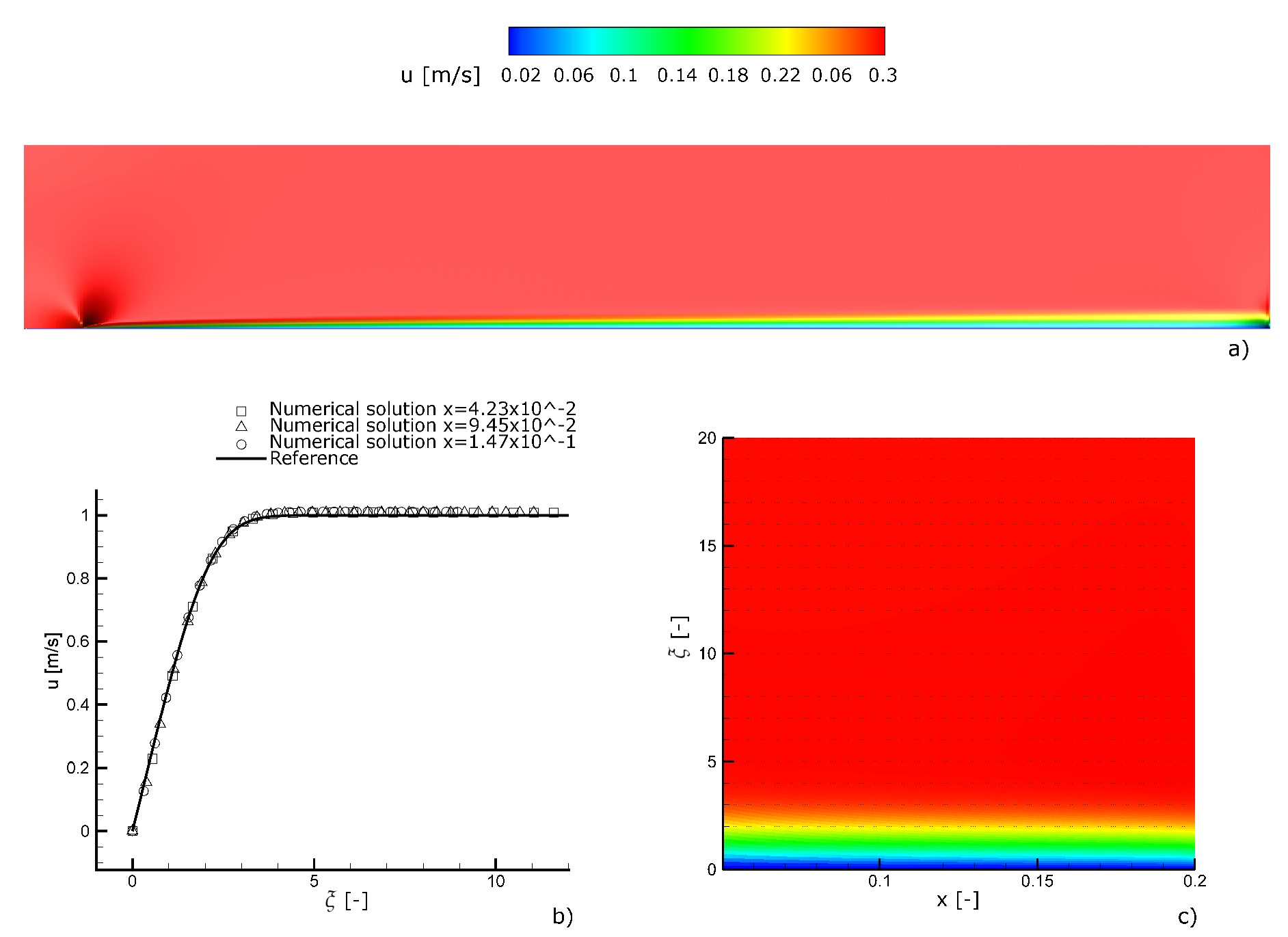
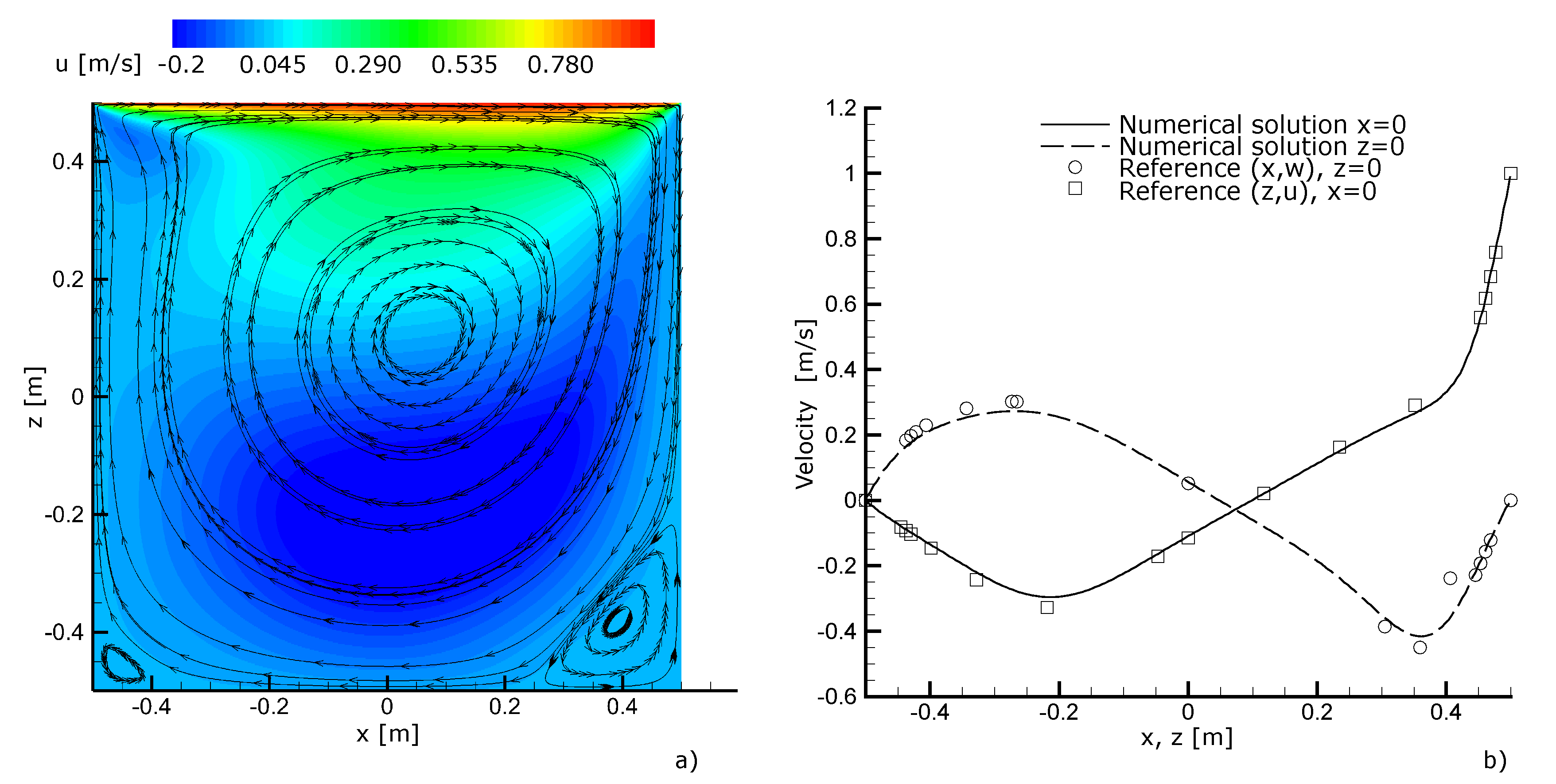
2.2. Validation Tests
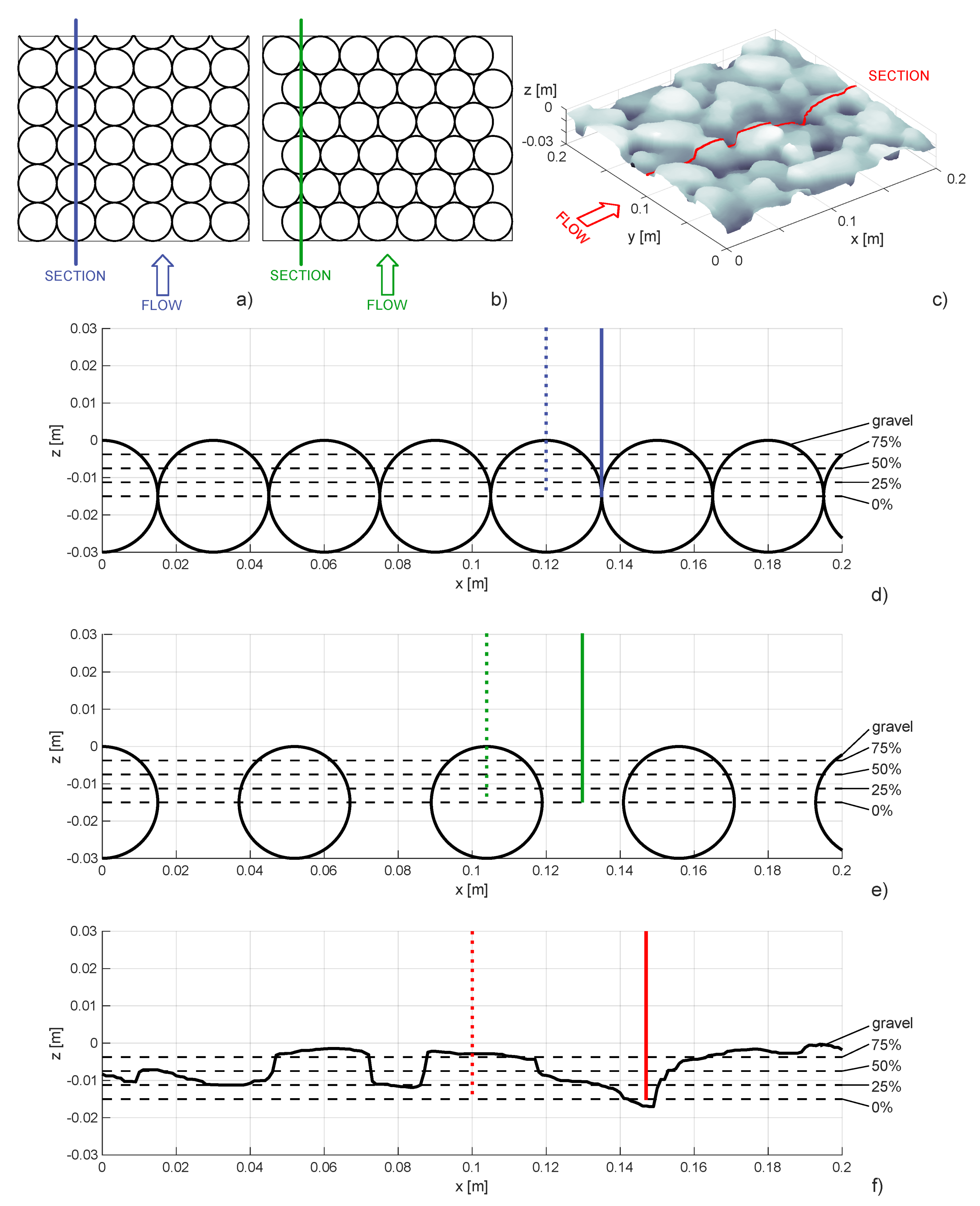
Numerical Experiments
3. Results and Discussion
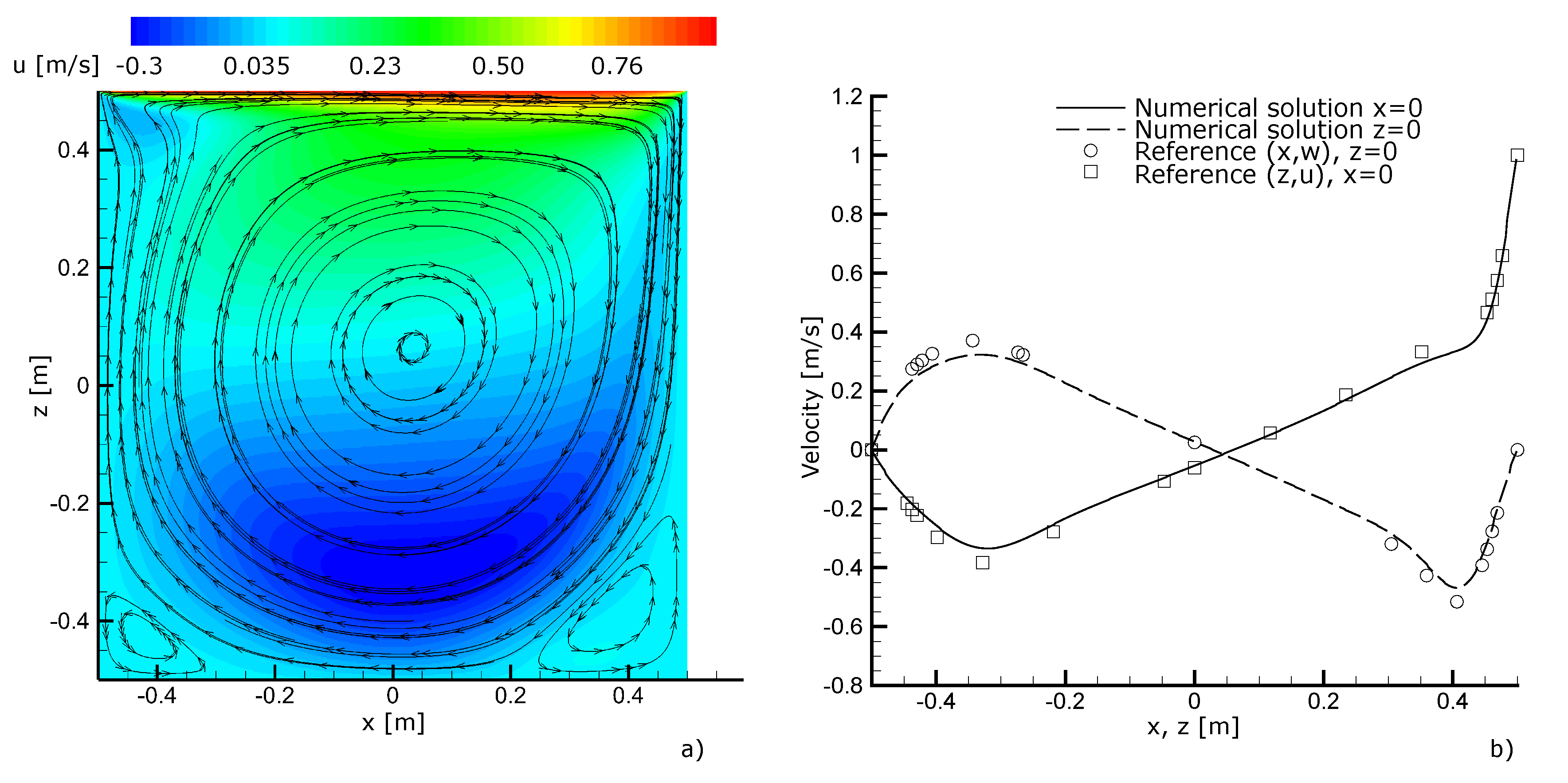
3.1. Validation Tests
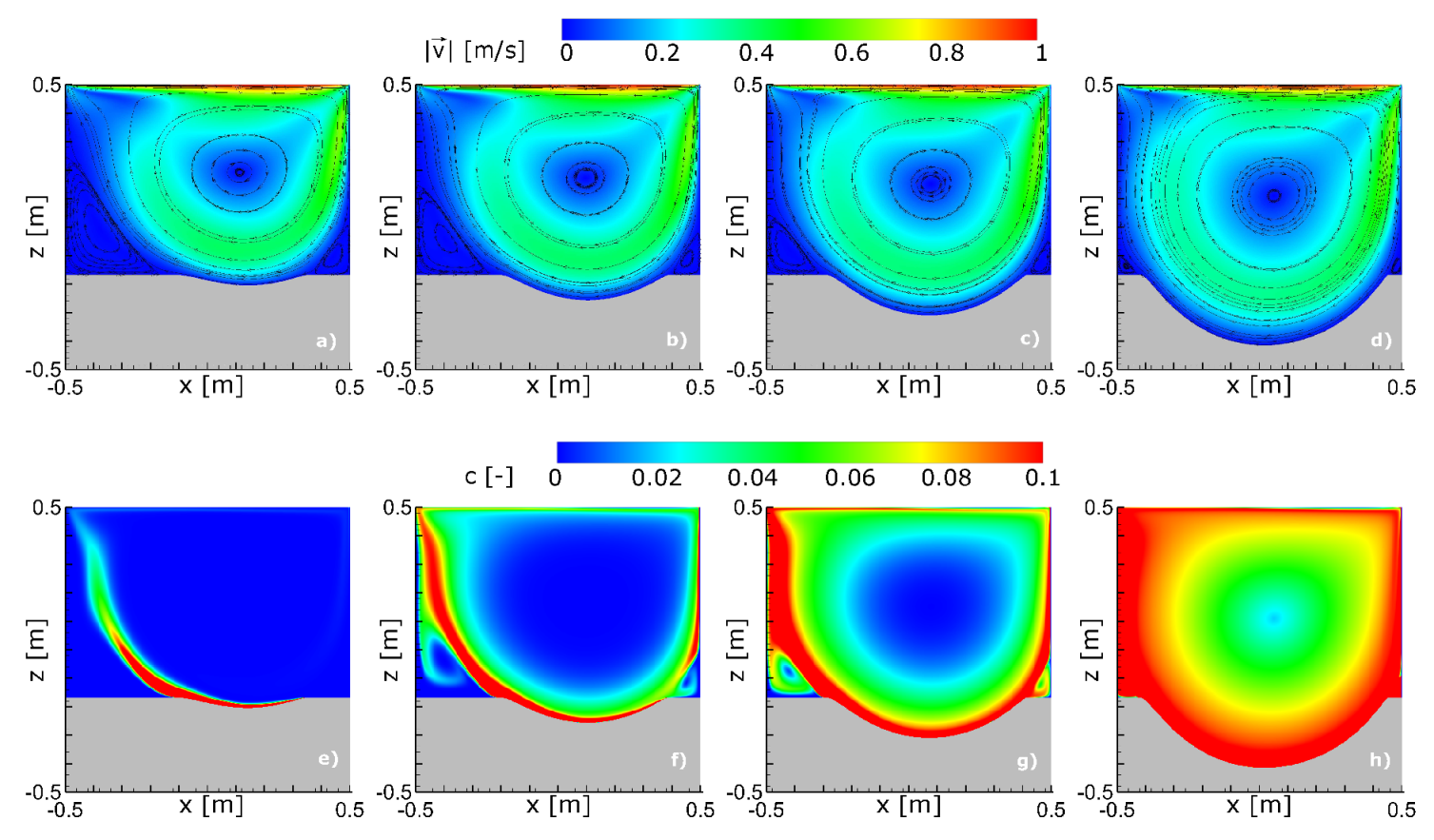
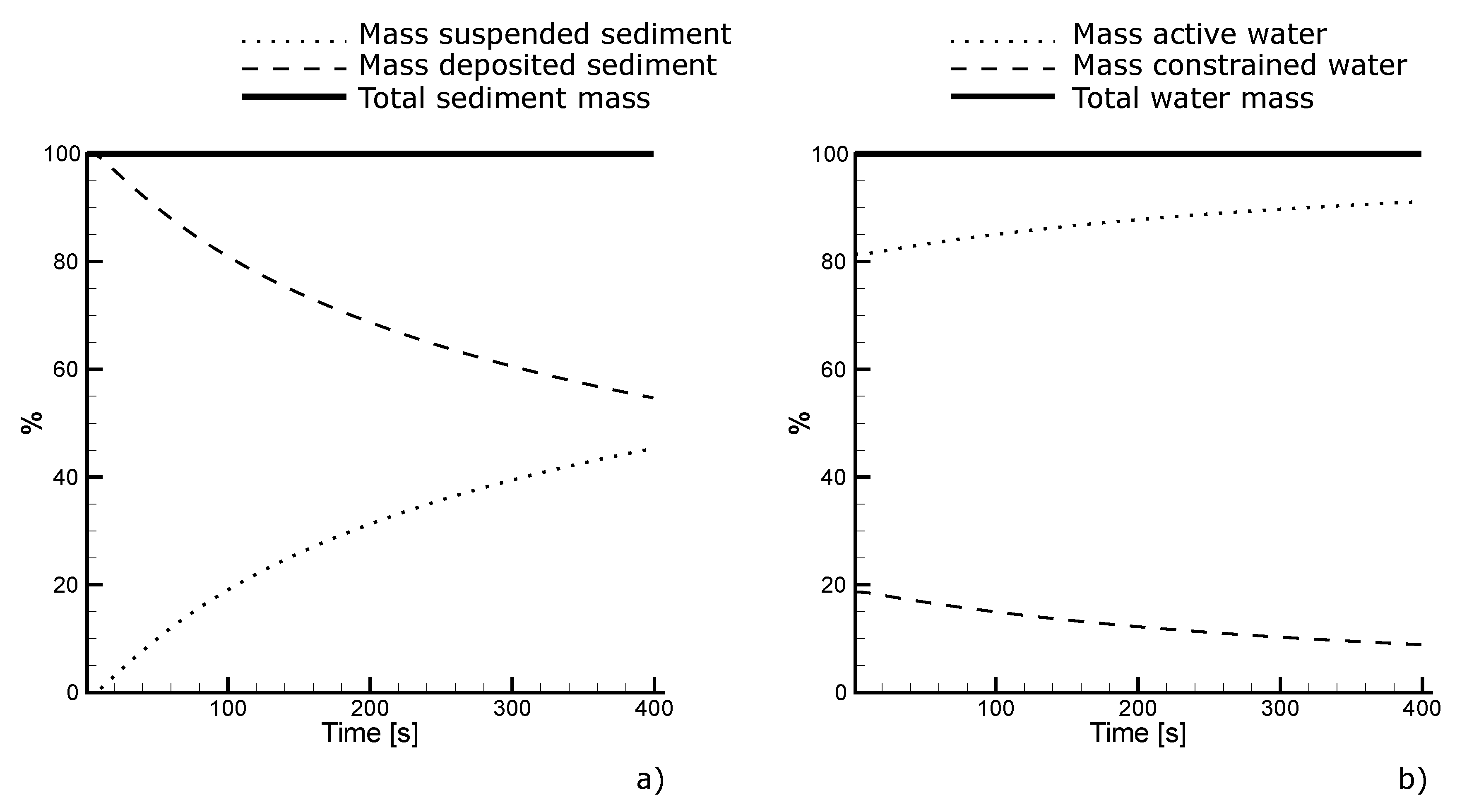
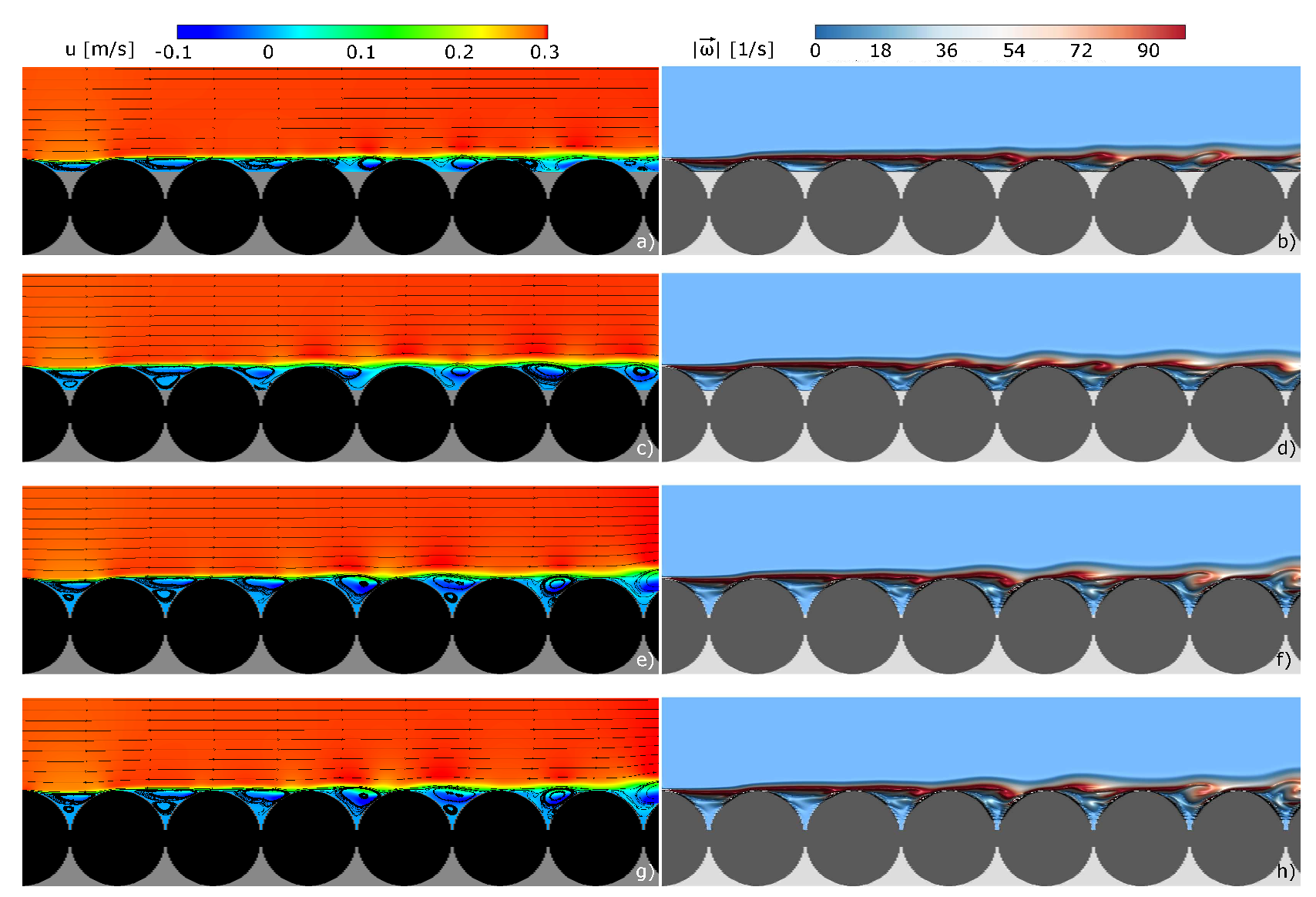
3.2. Numerical Experiments
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schleiss, A.J.; Franca, M.J.; Juez, C.; Cesare, G.D. Reservoir sedimentation. J. Hydraul. Res. 2016, 54, 595–614. [Google Scholar] [CrossRef]
- Kaffas, K.; Hrissanthou, V.; Sevastas, S. Modeling hydromorphological processes in a mountainous basin using a composite mathematical model and ArcSWAT. CATENA 2018, 162, 108–129. [Google Scholar] [CrossRef]
- ICOLD. Sedimentation and Sustainable Use of Reservoirs and River Systems; Technical Report; International Commission on Large Dams: Paris, France, 2009. [Google Scholar]
- Williams, G.P.; Wolman Gordon, M. Downstream Effects of Dams on Alluvial Rivers; Geological Survey Professional Paper 1286; U.S. Government Printing Office: Washington, DC, USA, 1984. [CrossRef]
- Brandt, S. Classification of geomorphological effects downstream of dams. CATENA 2000, 40, 375–401. [Google Scholar] [CrossRef]
- Juez, C.; Hassan, M.A.; Franca, M.J. The Origin of Fine Sediment Determines the Observations of Suspended Sediment Fluxes Under Unsteady Flow Conditions. Water Resour. Res. 2018, 54, 5654–5669. [Google Scholar] [CrossRef]
- Kondolf, G.M. Hungry Water: Effects of Dams and Gravel Mining on River Channels. Environ. Manag. 1997, 21, 533–551. [Google Scholar] [CrossRef]
- Shen, H.W.; Lu, J. Development and Prediction of Bed Armoring. J. Hydraul. Eng. 1983, 109, 611–629. [Google Scholar] [CrossRef]
- Dietrich, W.; Kirchner, J.; Ikeda, H.; Iseya, F. Sediment Supply and Development of Coarse Surface Layer in Gravel Bedded Rivers. Nature 1989, 340. [Google Scholar] [CrossRef]
- Wilcock, P.R.; DeTemple, B.T. Persistence of armor layers in gravel-bed streams. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Bui, V.; Bui, M.; Rutschmann, P. Advanced Numerical Modeling of Sediment Transport in Gravel-Bed Rivers. Water 2019, 11, 550. [Google Scholar] [CrossRef]
- Schälchli, U. The clogging of coarse gravel river beds by fine sediment. Hydrobiologia 1992, 235–236, 189–197. [Google Scholar] [CrossRef]
- Wu, F.C.; Huang, H.T. Hydraulic Resistance Induced by Deposition of Sediment in Porous Medium. J. Hydraul. Eng. 2000, 126. [Google Scholar] [CrossRef]
- Wharton, G.; Mohajeri, S.H.; Righetti, M. The pernicious problem of streambed colmation: A multi-disciplinary reflection on the mechanisms, causes, impacts, and management challenges. Wiley Interdiscip. Rev. Water 2017, 4, e1231. [Google Scholar] [CrossRef]
- Brunke, M.; Gonser, T. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef]
- Kemp, P.; Sear, D.; Collins, A.; Naden, P.; Jones, I. The impacts of fine sediment on riverine fish. Hydrol. Process. 2011, 25, 1800–1821. [Google Scholar] [CrossRef]
- Jones, J.; Collins, A.; Naden, P.; Sear, D. The relationship between fine sediment and macrophytes in rivers. River Res. Appl. 2012, 28, 1006–1018. [Google Scholar] [CrossRef]
- Jones, J.I.; Murphy, J.F.; Collins, A.L.; Sear, D.A.; Naden, P.S.; Armitage, P.D. The impact of fine sediment on macro-invertebrates. River Res. Appl. 2012, 28, 1055–1071. [Google Scholar] [CrossRef]
- Krause, S.; Hannah, D.M.; Fleckenstein, J.H. Hyporheic hydrology: Interactions at the groundwater-surface water interface. Hydrol. Process. 2009, 23, 2103–2107. [Google Scholar] [CrossRef]
- Sambrook Smith, G.H.; Nicholas, A.P. Effect on flow structure of sand deposition on a gravel bed: Results from a two-dimensional flume experiment. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Wren, D.; Langendoen, E.; Kuhnle, R. Effects of sand addition on turbulent flow over an immobile gravel bed. J. Geophys. Res. Earth Surf. 2011, 116, 1–12. [Google Scholar] [CrossRef]
- Mohajeri, S.H.; Righetti, M.; Wharton, G.; Romano, G.P. On the structure of gravel-bed flow with intermediate submergence: Implications for sediment transport. Adv. Water Resour. 2016, 92, 90–104. [Google Scholar] [CrossRef]
- Nikora, V.; Goring, D.; McEwan, I.; Griffiths, G. Spatially averaged open-channel flow over rough bed. J. Hydraul. Eng. 2001, 127, 123–133. [Google Scholar] [CrossRef]
- Mignot, E.; Barthelemy, E.; Hurter, D. Double-averaging analysis and local flow chracterization of near-bed turbulence in gravel-bed channel flow. J. Fluid Mech. 2009, 618, 279–303. [Google Scholar] [CrossRef]
- Dey, S.; Das, R. Gravel-bed hydrodynamics: Double-averaging approach. J. Hydraul. Eng. 2012, 138, 707–725. [Google Scholar] [CrossRef]
- Grams, P.E.; Wilcock, P.R. Equilibrium entrainment of fine sediment over a coarse immobile bed. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Wren, D.G.; Langendoen, E.J.; Rigby, J.R. Sand transport over an immobile gravel bed substrate. J. Hydraul. Eng. 2013, 139, 167–176. [Google Scholar] [CrossRef]
- Grams, P.E.; Wilcock, P.R. Transport of fine sediment over a coarse, immobile riverbed. J. Geophys. Res. Earth Surf. 2015, 119, 188–211. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Langendoen, E.J.; Wren, D.G. Prediction of sand transport over immobile gravel from supply-limited to capacity conditions. J. Hydraul. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Bertin, S.; Friedrich, H. Effects of Sand Addition and Bed Flushing on Gravel Bed Surface Microtopography and Roughness. Water Resour. Res. 2019. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Wren, D.G.; Langendoen, E.J. Erosion of Sand from a Gravel Bed. J. Hydraul. Eng. 2016, 142, 04015052. [Google Scholar] [CrossRef]
- Wren, D.G.; Kuhnle, R.A.; Langendoen, E.J.; Rigby, J.R. Turbulent Flow and Sand Transport over a Cobble Bed in a Laboratory Flume. J. Hydraul. Eng. 2014, 140, 04014001. [Google Scholar] [CrossRef]
- Fornarelli, F.; Vittori, G. Oscillatory boundary layer close to a rough wall. Eur. J. Mech. B/Fluids 2009, 28, 283–295. [Google Scholar] [CrossRef]
- Ghodke, C.D.; Apte, S.V. DNS study of particle-bed–turbulence interactions in an oscillatory wall-bounded flow. J. Fluid Mech. 2016, 792, 232–251. [Google Scholar] [CrossRef]
- Mazzuoli, M.; Blondeaux, P.; Simeonov, J.; Calantoni, J. Direct numerical simulation of the oscillatory flow around a sphere resting on a rough bottom. J. Fluid Mech. 2017, 822, 235–266. [Google Scholar] [CrossRef]
- Casulli, V. A semi-implicit numerical method for the free-surface Navier–Stokes equations. Int. J. Numer. Methods Fluids 2014, 74, 605–622. [Google Scholar] [CrossRef]
- Casulli, V.; Zanolli, P. Semi-implicit numerical modeling of nonhydrostatic free-surface flows for environmental problems. Math. Comput. Model. 2002, 36, 1131–1149. [Google Scholar] [CrossRef]
- Casulli, V.; Zanolli, P. High resolution methods for multidimensional advection–diffusion problems in free-surface hydrodynamics. Ocean Model. 2005, 10, 137–151. [Google Scholar] [CrossRef]
- Stelling, G.S.; Duinmeijer, S.P.A. A staggered conservative scheme for every Froude number in rapidly varied shallow water flows. Int. J. Numer. Methods Fluids 2003, 43, 1329–1354. [Google Scholar] [CrossRef]
- Gross, E.S.; Bonaventura, L.; Rosatti, G. Consistency with continuity in conservative advection schemes for free-surface models. Int. J. Numer. Methods Fluids 2002, 38, 307–327. [Google Scholar] [CrossRef]
- Casulli, V. Eulerian-Lagrangian methods for the Navier-Stokes equations at high Reynolds number. Int. J. Numer. Methods Fluids 1988, 8, 1349–1360. [Google Scholar] [CrossRef]
- Casulli, V.; Cattani, E. Stability, accuracy and efficiency of a semi-implicit method for three-dimensional shallow water flow. Comput. Math. Appl. 1994, 27, 99–112. [Google Scholar] [CrossRef]
- Blasius, H. Grenzschichten in Flüssigkeiten mit kleiner Reibung. Z. Math. Phys. 1908, 56, 1–37. [Google Scholar]
- Ghia, U.; Ghia, K.; Shin, C.T. High-resolutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- van Rijn, L.C. Sediment pick-up functions. J. Hydraul. Eng. 1984, 110, 1494–1502. [Google Scholar] [CrossRef]
- Manes, C.; Pokrajac, D.; McEwan, I.; Nikora, V. Turbulence structure of open channel flows over permeable and impermeable beds: A comparative study. Phys. Fluids 2009, 21, 125109. [Google Scholar] [CrossRef]
- Yager, E.M.; Kirchner, J.W.; Dietrich, W.E. Calculating bed load transport in steep boulder bed channels. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Dumbser, M. Arbitrary high order PNPM schemes on unstructured meshes for the compressible Navier–Stokes equations. Comput. Fluids 2010, 39, 60–76. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Casulli, V.; Zanolli, P. Iterative solutions of mildly nonlinear systems. J. Comput. Appl. Math. 2012, 236, 3937–3947. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tavelli, M.; Piccolroaz, S.; Stradiotti, G.; Pisaturo, G.R.; Righetti, M. A New Mass-Conservative, Two-Dimensional, Semi-Implicit Numerical Scheme for the Solution of the Navier-Stokes Equations in Gravel Bed Rivers with Erodible Fine Sediments. Water 2020, 12, 690. https://doi.org/10.3390/w12030690
Tavelli M, Piccolroaz S, Stradiotti G, Pisaturo GR, Righetti M. A New Mass-Conservative, Two-Dimensional, Semi-Implicit Numerical Scheme for the Solution of the Navier-Stokes Equations in Gravel Bed Rivers with Erodible Fine Sediments. Water. 2020; 12(3):690. https://doi.org/10.3390/w12030690
Chicago/Turabian StyleTavelli, Maurizio, Sebastiano Piccolroaz, Giulia Stradiotti, Giuseppe Roberto Pisaturo, and Maurizio Righetti. 2020. "A New Mass-Conservative, Two-Dimensional, Semi-Implicit Numerical Scheme for the Solution of the Navier-Stokes Equations in Gravel Bed Rivers with Erodible Fine Sediments" Water 12, no. 3: 690. https://doi.org/10.3390/w12030690
APA StyleTavelli, M., Piccolroaz, S., Stradiotti, G., Pisaturo, G. R., & Righetti, M. (2020). A New Mass-Conservative, Two-Dimensional, Semi-Implicit Numerical Scheme for the Solution of the Navier-Stokes Equations in Gravel Bed Rivers with Erodible Fine Sediments. Water, 12(3), 690. https://doi.org/10.3390/w12030690





