Modelling Effects of Rainfall Patterns on Runoff Generation and Soil Erosion Processes on Slopes
Abstract
:1. Introduction
2. Methodology
2.1. InHM Model
2.2. Model Setup
2.3. Rainfall Scenarios
3. Results
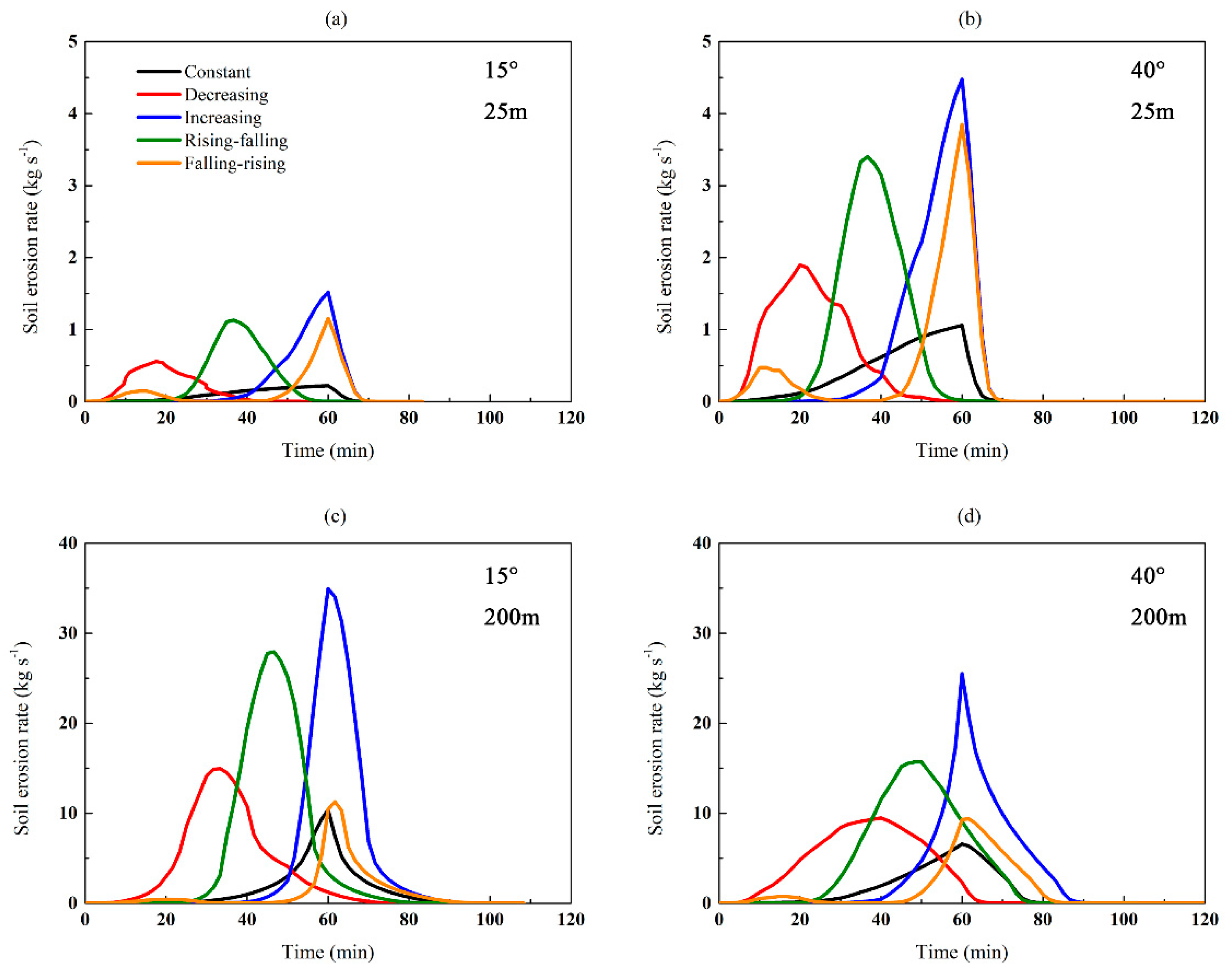
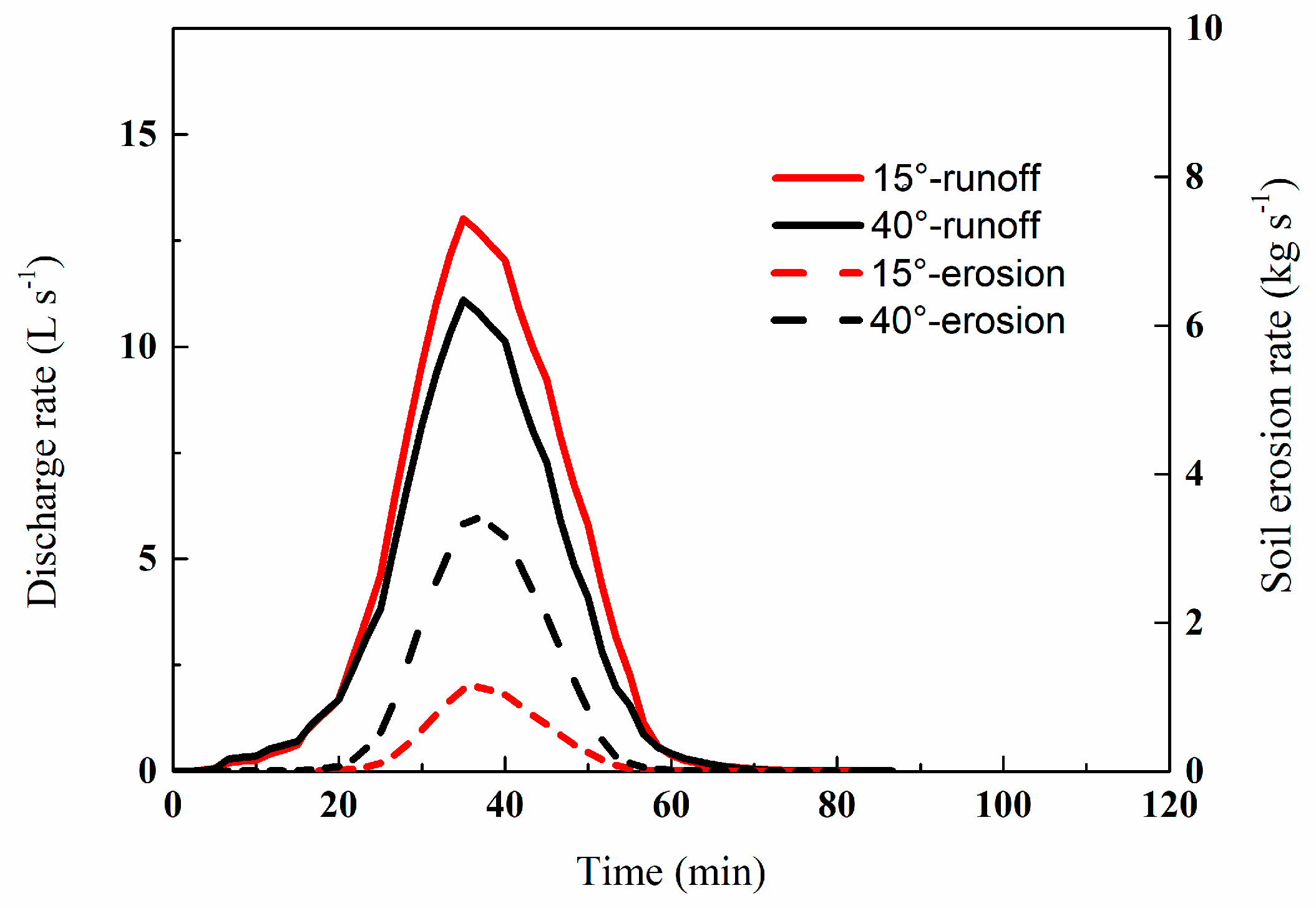
3.1. Hydrological Responses
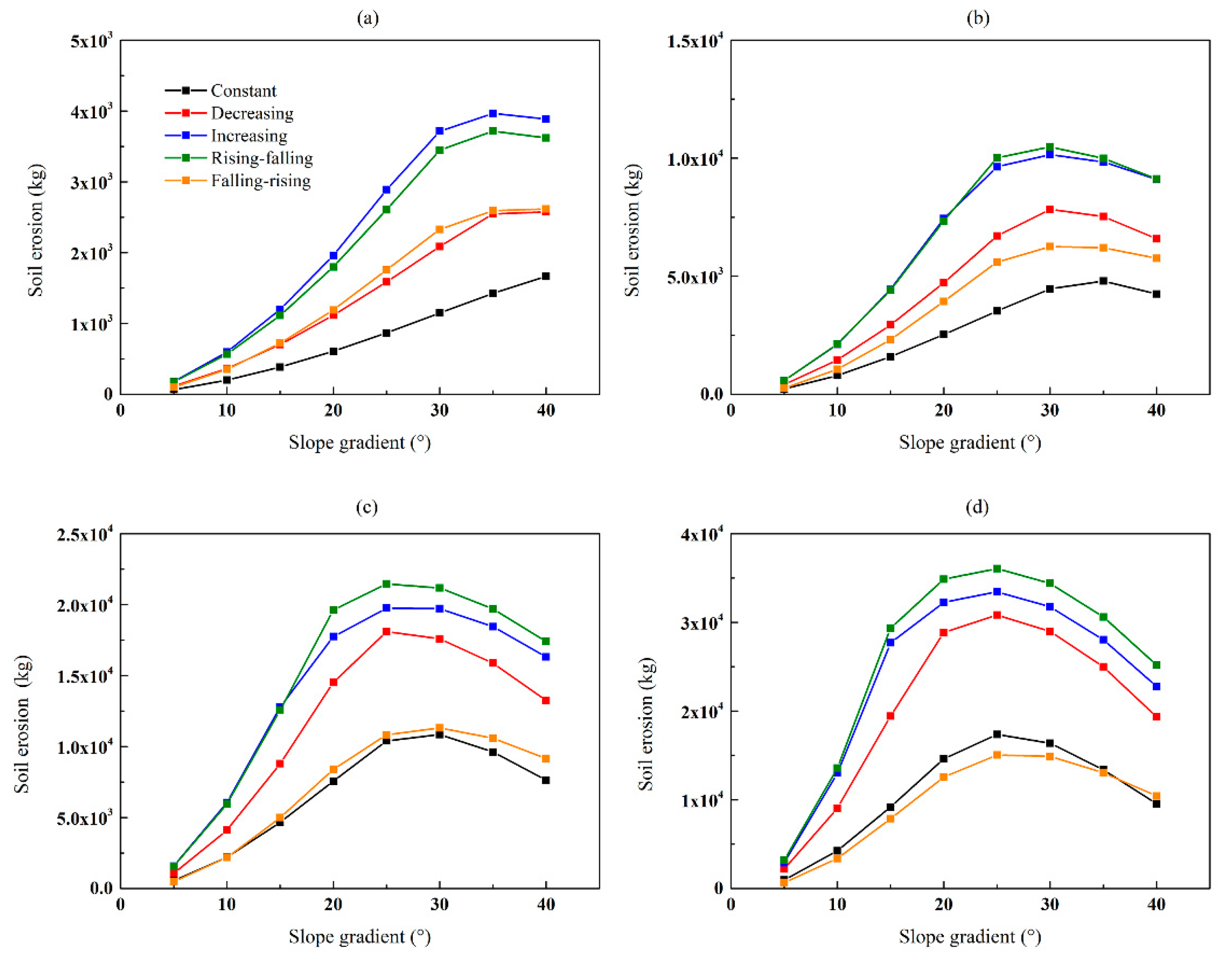
3.2. Soil Erosion
4. Discussion
4.1. Effect of Rainfall Patterns on Total Runoff and Soil Erosion at Different Slope Lengths
4.2. The Impact of Slope Gradient on Total Runoff and Erosion under Five Rainfall Patterns
4.3. Effect of Rainfall Patterns on Runoff and Soil Erosion Peaks
4.4. Benefits and Future Work
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dunkerley, D. Rain event properties in nature and in rainfall simulation experiments: A comparative review with recommendations for increasingly systematic study and reporting. Hydrol. Process. 2008, 22, 4415–4435. [Google Scholar] [CrossRef]
- Farrick, K.K.; Branfireun, B.A. Soil water storage, rainfall and runoff relationships in a tropical dry forest catchment. Water Resour. Res. 2014, 50, 9236–9250. [Google Scholar] [CrossRef]
- Dunkerley, D. Effects of rainfall intensity fluctuations on infiltration and runoff: Rainfall simulation on dryland soils, fowlers gap, australia. Hydrol. Process. 2012, 26, 2211–2224. [Google Scholar] [CrossRef]
- Singh, V.P. Effect of spatial and temporal variability in rainfall and watershed characteristics on stream flow hydrograph. Hydrol. Process. 1997, 11, 1649–1669. [Google Scholar] [CrossRef]
- Cerdan, O.; Bissonnais, Y.L.; Couturier, A.; Bourennane, H.; Souchère, V. Rill erosion on cultivated hillslopes during two extreme rainfall events in normandy, france. Soil Tillage Res. 2002, 67, 99–108. [Google Scholar] [CrossRef]
- Dolšak, D.; Bezak, N.; Šraj, M. Temporal characteristics of rainfall events under three climate types in slovenia. J. Hydrol. 2016, 541, 1395–1405. [Google Scholar] [CrossRef]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- An, J.; Zheng, F.L.; Han, Y. Effects of rainstorm patterns on runoff and sediment yield processes. Soil Sci. 2014, 179, 293–303. [Google Scholar] [CrossRef]
- Dunkerley, D. An approach to analysing plot scale infiltration and runoff responses to rainfall of fluctuating intensity. Hydrol. Process. 2017, 31, 191–206. [Google Scholar] [CrossRef]
- Parsons, A.J.; Stone, P.M. Effects of intra-storm variations in rainfall intensity on interrill runoff and erosion. Catena 2006, 67, 68–78. [Google Scholar] [CrossRef]
- Zhai, X.Y.; Guo, L.; Liu, R.H.; Zhang, Y.Y. Rainfall threshold determination for flash flood warning in mountainous catchments with consideration of antecedent soil moisture and rainfall pattern. Nat. Hazards 2018, 94, 605–625. [Google Scholar] [CrossRef]
- Chen, L.; Sela, S.; Svoray, T.; Assouline, S. Scale dependence of hortonian rainfall-runoff processes in a semiarid environment. Water Resour. Res. 2016, 52, 5149–5166. [Google Scholar] [CrossRef]
- Parsons, A.J.; Brazier, R.E.; Wainwright, J.; Powell, D.M. Scale relationships in hillslope runoff and erosion. Earth Surf. Process. Landf. 2006, 31, 1384–1393. [Google Scholar] [CrossRef]
- Langhans, C.; Govers, G.; Diels, J.; Stone, J.J.; Nearing, M.A. Modeling scale-dependent runoff generation in a small semi-arid watershed accounting for rainfall intensity and water depth. Adv. Water Resour. 2014, 69, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Guntner, A.; Bronstert, A. Representation of landscape variability and lateral redistribution processes for large-scale hydrological modelling in semi-arid areas. J. Hydrol. 2004, 297, 136–161. [Google Scholar] [CrossRef] [Green Version]
- Stomph, T.J.; Ridder, N.D.; Steenhuis, T.S.; Giesen, N.C.V.D. Scale effects of hortonian overland flow and rainfall-runoff dynamics: Laboratory validation of a process-based model. Earth Surf. Process. Landf. 2002, 27, 847–855. [Google Scholar] [CrossRef]
- Assouline, S.; Ben-Hur, M. Effects of rainfall intensity and slope gradient on the dynamics of interrill erosion during soil surface sealing. Catena 2006, 66, 211–220. [Google Scholar] [CrossRef]
- Essig, E.T.; Corradini, C.; Morbidelli, R.; Govindaraju, R.S. Infiltration and deep flow over sloping surfaces: Comparison of numerical and experimental results. J. Hydrol. 2009, 374, 30–42. [Google Scholar] [CrossRef]
- Defersha, M.B.; Quraishi, S.; Melesse, A. The effect of slope steepness and antecedent moisture content on interrill erosion, runoff and sediment size distribution in the highlands of ethiopia. Hydrol. Earth Syst. Sci. 2011, 15, 2367–2375. [Google Scholar] [CrossRef]
- Shi, Z.H.; Fang, N.F.; Wu, F.Z.; Wang, L.; Yue, B.J.; Wu, G.L. Soil erosion processes and sediment sorting associated with transport mechanisms on steep slopes. J. Hydrol. 2012, 454, 123–130. [Google Scholar] [CrossRef]
- Cheng, Q.; Ma, W.; Cai, Q. The relative importance of soil crust and slope angle in runoff and soil loss: A case study in the hilly areas of the loess plateau, north china. GeoJournal 2008, 71, 117–125. [Google Scholar] [CrossRef]
- Chaplot, V.A.M.; Le Bissonnais, Y. Runoff features for interrill erosion at different rainfall intensities, slope lengths, and gradients in an agricultural loessial hillslope. Soil Sci. Soc. Am. J. 2003, 67, 844–851. [Google Scholar] [CrossRef]
- Ebel, B.A.; Loague, K.; Montgomery, D.R.; Dietrich, W.E. Physics-based continuous simulation of long-term near-surface hydrologic response for the coos bay experimental catchment. Water Resour. Res. 2008, 44, 137–149. [Google Scholar] [CrossRef]
- Ran, Q.; Keith, L.; Verkwaak, J.E. Hydrologic-response-driven sediment transport at a regional scale, process-based simulation. Hydrol. Process. 2012, 26, 159–167. [Google Scholar] [CrossRef]
- Ebel, B.A.; Loague, K.; Borja, R.I. The impacts of hysteresis on variably saturated hydrologic response and slope failure. Environ. Earth Sci. 2010, 61, 1215–1225. [Google Scholar] [CrossRef]
- VanderKwaak, J.E.; Loague, K. Hydrologic-response simulations for the r-5 catchment with a comprehensive physics-based model. Water Resour. Res. 2001, 37, 999–1013. [Google Scholar] [CrossRef]
- VanderKwaak, J.E. Numerical Simulation of Flow and Chemical Transport in Integrated Surface-Subsurface Hydrologic Systems. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 1999. [Google Scholar]
- Ran, Q.; Heppner, C.S.; Vanderkwaak, J.E.; Loague, K. Further testing of the integrated hydrology model (inhm): Multiple-species sediment transport. Hydrol. Process. 2007, 21, 1522–1531. [Google Scholar] [CrossRef]
- Ran, Q.; Hong, Y.; Li, W.; Gao, J. A modelling study of rainfall-induced shallow landslide mechanisms under different rainfall characteristics. J. Hydrol. 2018, 563, 790–801. [Google Scholar] [CrossRef]
- Heppner, C.S.; Ran, Q.; Vanderkwaak, J.E.; Loague, K. Adding sediment transport to the integrated hydrology model (inhm): Development and testing. Adv. Water Resour. 2006, 29, 930–943. [Google Scholar] [CrossRef]
- Johansen, M.P.; Hakonson, T.E.; Breshears, D.D. Post-fire runoff and erosion from rainfall simulation: Contrasting forests with shrublands and grasslands. Hydrol. Process. 2001, 15, 2953–2965. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Gao, J.; Kirkby, M.; Holden, J. The effect of interactions between rainfall patterns and land-cover change on flood peaks in upland peatlands. J. Hydrol. 2018, 567, 546–559. [Google Scholar] [CrossRef] [Green Version]
- Flanagan, D.C.; Foster, G.R.; Moldenhauer, W.C. Storm pattern effect on infiltration, runoff, and erosion. Trans. ASAE 1988, 31, 546–559. [Google Scholar] [CrossRef]
- Wang, B.; Steiner, J.; Zheng, F.; Gowda, P. Impact of rainfall pattern on interrill erosion process. Earth Surf. Process. Landf. 2017, 42, 1833–1846. [Google Scholar] [CrossRef]
- Xue, J.; Gavin, K. Effect of rainfall intensity on infiltration into partly saturated slopes. Geotech. Geol. Eng. 2008, 26, 199–209. [Google Scholar] [CrossRef]
- Wu, S.; Yu, M.; Chen, L. Nonmonotonic and spatial-temporal dynamic slope effects on soil erosion during rainfall-runoff processes. Water Resour. Res. 2017, 53, 1369–1389. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Xiang, H.; Singh, V.P. A simulation model for unified interrill erosion and rill erosion on hillslopes. Hydrol. Process. 2006, 20, 469–486. [Google Scholar] [CrossRef]
- Dunkerley, D. Stemflow production and intrastorm rainfall intensity variation: An experimental analysis using laboratory rainfall simulation. Earth Surf. Process. Landf. 2014, 39, 1741–1752. [Google Scholar] [CrossRef]
- Fang, H.; Sun, L.; Tang, Z. Effects of rainfall and slope on runoff, soil erosion and rill development: An experimental study using two loess soils. Hydrol. Process. 2015, 29, 2649–2658. [Google Scholar] [CrossRef]
- Wirtz, S.; Seeger, M.; Ries, J.B. Field experiments for understanding and quantification of rill erosion processes. Catena 2012, 91, 21–34. [Google Scholar] [CrossRef]

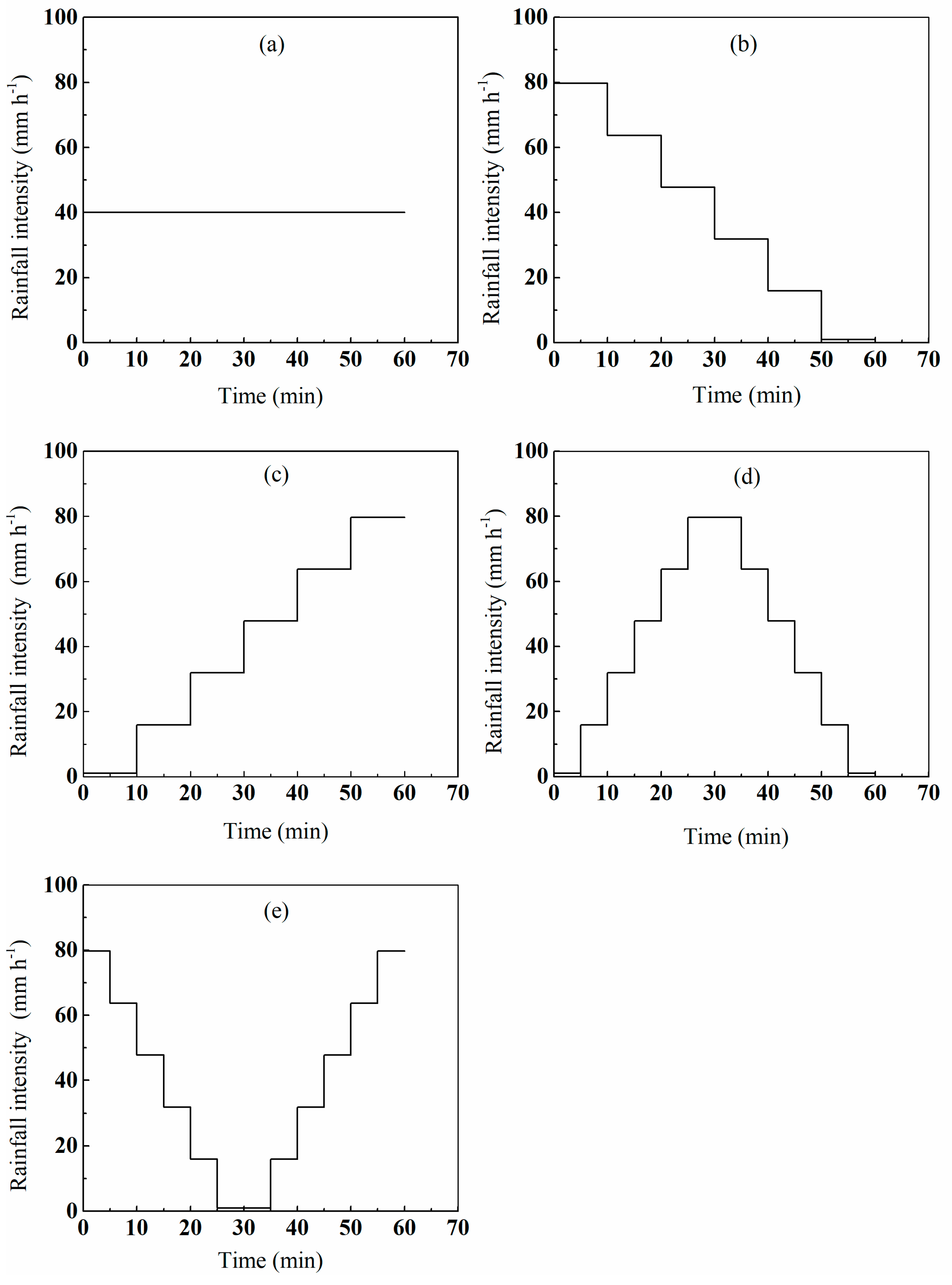





| Parameters | Value |
|---|---|
| Porosity | 0.46 |
| Species average grain diameter | 2.0 × 10−5 m |
| Manning coefficient | 0.275 |
| Initial water table | −5 m |
| Mobile water depth (i.e., depression storage) | 5 × 10−4 m |
| Height of microtopography | 0.01 m |
| Soil-water retention function (van Genuchten approach [32]) | α: 1.0 |
| n: 1.23 | |
| θr: 0.088 | |
| Saturated hydraulic conductivity (Ks) | 10.8 mm h−1 |
| Rainsplash coefficient | 2.93 |
| Projective Slope Length (m) | Rainfall Pattern | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° |
|---|---|---|---|---|---|---|---|---|---|
| 25 | Constant | 13.3 | 14.1 | 14.3 | 14.3 | 14.0 | 13.5 | 12.7 | 11.8 |
| Decreasing | 15.9 | 16.5 | 16.6 | 16.5 | 16.1 | 15.5 | 14.6 | 13.5 | |
| Increasing | 17.3 | 18.1 | 18.3 | 18.3 | 18.0 | 17.4 | 16.7 | 15.7 | |
| Rising-falling | 17.6 | 18.2 | 18.3 | 18.1 | 17.8 | 17.2 | 16.4 | 15.3 | |
| Falling-rising | 14.3 | 15.4 | 15.8 | 15.8 | 15.5 | 15.0 | 14.3 | 13.3 | |
| 50 | Constant | 21.7 | 23.4 | 23.7 | 23.4 | 22.5 | 21.1 | 19.2 | 16.9 |
| Decreasing | 27.8 | 29.2 | 29.3 | 28.7 | 27.7 | 26.1 | 24.0 | 21.4 | |
| Increasing | 29.4 | 31.3 | 31.9 | 31.7 | 31.0 | 29.7 | 28.0 | 25.7 | |
| Rising-falling | 30.5 | 32.3 | 32.6 | 32.3 | 31.4 | 30.1 | 28.2 | 25.7 | |
| Falling-rising | 22.0 | 24.6 | 25.5 | 25.4 | 24.7 | 23.5 | 21.7 | 19.6 | |
| 100 | Constant | 32.8 | 36.9 | 37.9 | 37.2 | 35.3 | 32.3 | 28.3 | 23.5 |
| Decreasing | 45.0 | 49.3 | 50.3 | 49.5 | 47.4 | 44.1 | 39.6 | 33.9 | |
| Increasing | 47.3 | 51.8 | 53.2 | 52.9 | 51.3 | 48.5 | 44.6 | 39.5 | |
| Rising-falling | 49.6 | 54.3 | 55.6 | 55.3 | 53.6 | 50.8 | 46.8 | 41.5 | |
| Falling-rising | 30.0 | 35.6 | 37.6 | 37.7 | 36.4 | 33.9 | 30.4 | 26.2 | |
| 200 | Constant | 43.4 | 51.5 | 53.9 | 52.9 | 49.2 | 43.3 | 35.7 | 27.4 |
| Decreasing | 65.9 | 74.9 | 77.8 | 76.8 | 73.0 | 66.3 | 57.2 | 45.7 | |
| Increasing | 69.7 | 79.9 | 82.8 | 82.0 | 78.3 | 72.1 | 63.4 | 52.2 | |
| Rising-falling | 75.4 | 84.6 | 87.3 | 86.6 | 83.0 | 76.9 | 68.0 | 56.6 | |
| Falling-rising | 35.8 | 44.9 | 48.4 | 48.4 | 46.0 | 41.4 | 35.5 | 29.1 |
| Projective Slope Length (m) | Rainfall Pattern | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° |
|---|---|---|---|---|---|---|---|---|---|
| 25 | Constant | 66 | 201 | 385 | 610 | 867 | 1149 | 1426 | 1666 |
| Decreasing | 116 | 364 | 703 | 1116 | 1586 | 2087 | 2546 | 2574 | |
| Increasing | 179 | 599 | 1198 | 1961 | 2888 | 3715 | 3965 | 3888 | |
| Rising-falling | 175 | 567 | 1114 | 1797 | 2607 | 3446 | 3717 | 3620 | |
| Falling-rising | 102 | 352 | 722 | 1191 | 1757 | 2329 | 2592 | 2618 | |
| 50 | Constant | 227 | 794 | 1590 | 2530 | 3527 | 4465 | 4800 | 4248 |
| Decreasing | 411 | 1452 | 2935 | 4729 | 6704 | 7837 | 7534 | 6590 | |
| Increasing | 586 | 2116 | 4442 | 7445 | 9636 | 10,154 | 9842 | 9102 | |
| Rising-falling | 581 | 2127 | 4426 | 7338 | 10,017 | 10,480 | 9993 | 9123 | |
| Falling-rising | 261 | 1058 | 2314 | 3931 | 5598 | 6258 | 6210 | 5762 | |
| 100 | Constant | 547 | 2199 | 4662 | 7566 | 10,401 | 10,845 | 9622 | 7629 |
| Decreasing | 1060 | 4111 | 8795 | 14,523 | 18,102 | 17,590 | 15,878 | 13,242 | |
| Increasing | 1571 | 6053 | 12,787 | 17,745 | 19,753 | 19,720 | 18,447 | 16,318 | |
| Rising-falling | 1559 | 5962 | 12,579 | 19,620 | 21,465 | 21,173 | 19,703 | 17,396 | |
| Falling-rising | 487 | 2186 | 4993 | 8389 | 10,827 | 11,320 | 10,589 | 9150 | |
| 200 | Constant | 955 | 4250 | 9193 | 14,618 | 17,358 | 16,384 | 13,373 | 9548 |
| Decreasing | 2205 | 9037 | 19,436 | 28,850 | 30,831 | 28,977 | 24,982 | 19,345 | |
| Increasing | 2895 | 13,002 | 27,699 | 32,262 | 33,449 | 31,753 | 28,030 | 22,777 | |
| Rising-falling | 3179 | 13,562 | 29,359 | 34,865 | 36,063 | 34,389 | 30,605 | 25,198 | |
| Falling-rising | 660 | 3370 | 7866 | 12,564 | 15,046 | 14,901 | 13,047 | 10,428 |
| Source | Experiment Setup | Scenario Arrangement | Finding | Comparison with This Study |
|---|---|---|---|---|
| Parsons and Stone [10] | 2.43 m-long, 0.9 m-width, 0.2 m-depth flume, 10° slope, three soil types. | Intensity from 46.4 to 170.8 mm h−1, 93.9 mm h−1 on average. | A constant-intensity storm are reduced by about 25% compared to varied-intensity storms. | 1. Conform part: Total runoff and soil erosion were lower than those of increasing, decreasing and rising-falling rainfalls. 2. Non conform part: The rising-falling rainfall generally had the largest runoff and soil erosion amount, while the constant rainfall did not have the lowest ones when the projective slope length was over 100 m. |
| An et al. [8] | 8 m-long, 1.6 m-width, 0.2 m-depth flume, 5° and 10° slope, pre wetted silt loam soil. | Intensity from 50 to 100 mm h−1, 75 mm h−1 on average. | Soil loss from varying-intensity rainfalls was 1.13 to 5.17 times greater than that from even-intensity rainfall. Soil loss under increasing rainfall were the highest. | |
| Dunkerley [3] | 0.5 m × 0.5 m plot, 0.2° slope, loam soil. | Intensity peaked at 30 mm h−1, 10 mm h−1 on average. | Late peak events had the highest peak runoff rate and runoff ratio, which were more than double those of the early peak events. The constant rainfall yielded the lowest total runoff and runoff rate. | |
| Wang et al. [35] | 2 m-long, 1 m-width, 0.5 m-depth flume, 10° slope, pre wetted clay loam soil. | Intensity from 50 to 100 mm h−1, 75 mm h−1 on average. | The constant rainfall produced the lowest sediment yield at around 61.8% of the average soil loss for the increasing rainfall, which had the highest soil loss. | |
| Zhai et al. [11] | Hydrological simulation study at catchment around 100 km2. | Intensity from 7 to 69 mm h−1, about 20 mm h−1 on average | The delayed rainfall pattern yield higher flood volume and peak than the early peak pattern. | Consensus |
| Wu et al. [37] | Theoretical framework work at 22.1 m long slopes from 0.5° to 60°. | No description. | Critical slope for runoff rate was around 11° regardless of rainfall duration and slope length | The critical slope of the runoff was close, and was also independent of slope length. |
| Cheng et al. [38] | 2 m × 5 m plot, 5° to 25° slope, sandy loam soil. | 72 mm h−1 rainfall for 30 min. | Soil loss increased with increasing slope angle till the critical slope angle of 20°–30°. | The range of critical slope of the soil erosion was close. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, Q.; Wang, F.; Gao, J. Modelling Effects of Rainfall Patterns on Runoff Generation and Soil Erosion Processes on Slopes. Water 2019, 11, 2221. https://doi.org/10.3390/w11112221
Ran Q, Wang F, Gao J. Modelling Effects of Rainfall Patterns on Runoff Generation and Soil Erosion Processes on Slopes. Water. 2019; 11(11):2221. https://doi.org/10.3390/w11112221
Chicago/Turabian StyleRan, Qihua, Feng Wang, and Jihui Gao. 2019. "Modelling Effects of Rainfall Patterns on Runoff Generation and Soil Erosion Processes on Slopes" Water 11, no. 11: 2221. https://doi.org/10.3390/w11112221
APA StyleRan, Q., Wang, F., & Gao, J. (2019). Modelling Effects of Rainfall Patterns on Runoff Generation and Soil Erosion Processes on Slopes. Water, 11(11), 2221. https://doi.org/10.3390/w11112221





