Numerical Simulation of Non-Homogeneous Viscous Debris-Flows Based on the Smoothed Particle Hydrodynamics (SPH) Method
Abstract
:1. Introduction
2. Fundamental Theories and Numerical Modeling
2.1. The SPH Method
2.1.1. SPH Interpolation
2.1.2. Gradient and Divergence
2.2. Governing Equations
2.2.1. Equation of State
2.2.2. Viscous Terms
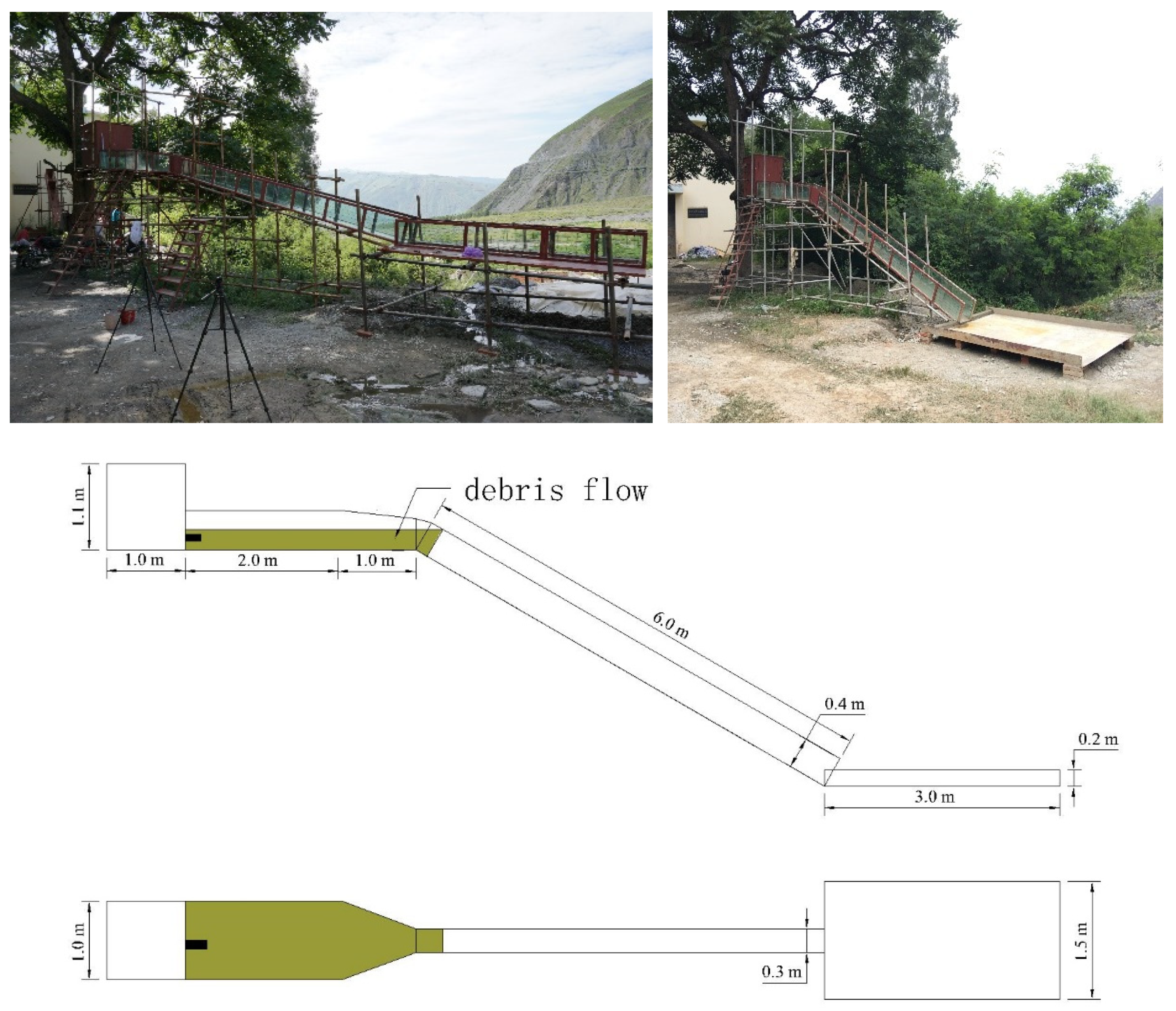
3. Experimental Setup and Boundary Conditions
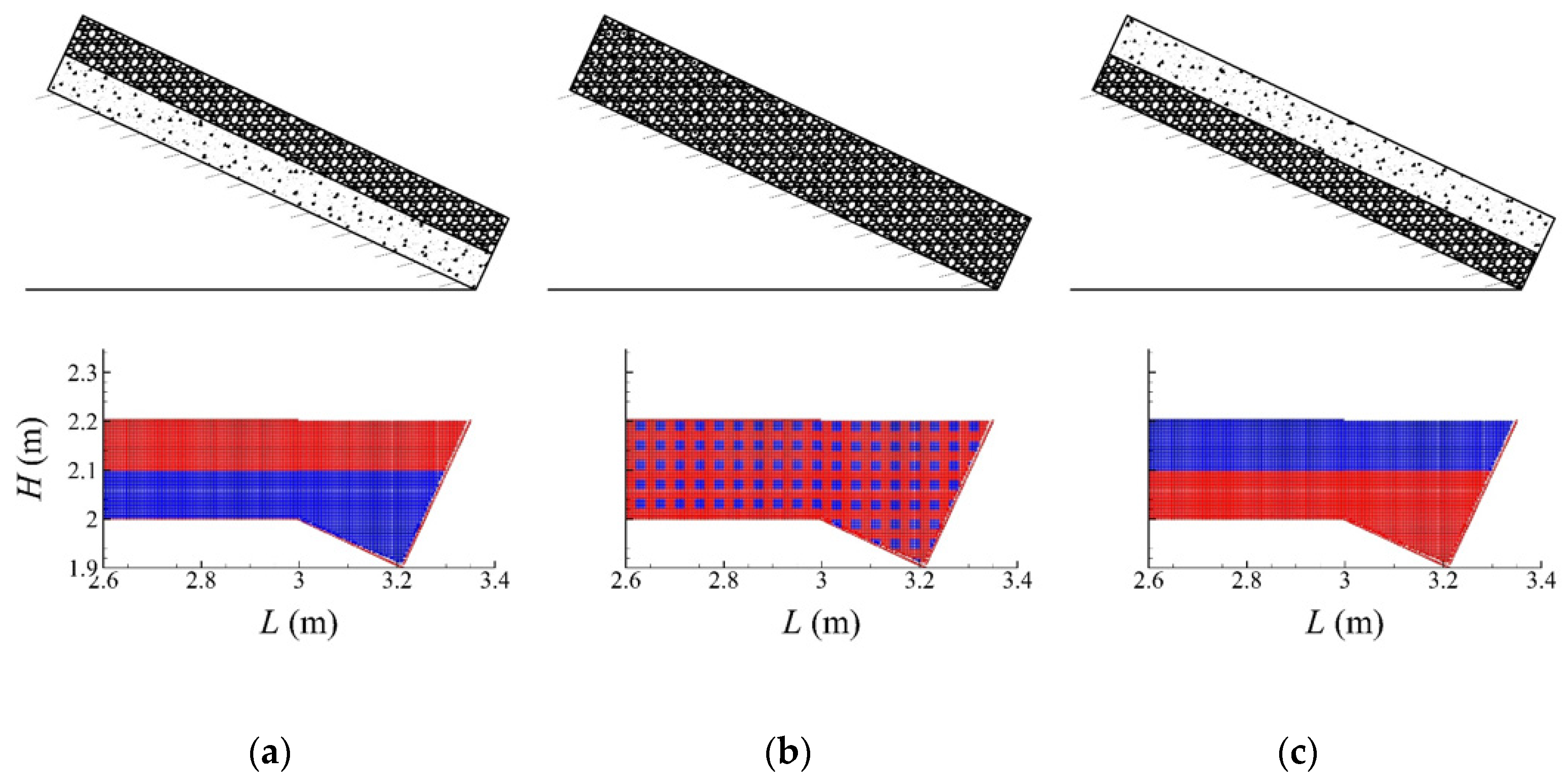
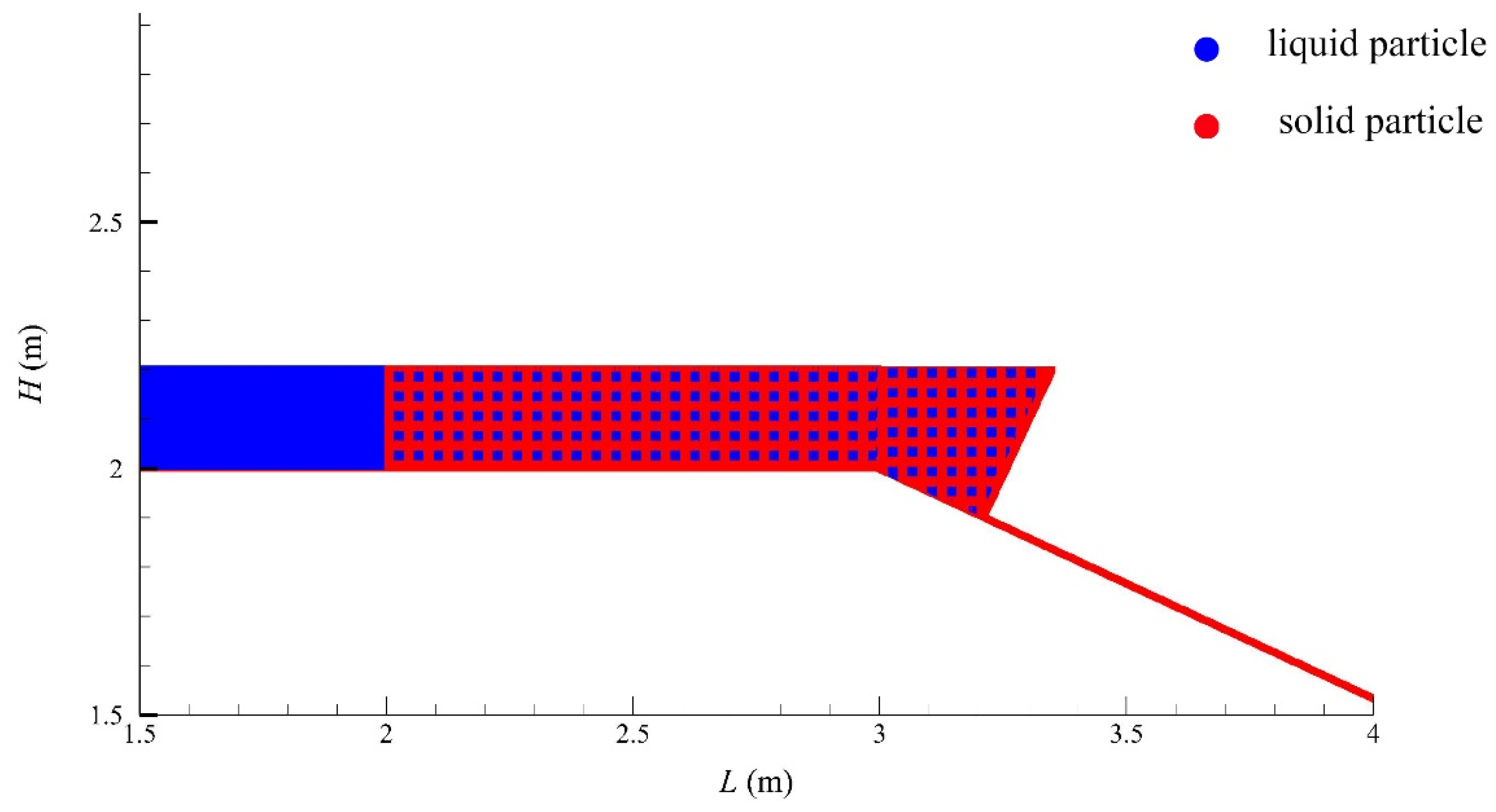
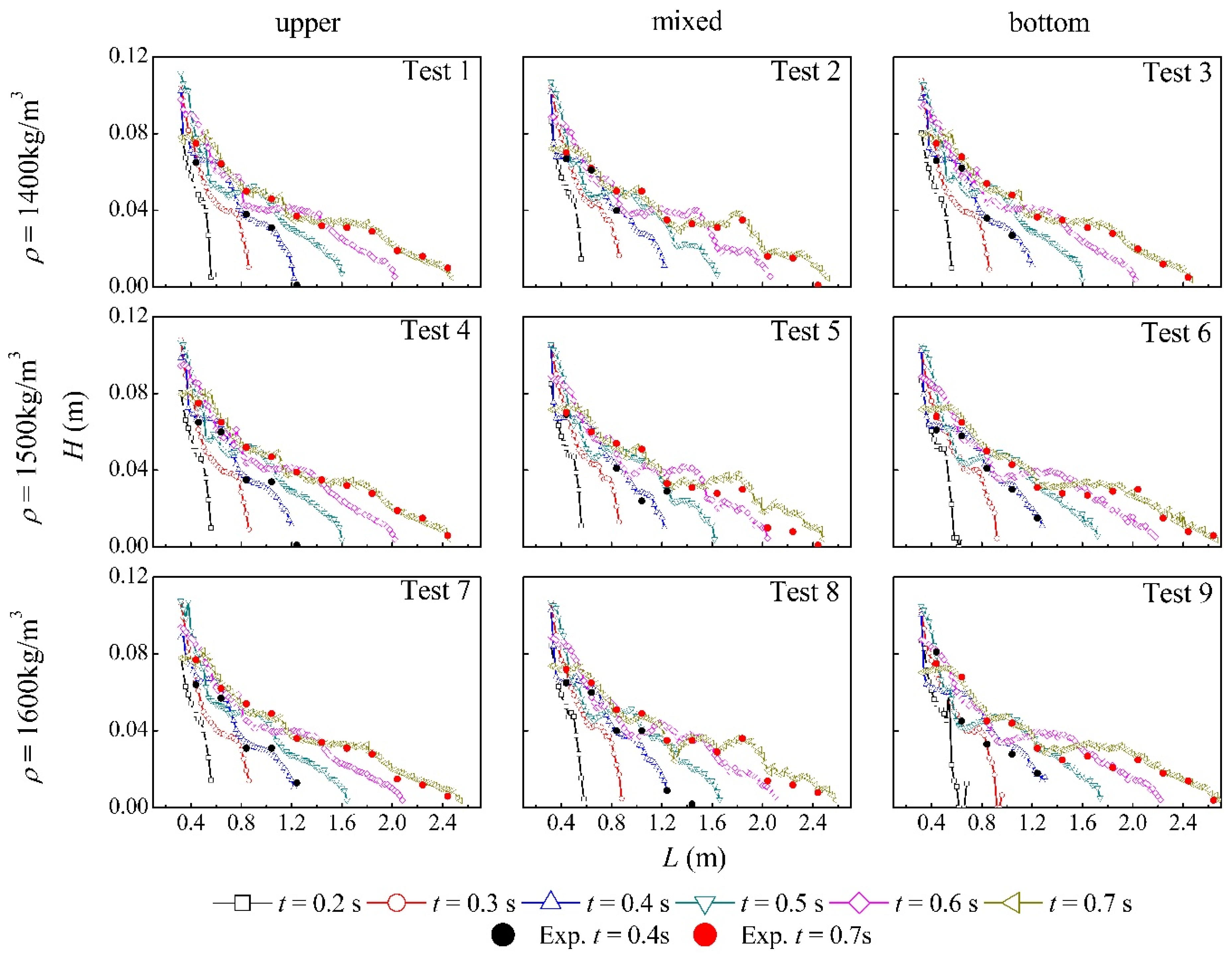
4. Simulation and Analysis
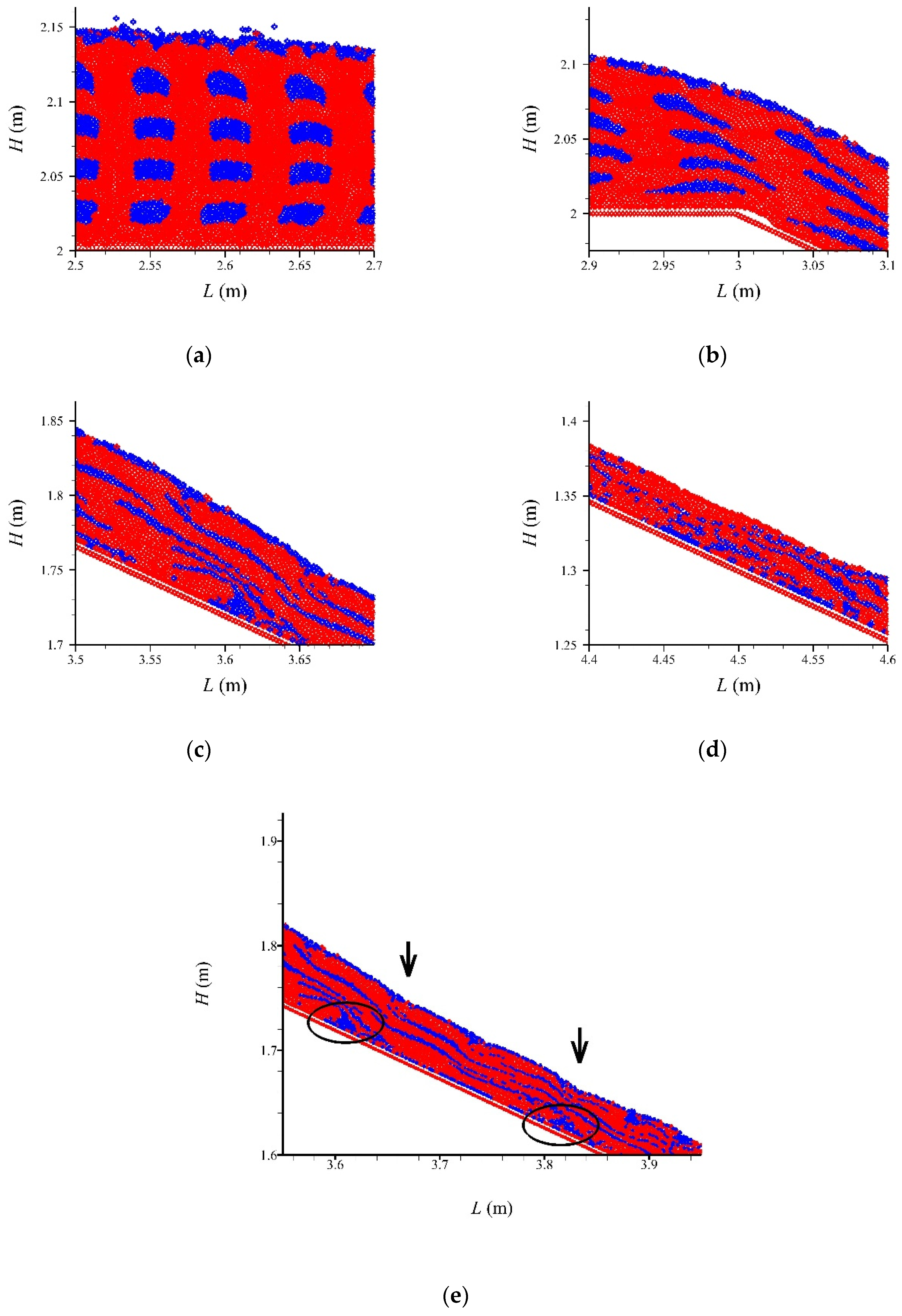
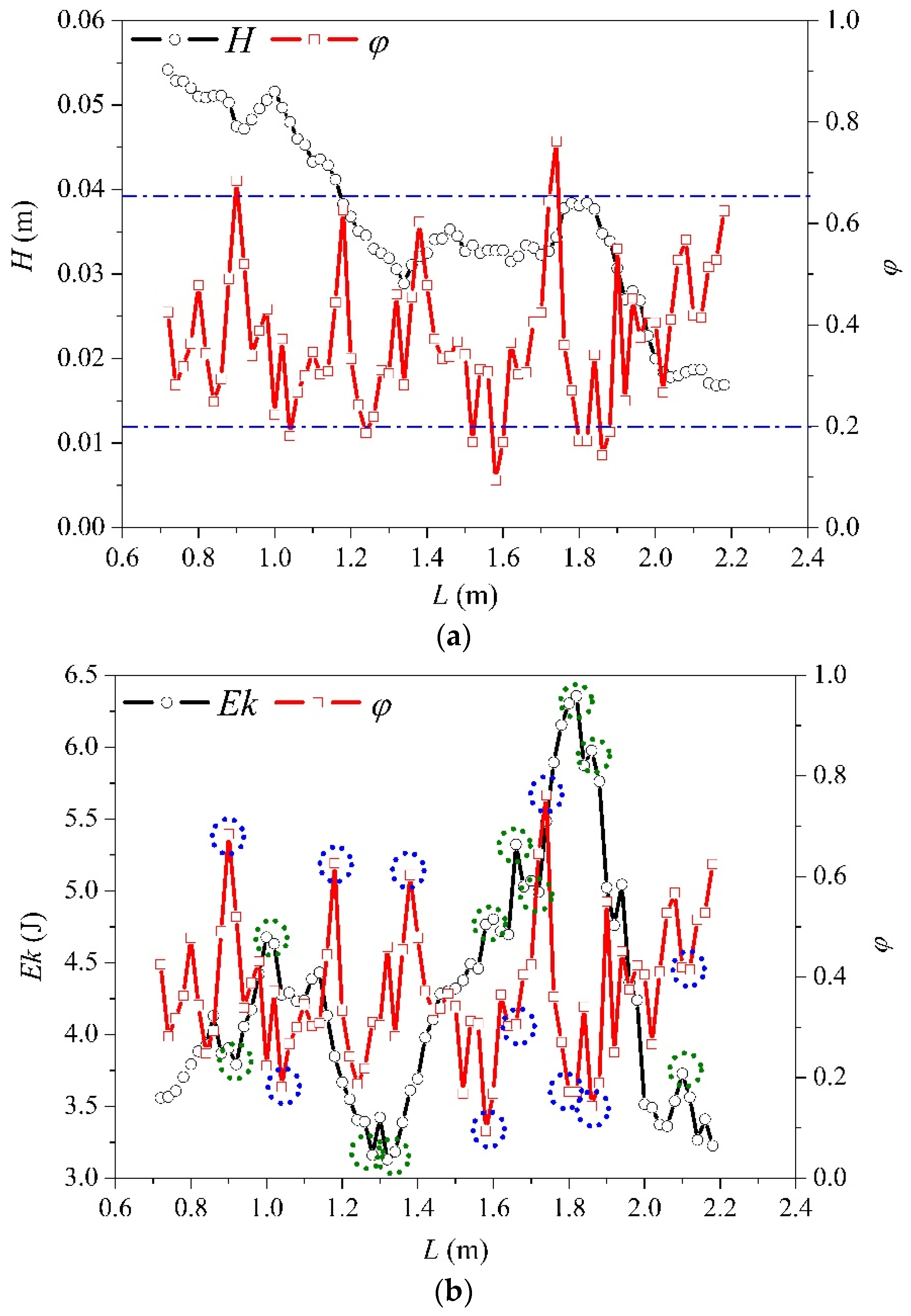
Characterization of Intermittent Debris Flow
5. Summary and Conclusions
- By comparing the shape and velocity of debris flows under different configurations, it was found that the vertical distribution of particles played a very important role in debris flow fluctuation, with a greater influence than on the viscous coefficient. The third configuration with mixed fine and coarse particles showed to fluctuate more violently, and this outcome confirmed one of the main assumptions for intermittent debris flows.
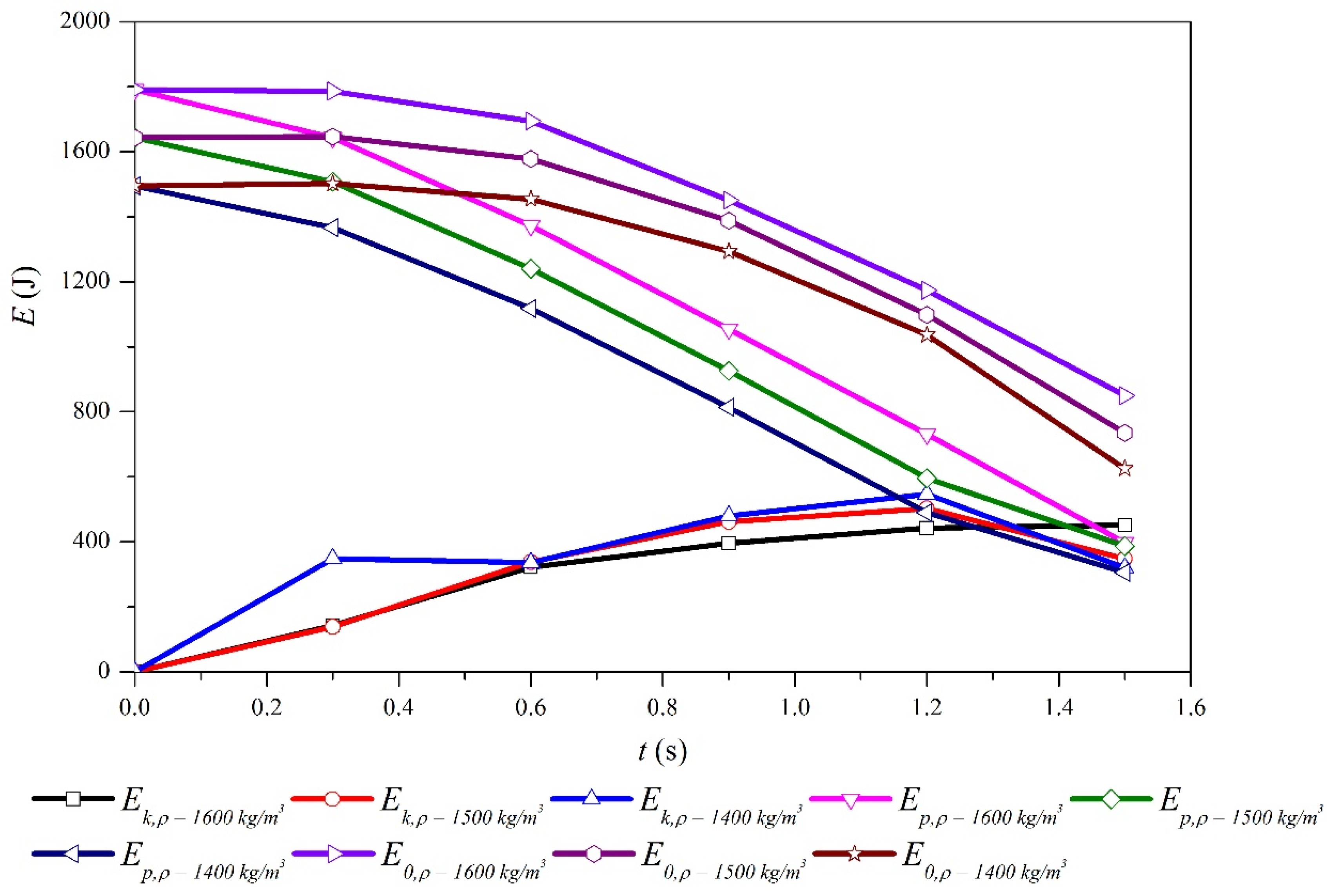
- By analyzing the characteristics of the fluid movement processes, it was found that when the two layers (fine and coarse particles) are mixed with the water, liquid particles tended to gather towards the bottom side of the debris flow causing a correspondent decrease of height. However, this effect could only be observed at small-scale areas. The potential energy was greatly affected by the magnitude of the moisture content, while the kinetic energy was significantly affected by the derivative of moisture content in the L direction.
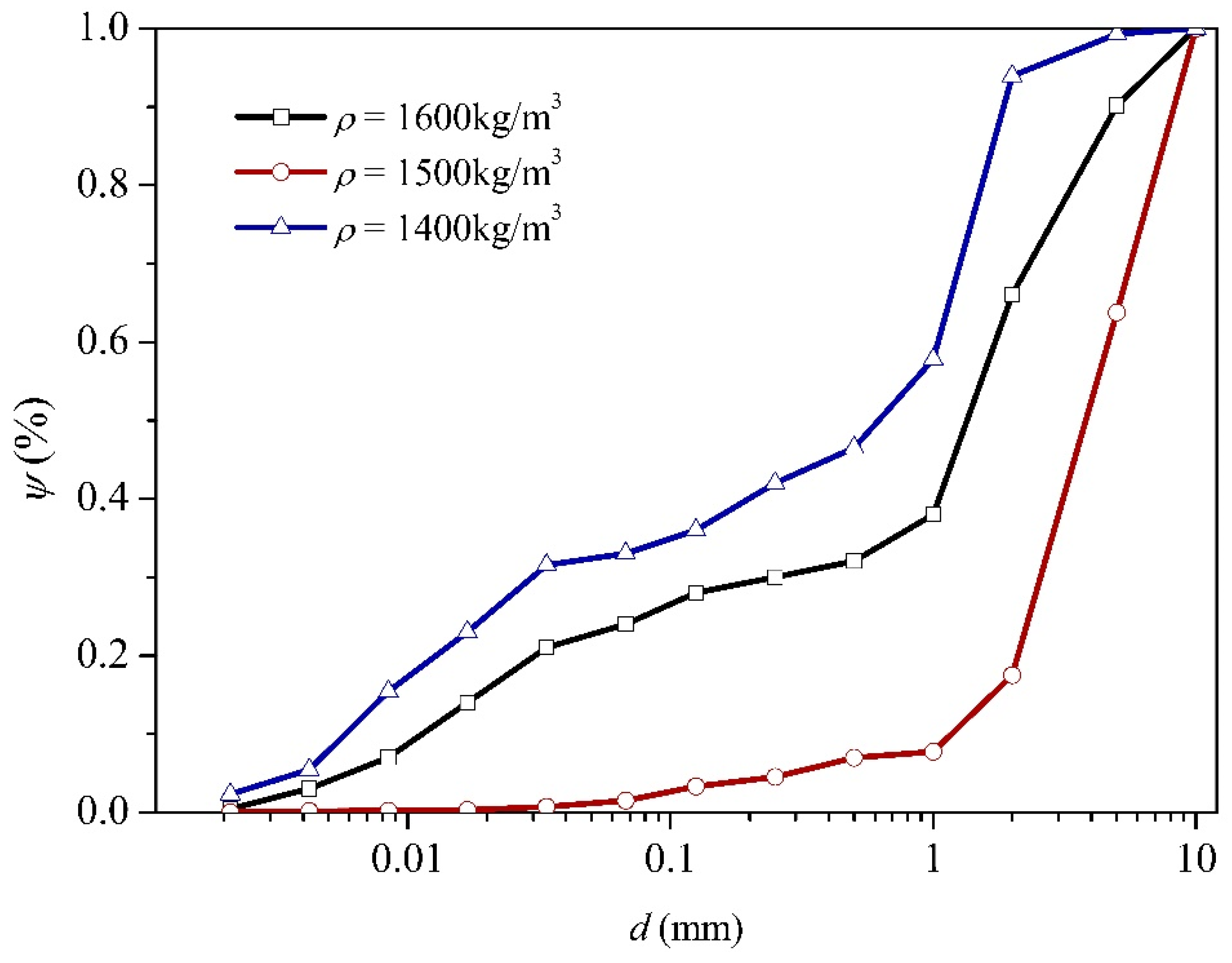
- The differences of the energy conversion curves associated to different viscous coefficients were mainly noticed in kinetic energies. Fluids with smaller densities exhibited higher initiation velocities and higher fluctuations values.
Author Contributions
Funding
Conflicts of Interest
References
- Kim, M.I.; Kwak, J.H.; Kim, B.S. Assessment of dynamic impact force of debris flow in mountain torrent based on characteristics of debris flow. Environ. Earth Sci. 2018, 77, 538. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.M. Impact of the 2008 Wenchuan earthquake in China on subsequent long-term debris flow activities in the epicentral area. Geomorphology 2017, 276, 86–103. [Google Scholar] [CrossRef]
- Silhan, K.; Tichavsky, R. Recent increase in debris flow activity in the Tatras Mountains: Results of a regional dendogeomorphic reconstruction. CATENA 2016, 143, 221–231. [Google Scholar] [CrossRef]
- Brandinoni, F.; Mao, L.; Recking, A.; Rickenmann, D.; Turowski, J.M. Morphodynamics of steep mountain channels. Earth Surf. Process. Landf. 2015, 40, 1560–1562. [Google Scholar] [CrossRef]
- Takahashi, T.; Das, D.K. Debris Flow: Mechanics, Prediction and Countermeasures; CRC Press: London, UK, 2014. [Google Scholar]
- Shu, A.P.; Tian, L.; Wang, S.; Rubinato, M.; Zhu, F.Y.; Wang, M.Y.; Sun, J.T. Hydrodynamic characteristics of the formation processes for non-homogeneous debris-flow. Water 2018, 10, 452. [Google Scholar] [CrossRef]
- Liu, J.J.; Li, Y. A review of study on drag reduction of viscous debris flow residual layer. J. Sedim. Res. 2016, 3, 72–80. (In Chinese) [Google Scholar]
- Johnson, A.M. Physical Processes in Geology; Freeman Cooper & Company: San Francisco, CA, USA, 1970. [Google Scholar]
- Bagnold, R.A. Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. Lond. Ser. A 1954, 22, 49–63. [Google Scholar]
- Takahashi, T. Mechanical characteristics of debris flow. J. Hydraul. Div. Am. Soc. Civ. Eng. 1978, 104, 1153–1169. [Google Scholar]
- Chen, C.L. Generalized viscoplastic modelling of debris flow. J. Hydraul. Div. Am. Soc. Civ. Eng. 1988, 114, 237–258. [Google Scholar] [CrossRef]
- Chen, C.L. General solutions for viscoplastic debris flow. J. Hydraul. Div. Am. Soc. Civ. Eng. 1988, 114, 259–282. [Google Scholar] [CrossRef]
- O’Brien, J.S.; Julien, P.Y. Laboratory analysis of mudflow properties. J. Hydraul. Div. Am. Soc. Civ. Eng. 1988, 114, 877–887. [Google Scholar] [CrossRef]
- O’Brien, J.S.; Julien, P.Y.; Fullerton, W.T. Two-dimensional water flood and mudflow simulation. J. Hydraul. Div. Am. Soc. Civ. Eng. 1993, 119, 244–261. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y.; Cheng, H.; Xu, Q. 3D Numerical modeling using smoothed particle hydrodynamics of flow-like landslide propagation triggered by the 2008 Wenchuan earthquake. Eng. Geol. 2014, 180, 21–33. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Manzari, M.T.; Hannani, S.K. A fully explicit three-step SPH algorithm for simulation of non-Newtonian fluid flow. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 715–735. [Google Scholar] [CrossRef]
- Rodriguez-Paz, M.X.; Bonet, J. A corrected smooth particle hydrodynamics method for the simulation of debris flows. Numer. Methods Part Differ. Equ. 2004, 20, 140–163. [Google Scholar] [CrossRef]
- Savage, S.B.; Hutter, K. The dynamics of avalanches of granular materials from initiation to run out. Acta Mech. Sin. 1991, 86, 201–223. [Google Scholar] [CrossRef]
- Trunk, F.J.; Dent, J.D.; Lang, T.E. Computer modeling of large rock slides. J. Geotech. Eng. 1986, 112, 348–360. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef] [Green Version]
- Xenakis, A.M.; Lind, S.J.; Stansby, P.K.; Rogersb, B.D. An incompressible SPH scheme with improved pressure predictions for free-surface generalised Newtonian flows. J. Non-Newton. Fluid Mech. 2015, 218, 1–15. [Google Scholar] [CrossRef]
- Springel, V.; Hernquist, L. Cosmological smoothed particle hydrodynamics simulations: A hybrid multiphase model for star formation. Mon. Not. R. Astron. Soc. 2003, 339, 289–311. [Google Scholar] [CrossRef]
- Gómez-Gesteira, M.; Dalrymple, R.A. Using a three-dimensional Smoothed Particle Hydrodynamics method for wave impact on a tall structure. J. Waterw Port Coast. 2004, 130, 63–69. [Google Scholar] [CrossRef]
- Flebbe, O.; Muenzel, S.; Herold, H.; Riffert, H. Smoothed Particle Hydrodynamics: Physical viscosity and the simulation of accretion disks. Astrophys. J. 1994, 431, 754–760. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Mesh-Free Particle Method; World Scientific Publishing Company: Singapore, 2003; pp. 27–33. [Google Scholar]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Kernel estimates as a basis for general particle methods in hydrodynamics. J. Comput. Phys. 1982, 46, 429–453. [Google Scholar] [CrossRef]
- Monaghan, J.J. Particle methods for hydrodynamics. Comput. Phys. Rep. 1985, 3, 71–124. [Google Scholar] [CrossRef]
- Fulk, D.A.; Quinn, D.W. An Analysis of 1-D Smoothed Particle Hydrodynamics kernels. J. Comput. Phys. 1996, 126, 165–180. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by Smoothed Particle Hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Bose, A.; Carey, G.F. Least-squares p-r finite element methods for incompressible non-Newtonian flows. Comput. Methods Appl. Mech. 1999, 180, 431–458. [Google Scholar] [CrossRef]
- Wood, D. Collapse and fragmentation of isothermal gas clouds. Mon. Not. R. Astron. Soc. 1981, 194, 201–218. [Google Scholar] [CrossRef] [Green Version]
- Bonet, J.; Lok, T.S.L. Variational and momentum preservation aspects of Smooth Particle Hydrodynamic formulations. Comput. Method Appl. Mech. 1999, 180, 97–115. [Google Scholar] [CrossRef]
- Loewenstein, M.; Mathews, W.G. Adiabatic particle hydrodynamics in three dimensions. J. Comput. Phys. 1986, 62, 414–428. [Google Scholar] [CrossRef]
- Shao, S.; Lo, E.Y.M. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Lo, E.Y.M.; Shao, S.D. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar]
- Yang, H.J.; Wei, F.Q.; Hu, K.H. Determination of the maximum packing fraction for calculating slurry viscosity of debris flow. J. Sediment. Res. 2018, 3, 382–390. [Google Scholar]

| Test No. | Factors | ||||
|---|---|---|---|---|---|
| ρ (kg/m3) | Solid Phase Level | μ0 (Pa) | μ1 (Pa·s) | μ2 (Pa·s2) | |
| 1 | 1400 | Upper | 0.00004 | 0.0048 | 0.0197 |
| 2 | 1400 | Mixed | |||
| 3 | 1400 | Bottom | |||
| 4 | 1500 | Upper | 0.00006 | 0.0051 | 0.1654 |
| 5 | 1500 | Mixed | |||
| 6 | 1500 | Bottom | |||
| 7 | 1600 | Upper | 0.0001 | 0.0034 | 0.8242 |
| 8 | 1600 | Mixed | |||
| 9 | 1600 | Bottom | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Shu, A.; Rubinato, M.; Wang, M.; Qin, J. Numerical Simulation of Non-Homogeneous Viscous Debris-Flows Based on the Smoothed Particle Hydrodynamics (SPH) Method. Water 2019, 11, 2314. https://doi.org/10.3390/w11112314
Wang S, Shu A, Rubinato M, Wang M, Qin J. Numerical Simulation of Non-Homogeneous Viscous Debris-Flows Based on the Smoothed Particle Hydrodynamics (SPH) Method. Water. 2019; 11(11):2314. https://doi.org/10.3390/w11112314
Chicago/Turabian StyleWang, Shu, Anping Shu, Matteo Rubinato, Mengyao Wang, and Jiping Qin. 2019. "Numerical Simulation of Non-Homogeneous Viscous Debris-Flows Based on the Smoothed Particle Hydrodynamics (SPH) Method" Water 11, no. 11: 2314. https://doi.org/10.3390/w11112314
APA StyleWang, S., Shu, A., Rubinato, M., Wang, M., & Qin, J. (2019). Numerical Simulation of Non-Homogeneous Viscous Debris-Flows Based on the Smoothed Particle Hydrodynamics (SPH) Method. Water, 11(11), 2314. https://doi.org/10.3390/w11112314






