Additional Value of Using Satellite-Based Soil Moisture and Two Sources of Groundwater Data for Hydrological Model Calibration
Abstract
1. Introduction
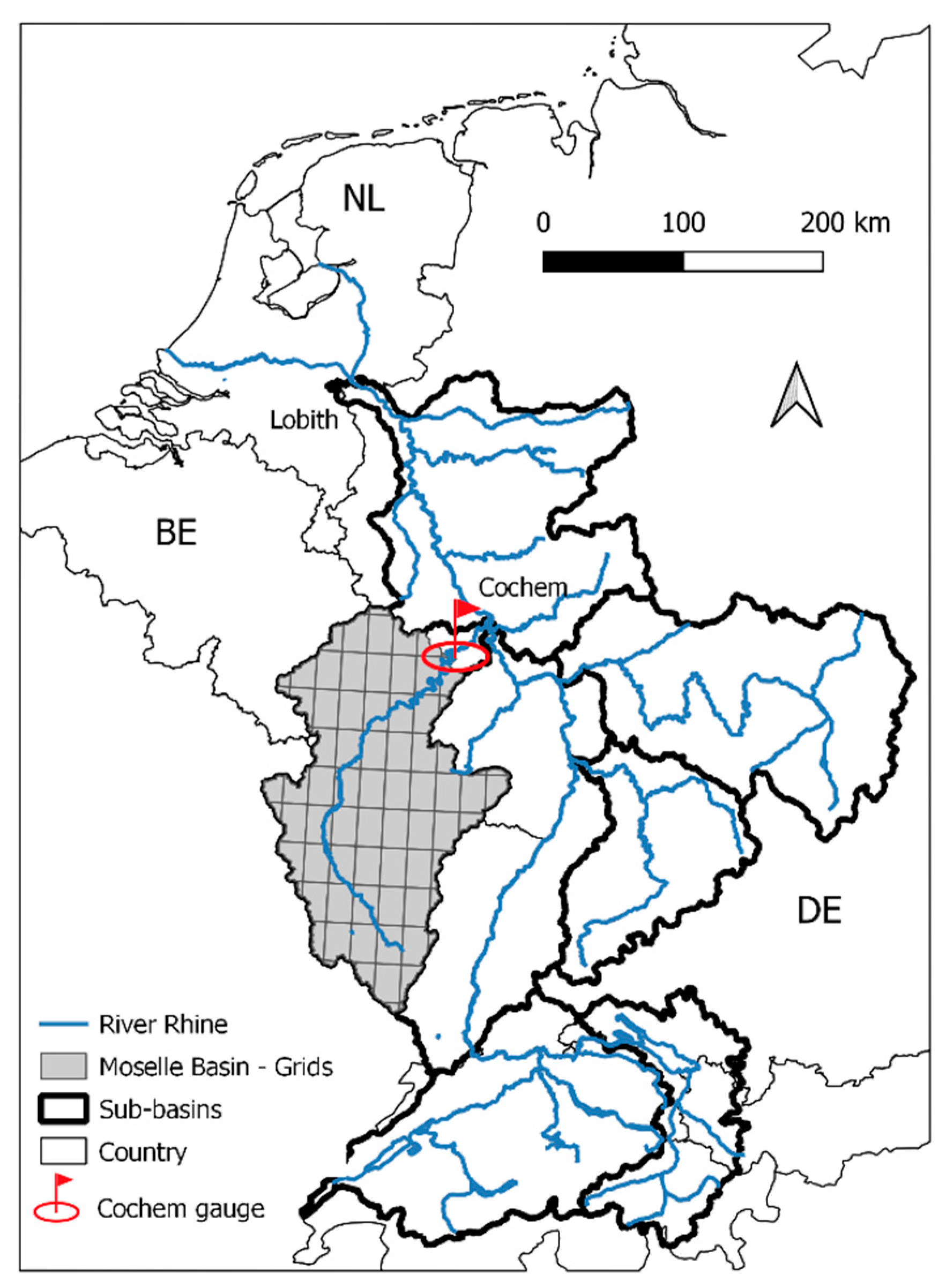
2. Study Area
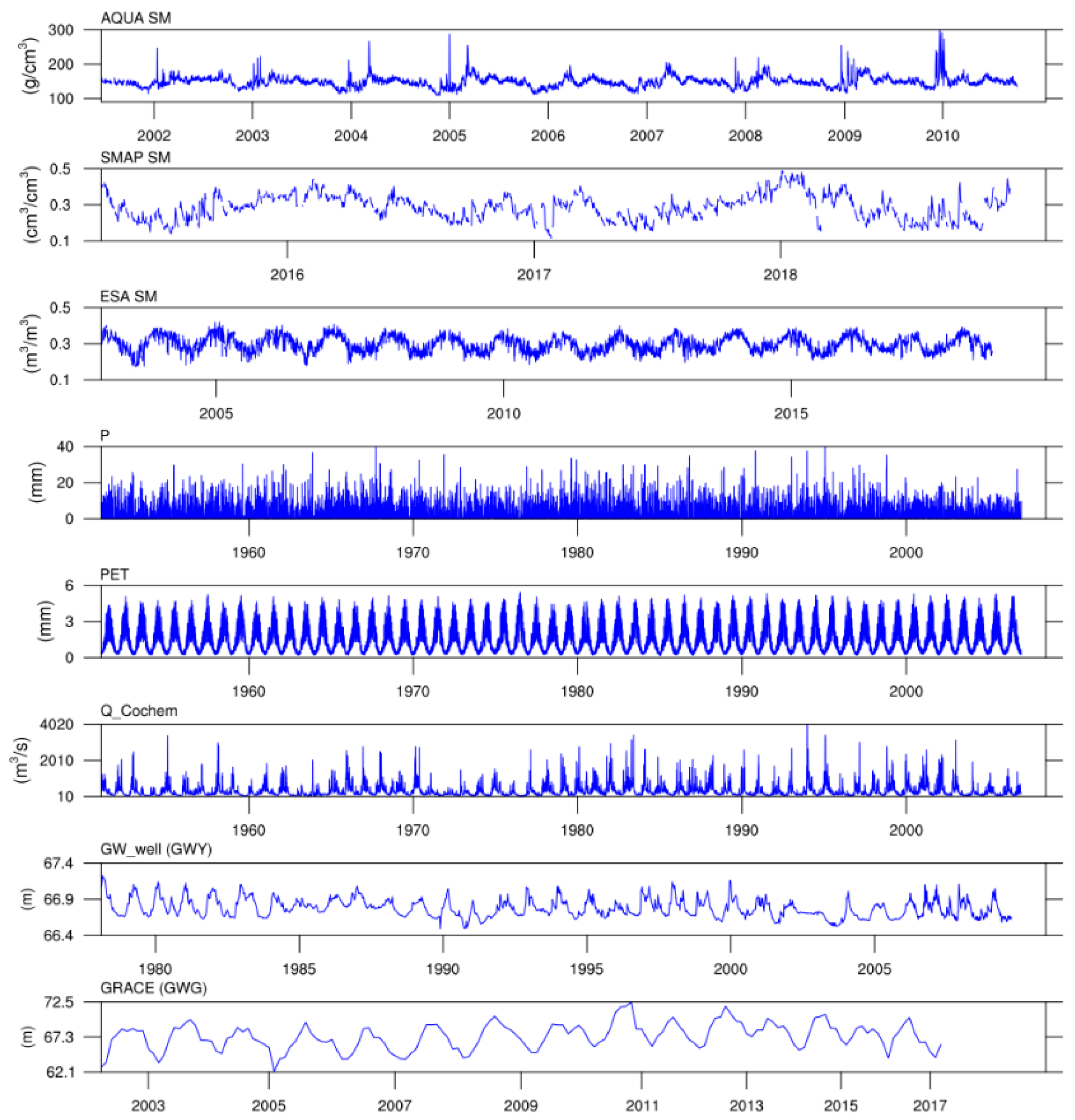
3. Data
3.1. European Space Agency (ESA CCI SM V04.4)
3.2. The Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E)
3.3. The Soil Moisture Active Passive (SMAP)
3.4. Gravity Recovery and Climate Experiment (GRACE)
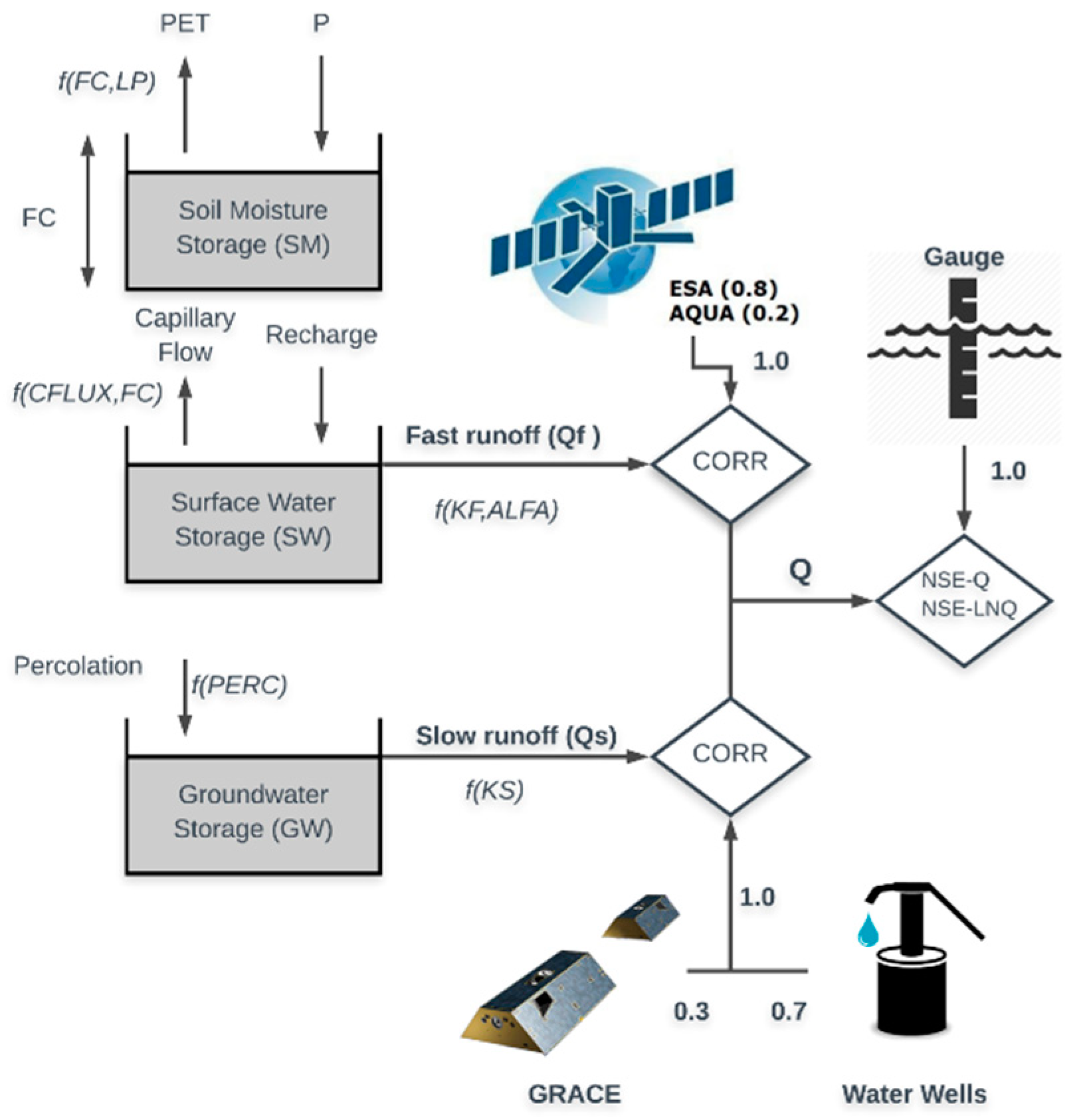
4. Methods
4.1. Hydrologic Model
4.2. Objective Functions
4.3. Latin Hypercube Sampling One-Factor-At-A-Time Sensitivity Analysis
4.4. Model Calibration and Validation
5. Results
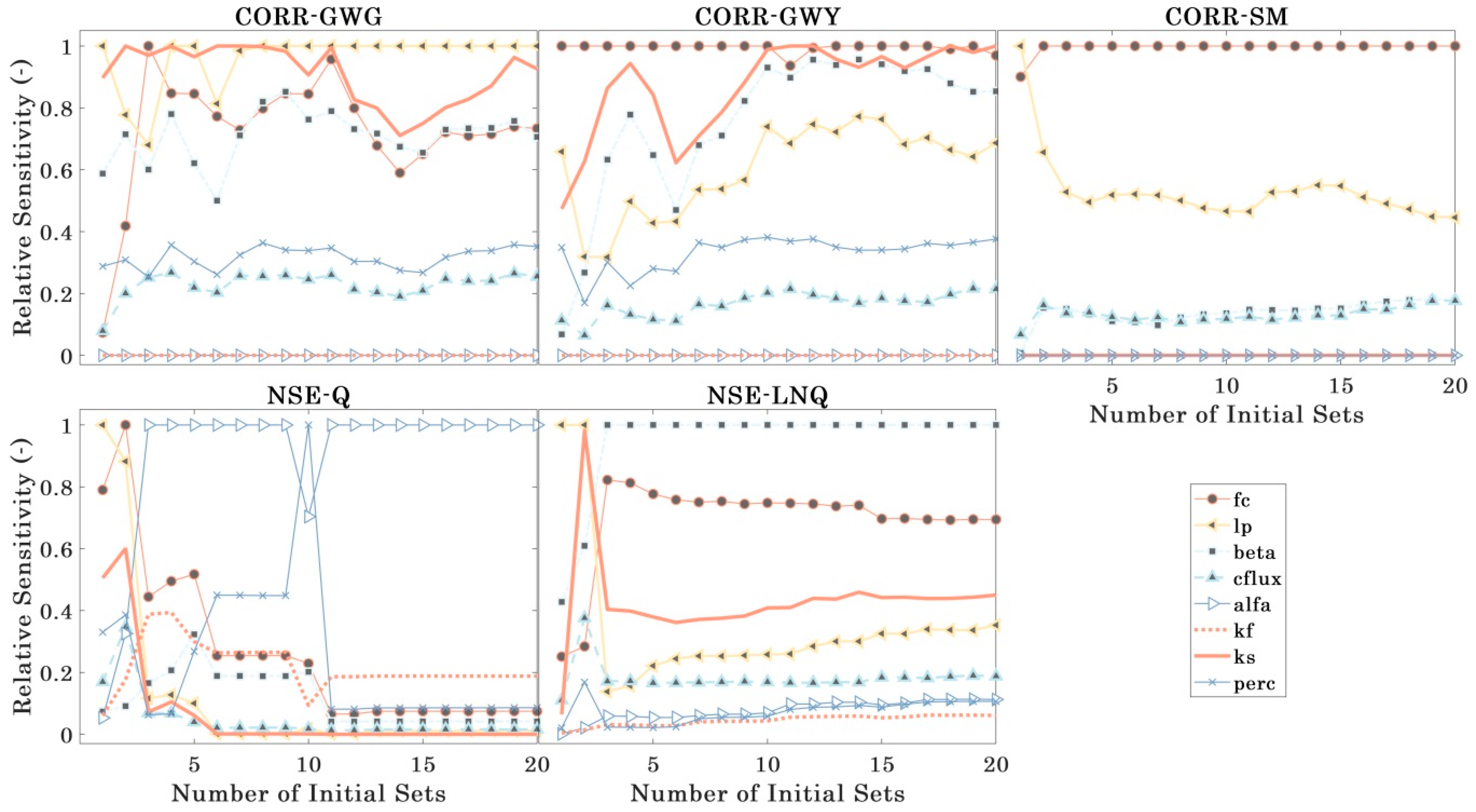
5.1. Sensitivity Analysis of the Model Parameters
5.2. Model Calibration and Validation
6. Discussion
7. Conclusions
- Based on the sensitivity analysis results, we find that different hydrologic processes are sensitive for different parameters. The HBV model’s groundwater performance (GWY) was most sensitive to the KS parameter, whereas the model’s soil moisture performance was most sensitive to the FC parameter.Also we confirm that 20 different initial parameter sets [64] using Latin Hypercube sampling are sufficient for globally encapsulating the most sensitive parameters.
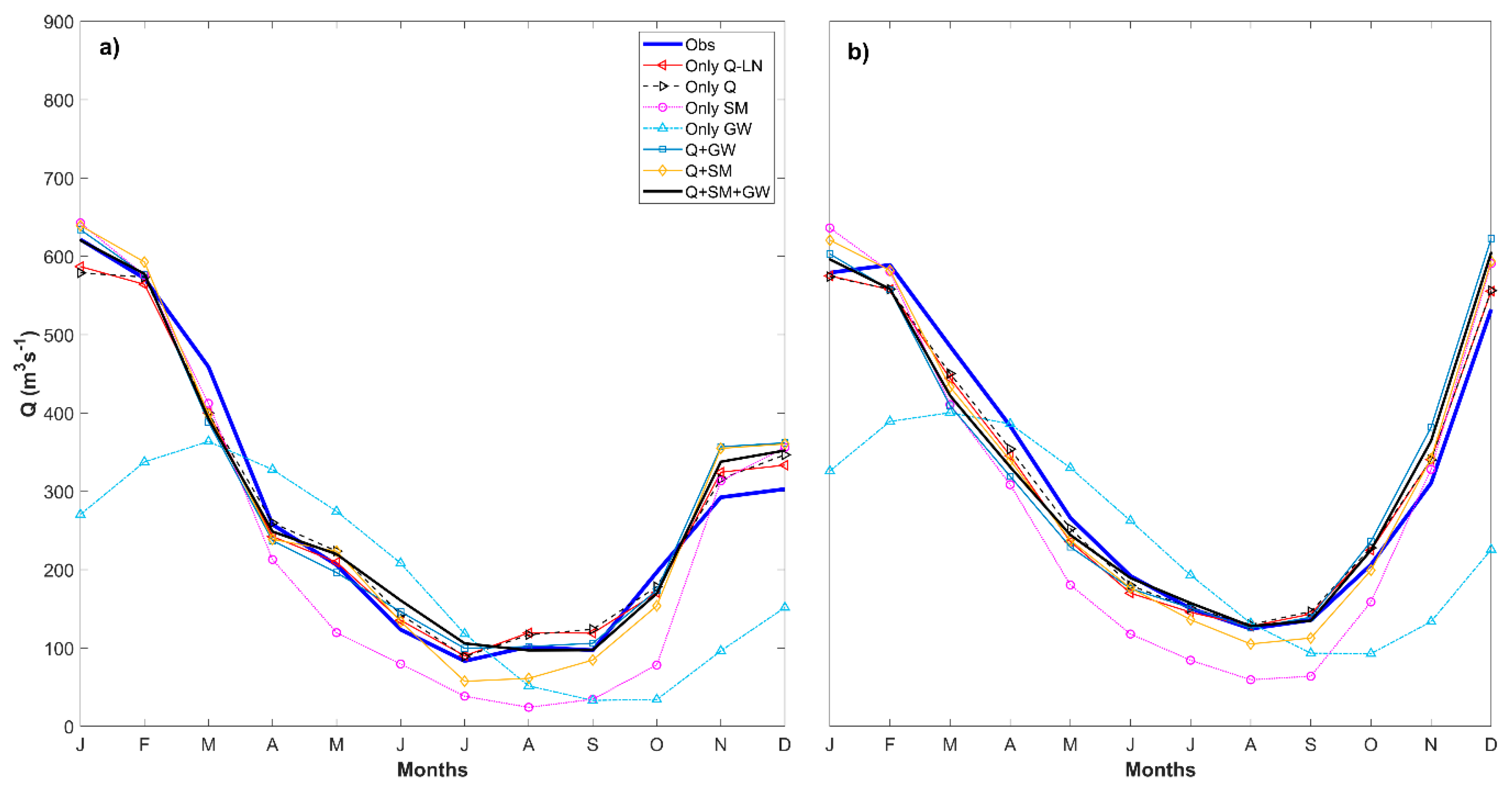
- Based on the calibration and validation results, we show that the two global methods perform better than the local Levenberg Marquardt method. An upper limit of 3,000 model runs appeared to be plausible for both the local and global optimization of the HBV model. Also including groundwater and remotely-sensed soil moisture information slightly (up to ~10%) improved not only the GW and SM simulation performances of the model, but also the simulation of the observed discharge behavior of the HBV model. This is only exploiting the temporal information of the satellite-based data, since we spatially averaged the distributed data to get the time series of SM and GW. This was also confirmed by a recent study by Nijzink et al. [2].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiang, D.; Wang, K. The Role of Satellite-Based Remote Sensing in Improving Simulated Streamflow: A Review. Water 2019, 11, 1615. [Google Scholar] [CrossRef]
- Nijzink, R.C.; Almeida, S.; Pechlivanidis, I.G.; Capell, R.; Gustafssons, D.; Arheimer, B.; Parajka, J.; Freer, J.; Han, D.; Wagener, T.; et al. Constraining Conceptual Hydrological Models with Multiple Information Sources. Water Resour. Res. 2018, 54, 8332–8362. [Google Scholar] [CrossRef]
- Demirel, M.C.; Mai, J.; Mendiguren, G.; Koch, J.; Samaniego, L.; Stisen, S. Combining satellite data and appropriate objective functions for improved spatial pattern performance of a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2018, 22, 1299–1315. [Google Scholar] [CrossRef]
- Becker, R.; Koppa, A.; Schulz, S.; Usman, M.; aus der Beek, T.; Schüth, C. Spatially distributed model calibration of a highly managed hydrological system using remote sensing-derived ET data. J. Hydrol. 2019, 577, 123944. [Google Scholar] [CrossRef]
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.G.; Booij, M.J.; Bhatti, H.A. Multi-variable calibration of a semi-distributed hydrological model using streamflow data and satellite-based evapotranspiration. J. Hydrol. 2013, 505, 276–290. [Google Scholar] [CrossRef]
- Li, Y.; Grimaldi, S.; Pauwels, V.R.N.; Walker, J.P. Hydrologic model calibration using remotely sensed soil moisture and discharge measurements: The impact on predictions at gauged and ungauged locations. J. Hydrol. 2018, 557, 897–909. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Rakovec, O.; Kumar, R.; Mai, J.; Cuntz, M.; Thober, S.; Zink, M.; Attinger, S.; Schäfer, D.; Schrön, M.; Samaniego, L. Multiscale and Multivariate Evaluation of Water Fluxes and States over European River Basins. J. Hydrometeorol. 2016, 17, 287–307. [Google Scholar] [CrossRef]
- Rakovec, O.; Kumar, R.; Attinger, S.; Samaniego, L. Improving the realism of hydrologic model functioning through multivariate parameter estimation. Water Resour. Res. 2016, 52, 7779–7792. [Google Scholar] [CrossRef]
- Zink, M.; Mai, J.; Cuntz, M.; Samaniego, L. Conditioning a Hydrologic Model Using Patterns of Remotely Sensed Land Surface Temperature. Water Resour. Res. 2018, 54, 2976–2998. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Xiong, L.; Zeng, L. Impacts of Introducing Remote Sensing Soil Moisture in Calibrating a Distributed Hydrological Model for Streamflow Simulation. Water 2019, 11, 666. [Google Scholar] [CrossRef]
- Kamamia, A.W.; Mwangi, H.M.; Feger, K.-H.; Julich, S. Assessing the impact of a multimetric calibration procedure on modelling performance in a headwater catchment in Mau Forest, Kenya. J. Hydrol. Reg. Stud. 2019, 21, 80–91. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Tobin, K.; Bennett, M. Improving Alpine Summertime Streamflow Simulations by the Incorporation of Evapotranspiration Data. Water 2019, 11, 112. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andréassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420–421, 171–182. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Koch, J.; Siemann, A.; Stisen, S.; Sheffield, J. Spatial validation of large scale land surface models against monthly land surface temperature patterns using innovative performance metrics. J. Geophys. Res. Atmos. 2016. [Google Scholar] [CrossRef]
- Mendiguren, G.; Koch, J.; Stisen, S. Spatial pattern evaluation of a calibrated national hydrological model—A remote-sensing-based diagnostic approach. Hydrol. Earth Syst. Sci. 2017, 21, 5987–6005. [Google Scholar] [CrossRef]
- Stisen, S.; Koch, J.; Sonnenborg, T.O.; Refsgaard, J.C.; Bircher, S.; Ringgaard, R.; Jensen, K.H. Moving beyond runoff calibration—Multi-variable optimization of a surface-subsurface-atmosphere model. Hydrol. Process. 2018. [Google Scholar] [CrossRef]
- Booij, M.J.; Krol, M.S. Balance between calibration objectives in a conceptual hydrological model. Hydrol. Sci. J. 2010, 55, 1017–1032. [Google Scholar] [CrossRef]
- Koch, J.; Jensen, K.H.; Stisen, S. Toward a true spatial model evaluation in distributed hydrological modeling: Kappa statistics, Fuzzy theory, and EOF-analysis benchmarked by the human perception and evaluated against a modeling case study. Water Resour. Res. 2015, 51, 1225–1246. [Google Scholar] [CrossRef]
- Koch, J.; Demirel, M.C.; Stisen, S. The SPAtial EFficiency metric (SPAEF): Multiple-component evaluation of spatial patterns for optimization of hydrological models. Geosci. Model Dev. 2018, 11, 1873–1886. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergstrom, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments; SMHI: Norrköping, Sweden, 1976. [Google Scholar]
- Asselman, N.E.M.; Middelkoop, H.; Van Dujk, P.M. The impact of changes in climate and land use on soil erosion, transport and deposition of suspended sediment in the River Rhine. Hydrol. Process. 2003, 17, 3225–3244. [Google Scholar] [CrossRef]
- Van Osnabrugge, B.; Weerts, A.H.; Uijlenhoet, R. genRE: A Method to Extend Gridded Precipitation Climatology Data Sets in Near Real-Time for Hydrological Forecasting Purposes. Water Resour. Res. 2017, 53, 9284–9303. [Google Scholar] [CrossRef]
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. The skill of seasonal ensemble low-flow forecasts in the Moselle River for three different hydrological models. Hydrol. Earth Syst. Sci. 2015, 19, 275–291. [Google Scholar] [CrossRef]
- Descy, J.P. Ecology of the phytoplankton of the River Moselle: Effects of disturbances on community structure and diversity. Hydrobiologia 1993, 249, 111–116. [Google Scholar] [CrossRef]
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. Effect of different uncertainty sources on the skill of 10 day ensemble low flow forecasts for two hydrological models. Water Resour. Res. 2013, 49, 4035–4053. [Google Scholar] [CrossRef]
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. Identification of appropriate lags and temporal resolutions for low flow indicators in the River Rhine to forecast low flows with different lead times. Hydrol. Process. 2013, 27, 2742–2758. [Google Scholar] [CrossRef]
- Secretariat, G. Implementation plan for the global observing system for climate in support of the UNFCCC (2010 Update). In Proceedings of the Conference of the Parties (COP), Copenhagen, Denmark, 7–18 December 2009; pp. 7–19. [Google Scholar]
- Wagner, W.; Dorigo, W.; De Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 315–321. [Google Scholar] [CrossRef]
- Dorigo, W.; Gruber, A.; Scanlon, T.; Hahn, S.; Kidd, R.; Paulik, C.; Reimer, C.; Van der Schalie, R.; Preimesberger, W.; De Jeu, R.W.W. ESA Soil Moisture Climate Change Initiative (Soil_Moisture_cci): Version 04.4 Data Collection. Available online: https://catalogue.ceda.ac.uk/uuid/dce27a397eaf47e797050c220972ca0e?jump=related-docs-anchor (accessed on 10 January 2019).
- Gruber, A.; Scanlon, T.; Van Der Schalie, R.; Wagner, W.; Dorigo, W. Evolution of the ESA CCI Soil Moisture climate data records and their underlying merging methodology. Earth Syst. Sci. Data 2019, 11, 717–739. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS Scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Naeimi, V.; Scipal, K.; Bartalis, Z.; Hasenauer, S.; Wagner, W. An improved soil moisture retrieval algorithm for ERS and METOP scatterometer observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1999–2013. [Google Scholar] [CrossRef]
- Scipal, K.; Wagner, W.; Trommler, M.; Naumann, K. The global soil moisture archive 1992–2000 from ERS scatterometer data: First results. Int. Geosci. Remote Sens. Symp. 2002, 3, 1399–1401. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Wagner, W.; Brocca, L.; Naeimi, V.; Reichle, R.; Draper, C.; De Jeu, R.; Ryu, D.; Su, C.H.; Western, A.; Calvet, J.C.; et al. Clarifications on the “comparison between SMOS, VUA, ASCAT, and ECMWF Soil Moisture Products over Four Watersheds in U.S.”. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1901–1906. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113, 1–17. [Google Scholar] [CrossRef]
- Parinussa, R.M.; Holmes, T.R.H.; De Jeu, R.A.M. Soil moisture retrievals from the windSat spaceborne polarimetric microwave radiometer. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2683–2694. [Google Scholar] [CrossRef]
- Li, L.; Gaiser, P.W.; Gao, B.C.; Bevilacqua, R.M.; Jackson, T.J.; Njoku, E.G.; Rüdiger, C.; Calvet, J.C.; Bindlish, R. WindSat global soil moisture retrieval and validation. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2224–2241. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Parinussa, R.M.; Holmes, T.R.H.; Wanders, N.; Dorigo, W.A.; De Jeu, R.A.M. A preliminary study toward consistent soil moisture from AMSR2. J. Hydrometeorol. 2015, 16, 932–947. [Google Scholar] [CrossRef]
- Njoku, E.G.; Entekhabi, D. Passive Microwave Remote Sensing of Soil Moisture. J. Hydrol. 1996, 184, 101–129. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Gruhier, C.; De Rosnay, P.; Hasenauer, S.; Holmes, T.; De Jeu, R.; Kerr, Y.; Mougin, E.; Njoku, E.; Timouk, F. Soil moisture active and passive microwave products: Intercomparison and evaluation over a Sahelian site. Hydrol. Earth Syst. Sci. 2010, 14, 141–156. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.; O’Neill, P.; Spencer, M.; Jackson, T.; Entin, J.; Im, E.; Kellogg, K. The {Soil Moisture Active/Passive Mission (SMAP)}. IEEE Int. Geosci. Remote Sens. Symp. 2008, 3, III-1–III-4. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Sadri, S.; Wood, E.F.; Pan, M. A SMAP-Based Drought Monitoring Index for the United States. Hydrol. Earth Syst. Sci. Discuss. 2018, 1–19. [Google Scholar] [CrossRef]
- Brown, M.E.; Escobar, V.; Moran, S.; Entekhabi, D.; O’Neill, P.E.; Njoku, E.G.; Doorn, B.; Entin, J.K. NASA’s soil moisture active passive (SMAP) mission and opportunities for applications users. Bull. Am. Meteorol. Soc. 2013, 94, 1125–1128. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J.; Bruijnzeel, L.A. Global-scale regionalization of hydrologic model parameters. Water Resour. Res. 2016. [Google Scholar] [CrossRef]
- Singh, S.K.; Bárdossy, A. Calibration of hydrological models on hydrologically unusual events. Adv. Water Resour. 2012, 38, 81–91. [Google Scholar] [CrossRef]
- Tian, Y.; Booij, M.J.; Xu, Y.-P. Uncertainty in high and low flows due to model structure and parameter errors. Stoch. Environ. Res. Risk Assess. 2014, 28, 319–332. [Google Scholar] [CrossRef]
- Uhlenbrook, S.; Leibundgut, C. Process-oriented catchment modelling and multiple-response validation. Hydrol. Process. 2002, 16, 423–440. [Google Scholar] [CrossRef]
- ASCE. Criteria for Evaluation of Watershed Models. J. Irrig. Drain. Eng. 1993. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ. Model. Softw. 2007. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007. [Google Scholar] [CrossRef]
- Reusser, D.E.; Blume, T.; Schaefli, B.; Zehe, E. Analysing the temporal dynamics of model performance for hydrological models. Hydrol. Earth Syst. Sci. 2009, 13, 999–1018. [Google Scholar] [CrossRef]
- Demirel, M.; Koch, J.; Mendiguren, G.; Stisen, S. Spatial Pattern Oriented Multicriteria Sensitivity Analysis of a Distributed Hydrologic Model. Water 2018, 10, 1188. [Google Scholar] [CrossRef]
- Iman, R.L.; Consultants, S.T. Latin Hypercube Sampling. Wiley StatsRef Stat. Ref. Online 1998. [Google Scholar] [CrossRef]
- Doherty, J. PEST: Model Independent Parameter Estimation. Fifth Edition of User Manual; Watermark Numerical Computing: Brisbane, QLD, Australia, 2005. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Adapting arbitrary normal mutation distributions in evolution strategies: The covariance matrix adaptation. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Van Esse, W.R.; Perrin, C.; Booij, M.J.; Augustijn, D.C.M.; Fenicia, F.; Kavetski, D.; Lobligeois, F. The influence of conceptual model structure on model performance: A comparative study for 237 French catchments. Hydrol. Earth Syst. Sci. 2013, 17, 4227–4239. [Google Scholar] [CrossRef]
- Kling, H.; Gupta, H. On the development of regionalization relationships for lumped watershed models: The impact of ignoring sub-basin scale variability. J. Hydrol. 2009, 373, 337–351. [Google Scholar] [CrossRef]
- Spearman Rank Correlation Coefficient. In The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2008; pp. 502–505.
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Benchmarking a Catchment-Aware Long Short-Term Memory Network (LSTM) for Large-Scale Hydrological Modeling. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–32. [Google Scholar] [CrossRef]
- Bowes, B.D.; Sadler, J.M.; Morsy, M.M.; Behl, M.; Goodall, J.L. Forecasting Groundwater Table in a Flood Prone Coastal City with Long Short-term Memory and Recurrent Neural Networks. Water 2019, 11, 1098. [Google Scholar] [CrossRef]
| Abbreviation | Description | Number of Sub-Basins | Spatiotemporal Resolution | Spatial Averaging | Period | Source |
|---|---|---|---|---|---|---|
| Q | Discharge | 1 gauge at Cochem | Catchment-scale (daily) | - | 1.1.1951–31.12.2015 | GRDC in Koblenz |
| P | Precipitation | 26 | 10 km (daily) | Areal weighting (sub-basins) | 1.1.1951–31.12.2015 | BfG in Koblenz, van Osnabrugge et al. [29] |
| PET | Potential evapotranspiration | 26 | 20 km (daily) | Areal weighting (sub-basins) | 1.1.1951–31.12.2015 | BfG in Koblenz, van Osnabrugge et al. [29] |
| GWG | Remotely sensed groundwater storage (GRACE) | 1 (Rhine basin) | 400 km (monthly) | - | 2002–2017 | GRACE |
| GWY | Groundwater well measurements | 80 | Point (daily) | Areal weighting (sub-basins) | 8.2.1978–7.10.2009 | BfG in Koblenz |
| ESA | Soil moisture (ESACCI_SM_V04.4 combined product) | - | 0.25 degree (daily) | Grids—arithmetic averaging | 01.11.1978–30.06.2018 | ftp.geo.tuwien.ac.at |
| AQUA | Soil moisture (AMSR-E/Aqua) | - | 25 km (daily) | Grids—arithmetic averaging | 19.06.2002–03.10.2011 | earthdata.nasa.gov |
| SMAP | Soil moisture | - | 36 km (daily) | Grids—arithmetic averaging | 31.03.2015–Present | earthdata.nasa.gov |
| Parameter | Unit | Range | Description |
|---|---|---|---|
| FC | mm | 100–800 | Maximum soil moisture capacity |
| LP | 0.1–1 | Soil moisture threshold for the reduction of evapotranspiration | |
| BETA | 1–6 | Shape coefficient | |
| CFLUX | mm day−1 | 0.1–1 | Maximum capillary flow from upper response box to soil moisture zone |
| ALFA | 0.1–2 | Measure for nonlinearity of quick runoff | |
| KF | day−1 | 0.005–0.5 | Recession coefficient for quick runoff |
| KS | day−1 | 0.0005–0.2 | Recession coefficient for base flow |
| PERC | mm day−1 | 0.01–6 | Maximum flow from upper to lower response box |
| Objective Functions | Formula | Range of Values |
|---|---|---|
| CORR | [−1, 1] | |
| NSE-Q | [−∞, 1] | |
| NSE-LNQ | [−∞, 1] |
| Calibration | Validation | |||
|---|---|---|---|---|
| Objective Function | Start | End | Start | End |
| CORR_GWG | 31.03.2002 | 31.12.2004 | 31.01.2005 | 31.12.2015 |
| CORR_GWY | 01.01.2002 | 31.12.2004 | 01.01.1979 | 31.12.2001 |
| CORR_SM | 19.06.2002 | 31.12.2004 | 01.01.2005 | 31.12.2015 |
| NSE-Q | 01.01.2002 | 31.12.2006 | 01.01.1954 | 31.12.2001 |
| NSE-LNQ | 01.01.2002 | 31.12.2006 | 01.01.1954 | 31.12.2001 |
| Parameter | Normalized Sensitivity | ||||
|---|---|---|---|---|---|
| Correlation Coefficient | NSE | ||||
| GWG (GRACE) | GWY (WELL) | SM (ESA and AQUA) | Q | LNQ | |
| FC | 0.733 | 0.970 | 1 | 0.075 | 0.695 |
| LP | 1 | 0.687 | 0.446 | 0.011 | 0.353 |
| BETA | 0.706 | 0.854 | 0.179 | 0.042 | 1 |
| CFLUX | 0.255 | 0.214 | 0.177 | 0.016 | 0.188 |
| ALFA | 0 | 0 | 0 | 1 | 0.112 |
| KF | 0 | 0 | 0 | 0.188 | 0.061 |
| KS | 0.926 | 1 | 0 | 0 | 0.450 |
| PERC | 0.352 | 0.376 | 0 | 0.086 | 0.106 |
| CAL | VAL | |||||||
|---|---|---|---|---|---|---|---|---|
| Case | Processes | Objective Function | PEST_LM | SCE-UA | CMAES | PEST_LM | SCE-UA | CMAES |
| 1 | Q—High flows | CORR_GWG | −0.14 | −0.36 | −0.38 | 0.02 | −0.05 | −0.03 |
| CORR_GWY | 0.51 | 0.71 | 0.73 | 0.61 | 0.67 | 0.68 | ||
| CORR_SM | 0.82 | 0.83 | 0.78 | 0.68 | 0.67 | 0.67 | ||
| NSE-Q | 0.77 | 0.90 | 0.89 | 0.77 | 0.90 | 0.89 | ||
| NSE-LNQ | 0.53 | 0.86 | 0.85 | 0.44 | 0.84 | 0.84 | ||
| Q—Low flows | CORR_GWG | −0.38 | −0.38 | −0.36 | −0.03 | 0.07 | 0.03 | |
| CORR_GWY | 0.73 | 0.62 | 0.72 | 0.66 | 0.75 | 0.73 | ||
| CORR_SM | 0.82 | 0.79 | 0.78 | 0.69 | 0.64 | 0.67 | ||
| NSE-Q | 0.84 | 0.84 | 0.81 | 0.84 | 0.84 | 0.81 | ||
| NSE-LNQ | 0.81 | 0.80 | 0.82 | 0.81 | 0.79 | 0.76 | ||
| 2 | GW—Only | CORR_GWG | −0.37 | −0.28 | −0.27 | −0.07 | −0.10 | −0.05 |
| CORR_GWY | 0.73 | 0.75 | 0.75 | 0.63 | 0.70 | 0.75 | ||
| CORR_SM | 0.79 | 0.83 | 0.84 | 0.68 | 0.61 | 0.58 | ||
| NSE-Q | 0.88 | −286 | 0.72 | 0.88 | −286 | 0.72 | ||
| NSE-LNQ | 0.85 | −0.68 | −0.91 | 0.83 | −1.18 | −0.48 | ||
| SM—Only | CORR_GWG | −0.05 | −0.38 | 0.18 | −0.04 | 0.01 | −0.08 | |
| CORR_GWY | 0.48 | 0.69 | 0.25 | 0.58 | 0.75 | 0.37 | ||
| CORR_SM | 0.83 | 0.85 | 0.85 | 0.71 | 0.65 | 0.66 | ||
| NSE-Q | 0.82 | −26.7 | 0.20 | 0.82 | −26.7 | 0.20 | ||
| NSE-LNQ | 0.63 | 0.17 | −1.39 | 0.54 | −0.24 | −1.39 | ||
| 3 | Q + GW | CORR_GWG | −0.11 | −0.37 | −0.31 | −0.03 | 0.00 | −0.04 |
| CORR_GWY | 0.54 | 0.72 | 0.73 | 0.61 | 0.72 | 0.67 | ||
| CORR_SM | 0.80 | 0.83 | 0.82 | 0.69 | 0.66 | 0.65 | ||
| NSE-Q | 0.45 | 0.87 | 0.85 | 0.45 | 0.87 | 0.85 | ||
| NSE−LNQ | 0.64 | 0.84 | 0.83 | 0.57 | 0.78 | 0.82 | ||
| Q + SM | CORR_GWG | −0.36 | −0.38 | −0.36 | 0.10 | 0.00 | 0.01 | |
| CORR_GWY | 0.68 | 0.72 | 0.68 | 0.70 | 0.74 | 0.75 | ||
| CORR_SM | 0.84 | 0.83 | 0.84 | 0.64 | 0.66 | 0.66 | ||
| NSE-Q | 0.85 | 0.88 | 0.87 | 0.71 | 0.88 | 0.87 | ||
| NSE-LNQ | 0.81 | 0.79 | 0.67 | −0.69 | 0.73 | 0.62 | ||
| 4 | Q + GW + SM | CORR_GWG | −0.15 | −0.37 | −0.34 | −0.02 | −0.06 | −0.07 |
| CORR_GWY | 0.55 | 0.73 | 0.73 | 0.64 | 0.67 | 0.65 | ||
| CORR_SM | 0.83 | 0.84 | 0.83 | 0.69 | 0.68 | 0.66 | ||
| NSE-Q | 0.80 | 0.88 | 0.87 | 0.80 | 0.88 | 0.87 | ||
| NSE-LNQ | 0.58 | 0.86 | 0.83 | 0.50 | 0.82 | 0.81 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demirel, M.C.; Özen, A.; Orta, S.; Toker, E.; Demir, H.K.; Ekmekcioğlu, Ö.; Tayşi, H.; Eruçar, S.; Sağ, A.B.; Sarı, Ö.; et al. Additional Value of Using Satellite-Based Soil Moisture and Two Sources of Groundwater Data for Hydrological Model Calibration. Water 2019, 11, 2083. https://doi.org/10.3390/w11102083
Demirel MC, Özen A, Orta S, Toker E, Demir HK, Ekmekcioğlu Ö, Tayşi H, Eruçar S, Sağ AB, Sarı Ö, et al. Additional Value of Using Satellite-Based Soil Moisture and Two Sources of Groundwater Data for Hydrological Model Calibration. Water. 2019; 11(10):2083. https://doi.org/10.3390/w11102083
Chicago/Turabian StyleDemirel, Mehmet Cüneyd, Alparslan Özen, Selen Orta, Emir Toker, Hatice Kübra Demir, Ömer Ekmekcioğlu, Hüsamettin Tayşi, Sinan Eruçar, Ahmet Bilal Sağ, Ömer Sarı, and et al. 2019. "Additional Value of Using Satellite-Based Soil Moisture and Two Sources of Groundwater Data for Hydrological Model Calibration" Water 11, no. 10: 2083. https://doi.org/10.3390/w11102083
APA StyleDemirel, M. C., Özen, A., Orta, S., Toker, E., Demir, H. K., Ekmekcioğlu, Ö., Tayşi, H., Eruçar, S., Sağ, A. B., Sarı, Ö., Tuncer, E., Hancı, H., Özcan, T. İ., Erdem, H., Koşucu, M. M., Başakın, E. E., Ahmed, K., Anwar, A., Avcuoğlu, M. B., ... Booij, M. J. (2019). Additional Value of Using Satellite-Based Soil Moisture and Two Sources of Groundwater Data for Hydrological Model Calibration. Water, 11(10), 2083. https://doi.org/10.3390/w11102083










