IDF Curve Modification Under Climate Change: A Case Study in the Lombardy Region Using EURO-CORDEX Ensemble

Abstract

Intensity–Frequency–Duration Curves (IDF curves) are a tool applied in hydraulic and hydrology engineering to design infrastructure for rainfall management. They express how precipitation, with a defined duration (D) and intensity (I), is frequent in a certain area. They are built from past recorded rainfall series, applying the extreme value statistics, and they are considered invariant in time. However, the current climate change projections are showing a detectable positive trend in temperatures, which, according to Clausius–Clapeyron, is expected to intensify extreme precipitation (higher temperatures bring more water vapour available for precipitation). According to the IPCC (Intergovernmental Panel on Climate Change) reports, rainfall events are projected to intensify their magnitude and frequency, becoming more extreme, especially across “climatic hot-spot” areas such as the Mediterranean basin. Therefore, a sensible modification of IDF curves is expected, posing some challenges for future hydraulic infrastructure design (i.e., sewage networks), which may experience damage and failure due to extreme intensification. In this paper, a methodology for reconstructing IDF curves by analysing the EURO-CORDEX climate model outputs is presented. The methodology consists of the analysis of climatic rainfall series (that cover a future period up to 2100) using GEV (Generalised Extreme Value) techniques. The future anomalies of rainfall height (H) and their return period (RP) have been evaluated and then compared to the currently adopted IDF curves. The study is applied in Lombardy (Italy), a region characterised by strong orographic precipitation gradients due to the influence of Alpine complex orography. The future anomalies of H evaluated in the study show an increase of 20–30 mm (2071–2100 ensemble median, RCP 8.5) in rainfall depth. Conversely, a significant reduction in the return period by 40–60% (i.e., the current 100-year event becomes a ≈40–60-year event by 2071–2100 under RCP 8.5) is reported, leading to an intensification of extreme events. The former have been considered to correct the currently adopted IDF curves, taking into account climate change drivers. A series of applications in the field of hydraulic infrastructure (a stormwater retention tank and a sewage pipe) have demonstrated how the influence of IDF curve modification may change their design. The latter have shown how future RP modification (i.e., reduction) of the design rainfall may lead to systematic under-design and increased flood risk if not addressed properly.

1. Introduction

Rainfall is a meteorological phenomenon that interacts significantly with the surface environment [1]. It is part of the water cycle, able to convey water flux across a territory and influence human life and its developments [2]. Its distribution is generally associated with synoptic configurations of humid air masses at large scales that may interact with the local topography [3]. Extratropical cyclones coming from the Atlantic Ocean are the most common in Europe and the Mediterranean areas [4]. They contribute to a large portion of precipitation falling to the ground, influencing the local climatology [4]. Rainfall is functional for several purposes (agriculture, economy, etc.) but, under certain situations, may cause several issues for the territory, triggering geo-hydrological hazards [5,6,7,8]. The presence of mountain ranges (such as the Alps and Apennine chain in Italy) represents an orographic element capable of significantly enhancing the magnitude of these phenomena, often also leading to risk conditions in the hydrogeological field (landslides, floods, etc.) [4,9,10,11]. The latter are said to be rainfall-triggered when heavy or extreme precipitation events occur, especially when a significant amount of water is poured on the ground in a relatively short time [12]. Therefore, rainfall events can be characterised by four main properties, which are their duration (D), intensity (I), height or depth (H = I·D), and frequency or return period (RP) [1,13]. These properties are site-specific, characterising the local climatology and the expected magnitude of a specific rainfall event, which is strongly linked to geo-hydrological hazards through a cause-and-effect process [5,6].

The analysis of precipitation is crucial in the hydrologic and hydraulic fields where water infrastructure design is required to deal with and prevent geo-hydrological hazards [14,15,16]. Among others, flash floods are the most critical, since they may generate in a very short time due to thunderstorm formation and impact the local sewage network, causing damage and pipe failures [17]. Therefore, these infrastructures are built starting from the definition of a “design rainfall”, characterised by a certain D, I, and RP [1,14]. These three quantities are merged together within the Intensity–Duration–Frequency Curves (IDF curves) or Depth–Duration–Frequency Curves (DDFCs), analytical functions able to describe the frequency (RP) of a design precipitation (D, I) or (D, H) [1,18,19,20]. IDF curves are obtained from the statistical analysis of rain-gauge historical series, which contain a sequence of rainfall events that can be isolated and analysed to retrieve their probability. The statistical analysis of the annual maxima precipitation using the Generalised Extreme Value (GEV) technique is generally adopted in a similar way all over the world and is a fundamental tool in the hydraulic field [1,14,19,21]. In Italy, the currently adopted IDF curves were built in the past from rainfall data collected by the former SIMN (Servizio Idrografico Mareografico Nazionale) and elaborated at a national scale within the VAPI (VAlutazione Piene Italiane) project [18,19]. The data were then aggregated for different durations ranging from 1 h to 5 days, and for each year, the corresponding annual maximum was evaluated. IDF curves are applied by setting a critical D of the design rainfall event (generally related to the minimum time of concentration of the sewer network [1,14,22]) and assigning a design RP (generally between 10 and 100 years, depending on the application). Using the IDF curves, the maximum expected rainfall height is evaluated, representing the initial data for the subsequent hydrological and hydraulic analysis required for completing the infrastructure design.

However, ongoing climate change is modifying the frequency and magnitude of rainfall, causing a potential deviation of the current IDF curves from the past [23,24,25,26,27,28]. In fact, the hypothesis of climate invariance on which past studies were based is no longer considered valid, as statistically significant deviations from historical climatology are starting to emerge [25]. Even in Italy, the effects of the change are now visible with a clear tendency to increase the severity of rainfall events interspersed with long periods of drought [29,30]. However, as highlighted in a previous study [23], detecting climate change on IDF curves is not a simple task, since hidden climatic feedback in rainfall generation is not completely understood [31]. The latter may be site-specific and is strongly linked to local climatology. Moreover, IDF curves future modifications are evaluated using the climate models’ outputs. Even though they are calibrated and validated from the past, they remain numerical routines, which may make errors in future predictions, especially looking at long-term periods (i.e., at the end of the century) [31,32]. Even though downscaling and bias-correction procedures may be applied, these techniques may degrade the rainfall outputs, impacting the extreme rainfall analysis [31,33].

As a matter of fact, the studies of IDF curves revisions are now at the very beginning stage [20,23], starting to apply consolidated GEV theory to the climate model rainfall series to detect the future D, I, H or RP modifications for rainfall. In this work, a possible methodology that tries to detect the effects of climate change on intense rainfall will be illustrated. In the Materials and Methods section, the entire theory about the climatic model and the analysis of extreme rainfall events using GEV is described. This methodology has been tested across the Lombardy region (Northern Italy), an area characterised by strong yearly mean rainfall gradients that is suspected to experience significant changes in IDF curves due to climate change [30,34]. The Results section contains all the IDF curve analyses carried out, describing the characteristics of the currently adopted IDF curves and showing the application of climate models in the correction of IDF curves. The analysis of future anomalies in terms of rainfall height (H) and return period (RP) variations has been reported for a duration of 1 to 5 days. A possible strategy for assessing IDF curve variation for a sub-daily duration has been proposed, considering the duration dependence of the future anomaly trends, and an application of the new IDF curves on sewage infrastructure design is reported. All the outcomes of the study have been extensively discussed in a dedicated Section 4 (Discussion), reporting also the main challenges currently faced by other authors exploring this subject. In the Conclusions, the most significant results of the presented study are summed up.

2. Materials and Methods

This section illustrates the methodologies applied to evaluate the influence of climate change on rainfall statistics showing the relation between precipitation intensity and temperature (Clausius–Clapeyron equation) [35,36], the theory of the extreme value distribution (GEV) [21,37], the climatic model structure (EURO-CORDEX) [31,38], and the presentation of the case study.

2.1. Empirical Methods, Clausius–Clapeyron Equation and GEV Distribution for Future IDF Curve Corrections

The study of intense precipitation processes in the climate change context began from the literature review carried out in [23]. There, the methodologies for the study’s possible future modification of intense precipitation data were illustrated, addressing empirically and physically based approaches currently adopted worldwide. These approaches have the scope to correct or recalculate the IDF curves, modifying for a certain duration (D) and return period (RP) the values of rainfall height (H) or intensity (I). In Equation (1), the analytical function of the IDF curves in the two forms generally adopted by hydraulic engineers is reported: the DDF (depth duration frequency form, when the rainfall height (or depth H) is explicit), and the IDF (intensity duration frequency), when rainfall intensity is used instead. The curve coefficients depending on the characteristics of precipitation and on its magnitude are a₁, w_RP, and n [1].

$$H=a_1{w}_{RP}{D}^n or I={\displaystyle \frac{H}{D}}=a_1{w}_{RP}{D}^{n-1}$$

(1)

Among the empirical approaches examined, three main groups have been analysed, consisting of a weight-based/percentage correction of the future precipitation intensity (I) or height (H). The first two methods presented in [23] use percentage approaches in which the rainfall intensity is simply rescaled, increasing its values by 20% and 30% to include climate change influence. More precisely, in the first one, rainfall intensity increases are uniform among IDF curves, since a fixed percentage increment is adopted, while in the second, this rate may change (increase) as a function of RP. The formers are already applied within the building codes of some European and American states [23]. The simplest adaptation strategy is a constant percentage increase in I, which is supposed to be constant with D and RP. This method is currently used in Belgium and the United Kingdom, respectively, applying a 30% and 20% increase on precipitation computed from reference IDF curves; and similar factors, around 18–20%, are also applied by the Canadian government [23]. The adaptive percentage approach recognises that in the future, increases in extreme precipitation will probably not be uniform and will depend on various factors, such as the temperature increase (ΔT) and frequency of precipitation (RP). A strategy used at the national level by Denmark and Sweden for rainfall design is to implement different safety factors based on the frequency of the event selected in the project (i.e., increases of 20%, 30%, and 40% are added to the return periods of 2, 10, and 100 years, respectively) [23]. Conversely, the UK Department for Infrastructure selected a single factor of 20% nationwide with incremental safety factors for rainfall design across England based on the time horizon (i.e., up to 10%, 20%, and 40% by 2040, 2070, and 2115, respectively) [23].

In the third method, a direct connection between rainfall intensity and temperature trends is made, considering the Clausius–Clapeyron relationship [3,36,39,40] (see Appendix A). This approach is interesting because it allows the engineers to easily correct the coefficients of the IDF curves by simply knowing the deviation in future temperature ΔT_cc, a datum easily available from the most recent climate projections [25,38,40]. Equation (2) is derived from (A10); substituting P₁ with I_reference, P₂ with I_future, and (T₂ − T₁) with ΔT_cc, it can be applied for the correction of the precipitation intensity as a function of the parameter R_sc = α_cc = 7% °C⁻¹ (Rainfall Scaling Factor) and the future temperature increase ΔT_cc.

$$I_{future}=I_{reference}\times {\left({\displaystyle \frac{100+R_{sc}}{100}}\right)}^{∆T_{cc}}$$

(2)

Several authors [39,41,42,43,44,45] have tried to retrieve and estimate the 7% °C⁻¹ rate (also reported as Clausius-Clapeyron rate (CC rate)) from local observations and form regional reanalysis datasets all around the world, finding a general agreement with respect to the theory. They have demonstrated that the α_cc coefficient of Equation A8 (i.e. CC rate) is equal to 7%, according to which, when the temperature increases by one degree (+1 °C), the average intensity of precipitation can increase by 7%. They applied a least-squares linear regression to the logarithm of precipitation intensities, considering the temperature values up to peak precipitation intensities (see Equation (A9)). Among them, the analysis carried out in [44] across the Alpine Mountain range (Figure 1) exhibits how the 7% °C⁻¹ could be directly measured considering the relation between 10 min intensity I₁₀ (or the 1 h intensity I₆₀) and the recorded ground temperature T_ground. The latter was retrieved by analysing the Austrian and Swiss Alps [42], confirming that the CC rate can sometimes be larger, approaching 2×CC scaling for extreme events. In Figure 2, the means of the intensity-temperature scaling rates for different areas of the Swiss Alps are reported. The CC rate is between 7% °C⁻¹ and 14% °C⁻¹, showing a larger rate for convective storms with respect to non-convective ones. Regression was conducted using I₁₀ and I₆₀ as the maximum rainfall intensity, showing that the CC evaluated with I₁₀ was higher than that calculated from I₆₀.

The methods mentioned above can be used for rapid IDF curve correction, simply by modifying (i.e., increasing) the rainfall intensity I or height H. An alternative approach is based on the statistical analysis of the extreme value distribution [1,14,19] of the future rainfall series computed by climate models. This methodology is not different from the one applied to the ground-based rain gauge timeseries and consists of studying the samples of annual maxima P_max-y for different precipitation durations D using the Generalised Extreme Value distributions (GEV) and measuring the return period RP (i.e., the frequency) of the rainfall events. The GEV distribution incorporates three asymptotic forms of maximum extreme values in a single expression, which includes the Gumbel, Fréchet, and Weibull distributions [14,19] (see Appendix B). In Equation (3), the analytical function of IDF curves is reported where the dependence on GEV coefficients ($\alpha ,\epsilon ,k$) is highlighted within the parameter w_RP.

$$H=a_1{w}_{RP}{D}^n\to where w_{RP}f(\alpha ,\epsilon ,k,RP)$$

(3)

The theory of extremes [1,37] tells us that the precipitation maxima converge (asymptotically) to a GEV distribution. However, considering a length of data sample equal to 30 years (according to the climatic definition of the minimum period of investigation for the future [25,30]), this may represent a limitation to the application of extreme value distribution using climate model outputs. According to [46,47], trying to assess the extreme distribution of a certain quantity (rainfall, discharges, etc.) in a deterministic way represents a critical task that strongly depends on the quality and consistency of the adopted timeseries. Sometimes, the convergence is perturbed by rare and very rare events that are often difficult to record (due to instrumentation failure) or are assessed in terms of the order of magnitude (such as for discharges). In this regard, the literature has provided several strategies to deal with extremes, with some that are more statistically based (looking at the tails of the distribution, i.e., 90% and 99% percentages) and others that aim to retrieve the extreme distribution more analytically, such as GEV. According to [14,19,46,48], the GEV distributions are the ones that provide the highest accuracy and flexibility in dealing with extreme values (especially for rainfall events), and they are mentioned in national guidelines for hydraulic infrastructure design [14,49]. However, the spatial distribution of GEV’s parameters, since they depend on the provided timeseries, should be corrected and updated every time an intense or significant event is recorded in the area. In fact, a slight modification in the fitting parameters means a non-negligible variation in the RP estimation of extreme quantities. Moreover, the choice of the most suitable distribution within GEV is sometimes critical, especially in cases where the combined model (the GEV) may fail to converge to finite values for high RP [14,19].

With a few annual maxima observations N ≤ 30 (where N is the size of the sample data corresponding to the n° of years), the asymptotic regime may not be assured in all situations: convergence to the true limit distribution can still be very slow and unstable. In these cases, the Gumbel distribution (i.e., k ≈ 0, the scale parameter of GEV) is often used as a compromise according to [37,50], because it is asymptotically neutral (this is the borderline case between Weibull and Fréchet), more numerically stable in estimation methods, and more “robust” for small samples. The Gumbel is preferred to the Fréchet because is less prone to overestimating heavy tails and outliers. Conversely, the Fréchet is more suitable for very heavy tails but requires more data (i.e. longer data series) for a reliable estimation of its parameters. The choice depends on the nature of the extremes observed, but in general, the Gumbel provides more robust predictions. The Gumbel has a tail that decays exponentially (like the Weibull), while the Fréchet has a heavier tail (Pareto/student-t type), which means that the Fréchet is sensitive to very large extreme values that may not be present in a small dataset [1,14,46]. Regarding the parameter stability, the Gumbel has all its finite moments, which makes it more stable to estimate than the Fréchet (whose first moment can be infinite, making the average estimate unstable) when the data is scarce. In these cases, estimating the parameters of a heavy tail like Fréchet’s can lead to very inaccurate estimates or even illogical results (e.g., infinite averages). The former was confirmed through several tests carried out at preliminary steps in this study (not reported) on small sample timeseries, showing a non-convergent behaviour of Fréchet’s for rather higher RP (≥100 years). In this regard, GEV could, in principle, be estimated with 20–30 points, but the estimate of the k parameter is difficult, so that fixing k = 0 (Gumbel) for small samples, if there is no strong evidence of heavy or truncated tails, could simplify the IDF curves calculation. Generally speaking, for small samples (N < 50), Gumbel is often preferable to a full estimate of the GEV [1,14,37]. If the physics of the problem does not suggest truncations (→Weibull) or low-probability catastrophic events (→Fréchet), the Gumbel represents a conservative choice.

Empirical methods, the Clausius–Clapeyron equation, and the GEV distribution applied to climate change projections represent valid strategies for future IDF curve corrections. In this study, some insights about the Clausius–Clapeyron theory and a full application of the GEV distribution to EURO-CORDEX climatic regional models are presented. As mentioned above, the Clausius–Clapeyron method is rather straightforward to apply, knowing the future temperature trend, while the GEV analysis requires processing the rainfall data coming from the climate model. Therefore, since the methodology of recalculating IDF curves using GEV is also retained as the most accurate and scientifically rigorous, it will be presented in detail in the next paragraph, starting from the description of the EURO-CORDEX ensemble and reporting the working hypothesis adopted in the study.

2.2. Regional Climate Change Projection Using EURO-CORDEX Models Ensemble

To evaluate the possible future anomalies of the IDF curves as a function of climate change, by applying the Clausius–Clapeyron correction or recalculating them using GEV, the climate models’ outputs of the European consortium EURO-CORDEX are used [31,38]. The EURO-CORDEX consortium brought together 15 climate models in an ensemble with the aim of reproducing the climatology of the European area from 1976 to 2100. These models use the observed data to reconstruct the historical period between 1976 and 2005 and make future projections from the year 2006 to 2100. The peculiarity of this ensemble is that each of the models is the result of the union of a climate model on a global scale (GCM, Global Circulation Model) that provides the boundary conditions to a climate model on a European scale at higher resolution (RCM, Regional Circulation Model), for which 15 possible combinations have been selected (

Table 1. The 15 EURO-CORDEX climatic models utilised in the current study are listed. The entire name is specified with the relative GCM (Global Circulation Model) and RCM (Regional Circulation Model).

Id	Name	EURO-CORDEX Climatic Model	GCM	RCM
1	mod1	CNRM-CERFACS-CNRM-CM5_CNRM-ALADIN53	CNRM-CM5	CNRM-ALADIN53
2	mod2	ICHEC-EC-EARTH_CLMcom-CCLM4-8-17	EC-EARTH	CLMcom-CCLM4-8-17
3	mod3	MPI-M-MPI-ESM-LR_CLMcom-CCLM4-8-17	M-MPI-ESM-LR	CLMcom-CCLM4-8-17
4	mod4	CNRM-CERFACS-CNRM-CM5_CLMcom-CCLM4-8-17	CNRM-CM5	CLMcom-CCLM4-8-17
5	mod5	CNRM-CERFACS-CNRM-CM5_KNMI-RACMO22E	CNRM-CM5	KNMI-RACMO22E
6	mod6	CNRM-CERFACS-CNRM-CM5_SMHI-RCA4	CNRM-CM5	SMHI-RCA4
7	mod7	ICHEC-EC-EARTH_KNMI-RACMO22E	EC-EARTH	KNMI-RACMO22E
8	mod8	ICHEC-EC-EARTH_r1i1p1_KNMI-RACMO22E	EC-EARTH_r1i1p1	KNMI-RACMO22E
9	mod9	ICHEC-EC-EARTH_r12i1p1_KNMI-RACMO22E	EC-EARTH_r12i1p1	KNMI-RACMO22E
10	mod10	ICHEC-EC-EARTH_SMHI-RCA4	EC-EARTH	SMHI-RCA4
11	mod11	IPSL-IPSL-CM5A-MR_SMHI-RCA4	CM5A-MR	SMHI-RCA4
12	mod12	MOHC-HadGEM2-ES_CLMcom-CCLM4-8-17	HadGEM2-ES	CLMcom-CCLM4-8-17
13	mod13	MOHC-HadGEM2-ES_KNMI-RACMO22E	HadGEM2-ES	KNMI-RACMO22E
14	mod14	MOHC-HadGEM2-ES_SMHI-RCA4	HadGEM2-ES	SMHI-RCA4
15	mod15	MPI-M-MPI-ESM-LR_SMHI-RCA4	M-MPI-ESM-LR	SMHI-RCA4

). This number is necessary to perform statistical uncertainties related to future projections. The radiative forcing scenario considered in the elaboration is the RCP 8.5 (Representative Concentration Pathway), identified by the IPCC (Intergovernmental Panel on Climate Change) as the most critical for the future (called also “Business as usual”) [25,51,52], as it indicates a scenario with little or negligible climate change mitigation initiatives and that represents the most probable in the upcoming decades. RCP 8.5 is an emission scenario used in IPCC reports for where the “worst case” or “extreme” scenario, with a global temperature increase that can vary between 3.0 °C and 5.1 °C, is considered. In the RCP 8.5 scenario, the climate change effects are exacerbated since no mitigation measures or strategies to reduce CO₂ emissions are implemented at the global scale [30,34].

2.3. Methodology for Recalculating Future IDF Curves Using EURO-CORDEX Models and GEV Distributions

The future IDF curve reconstruction methodology using EURO-CORDEX models and GEV distributions was automated using Python 3.11 version (an open-source programming language), following these steps:

• The EURO-CORDEX ensemble has been organised using the NETCDF (.nc) file format, subdividing for each climate model the historical period (1976–2005) from the future period (2006–2100). The RCP scenario selected for the simulation was the RCP 8.5, the most severe among the IPCC scenarios, which corresponds to the highest anthropogenic radiative forcing. This choice was made since, according to the monitoring, current climate trends are moving between RCP 4.5 and RCP 8.5, where 4.5 is a more optimistic scenario, while 8.5 is the pessimistic one [34].
• The EURO-CORDEX data for each model have been aggregated, calculating the rainfall accumulations at 1-2-3-4-5 days. Here, the rainfall data were not conditioned or downscaled in order to preserve, as much as possible, the integrity of the model result and its relationship with the temperature data. Even if downscaling techniques may resolve some systematic errors in cumulative rainfall, these are complex and may introduce distortions in the sample distribution that may afflict the extreme value statistics [30,31,53].
• For obtaining the IDF curve parameters by applying the GEV distribution, a return period (RP) array containing reference RPs of 2-5-10-20-50-50-100-200-500 years was assumed in the methodology. The array is the same adopted by ARPA (Regional Environmental Protection Agency) [54] reference IDF curves that span from frequent events (with RPs from 2 to 5 years) to rather rare events (with RPs from 200 to 500 years). The latter are generally required by Italian regulations [55] for assessing flood magnitude (200 years) and for dam construction (1000 years).
• The procedure of IDF curve calculation was applied four times for each climate model, considering sample time windows of 30 years, and labelled with the “central-year” of each sample, as reported in

  Table 2. Climatic model periods chosen in the analysis. The reference period is distinguished from future periods, considering a length of 30 years. Within reference periods, climatic models are tested and calibrated in order to reproduce the past climatology.

  Period	Years	Period Length	Label (Central Year)
  Reference	1976–2005	30 years	1991
  Future—Short-Term	2006–2035	30 years	2021
  Future—Mid-Term	2036–2065	30 years	2051
  Future—Long-Term	2066–2100	34 years	2081

  . According to the climatic definition of the minimum period of investigation for the future [25,30], 30 years represents a standard used for evaluating the possible modification of climatic statistics across an area. In particular, the periods of investigation analysed were (1976–2005) for the historical (reference) period, (2006–2035) for the near-future (short-term) period, (2036–2065) for the mid-future (mid-term) period, and (2066–2100) for the far-future (long-term) period.

2.3.1. Climate Models Validation Using ARPA Reference IDF Curves

After the application of the methodology, the IDF curves obtained for the historical period 1976–2005 were compared and validated with respect to the local reference IDF curves provided by ARPA (Regional Environmental Protection Agency) [54]. Since IDF curves are multiparametric functions depending on duration D and return period RP of the rainfall, the validation comparison was simplified, evaluating the agreement between the two main characterising parameters of the IDF curves (i.e., a₁ and n), discarding at first the dependence on RP, which acts as an “amplificatory factor” for the curves. The statistics considered in the error analysis of a₁ and n were the anomaly (BIAS, in Equation (4)), the relative anomaly (BIAS%, in Equation (5)), the Root Mean Square Error (RMSE, in Equation (6)), and the RMSE% (in Equation (7)) [30,37,56] between the IDF curve parameters reconstructed from the EURO-CORDEX data (E_i, estimated) and the ARPA reference ones (O_ARPA, observed).

$$BIAS={\displaystyle \frac{1}{N}}\sum _{i=1}^N{E}_i-O_{ARPA}$$

(4)

$$BIAS\%=100·BIAS/O_{ARPA}$$

(5)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(E_i-O_{ARPA}\right)}^2}$$

(6)

$$RMSE\%=100· RMSE/O_{ARPA}$$

(7)

As can be appreciated, the statistics take into account the possible variabilities among the 15 EURO-CORDEX models, giving an average quantification of the errors among the 15 different model realisations. According to the literature [57,58], the EURO-CORDEX ensemble generally reproduces climate patterns, but has systematic biases like widespread precipitation overestimation, especially in winter, and some temperature biases in certain regions. For precipitation data, biases are often seasonal. While models often show “added value” at higher resolutions, especially for representing local-scale features like orography, their performance varies by model and region, with no single model ranking consistently on top across all metrics. Therefore, the spread of the results across the ensemble helps to quantify uncertainty in future climate projections [30,34].

2.3.2. Climatological Anomaly, Rainfall Anomaly and Return Period Anomaly

After the historical period validation, the methodology concentrates on future anomalies of the precipitation height (H) [30]. Primarily, the climatological anomalies were investigated by comparing the mean precipitation of the historical period against the future projected one (see Appendix E). Then, the number of mean wet-rain days has been calculated following the WMO (World Meteorological Organisation—WMO) indication (P_day ≥ 1 mm). The historical period (1976–2005) was compared with the three future periods, comprising 2006 to 2100, in Table 2. Then, the anomalies of future wet and dry days and of the mean annual precipitation have been calculated using Equations (8)–(10):

$$C{A}_{Pmean}=P_{mean}\left(Future\right)-P_{mean}\left(Historical\right)$$

(8)

$$C{A}_{WetDays}=P_{mean}\left(P_{future}\ge 1 \mathrm{m}\mathrm{m}\right)-P_{mean}\left(P_{historical}\ge 1 \mathrm{m}\mathrm{m}\right)$$

(9)

$$C{A}_{DryDays}=P_{mean}\left(P_{future}<1 \mathrm{m}\mathrm{m}\right)-P_{mean}\left(P_{historical}<1 \mathrm{m}\mathrm{m}\right)$$

(10)

The same approach has been applied to IDF curves, comparing, for each climate model, the future precipitation within a certain scenario (short, medium, and long) and with an assigned duration D and return period RP against the historical one. This anomaly (BIAS) measures the actual increase or decrease in the precipitation amounts in the future as compared to the past, highlighting possible trends of the future climatology. Also, for the return period (RP), it is possible to assess an indicator of future climate trends. However, with respect to the rainfall height (H) anomaly that is measured in mm, the variation in RP could be quantified in terms of a ratio, comparing the future with respect to the past. The reason for this choice resides in the distribution of the two quantities in IDF curves with respect to a fixed duration D. Maximum precipitation increases linearly with the logarithm of the RP [1,19]. Therefore, a small maximum precipitation variation may lead to significant return period modification. This is why precipitation anomalies are generally expressed in dimensional form (i.e., as A_P, Equation (11)) while the return period variations are expressed with a ratio (i.e., R_RP, Equation (12)), showing an increase or decrease in % terms as compared to the historical scenario.

$$A_P=1/N\sum _{i=1}^{15}{P}_{future}{\left(RP,D\right)}_i-P_{historical}{\left(RP,D\right)}_i$$

(11)

$$R_{RP}=1/N\sum _{i=1}^{15}{RP}_{future}{\left(H,D\right)}_i/R{P}_{historical}{\left(H,D\right)}_i$$

(12)

2.3.3. Significance of the Climatic Trends

Statistical tests have been performed throughout the study to verify the significance of the anomalies calculated, identifying possible deviations between the historical and future 30-year periods of the IDF curves. The IDF curve distributions, the statistical test on the sample mean, the t-test [59] (Equation (12)), and the Welch test [60] (Equation (13)) were taken into consideration, considering a significance level of 0.05 and treating each climate model independently from the others (i.e., as an independent realisation of the stochastic process). The latter are two-tailed statistical tests that allow you to verify the hypothesis of equality of the average between the two samples (i.e., the historical/reference period and the future period). The first requires a sample of a number between 20 and 30, where the distribution is normal and it has the same variance. The second test is similar to the first, but is more general, because it does not require a hypothesis on the equality of the variance of the two samples. Equations (13) and (14) report the tests evaluated.

▪

x₁ and x₂: the mean of the first (future) and second (historical) sample, respectively.

▪

n₁ and n₂: the number of observations of the first (future) and second (historical) sample, i.e., ~30 observations.

▪

s_p: the pooled standard deviation, a measure of the combined variance of both groups (for the t-test)

▪

s₁ and s₂: the standard deviation of the first (future) and second (historical) sample (for the Welch test).

Since IDF curves are multiparametric functions depending on duration D and return period RP of the rainfall, the statistical tests were carried out as follows. The 15 climate models were considered together, evaluating the statistical mean and median of the ensemble for the historical period (1976–2005), and for the three future climate periods (2006–2035, 2036–2065, and 2066–2100). Then, for three reference RPs (2 years, 20 years, and 200 years) and three representative durations (1 day, 3 days, and 5 days), the mean H (in mm) of corresponding IDF curves were selected for carrying out the statistical tests on the anomalies. The two tests (t-test and Welch-test) were performed, comparing the reference period (1976–2005) with each one of the future periods (short-, medium-, and long-term) and testing the null hypothesis H_o separately for each combination of D, RP, and future period: if H_o is verified, the two samples may admit the same mean values. Each sample was tested independently, comparing its future period with its past period and giving a score of 0 for a test passed (i.e., the same mean) and 1 for a test not passed (i.e., a different mean).

According to [61,62,63], when multi-hypothesis tests are conducted, a correction for the significance level α (considered in this analysis equal to 0.05) should be advisable. In this regard, the Bonferroni correction is sometimes applied [63]. With the Bonferroni approach, the significance level α is divided by the number m of null hypotheses that are tested. If a p-value is below α/m, then the null hypothesis is rejected at level α. However, this technique is sensitive to the number of null hypotheses tested, which in our case, is 27, since 3 Ds, 3 RPs, and 3 future periods have been combined and tested. Since the Bonferroni correction is reported to be rather conservative, reducing the Type I error (i.e., the true positives) but increasing the Type II error (i.e., the false negatives), the correction was not applied to the analysis, considering each test conducted for each sub-sample as independent, and simply anchoring them with 0–1 score. Then, an overall score of the test applied (one for the t-test and one for the Welch-test) has been evaluated by summing each test’s results (0–1), dividing it by 27 combinations, and assuming the anomalies as significant for a ratio > 0.7. However, since in some cases, the RP or D averages have been adopted, the effective combinations may have varied (i.e., reduced).

$$t={\displaystyle \frac{{\overline{x}}_1-{\overline{x}}_2}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}}\to Student’s t-test$$

(13)

$$t={\displaystyle \frac{{\overline{x}}_1-{\overline{x}}_2}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}}\to Welch Test$$

(14)

In addition, the test on the significance of a possible future linear trend of yearly maximum rainfall amounts (P_max-y) for durations between 1 and 5 days [29] was applied. The test verifies that among the variables of the regression (the independent variable “$x$”, the years, and the dependent variable “$y$” that describes one of the quantities examined, such as P_max-y), the null hypothesis H_o is verified, which affirms the non-existence of a linear trend. The test verifies that the calculated p-value is lower than the significance level, which, in the case in question, is chosen to be equal to 0.05. Another way to perform the test is to calculate the test statistic t in Equation (15), which depends on the sample size (length of the data series, n) as well as the value of the Pearson regression coefficient $r$, and to verify that it is >2.0 or <−2.0. These limits correspond to the critical value of t by setting a significance level of 0.05 and considering the degrees of freedom $df$ equal to n − 2. Here, the trend analysis has been conducted separately for each model of the EURO-CORDEX ensemble, taking into account the whole future period from 2006 to 2100, and a ranking of the test was adopted using a 0–1 score for verified H_o (non-linear trend, 0) and for non-verified H_o (linear trend, 1), respectively.

$$t={\displaystyle \frac{r}{\sqrt{\frac{1-r^2}{n-2}}}}\to Pearson Trend Test$$

(15)

2.4. Case Study of Lombardy Region

The application of the IDF curve correction considering future climate change was tested and developed across the Lombardy Region (Italy). The area is characterised by sharp maximum and mean rainfall gradients (Figure 3), which are related to the orographic precipitation that frequently occurs across the Alps and Pre-Alps Mountain range [19]. A sharp rainfall gradient may locally lead to a significant variation in IDF curves [40,64], so their correction under a climate change scenario is mandatory in order to enhance the prediction of possible extreme precipitation. The IDF curves currently in use in Lombardy are built using historical observations between 1950 and 2001 and are divided into two sets: IDF curves for short-term events between 1 and 24 h, and IDF curves for long-duration events between 1 and 5 days [18,19]. This distinction is related to the different sampling techniques used in the past by weather stations before mechanical rain gauges were installed. The two datasets, although used to reconstruct IDF curves, are not completely overlapping and lead to substantial differences between the IDF curves evaluated for 24 h and the one corresponding to 1 day (note the discontinuity of the IDF curves represented in Figure 4). Namely, the hourly and daily IDF curves tend to coincide in the area with significant rainfall amounts (Varese and Lecco), while in drier regions (Sondalo and Mantova), the discontinuity is more pronounced (see Appendix D). From a hydraulic design perspective, this represents a significant uncertainty that may lead to an incorrect interpretation of the extreme rainfall phenomena statistics across the region.

3. Results

3.1. Clausius–Clapeyron and Intensity-Temperature Graphs

Before starting with the study on IDF curves, the Clausius–Clapeyron theory has been applied to a group of heavy rainfall events recorded across the Lombardy area. The aim was to try to determine if the relationship between the temperature and intensity was detectable, showing R_cs was between CC and 2CC rates. An ensemble of heavy rainfall events that hit the Lombardy region between 2018 and 2022 was gathered from historical chronicles. Then, the meteorological data of each event, the temperature, and the maximum intensity have been extracted from the nearest rain gauge from the ARPA Lombardia weather station network [54]. The temperature is representative of the amount of energy available in the environment, and it should be collected at the very beginning of the rainfall event investigated [43,66]. Therefore, the former was the temperature recorded on the ground averaged between 1 h and 4 h before the rainfall started [56,67,68], while for the rainfall intensity, the maximum recorded within the event was considered. Since this data could be measured virtually at a higher frequency (i.e., 10 min) but not in all rain gauge stations (some have 1 h sample frequency), the maximum rainfall intensity has been rescaled in mm h⁻¹ to homogenise the measures.

In Figure 5, the result of the Clausius–Clapeyron regression analysis is reported, where the T-I (Temperature-Intensity) points are compared against the CC and 2CC rates. As can be appreciated, the points lie between the two curves, confirming the analysis conducted in [44] for the Ticino area located across the Southern Alps, in Switzerland, close to the Lombardy Region (Figure 2). The data dispersion is rather high, showing the complexity of retrieving this relationship. Among the events, a large part of them occurred during the summer period, characterised by a mean T ≥ 15–20 °C, which implied the activation of moist convection [69]. According to [43,69], moist convection is able to deplete environmental energy more efficiently, leading also to thunderstorm and cloudburst generation, which are characterised by a higher rainfall rate compared to stratiform precipitation. Among the events reported, the extreme precipitation that occurred in Cantiano (in the Marche Region), which triggered a sudden flash flood on 16 September 2022, was included within the T-I graph [70]. The Cantiano event occurred in the late summer (T ≈ 25 °C) due to a V-shaped thunderstorm that became stationary (i.e., persistent) and showed a maximum rainfall intensity of 52 mm h⁻¹. As was suspected, the return period of Cantiano rainfall amounts was calculated around ≥ 500 years [70,71], and the T-I scaling of this event lies on 2CC curves, confirming the fact that the Clausius–Clapeyron method is valid and able to detect the extreme rainfall events.

Considering the limited extension of the dataset studied, the research for CC—2CC scaling between T and I was extended, analysing rain gauge series for 45 stations across the Lombardy area. Here, the length of the series was comprised from 1993 to 2024, covering 30 years. The analysis was carried out considering all the events with I ≥ 5 mm h⁻¹ to concentrate the analysis only for the most intense rainfall events. As can be appreciated from the reported graph in Figure 6, the CC rule also holds for this second dataset, showing a R_cs coefficient in the order of 7% °C⁻¹. Figure 6a shows the entire dataset where 4140 events were detected between 1993 and 2024, and where the extreme events recorded between 2018 and 2022 are superimposed. As can be noticed, the total regression is rather dispersed, giving an R_cs coefficient around 4.89% °C⁻¹, which is slightly lower with respect to 7% °C⁻¹ and significantly lower than 12.6% °C⁻¹ obtained for extreme events. Therefore, the sample has been manipulated to retrieve a stronger T-I relationship, calculating for each station and for each year of the investigated series the monthly average of T and I and then plotting the data in Figure 6b. The scatter has significantly reduced (there are 345 points with respect to 4140) and T-I regression is now clearly detectable, showing CC comprised between 6.35% °C⁻¹ and 7% °C⁻¹. Moreover, according to the theory [43,44,66], reducing the dataset by filtering out lower temperatures, CC tend to rise (6.35% °C⁻¹ for T > 5 °C in blue, 6.42% °C⁻¹ for T > 10 °C in green, and 7.03% °C⁻¹ for T > 15 °C in yellow in Figure 6b), confirming the trend shown for extreme events, where higher CC can occur with higher T.

According to Figure 5 and Figure 6, the Clausius–Clapeyron approach is consistent with the observations recorded in the Lombardy region. Therefore, the application of Equation (2) could, in principle, be adopted for correcting the IDF curve intensity. However, posing 7% °C⁻¹ ≤ R_cs ≤ 14% °C⁻¹, ΔT_cc needs to be specified. Following the indication of IPCC reports [24,25] over the Mediterranean area and Alpine Mountain range, the increase in the mean temperature is between 2 °C and 4 °C. As a result, the expected intensity increments are listed in

Table 3. The IDF curve’s correction factor is evaluated for suggested ranges of temperature difference ΔT_cc and CC scaling coefficients. Increasing ΔT_cc and CC leads to a higher correction factor (colours moves from green to red), increasing sensibly (up to 50–60%) the reference rainfall intensity.

	Temperature [°C]
CC Ratio [% °C−1]	1.5	2	2.5	3	3.5	4
7	1.11	1.14	1.18	1.23	1.27	1.31
8	1.12	1.17	1.21	1.26	1.31	1.36
9	1.14	1.19	1.24	1.30	1.35	1.41
10	1.15	1.21	1.27	1.33	1.40	1.46
11	1.17	1.23	1.30	1.37	1.44	1.52
12	1.19	1.25	1.33	1.40	1.49	1.57
13	1.20	1.28	1.36	1.44	1.53	1.63
14	1.22	1.30	1.39	1.48	1.58	1.69
Years	2020	2050	2080	2110	2140	2170

.

As can be appreciated, as the CC rates increase, the future intensity tends to rise. However, ΔT_cc is the other factor that may perturb it. Even if in the current climate situation, where ΔT_cc ≈ 1.5 °C, we are experiencing a slight increase in extreme phenomena [24] (in the green sector of Table 3), in the future, a transition to a more intensified state will be more likely (moving to yellow, then up to the red sectors). For example, an event with intensity 15 mm h⁻¹ in 2020 (with ΔT_cc ≈ +1.5 °C), admitting a R_cs = 10% °C⁻¹, will become (with ΔT_cc ≈ +3 °C) 20 mm h⁻¹ in 2100, increasing its magnitude by around 30%.

The Clausius–Clapeyron correction for IDF curves is undoubtedly fast and straightforward to apply, simply using reference data and considering them as not already affected by climate change. Nevertheless, this methodology remains semi-empirical, leaving the user the choice of the CC factor and the ΔT_cc scenario [40]. Behind the choice of those parameters still exist some uncertainties (i.e., CC factor is highly variable depending on the typology of the rainfall event [23,43], while the expected ΔT_cc can change with the location and the radiative scenario [25,29]). Moreover, according to [23], it requires some modifications to integrate the expectation of intensification of projected rainfall extremes with frequency (as the return period increases) and with shorter durations (sub-daily). So, this approach has been integrated with the physically based reconstruction of IDF curves using EURO-CORDEX climatic models and GEV distributions.

3.2. Preliminary Application of the GEV Distribution for Future IDF Curve Reconstruction in the Alpine Environment

The preliminary application of the GEV distribution for future IDF curve reconstruction has started with the analysis of the currently adopted IDF curves. The former have been derived from historically recorded rainfall data that in Italy have been conventionally collected within hydrological annals [49]. The hydrological annals, edited by the local environmental monitoring services (ARPAs), contain the data series of maximum rainfall height for an appropriate number of durations less than a day (1–24 h), and for several consecutive days (1–5 days) [19,49]. For each rainfall station, the maximum rainfall heights in 1, 3, 6, 12, and 24 consecutive hours (using a sliding window scheme) and the maximums from 1 to 5 consecutive days, however, referring to fixed-step readings (from 9 a.m. to 9 a.m. the following day), are reported. So, the 1–24 h and 1–5 day samples cannot be merged in the currently adopted IDF curves, giving two separate products in the GEV analysis of the precipitation [19]. This distinction is shown in the following Figure 7 and Figure 8. Here, the rain gauge networks adopted for retrieving the two IDF curve groups, and the hourly rainfall coefficient a₁, evaluated for both, are presented. For the Lombardy region, according to [19], the 2D spatialization of a₁ was carried out using a spherical variogram for the Kriging interpolation technique [72], which was performed to interpret the variability of the parameters considered.

Moving to the climate dataset, among the 15 models of the EURO-CORDEX ensemble, the three considered most accurate compared to the past local observation were applied (

Table 4. EURO-CORDEX climatic models are considered for methodology tests in the upper Lombardy region.

Id	Name	EURO-CORDEX Climatic Model
2	mod2	ICHEC-EC-EARTH_CLMcom-CCLM4-8-17
3	mod3	MPI-M-MPI-ESM-LR_CLMcom-CCLM4-8-17
4	mod4	CNRM-CERFACS-CNRM-CM5_CLMcom-CCLM4-8-17

). This data of CORDEX simulations with the CCLM4-8-17 regional climate model for Europe—high resolution (EUR-11) is provided by CLMcom (Climate Limited-area Modelling Community) [73,74,75]. It includes historical and RCP 8.5 using forcing data derived from the CMIP5 (Coupled Model Intercomparison Project Phase 5) model outputs of EC-EARTH, MPI-ESM-LR, and CNRM-CM5 global circulation models. The three models are constituted by the COSMO-CLM (Consortium for Small-Scale Modelling (COSMO) model in Climate Mode (CLM), abbreviated as CCLM, as a regional climate model (RCM). The latter is the climate version of the COSMO LM model [76], which is the operational non-hydrostatic mesoscale weather forecast model. This choice was validated within the study presented in [30,77], where those models have been reported to be less biassed with respect to the others in the reconstruction of the past rainfall amounts and rainfall extremes, during the reference period 1976–2005 and across the Northern Italy area. No further downscaling procedure of the data was carried out in order to preserve the original model’s outputs, using them at its native resolution of ~12 km.

The extension of this preliminary application of the methodology was carried out in the northern part of the Lombardy region (Figure 9). Assuming that one climate pixel is approximately equal to a rain gauge, the information available from climate data was virtually constituted by a matrix with six rows and 14 columns that resulted in 84 rain gauges. These numbers are significantly greater than the number of historical rain series adopted by ARPA for building reference IDF curves (15 stations in Figure 9a). Therefore, the information brought by the climatic model, even if at first glance it may seem coarse in resolution, contains more data with respect to the reference timeseries. To speed up the preliminary analysis, the climate models’ time series were simply investigated, separating them into two parts: a historical period 1976–2005 (reference period—R) and the future period 2005–2100 (climate period—C), where 30-year aggregation was not considered for the future. The IDF curves are reconstructed separately for the two periods using applying GEV distribution analysis.

The analysis on future IDF curves concentrated on the quantification of the projected future H anomalies using Equation (7). Anomalies evaluated for a specific D and RP have the advantage of being added to the reference IDF curves, neglecting the discontinuity problems which may be encountered trying to extrapolate and temporally downscale the 1–5 day climatic result to short durations. For each climate model of Table 4 (mod2, mod3, and mod4) and for each scenario (reference period-R) and (future period-C), the average anomalies of H were evaluated. The analysis was not carried out on a pixel basis, but on sampling rainfall data in correspondence with the new monitoring station’s network of ARPA Lombardia, located in the investigated area. The former has increased in recent decades from 15 to 50 rain gauges, giving a larger sample size (orange spots in Figure 9b) with a homogeneous spatial distribution in the area.

Firstly, reference IDF curves from the ARPA Lombardia dataset have been compared against the IDF curves recalculated using the reference period of the three climate models in Figure 10. The anomaly between the two datasets is shown as a function of the duration D and the return period RP. As can be appreciated, the anomalies are not negligible, and, taking the average of the three models (dashed line), they amount to around +10–20 mm. Namely, the differences are higher for mod3 and mod4, while mod2 seems closer to the ARPA data. Figure 10b reports the relative anomaly where its dependence on RP is clearly visible. The differences between the two datasets are higher for lower RPs (up to 15–20%) while reduced for higher RPs (between 5 and 10%). Averaging with respect to RPs, the mean relative anomaly assesses around (10–15%), and the mod2 is the one best in accordance with the ARPA Lombardia dataset. Here, the analysis clearly depicts how difficult it is to compare two datasets that come from different sources (i.e., ground-based station and climate model) and justify why climate ensembles are advisable for carrying out rainfall statistics.

The same analysis has been repeated, also considering climate change, evaluating the anomalies between future and reference periods of the three climate models. As can be appreciated in Figure 11a, the anomalies are always positive and tend to increase in function of RP, while the dependence of D is significant only for higher RPs. Averaging with respect to RPs, the mean anomaly is around +10–30 mm, progressively increasing moving from D = 1 day to D = 5 days. Looking at Figure 11b, the relative anomaly is depicted, showing an increase with RPs but a non-significant dependence on rainfall duration. On average, the relative anomaly of rainfall height is around +10–15% if compared to the reference period.

In Figure 12, the dependence of D has been neglected, taking the mean H for D between 1 and 5 days. Therefore, the anomaly is calculated from H, only considering the RP dependence. For the three investigated climate models, a positive anomaly (A_p) of around +23 mm of the maximum rainfall within the climatic data has been clearly detected for the area of Northern Lombardy. In particular:

▪

The A_p evaluated tends to increase as a function of the RP. In fact, it ranges from a minimum of +5/10 mm for RP = 2 years up to +50/60 mm for RP = 500 years;

▪

The uncertainties in the A_p increase proportionally with the RP, and this is well described by the three climate models that provide similar results for low RPs, while they are divergent for high RPs;

▪

Averaging the results with respect to RP, the IDF curve increases are +33 mm (mod2), +12 mm (mod3), and +28 mm (mod4), which corresponds to a mean of about +23 mm.

To appreciate the climate change perturbation on historical IDF curves, the computed positive anomalies (+23 mm on average) have been applied to a pair of local IDF curves located within the investigated area, showing a rising curve (Figure 11). From the RP viewpoint, moving upwards, the curves correspond to a reduction in the RP of the rainfall phenomena. Looking more closely at Figure 13, for the two stations of Morbegno and Bormio, the new IDF curves (dashed lines) are higher than the reference IDF curves. The RP decreasing due to this upper shifting is between 0.3 and 0.7, with a central tendency of ~0.5. Therefore, in the future, a reduction in RP of about 50% is likely.

The preliminary results obtained from the reconstruction of the IDF curves in Northern Lombardy are in line with the IPCC [25] and CMCC (Centro euro-Mediterraneo Cambiamenti Climatici) [24] reports, which underline a non-negligible increase in the frequency and intensity of extreme rainfall events in Northern Italy. In this regard, the statistical significance of the anomalies computed has been verified by applying the statistical t-test and the Welch test. Both tests, conducted separately for each analysed model, have confirmed that the future rainfall distribution, even with a similar shape to the reference one, will have a mean and a median statistically different from the past, revealing a possible increase in extreme events. Also, the Pearson Trend test has been applied to the future series from 2006 to 2100 of the yearly maximum rainfall, considering the 1 to 5 day durations, confirming a statistically significant trend that is in accordance with the possible increase in extreme rainfall intensities [24]. Given these promising results obtained by this test case in Northern Lombardy, the methodology has been further extended to the domain of the entire Lombardy Region, considering a larger number of climate models (up to 15 of the EURO-CORDEX ensemble), useful for the most complete quantification of uncertainty.

3.3. Extension to the Entire Lombardy Region

For the update of the IDF curves throughout the Lombardy region, the GEV technique was applied to the 15 EURO-CORDEX climate models. Firstly, a climatological analysis of the study area has been conducted to evaluate possible trends embedded within the mean precipitation analysis. The analysis (fully reported in Appendix E) has shown the existence of three different rainfall regimes which have been considered for subdividing the region into three principal sectors: the Po Valley sector (PN) is located in the southern part of Lombardy and is characterised by a yearly average precipitation (P_mean-y) < 1000 mm; the Pre-Alps sector (PR), located in the central part of Lombardy in correspondence with the Maggiore, Como, and Garda Lakes and the Orobie Pre-Alps, is characterised by P_mean-y ≥ 1000 mm; and the Alta Valtellina sector (AV) is located in the north eastern part of the region and is characterised by a significant decrease in P_mean-y < 1000 mm. This sub-regionalisation was adopted to clusterize the IDF curve reconstruction across the investigation area (Figure 14). To retrieve the IDF statistics, the currently operating 266 rain gauge stations (80 in the PN sector, 160 in the PR sector, and 26 in the AV sector) were adopted to sample climatic conditions, considering their rather uniform distribution across the Lombardy region.

3.3.1. IDF Curve Reconstruction: Reference Periods Comparison

Before proceeding with future IDF curve reconstruction, a verification of the climate model’s performance in past IDF curve reconstruction has been carried out. The coefficients a₁ and n of ARPA reference IDF curves have been compared with the ones retrieved from the 15 climate models applying the GEV distribution to yearly maximum precipitation simulated for the reference period 1976–2005. The comparisons are reported in

Table 5. Comparison of the coefficient a₁ of IDF curves calculated from EURO-CORDEX climate models with reference ARPA Lombardia a_{1–24 h} and a_{1–5 day} coefficients.

Par a1	Climate Model Reference 1976–2005		ARPA Lombardia 1951–2001
Sector	1991_mean	1991_median	a_1-24 h_mean	a_1-24 h_median	a_1-5 d_mean	a_1-5 d_median
ALL	17.5083	17.5583	25.99	26.78	20.84	20.57
AV	19.9357	20.7388	18.06728	17.97	17.48547	16.90816
PR	16.7502	16.7138	28.33431	29.03	22.27761	21.9701
PN	17.5083	17.5583	26.85211	26.75	21.37658	21.10925

and

Table 6. Comparison of the coefficient n₁ of IDF curves calculated from EURO-CORDEX climate models with reference ARPA Lombardia n_{1–24 h} and n_{1–5 day} coefficients.

Par n	Climate Model Reference 1976–2005		ARPA Lombardia 1951–2001
Sector	n_1991_mean	n_1991_median	n_1-24 h_mean	n_1-24 h_median	n_1-5 d_mean	n_1-5 d_median
ALL	0.3731	0.3707	0.333952	0.3097	0.366825	0.381093
AV	0.4363	0.4289	0.448513	0.458	0.415258	0.412051
PR	0.3734	0.3699	0.345235	0.3387	0.398397	0.398893
PN	0.3569	0.3560	0.280178	0.279	0.318024	0.320056

, while the BIAS and RMSE error indices calculated are listed in

Table 7. BIAS and RMSE errors computed for the four Lombardy sectors with respect to a_{1–5 day}, and n_{1–5 day} coefficients. Climatic models are closer to the 1–5 day statistics, admitting low BIAS (between 10 and 20%) and RMSE errors (between 20 and 30%), confirming their accuracy for reconstructing the historical period.

Par a1	BIAS [mm/h]	BIAS %	RMSE [mm/h]	RMSE %
Sector
AV	2.9130	17.01	3.0363	14.57
PR	−5.2052	−23.90	6.5618	37.53
PN	−3.6614	−17.30	4.4483	19.97
ALL	−3.5360	−16.86	5.7229	26.77
Par n	BIAS [−]	BIAS %	RMSE [−]	RMSE %
Sector
AV	0.03682	9.2	0.0505	13.77
PR	−0.03521	−8.7	0.0439	10.57
PN	0.03886	12.30	0.057	14.31
ALL	0.01003	2.78	0.0491	15.44

. Moreover, the analysis of the entire Lombardy region (ALL) was also disaggregated for the three climatic sectors AV, PR, and PN.

As can be appreciated, the a₁ and n parameters (expressed in terms of the mean and median of 15 climatic models) are very close to the reference ones, especially for the 1–5-day ARPA coefficients. This result was expected since the EURO-CORDEX model has been validated on a historical period in the European domain, theoretically also matching with extreme statistics. Moreover, means and medians are rather close, showing a Gaussian distribution of the coefficient among 15 EURO-CORDEX models. Looking at BIAS and RMSE calculated considering all the Lombardy sectors, the minimum errors are obtained for 1–5 day ARPA coefficients. This was expected since both methods are coherent in evaluating the extremes using a fixed window sampling, while for 1–24 h coefficients, the moving window method was carried out. The climatic models are closer to the 1–5 day statistics, admitting low BIAS (between 10 and 20%) and RMSE errors (around 20–30%) on average. Among the three sectors, the PR admits the highest errors, especially for the a₁ coefficient with a negative BIAS% = −23.9 and the highest RMSE% = 37.53. This evidence is consistent with the fact that the southern Pre-Alps exhibit the highest rainfall amounts and the most important orographic rainfall gradients [10]. In addition, the relatively coarse resolution of climate models in reproducing complex orography may have played an important role in changing the extreme rainfall regime and degrading the IDF reconstruction [23]. In fact, biases are negative, showing a possible smoothing of the rainfall extremes due to the coarse resolution and the local moist convection parameterisation implemented within the climate models. With respect to the previous analysis, where only three climatic models were investigated, the ensemble investigation can sensibly reduce the BIASES with the ARPA reference data, taking into account a larger number of time series for IDF curve rain reconstruction within the reference period, and also reducing the outliers’ weight. As a result, the IDF curves calculated from climatic models seem to be representative of the past climatology and are close to the 1–5 day statistics calculated from the ARPA timeseries (Figure 15).

3.3.2. IDF Curve Reconstruction: Rainfall Anomaly

As shown in Figure 16, merging 15 climate models identifies a statistically significant anomaly of the IDF curves (according to the t-Test and Welch test) if averaged over all the durations of the rainfall event (1–5 days) across the Lombardy region. This anomaly is progressively increasing, moving from short (Figure 16a) to medium (Figure 16b) and to long (Figure 16c) scenarios, yielding mean (median) values of +15.6 (+10.9) mm, +20.6 (+23.6) mm, and +39.3 (+29.1) mm, respectively. The anomaly becomes higher and more dispersed, increasing the RP in all three scenarios. Moreover, even if mean and median statistics are coincident for a small RP (i.e., the data have a Gaussian distribution), the sample distortion tends to increase with the highest RP (especially for RP > 100 yr). This behaviour is also linked to the number and the characteristics of each climate model considered in the study, which, for rare rainfall events, exhibit a higher-lower tendency to amplify or dampen the modelled solution. The statistics reported in Figure 16 are related to the entire Lombardy region, but similar results have been obtained for the AV, PR, and PR sectors (

Table 8. Mean anomalies were evaluated for increased RPs and future periods (2021–2051–2081), considering the three sectors of the Lombardy region. Higher values are recorded for PR and PN, while AV will experience lower anomalies.

Sector (Mean)	Period	RP 2 yr	RP 5 yr	RP 10 yr	RP 20 yr	RP 50 yr	RP 100 yr	RP 200 yr	RP 500 yr	Avg
AV	2021	3.2	5.9	7.8	10	13.9	18.5	26.2	47	16.6
AV	2051	8.3	12.5	15.4	18.5	23.7	29.3	38	60	25.7
AV	2081	10.8	16.6	20.8	25	31.7	38.3	48.1	71.5	32.9
PR	2021	5.2	7.2	8.6	10.3	13.6	17.8	25.1	45.2	16.6
PR	2051	8.6	11.6	13.9	16.3	20.6	25.6	33.7	54.8	23.1
PR	2081	15.5	23.1	28.3	33.6	41.6	49.3	60	84.8	42.0
PN	2021	4.2	5.6	6.8	8.3	11.2	15.2	22.2	42	14.4
PN	2051	6.5	8.1	9.4	11	14	18.1	25.2	45.1	17.2
PN	2081	13.3	20.7	25.7	30.9	38.7	46.3	56.9	81.5	39.3

and

Table 9. Median anomalies were evaluated for increased RPs and future periods (2021–2051–2081), considering the three sectors of the Lombardy region. Higher values are recorded for PR and PN, while AV will experience lower anomalies.

Sector (Median)	Period	RP 2 yr	RP 5 yr	RP 10 yr	RP 20 yr	RP 50 yr	RP 100 yr	RP 200 yr	RP 500 yr	Avg
AV	2021	2.3	5.2	9.3	15.6	21.8	26.4	31	37.2	18.6
AV	2051	7.3	13.5	16.4	19.1	23.3	26.2	29.2	33.1	21.0
AV	2081	11.1	17.5	20.2	23.1	29.8	33.3	36.2	39.9	26.4
PR	2021	2.9	5.1	8.2	12.6	15.1	16.9	18.7	21	12.6
PR	2051	9.8	15.1	19.1	22.8	31.8	36.6	41.3	47.6	28.0
PR	2081	16.6	20.2	23.2	27.3	32	35.8	39.5	44.5	29.9
PN	2021	3.9	4.8	7.2	8.6	9.7	10.6	11.4	12.5	8.6
PN	2051	6.3	9.7	11.4	13.3	14.9	16.3	17.7	19.5	13.6
PN	2081	11.9	17.9	21.8	25.5	33.6	38.1	42.6	48.4	30.0

). Moreover, the Pearson Trend test has been applied to the future series from 2006 to 2100 of the P_max-y, for the 1 to 5 days durations, confirming a statistically significant linear trend for most models of the ensemble, but characterised by important data variance.

Across the AV, PR, and PN sectors, the anomaly increases with RP and when moving forward into the future. The anomaly calculated using the mean values is higher compared to the medians, since it is a statistic that is much more sensitive to possible outliers. However, the sharpest increments are projected to involve mainly the PR sector (which is the wettest area of the region, +42 (+29.9) mm) and the PN sector (located across the floodplain where intense convective thunderstorms are more likely to be triggered, +39.3 (+30) mm). Conversely, the internal and driest area of AV will experience a slightly lower anomaly of +32.9 (+26.4) mm by the end of the century. These discrepancies, even though they are small, show how differently Lombardy can respond to climate change in relation to their location and their typical rainfall regime. The most critical horizon seems to be the long-term one of the thirty-year periods 2066–2100, in which significant deviations from past climatology are expected in the Lombardy area. These data are in accordance with the studies carried out at both the Italian and European level [23,42,44,56,68], which agree on identifying a possible increase in the intensity of intense precipitation events in the Alpine area.

The anomalies reported exhibit a positive temporal and statistically significant trend (using the Pearson Trend test) that has been summarised in Figure 17. This trend is expressed in mm yr⁻¹ (mm/yr in the graphs) and was calculated firstly by computing, for each climate model, the anomaly trends for the periods 2021, 2051, and 2081, which were then merged together within a box plot. The average trend in the anomaly is around 0.35 mm yr⁻¹_, which, if temporally integrated for 100 years, is compatible with the average +30 mm already found. As can be appreciated, these trends are different across the Lombardy region, where they are higher in the PR (0.38 mm yr⁻¹) and PN (0.34 mm yr⁻¹) sectors and lower in the AV (0.30 mm yr⁻¹) sector. Moreover, the AV and PN sectors exhibit the highest scattering of the data, highlighting a possible significant variability of the precipitation across those areas. Conversely, the trends across the PR area are less dispersed, even though some outliers are found.

In the previous graph, only the influence of RP on anomaly has been taken into account, since the dependence on D has been neglected (i.e., the five durations have been averaged). However, it is also interesting to investigate the anomalous behaviour by varying the duration of the precipitation. For clarity, the durations of 1 day, 3 days, and 5 days, and the return period of 2 years, 20 years, and 200 years, are shown in the next figures. Moreover, to simplify the presentation, only the anomaly trends in mm yr⁻¹ evaluated for the 2021, 2051, and 2081 periods have been investigated. In Figure 18, the trends of the anomaly for durations of 1–3–5 days and for 2–20–200 RPs are shown. As can be observed, duration has a strong influence on the trend dispersion: increasing the duration of the rainfall phenomena, the combination of the rainfall values increases sharply, leading to a higher dispersion due to rainfall intermittency [78,79]. Moreover, it is also possible that no rainy days will occur within the five days, which may influence the final statistics, increasing the variability. With increasing RP, the events become rarer, causing the oscillation of the anomaly to become more pronounced, especially if RPs > 100 years are considered. Here, the GEV statistic carries out a sort of extrapolation of the statistical solution: according to [1,80], the GEV statistic is valid for RP ≈ 3 × N, where N is the size of the sample data (i.e., the 30 values of the yearly maximum precipitation). Therefore, in principle, the statistics computed are valid up to RP ≈ 100 years, while the others represent a statistical extrapolation of the extreme values.

In Figure 19, the anomaly trends are reported for the duration of 1 and 5 days, for the 2–20–200 years RP, and show the differences among the three sectors of the Lombardy region. As can be appreciated, the increase in anomaly with RP and D is detectable in all sectors:

▪

The duration influence is more pronounced in the AV sector for a higher RP and a duration of 5 days. Here, the trends increase up to 0.5 mm yr⁻¹ (RP = 200 years), suggesting a stronger perturbation of the extreme rainfall in that area. Similar values are shown for the PR and PN sectors, but with significantly less dispersion, confirming the greater variabilities of the rainfall across internal and orographic complex areas.

▪

The amplification due to RP and D increasing shows how non-linearities exist: IDF curves cannot be raised by the same amount, neglecting the anomaly dependence of RP and D; otherwise, underestimation may occur. So, considering the magnitude of anomaly trends as a function of RP and D is advisable to consistently adjust the IDF curves under climate change scenarios.

3.3.3. IDF Curve Reconstruction: RP Anomaly

A positive anomaly of the IDF curves corresponds graphically to a rise in the curves. This increase translates into a significant reduction in the return period, which does not scale linearly with respect to the anomaly. According to several studies conducted at the European level using EURO-CORDEX ensembles [23,56,68], the increase of about 10–20% of the annual maximum precipitation will correspond to a reduction of about 50% of the return period. This halving is important, especially if related to the project payback times currently in force by legislation for hydraulic works. In particular, it is expected that the current payback time of 20 years, as a result of climate change, may become about 10 years, with a consequent increase in situations of potential criticality or insufficiency of planned infrastructure.

This trend was also highlighted by the present study using EURO-CORDEX models. After choosing a set of reference rainfall heights H (100 mm, 150 mm, 200 mm, 250 mm, and 300 mm) with fixed durations D between 1 and 5 days, the corresponding RPs have been retrieved from the reference period (1991) and future period (2021–2051–2081). Then, as shown in Figure 20, the RPs were plotted against the rainfall duration for each period, showing a progressive reduction in RP moving forward in the future. This reduction has been quantified with respect to the historical period (Figure 17), showing an RP reduction in 2081 of about 50%. As shown in Figure 14, a reduction of between 40 and 60% of the return period is expected, approaching 2100. By analogy, this is a confirmation of what was observed with the anomalies, where the most significant reductions will be mainly in the medium- and long-term. As can be appreciated, all the rainfall durations exhibit the same behaviour (i.e., RP reduction), which is reported to be more pronounced for longer events (D = 5 days) compared to shorter ones (D = 1 day).

3.3.4. a₁ and n Coefficient Variation

Up to this point, the investigation was concentrated on the quantification of the anomaly increase and of the RP reduction. Undoubtedly, the variables, parameters, and the coefficient involved are many, but a simplification can be adopted by evaluating the trend analysis solely for the two main parameters of the IDF curves: a₁ and n. The general mathematical expression of IDF curves can be simplified as reported in Equation (16), reducing their complexity in the study to only two parameters. For a_1RP and n parameters, it is possible to retrieve the future anomaly, highlighting the possible variations. In this way, the analysis simplifies, since the dependency for duration D is dropped.

$$H=a_1{w}_{RP}{D}^n\to simplify\to H=a_{1RP}{D}^n$$

(16)

The analysis of future anomalies has been conducted for both the a_1RP and n coefficients, but when applying the statistical test on the mean variation, the statistically significant trends have been found only for the a_1RP. The n coefficient was reported to remain quite stable with respect to climate forcing, highlighting the fact that modifications in the phenomena scale (i.e., changes in orographically driven rainfall mechanisms) are not expected in the future. The exponent in rainfall probability curves represents a parameter that indicates the sensitivity of maximum precipitation (or rainfall intensity) to its duration [1]. It explains how the amount of rain (or its intensity) changes as the duration of the rainfall event changes. A higher value of n indicates greater variability in precipitation as the duration changes, while a lower value suggests greater uniformity. Conversely, a_1RP is reported to increase more sharply in the future with higher RP (Figure 21). The variation in the parameter with respect to the reference period (1991) is always positive and higher in the long-term (2081). The dispersion also increases, showing a +30–40% increase for RP = 200 years in the 2081 period. The figure considers the a_1RP for the entire Lombardy region, but similar behaviour has been highlighted for the other three sectors (not reported). According to the literature [1,14,19], the a_1RP parameter primarily depends on local rainfall climatology, where regions with higher extreme rainfall intensities will have larger a_1RP values. Moreover, since it embeds the RP statistic, it reflects the scale (magnitude) of extreme rainfall at that location.

3.3.5. Sub-Daily Precipitations

The climatic evaluations carried out in this study are to be considered valid for rainfall lasting more than or equal to 1 day. The data available for durations of less than one day require the use of climate models that explicitly resolve the convective mechanism linked to the generation of thunderstorms (Convective Permitting Climate Model, CPCM), which, according to recent literature analysis [23,35,81], however, are not too reliable, as they do not accurately reproduce the statistical distribution of such precipitation. They represent an active frontier of rather recent research [23], so they have not been considered by the presented analysis.

Taking into account the discontinuities between the reference ARPA Lombardia daily and sub-daily IDF curves (see Appendix D), it was decided to propose an extrapolation of the IDF curves’ values using the trend of the climatic anomaly expected for the future period [1,80,82] and presented in Figure 22. By applying the extrapolation functions described on the precipitation height anomaly previously assessed, the future variation in IDF curves, also for sub-day durations, has been retrieved. As can be seen in Figure 22, the linear and power-law interpolation functions of the anomalies evaluated for 1 day, 3 days, and 5 days are derived for RPs equal to 2, 20, and 200 years. Adopting linear extrapolation by reducing the duration of the event, the positive anomaly tends to decrease significantly, decreasing in the order of 50% if we consider events lasting 5 days compared to those lasting 1 h. In addition, for a rather short RP (2 years) and short durations (around one hour), the positive anomalies are calculated around +10 mm (both regarding the statistics on the mean and median values of the distributions); for medium RP (20 years) and short durations (1 h), the positive anomalies are evaluated around +20 mm; while for high return periods (200 years) and short durations (1 h), the positive anomalies are assessed around 30 mm.

The linear extrapolation adopted appears rather approximate in the absence of climatic data verifying this trend. Therefore, a power-law extrapolation has been applied instead, showing a significant evolution of the anomaly, especially for short-duration precipitation. The curves exhibit values between 5 and 20 mm for D = 1 h, which are sensibly lower than the anomaly predicted with the linear interpolation (between 12 and 33 mm), especially for higher RP. Moreover, the curves obtained from the mean statistic are higher than the median curves, showing that the difference progressively increases with RP. The results obtained are interesting for the purposes of a “first guess” estimate of the future trend, but are based on the hypothesis that the anomalies evaluated for daily durations are likely to also be maintained for sub-day durations [82]. This is not automatically verified because the ranges of variability are very high, linked to the different nature of the short-lived convective phenomenon compared to the stratiform one that tends to last longer [83].

3.4. IDF Curves’ Influence on the Public Hydraulic Network

In this section, the practical applications of the results of the IDF curve study are presented. According to the results of the analysis, the future trend of the rainfall probability curves substantially foresees a halving of the expected return periods: the current event with a RP of 20 years will increase its frequency by lowering the return period by about 50% or 10 years. Therefore, some simulations relating to two hydraulic interventions planned by the local municipalities will be compared, using reference IDF curves and their future correction obtained from GEV analysis, considering a design RP of 10 years. Specifically, the following case studies are examined: the construction of a stormwater detention tank for the lamination of rainwater and the upgrading of a sewer pipe. Both case studies were conducted in Monza-Brianza province, located in the central part of the Lombardy region (see Figure 3), where the IDF curve analysis was carried out.

3.4.1. Stormwater Detention Tank for Rainwater Control

Stormwater detention tanks are small reservoirs able to temporarily store, in a relatively small volume, the water coming from the sewage network. They are implemented to reduce the water flow peak that could happen during intense thunderstorms, smoothing the outflow discharge curve with respect to the inflow one. Their design considers short precipitation (with a duration of a few hours or less, comparable with the time of concentration the sewage network) and a rather low RP (of about 10 years, RP_10y) [1]. Critical rainfall height or D < 1 h was evaluated through the “Bell” formulation in Equation (A16), extrapolating H from IDF curves with D = 1 h.

Considering climate change, the future RP_10y will have the same frequency as the current RP_20y; rainfall intensity will increase while RP will reduce by 50%. Figure 23 reports the effect on the design of two stormwater detention tanks with a volume of 2000 m³ and 800 m³. In the current situation, using the reference IDF curves with RP_10yr, the designed volumes are able to contain the predicted inflow volume (blue line), coming from the upstream sewage system: 2000 m³ > 1920 m³ (for BR-03) and 800 m³ > 780 m³ (for BR-13). However, applying the future IDF curves with RP = 10 years (i.e., current IDF curves with RP_20yr, orange line), the stormwater detention tanks are no longer verified, yielding 2000 m³ < 2280 m³ (for BR-03) and 800 m³ < 890 m³ (for BR-13). This example shows how hydraulic infrastructure verified by old IDF curves will probably incur issues or failures in the future, due to rainfall intensification.

3.4.2. Upgrading of a Sewer Pipe

Another application has analysed the behaviour of a long sewer pipe, which was primarily designed to satisfy a short-duration rainfall with an RP of 10 years. As can be noticed from Figure 24, applying the RP 10-year rainfall, the pipe works correctly, not showing any issues related to uncontrolled outflow and maintaining the piezometric level at least 1 m below the terrain surface. The pipe does not work under pressure mode, so the tube is able to discharge the inflow precipitation without any problem [14]. Conversely, applying a rainfall of RP = 20 years (i.e., the future RP_10yr), the same pipe exhibits some critical issues. During the design event, the pipe will be completely under pressure, which means a sharp reduction in the maximum discharge due to the abrupt reduction in the wet perimeter within the tube [14]. Moreover, the piezometric line is now higher and very close to the superficial terrain (<30 cm), causing potential overflowing and sudden floods across the most depressed areas.

Even though the intensity variation in the design precipitation predicted using reference or future IDF curves might seem small (+20%), the RP changes are more evident (−50%). Therefore, the design of hydraulic infrastructure, especially if deputed to rainfall control, means taking into account that critical events will probably increase their frequency in the future. At first glance, increasing the size of hydraulic structures could be a primary solution, but it might not be economically feasible, especially for old structures and pipes across cities. Therefore, a more extensive retrofitting and sewage network reorganisation should be advisable in order to increase the strength and resilience of these infrastructures against climate change side effects.

4. Discussion

In this section, the key points of the methodology proposed to study the influence of climate change on IDF curves are discussed. The chapter is subdivided into four sub-sections where the Clausius–Clapeyron correction, the GEV reconstruction from the EURO-CORDEX ensemble, the effects of climate change on hydraulic infrastructures design and the possible future developments of this study are discussed.

4.1. IDF Curves and Clausius–Clapeyron Correction

In the first part of this paper, the Clausius–Clapeyron theory has been presented. The existing relation between the temperature and rainfall rates derives from the assumption that as the temperature increases, the atmosphere increases its capability to store water vapour [43,44,66]. An additional amount of vapour means more fuel for precipitation occurrence. This behaviour has been detected by several authors around the world and was also confirmed across the Alpine mountain range [23,42,43,44] (

Table 10. Reference studies across Europe where the CC relation has been studied, from [66].

Localization	T Threshold [°C]	CC Scaling % °C−1
Netherlands	12	7–14
West Europe	10	7–14
Germany	10	≥7
Austria	12	≥7
Romania	10	≈14
UK	10–15	≥7
Italy	10–15	≥7

). In this light, this study conducted across the Lombardy region (located in the Southern Alps) has shown how the intensity of precipitation may scale with the temperature, following CC (7% °C⁻¹) and 2CC rates (14% °C⁻¹), in accordance with the literature studies conducted and reported in Table 5. Thanks to the robustness of this atmospheric property, following the work presented in [41], a possible correction of IDF curves based on the Clausius–Clapeyron relation has been evaluated. Taking into account Equation (2), the new rainfall intensity I or height H could be easily retrieved by rescaling the currently available IDF curves and simply considering two pieces of information: the R_sc scaling coefficient (which has been demonstrated to lie between 7 and 14% °C⁻¹) and the possible temperature increments due to climate change. In Table 3, a possible combination of the two parameters has been described, showing how the correction is perturbed: for small R_sc and ΔT_cc, the new rainfall intensity is very close to the previous one with variation < 10%, and while increasing the parameters (CC = 14% °C⁻¹) and ΔT_cc = +4 °C, the intensity increases up to 60%.

The method proposed is undoubtedly straightforward to apply to adjust currently adopted IDF curves, and it is more physically based with respect to the empirical methods that simply increase the intensity or height by a fixed percentage. However, the method described is not the most accurate one that considers the Clausius–Clapeyron relationship. According to [23], it could be improved by also considering the dependence of rainfall duration D and RP with respect to the evaluation of the new intensity. These dependences are included in Equation (2) as corrective factors, but they need to be estimated using the data available, which may depend on the site-specific characteristics, such as rainfall types that occur at a particular location. Moreover, even though the CC relationship is robust, the ranges of R_sc ratio and temperature T are quite wide, and may experience greater spatial variability, especially across complex orography environments [66,84] (Figure 5 and Figure 6). Regional Climate Model (RCM) projections show that intense daily precipitation (corresponding to the 99.9th percentile of distributions) will increase at rates of between 6% and 15%, compared to past observations [29,30]. According to [23], the value of R_sc could also be a direct function of the duration of the event. In fact, by increasing the duration, the average tends to decrease up to values of 5–7% °C⁻¹, while for heavy and extreme rains of short and very short duration, R_sc can increase up to 15% °C⁻¹. It can also vary with other parameters, but the relationships are still partly unknown or rather complex to extrapolate [23].

According to IPCC [25], the Alps have already experienced a more significant rise in temperature due to their location near the Mediterranean hot spot [30]. Across the Alps, several types of precipitation may occur (convective and stratiform) depending on the season, which are locally perturbed by orographic uplift and moist southerly flows [10,83,84], that significantly increase the dispersion of the R_sc coefficient [66,85,86]. Therefore, a transition between CC and 2CC is expected for more extreme events. According to [66,85], the CC value is obtained for stratiform precipitation, while for convective precipitation, it is possible to reach 2CC values. When the precipitation is characterised by a mixed type or with characteristics tending to be convective, an intermediate situation may occur. It should be noted that the linear growth behaviour is, however, limited beyond a certain temperature threshold (~25 °C) [66,85,86]. Beyond this value, the loss of the saturation capacity of the atmosphere (the amount of vapour required to saturate a volume of air increases as the temperature increases) acts as a limiting factor that could inhibit the mechanisms of initiation of convective precipitation (Figure 25).

As a matter of fact, the methodology that implements the CC correction represents a wise attempt to approximately infer the influence of climate change on IDF curves, taking into account the strong climatic drivers such as the temperature increments. In our opinion, this correction is suitable for gaining an idea of the effects of the climate change process without digging into deep climatological studies. The formula is valuable for practical and expeditious studies (such ones those deputed for urban planning), bearing in mind that its parameterisation of R_sc should be carried out with care, considering site-specific rainfall characteristics. However, for a better depiction of the climate change influence of IDF curves following a more rigorous methodology based on climate models’ outputs, the extreme value analysis is preferable.

4.2. IDF Curves and Climate-Change GEV Analysis

The insights into the temperature-intensity (T-I) relationship that come from the Clausius–Clapeyron theory are implicitly embedded in the climate change models. The former aim to find projections of the atmospheric state in the future under a specific radiative scenario (RCP 8.5 in this study) that corresponds to a CO₂ concentration forcing generated by human activities [38]. Since climate models make future projections, the errors embedded in the output data could be significant, especially moving forward in the future up to the 2100 horizon, where sometimes, divergent behaviour may be detected [30]. In order to cope with these uncertainties, the EURO-CORDEX consortium has proposed an ensemble of climate models with the aim of studying, in a more statistical and probabilistic way, the effects of climate change [31,38]. In this work, the focus concentrated on precipitation variables. The 15 climate models’ rainfall series (from 1976 up to 2100) have been studied across the Lombardy region, applying the extreme value analysis (GEV) to detect possible variation in the future trend of IDF curves.

From a methodological viewpoint, rebuilding IDF curves using a climatic model has faced some issues presented here. Firstly, the reference IDF curves, currently adopted in the Lombardy area and provided by ARPA Lombardia environmental agency, are distinguished into two different samples (1–24 h short-duration and 1–5 day long-duration rainfall IDF curves). The reference IDF curves exhibit important discontinuities at D = 24 h that, even if they are not physical, can make it difficult to compare them with climatic model elaboration [19,49,87]. This “methodological” difference can be appreciated by comparing the differences between the IDF curves’ statistics at 24 h and 1 day. As was presented in the results, this difference is negligible at the wettest location of the Lombardy region (i.e., the western part), while it is in the order of 40–50% in the dryest locations (i.e., the eastern part). This discrepancy should be taken into account when IFD curves are applied for hydraulic projects, because it does not have a physical meaning and is just related to the sampling method of the rain gauge data. Our analysis has pointed out a possible correlation with the 2D spatial distribution of the a₁ parameter of the curves (see Appendix D), which is representative of the “energy” of precipitation [19], namely looking at Figure 4, which is the corrected IDF value at D = 24 h or D = 1 day. Probably the most precise and rigorous evaluation is the one coming from the “moving widow” sample (i.e., the 1–24 h curves), but currently used climatic models provide output data on a daily basis, which allows the application of a “fixed window” sampling method. For this reason, only the long-duration 1–5 days rainfall IDF curves could be, in principle, reconstructed using the EURO-CORDEX models.

Secondly, the reference IDF curves were evaluated using recorded rain gauge data on a historical period between 1951 and 2001 [19,49], while the reference period for the EURO-CORDEX model is generally between 1976 and 2005 [38]. Therefore, a complete overlapping of the two series is partially missed, bearing in mind that, in both cases, the datasets were probably already affected by climate change due to the steep rising CO₂ concentration experienced during that period [25]. IDF curves require long and continuous rain gauge time series. The latter is not always guaranteed due to instrumentation failure, poor maintenance, moving location, etc. [10]. Therefore, the number of stations available for the effective IDF curves calculus could be significantly lower than the entire network, giving a poor representation of IDF curves statistics in those areas where stations are less dense than normally occur across mountain ranges [19]. Conversely, even though the climate pixel is not punctual, they are uniformly distributed in a grid, covering the entire domain with a constant density. As a result, the information contained in the climate model rainfall series could sometimes be higher than the one considered to build reference IDF curves.

Thirdly, the reference IDF curves in the Lombardy region have been evaluated using the GEV methodology, but other strategies have been implemented in other parts of the Italian territory (such as TCEV, the Two-Component Extreme Value distribution [88]), sometimes preferring large area regionalisation of the IDF curve parameters [49,64,82] against the single rain-gauge statistics. So, the differences between the spatial resolution of the climatic model (expressed in terms of the cell dimension of the calculation grid domain) with respect to the spatial aggregation/regionalisation of the coefficients of the reference IDF curve analysis may represent another source of uncertainty in the method. In this regard, the spatial and temporal resolution of each climate model’s output data represents a critical aspect. In fact, implementing GEV statistics on rain gauges with respect to climate change model outputs should consider that the rainfall data are provided on a ‘single-cell’ basis at a spatial resolution in the order of ~11–12 km. This means that the precipitation is considered uniform in space within an area of ~100 km², which is not always a correct assumption from a physical viewpoint [19,32] since rainfall amounts may change abruptly across the landscape, especially across mountain ranges due to orographic effects [4]. Thunderstorms (i.e., the phenomena that bring the highest rainfall ratios) have a circular-elliptical shape where the rainfall intensity is higher in the centre and lower at the border, so uniform precipitation could not be representative, since a smoothing of the highest rainfall rates is applied by the model [19,89]. The loss in spatial resolution is crucial to take into account when extreme precipitation is studied, especially for short-duration phenomena [23]. Another difference is the temporal resolution, which for climate models is generally fixed at 1 day. Sub-hourly data are generally not investigated since, in reproducing short-rainfall statistics, they are not retained with sufficient accuracy [23,90]. Nonetheless, the EURO-CORDEX dataset contains data at a maximum temporal aggregation of three hours, but, due to the coarser spatial scale, short-duration rainfall events (i.e., moist convection) are not resolved explicitly [57]. According to [33], RCMs and GCMs have shown some issues with their sub-grid scale parameterisations of convective processes, which affect their ability to reproduce, for example, the diurnal cycle of rainfall intensity, the peak storm intensities, and extreme hourly intensities. It is therefore questionable to what extent such RCMs are capable of describing short-duration extremes in the present as well as in the future climate. Within the EURO-CORDEX ensemble, only a subset of model outputs is available on an hourly basis [33]: the sub-daily extreme statistics are limited to a small number of models, increasing the possible uncertainties in their evaluation. In addition, temporal and spatial downscaled models may be available locally over a particular region, not completely covering the European domain [91]. Sub-daily data could be retrieved from Convection-Permitting climate Models (CPMs) [35,81,92], high-resolution regional climate models that explicitly represent deep moist convection, a crucial atmospheric process required for understanding and predicting weather extremes like intense rainfall. Unlike traditional climate models that parameterise convection, CPMs resolve it directly on their grid, leading to more accurate simulations of local-scale phenomena. CPMs are better at capturing the complexities of localised weather events, such as heavy rainfall and extreme temperatures, which are often missed or misrepresented by models with coarser resolutions. Nevertheless, they also come with significant challenges. These include high computational demands, the need for high-resolution observations, and uncertainties in representing certain physical processes, particularly at the sub-kilometre scale [81,93,94]. CPMs are experimental, since the moist convection analysis is difficult to reproduce at a large scale and considering a long-term horizon (such as in the case of climate models) [64,82]. Moreover, the overall performance in reproducing convective precipitation with realistic and physically consistent rainfall rates is not always accurate, providing a statistical distribution of sub-daily extremes that is sometimes too smoothed and that is significantly different from real data [30,34,95].

Bearing in mind all these issues, in our analysis, only the 15 EURO-CORDEX models have been considered, excluding the common reanalysis downscaling simulations and hourly basis data, in order to not introduce some additional uncertainty propagation through the IDF curve methodology. Extreme value analysis was carried out, adopting the following working hypotheses. Looking at the differences between climate and reference datasets, the analysis did not concentrate on the direct recalculation of the IDF curves. EURO-CORDEX data provide rainfall series from 1976 up to 2100, where 1976–2005 represents the reference period where the climate model is generally calibrated and initialised. Recalling that the historical period (centred in 1991) that partially overlaps with the reference IDF curves (evaluated from 1951 and 2001), the past climatology agreement of the EURO-CORDEX ensemble was verified by comparing the IDF curve parameters (a₁ and n) computed for the historical period (1976–2005) with the reference IDF curve parameters. The error analysis has confirmed that the reference period was assessed differently by each climate model, but, on average, the BIAS% and RMSE% in the rainfall statistics are rather low, around 10–15% in the preliminary test case of Northern Lombardy, while they are around 20–30% (for a₁) and 10–20% for n, considering the entire ensemble over the Lombardy region. These errors are not uniformly distributed across the investigated area (Figure 15), but they were reported more frequently across the PR sector, the one that exhibits the highest precipitation amounts and the steepest orographic rainfall gradients.

After validation of the past climatic time series, IDF curve analysis was carried out considering climate change influence by applying (adding) the mean climate anomalies evaluated in the comparison between the future projection IDF curve statistics (from 2006 to 2100) against the ones reconstructed for the reference period (from 1976 to 2005) for the entire EURO-CORDEX ensemble. Moreover, the future period was subdivided into three sub-periods corresponding to the short, medium, and long term. The analysis of the anomalies has been distinguished as a function of the duration D, the return period RP, and the future horizon (short-term centred in 2021, medium-term centred in 2051, and long-term centred in 2081), and produced the following main outcomes.

The climate anomaly will increase progressively moving forward in the future by about +20–30 mm if all durations and RPs are averaged. This data can be interpreted as a long-term linear trend of +0.2–0.3 mm yr^-1 that embeds a certain grade of variability depending on the Lombardy area investigated. This trend was retrieved as more stable and less variable across the pre-alpine areas, which are the wettest areas of the region, while it is more dispersed across the Po floodplain and the internal AV sector. In the drier areas, a clear tendency is difficult to establish since extreme events are sometimes very rare and exceptional if compared to the wettest areas. However, climate change is likely to impact the climatology of the overall Lombardy region, increasing the IDF curves with positive anomalies, as was reported in [23,30,40,64,82].

The positive anomalies calculated will cause upper shifting of an IDF curve, which translates to a reduction in rainfall RP. In this study, the RP contraction was assessed to be in the order of −40–60%, confirming several literature studies that have conducted similar elaborations across European countries [23,56,67,68]. The half-reduction in RP is significant and highlights how climate change impacts the IDF curves. Temperature increasing scales linearly with the rainfall intensity variation (following Clausius-Clapeyron relation), while the logarithm of RP tends to reduce linearly. That means that a linear increase in intensity (i.e. a positive climate anomaly) corresponds to an exponential decrease in RP. This outcome is interesting, especially for hydraulic structure projects and retrofitting that, under a climate change scenario, may be unverified due to RP shifting [64,82].

Another point touched on in the analysis is related to the sub-daily anomaly estimation. Since the climate model ensemble does not provide hourly data, the anomaly cannot be directly evaluated [82]. However, having calculated the daily anomaly (1 to 5 days), a duration–anomaly function for a specified RP was retrieved. The data were interpolated using linear and power-law trend curves and then extrapolated to sub-daily data, giving a simplified estimation of the possible anomalies. Among the two curves, the linear approximation appears more ‘crude’ with respect to the power-law, admitting more anomalies (double) for short-duration events. This technique has been proposed in order to cope with the climate data limitations, and, in our opinion, it represents a straightforward way to at least take into account the climate change influence for sub-daily IDF curves. In this regard, sub-daily data future projections are crucial, since they are frequently applied in the design of sewage networks, which are characterised by a correlation time in the order of a few hours [14]. However, the main drawback of this extrapolation method consists of the fact that IDF curves for sub-daily duration are steeper, since the representative phenomena, rainfall phenomena (i.e., thunderstorms), have slightly different characteristics with respect to the longer ones (i.e., stratiform precipitation). This transition is continuous in nature and cannot be clustered with a threshold on rainfall duration [1,2]. Therefore, this anomaly trend should be treated and interpreted carefully.

4.3. Adaptation to Climate Change in Hydraulic Infrastructures

Applying the extreme value statistics to the climate model ensemble has allowed us to quantify the uncertainties behind the IDF curve reconstruction. All the evaluations presented in this work have been provided in terms of mean, median, and standard deviation in order to highlight their derivation from the EURO-CORDEX ensemble (Figure 26). According to [24,25,86], an increase in mean temperature is likely to occur in the future, while for precipitation, even if the mean will remain the same, an increase in variance (i.e., more extreme rainfall events) is expected. Our study has addressed this statement across the Lombardy region under the RCP 8.5 scenario, showing the negligible variation in mean precipitation compensated for by an increase in extremes by the end of the current century. These results have been validated statistically through the t-test and Welch test, studying the mean anomalies in the future calculated from the entire EURO-CORDEX ensemble. Moreover, applying the Pearson test to P_max-y from 2006 to 2100 projections, a statistically significant tendency was detected in the datasets. So, increases in precipitation variance (and in mean rainfall intensities) seem to be the most probable effect of climate change in the future [29,30,34,95].

The climate model yearly maximum rainfall series increase their dispersion with the return period RP, with the duration D, and when moving forward into the future with rather variable but clear positive trends. Therefore, ongoing climate change will significantly impact the IDF curve’s statistics with direct consequences on the management of hydraulic infrastructures and the sewage network [23,25,40]. Therefore, the frequency of intense precipitation outside the design RP range (i.e., higher) may increase in the future, raising infrastructure issues and maintenance/replacement costs. In this work, two experiences of a stormwater detention tank and a sewage pipe have been reported in order to practically see the effects of IDF curves variation induced by climate change. As was described, the two infrastructures need to be redesigned, increasing their dimensions (i.e., the storage volume for the stormwater detention tank and the size of the pipe) in order to be able to contain or transport a large amount of water coming from the sewage network. Recently, these climate change side effects have started to be included within the guidelines of local regulation [96,97], where the urgency of considering climate change adaptation is highlighted [98,99]. In this regard, recalling the validity of the GEV procedure is essential for future projections of higher RPs. Generally speaking, to carry out an accurate GEV for high RPs, longer time series are required. However, in climatology, 30 years is taken as a reference period for establishing the climate variation, and this sample length may limit the extrapolation of GEV statistics for higher RPs, degrading their accuracy. Nevertheless, these statistics, even though they are sometimes approximated, are a crucial indication for future climate assessment of the infrastructure [100]. In fact, RPs ≤ 100 years are applied in the larger part of civil hydraulic infrastructure (bridges, sewage networks, etc.); RPs > 100 years are taken into account for flood risk analysis (European and Italian regulations considered a RP of 200 years for floods), while RPs equal to 500 or 1000 years are adopted for large dam projects [14].

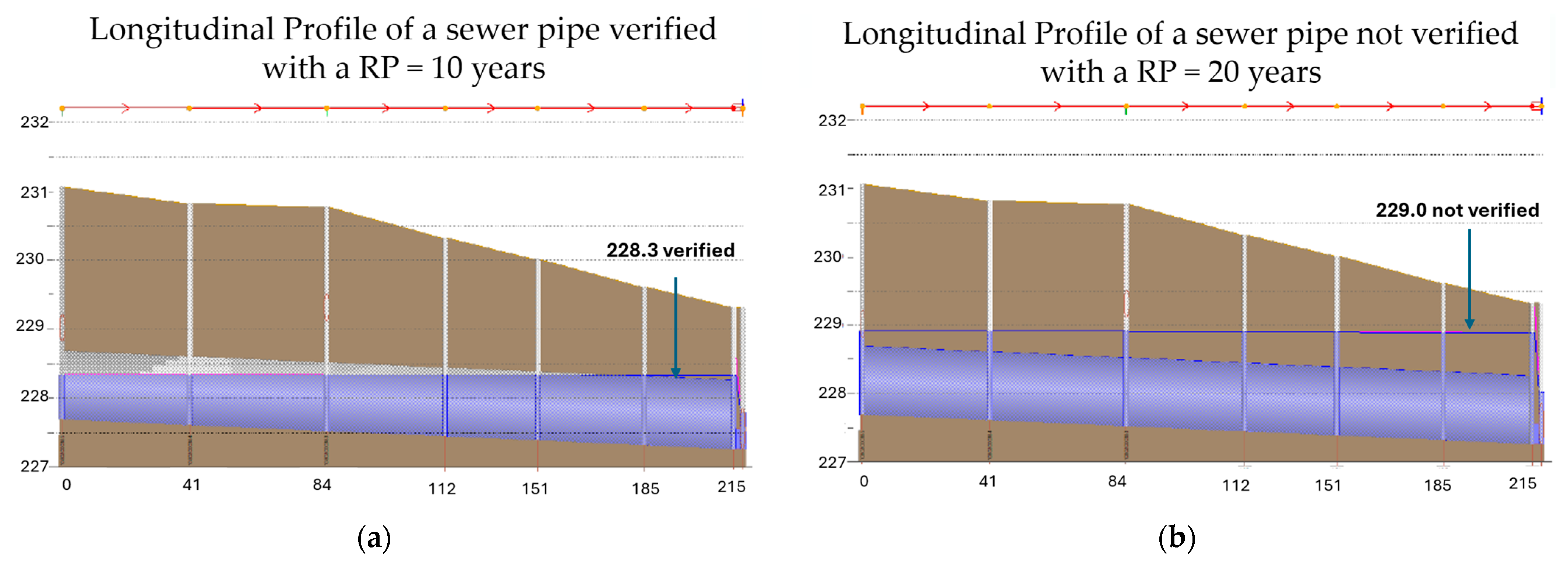
According to [23,24,25,101], climate change effects should be taken into account not only for new projects (which is easier), but adaptation and mitigation measures should be applied to the existing sewage network in order to prevent potentially severe damages. The RP exponential reduction against rising temperature should be considered, because a critical rainfall with RP = 100 years will become more likely with RP = 50 years, reducing its value by half and doubling its frequency. Among the infrastructure analysed, the sewage pipe is the most sensitive, since it is located underground and retrofitting is sometimes difficult because it implies a complete diameter resizing of the pipe, excavation, etc. Another possibility could be to double the number of pipes to improve the rainfall drainage locally, taking into account the enlarged volumes predicted by modified IDF curves. All of these interventions will not be costless, so it is advisable to evaluate a cost–benefit analysis, highlighting the most critical situations within the analysed network [102]. Moreover, since the IDF curves exhibit a smoother but not negligible variability across the territory, the anomaly correction should be performed taking into account the site-specific statistics, or at least considering aggregated sectors, as was presented in this study.

4.4. Future Developments

The IDF curve reconstruction methodology presented in this work follows an articulated framework that mainly depends on both the quality of the climatic model data output and on the integrity of the reference IDF curve dataset [31]. Future developments will be mainly related to the improvement in climate change reconstruction to allow us to study short-duration rainfall events at a refined spatial scale. As mentioned throughout the text, the new CPMs (Convective Permitting Models) will help in this way, but up to now, only a few examples of these models have been validated and are not yet included within a climate ensemble [23,69,89] like EURO-CORDEX. On the other hand, a future homogeneization of the reference IDF curves would be expected, slightly enlarging the historical data series (comprising at least the last 20–25 years of data) and hopefully resolving (and closing) the gap between the 1–24 h and 1–5 days statistics. This gap might perturb the infrastructure design, especially across drier areas of the Lombardy region, where the errors detected are larger (Figure 4). According to hydraulic engineers working in this sector, a possible suggestion for solving this issue is to consider, among the durations of 1 day or 24 h, the worst-case scenario (i.e., the highest intensity, for a selected RP).

Nowadays, automated rain gauge stations are able to work with higher temporal resolution up to 10–5 min, so they could potentially resolve the issues encountered throughout the text regarding the IDF extrapolation for sub-daily and sub-hourly durations [14]. In this regard, we retain that the accuracy of the GEV methodology is lower than for daily statistics, so that the Clausius–Clapeyron correction could be adopted in combination and privileging the most conservative approach among the two (i.e., the one who admits highest rainfall intensity I or height H for a certain RP and D).

However, the results obtained in the analysis are in accordance with other studies that have applied the extreme value methodology to climate datasets [23,56,67,68], so that future analysis will improve the robustness of the presented framework, taking into account possible data preprocessing (such as a tailor-made statistical downscaling of the rainfall data both in space and time) with further investigation across the three climatic areas evaluated for the Lombardy region. In principle, the methodology presented is rather general and could be applied across other areas of the Alps to see if the climatic trends of IDF curves hold similarly or may change in the future. Another extension of the methodology could be the analysis of other RCP scenarios, considering not only the 8.5 (the most critical) but also at least the RCP 4.5, according to [34]. Currently, IPCC [25] has revised the climate scenarios in the sixth report, which have been distinguished taking into account other parameters and, therefore, they are slightly different from the scenarios adopted in this study, which refers to the timeline of the Fifth Assessment Report (AR5) of the IPCC. Unfortunately, EURO-CORDEX ensembles are not yet available for addressing regional climate investigation using the Sixth Assessment Report (AR6), but they will surely open new perspectives for more accurate extreme rainfall analysis.

5. Conclusions

In this study, IDF curves under climate change have been recalculated using the EURO-CORDEX ensemble. The analysis has applied the theory of extreme value to evaluate the future rainfall anomalies for a certain RP and D to be applied to the reference IDF curves currently in use. The case study of the Lombardy region was selected for the methodology since its climatology is interesting, showing strong orographic precipitation gradients among the Pre-Alps, Po Floodplain, and internal mountain region.

The study started with the analysis of the Clausius–Clapeyron principle under which IDF curve correction is evaluated empirically using the CC rates and an estimation of ΔT_cc. Even if it is a straightforward correction, the RP and duration D dependencies are not explicitly taken into account, making the method useful for a first-step expeditious analysis. Conversely, GEV techniques represent a robust methodology that could, in principle, be applied to climatic model rainfall series. Considering the EURO-CORDEX ensemble, a positive anomaly of +20–30 mm on average has been found in IDF curves at the 2100 horizon. These results have been further analysed, disentangling the RP and duration influence and showing how the ensemble data dispersion tends to progressively increase with them. RCP 8.5 scenario was considered in this work, depicting a statistically significant positive signal in the anomalies calculated, which translates into a sharp RP reduction of about −50%. The anomalies have been added to reference IDF curves, maintaining the shape of the reference IDF curves, which exhibit a non-physical discontinuity due to different sampling methods of the rain gauge data. This fact, in addition to the incomplete temporal series overlapping and daily based climate model data, has not permitted a direct comparison of the IDF curves computed with climate model data with the reference ones. In addition, an extrapolation of the daily anomaly has been extended to sub-daily durations in order to consider climatic influence on short-term precipitation. In the end, the application of new IDF curves has been applied to two sewage infrastructures, highlighting their non-negligible influence in perturbing the “design rainfall”. The side-effects consist of a significant RP reduction (−50%) in intense precipitation that may hit, with higher frequency, the sewage network infrastructures, causing pluvial floods and extensive damage.

It is important to underline that the studies conducted and reported here have a purely statistical value. While GEV is considered a robust and widely used methodology, climate models can be affected by important uncertainties related to both their architecture and the validation and calibration processes, which can show significant errors depending on the area examined [30,31]. In this context, the Italian peninsula and the Alpine chain are located in correspondence with the “climatic hot spot” of the Mediterranean Sea, which is able to accentuate the possible effects of climate change through feedback processes that are still the subject of research and study [24]. It is precisely for this reason that the use of climate ensembles is promoted to provide an overview of possible future projections, taking into account modelling uncertainties. We therefore believe that the study carried out is valid, above all for implementing intervention planning procedures that consciously take into account future the climatic effects of intense rainfall. The study represents one of the first carried out in the Italian country showing not only empirical (i.e. CC) and physical methodologies (i.e. GEV) for IDF curve correction, but also providing practical evidence of the climate change rainfall intensity increase on the functionality of some critical hydraulic infrastructure.