Neural Hierarchical Interpolation for Standardized Precipitation Index Forecasting
Abstract
1. Introduction
2. Materials and Methods
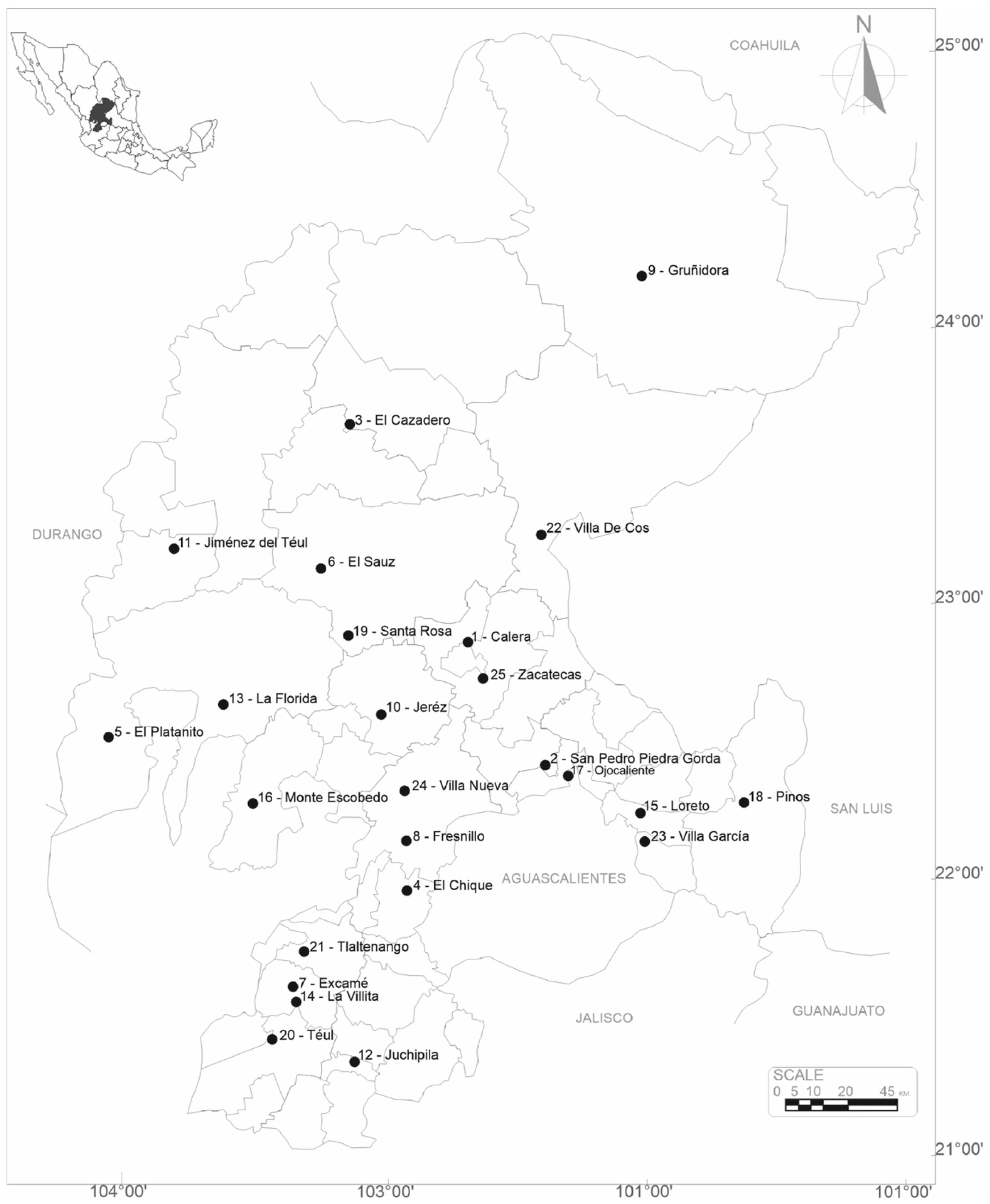
2.1. Study Region and Datasets
2.2. Standardized Precipitation Index
Cluster Analysis
2.3. Neural Time Series Forecasting
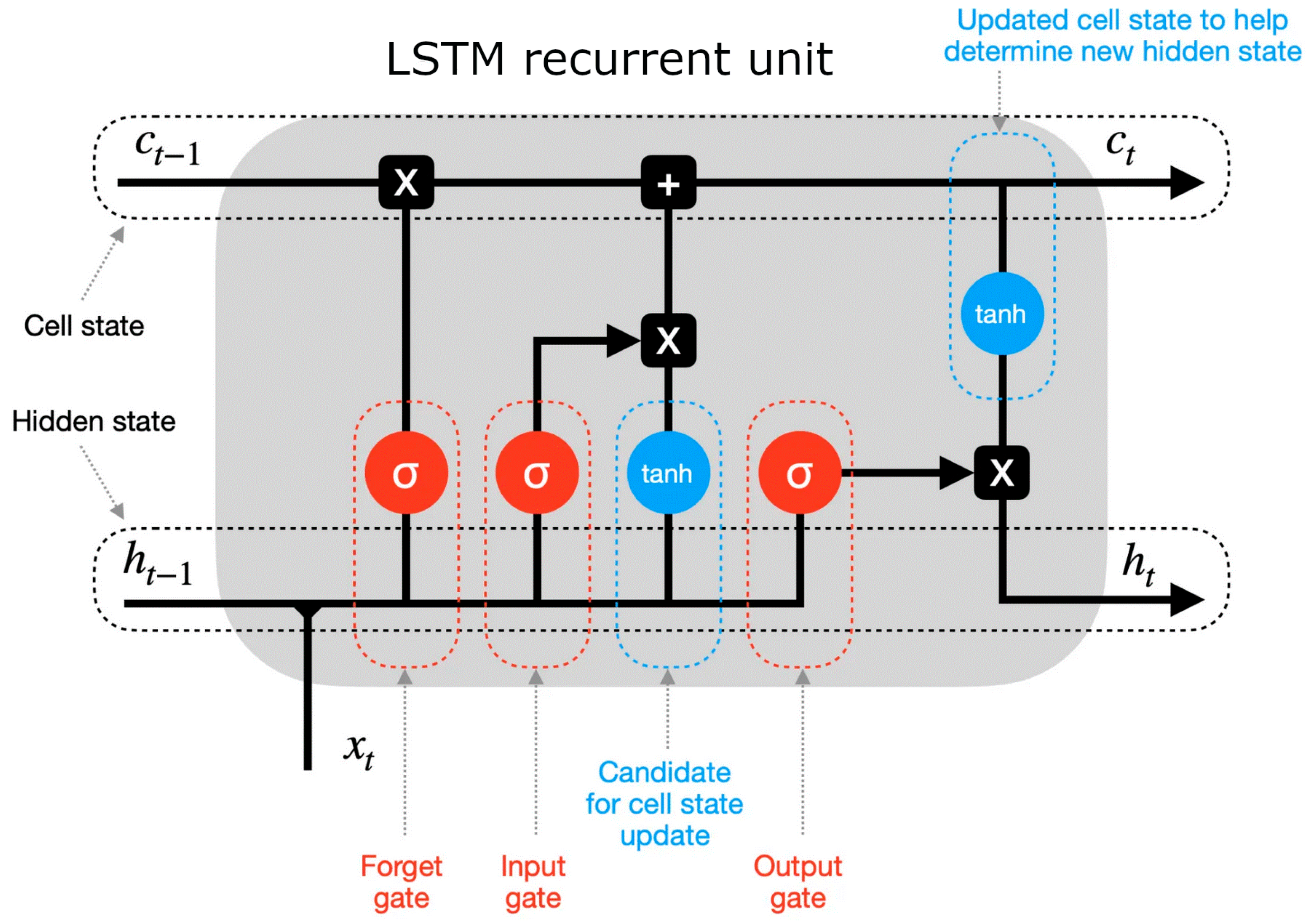
2.3.1. Long Short-Term Memory Networks
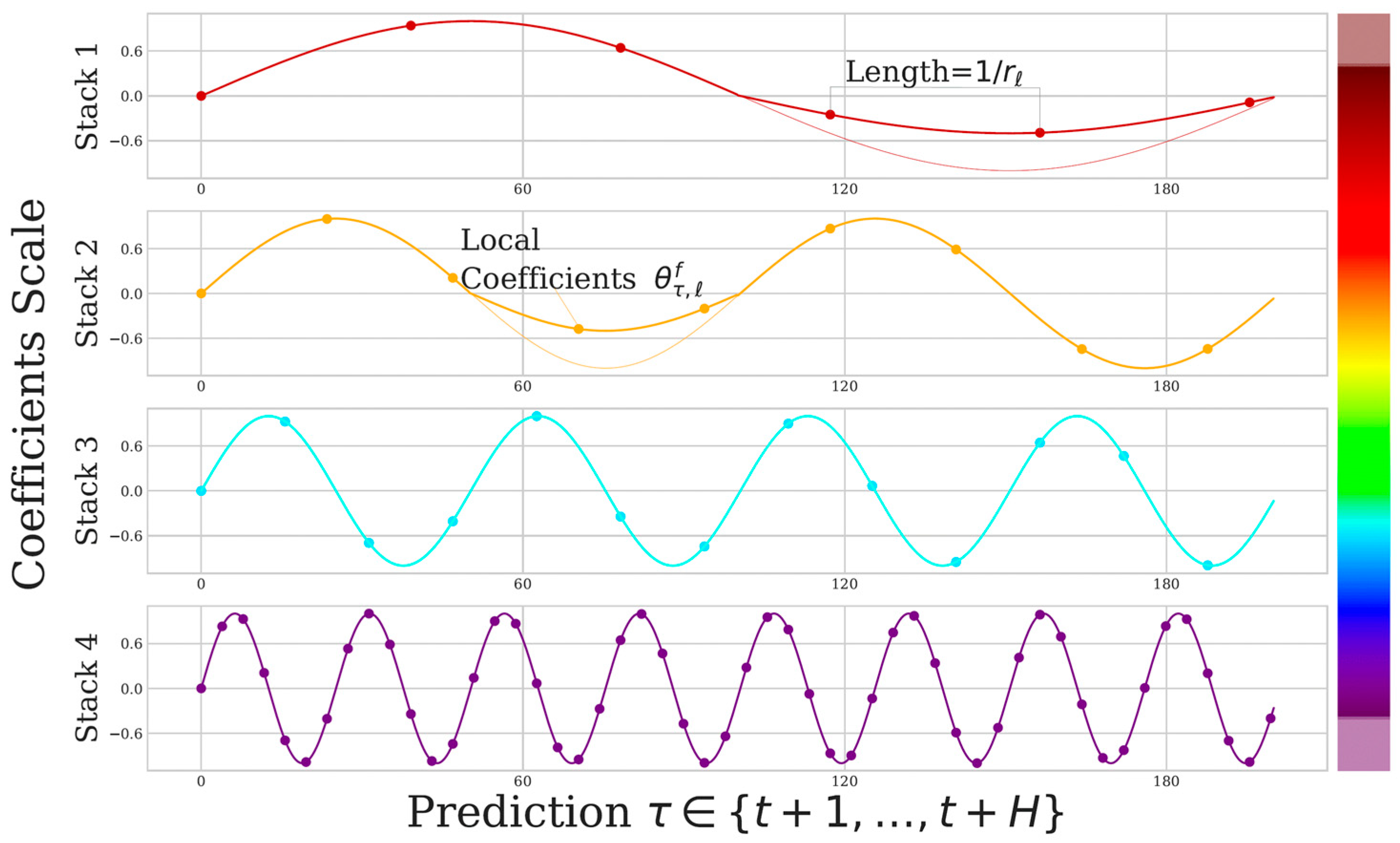
2.3.2. Neural Hierarchical Interpolation for Time Series Forecasting
Multi-Rate Signal Sampling
Nonlinear Regression
Hierarchical Interpolation
2.3.3. Forecasting Performance
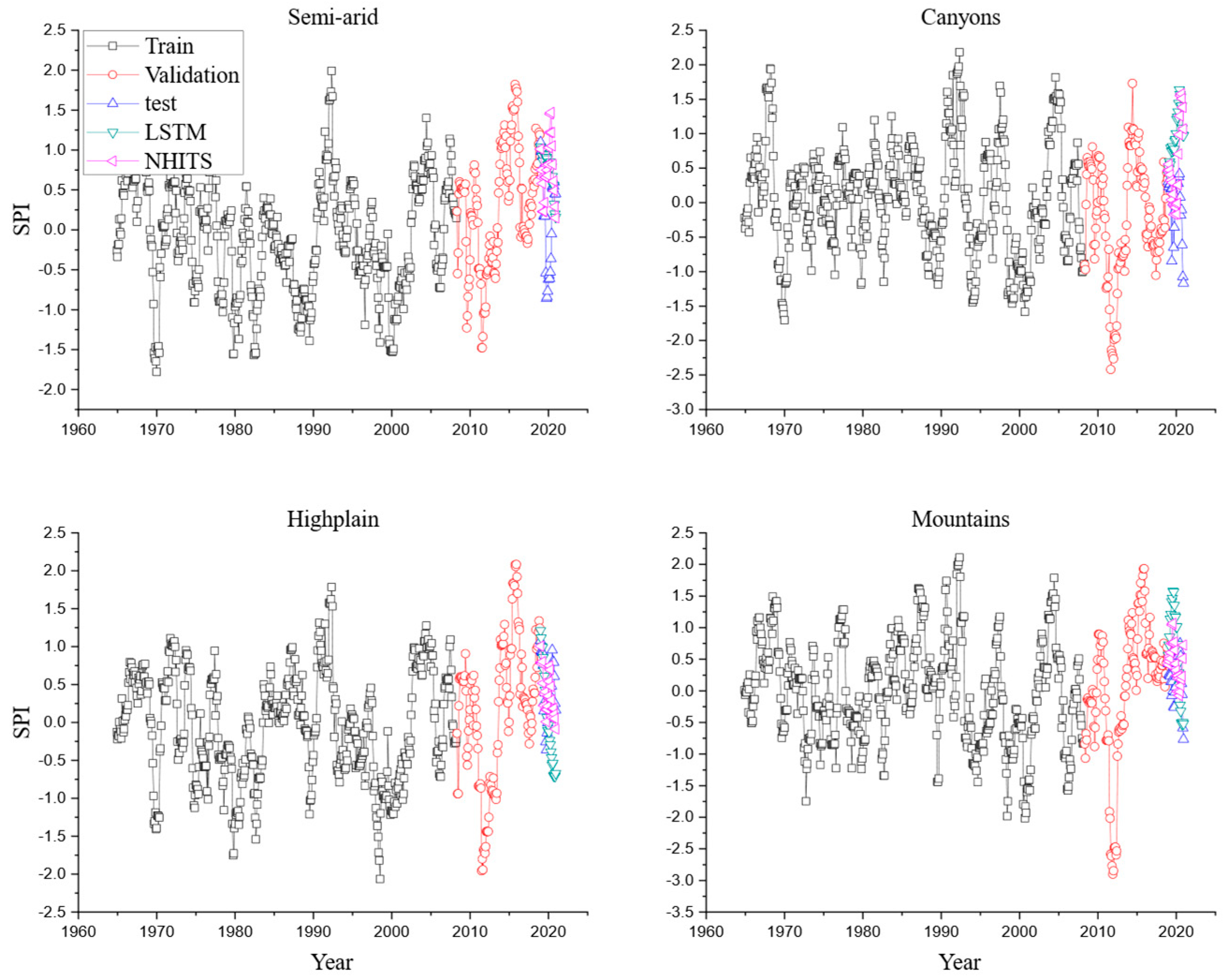
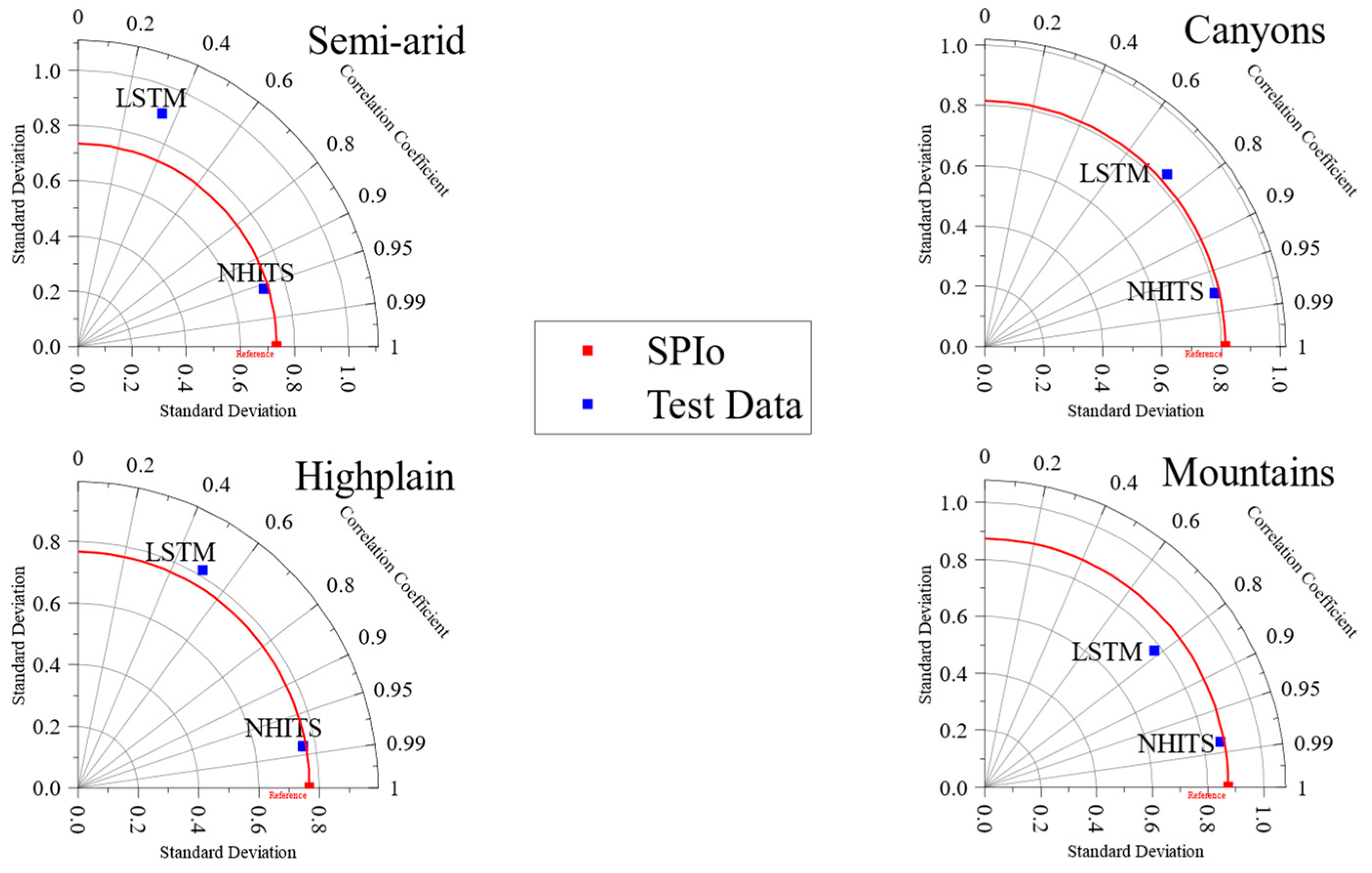
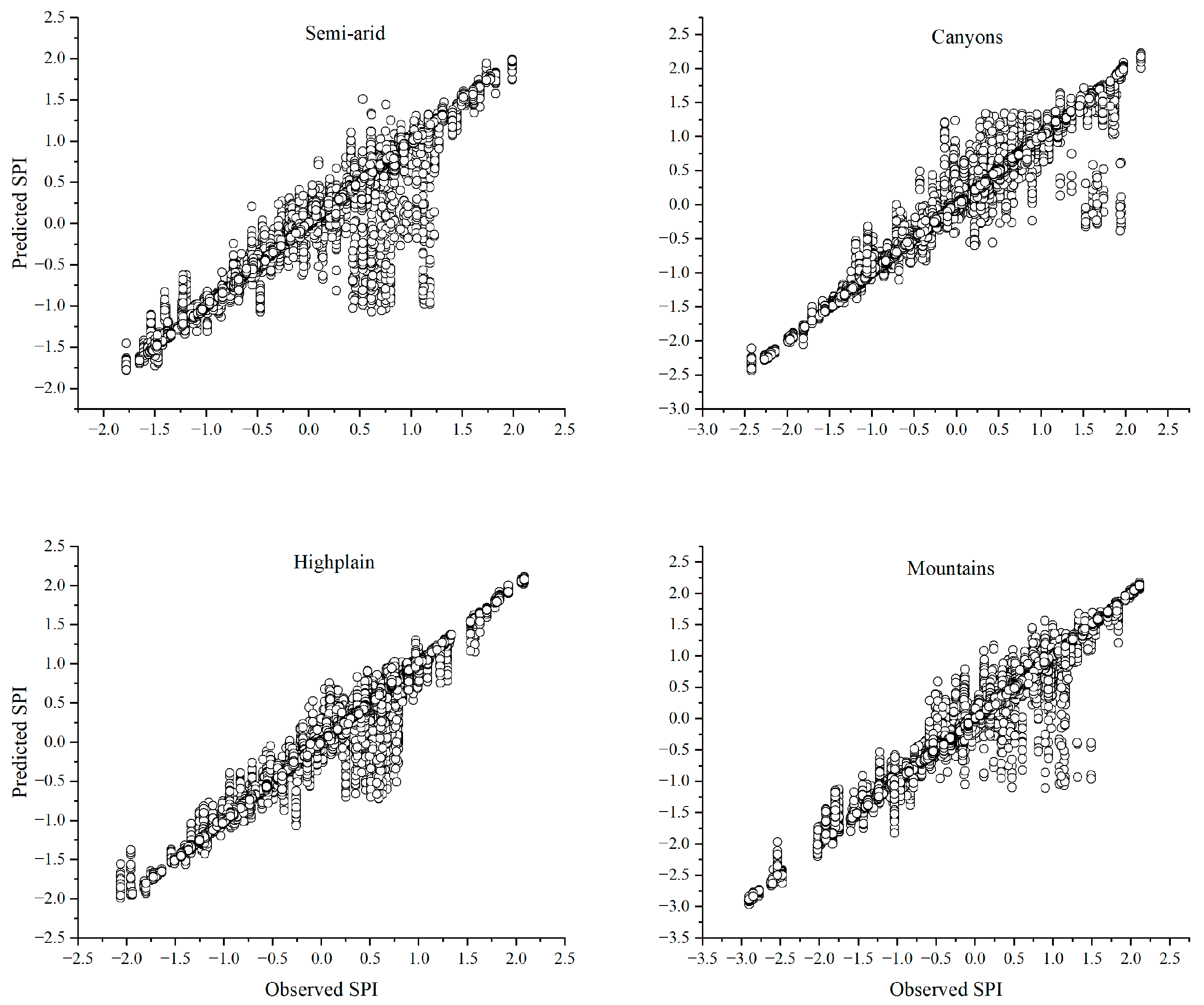
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Liu, Y.; Guo, X.; Wu, H.; Wang, H.; Liu, Y. An Energy Consumption Prediction Method for HVAC Systems Using Energy Storage Based on Time Series Shifting and Deep Learning. Energy Build. 2023, 298, 113508. [Google Scholar] [CrossRef]
- Kaushik, S.; Choudhury, A.; Sheron, P.K.; Dasgupta, N.; Natarajan, S.; Pickett, L.A.; Dutt, V. AI in Healthcare: Time-Series Forecasting Using Statistical, Neural, and Ensemble Architectures. Front. Big Data 2020, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Shuvo, M.A.R.; Zubair, M.; Purnota, A.T.; Hossain, S.; Hossain, M.I. Traffic Forecasting Using Time-Series Analysis. In Proceedings of the 2021 6th International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 20 January 2021; pp. 269–274. [Google Scholar]
- Basher, R. Global Early Warning Systems for Natural Hazards: Systematic and People-Centred. Phil. Trans. R. Soc. A 2006, 364, 2167–2182. [Google Scholar] [CrossRef] [PubMed]
- Field, C.B. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012; ISBN 1-107-02506-0. [Google Scholar]
- Bonaldo, D.; Bellafiore, D.; Ferrarin, C.; Ferretti, R.; Ricchi, A.; Sangelantoni, L.; Vitelletti, M.L. The Summer 2022 Drought: A Taste of Future Climate for the Po Valley (Italy)? Reg. Env. Change 2023, 23, 1. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Poornima, S.; Pushpalatha, M. Drought Prediction Based on SPI and SPEI with Varying Timescales Using LSTM Recurrent Neural Network. Soft Comput. 2019, 23, 8399–8412. [Google Scholar] [CrossRef]
- Chen, L.; Han, B.; Wang, X.; Zhao, J.; Yang, W.; Yang, Z. Machine Learning Methods in Weather and Climate Applications: A Survey. Appl. Sci. 2023, 13, 12019. [Google Scholar] [CrossRef]
- Choubin, B.; Malekian, A.; Golshan, M. Application of Several Data-Driven Techniques to Predict a Standardized Precipitation Index. Atmosfera 2016, 29, 121–128. [Google Scholar] [CrossRef]
- Ali, Z.; Hussain, I.; Faisal, M.; Nazir, H.M.; Hussain, T.; Shad, M.Y.; Mohamd Shoukry, A.; Hussain Gani, S. Forecasting Drought Using Multilayer Perceptron Artificial Neural Network Model. Adv. Meteorol. 2017, 2017, 5681308. [Google Scholar] [CrossRef]
- Ozger, M.; Mishra, A.K.; Singh, V.P. Estimating Palmer Drought Severity Index Using a Wavelet Fuzzy Logic Model Based on Meteorological Variables. Int. J. Climatol. 2011, 31, 2021–2032. [Google Scholar] [CrossRef]
- Masinde, M. Artificial Neural Networks Models for Predicting Effective Drought Index: Factoring Effects of Rainfall Variability. Mitig. Adapt. Strateg. Glob. Change 2014, 19, 1139–1162. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-Term SPI Drought Forecasting in the Awash River Basin in Ethiopia UsingWavelet Neural Network andWavelet Support Vector Regression Models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Deo, R.C.; Sahin, M. Application of the Artificial Neural Network Model for Prediction of Monthly Standardized Precipitationband Evapotranspiration Index Using Hydrometeorological Parameters and Climate Indices in Eastern Australia. Atmos. Res. 2015, 161–162, 65–81. [Google Scholar] [CrossRef]
- Soh, Y.W.; Koo, C.H.; Huang, Y.F.; Fung, K.F. Application of Artificial Intelligence Models for the Prediction of Standardized Precipitation Evapotranspiration Index (SPEI) at Langat River Basin, Malaysia. Comput. Electron. Agric. 2018, 144, 164–173. [Google Scholar] [CrossRef]
- Magallanes-Quintanar, R.; Galván-Tejada, C.E.; Galvan-Tejada, J.I.; Méndez-Gallegos, S.d.J.; Blanco-Macías, F.; Valdez-Cepeda, R.D. Artificial Neural Network Models for Prediction of Standardized Precipitation Index in Central Mexico. Agrociencia 2023, 57, 11–20. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Challu, C.; Olivares, K.G.; Oreshkin, B.N.; Ramirez, F.G.; Canseco, M.M.; Dubrawski, A. Nhits: Neural Hierarchical Interpolation for Time Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2023, 37, 6989–6997. [Google Scholar] [CrossRef]
- Koudahe, K.; Kayode, A.J.; Samson, A.O.; Adebola, A.A.; Djaman, K. Trend Analysis in Standardized Precipitation Index and Standardized Anomaly Index in the Context of Climate Change in Southern Togo. Atmos. Clim. Sci. 2017, 7, 401–423. [Google Scholar] [CrossRef]
- Caloiero, T. Drought Analysis in New Zealand Using the Standardized Precipitation Index. Environ. Earth Sci. 2017, 76, 569. [Google Scholar] [CrossRef]
- R CoreTeam. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Beguería, S.; Vicente-Serrano, S.M. SPEI: Calculation of the Standardized Precipitation-Evapotranspiration Index. In R Package Version 1.8.1 2017; R Foundation for Statistical Computing: Vienna, Austria, 2017; Volume 1. [Google Scholar]
- The Comprehensive R Archive Network. Available online: https://cran.r-project.org/ (accessed on 1 June 2024).
- Unal, Y.; Kindap, T.; Karaca, M. Redefining the Climate Zones of Turkey Using Cluster Analysis. Intl. J. Climatol. 2003, 23, 1045–1055. [Google Scholar] [CrossRef]
- Karmalkar, A.V.; Bradley, R.S.; Diaz, H.F. Climate Change in Central America and Mexico: Regional Climate Model Validation and Climate Change Projections. Clim. Dyn. 2011, 37, 605–629. [Google Scholar] [CrossRef]
- Tan, P.-N.; Kumar, V. Introduction to Data Mining; Pearson: London, UK, 2018; ISBN 978-0133128901. [Google Scholar]
- Paradis, E.; Schliep, K. Ape 5.0: An Environment for Modern Phylogenetics and Evolutionary Analyses in R. Bioinformatics 2019, 35, 526–528. [Google Scholar] [CrossRef] [PubMed]
- Farajzadeh, J.; Fakheri Fard, A.; Lotfi, S. Modeling of Monthly Rainfall and Runoff of Urmia Lake Basin Using “Feed-Forward Neural Network” and “Time Series Analysis” Model. Water Resour. Ind. 2014, 7–8, 38–48. [Google Scholar] [CrossRef]
- Lara-Benítez, P.; Carranza-García, M.; Riquelme, J.C. An Experimental Review on Deep Learning Architectures for Time Series Forecasting. Int. J. Neural Syst. 2021, 31, 2130001. [Google Scholar] [CrossRef] [PubMed]
- Shenfield, A.; Howarth, M. A Novel Deep Learning Model for the Detection and Identification of Rolling Element-Bearing Faults. Sensors 2020, 20, 5112. [Google Scholar] [CrossRef] [PubMed]
- Olivares, K.G.; Challú, C.; Garza, F.; Canseco, M.M.; Dubrawski, A. NeuralForecast: User Friendly State-of-the-Art Neural Forecasting Models. PyCon Salt Lake City Utah US 2022, 2022, 6. [Google Scholar]
- Nixtla. Available online: https://nixtlaverse.nixtla.io/ (accessed on 1 June 2024).
- Chatterjee, S. A New Coefficient of Correlation. J. Am. Stat. Assoc. 2021, 116, 2009–2022. [Google Scholar] [CrossRef]
- Chatterjee, S.; Holmes, S. XICOR. In R Package Version 0.4.1 2023; R Foundation for Statistical Computing: Vienna, Austria, 2023; Volume 1. [Google Scholar]
- Moustris, K.P.; Larissi, I.K.; Nastos, P.T.; Paliatsos, A.G. Precipitation Forecast Using Artificial Neural Networks in Specific Regions of Greece. Water Resour. Manag. 2011, 25, 1979–1993. [Google Scholar] [CrossRef]
- Smyl, S. A Hybrid Method of Exponential Smoothing and Recurrent Neural Networks for Time Series Forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Bandara, K.; Bergmeir, C.; Smyl, S. Forecasting across Time Series Databases Using Recurrent Neural Networks on Groups of Similar Series: A Clustering Approach. Expert Syst. Appl. 2020, 140, 112896. [Google Scholar] [CrossRef]
- Magallanes-Quintanar, R.; Galván-Tejada, C.E.; Galván-Tejada, J.I.; Méndez-Gallegos, S.d.J.; García-Domínguez, A.; Gamboa-Rosales, H. Narx Neural Networks Models for Prediction of Standardized Precipitation Index in Central Mexico. Atmosphere 2022, 13, 1254. [Google Scholar] [CrossRef]
- Giddings, L.; Soto, M.; Rutherford, B.M.; Maarouf, A. Standardized Precipitation Index Zones for México. Atmosfera 2005, 18, 33–56. [Google Scholar]

| SPI Value | Class |
|---|---|
| ≥2.0 | Extremely wet |
| 1.5 to 1.99 | Severely wet |
| 1.0 to 1.49 | Moderately wet |
| −0.99 to 0.99 | Near normal |
| −1.49 to −0.99 | Moderately dry |
| −1.99 to −1.49 | Severely dry |
| ≤2.0 | Extremely dry |
| LSTM | N-HiTS | |||
|---|---|---|---|---|
| Region | MSE | MAE | MSE | MAE |
| Semi-Arid | 0.4918 | 0.5861 | 0.3264 | 0.4849 |
| High plain | 0.1723 | 0.3117 | 0.0455 | 0.1696 |
| Mountains | 1.6711 | 1.2016 | 0.5472 | 0.6661 |
| Canyons | 0.6456 | 0.7639 | 0.4433 | 0.5769 |
| Region | R2 | ξ | ||
|---|---|---|---|---|
| LSTM | N-HiTS | LSTM | N-HiTS | |
| Semi-Arid | 0.1206 | 0.9162 | 0.5925 | 0.9222 |
| High plain | 0.5409 | 0.9513 | 0.7079 | 0.9316 |
| Mountains | 0.2557 | 0.9684 | 0.5999 | 0.9368 |
| Canyons | 0.6163 | 0.9668 | 0.6659 | 0.9293 |
| Region | PE < 0 | PE > 0 |
|---|---|---|
| Semi-Arid | 0.4241 | 0.5759 |
| High plain | 0.5540 | 0.4460 |
| Mountains | 0.5636 | 0.4364 |
| Canyons | 0.5198 | 0.4802 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magallanes-Quintanar, R.; Galván-Tejada, C.E.; Galván-Tejada, J.I.; Gamboa-Rosales, H.; Méndez-Gallegos, S.d.J.; García-Domínguez, A. Neural Hierarchical Interpolation for Standardized Precipitation Index Forecasting. Atmosphere 2024, 15, 912. https://doi.org/10.3390/atmos15080912
Magallanes-Quintanar R, Galván-Tejada CE, Galván-Tejada JI, Gamboa-Rosales H, Méndez-Gallegos SdJ, García-Domínguez A. Neural Hierarchical Interpolation for Standardized Precipitation Index Forecasting. Atmosphere. 2024; 15(8):912. https://doi.org/10.3390/atmos15080912
Chicago/Turabian StyleMagallanes-Quintanar, Rafael, Carlos Eric Galván-Tejada, Jorge Isaac Galván-Tejada, Hamurabi Gamboa-Rosales, Santiago de Jesús Méndez-Gallegos, and Antonio García-Domínguez. 2024. "Neural Hierarchical Interpolation for Standardized Precipitation Index Forecasting" Atmosphere 15, no. 8: 912. https://doi.org/10.3390/atmos15080912
APA StyleMagallanes-Quintanar, R., Galván-Tejada, C. E., Galván-Tejada, J. I., Gamboa-Rosales, H., Méndez-Gallegos, S. d. J., & García-Domínguez, A. (2024). Neural Hierarchical Interpolation for Standardized Precipitation Index Forecasting. Atmosphere, 15(8), 912. https://doi.org/10.3390/atmos15080912








