Influence of Short-Term Variations in Solar Activity on Total Electron Content

Abstract

In the present work, the variations in Total Electron Content (TEC) induced by changes in the ionizing radiation of the Sun, which are related to the rotation period (about 27 days), were investigated. This study was based on a 30-year period. The relative deviations in the TEC and F10.7 values were used in the data analysis. The use of this modification aimed to eliminate the stationary diurnal, seasonal, and solar course of the TEC over the course of the long-term variations in solar activity, preserving the variations within a time scale of 27 days and less. As a result, the values of the linear regression coefficient between the relative deviations in the two considered quantities from the median (quiet conditions) for one rotation period were obtained. Depending on the general level of solar activity, the season, and the latitude, this coefficient varied between 40% and 60%. The analysis showed that the minimum values were observed during high solar activity. The latitudinal distribution demonstrated an increase in the area of the Equatorial Ionization Anomaly (EIA) under the influence of the so-called “fountain effect”. As a result, there was a seasonal variation and an increase in the winter months at mid and high latitudes and a decrease in the months of the minimum zenith angle of the Sun at low latitudes. A well-pronounced asymmetry in the equinox months was also obtained. The obtained results are the novelty of this study and can be used to improve empirical models for short-term TEC forecasting.

1. Introduction

Scientists working in the fields of solar–terrestrial physics and space weather have studied the influence of variations in solar activity during the 11-year solar cycle in sufficient detail. It is well known that solar radiation significantly modulates the behavior of the ionosphere. The dependence of solar activity on the ionosphere is essential for ionospheric physics scientists to understand ionospheric variations and processes [1].

In recent decades, a significant number of empirical background TEC models have been developed based on smoothed values, sunspot numbers, and the radio flux of the Sun at a wavelength of 10.7 cm [2,3,4,5]. The present study is focused on the influence of short-term variations in solar ionizing radiation associated with the Sun’s rotation, in the case of an irregular distribution of active centers on it, which has been described and defined in detail for so-called medium-term ionospheric changes [6].

According to some studies, the solar radiation flux F10.7 is the most suitable solar index for investigation, characterizing the level of extreme ultraviolet radiation, which is the main ionizing factor in the ionospheric F-region [7]. Other authors suggest it is more appropriate to describe the behavior of the F-region based on solar activity proxies, such as the following indices: MgII, Ly-α, and F30 [8,9]. In the present study, the authors used the traditional solar activity index F10.7 due to the fact that there is a sufficiently long series of uniform data of good quality on it.

In the behavior of the daily values of F10.7, there is a periodicity of about 27 days (recurrent variations), which also exists in the variability in the electron density of the ionospheric F-region, including in the TEC [10]. Recurrent variations are an important part of the day-to-day variability in the ionosphere [11]. These variations include both the influence of ionizing radiation and the influence of solar wind. Mansoori et al. (2013) [10] provided a detailed analysis of TEC variations for the period of 1998 to 2003 (23 and 24 solar cycles). The influence of solar activity on the ionosphere and their inter-relationship are well known and has been studied in detail [12,13,14,15]. A significant and high correlation was found both between the TEC and F10.7 and between the TEC and the solar EUV flux (26–34 nm), which proves the correct selection of using F10.7 as an indicator of solar ionizing radiation variations.

Of special interest to scientists are studies on the delay in the ionospheric response to changes in ionizing radiation. Ren et al. (2018) [16] studied the solar EUV flux variations observed by TIMED/SEE and the electron density variations measured by the same satellite. The main conclusion of the analysis was that the electron density variations were delayed by about one day compared with the EUV variations. In the same study [14], it was specified that the time delay of the production rate was about 0, while the delay of the loss coefficient depended on the latitude (1.4 at the equator and 1.8 at 60°). A significant result of the study was the dependence of the O/N₂ ratio on the 27-day variations in solar activity. This ratio, on which the loss coefficient depends, has a positive correlation with solar activity and changes as a result of variations in the neutral temperature.

Schmölter et al. (2021) [17] investigated the variations in F10.7, solar EUV flux, and TEC in 2019. The results confirmed the high correlation between F10.7 and EUV flux. An attempt to find a regression relationship between the daily values of the TEC and F10.7 (see Figure 4; in reference [15]) was unsuccessful due to the presence of seasonal and spatial variations in the TEC. After applying the interpolation of the correlation coefficient values between the TEC and F10.7, it became 0.69. In the present work, another method is proposed to eliminate the influence of seasonal and spatial variations. This paper presents results indicating a correlation between F10.7 and the TEC, which turned out to have zero lag. The time interval (28 days) for which the correlation was calculated was insufficient to obtain reliable results.

Of interest is the study by Rich et al. (2003) [18] on the correlation between F10.7 and the electron density measured by the DMSP satellite in 1989 at 18:00 local time as a function of the magnetic latitude. Correlation coefficient values of around 0.6 were obtained for magnetic latitudes between −60° and 60° at low values (below 4) of the geomagnetic activity index Kp.

Min et al. (2009) [19] used Fast Fourier Transform (FFT) to determine the correlation between F10.7, the TEC, and neutral density in CHAMP satellite data from 2002 under nighttime conditions. The presented correlation amplitudes depending on the time lag showed a delay of one day, and the correlation between both quantities (the TEC and neutral density) was positive. Because there is no direct ionization in nighttime conditions, the article by Min et al. (2009) [19] concluded that the influence of variations in solar activity on the TEC is due to changes in the scale height of the topside ionosphere, leading to a redistribution of the neutral components on which the recombination depends.

Afraimovich et al. (2006) [20] studied the influence of variations in solar activity on the global electron content, defined as the Total Electron Content of the entire Earth’s ionosphere for the period of 1998–2005. The delay of the global electron content was 1.5–2.5 days, which coincided with the delay of the TEC obtained by other authors. In this paper, the linear dependence obtained by the authors is published as G = 0.013 [F-60] + 0.5.

The aim of the present research was to obtain the qualitative and quantitative relationships between the rotational variations in solar activity represented by F10.7 and the corresponding variations in the TEC based on the global data of nearly three solar cycles (30 years), taking into account the spatial (latitudinal) peculiarities.

Special attention to the dependence of variations on a general level of solar activity within the 11-year periodicity was paid. Seasonally dependent and associated anomalous behaviors and physical interaction mechanisms were also analyzed.

2. Data and Methods

The data used in the analysis of the present investigation will be described in detail in this section. This work used TEC data from 1994 to 2023 downloaded from https://www.izmiran.ru/ionosphere/weather/grif/Maps/TEC/, accessed on 13 July 2024. These data are a product of the NASA JPL (Jet Propulsion Laboratory, the California Institute of Technology, USA). These hourly-type data have a spatial grid in geographic coordinates between 87.5° S and 87.5° N. The data for F10.7 are freely available at https://omniweb.gsfc.nasa.gov/form/dx1.html, accessed on 13 July 2024. The TEC data were converted into a coordinate system with modip latitude and geographical longitude [21]. Modip latitude at low latitudes is close to the values of the inclination of the Earth’s magnetic field, which is a condition for the correct study of the features of the EIA area. The creation of the EIA is described as the removal of plasma from the equator, as a result of which a reduction is observed in the equatorial region, while at around ~±20° magnetic latitudes, areas called crests with a low accumulation of plasma in quiet conditions are formed. As a result of geomagnetic storms, the EIA extends over ~±30° magnetic latitudes [22]. The explanations for the observed anomalies in the EIA at low latitudes are related to the direct penetration of the magnetospheric electric fields and the thermospheric–ionospheric disturbances [23]. In their study, Bojilova and Mukhtarov (2024) [24] found that the observed positive reaction at low latitudes occurs at the modip latitudes 30° N and 30° S and is relatively stationary.

The analysis of the dependence of the TEC on short-term variations in solar activity in the present study was performed based on the relative deviations in the two quantities, denoted by rTEC and rF10.7, respectively:

$$rTEC\left(t\right)={\displaystyle \frac{TEC\left(t\right)-{TEC}_{med}\left(UT\right)}{{TEC}_{med}\left(UT\right)}}$$

(1)

where TEC(t) denotes the TEC value at the moment t, TEC_med(UT) is the median TEC obtained from the TEC values for the universal time UT coinciding with the universal time at the moment t during a 27-day period centered on the current day.

$$rF107\left(day\right)={\displaystyle \frac{F10.7\left(day\right)-{F10.7}_m\left(day\right)}{{F10.7}_m\left(day\right)}}$$

(2)

where F10.7(day) is the value of F10.7 for a selected day, and F10.7_m(day) is the median value of F10.7 for a period of 27 days, centered on the current day.

The study conducted by Mukhtarov et al. (2018) [25] described in detail the properties of these transformations. These modifications aim to eliminate the stationary diurnal, seasonal, and solar course of the TEC over the course of the long-term variations in F10.7 in the 11-year cycle of solar activity, keeping the variations within a time scale of 27 days and less.

For the purposes of the present study, the relative TEC was averaged by days, which removed variations with a time scale smaller than the diurnal variability due to the fact that solar activity data are averaged daily. In addition, the averaging of the geographic longitude for the purpose of studying the latitudinal regularities was performed.

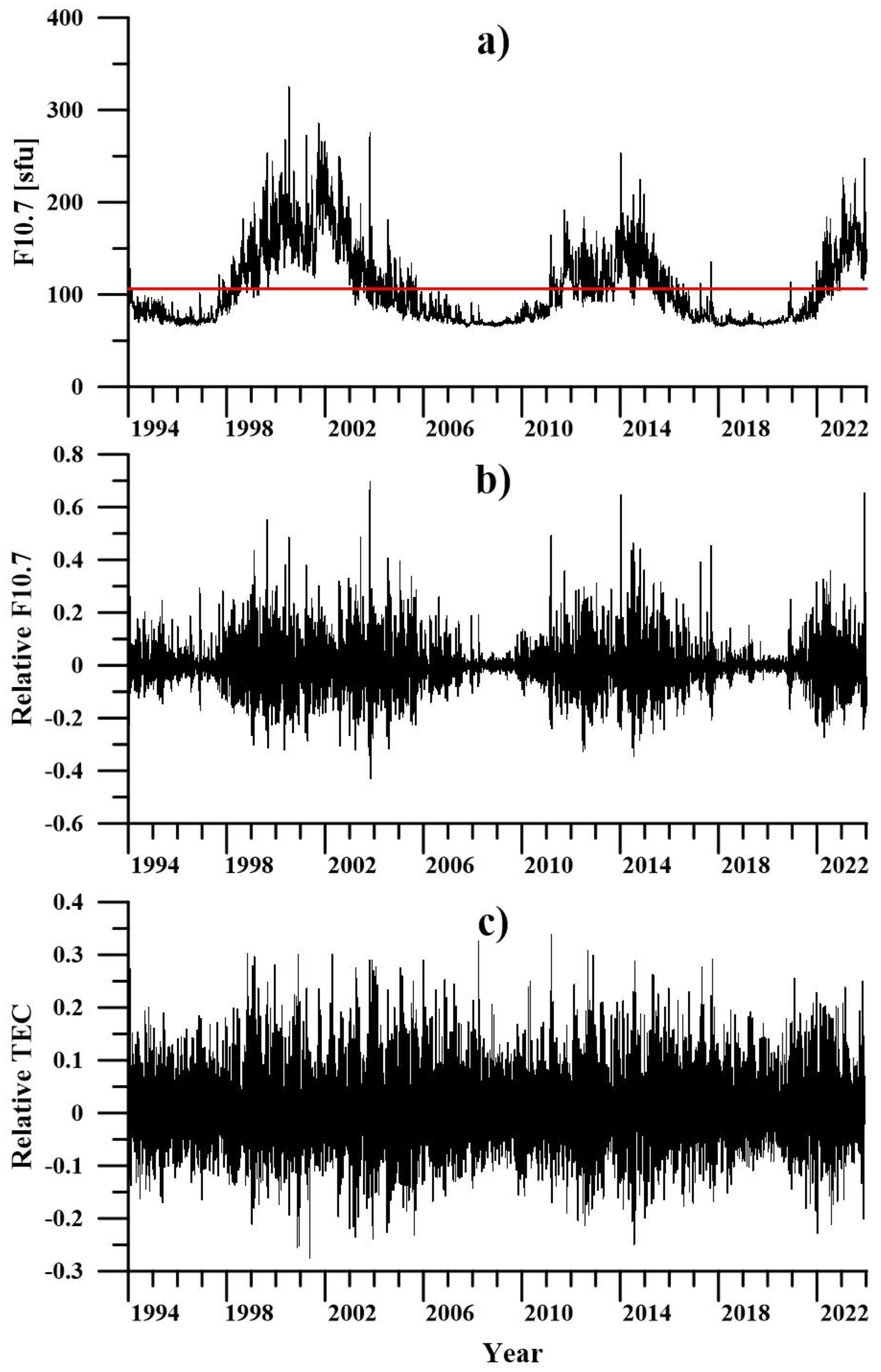
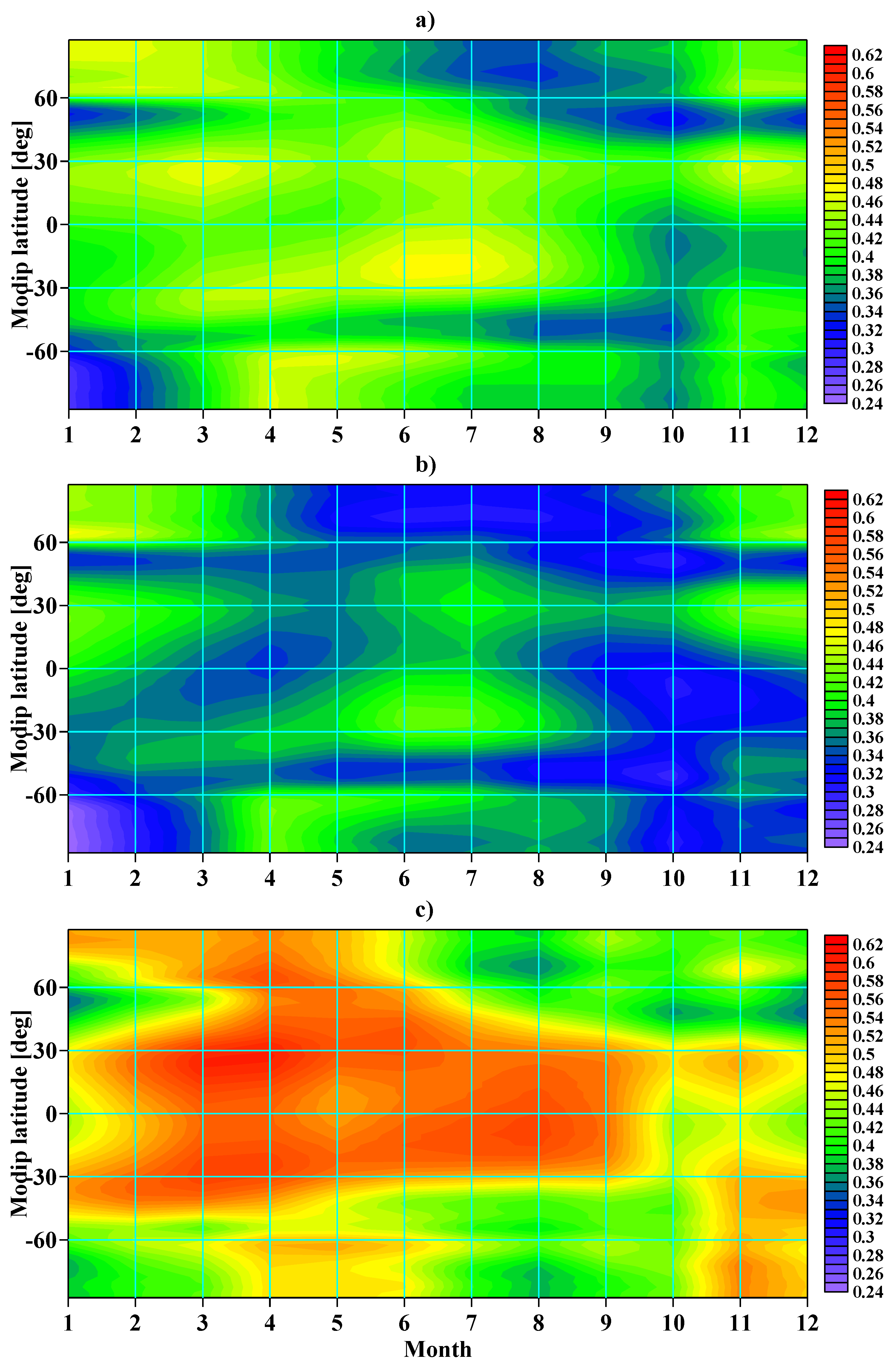
Before researching the influence of short-term variations in the Sun on the TEC, it was necessary to first analyze the behavior and statistical characteristics of solar activity for the considered time interval of 30 years. Figure 1 shows the behavior of the daily values of (a) the measured F10.7, (b) the relative F10.7, and (c) the relative TEC for the period from 1994 to 2023. The average value shown with a red line in Figure 1a is 106 sfu, and this value is used to separate low and high solar activity. Figure 1 clearly shows the different behavior of the solar activity during the 23, 24, and 25 solar cycles. In order to reduce the influence of variations due to geomagnetic activity, the days on which the daily average value of the Kp index was greater than 6 were removed from the analyses.

Figure 2, Figure 3, Figure 4 and Figure 5 show the main statistical characteristics of the two relative deviations (in the quantities of TEC and F10.7).

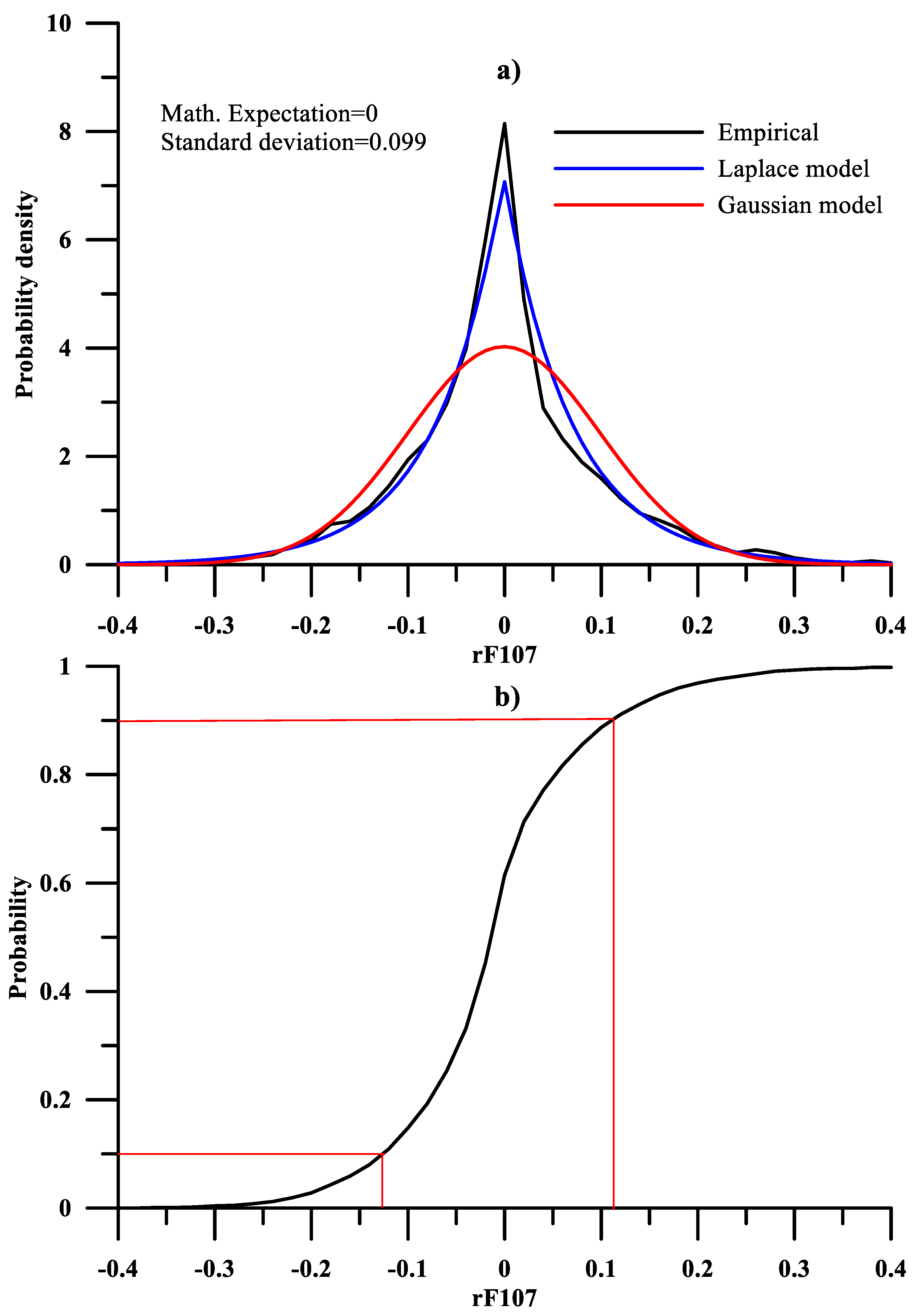
Figure 2a shows a comparison of the probability density distribution of rF107, empirically modeled (black line) and using Laplace (blue line) and Gaussian (red line) models. Figure 2b illustrates the probability and deciles, bounded by the upper decile (90% probability) and lower decile (10% probability), marked with red lines. As can be seen in Figure 2a, the probability density distribution of rF10.7 is symmetrically located, with a practically zero mean value and a shape close enough to the Laplace distribution. The probability, shown in Figure 2b, allows estimating, by the empirical 90% quantiles, the range of values in which 80% of the values (bounded by the upper and lower deciles) are located. According to the probability distribution shown in Figure 2b for rF10.7, this range is from −0.12 to 0.11, and the range from −0.4 to 0.4 for rF10.7 shown in Figure 2a includes practically all values of the quantity. The resulting Math. Expectation and standard deviation of rF10.7 are close to zero.

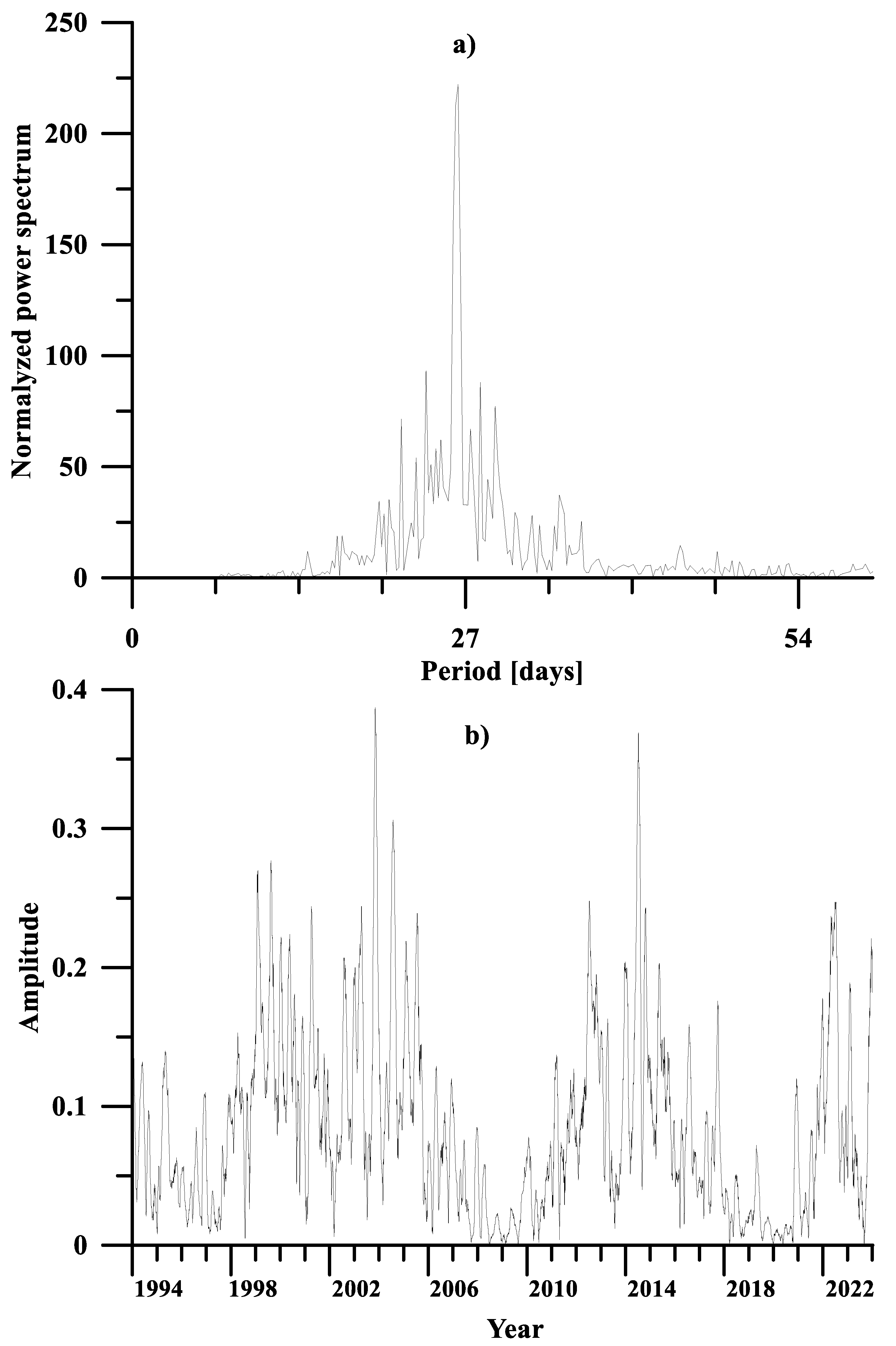
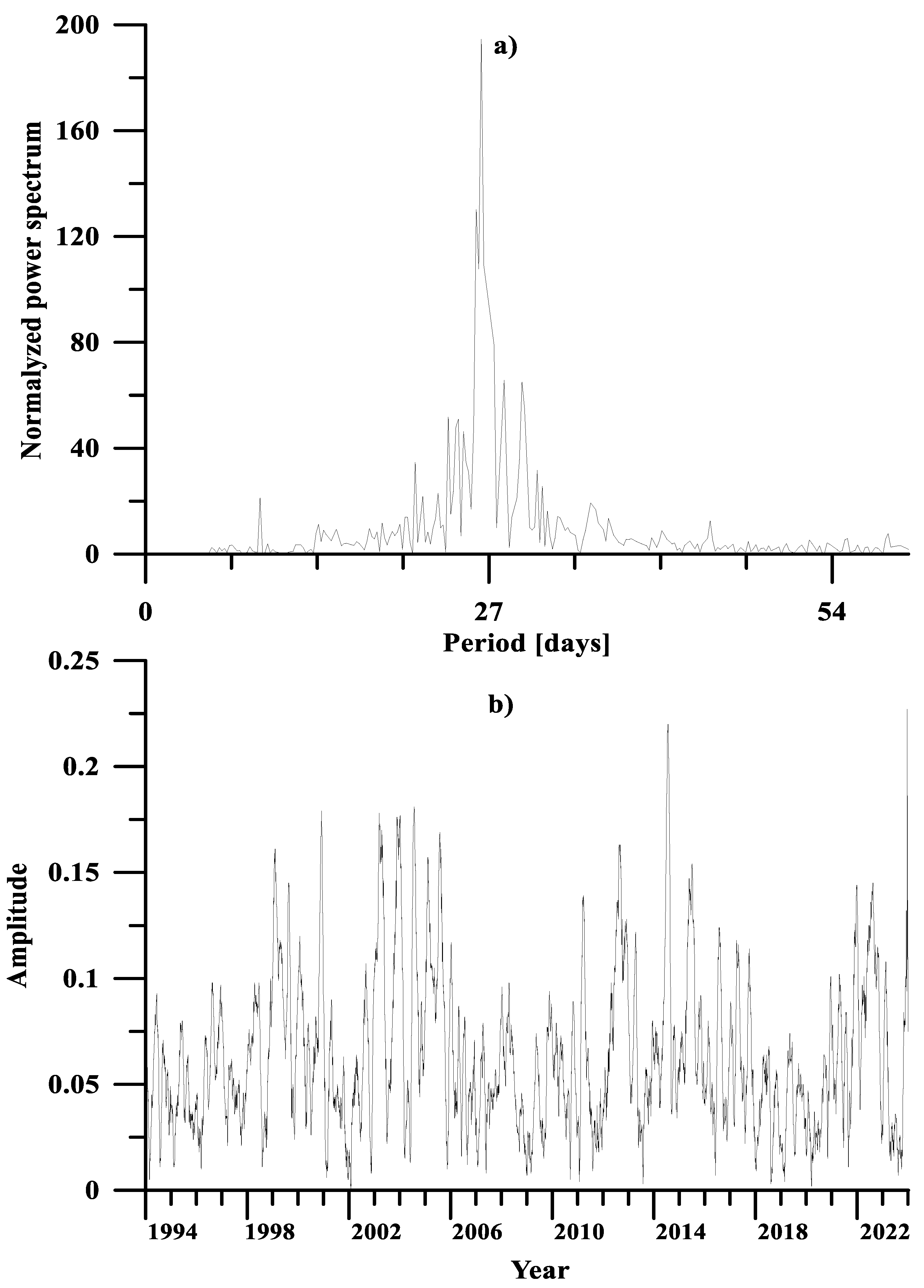
Figure 3a shows the normalized power spectrum (the Fourier transform of the normalized autocorrelation function) of the relative deviation in F10.7. As can be seen in the figure above for rF10.7, at the equator, the predominant component has a period of 26.4 days, which is the mean period of rotation of the Sun.

Figure 3b shows the amplitudes of the 27-day variation in rF10.7 at the equator obtained by 27-day moving segment decomposition. The amplitudes are of the same order and apparently depend on the level of solar activity shown in Figure 1.

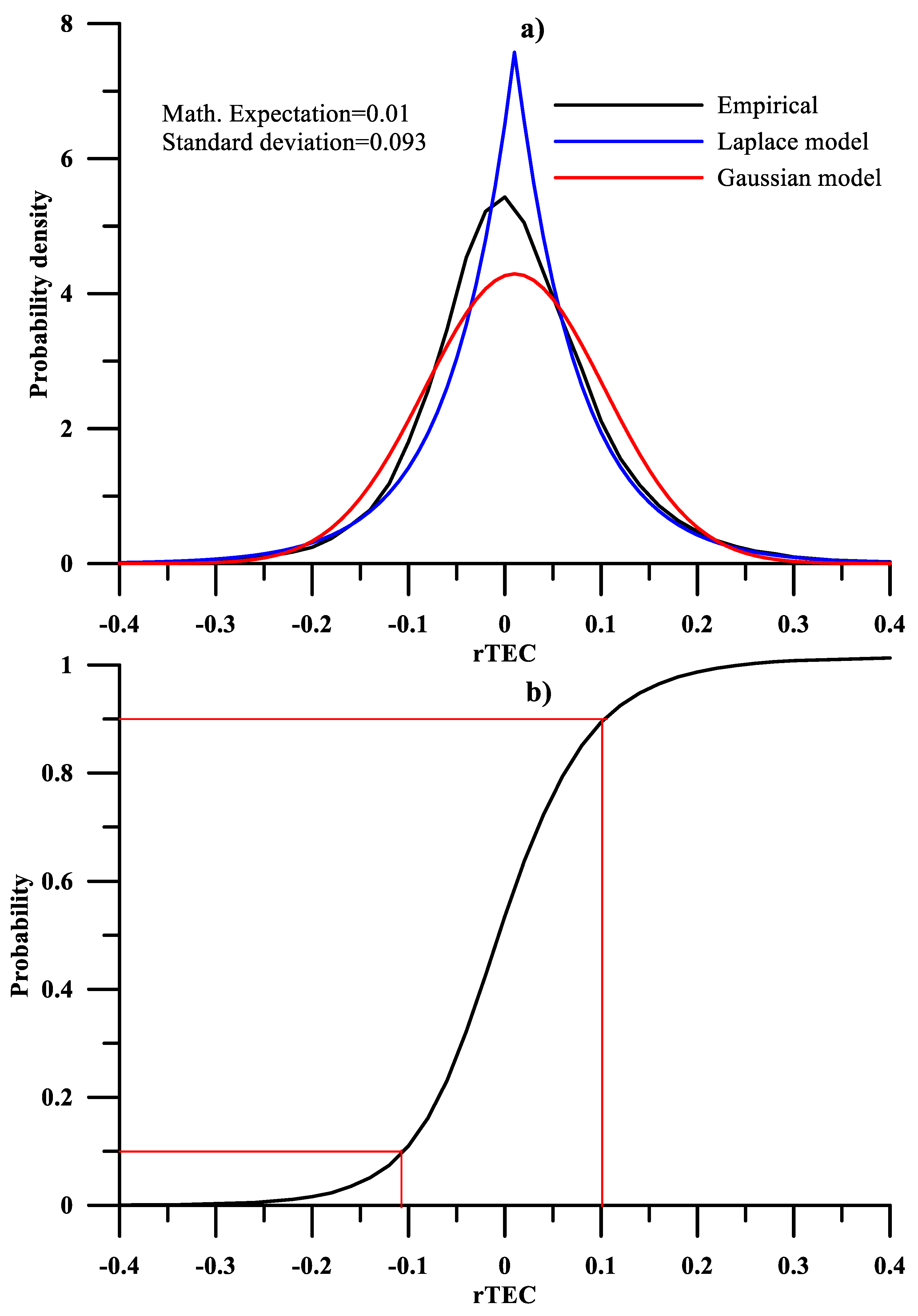
Figure 4a is analogous to Figure 2a and shows the probability density distribution of rTEC, empirically modeled (black line) and using Laplace (blue line) and Gaussian (red line) models. Figure 4b illustrates the probability and deciles of the rTEC limited by the upper and lower deciles, marked with red lines. The shown probability density distribution of the rTEC (see Figure 4a) is closer to a Gaussian distribution and has some asymmetry, with a practically zero mean value. The mathematical expectation and standard deviation are close to those obtained for the rF10.7. For the rTEC quantity, the probability range shown in Figure 4b is from −0.11 to 0.11, which includes 80% of the values. The results show that the rTEC is in the range from −0.4 to 0.4, which includes practically all values of the quantity.

Figure 5 is analogous to Figure 3. Figure 5a shows the normalized power spectrums (the Fourier transform of the normalized autocorrelation function) of the rTEC. The analogous result to that for the rF10.7 at the equator shows that the predominant component has a period of 26.4 days. Figure 5b shows the amplitudes of the 27-day variation in the rTEC at the equator obtained by 27-day moving segment decomposition.

The similarity between the main statistical characteristics of the two relative quantities, as well as the coincidence of the main periodicity in them, shows the justification of their use and the search for a relationship between the variations in them.

3. Results

A general concept shows that the cross-correlation function gives the causal relationship between two physical quantities. In cases where time series are considered, the cross-correlation function is a measure of the similarity between their time variations. In general, this similarity is not proof of a causal relationship, but it is an important argument for it. The content of this section is related to the search for a relationship between solar activity and TEC variations.

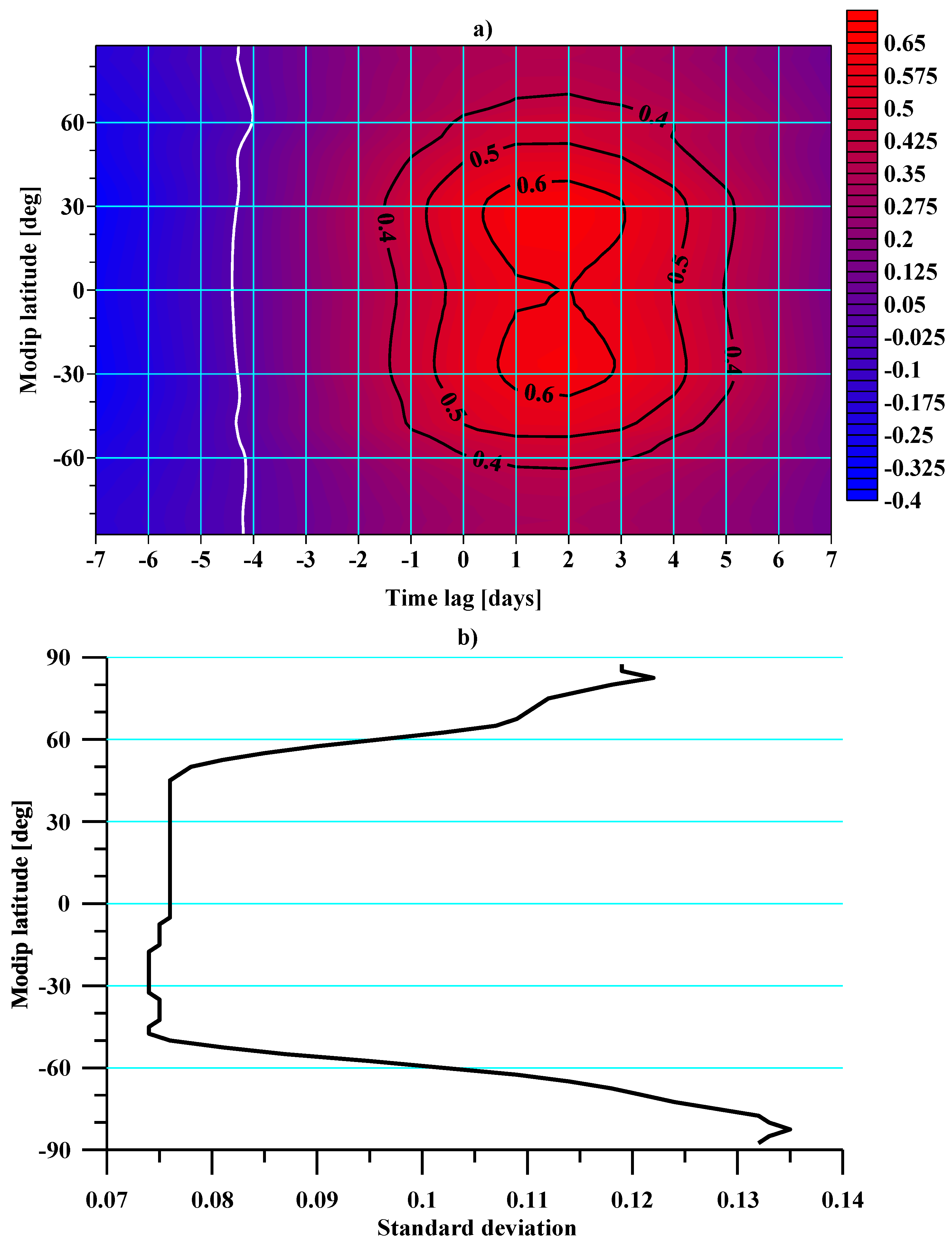
Figure 6a shows the normalized cross-correlation function between the relative F10.7 and the relative TEC calculated for each modip latitude by time lags between −7 and 7 days. The presented analysis was conducted under the assumption that solar activity is the cause and the response of the TEC is the effect. Values at close to zero time lags showed a significant correlation (about 0.5) with the maximum values observed close to modip latitudes of ±30°. Analysis of the figure showed a time lag of about 1–2 days. Due to the data-sampling step, it was not possible to give the correct value of the delay. The cross-correlation and time delay values were close to those published by Rich et al. (2003) [18], despite the fact that the present ones were obtained by a different methodology. The values of the normalized cross-correlation function shown in Figure 6a give an approximate idea of the coefficient of linear regression between the solar activity represented by F10.7 and the TEC under the condition that the dispersions of the two quantities are equal (see Figure 2a and Figure 4a).

Figure 6b illustrates the latitudinal distribution of the standard deviation of the relative TEC, which shows its increase at modip latitudes higher than 60° (for both hemispheres). This result is due to the influence of the processes in the polar region under the action of solar wind and the effects on the electron density.

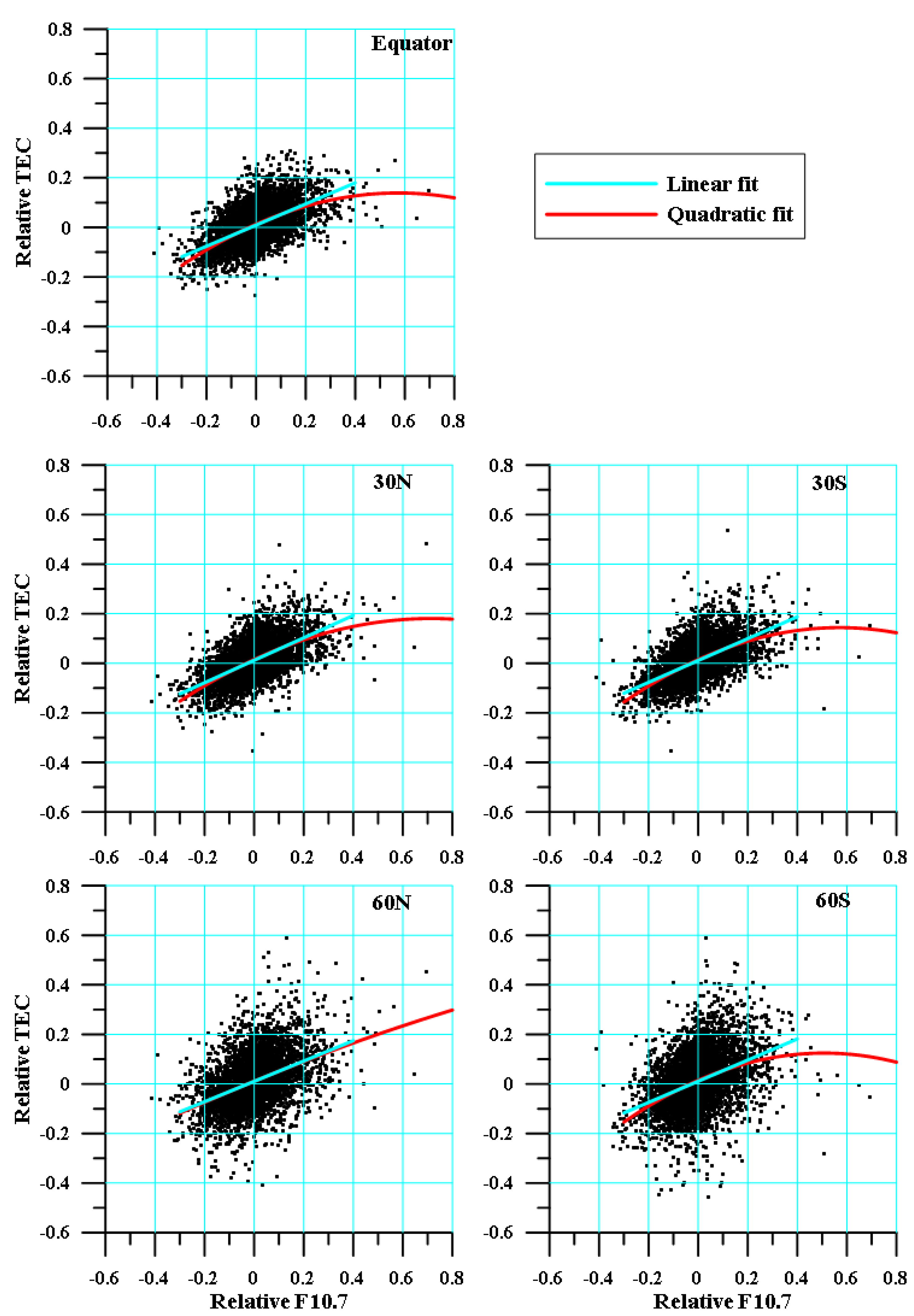
Figure 7 shows the scatter plots of the relative F10.7 and relative TEC for different modip latitudes. The figure shows the increase in scattering at high latitudes. Shown in the figure are the linear (marked with the cyan color) and quadratic fit regressions (marked with the red color). It follows from the figure that in the range of values of the relative F10.7 between −0.4 and 0.4, the two regressions practically coincide. At values above 0.4 (which are very few counts), the quadratic regression shows a trend toward definite saturation.

The authors Liu and Chen (2009) [26] obtained a similar result. Due to the fact that in this study, the measured values of the F10.7 and TEC were used, the local time and longitude were fixed. The results show that the obtained variations in the TEC associated with the variations in solar activity were more significant during the day and at low latitudes. Another result of this work shows that in the equatorial and low-latitude regions, the dependence of the ionosphere on solar activity had a minimum around the dip equator, and on both sides of the dip equator, maxima were observed [26].

Another paper related to the influence of solar activity on the global electron content showed significant semi-annual ionospheric variations with the maximum relative amplitude (10%) during the rising and declining parts of the solar cycle and reaching up to 30% during the period of the maximum [27].

An investigation of a similar influence of solar activity on the ionosphere proved the presence of a linear relationship between the daily mean value of the electron content and the solar radio flux at 2.8 GHz. It was also found that the coefficients of the linear regression had an annual variation. A delay in the ionospheric response was observed between 1 and 3 days compared with the fluctuations in solar flux. The authors of this research conclude that the use of linear dependence allows predicting, with sufficient accuracy, the state of the mean daily value of the electron content in the presence of data on solar activity [28].

The Discussion Section of the present work presents an additional analysis of the so-called “saturation” phenomenon. Subsequently, the representation of the relationship between the F10.7 and TEC by the simplest linear relationship obtained by the method of least squares was adopted. The linear dependence calculated in this way describes the area of relatively small deviations in the solar activity from the average condition, where a significant part of the measured TEC values is concentrated. In cases of the empirical modeling of the ionosphere, it is appropriate to use a parabolic relationship between the level of solar activity and ionospheric characteristics [25].

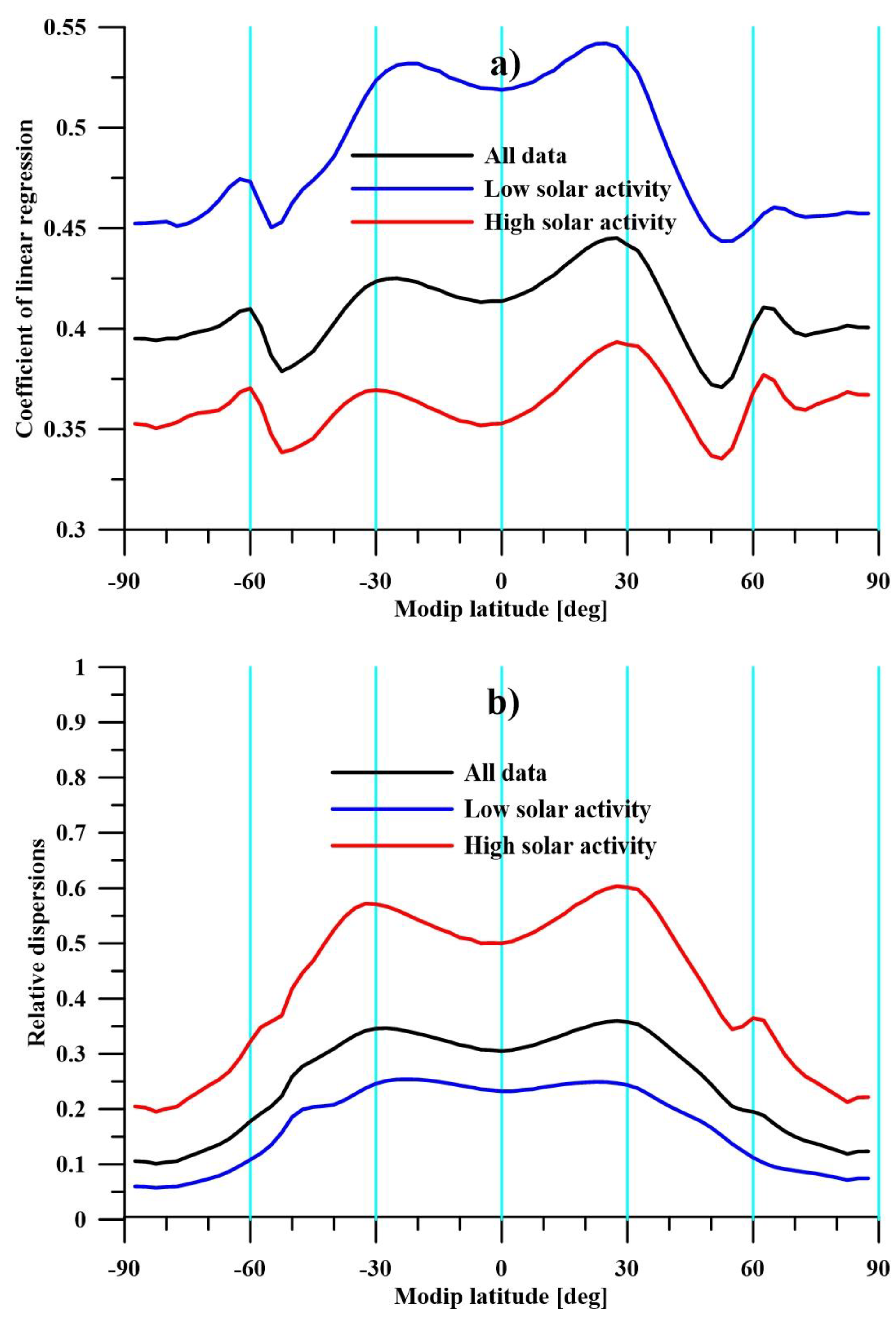
Due to the fact that the purpose of the present research was not modeling, a simplified linear dependence was assumed, which gave a better opportunity to visualize the latitudinal distribution of the TEC response to short-term variations in solar activity, and the results are presented in Figure 8a. Using all the data (i.e., with any type of solar activity), the linear coefficient was about 0.4. From the resulting ratio between the relative values, this means that the ionospheric TEC response was about 40% of the F10.7 variation. It is obvious that the obtained value cannot be compared with the linear coefficient 0.013 obtained by Afraimovich et al. (2006) [20] because it describes the response of the global electron content.

The latitudinal dependence of the linear coefficient had some features that were most probably related to the basic regularities of the latitudinal distribution of the ionospheric plasma. The two maxima at modip latitudes of ±30° coincided with the EIA maxima. As a result of the fact that these maxima were due to the transfer of plasma from the equator by the “fountain effect”, it can be assumed that the additional ionization of the equator also affected these latitudes. It is more difficult to explain the two local minima at ±50° and the two local maxima at ±60°. There is a possibility that they were due to the influence of geomagnetic activity on the ionosphere; however, in the present analysis, the days during which ionospheric storms of geomagnetic origin were registered were removed. Variations in geomagnetic activity associated with the rotation of the Sun that do not cause storms and that affect the ionosphere exist even in the quietest periods of solar activity [29]. The local minima were located at mid-latitudes, where a negative response of the TEC occurred during geomagnetic storms, and at ±60°, positive responses occurred [24]. The explanation for the two observed minima can be given by the general signatures of the plasma density bottom, while the two local maxima can be signatures of auroral ionization (originating in the auroral oval and produced by particle precipitation). The plasma density (created by the depletion of the solar-produced ionization) trough also represents the poleward boundary of the solar-produced ionization, since the auroral oval is created by particle precipitations. Regarding the influence of geomagnetic activity on the plasma density trough and auroral oval, both move equatorward during magnetically active times and poleward during magnetically quiet times [30].

Additional analysis of this possible influence is presented in the Discussion Section.

Figure 8a shows the latitudinal distribution of the linear coefficient during low and high solar activities. The average value of F10.7 for the considered period 106 sfu was taken as a conditional limit. As can be seen in Figure 8a, the dependence of the TEC response on the level of solar activity was significant, while the latitudinal dependence was preserved. The increase in the linear coefficient during low solar activity to 0.5 (and its decrease to 0.35 during high solar activity) can be explained by the change in the temperature regime of the thermosphere. During high solar activity, the temperature in the thermosphere increases compared with the temperature during low solar activity, which means higher recombination. This is the explanation of why the response of the TEC to short-term variations in solar activity decreases during high solar activity. Specific data for this statement are presented in Ren et al.’s (2018) study [16]. The same mechanism also operates in short-term warming associated with the heating of the polar region during geomagnetic storms and causes a negative response in the electron density of the ionospheric F-region [31].

Figure 8b shows the relationships between the dispersions of the rTEC values obtained according to the linear representation and the dispersion of the rTEC data. For this purpose, rTEC values were generated for each latitude and for each day as the product of rF10.7 and the linear regression coefficient according to Figure 8a. The values of dispersions obtained for all rF10.7 data, only for high and only for low solar activity, were divided by the dispersion of the rTEC data. These relationships characterized the relative contribution of rTEC variations caused by solar activity variations to the overall variability.

The relative contribution was strongest during high solar activity and least significant during low solar activity. It decreased with increasing latitude due to the dominance at mid and high latitudes of variations caused by geomagnetic activity and intra-atmospheric processes.

Figure 9 shows the seasonal variability in the linear coefficient (a) for all data, (b) during high solar activity, and (c) during low solar activity. For each calendar month, the data for that month and for the two months before and after the selected month were used; therefore, the seasonal trend is represented by a sliding segment of three months.

During the winter period, an increase in the linear coefficient was observed at high latitudes, which was probably due to the seasonal changes in the temperature regime (during the winter season, temperatures are lower; therefore, recombination decreases). In this case, the influence of geomagnetic activity related to predominantly positive ionospheric responses to geomagnetic disturbances cannot be excluded. In the tropical region at ±30°, the seasonal course had a distinct semi-annual course, which was most likely due to the semi-annual course of the zenith angle of the Sun and, accordingly, the temperature changes.

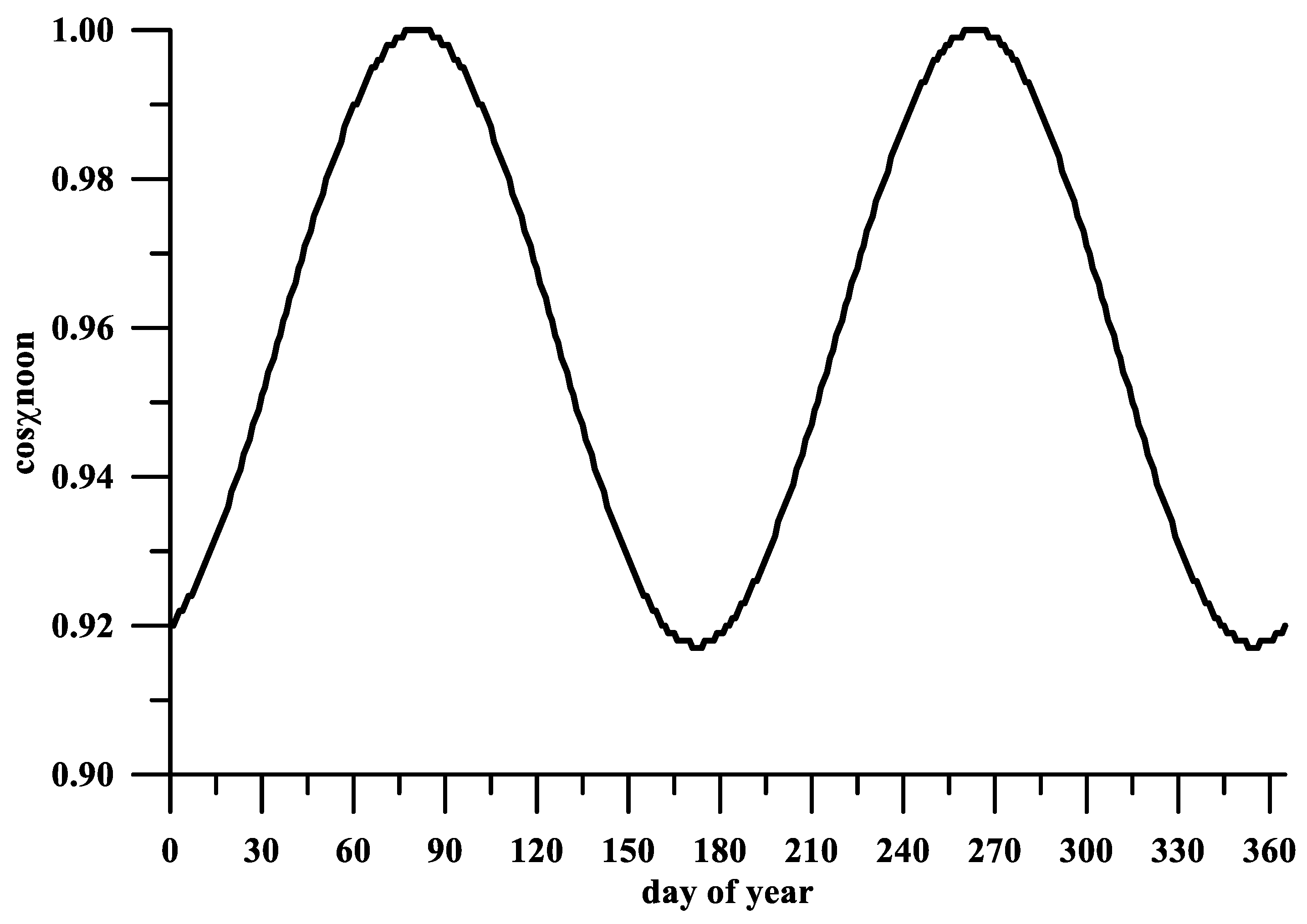
Figure 10 shows the variability cosine at the noon solar zenith angle on the equator. The minima that should cause a decrease in temperature and a corresponding increase in the response due to a decrease in recombination were at the beginning, middle, and end of the year, which coincided with the seasonal course of the linear coefficient. The significant decrease in the linear coefficient observed in the month of October at all latitudes cannot be explained by the normal seasonal course of the neutral temperature. Studies of the ionospheric D region show a phenomenon known as the “October effect”. This phenomenon is expressed as a sharp change in the amplitude of radio waves with a very low frequency (VLF), reflected in the lowest ionosphere in October [32,33].

The physical mechanism of this phenomenon has not been discovered, but it is probably related to some features of the transition of the atmosphere from the summer to winter regime, asymmetrical to the corresponding winter–summer transition. However, the “October effect” obtained in the present work also occurred at low latitudes. Liu and Chen (2009) [26] noted a decrease in the linear coefficient of dependence between solar activity and the TEC for days 160 to 220 of the year but did not note asymmetry.

4. Discussion

This section will discuss two issues mentioned in the previous section. The first of them is whether the variations in geomagnetic activity can affect the results of the present study. The presence of periodicity in ionospheric disturbances of geomagnetic origin, which is related to the rotation of the Sun, is well known [34], and it can be assumed that the ionospheric disturbances caused by them may affect the dependence of the TEC on variations in the ionizing radiation if there is substantial synchronism between geomagnetic and radiation variations.

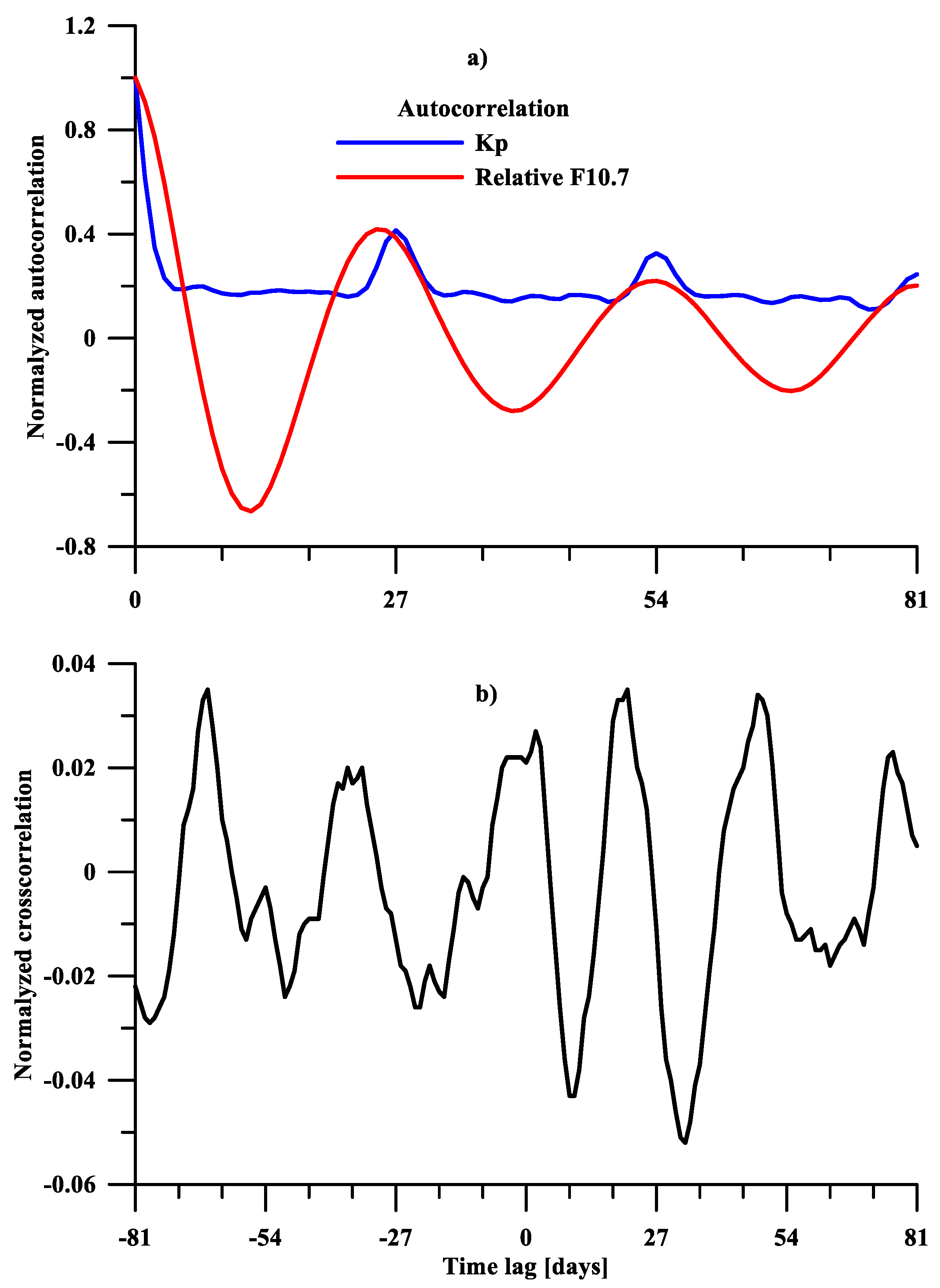
Figure 11a shows the autocorrelation functions of the geomagnetic activity index Kp (marked with the blue color) and the relative F10.7 (marked with the red color). The presence of a 27-day autocorrelation in both quantities confirms the presence of a 27-day periodicity in both geomagnetic activity and ionizing radiation. As can be seen in the figure, the autocorrelation of the geomagnetic activity was significantly smaller than that of F10.7.

The cross-correlation shown in Figure 11b between the two quantities turned out to be too small, about 5%. This means that the coincidence in the time of the variations was of low probability; therefore, any significant influence of geomagnetically disturbed periods on the dependence of the TEC on solar activity was not expected.

Figure 12 shows the linear regression coefficients when using all the data (including geomagnetically disturbed days) (marked with the black color), the data for excluded days with an average daily value of Kp greater than 6 (analogous to Figure 8a) (marked with the blue color), and when excluding days with a Kp of ≥4 (marked with the red color). It can be seen in the figure that the difference between the second and third cases was quite insignificant, which justifies the threshold of the geomagnetic activity adopted in the present work when days were removed from the analysis.

When geomagnetically disturbed days were removed, the linear coefficients slightly increased without changing their latitudinal distribution. This result coincides with the one obtained in the article of Rich et al. (2003) [18].

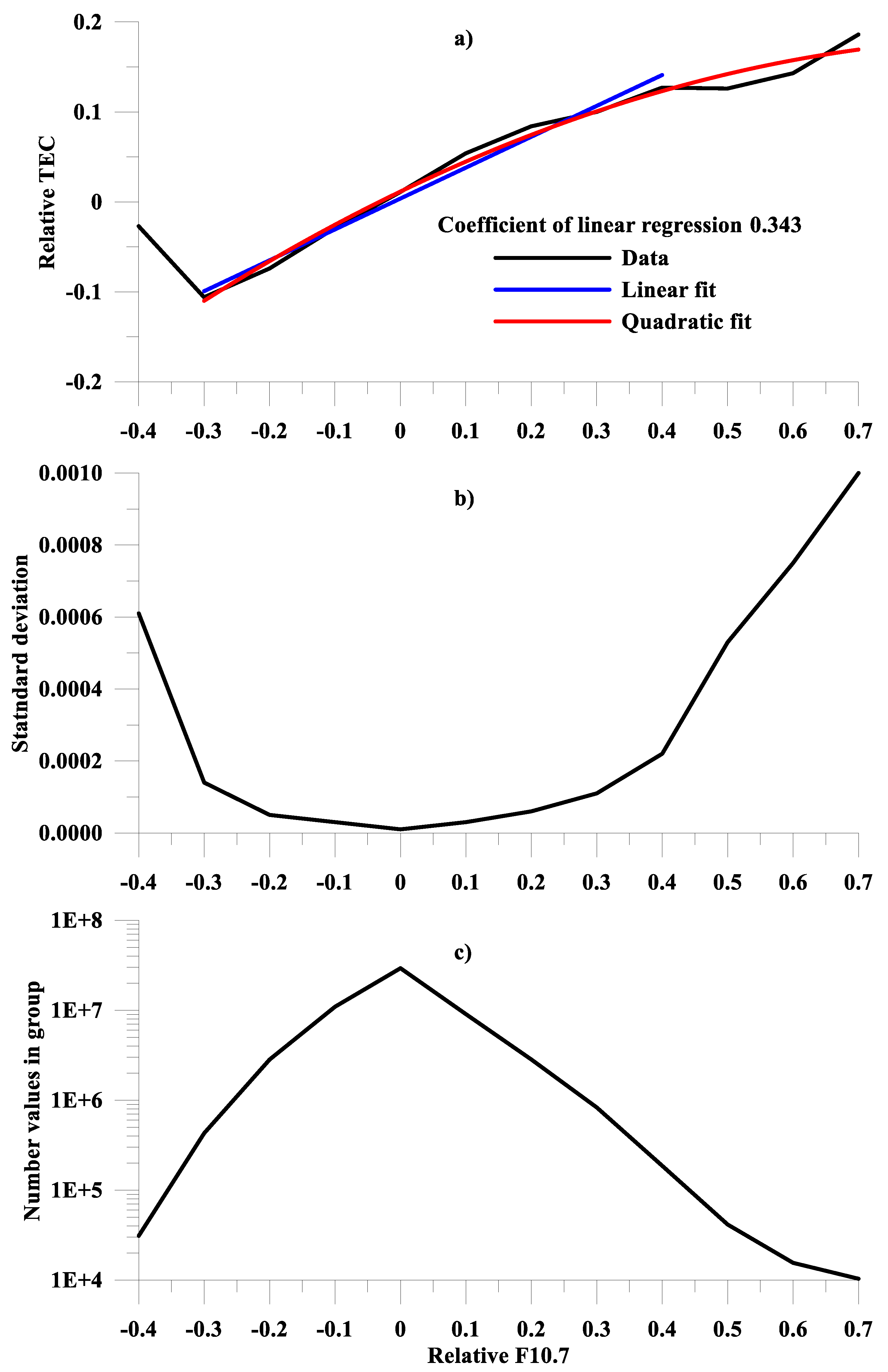
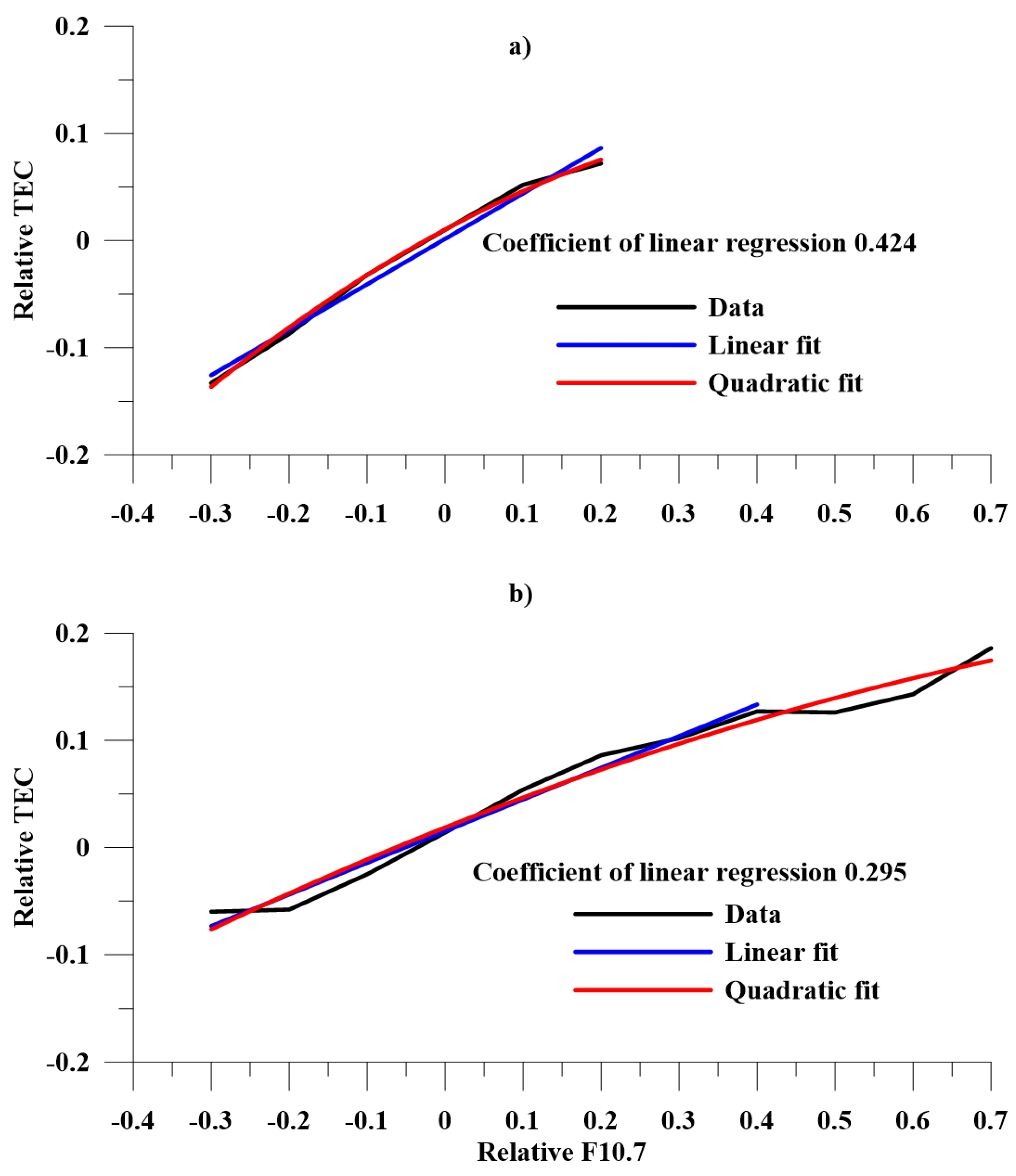
The next discussion problem was the presence of “saturation” at high values of the relative F10.7, which, in the present work, was neglected due to the adopted linear regression. For this purpose, a regression analysis was performed based on the group mean values, in which the “weights” of the bin values participating in the regression were equalized, and the sections where there were very few values participated in the regression equally to the others. Bins of the relative F10.7 values equal to 0.1 were assumed. Figure 13a shows the mean values by bins for the entire data series and for all latitudes. Figure 13b shows the standard deviations by bins. Figure 13c illustrates the number of values for each bin. A comparison of the results shows that analogous to Figure 7, the linear and quadratic regression practically coincided in the range of −0.4 to 0.4.

Figure 14a shows the group regression data for low solar activity and Figure 14b for high solar activity. During low solar activity, the linear and quadratic regressions practically coincided. During high solar activity, significant positive deviations were obtained. The results show that the values of the linear regression coefficients were close to those shown in Figure 8a. Unfortunately, attempts to apply the group regression method when splitting the data by latitude and season were unsuccessful due to insufficient statistics.

5. Conclusions

The behavior of the TEC was investigated depending on the variations in the ionizing radiation of the Sun represented by the radio radiation flux with a wavelength of 10.7 cm. In the analysis, the two quantities were transformed into relative deviations from the average state in a 27-day period centered on each current day, which was newly highlighted in this investigation. The representation of the ionospheric TEC was in modified dip coordinates.

A 30-year time series (from 1994 to 2023) was included in this study. Quantitative characteristics via the root-mean-square linear regression of the influence of short-term variations in solar activity (with a time scale below one calendar month) were obtained. The ratio between the relative variation in solar activity with respect to its monthly mean level and the corresponding relative deviation in the TEC from the medians was between 40% and 60% depending on the general level of solar activity and the season.

During high solar activity, the coefficient of linear dependence dropped to minimum values compared with those during low solar activity. The latitudinal distribution showed an increased response in the EIA area, which can be explained by the influence of the “fountain effect”.

In this research, an assessment was made of the possible influence of geomagnetic disturbances related to the rotation of the Sun, which, with a sufficient probability, have a secondary influence on the ionosphere, which can be manifested at latitudes close to the polar regions of the Earth.

The changes in the temperature regime and recombination could be an explanation for the results of the seasonal dependence, which showed an enhanced response in the winter months at mid and high latitudes. Probably for the same reason, at low latitudes, an enhanced response in the months of January, June, and December was observed, when the zenith angle of the Sun is at a maximum and, correspondingly, the cosine of it is at a minimum.

The presented results show an equinoctial asymmetry in autumn (October), in which there is a significant decrease in the response coefficient. This effect, which is similar to the well-known “October effect” in the lower-latitude ionosphere, is most probably related to the peculiarities of the summer–winter transition.

Studying the relationship between variations in the thermosphere and ionosphere as a result of changes in solar activity is an important part of the space weather issue due to the importance of human space-based activity.

The obtained results of the present study can be applied for the purposes of the empirical modeling and short-term forecasting of the TEC. The short-term variations in solar activity represented by F10.7 have a significant amplitude (see Figure 3), and their influence on the TEC is also significant (see Figure 8). Incorporating the resulting latitudinal, seasonal, and 11-year solar cycle dependencies, which are also novel contributions of this investigation, will improve the prediction accuracy of the ionospheric TEC. It is planned that the obtained dependencies will be implemented in improved models for forecasting the ionosphere.