Abstract
In the Qinghai-Tibet Plateau region, operational deficiencies and limited maintenance capacities often impair automatic air quality monitoring stations. This results in frequent data omissions, compromising the reliability of environmental assessment data. Therefore, an effective data imputation method is required to address the gaps in observational records. Utilizing a Sequence-to-Sequence framework, we introduce a model termed Bidirectional Recurrent Imputation for Time Series-Attention-based Long Short-Term Memory (BRITS-ALSTM). The encoder of BRITS-ALSTM applies BRITS to integrate single-station historical characteristics with multi-station correlation features. Concurrently, the decoder employs LSTM within an attention mechanism to capitalize on previously observed data, thereby generating hourly imputations for missing air quality data values. The model was trained using six types of air quality data from 16 stations across Qinghai Province. Through localized testing and parameter optimization, BRITS-ALSTM achieved a reduction in mean relative error (MRE) by 74.88% compared to the baseline mean-filling approach. Additionally, ablation studies demonstrated an improvement in the coefficient of determination R-squared (R2) from 0.67 to 0.76, outperforming the standalone BRITS. Consequently, BRITS-ALSTM enhances the accuracy of air quality data evaluations in the Tibetan Plateau and offers an efficacious strategy for data imputation in elevated terrains.
1. Introduction
Precision in the prevention and control of air pollution is contingent upon a comprehensive grasp of atmospheric pollutant characteristics [1]. An objective assessment of air pollution is derived from meticulous monitoring and analysis of key air quality indicators, enabling an accurate exploration of time series data. Such insights are pivotal for decision-makers, facilitating the formulation of tailored improvement measures aimed at mitigating the adverse impacts of air pollution on both human health and the environment [2,3,4,5,6]. Consequently, the imperative of acquiring precise air quality data is underscored [7]. Progress is noted in the enhancement of air quality monitoring networks globally, a response to the burgeoning necessity for refined data, essential in the nuanced management of air pollution [8,9,10]. Air quality monitoring stations are integral in this endeavor, renowned for delivering precise data. However, their efficacy is compromised in elevated terrains characterized by harsh climatic conditions. Data collection is often impeded by equipment malfunctions, adverse weather, and delayed maintenance, injecting a degree of uncertainty into the process [11,12,13,14]. The resultant data voids undermine the attainment of the minimum requisites stipulated by the Ambient Air Quality Standards (GB3095-2012), particularly concerning the validity of annual and daily average data statistics for air pollutants [15]. Air quality exhibits a high degree of time sensitivity, necessitating the monitoring of hourly data to accurately capture rapid changes. This approach enables real-time broadcasting of the Air Quality Index (AQI). Consequently, the strategic imputation of missing data at the hourly level becomes crucial. Such intervention significantly enhances the completeness and precision of air quality monitoring data [16,17,18,19].
The primary strategies for addressing missing values encompass direct deletion and data imputation [20]. Direct deletion serves as a straightforward tactic where data entries with absent attributes are eliminated, especially when the proportion of such missing values remains low. However, this approach becomes impractical as the missing rate escalates; valuable information is discarded, leading to the degradation of experimental outcomes due to compromised data integrity [21,22]. In contrast, missing value imputation has gained prominence as an efficient alternative. The judicious selection of an appropriate imputation method is pivotal, not only for ensuring the integrity of subsequent research but also for enhancing the precision of the outcomes [23,24].
Imputation methods primarily rely on statistical models, machine learning algorithms, or deep learning architectures, each possessing distinct merits and limitations [25]. Statistical models compute missing values using established algorithms, predominantly employing mean, median, and regression imputation techniques [26]. For instance, Worden et al. utilized least squares curves to impute datasets under sparse normality conditions [27], while Noor et al. employed linear, quadratic, and cubic imputation methods for processing PM10 data [28]. Although effective, statistical methods can introduce errors and perform suboptimally when dealing with complex variable relationships or substantial missing data gaps. In contrast, machine learning and deep learning approaches often yield superior imputation results but typically necessitate extended imputation durations compared to statistical methods. Concurrently, traditional machine learning approaches, encompassing K-Nearest Neighbor, fuzzy methods, decision trees, support vectors, and other models, have been integrated into the repertoire of techniques for addressing missing values [29,30,31]. A case in point is the work of Honghai et al., where Support Vector Machine (SVM) regression was employed to estimate missing conditional attribute values, illustrating the efficacy of machine learning in enhancing data completeness, but not with large datasets [32]. In a similar vein, Patil et al. innovated a weighted distance-based k-means algorithm. This method hinges on computing the mean of the center of mass values and center of mass distances of proximate neighbors to impute missing values, marking a stride in precision and reliability, but it is less effective for high-dimensional sparse data [33]. Complementing these, Kornelsen et al. amalgamated Artificial Neural Network (ANN) and Evolutionary Polynomial Regression (EPR) techniques. They capitalized on the Multilayer Perceptrons (MLP) algorithm to impute randomly missing values in high-resolution soil water data, underscoring the versatility and robustness of combined methodologies, but prone to the problem of local minima [34].
Deep learning models, particularly those founded on neural networks, have become a cornerstone in endeavors to enhance the precision of missing data imputation [35]. Che et al. deployed missing mode representation of masks and time intervals, an approach instrumental in capturing intricate long-term dependencies in time series. They manipulated the decay of hidden states within the Gated Recurrent Unit-Decay (GRU-D) model, fostering a notable enhancement in accuracy [36]. Similarly, Cao et al. introduced the Bidirectional Recurrent Imputation for Time Series (BRITS) algorithm, an innovation grounded in Recurrent Neural Network (RNN) technology, adept at managing multiple correlated missing values within time series [37]. These methodologies, though diverse, share a common foundation in variations of neural networks derived from RNNs. They adeptly navigate the challenges of gradient vanishing or explosion, ensuring optimal learning of the data’s temporal dependencies [36,37]. In another significant development, Yoon et al. unveiled the Generative Adversarial Imputation Nets (GAIN), a model designed for missing value imputation. By feeding additional information to the Discriminator, they ensured that the model’s Generator mastered the correct expected distribution [38]. Furthermore, Cini et al. pioneered the Graph Recurrent Imputation Network (GRIN), a novel multivariate time-series imputation framework for graph neural networks. GRIN excels in reconstructing lost data information transfer across various channels by mastering spatio–temporal representations [39]. In essence, deep learning underscores a superior efficacy in imputing large datasets, outperforming conventional padding and statistical methodologies.
Traditional recurrent neural networks, including RNN and LSTM (Long Short-Term Memory), are recognized for their adeptness in mining complex temporal features. This is achieved through the employment of cyclic feedback network structures and the continuous recursive replacement of temporal information [40,41,42]. A limitation, however, is their focus on restricted sequence information, resulting in a compromise in model performance when processing extensive sequence data [43]. To mitigate this limitation, the Sequence-to-Sequence (Seq2Seq) structure, a prevalent Encoder–Decoder model, has been introduced. It operates by encoding an input sequence into a fixed-length vector and subsequently decoding this vector into an output sequence [44,45,46]. This architectural innovation amplifies the model’s capacity to process and memorize extended temporal sequences, circumventing the constraints inherent in traditional RNN and LSTM networks.
This study introduces the Bidirectional Recurrent Imputation for Time Series-Attention Long Short-Term Memory (BRITS-ALSTM) model, innovatively designed to grasp the global dependencies and multivariate local correlations within time series data. With the Sequence-to-Sequence structure serving as its foundational architecture, the model integrates the BRITS as the encoder within an Encoder–Decoder configuration, paired with LSTM acting as the decoder [47]. This structure has proven instrumental in addressing the imputation of missing air quality values. In the encoding phase, multivariate time series vectors containing missing values are adeptly encoded utilizing BRITS. Progressing to the decoding phase, an attention mechanism is employed to adjust the weights associated with long time series information vectors. This adjustment enhances the model’s ability to discern the spatio-temporal characteristics of air quality data at pivotal time junctures [48]. Consequently, the model attains a comprehensive understanding of the underlying data representations and temporal dependencies between sequences. The decoding process subsequently facilitates high-precision imputation of the missing data values. Key contributions of this study are encapsulated in the introduction of the BRITS-ALSTM model, its adept handling of global dependencies, and the intricate extraction of multivariate local correlations within time series data.
- The BRITS-ALSTM model employs a bidirectional encoding scheme complemented by a decoding architecture that incorporates an attention mechanism. This model is designed to capture both temporal dependencies and spatial correlations among adjacent stations at hourly intervals within a specified timeframe. Through the integration of the attention mechanism, it is possible to discern the significance of various informational inputs by assigning appropriate weight ratios, thereby fine-tuning the current state’s dependencies throughout the LSTM’s decoding phase.
- An analysis was conducted on the imputation of missing values in six categories of air quality data from 16 monitoring stations in Qinghai Province using three methods: mean-filling, BRITS (Bidirectional Recurrent Imputation for Time Series), and BRITS-ALSTM. The findings indicate that the BRITS-ALSTM model exhibits superior imputation accuracy, thereby enhancing the assessment of regional air quality data on the Tibetan Plateau.
2. Materials and Methods
2.1. Data
This study focuses on Qinghai Province, a strategically significant area for ecological preservation and development in China, nestled in the northeastern sector of the Qinghai-Tibetan Plateau [49]. Characterized by an altitude exceeding 3000 m and annual temperatures fluctuating between −1 °C and 15 °C, this region presents a unique environment for air quality study. The unique climatic conditions and elevated altitude of the study area contribute to a sparse population, resulting in an insufficient number of grassroots environmental protection personnel [50]. Consequently, efforts in air pollution prevention and control are hampered, and the capacity for station operation and maintenance is limited. Instances of missing monitoring data often occur due to routine maintenance activities, such as the calibration of monitoring instruments, and unforeseen challenges, like instrument failures, communication breakdowns, and power outages [51]. The state-controlled station dataset incorporates air quality readings from eight centrally administered ambient air automatic stations, offering comprehensive coverage across Qinghai Province’s expanse, inclusive of two cities and six prefectures. Similarly, the province-controlled station dataset derives its data from eight regional ambient air automatic stations stationed in Haidong City, ensuring complete coverage of the entire city, encompassing two districts and four counties. Figure 1 elucidates the geospatial distribution of these stations.
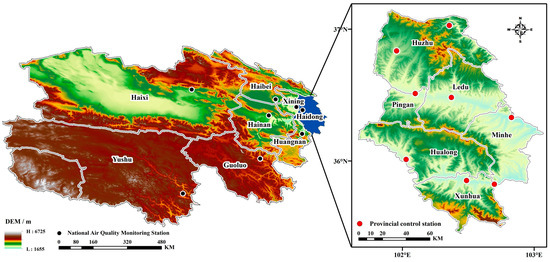
Figure 1.
Distribution of ambient air quality monitoring stations in the study area. The left figure shows the distribution of state-controlled stations in Qinghai Province, and the right figure shows the distribution of province-controlled stations in Haidong City.
The China National Environmental Monitoring Center (CNEMC) plays a pivotal role in China’s environmental monitoring efforts, providing real-time air quality data from all provinces and cities. This data, collected through nationwide environmental monitoring stations, undergoes rigorous testing for accuracy, quality control, and data review before public dissemination, thereby making it a highly authoritative and frequently utilized dataset for air quality research in China. The current study acquired hourly observation data on six ambient air pollutants (PM2.5, PM10, O3, NO2, SO2, and CO) from eight state-controlled stations in Qinghai Province (2019–2021) and eight provincial-controlled stations in Haidong City, Qinghai Province (2020–2022). Variability was observed in data missingness and validity across the 16 stations, with each station’s data evaluated against national standards. Table 1 shows the minimum requirements for evaluating the validity of pollutant concentration data in the Ambient Air Quality Standards (GB3095-2012).

Table 1.
Minimum requirements for validity of pollutant concentration data.
Figure 2 and Figure 3 delineate the disparity between the obtained and missing data, contextualized within the annual evaluation timeframe. The average rate of missing data for state-controlled stations is about 5% (Figure 2a,c), with the phenomenon that the higher the altitude, the more severe the missing data at the station. When annual averaging was evaluated for the state-controlled stations, all stations met the requirement of having at least 89% of the daily averages for each year (Figure 2b,d), but only two stations also met Condition 2. State-controlled station data are not far from meeting the requirements of Condition 2. Figure 2e shows that absences were concentrated in February, June, August, and September. The analysis revealed that data gaps at the state-controlled station predominantly occur between 16:00 and 20:00 (refer to Figure 2f). This pattern suggests a potential correlation with disruptions in communication signals or power outages during this time frame. These statistics help to better target the maintenance of state-controlled monitoring stations and reduce deficiencies in the monitoring process.
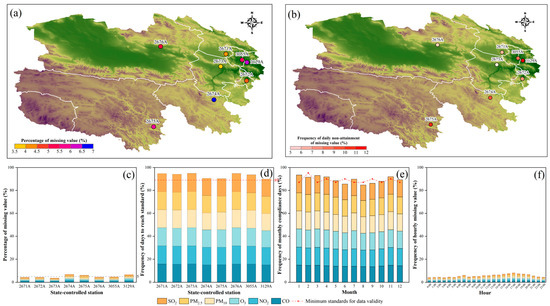
Figure 2.
Statistical data related to the occurrence of missing values in the monitoring of six pollutants at state-controlled stations. (a) Percentage of missing values at stations, (b) frequency of days with non-attainment of the daily average evaluation at the stations, (c) histogram of the percentage of missing values for the six pollutants at the stations, (d) frequency of days with daily average evaluations of compliance for the six pollutants at stations, (e) frequency of days evaluated to meet the standard for each month for the six pollutants, (f) percentage of missing values by hour for each of the six pollutants.
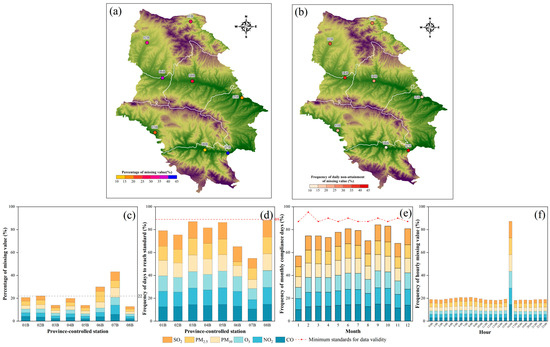
Figure 3.
Statistical data related to the occurrence of missing values in the monitoring of six pollutants at province-controlled stations. (a) Percentage of missing values at stations, (b) frequency of days with non-attainment of the daily average evaluation at the stations, (c) histogram of the percentage of missing values for the six pollutants at the stations, (d) frequency of days with daily average evaluations of compliance for the six pollutants at stations, (e) frequency of days evaluated to meet the standard for each month for the six pollutants, (f) percentage of missing values by hour for each of the six pollutants.
There is a more serious situation of missing data in the province-controlled stations, with an average missing rate of about 22% (Figure 3a,c), and up to 43.29% in station 07B. When evaluating the annual averages for the state-controlled stations, none of the stations met the requirement of having at least 89% of daily averages per year (Figure 3b,d), and none of them met Condition 2. Province-controlled stations had the most serious deficiencies in the month of January (Figure 3e). Data scarcity at 16:00 was notably evident at provincially controlled stations during daytime hours (see Figure 3f). This phenomenon is attributed to the calibration procedures of instruments at newly established stations. Therefore, it is important to perform hourly imputation of data from provincial control stations with high missing rates and high randomness to make the data meet the national evaluation standards.
2.2. Methodology
The BRITS model excels in the imputation of time series data within the realm of deep learning and has consistently demonstrated superior accuracy in imputing missing values across a variety of public datasets. Its conceptual framework exhibits broad applicability and utility. Drawing inspiration from established models, like BRITS [37] and BiLSTM-I [52], this study introduces the BRITS-ALSTM, a nuanced model engineered for the intricate task of correlating multivariate time series imputation, with BRITS serving as its foundational element. The integration of the BRITS structure and the sophisticated Encoder–Decoder network intrinsic to the Seq2Seq model facilitates a profound extraction of both the temporal dependencies characteristic of extensive time series data at individual stations and the spatial correlations manifesting synchronously across diverse locations. The incorporation of an attention mechanism amplifies the delineation of pivotal temporal nodes within the contemporaneous imputed data. In the encoder segment, BRITS takes precedence, with RITS at its core, functioning as a feature correlation algorithm within unidirectional recursive recurrent dynamical systems. Conversely, the decoder segment assimilates attention distribution and employs LSTM to actualize data imputation with precision and efficiency.
2.2.1. Basic Definition
The air quality data are stored separately in chronological order for each station, and the time series data are noted as ; represents the station code and represents the timestamp. The absence of temporal and quantitative patterns and the presence of various uncertainties in the absence of air quality data lead to the presence of null values in . To explicitly represent the missing cases in the station collection data, introduce a mask vector , where:
Define as the time gap from the last observing to the current timestamp, where:
In summary, the data set , mask vector and time gap vector are obtained for all stations. Taking the data from 1 January 2019 0:00 to 1 January 2019 7:00 as an example, the corresponding mask and time gap vectors are generated as shown in Table 2.

Table 2.
Example of a multivariate time series with missing values.
2.2.2. BRITS-ALSTM Model
The model structure is shown in Figure 4, where the input sequence is denoted as , the mask sequence is denoted as , the time gap sequence is denoted as , and the output sequence generated after imputation is denoted as .
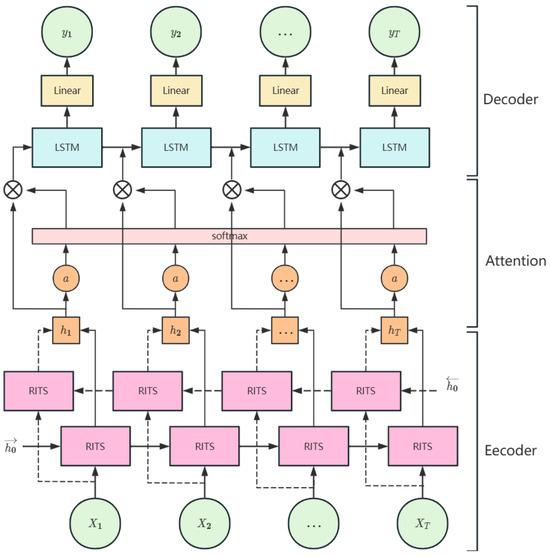
Figure 4.
Neural network structure for imputing missing value of air quality data.
- Encoder
To construct BRITS, the hidden states are initialized to all-zero vectors, and the model is updated by the following equation:
Equation (3) inputs the historical data of a single station into the model and converts the hidden states into estimated vectors to obtain the history-based estimates. Equation (4) replaces the missing values in with the history-based estimates to obtain the imputed vector . Equation (5) inputs the historical estimates of other stations and synthesizes the effects of multivariate correlation on a single station to obtain the estimates of the station based on other features. Where and are the corresponding parameters, the diagonal of the restriction parameter matrix is 0. Thus, the dth element in is the estimate of based on other features. Due to the irregularity of missing time series data, Equation (6) introduces a time decay factor to represent missing patterns in the time series. In Equation (7), is used as the mode for combining the history-based estimation and the feature-based estimation . The weights are learned by considering the time decay factor and the mask vector . Equation (8) assigns the history-based and feature-based estimation weights as calculated in Equation (7) to obtain the joint estimate of the two. Equation (9) replaces the missing values in a using to obtain the new imputed vector . Equation (10) is used to update the decay-based hidden state to realize the prediction of the next , where denotes the join operation. Equation (11) loss function uses the sum of the errors of all the estimates (history-based estimates , feature-based estimates , and joint estimates of both ).
BRITS’ bidirectional RITS neural network a reads inputs from the beginning to the end of a time series that produces a forward hidden state sequence and unit state sequence ; the other reads the input in reverse from the end to the beginning of the time sequence, producing the backward hidden state sequence and the unit state sequence . The forward and backward hidden state sequences and unit states are spliced together to form the coded outputs and of the encoding layer, where and .
Error in BRITS consists of both forward estimation error and backward estimation error (Equation (12)).
- 2.
- Attention Mechanism
In the encoding process, each input time point of the time series does not contribute equally to the imputation value at the current moment, so the attention mechanism is introduced to allocate the probability distribution of attention to extract the input information that is more important to the imputation at the current moment and to improve the accuracy of the imputation. The specific equation of the principle of the attention mechanism is as follows:
In Equation (13), the encoder compiles the input information to obtain the output hidden state sequence, for the last moment of the hidden state in the encoder, through a fully-connected layer and activation function, to calculate the correlation between the last moment of the hidden state and the encoder output hidden state, scoring mapping to generate the attention weights, and normalized to obtain the final attention weights.
- 3.
- Decoder
The decoder processes the output sequence of the encoder by receiving the attentional weights and produces the imputed time sequence . The decoding structure using a combination of LSTM and linear layers is given in the following equation:
Equations (14)–(16) sum the hidden states of the input information weighted according to the attention distribution to obtain a feature vector that contains both the encoder output state information and the decoder current moment feature timing attention correlation information. The updated is passed to the LSTM, and Equation (16) shows the decoding process of the LSTM layer. Equation (17) is the linear fully connected layer that outputs the imputation result sequence . Equation (18) is the estimation error of decoder imputation.
The error of the whole neural network consists of two parts:
where is the estimation error in the model coding layer and is the estimation error in the model decoding layer.
2.2.3. Evaluation Metrics
The BRITS-ALSTM is deployed utilizing the PyTorch open-source machine learning framework, executing the model across two distinct datasets. Air quality data is inherently characterized by its periodicity and seasonality; thus, data corresponding to March, June, September, and December from both datasets are allocated as test sets. The remaining monthly data form the training sets, establishing a 2:1 ratio between training and test data. The study establishes ‘eval’ and ‘eval_masks’ vectors for evaluation purposes. ‘Eval’ encompasses all true observations, while ‘eval_masks’ introduces a random 30% masking in the dataset where the actual observations are known, simulating missing data. The BRITS-ALSTM model is then employed to impute these artificially missing locations, yielding the model’s imputation results. These results, compared with the true monitoring values, are instrumental in calculating the model’s loss function and assessing its parameters. The performance of the BRITS-ALSTM model in imputing missing values is meticulously evaluated and benchmarked against an array of baseline imputation methods, as enumerated in Table 3. Each method is subjected to rigorous testing under identical dataset conditions to ensure a comprehensive and objective comparative analysis.

Table 3.
Introduction to baseline imputation methods.
The BRITS-ALSTM imputation model constructed in this study is a kind of regression model, which can evaluate the imputation results from the deviation between the imputed value and the true value. Therefore, Mean Absolute Error (MAE) and Mean Relative Error (MRE) are selected as evaluation indexes. Among them, MAE and MRE characterize the deviation of the model fitting to the true value, and the smaller the means the more accurate the result, as follows:
In Equations (18) and (19), is the real value, is the imputed value, and is the total number of samples.
3. Results
The state-controlled station dataset exhibits an average missing rate of 5%. Table 4 presents the results of a comparative analysis of missing value imputation between the BRITS-ALSTM model and other baseline imputation methods, utilizing the state-controlled station dataset. Notably, the BRITS, BRITS-LSTM, and BRITS-ALSTM approaches demonstrate superior performance over statistical modeling methods, including Mean, KNN, MF, MICE, and the M-RNN method, particularly in the context of six air pollutants. Each of these BRITS-based deep learning methods delivers enhanced imputation accuracy and reduced relative error, distinguishing themselves from traditional imputation methodologies. This enhanced performance is attributed to the nonlinear modeling capacity of deep learning methods, enabling a more nuanced fit to real-world data complexities. The variance in performance among these methods, contingent on the specific ambient air pollutant data being imputed, underscores the nuanced advantages and limitations inherent to their application across diverse data sets.

Table 4.
Comparison of imputation results for state-controlled station dataset.
Table 5 delineates the performance metrics of all evaluated models in imputation air quality data, utilizing the province-controlled station dataset. This particular dataset has a substantial missing rate of approximately 22%, representing a more pronounced data insufficiency. The empirical results underscore the pronounced efficacy of the BRITS, BRITS-LSTM, and BRITS-ALSTM models over both the conventional statistical modeling techniques and the M-RNN method. Combining the imputation results of air quality data from state-controlled and provincial-controlled stations, BRITS-ALSTM has the highest accuracy for PM2.5, O3, NO2, SO2, and CO, and BRITS-LSTM has the highest accuracy for PM10.

Table 5.
Comparison of imputation results for province-controlled station dataset.
To elucidate the distinctions between the imputed values and the observed values, Figure 5 shows the results of the BRITS-ALSTM model in imputing the missing hourly PM2.5 data at the state-controlled station 2676A from 1–8 January 2019, compared with the actual observations. In Figure 5 and Figure 6, the blue line represents the actual PM2.5 observations. The yellow line models data gaps in locations where true observations are present, simulating missing data scenarios. The red line depicts the outcomes of imputation derived from the BRITS-ALSTM model. It can be seen that the imputation values of the BRITS-ALSTM model are more consistent with the actual observations. Figure 6 shows the zoomed-in comparison between the imputed values and the actual observations of the BRITS-ALSTM model in 24 h for the first four days of Figure 5. It can be seen that the imputed results of the BRITS-ALSTM model have a small numerical difference from the real values. It can predict the rising or falling trend of pollutant concentration more accurately when filling the inflection time.
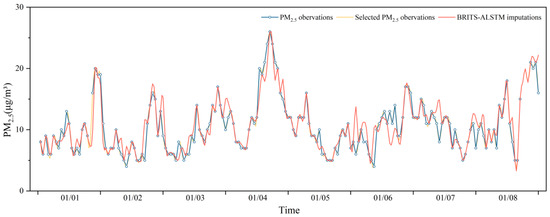
Figure 5.
Comparison of imputed and observed hourly PM2.5 concentrations at the state-controlled station 2676A, 1–8 January 2019.
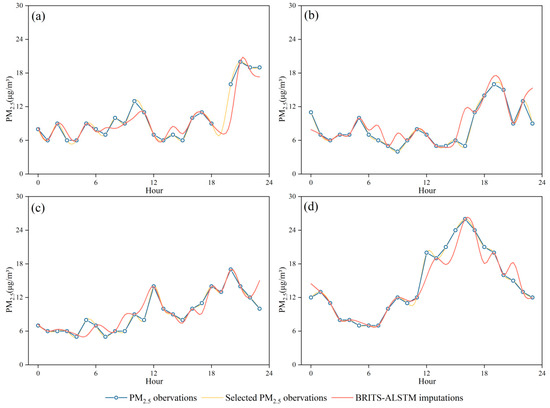
Figure 6.
Comparison of 24-h imputed values with observed values.
4. Discussion
4.1. BRITS vs. BRITS-ALSTM
Performance variations are observable among the BRITS, BRITS-LSTM, and BRITS-ALSTM models in the context of six types of air quality datasets. As depicted in Figure 7, the BRITS-ALSTM model performs best when imputing PM2.5, O3, NO2, SO2, and CO data compared to the BRITS and BRITS-LSTM models. During the accuracy validation of the model using the test set, imputing the CO data from the state-controlled stations had the highest accuracy compared to imputing the other five types of air quality data. Taking CO as an example, Figure 8a shows the correlation between the imputation results of the BRITS model and the CO observations, and Figure 8b shows the correlation between the imputation results of the BRITS-ALSTM model, the CO observations, and the coefficient of determination R-squared (R2) of the BRITS and BRITS-ALSTM models are 0.67 and 0.76, respectively, and the accuracy of the improved model is increased by 13.43%. The BRITS-ALSTM reduces the MAE metrics by 0.0258 and 0.0554, equivalent to reductions of 20.03% and 34.97%, when compared with the BRITS and BRITS-LSTM models. The MRE metrics decline by 0.0408 and 0.0877, marking improvements of 20.01% and 34.98% over the BRITS and BRITS-LSTM models. These findings underline the superior imputation capability of the BRITS-ALSTM model, enhanced by the integration of the Seq2Seq structure and attention mechanism. The BRITS-LSTM model, incorporating only the Seq2Seq structure, is secondary in performance, while the BRITS model trails as the least effective.
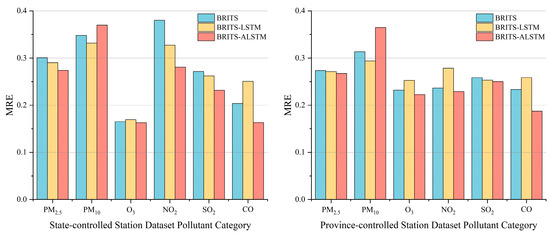
Figure 7.
Comparison of MRE performance of three BRITS-based models.
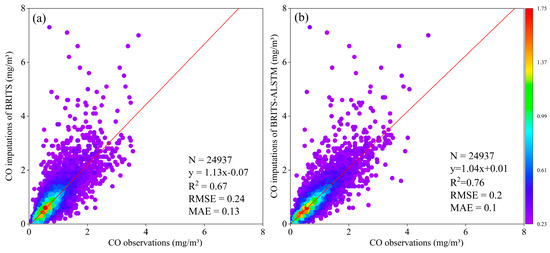
Figure 8.
Correlation of model imputation results with CO observations. (a) Correlation between BRITS estimates and CO observations, and (b) correlation between BRITS-ALSTM estimates and CO observations.
The datasets from the state-controlled and province-controlled stations are indicative of the imputation contexts influenced by diverse data omission rates. The three BRITS-based models’ imputation efficiency manifests distinct trends and dynamics within these separate contexts. To elucidate the disparities between the BRITS variants, which integrate Seq2Seq architecture and attention mechanisms, two supplementary parameters are introduced. The first parameter is denoted as . This metric evaluates the enhancement in the MRE for each technique compared to the imputation performed using the Mean method, as quantified by the subsequent equation.
denotes the average MRE value assessed at diverse missing rates. The second metric introduced is the Sensitivity to the Missing Rate . This metric quantifies the impact of varying missing rates on the performance of a given model. It is computed through the determination of the slope between the Missing Rate and , as expressed in the subsequent equation.
Table 6 presents a comparative analysis of model performance across varied missing rate scenarios. It is evident from the data that the integration of the Seq2Seq structure elevates the of the standard BRITS model from 72.08% to 72.72% under a 5% missing rate condition. Further enhancement is observed with the incorporation of the attention mechanism, pushing to an impressive 75.22%. Conversely, at a 22% missing rate, the Seq2Seq structure alone fails to augment . Nevertheless, its combination with the attention mechanism elevates the metric to 74.54%. This underscores the pivotal role of the attention mechanism in optimizing MRE for the imputation of extensive time-series data across diverse missing rate contexts. While the Seq2Seq structure does not consistently bolster performance across all missing rate conditions, its contribution to model robustness is unequivocal. This is evidenced by the marked reduction in the of the BRITS-ALSTM model by 90.58% and 63.39%, respectively, attesting to its capacity to stabilize model performance amidst fluctuating data missing rates.

Table 6.
Comparison of method performance at different missing data rates.
In conclusion, the BRITS-ALSTM model demonstrates substantial enhancement in handling long-time series air quality data with varied missing rates, compared to the original BRITS and BRITS-LSTM models. This underscores the efficacy of incorporating the Seq2Seq structure and attention mechanism, attesting to their collective contribution in augmenting the accuracy of imputing missing values in extended time series.
4.2. Application of BRITS-ALSTM Imputed Dataset
Air pollutant prediction experiments were carried out using the BRITS-ALSTM model imputed with the complete dataset of state and provincial control stations. The pollutant concentrations for the next 24 h were predicted using a two-layer LSTM network with units = 64, batch-size = 32, and epochs = 100, and the performance was compared with that of the dataset using the mean-filled dataset on the same prediction model. Table 7 shows the results of air quality prediction accuracy evaluation of the datasets imputed by mean and BRITS-ALSTM models respectively on the LSTM model. The datasets imputed using the BRITS-ALSTM model are all better than the datasets imputed using the mean-filling method. The complete dataset imputed by BRITS-ALSTM contributes to the improvement of the prediction accuracy.

Table 7.
Effect of different imputation method datasets on prediction results.
5. Conclusions
In this research, the BRITS-ALSTM model was developed, augmenting the original BRITS model with an integration of the Seq2Seq structure and an attention mechanism. This model achieved high-precision imputation of missing data using the air quality dataset from state-controlled and provincial-controlled stations in Qinghai Province for the years 2019–2022. It was compared with various methods, including Mean, KNN, MF, MICE, M-RNN, and BRITS, as well as BRITS-LSTM. The BRITS-ALSTM model effectively addresses the challenges of high rates of missing data and low validity of evaluated data at the Qinghai-Tibetan Plateau automated air monitoring stations, demonstrating its suitability for processing missing air quality values in alpine regions. Future studies on the BRITS-ALSTM model will consider the influence of meteorological and geographic environments surrounding the automatic air monitoring stations [57].
Author Contributions
Conceptualization, Y.W., K.L. and Y.H.; methodology, Y.W. and Q.F.; software, W.L. (Wei Luo); data curation, Y.W., Q.F. and P.W.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W., K.L. and Y.H.; visualization, Y.W., W.L. (Wentao Li), X.L. and S.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by North China Institute of Aerospace Engineering Doctoral Fund: Research on Spatio-Temporal Data Fusion Analysis of Beijing-Tianjin-Hebei City Cluster (BKY-2020-33) and Qinghai Province Air Pollution Status Assessment and Refined Management Support Project (2023-005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
State-controlled station data and province-controlled station data published by the China National Environmental Monitoring Centre: https://quotsoft.net/air/, accessed on 22 January 2023.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, Y.; Luo, B.; Li, J.; Hao, Y.; Yang, W.; Shi, F.; Chen, Y.; Simayi, M.; Xie, S. Characteristics of six criteria air pollutants before, during, and after a severe air pollution episode caused by biomass burning in the southern Sichuan Basin, China. Atmos. Environ. 2019, 215, 116840. [Google Scholar] [CrossRef]
- Ebelt, S.T.; D’Souza, R.R.; Yu, H.; Scovronick, N.; Moss, S.; Chang, H.H. Monitoring vs. modeled exposure data in time-series studies of ambient air pollution and acute health outcomes. J. Expo. Sci. Environ. Epidemiol. 2023, 33, 377–385. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Zhao, C.; Yang, Y. A comprehensive analysis of the spatio-temporal variation of urban air pollution in China during 2014–2018. Atmos. Environ. 2020, 220, 117066. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J.; Oh, S.; Park, S.; Mayer, H. Air pollution assessment in Seoul, South Korea, using an updated daily air quality index. Atmos. Pollut. Res. 2023, 14, 101728. [Google Scholar] [CrossRef]
- Zou, B.; You, J.; Lin, Y.; Duan, X.; Zhao, X.; Fang, X.; Campen, M.J.; Li, S. Air pollution intervention and life-saving effect in China. Environ. Int. 2019, 125, 529–541. [Google Scholar] [CrossRef]
- Tzanis, C.G.; Alimissis, A.; Koutsogiannis, I. Addressing missing environmental data via a machine learning scheme. Atmosphere 2021, 12, 499. [Google Scholar] [CrossRef]
- Kadow, C.; Hall, D.M.; Ulbrich, U. Artificial intelligence reconstructs missing climate information. Nat. Geosci. 2020, 13, 408–413. [Google Scholar] [CrossRef]
- Singh, D.; Dahiya, M.; Kumar, R.; Nanda, C. Sensors and systems for air quality assessment monitoring and management: A review. J. Environ. Manag. 2021, 289, 112510. [Google Scholar] [CrossRef]
- Motlagh, N.H.; Lagerspetz, E.; Nurmi, P.; Li, X.; Varjonen, S.; Mineraud, J.; Siekkinen, M.; Rebeiro-Hargrave, A.; Hussein, T.; Petaja, T. Toward massive scale air quality monitoring. IEEE Commun. Mag. 2020, 58, 54–59. [Google Scholar] [CrossRef]
- Nasir, H.; Goyal, K.; Prabhakar, D. Review of air quality monitoring: Case study of India. Indian J. Sci. Technol. 2016, 9, 105255. [Google Scholar] [CrossRef]
- Feng, Y.; Ning, M.; Lei, Y.; Sun, Y.; Liu, W.; Wang, J. Defending blue sky in China: Effectiveness of the “Air Pollution Prevention and Control Action Plan” on air quality improvements from 2013 to 2017. J. Environ. Manag. 2019, 252, 109603. [Google Scholar] [CrossRef] [PubMed]
- Feenstra, B.; Papapostolou, V.; Hasheminassab, S.; Zhang, H.; Der Boghossian, B.; Cocker, D.; Polidori, A. Performance evaluation of twelve low-cost PM2.5 sensors at an ambient air monitoring site. Atmos. Environ. 2019, 216, 116946. [Google Scholar] [CrossRef]
- Zhao, A.; Nie, Y.; Hou, X.; Li, Y.; Li, H. Development of an unmanned 10-factor automatic weather station for cold and arid regions. Highl. Meteorol. 2003, 2003, 646–649. [Google Scholar]
- Wijesekara, L.; Liyanage, L. Mind the Large Gap: Novel Algorithm Using Seasonal Decomposition and Elastic Net Regression to Impute Large Intervals of Missing Data in Air Quality Data. Atmosphere 2023, 14, 355. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.; Lu, J. Exploring the relationship between air pollution and meteorological conditions in China under environmental governance. Sci. Rep. 2020, 10, 14518. [Google Scholar] [CrossRef]
- Zhang, Y.; Thorburn, P.J. Handling missing data in near real-time environmental monitoring: A system and a review of selected methods. Future Gener. Comput. Syst. 2022, 128, 63–72. [Google Scholar] [CrossRef]
- Ottosen, T.-B.; Kumar, P. Outlier detection and gap filling methodologies for low-cost air quality measurements. Environ. Sci. Process. Impacts 2019, 21, 701–713. [Google Scholar] [CrossRef]
- Rashid, W.; Gupta, M.K. A perspective of missing value imputation approaches. In Proceedings of the Advances in Computational Intelligence and Communication Technology (CICT 2019), Allahabad, India, 6–8 December 2019; Springer: Berlin/Heidelberg, Germany, 2021; pp. 307–315. [Google Scholar]
- Armina, R.; Zain, A.M.; Ali, N.A.; Sallehuddin, R. A review on missing value estimation using imputation algorithm. J. Phys. Conf. Ser. 2017, 892, 012004. [Google Scholar] [CrossRef]
- Egigu, M. Techniques of Filling Missing Values of Daily and Monthly Rain Fall Data: A Review. SF J. Environ. Earth Sci. 2020, 3, 1036. [Google Scholar]
- Mao, Y.; Zhang, J.; Qi, H.; Wang, L. DNN-MVL: DNN-multi-view-learning-based recover block missing data in a dam safety monitoring system. Sensors 2019, 19, 2895. [Google Scholar] [CrossRef]
- Samal, K.K.R.; Babu, K.S.; Das, S.K. Multi-directional temporal convolutional artificial neural network for PM2.5 forecasting with missing values: A deep learning approach. Urban Clim. 2021, 36, 100800. [Google Scholar] [CrossRef]
- Marchang, N.; Tripathi, R. KNN-ST: Exploiting spatio-temporal correlation for missing data inference in environmental crowd sensing. IEEE Sens. J. 2020, 21, 3429–3436. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.; Ding, Y.; Lin, C.; Jiang, F.; Wang, M.; Zhai, C. Transfer learning for long-interval consecutive missing values imputation without external features in air pollution time series. Adv. Eng. Inform. 2020, 44, 101092. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, X.; Yin, W.; Zou, Y.; Wang, Y. Missing data imputation for traffic flow based on combination of fuzzy neural network and rough set theory. J. Intell. Transp. Syst. 2021, 25, 439–454. [Google Scholar] [CrossRef]
- Baloch, M.A.; Wang, B. Analyzing the role of governance in CO2 emissions mitigation: The BRICS experience. Struct. Chang. Econ. Dyn. 2019, 51, 119–125. [Google Scholar]
- Worden, K.; Sohn, H.; Farrar, C.R. Novelty detection in a changing environment: Regression and interpolation approaches. J. Sound Vib. 2002, 258, 741–761. [Google Scholar] [CrossRef]
- Noor, M.; Yahaya, A.; Ramli, N.A.; Al Bakri, A.M. Filling missing data using interpolation methods: Study on the effect of fitting distribution. Key Eng. Mater. 2014, 594, 889–895. [Google Scholar] [CrossRef]
- Junninen, H.; Niska, H.; Tuppurainen, K.; Ruuskanen, J.; Kolehmainen, M. Methods for imputation of missing values in air quality data sets. Atmos. Environ. 2004, 38, 2895–2907. [Google Scholar] [CrossRef]
- Norazian, M.; Al Bakri, A.M.M.; Shukri, Y.A.; Azam, R.N. Estimation of missing values for air pollution data using interpolation technique. Simulation 2006, 75, 94. [Google Scholar]
- Saeipourdizaj, P.; Sarbakhsh, P.; Gholampour, A. Application of imputation methods for missing values of PM10 and O3 data: Interpolation, moving average and K-nearest neighbor methods. Environ. Health Eng. Manag. J. 2021, 8, 215–226. [Google Scholar] [CrossRef]
- Honghai, F.; Guoshun, C.; Cheng, Y.; Bingru, Y.; Yumei, C. A SVM regression based approach to filling in missing values. In Proceedings of the International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, Melbourne, Australia, 14–16 September 2005; pp. 581–587. [Google Scholar]
- Patil, B.M.; Joshi, R.C.; Toshniwal, D. Missing value imputation based on k-mean clustering with weighted distance. In Proceedings of the Contemporary Computing: Third International Conference (IC3 2010), Noida, India, 9–11 August 2010; Proceedings Part I3. Springer: Berlin/Heidelberg, Germany, 2010; pp. 600–609. [Google Scholar]
- Kornelsen, K.; Coulibaly, P. Comparison of interpolation, statistical, and data-driven methods for imputation of missing values in a distributed soil moisture dataset. J. Hydrol. Eng. 2014, 19, 26–43. [Google Scholar] [CrossRef]
- Ye, Z.; Yang, J.; Zhong, N.; Tu, X.; Jia, J.; Wang, J. Tackling environmental challenges in pollution controls using artificial intelligence: A review. Sci. Total Environ. 2020, 699, 134279. [Google Scholar] [CrossRef] [PubMed]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef]
- Cao, W.; Wang, D.; Li, J.; Zhou, H.; Li, L.; Li, Y. Brits: Bidirectional recurrent imputation for time series. In Proceedings of the Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montréal, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Yoon, J.; Jordon, J.; Schaar, M. Gain: Missing data imputation using generative adversarial nets. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5689–5698. [Google Scholar]
- Cini, A.; Marisca, I.; Alippi, C. Filling the g_ap_s: Multivariate time series imputation by graph neural networks. arXiv 2021, arXiv:2108.00298. [Google Scholar]
- Ma, J.; Cheng, J.C.; Jiang, F.; Chen, W.; Wang, M.; Zhai, C. A bi-directional missing data imputation scheme based on LSTM and transfer learning for building energy data. Energy Build. 2020, 216, 109941. [Google Scholar] [CrossRef]
- Yin, Y.; Shi, C.; Zou, C.; Liu, X. Fusion of Seq2Seq and temporal attention mechanism for process quality prediction. Mech. Sci. Technol. 2019, 107, 287–300. [Google Scholar] [CrossRef]
- Weerakody, P.B.; Wong, K.W.; Wang, G.; Ela, W. A review of irregular time series data handling with gated recurrent neural networks. Neurocomputing 2021, 441, 161–178. [Google Scholar] [CrossRef]
- Iskandaryan, D.; Ramos, F.; Trilles, S. Air quality prediction in smart cities using machine learning technologies based on sensor data: A review. Appl. Sci. 2020, 10, 2401. [Google Scholar] [CrossRef]
- Chen, H.; Guan, M.; Li, H. Air quality prediction based on integrated dual LSTM model. IEEE Access 2021, 9, 93285–93297. [Google Scholar] [CrossRef]
- Liu, B.; Yan, S.; Li, J.; Qu, G.; Li, Y.; Lang, J.; Gu, R. A sequence-to-sequence air quality predictor based on the n-step recurrent prediction. IEEE Access 2019, 7, 43331–43345. [Google Scholar] [CrossRef]
- Zhu, Z.; Rao, Y.; Wu, Y.; Qi, H.; Zhang, Y. Research Progress of Attentional Mechanisms in Deep Learning. J. Chin. Inf. 2019, 33, 1–11. [Google Scholar]
- Utama, I.B.K.Y.; Tran, D.H.; Jang, Y.M. Short-term PM2.5 Prediction using Modified Attention Seq2Seq BiLSTM. In Proceedings of the 2022 Thirteenth International Conference on Ubiquitous and Future Networks (ICUFN), Barcelona, Spain, 5–8 July 2022; pp. 462–465. [Google Scholar]
- Tu, X.-Y.; Zhang, B.; Jin, Y.-P.; Zou, G.-J.; Pan, J.-G.; Li, M.-Z. Longer time span air pollution prediction: The attention and autoencoder hybrid learning model. Math. Probl. Eng. 2021, 2021, 5515103. [Google Scholar] [CrossRef]
- Caiji, Z. Construction and empirical research on differentiated evaluation index system for ecological civilization construction in Qinghai Province. Ecol. Econ. 2023, 39, 214–220. [Google Scholar]
- Sun, H.; Zheng, D.; Yao, T.; Zhang, Y. Protection and construction of national ecological security barriers on the Tibetan Plateau. J. Geogr. 2012, 67, 3–12. [Google Scholar]
- Liang, G. Practical exploration of intelligent operation and maintenance platform construction for ambient air automatic stations. Sci. Technol. Innov. 2020, 2020, 138–139. [Google Scholar] [CrossRef]
- Xie, C.; Huang, C.; Zhang, D.; He, W. BiLSTM-I: A deep learning-based long interval gap-filling method for meteorological observation data. Int. J. Environ. Res. Public Health 2021, 18, 10321. [Google Scholar] [CrossRef]
- Shuai, P.; Li, X.; Zhou, X.; Liu, Y. Research Progress on Statistical Processing Methods for Missing Data. China Health Stat. 2013, 30, 135–139+142. [Google Scholar]
- Hwang, W.-S.; Li, S.; Kim, S.-W.; Lee, K. Data imputation using a trust network for recommendation via matrix factorization. Comput. Sci. Inf. Syst. 2018, 15, 347–368. [Google Scholar] [CrossRef]
- Van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Yoon, J.; Zame, W.R.; van der Schaar, M. Multi-directional recurrent neural networks: A novel method for estimating missing data. In Proceedings of the Time Series Workshop in International Conference on Machine Learning, New Orleans, LA, USA, 18–21 November 2017. [Google Scholar]
- Xing, Y.; Brimblecombe, P. Role of vegetation in deposition and dispersion of air pollution in urban parks. Atmos. Environ. 2019, 201, 73–83. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).