Parameter Optimisation-Based Hybrid Reference Evapotranspiration Prediction Models: A Systematic Review of Current Implementations and Future Research Directions
Abstract
1. Introduction
2. Methodology
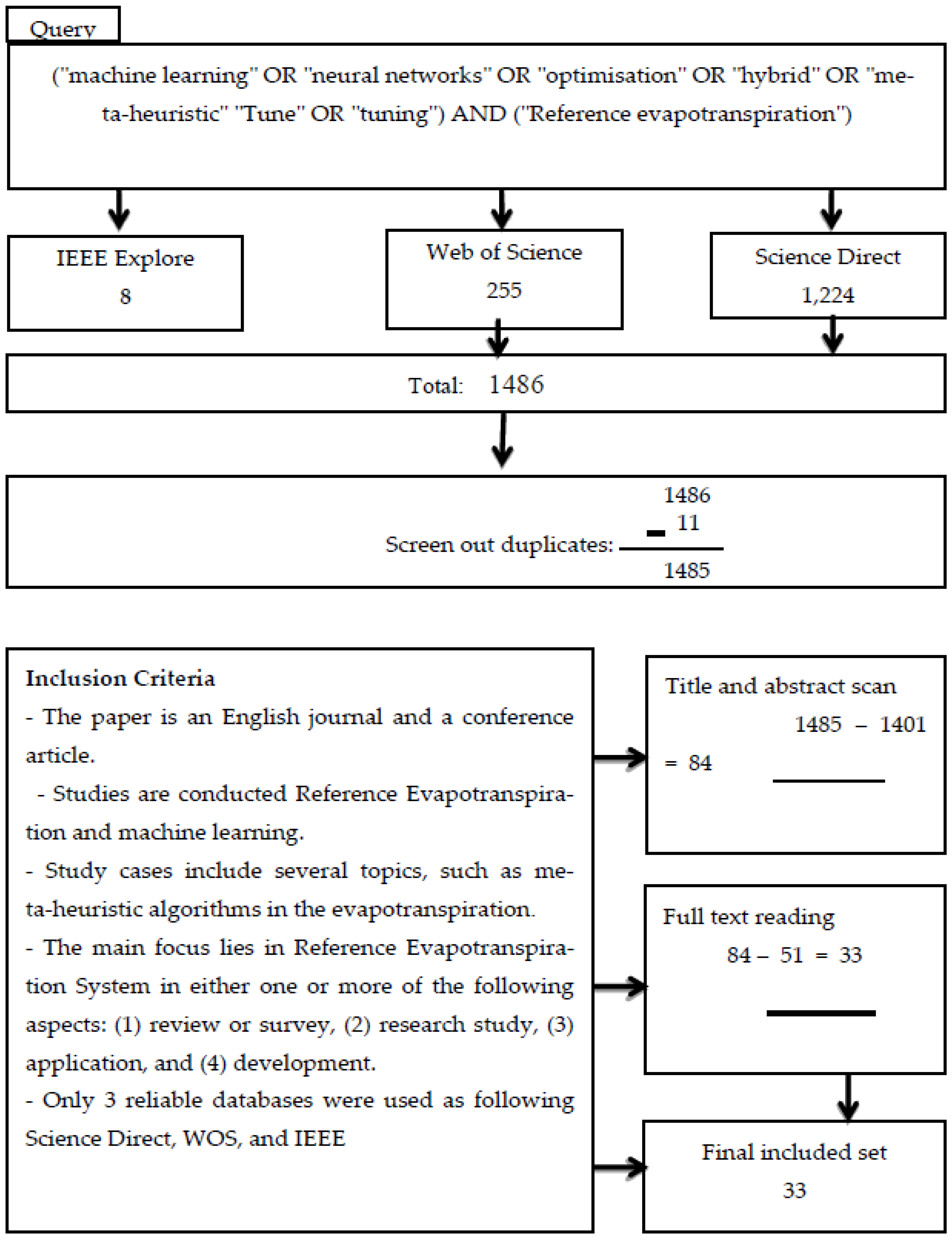
2.1. Information Sources
2.2. Study Selection
2.3. Search
2.4. Eligibility Criteria
2.5. Data Collection Process
2.6. Articles Search Results and Statistical Information
3. Results
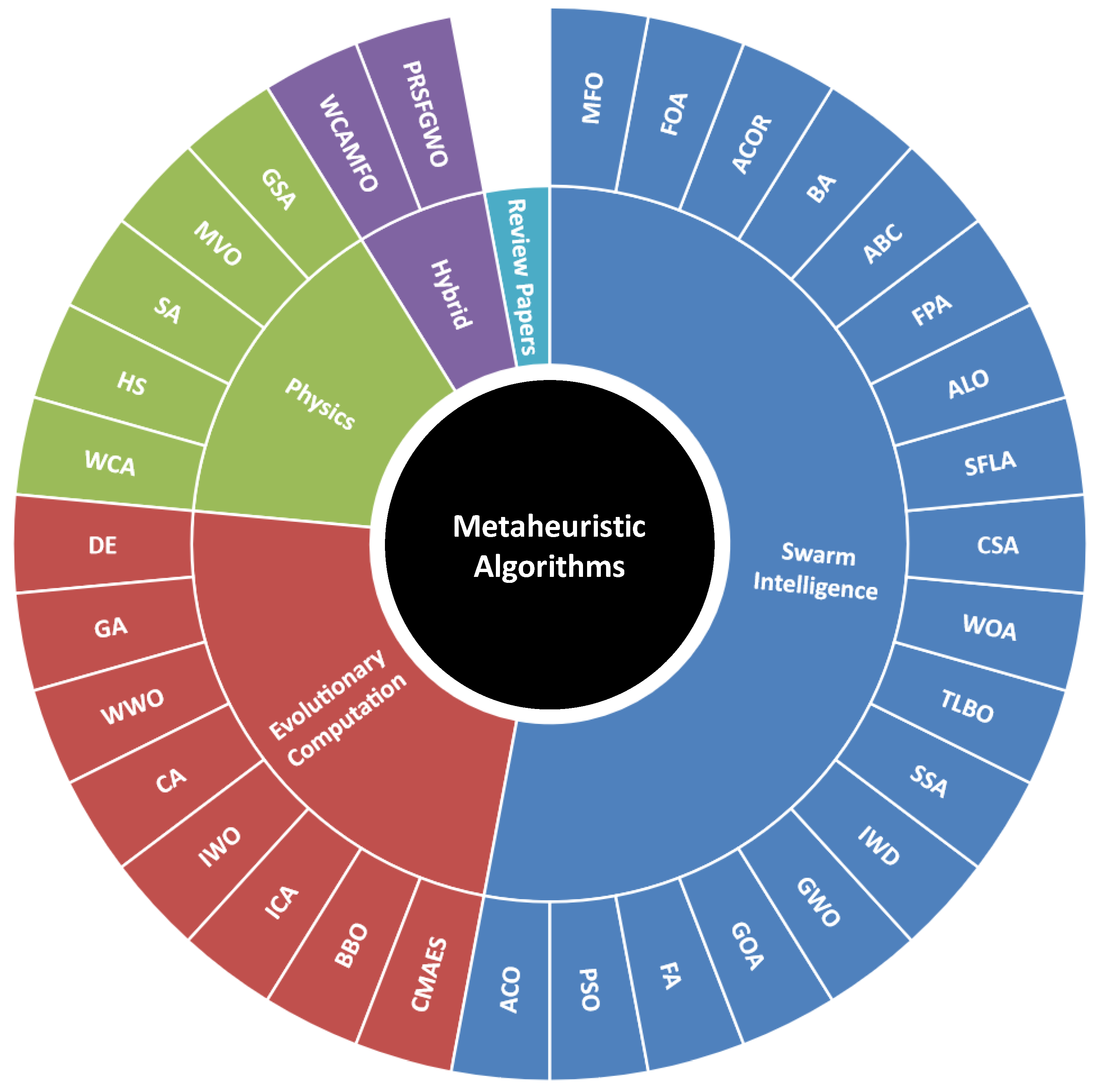
3.1. Meta-Heuristic Algorithms
3.1.1. Swarm Intelligence-Based Algorithms (SI)
- a
- Particle Swarm Optimisation (PSO)
- b
- Ant Colony Optimisation (ACO)
- c
- Shuffled Frog-Leaping Algorithm (SFLA)
- d
- Firefly Algorithm (FA)
- e
- Grasshopper Optimisation Algorithm (GOA)
- f
- Grey Wolf Optimiser Algorithm (GWO)
- g
- Intelligent Water Drops (IWD)
- h
- Salp Swarm Algorithm (SSA)
- i
- Whale Optimisation Algorithm (WOA)
- j
- Cuckoo Search Algorithm (CSA)
- k
- Flower Pollination Algorithm (FPA)
- l
- Artificial Bee Colony (ABC)
- m
- Bee Algorithm (BA)
- n
- Continuous Ant Colony Optimisation (ACOR)
- o
- Ant Lion Optimiser (ALO)
- p
- Moth-Flame Optimisation Algorithm (MFO)
- q
- Teaching-Learning-Based Optimisation (TLBO)
- r
- Fruit fly Optimisation Algorithm (FOA)
3.1.2. Evolutionary Computation-Based Algorithms (EC)
- Genetic Algorithm (GA)
- b
- Differential Evolution (DE)
- c
- Biogeography-Based Optimisation (BBO)
- d
- Covariance Matrix Adaptation Evolution Strategy (CMAES)
- e
- Imperialist Competitive Algorithm (ICA)
- f
- Invasive Weed Optimisation (IWO)
- g
- Cultural Algorithms (CA)
- h
- Water Wave Optimisation (WWO)
3.1.3. Physics-Based Algorithms (PH)
- a
- Gravitational Search Algorithm (GSA)
- b
- Multi-Verse Optimiser (MVO)
- c
- Simulated Annealing Optimisation Algorithm (SA)
- d
- Harmony Search (HS)
- e
- Water Cycle Optimisation Algorithm (WCA)
3.1.4. Hybrid Meta-Heuristic Algorithms
- a
- Adaptive Dynamic Algorithm Coupled with the Grey Wolf Optimiser (PRSFGWO)
- b
- Water Cycle-Moth Flame Optimisation (WCAMFO)
3.2. Review and Survey Articles
4. Discussion
5. Analysing Scientific Maps
5.1. Main Information
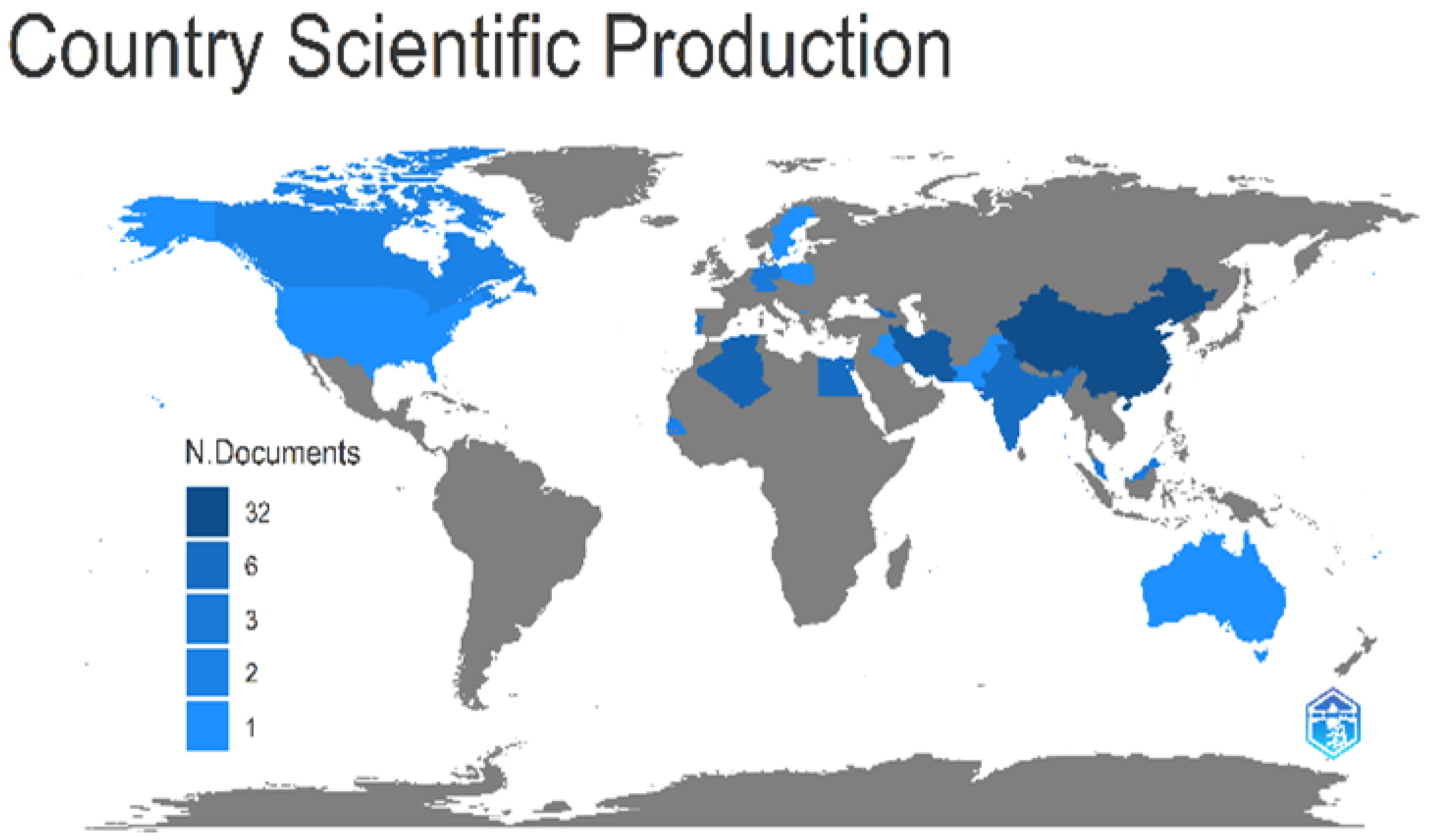
5.2. Country Scientific Production
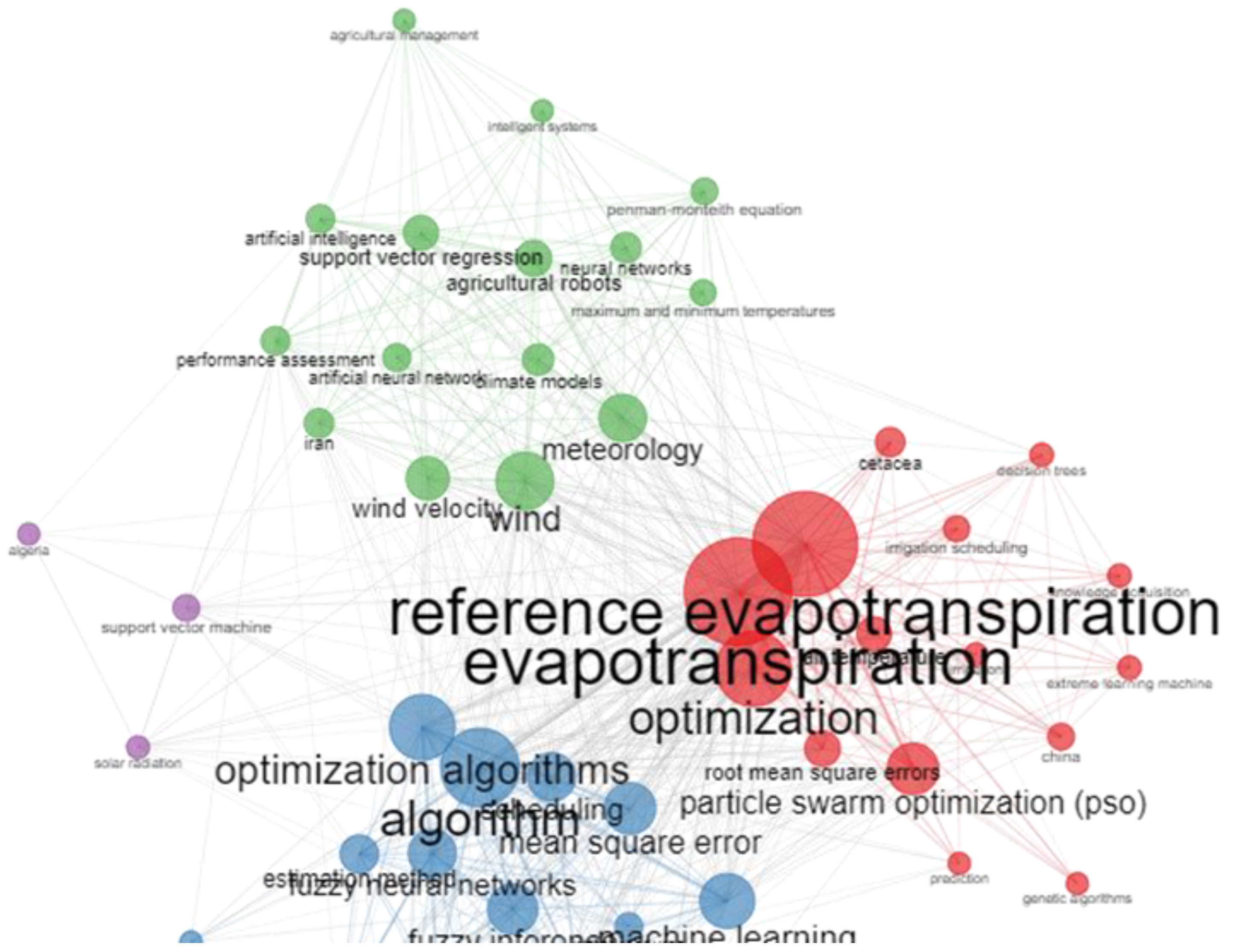
5.3. Cloud of Words
5.4. Distribution Based on Affiliations
5.5. Co-Occurrence
6. Recommendations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | Explanation |
| ABC | Artificial Bee Colony |
| Acc | Accuracy |
| ACO | Ant Colony Optimisation |
| ACOR | Continuous Ant Colony Optimisation |
| AI | Artificial Intelligence |
| ALO | Ant Lion Optimizer |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN | Artificial Neural Network |
| BA | Bee Algorithm |
| BBO | Biogeography-Based Optimisation |
| BMA | Bayesian Model Averaging |
| BSS | Bright Sunshine Hours |
| CART | Classification and Regression Tree |
| CMAES | Covariance Matrix Adaptation Evolution Strategy |
| COR | Pearson’s correlation |
| CSA | Cuckoo Search Algorithm |
| DE | Differential Evolution |
| DENFIS | Dynamic Evolving Neural-Fuzzy Inference System |
| DET | Decision Tree Regressor |
| DFA | Dragonfly Algorithm |
| EC | Evolutionary Computing |
| ELM | Extreme Learning Machine |
| EP | Weekly Cumulative Pan Evaporation |
| Epan | Pan Evaporation |
| ET | Evapotranspiration |
| ETo | Reference Evapotranspiration |
| FA | Firefly Algorithm |
| FIS | Fuzzy Inference System |
| FOA | Fruit Fly Optimisation Algorithm |
| FPA | Flower Pollination Algorithm |
| GA | Genetic Algorithm |
| GOA | Grasshopper Optimisation Algorithm |
| GP | Genetic Programming |
| GPI | Global Performance Index |
| GSA | Gravitational Search Algorithm |
| GWO | Grey Wolf Optimizer |
| HFS | Hierarchical Fuzzy System |
| HS | Harmony Search |
| ICA | Imperialist Competitive Algorithm |
| IOA | Willmott’s Index of Agreement |
| IOS | Index Of Scattering |
| IWD | Intelligent Water Drops |
| IWO | Invasive Weed Optimisation |
| KGE | Kling–Gupta Efficiency |
| KHA | Krill Herd Algorithm |
| KNR | K-Neighbours Regressor |
| LSSVM | Least Square Support Vector Machine |
| LSSVR | Least Squares Support Vector Regression |
| M5 | Model Tree |
| MAD | Mean Absolute Deviation |
| MADE | Median Absolute Deviation |
| MAE | Mean Absolute Error |
| MAX | Maximum Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MBE | Mean Bias Error |
| MEMD | Multivariate Empirical Mode Decomposition |
| MFO | Moth-Flame Optimisation Algorithm |
| MLP | Multilayer Perceptron |
| MLR | Multiple Linear Regression |
| MRE | Mean Relative Error |
| MSE | Mean Square Error |
| MVC | Model Validity Coefficient |
| MVO | Multi-Verse Optimizer |
| NNE | Non-Linear Neural Ensemble |
| NRMSE | Normalised Root Mean Squared Error |
| NSE | Nash–Sutcliffe Coefficient of Efficiency |
| P | Precipitation |
| PBIAS | Percent bias |
| PCA | Principal Component Analysis |
| FAO-56 PM | Penman–Monteith Model |
| PRSFGWO | Adaptive Dynamic Algorithm Coupled with the Grey Wolf Optimizer |
| PSO | Particle Swarm Optimisation |
| R | Correlation Coefficient |
| R² | Coefficient of Determination |
| Ra | Extraterrestrial Solar Radiation |
| RF | Random Forest |
| RFR | Random Forest Regressor |
| RH | Relative Humidity |
| RH1 | Morning Relative Humidity During |
| RH2 | Afternoon Relative Humidity |
| RL | Relief |
| RMSE | Root Mean Square Error |
| RMSRE | Root Mean Square Relative Error |
| RRMSE | Relative Root Mean Square Error |
| Rs | Global Solar Radiation |
| RT | Regression Tree |
| SA | Simulated Annealing Optimisation Algorithm |
| SFLA | Shuffled Frog-Leaping Algorithm |
| SIndex | Scatter Index |
| SONN | Second-Order Neural Network |
| SSA | Salp Swarm Algorithm |
| SSD | Sunshine Duration |
| SSWC | Average Surface Soil Water Content |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| T | Air Temperature |
| Tave | Average Temperature |
| Tmax | Maximum Temperature |
| Tmean | Mean Air Temperature |
| Tmin | Minimum Temperature |
| TD | Taylor Diagram |
| Tstat | T-statistic Test |
| TLBO | Teaching-Learning-Based Optimisation |
| U2 | Wind Speed at a Height of 2 m |
| U95 | Uncertainty with 95% Confidence Level |
| U | Theil Inequality Statistic |
| UB | Bias Proportion of Theil Inequality Statistic |
| UC | Covariance Proportion of Theil Inequality Statistic |
| UV | Variance Proportion of Theil Inequality Statistic |
| Vp | Vapour Pressure |
| VPD | Saturated Water Vapour Pressure Deficit |
| WCA | Water Cycle Optimisation Algorithm |
| WCAMFO | Water Cycle-Moth Flame Optimisation |
| WoS | Web of Science |
| WOA | Whale Optimisation Algorithm |
| WS | Wind Speed |
| WWO | Water Wave Optimisation |
| XGB | Extreme Gradient Boosting |
References
- Kumar, R.; Shankar, V.; Kumar, M.J. Modelling of Crop Reference Evapotranspiration: A Review. J. Environ. Res. Technol. 2011, 1, 239–246. [Google Scholar]
- Čadro, S.; Cherni-Čadro, S.; Marković, M.; Žurovec, J. A reference evapotranspiration map for Bosnia and Herzegovina. Int. Soil Water Conserv. Res. 2019, 7, 89–101. [Google Scholar] [CrossRef]
- Yahaya, O.; Hope, I. Assessment of Reference Evapotranspiration Estimation Models. Asian Rev. Environ. Earth Sci. 2020, 7, 26–34. [Google Scholar] [CrossRef][Green Version]
- Raza, A.; Hu, Y.; Shoaib, M.; Abd Elnabi, M.K.; Zubair, M.; Nauman, M.; Syed, N. A Systematic Review on Estimation of Reference Evapotranspiration under Prisma Guidelines. Pol. J. Environ. Stud. 2021, 30, 5413–5422. [Google Scholar] [CrossRef]
- Jawale, B.; Awari, V.K.I.; Khodke, U.M. Spatial Distribution of Reference Evapotranspiration for Aurangabad District. Int. J. Curr. Microbiol. Appl. Sci. 2022, 11, 50–60. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H. Improving reference evapotranspiration estimation using novel inter-model ensemble approaches. Comput. Electron. Agric. 2021, 187, 106227. [Google Scholar] [CrossRef]
- Exner-Kittridge, M.G.; Rains, M.C.J. Case study on the accuracy and cost/effectiveness in simulating reference evapotranspiration in West-Central Florida. J. Hydrol. Eng. 2010, 15, 696–703. [Google Scholar] [CrossRef]
- Wu, L.; Peng, Y.; Fan, J.; Wang, Y.; Huang, G. A novel kernel extreme learning machine model coupled with K-means clustering and firefly algorithm for estimating monthly reference evapotranspiration in parallel computation. Agric. Water Manag. 2021, 245, 106624. [Google Scholar] [CrossRef]
- Dong, J.; Liu, X.; Huang, G.; Fan, J.; Wu, L.; Wu, J. Comparison of four bio-inspired algorithms to optimize KNEA for predicting monthly reference evapotranspiration in different climate zones of China. Comput. Electron. Agric. 2021, 186, 106594. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H. Swarm-based optimization as stochastic training strategy for estimation of reference evapotranspiration using extreme learning machine. Agric. Water Manag. 2021, 243, 106211. [Google Scholar] [CrossRef]
- Yan, S.; Wu, L.; Fan, J.; Zhang, F.; Zou, Y.; Wu, Y. A novel hybrid WOA-XGB model for estimating daily reference evapotranspiration using local and external meteorological data: Applications in arid and humid regions of China. Agric. Water Manag. 2021, 244, 106594. [Google Scholar] [CrossRef]
- Rashid Niaghi, A.; Hassanijalilian, O.; Shiri, J.J.H. Estimation of reference evapotranspiration using spatial and temporal machine learning approaches. Hydrology 2021, 8, 25. [Google Scholar] [CrossRef]
- El-Kenawy, E.M.; Zerouali, B.; Bailek, N.; Bouchouich, K.; Hassan, M.A.; Almorox, J.; Kuriqi, A.; Eid, M.; Ibrahim, A. Improved weighted ensemble learning for predicting the daily reference evapotranspiration under the semi-arid climate conditions. Environ. Sci. Pollut. Res. Int. 2022, 81279–81299. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Fernandes Filho, E.I. Estimation of reference evapotranspiration in Brazil with limited meteorological data using ANN and SVM—A new approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Keshtegar, B.; Kisi, O.; Ghohani Arab, H.; Zounemat-Kermani, M.J.W. Subset modeling basis ANFIS for prediction of the reference evapotranspiration. Water Resour. Manag. 2018, 32, 1101–1116. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Gong, D.; Zhang, Q.; Zhao, L. Evaluation of random forests and generalized regression neural networks for daily reference evapotranspiration modelling. Agric. Water Manag. 2017, 193, 163–173. [Google Scholar] [CrossRef]
- Wen, X.; Si, J.; He, Z.; Wu, J.; Shao, H.; Yu, H.J.W. Support-vector-machine-based models for modeling daily reference evapotranspiration with limited climatic data in extreme arid regions. Water Resour. Manag. 2015, 29, 3195–3209. [Google Scholar] [CrossRef]
- Abdullah, S.S.; Malek, M.A.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme Learning Machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid particle swarm optimization with extreme learning machine for daily reference evapotranspiration prediction from limited climatic data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Mohamed Shah, N.J. Review on forecasting of photovoltaic power generation based on machine learning and metaheuristic techniques. IET Renew. Power Gener. 2019, 13, 1009–1023. [Google Scholar] [CrossRef]
- Maroufpoor, S.; Bozorg-Haddad, O.; Maroufpoor, E. Reference evapotranspiration estimating based on optimal input combination and hybrid artificial intelligent model: Hybridization of artificial neural network with grey wolf optimizer algorithm. J. Hydrol. 2020, 588, 125060. [Google Scholar] [CrossRef]
- Tao, H.; Diop, L.; Bodian, A.; Djaman, K.; Ndiaye, P.M.; Yaseen, Z.M. Reference evapotranspiration prediction using hybridized fuzzy model with firefly algorithm: Regional case study in Burkina Faso. Agric. Water Manag. 2018, 208, 140–151. [Google Scholar] [CrossRef]
- Hajirahimi, Z.; Khashei, M.J.A.I.R. Hybridization of hybrid structures for time series forecasting: A review. Artif. Intell. Rev. 2022, 1–61. [Google Scholar] [CrossRef]
- Khudhair, Z.S.; Zubaidi, S.L.; Ortega-Martorell, S.; Al-Ansari, N.; Ethaib, S.; Hashim, K.J.E. A Review of Hybrid Soft Computing and Data Pre-Processing Techniques to Forecast Freshwater Quality’s Parameters: Current Trends and Future Directions. Environments 2022, 9, 85. [Google Scholar] [CrossRef]
- Krishnashetty, P.H.; Balasangameshwara, J.; Sreeman, S.; Desai, S.; Kantharaju, A.B. Cognitive computing models for estimation of reference evapotranspiration: A review. Cogn. Syst. Res. 2021, 70, 109–116. [Google Scholar] [CrossRef]
- Jing, W.; Yaseen, Z.M.; Shahid, S.; Saggi, M.K.; Tao, H.; Kisi, O.; Salih, S.Q.; Al-Ansari, N.; Chau, K.-W. Implementation of evolutionary computing models for reference evapotranspiration modeling: Short review, assessment and possible future research directions. Eng. Appl. Comput. Fluid Mech. 2019, 13, 811–823. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic algorithms: A comprehensive review. Comput. Intell. Multimed. Big Data Cloud Eng. Appl. 2018, 185–231. [Google Scholar] [CrossRef]
- Mirjalili, S.J. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Ridha, H.M.; Hizam, H.; Mirjalili, S.; Othman, M.L.; Ya’acob, M.E.; Abualigah, L.J.I.A. A novel theoretical and practical methodology for extracting the parameters of the single and double diode photovoltaic models. IEEE Access 2022, 10, 11110–11137. [Google Scholar] [CrossRef]
- Majhi, B.; Naidu, D. Differential evolution based radial basis function neural network model for reference evapotranspiration estimation. SN Appl. Sci. 2021, 3, 56. [Google Scholar] [CrossRef]
- Roy, D.K.; Saha, K.K.; Kamruzzaman, M.; Biswas, S.K.; Hossain, M.A. Hierarchical Fuzzy Systems Integrated with Particle Swarm Optimization for Daily Reference Evapotranspiration Prediction: A Novel Approach. Water Resour. Manag. 2021, 35, 5383–5407. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, W.; Xu, L.; Zhangzhong, L.; Zhang, G.; Shan, F. A PSO-XGBoost Model for Estimating Daily Reference Evapotranspiration in the Solar Greenhouse. Intell. Autom. Soft Comput. 2020, 26, 989–1003. [Google Scholar] [CrossRef]
- Alizamir, M.; Kisi, O.; Muhammad Adnan, R.; Kuriqi, A. Modelling reference evapotranspiration by combining neuro-fuzzy and evolutionary strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Afshar, A.; Massoumi, F.; Afshar, A.; Mariño, M.A. State of the art review of ant colony optimization applications in water resource management. Water Resour. Manag。 2015, 29, 3891–3904. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F.J. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Zhen, Z.; Wang, D.; Liu, Y. Improved shuffled frog leaping algorithm for continuous optimization problem. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 2992–2995. [Google Scholar]
- Mehdizadeh, S.; Mohammadi, B.; Pham, Q.B.; Duan, Z. Development of Boosted Machine Learning Models for Estimating Daily Reference Evapotranspiration and Comparison with Empirical Approaches. Water 2021, 13, 3489. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. arXiv 2010, arXiv:1003.1409. [Google Scholar] [CrossRef]
- Roy, D.K.; Lal, A.; Sarker, K.K.; Saha, K.K.; Datta, B. Optimization algorithms as training approaches for prediction of reference evapotranspiration using adaptive neuro fuzzy inference system. Agric. Water Manag. 2021, 255, 107003. [Google Scholar] [CrossRef]
- Shiri, J.; Zounemat-Kermani, M.; Kisi, O.; Mohsenzadeh Karimi, S. Comprehensive assessment of 12 soft computing approaches for modelling reference evapotranspiration in humid locations. Meteorol. Appl. 2019, 27, e1841. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A.J. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A.J. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Lu, X.; Fan, J.; Lifeng, W.; Dong, J. Forecasting Multi-Step Ahead Monthly Reference Evapotranspiration Using Hybrid Extreme Gradient Boosting with GreyWolf Optimization Algorithm. Comput. Model. Eng. Sci. 2020, 125, 699–723. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Kumar, A.; Souag-Gamane, D.; Kisi, O. Estimation of monthly reference evapotranspiration using novel hybrid machine learning approaches. Hydrol. Sci. J. 2019, 64, 1824–1842. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Souag-Gamane, D.; Kisi, O. Artificial intelligence models versus empirical equations for modeling monthly reference evapotranspiration. Environ. Sci. Pollut. Res. Int. 2020, 27, 30001–30019. [Google Scholar] [CrossRef]
- Hosseini, H.S. Problem solving by intelligent water drops. In Proceedings of the 2007 IEEE congress on evolutionary computation, Singapore, 25–28 September 2007; pp. 3226–3231. [Google Scholar]
- Ahmadi, F.; Mehdizadeh, S.; Mohammadi, B.; Pham, Q.B.; Doan, T.N.C.; Vo, N.D. Application of an artificial intelligence technique enhanced with intelligent water drops for monthly reference evapotranspiration estimation. Agric. Water Manag. 2021, 244, 106622. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A.J. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agric. Water Manag. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Pandey, K.; Sammen, S.S.; Souag-Gamane, D.; Heddam, S.; Kisi, O. Monthly evapotranspiration estimation using optimal climatic parameters: Efficacy of hybrid support vector regression integrated with whale optimization algorithm. Env. Monit Assess 2020, 192, 696. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Wu, L.; Zhou, H.; Ma, X.; Fan, J.; Zhang, F. Daily reference evapotranspiration prediction based on hybridized extreme learning machine model with bio-inspired optimization algorithms: Application in contrasting climates of China. J. Hydrol. 2019, 577, 123960. [Google Scholar] [CrossRef]
- Yang, X.-S. Flower pollination algorithm for global optimization. In Proceedings of the International conference on unconventional computing and natural computation, Orléans, France, 3–7 September 2012; pp. 240–249. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- Pham, D.T.; Ghanbarzadeh, A.; Koç, E.; Otri, S.; Rahim, S.; Zaidi, M. The bees algorithm—A novel tool for complex optimisation problems. In Intelligent Production Machines and Systems; Elsevier: Amsterdam, The Netherlands, 2006; pp. 454–459. [Google Scholar]
- Yuce, B.; Packianather, M.S.; Mastrocinque, E.; Pham, D.T.; Lambiase, A.J.I. Honey bees inspired optimization method: The bees algorithm. Insects 2013, 4, 646–662. [Google Scholar] [CrossRef] [PubMed]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Mani, M.; Bozorg-Haddad, O.; Chu, X. Ant lion optimizer (ALO) algorithm. In Advanced Optimization by Nature-Inspired Algorithms; Springer: Berlin/Heidelberg, Germany, 2018; pp. 105–116. [Google Scholar]
- Mirjalili, S.J. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Roy, D.K.; Barzegar, R.; Quilty, J.; Adamowski, J. Using ensembles of adaptive neuro-fuzzy inference system and optimization algorithms to predict reference evapotranspiration in subtropical climatic zones. J. Hydrol. 2020, 591. [Google Scholar] [CrossRef]
- Zeinolabedini Rezaabad, M.; Ghazanfari, S.; Salajegheh, M. ANFIS Modeling with ICA, BBO, TLBO, and IWO Optimization Algorithms and Sensitivity Analysis for Predicting Daily Reference Evapotranspiration. J. Hydrol. Eng. 2020, 25, 125509. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.J. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Pan, W.-T. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowl. Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Ruiming, F.; Shijie, S. Daily reference evapotranspiration prediction of Tieguanyin tea plants based on mathematical morphology clustering and improved generalized regression neural network. Agric. Water Manag. 2020, 236, 106177. [Google Scholar] [CrossRef]
- Kokash, N. Telecommunications. An introduction to heuristic algorithms. Dep. Inform. Telecommun. Zogr. Greece 2005, 1–8. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Mohammed, S.J.; Zubaidi, S.L.; Ortega-Martorell, S.; Al-Ansari, N.; Ethaib, S.; Hashim, K.J.C.E. Application of hybrid machine learning models and data pre-processing to predict water level of watersheds: Recent trends and future perspective. Cogent Eng. 2022, 9, 2143051. [Google Scholar] [CrossRef]
- Jiao, P.; Hu, S.-J. Optimal Alternative for Quantifying Reference Evapotranspiration in Northern Xinjiang. Water 2021, 14, 1. [Google Scholar] [CrossRef]
- Robič, T.; Filipič, B. Differential evolution for multiobjective optimization. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guanajuato, Mexico, 9–11 March 2005; pp. 520–533. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P.J.E.C. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Mehrabian, A.R.; Lucas, C.J.E. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inf. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Reynolds, R.G. An introduction to cultural algorithms. In Proceedings of the Third Annual Conference on Evolutionary Programming, San Diego, CA, USA, 24–26 February 1994; pp. 131–139. [Google Scholar]
- Zheng, Y.-J.J.C.; Research, O. Water wave optimization: A new nature-inspired metaheuristic. Comput. Oper. Res 2015, 55, 1–11. [Google Scholar] [CrossRef]
- Sayyahi, F.; Farzin, S.; Karami, H.; Cai, N. Forecasting Daily and Monthly Reference Evapotranspiration in the Aidoghmoush Basin Using Multilayer Perceptron Coupled with Water Wave Optimization. Complexity 2021, 2021, 6683759. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S.J.I. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Muhammad Adnan, R.; Chen, Z.; Yuan, X.; Kisi, O.; El-Shafie, A.; Kuriqi, A.; Ikram, M. Reference Evapotranspiration Modeling Using New Heuristic Methods. Entropy 2020, 22, 547. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A.J.N.C. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Černý, V. Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M.J.C. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110, 151–166. [Google Scholar] [CrossRef]
- Ting, T.; Yang, X.-S.; Cheng, S.; Huang, K. Hybrid metaheuristic algorithms: Past, present, and future. Recent Adv. Swarm Intell. Evol. Comput. 2015, 71–83. [Google Scholar]
- Poorzahedy, H.; Rouhani, O.M. Hybrid meta-heuristic algorithms for solving network design problem. Eur. J. Oper. Res. 2007, 182, 578–596. [Google Scholar] [CrossRef]
- Abdul Kareem, B.; Zubaidi, S.L.; Ridha, H.M.; Al-Ansari, N.; Al-Bdairi, N.S.S.J.H. Applicability of ANN Model and CPSOCGSA Algorithm for Multi-Time Step Ahead River Streamflow Forecasting. Hydrology 2022, 9, 171. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S.J.S.C. An efficient hybrid algorithm based on Water Cycle and Moth-Flame Optimization algorithms for solving numerical and constrained engineering optimization problems. Methodol. Appl. 2019, 23, 1699–1722. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Heddam, S. Estimating reference evapotranspiration using hybrid adaptive fuzzy inferencing coupled with heuristic algorithms. Comput. Electron. Agric. 2021, 191, 106541. [Google Scholar] [CrossRef]


| Authors | Location | Size of Data | Scale | Predictors | Target | Models Used | Best Model | Measures of Accuracy |
|---|---|---|---|---|---|---|---|---|
| [51] | Iran | 2000–2014 | Daily | Tmin, Tmax, RH, U2, Rs, SSD | ETO | SVR, RL-SVR-WOA, RF-SVR-WOA, PCA-SVR-WOA, COR-SVR-WOA | RF-SVR-WOA | NSE, NRMSE, MAE, R2, RMSE |
| [30] | India | 2000–2019 | Weekly | Tmin, Tmax, Rs, BSS, WS, RH1, RH2, EP | ETO | ML-ANN, RBF-PSO, RBF-NN, RBF-DE | RBF-DE | NSE, RMSE, R2, MAPE |
| [62] | Bangladesh and USA | 2004–2019, 2009–2014, 2007–2010 | Daily | Tmin, Tmax, WS, RH, SSD, sensible heat flux, latent heat | ETO | ANFIS, ANFIS-BBO, ANFIS-FA, ANFIS-PSO, ANFIS-TLBO, LSGD, | ANFIS-FA | R, UC, RRMSE, SI, MAE, MBE, Tstat, U95, GPI, NSE, KGE, U, UB, UV, Shannon’s entropy, COV, GRA |
| [31] | Bangladesh | 2004–2019, 2015–2020 | Daily | Tmin, Tmax, RH, WS, SSD, Rs | ETO | RT, FIS, M5Tree, HFS, HFS-PSO | HFS-PSO | R, RMSE, NRMSE, Acc, NSE, IOA, MAE, MADE, Shannon’s entropy |
| [9] | China | 1966–2015 | Monthly | Tmin, Tmax, RH, WS, Rs, Ra | ETO | KNEA, KNEA-SSA, KNEA-PSO, KNEA-GWO, KNEA-GOA | KNEA-GWO | NRMSE, RMSE, MAE, R2 |
| [13] | Spain | 2000–2020 | Daily | Tmean, Tmin, Tmax, RH, WS | ETO | PRSFGWO, MLP, RFR, SVR, KNR, DET | PRSFGWO | MAE, RMSE, RRMSE, R2, IOA, ANOVA tests |
| [66] | China | 2018–2019 | Daily | Tmean, SSD, RH | ETO | MMC, GRNN, GRNN-FOA | GRNN-FOA | MVC, MAE, RMSE |
| [48] | Iran | 1973–2018 | Monthly | Tmean, Tmin, Tmax, RH, SSD, U2 | ETO | SVR-IWD, SVR, GEP | SVR-IWD | R, MAE, RMSE |
| [78] | Iran | 1987–2000 | Daily and Monthly | the lagged ETo values | ETO | MLP, MLP-GA, MLP-WWO, MLP-PSO | MLP-WWO | NSE, PBIAS, MAE, Scatter plots |
| [22] | Burkina Faso | 1998–2012 | Daily | Tmin, Tmax, RH, WS, Rs, Vp | ETO | ANFIS-FA, ANFIS | ANFIS-FA | TD, MAPE, RMSE, RMSRE, MRE, MAE, R2, RE, SIndex |
| [41] | Iran | 2001–2012 | Daily | T, RH, WS, Rs | ETO | ELM, NF-GP, NF-SC, MARS, MT, RF, BT, SVM, GEP | SVM-FA and NF-GP | NSE, RMSE, SIndex, MAE, R2 |
| [32] | China | 2018–2019 | Hourly | Tmean, VPD, RH, RS, SSWC | ETO | XGB-PSO, CatBoost, Bagging, XGB, AdaBoost, RF, ANN, KNN, Tree | XGB-PSO | RMSE, MSE, MAE, R2 |
| [8] | China | 1966–2000, 2001–2015 | Monthly | Tave, Tmax, Tmin, RH, WS, SSD | ETO | RF, M5P, ANFIS, KELM-FA, Kmeans-FA-KELM | Kmeans-KELM-FA | NSE, RMSE, MAE, SI, R2 |
| [54] | China | 2001–2015 | Daily | Tmin, Tmax, RH, WS, Rs | ETO | ELM, ELM-FPA, ELM-ACO, ELM-GA, ELM-CSA | ELM-FPA | MAE, RMSE, NRMSE, R2 |
| [63] | Iran | 2000–2015 | Daily | Tmin, Tmax, RH, U2, Rs, SSD, Epan, ETo- FAOPM56 | ETO | ANFIS, ANFIS-IWO, ANFIS-BBO, ANFIS-TLBO, ANFIS-ICA | ANFIS-ICA | NSE, MAE, IOA, R, RMSE |
| [33] | Turkey | 1982–2006 | Monthly | Tave, RH, WS, Rs | ETO | ANN, CART, ANFIS-PSO, ANFIS-GA, ANFIS | ANFIS-PSO, ANFIS-GA | R2, NSE, RMSE |
| [10] | Malaysia | 2014–20 | Daily | Tmean, Tmin, Tmax, RH, Rs, U2 | ETO | ELM, ELM-WOA, ELM-PSO, ELM-MFO | ELM-WOA | R2, RMSE, MAE |
| [6] | Malaysia | 2000–2019 | Daily | Tmean, Tmin, Tmax, RH, Rs, WS | ETO | ANFIS, SVM, MLP, BMLP, BSVM, BANFIS, BMA-E, ELM-WOA-E | ELM-WOA-E | MBE, RMSE, R2, MAE |
| [70] | China | 2000–2020 | Daily, Monthly, and Seasonal Scales | Tmean, RH, WS, Rainfall, VPD, Ra | ETO | BP-GA, Bi-LSTM, LSSVR | BP-GA, LSSVR | GPI, MAE, MBE, R2, RMSE |
| [80] | China | 1961–2012 | Monthly | Tave, Ra, ETo | ETO | LSSVR-GSA, DENFIS, M5RT, LSSVR | LSSVR-GSA | R2, MAE, RMSE |
| [89] | Bangladesh | 1982–2017 | Monthly | Tmin, Tmax, RH, U2 | ETO | ANFIS, ANFIS-WCA, ANFIS-MFO, ANFIS-WCAMFO | ANFIS-WCAMFO | R2, MAE, NSE, RMSE |
| [38] | Iran | 2000–2014 | Daily | Tave, Tmax, Tmin, RH, U2, Rs, SSD | ETO | ANFIS, ANFIS-SFLA, ANFIS-IWO | ANFIS-SFLA | NSE, RRMSE, MAE, R2, RMSE |
| [21] | Iran | 2012–2017 | Monthly | Tmin, Tmax, RH, U2, SSD, P | ETO | ANN-GWO, ANN, LSSVR | ANN-GWO | GPI, R2, MAE, U95, SI, TD |
| [11] | China | 1966–2015 | Daily | Tmin, Tmax, RH, U2, SSD | ETO | XGB-WOA, XGB | XGB-WOA | NSE, MAE, RMSE |
| Lu, et al. [44] | China | 1966–2015 | Monthly | T, RH, WS, SSD | ETO | XGB- GWO, MLP, M5, XGB | MLP best in summer, XGB- GWO best in autumn | RMSE, NSE, MAE |
| [45] | India and Algeria | 1994–2012, 1990–2016 | Monthly | Tmin, Tmax, RH, WS, Rs | ETO | ANN, ANN-ALO, ANN-GWO, ANN-MVO, ANN-PSO, ANN-WOA, | ANN-GWO | IOA, NSE, R, IOS, RMSE Scatter plots and TD |
| [52] | Algeria | 2000–2013 | Monthly | Tmin, Tmax, RH, WS, Rs | ETO | SVR, SVR-ALO, SVR-MVO, SVR-WOA, | SVR-WOA | NSE, RMSE, IOA, R, MAE, IOS, and graphical interpretation (time-variation and scatter plots, and TD). |
| [46] | Algeria | 2000–2014 | Monthly | Tmin, Tmax, RH, WS, Rs | ETO | SVR, SVR-PSO, SVR-GA, SVR-GWO | SVR-GWO | IOA, NSE, R, RMSE |
| [40] | Bangladesh | 2004–2019 | Daily | Tmin, Tmax, RH, WS, SSD | ETO | ANFIS, ANFIS-ABC, ANFIS-BA, ANFIS-BBO, ANFIS-ACOR, ANFIS-CMAES, ANFIS-CA, ANFIS-DE, ANFIS-FA, ANFIS-GA, ANFIS-HS, ANFIS-ICA, ANFIS-IWO, ANFIS-PSO, ANFIS-SA, ANFIS-TLBO, ANFIS-LSE-GD | ANFIS-FA | NRMSE, NSE, IOA, KGE, RMSE, MAE, MADE, R |
| [19] | Northwest China | 2002–2016 | Daily | Tmin, Tmax, RH, U2, Rs | ETO | ELM-PSO, ANN, RF, ELM, | ELM-PSO | R2, RRMSE, NSE, MAE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khairan, H.E.; Zubaidi, S.L.; Muhsen, Y.R.; Al-Ansari, N. Parameter Optimisation-Based Hybrid Reference Evapotranspiration Prediction Models: A Systematic Review of Current Implementations and Future Research Directions. Atmosphere 2023, 14, 77. https://doi.org/10.3390/atmos14010077
Khairan HE, Zubaidi SL, Muhsen YR, Al-Ansari N. Parameter Optimisation-Based Hybrid Reference Evapotranspiration Prediction Models: A Systematic Review of Current Implementations and Future Research Directions. Atmosphere. 2023; 14(1):77. https://doi.org/10.3390/atmos14010077
Chicago/Turabian StyleKhairan, Hadeel E., Salah L. Zubaidi, Yousif Raad Muhsen, and Nadhir Al-Ansari. 2023. "Parameter Optimisation-Based Hybrid Reference Evapotranspiration Prediction Models: A Systematic Review of Current Implementations and Future Research Directions" Atmosphere 14, no. 1: 77. https://doi.org/10.3390/atmos14010077
APA StyleKhairan, H. E., Zubaidi, S. L., Muhsen, Y. R., & Al-Ansari, N. (2023). Parameter Optimisation-Based Hybrid Reference Evapotranspiration Prediction Models: A Systematic Review of Current Implementations and Future Research Directions. Atmosphere, 14(1), 77. https://doi.org/10.3390/atmos14010077













