Evolving Hybrid Generalized Space-Time Autoregressive Forecasting with Cascade Neural Network Particle Swarm Optimization

Abstract

Background: The generalized space-time autoregressive (GSTAR) model is one of the most widely used models for modeling and forecasting time series and location data. Methods: In the GSTAR model, there is an assumption that the research locations are heterogeneous. In addition, the differences between these locations are shown in the form of a weighting matrix. The novelty of this paper is that we propose the hybrid time-series model of GSTAR uses the cascade neural network and obtains the best parameters from particle swarm optimization. Results and conclusion: This hybrid model provides a high accuracy value for forecasting PM_2.5, PM₁₀, NO_x, and SO₂ with high accuracy forecasting, which is justified by a mean absolute percentage error (MAPE) accuracy of around 0.01%.

1. Introduction

Many countries experienced an increased rate of urbanization and economic growth in the past few decades, leading to an increase in population, resource consumption, and environmental pollution. Air pollutants are a mixture of particulate matter, including PM_2.5 and PM_10, and gas-phase pollutants, including NO₂, CO, O₃, and SO_2, which have been shown to start reducing visibility and cause respiratory, cardiovascular, and immune system disorders, as well as mental disorders [1,2]. The World Health Organization (WHO) classifies some particulate matter as a class 1 cancer-causing agent, a designation given when there is sufficient evidence of carcinogenic effects [3]. The importance of data science in the environment can be beneficial in supporting national health risk management and environmental planning [4].

Precise forecasting is needed for decision-making. In the big data era paradigm, data availability is very abundant, diverse, and complex, and a high volume of data is accompanied by high data speed [5,6,7]. The motivation to provide high forecasting results has also been described in M-Competitions [6,7,8]. These M-Competitions are available studies that have compared the efficiency of a huge series of prominent forecasting models using acknowledged scientists who provide estimations of their knowledge and experience, using methods that include the application of recent statistics and parametric, semi-parametric, machine learning, deep learning, and expert systems [9,10,11,12,13,14].

Several studies that used hybrid time series by combining neural networks with traditional time series proved more beneficial for reasoning, such as the roll-motion Arima-neural networks [15], hybrid VAR-SVR [16], SARIMA-ANN [17], SARIMA-CNN-LSTM [18], and fuzzy neural network [19]. Meanwhile, the challenges in forecasting neural networks include determining the right pre-processing method and the appropriate neural network architecture, and finding the optimal parameter values. Thus, the most reasonable method during the existence of the time series model is to conduct pre-processing or inputting using the partial autocorrelation function (PACF) by justifying the correlation of a stationary time series with its own lagged values [20,21,22].

The neural network architecture is made of individual units called neurons that mimic the biological behavior of the brain. Regarding the neural network architecture, it can be used to develop a feed-forward neural network [22,23,24,25,26,27,28], radial basis neural network [29,30], deep feed-forward neural network [26], recurrent neural network [31], long-short term memory [32,33], gated recurrent unit (GRU) neural network [34], and much more. Optimization techniques also have an essential role in obtaining optimal machine learning parameters. Many types of optimization are used, such as a genetic algorithm (GA) nearest neighbor search (NNS), or simulated annealing (SA). In addition, metaheuristics, such as a tabu search (TS), can reduce the risk of falling into the local optimal according to the calculation used or by adjusting the parameter value. Using a metaheuristic makes it possible to increase the diversity of the population, thereby reducing the risk of falling into the local optimum. In the case of particle swarm optimization (PSO), the uniform arrangement of particles initially located in the solution space is of considerable value to the inertia constant and to the randomness added to the acceleration stability. The risk of falling into the local optimum can be reduced through the size of the swarm. Since PSO swarms solutions with slightly different directions of improvement (particle), it cannot be called a complete greedy hill-climbing approach with individual particles. Several studies have also conducted neural networks with PSO that provided excellent accuracy, such as the PSO-enabled LSTM neural network [35], artificial neural network, and PSO algorithm [36,37,38].

In this paper, we enhance the cascade neural network with particle swarm optimization (PSO). PSO improves the solutions in pbest and gbest, but it is not known if they add randomness through random numbers. It can be said that the risk is inherent in the algorithm itself. In this study, to solve the early convergence of the basic PSO, the swarm is divided into positive and negative swarms, and the positive swarm improves the solution in the direction of the basic PSO. The particle swarm moves the solution position in the opposite direction of the fitness value (pbest) and best value of any particle in its neighborhood (gbest). A bidirectional repositioning strategy was used. Particles belonging to the swarm played a role in improving the solution by following pbest and gbest over generations, similar to players in the existing PSO. Particles belonging to the particle swarm moving in the opposite direction were, until then, moving in the same direction and speed as the swarm. At a certain point in time, they start to move in the opposite direction to the pbest and gbest to increase the diversity of the entire swarm. To spread the particles evenly and radially in the multidimensional space centered on the negative swarm gbest, it is appropriate to use the time when it is judged that the local optimum has been reached to some extent, such as when the improvement of the solution is not made for several generations, as the detonation time. This article is organized as follows; in Section 2, we review the multivariate time series VAR and GSTAR and training using cascade neural network, and employ the model using PSO. Their performance is examined in Section 3 via simulation studies and four accurate air pollution data benchmark datasets. Finally, Section 4 presents the summary and conclusion.

2. Methodology

Multivariate Time Series VAR and GSTAR

Time series analysis is used when the data used are time-bound. Therefore, there is a correlation between the current event data and data from one previous period [5]. It means that events also influence current events in an earlier period [6,7]. Time series analysis that uses only one variable is called a univariate time series. In everyday life, a variable is often related to several other variables and when conducting research, more than one variable is involved [39,40,41]. Analysis using many variables is called a multivariate time series. Multivariate time series analysis is generally used to model and explain the interactions and movements between several time series variables [42].

A multivariate time series is a series of data consisting of several variables taken from time to time and recorded sequentially according to the time of occurrence with fixed time intervals. Time intervals include seconds, minutes, hours, days, months, years, and other periods. Similar to univariate time series, the stationarity of multivariate time series data can also be justified from the matrix autocorrelation function (MACF), and matrix partial autocorrelation function (MPACF) plots [43,44]. The MACF plot that decreases slowly indicates that the data do not have a stationary average; thus, it is necessary to perform differencing to stabilize the data. Likewise, when the information is not stationary in the variance, it must transform to obtain stationary data. If there is a time series vector with $\mathrm{n}$ observations, that is, Z₁, Z₂, …, Z_n, then the sample correlation matrix equation is as follows:

$$\widehat{\mathsf{\rho }}\left(\mathrm{k}\right)=\left[{\widehat{\mathsf{\rho }}}_{\mathrm{ij}}\left(\mathrm{k}\right)\right]$$

(1)

where ${\widehat{\mathsf{\rho }}}_{\mathrm{ij}}\left(\mathrm{k}\right)$ is the sample cross-correlation for the $\mathrm{i}-\mathrm{th}$ and $\mathrm{j}-\mathrm{th}$ series components, which are expressed in the following equation:

$$\widehat{{\mathsf{\rho }}_{\mathrm{ij}}}\left(\mathrm{k}\right)=\frac{{{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{n}-\mathrm{k}}\left({\mathrm{Z}}_{\mathrm{i},\mathrm{t}}-\overline{{\mathrm{Z}}_{\mathrm{i}}}\right)\left({\mathrm{Z}}_{\mathrm{j},\mathrm{t}+\mathrm{k}}-{\mathrm{Z}}_{\mathrm{j}}\right)}{{\left[{{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{n}}{\left({\mathrm{Z}}_{\mathrm{i},\mathrm{t}}-\overline{{\mathrm{Z}}_{\mathrm{i}}}\right)}^2{{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{n}}{\left({\mathrm{Z}}_{\mathrm{j},\mathrm{t}}-\overline{{\mathrm{Z}}_{\mathrm{j}}}\right)}^2\right]}^{\frac{1}{2}}}$$

(2)

Meanwhile, ${\overline{\mathrm{Z}}}_{\mathrm{i}}$ and ${\overline{\mathrm{Z}}}_{\mathrm{j}}$ are the sample means of the corresponding series components. In line with this, the matrices and graphs become more complex as the dimensions and vectors become more extensive, making identification difficult. To overcome this, [45] introduced a suitable method for summarizing the explanation of sample correlation, namely, by using symbols denoted by (+), (−), and (.) in the sample correlation matrix for $\left(\mathrm{i}\right)\mathrm{and}\left(\mathrm{j}\right)$. The standard error (SE) of a statistic is the standard deviation of its sampling distribution or an estimate of that standard deviation.

• The symbol (+) is defined as ${\widehat{\mathsf{\rho }}}_{\mathrm{ij}}\left(\mathrm{k}\right)$ greater than two times the standard error and indicates the relationship has a positive correlation.
• The symbol (−) represents a value of ${\widehat{\mathsf{\rho }}}_{\mathrm{ij}}\left(\mathrm{k}\right)$ less than −2 times the standard error. It indicates that the relationship has a negative correlation.
• The symbol (.) denotes ${\widehat{\mathsf{\rho }}}_{\mathrm{ij}}\left(\mathrm{k}\right)$, which is between ±2 times the standard error and indicates no correlation.

The field carried out the generalization of the PACF concept into a time series vector [45] and defined a partial autocorrelation matrix at lag $\mathrm{s}$ with the notation $\mathcal{P}\left(\mathrm{s}\right)$. The equation for the partial autocorrelation matrix is as follows:

$$\mathcal{P}\left(\mathrm{s}\right)=\left\{\begin{array}{c}{\mathsf{\Gamma }}^{\prime }\left(1\right){\left[\mathsf{\Gamma }\left(0\right)\right]}^{-1},\mathrm{s}=1\\ \left({\mathsf{\Gamma }}^{\prime }\left(\mathrm{s}\right)-{\mathrm{c}}^{\prime }\left(\mathrm{s}\right){\left[\mathrm{A}\left(\mathrm{s}\right)\right]}^{-1}\mathrm{b}\left(\mathrm{s}\right)\right){\left(\mathsf{\Gamma }\left(0\right)-{\mathrm{b}}^{\prime }\left(\mathrm{s}\right){\left[\mathrm{A}\left(\mathrm{s}\right)\right]}^{-1}\mathrm{b}\left(\mathrm{s}\right)\right)}^{-1},\mathrm{s}>1\end{array}\right.$$

(3)

For $\mathrm{s}\ge 2,$ then the value of $\mathrm{A}\left(\mathrm{s}\right),\mathrm{b}\left(\mathrm{s}\right), \mathrm{c}\left(\mathrm{s}\right)$can be expressed as follows:

$$\mathrm{A}\left(\mathrm{s}\right)=\left[\begin{array}{cccc}\mathsf{\Gamma }\left(0\right)& {\mathsf{\Gamma }}^{\prime }\left(1\right)& \dots & {\mathsf{\Gamma }}^{\prime }\left(\mathrm{s}-2\right)\\ \mathsf{\Gamma }\left(1\right)& \mathsf{\Gamma }\left(0\right)& \cdots & {\mathsf{\Gamma }}^{\prime }\left(\mathrm{s}-3\right)\\ ⋮& ⋮& & ⋮\\ \mathsf{\Gamma }\left(\mathrm{s}-2\right)& \mathsf{\Gamma }\left(\mathrm{s}-3\right)& \cdots & \mathsf{\Gamma }\left(0\right)\end{array}\right],\mathrm{b}\left(\mathrm{s}\right)=\left[\begin{array}{c}{\mathsf{\Gamma }}^{\prime }\left(\mathrm{s}-1\right)\\ {\mathsf{\Gamma }}^{\prime }\left(\mathrm{s}-2\right)\\ ⋮\\ {\mathsf{\Gamma }}^{\prime }\left(1\right)\end{array}\right],\mathrm{c}\left(\mathrm{s}\right)=\begin{array}{c}\mathsf{\Gamma }\left(1\right)\\ \mathsf{\Gamma }\left(2\right)\\ ⋮\\ \mathsf{\Gamma }\left(\mathrm{s}-1\right)\end{array}$$

(4)

where $\mathsf{\Gamma }\left(\mathrm{s}\right)$ is the s-lag covariance matrix. The sample estimate of $\mathcal{P}\left(\mathrm{s}\right)$can be calculated by $\mathsf{\Gamma }\left(\mathrm{s}\right)$, replacing the unknown with the sample covariance matrix $\mathsf{\Gamma }\left(\mathrm{s}\right)$:

$$\widehat{\mathsf{\Gamma }}\left(\mathrm{s}\right)=\frac{1}{\mathrm{n}}{\displaystyle \sum }_{\mathrm{t}=1}^{\mathrm{n}-\mathrm{s}}\left({\mathrm{Z}}_{\mathrm{t}}-\overline{\mathrm{Z}}\right){\left(({\mathrm{Z}}_{\mathrm{t}+\mathrm{s}}-\overline{\mathrm{Z}}\right)}^{\prime }) ,\mathrm{s}=1,2,\dots$$

(5)

where $\overline{\mathrm{Z}}=\left(\overline{{\mathrm{Z}}_1},\overline{{\mathrm{Z}}_2},\overline{{\mathrm{Z}}_3},\overline{{\mathrm{Z}}_4}\right)$ is the sample mean vector. The data identification based on MPACF values is also denoted in the form of (+), (−), and (.) as in the MACF. Like the partial autocorrelation equation in the univariate case, the partial autocorrelation matrix equation $\mathcal{P}\left(s\right)$ also has a cut-off property for the AR process.

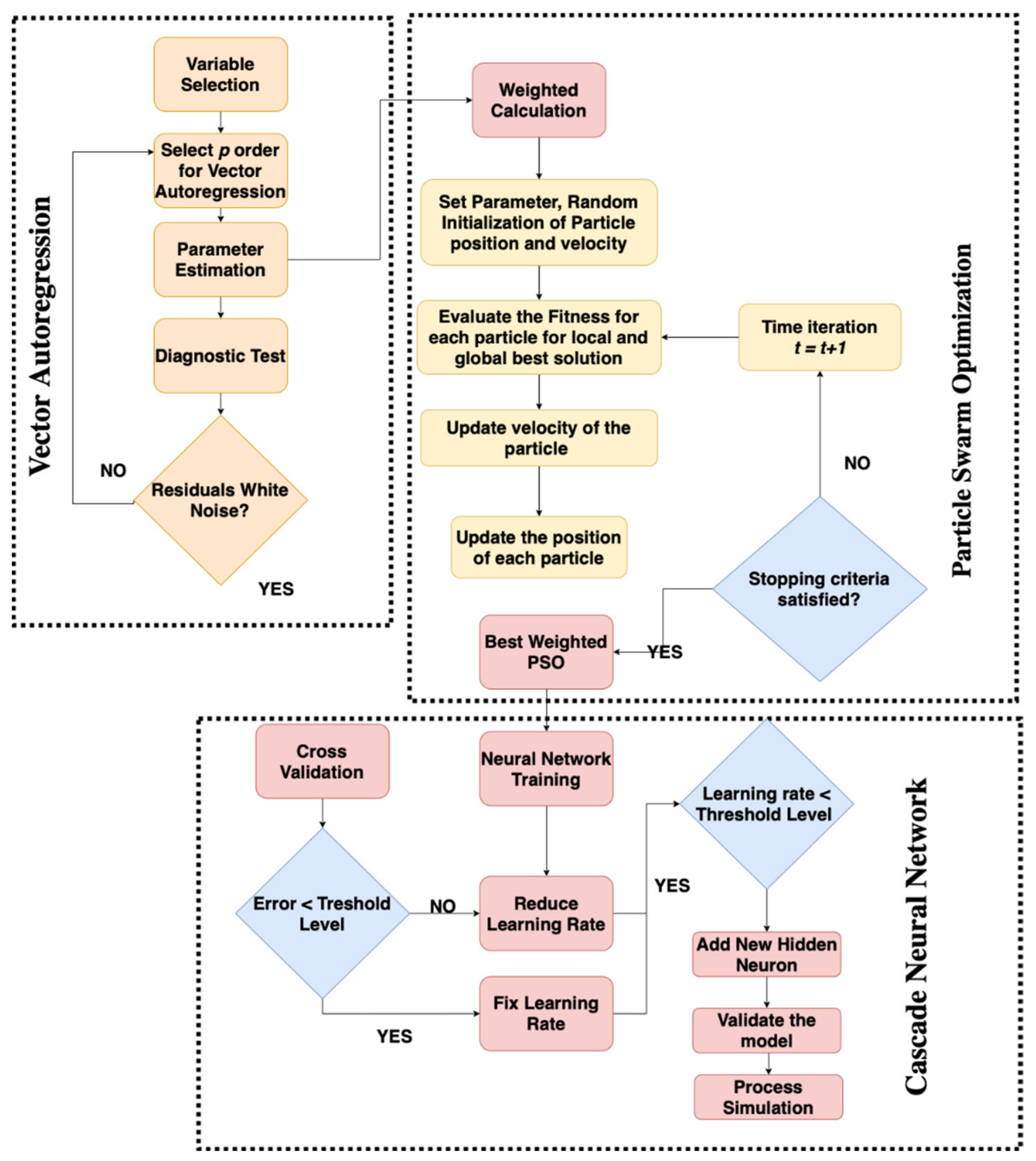
3. The Step Construction Cascade Neural Network with Particle Swarm Optimization

The basic idea is to imitate nature-inspired optimization and social behavior patterns such as birds and fish acting in colonies for self-defense against natural enemies or bees and ants acting in groups to find food. When a colony is formed, individuals can effectively achieve their goals through cooperation. The particle swarm optimization (PSO) was first introduced by [46]. PSO is a population-based optimization technique similar to the genetic algorithm developed by Holland in 1975. The genetic algorithm imitates the evolutionary mechanism of natural selection, whereas PSO reflects the social behavior patterns of biological communities such as flocks of birds and fish [47,48,49,50].

The particle swarm optimization (PSO) is a tool to solve the optimization problem and imitates the social behavior of these organisms. However, PSO is one of the most widely used optimization techniques to solve several issues looking for the optimal point and solution of the function. In PSO, individual latent solutions are represented by particles, which is explained in Figure 1. If the number of decision variables is $\mathrm{m}$, the search space in PSO becomes the real space of $\mathrm{m}$ and the $\mathrm{j}-\mathrm{th}$ particle at time $\mathrm{t}$. In addition, ${\mathrm{x}}_{\mathrm{j}}\left(\mathrm{t}\right)$ is expressed as a real vector of ${\mathrm{parent} \mathrm{x}}_{\mathrm{j}}\left(\mathrm{t}\right)={\mathrm{x}}_{\mathrm{j}1}\left(\mathrm{t}\right),{\mathrm{x}}_{\mathrm{j}2}\left(\mathrm{t}\right),\dots ,{\mathrm{x}}_{\mathrm{jm}}\left(\mathrm{t}\right)$. Meanwhile, a ‘swarm’ is a set of these particles. In addition, $\mathrm{t}$ can be expressed as $\mathrm{S}\left(\mathrm{t}\right)={\left({\mathrm{x}}_1\left(\mathrm{t}\right),{\mathrm{x}}_2\left(\mathrm{t}\right), \dots ,{ \mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)\right)}^{\mathrm{T}}$. Each particle frame has the properties of the current position and ‘velocity’. In the iterative process, particles move through the multi-dimensional search space and have the fitness function value evaluated by the fitness function. Based on this, they move to a location with a higher fitness function value. At this time, the particles lock the two optimal positions and move to the next position. The optimal solution (pbest) is found through the iteration of each particle. The overall optimal solution (gbest) found through iteration of all leaflets is the $\mathrm{j}-\mathrm{th}$ particle at time $\mathrm{t}$. Equation (6) explains the velocity of PSO.

$${\mathrm{v}}_{\mathrm{j}}\left(\mathrm{t}+1\right)=\mathrm{w}\left(\mathrm{t}\right)·{\mathrm{v}}_{\mathrm{j}}\left(\mathrm{t}\right)+{\mathrm{c}}_1·{\mathrm{r}}_1·\left({\mathrm{p}}_{{\mathrm{best}}_{\mathrm{j}}}\left(\mathrm{t}\right)-{\mathrm{x}}_{\mathrm{j}}\left(\mathrm{t}\right)\right)+{\mathrm{c}}_2·{\mathrm{r}}_2·\left({\mathrm{g}}_{\mathrm{best}}\left(\mathrm{t}\right)-{\mathrm{x}}_{\mathrm{j}}\left(\mathrm{t}\right)\right)$$

(6)

Here, $\mathrm{w}\left(\mathrm{t}\right)$ is the inertial load for the previous speed. Meanwhile, ${\mathrm{C}}_1,{\mathrm{C}}_2$ is the acceleration constant, and ${\mathrm{r}}_1,{\mathrm{r}}_2$ is a random number of $\left(0,1\right)$. Additionally, it is required to select an appropriate value. The GSTAR model is a specific vector autoregressive (VAR) model. This model shows a linear dependence of location and time, where the main difference with VAR is in the spatial support; in the GSTAR model, it is shown in a weighted matrix [22,51,52]. The GSTAR model also generalizes the space-time autoregressive (STAR) model [53]. The fundamental difference between the GSTAR and STAR models lies in assuming the parameters [9,54]. The STAR model assumes the locations used in the study are the same, thus this model can only be applied to uniform locations. Meanwhile, in the GSTAR model, there is an assumption that the research locations are heterogeneous [43,51,52]. In line with this, Equation (7) expresses the GSTAR model with $\mathrm{p}$ autoregressive orders and ${\mathsf{\lambda }}_1,{\mathsf{\lambda }}_2,\dots ,{\mathsf{\lambda }}_{\mathrm{p}}$ spatial order, as well as GSTAR $({\mathrm{p} \mathsf{\lambda }}_1,{\mathsf{\lambda }}_2,\dots ,{\mathsf{\lambda }}_{\mathrm{p}})$.

$$\mathrm{Z}\left(\mathrm{t}\right)={\displaystyle \sum }_{\mathrm{s}=1}^{\mathrm{p}}\left[{\mathsf{\varphi }}_{\mathrm{s}0}+{\displaystyle \sum }_{\mathrm{k}=1}^{\mathsf{\lambda }\mathrm{s}}{\mathsf{\varphi }}_{\mathrm{sk}}{\mathrm{W}}^{\left(\mathrm{k}\right)}\right]\mathrm{Z}\left(\mathrm{t}-\mathrm{s}\right)+{\mathrm{e}}_{\mathrm{t}}$$

(7)

However, ${\mathsf{\varphi }}_{\mathrm{s}0}$ is the autoregressive parameter $\mathrm{s}=1,2,\dots ,\mathrm{p}$; ${\mathsf{\varphi }}_{\mathrm{sk}}$ is the regression spatial parameter $\mathrm{k}=1,2,\dots ,{\mathsf{\lambda }}_{\mathrm{s}}$; ${\mathsf{\varphi }}_{\mathrm{s}0}=\mathrm{diag} \left({\mathsf{\varphi }}_{\mathrm{s}0}^{\prime },\dots ,{\mathsf{\varphi }}_{\mathrm{s}0}^{\mathrm{N}}\right)$; and ${\mathsf{\varphi }}_{\mathrm{sk}}=\mathrm{diag} \left({\mathsf{\varphi }}_{\mathrm{sk}}^{\prime },\dots ,{\mathsf{\varphi }}_{\mathrm{sk}}^{\mathrm{N}}\right)$. Meanwhile, the weighted matrix $\mathrm{N}\times \mathrm{N}$ can be expressed as ${\mathrm{W}}^{\mathrm{k}}$ with the weighted value selected to meet ${\mathrm{w}}_{\mathrm{ii}}^{\left(\mathrm{k}\right)}=0$ and ${\displaystyle \sum }_{\mathrm{i}\ne \mathrm{j}}{\mathrm{w}}_{\mathrm{ii}}^{\left(\mathrm{k}\right)}=1, \mathrm{i}=1,2,\dots ,\mathrm{N}$. If the spatial order is $\mathrm{k}=1,$then the GSTAR model formed is GSTAR(p1) with the following formula:

$$\mathrm{Z}\left(\mathrm{t}\right)={\displaystyle \sum }_{\mathrm{s}=1}^{\mathrm{p}}\left[{\mathsf{\varphi }}_{\mathrm{s}0}+{\mathsf{\varphi }}_{\mathrm{s}1}\mathrm{W}\right]{\mathrm{Z}}_{\mathrm{t}-\mathrm{s}}+{\mathrm{e}}_{\mathrm{t}}$$

(8)

GSTAR(1,1)

$$\mathrm{Z}\left(\mathrm{t}\right)=\left[{\mathsf{\varphi }}_{\mathrm{s}0}+{\mathsf{\varphi }}_{\mathrm{s}1}\mathrm{W}\right]{\mathrm{Z}}_{\mathrm{t}-1}+{\mathrm{e}}_{\mathrm{t}}$$

(9)

GSTAR(2,1)

$$\begin{gathered} \mathrm{Z}\left(\mathrm{t}\right)={\displaystyle \sum }_{\mathrm{s}=1}^2\left[{\mathsf{\varphi }}_{\mathrm{s}0}+{\mathsf{\varphi }}_{\mathrm{s}1}\mathrm{W}\right]{\mathrm{Z}}_{\mathrm{t}-\mathrm{s}}+{\mathrm{e}}_{\mathrm{t}} \\ \mathrm{Z}\left(\mathrm{t}\right)=\left[{\mathsf{\varphi }}_{10}+{\mathsf{\varphi }}_{11}\mathrm{W}\right]{\mathrm{Z}}_{\mathrm{t}-1}+\left[{\mathsf{\varphi }}_{20}+{\mathsf{\varphi }}_{21}\mathrm{W}\right]{\mathrm{Z}}_{\mathrm{t}-\mathrm{s}}+{\mathrm{e}}_{\mathrm{t}} \end{gathered}$$

(10)

The study areas included the cities of Taipei, Hsinchu, Taichung, and Kaohsiung, which consist of pollution data, namely, nitrogen oxide (NO_x), atmospheric particulate matter (PM_2,5), atmospheric particulate matter (PM₁₀), and sulfur dioxide (SO₂), respectively.

4. Results and Discussion

This paper is an extended version of previous research that uses a hybrid VAR neural network genetic algorithm [9] and cascade neural network genetic algorithm [53]. In

Table 1. Model Comparison based on Pollution.

GSTAR CFNN	Dataset	FVAL	OBJ	Training			Testing			Average			Elapsed Time (Seconds)
				RMSE	MAE	SMAPE	RMSE	MAE	SMAPE	RMSE	MAE	SMAPE
GSTAR (1)	NOX	0.7470	0.7470	5.2660	3.2622	0.0049	4.7143	2.4282	0.0268	4.9902	2.8452	0.0159	229.0739
	PM2.5	1.1580	1.1580	9.2831	6.5054	0.0041	6.7955	4.9921	0.0205	8.0393	5.7488	0.0123	91.236504
	PM10	0.735571	0.7356	13.0906	9.1146	0.0038	9.2994	6.5805	0.016	11.1950	7.8476	0.0099 *	90.51314
	SO2	2.643	2.643	1.5409	1.0592	0.0057	0.9035	0.6893	0.0265	1.2222	0.8743	0.0161	95.544592
GSTAR (2)	NOX	0.715855	0.7159	5.203	3.2747	0.005	3.7358	2.4901	0.0239	4.4694	2.8824	0.0145 *	106.778741
	PM2.5	2.02728	2.0273	9.2237	6.4361	0.0042	6.7847	4.9562	0.0199	8.0042	5.6962	0.0121 *	120.178632
	PM10	2.4187	2.4187	12.9489	8.9896	0.0036	9.1351	6.4255	0.0167	11.0420	7.7076	0.0102	196.033143
	SO2	7.79396	7.794	1.5172	1.0465	0.0056	0.8858	0.6726	0.0257	1.2015	0.8596	0.0157 *	206.967525
VAR (1)	NOX	3.20116	3.2012	5.1847	3.2426	13.5834	3.7378	2.4028	12.4158	4.4613	2.8227	12.9996	83.651723
	PM2.5	5.99995	6	9.2164	6.4473	7.5802	6.8311	5.0247	6.8707	8.0238	5.7360	7.2255	83.842196
	PM10	3.31837	3.3184	12.9178	8.9778	7.23	9.2731	6.5761	8.4924	11.0955	7.7770	7.8612	84.947817
	SO2	2.65504	2.655	1.5349	1.0506	6.8211	0.9185	0.7007	6.4913	1.2267	0.8757	6.6562	75.589595
VAR (2)	NOX	7.50572	7.5057	5.0466	3.1183	12.0234	3.6744	2.3254	11.8713	4.3605	2.7219	11.9474	82.196178
	PM2.5	5.31512	5.3151	9.1431	6.3854	7.8689	6.777	5.0306	7.2665	7.9601	5.7080	7.5677	269.645339
	PM10	3.72273	3.7227	12.7213	8.7579	6.9237	9.0049	6.3091	7.9569	10.8631	7.5335	7.4403	105.356041
	SO2	5.47567	5.4757	1.493	1.027	6.7956	0.9068	0.6823	7.1553	1.1999	0.8547	6.9755	161.550041

* Best model.

, we made a comparison of accuracy using RMSE, MAE, and SMAPE. We decided to use SMAPE as the basis for selecting the best model because this technique can be used to evaluate the diversity between training and testing in more detail. If the cascade neural network method is used for VAR, it provides a speedy computing time compared to GSTAR. This could be due to the complexity of the weights obtained between the different VAR and GSTAR methods. However, we can use modeling for PM₁₀ (GSTAR(1)-CFNN-PSO), PM_2.5 (GSTAR(2)-CFNN-PSO), NO_x (GSTAR(2)-CFNN-PSO), and SO₂ (GSTAR(2)-CFNN-PSO). VAR computing time is faster than GSTAR because the parameters in VAR are fewer than in GSTAR. Nevertheless, in GSTAR we used weighted information for modeling. In line with this, the time-lapse computing of GSTAR should be more complicated than of VAR. The evaluation function of PSO was justified by mean square error. In Figure 2, the variables used as inputs are NOx, PM_2.5, PM₁₀, and SO₂. Each of these variables already included spatial location. Then, before the initiation using PSO, an analysis using the sigmoid activation function was carried out; after obtaining the best weight, it was retrained with a linear activation function so that forecasting could be performed for each space-time variable.

The cascade neural network is a pyramid-like cascade of basic FFNN units that is modifiable. Each neural unit has to have a simple network architecture to handle only one task at hand, including data transformation, data integration, or prediction output. A cascade neural network model, in concept, could host vast volumes of data concurrently. Though a single input has poor prediction accuracy, a considered reliable prediction is assured if oriented data is given. The set of input hyperparameters is determined by the ability to inspect for the best model.

In addition to the time dimension, time series can also have space and time or space-time dimensions. The space-time model is a model that combines elements of time and location dependencies in multivariate time series data, for example, the hourly level of air pollution at several observation points in one area. The generalized space-time autoregressive (GSTAR) model is a model that can overcome the assumption that research locations are heterogeneous; thus, the parameters for each location are different, which is represented in Figure 3, Figure 4, Figure 5 and Figure 6. Based on the best model we forecasted for the next 30 days, it can be seen in Figure 7 that in Taiwan, Taichung city has the most significant values for PM_2.5, PM₁₀, NO_x, and SO₂ values compared to Taipei, Hsinchu, and Kaohsiung. It can be said that the city of Taichung is significantly impacting air pollution; thus, special handling is needed to solve this air pollution problem, especially with penta-helix contributors. Excessive industrial activities can also cause air pollution. In addition, the number of fossil-fueled vehicles contributes to an increase in the amount of carbon dioxide and other toxic gases in the air. Forecasting using GSTAR-CFNN-PSO can be used as a reference for long-term forecasting because it provides a high accuracy value [22,35,40,54,55,56]. In this study, we compared the performance of neural network methods to air pollution. We proposed using two hybrid models that combine VAR and GSTAR with neural network models to forecast pollution. In our proposed model, a time series is considered a nonlinear function of several past observations and random errors. Therefore, VAR and GSTAR models are used to generate the residuals. We first examined the accuracy of these three models using simulated data and then the pollution data. All of our methods yielded almost the same values regardless of leading time. The cascade neural network with PSO was better for the pollution forecast if we consider the training time.

Pollution issues in several countries are specifically related to traffic jams, air and noise pollution, traffic accidents, and delays (increased travel time) [57,58,59,60,61,62,63,64,65,66]. In the late 1980s, developed countries reached a much more advanced stage in transportation planning than they had 20 years earlier. The rapid advancement of knowledge in electronics and computer equipment has enabled the development of several previously unimagined transportation infrastructure concepts. On the other hand, many developing countries are dealing with transportation issues, some of which are already critical. Problems caused by limited existing transportation infrastructure have been added to other issues such as low per capita income, rapid urbanization, limited resources (particularly funds), and the quality and quantity of data related to transportation [4,67,68,69]. It is simple to determine the cause of traffic jams in Taiwan with our bare eyes. Congestion is caused by an increasing uncontrolled number of vehicles, including cars, motorcycles, public transit, and other vehicles, which then spill into traffic, causing this general problem. Furthermore, the number of private cars is increasing. It can be seen that the number of cars on major roads outnumbers other vehicles such as motorcycles, public transportation, and so on.

5. Conclusions

The GSTAR model has limitations, as it cannot model nonlinear time series. This can be overcome by applying a hybrid model to the GSTAR. The hybrid model works by combining linear and nonlinear models to handle linear and nonlinear correlation structures. Each model produces different error values, and it has been discussed that, overall, the GSTAR-cascade-neural-network model provides better accuracy when compared to the VAR model. Therefore, the pollution conditions, including NO_x, PM_2.5, PM₁₀, and SO₂ in the four locations of Taichung, Taipei, Kaohsiung, and Hsinchu, can be generalized for spatial forecasting using the GSTAR-cascade-neural-network with a reasonably high accuracy up to 0.01% (close to zero). Further research also needs to involve subset elements in the GSTAR model to improve forecast accuracy. In addition, it is possible to develop a GSTARX-ANN 1-level hybrid model for space-time data forecasting as a comparison of the GSTARX-ANN 2-level hybrid model for forecasting data containing trend, seasonal, calendar variation, and linear and nonlinear noise series components. In addition, we recommend using other types of architecture on neural networks and deep neural networks. Further research can be conducted with simulation studies for seasonal data only and seasonal and non-seasonal using the GSTAR-GLS and GSTAR-SUR models. Due to rapid urbanization and industrialization over the last decades, Taiwan has faced severe environmental problems, including air pollution. To address the issue of air pollution, the government has undertaken a number of defensive measures. In line with this, spatial-temporal empirical studies of air quality using monitoring data from the last ten years revealed that air quality changed with urban development. The evaluations are used to make future specific recommendations and policy advice [66,70,71,72,73,74]. In many countries, traffic is the leading cause of serious air pollution. Traffic is a serious threat to the environment not only because of the number of cars on the road, but also because of the fuel efficiency. The per-vehicle mileage in Taiwan is excessively high when compared to other metropolitan cities because Taiwan’s transportation policy has emphasized expanding the supply of traffic utilities, such as through road construction, and expanding intersections and parking lots due to low fuel and parking fees.

Many researchers make observations about pollutant gases, such as ozone (O₃), nitrogen oxide (NO), nitrogen dioxide (NO₂), sulfur dioxide (SO₂), and particulate matter, to determine the air quality in an area and control the stability of its air quality. The research process is carried out by forming an air quality model and then creating a control device to prevent or reduce pollutant substances in the air. Due to the high cost of these controllers and the high maintenance costs, it is not possible to place and use as many tools as possible to measure pollutant concentrations. Therefore, the estimation of pollutant concentration is essential in predicting pollutant concentrations in the future and estimating pollutant concentrations in areas that are not included in the radius of a measuring instrument. The next research can use the air pollution model with chemical transport. This model is a linear dynamic model that is then formed into a state-space model and discrete model, which can be performed using VAR. After that, it is processed at the prediction, correction, and simulation stages.

$$\begin{gathered} \frac{\partial \mathrm{C}}{\partial \mathrm{t}}~\frac{{\partial }^2\mathrm{C}}{{\mathrm{x}}^2} \\ \frac{\partial \mathrm{C}}{\partial \mathrm{t}}~{\mathrm{K}}_{\mathrm{x}}\frac{{\partial }^2\mathrm{C}}{\partial {\mathrm{x}}^2} \end{gathered}$$

$\mathrm{C}$ is the concentration of the substance in the air and t is time in seconds. However, ${\mathrm{K}}_{\mathrm{x}}$ is the proportional constant in units of $\frac{{\mathrm{m}}^2}{\mathrm{second}}$.

We have explained how to perform vector autoregression with a cascade neural network and particle swarm optimization. The disadvantage of VAR models is that they only can capture the relationship between multiple quantities as they change over time. Every region has different uniqueness of climate phenomena and pollution, making the accuracy for forecasting not really robust.