Abstract
Experimental field campaigns are an essential part of atmospheric research, as well as of university education in the field of atmospheric physics and meteorology. Experimental field observations are needed to improve the understanding of the surface-atmosphere interaction and atmospheric boundary layer (ABL) physics and develop corresponding model parameterizations. Information on the ABL wind profiles is essential for the interpretation of other observations. However, wind profile measurements above the surface layer remain challenging and expensive, especially for the field campaigns performed in remote places and harsh conditions. In this study, we consider the experience of using two low-cost methods for the wind profiling, which may be easily applied in the field studies with modest demands on logistical opportunities, available infrastructure, and budget. The first one is a classical and well-known method of pilot balloon sounding, i.e., when balloon is treated as a Lagrangian particle and tracked by theodolite observations of angular coordinates. Second one is based on a vertical sounding with a popular and relatively cheap mass-market quadcopter DJI Phantom 4 Pro and utilizes its built-in opportunity to restore the wind vector from quadcopter tilt angles. Both methods demonstrated reasonable agreement and applicability even in harsh weather conditions and complex terrain. Advantages and shortcomings of these methods, as well as practical recommendations for their use are discussed. For the drone-based wind estimation, the importance of calibration by comparison to high-quality wind observations is shown.
1. Introduction
Information on the vertical distribution (profile) of wind speed in the troposphere is important for various tasks, ranging from the safety of aviation flights to the forecast of disastrous meteorological phenomena and the development of atmospheric boundary layer (ABL) theories and model parameterizations. It is critical in aeronautical meteorology and wind energy. The vertical profiles of the average wind speed within the ABL depend on several parameters, including the upwind surface properties, surface roughness, atmospheric stratification, synoptic-scale pressure gradient, etc. The wind profile is highly variable in time especially when a point of observations is passed by squalls, atmospheric fronts, mesoscale convective systems.
Specific need for ABL wind observations is associated with field campaigns, that are regularly carried out by research institutions to improve the understanding of the surface-atmosphere interaction and ABL physics. Basic theories of the ABL physical processes, including Monin–Obukhov similarity theory and turbulence closures of different orders have been developed since the middle of the 20th century [1] allowing the representation of the ABL processes in weather and climate models [2]. However, atmospheric physics still faces challenges in understanding and parameterizing ABL processes under specific conditions, e.g., in case of strongly stable temperature stratification [3] or over inhomogeneous terrains [4,5] including coastal zones, polynyas, urban areas, mountain landscapes etc. Comprehensive information on the ABL structure under such specific conditions is usually obtained in targeted experimental field campaigns. In addition, information on the profiles of wind speed, temperature, and humidity is an important accompaniment to field studies of the gas and aerosol composition of the atmosphere and an integral part of various subsatellite experiments. Moreover, short-term field campaigns with wind measurements are essential not only for atmospheric research but also for educating university students learning meteorology, atmospheric physics, and adjacent areas of knowledge.
Even when the field campaigns are focused on surface-layer processes, information on temperature and wind ABL profiles is extremely important for data interpretation; especially for very stable stratification, where wind profile may indicate proximity of ABL height to surface and hence the necessity for reconsidering the Monin-Obukhov theory, which assumes invariance of fluxes with height. Field campaigns in atmospheric studies often face logistical challenges in taking measurements at remote sites that are difficult to reach and are often characterized by harsh weather conditions [6]. Despite the numerous methods for ABL wind profile measurements have been suggested, the most of them have limited applicability for such field campaigns, which is shown in a brief review below.
Sounding with pilot balloons (pibals) is a classical method of wind proofing that enjoys a history lasting more than two centuries [7]. The principle behind this type of measurements assumes that a balloon may be treated as a Lagrangian particle in its horizontal motion, while having a buoyancy-driven vertical velocity with respect to air. Thus, if the trajectory of a balloon is known, it provides the distribution of horizontal air speed along the trajectory; with respect to large-scale atmospheric circulations this distribution may be treated as a local vertical profile of wind. The classical method of pibal sounding assumes the determination of balloon’s trajectory from the theodolite angular observations. Later, invention of radio allowed tracking balloons using radio directional finding, and receiving data from meteorological sensors attached to the balloon, which originated the atmospheric radio sounding.
Since 1930th, radiosondes are a routine tool for areological observations, and remain one of the most important sources of the wind profile data for atmospheric research and weather forecast [8,9,10]. However, the use of one-off sondes determines the high cost of this method. Therefore, areological network is scarce, and soundings are typically performed only twice a day [10]. Another frequently used method for wind profile monitoring is multilevel contact measurements at meteorological masts [11,12]. Disadvantage of such measurements are discreteness, coverage of only the lower part of the ABL with a maximum height of few hundred meters, and a high cost of mast construction.
Promising opportunities for wind profile monitoring are provided by remote sensing techniques. All such methods are based on the emission, atmospheric backscattering, and recording of received signal of waves differing in nature and wavelength: these are sodars (acoustic waves), lidars (optical radiation), radars (radio waves), and radio-acoustic systems which combine acoustic and electromagnetic radiation.
Sodars (acoustic locators) provide measurements of wind magnitude and direction in an altitude range from 20 to 200–800 m [13,14,15,16]. However, the height of sounding is highly dependent on meteorological conditions. Sodars are sensitive to background atmospheric noise and practically do not operate during liquid precipitation and high wind speeds. An extension of the acoustic sounding technique is RASS (Radio Acoustic Sounding System), i.e., when sodar is supplemented by a radar [14,17]. RASS systems have similar limitations in height and operation conditions as sodars but simultaneously provide information on the vertical distribution of wind and temperature.
Optical wind profilers (lidars) record an optical signal scattered by aerosols or air molecules [18,19,20,21,22,23,24]. They are capable of sensing the atmosphere to very high altitudes [25], and are widely used in wind industry [26,27]. A common property of all optical wind profilers is that they work well in clear and calm weather. However, lidars are practically inoperative under conditions with strong turbulence, wind, and precipitation, fog, low cloud cover, and high dust concentration.
Contrary to lidars, radars provide the best results in the presence of cloudiness and precipitation. Radar wind profilers use the reflection of electromagnetic waves from liquid and solid water particles suspended in the air [28,29,30]. An analysis of reflected signals enables to obtain in real-time the wind distribution, turbulence intensity, and wind shear in altitude and time [31]. Radar measurements of the wind are traditionally complicated due to the high variability of the air speed and the spatial heterogeneity of the diffusers’ reflectivity. Also, in the radar measurements, the information on the wind speed is typically not available in the layer below 300–400 m.
According to the presented review, currently there is no “universal” remote wind profiler applicable in any weather conditions. In addition to the listed technical and methodological limitation of the reviewed methods, their application in the field campaigns, especially in remote areas, is strongly limited by the logistical and infrastructural challenges. Most remote sensing devises are hard-to-transport and difficult to maintain, so their transportation and operation are expensive and labor-demanding tasks. The exception is portable sodars [32], however, as shown above, their operation is subject to weather restrictions. Additionally, most of the methods lack opportunity to provide reliable data for the lowest part of the atmosphere, which is a primary interest in the field studies focused on the surface-atmosphere interactions. Another limitation is the high cost of the remote sensing devices, which limits their operation by small research groups, especially in developing countries. Therefore, for field measurements mentioned, it is practical to use a relatively simple, low-cost wind profiling method applicable in wide range of weather conditions.
Emerging opportunities for atmospheric monitoring, including wind profiling, are opened by rapid development of the unmanned aerial vehicles (UAVs) or the so-called drones [33,34]. There are two types of the UAVs, namely fixed-wing and rotary-wing ones. Among the rotary-wing UAVs, the most popular are the multirotor aircrafts or multicopters, which are equipped with a number of (usually 4 or 6) rotary engines. The multirotor UAVs started their development later than other models, only in the 21st century, but have already become the most popular UAV type. The recent software and hardware developments have dramatically improved the ease of use of the multirotor UAVs and turned them to popular devices which experience a commercial boom nowadays. The multirotor UAVs found their application in different industries, including photo and video production, security, transport, etc., as well in scientific research, mostly in field of cartography and remote sensing. For example, multirotor UAVs could be used for agricultural monitoring [35,36], creation of high-resolution digital elevation models [37,38], snow depth estimations [39], and monitoring of the land/water surface temperature using the infra-red radiometers [36,40,41,42].
The first attempts of using the fixed-wing UAVs for atmospheric research go back to the 1970s [43]. Further technological advances in manufacturing and signal processing have led to the miniaturization of sensors and moved the fixed-wing UAVs to the forefront of atmospheric measurements in 2000th, see e.g., [6,44,45,46,47]. The pioneering studies in the use of the multirotor UAVs for atmospheric measurements appeared only in 2010th, but have already demonstrated that multicopters, equipped by meteorological sensors, could be effectively used for profile measurements in the lower atmosphere, including the harsh Arctic and Antarctic conditions [6,48,49,50]. The multicopters have several noticeable advantages against the fixed-wing UAVs for the profile measurements in field campaigns. They have opportunity to take off in a limited space and to hover or to make strictly vertical profiles over a given point. The latter is especially important for taking measurements in a complex environment such as urban canopy or over a heterogeneous surface, e.g., over an ice-water border or a hilly terrain. Another advantage of multicopters is an opportunity to move with a low vertical or horizontal speed, which is important for better resolving the sharp gradients of temperature and other parameters, e.g., near the surface.
Both fixed-wing and rotary-wing UAVs could be used to measure the wind speed and direction. Fixed-wing UAVs are typically equipped by Pitot tubes, which provide high-quality and high-frequency measurements of 3D wind vector, suitable for wind profiling as well as for turbulence studies [46,51]. However, the use of such high-quality measurements is limited by a significant cost of the Pitot probes and by the need of additional high-quality data loggers and other supporting equipment. Multirotor aircrafts provide a unique low-cost opportunity to estimate the wind speed without any additional sensors based only on the attitude data (pitch and roll angles) from the internal measurement unit [52,53]. Such method is too coarse for turbulence-resolving studies, however the recent studies found it to be enough accurate for the vertical mean wind profiling [33,34]. The opportunity for low-cost wind speed measurements together with other listed advantages turn the multirotor UAVs to a very attractive tool for meteorological monitoring in the lower atmosphere.
A big part of existing studies on the use of the UAVs for atmospheric measurements consider the custom-built drones, which were designed specifically for atmospheric measurements. The examples are the MACS-3 [51] and SUMO [47] fixed-wing UAVs or the CopterSonde quadcopter [33]. A custom-built UAV could be deeply optimized for better efficiency and higher-precision measurements. However, its development requires months or years of highly qualified engineering work, and its further applications are usually limited by the group of its developers. Even after development and debugging, creating the next instance or repairing after an accident remains a difficult and time-consuming task. Drones designed specifically for atmospheric measurements are also available commercially, e.g., the MeteoDrone from Meteomatics company [54] (https://www.meteomatics.com/en/meteodrones-meteobase/, accessed on 13 March 2021), however their price is far away from the low-cost segment. Alternative option is to use mass-market drones. For example, the mass-market multirotor UAVs manufactured by DJI company, e.g., DJI Matrice or DJI Phantom 4, are originally designed for photo and video production or industrial applications, but have been efficiently used to carry temperature, humidity, and atmospheric composition sensors [48,55,56]. The cost of such drones starts with the first thousand USD, which allows to consider them as low-cost tools in comparison to the special commercial solutions and remote sensing equipment. The opportunity to obtain the wind speed estimate is also available for such drones, however it has not been extensively tested and evaluated in previous field studies by comparing with conventional wind measurements.
Among the reviewed wind profiling methods, only two can be considered as the low-cost solutions, suitable for the wind profiling in the lower atmosphere during the remote field campaigns, namely the classic method of pilot balloon sounding, and novel drone-based vertical profiling with mass-market quadcopters. This study aims to conduct intercomparison between these two methods applied in a field campaign under harsh winter conditions and complex terrain in the Russian Arctic.
2. Methods
2.1. Study Area and Research Campaign
The White Sea Biological Station (WSBS) of Moscow State University (MSU) is located on the North Western coast of White Sea, Russia, almost at the Arctic Circle (66°34′ N, 33°08′ E). Surrounding terrain is highly inhomogeneous. The site is located at Kindo peninsula with an altitude range about 100 m at the coast of Bolshaya Salma straight (Figure 1a). The most of the straight is typically covered by ice in winter, however its part remains unfreezing as a polynya [57]. WSBS has been a base infrastructure for numerous biological, geomorphological, oceanological studies since its foundation in 1938. It is extensively used for undergraduate student field practices by Faculties of Biology, Geography and Physics, MSU. Recently, a number of winter short-term (ca. two weeks) field campaigns were carried out here jointly by MSU and A.M. Obukhov Institute of Atmospheric Physics RAS for studying thermodynamic and biogeochemical regime of meromictic lakes and statistical properties of atmospheric turbulence in heterogeneous landscape formed by lakes and surrounding forest over hilly surface. Among significant results, it was first established that over small clearings in a forest, certain statistical properties of wind and temperature series resemble that of a convective boundary layer, indicating a presence of coherent structures in a turbulent flow [4,5].

Figure 1.
Location of the White Sea Biological Station (WSBS) site (a) and aerial photo of WSBS pier where the discussed observations were performed (b). Colored shading in (a) represents the elevation above the sea level according to Arctic DEM, and cyan line indicate the typical location of the unfreezing polynya in the Bolshaya Salma straight.
Our study is based on the results of the field campaign, that was performed at WSBS site from the period 25th of January to 4th of February 2020 (WSBS-2020 campaign). As previous campaigns at this site, the WSBS-2020 campaign was focused on surface-atmosphere interaction over complex terrain in winter. It consisted of different kinds of observations, including routine meteorological observations, eddy covariance measurements and vertical profiling. One of the campaign objectives was testing and comparison of the methods for measuring the vertical wind profile, suitable for use in the field with limited infrastructure, namely vertical sounding with pilot balloons and quadcopters.
Most of the observations were carried out at the WSBS pier (66.5533° N, 33.10396° E) (Figure 1b). Measurements at this site included routine meteorological observations by Vaisala WXT520 automatic weather station (AWS), temperature profile measurements by MTP-5 microwave temperature profiler, and high-quality wind speed measurements with 20 Hz frequency by acoustic anemometer, built in to IRGASON EC150 CO2/H2O Open-Path Gas Analyzer (Campbell Scientific, Inc., Logan, UT, USA). The latter was installed at the end of pier, at the height about 4 m above the sea ice. Balloon and quadcopter-based vertical soundings were performed onshore in the vicinity of the pier (Figure 1b).
2.2. Balloon Sounding
A crucial component of pilot balloon sounding method is a measurement of 3D balloon trajectory, from which the vertical wind profile is then computed. This measurement may be performed by a variety of methods; the cheapest and realizable way in a wide range of environmental conditions (except the cases of low cloudiness) involves theodolite optical observations of two angle coordinates and a model for vertical motion of a balloon. This method is applicable for lower atmosphere measurements, owing to the limitations of balloon visibility. An important uncertainty in this method is imposed by formulation and parameters of a vertical motion model. A number of balloon ascent models have been developed [58,59,60,61,62]. All of them are subject to one or another limitation: a perfect balance between buoyancy and friction forces is usually assumed, the heat balance equation of a balloon skin is substituted by equality of balloon skin temperature to ambient air temperature [60], the temperature distribution inside a balloon is taken homogeneous [58], and others. One of the most important parameters of the model is aerodynamic drag coefficient, usually parameterized as function of Reynolds number [60]. Most of the parameter uncertainties and simplifications of model equations become important during soundings of the higher atmosphere, where the ambient conditions (temperature, pressure, radiation fluxes) as well as the balloon’s characteristics alter significantly through the balloon route from the Earth surface; in this case, model parameterizations should be applicable in a wide range of balloon diameters, temperature, vertical velocity with respect to air.
In our study, soundings have been performed up to 500 m. The model for balloon ascent developed in this study follows basically Gallice et al. (2011) [60], the latter is extended by using unsteady vertical motion equation and inclusion of full heat balance equation at the balloon surface [58]. The full equation for vertical balloon motion reads:
where is vertical coordinate of the balloon, t is time, is its vertical speed, Vb is the balloon volume, Sb is the reference area (=, R—balloon radius), mb is the balloon mass (assumed constant, neglecting slow diffusion of helium through the balloon skin), is the ambient air density, is an aerodynamic drag coefficient, taken as semi-empirical function of Reynolds number [60]. The ambient pressure and air density are computed from hydrostatic equation using vertical air temperature distribution Ta measured by MTP-5 temperature profiler. The balloon radius at each height is found from ideal gas law given ambient pressure and mean temperature inside the balloon. The mean temperature over the balloon volume is found by averaging the solution of 1D heat conductance equation (valid under condition of spherical symmetry):
where is the thermal conductivity coefficient of helium, is helium density, cp is helium heat capacity at constant pressure, is a normalized radial coordinate. The use of normalized radial coordinate simplifies the solution of temperature diffusion problem inside a balloon, as it allows to avoid adjustment of the numerical grid of non-normalized radial coordinate to the balloon expansion.
The vertical motion model describes an ascent of a balloon respective to air, so that the vertical coordinate of a balloon with respective to the earth surface in general case should be computed using the sum of balloon velocity and air vertical velocity. Vice versa, the air vertical velocity can be computed if the balloon coordinates are measured and the balloon vertical velocity with respect to air is simulated [59,60,62]. Vertical balloon motion with respect to air could be fairly used to estimate the balloon height and, ultimately, vertical distribution of horizontal speed.
When the vertical wind profile is estimated via balloon tracking by visual measurements of vertical () and horizontal () angles with theodolite, the error of angles measurements and lead to corresponding error in wind module and direction calculation. Under the assumption that theodolite angle measurements are non-correlated in time, and and are uncorrelated (i.e., , where overline denotes mathematical expectation), one gets the following estimates:
where is a true velocity vector, is wind direction, is an error of velocity measurement, subscript “m” denotes measured values. The variances and covariance of velocity vector measurement errors computed for a period between two observations of balloon angle coordinates by theodolite are given as:
here, the coefficients relating the errors of angle coordinates to that of wind speed components are proportional to (Appendix A). These formulas imply that assuming constant values and (which are defined by construction properties of theodolite) the errors of wind components increase with height of balloon position. However, the errors of velocity module and direction are dependent on covariance and may become non-monotonic with height. For the theodolite model used in this study, =
2.3. Quadcopter-Based Measurements of the Wind Speed and Direction
The multi-rotor UAVs provide an opportunity to estimate the wind speed without any additional sensors based only on the records of inertial measurement unit (IMU). Such opportunity follows from the principle of motion of multirotor aircraft. Its horizontal motion is performed by redistributing the engine power to change the roll and pitch angles and, accordingly, to deviate the thrust vector in the required direction. To follow the pilot’s commands (to hover at the fixed point or to move in requested direction), the drone needs to compensate the airflow. Such compensation is performed by flight controller using the data from IMU that usually include gyroscopes, accelerometers, and GPS. E.g., when the drone is hovering over the given point, it is still moving against the airflow. The wind speed and direction could be estimated based on the drone tilt and other variables from IMU. The theoretical description of this method and its application is described in recent literature [52,53]. However, implementation of such method for a specific aircraft model remains a challenging task due to the need for an accurate adjustment and calibration taking into account the features of the aircraft design [33].
In this study, we use the commercial mass-market quadcopters DJI Phantom 4 to obtain the wind profiles in lower atmosphere together with temperature and humidity profiles. Successful experience to use such drones to obtain temperature and humidity profiles was discussed in author’s previous study [48]. In contrast to many other drones, the DJI flight controller includes the built-in software for estimation of the wind speed to warn the pilot about the dangerous wind. The estimated values are transmitted to the remote controller and stored in the flight logs. Unfortunately, the description of the specific algorithm, used to obtain the wind vector estimate, is not publicly available, so the user can only consider it as a “black box.”
The flight logs from DJI can be accessed using DJI Assistant software and further converted to csv format using CsvView software (, accessed on 13 March 2021). The logs contain various information about the aircraft state, including the IMU data. The available data gives several options to obtain the wind speed and direction. First, there are variables called “AirSpeedBody:X” and “AirSpeedBody:Y” (or “air_vbx” and “air_vbx” in latter CsvView versions), which correspond to the airflow speed in the drone-based coordinate system. The information of the horizontal speed of a drone with respect to the ground , obtained by GPS module, is also known from the flight logs, so the wind speed could be easily estimated as
Second, the flight logs already include the variables called “WindSpeed,” “Wind:X,” and “Wind:Y,” which correspond to the wind speed estimate that is used to warn the pilot, and its zonal and meridional components. and are expected to be equal, however we found that their relationship is not so simple. The values are smoothed with respect to with a window of about 10–15 s and scaled by a non-constant factor of about 1–1.5. Third, the available data allows application of the original algorithms based on theoretical tilt–wind relationships from a literature. However, application of these algorithms based on Phantom 4 flight logs requires an accurate calibration, which should be already done by the manufacturer. Hence, in this study we evaluate the wind estimates which are already available in the flight logs. We further use estimate, which corresponds to a lower level of data processing and include fewer unknown factors in comparison to . However, the presence of the data fields, used for and estimates, depends on the drone’s firmware version. In case of missing fields needed for estimate, the approaches discussed below can be applied to estimate.
During the WSBS-2020 campaign, we used two DJI Phantom 4 drones (D1 and D2) for different missions, including the vertical profiling. These drones were equipped by meteorological sensors produced by Intermetsystem (https://www.intermetsystems.com/, accessed on 13 March 2021), namely the iMet-XF and iMet-XQ2 sensor packages. iMet-XQ2 is a compact ready-to-use system that includes internal memory, GPS and temperature, humidity and pressure sensors. iMet-XF sensor package was used as a part of customized system that also includes the data logger and power supply, packed in a plastic box [48]. It is more flexible and allows to plug in a variety of sensors but is significantly heavier than iMet-XQ2. Both sensor packages were mounted at the drones’ chassis with the sensors placed under the front rotors for better aspiration (Figure 2a). The D1 drone was equipped by iMet-XQ system, and D2 was equipped by both iMet-XQ2 and iMet-XF sensor packages.

Figure 2.
Two drones D1 and D2, equipped by meteorological sensors, used in the study (a). The photo in (b) shows the experiment when the drones were hovering near the acoustic anemometer.
Vertical profile measurements were performed one or two times per day together with balloon sounding (in total 14 times during the campaign). Balloons and drones were launched from the same point near WSBS pier. We tried to synchronize the launch time for balloon and drone as close as possible, however in some cases due to the technical problems the launch times differed by tens of minutes. The profile measurements by the drone were performed during an ascent to the height of 400–500 m with a vertical speed of about 0.5–1 m/s in the lowest 50 m and 1–2 m/s above, hovering at the highest point for 10–20 s and descending back to the surface with the same vertical speed. Hence, the profiling missions usually took 15 min. In most of the cases, the drone was piloted manually and kept over a fixed point during ascent and descent. In some cases, we used the autopilot software DJI GS Pro that automatically leads the drone along a prescribed path. This software does not allow to prescribe the ascending/descending motion over a fixed point, so the vertical motion along the profile was represented by the series of zigzags within approx. 200 m from the starting point. In usual, the vertical profiles were measured by D1 drone and occasionally by D2.
The data processing was performed by the set of routines, which synchronize the data from meteorological sensors and from the flight logs, interpolate all variables to the same time intervals with 1 Hz frequency, separate the ascending and descending segments of the flight, determine the height above the ground, and average the meteorological variables for regular height intervals. The height above the ground was estimated based on iMet-XQ2 pressure readings taking into account the observed vertical temperature profile [48]. Finally, processing routines provide the vertical profiles of the meteorological variables including the wind speed and direction. The known problem of the aircraft-based vertical sounding is a difference between the ascending and descending profiles due to the sensors’ inertia as well as due to the atmospheric unsteadiness [63]. In our previous research, the noticeable effects of the sensor’s inertia on the temperature and humidity profiles was found, and a simple correction based on a time shift of the sensors’ readings was proposed [48]. However, we did not find such effect for the drone-estimated wind profiles. In the following, we use the profiles of the wind speed and direction, averaged between measurements in ascending and descending flight segments; the difference between “ascending” and “descending” profiles is used as a measure for uncertainty of the drone-observed wind.
2.4. Verification of Quadcopter Wind Measurements versus Ground-Based Observations
To verify and calibrate the drone-based wind measurement, we performed series of experiments when the drones were hovering near the acoustic anemometer (Figure 2b). In each experiment one or two drones were hovering over the sea ice in front of the WSBS pier, in the vicinity of 5–10 m from the anemometer for 10–12 min. The hovering height was controlled to be as close to the height of anemometer (approx. 4 m above the sea level) as possible. In total, we performed seven experiments for the cases with different wind speed and direction, and with different orientation of the drones with respect to airflow.
3. Results
3.1. Calibration of the Drone Wind Measurements versus Ground-Based Observations
The experiments when the drones were hovering near the IGRASON acoustic anemometer have shown a relatively good agreement between anemometer measurements and drone-based estimates in terms of the mean values and wind speed temporal variations with an averaging period about 20–30 s and more (Figure 3a). However, we found a systematic underestimation of the drone-estimated wind speed when the drones were aligned parallel to the airflow (Figure 3b).
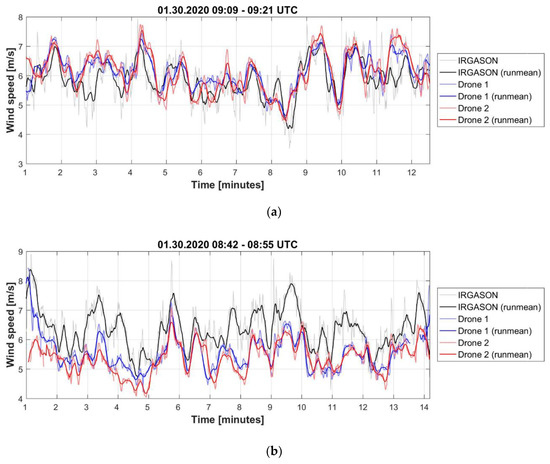
Figure 3.
Comparison of the wind speed series, measured by IGRASON anemometer and estimated by the drones during hovering near anemometer, for cases when the drones were headed perpendicular the airflow (a) and along the airflow (b). Data are shown with 1 Hz frequency and after applying a running mean with 10 s window.
To investigate the revealed dependence of the wind speed bias on the wind direction relative to drone, we analyzed the wind speed components and in a coordinate system of the drone, where X axis is directed from the drone’s front side to backside, and Y axis is aligned from the drone’s right side to the left side. Hence, is positive for the headwind, is positive for the right crosswind. Reference anemometer measurements were rotated to drone-based coordinates using the drone’s yaw angle. Comparison between reference and estimated and values shows relatively good agreement with trend determination coefficient equal to 0.78 and 0.92 correspondingly. However, the drone-estimated values are generally underestimated, especially when reference is higher than 4 m/s. The slope of the linear trend for estimated is less than 1 (0.75 as a mean value for all cases), while linear trend slope for is almost 1 (Figure 4a,b). In other words, the drones are less sensitive to the headwind than to the crosswind.
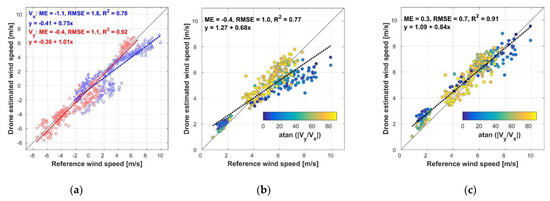
Figure 4.
Comparison between (red markers) and (blue markers) components (a) and wind speed (b), averaged over 30-s intervals, according to the reference IRGASON measurements and the drone-based estimate before correction, and for the wind speed after applying the proposed correction for component (c). and values are shown in (a) by blue and red color, respectively. Different symbols in (a) indicated to different hovering experiments.
The absence of the publicly available description of the wind-estimation algorithm, used by DJI flight controller, complicates an accurate interpretation of the revealed differences in drones’ sensitivity to headwind and crosswind. One may suggest a possible reason for this related with influence of payload, i.e., iMet-XQ and iMet-XF sensors installed on the drone’s chassis. Installation of iMet-XQ and iMet-XF sensors should increase the drone’s windage to the crosswind and modify the optimal calibration parameters of the wind-estimation algorithm. However, there is no significant difference between the wind speed evaluation results for D1 drone equipped with iMet-XQ sensor and D2 drone with both iMet-XQ and iMet-XF sensors, despite the later should be strongly affected by the payload. Moreover, additional calibration experiments, performed later with and without payload, suggests that drone’s sensitivities to the headwind and crosswind are still different even when payload is not installed (details are not shown).
Despite the available data have not clearly revealed the reasons for the differences between reference and drone-estimated wind, it allows introducing a simple correction for the drone-estimated headwind component. Based on the comparison results for seven experiments and two drones, we introduced a correction in a form of scaling multiplier 1/0.75 = 1.33 for component. This correction noticeably decreased the errors of the drone-estimated wind speed. The root-mean square error (RMSE) for the wind speed, averaged over 30-s intervals, decreased from 1 to 0.7 m/s, and correlation coefficient increased from 0.87 to 0.95. Such error values are close to those ones obtained for CopterSonde [34] in comparison to the radiosondes and acoustic anemometer on 15-m tower [33].
3.2. Comparison between Vertical Wind Profiles, Obtained by Two Methods
Performed synchronous balloon and drone-based vertical soundings allow comparing two methods for diverse conditions, i.e., with different wind speed and direction and with different shape of vertical wind profile. In general, two methods demonstrated reasonable agreement with a range of wind speed up to 20 m/s, which is illustrated by examples in Figure 5a–c for three cases with lower or higher wind shear. For the wind direction in Figure 5a–c, the methods agree in terms of basic wind direction intervals, but not always agree even in a shape of the profile. For example, case for 29th of January from Figure 5b,e demonstrates the best agreement for the wind speed, however for the wind direction there is no agreement even for the sign of vertical wind rotation, with right wind rotation for the drone-estimated profile and opposite for balloon sounding results. Disagreement for wind direction in this specific case may be explained by the orography-induced spatial inhomogeneity of the airflow, which is further discussed in Discussion.
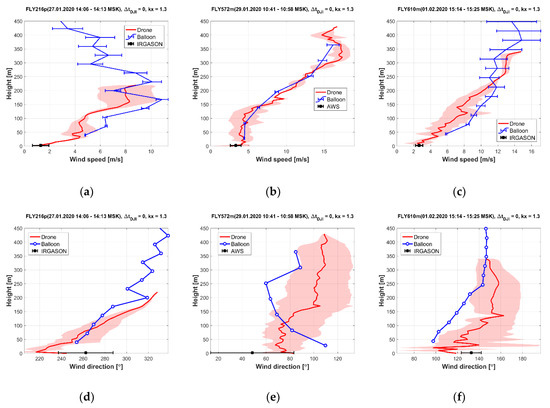
Figure 5.
Examples of comparison between balloon and drone soundings for wind speed (a–c) and direction (d–f) profiles for three cases. For the drone-based profiles, red shading indicates the spread between ascending and descending segments of flight. For balloon-based wind speed profiles, error bars indicate uncertainty as described in Section 2.2. For ground-based observations (IRGASON anemometer or Vaisala AWS if the first is not available), error bars indicate the standard deviation of the wind speed/direction during the drone flight.
Especially interesting example of comparison between two methods is provided by the case of 28th of January, when intense temperature inversion was developed under clear-sky conditions (Figure 6). The temperature profiles, measured by quadcopter and MTP-5 temperature profiler, indicate the inversion strength of 8 °C in a layer from 0 to 350 m, with the sharpest temperature gradient at the height about 100 m. As typical for stably boundary layer, inversion was accompanied by a low-level jet [64]. Wind speed peak of about 7 m/s at the height of 150–200 m was nicely captured by the drone and balloon as well. Unfortunately, in this case the balloon was lost by observer just in the beginning of the sounding and then was captured again at the height about 100 m, therefore there is no data for balloon-based wind profile lower than 100 m. The drone-based wind direction profile, together with near-surface observations by IRGASON anemometer clearly shows the sharp wind rotation by almost 180° in the lowest 100 m, with eastern wind near the surface and western wind above. So sharp wind rotation may be explained by the mesoscale orography-induced circulation in the layer below the temperature inversion. Thus, it is not surprising that the balloon was lost by the observer with such a sharp turn of the wind.
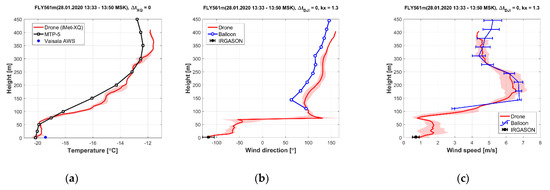
Figure 6.
Vertical profiles of the air temperature (a), wind speed (b) and wind direction (c) according to drone-based sounding, balloon sounding and observations of MTP-5 temperature profiler for a case with a strong temperature inversion (28 January 2020). Designations are similar to Figure 5.
For three cases, the balloon-based sounding was consequently repeated (with a delay of about 15 min) with an aim to estimate uncertainty of the consequently measured wind profiles. Plots on Figure 7 demonstrate the wind speed and direction profiles for these cases. One may note that for the wind speed, the difference between consequent balloon-derived profiles may reach 2–3 m/s and is higher than the difference between the uncertainty of drone-estimated profiles (difference between profiles for ascending and descending flight segments). Moreover, differences in balloon-derived wind speed between two soundings in cases (a) and (c) significantly exceed the estimated uncertainty of the method (see Equations (5) and (6)), which might indicate individual errors of an observer or non-stationarity of the flow. For wind direction, on contrary, the difference between two consequent balloon-derived profiles is typically lower than the uncertainty of the drone-estimated profile. High uncertainty of the drone-based wind direction profiles seems to be a shortcoming of the wind estimation algorithm, which should be investigated in more detail in further studies.
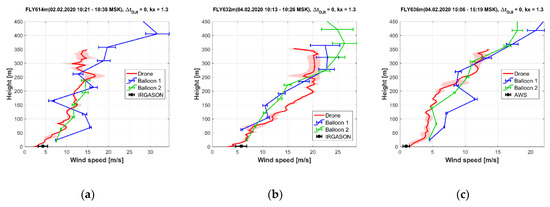
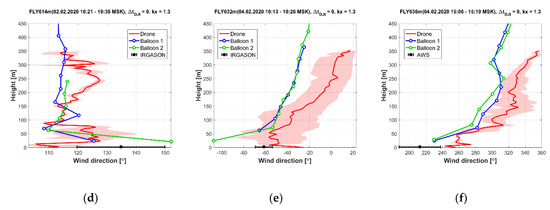
Figure 7.
Examples of comparison between balloon and drone sounding for wind speed (a–c) and direction (d–f) profiles for three cases, when balloon sounding was performed twice. Designations are similar to Figure 5.
During the WSBS-2020 campaign, we tested different possibilities to perform the drone-based vertical sounding. The simplest option is to manually control the aircraft. In manual mode, the aircraft was moving strictly vertical way with ascend/descent speed about 1–2 m/s, and the yaw angle was typically kept constant during ascending and descending (allowing rotation at the top point). However, manual piloting becomes challenging in cold weather due to the freezing of the pilot’s fingers. An attempt to automatize the drone-based sounding was performed using DJI GS Pro autopilot software (https://www.dji.com/ground-station-pro, accessed on 13 March 2021). DJI GS Pro allows to drive the drone along a given trajectory specified as a sequence of points on a map. For each point, it is possible to specify the requested height, however it is not possible to drive aircraft strictly vertical using this software. Various options were tested for raising the aircraft to a height of 500 m in such a way as to minimize its distance from the starting point and keep the quasi-vertical profile. One of the options was to drive the drone along the trajectory with multiple zigzags around starting point, rotating by 180° every 50 m of altitude (Figure 8a). However, such method led to unexpected artifacts in the wind profiles, namely the unrealistic step-like variations every 50 m (Figure 8b,d). For the wind speed profile, such step-like variations are less expressed, but still noticeable. Such behavior seems to be not related with the influence of the payload or other yaw-dependent systematic error, since the drone’s orientation during ascent and descent was mirrored opposite. Nevertheless, the same step-like variations were obtained on the descent and ascent wind direction profile. While the reasons of observed behavior require further investigation, it could be concluded that it is better not to change drone’s yaw when making vertical profiles. Next profiles were performed using DJI GS Pro software with a same trajectory, but drone’s yaw was kept constant, which eliminated the described problem.
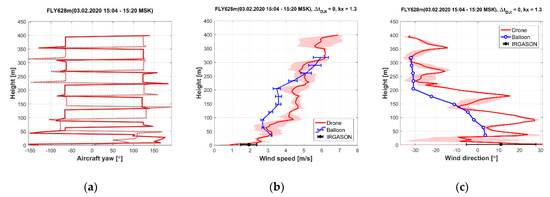
Figure 8.
Comparison between aircraft yaw (a), wind speed (b) and direction (c) profiles for the cases at 3.02.2020, when drone was piloted by GS Pro software following predefined zigzag ascending and descending trajectory. For yaw (a), dotted and solid lines show the values for ascending and descending segments of the flight, respectively. Other designations are similar to Figure 5.
To evaluate the formal metrics of comparison between two methods such as correlation coefficient (R), mean error (ME), and root-mean square error (RMSE), we set up a correspondence between each balloon-estimated value at i-th vertical level, , and the mean drone-estimate values within the elevation range from to , including both ascending and descending segments of the flight. Comparison between such values of wind speed over all 14 available cases indicates a relatively good agreement with R = 0.86, R2 = 0.75, near-zero ME and RMSE = 2.3 m/s (Figure 9b). These metrics are obtained for the drone-estimated wind profiles, corrected as proposed in Section 3.1. Otherwise, the agreement between two methods is worse, with higher RMSE = 2.7 m/s and negative ME = −1.2 m/s indicating the underestimation of the drone-estimated wind speed with respect to balloon-estimated values. Thus, the proposed correction is additionally supported. For the wind direction, the ME is 13.3°, which means that the drone-estimated wind direction is systematically biased to the right side. Such systematic bias could be caused by the drone’s misbalance induced by the attached sensors; however, this should be confirmed in further studies. Despite the high correlation coefficient, the RMSE value is 27°, which ensures the agreement in terms of eight principal wind direction segments.
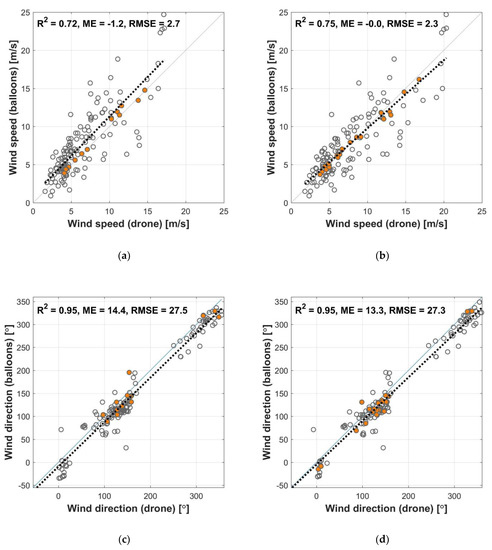
Figure 9.
Comparison between balloon-based and drone-based vertical soundings for the wind speed (a,b) and direction (c,d) values, before (a,c) and after (b,d) applying correction for drone-estimated crosswind component. Orange dots indicate, when the drone-estimate wind speed lies within uncertainty range of balloon-based wind speed estimate, related with imperfect tracking of the balloon by the theodolite.
4. Discussion: What Are the Sources of Discrepancies between Two Methods?
The comparison between the two methods of wind profiling, i.e., by pilot balloons and DJI Phantom 4 Pro drones demonstrated unbiased agreement. However, high scatter between wind profiles obtained by each of these methods (with RMSE of 2.3 m/s for wind speed and 27° for wind direction) indicates several uncertainties. Such uncertainties are noticeably higher than errors of the drone-estimated wind speed in comparison to reference measurements by acoustic anemometer. The latter demonstrated the RMSE of 0.7 m/s, which is comparable to RMSE in other recent studies where quadcopter-estimated wind speed was evaluated against acoustic anemometer [33,52,53,65]. Significantly higher uncertainties between two wind profiling methods may be caused by several factors, including the following:
- (1)
- The model, that is used to derive the height of acceding balloon uses a number of parameterizations e.g., drag coefficient dependence on Reynolds number of uncertain accuracy.
- (2)
- As shown in Section 2.2., the other source of errors of the balloon-estimated wind speed and direction is uncertainty of measuring balloons’ angular coordinates by the theodolite, where both errors caused by construction of theodolite and those of the observer come in play; the errors, permitted by construction are 0.2° in vertical and horizontal angles, which translates to 0.1–1 m/s standard error of measured wind speed (Section 2.2 and Section 3.2); this error magnitude, however, does not explain deviations between two methods in a number of cases.
- (3)
- The balloon wind sounding method assumes the absence of vertical air motion, which is actually present leading to errors in computed wind profile [60]; in a case of this study, significant vertical velocities might have been generated in a convective boundary layer (CBL) over polynya; we estimated CBL thickness to be several dozens of meters, while above CBL stratification was stable and significant vertical velocities (i.e., comparable to balloon velocity) in the lower atmosphere were unlikely.
- (4)
- Other uncertainties related with observing balloon in the theodolite can be related with inaccurate theodolite installation and with irregular time intervals between actual angle measurements.
- (5)
- Limitations and uncertainties of the drone’s built-in wind estimation algorithm are not fully understood; however, a correction multiplier may be derived when comparing drone wind measurements to data of sonic anemometers, which noticeably improves the agreement between drones and anemometers, and between drones and balloons.
- (6)
- Airflow in the ABL is non-stationary, which may result in significant differences between the profiles measured with a time lag of few minutes. This may be especially important since the drone-based and balloon-based soundings are difficult to synchronize.
- (7)
- Additional uncertainties may arise from the horizontal displacement of locations of wind measurements by drones and balloons. While the drone measures the wind along a vertical profile over a given site, balloon is blown away for hundreds of meters from the launch point (Figure 10); this is likely to be especially important for the measurements over inhomogeneous landscape with high horizontal variability of wind field.
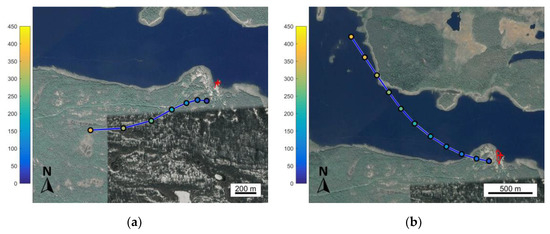 Figure 10. Example of the balloon’s trajectories at 29th of January (a) and 1st of February (b). White line with colored markers indicates the balloon’s trajectory within the lowest 500 m (height is shown by color) and read “+” symbol indicates the location where drone-based sounding was performed. Google maps images are used as background. Presented cases at (a) and (b) plots corresponds to wind profiles shown in Figure 5b,e and Figure 5c,f respectively.
Figure 10. Example of the balloon’s trajectories at 29th of January (a) and 1st of February (b). White line with colored markers indicates the balloon’s trajectory within the lowest 500 m (height is shown by color) and read “+” symbol indicates the location where drone-based sounding was performed. Google maps images are used as background. Presented cases at (a) and (b) plots corresponds to wind profiles shown in Figure 5b,e and Figure 5c,f respectively.
Below, we discuss the significance of some of the listed factors. The balloon ascent model presented in Section 2.2 (factor no. 1) is the fullest in terms of a set of physical processes accounted for, according to the knowledge of authors. However, several effects of balloon dynamics remain minor in the interval of altitudes 0–1 km which is a focus in this study. Specifically, neglecting vertical balloon acceleration and solving the Equation (3) by assuming the helium temperature homogeneous inside the balloon and equal to ambient air temperature or even the near-surface temperature (2 m), change the computed vertical wind profiles negligibly. Another possible inaccurate model assumption is related to estimation of the balloon’s drag coefficient. The systematic consideration of optimal specification for dependence is presented in [60]; in this study we use the dependence derived there. This function has been calibrated for whereas typical values for small balloons used in this study are . Though there is no firm justification in the literature for using selected function for such small , should the actual be systematically misestimated by our balloon ascent model, this would lead to systematically wrong computed vertical balloon speed, and consequently the emergence of systematic vertical shifts between balloon-based and drone-based wind profiles, which are not observed in our case.
One more feature of balloon-based compared to drone-based measurements is the presence of “saw-like” fluctuations (Figure 5a,d and Figure 6a,d) exceeding the predicted ranges of standard error. Gallice et al. (2011) [60] observes similar effects at much larger vertical scales and attributes them to internal waves under stable stratification. In our case of the lower 1 km, such kind of disturbances might occur from non-homogeneity of horizontal wind distribution over complex terrain as well as from errors of the observer.
Based on the available data, we firmly conclude that uncertainty of measuring balloons’ angular coordinates by the theodolite (factor no. 2) is likely not be the main reason for the observed differences. Cases when the drone-estimated wind speed is inside the range of possible values of balloon-estimated wind, determined by the accuracy of angular measurements in the theodolite, are highlighted in orange in the Figure 9. Such cases have much better agreement than the others and almost ideally fit the one-to-one line for the wind speed. Hence, this factor of the uncertainty seems to be less important in comparison with other ones.
To investigate the contribution of other possible factors, we analyzed the dependencies of the difference between drone-estimated and balloon-estimated wind speed on a set of variables that included heigh over the ground, balloon’s horizontal displacement from the launch point, angle between the drone’s yaw and wind direction and wind direction. We did not reveal any significant dependence between the wind speed difference and any of these variables. Most likely, the observed uncertainties are caused by a complex interplay of all listed factors. For example, balloon displacement should be important on the low altitudes in cases when the underlying terrain is inhomogeneous along the balloon’s trajectory, which is illustrated by the case of 29th of January (Figure 5b,e). At this day, east-north-eastern prevailing wind was observed. The drone, launched above the WSBS pier, captured the airflow before it was disturbed by the orography of Kindo peninsula. Hover, the balloon just after release was blown away from the coastline over the forest and slope of the hill with altitude range from 0 to ≈100 m (Figure 10a). Orography-induced perturbations of the airflow are likely to be the reason for noticeable disagreement between drone-estimated and balloon-estimated wind direction profiles in the lowest 200 m for this case (Figure 5e). Another example is a case at 01.02.2020 (Figure 5c,f), when the drone’s launch site was shielded from the prevailing south-eastern wind by Kindo peninsula, which is a possible reason for significant difference in wind direction between two methods (Figure 5f).
5. Conclusions
Presented study compared two low-cost methods of wind profiling in the lower atmosphere, namely vertical sounding with pilot balloons, tracked by theodolite angular observations, and vertical sounding with mass-market unmanned quadcopters DJI Phantom 4 Pro. Each of these methods prone to errors due to different reasons (e.g., observer’s errors and shortcomings of the balloon ascent model for the balloon-based method, imperfectness of the wind-estimation algorithm and disturbances of the drone’s calibration by attached meteorological sensors for quadcopter-based sounding) and the non-stationary nature of the atmospheric flow, especially over heterogeneous terrain. Despite these uncertainties, during the field campaign at the White Sea Biological Station in 2020 (WSBS-2020) these methods demonstrated reasonable agreement in wide range of environmental conditions and wind speeds from 0 to 20 m/s, with RMSE of 2.3 m/s for the wind speed and 27° for wind direction. Beyond formal metrics, in most of the cases both methods agreed in the shape of wind profile and its important characteristics such as vertical wind shear and rotation. The accuracy of quadcopter-estimated wind speed was additionally examined in comparison against reference near-surface wind speed measurements by acoustic anemometer. After introducing an empirical correction to the crosswind component of the quadcopter-estimated wind, we found a good agreement between the latter and reference observations with RMSE of 0.7 m/s. Application of the both wind profiling methods during WSBS-2020 allowed us to reveal high temporal and spatial variability of the boundary layer wind speed over heterogenous terrain, which will be analyzed with a linkage to other performed observations in further studies.
Of course, discussed wind profiling methods are not recommended to substitute high-precision and regular wind profile observations by masts, lidars, and other sophisticated techniques. Nonetheless, we found both to be effective for short-term field atmospheric research campaigns, especially in remote places, and for educational events, since both of the methods allow better understanding of the full chain of data acquisition, processing and collection. Required equipment is easy to transport (with a total weight not exceeding 10 kg for each method) and does not need any specific infrastructure. In our case, both methods were quite time- and labor consuming. One balloon-based sounding required work of two persons for about 30 min, and drone-based sounding requires work of one person for the same time. However, possibilities to partially automate both methods are foreseen. For the DJI drones, several solutions are already proposed to automate the almost whole process from the battery charging to performing flights. Even the use of GS Pro autopilot software strongly simplifies the drone-based soundings.
Both methods have their advantages and shortcomings. Novel method of the quadcopter-based sounding is simpler in operation and provides higher-resolution data in comparison to the classic method of balloon-based sounding. Another key advantage of the quadcopter-based sounding is an opportunity to simultaneously obtain profiles of wind and other meteorological variables (temperature, in our case) and to get comprehensive understanding of the boundary layer processes. Additionally, quadcopter-based profiles are not affected by random errors of the observer. However, application of the quadcopter-based sounding is limited by flight restriction rules, e.g., it may be difficult to apply this method in urban areas or near airports. Despite the drone-based sounding may be performed even in case of low cloudiness, it is still limited in height. The maximum altitude for DJI Phantom 4 Pro as well as other DJI drones is limited to 500 m by software, while the vertical range of the balloon-based sounding in clear weather is limited only by observer’s ability to track the ball. In our study, several balloons reached the height of more than 1 km. Another limitation of the drone-based sounding is high wind speed. In our case, the drone was not able to keep its position when the wind speed exceeded approximately 15 m/s. On contrary, balloon-based sounding could be challenging in case of sharp wind rotation with height, as it was shown in this paper for a case with intense temperature inversion.
Another problem of the wind measurements by mass-market DJI drones is absence of publicly available documentation of the built-in wind estimation algorithm and its possible dependence on the drone’s firmware version. For example, the flight logs of the recently updated DJI Phantom 4 Pro drone (2.0 version) does not contain the airflow speed with respect to a drone, that we used in our study to calculate final wind speed estimate, but still contain more smoothed wind speed estimate with respect to a ground. For another popular mass-market drone, DJI Mavic, wind speed estimate by built-in algorithms is even not available since the flight logs are encoded. Additionally, it is still difficult to judge about the influence of the payload (meteorological sensors attached to a drone) on the drone-based wind speed estimate. Thus, we highly recommend performing calibration of the drone-based wind speed estimate against reference observations for each new drone, each new version of its firmware, and each new payload type. Experiments with rotating drone with respect to airflow performed in our field campaign may be used as a basic scheme for such calibration. Among the other recommendations, our experience suggests keeping the drone’s yaw as constant when performing the vertical sounding, event when the drone is controlled by autopilot software, since the fast rotations may disturb the proper functioning of the drone’s built-in wind estimation algorithm.
Author Contributions
Conceptualization, M.V., V.S., I.R., and V.B.; methodology, M.V., V.S., I.R., V.B., A.A.; software, M.V., V.S., V.B., E.M.; validation, M.V. and E.M.; formal analysis, M.V., E.M., A.V., N.K.; investigation, all authors; resources, M.V., V.S., I.R., A.A., A.P.; data curation, M.V., E.M., A.V., N.K.; writing—original draft preparation, M.V., V.S., and I.R.; writing—review and editing, M.V., V.S., and I.R.; visualization, M.V., N.K., A.V.; supervision, V.S. and I.R. All authors have read and agreed to the published version of the manuscript.
Funding
Development of the quadcopter-based sounding technique was funded by Russian Foundation for Basic Research (RFBR) projects no. 18-05-60126 and 20-55-71004. Field campaign in coastal zone of the White sea was supported by RFBR projects 20-05-00834 and 18-05-80065. Data analysis and model development performed by V.S., I.R. and A.A. was carried out within the grant of the Tyumen region Government in accordance with the Program of the World-Class West Siberian Interregional Scientific and Educational Center (National Project “Nauka”).
Data Availability Statement
The datasets analyzed and generated during our study are available on request to corresponding author.
Acknowledgments
The authors are thankful for administration and staff of the White Sea Biological Station of the Lomonosov Moscow State University for hosting the field campaign and unvaluable help and support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Consider balloon tracking in a cylindrical coordinate system , where is the vertical angle, is the horizontal angle (azimuth), and is the height; the first two coordinates are measured (in our case by theodolite), and the last one is computed model of vertical motion described in Section 2.2. Introducing an error , and a measured value so that, , where , assuming (as there is no information on this error), one gets:
where are eastward and northward Cartesian coordinates of a balloon, respectively, and
We have neglected the quadratic terms in above expressions, assuming errors are small. Now, introduce the balloon velocity components as finite differences, and using (A1) and (A2) we get:
and analogous expression for . Now, assuming that errors of two angles are uncorrelated, and are also uncorrelated in time, yields equations for and ((7)–(9) in the main text of the paper).
References
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows, Their Structure and Measurements; Oxford University Press: New York, NY, USA; Oxford, UK, 1994. [Google Scholar]
- Baklanov, A.; Grisogono, B. Atmospheric Boundary Layers: Nature, Theory and Applications to Environmental Modelling and Security; Springer: New York, NY, USA, 2007. [Google Scholar]
- Holtslag, A.A.M.; Svensson, G.; Baas, P.; Basu, S.; Beare, B.; Beljaars, A.C.M.; Bosveld, F.C.; Cuxart, J.; Lindvall, J.; Steeneveld, G.J.; et al. Stable atmospheric boundary layers and diurnal cycles: Challenges for weather and climate models. Bull. Am. Meteorol. Soc. 2013, 94, 1691–1706. [Google Scholar] [CrossRef]
- Barskov, K.V.; Chernyshev, R.V.; Stepanenko, V.M.; Repina, I.A.; Artamonov, A.Y.; Guseva, S.P.; Gavrikov, A.V. Experimental study of heat and momentum exchange between a forest lake and the atmosphere in winter. IOP Conf. Ser. Earth Environ. Sci. 2017, 96, 012003. [Google Scholar] [CrossRef]
- Barskov, K.; Stepanenko, V.; Repina, I.; Artamonov, A.; Gavrikov, A. Two Regimes of Turbulent Fluxes Above a Frozen Small Lake Surrounded by Forest. Bound.-Layer Meteorol. 2019, 173, 311–320. [Google Scholar] [CrossRef]
- Kral, S.; Reuder, J.; Vihma, T.; Suomi, I.; O’Connor, E.; Kouznetsov, R.; Wrenger, B.; Rautenberg, A.; Urbancic, G.; Jonassen, M.; et al. Innovative Strategies for Observations in the Arctic Atmospheric Boundary Layer (ISOBAR)—The Hailuoto 2017 Campaign. Atmosphere 2018, 9, 268. [Google Scholar] [CrossRef]
- Pfotzer, G. History of the use of balloons in scientific experiments. Space Sci. Rev. 1972, 13, 199–242. [Google Scholar] [CrossRef]
- Ingleby, B. An Assessment of Different Radiosonde Types 2015/2016; ECMWF Technical Memoranda; ECMWF: Reading, UK, 2017; p. 69. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Seidel, D.J.; Hunt, D.C. Comparing radiosonde and COSMIC atmospheric profile data to quantify differences among radiosonde types and the effects of imperfect collocation on comparison statistics. J. Geophys. Res. Atmos. 2010, 115, 1–16. [Google Scholar] [CrossRef]
- Durre, I.; Vose, R.S.; Wuertz, D.B. Overview of the integrated global radiosonde archive. J. Clim. 2006, 19, 53–68. [Google Scholar] [CrossRef]
- Peña, A.; Floors, R.; Sathe, A.; Gryning, S.-E.; Wagner, R.; Courtney, M.S.; Larsén, X.G.; Hahmann, A.N.; Hasager, C.B. Ten Years of Boundary-Layer and Wind-Power Meteorology at Høvsøre, Denmark. Bound.-Layer Meteorol. 2016, 158, 1–26. [Google Scholar] [CrossRef]
- Novitskii, M.A.; Mazurin, N.F.; Kulizhnikova, L.K.; Kalinicheva, O.Y.; Tereb, L.A.; Nechaev, D.R.; Sapronov, V.L. Comparison of wind measurements by means of industrially produced sodar and high-altitude meteorological mast in Obninsk. Russ. Meteorol. Hydrol. 2011, 36, 693–699. [Google Scholar] [CrossRef]
- Gilman, G.W.; Coxhead, H.B.; Willis, F.H. Reflection of Sound Signals in the Troposphere. J. Acoust. Soc. Am. 1946, 18, 274–283. [Google Scholar] [CrossRef]
- Kallistratova, M.A. Acoustic and radio-acoustic remote sensing studies in C.I.S. (Former U.S.S.R.)-current status. Int. J. Remote Sens. 1994, 15, 251–266. [Google Scholar] [CrossRef]
- Coulter, R.L.; Kallistratova, M.A. The Role of Acoustic Sounding in a High-Technology Era. Meteorol. Atmos. Phys. 1999, 71, 3–13. [Google Scholar] [CrossRef]
- Kallistratova, M.A.; Petenko, I.V.; Kouznetsov, R.D.; Kulichkov, S.N.; Chkhetiani, O.G.; Chunchusov, I.P.; Lyulyukin, V.S.; Zaitseva, D.V.; Vazaeva, N.V.; Kuznetsov, D.D.; et al. Sodar Sounding of the Atmospheric Boundary Layer: Review of Studies at the Obukhov Institute of Atmospheric Physics, Russian Academy of Sciences. Izvestiya Atmos. Ocean. Phys. 2018, 54, 242–256. [Google Scholar] [CrossRef]
- Emeis, S. Upper limit for wind shear in stably stratified conditions expressed in terms of a bulk Richardson number. Meteorol. Z. 2017, 26, 421–430. [Google Scholar] [CrossRef]
- Banakh, V.; Smalikho, I. Lidar Studies of Wind Turbulence in the Stable Atmospheric Boundary Layer. Remote Sens. 2018, 10, 1219. [Google Scholar] [CrossRef]
- Baker, W.E.; Atlas, R.; Cardinali, C.; Clement, A.; Emmitt, G.D.; Gentry, B.M.; Hardesty, R.M.; Källén, E.; Kavaya, M.J.; Langland, R.; et al. Lidar-Measured Wind Profiles: The Missing Link in the Global Observing System. Bull. Am. Meteorol. Soc. 2014, 95, 543–564. [Google Scholar] [CrossRef]
- Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Weitkamp, C., Ed.; Springer Science & Business: Berlin/Heidelberg, Germany, 2005; ISBN 0 387 40075 3. [Google Scholar]
- Chanin, M.L.; Garnier, A.; Hauchecorne, A.; Porteneuve, J. A Doppler lidar for measuring winds in the middle atmosphere. Geophys. Res. Lett. 1989, 16, 1273–1276. [Google Scholar] [CrossRef]
- Rees, D.; McDermid, I.S. Doppler lidar atmospheric wind sensor: Reevaluation of a 355-nm incoherent Doppler lidar. Appl. Opt. 1990, 29, 4133. [Google Scholar] [CrossRef] [PubMed]
- Frehlich, R.G.; Kavaya, M.J. Coherent laser radar performance for general atmospheric refractive turbulence. Appl. Opt. 1991, 30, 5325. [Google Scholar] [CrossRef]
- Boquet, M.; Royer, P.; Cariou, J.P.; Machta, M.; Valla, M. Simulation of Doppler lidar measurement range and data availability. J. Atmos. Ocean. Technol. 2016, 33, 977–987. [Google Scholar] [CrossRef]
- Liu, Z.; Barlow, J.F.; Chan, P.W.; Fung, J.C.H.; Li, Y.; Ren, C.; Mak, H.W.L.; Ng, E. A review of progress and applications of pulsed DopplerWind LiDARs. Remote Sens. 2019, 11, 2522. [Google Scholar] [CrossRef]
- Mikkelsen, T. Lidar-based research and innovation at DTU wind energy—A review. J. Phys. Conf. Ser. 2014, 524. [Google Scholar] [CrossRef]
- Hildebrand, J.; Baumgarten, G.; Fiedler, J.; Lübken, F.J. Wind measurements with the ALOMAR RMR-Lidar: Method description and initial results. In Proceedings of the 19th ESA Symposium on European Rocket and Balloon Programmes and Related Research, Bad Reichenhall, Germany, 7–11 June 2009; pp. 7–11. [Google Scholar]
- Woodman, R.F.; Guillen, A. Radar Observations of Winds and Turbulence in the Stratosphere and Mesosphere. J. Atmos. Sci. 1974, 31, 493–505. [Google Scholar] [CrossRef]
- Zhou, S.; Cui, Y.; Zheng, H.; Zhang, T. Wind shear identification with the retrieval wind of doppler wearth radar. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII–3, 2553–2555. [Google Scholar] [CrossRef]
- Muschinski, A.; Lehmann, V.; Justen, L.; Teschke, G. Advanced radar wind profiling. Meteorol. Z. 2005, 14, 609–625. [Google Scholar] [CrossRef]
- Teschke, G.; Lehmann, V. Mean wind vector estimation using the velocity-Azimuth display (VAD) method: An explicit algebraic solution. Atmos. Meas. Tech. 2017, 10, 3265–3271. [Google Scholar] [CrossRef]
- Lyulyukin, V.; Kallistratova, M.; Zaitseva, D.; Kuznetsov, D.; Artamonov, A.; Repina, I.; Petenko, I.; Kouznetsov, R.; Pashkin, A. Sodar observation of the ABL structure and waves over the black sea offshore site. Atmosphere 2019, 10, 811. [Google Scholar] [CrossRef]
- Segales, A.R.; Greene, B.R.; Bell, T.M.; Doyle, W.; Martin, J.J.; Pillar-Little, E.A.; Chilson, P.B. The CopterSonde: An insight into the development of a smart unmanned aircraft system for atmospheric boundary layer research. Atmos. Meas. Tech. 2020, 13, 2833–2848. [Google Scholar] [CrossRef]
- Bell, T.; Greene, B.; Klein, P.; Carney, M.; Chilson, P. Confronting the Boundary Layer Data Gap: Evaluating New and Existing Methodologies of Probing the Lower Atmosphere. Atmos. Meas. Tech. Discuss. 2019, 1–23. [Google Scholar] [CrossRef]
- Roldán, J.J.; Joossen, G.; Sanz, D.; del Cerro, J.; Barrientos, A. Mini-UAV based sensory system for measuring environmental variables in greenhouses. Sensors 2015, 15, 3334–3350. [Google Scholar] [CrossRef]
- Patel, P.N.; Patel, M.A.; Faldu, R.M.; Dave, Y.R. Quadcopter for Agricultural Surveillance. Adv. Electron. Electr. Eng. 2013, 3, 427–432. [Google Scholar]
- Ajayi, O.G.; Salubi, A.A.; Angbas, A.F.; Odigure, M.G. Generation of accurate digital elevation models from UAV acquired low percentage overlapping images. Int. J. Remote Sens. 2017, 38, 3113–3134. [Google Scholar] [CrossRef]
- Voskresensky, I.S.; Suchilin, A.A.; Ushakova, L.A.; Shaforostov, V.M.; Entin, A.L.; Ivanov, M.M. Study of the landslide morphology based on GNSS data and airborne sounding (on the example of a section of the Protva river valley) (in Russian). Eng. Surv. 2018, 12, 50–57. [Google Scholar] [CrossRef]
- Cimoli, E.; Marcer, M.; Vandecrux, B.; Bøggild, C.E.; Williams, G.; Simonsen, S.B. Application of Low-Cost UASs and Digital Photogrammetry for High-Resolution Snow Depth Mapping in the Arctic. Remote Sens. 2017, 9, 1144. [Google Scholar] [CrossRef]
- Nishar, A.; Richards, S.; Breen, D.; Robertson, J.; Breen, B. Thermal infrared imaging of geothermal environments and by an unmanned aerial vehicle (UAV): A case study of the Wairakei-Tauhara geothermal field, Taupo, New Zealand. Renew. Energy 2016, 86, 1256–1264. [Google Scholar] [CrossRef]
- Li, F.; Yang, W.; Liu, X.; Sun, G.; Liu, J. Using high-resolution UAV-borne thermal infrared imagery to detect coal fires in Majiliang mine, Datong coalfield, Northern China. Remote Sens. Lett. 2018, 9, 71–80. [Google Scholar] [CrossRef]
- DeMario, A.; Lopez, P.; Plewka, E.; Wix, R.; Xia, H.; Zamora, E.; Gessler, D.; Yalin, A. Water Plume Temperature Measurements by an Unmanned Aerial System (UAS). Sensors 2017, 17, 306. [Google Scholar] [CrossRef] [PubMed]
- Konrad, T.G.; Hill, M.L.; Rowland, J.R.; Meyer, J.H. A Small, Radio-Controlled Aircraft as A Platform for Meteorological Sensors. APL Tech. Dig. 1970, 10, 11–19. [Google Scholar]
- Spiess, T.; Bange, J.; Buschmann, M.; Vörsmann, P. First application of the meteorological Mini-UAV “M2AV”. Meteorol. Z. 2007, 16, 159–169. [Google Scholar] [CrossRef]
- Boer, G.; Ivey, M.; Schmid, B.; Lawrence, D.; Dexheimer, D.; Mei, F.; Hubbe, J.; Bendure, A.; Hardesty, J.; Shupe, M.D.; et al. A bird’s-eye view: Development of an operational ARM unmanned aerial capability for atmospheric research in arctic Alaska. Bull. Am. Meteorol. Soc. 2018, 99, 1197–1212. [Google Scholar] [CrossRef]
- Wildmann, N.; Bernard, S.; Bange, J. Measuring the local wind field at an escarpment using small remotely-piloted aircraft. Renew. Energy 2017, 103, 613–619. [Google Scholar] [CrossRef]
- Reuder, J.; Brisset, P.; Jonassen, M.; Müller, M.; Mayer, S. The Small Unmanned Meteorological Observer SUMO: A new tool for atmospheric boundary layer research. Meteorol. Z. 2009, 18, 141–147. [Google Scholar] [CrossRef]
- Varentsov, M.I.; Yu Artamonov, A.; Pashkin, A.D.; Repina, I.A. Experience in the quadcopter-based meteorological observations in the atmospheric boundary layer. IOP Conf. Ser. Earth Environ. Sci. 2019, 231, 012053. [Google Scholar] [CrossRef]
- Jonassen, M.O.; Tisler, P.; Altstädter, B.; Scholtz, A.; Vihma, T.; Lampert, A.; König-Langlo, G.; Lüpkes, C. Application of remotely piloted aircraft systems in observing the atmospheric boundary layer over Antarctic sea ice in winter. Polar Res. 2015, 34, 1–15. [Google Scholar] [CrossRef]
- Lampert, A.; Altstädter, B.; Bärfuss, K.; Bretschneider, L.; Sandgaard, J.; Michaelis, J.; Lobitz, L.; Asmussen, M.; Damm, E.; Käthner, R.; et al. Unmanned Aerial Systems for Investigating the Polar Atmospheric Boundary Layer—Technical Challenges and Examples of Applications. Atmosphere 2020, 11, 416. [Google Scholar] [CrossRef]
- Rautenberg, A.; Schön, M.; zum Berge, K.; Mauz, M.; Manz, P.; Platis, A.; van Kesteren, B.; Suomi, I.; Kral, S.T.; Bange, J. The Multi-Purpose Airborne Sensor Carrier MASC-3 for Wind and Turbulence Measurements in the Atmospheric Boundary Layer. Sensors 2019, 19, 2292. [Google Scholar] [CrossRef]
- Neumann, P.P.; Bartholmai, M. Real-time wind estimation on a micro unmanned aerial vehicle using its inertial measurement unit. Sens. Actuators A Phys. 2015, 235, 300–310. [Google Scholar] [CrossRef]
- Palomaki, R.T.; Rose, N.T.; van den Bossche, M.; Sherman, T.J.; De Wekker, S.F.J. Wind estimation in the lower atmosphere using multirotor aircraft. J. Atmos. Ocean. Technol. 2017, 34, 1183–1191. [Google Scholar] [CrossRef]
- Wilgan, K.; Stauffer, R.; Meindl, M.; Geiger, A. Comparison of tropospheric parameters from Meteodrone measurements with GNSS estimates from ground-based stations. Adv. Space Res. 2020. [Google Scholar] [CrossRef]
- Lee, T.R.; Buban, M.; Dumas, E.; Baker, C.B. Correction: On the use of rotary-wing aircraft to sample near-surface thermodynamic fields: Results from recent field campaigns (Sensors (2019), 19(1), 10). Sensors 2019, 19, 2197. [Google Scholar] [CrossRef]
- Shah, A.; Allen, G.; Pitt, J.R.; Ricketts, H.; Williams, P.I.; Helmore, J.; Finlayson, A.; Robinson, R.; Kabbabe, K.; Hollingsworth, P.; et al. A Near-Field Gaussian Plume Inversion Flux Quantification Method, Applied to Unmanned Aerial Vehicle Sampling. Atmosphere 2019, 10, 396. [Google Scholar] [CrossRef]
- Stepanenko, V.M.; Debolsky, A.; Varentsov, M.I.; Kuznetsov, D.; Zimin, M. Study of Atmospheric Convection Over the Arctic Ice Opening Applying Supercomputer Computations and High Resolution Satellite Data [in Russian]. Earth from Space 2011, 10, 52–55. [Google Scholar]
- Carlson, L.A.; Horn, W.J. New thermal and trajectory model for high-altitude balloons. J. Aircr. 1983, 20, 500–507. [Google Scholar] [CrossRef]
- Wang, J.; Bian, J.; Brown, W.O.; Cole, H.; Grubišić, V.; Young, K. Vertical Air Motion from T-REX Radiosonde and Dropsonde Data. J. Atmos. Ocean. Technol. 2009, 26, 928–942. [Google Scholar] [CrossRef]
- Gallice, A.; Wienhold, F.G.; Hoyle, C.R.; Immler, F.; Peter, T. Modeling the ascent of sounding balloons: Derivation of the vertical air motion. Atmos. Meas. Tech. 2011, 4, 2235–2253. [Google Scholar] [CrossRef]
- Harstad, E. Analysis of Balloon Trajectory Prediction Methods. In Proceedings of the Academic High Altitude Conference 2012, Nashville, TN, USA, 27–29 June 2012; pp. 103–108. [Google Scholar]
- Zhang, J.; Chen, H.; Zhu, Y.; Shi, H.; Zheng, Y.; Xia, X.; Teng, Y.; Wang, F.; Han, X.; Li, J.; et al. A Novel Method for Estimating the Vertical Velocity of Air with a Descending Radiosonde System. Remote Sens. 2019, 11, 1538. [Google Scholar] [CrossRef]
- Jacobi, C.; Scherf, A.; Siemer, A.H.; Roth, R. On the influence of sensor inertia on the estimation of turbulent fluxes from aircraft measurements. Bound.-Layer Meteorol. 1995, 76, 97–108. [Google Scholar] [CrossRef]
- Andreas, E.L.; Claffey, K.J.; Makshtas, A.P. Low-level atmospheric jets and inversions over the western Weddell Sea. Bound.-Layer Meteorol. 2000, 97, 459–486. [Google Scholar] [CrossRef]
- González-Rocha, J.; Woolsey, C.A.; Sultan, C.; De Wekker, S.F.J. Sensing wind from quadrotor motion. J. Guid. Control Dyn. 2019, 42, 836–852. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).