Sensitivity Operator Framework for Analyzing Heterogeneous Air Quality Monitoring Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemical Transport Model
- We suppose that only a given set of species is emitted. For the rest of species , .
- The emission sources are supposed to be constant in time ().
- We do not require the emission sources to be positive since variables unconsidered in the model, chemical transformations, various land types, and meteorological conditions, such as rains and snowfalls, can act as sinks for the specific chemicals.
- In the Inverse problem, the uncertainty function has to be identified from the partial information (“measurement data”) about , described in Section 2.3.
2.2. Sensitivity-Operator Based Representation of Measurement Data
2.3. Measurement Data Types
- “Timeseries”: time series of concentrations of the specific species in the specific points. In the state function terms:Projection system:For any element of , the parameter ranges from 0 to . The number of the frequencies is the parameter of the projection system. This parameter is responsible for the temporal resolution of the considered data. Hence the total number of projection functions corresponding to the Timeseries is
- “Pointwise”: Pointwise concentration measurements of the specific species at specific moments and specific points. In the state function terms:Projection system:The projection system is naturally defined by the measurement points. Hence the total number of the projection functions is . In the case of a large number of points, these data can be aggregated.
- “Integral”: Integrals of concentrations over the time interval of the specific species in the specific points. In the state function terms:Projection system:Here . Integral measurements are equivalent to “Timeseries” measurements with .
- “Snapshot”: specific species concentration fields images at specific moments in time. In the state function terms:Projection system:The projection system has two parameters: and , which define the spatial resolution of the considered data. For any image, and range in and , respectively. Hence .
2.4. Sensitivity-Operator-Based Analysis of Measurement System
2.4.1. Inverse Problem Solution
- (1)
- The “exact” solution is given. In our case, this is the location and capacity of the emission sources.
- (2)
- The “exact” solution is then used to simulate the “measurement data“. This “measurement data” is used in the algorithm to solve the inverse problem.
- (3)
- The result of the algorithm is compared with the “exact” solution. In this case, both the reconstruction of the source is estimated, and the convergence parameters of the algorithm are analyzed.
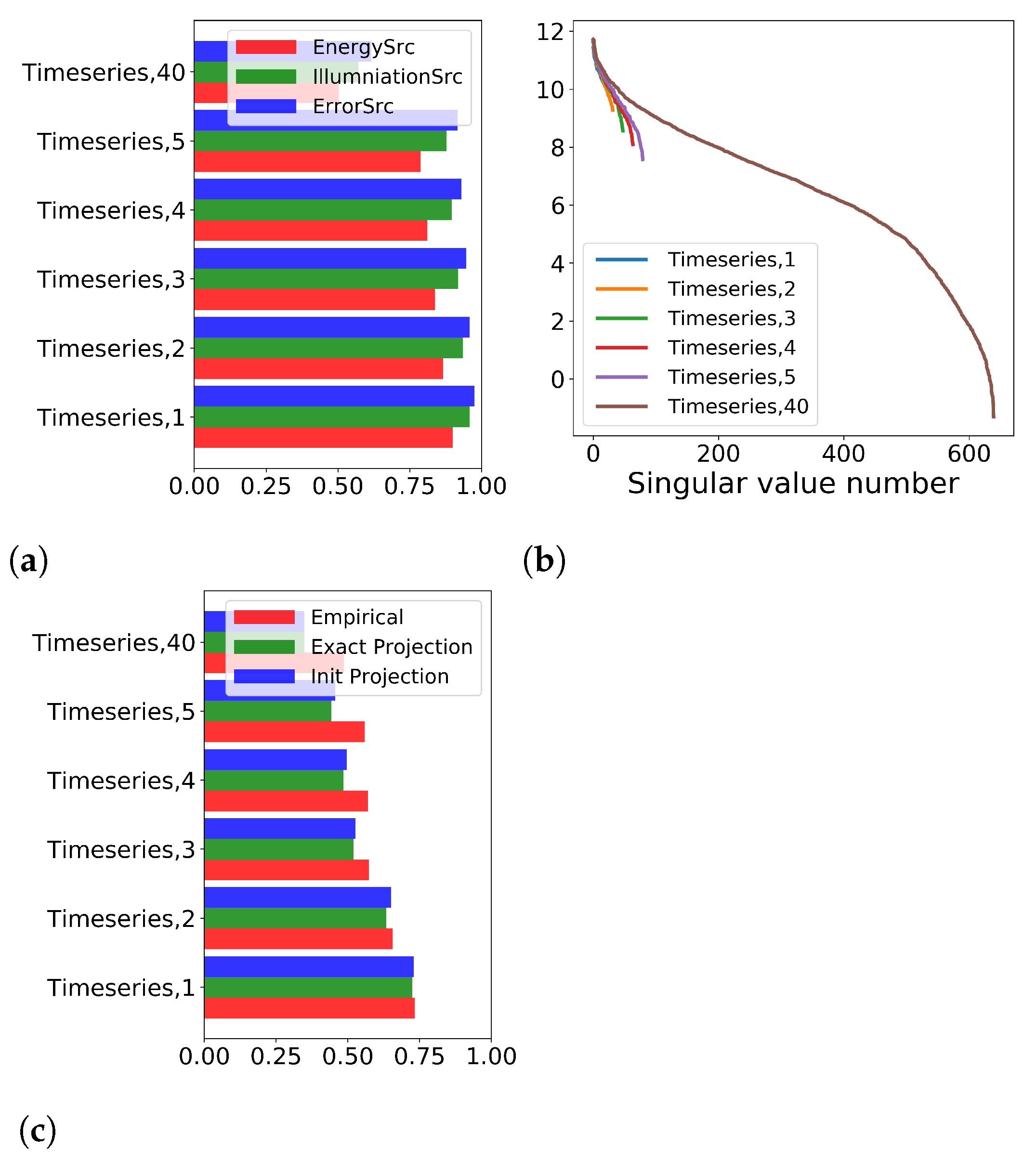
2.4.2. Sensitivity Operator Properties Analysis
2.5. Inverse Modeling Scenario
- Geographical domain.
- Monitoring system characteristics: locations and accuracy.
- Main emission sources to construct the “exact” solution.
- Chemical transformation mechanism, initial, and boundary conditions.
- Meteorological conditions, determining CTM model coefficients.
3. Results
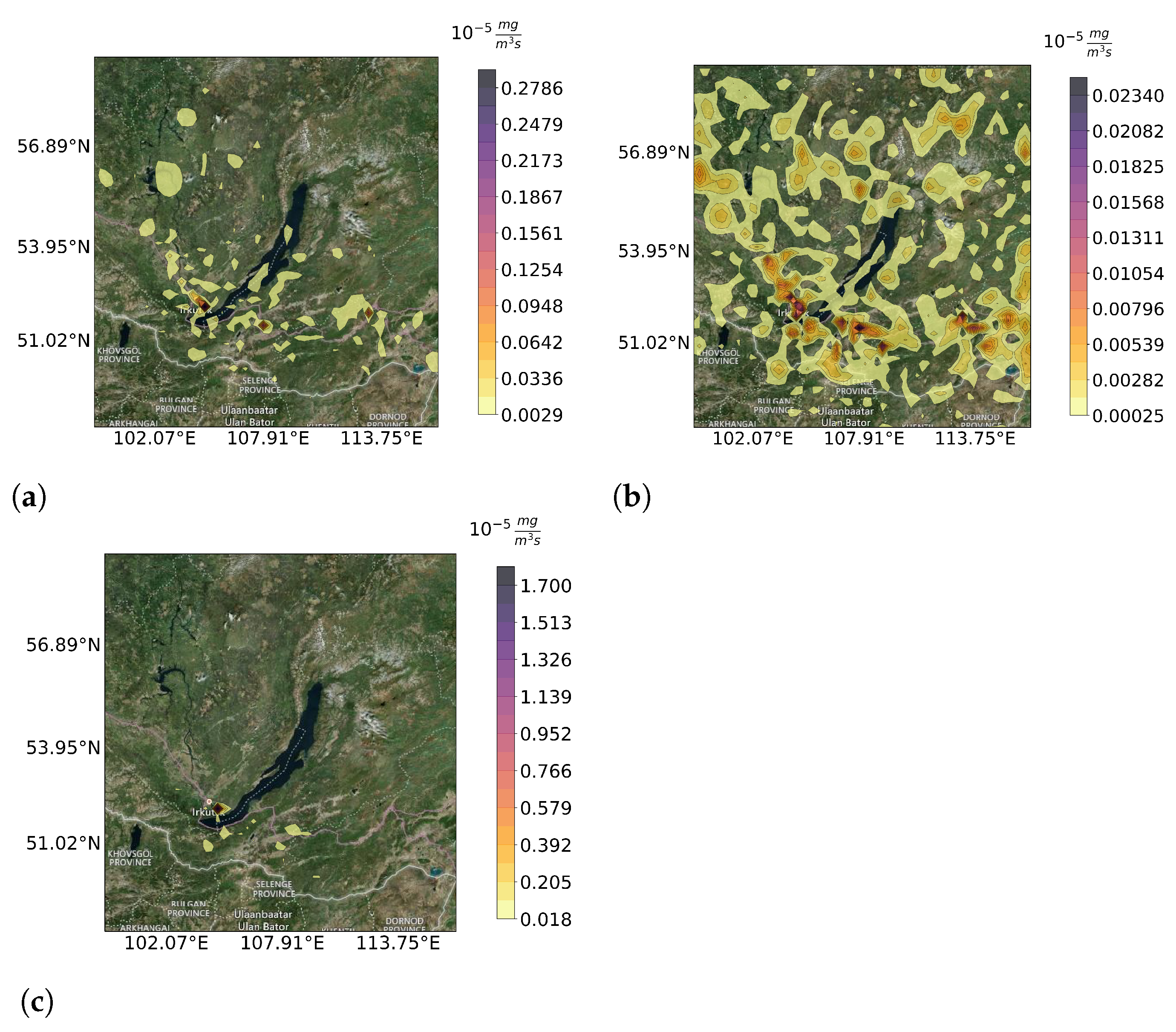
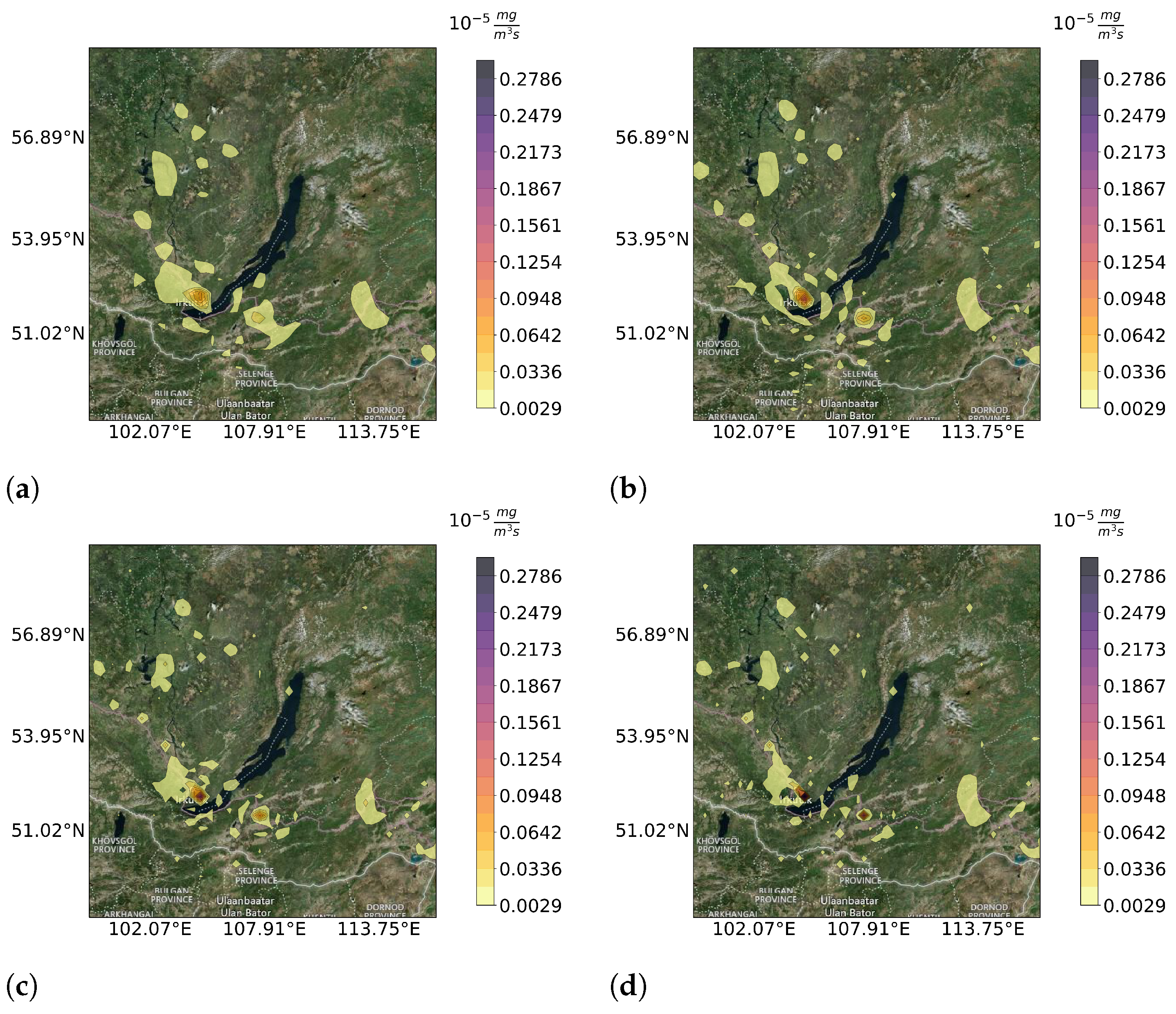
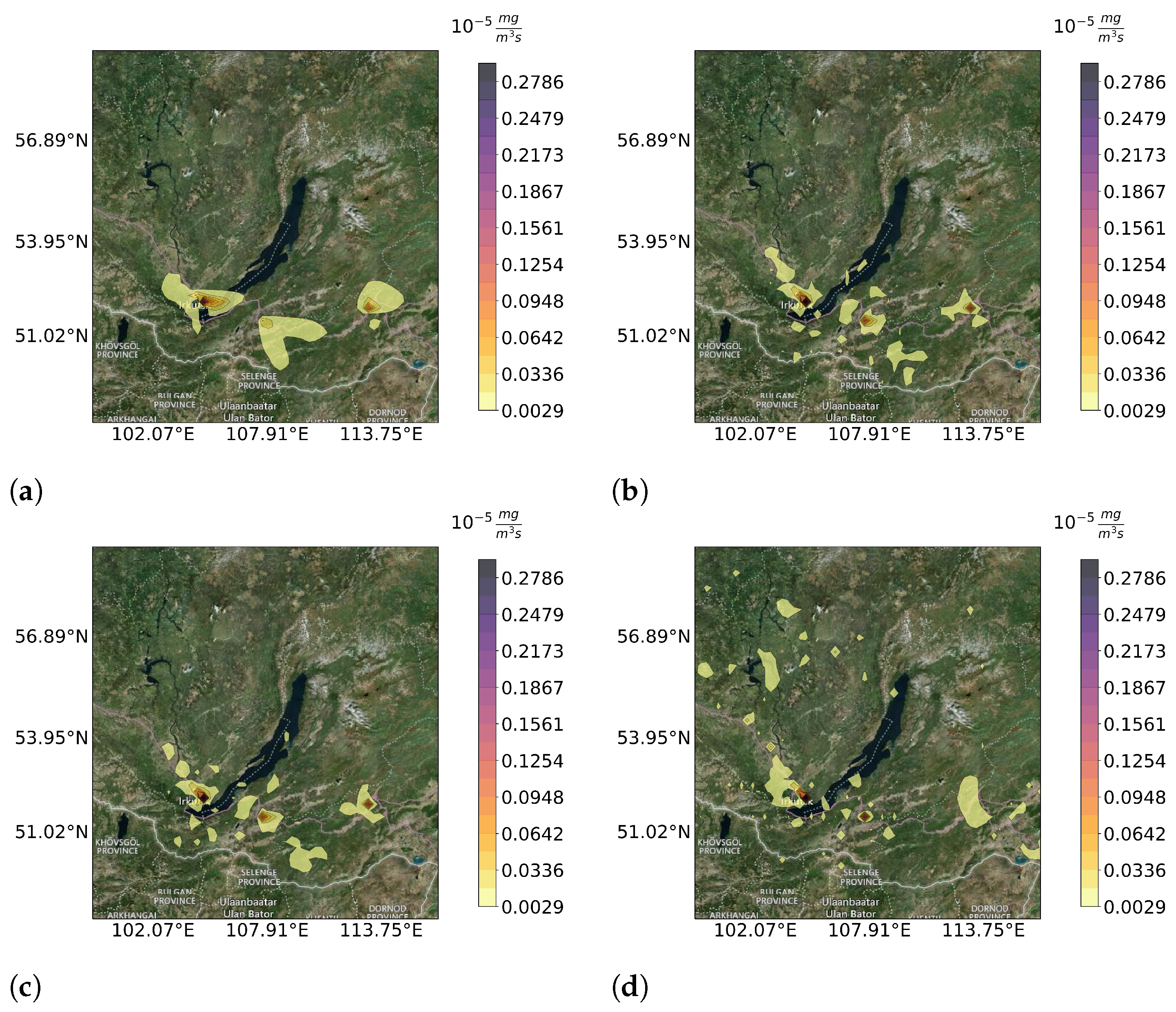
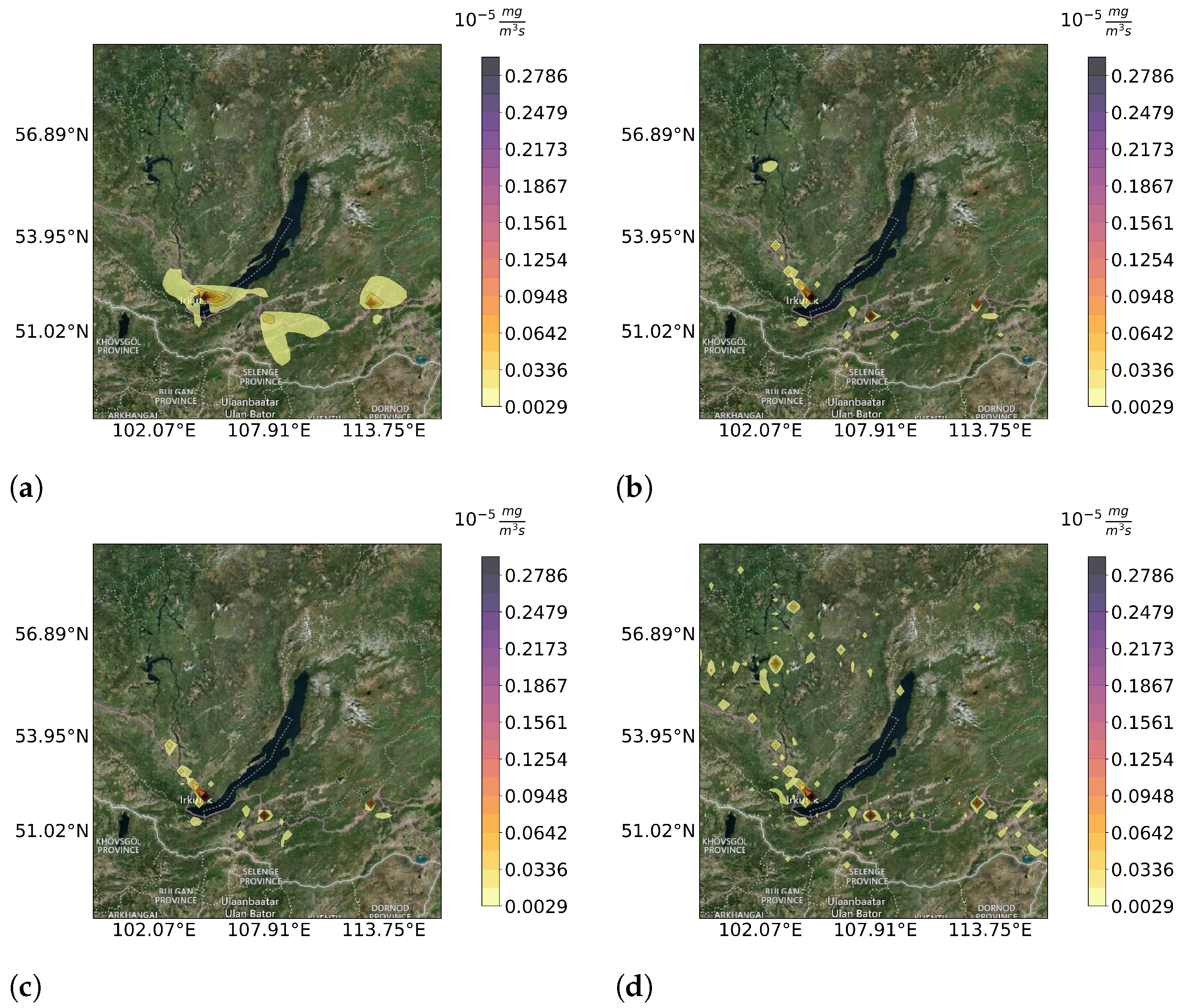
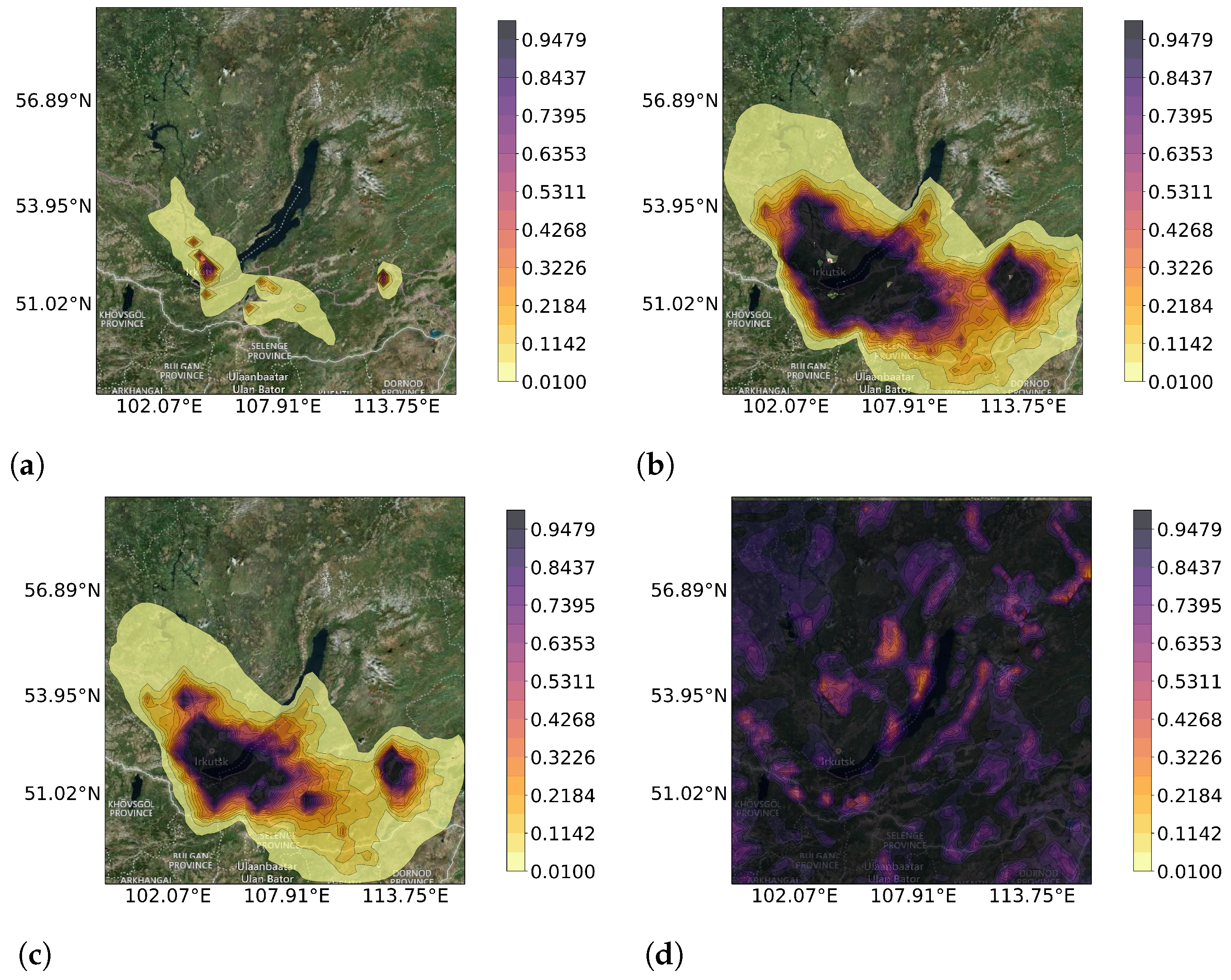
3.1. Heterogeneous Measurements
3.2. Specific Measurement Types
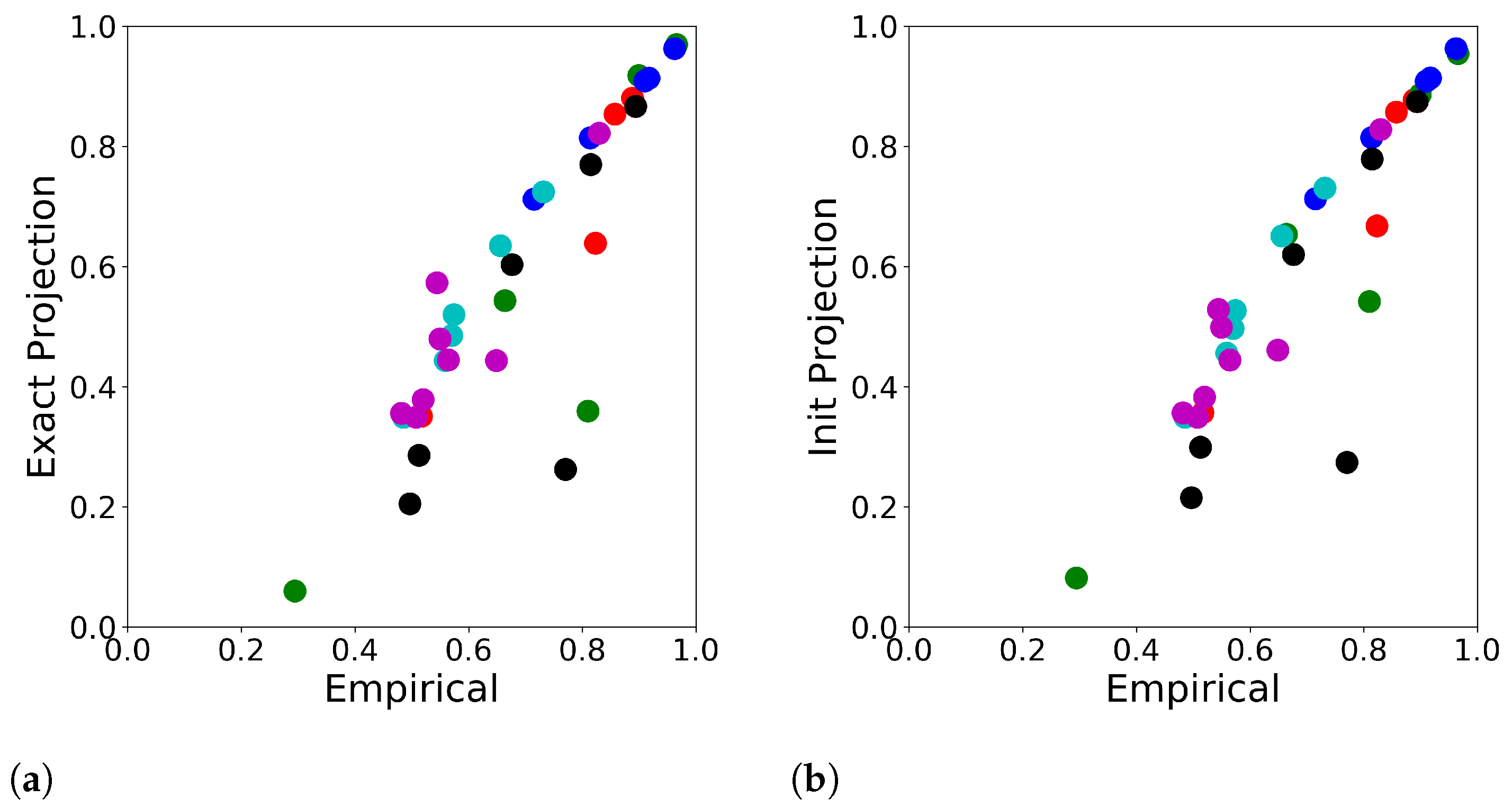
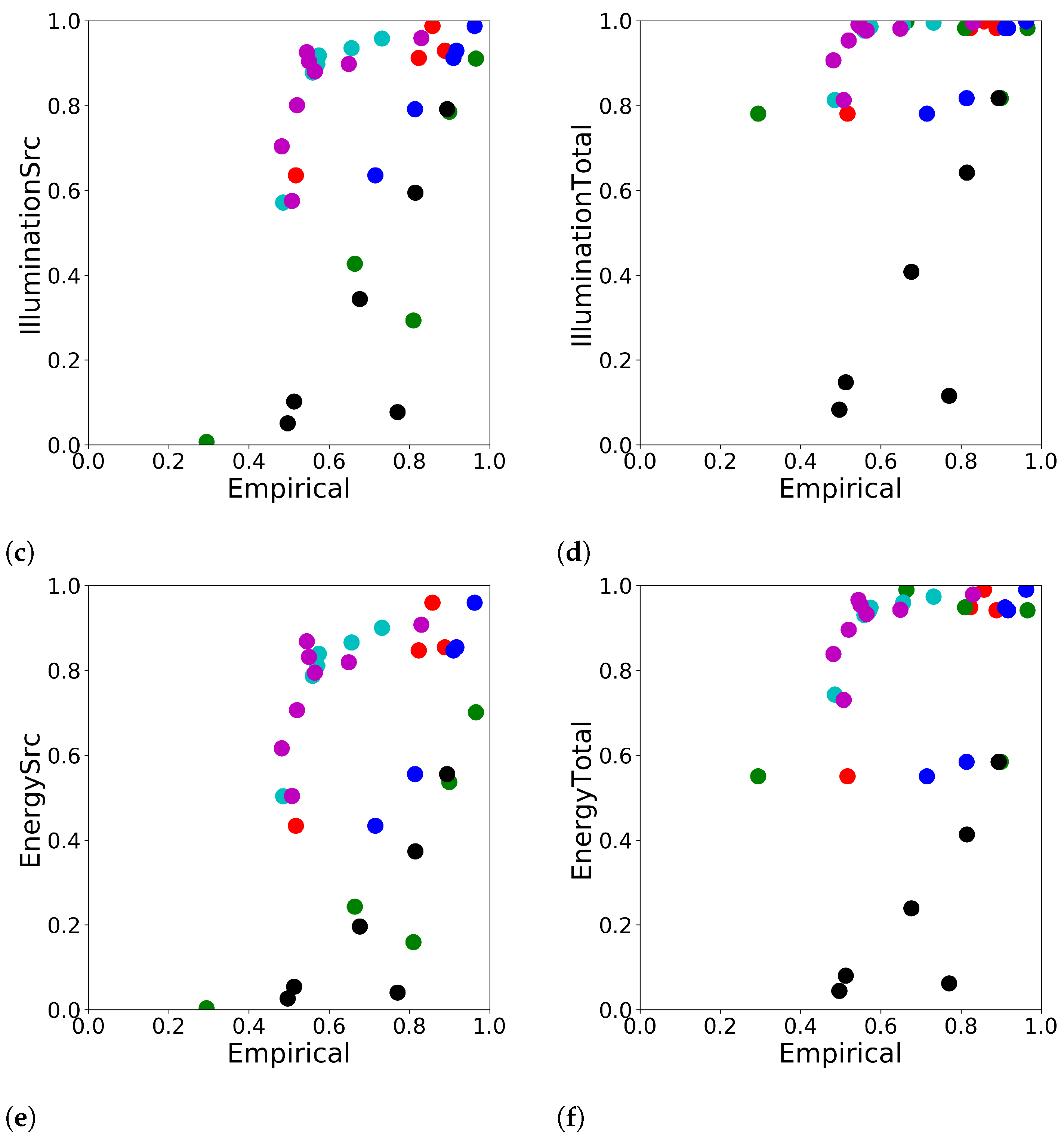
3.3. Accuracy of the Reconstruction’s Prediction
- Red: Section 3.1, “realistic” source case;
- Green: Section 3.1, “single” source case;
- Blue: Section 3.1, “unified” source case;
- Black: Section 3.2, Timeseries experiment;
- Cyan: Section 3.2, Pointwise experiment;
- Magenta: Section 3.2, Snapshot experiment.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BNT | Baikal Natural Territory |
| SVD | Singular value decomposition |
| COSMO | Consortium for Small-scale Modeling |
| CTM | Chemical transport model |
Appendix A. Newton–Kantorovich-Type Algorithm
| Algorithm A1 Newton–Kantorovich-type Algorithm |
|
Appendix B. Projection Equivalence
Appendix C. Chemical Transformation Model (Leighton Relationship-Based)
Appendix D. The Description of the Meteorological Scenario
- 23.07 Rain zone in the foothills of the Altai, in the Kuzbass. The cold front from the west offset to the east. There is practically no leading stream. Weak variable wind in the west of Lake Baikal.
- 24.07 Rain zone in the foothills of Altai-Sayan (Khakassia), Western Sayan (Daily precipitation HMS 29698 Nizhneudinsk-57mm). With the approach of a cold front from the west, the wind is mainly south-easterly.
- 25.07 The rain zone encircles the Western Sayans from the north. Cold front, offset to the east, the wind weakens and changes direction to mainly western.
- 26.07 The cold front approaches the Hangar from the west. Baikal, in the warm sector orographically cut off in the south (baric depression, thunderstorms south and north of Lake Baikal).

References
- Brunet, G. Seamless Prediction of the Earth System: From Minutes to Months; World Meteorological Organization: Geneva, Switzerland, 2015. [Google Scholar]
- WMO. Measurement of Meteorological Variables, chapter Measurement of atmospheric composition. In Guide to Instruments and Methods of Observation; World Meteorological Organization: Geneva, Switzerland, 2018; Volume I, pp. 506–541. [Google Scholar]
- Penenko, V.; Raputa, V.; Panarin, A. Planning an experiment for determining the position and strength of a pollution source. Sov. Meteorol. Hydrol. 1985, 11, 10–16. [Google Scholar]
- Penenko, V.; Raputa, V.; Bykov, A. Design of an experiment for the Pollution Source Power Estimation problem. Izv. Atmos. Ocean. Phys. 1986, 21, 705–710. [Google Scholar]
- Abida, R.; Bocquet, M.; Vercauteren, N.; Isnard, O. Design of a monitoring network over France in case of a radiological accidental release. Atmos. Environ. 2008, 42, 5205–5219. [Google Scholar] [CrossRef]
- Saunier, O.; Bocquet, M.; Mathieu, A.; Isnard, O. Model reduction via principal component truncation for the optimal design of atmospheric monitoring networks. Atmos. Environ. 2009, 43, 4940–4950. [Google Scholar] [CrossRef]
- Keats, A.; Yee, E.; Lien, F.S. Information-driven receptor placement for contaminant source determination. Environ. Model. Softw. 2010, 25, 1000–1013. [Google Scholar] [CrossRef]
- Araki, S.; Iwahashi, K.; Shimadera, H.; Yamamoto, K.; Kondo, A. Optimization of air monitoring networks using chemical transport model and search algorithm. Atmos. Environ. 2015, 122, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Ngae, P.; Kouichi, H.; Kumar, P.; Feiz, A.A.; Chpoun, A. Optimization of an urban monitoring network for emergency response applications: An approach for characterizing the source of hazardous releases. Q. J. R. Meteorol. Soc. 2019, 145, 967–981. [Google Scholar] [CrossRef]
- Kouichi, H.; Ngae, P.; Kumar, P.; Feiz, A.A.; Bekka, N. An optimization for reducing the size of an existing urban-like monitoring network for retrieving an unknown point source emission. Geosci. Model Dev. 2019, 12, 3687–3705. [Google Scholar] [CrossRef] [Green Version]
- Cao, S.J.; Ding, J.; Ren, C. Sensor deployment strategy using cluster analysis of Fuzzy C-Means Algorithm: Towards online control of indoor environment’s safety and health. Sustain. Cities Soc. 2020, 59, 102190. [Google Scholar] [CrossRef]
- Fattoruso, G.; Nocerino, M.; Toscano, D.; Pariota, L.; Sorrentino, G.; Manna, V.; Vito, S.D.; Cartenì, A.; Fabbricino, M.; Francia, G.D. Site Suitability Analysis for Low Cost Sensor Networks for Urban Spatially Dense Air Pollution Monitoring. Atmosphere 2020, 11, 1215. [Google Scholar] [CrossRef]
- deSouza, P.; Anjomshoaa, A.; Duarte, F.; Kahn, R.; Kumar, P.; Ratti, C. Air quality monitoring using mobile low-cost sensors mounted on trash-trucks: Methods development and lessons learned. Sustain. Cities Soc. 2020, 60, 102239. [Google Scholar] [CrossRef]
- Schafer, K.; Lande, K.; Grimm, H.; Jenniskens, G.; Gijsbers, R.; Ziegler, V.; Hank, M.; Budde, M. High-Resolution Assessment of Air Quality in Urban Areas—A Business Model Perspective. Atmosphere 2021, 12, 595. [Google Scholar] [CrossRef]
- Hadi-Vencheh, A.; Tan, Y.; Wanke, P.; Loghmanian, S.M. Air Pollution Assessment in China: A Novel Group Multiple Criteria Decision Making Model under Uncertain Information. Sustainability 2021, 13, 1686. [Google Scholar] [CrossRef]
- Marchuk, G. Mathematical Models in Environmental Problems. In Studies in Mathematics and Its Applications Book Series; Elsevier Science & Techn.: Amsterdam, The Netherlands, 1986; Volume 16. [Google Scholar]
- Pudykiewicz, J.A. Application of adjoint tracer transport equations for evaluating source parameters. Atmos. Environ. 1998, 32, 3039–3050. [Google Scholar] [CrossRef]
- Desyatkov, B.M.; Sarmanaev, S.P.; Borodulin, A.I.; Kotlyarova, S.S.; Selegei, V.V. Determination of some characteristics of an aerosol pollution source by solving the inverse problem of pollutant spread in the atmosphere. Atmos. Ocean. Opt. 1999, 12, 130–133. [Google Scholar]
- Issartel, J.P. Rebuilding sources of linear tracers after atmospheric concentration measurements. Atmos. Chem. Phys. 2003, 3, 2111–2125. [Google Scholar] [CrossRef] [Green Version]
- Mamonov, A.V.; Tsai, Y.H.R. Point source identification in nonlinear advection-diffusion-reaction systems. Inverse Probl. 2013, 29, 035009. [Google Scholar] [CrossRef] [Green Version]
- Turbelin, G.; Singh, S.K.; Issartel, J.P. Reconstructing source terms from atmospheric concentration measurements: Optimality analysis of an inversion technique. J. Adv. Model. Earth Syst. 2014, 6, 1244–1255. [Google Scholar] [CrossRef]
- Kumar, P.; Feiz, A.A.; Singh, S.K.; Ngae, P.; Turbelin, G. Reconstruction of an atmospheric tracer source in an urban-like environment. J. Geophys. Res. Atmos. 2015, 120, 12589–12604. [Google Scholar] [CrossRef] [Green Version]
- Bieringer, P.E.; Young, G.S.; Rodriguez, L.M.; Annunzio, A.J.; Vandenberghe, F.; Haupt, S.E. Paradigms and commonalities in atmospheric source term estimation methods. Atmos. Environ. 2017, 156, 102–112. [Google Scholar] [CrossRef] [Green Version]
- Bocquet, M.; Elbern, H.; Eskes, H.; Hirtl, M.; Žabkar, R.; Carmichael, G.R.; Flemming, J.; Inness, A.; Pagowski, M.; Camaño, J.L.P.; et al. Data assimilation in atmospheric chemistry models: Current status and future prospects for coupled chemistry meteorology models. Atmos. Chem. Phys. Discuss. 2014, 14, 32233–32323. [Google Scholar] [CrossRef] [Green Version]
- Carrassi, A.; Bocquet, M.; Bertino, L.; Evensen, G. Data assimilation in the geosciences: An overview of methods, issues, and perspectives. Wiley Interdiscip. Rev. Clim. Chang. 2018, 9, e535. [Google Scholar] [CrossRef] [Green Version]
- Elbern, H.; Friese, E.; Nieradzik, L.; Schwinger, J. Data assimilation in atmospheric chemistry and air quality. In Advanced Data Assimilation for Geosciences; Oxford University Press: Oxford, UK, 2014; pp. 507–534. [Google Scholar] [CrossRef]
- Silver, J.D.; Christensen, J.H.; Kahnert, M.; Robertson, L.; Rayner, P.J.; Brandt, J. Multi-species chemical data assimilation with the Danish Eulerian hemispheric model: System description and verification. J. Atmos. Chem. 2015, 73, 261–302. [Google Scholar] [CrossRef]
- Nguyen, C.; Soulhac, L.; Salizzoni, P. Source Apportionment and Data Assimilation in Urban Air Quality Modelling for NO2: The Lyon Case Study. Atmosphere 2018, 9, 8. [Google Scholar] [CrossRef] [Green Version]
- Xing, J.; Li, S.; Ding, D.; Kelly, J.T.; Wang, S.; Jang, C.; Zhu, Y.; Hao, J. Data Assimilation of Ambient Concentrations of Multiple Air Pollutants Using an Emission-Concentration Response Modeling Framework. Atmosphere 2020, 11, 1289. [Google Scholar] [CrossRef] [PubMed]
- Mijling, B. High-resolution mapping of urban air quality with heterogeneous observations: A new methodology and its application to Amsterdam. Atmos. Meas. Tech. 2020, 13, 4601–4617. [Google Scholar] [CrossRef]
- Nguyen, C.V.; Soulhac, L. Data assimilation methods for urban air quality at the local scale. Atmos. Environ. 2021, 253, 118366. [Google Scholar] [CrossRef]
- Elbern, H.; Strunk, A.; Schmidt, H.; Talagrand, O. Emission rate and chemical state estimation by 4-dimensional variational inversion. Atmos. Chem. Phys. Discuss. 2007, 7, 1725–1783. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.S.; Griffith, S.M.; Lin, Y.C.; Chen, Y.C.; Lee, C.T.; Chou, C.C.K.; Chuang, M.T.; Wang, S.H.; Lin, N.H. Satellite-based Emission Inventory Adjustments Improve Simulations of Long-range Transport Events. Aerosol Air Qual. Res. 2021, 21, 210121. [Google Scholar] [CrossRef]
- Markakis, K.; Valari, M.; Perrussel, O.; Sanchez, O.; Honore, C. Climate-forced air-quality modeling at the urban scale: Sensitivity to model resolution, emissions and meteorology. Atmos. Chem. Phys. 2015, 15, 7703–7723. [Google Scholar] [CrossRef] [Green Version]
- Holnicki, P.; Nahorski, Z. Emission Data Uncertainty in Urban Air Quality Modeling—Case Study. Environ. Model. Assess. 2015, 20, 583–597. [Google Scholar] [CrossRef] [Green Version]
- Munir, S.; Mayfield, M.; Coca, D. Understanding Spatial Variability of NO2 in Urban Areas Using Spatial Modelling and Data Fusion Approaches. Atmosphere 2021, 12, 179. [Google Scholar] [CrossRef]
- Ponomarev, N.; Yushkov, V.; Elansky, N. Air Pollution in Moscow Megacity: Data Fusion of the Chemical Transport Model and Observational Network. Atmosphere 2021, 12, 374. [Google Scholar] [CrossRef]
- Carnevale, C.; Angelis, E.D.; Finzi, G.; Turrini, E.; Volta, M. Application of Data Fusion Techniques to Improve Air Quality Forecast: A Case Study in the Northern Italy. Atmosphere 2020, 11, 244. [Google Scholar] [CrossRef] [Green Version]
- Penenko, V.V.; Penenko, A.V.; Tsvetova, E.A.; Gochakov, A.V. Methods for Studying the Sensitivity of Air Quality Models and Inverse Problems of Geophysical Hydrothermodynamics. J. Appl. Mech. Tech. Phys. 2019, 60, 392–399. [Google Scholar] [CrossRef]
- Penenko, A. A Newton-Kantorovich Method in Inverse Source Problems for Production-Destruction Models with Time Series-Type Measurement Data. Numer. Anal. Appl. 2019, 12, 51–69. [Google Scholar] [CrossRef]
- Penenko, A. Convergence analysis of the adjoint ensemble method in inverse source problems for advection-diffusion-reaction models with image-type measurements. Inverse Probl. Imaging 2020, 14, 757–782. [Google Scholar] [CrossRef]
- Penenko, A.; Zubairova, U.; Mukatova, Z.; Nikolaev, S. Numerical algorithm for morphogen synthesis region identification with indirect image-type measurement data. J. Bioinform. Comput. Biol. 2019, 17, 1940002. [Google Scholar] [CrossRef]
- Penenko, A.; Gochakov, A.; Penenko, V. Algorithms based on sensitivity operators for analyzing and solving inverse modeling problems of transport and transformation of atmospheric pollutants. IOP Conf. Ser. Earth Environ. Sci. 2020, 611, 012032. [Google Scholar] [CrossRef]
- Khodzher, T.V.; Zhamsueva, G.S.; Zayakhanov, A.S.; Dementeva, A.L.; Tsydypov, V.V.; Balin, Y.S.; Penner, I.E.; Kokhanenko, G.P.; Nasonov, S.V.; Klemasheva, M.G.; et al. Ship-Based Studies of Aerosol-Gas Admixtures over Lake Baikal Basin in Summer 2018. Atmos. Ocean. Opt. 2019, 32, 434–441. [Google Scholar] [CrossRef]
- Antokhin, P.N.; Arshinova, V.G.; Arshinov, M.Y.; Belan, B.D.; Belan, S.B.; Davydov, D.K.; Ivlev, G.A.; Fofonov, A.V.; Kozlov, A.V.; Paris, J.D.; et al. Distribution of Trace Gases and Aerosols in the Troposphere Over Siberia during Wildfires of Summer 2012. J. Geophys. Res. Atmos. 2018, 123, 2285–2297. [Google Scholar] [CrossRef]
- Gu, Q.; Michanowicz, D.R.; Jia, C. Developing a Modular Unmanned Aerial Vehicle (UAV) Platform for Air Pollution Profiling. Sensors 2018, 18, 4363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arshinov, M.Y.; Belan, B.D.; Davydov, D.K.; Kozlov, A.V.; Fofonov, A.V.; Arshinova, V.G. Study of the Spatial Distributions of CO2 and CH4 in the Surface Air Layer over Western Siberia Using a Mobile Platform. Atmos. Ocean. Opt. 2020, 33, 661–670. [Google Scholar] [CrossRef]
- Roshydromet. Unified Information System for Monitoring Atmospheric Air Pollution. Available online: http://www.feerc.ru/uisem/portal/ad/irkutsk (accessed on 1 November 2021). (In Russian).
- Marchuk, G.I. Formulation of some converse problems. Sov. Math. Dokl. 1964, 5, 675–678. [Google Scholar]
- Penenko, V. Methods for Numerical Simulation of Atmospheric Processes; Hydrometeoizdat: Leningrad, Russia, 1981. (In Russian) [Google Scholar]
- Murio, D.A. The Mollification Method and the Numerical Solution of Ill-Posed Problems; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Dimet, F.X.L.; Souopgui, I.; Titaud, O.; Shutyaev, V.; Hussaini, M.Y. Toward the assimilation of images. Nonlinear Process. Geophys. 2015, 22, 15–32. [Google Scholar] [CrossRef] [Green Version]
- Penenko, V.V.; Obraztsov, N.N. A variational initialization method for the fields of the meteorological elements. Engl. Transl. Sov. Meteorol. Hydrol. 1976, 11, 3–16. [Google Scholar]
- Marchuk, G.I.; Penenko, V.V. Application of optimization methods to the problem of mathematical simulation of atmospheric processes and environment. In Modelling and Optimization of Complex System; Springer: Berlin/Heidelberg, Germany, 1978; pp. 240–252. [Google Scholar] [CrossRef]
- Dimet, F.X.L.; Talagrand, O. Variational algorithms for analysis and assimilation of meteorological observations: Theoretical aspects. Tellus 1986, 38A, 97–110. [Google Scholar] [CrossRef]
- Issartel, J.P. Emergence of a tracer source from air concentration measurements, a new strategy for linear assimilation. Atmos. Chem. Phys. 2005, 5, 249–273. [Google Scholar] [CrossRef] [Green Version]
- Penenko, A.V.; Gochakov, A.; Antokhin, P. Numerical study of emission sources identification algorithm with joint use of in situ and remote sensing measurement data. In Proceedings of the 26th International Symposium on Atmospheric and Ocean Optics, Atmospheric Physics, Moscow, Russia, 29 June–3 July 2020; Matvienko, G.G., Romanovskii, O.A., Eds.; SPIE: Bellingham, WA, USA, 2020. [Google Scholar] [CrossRef]
- UNESCO. Lake Baikal. Available online: https://whc.unesco.org/en/list/754/ (accessed on 1 December 2021).
- Plyusnin, V.; Vladimirov, I.; Sorokovoi, A. Baikal region in the UNESCO “Man and Biocphere” Programme. Probl. Geogr. 2021, 152, 202–221. (In Russian) [Google Scholar] [CrossRef]
- Golobokova, L.; Khodzher, T.; Khuriganova, O.; Marinayte, I.; Onishchuk, N.; Rusanova, P.; Potemkin, V. Variability of Chemical Properties of the Atmospheric Aerosol above Lake Baikal during Large Wildfires in Siberia. Atmosphere 2020, 11, 1230. [Google Scholar] [CrossRef]
- Efimova, N.V.; Rukavishnikov, V.S. Assessment of Smoke Pollution Caused by Wildfires in the Baikal Region (Russia). Atmosphere 2021, 12, 1542. [Google Scholar] [CrossRef]
- Popovicheva, O.; Molozhnikova, E.; Nasonov, S.; Potemkin, V.; Penner, I.; Klemasheva, M.; Marinaite, I.; Golobokova, L.; Vratolis, S.; Eleftheriadis, K.; et al. Industrial and wildfire aerosol pollution over world heritage Lake Baikal. J. Environ. Sci. 2021, 107, 49–64. [Google Scholar] [CrossRef]
- Gorshkov, A.G.; Izosimova, O.N.; Kustova, O.V.; Marinaite, I.I.; Galachyants, Y.P.; Sinyukovich, V.N.; Khodzher, T.V. Wildfires as a Source of PAHs in Surface Waters of Background Areas (Lake Baikal, Russia). Water 2021, 13, 2636. [Google Scholar] [CrossRef]
- Grigorieva, M.A.; Ippolitova, N.A. Big business in socio-economic development of cities in the Baikal region. Geogr. Nat. Resour. 2011, 32, 166–171. [Google Scholar] [CrossRef]
- Akhtimankina, A.; Arguchintseva, A. Zagryaznenie atmosfernogo vozduha promyshlennymi predpriyatiyami g. Irkutska. IZVESTIYA Irkutsk. Gos. Univ. 2013, 6, 3–19. (In Russian) [Google Scholar]
- Brown, K.P.; Gerber, A.; Bedulina, D.; Timofeyev, M.A. Human impact and ecosystemic health at Lake Baikal. WIREs Water 2021, 8, e1528. [Google Scholar] [CrossRef]
- Khuriganova, O.I.; Obolkin, V.A.; Golobokova, L.P.; Bukin, Y.S.; Khodzher, T.V. Passive Sampling as a Low-Cost Method for Monitoring Air Pollutants in the Baikal Region (Eastern Siberia). Atmosphere 2019, 10, 470. [Google Scholar] [CrossRef] [Green Version]
- Zayakhanov, A.S.; Zhamsueva, G.S.; Tcydypov, V.V.; Balzhanov, T.S.; Dementeva, A.L.; Khodzher, T.V. Investigation of Transport and Transformation of Tropospheric Ozone in Terrestrial Ecosystems of the Coastal Zone of Lake Baikal. Atmosphere 2019, 10, 739. [Google Scholar] [CrossRef] [Green Version]
- Mashyanov, N.; Obolkin, V.; Pogarev, S.; Ryzhov, V.; Sholupov, S.; Potemkin, V.; Molozhnikova, E.; Khodzher, T. Air Mercury Monitoring at the Baikal Area. Atmosphere 2021, 12, 807. [Google Scholar] [CrossRef]
- Golobokova, L.; Netsvetaeva, O.; Khodzher, T.; Obolkin, V.; Khuriganova, O. Atmospheric Deposition on the Southwest Coast of the Southern Basin of Lake Baikal. Atmosphere 2021, 12, 1357. [Google Scholar] [CrossRef]
- Obolkin, V.; Molozhnikova, E.; Shikhovtsev, M.; Netsvetaeva, O.; Khodzher, T. Sulfur and Nitrogen Oxides in the Atmosphere of Lake Baikal: Sources, Automatic Monitoring, and Environmental Risks. Atmosphere 2021, 12, 1348. [Google Scholar] [CrossRef]
- Engl, H.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Kluwer: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Voronina, T.A.; Tcheverda, V.A.; Voronin, V.V. Some properties of the inverse operator for a tsunami source recovery. Sib. Elektron. Mat. Izv. 2014, 11, 532–547. [Google Scholar]
- Judd, L.M.; Al-Saadi, J.A.; Valin, L.C.; Pierce, R.B.; Yang, K.; Janz, S.J.; Kowalewski, M.G.; Szykman, J.J.; Tiefengraber, M.; Mueller, M. The Dawn of Geostationary Air Quality Monitoring: Case Studies From Seoul and Los Angeles. Front. Environ. Sci. 2018, 6, 1–17. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, U.; Ahn, M.H.; Kim, J.H.; Park, R.J.; Lee, H.; Song, C.H.; Choi, Y.S.; Lee, K.H.; Yoo, J.M.; et al. New Era of Air Quality Monitoring from Space: Geostationary Environment Monitoring Spectrometer (GEMS). Bull. Am. Meteorol. Soc. 2020, 101, E1–E22. [Google Scholar] [CrossRef] [Green Version]
- Mettig, N.; Weber, M.; Rozanov, A.; Arosio, C.; Burrows, J.P.; Veefkind, P.; Thompson, A.M.; Querel, R.; Leblanc, T.; Godin-Beekmann, S.; et al. Ozone profile retrieval from nadir TROPOMI measurements in the UV range. Atmos. Meas. Tech. 2021, 14, 6057–6082. [Google Scholar] [CrossRef]
- Liu, S.; Valks, P.; Pinardi, G.; Xu, J.; Chan, K.L.; Argyrouli, A.; Lutz, R.; Beirle, S.; Khorsandi, E.; Baier, F.; et al. An improved TROPOMI tropospheric NO2 research product over Europe. Atmos. Meas. Tech. 2021, 14, 7297–7327. [Google Scholar] [CrossRef]
- Stebel, K.; Stachlewska, I.S.; Nemuc, A.; Horálek, J.; Schneider, P.; Ajtai, N.; Diamandi, A.; Benešová, N.; Boldeanu, M.; Botezan, C.; et al. SAMIRA-SAtellite Based Monitoring Initiative for Regional Air Quality. Remote Sens. 2021, 13, 2219. [Google Scholar] [CrossRef]
- Wolfram Research. Wolfram Alpha. Available online: https://www.wolframalpha.com/ (accessed on 12 December 2020).
- Hundsdorfer, W.; Verwer, J.G. Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hauglustaine, D.A.; Brasseur, G.P.; Walters, S.; Rasch, P.J.; Muller, J.F.; Emmons, L.K.; Carroll, M.A. MOZART, a global chemical transport model for ozone and related chemical tracers: 2. Model results and evaluation. J. Geophys. Res. Atmos. 1998, 103, 28291–28335. [Google Scholar] [CrossRef]
- Baldauf, M.; Seifert, A.; Forstner, J.; Majewski, D.; Raschendorfer, M.; Reinhardt, T. Operational Convective-Scale Numerical Weather Prediction with the COSMO Model: Description and Sensitivities. Mon. Weather. Rev. 2011, 139, 3887–3905. [Google Scholar] [CrossRef]
- Griewank, A.; Walther, A. Evaluating Derivatives; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar] [CrossRef]
- Vlasenko, A.; Kohl, A.; Stammer, D. The efficiency of geophysical adjoint codes generated by automatic differentiation tools. Comput. Phys. Commun. 2016, 199, 22–28. [Google Scholar] [CrossRef] [Green Version]
- Naumann, U. Adjoint Code Design Patterns. ACM Trans. Math. Softw. 2019, 45, 1–32. [Google Scholar] [CrossRef]
- Penenko, A.; Gochakov, A. Parallel speedup analysis of an adjoint ensemble-based source identification algorithm. J. Phys. Conf. Ser. 2021, 1715, 012072. [Google Scholar] [CrossRef]
- Koh, J.; Lee, J.; Yoon, S. Single-image deblurring with neural networks: A comparative survey. Comput. Vis. Image Underst. 2021, 203, 103134. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, Z.; Jiang, C.; Zheng, H.; Ge, Y.; Liang, D. Artifact removal using a hybrid-domain convolutional neural network for limited-angle computed tomography imaging. Phys. Med. Biol. 2020, 65, 155010. [Google Scholar] [CrossRef]
- Xie, S.; Zheng, X.; Chen, Y.; Xie, L.; Liu, J.; Zhang, Y.; Yan, J.; Zhu, H.; Hu, Y. Artifact Removal using Improved GoogLeNet for Sparse-view CT Reconstruction. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [Green Version]
- Penenko, A.; Nikolaev, S.; Golushko, S.; Romashenko, A.; Kirilova, I. Numerical Algorithms for Diffusion Coefficient Identification in Problems of Tissue Engineering. Math. Biol. Bioinform. 2016, 11, 426–444. [Google Scholar] [CrossRef] [Green Version]
- Cheverda, V.A.; Kostin, V.I. R-pseudoinverses for compact operators in Hilbert spaces: Existence and stability. J. Inverse Ill-Posed Probl. 1995, 3, 131–148. [Google Scholar] [CrossRef]
- Penenko, A.V.; Salimova, A.B. Source Identification for the Smoluchowski Equation Using an Ensemble of Adjoint Equation Solutions. Numer. Anal. Appl. 2020, 13, 152–164. (In Russian) [Google Scholar] [CrossRef]








| Type | Description | ||
|---|---|---|---|
| Pointwise | 60 | 60 | |
| Timeseries | 60 | 6 | |
| Integral | 5 | 5 | |
| Snapshot | 625 | 1 | |
| Composite | 750 | Sum of the above |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penenko, A.; Penenko, V.; Tsvetova, E.; Gochakov, A.; Pyanova, E.; Konopleva, V. Sensitivity Operator Framework for Analyzing Heterogeneous Air Quality Monitoring Systems. Atmosphere 2021, 12, 1697. https://doi.org/10.3390/atmos12121697
Penenko A, Penenko V, Tsvetova E, Gochakov A, Pyanova E, Konopleva V. Sensitivity Operator Framework for Analyzing Heterogeneous Air Quality Monitoring Systems. Atmosphere. 2021; 12(12):1697. https://doi.org/10.3390/atmos12121697
Chicago/Turabian StylePenenko, Alexey, Vladimir Penenko, Elena Tsvetova, Alexander Gochakov, Elza Pyanova, and Viktoriia Konopleva. 2021. "Sensitivity Operator Framework for Analyzing Heterogeneous Air Quality Monitoring Systems" Atmosphere 12, no. 12: 1697. https://doi.org/10.3390/atmos12121697
APA StylePenenko, A., Penenko, V., Tsvetova, E., Gochakov, A., Pyanova, E., & Konopleva, V. (2021). Sensitivity Operator Framework for Analyzing Heterogeneous Air Quality Monitoring Systems. Atmosphere, 12(12), 1697. https://doi.org/10.3390/atmos12121697






