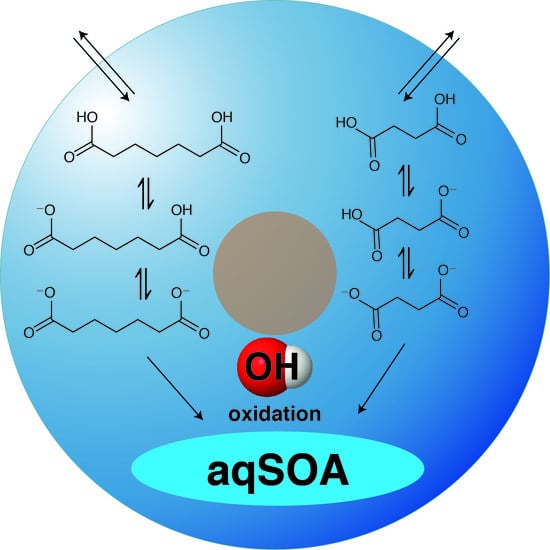
pH- and Temperature-Dependent Kinetics of the Oxidation Reactions of OH with Succinic and Pimelic Acid in Aqueous Solution
Abstract
1. Introduction
2. Experiments
2.1. Materials
2.2. Methods
2.2.1. Experimental Setup
2.2.2. Competition Kinetics Method
3. Results and Discussion
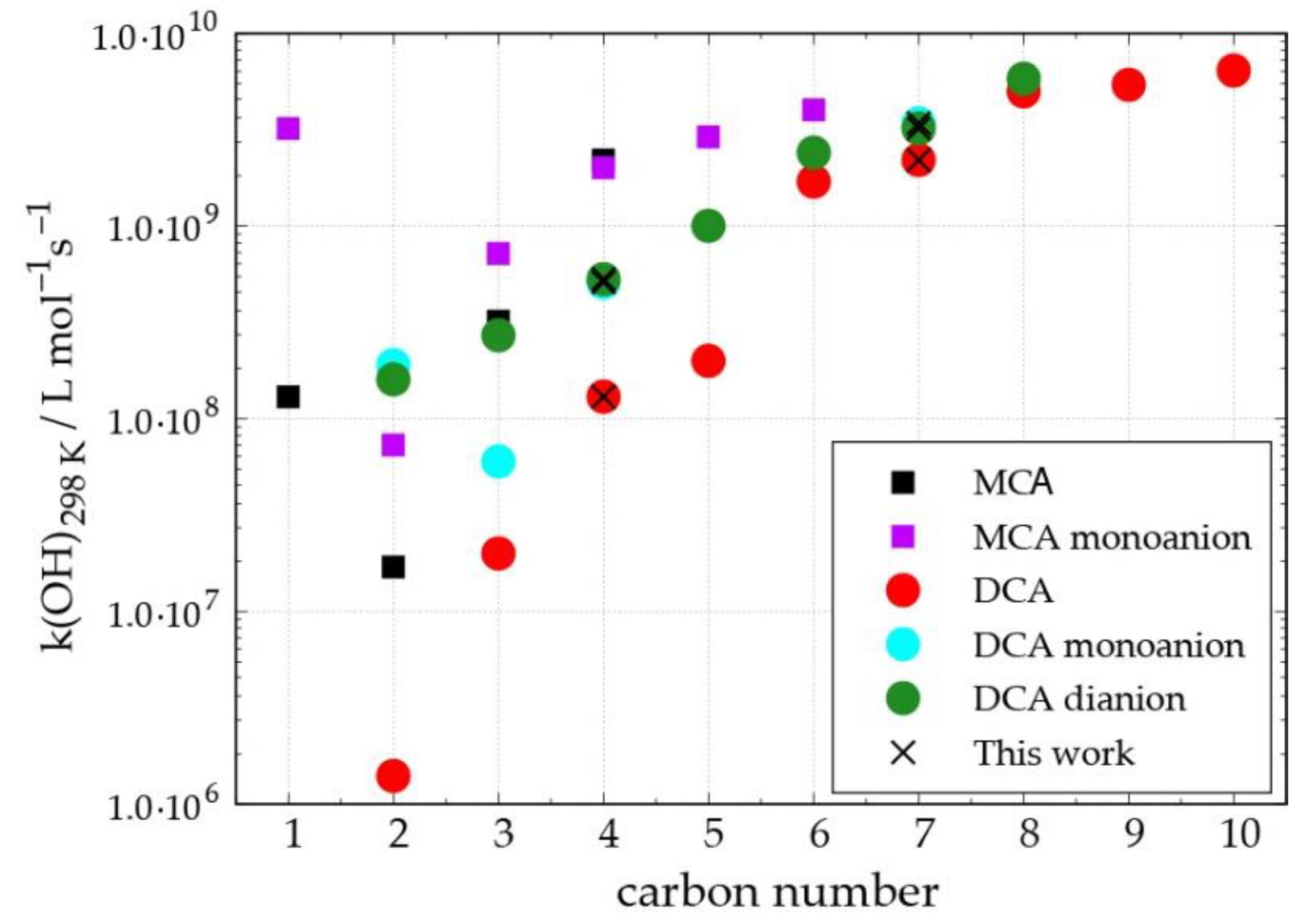
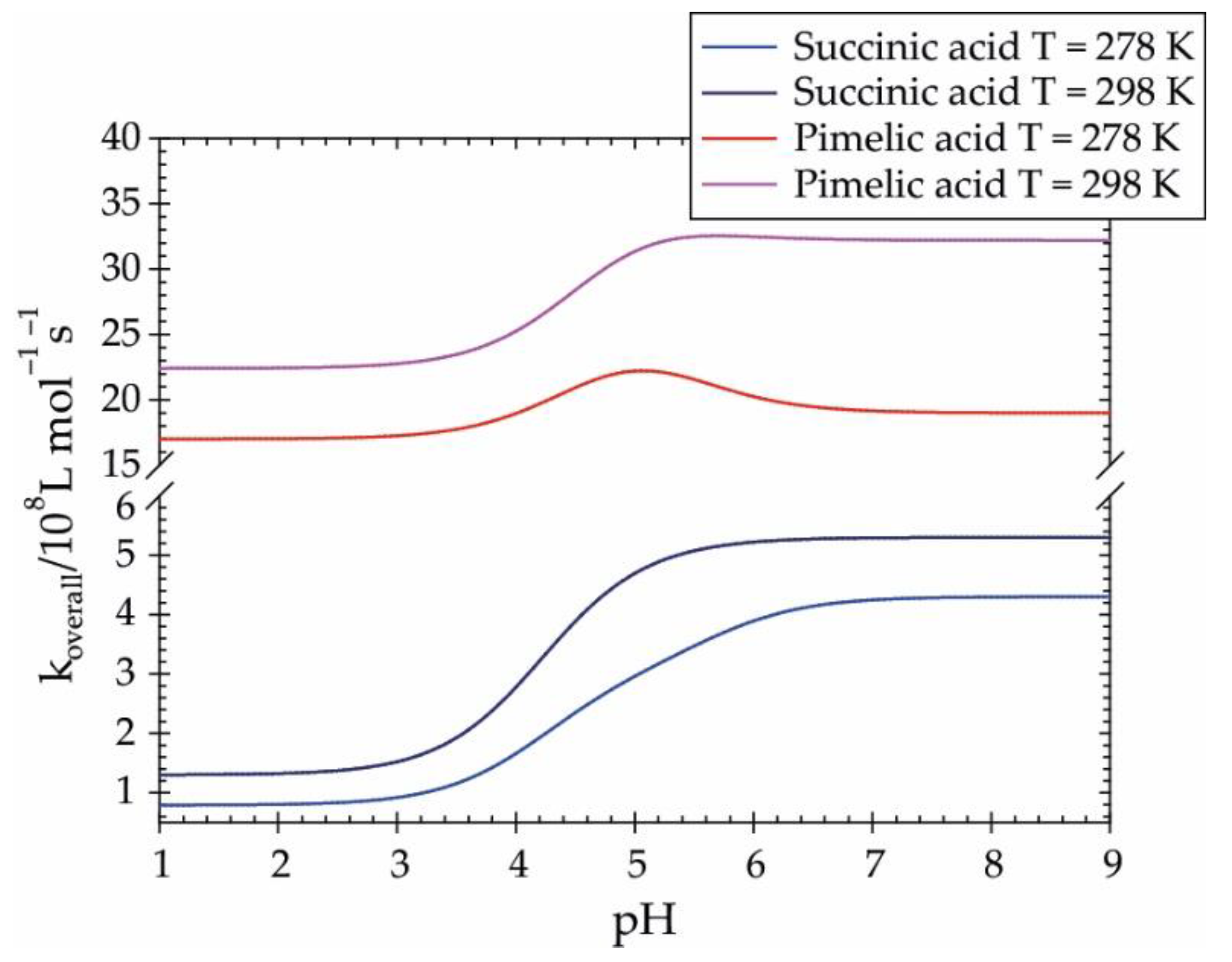
3.1. Oxidation Mechanism
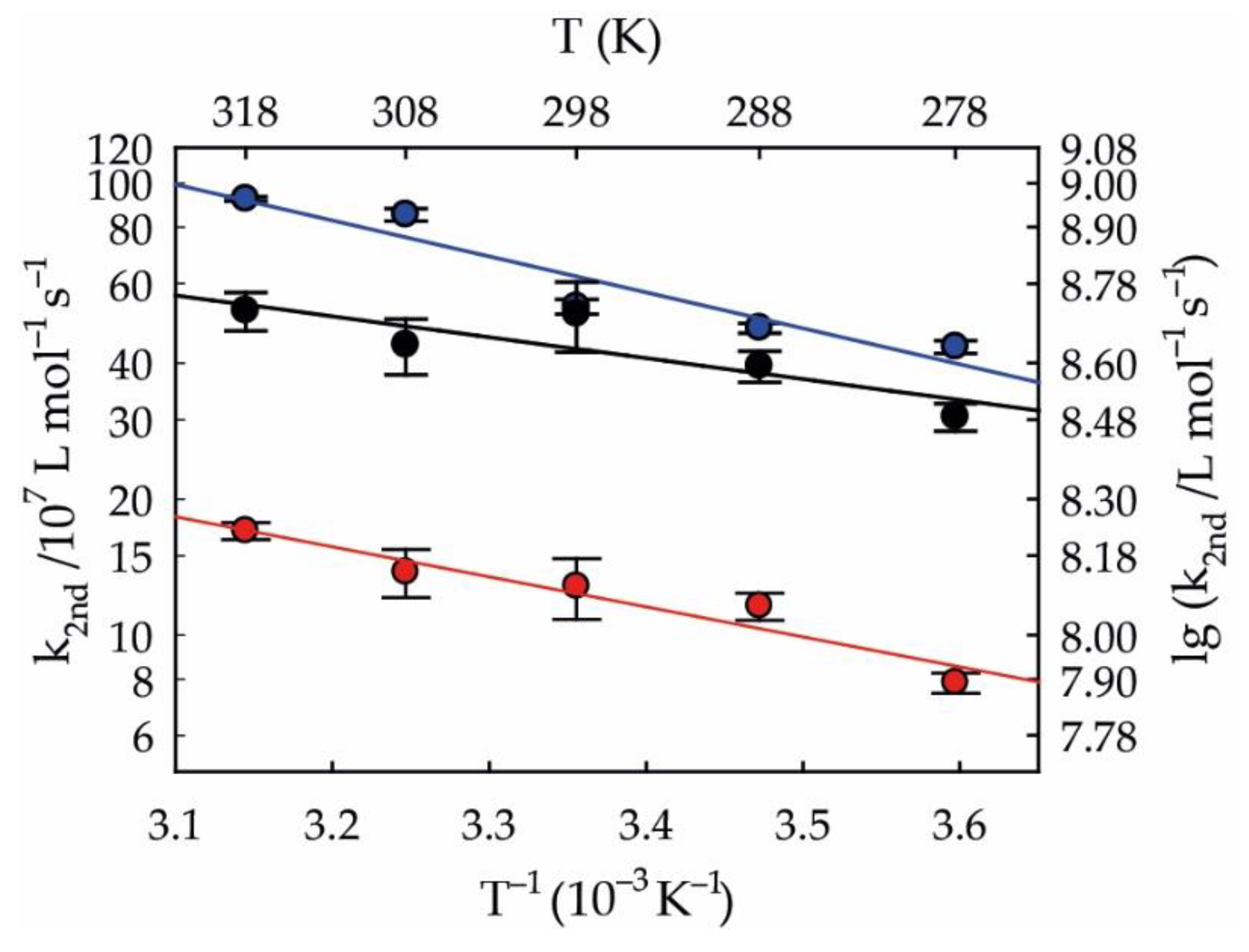
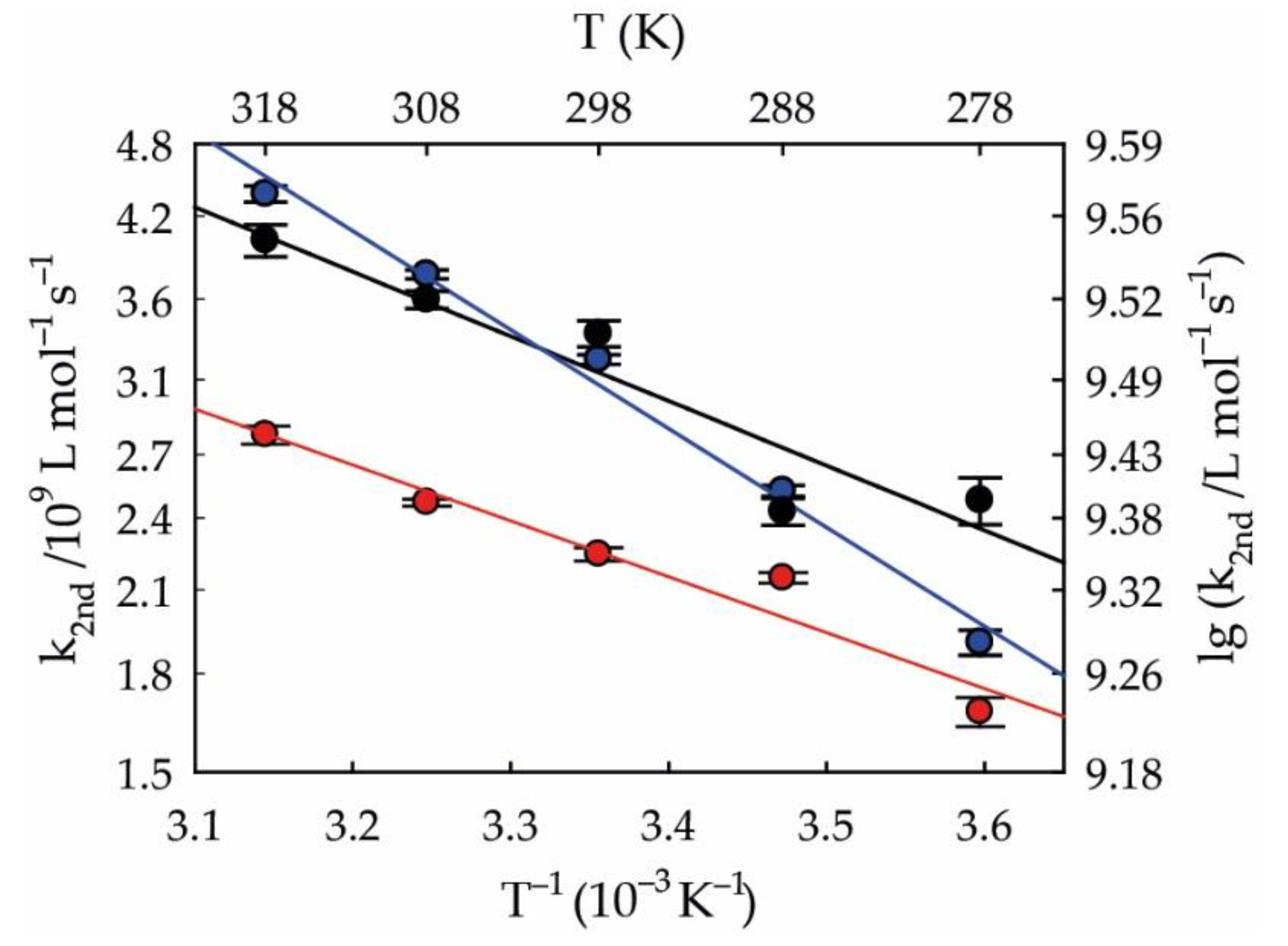
3.2. Activation Parameters
4. Atmospheric Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Compernolle, S.; Müller, J.F. Henry’s law constants of diacids and hydroxy polyacids: Recommended values. Atmos. Chem. Phys. 2014, 14, 2699–2712. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Chebbi, A.; Carlier, P. Carboxylic acids in the troposphere, occurrence, sources, and sinks: A review. Atmos. Environ. 1996, 30, 4233–4249. [Google Scholar] [CrossRef]
- Kawamura, K.; Bikkina, S. A review of dicarboxylic acids and related compounds in atmospheric aerosols: Molecular distributions, sources and transformation. Atmos. Res. 2016, 170, 140–160. [Google Scholar] [CrossRef]
- Kawamura, K.; Kasukabe, H.; Barrie, L.A. Secondary formation of water-soluble organic acids and α-dicarbonyls and their contributions to total carbon and water-soluble organic carbon: Photochemical aging of organic aerosols in the Arctic spring. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Kawamura, K.; Seméré, R.; Imai, Y.; Fujii, Y.; Hayashi, M. Water soluble dicarboxylic acids and related compounds in Antarctic aerosols. J. Geophys. Res. Atmos. 1996, 101, 18721–18728. [Google Scholar] [CrossRef]
- Teich, M.; van Pinxteren, D.; Herrmann, H. A one year study of functionalised medium-chain carboxylic acids in atmospheric particles at a rural site in Germany revealing seasonal trends and possible sources. J. Atmos. Chem. 2019, 76, 115–132. [Google Scholar] [CrossRef]
- Van Pinxteren, D.; Neusüß, C.; Herrmann, H. On the abundance and source contributions of dicarboxylic acids in size-resolved aerosol particles at continental sites in central Europe. Atmos. Chem. Phys. 2014, 14, 3913–3928. [Google Scholar] [CrossRef]
- Herrmann, H.; Schaefer, T.; Tilgner, A.; Styler, S.A.; Weller, C.; Teich, M.; Otto, T. Tropospheric aqueous-phase chemistry: Kinetics, mechanisms, and its coupling to a changing gas phase. Chem. Rev. 2015, 115, 4259–4334. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Altieri, K.E.; Seitzinger, S.P.; Carlton, A.G.; Turpin, B.J.; Klein, G.C.; Marshall, A.G. Oligomers formed through in-cloud methylglyoxal reactions: Chemical composition, properties, and mechanisms investigated by ultra-high resolution FT-ICR mass spectrometry. Atmos. Environ. 2008, 42, 1476–1490. [Google Scholar] [CrossRef]
- Liu, T.; Clegg, S.L.; Abbatt, J.P.D. Fast oxidation of sulfur dioxide by hydrogen peroxide in deliquesced aerosol particles. Proc. Natl. Acad. Sci. USA 2020, 117, 1354. [Google Scholar] [CrossRef] [PubMed]
- Hazra, M.K.; Sinha, A. Formic acid catalyzed hydrolysis of SO3 in the gas phase: A barrierless mechanism for sulfuric acid production of potential atmospheric importance. J. Am. Chem. Soc. 2011, 133, 17444–17453. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, H.; Hoffmann, D.; Schaefer, T.; Bräuer, P.; Tilgner, A. Tropospheric aqueous-phase free-radical chemistry: Radical sources, spectra, reaction kinetics and prediction tools. ChemPhysChem 2010, 11, 3796–3822. [Google Scholar] [CrossRef] [PubMed]
- Vel Leitner, N.K.; Dore, M. Hydroxyl radical induced decomposition of aliphatic acids in oxygenated and deoxygenated aqueous solutions. J. Photochem. Photobiol. A 1996, 99, 137–143. [Google Scholar] [CrossRef]
- Gao, S.S.; Abbatt, J.P.D. Kinetics and mechanism of OH oxidation of small organic dicarboxylic acids in ice: Comparison to behavior in aqueous solution. J. Phys. Chem. A 2011, 115, 9977–9986. [Google Scholar] [CrossRef]
- Chan, M.N.; Zhang, H.; Goldstein, A.H.; Wilson, K.R. Role of water and phase in the heterogeneous oxidation of solid and aqueous succinic acid aerosol by hydroxyl radicals. J. Phys. Chem. C 2014, 118, 28978–28992. [Google Scholar] [CrossRef]
- Chin, M.; Wine, P.H. A Temperature-Dependent Competitive Kinetics Study of the Aqueous-Phase Reactions of OH Radicals with Formate, Formic Acid, Acetate, Acetic Acid, and Hydrated Formaldehyde; Lewis: Hangzhou, China, 1994; pp. 85–96. [Google Scholar] [CrossRef]
- Ervens, B.; Gligorovski, S.; Herrmann, H. Temperature-dependent rate constants for hydroxyl radical reactions with organic compounds in aqueous solutions. Phys. Chem. Chem. Phys. 2003, 5, 1811–1824. [Google Scholar] [CrossRef]
- Gligorovski, S.; Rousse, D.; George, C.H.; Herrmann, H. Rate constants for the OH reactions with Oxygenated organic compounds in aqueous solution. Int. J. Chem. Kinet. 2009, 41, 309–326. [Google Scholar] [CrossRef]
- Logan, S.R. Redox reactions of organic radicals with ferrocene/ferricenium species in aqueous solution. Part 1. Radicals derived from carboxylic acids. J. Chem. Soc. Perkin Trans. 2 1989, 751–754. [Google Scholar] [CrossRef]
- Martin, L.R.; Mezyk, S.P.; Mincher, B.J. Determination of arrhenius and thermodynamic parameters for the aqueous reaction of the hydroxyl radical with lactic acid. J. Phys. Chem. A 2009, 113, 141–145. [Google Scholar] [CrossRef]
- Otto, T.; Schaefer, T.; Herrmann, H. Aqueous-phase oxidation of terpene-derived acids by atmospherically relevant radicals. J. Phys. Chem. A 2018, 122, 9233–9241. [Google Scholar] [CrossRef] [PubMed]
- Walling, C.; El-Taliawi, G.M. Fenton’s reagent. II. Reactions of carbonyl compounds and alpha, beta-unsaturated acids. J. Am. Chem. Soc. 1973, 95, 844–847. [Google Scholar] [CrossRef]
- Adler, H.; Sirén, H. Study on dicarboxylic acids in aerosol samples with capillary electrophoresis. J. Anal. Methods Chem. 2014, 2014, 498168. [Google Scholar] [CrossRef] [PubMed]
- Martinsson, J.; Monteil, G.; Sporre, M.K.; Kaldal Hansen, A.M.; Kristensson, A.; Eriksson Stenström, K.; Swietlicki, E.; Glasius, M. Exploring sources of biogenic secondary organic aerosol compounds using chemical analysis and the FLEXPART model. Atmos. Chem. Phys. 2017, 17, 11025–11040. [Google Scholar] [CrossRef]
- Zhu, L.; Nicovich, J.M.; Wine, P.H. Temperature-dependent kinetics studies of aqueous phase reactions of hydroxyl radicals with dimethylsulfoxide, dimethylsulfone, and methanesulfonate. Aquat. Sci. 2003, 65, 425–435. [Google Scholar] [CrossRef]
- Schaefer, T.; Herrmann, H. Competition kinetics of OH radical reactions with oxygenated organic compounds in aqueous solution: Rate constants and internal optical absorption effects. Phys. Chem. Chem. Phys. 2018, 20, 10939–10948. [Google Scholar] [CrossRef]
- Herrmann, H. Kinetics of aqueous phase reactions relevant for atmospheric chemistry. Chem. Rev. 2003, 103, 4691–4716. [Google Scholar] [CrossRef]
- Martell, A.E.; Smith, R.M. Critical Stability Constants; Plenum Press: New York, NY, USA, 1976; pp. 1–4. [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Versuch einer mathematischen theorie der koagulations kinetic kolloider lösungen. Z. Phys. Chem. 1917, 92, 129. [Google Scholar] [CrossRef]
- He, L.; Schaefer, T.; Otto, T.; Kroflič, A.; Herrmann, H. Kinetic and theoretical study of the atmospheric aqueous-phase reactions of OH radicals with methoxyphenolic compounds. J. Phys. Chem. A 2019, 123, 7828–7838. [Google Scholar] [CrossRef]
- Kroflič, A.; Schaefer, T.; Huš, M.; Phuoc Le, H.; Otto, T.; Herrmann, H. OH radicals reactivity towards phenol-related pollutants in water: Temperature dependence of the rate constants and novel insights into the [OH–phenol] adduct formation. Phys. Chem. Chem. Phys. 2020, 22, 1324–1332. [Google Scholar] [CrossRef]
- Otto, T.; Schaefer, T.; Herrmann, H. Aqueous-phase oxidation of cis-β-Isoprene epoxydiol by hydroxyl radicals and its impact on atmospheric isoprene processing. J. Phys. Chem. A 2019, 123, 10599–10608. [Google Scholar] [CrossRef] [PubMed]
- Atkins, P.; De Paula, J. Physical Chemistry, 8th ed.; W. H. Freeman and Company: New York, NY, USA, 2006. [Google Scholar]
- Asmus, K.D.; Moeckel, H.; Henglein, A. Pulse radiolytic study of the site of hydroxyl radical attack on aliphatic alcohols in aqueous solution. J. Phys. Chem. 1973, 77, 1218–1221. [Google Scholar] [CrossRef]
- Hoffmann, D.; Weigert, B.; Barzaghi, P.; Herrmann, H. Reactivity of poly-alcohols towards OH, NO3 and SO4- in aqueous solution. Phys. Chem. Chem. Phys. 2009, 11, 9351–9363. [Google Scholar] [CrossRef] [PubMed]
- Buxton, G.V.; Greenstock, C.L.; Helman, W.P.; Ross, A.B. Critical review of rate constants for reactions of hydrated electrons, hydrogen atoms and hydroxyl radicals (OH/O-) in aqueous solution. J. Phys. Chem. Ref. Data 1988, 17, 513–886. [Google Scholar] [CrossRef]
- Luo, Y.R. Handbook of Bond Dissociation Energies in Organic Compounds; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar] [CrossRef]
- Denisov, E.T.; Tumanov, V.E. Estimation of the bond dissociation energies from the kinetic characteristics of liquid-phase radical reactions. Russ. Chem. Rev. 2005, 74, 825–858. [Google Scholar] [CrossRef]
- Neta, P.; Huie, R.E.; Ross, A.B. Rate constants for reactions of peroxyl radicals in fluid solutions. J. Phys. Chem. Ref. Data 1990, 19, 413–513. [Google Scholar] [CrossRef]
- Von Sonntag, C.; Schuchmann, H.-P. The Elucidation of peroxyl radical reactions in aqueous solution with the help of radiation-chemical methods. Angew. Chem. Int. Ed. Engl. 1991, 30, 1229–1253. [Google Scholar] [CrossRef]
- Russell, G.A. Deuterium-isotope effects in the autoxidation of Aralkyl hydrocarbons. Mechanism of the interaction of Peroxy Radicals1. J. Am. Chem. Soc. 1957, 79, 3871–3877. [Google Scholar] [CrossRef]
- Bennett, J.E.; Summers, R. Product studies of the mutual termination reactions of sec-alkylperoxy radicals: Evidence for non-cyclic termination. Can. J. Chem. 1974, 52, 1377–1379. [Google Scholar] [CrossRef]
- Schaefer, T.; van Pinxteren, D.; Herrmann, H. Multiphase chemistry of glyoxal: Revised kinetics of the alkyl radical reaction with molecular oxygen and the reaction of glyoxal with OH, NO3, and SO4– in aqueous solution. Environ. Sci. Technol. 2015, 49, 343–350. [Google Scholar] [CrossRef]
- Scholes, G.; Willson, R.L. γ-Radiolysis of aqueous thymine solutions. Determination of relative reaction rates of OH radicals. Trans. Faraday Soc. 1967, 63, 2983–2993. [Google Scholar] [CrossRef]
- Cabelli Diane, E.; Bielski Benon, H.J. A pulse radiolysis study of some dicarboxylic acids of the citric acid cycle. The kinetics and spectral properties of the free radicals formed by reaction with the OH radical. Z. Naturforsch. B Chem. Sci. 1985, 40, 1731. [Google Scholar] [CrossRef]
- Minakata, D.; Li, K.; Westerhoff, P.; Crittenden, J. Development of a group contribution method to predict aqueous phase hydroxyl radical (HO•) reaction rate constants. Environ. Sci. Technol. 2009, 43, 6220–6227. [Google Scholar] [CrossRef] [PubMed]
- Doussin, J.F.; Monod, A. Structure-activity relationship for the estimation of OH-oxidation rate constants of carbonyl compounds in the aqueous phase. Atmos. Chem. Phys. 2013, 13, 11625–11641. [Google Scholar] [CrossRef]
- Chin, M.; Wine, P.H. A temperature-dependent kinetics study of the aqueous phase reactions OH + SCN− → SCNOH− and SCN + SCN− ⇆ (SCN)2−. J. Photochem. Photobiol. A 1992, 69, 17–25. [Google Scholar] [CrossRef]
- NIST. Solution Kinetics Database Version 3.0; NIST: Gaithersburg, MD, USA, 1998. [Google Scholar]
- Vel Leitner, N.K.; Doré, M. Mecanisme d’action des radicaux OH sur les acides glycolique, glyoxylique, acetique et oxalique en solution aqueuse: Incidence sur la consammation de peroxyde d’hydrogene dans les systemes H2O2UV et O3H2O2. Water Res. 1997, 31, 1383–1397. [Google Scholar] [CrossRef]
- Barker, J.R.; Steiner, A.L.; Wallington, T.J. Advances in Atmospheric Chemistry; World Scientific: Singapore, 2017; Volume 1, p. 608. [Google Scholar] [CrossRef]
| Compounds and pH Values | k(278 K)/L mol−1 s−1 | k(288 K)/L mol−1 s−1 | k(298 K)/L mol−1 s−1 | k(308 K)/L mol−1 s−1 | k(318 K)/L mol−1 s−1 |
|---|---|---|---|---|---|
| Succinic acid | |||||
| pH = 2 | (7.9 ± 0.4) · 107 | (1.2 ± 0.1) · 108 | (1.3 ± 0.2) · 108 | (1.4 ± 0.4) · 108 | (1.7 ± 0.1) · 108 |
| pH = 8- | (4.3 ± 0.1) · 108 | (4.8 ± 0.1) · 108 | (5.3 ± 0.2) · 108 | (8.5 ± 0.3) · 108 | (9.2 ± 0.1) · 108 |
| pH = 4.9 | (2.9 ± 0.1) · 108 | (3.6 ± 0.1) · 108 | (4.6 ± 0.3) · 108 | (4.5 ± 0.3) · 108 | (3.6 ± 0.1) · 108 |
| Pimelic acid | |||||
| pH = 2 | (1.7 ± 0.1) · 109 | (2.2 ± 0.1) · 109 | (2.2 ± 0.1) · 109 | (2.5 ± 0.1) · 109 | (2.8 ± 0.1) · 109 |
| pH = 8- | (1.9 ± 0.1) · 109 | (2.5 ± 0.1) · 109 | (3.2 ± 0.1) · 109 | (3.8 ± 0.1) · 109 | (4.4 ± 0.1) · 109 |
| pH = 4.61 | (2.1 ± 0.1) · 109 | (2.3 ± 0.1) · 109 | (2.8 ± 0.1) · 109 | (3.2 ± 0.1) · 109 | (3.5 ± 0.1) · 109 |
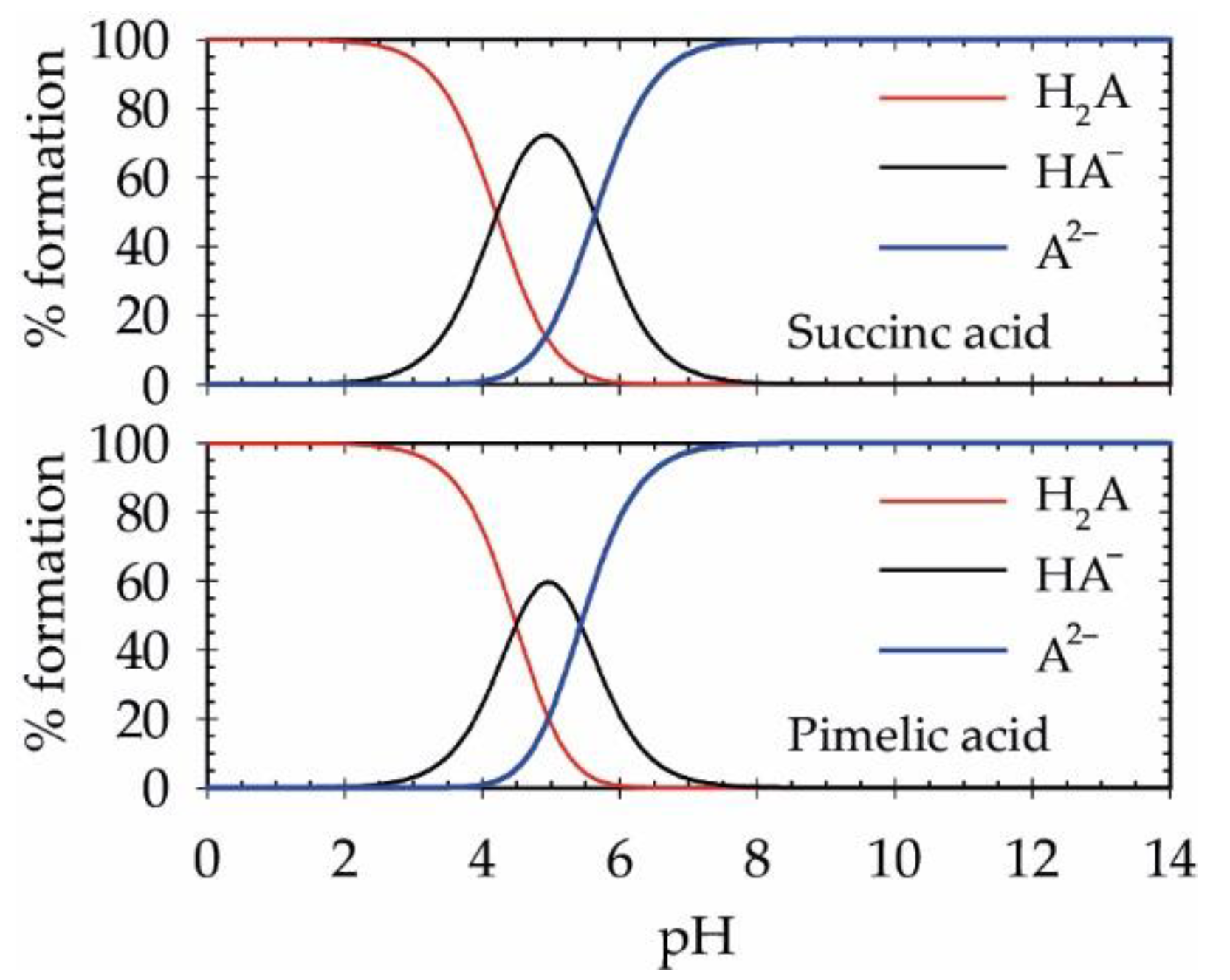
| Compounds, pKa Values and Rate Constants | 278 K | 288 K | 298 K | 308 K | 318 K |
|---|---|---|---|---|---|
| Succinic acid | |||||
| pKa,1 | 4.243 | 4.224 | 4.207 | 4.191 | 4.176 |
| pKa,2 | 5.634 | 5.635 | 5.636 | 5.637 | 5.638 |
| k2nd(AH−)/L mol−1 s−1 | (3.0 ± 0.1) · 108 | (3.9 ± 0.1) · 108 | (5.1 ± 0.1) · 108 | (4.4 ± 0.1) · 108 | (5.3 ± 0.1) · 108 |
| Pimelic acid | |||||
| pKa,1 | 4.474 | 4.482 | 4.490 | 4.497 | 4.504 |
| pKa,2 | 5.383 | 5.407 | 5.430 | 5.451 | 5.471 |
| k2nd(AH−)/L mol−1 s−1 | (2.5 ± 0.1) · 109 | (2.4 ± 0.1) · 109 | (3.4 ± 0.1) · 109 | (3.6 ± 0.1) · 109 | (4.0 ± 0.1) · 109 |
| Compounds | A/L mol−1 s−1 | EA/kJ mol−1 | ΔH‡/kJ mol−1 | ΔS‡/J K−1 mol−1 | ΔG‡/kJ mol−1 |
|---|---|---|---|---|---|
| Succinic acid | |||||
| Diacid | (2.1 ± 0.1) · 1010 | 13 ± 2 | 10 ± 2 | −(56 ± 3) | 27 ± 7 |
| Monoanion | (1.5 ± 0.1) · 1010 | 9 ± 3 | 7 ± 3 | −(57 ± 4) | 24 ± 11 |
| Dianion | (2.9 ± 0.2) · 1011 | 15 ± 3 | 13 ± 3 | −(34 ± 2) | 23 ± 7 |
| Pimelic acid | |||||
| Diacid | (7.3 ± 0.2) · 1010 | 9 ± 1 | 6 ± 1 | −(45 ± 1) | 20 ± 4 |
| Monoanion | (1.8 ± 0.1) · 1011 | 10 ± 2 | 8 ± 2 | −(38 ± 2) | 19 ± 6 |
| Dianion | (1.4 ± 0.1) · 1012 | 15 ± 1 | 13 ± 1 | −(21 ± 1) | 19 ± 2 |
| Compounds | kOH/L mol−1 s−1 | Remarks | Reference |
|---|---|---|---|
| Succinic acid | |||
| AH2 | 1.0 · 108 a | pH = 2, T = not reported/room temperature, PR-comp. kinetics, ref. thymine (slope 0.023) | [46] |
| 1.33 · 108 a | pH = 2.0–2.2, T = 303.15 K, Fenton type-comp. kinetics, ref. methanol (slope 0.097) | [24] | |
| (3.1 ± 0.3) · 108 a | pH = 1.5–10, T = 298.25 K, PR-build-up kinetics at λ = 250–350 nm, (pKa 4.16, 5.61) | [47] | |
| (1.1 ± 0.1) · 108 a, b (1.06 ± 0.1) · 108 c | pH = 1.5, T = 298.15 K, PR-comp. kinetics, ref. SCN− (slope 0.0089), T-dependent measurement, (pKa 4.16, 5.61) | [19]d | |
| 1.1 · 108 | Estimation method | [48] | |
| 7.7 · 107 | Estimation method | [49] | |
| (1.3 ± 0.2) · 108 b | pH = 2, T = 298.15 K | This work | |
| AH− | 2.0 · 108 | Estimation method | [49] |
| (5.1 ± 0.1) · 108 b | pH = 4.9, T = 298.15 K | This work | |
| A2− | (5.3 ± 0.5) · 108 a | pH = 9, borax buffer, T = 293.15 K, FP-comp. kinetics, ref. 4-ferrocenyl-butanoate (slope 0.049) | [21] |
| (5.0 ± 0.5) · 108 a, b (4.8 ± 0.48) · 108 c | pH = 7.8, T = 298.15 K, LFP-comp. kinetics, ref. SCN- (slope 0.0403), T-dependent measurement, (pKa 4.16, 5.61) | [19] | |
| 4.6 · 108 | Estimation method | [49] | |
| (5.3 ± 0.2) · 108 b | pH = 8, T = 298.15 K | This work | |
| Pimelic acid | |||
| AH2 | 2.4 · 109 a 3.5 · 109 e | pH = 2, T = not reported/room temperature, PR-comp. kinetics, ref. thymine (slope 0.558) | [46] |
| (2.4 ± 0.7) · 109 | pH = 2, T = 298.15 K, LFP-build-up kinetics at λ = 244 nm | [29] | |
| 4.3 · 109 | Estimation method | [48] | |
| 1.6 · 109 | Estimation method | [49] | |
| (2.2 ± 0.1) · 109 b | pH = 2, T = 298.15 K | This work | |
| AH− | 2.3 · 109 | Estimation method | [49] |
| (3.4 ± 0.1) · 109 b | pH = 4.6, T = 298.15 K | This work | |
| A2− | (2.9 ± 0.8) · 109 | pH = 9, T = 298.15 K, LFP-build-up kinetics at λ = 244 nm | [29] |
| 3.0 · 109 | Estimation method | [49] | |
| (3.2 ± 0.1) · 109 b | pH = 8, T = 298.15 K | This work | |
| Compounds | Cloud Case Urban | Cloud Case Remote | Aerosol Case Urban | Aerosol Case Remote |
|---|---|---|---|---|
| [OH] = 3.5 · 10−15 /mol L−1 | [OH] = 2.2 · 10−14 /mol L−1 | [OH] = 4.4 · 10−13 /mol L−1 | [OH] = 3.0 · 10−12 /mol L−1 | |
| Succinic acid | ||||
| AH2 | 25.4–41.9 d | 4.0–6.7 d | 4.9–8.0 h | 43–70 min |
| AH− | 6.2–7.7 d | 23.8–29.4 h | 72–88 min | 11–13 min |
| A2− | 6.5–11 d | 24.8–42.1 h | 74–126 min | 11–19 min |
| Pimelic acid | ||||
| AH2 | 36.1–46.7 h | 5.7–7.4 h | 17–22 min | 2–3 min |
| AH− | 24.8–41.8 h | 3.9–6.6 h | 12–20 min | 2–3 min |
| A2− | 24.8–41.8 h | 3.9–6.6 h | 12–20 min | 2–3 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schaefer, T.; Wen, L.; Estelmann, A.; Maak, J.; Herrmann, H. pH- and Temperature-Dependent Kinetics of the Oxidation Reactions of OH with Succinic and Pimelic Acid in Aqueous Solution. Atmosphere 2020, 11, 320. https://doi.org/10.3390/atmos11040320
Schaefer T, Wen L, Estelmann A, Maak J, Herrmann H. pH- and Temperature-Dependent Kinetics of the Oxidation Reactions of OH with Succinic and Pimelic Acid in Aqueous Solution. Atmosphere. 2020; 11(4):320. https://doi.org/10.3390/atmos11040320
Chicago/Turabian StyleSchaefer, Thomas, Liang Wen, Arne Estelmann, Joely Maak, and Hartmut Herrmann. 2020. "pH- and Temperature-Dependent Kinetics of the Oxidation Reactions of OH with Succinic and Pimelic Acid in Aqueous Solution" Atmosphere 11, no. 4: 320. https://doi.org/10.3390/atmos11040320
APA StyleSchaefer, T., Wen, L., Estelmann, A., Maak, J., & Herrmann, H. (2020). pH- and Temperature-Dependent Kinetics of the Oxidation Reactions of OH with Succinic and Pimelic Acid in Aqueous Solution. Atmosphere, 11(4), 320. https://doi.org/10.3390/atmos11040320