Characterization of Wind-Sea- and Swell-Induced Wave Energy along the Norwegian Coast
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Wave Climate in the Northeast Atlantic: The North Sea, the Norwegian Sea, and the Barents Sea
3.2. WEF along the Norwegian Coast
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Marine Renewable Energy | |
| Significant wave height | |
| Swell significant wave height | |
| Wind sea significant wave height | |
| Peak wave period | |
| Swell peak wave period | |
| Wind sea peak wave period | |
| (Total) Wave Energy Flux | |
| Swell Wave Energy Flux | |
| Wind Sea Wave Energy Flux | |
| Average Swell Wave Energy Flux | |
| Average Wind Sea Wave Energy Flux |
References
- European Commission. A Clean Planet for All—A European Long-Term Strategic Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy; Technical Report; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Twidell, J.; Weir, T. Renewable Energy Resources; Routledge: London, UK, 2015. [Google Scholar] [CrossRef]
- Borthwick, A.G.L. Marine Renewable Energy Seascape. Engineering 2016, 2, 69–78. [Google Scholar] [CrossRef]
- Grabbe, M.; Lalander, E.; Lundin, S.; Leijon, M. A review of the tidal current energy resource in Norway. Renew. Sustain. Energy Rev. 2009, 13, 1898–1909. [Google Scholar] [CrossRef]
- Astariz, S.; Iglesias, G. The economics of wave energy: A review. Renew. Sustain. Energy Rev. 2015, 45, 397–408. [Google Scholar] [CrossRef]
- Magagna, D.; Uihlein, A. Ocean energy development in Europe: Current status and future perspectives. Int. J. Mar. Energy 2015, 11, 84–104. [Google Scholar] [CrossRef]
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A review of combined wave and offshore wind energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef]
- Uihlein, A.; Magagna, D. Wave and tidal current energy—A review of the current state of research beyond technology. Renew. Sustain. Energy Rev. 2016, 58, 1070–1081. [Google Scholar] [CrossRef]
- Chatzigiannakou, M.; Temiz, I.; Leijon, M. Offshore Deployments of Wave Energy Converters by Seabased Industry AB. J. Mar. Sci. Eng. 2017, 5, 15. [Google Scholar] [CrossRef]
- Wang, Z. New wave power. Nature 2017, 542, 159–160. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean Wave Energy Converters: Status and Challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef]
- Lavidas, G. Energy and socio-economic benefits from the development of wave energy in Greece. Renew. Energy 2019, 132, 1290–1300. [Google Scholar] [CrossRef]
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A recent increase in global wave power as a consequence of oceanic warming. Nat. Commun. 2019, 10, 205. [Google Scholar] [CrossRef] [PubMed]
- Clément, A.; McCullen, P.; Falcão, A.; Fiorentino, A.; Gardner, F.; Hammarlund, K.; Lemonis, G.; Lewis, T.; Nielsen, K.; Petroncini, S.; et al. Wave energy in Europe: Current status and perspectives. Renew. Sustain. Energy Rev. 2002, 6, 405–431. [Google Scholar] [CrossRef]
- Gunn, K.; Stock-Williams, C. Quantifying the global wave power resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- Falnes, J. Research and development in ocean-wave energy in Norway. In Proceedings of the International Symposium on Ocean Energy Development, Muroran, Hokkaido, Japan, 26–27 August 1993; pp. 27–39. [Google Scholar]
- Kalogeri, C.; Galanis, G.; Spyrou, C.; Diamantis, D.; Baladima, F.; Koukoula, M.; Kallos, G. Assessing the European offshore wind and wave energy resource for combined exploitation. Renew. Energy 2017, 101, 244–264. [Google Scholar] [CrossRef]
- Saha, P.; Idsø, J. New hydropower development in Norway: Municipalities’ attitude, involvement and perceived barriers. Renew. Sustain. Energy Rev. 2016, 61, 235–244. [Google Scholar] [CrossRef]
- Cheliotis, I.; Varlas, G.; Christakos, K. The Impact of Cyclone Xaver on Hydropower Potential in Norway. In Perspectives on Atmospheric Sciences; Springer International Publishing: Cham, Switzerland, 2017; pp. 175–181. [Google Scholar]
- Strbac, G.; Hatziargyriou, N.; Lopes, J.P.; Moreira, C.; Dimeas, A.; Papadaskalopoulos, D. Microgrids: Enhancing the Resilience of the European Megagrid. IEEE Power Energy Mag. 2015, 13, 35–43. [Google Scholar] [CrossRef]
- Rusu, E.; Onea, F. A review of the technologies for wave energy extraction. Clean Energy 2018, 1. [Google Scholar] [CrossRef]
- Katsafados, P.; Papadopoulos, A.; Korres, G.; Varlas, G. A fully coupled atmosphere–ocean wave modeling system for the Mediterranean Sea: Interactions and sensitivity to the resolved scales and mechanisms. Geosci. Model Dev. 2016, 9, 161–173. [Google Scholar] [CrossRef]
- Varlas, G.; Katsafados, P.; Papadopoulos, A.; Korres, G. Implementation of a two-way coupled atmosphere-ocean wave modeling system for assessing air-sea interaction over the Mediterranean Sea. Atmos. Res. 2018, 208, 201–217. [Google Scholar] [CrossRef]
- Katsafados, P.; Varlas, G.; Papadopoulos, A.; Spyrou, C.; Korres, G. Assessing the Implicit Rain Impact on Sea State During Hurricane Sandy (2012). Geophys. Res. Lett. 2018. [Google Scholar] [CrossRef]
- Zheng, C.; Shao, L.; Shi, W.; Su, Q.; Lin, G.; Li, X.; Chen, X. An assessment of global ocean wave energy resources over the last 45 a. Acta Oceanol. Sin. 2014, 33, 92–101. [Google Scholar] [CrossRef]
- Cornett, A. A Global Wave Energy Resource Assessment. In Proceedings of the Eighteenth International Offshore and Polar Engineering Conference, Vancouver, BC, Canada, 6–11 July 2008; Volume 50. [Google Scholar]
- The WAVEWATCHIII® Development Group. User Manual and System Documentation of WAVEWATCH III® Version 5.16; Technical Report 329; NOAA/NWS/NCEP/MMAB: College Park, MD, USA, 2016. [Google Scholar]
- Reistad, M.; Breivik, Ø.; Haakenstad, H.; Aarnes, O.J.; Furevik, B.R.; Bidlot, J.R. A high-resolution hindcast of wind and waves for the North Sea, the Norwegian Sea, and the Barents Sea. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Furevik, B.R.; Haakenstad, H. Near-surface marine wind profiles from rawinsonde and NORA10 hindcast. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Uppala, S.; Kallberg, P.; Simmons, A.J.; Andrae, U.; Da Costa Bechtold, V.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez-Carrascal, A.; Kelly, G.A.; et al. The Era-40 Re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Undén, P.; Rontu, L.; Järvinen, H.; Lynch, P.; Calvo-Sanchez, J.; Cats, G.; Cuxart, J.; Eerola, K.; Fortelius, C.; García-Moya, J. HIRLAM-5 Scientific Documentation; Technical Report; Sveriges Meteorologiska Och Hydrologiska Institut: Norrköping, Sweden, 2002. [Google Scholar]
- ECMWF. Part VII: ECMWF Wave Model. In IFS Documentation CY45R1; Number 7 in IFS Documentation; ECMWF: Reading, UK, 2018; Chapter 10; p. 70. [Google Scholar]
- Aarnes, O.J.; Breivik, Ø.; Reistad, M. Wave Extremes in the Northeast Atlantic. J. Clim. 2012, 25, 1529–1543. [Google Scholar] [CrossRef]
- Iglesias, G.; López, M.; Carballo, R.; Castro, A.; Fraguela, J.; Frigaard, P. Wave energy potential in Galicia (NW Spain). Renew. Energy 2009, 34, 2323–2333. [Google Scholar] [CrossRef]
- Herbich, J.B. Handbook of Coastal Engineering, 1st ed.; McGraw-Hill Professional: New York, NY, USA, 2000. [Google Scholar]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Izadparast, A.H.; Niedzwecki, J.M. Estimating the potential of ocean wave power resources. Ocean Eng. 2011, 38, 177–185. [Google Scholar] [CrossRef]
- Bento, A.R.; Martinho, P.; Guedes Soares, C. Wave energy assessement for Northern Spain from a 33-year hindcast. Renew. Energy 2018, 127, 322–333. [Google Scholar] [CrossRef]
- Akpınar, A.; Jafali, H.; Rusu, E. Temporal Variation of the Wave Energy Flux in Hotspot Areas of the Black Sea. Sustainability 2019, 11, 562. [Google Scholar] [CrossRef]
- Holthuijsen, L. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Cahill, B.; Lewis, T. Wave period ratios and the calculation of wave power. In Proceedings of the 2nd Marine Energy Technology Symposium METS2014, Seattle, WA, USA, 15–18 April 2014. [Google Scholar]
- Santo, H.; Taylor, P.H.; Woollings, T.; Poulson, S. Decadal wave power variability in the North-East Atlantic and North Sea. Geophys. Res. Lett. 2015, 42, 4956–4963. [Google Scholar] [CrossRef]
- Varlas, G.; Christakos, K.; Cheliotis, I.; Papadopoulos, A.; Steeneveld, G.J. Spatiotemporal variability of marine renewable energy resources in Norway. Energy Procedia 2017, 125, 180–189. [Google Scholar] [CrossRef]
- Sasaki, W. Changes in wave energy resources around Japan. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Míguez, B.M.; McIlvenny, J.; Gleizon, P. Wave energy resource assessment with AltiKa satellite altimetry: A case study at a wave energy site. Geophys. Res. Lett. 2015, 42, 5452–5459. [Google Scholar] [CrossRef]
- Boronowski, S.; Wild, P.; Rowe, A.; Cornelis van Kooten, G. Integration of wave power in Haida Gwaii. Renew. Energy 2010, 35, 2415–2421. [Google Scholar] [CrossRef]
- Semedo, A.; Vettor, R.; Breivik, O.; Sterl, A.; Reistad, M.; Lima, D. The wind sea and swell waves climate in the Nordic seas. Ocean Dyn. 2014, 65. [Google Scholar] [CrossRef]
- Lavidas, G.; Polinder, H. North Sea Wave Database (NSWD) and the Need for Reliable Resource Data: A 38 Year Database for Metocean and Wave Energy Assessments. Atmosphere 2019, 10, 551. [Google Scholar] [CrossRef]
- Christakos, K.; Varlas, G.; Reuder, J.; Katsafados, P.; Papadopoulos, A. Analysis of a Low-level Coastal Jet off the Western Coast of Norway. Energy Procedia 2014, 53, 162–172. [Google Scholar] [CrossRef]
- Christakos, K.; Cheliotis, I.; Varlas, G.; Steeneveld, G.J. Offshore Wind Energy Analysis of Cyclone Xaver over North Europe. Energy Procedia 2016, 94, 37–44. [Google Scholar] [CrossRef]
- SWAN Team. Scientific and Technical Documentation SWAN Cycle III Version 41.31; Delft University of Technology: Delft, The Netherlands, 2019. [Google Scholar]
- Christakos, K.; Furevik, B.R.; Aarnes, O.J.; Breivik, Ø.; Tuomi, L.; Byrkjedal, Ø. The importance of wind forcing in fjord wave modelling. Ocean Dyn. 2020, 70, 57–75. [Google Scholar] [CrossRef]
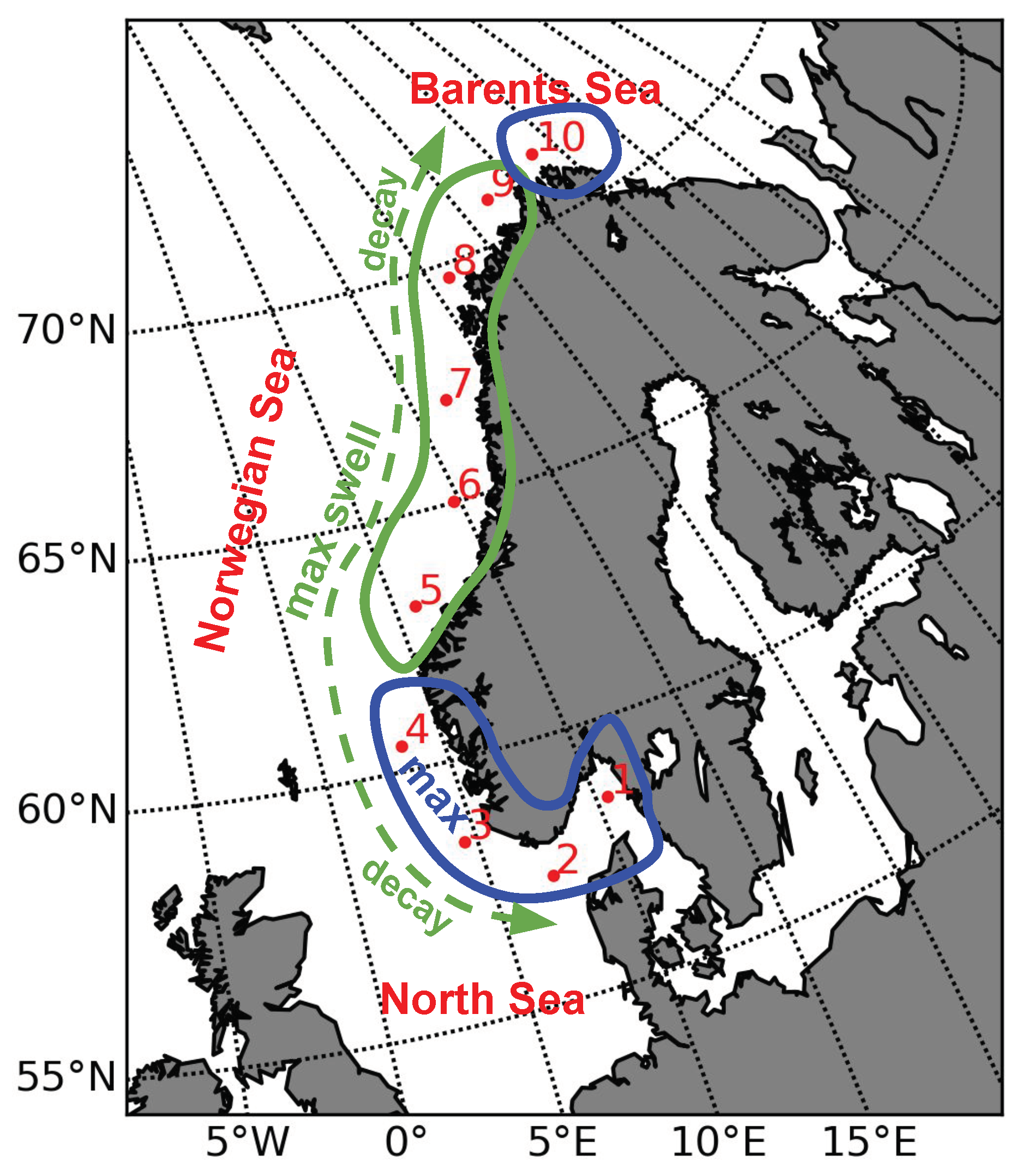
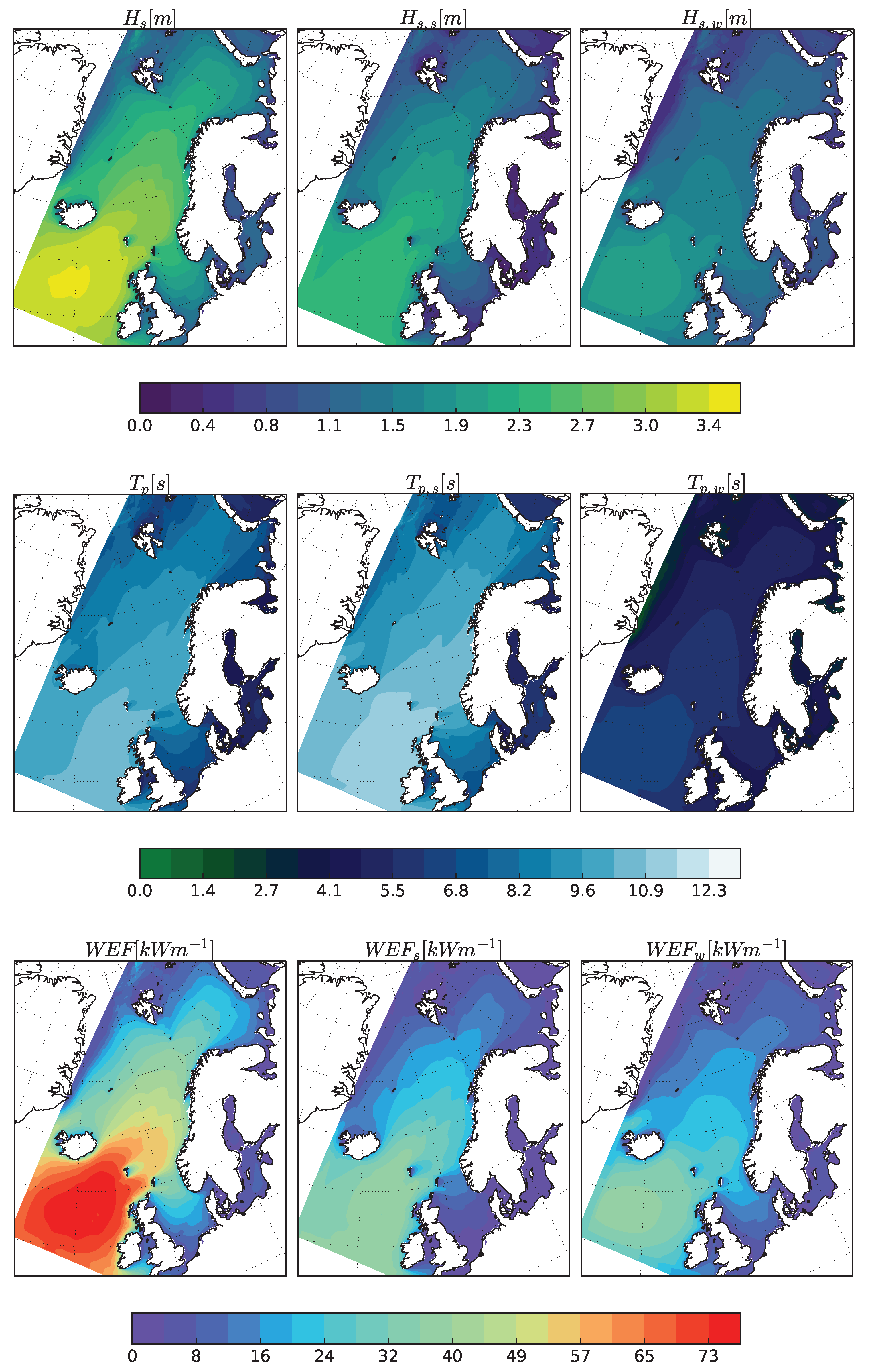
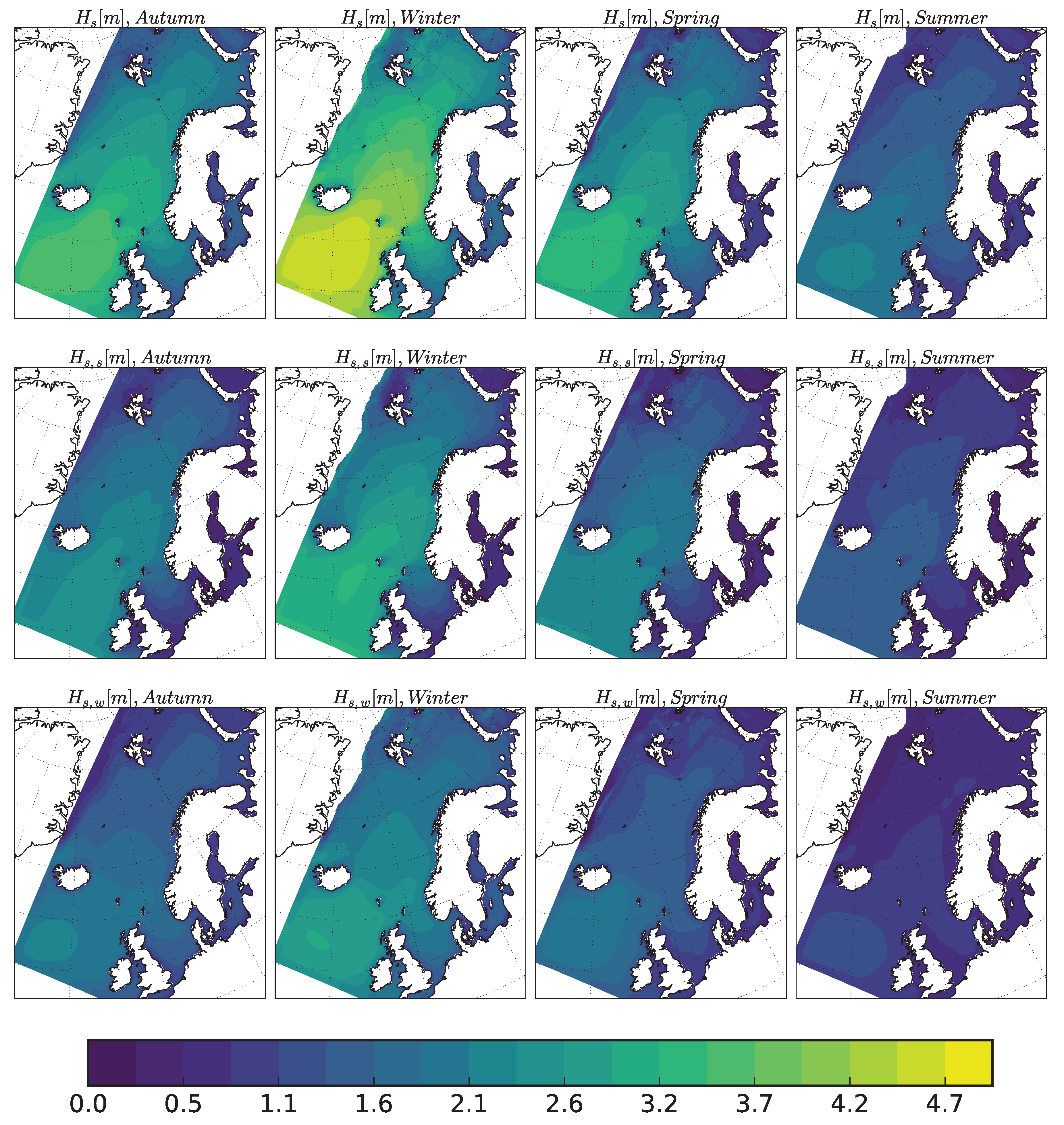

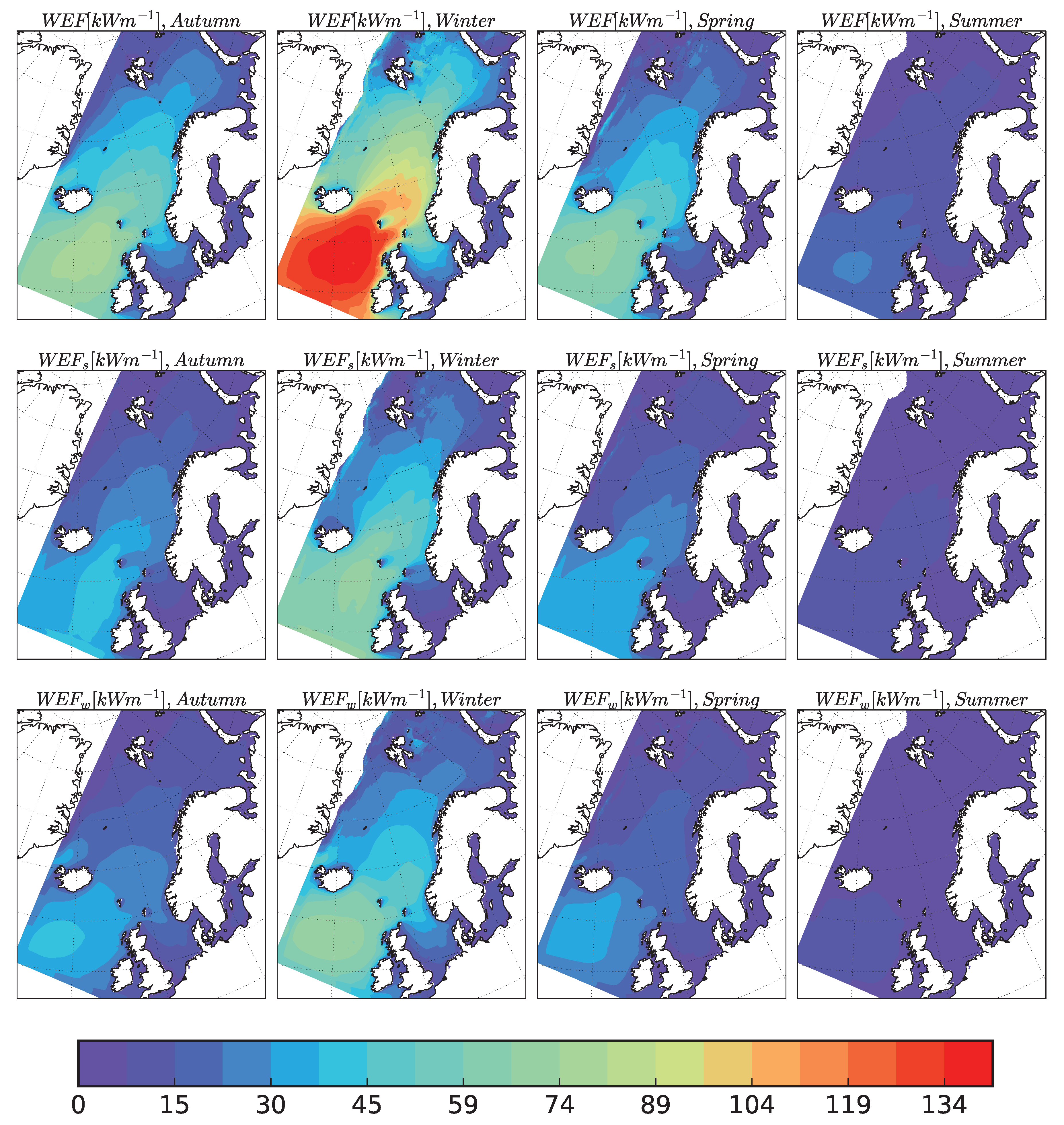
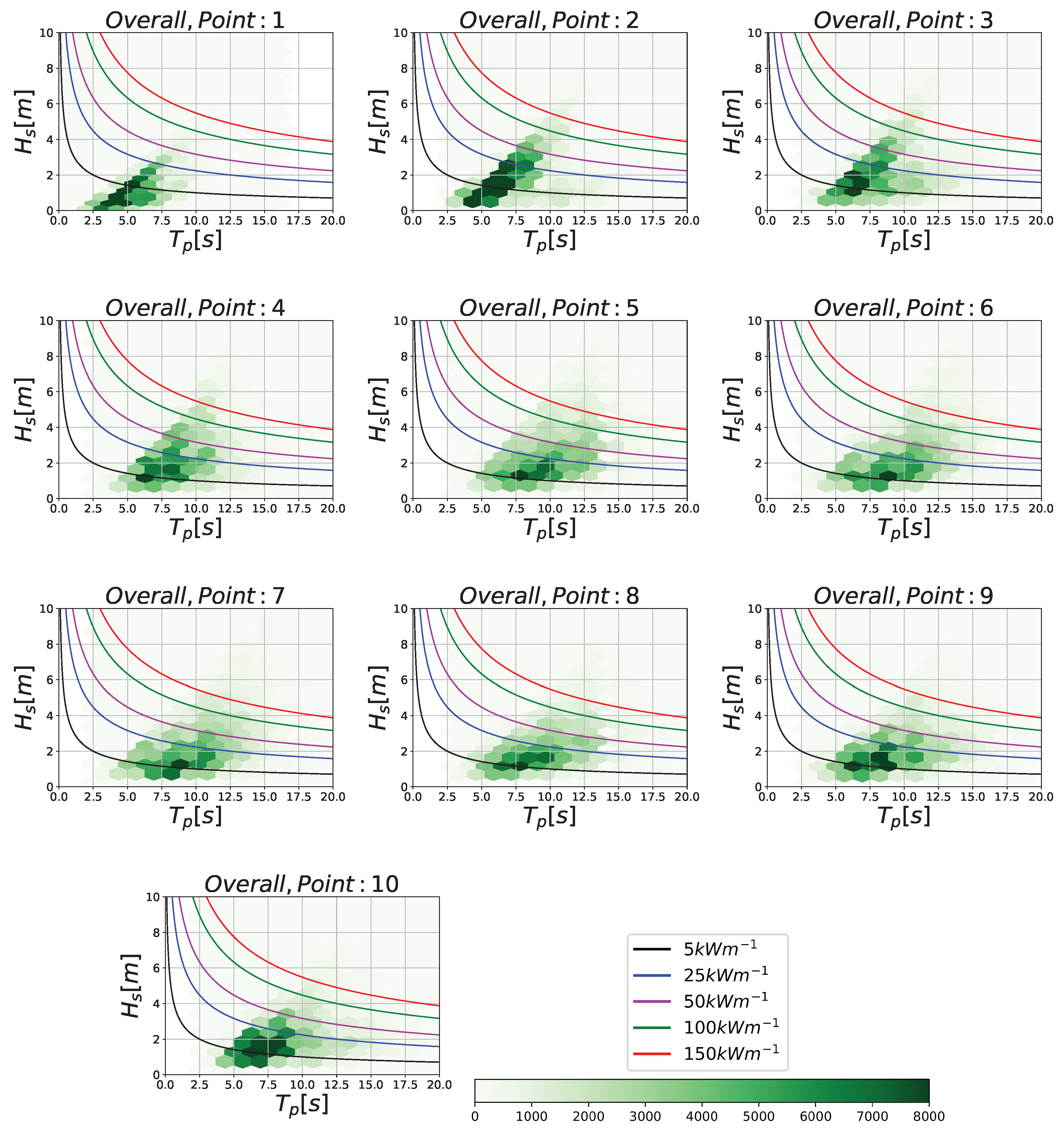
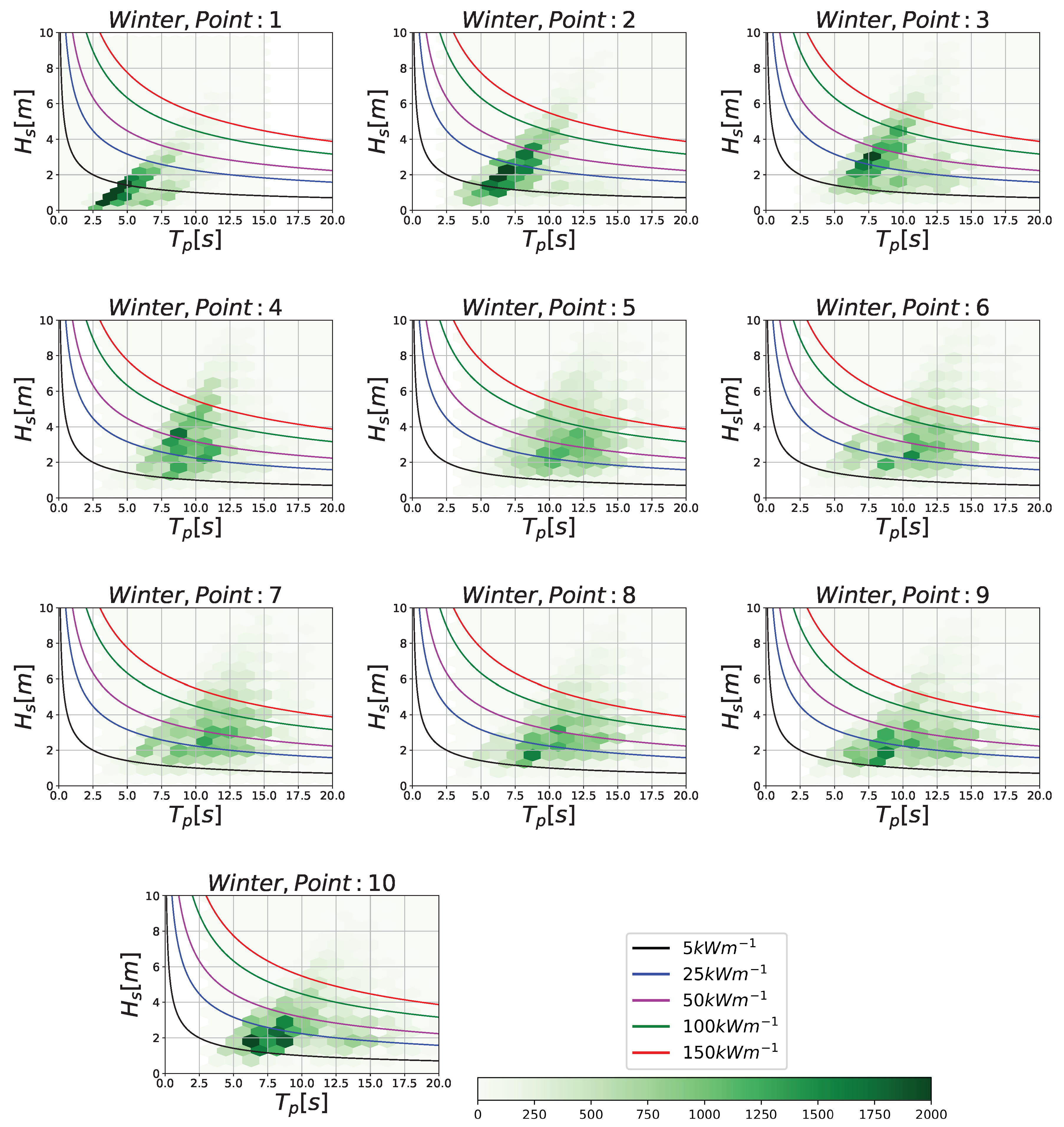



| Point | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15.97 | 10.64 | 8.11 | 3.95 | 3.38 | 3.99 | 3.91 | 3.97 | 7.07 | 10.05 | 12.52 | 15.42 | 8.25 |
| 2 | 37.95 | 29.07 | 23.53 | 13.15 | 8.40 | 8.69 | 8.14 | 8.70 | 15.99 | 23.31 | 30.97 | 36.63 | 20.38 |
| 3 | 56.83 | 45.26 | 38.58 | 21.13 | 12.16 | 9.37 | 7.94 | 9.65 | 20.89 | 34.57 | 45.16 | 55.10 | 29.72 |
| 4 | 68.80 | 54.98 | 46.52 | 26.11 | 14.60 | 10.68 | 8.64 | 10.37 | 23.85 | 40.07 | 52.03 | 65.70 | 35.20 |
| 5 | 89.75 | 79.54 | 63.32 | 33.03 | 16.69 | 12.88 | 10.42 | 12.37 | 31.00 | 48.61 | 62.31 | 86.15 | 45.51 |
| 6 | 85.95 | 79.07 | 59.67 | 30.16 | 14.65 | 11.55 | 8.97 | 10.92 | 28.67 | 45.75 | 58.73 | 81.40 | 42.96 |
| 7 | 80.41 | 74.88 | 56.41 | 27.23 | 12.98 | 10.13 | 7.97 | 9.90 | 25.98 | 42.80 | 54.43 | 74.90 | 39.83 |
| 8 | 68.06 | 66.05 | 50.39 | 24.71 | 13.00 | 10.41 | 7.88 | 9.67 | 22.24 | 39.17 | 46.26 | 62.46 | 35.02 |
| 9 | 58.22 | 58.58 | 45.27 | 21.99 | 12.10 | 9.79 | 7.26 | 9.09 | 19.78 | 35.36 | 39.83 | 53.84 | 30.92 |
| 10 | 47.29 | 48.30 | 37.33 | 19.44 | 11.39 | 9.24 | 6.97 | 8.92 | 17.67 | 30.85 | 33.76 | 43.71 | 26.24 |
| Point | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3.19 | 2.43 | 1.92 | 1.05 | 0.90 | 1.04 | 1.03 | 1.10 | 1.45 | 2.17 | 2.70 | 3.01 | 1.83 |
| 2 | 10.66 | 9.15 | 7.51 | 4.60 | 2.84 | 2.39 | 2.09 | 2.50 | 4.69 | 6.68 | 9.15 | 10.71 | 6.08 |
| 3 | 20.02 | 17.75 | 15.65 | 9.75 | 5.55 | 3.89 | 3.39 | 4.12 | 8.58 | 12.96 | 17.35 | 20.75 | 11.65 |
| 4 | 27.00 | 23.88 | 21.14 | 12.82 | 7.22 | 5.00 | 4.27 | 5.08 | 11.05 | 17.72 | 22.55 | 27.80 | 15.46 |
| 5 | 43.69 | 39.62 | 33.03 | 19.21 | 10.35 | 7.55 | 6.27 | 7.26 | 15.85 | 24.31 | 31.43 | 41.31 | 23.32 |
| 6 | 45.14 | 41.03 | 33.75 | 18.57 | 9.48 | 7.31 | 5.85 | 6.86 | 15.83 | 24.43 | 31.03 | 42.41 | 23.47 |
| 7 | 43.32 | 40.45 | 31.79 | 16.99 | 8.63 | 6.60 | 5.17 | 6.37 | 15.09 | 22.57 | 28.87 | 40.05 | 22.16 |
| 8 | 37.66 | 35.18 | 27.92 | 15.20 | 8.02 | 6.17 | 4.91 | 6.02 | 13.72 | 21.39 | 26.31 | 35.02 | 19.79 |
| 9 | 29.80 | 28.51 | 22.45 | 12.31 | 6.63 | 5.27 | 4.26 | 5.30 | 11.49 | 17.76 | 21.18 | 27.83 | 16.07 |
| 10 | 21.47 | 20.69 | 16.52 | 9.62 | 5.42 | 4.63 | 3.58 | 4.60 | 9.28 | 14.48 | 16.13 | 20.31 | 12.23 |
| Point | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 12.67 | 8.11 | 6.14 | 2.88 | 2.45 | 2.92 | 2.86 | 2.84 | 5.59 | 7.82 | 9.74 | 12.32 | 6.36 |
| 2 | 27.36 | 19.90 | 15.99 | 8.47 | 5.50 | 6.26 | 6.03 | 6.18 | 11.28 | 16.59 | 21.76 | 25.94 | 14.27 |
| 3 | 36.93 | 27.48 | 22.79 | 10.99 | 6.39 | 5.38 | 4.45 | 5.41 | 12.13 | 21.41 | 27.49 | 34.25 | 17.93 |
| 4 | 41.70 | 30.93 | 25.16 | 12.83 | 7.16 | 5.54 | 4.26 | 5.12 | 12.59 | 22.01 | 29.09 | 37.47 | 19.49 |
| 5 | 43.27 | 37.30 | 28.21 | 12.70 | 5.80 | 4.93 | 3.78 | 4.71 | 14.28 | 22.92 | 28.89 | 42.23 | 20.75 |
| 6 | 37.38 | 34.76 | 23.54 | 10.36 | 4.63 | 3.84 | 2.80 | 3.68 | 11.91 | 19.66 | 25.40 | 35.73 | 17.81 |
| 7 | 33.43 | 30.90 | 21.87 | 8.97 | 3.79 | 3.08 | 2.47 | 3.13 | 9.80 | 18.39 | 22.95 | 31.51 | 15.86 |
| 8 | 27.49 | 28.33 | 20.25 | 8.60 | 4.55 | 3.88 | 2.69 | 3.28 | 7.64 | 16.36 | 17.83 | 24.89 | 13.82 |
| 9 | 26.23 | 27.81 | 20.99 | 8.90 | 5.13 | 4.24 | 2.77 | 3.48 | 7.56 | 16.47 | 16.93 | 23.93 | 13.70 |
| 10 | 24.23 | 25.87 | 19.48 | 9.29 | 5.74 | 4.37 | 3.24 | 4.09 | 7.79 | 15.41 | 16.25 | 21.78 | 13.13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christakos, K.; Varlas, G.; Cheliotis, I.; Spyrou, C.; Aarnes, O.J.; Furevik, B.R. Characterization of Wind-Sea- and Swell-Induced Wave Energy along the Norwegian Coast. Atmosphere 2020, 11, 166. https://doi.org/10.3390/atmos11020166
Christakos K, Varlas G, Cheliotis I, Spyrou C, Aarnes OJ, Furevik BR. Characterization of Wind-Sea- and Swell-Induced Wave Energy along the Norwegian Coast. Atmosphere. 2020; 11(2):166. https://doi.org/10.3390/atmos11020166
Chicago/Turabian StyleChristakos, Konstantinos, George Varlas, Ioannis Cheliotis, Christos Spyrou, Ole Johan Aarnes, and Birgitte Rugaard Furevik. 2020. "Characterization of Wind-Sea- and Swell-Induced Wave Energy along the Norwegian Coast" Atmosphere 11, no. 2: 166. https://doi.org/10.3390/atmos11020166
APA StyleChristakos, K., Varlas, G., Cheliotis, I., Spyrou, C., Aarnes, O. J., & Furevik, B. R. (2020). Characterization of Wind-Sea- and Swell-Induced Wave Energy along the Norwegian Coast. Atmosphere, 11(2), 166. https://doi.org/10.3390/atmos11020166






