Multifractal Cross Correlation Analysis of Agro-Meteorological Datasets (Including Reference Evapotranspiration) of California, United States
Abstract
1. Introduction
2. Materials and Methods
2.1. MFDFA Method
- (1)
- Determine the accumulated deviation of the time series signal X (x1, x2… xL) from its mean (so called ‘profile’) as:where i = 1, 2,..., L, with mean and length L.
- (2)
- Identify different independent sub-series of different lengths (called scale s) both in forward and backward directions.
- (3)
- Fit polynomial to each sub-series and find the difference between original sub-series and its fitted polynomial as:and:Here yυ(i) is the polynomial used for fitting in fragment υ.
- (4)
- Determine the fluctuation function (FF) for different combination of scale s and statistical moment order q, based on step 3:
- (5)
- Develop the log-log plot of fluctuation function FFq(s) vs. scale s. The slope of logarithmic plot of FF versus s is called generalized Hurst exponent (GHE) h(q) for different moment order q. The non-linear behavior of the plot between h(q) and q indicates the multifractality of the time series. For monofractal time series h(q) is independent of q. Multifractal behavior (a significant dependence of h(q) on q) will manifest itself only if small and large fluctuations scale differently in the time series. For positive values of q, h(q) describes the scaling behavior of the segments with large fluctuations, whereas for negative values of q, the scaling behavior of the segments with small fluctuations is described. While the precision of h(q) estimation depends mostly on the length of the time series, for large negative values of q (very small fluctuations) the precision of measurement is also starting to play a role. A detailed analysis on the precision of h(q) estimation for the MFDFA method was performed by López and Contreras [71]. The GHE value for q = 2 is considered to be equivalent to the classical Hurst exponent (H) [27,28]. From h(q) other useful exponents like mass exponent τ(q) or singularity exponent f(α) can be derived as follows:
2.2. MFCCA Method
- (1)
- For two time series xi and yi (I = 1, 2,…, N), determine the profiles as:and:where j = 1, 2,…, N and and are the mean of the two time series xi and yi.
- (2)
- Divide each profile Px(j) and Py(j) into Ns non-overlapping segments both in progressive and retrograde directions, to avoid any omission of time series data from the head or tail end of the series.
- (3)
- For each 2Ns segments, compute local trend of both “profiles” Px(j) and Py(j) by fitting polynomials pX,υm(j) and pY,υm(j) of appropriate order m. The subtraction of the fitted polynomial from the original segment gives the covariance as given below:where s is the length of υ segment.
- (4)
- Calculate detrended covariance by summation over all segments:
- (5)
- Check if FqXY(s) behaves as a power-law function of s (the scaling behavior), where s is the segmental sample size:
2.3. Study Area and Data
3. Results and Discussion
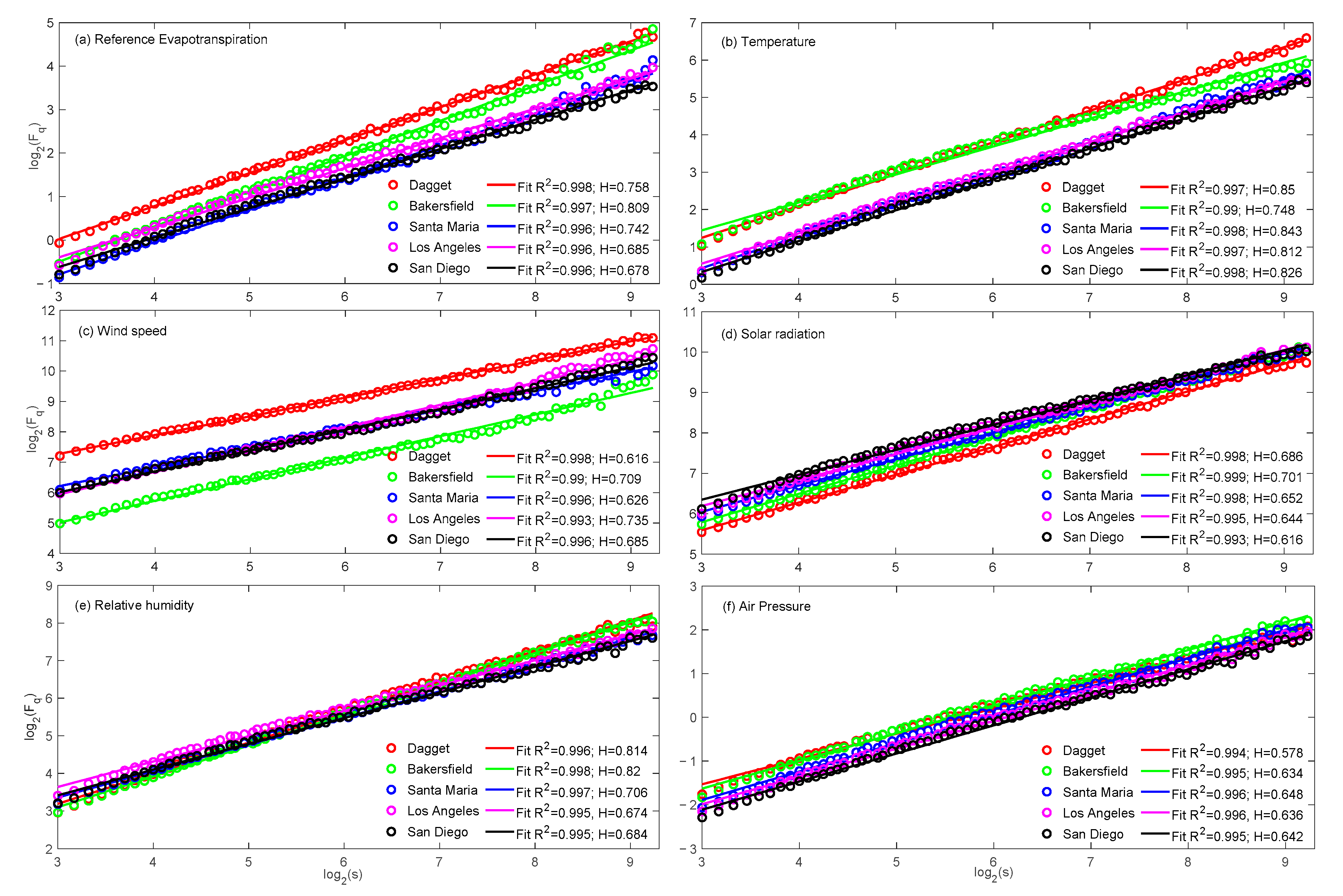
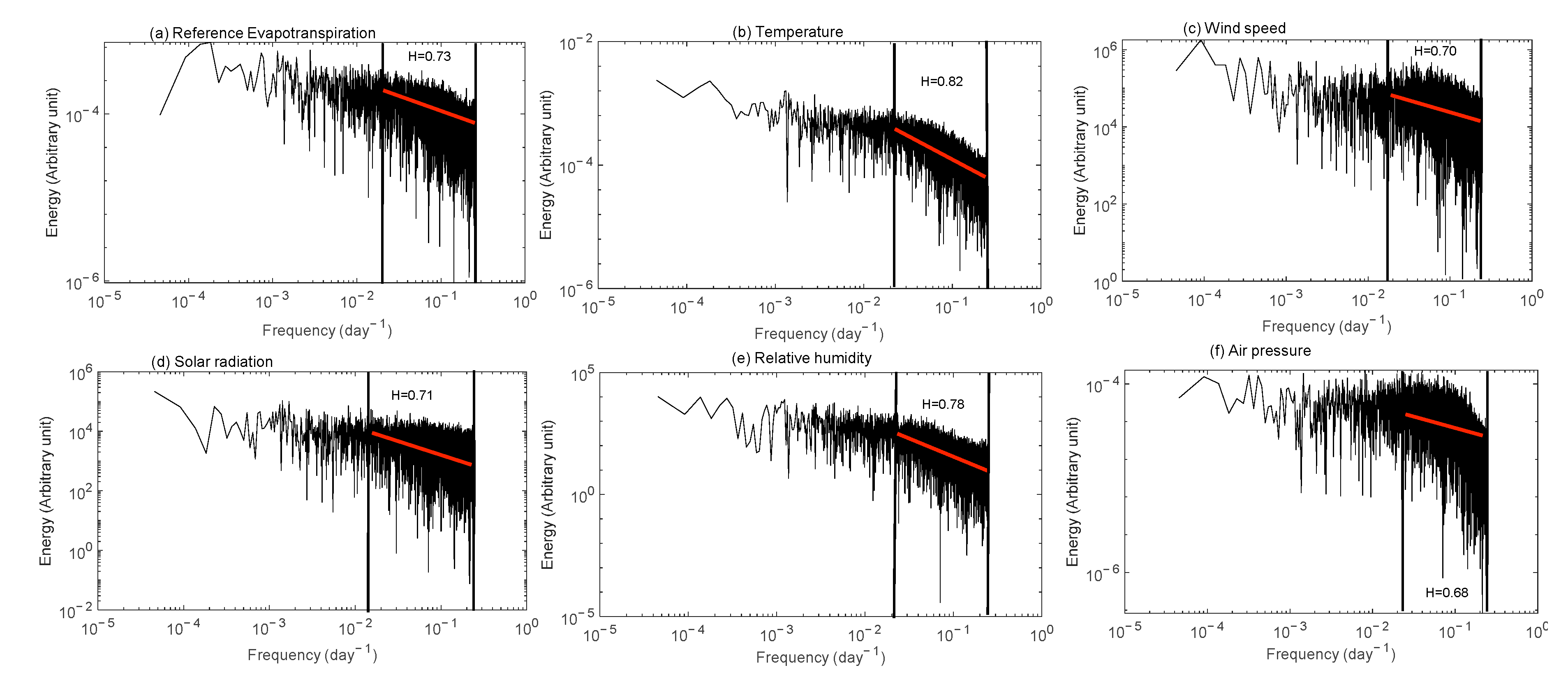
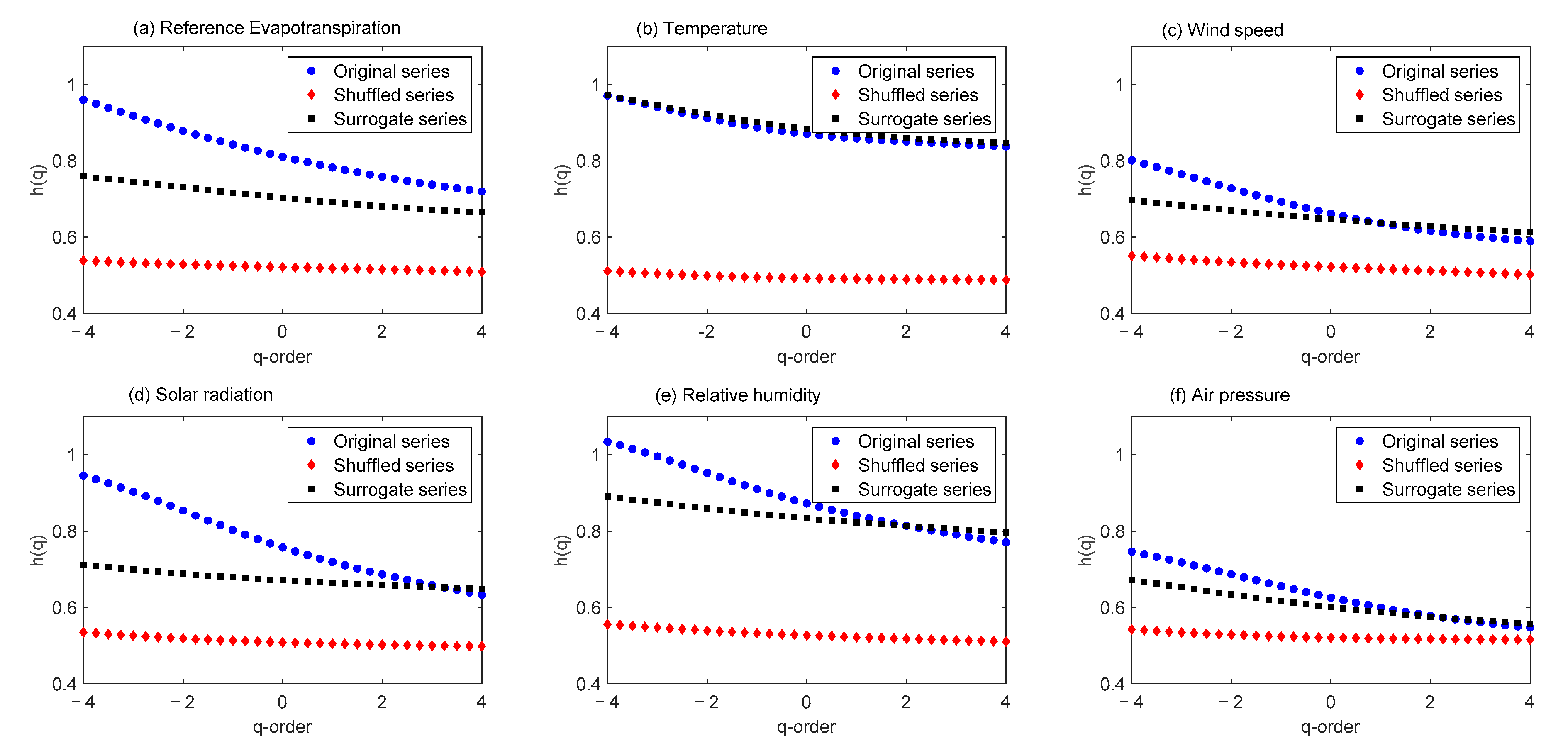
3.1. MFDFA of Agro-Meteorological Time Series
Origin of Multifractality
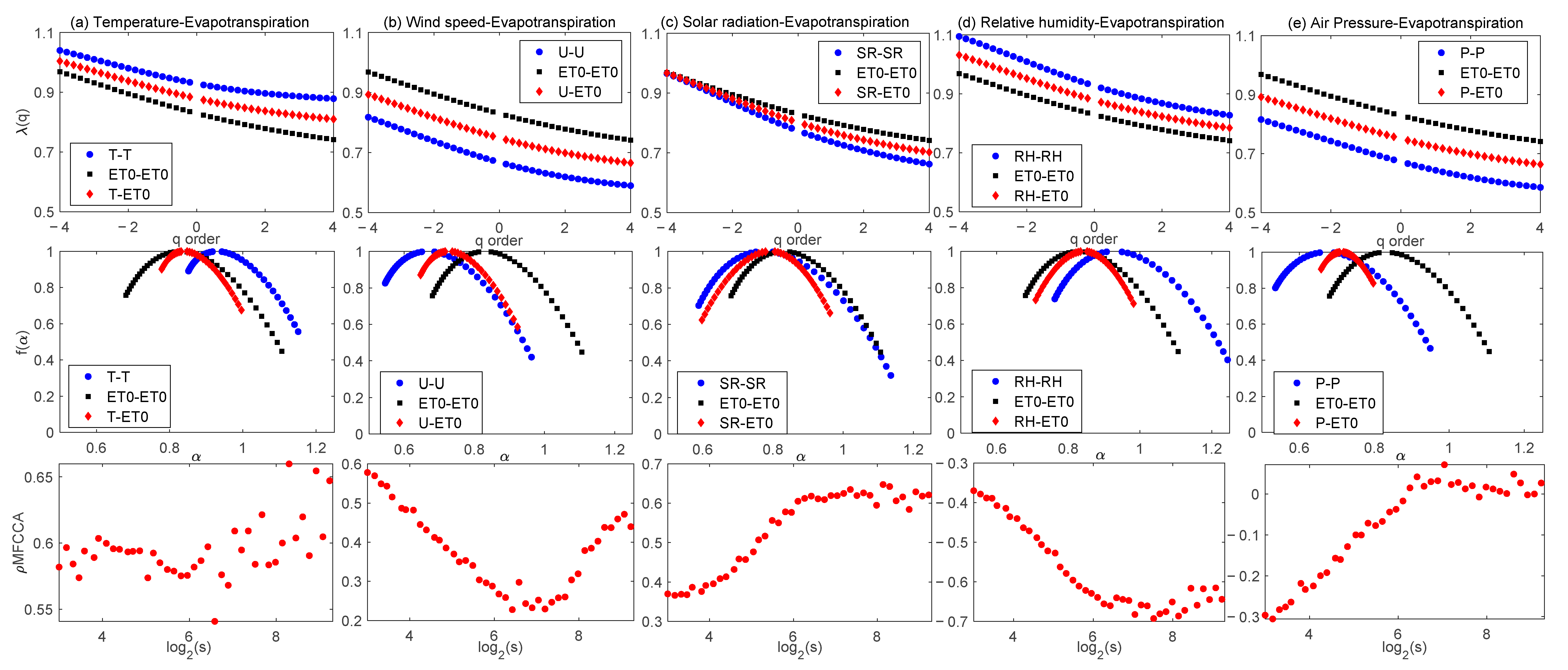
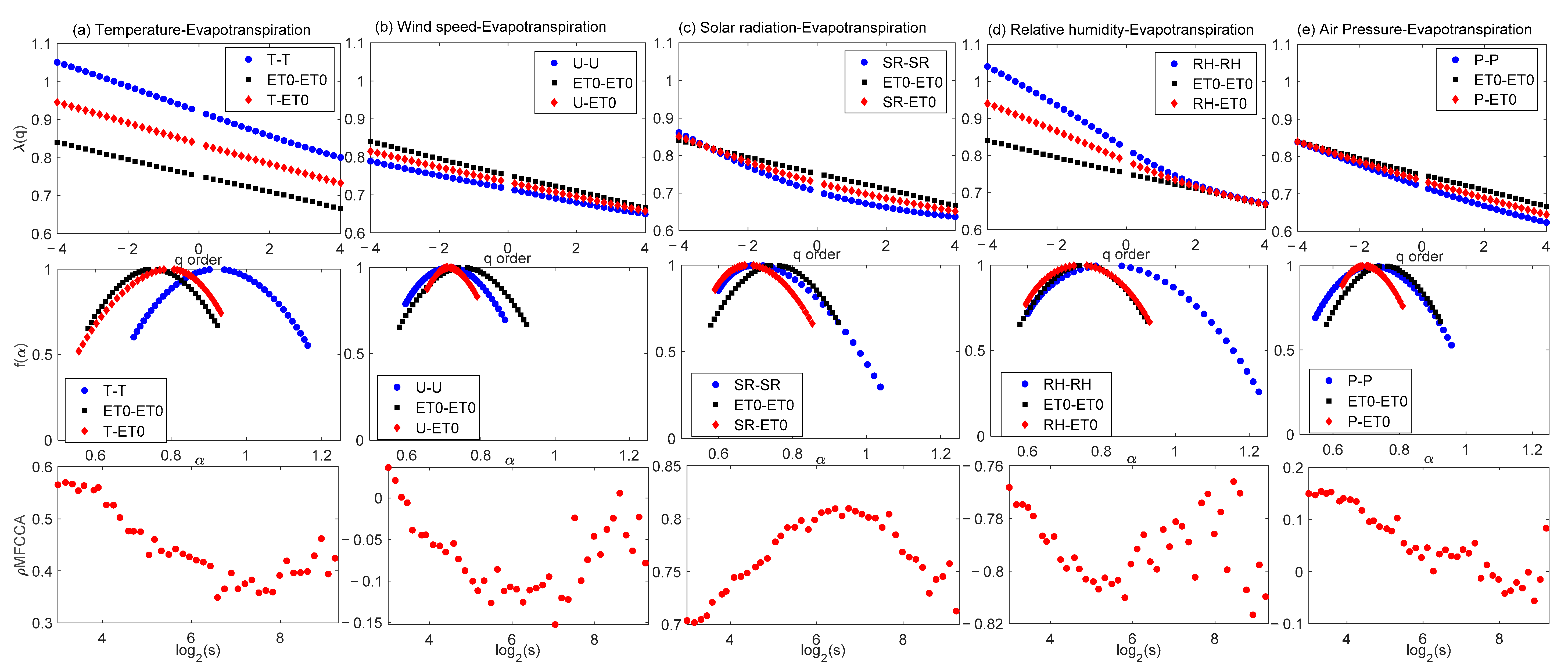
3.2. MFCCA of Meteorological Variables with ET0
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Hoffmann, H. Temporal scale influence on multifractal properties of agro-meteorological time series. Agric. For. Meteorol. 2017, 239, 223–235. [Google Scholar] [CrossRef]
- Verrier, S.; de Montera, L.; Barthès, L.; Mallet, C. Multifractal analysis of African monsoon rain fields, taking into account the zero rain-rate problem. J. Hydrol. 2010, 389, 111–120. [Google Scholar] [CrossRef]
- Shang, P.; Kame, S. Fractal nature of time series in the sediment transport phenomenon. Chaos Solitons Fractals 2005, 26, 997–1007. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; WH Freeman Publishers: New York, NY, USA, 1982. [Google Scholar]
- Kolmogorov, A.N. Local structure of turbulence in an incompressible liquid for very large Reynolds numbers. Proc. Acad. Sci. URSS. Geochem. Sect. 1941, 30, 299–303. [Google Scholar]
- Obukhov, A.M. Spectral Energy Distribution in a Turbulent Flow. Izv. Akad. Nauk. S.S.S.R. Ser. Geogr. Geophys. 1941, 5, 453–466. [Google Scholar]
- Obukhov, A.M. Structure of the temperature field in a turbulent flow. Izv. Akad. Nauk. S.S.S.R Ser. Geogr. Geofiz. 1949, 13, 58–69. [Google Scholar]
- Corrsin, S. On the Spectrum of Isotropic Temperature Fluctuations in an Isotropic Turbulence. J. Appl. Phys. 1951, 22, 469–473. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Obukhov, A.M. Some specific features of atmospheric turbulence. J. Fluid Mech. 1962, 13, 77–81. [Google Scholar] [CrossRef]
- Novikov, E.A.; Stewart, R. Intermittency of turbulence and spectrum of fluctuations in energy-disspation. Izv. Akad. Nauk. SSSR. Ser. Geofiz. 1964, 3, 408–412. [Google Scholar]
- Yaglom, A.M. The influence of the fluctuation in energy dissipation on the shape of turbulent characteristics in the inertial interval. Sov. Phys. Dokl. 1966, 2, 26–30. [Google Scholar]
- Mandelbrot, B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of the carrier. J. Fluid Mech. 1974, 62, 331–350. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence: The Legacy of A.N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Seuront, L.; Schmitt, F.; Sherzter, D.; Lagadeue, Y.; Lovejoy, S. Multifractal intermittency of Eulerian and Lagrangian turbulence of ocean temperature and plankton fields. Nonlinear Process. Geophys. 1996, 3, 236–246. [Google Scholar] [CrossRef]
- Schmitt, F.G.; Huang, Y.-X. Stochastic Analysis of Scaling Time Series; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Hurst, H.E. The long-term Storage capacity of Reservoir. Trans. Am. Soc. Civil Eng. 1951, 116, 770–779. [Google Scholar]
- Tessier, Y.; Lovejoy, S.; Hubert, P.; Schertzer, D.; Pecknold, S. Multifractal analysis and modeling of rainfall and river flows and scaling, causal transfer functions. J. Geophys. Res. 1996, 101, 26427–26440. [Google Scholar] [CrossRef]
- Schaefer, A.; Brach, J.S.; Perera, S.; Sejdić, E.A. Comparative analysis of spectral exponent estimation techniques for 1/fβ processes with applications to the analysis of stride interval time series. Neurosci. Methods 2014, 222, 118–130. [Google Scholar] [CrossRef]
- Szolgayova, E.; Laaha, G.; Blöschl, G.; Bucher, C. Factors influencing long range dependence in streamflow of European rivers. Hydrol. Process. 2014, 28, 1573–1586. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Physical modelling and analysis of rain and clouds by aniso–tropic scaling multiplicative processes. J. Geophys. Res. 1987, 92, 9693–9714. [Google Scholar] [CrossRef]
- Muzy, J.-F.; Bacry, E.; Arneodo, A. Multifractal formalism for fractal signals: The structure-function approach versus the wavelet-transform modulus-maxima method. Phys. Rev. E 1993, 47, 875–884. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of non-stationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Dahlstedt, K.; Jensen, H. Fluctuation spectrum and size scaling of river flow and level. Phys. A 2005, 348, 596–610. [Google Scholar] [CrossRef]
- Huang, Y.-X. Arbitrary Order Hilbert Spectral Analysis Definition and Application to Fully Developed Turbulence and Environmental Time-series. Ph.D. Thesis, University of Lille France, Lille, France, 2009. [Google Scholar]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rybski, D.; Braun, P.; Bunde, A.; Havlin, S. Long-term persistence and multifractality of precipitation and river runoff records. J. Geophys. Res. Atmos. 2006, 111, D1. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.-Y.; Yu, Z.; Liu, C.-L.; Chen, Y.-D. Multifractal analysis of streamflow records of the East river basin (Pearl river), China. Phys. A 2009, 388, 927–934. [Google Scholar] [CrossRef]
- Li, E.; Mu, X.; Zhao, G.; Gao, P. Multifractal detrended fluctuation analysis of streamflow in the Yellow River Basin, China. Water 2015, 7, 1670–1686. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.W. Multifractality of Canadian precipitation and streamflow. Int. J. Climatol. 2017, 37, 1221–1236. [Google Scholar] [CrossRef]
- Lin, G.; Chen, X.; Fu, Z. Temporal–spatial diversities of long-range correlation for relative humidity over China. Phys. A 2007, 383, 585–594. [Google Scholar] [CrossRef]
- Lin, G.; Fu, Z. A universal model to characterize different multi-fractal behaviors of daily temperature records over China. Phys. A 2008, 387, 573–579. [Google Scholar] [CrossRef]
- Yu, Z.G.; Leung, Y.; Chen, Y.D.; Zhang, Q.; Anh, V.; Zhou, Y. Multifractal analyses of daily rainfall time series in Pearl River basin of China. Phys. A 2014, 405, 193–202. [Google Scholar] [CrossRef]
- Burgueño, A.; Lana, X.; Serra, C.; Martínez, M.D. Daily extreme temperature multifractals in Catalonia (NE Spain). Phys. Lett. A 2014, 378, 874–885. [Google Scholar] [CrossRef]
- Ariza-Villaverde, A.B.; Pavón-Domínguez, P.; Carmona-Cabezas, R.; Gutierrez de Rave, E.; Jimenez-Honero, F.J. Joint multifractal analysis of air temperature, relative humidity and reference evapotranspiration in the middle zone of the Guadalquivir river valley. Agric. For. Meteorol. 2019, 278, 107657. [Google Scholar] [CrossRef]
- Baranowski, P.; Krzyszczak, J.; Slawinski, C.; Hoffmann, H.; Kozyra, J.; Nieróbca, A.; Siwek, K.; Gluza, A. Multifractal analysis of meteorological time-series to assess climate impacts. Clim. Res. 2015, 65, 39–52. [Google Scholar] [CrossRef]
- Kalamaras, N.; Philippopoulos, K.; Deligiorgi, D.; Tzanis, C.G.; Karvounis, G. Multifractal scaling properties of daily air temperature time series. Chaos Solitons Fractals 2017, 98, 38–43. [Google Scholar] [CrossRef]
- Madanchi, A.; Absalan, M.; Lohmann, G.; Anvari, M.; Tabar, M.R.R. Strong short-term non-linearity of solar irradiance fluctuations. Sol. Energy 2017, 144, 1–9. [Google Scholar] [CrossRef]
- Hou, W.; Feng, G.; Yan, P.; Li, S. Multifractal analysis of the drought area in seven large regions of China from 1961 to 2012. Meteorol. Atmos. Phys. 2018, 130, 459–471. [Google Scholar] [CrossRef]
- Adarsh, S.; Kumar, D.N.; Deepthi, B.; Gayathri, G.; Aswathy, S.S.; Bhagyasree, S. Multifractal characterization of meteorological drought in India using detrended fluctuation analysis. Int. J. Climatol. 2019, 39, 4234–4255. [Google Scholar] [CrossRef]
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Kazandjiev, V.; Georgieva, V.; Sławiński, C.; Siwek, K.; Kozyra, J.; Nieróbca, A. Multifractal characterization and comparison of meteorological time series from two climatic zones. Theor. Appl. Climatol. 2019, 137, 1811–1824. [Google Scholar] [CrossRef]
- Krzyszczak, J.; Baranowski, P.; Hoffmann, H.; Zubik, M.; Sławiński, C. Advances in time series Analysis and Forecasting. In Analysis of Climate Dynamics Across a European Transect Using a Multifractal Method; Rojas, I., Pomares, H., Valenzuela, O., Eds.; Springer International Publishing AG: Cham, Switzerland, 2017; pp. 1–14. [Google Scholar]
- Adarsh, S.; Nourani, V.; Archana, D.S.; Dharan, D.S. Multifractal description of rainfall fields over India. J. Hydrol. 2020, 586, 124913. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W.O. Crop water requirements. FAO Irrig. Drain. Pap. 1977, 24, 1–179. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration. Guidelines for computing crop water requirements. FAO Irrig. Drain. Pap. 1998, 56, D05109. [Google Scholar]
- Tabari, H.; Grismer, M.E.; Trajkovic, S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2013, 31, 107–117. [Google Scholar] [CrossRef]
- Kisi, O.; Çimen, M. Evapotranspiration modeling using support vector machines. Hydrol. Sci. J. 2009, 54, 918–928. [Google Scholar] [CrossRef]
- Cobaner, M. Reference evapotranspiration based on Class A pan evaporation via wavelet regression technique. Irrig. Sci. 2013, 31, 119–134. [Google Scholar] [CrossRef]
- Valipour, M.; Sefidkouhi, M.A.G.; Raeini-Sarjaz, M.; Guzman, S.M. A Hybrid Data-Driven Machine Learning Techniquefor Evapotranspiration Modeling in Various Climates. Atmosphere 2019, 10, 311. [Google Scholar] [CrossRef]
- Adarsh, S.; Sulaiman, S.; Murshida, K.K.; Nooramol, P. Scale-dependent prediction of reference evapotranspiration based on Multivariate Empirical Mode Decomposition. Ain Shams Eng. J. 2018, 9, 1839–1848. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abdullah, J. Multi-station artificial intelligence based ensemble modeling of reference evapotranspiration using pan evaporation measurements. J. Hydrol. 2019, 577, 123958. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in Atmospheric Sciences, 2nd ed.; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Bassingthwaighte, J.B.; Beyer, R.P. Fractal correlation in heterogeneous systems. Phys. D 1991, 53, 71–84. [Google Scholar] [CrossRef]
- Adarsh, S.; Reddy, M.J. Multi-Scale Spectral Analysis in Hydrology: From Theory to Practice; Taylor & Francis Ltd.: Abingdon, UK; CRC Press: Boca Raton, FL, USA, 2021; p. 400852. [Google Scholar]
- Piao, L.; Fu, Z. Quantifying distinct associations on different temporal scales: Comparison of DCCA and Pearson methods. Sci. Rep. 2016, 6, 36759. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended cross-correlation analysis: A new method for analyzing two non-stationary time series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef]
- Zhou, W.X. Multifractal detrended cross-correlation analysis for two non-stationary signals. Phys. Rev. E 2008, 77, 066211. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Zhou, W.X. Multifractal detrending moving-average cross-correlation analysis. Phys. Rev. E 2011, 84, 016106. [Google Scholar] [CrossRef] [PubMed]
- Oświȩcimka, P.; Drożdż, S.; Forczek, M.; Jadach, S.; Kwapień, J. Detrended cross-correlation analysis consistently extended to multifractality. Phys. Rev. E 2014, 89, 023305. [Google Scholar] [CrossRef] [PubMed]
- Wątorek, M.; Drożdż, S.; Oświęcimka, P.; Stanuszek, M. Multifractal cross-correlations between the world oil and other financial markets in 2012–2017. Energy Econ. 2019, 81, 874–885. [Google Scholar] [CrossRef]
- Drożdż, S.; Minati, L.; Oświȩcimka, P.; Stanuszek, M.; Wątorek, M. Signatures of the Crypto-Currency Market Decoupling from the Forex. Future Internet 2019, 11, 154. [Google Scholar] [CrossRef]
- Zhang, C.; Ni, Z.; Ni, L. Multifractal detrended cross-correlation analysis between PM2.5 and meteorological factors. Phys. A 2015, 438, 114–123. [Google Scholar] [CrossRef]
- Kar, A.; Chatterjee, S.; Ghosh, D. Multifractal detrended cross-correlation analysis of Land-surface temperature anomalies and Soil radon concentration. Phys. A 2019, 521, 236–247. [Google Scholar] [CrossRef]
- Tzanis, C.G.; Koutsogiannis, I.; Philippopoulos, K.; Kalamaras, N. Multifractal Detrended Cross-Correlation Analysis of Global Methane and Temperature. Remote Sens. 2020, 12, 557. [Google Scholar] [CrossRef]
- Zebende, G.F. DCCA cross-correlation coefficient: Quantifying level of cross-correlation. Phys. A 2011, 390, 614–618. [Google Scholar] [CrossRef]
- Vassoler, R.T.; Zebende, G.F. DCCA cross-correlation coefficient apply in time series of air temperature and air relative humidity. Phys. A 2012, 391, 2438–2443. [Google Scholar] [CrossRef]
- Wu, Y.; He, Y.; Wu, M.; Lu, C.; Gao, S.; Xu, Y. Multifractality and cross correlation analysis of streamflow and sediment fluctuation at the apex of the Pearl River Delta. Sci. Rep. 2018, 8, 16553. [Google Scholar] [CrossRef]
- Dey, P.; Mujumdar, P.P. Multiscale evolution of persistence of rainfall and streamflow. Adv. Water Resour. 2018, 121, 285–303. [Google Scholar] [CrossRef]
- Adarsh, S.; Dharan, D.S.; Nandhu, A.R.; Vishnu, B.A.; Mohan, V.K.; Watorek, M. Multifractal description of streamflow and suspended sediment concentration data from Indian river basins. Acta Geophys. 2020, 68, 519–535. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- López, J.L.; Contreras, J.G. Performance of multifractal detrended fluctuation analysis on short time series. Phys. Rev. E 2013, 87, 022918. [Google Scholar] [CrossRef] [PubMed]
- Baranowski, P.; Gos, M.; Krzyszczak, J.; Siwek, K.; Kieliszek, A.; Tkaczyk, P. Multifractality of meteorological time series for Poland on the base of MERRA-2 data. Chaos Solitons Fractals 2019, 127, 318–333. [Google Scholar] [CrossRef]
- Ihlen, E.A.F.E. Introduction to multifractal detrended fluctuation analysis in MATLAB. Front. Physiol. 2012, 3, 141. [Google Scholar] [CrossRef]
- Yuan, N.; Fu, Z.; Mao, J. Different scaling behaviors in daily temperature records over China. Phys. A 2010, 389, 4087–4095. [Google Scholar] [CrossRef]
- Köppen, W. VersucheinerKlassifikation der Klimate, vorzugsweise nach ihren Beziehungen zur Pflanzenwelt. Geogr. Z. 1900, 6, 657–679. [Google Scholar]
- Center for Exposure Assessment Modeling (CEAM), United States Environmental Protection Agency (EPA). Meteorological Data for California. Available online: https://www.epa.gov/ceam/meteorological-data-california (accessed on 18 October 2020).
- Feng, S.; Hu, Q.; Qian, W. Quality control of daily meteorological data in China, 1951–2000: A new dataset. Int. J. Climatol. 2004, 24, 853–870. [Google Scholar] [CrossRef]
- Estévez, J.; García-Marín, A.P.; Morábito, J.A.; Cavagnaro, M. Quality assurance procedures for validating meteorological inputvariables of reference evapotranspiration in Mendoza province (Argentina). Agric. Water Manag. 2016, 172, 96–109. [Google Scholar] [CrossRef]
- Herrera-Grimaldi, P.; Garcia-Marin, A.P.; Estevez, J. Multifractal analysis of diurnal temperature range over Southern Spain using validated datasets. Chaos 2019, 29, 063105. [Google Scholar] [CrossRef] [PubMed]
- Kisi, O. Daily pan evaporation modelling using a neuro-fuzzy computing technique. J. Hydrol. 2006, 329, 636–646. [Google Scholar] [CrossRef]
- Makowiec, D.; Fuliński, A. Multifractal Detrended Fluctuation Analysis as the Estimator of Long-range Dependence. Acta Phys. Polonica B 2010, 41, 1025. [Google Scholar]
- Movahed, M.S.; Jafari, G.R.; Ghasemi, F.; Rahvar, S.; Tabar, M.R.R. Multifractal detrended fluctuation analysis of sunspot time-series. J. Stat. Mech. Theory Exp. 2006, 2006, P02003. [Google Scholar] [CrossRef]
- Matia, K.; Ashkenazy, Y.; Stanley, H.E. Multifractal properties of price fluctuations of stocks and commodities. Europhys. Lett. 2003, 61, 422–428. [Google Scholar] [CrossRef]
- Keylock, C.J. A resampling method for generating synthetic hydrological time-series with preservation of cross correlative structure and higher-order properties. Water Resour. Res. 2012, 48, W12521. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef] [PubMed]
- Keylock, C.J. Hypothesis testing for nonlinear phenomena in the geosciences using synthetic, surrogate data. Earth Space Sci. 2019, 6, 41–58. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Huang, Y.-X.; Schmitt, F.G. Time dependent intrinsic correlation analysis of temperature and dissolved oxygen time series using empirical mode decomposition. J. Mar. Syst. 2014, 130, 90–100. [Google Scholar] [CrossRef]
- Hajian, S.; Movahed, M.S. Multifractal detrended cross-correlation analysis of sunspot numbers and river flow fluctuations. Phys. A 2010, 389, 4942–4954. [Google Scholar] [CrossRef]
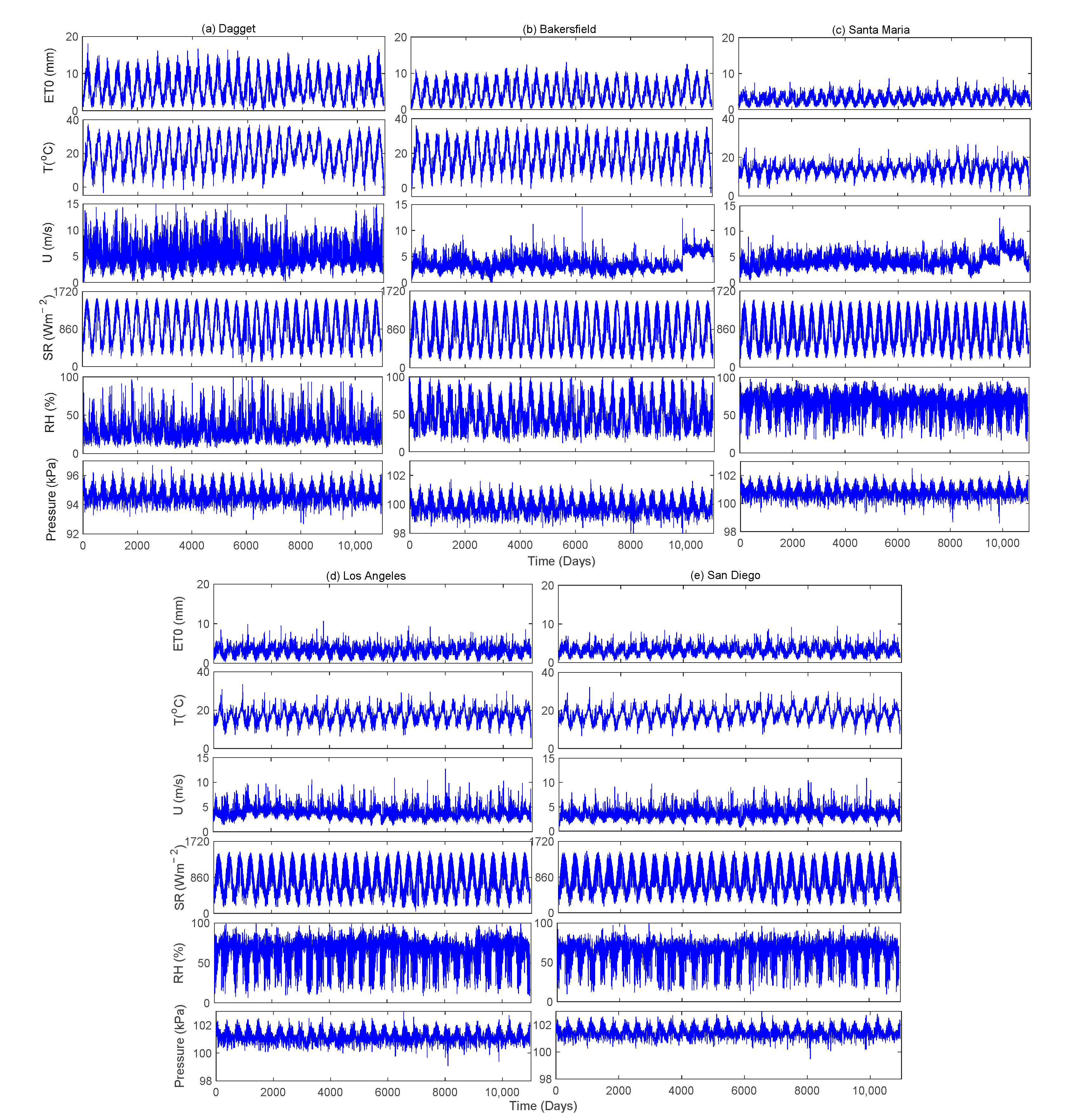

| Station | Variable | Maximum | Minimum | Mean | Standard Deviation |
|---|---|---|---|---|---|
| Dagget | ET0 (mm) | 18 | 0.2 | 6.42 | 3.37 |
| T (°C) | 37.2 | −5.3 | 19.72 | 8.47 | |
| U (m/s) | 15.973 | 0.174 | 5.04 | 2.22 | |
| SR (Wm−2) | 1576.2 | 102 | 993.9 | 359.5 | |
| RH (%) | 100 | 7 | 30.20 | 14.29 | |
| P (kPa) | 96.7 | 92.7 | 94.66 | 0.48 | |
| Bakersfield | ET0 (mm) | 13 | 0.2 | 4.68 | 2.78 |
| T (°C) | 37 | −2.8 | 18.58 | 8.04 | |
| U (m/s) | 14.564 | 0 | 3.49 | 1.32 | |
| SR (Wm−2) | 1521.3 | 129.6 | 895.3 | 400.7 | |
| RH (%) | 100 | 12 | 48.10 | 18.56 | |
| P (kPa) | 101.7 | 97.7 | 99.83 | 0.50 | |
| Santa Maria | ET0 (mm) | 10.6 | 0.3 | 3.21 | 1.22 |
| T (°C) | 33.3 | 5.7 | 16.72 | 3.36 | |
| U (m/s) | 12.719 | 1.257 | 3.77 | 1.00 | |
| SR (Wm−2) | 1492.7 | 49.6 | 850.7 | 327.4 | |
| RH (%) | 100 | 7 | 65.22 | 16.07 | |
| P (kPa) | 103 | 99.1 | 101.19 | 0.37 | |
| Los Angeles | ET0 (mm) | 9 | 0.5 | 3.03 | 1.21 |
| T (°C) | 26.7 | 0.5 | 13.35 | 2.80 | |
| U (m/s) | 12.53 | 0.453 | 4.07 | 1.31 | |
| SR (Wm−2) | 1527.7 | 157.2 | 889.6 | 346.7 | |
| RH (%) | 98 | 16 | 65.34 | 13.78 | |
| P (kPa) | 102.5 | 98.6 | 100.80 | 0.38 | |
| San Diego | ET0 (mm) | 9.4 | 0.5 | 3.31 | 1.18 |
| T (°C) | 32.2 | 6.7 | 17.55 | 3.43 | |
| U (m/s) | 10.897 | 0.697 | 3.55 | 0.99 | |
| SR (Wm−2) | 1488.5 | 156.8 | 864.5 | 314.1 | |
| RH (%) | 100 | 10 | 63.99 | 14.02 | |
| P (kPa) | 103.1 | 99.5 | 101.46 | 0.35 |
| Variable | Multifractal Properties | |||||
|---|---|---|---|---|---|---|
| H | W | AI | ∆f(α) | ∆h(q) | α0 | |
| Dagget | ||||||
| ET0 | 0.758 | 0.458 | 0.362 | 0.370 | 0.240 | 0.804 |
| T | 0.851 | 0.270 | 0.596 | 0.344 | 0.133 | 0.867 |
| U | 0.616 | 0.383 | 0.454 | 0.371 | 0.212 | 0.655 |
| SR | 0.687 | 0.551 | 0.260 | 0.232 | 0.313 | 0.747 |
| RH | 0.814 | 0.472 | 0.308 | 0.271 | 0.264 | 0.864 |
| P | 0.578 | 0.348 | 0.320 | 0.223 | 0.199 | 0.619 |
| Bakersfield | ||||||
| ET0 | 0.810 | 0.279 | 0.529 | 0.307 | 0.147 | 0.831 |
| T | 0.748 | 0.325 | 0.403 | 0.275 | 0.173 | 0.778 |
| U | 0.710 | 0.246 | 0.300 | 0.109 | 0.120 | 0.728 |
| SR | 0.701 | 0.523 | 0.377 | 0.385 | 0.293 | 0.755 |
| RH | 0.820 | 0.269 | 0.527 | 0.305 | 0.138 | 0.840 |
| P | 0.634 | 0.309 | 0.210 | 0.132 | 0.172 | 0.672 |
| Santa Maria | ||||||
| ET0 | 0.742 | 0.207 | 0.411 | 0.176 | 0.105 | 0.759 |
| T | 0.843 | 0.381 | 0.390 | 0.292 | 0.218 | 0.885 |
| U | 0.626 | 0.464 | 0.522 | 0.460 | 0.260 | 0.665 |
| SR | 0.652 | 0.421 | 0.405 | 0.350 | 0.224 | 0.690 |
| RH | 0.706 | 0.477 | 0.373 | 0.336 | 0.286 | 0.765 |
| P | 0.648 | 0.413 | 0.286 | 0.268 | 0.220 | 0.693 |
| Los Angeles | ||||||
| ET0 | 0.685 | 0.380 | 0.245 | 0.196 | 0.198 | 0.724 |
| T | 0.812 | 0.501 | 0.185 | 0.162 | 0.289 | 0.876 |
| U | 0.735 | 0.239 | 0.381 | 0.203 | 0.148 | 0.772 |
| SR | 0.644 | 0.417 | 0.528 | 0.471 | 0.229 | 0.682 |
| RH | 0.674 | 0.611 | 0.378 | 0.419 | 0.389 | 0.760 |
| P | 0.636 | 0.337 | 0.209 | 0.138 | 0.182 | 0.673 |
| San Diego | ||||||
| ET0 | 0.678 | 0.336 | 0.128 | 0.070 | 0.172 | 0.712 |
| T | 0.826 | 0.426 | 0.121 | 0.078 | 0.247 | 0.883 |
| U | 0.685 | 0.205 | 0.111 | 0.047 | 0.109 | 0.709 |
| SR | 0.616 | 0.441 | 0.510 | 0.498 | 0.235 | 0.655 |
| RH | 0.684 | 0.497 | 0.247 | 0.212 | 0.321 | 0.763 |
| P | 0.642 | 0.338 | 0.213 | 0.145 | 0.179 | 0.678 |
| Link | MFCCA Parameters | Pearson Correlation Coefficient | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scaling Exponent | Spectral Width | Asymmetry Index | Cross Correlation Coefficient | |||||||||
| λXX | λYY | λXY | WXX | WYY | WXY | AIXX | AIYY | AIXY | ρXY(90) | ρXY(365) | ρ | |
| Dagget | ||||||||||||
| T-ET0 | 0.896 | 0.778 | 0.837 | 0.300 | 0.426 | 0.218 | −0.522 | −0.325 | −0.473 | 0.575 | 0.610 | 0.560 |
| U-ET0 | 0.619 | 0.778 | 0.699 | 0.417 | 0.426 | 0.276 | −0.452 | −0.325 | −0.454 | 0.256 | 0.416 | 0.465 |
| SR-ET0 | 0.708 | 0.778 | 0.743 | 0.548 | 0.426 | 0.365 | −0.348 | −0.325 | 0.071 | 0.615 | 0.610 | 0.447 |
| RH-ET0 | 0.868 | 0.778 | 0.823 | 0.482 | 0.426 | 0.273 | −0.341 | −0.325 | −0.018 | −0.652 | −0.633 | −0.508 |
| P-ET0 | 0.619 | 0.778 | 0.699 | 0.413 | 0.426 | 0.139 | −0.369 | −0.325 | −0.237 | 0.033 | 0.019 | −0.169 |
| Bakersfield | ||||||||||||
| T-ET0 | 0.824 | 0.804 | 0.814 | 0.374 | 0.440 | 0.276 | −0.379 | −0.468 | −0.138 | 0.707 | 0.585 | 0.617 |
| U-ET0 | 0.690 | 0.805 | 0.748 | 0.369 | 0.515 | 0.351 | −0.786 | −0.468 | 0.068 | 0.136 | 0.310 | 0.402 |
| SR-ET0 | 0.719 | 0.804 | 0.762 | 0.491 | 0.440 | 0.317 | −0.396 | −0.468 | −0.019 | 0.668 | 0.684 | 0.571 |
| RH-ET0 | 0.855 | 0.804 | 0.830 | 0.309 | 0.440 | 0.210 | −0.445 | −0.468 | −0.287 | −0.784 | −0.706 | −0.700 |
| P-ET0 | 0.675 | 0.804 | 0.739 | 0.345 | 0.440 | 0.075 | −0.220 | −0.468 | −0.745 | −0.145 | −0.113 | −0.118 |
| Santa Maria | ||||||||||||
| T-ET0 | 0.881 | 0.748 | 0.815 | 0.351 | 0.281 | 0.249 | −0.392 | −0.463 | −0.193 | 0.462 | 0.452 | 0.505 |
| U-ET0 | 0.630 | 0.715 | 0.672 | 0.483 | 0.375 | 0.288 | −0.450 | −0.220 | −0.325 | 0.084 | 0.163 | 0.159 |
| SR-ET0 | 0.672 | 0.748 | 0.710 | 0.469 | 0.281 | 0.272 | −0.432 | −0.463 | −0.354 | 0.742 | 0.627 | 0.679 |
| RH-ET0 | 0.739 | 0.748 | 0.743 | 0.503 | 0.281 | 0.282 | −0.381 | −0.463 | −0.432 | −0.811 | −0.822 | −0.791 |
| P-ET0 | 0.679 | 0.748 | 0.713 | 0.405 | 0.281 | 0.154 | −0.180 | −0.463 | −0.315 | 0.087 | 0.088 | 0.081 |
| Los Angeles | ||||||||||||
| T-ET0 | 0.853 | 0.708 | 0.781 | 0.514 | 0.425 | 0.400 | −0.116 | −0.177 | 0.102 | 0.428 | 0.454 | 0.522 |
| U-ET0 | 0.708 | 0.708 | 0.708 | 0.326 | 0.425 | 0.193 | −0.158 | −0.177 | −0.219 | 0.057 | −0.011 | 0.172 |
| SR-ET0 | 0.676 | 0.708 | 0.692 | 0.400 | 0.425 | 0.266 | −0.566 | −0.177 | −0.328 | 0.764 | 0.716 | 0.681 |
| RH-ET0 | 0.712 | 0.708 | 0.710 | 0.604 | 0.425 | 0.456 | −0.286 | −0.177 | −0.358 | −0.863 | −0.853 | −0.848 |
| P-ET0 | 0.659 | 0.708 | 0.684 | 0.407 | 0.425 | 0.255 | −0.176 | −0.177 | −0.233 | 0.031 | −0.003 | 0.060 |
| San Diego | ||||||||||||
| T-ET0 | 0.857 | 0.711 | 0.784 | 0.462 | 0.344 | 0.377 | −0.049 | 0.003 | 0.289 | 0.385 | 0.397 | 0.460 |
| U-ET0 | 0.681 | 0.711 | 0.696 | 0.268 | 0.344 | 0.135 | −0.121 | 0.003 | −0.147 | −0.110 | −0.013 | −0.009 |
| SR-ET0 | 0.662 | 0.711 | 0.686 | 0.437 | 0.344 | 0.263 | −0.564 | 0.003 | −0.326 | 0.807 | 0.745 | 0.738 |
| RH-ET0 | 0.722 | 0.711 | 0.717 | 0.626 | 0.344 | 0.335 | −0.337 | 0.003 | −0.132 | −0.798 | −0.768 | −0.768 |
| P-ET0 | 0.668 | 0.711 | 0.689 | 0.410 | 0.344 | 0.181 | −0.168 | 0.003 | −0.285 | 0.037 | −0.025 | 0.103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sankaran, A.; Krzyszczak, J.; Baranowski, P.; Devarajan Sindhu, A.; Kumar, N.P.; Lija Jayaprakash, N.; Thankamani, V.; Ali, M. Multifractal Cross Correlation Analysis of Agro-Meteorological Datasets (Including Reference Evapotranspiration) of California, United States. Atmosphere 2020, 11, 1116. https://doi.org/10.3390/atmos11101116
Sankaran A, Krzyszczak J, Baranowski P, Devarajan Sindhu A, Kumar NP, Lija Jayaprakash N, Thankamani V, Ali M. Multifractal Cross Correlation Analysis of Agro-Meteorological Datasets (Including Reference Evapotranspiration) of California, United States. Atmosphere. 2020; 11(10):1116. https://doi.org/10.3390/atmos11101116
Chicago/Turabian StyleSankaran, Adarsh, Jaromir Krzyszczak, Piotr Baranowski, Archana Devarajan Sindhu, Nandhineekrishna Pradeep Kumar, Nityanjali Lija Jayaprakash, Vandana Thankamani, and Mumtaz Ali. 2020. "Multifractal Cross Correlation Analysis of Agro-Meteorological Datasets (Including Reference Evapotranspiration) of California, United States" Atmosphere 11, no. 10: 1116. https://doi.org/10.3390/atmos11101116
APA StyleSankaran, A., Krzyszczak, J., Baranowski, P., Devarajan Sindhu, A., Kumar, N. P., Lija Jayaprakash, N., Thankamani, V., & Ali, M. (2020). Multifractal Cross Correlation Analysis of Agro-Meteorological Datasets (Including Reference Evapotranspiration) of California, United States. Atmosphere, 11(10), 1116. https://doi.org/10.3390/atmos11101116







