Using a Statistical Crop Model to Predict Maize Yield by the End-Of-Century for the Azuero Region in Panama
Abstract
1. Introduction
2. Materials and Methods
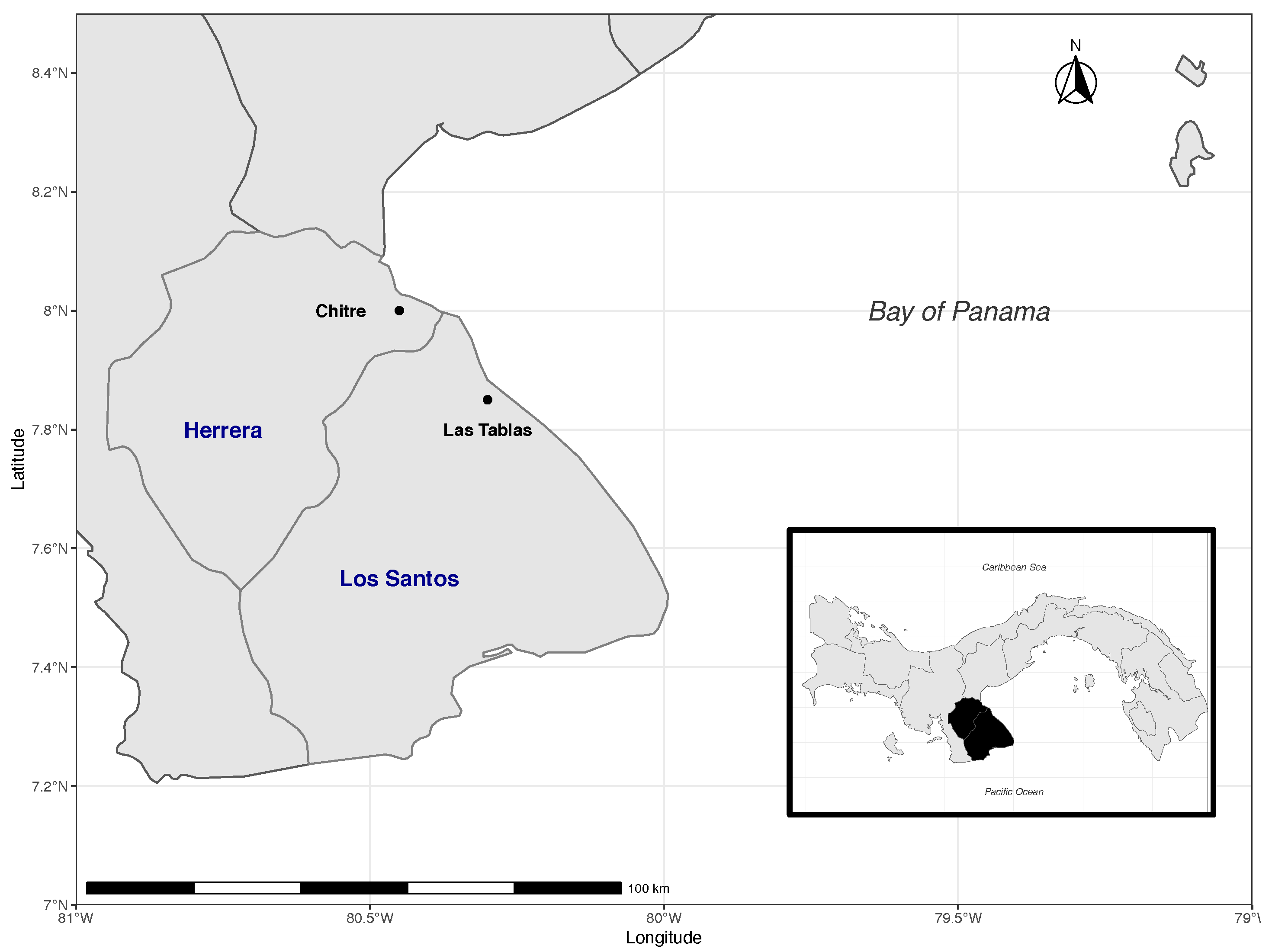
2.1. Location of the Study
2.2. Meteorological Data Source
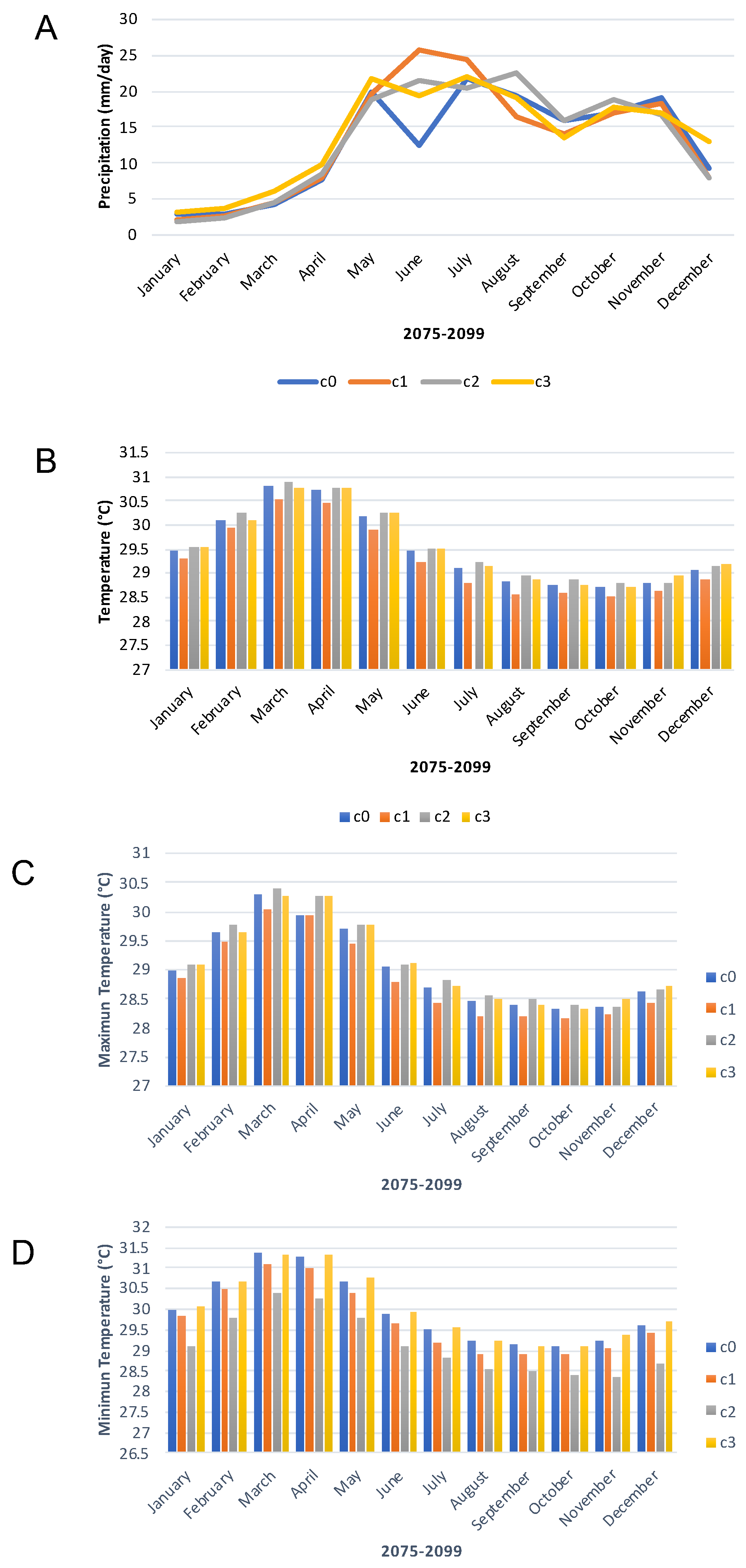
2.3. Projected Metereological Data
2.4. Historical Maize Production in Panama and Azuero
Maize Yield Model
- The first stage goes from germination to V9 (0 to 30 days after planting – DAP); in this stage, the hydric deficiency affects very little the grain yield and there are no losses in the yield if hydric deficiencies appear.
- The second stage begins in V10 until VT (31 to 50 DAP), in this period several components of the yield are defined, such as the number of rows and the number of grain per row of the ears. A deficiency in this stage can cause up to a 25% reduction in performance potential.
- The fourth and last stage comprises from R4 to R6, and in this stage there may be a 25% reduction in the presence of water deficiencies in the development of the crop.
2.5. Determining the Impact of Future Climate in Maize Yield at the End-of-century
2.6. Bias Correction for Projections
3. Results and Discussion
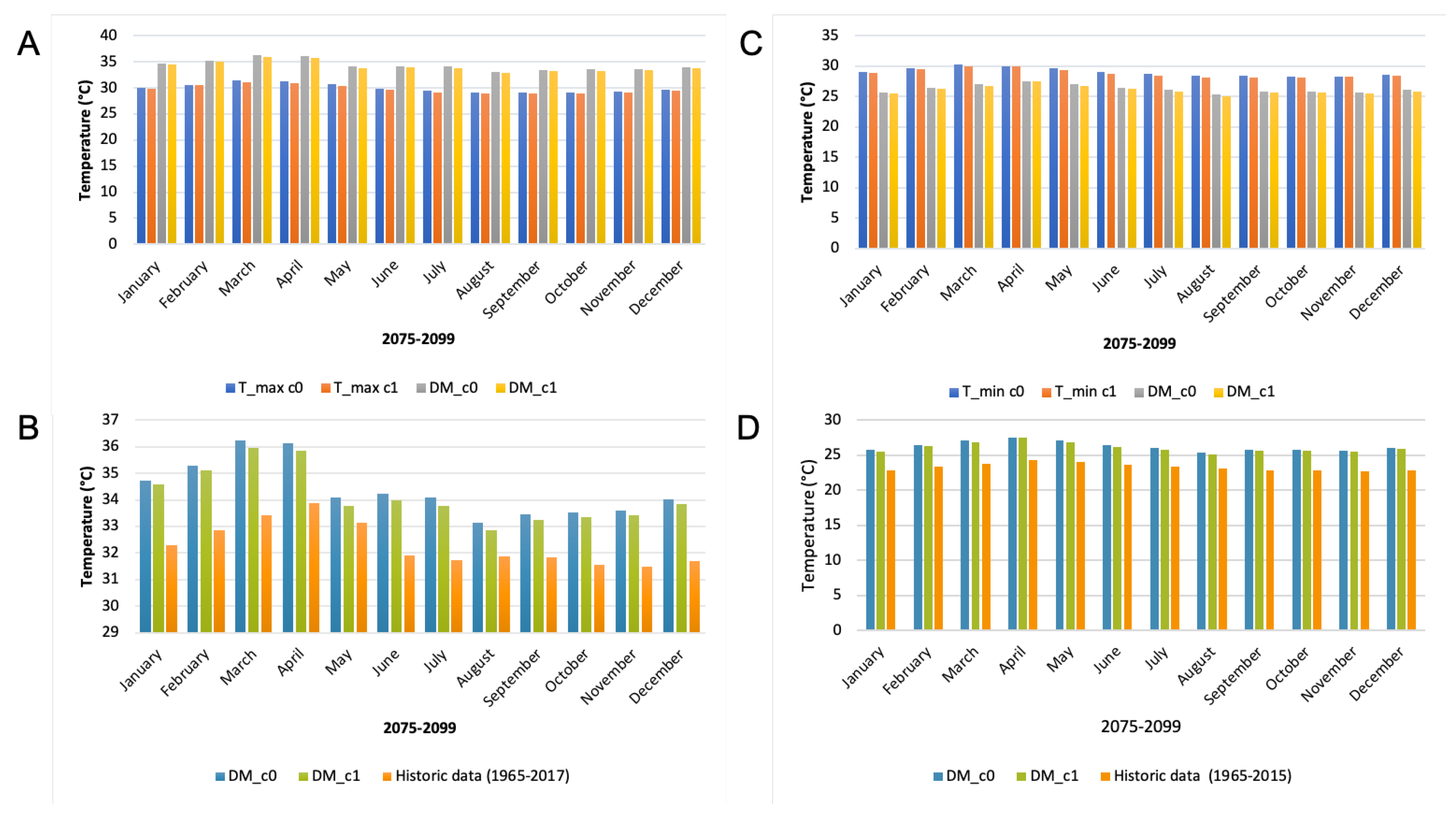
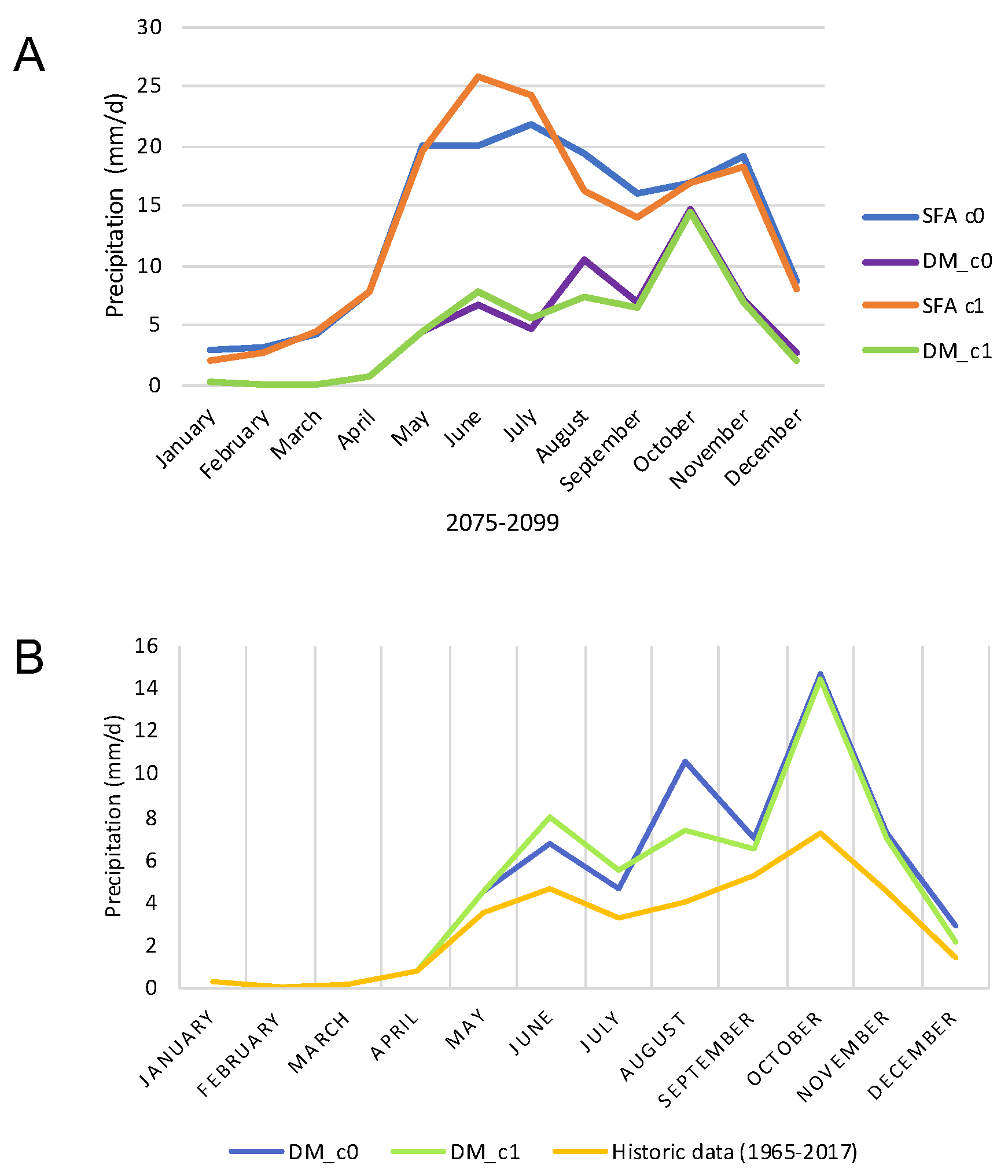
3.1. Assessment of the Projected Data
3.2. Crop Yield
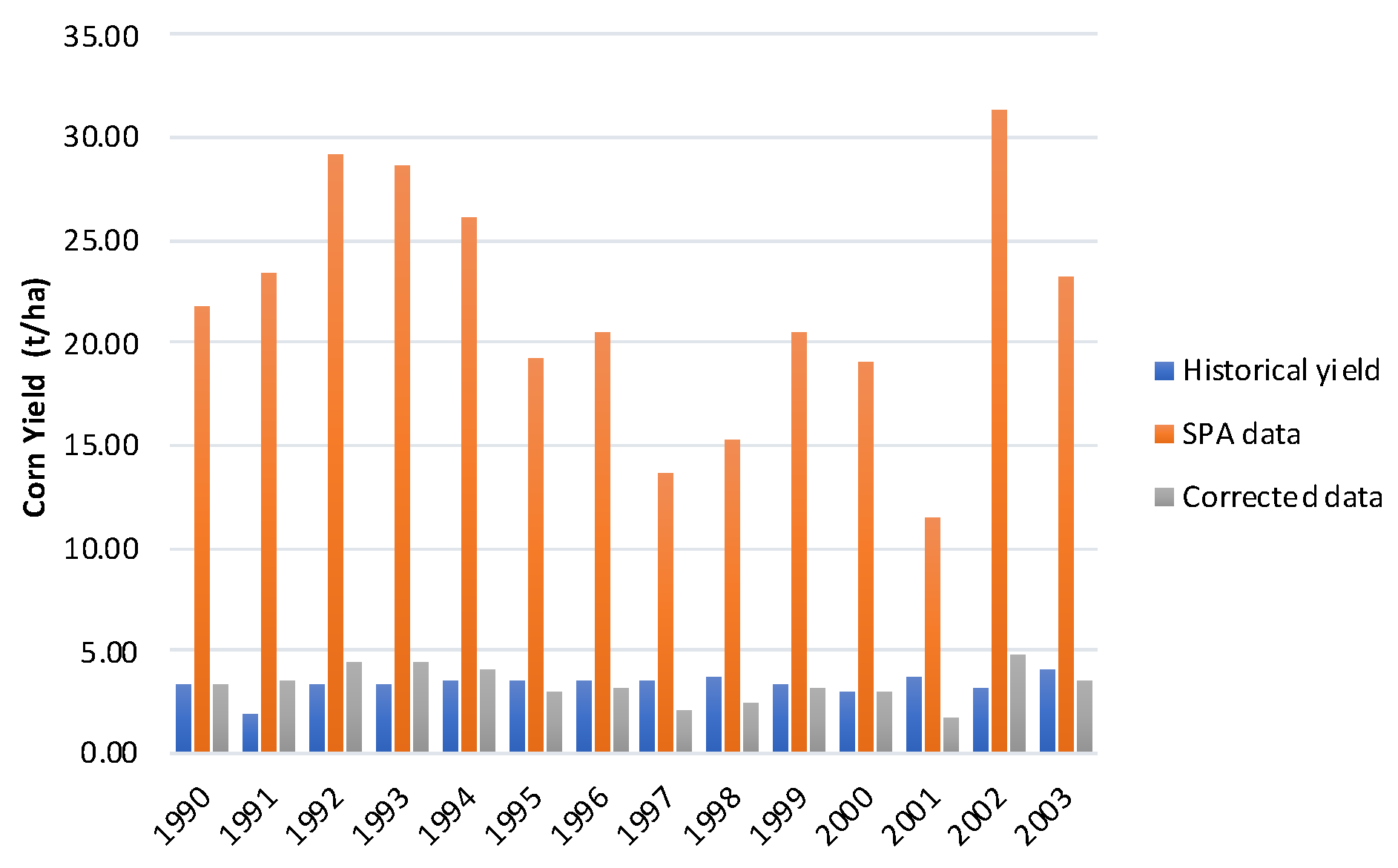
3.3. Bias Correction of Projected Estimates
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Regression Model Validation
| Variable | DF | Parameter Estimate | Standard Error | t-Value | p >|t| |
|---|---|---|---|---|---|
| PRE3 | 1 | 0.0282 | 0.01 | 2.9 | 0.03 |
| PRE4 | 1 | 0.0446 | 0.01 | 3.08 | 0.03 |
| TEMP3 | 1 | −2.0786 | 0.96 | −2.16 | 0.08 |
| TEMP4 | 1 | 2.1093 | 0.95 | 2.21 | 0.08 |
| Year | Planting Date | Observed Yield | Predicted Yield | Residual |
|---|---|---|---|---|
| 21 August | 9.42 | 6.69 | 2.73 | |
| 23 September | 6.69 | 3.26 | 3.42 | |
| 2018 | 10 October | 1.31 | 0.93 | 0.38 |
| 21 August | 7.95 | 5.20 | 2.75 | |
| 23 September | 6.15 | 3.67 | 2.48 | |
| 2019 | 10 October | 1.49 | 4.39 | −2.90 |
| Average | 1.47 |
References
- Adams, R.M.; Hurd, B.H.; Lenhart, S.; Leary, N. Effects of global climate change on agriculture: An interpretative review. Clim. Res. 1998, 11, 19–30. [Google Scholar] [CrossRef]
- Nelson, G.C.; Valin, H.; Sands, R.D.; Havlík, P.; Ahammad, H.; Deryng, D.; Elliott, J.; Fujimori, S.; Hasegawa, T.; Heyhoe, E.; et al. Climate change effects on agriculture: Economic responses to biophysical shocks. Proc. Natl. Acad. Sci. USA 2014, 111, 3274–3279. [Google Scholar] [CrossRef] [PubMed]
- Morton, J.F. The impact of climate change on smallholder and subsistence agriculture. Proc. Natl. Acad. Sci. USA 2007, 104, 19680–19685. [Google Scholar] [CrossRef] [PubMed]
- Lobell, D.B.; Field, C.B. Global scale climate–crop yield relationships and the impacts of recent warming. Environ. Res. Lett. 2007, 2, 014002. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Elliott, J.; Deryng, D.; Ruane, A.C.; Müller, C.; Arneth, A.; Boote, K.J.; Folberth, C.; Glotter, M.; Khabarov, N.; et al. Assessing agricultural risks of climate change in the 21st century in a global gridded crop model intercomparison. Proc. Natl. Acad. Sci. USA 2014, 111, 3268–3273. [Google Scholar] [CrossRef]
- Gregory, P.J.; Ingram, J.S.; Brklacich, M. Climate change and food security. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 2139–2148. [Google Scholar] [CrossRef]
- Pipitpukdee, S.; Attavanich, W.; Bejranonda, S. Climate Change Impacts on Sugarcane Production in Thailand. Atmosphere 2020, 11, 408. [Google Scholar] [CrossRef]
- Mall, R.; Gupta, A.; Sonkar, G. Effect of climate change on agricultural crops. In Current Developments in Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2017; pp. 23–46. [Google Scholar]
- Jones, P.G.; Thornton, P.K. The potential impacts of climate change on maize production in Africa and Latin America in 2055. Glob. Environ. Chang. 2003, 13, 51–59. [Google Scholar] [CrossRef]
- Ruane, A.C.; Cecil, L.D.; Horton, R.M.; Gordón, R.; McCollum, R.; Brown, D.; Killough, B.; Goldberg, R.; Greeley, A.P.; Rosenzweig, C. Climate change impact uncertainties for maize in Panama: Farm information, climate projections, and yield sensitivities. Agric. For. Meteorol. 2013, 170, 132–145. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asseng, S. Comparing estimates of climate change impacts from process-based and statistical crop models. Environ. Res. Lett. 2017, 12, 015001. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Roberts, M.J.; Braun, N.O.; Sinclair, T.R.; Lobell, D.B.; Schlenker, W. Comparing and combining process-based crop models and statistical models with some implications for climate change. Environ. Res. Lett. 2017, 12, 095010. [Google Scholar] [CrossRef]
- Kogo, B.K.; Kumar, L.; Koech, R.; Langat, P. Modelling Impacts of Climate Change on Maize (Zea mays L.) Growth and Productivity: A Review of Models, Outputs and Limitations. J. Geosci. Environ. Prot. 2019, 7, 76. [Google Scholar]
- Holzkämper, A.; Calanca, P.; Fuhrer, J. Statistical crop models: Predicting the effects of temperature and precipitation changes. Clim. Res. 2012, 51, 11–21. [Google Scholar] [CrossRef]
- Holzkämper, A.; Calanca, P.; Honti, M.; Fuhrer, J. Projecting climate change impacts on grain maize based on three different crop model approaches. Agric. For. Meteorol. 2015, 214, 219–230. [Google Scholar] [CrossRef]
- Auffhammer, M.; Schlenker, W. Empirical studies on agricultural impacts and adaptation. Energy Econ. 2014, 46, 555–561. [Google Scholar] [CrossRef]
- Nakayama, K.; Beitia, C.; Vallester, E.; Pinzon, R.; Fábrega, J.; Nakaegawa, T.; Maruya, Y.; Espinosa, J.; Olmedo, B.; Kato, J. Increase in simple precipitation intensity index in Panama. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraulic Eng.) 2012, 68, I_163–I_168. [Google Scholar] [CrossRef]
- Beitia, C. Aplicación del Modelo del Clima Global MRI-AGCM en la Proyección de Precipitación en la República de Panamá. Bachelor’s Thesis, Faculty of Civil Engineering, Universidad Tecnologica Panamá, Panama City, Panama, 2012. [Google Scholar]
- Fábrega, J.; Nakaegawa, T.; Pinzón, R.; Nakayama, K.; Arakawa, O. Hydroclimate projections for Panama in the late 21st Century. Hydrol. Res. Lett. 2013, 7, 23–29. [Google Scholar]
- Kusunoki, S.; Nakaegawa, T.; Pinzón, R.; Sanchez-Galan, J.E.; Fábrega, J.R. Future precipitation changes over Panama projected with the atmospheric global model MRI-AGCM3. 2. Clim. Dyn. 2019, 53, 5019–5034. [Google Scholar] [CrossRef]
- Espinosa, D.; Mendez, A.; Madrid, I.; Rivera, R. Assessment of climate change impacts on the water resources of Panama: The case of the La Villa, Chiriqui and Chagres River Basins. Clim. Res. 1997, 9, 131–137. [Google Scholar] [CrossRef]
- Hobeika, M.; Wagner, A.C. The Impacts of Climate Change on Agriculture in Tierras Altas, Panama and Recommendations for Adaptation: Perspectives of Local Farmers; Panama Field Study Semester; McGill University: Montreal, QC, Canada, April 2018. [Google Scholar]
- García, K.; Del Castillo, L.; Saavedra, C. Analysis of climate anomalies for La Villa river basin, Panama, based on RCP scenarios. I+ D Tecnológico 2020, 16, 84–90. [Google Scholar]
- Gordón, R. Los Granos Básicos y la Variabilidad Climática en Azuero: Caso Maíz; Primer Congreso Científico Universidad de Panamá, Centro Regional Universitario de Los Santos: Las Tablas, Panama, 2014. [Google Scholar] [CrossRef]
- Empresa de Transmision Electrica S.A., (ETESA). Datos Climaticos Historicos. 2019. Available online: http://www.hidromet.com.pa/clima_historicos.php (accessed on 2 February 2019).
- Gordón-Mendoza, R. Variabilidad Climática y su Efecto en la Producción del Maíz; Instituto de Investigación Agropecuaria de Panamá: Calle Carlos Lara, Panama, 2020; 48p. [Google Scholar]
- Mizuta, R.; Yoshimura, H.; Murakami, H.; Matsueda, M.; Endo, H.; Ose, T.; Kamiguchi, K.; Hosaka, M.; Sugi, M.; Yukimoto, S.; et al. Climate simulations using MRI-AGCM3. 2 with 20-km grid. J. Meteorol. Soc. Japan. Ser. II 2012, 90, 233–258. [Google Scholar] [CrossRef]
- Mizuta, R.; Oouchi, K.; Yoshimura, H.; Noda, A.; Katayama, K.; Yukimoto, S.; Hosaka, M.; Kusunoki, S.; Kawai, H.; Nakagawa, M. 20-km-mesh global climate simulations using JMA-GSM model—Mean climate states. J. Meteorol. Soc. Japan. Ser. II 2006, 84, 165–185. [Google Scholar] [CrossRef]
- Kitoh, A.; Kusunoki, S.; Nakaegawa, T. Climate change projections over South America in the late 21st century with the 20 and 60 km mesh Meteorological Research Institute atmospheric general circulation model (MRI-AGCM). J. Geophys. Res. Atmos. 2011, 116, 21. [Google Scholar] [CrossRef]
- Nakaegawa, T.; Kitoh, A.; Kusunoki, S.; Murakami, H.; Arakawa, O. Hydroclimate change over Central America and the Caribbean in a global warming climate projected with 20-km and 60-km mesh MRI atmospheric general circulation models. Pap. Meteorol. Geophys 2014, 65, 15. [Google Scholar] [CrossRef][Green Version]
- Change, I.C. Synthesis Report. Contribution of working groups I. II III Fifth Assess. Rep. Intergov. Panel Clim. Chang. 2014, 151. [Google Scholar]
- Murakami, H.; Mizuta, R.; Shindo, E. Future changes in tropical cyclone activity projected by multi-physics and multi-SST ensemble experiments using the 60-km-mesh MRI-AGCM. Clim. Dyn. 2012, 39, 2569–2584. [Google Scholar] [CrossRef]
- Murakami, H.; Sugi, M.; Kitoh, A. Future changes in tropical cyclone activity in the North Indian Ocean projected by high-resolution MRI-AGCMs. Clim. Dyn. 2013, 40, 1949–1968. [Google Scholar] [CrossRef]
- Ministerio de Desarrollo Agropecuario. Cierre Agrícola 2018–2019. 2020. Available online: https://www.mida.gob.pa/upload/documentos/cierre___2018-2019_ok.pdf (accessed on 15 August 2020).
- Ministerio de Desarrollo Agropecuario. Serie Histórica de los Rubros Agrícolas 1992–2019. 2019. Available online: https://www.mida.gob.pa/direcciones/direcciones_nacionales/direcci-n-de-agricultura/serie-hist-rica-de-los-rubros-agr-colas-1992-2019.html (accessed on 3 February 2019).
- Sáez-Cigarruista, A.E.; Gordón-Mendoza, R.; Núñez-Cano, J.I.; Jaén-Villarreal, J.E.; Franco-Barrera, J.E.; Ramos-Manzané, F.; Ávila-Guevara, A. Coeficientes genéticos de dos cultivares de maíz, Azuero-Panamá. Cienc. Agropecu. 2018, 29, 80–99. [Google Scholar]
- Denmead, O.; Shaw, R.H. The Effects of Soil Moisture Stress at Different Stages of Growth on the Development and Yield of Corn 1. Agron. J. 1960, 52, 272–274. [Google Scholar] [CrossRef]
- McWilliams, D.A.; Berglund, D.R.; Endres, G. Corn growth and management quick guide. In North Dakota Cooperative Extension Service; North Dakota State University: Fargo, ND, USA, 1999; pp. 1–8. [Google Scholar]
- Sah, R.; Chakraborty, M.; Prasad, K.; Pandit, M.; Tudu, V.; Chakravarty, M.; Narayan, S.; Rana, M.; Moharana, D. Impact of water deficit stress in maize: Phenology and yield components. Sci. Rep. 2020, 10, 2944. [Google Scholar] [CrossRef] [PubMed]
- Kranz, W.L.; Irmak, S.; Van Donk, S.J.; Yonts, C.D.; Martin, D.L. Irrigation management for corn. Neb Guid. Univ. Nebraska Linc. 2008, 10, 1–8. [Google Scholar]
- Araya, A.; Kisekka, I.; Lin, X.; Prasad, P.V.; Gowda, P.; Rice, C.; Andales, A. Evaluating the impact of future climate change on irrigated maize production in Kansas. Clim. Risk Manag. 2017, 17, 139–154. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W. Equiratio cumulative distribution function matching as an improvement to the equidistant approach in bias correction of precipitation. Atmos. Sci. Lett. 2014, 15, 1–6. [Google Scholar] [CrossRef]
- Piani, C.; Weedon, G.; Best, M.; Gomes, S.; Viterbo, P.; Hagemann, S.; Haerter, J. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Madrigal, J.; Flores Fernandez, G.; Solera, A.; Abreu, J. Corrección del sesgo en los estadísticos de las series de precipitación de cambio climático, en la cuenca del río Angulo. In Proceedings of the 5th Young Water Professionals Conference, Morelia, Mexico, 5–7 July 2017. [Google Scholar]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias correction of GCM precipitation by quantile mapping: How well do methods preserve changes in quantiles and extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Hidalgo, H.; Alfaro, E.; Quesada-Montano, B. Observed (1970–1999) climate variability in Central America using a high-resolution meteorological dataset with implication to climate change studies. Clim. Chang. 2017, 141, 13–28. [Google Scholar] [CrossRef]
- Gordón Mendoza, R.; Franco Barrera, J.E.; Camargo Buitrago, I. Impacto de la tecnología generada en el cultivo de maíz para la Región de Azuero. Cienc. Agropecu. 2016, 24, 1–18. [Google Scholar]
- Nakaegawa, T.; Arakawa, O.; Kamiguchi, K. Investigation of climatological onset and withdrawal of the rainy season in Panama based on a daily gridded precipitation dataset with a high horizontal resolution. J. Clim. 2015, 28, 2745–2763. [Google Scholar] [CrossRef]
- Dhakhwa, G.B.; Campbell, C.L.; LeDuc, S.; Cooter, E. Maize growth: Assessing the effects of global warming and CO2 fertilization with crop models. Agric. For. Meteorol. 1997, 87, 253–272. [Google Scholar] [CrossRef]
- Sugasti, L.; Pinzón, R. First Approach of Abiotic Drivers of Soil CO2 Efflux in Barro Colorado Island, Panama. Air Soil Water Res. 2020, 13, 1178622120960096. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
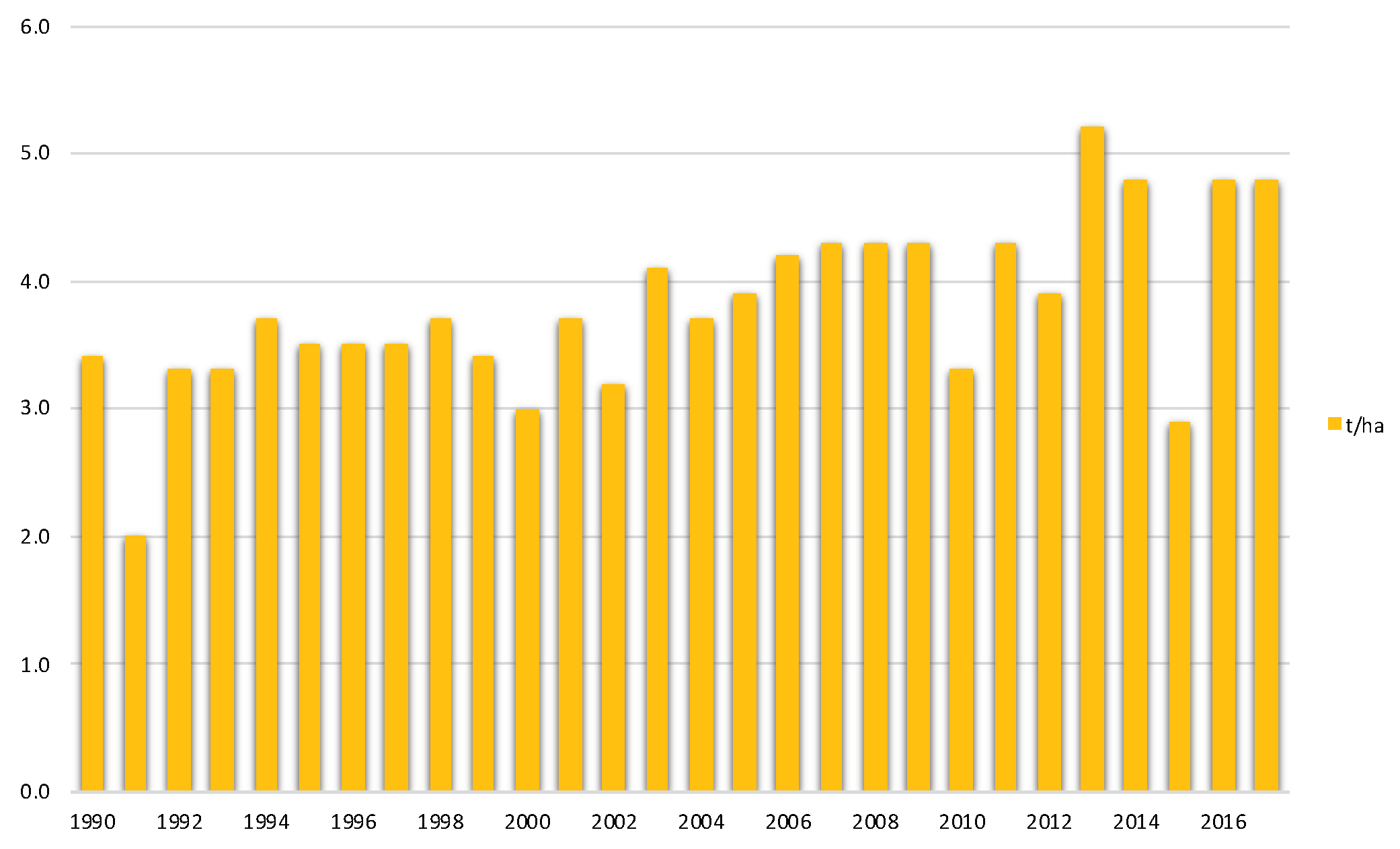
| C0 | C1 | |||||
|---|---|---|---|---|---|---|
| Year | 21 August | 23 September | 10 October | 21 August | 23 September | 10 October |
| 2075 | 36.3 | 18.0 | 13.4 | 18.1 | 13.5 | 13.4 |
| 2076 | 40.4 | 11.0 | 16.7 | 28.1 | 16.2 | 12.9 |
| 2077 | 29.5 | 30.8 | 14.4 | 22.5 | 19.8 | 10.0 |
| 2078 | 7.6 | 7.6 | 2.5 | 3.7 | 4.3 | 3.7 |
| 2079 | 16.3 | 50.2 | 24.8 | 22.9 | 30.3 | 14.1 |
| 2080 | 36.4 | 32.1 | 10.7 | 20.0 | 32.9 | 23.6 |
| 2081 | 28.6 | 24.9 | 6.8 | 11.9 | 17.0 | 15.5 |
| 2082 | 29.1 | 43.9 | 11.1 | 15.4 | 17.6 | 5.5 |
| 2083 | 37.2 | 56.4 | 16.8 | 26.3 | 28.5 | 13.9 |
| 2084 | 29.3 | 27.1 | 17.3 | 24.1 | 19.1 | 11.8 |
| 2085 | 33.9 | 39.0 | 17.9 | 22.8 | 20.9 | 5.4 |
| 2086 | 23.6 | 38.1 | 19.5 | 22.6 | 21.9 | 10.9 |
| 2087 | 28.1 | 24.3 | 10.3 | 11.5 | 14.5 | 9.9 |
| 2088 | 50.7 | 30.6 | 12.9 | 20.8 | 16.7 | 7.5 |
| 2089 | 37.3 | 62.8 | 13.5 | 16.8 | 28.9 | 5.8 |
| 2090 | 36.3 | 30.1 | 4.8 | 12.5 | 18.2 | 7.7 |
| 2091 | 63.2 | 60.9 | 34.8 | 48.5 | 35.9 | 20.4 |
| 2092 | 24.3 | 22.6 | 15.5 | 20.0 | 18.0 | 10.6 |
| 2093 | 15.2 | 12.2 | 4.2 | 5.2 | 6.7 | 4.2 |
| 2094 | 32.4 | 45.7 | 19.2 | 24.2 | 27.9 | 21.1 |
| 2095 | 40.1 | 22.2 | 20.9 | 34.9 | 22.1 | 14.6 |
| 2096 | 49.6 | 28.3 | 18.7 | 29.1 | 16.1 | 9.7 |
| 2097 | 38.0 | 22.6 | 16.9 | 31.9 | 25.7 | 14.2 |
| 2098 | 20.0 | 24.8 | 5.6 | 6.2 | 12.8 | 8.6 |
| 2099 | 24.2 | 63.6 | — | 16.6 | 24.3 | — |
| Average | 32.3 | 33.2 | 14.6 | 20.7 | 20.4 | 11.4 |
| C2 | C3 | |||||
|---|---|---|---|---|---|---|
| Year | 21 August | 23 September | 10 October | 21 August | 23 September | 10 October |
| 2075 | 27.3 | 10.7 | 7.6 | 23.7 | 29.9 | 24.2 |
| 2076 | 34.6 | 19.2 | 11.8 | 34.6 | 18.9 | 7.3 |
| 2077 | 27.3 | 15.9 | 10.2 | 11.5 | 14.2 | 13.4 |
| 2078 | 6.1 | 3.1 | 3.0 | 8.8 | 6.3 | 4.5 |
| 2079 | 31.0 | 31.7 | 18.6 | 30.7 | 31.2 | 23.8 |
| 2080 | 32.1 | 17.2 | 11.1 | 24.1 | 12.1 | 12.9 |
| 2081 | 33.1 | 17.5 | 16.6 | 48.2 | 18.0 | 5.4 |
| 2082 | 21.6 | 5.5 | 3.7 | 31.8 | 26.6 | 20.5 |
| 2083 | 34.1 | 30.8 | 25.2 | 33.9 | 60.0 | 48.3 |
| 2084 | 35.4 | 34.8 | 24.2 | 30.8 | 20.6 | 15.8 |
| 2085 | 35.6 | 42.1 | 28.1 | 35.7 | 25.4 | 20.0 |
| 2086 | 22.2 | 16.8 | 15.4 | 34.7 | 13.7 | 11.0 |
| 2087 | 19.4 | 5.4 | 4.1 | 18.4 | 12.2 | 9.5 |
| 2088 | 49.4 | 21.2 | 8.8 | 53.2 | 27.5 | 16.3 |
| 2089 | 30.2 | 25.9 | 11.2 | 20.8 | 24.1 | 17.4 |
| 2090 | 16.9 | 6.8 | 5.3 | 34.2 | 22.2 | 13.4 |
| 2091 | 55.6 | 34.9 | 25.6 | 24.9 | 28.2 | 21.2 |
| 2092 | 31.1 | 28.2 | 23.8 | 44.3 | 46.1 | 31.1 |
| 2093 | 18.2 | 2.9 | 2.1 | 20.0 | 11.1 | 8.7 |
| 2094 | 38.7 | 15.0 | 13.2 | 34.1 | 55.1 | 36.6 |
| 2095 | 31.5 | 20.2 | 18.9 | 30.3 | 22.8 | 20.4 |
| 2096 | 30.8 | 13.3 | 10.1 | 50.7 | 38.4 | 25.7 |
| 2097 | 31.7 | 21.2 | 11.7 | 34.2 | 22.6 | 15.6 |
| 2098 | 41.2 | 13.8 | 5.3 | 14.7 | 7.5 | 6.3 |
| 2099 | 36.8 | 25.3 | — | 54.9 | 34.1 | — |
| Average | 30.9 | 19.2 | 13.1 | 31.3 | 25.2 | 17.9 |
| C0 | C1 | |||||
|---|---|---|---|---|---|---|
| Period | 21 August | 23 September | 10 October | 21 August | 23 September | 10 October |
| 2075–2079 | 20% | 8% | −34% | −12% | −23% | −50% |
| 2080–2084 | 48% | 70% | −42% | −10% | 6% | −35% |
| 2085–2089 | 60% | 79% | −32% | −13% | −5% | −64 % |
| 2090–2094 | 58% | 58% | −28% | 2% | −2% | −41% |
| 2095–2099 | 58% | 49% | −29% | 9% | −7% | −46% |
| 2075–2099 | 49% | 53% | -33% | −5% | −6% | −47% |
| C2 | C3 | |||||
|---|---|---|---|---|---|---|
| Period | 21 August | 23 September | 10 October | 21 August | 23 September | 10 October |
| 2075–2079 | 16% | −26% | −53% | 1% | −7% | −33% |
| 2080–2084 | 44% | −2% | −25% | 56% | 27% | −5% |
| 2085–2089 | 45% | 3% | −38% | 50% | −5% | −32% |
| 2090–2094 | 48% | −19% | −36% | 45% | 50% | 2% |
| 2095–2099 | 58% | −13% | −47% | 70% | 16 | −22% |
| 2075–2099 | 42% | −12% | −39% | 44% | 16% | −18% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez, M.M.; Nakaegawa, T.; Pinzón, R.; Kusunoki, S.; Gordón, R.; Sanchez-Galan, J.E. Using a Statistical Crop Model to Predict Maize Yield by the End-Of-Century for the Azuero Region in Panama. Atmosphere 2020, 11, 1097. https://doi.org/10.3390/atmos11101097
Martínez MM, Nakaegawa T, Pinzón R, Kusunoki S, Gordón R, Sanchez-Galan JE. Using a Statistical Crop Model to Predict Maize Yield by the End-Of-Century for the Azuero Region in Panama. Atmosphere. 2020; 11(10):1097. https://doi.org/10.3390/atmos11101097
Chicago/Turabian StyleMartínez, Marlemys M., Tosiyuki Nakaegawa, Reinhardt Pinzón, Shoji Kusunoki, Román Gordón, and Javier E. Sanchez-Galan. 2020. "Using a Statistical Crop Model to Predict Maize Yield by the End-Of-Century for the Azuero Region in Panama" Atmosphere 11, no. 10: 1097. https://doi.org/10.3390/atmos11101097
APA StyleMartínez, M. M., Nakaegawa, T., Pinzón, R., Kusunoki, S., Gordón, R., & Sanchez-Galan, J. E. (2020). Using a Statistical Crop Model to Predict Maize Yield by the End-Of-Century for the Azuero Region in Panama. Atmosphere, 11(10), 1097. https://doi.org/10.3390/atmos11101097





